Mechanism Analysis of Wide-Band Oscillation Amplification for Long-Distance AC Transmission Lines
Abstract
1. Introduction
2. Establishment of Long-Distance AC Transmission Line and Asynchronous Motor Model
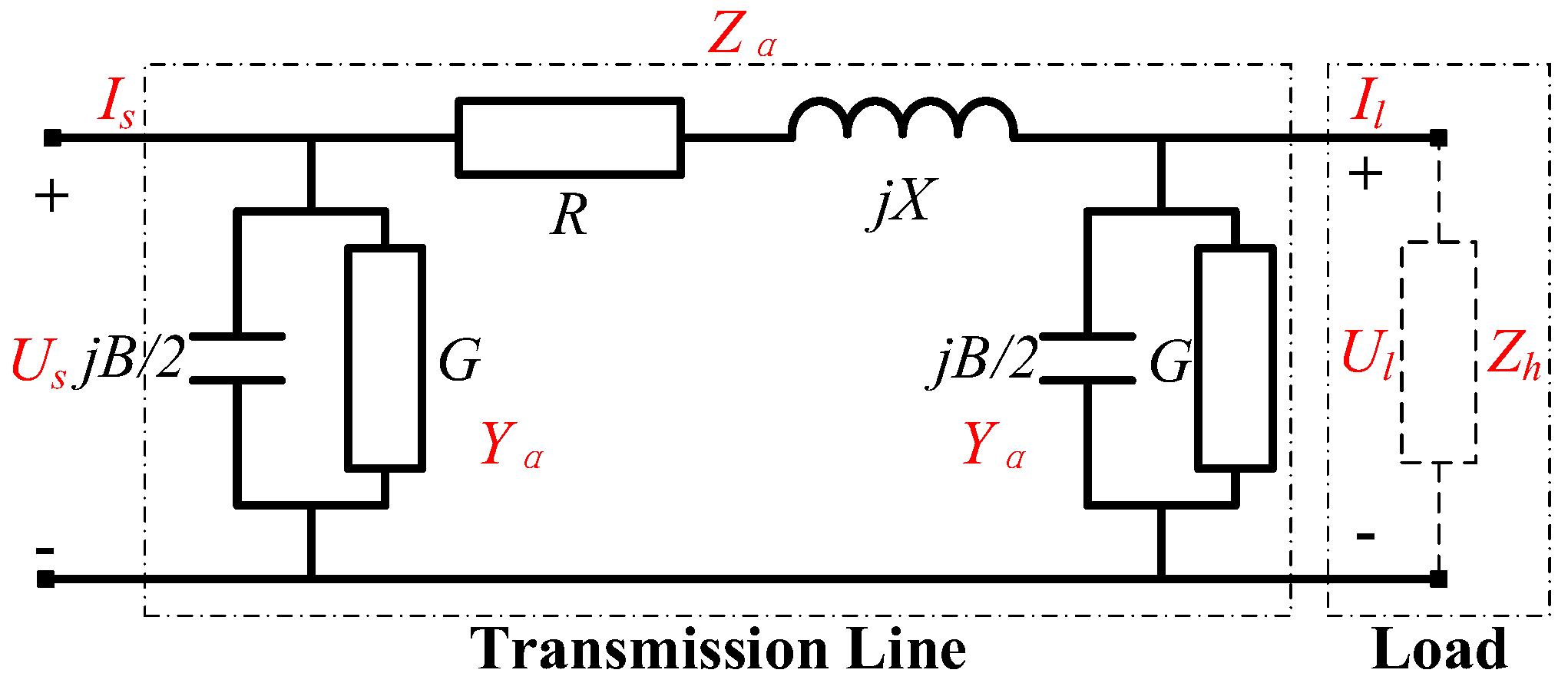
2.1. Long-Distance AC Transmission Line Model
2.2. Asynchronous Motor Model
- (1)
- and remain constant.
- (2)
- The current of the inter-harmonic frequency component remains three-phase symmetrical.
- (3)
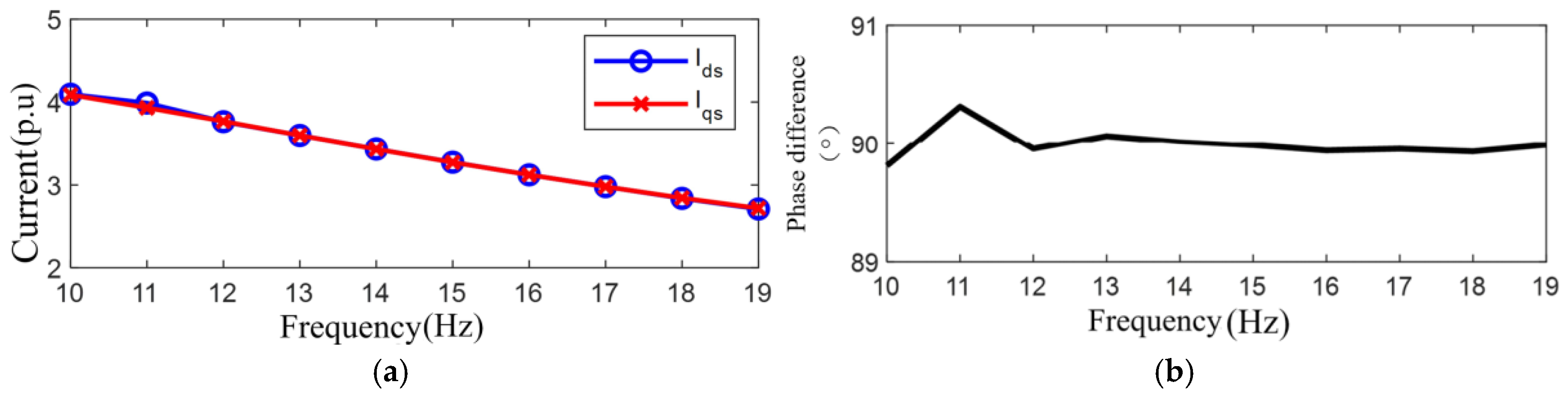
- Impedance model verification of the asynchronous motor.
3. Mechanism Analysis of Inter-Harmonic Amplification Characteristics
4. Influencing Factors and Suppression Measures of Inter-Harmonic Amplification Characteristics
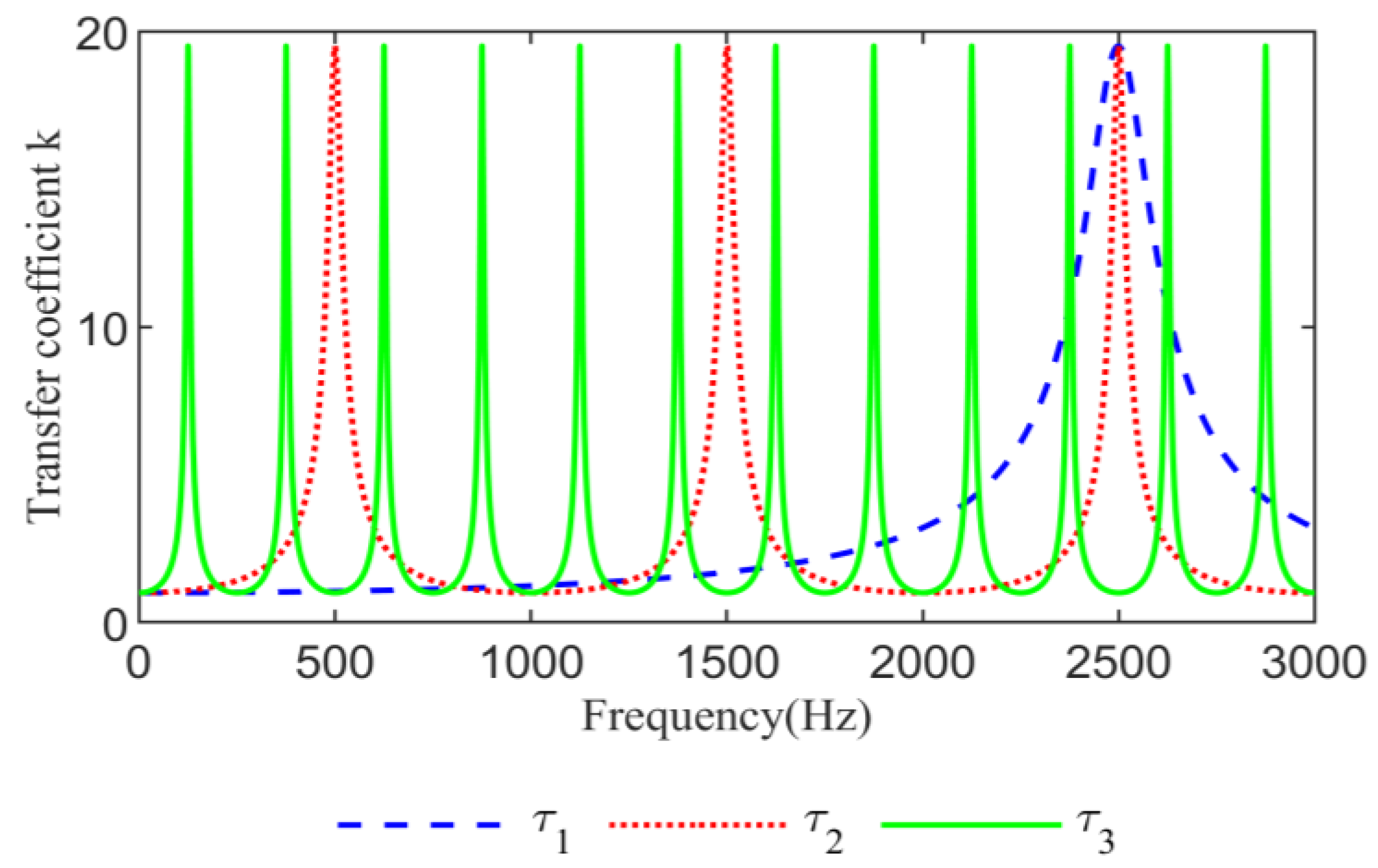
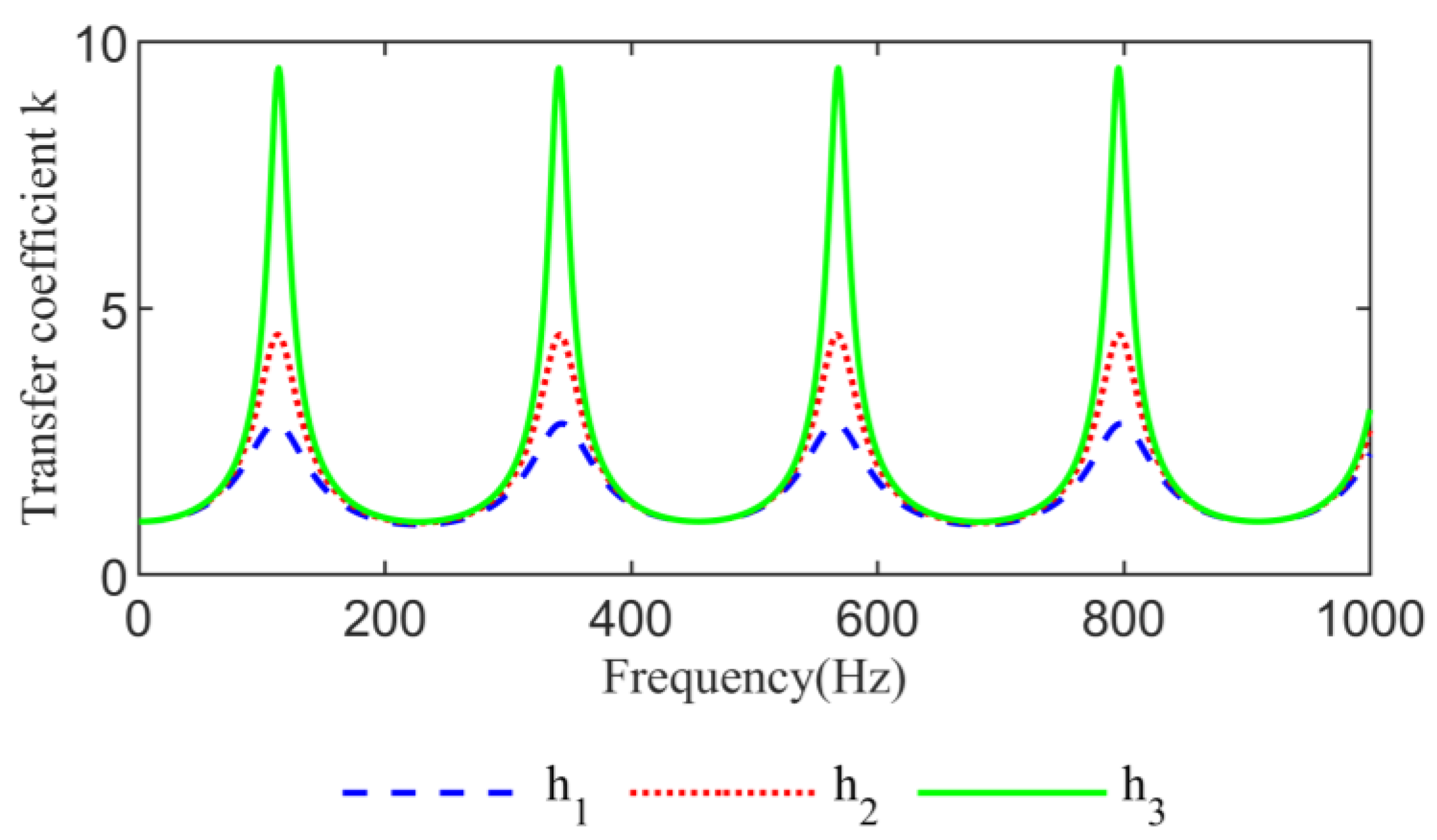
4.1. Analysis of Influencing Factors
4.2. Sensitivity Analysis
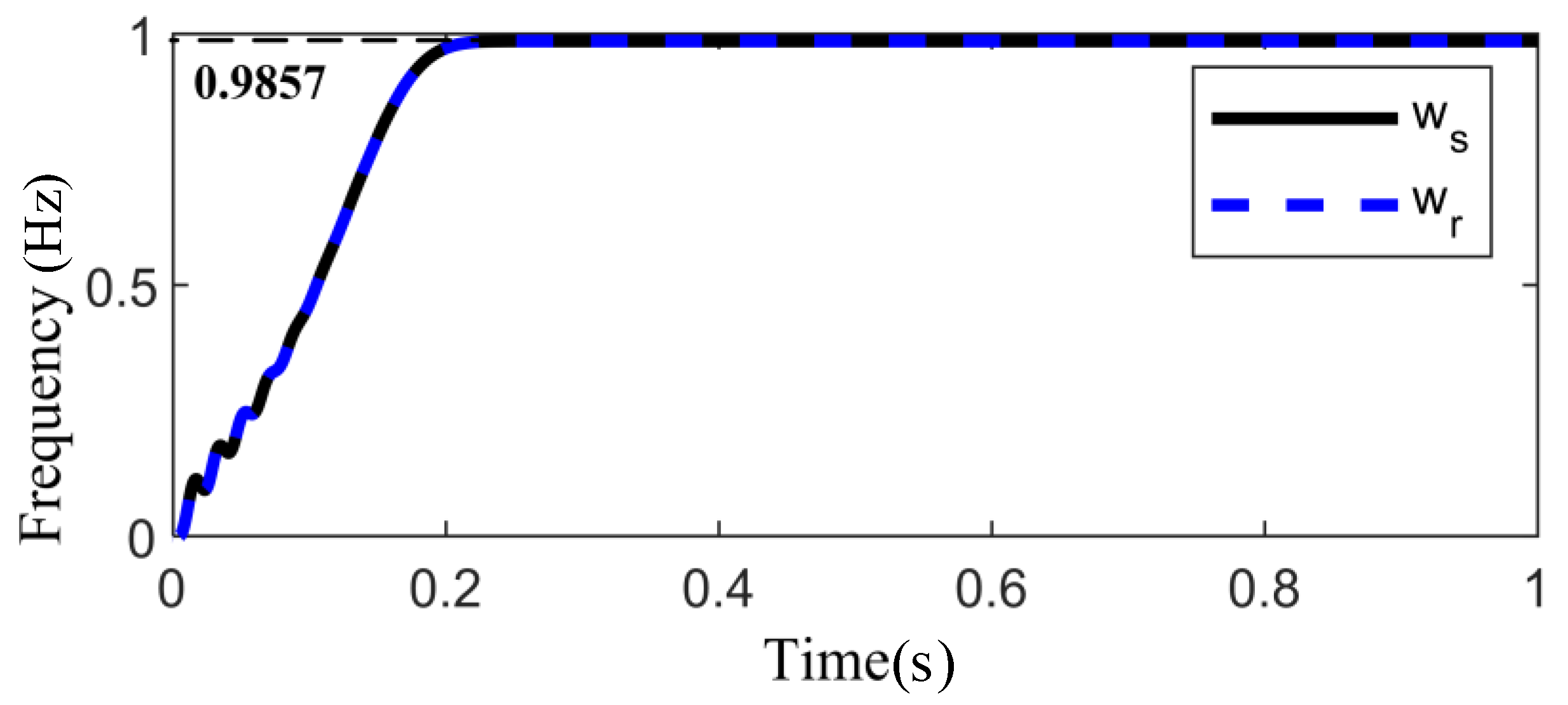
4.3. Suppression Measures
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbols and Parameters | Interpretations |
|---|---|
| and | The inflow current and outflow current of a two-port transmission line |
| and | The input and output terminal voltages of a two-port transmission line |
| and | The line impedance and line-to-ground admittance of a two-port transmission line |
| The load impedance of a two-port transmission line | |
| The line structure parameter of a long-distance transmission line | |
| The line delay of a long-distance transmission line | |
| The impedance of a long-distance transmission line | |
| and | The transferred current at the head and end of a long-distance transmission line |
| , and | The resistance, inductance, and capacitance of a long-distance transmission line per kilometer |
| and | The voltage of the stator d-axis and stator q-axis of an asynchronous motor |
| and | The voltage of the rotor d-axis and rotor q-axis of an asynchronous motor |
| and | The resistance of the stator winding and rotor winding of an asynchronous motor |
| and | The flux linkage of the stator d-axis and stator q-axis of an asynchronous motor |
| and | The flux linkage of the rotor d-axis and rotor q-axis of an asynchronous motor |
| and | The current of the stator d-axis and stator q-axis of an asynchronous motor |
| and | The current of the rotor d-axis and rotor q-axis of an asynchronous motor |
| and | The electrical angular velocity of the stator and rotor of an asynchronous motor |
| , and | The stator inductance, rotor inductance, and mutual inductance of an asynchronous motor |
| The amplitude of the stator side inter-harmonic current of an asynchronous motor | |
| The angular frequency of the stator side inter-harmonic component of an asynchronous motor | |
| The initial phase of the stator side inter-harmonic current of an asynchronous motor | |
| The equivalent impedance of an asynchronous motor | |
| The transfer coefficient | |
| The load impedance of multi-machine systems | |
| The frequency of the extreme value of the transfer coefficient | |
| The extreme value of the transfer coefficient | |
| , and | The normalized sensitivity for , , and |
| Parameters | Value |
|---|---|
| 150 (Hz) | |
| 5 + j3 () | |
| 0.1 + j0.5 () | |
| 0.3846 − j1.9231 () | |
| 5 + j3 () | |
| 110 (km) | |
| 0.0014 (H/km) | |
| 0.0529 (/km) | |
| (S/km) |



References
- Wang, G.; Konstantinou, G.; Townsend, C.D.; Pou, J.; Vazquez, S.; Demetriades, G.D.; Agelidis, V.G. A Review of Power Electronics for Grid Connection of Utility-Scale Battery Energy Storage Systems. IEEE Trans. Sustain. Energy 2016, 7, 1778–1790. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Dragicevic, T.; Blaabjerg, F. A New Perspective for Relating Virtual Inertia with Wideband Oscillation of Voltage in Low-Inertia DC Microgrid. IEEE Trans. Ind. Electron. 2022, 69, 7029–7039. [Google Scholar]
- Xie, X.; Zhan, Y.; Shair, J.; Ka, Z.; Chang, X. Identifying the Source of Subsynchronous Control Interaction via Wide-Area Monitoring of Sub/Super-Synchronous Power Flows. IEEE Trans. Power Deliv. 2020, 35, 2177–2185. [Google Scholar] [CrossRef]
- Shair, J.; Xie, X.; Yang, J.; Li, J.; Li, H. Adaptive Damping Control of Subsynchronous Oscillation in DFIG-Based Wind Farms Connected to Series-Compensated Network. IEEE Trans. Power Deliv. 2022, 37, 1036–1049. [Google Scholar]
- Li, C.; Sun, C.; Chen, Z.; Zhang, Y. Broad Learning System Using Rectified Adaptive Moment Estimation for Harmonic Detection and Analysis. IEEE Trans. Ind. Electron. 2024, 71, 2873–2882. [Google Scholar]
- Hou, C.; Zhu, M.; Li, Z.; Li, Y.; Cai, X. Inter Harmonic THD Amplification of Voltage Source Converter: Concept and Case Study. IEEE Trans. Power Electron. 2020, 35, 12651–12656. [Google Scholar] [CrossRef]
- Testa, A.; Akram, M.F.; Burch, R.; Carpinelli, G.; Chang, G.; Dinavahi, V.; Hatziadoniu, C.; Grady, W.M.; Gunther, E.; Halpin, M.; et al. Interharmonics: Theory and Modeling. IEEE Trans. Power Deliv. 2007, 22, 2335–2348. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Wang, F.; Wang, Q.; Huang, S. An Interharmonic Phasor and Frequency Estimator for Subsynchronous Oscillation Identification and Monitoring. IEEE Trans. Instrum. Meas. 2019, 68, 1714–1723. [Google Scholar] [CrossRef]
- Xiong, L.; Liu, X.; Liu, Y. Decaying DC and Harmonic Components Detection for Absorbing Impact Load Currents in Weak Grids. IEEE Trans. Power Deliv. 2021, 36, 1907–1910. [Google Scholar] [CrossRef]
- Friedemann, D.F.; Motter, D.; Oliveira, R.A. Stator-Ground Fault Location Method Based on Third-Harmonic Measures in High-Impedance Grounded Generators. IEEE Trans. Power Deliv. 2021, 36, 794–802. [Google Scholar]
- Ji, K.; Yang, Y. Harmonic Power Detection-Based Adaptive Resonance Suppression for Power Converters. IEEE Trans. Power Deliv. 2024, 39, 601–612. [Google Scholar]
- Jia, J.R.; Duan, X.B.; Lu, J.L.; Zhou, W.; Ren, R. Research on the Harmonic Transmission Characteristics of Transformers. Electric Power 2017, 50, 92–96+157. [Google Scholar] [CrossRef]
- Wang, J.; Wang, G.; Kuang, Y.; Tian, Z. Explorative research on harmonic transmission characteristics and corresponding measures of the UHV half-wavelength transmission lines. In Proceedings of the 2017 China International Electrical and Energy Conference (CIEEC), Beijing, China, 25–27 October 2017; pp. 360–364. [Google Scholar]
- Zhang, L.; Liang, S.; Li, X. Research on the harmonic in new continuous cable traction power supply system and its transmission characteristic. IET Gener. Transm. Distrib. 2020, 14, 2710–2718. [Google Scholar] [CrossRef]
- Li, Z.; Hu, H.; Tang, L.; Wang, Y.; Zang, T.; He, Z. Quantitative Severity Assessment and Sensitivity Analysis Under Uncertainty for Harmonic Resonance Amplification in Power Systems. IEEE Trans. Power Deliv. 2020, 35, 809–818. [Google Scholar]
- Pu, Y.; Shu, Q.; Xu, F. Harmonic Amplification Analysis of Cable Lines with Distributed Parameters Based on Kalman Filter and Convolution Inversion. J. Mod. Power Syst. Clean Energy 2023, 11, 1804–1813. [Google Scholar] [CrossRef]
- Chang, T.Y.; Wang, S.L.; Zhang, Y.M.; Ma, J.P.; Zhang, Y.H.; Liu, T.Q. Harmonic current amplification characteristics of DC lines based on distribution parameters. High Volt. Eng. 2023, 49, 4654–4664. [Google Scholar] [CrossRef]
- Yang, Y.; Xue, H.; Xu, R.; Zhang, S.; Chang, Z.; Xiao, Z. Conduction and Amplification of Harmonics in Distribution Network. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 2100–2105. [Google Scholar]
- Wang, Y.; Zhou, Y.; Dang, J.; Ma, S.; Tian, C.; Cheng, S. Study on Main Factors of Dynamic Stability for Regional Interconnected Power System. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 1653–1658. [Google Scholar]
- Skinder, K.S.; Kerdphol, T.; Mitani, Y.; Turschner, D. Frequency Stability Assessment of Multiple Virtual Synchronous Generators for Interconnected Power System. IEEE Trans. Ind. Appl. 2022, 58, 91–101. [Google Scholar]
- Lu, D.; Liu, Y.; Liao, Q.; Wang, B.; Huang, W.; Xi, X. Time-Domain Transmission Line Fault Location Method With Full Consideration of Distributed Parameters and Line Asymmetry. IEEE Trans. Power Deliv. 2020, 35, 2651–2662. [Google Scholar] [CrossRef]
- Benato, R.; Gardan, G.; Milano, F. Effect of Uniformly Distributed Parameter Line Models on the Evaluation of PV Curves and of the Maximum Loading Condition. IEEE Trans. Power Syst. 2022, 37, 4974–4977. [Google Scholar] [CrossRef]
- Song, G.; Chu, X.; Gao, S.; Kang, X.; Jiao, Z.; Suonan, J. Novel Distance Protection Based on Distributed Parameter Model for Long-Distance Transmission Lines. IEEE Trans. Power Deliv. 2013, 28, 2116–2123. [Google Scholar] [CrossRef]
- Ma, S.; Guo, J.; Sun, H.; Yu, Y. The comparison and analysis of lumped parameter equivalent circuits of transmission line. In Proceedings of the 2011 International Conference on Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011; pp. 1225–1229. [Google Scholar]
- Dommel, H.W. Digital Computer Solution of Electromagnetic Transients in Single-and Multiphase Networks. IEEE Trans. Power Appar. Syst. 1969, PAS-88, 388–399. [Google Scholar] [CrossRef]
- Dong, C.; Wu, Z.; Huang, R.; Wang, Z. Stability Analysis of Hybrid Systems Containing the Grid-Forming Inverter and the Grid-Following Inverter Based on Sequential Impedance Modelling. In The Proceedings of the 11th Frontier Academic Forum of Electrical Engineering (FAFEE2024); FAFEE 2024. Lecture Notes in Electrical Engineering; Yang, Q., Li, J., Eds.; Springer: Singapore, 2025; Volume 1287. [Google Scholar]

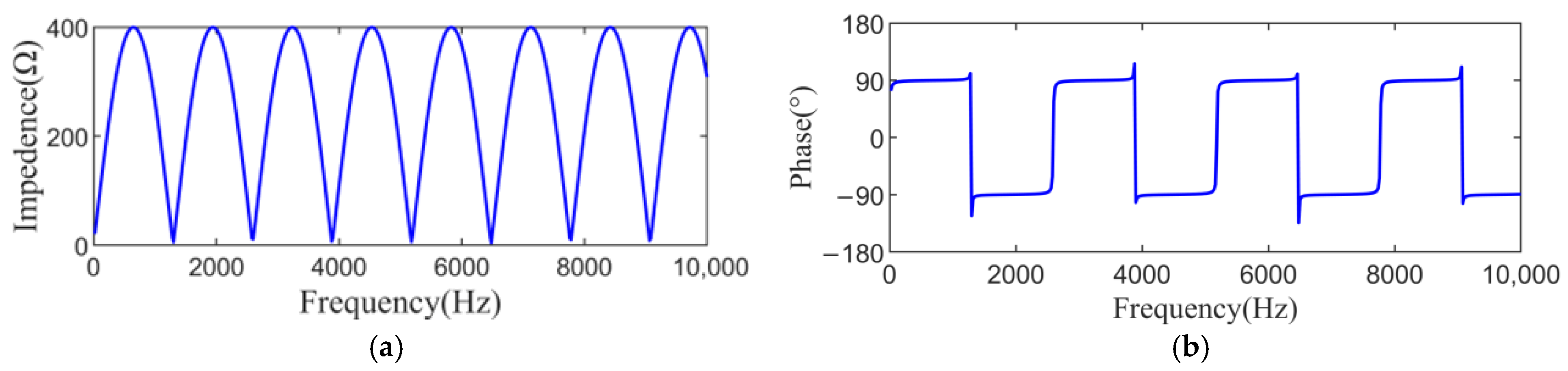


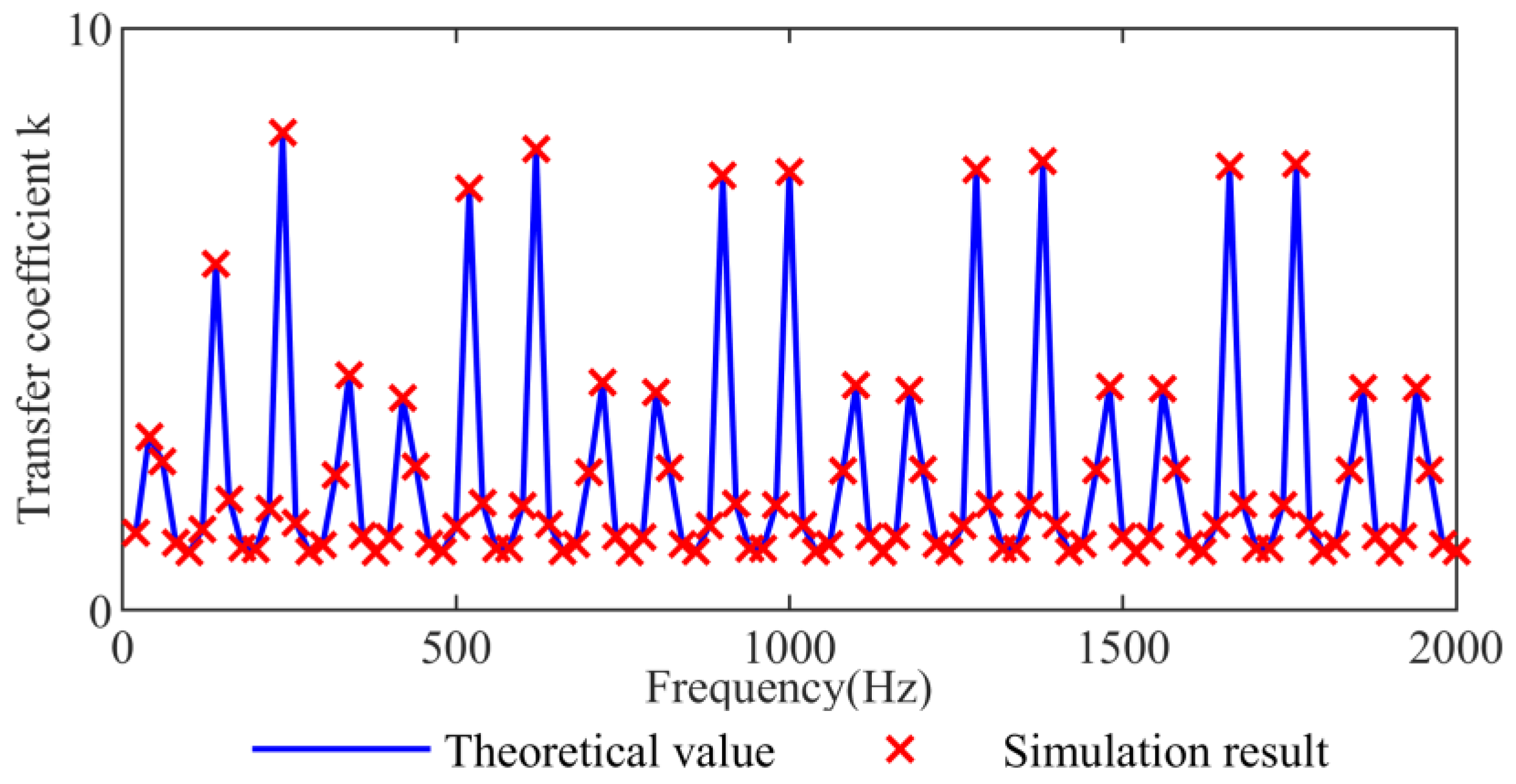



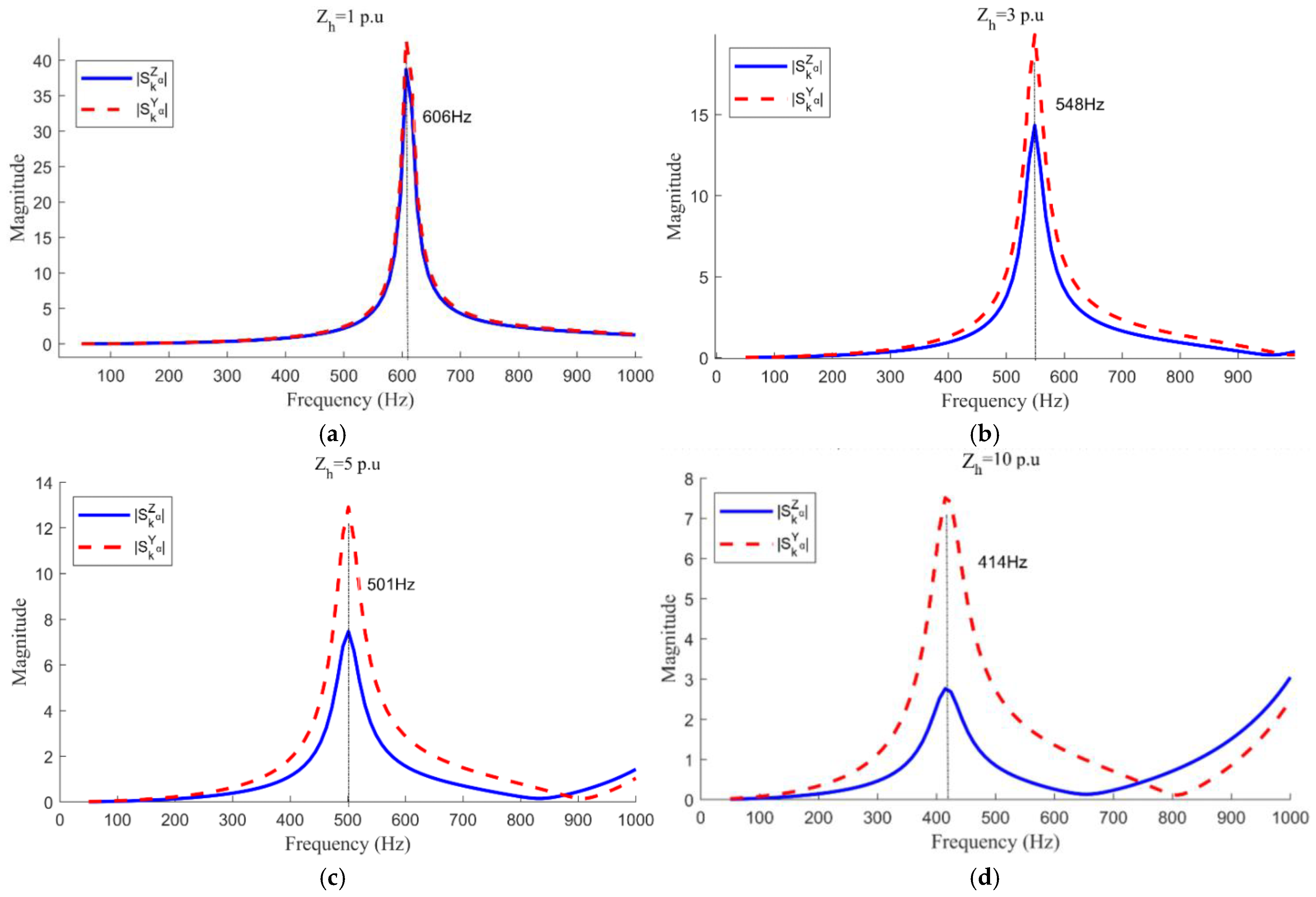
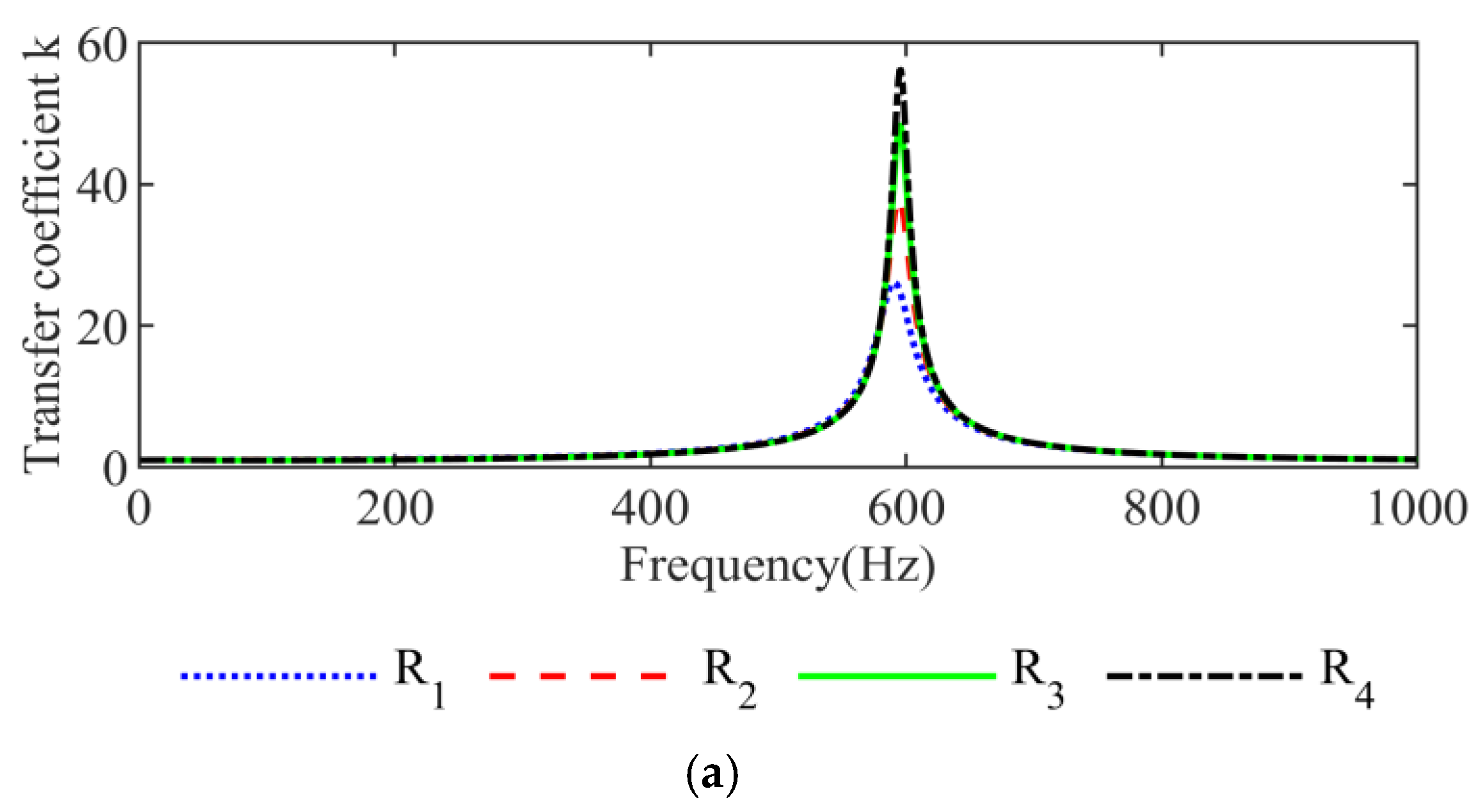
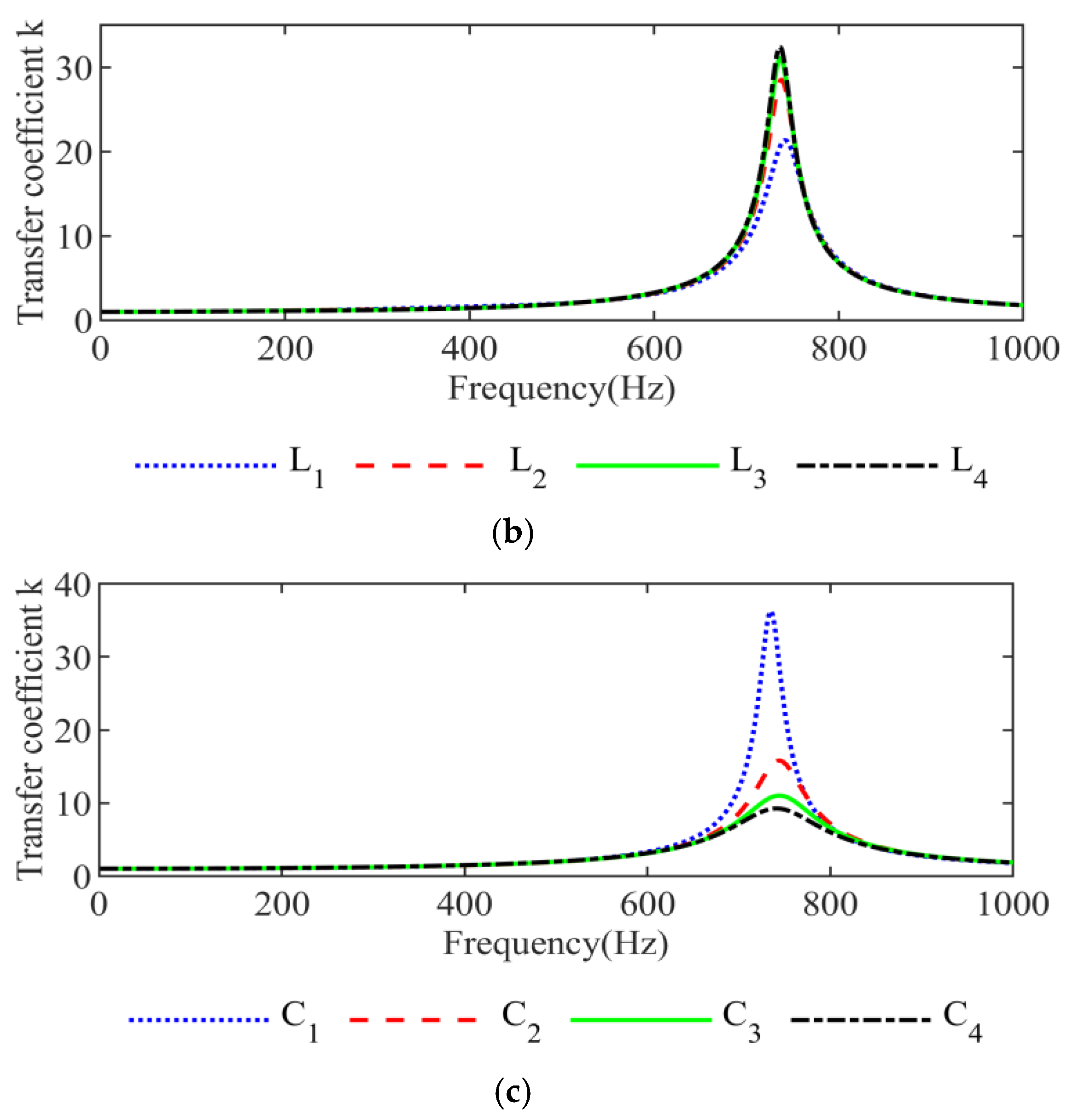
| Group | Theoretical Frequency of Extreme Value (Hz) | Simulation Frequency of Extreme Value (Hz) |
|---|---|---|
| 1 | 67 | 67.30 |
| 2 | 202 | 201.91 |
| 3 | 336 | 336.51 |
| 4 | 471 | 471.12 |
| 5 | 606 | 605.73 |
| 6 | 740 | 740.33 |
| 7 | 875 | 875.21 |
| 8 | 1010 | 1009.55 |
| Group | Theoretical Extreme Value (A) | Simulation Extreme Value (A) |
|---|---|---|
| 1 | 15.12 | 15.09 |
| 2 | 21.38 | 20.79 |
| 3 | 26.19 | 26.15 |
| 4 | 30.24 | 29.92 |
| 5 | 60.47 | 60.47 |
| 6 | 75.59 | 75.38 |
| 7 | 120.95 | 120.94 |
| 8 | 151.18 | 150.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, N.; Fan, C.; Li, Y.; Jin, B.; Yang, X.; Yu, Y. Mechanism Analysis of Wide-Band Oscillation Amplification for Long-Distance AC Transmission Lines. Energies 2025, 18, 5106. https://doi.org/10.3390/en18195106
Li N, Fan C, Li Y, Jin B, Yang X, Yu Y. Mechanism Analysis of Wide-Band Oscillation Amplification for Long-Distance AC Transmission Lines. Energies. 2025; 18(19):5106. https://doi.org/10.3390/en18195106
Chicago/Turabian StyleLi, Ning, Chen Fan, Yudun Li, Biao Jin, Xuchen Yang, and Yiping Yu. 2025. "Mechanism Analysis of Wide-Band Oscillation Amplification for Long-Distance AC Transmission Lines" Energies 18, no. 19: 5106. https://doi.org/10.3390/en18195106
APA StyleLi, N., Fan, C., Li, Y., Jin, B., Yang, X., & Yu, Y. (2025). Mechanism Analysis of Wide-Band Oscillation Amplification for Long-Distance AC Transmission Lines. Energies, 18(19), 5106. https://doi.org/10.3390/en18195106





