Void Reactivity Coefficient for Hybrid Reactor Cooled Using Liquid Metal

Abstract

A negative value of the void reactivity coefficient (α_V) is one of the most important passive safety properties for the operation of nuclear reactor. Herein, are presented calculated values of the void reactivity coefficient for different geometries of reactors cooled by liquid lead (LFR) and sodium (SFR) with U-238-Pu-239 and Th-232-U-233 fuels. The calculations were carried out for the reactors filled with either one or two types of fuel assemblies. The most interesting results are obtained for reactor filled with two different types of fuel assemblies (hybrid reactor). Hybrid reactors consist of central and peripheral types of fuel assemblies using low enrichment fuel and high enrichment fuel, respectively. Both hybrid reactors based on the uranium cycle (U-cycle) and the thorium cycle (Th-cycle) can maintain a negative void reactivity coefficient value for wide range of reactor parameters. The calculation results of the hybrid reactor matched those from FBR-IME reactor.

1. Introduction

Liquid metal cooled reactors can be considered the future of nuclear plants due to of their potential for breeding efficiency and, consequently, economic advantages. This type of reactor can achieve high coolant temperatures. Metal coolants remove heat from the reactor core more rapidly, allowing for much higher power density. In other words, using this type of reactor offers several advantages, including economic viability, high power density, and high coolant temperature.

The first experimental fast reactor was built in 1946 at Los Alamos. It was operated until 1953. The reactor was fueled with 2.5 L of metallic plutonium, and the reactor core was cooled by mercury [1]. In 1951, first experimental fast breeder reactor, EBR-I, which generated practical amount of useful power of 200 kWe, was constructed at the National Reactor Testing Station in Idaho [1]. Eutectic sodium-potassium served as the coolant of the reactor. Unfortunately, there are only about 20 experimental and commercial fast neutron reactors in operation worldwide [2,3]. One reason for this limited number is that fast reactors are typically cooled by liquid metal and have positive α_V coefficient value, it is difficult to reduce this coefficient.

A negative value of α_V is a fundamental property of passive safety of all types of nuclear reactors. The second important property is the passive removal of shutdown heat after a loss of coolant accident.

In recent years there has been stagnation in the development of liquid metal cooled fast reactors. However, interest in fast reactors has been renewed due to necessity of limiting CO₂ emission and addressing global warming.

Fast reactors have nuclear characteristics that enable the efficient use of uranium fuel and the ability to burn the long-lived actinides found in nuclear waste [2]. The authors of [2] presented the results of their calculations of reactivity feedback for a Sodium Fast Reactor (SFR) with a U-cycle. Their study provided a detailed description of neutron physics and included calculation results obtained using the perturbation method for voided condition in the SFR. Unfortunately, the study did not provide an estimated value for α_V.

To mitigate the overall reactivity increase during an accident, different concepts are used, including axial fuel expansion and radial core expansion. Core shape expansion is a passive method that utilizes thermal expansion and bowing of the ducts [4,5]. Additionally, there are other methods, such as control rod driveline expansion or a special coolant cavity over core to reduce the α_V, as well as passive shutdown systems with hydraulically suspended rods [4,5].

The European Lead Cooling System (ELSY) is a research project aimed developing nuclear reactors cooled using lead [6,7]. Lead Fast Reactors (LFRs) (1530 MWth) have a core composed of MOX fuel and a lead reflector [6]. The heterogeneous reactor core consists of a square fuel lattice. The core has three fuel zones, i.e., inner, intermediate and outer, with enrichment of 13.4 vol. %, 15 vol. %, 18.5 vol. %, respectively. The authors of [6] presented interesting results of the void reactivity effect, which was significantly positive in the inner zone and near zero in the outer zone.

The estimation of the value of α_V was studied in a water-cooled reactor with a flexible fuel cycle, which is a type of Boiling Water Reactor (BWR) [8]. In that work, exact perturbation calculations were applied, which quantitatively estimated α_V as a function of fuel rod diameter.

The effect on α_V of distribution of voids inside a reactor was studied in the Na-cooled FBR-IME reactor, based on the Japanese JOYO experimental reactor. The central part of the reactor consists of 95 heterogeneous fuel assemblies, while peripheral part (outer/fertile) consists 295 assemblies of U-238 [9,10]. The peripheral part is used for the conversion of U-238 to Pu-239. Unfortunately, it also plays a role as a reflector, which increases α_V. This work provides the exact result of α_V for several distributions of no-sodium assemblies in central part of reactor.

The void reactivity was studied as the effect of an unprotected loss of flow event (ULOF) in a MOX-fueled core based on the MONJU prototype reactor [11,12]. This reactor also utilized an inner core and an outer/fertile region.

The saturation concentration of U-233 in Th-cycle achieved 0.11 in fast reactor, while in in thermal reactor, it was only 0.0137 [13,14]. Breeding and criticality in Th-cycle occured simultaneously in the fast reactor only [15]. In other words, to achieve the most effective and safe thorium reactor, a fast reactor with a negative value of α_V should be constructed [13,14,15,16].

Two large FSRs (3600 MWth), i.e., MOX-3600 and CAR-3600, and two medium FSRs (1000 MWth), i.e., MET-1000 and MOX-1000, with different fuel types were compared in [17]. This excellent work presented various technical parameters of these reactors including numerical values for α_v for 100% void. All values of α_v were positive.

Reactors with a low value of αv, referred to as “the low void worth core” (CFV) possess relatively complex core geometries [18,19,20,21,22,23,24]. The cores are designed with radially or axially heterogeneous geometries, incorporating sodium plenums, fuel zones, fertile zones, and absorbing zones. There are several reactors based on low void worth cores including the Russian BN-800 reactor [18,23], the Japanese concepts of Takeda [21,22,23] and Saito [20,23] and the French concepts CFV of Sciora [23] and ASTRID CFV of Beck [24]. For the CFV concept, the value of α_v is positive when a decrease in coolant density occurs in central part of the core (fissile and fertile zone) and negative when it occurs in the upper sodium plenum zone. This concept does not eliminate the risk of sodium boiling.

A characteristic feature of CFV cores is the leakage of neutrons primarily through the upper sodium plenum, during the voided conditions. This concept restricts the neutron leakage to the top of core base, which, in turn limits, the height of the active core.

This paper presents a concept for a hybrid reactor in which neutron leakage primarily occurs through the radial side area of the core. This approach allows for a higher value of neutron leakage rate that is proportional to the height of the core. The hybrid concept consists of two kinds of fuel assemblies; assemblies with high enrichment fuel placed in the peripheral region, and with low enrichment fuel located in central part of core. The study focuses on the influence of the average fuel density and coolant volume fraction in the fuel cell on the decrease the value of α_v.

Additionally, the calculation results from hybrid model and FBR-IME reactor are compared (Section 8, [9,10]).

2. Materials and Methods

Current Fast Reactors have a low height of the active core (about 1 m) and large reflectors. This geometry makes it difficult to increase neutron leakage through the radial side of the core when it is in a voided state. The amount of radial leakage is proportional to the area of the radial side of the core, which is proportional to the height of the core. For this reason, a modified geometry of the European Pressurized Reactor (EPR) [25,26] was used for our computer simulation. This modified geometry was selected as it provides a sufficiently wide and high reactor core without a reflector, which is necessary for a comprehensive study of the α_V in a general context.

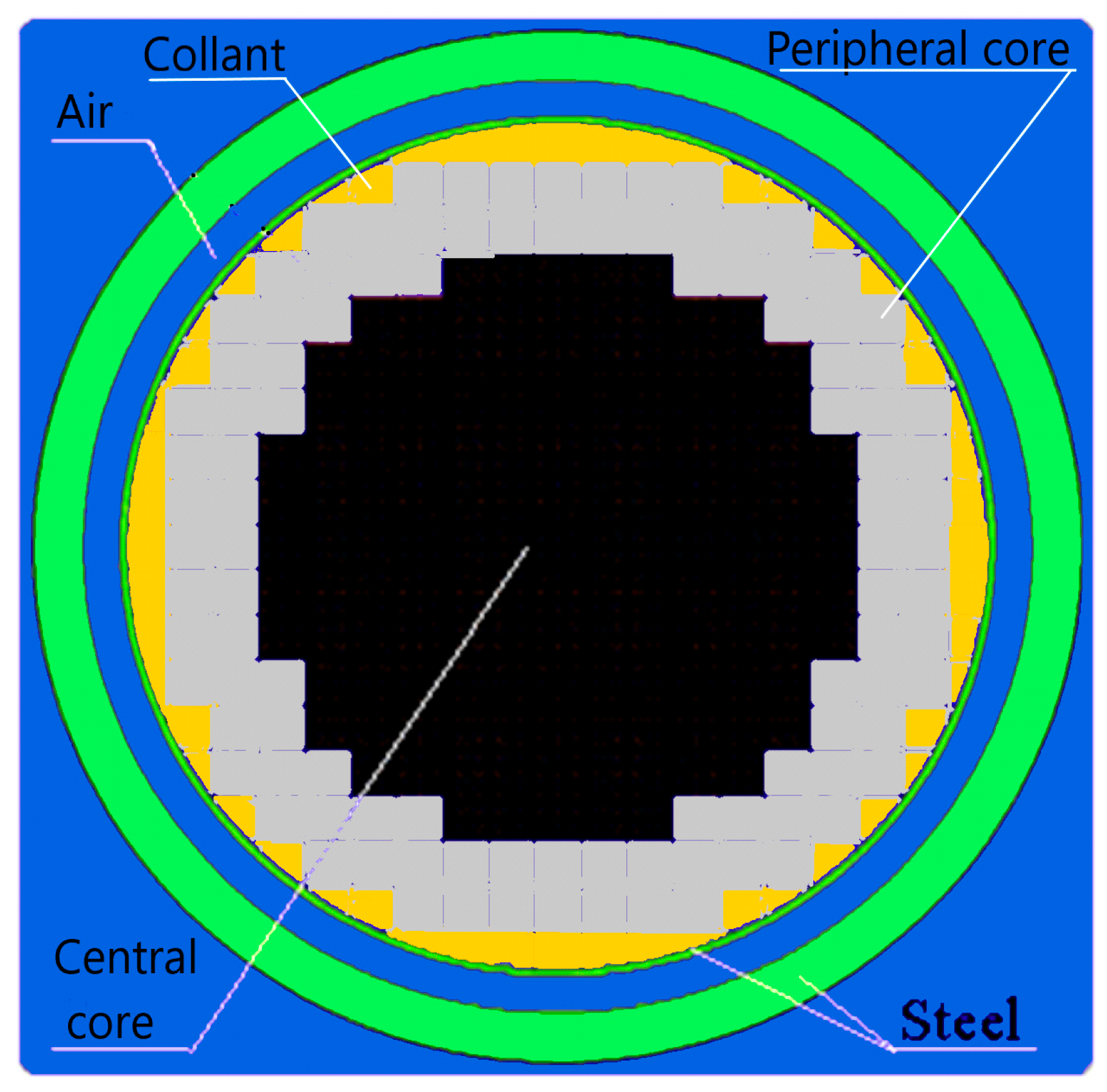
The modified model incorporates various type of coolants i.e., liquid sodium (Na) or lead (Pb). Additionally, it accounts for changeable volumes of fuel and coolant (Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 and

Table 1. Dependence of VCR and VCFR parameters on the radius of fuel rods.

Radius of Fuel Rod [cm]	VCR	$\mathit{V}\mathit{C}\mathit{F}\mathit{R}=\frac{\mathit{V}\mathit{C}\mathit{R}}{1-\mathit{V}\mathit{C}\mathit{R}}$
0.11	0.976	40.7
0.21	0.913	10.5
0.31	0.810	4.3
0.41	0.667	2.0
0.51	0.485	0.94
0.62	0.239	0.32

,

Table 2. Base parameters of assembly A1 [25].

Name	Number
Cells	289
Fuel rod	265
Guide tubes	23
Instrument tube	1
Hight of fuel rod	420 cm

and

Table 3. Basic parameters of the reactor used for the computation of ${\alpha }_V$.

Geometry of Core	Number of Assemblies	Value of VCR	Fuel: U-Cycle [g/cm3]	Fuel: Th-Cycle [g/cm3]	Coolant
Figure 1	241	0.976,	U-238 + Pu-239 Density: 19.05, 11.0 (U-238+Pu-239)O2 Density: 11.0, 8.0, 6.0	Th-232 + U-233 Density 11.7	Pb, Na
		0.913,
		0.810,
		0.667,
		0.485,
		0.239 for the entire core
Figure 2	137 + steel reflector	as above	U-238 + Pu-239 Density 19.05	as above	as above
Figure 3	137 Small core	as above	U-238 + Pu-239, Density: 19.05 (U-238 + Pu-239) O2 Density: 11.0, 8.0, 6.0	Th-232 + U-233, Density 11.7 (Th-232 + U-233) O2 Density 10.0	as above
Figure 3	101 Very small core	as above	(U-238 + Pu-239)O2 Density 11.0, 8.0, 6.0	Not used	as above
Figure 5	137-central 104-peripheral	0.485, 0.239—for the central part and 0.810, 0.667, 0.485—for the peripheral part	(U-238 + Pu-239) O2 Density: 11.0—for the central part Density: 11.0, 8.0, 6.0—for the peripheral part	(Th-232 + U-233)O2 Density:10.0 for the central part Density: 11.0, 8.0, 6.0—for the peripheral part	Na Pb

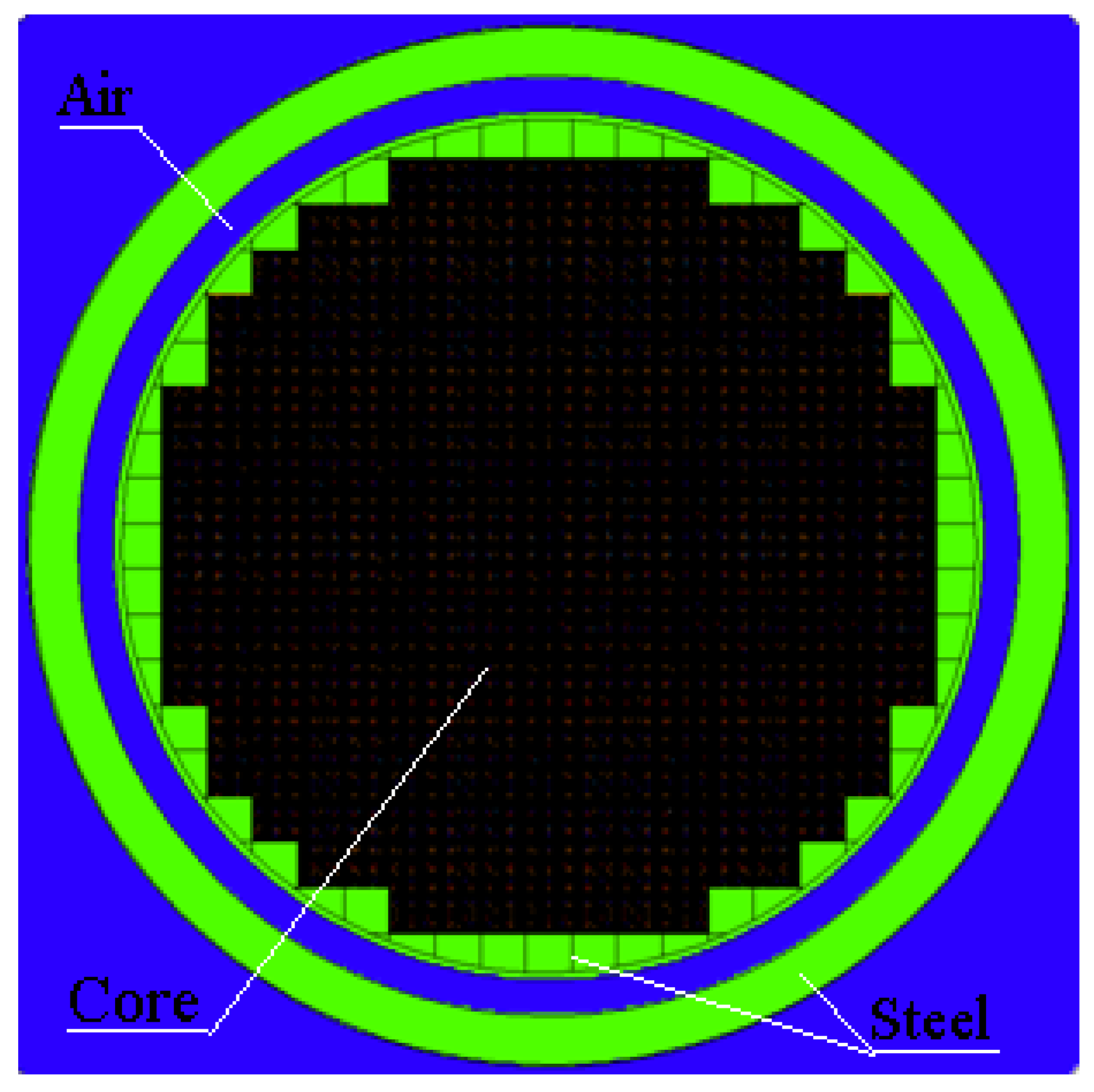
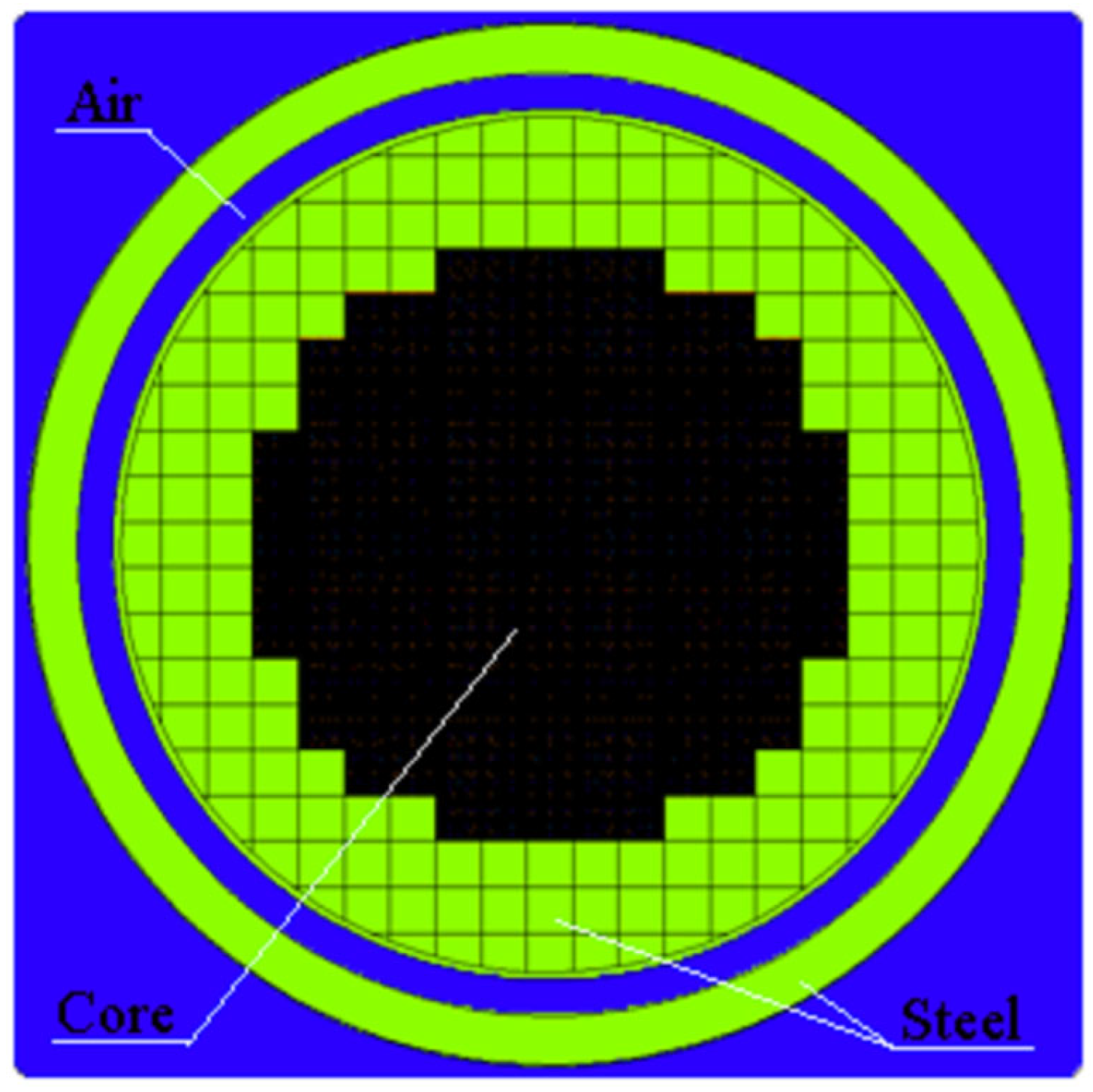
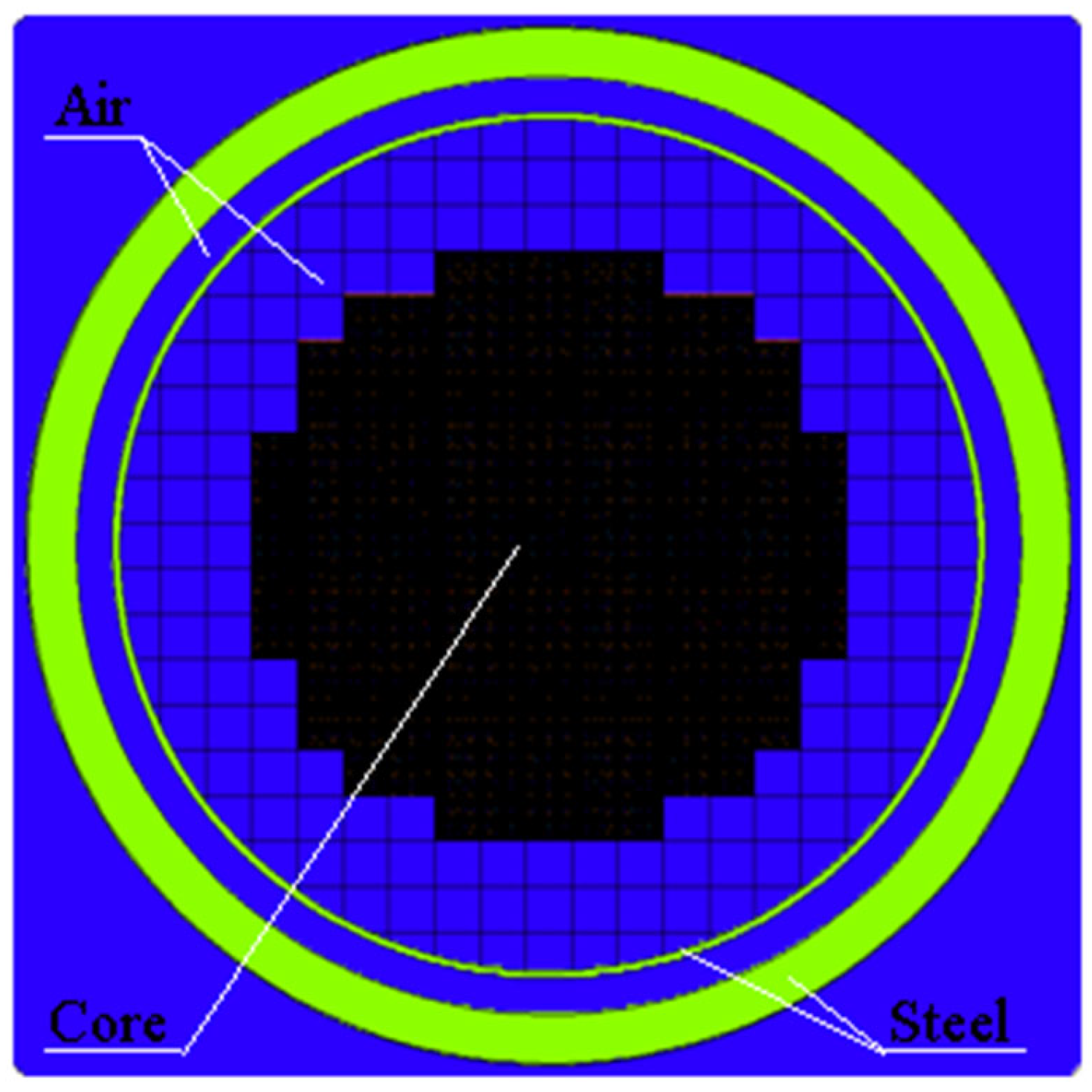
), as well as different numbers of fuel assemblies [15,16]. The reactor core model consists of 241, 137 or 101 assemblies (Figure 1, Figure 2, Figure 3 and Figure 4). We use the A1 assembly in the reactor model, which employs a single type of fuel rod (Figure 6, [25]). The fuel is a mixture of U-238 and Pu-239 or Th-232 and U-233 to study the U-cycle and Th-cycle, respectively. Furthermore, three different values of fuel density are applied.

The reactor model has a changeable fraction of coolant in the volume of the fuel cell (VCR)

$$VCR={\displaystyle \frac{Coolant\_Volume}{Cell\_Volume}}$$

(1)

The width values of the VCR parameters are in the range of <0.239, 0.976>.

Other parameter often used in the literature are the volume ratio of coolant and fuel (VCFR)

$$VCFR={\displaystyle \frac{Coolant\_Volume}{Fuel\_Volume}}$$

(2)

It is assumed that, the thickness of cladding of the fuel rods is equal to zero. For this reason, VCFR = VCR/(1 − VCR). This assumption is made to reduce the number of computations. It is a simplified model, intended solely for computational purposes, rather than for experimental research.

The wide range of values of the VCR or VCFR (Table 1) parameters allowed us to study a broad range of neutron flux spectrum (Section 4). However, in the hybrid reactor, we used only practical values of these parameters. This reactor model can achieve neutron flux characteristics typical of a fast reactor. For example, the average neutron energy (ANE) in fuel rods reaches 0.5 MeV, while the average neutron energy causing fission (ANFE) for the hybrid reactor based on a Na-cooled U-cycle is approximately 0.9 MeV in normal operating conditions and 1.1 MeV for voided core state (Section 6).

The change of the VCR or VCFR parameter of the reactor model can be achieved by using assemblies with appropriate cell configurations, which entail the suitable fuel and coolant volumes (Figure 5, Table 1).

To reduce the density of fuel, one can utilize porous materials or fill part of the fuel volume with air, for example. The simplest method for decreasing the average fuel density of fuel rods is to fill the central part of the rods with air. The calculation results in this work utilize a homogeneous fuel density distribution within the fuel rods. However, the homogeneous distribution is compared with a method featuring an empty central part of the fuel rod. The differences between these methods are found to be less than the standard deviation of αv.

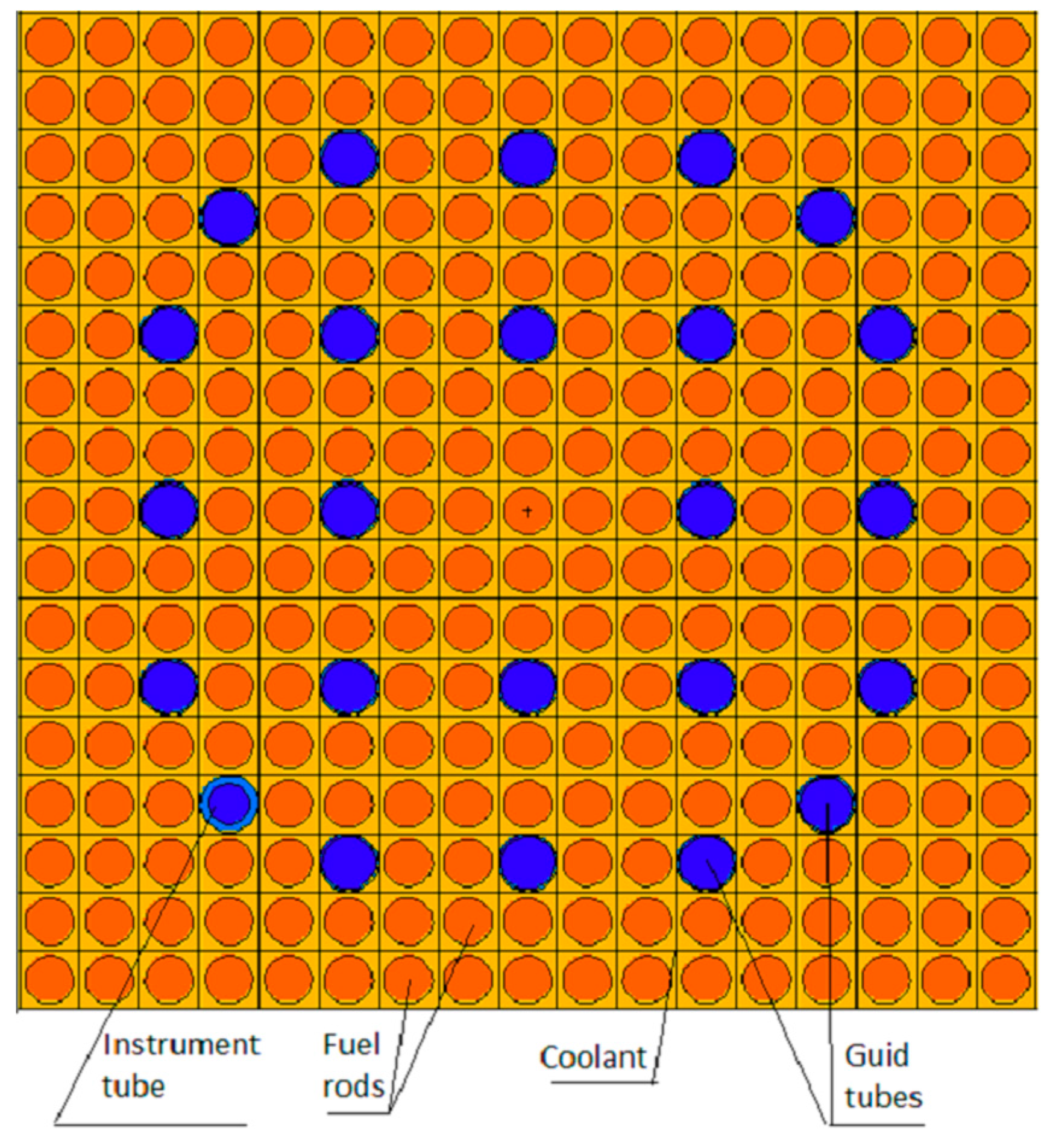
The initial value of the effective multiplication factor (k_eff) is in the range of 1.05 ± 0.02 for all cases. The uncertainty of α_V is discussed in Section 7. In other words, the initial enrichment of fuel is determined for each case before the reactor is voided for all values of the VCR parameter, fuel type and geometry. Herein, the reactor core may contain fuel assemblies of a single type (Figure 1, Figure 2 and Figure 3) or a two types (hybrid reactor, see Figure 4). The base parameters of the reactor cores are presented in Table 3. The core configuration presented in Figure 3 consists of 137 assemblies, referred to as the ‘small core’, or 101 assemblies, referred as the ‘very small core’.

The calculation results are obtained using Monte Carlo method, specifically employing the MCNP6.2 code [27]. The MCNP 6.2 code was developed by Los Alamos National Laboratory (USA) and is designed to track various particle types over a wide range of energies. For the calculations, only tabulated corresponding neutron cross sections from ENDF/B-VII.1 nuclear data library are used.

3. Definitions

There are different definitions for the void reactivity coefficient [8]. For example, the void reactivity coefficient for BWR is defined as the α_V at which the coolant flow rate reaches 90% of the nominal value [8]. In other case, the coolant has fully flowed out, and the reactor vessel is filled with saturated steam. The latter case is named as “the 100% void reactivity coefficient”. The following definition of α_V is presented in [8].

$${\alpha }_V={\displaystyle \frac{\frac{k_1-k_0}{k_1{k}_0}}{V_1-V_0}}.$$

(3)

where,

α_V: void reactivity coefficient

k₁, k₀: effective multiplication factor at void fraction of V₁ and V₀, respectively:

V₁, V₀: void fraction under varied and nominal conditions [%], respectively:

The definition in Equation (3) suggests that α_V is a linear function of the void fraction.

However, this is not accurate, as α_V is not generally a linear function (see Section 4 and Section 5).

For this reason, we employed the following definition of α_V:

$${\alpha }_V\left(void\right)={\displaystyle \frac{k_{void}-k_{norm}}{k_{norm}}},$$

(4)

where,

void [%] is an average value of the void fraction in the fuel cells,

k_norm, k_void are effective multiplication factors in a normally working and voided reactor core, respectively.

The following definition often is used in the literature:

$$∆\rho \left(void\right)={\rho }_{void}-{\rho }_{norm},$$

(5)

where,

${\rho }_{norm}$, ${\rho }_{void}$ indicate the reactivity of the reactor under normal operating condition and in a voided reactor core, respectively.

The definitions of α_V and $∆\rho$ are compared in Section 7.

The definitions provided by Equations (4) and (5) are more general than that of Equation (3), because they do not assume a linear void dependence of ${\alpha }_V\left(void\right)$ on the void fraction. In other words, all values of ${\alpha }_V\left(void\right)$ are calculated directly for each specific value of void parameter value.

${\alpha }_V\left(100\%void\right)$ means 0% of coolant density, i.e., the volume of coolant is filled by air at atmospheric pressure. This case simulates a Loss of Coolant Accident (LOCA).

${\alpha }_V\left(n\%void\right)$ means that the n% of part of the coolant is evaporated and the average density of the coolant is equal to (100 − n)% of its normal value. The normal value of the coolant density is equal to the density of liquid metal.

Magnitude ${\alpha }_V\left(void\right)$ depends on a various parameters, such as the VCR or the type of fuel, and the size and shape of the reactor core (See Section 4). If we are interested in ${\alpha }_V$ as a function of the VCR parameter and a constant void value, we can write it in the following form:

$${\alpha }_V^{void}\left(VCR\right)$$

(6)

Meanwhile, if we are interested in ${\alpha }_V$ as a function of the void parameter and with a constant value of the VCR parameter we can express it in the following form:

$${\alpha }_V^{VCR}\left(void\right)$$

(7)

Both function ${\alpha }_V^{void}\left(VCR\right)$ and ${\alpha }_V^{VCR}\left(void\right)$ are not linear functions of the void and VCR parameters (See Section 4 and Section 5).

4. Calculation Results for the Reactor Core Filled with Single-Type of Assemblies

This section presents ${\alpha }_V$ for the geometry of reactor cores depicted in the Figure 1, Figure 2 and Figure 3, considering different parameter values as VCR, type of fuel, type of coolant, geometry and fuel assembly (Table 3). In this section we assume that the reactors consist of a single type of fuel assembly. The initial values of fuel enrichments are the same for both normal operation and during the reactor void condition.

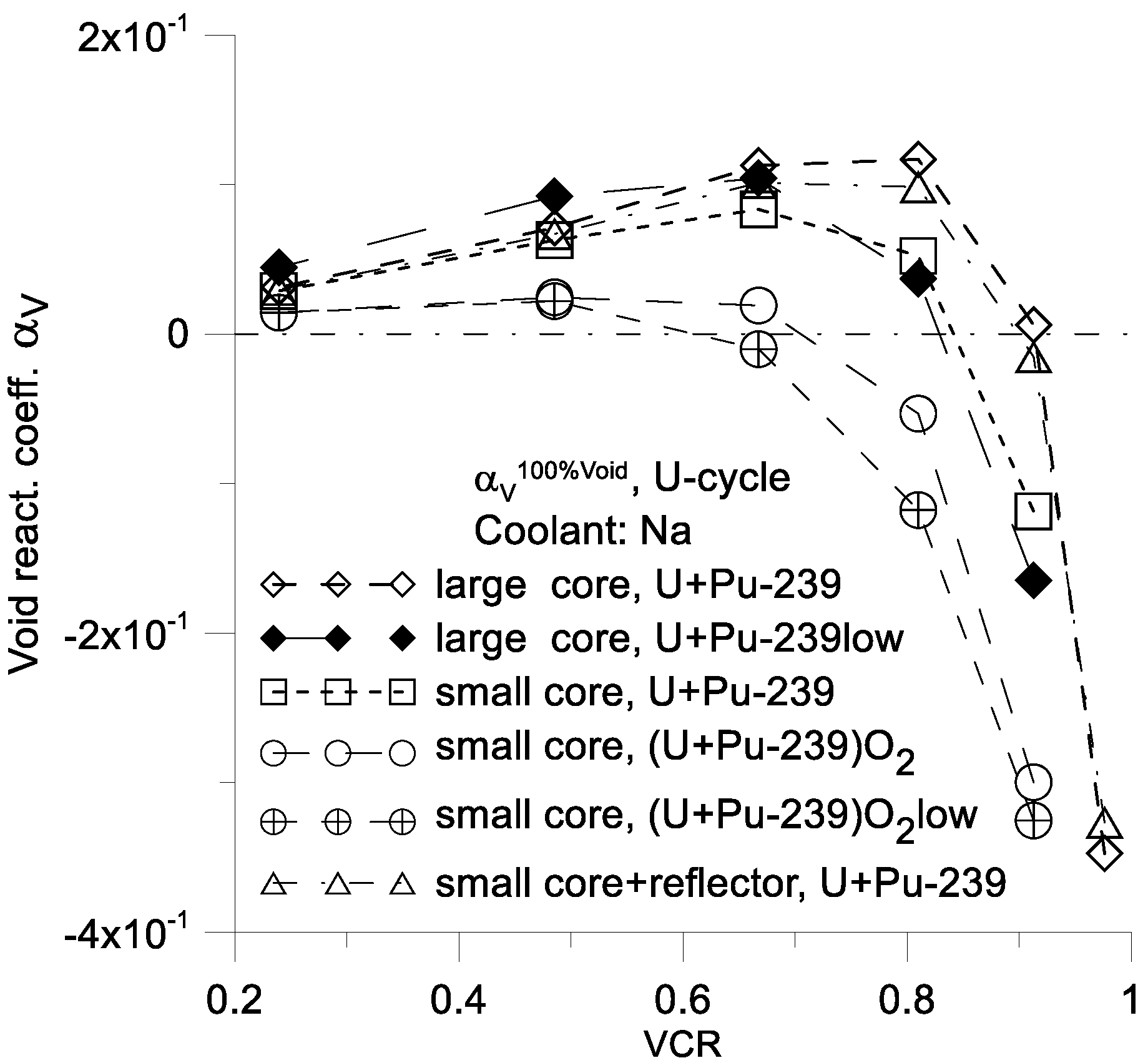
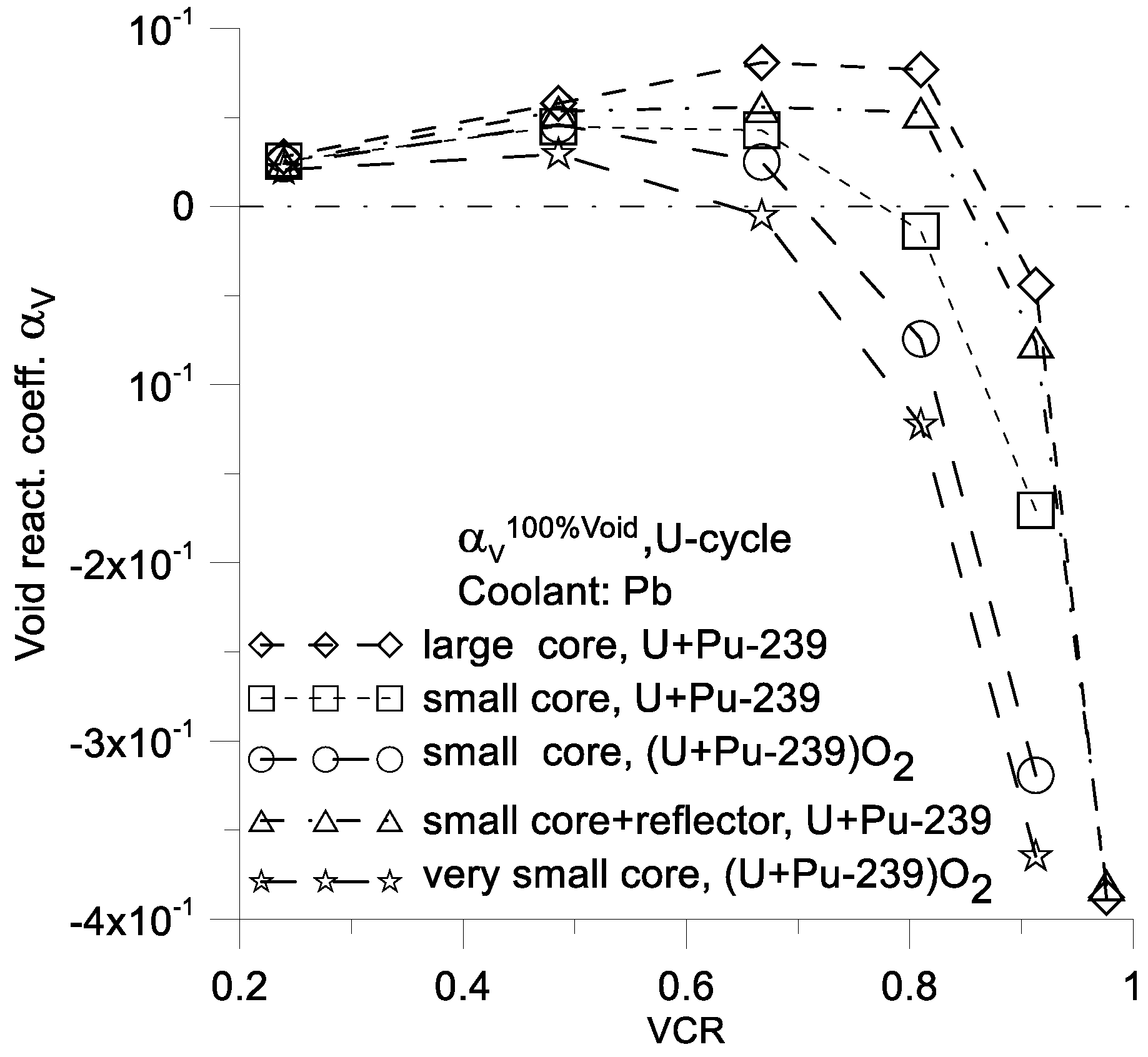
The Figure 7, Figure 8, Figure 9 and Figure 10 present values of ${\alpha }_V^{100\%void}\left(VCR\right)$ for different types of cores (Figure 1, Figure 2 and Figure 3) and various combinations of fuel and coolant (from Table 3). These values can be both positive and negative. The values of ${\alpha }_V^{100\%void}$(VCR) are important because they indicate the maximal positive value of ${\alpha }_V$ and minimal negative value for the maximal value of the void parameter.

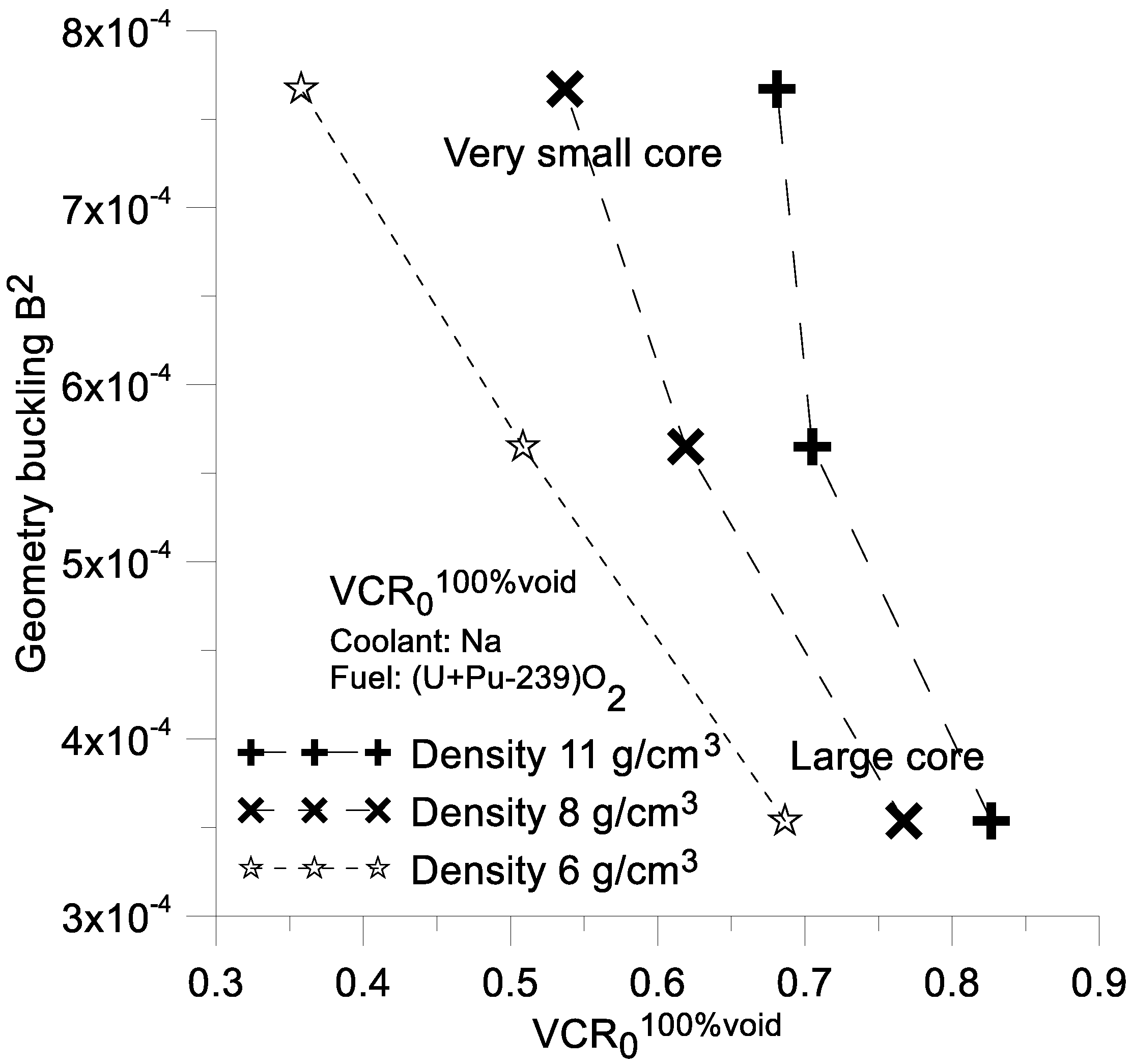
The value of ${VCR}_0^{100\%void}$, for which ${\alpha }_V^{100\%void}$(${VCR}_0^{100\%void}$) = 0, is very important. In other words, the ${VCR}_0^{100\%void}$ parameter is the zero (root) of a function ${\alpha }_V^{100\%void}$(VCR). This is significant because for VCR < ${VCR}_0^{100\%void}$, it is not possible to obtain a negative value of ${\alpha }_V$. For these values of the VCR, the reactor does not passively decrease the number of neutrons during a LOCA accident. In contrast, for reactors with a VCR greater than ${VCR}_0^{100\%void}$, the value of ${\alpha }_V^{100\%void}$ becomes negative, indicating that the reactor should be turned off during such an accident. Please note that ${VCR}_0^{100\%void}$ is a characteristic parameter of a class (set) of reactors that differ only in the VCR parameter.

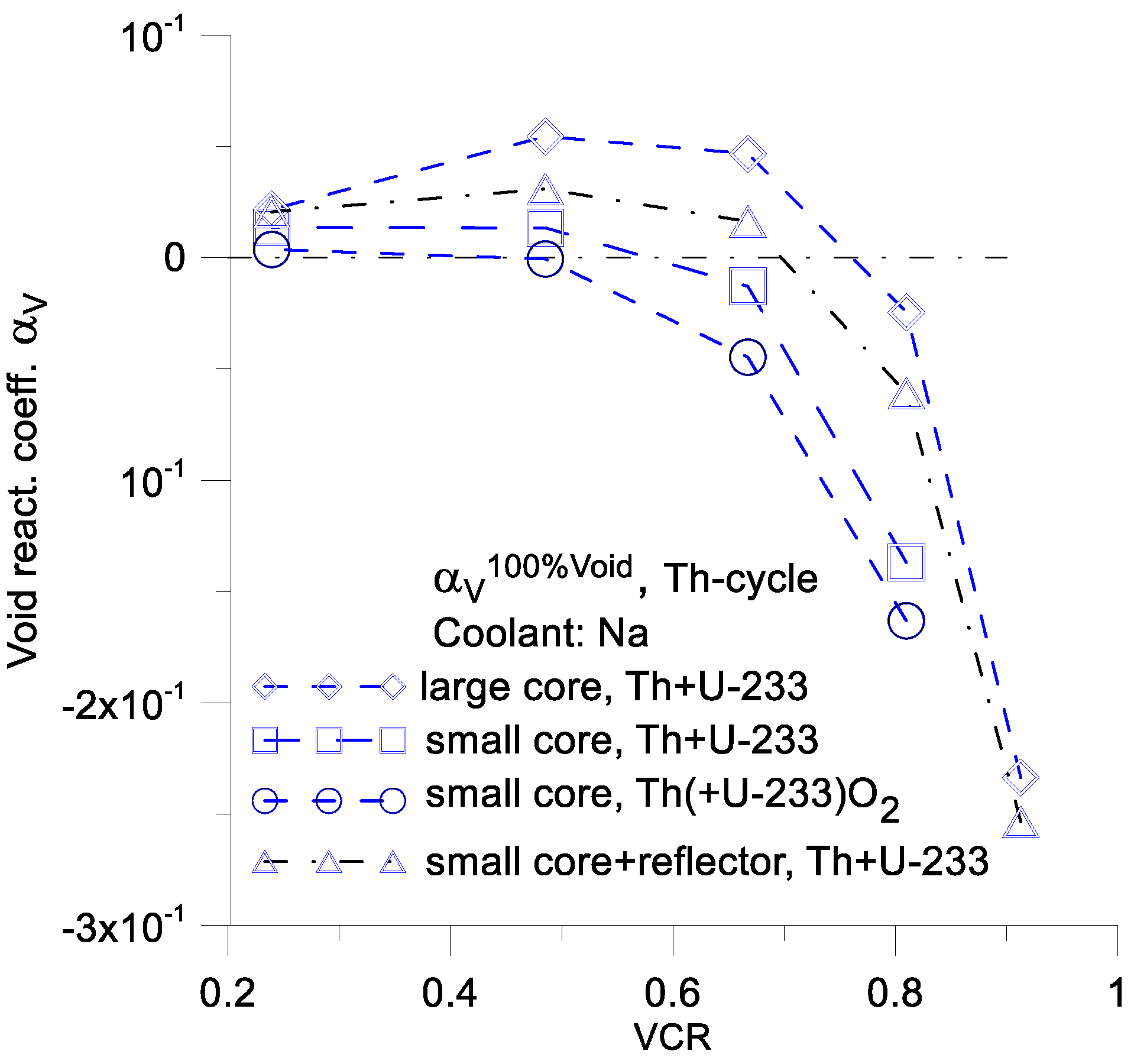
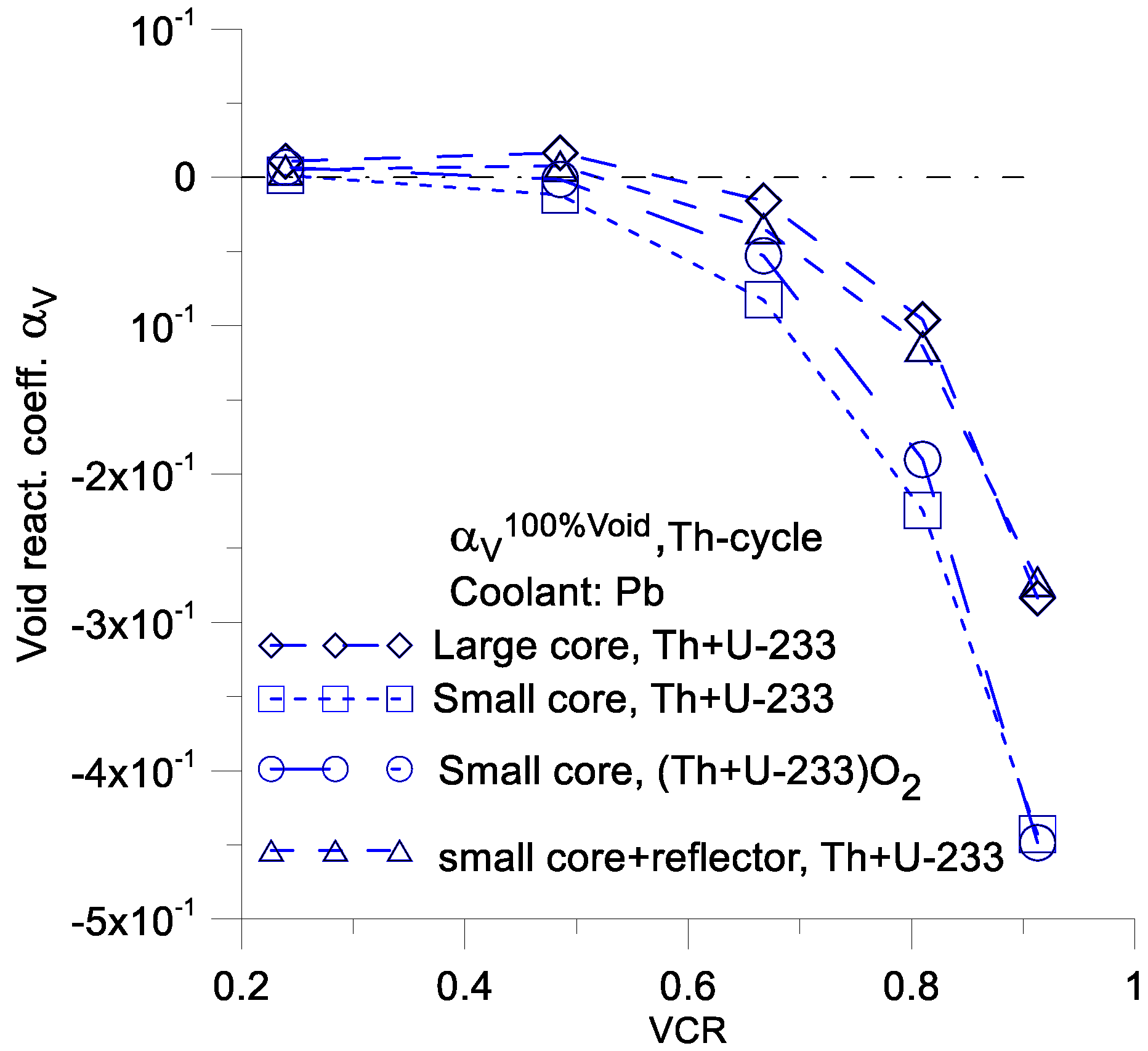
All the ${\alpha }_V^{100\%void}\left(VCR\right)$ functions have negative values for sufficiently high values of VCR. For this reason, VCR is the most important factor to reduce the value of ${\alpha }_V^{100\%void}\left(VCR\right)$.

The greatest positive values of ${\alpha }_V^{100\%void}\left(VCR\right)$ one can be achieved with large cores or small cores that incorporate a reflector and use metallic fuel of type U-238 + Pu-239 (Figure 7, Figure 8, Figure 9 and Figure 10). For this reason, both a reflector and high value of a fuel density are unfavorable when the goal is to reduce the value of ${\alpha }_V$.

Lower positive values of ${\alpha }_V^{100\%void}\left(VCR\right)$ are obtained for the thorium cycle (Figure 9 and Figure 10), the primary reason for this result is the lower density of metallic thorium compared to metallic uranium (see Section 6).

A negative value of ${\alpha }_V^{100\%void}\left(VCR\right)$ one can easily be obtained with a Pb-cooled Th-cycle (Figure 10). For this type of reactor, it is possible to obtain a negative value of ${\alpha }_V^{100\%void}$ over a wide range of VCR parameter values.

The ${\alpha }_V^{100\%void}\left(VCR\right)$ function increases or decreases with low and high values of VCR, respectively. The absorption and leakage components of α_v are responsible for the increasing and decreasing part of the α_v function, respectively. To obtain a negative α_v value, than the leakage component must be greater than the sum of absorption and spectrum components α_v [23].

The components mentioned above are closely interconnected. A high value of VCR indicates a high positive value of the absorption component; however, this does not necessarily imply a higher value of αv. In fact, a high value of VCR parameter generally corresponds to lower value of fuel mass in the fuel cell which increases the leakage component. As the VCR value becomes sufficiently high, αv tends to decrease.

A small core makes it easier to obtain a negative value of ${\alpha }_V^{100\%void}$ for in different type of reactors cores without reflectors (Figure 7, Figure 8, Figure 9 and Figure 10). This finding extends the existing literature [2,3,4,5,17]. However, another significant parameter that decreases the value of ${\alpha }_V^{100\%void}$ is the density of the fuel (Figure 7). The most effective method of reducing of ${\alpha }_V^{100\%void}$ is to apply the three methods simultaneously: reducing fuel density, decreasing the size of core, and increasing the value of VCR (Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11).

The average fuel density plays important role in decreasing the value of ${VCR}_0^{100\%void}$_. Unfortunately, only a very small core with a fuel density of 6 g/cm³ achieves a ${VCR}_0^{100\%void}$ value of less than 0.5. The method of reducing the average density of the fuel does not practically allow for the construction of a large reactor filled solely with a single-type of fuel assembly with a negative ${\alpha }_V$ (Figure 11).

Please note that the above conclusion applies to reactor core containing only a single-type of fuel assembly using the U-cycle.

The large and medium reactors presented in Reference [17] have reflectors and positive α_v values.

The results in this section predict that large reactors without the reflectors also exhibit a positive value of α_v. Why it is so difficult to obtain a low value of ${VCR}_0^{100\%void}$? This is because decreasing this value simultaneously increases the fuel mass in the fuel cell, which, in turn, decreases the neutron flux leakage.

Unfortunately, the results presented in this section exhibit a high value of ${VCR}_0^{100\%void}$_. However, they provide guidance on how to significantly reduce this quantity (see Section 6).

5. Loss of Neutrons

This section presents the relationship between α_v and neutron loss coefficient Loss Equation (8), and β_v Equation (10) as a functions of VCR. The fraction of lost neutrons can be defined in the following form:

$$Loss\left(VCR\right)=Absorption\left(VCR\right)+Escape\left(VCR\right),$$

(8)

$$Fission\left(VCR\right)=1-Loss\left(VCR\right),$$

(9)

where:

Absorption—means the absorption fraction without absorption neutrons inducing fissions i.e., (n,γ)

Escape—means the total escaped fraction of neutrons,

Fission—means the fraction of all actinides fission reactions.

Loss is a function of VCR and the void parameter.

The β_v function can be defined as relative change in the Loss(VCR) function

$${\beta }_V^{n\%void}={\displaystyle \frac{{Loss}_{void}-{Loss}_{norm}}{{Loss}_{norm}}}$$

(10)

where

Loss_norm, Loss_void—mean the loss neutrons fraction at 0% void (normal work) and n% void, respectively.

The Incore(VCR) function can be defined as the neutron fraction inside the core in the following form:

$$Incore\left(VCR\right)=1-Escape\left(VCR\right)=Absorption\left(VCR\right)+Fission\left(VCR\right).$$

(11)

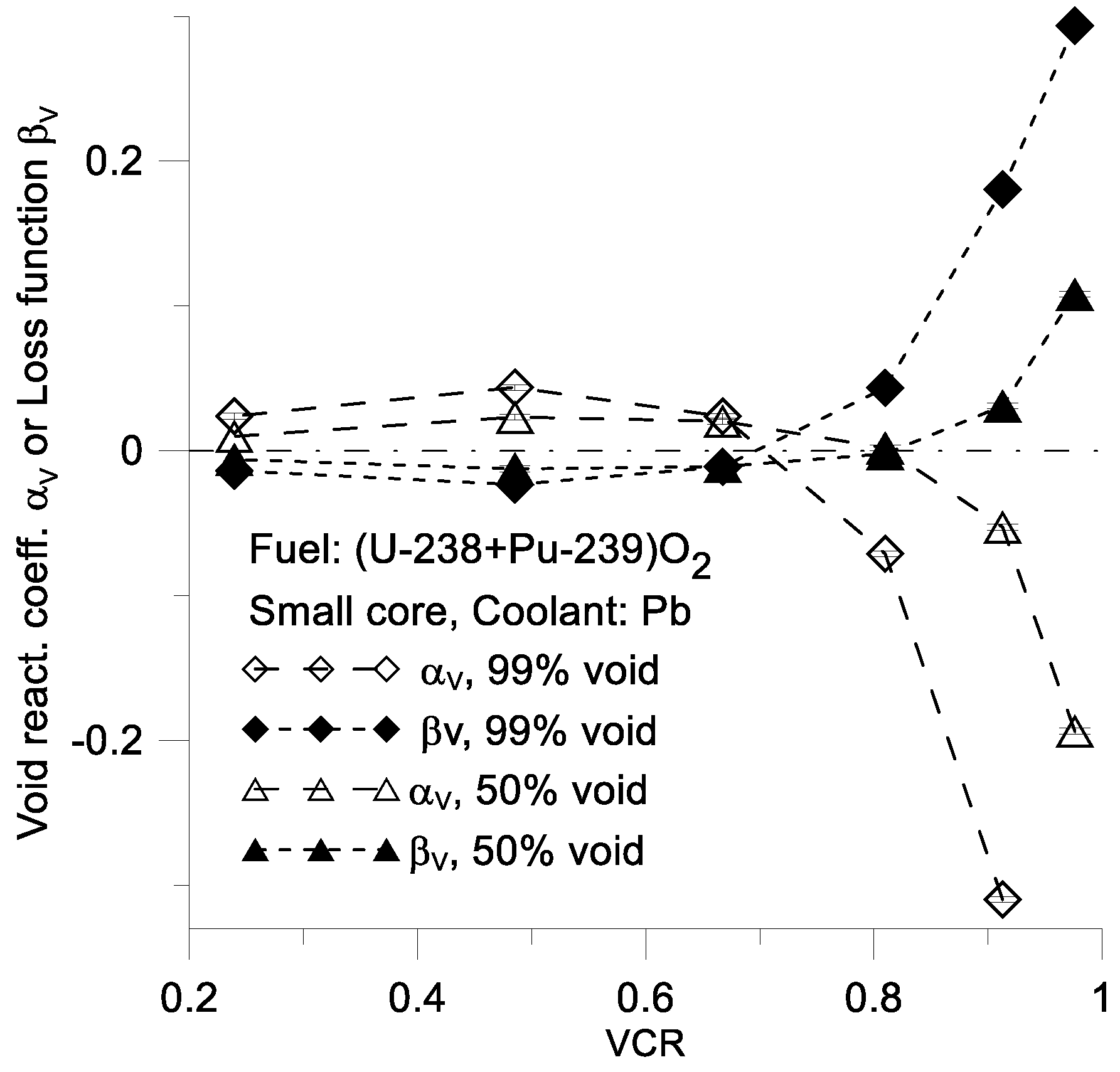
Comparisons between ${\alpha }_V^{\mathrm{n}\mathrm{\%}\mathrm{v}\mathrm{o}\mathrm{i}\mathrm{d}}$ and ${\beta }_V^{n\%void}$ for the Pb-cooled U-cycle in a small core reactor as a function of VCR are presented in Figure 12. Similarly, we determined the relationships between ${\alpha }_V^{\mathrm{n}\mathrm{\%}\mathrm{v}\mathrm{o}\mathrm{i}\mathrm{d}}$ and ${\beta }_V^{n\%void}$ for all cases discussed in this work.

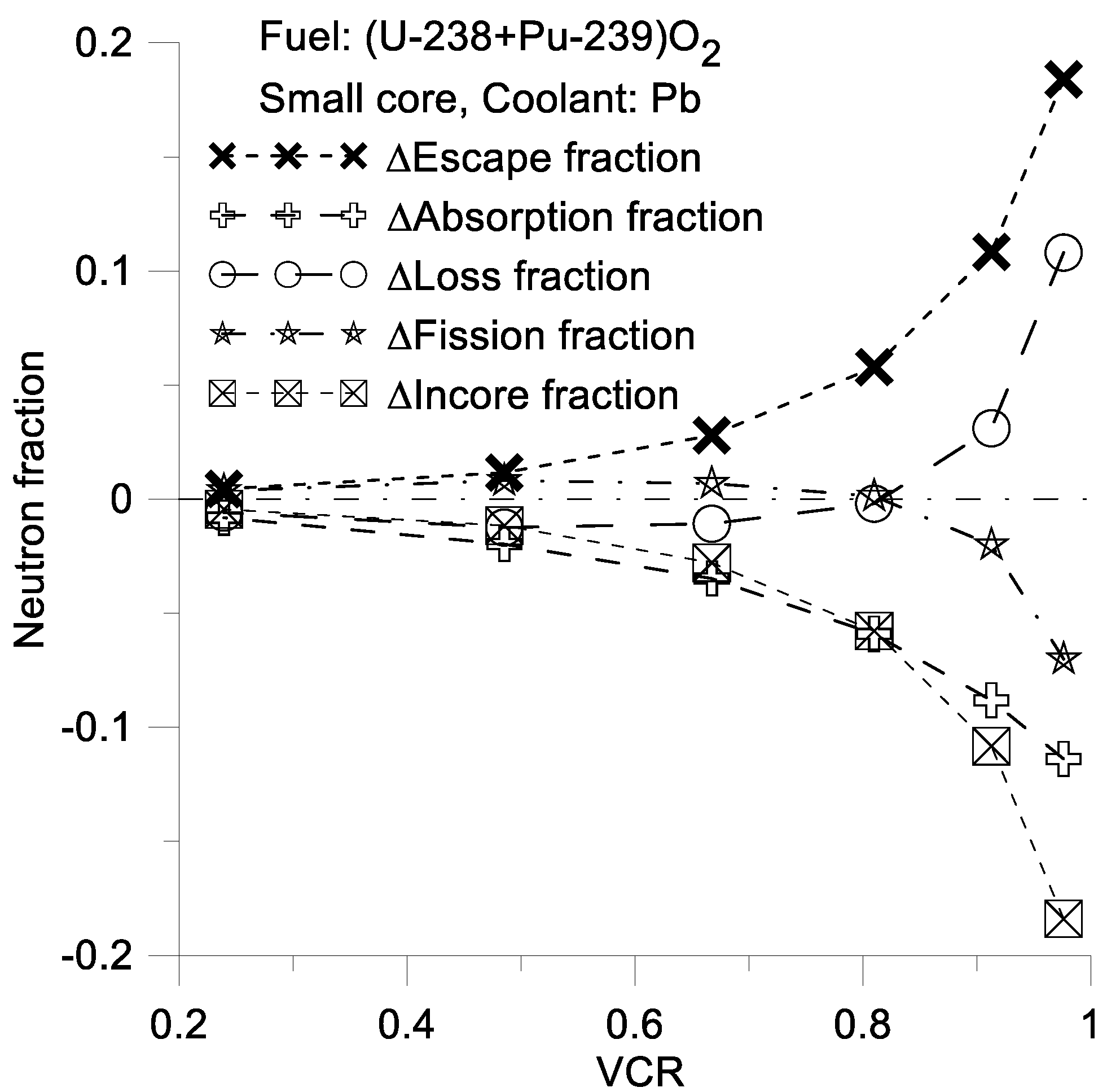
It is important to note, that ${\beta }_V^{100\%void}$ has negative and positive values. A positive values means positive values of ${\Delta Loss=Loss}_{void}-{Loss}_{norm}$ and a decreasing number of neutrons in the core. Conversely, a negative value of $\Delta Loss$ suggests an increase in the number of neutrons in the reactor core. In other words, the presence of a void can either increase or decrease the neutron populations in the core, which, in turn, changes the value of ${\alpha }_V$.

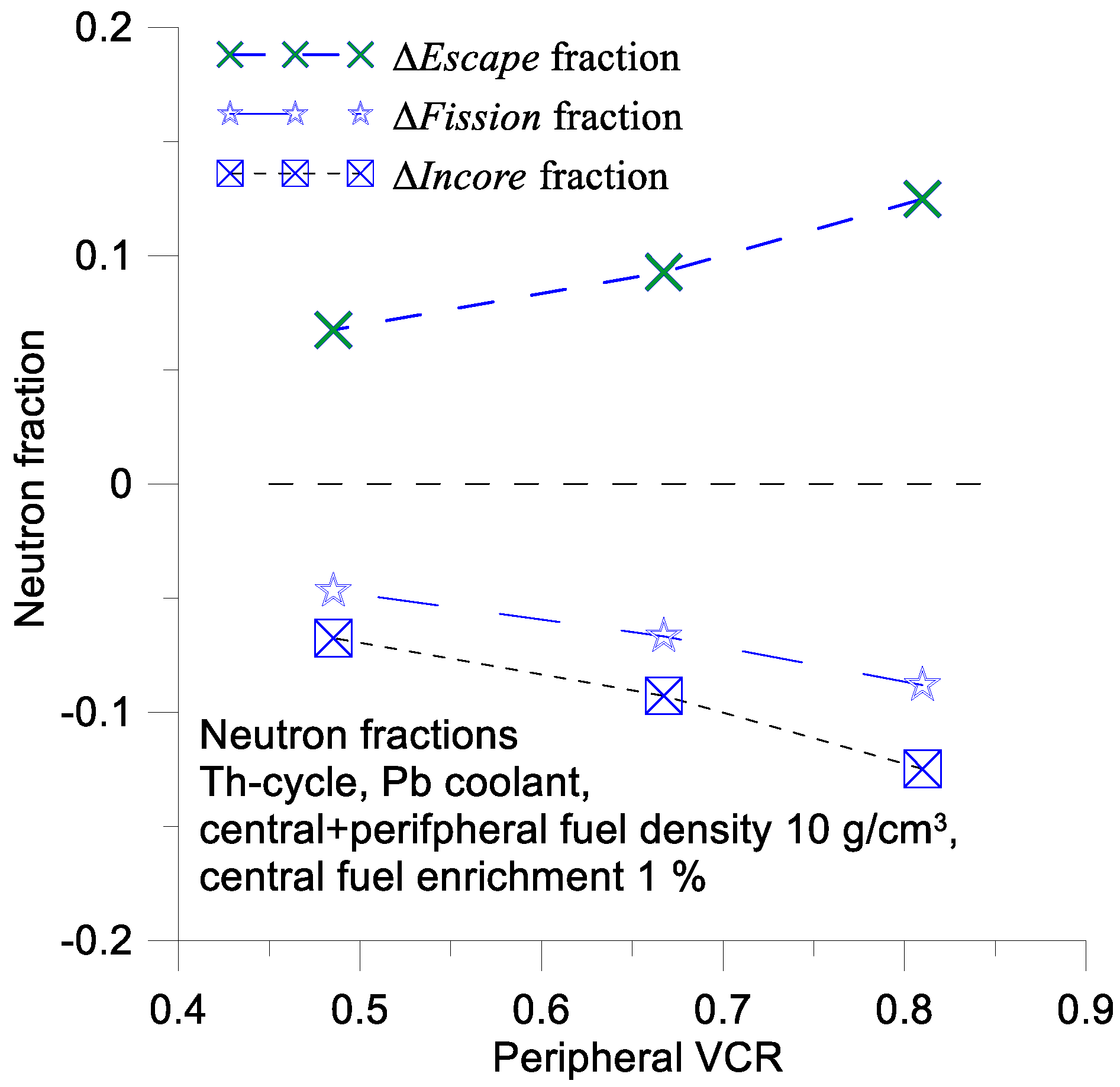
Note that the ΔLoss fraction is equal to the negative value of the Δfission fraction (Figure 13). In other words, a positive value of the ΔLoss fraction indicates a decrease in the fission fraction and a negative value of ${\alpha }_V$. The primary reason for this is the high value of the ΔEscape fraction during evaporative cooling. These calculations results take into account changes in the neutron flux energy distribution and cross sections of the corresponding reactions during reactor voiding. Specifically, the results consider the increase in fission cross sections induced by an increase in the average neutron energy. However, such an increase in the fission cross section can be mitigated by a decrease in the neutron fraction within the reactor core, which is caused by neutron escape. The Incore(VCR) function can be useful for illustrating this effect (Figure 13).

The results obtained in this section help us to get negative value of ${\alpha }_V$ for a hybrid reactor (see Section 6).

6. Calculation Results for Hybrid Reactor

The primary physical phenomenon that reduces the number of neutrons in the core in a voided state is their escape from the core. This can be achieved using the appropriate reactor geometry and material properties. Since the main goal of the present work is to increase the neutron leakage through the radial side surface of the core, a reactor should be designed without a radial reflector. The fuel arrangement in the reactor is also crucial, i.e., highly enriched fuel should be placed in the peripheral region of the reactor. In addition, the assemblies in the peripheral zone of the reactor should employ an increased VCR value and a reduced fuel density. These parameters contribute to an additional increase in neutron leakage.

Using the results from the previous sections, we can derive intriguing outcomes for the hybrid reactor (Figure 4, Table 3). In this study, the hybrid reactor core contains two parts: the central core and the peripheral core. The central core contains the fuel assembly with an optimal value for VCR, i.e., 0.485 (VCFR = 0.94), a standard fuel density and a low value of fuel enrichment. In contrast, the peripheral core is composed of a fuel assembly with a high level of fuel enrichment and three values of both the VCR parameter and fuel density. By simultaneously utilizing these three parameters and characteristics for the peripheral assemblies, we achieve the smallest values for ${\alpha }_V$. The calculations were conducted with central fuel enrichments of 1 and 5 at. % for both U-cycle and Th-cycle reactors. The enrichment of peripheral fuel was adjusted to ensure k_eff = 1.05 ± 0.02.

Herein two examples of hybrid reactors are presented: Na-cooled U-cycle and Pb-cooled Th-cycle. It is important to note that the Na-cooled U-cycle predicts maximal values of ${\alpha }_V$ whereas the Pb-cooled Th-cycle exhibits minimal values of ${\alpha }_V$ when the reactor core is filled with a single type of assembly (compare Figure 7, Figure 8, Figure 9 and Figure 10).

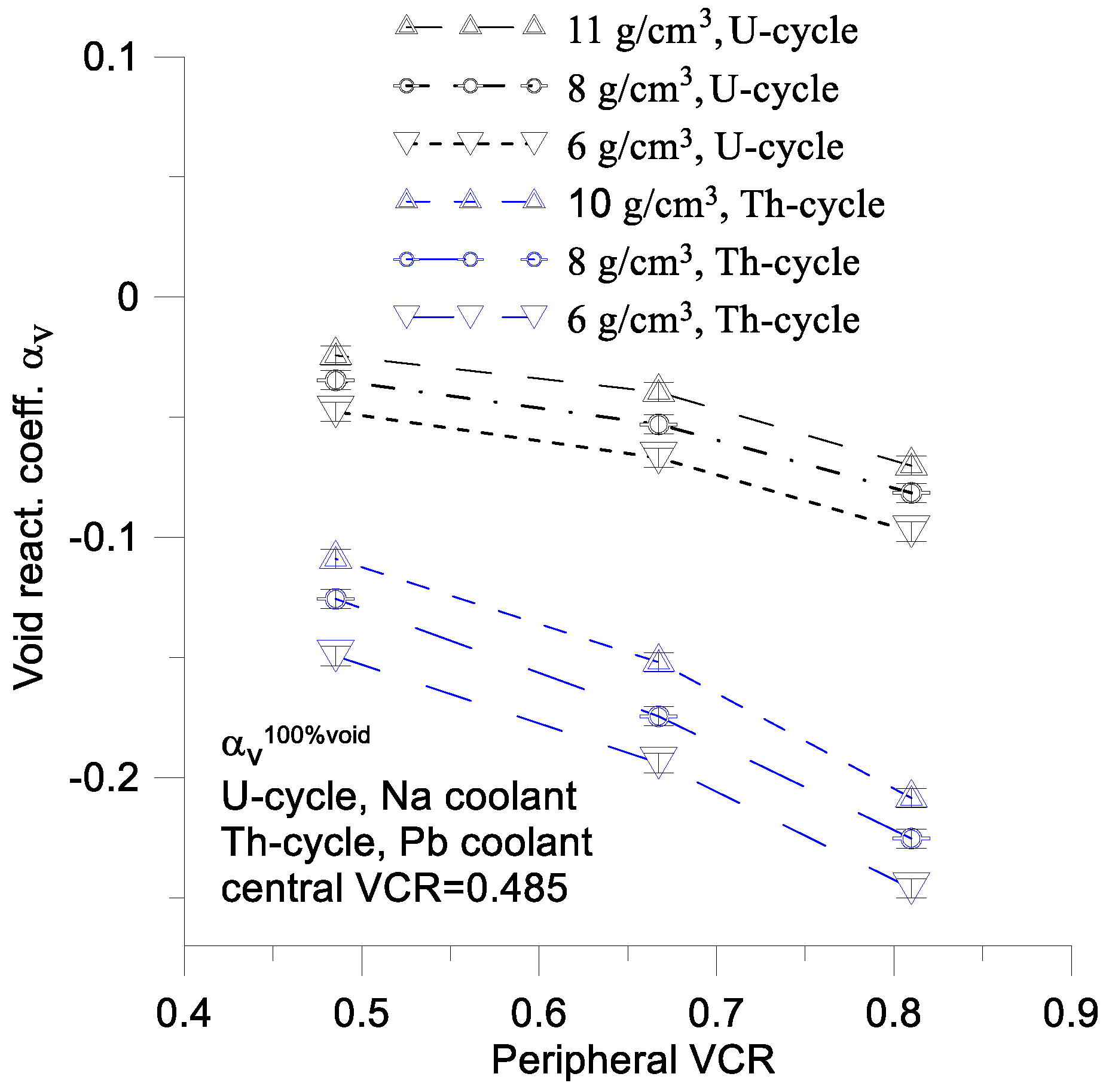
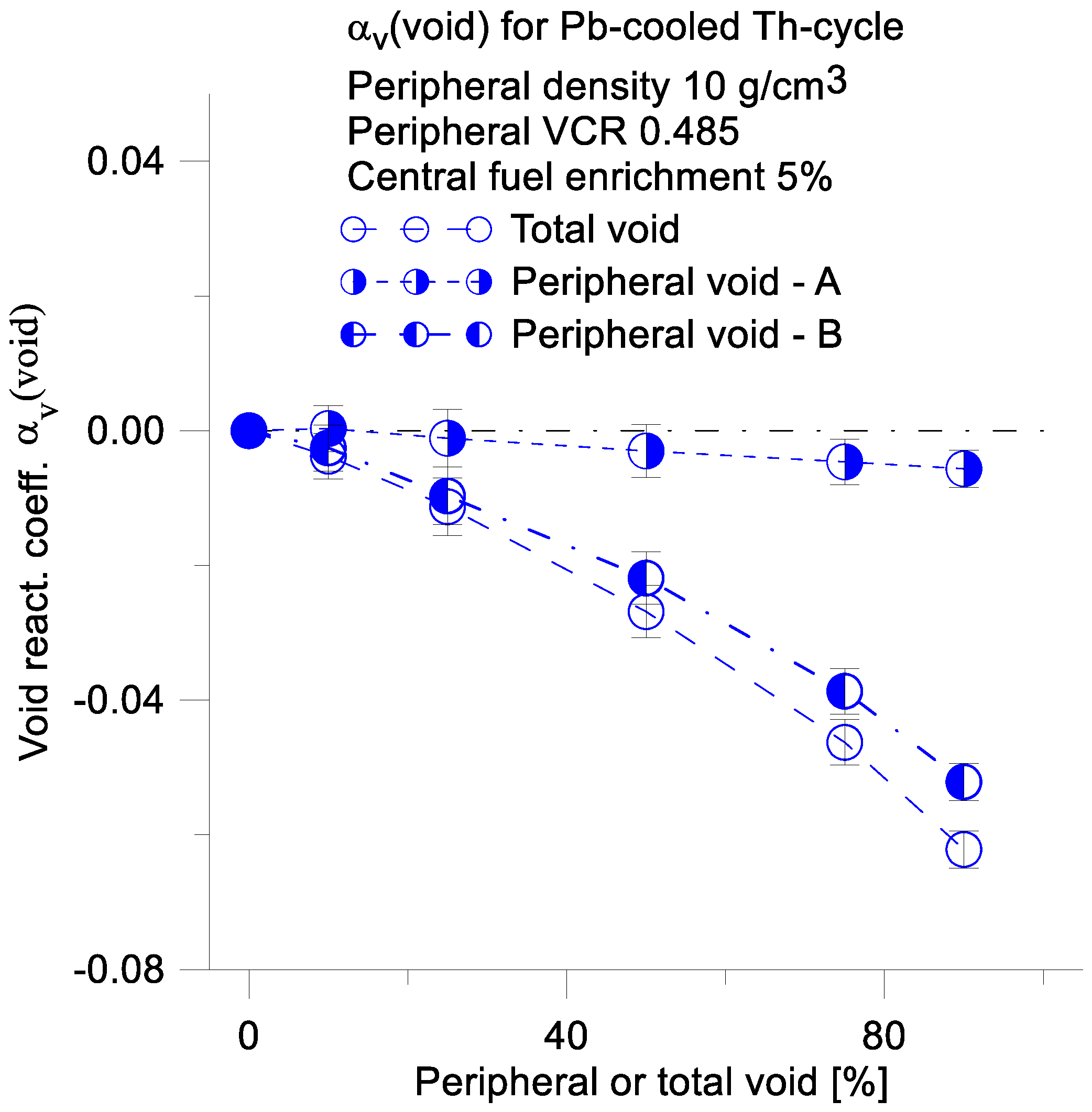
The Pb-cooled Th-cycle hybrid reactor has significantly lower value of ${\alpha }_V$ compared to the Na-cooled U-cycle reactor (Figure 14 and Figure 15). This indicates that Th-cycle reactors are characterized by substantially greater passive safety than U-cycle reactors.

The values of ${VCR}_0^{100\%void}$ are significantly less than 0.485 for all presented cases. While the exact values of ${VCR}_0^{100\%void}$ were not calculated, they can be easily estimated using the ${\alpha }_V\left(VCR\right)$ function and extrapolation method (Figure 14, Figure 16 and Figure 17). It is important to note that the values of VCR for the central and peripheral parts are significantly greater than ${VCR}_0^{100\%void}$. This can be expressed in the following inequalities: VCR^central > ${VCR}_0^{100\%void}$ and VCR^peripheral > ${VCR}_0^{100\%void}$. These results indicate that ${\alpha }_V$ has a negative value (see Section 5).

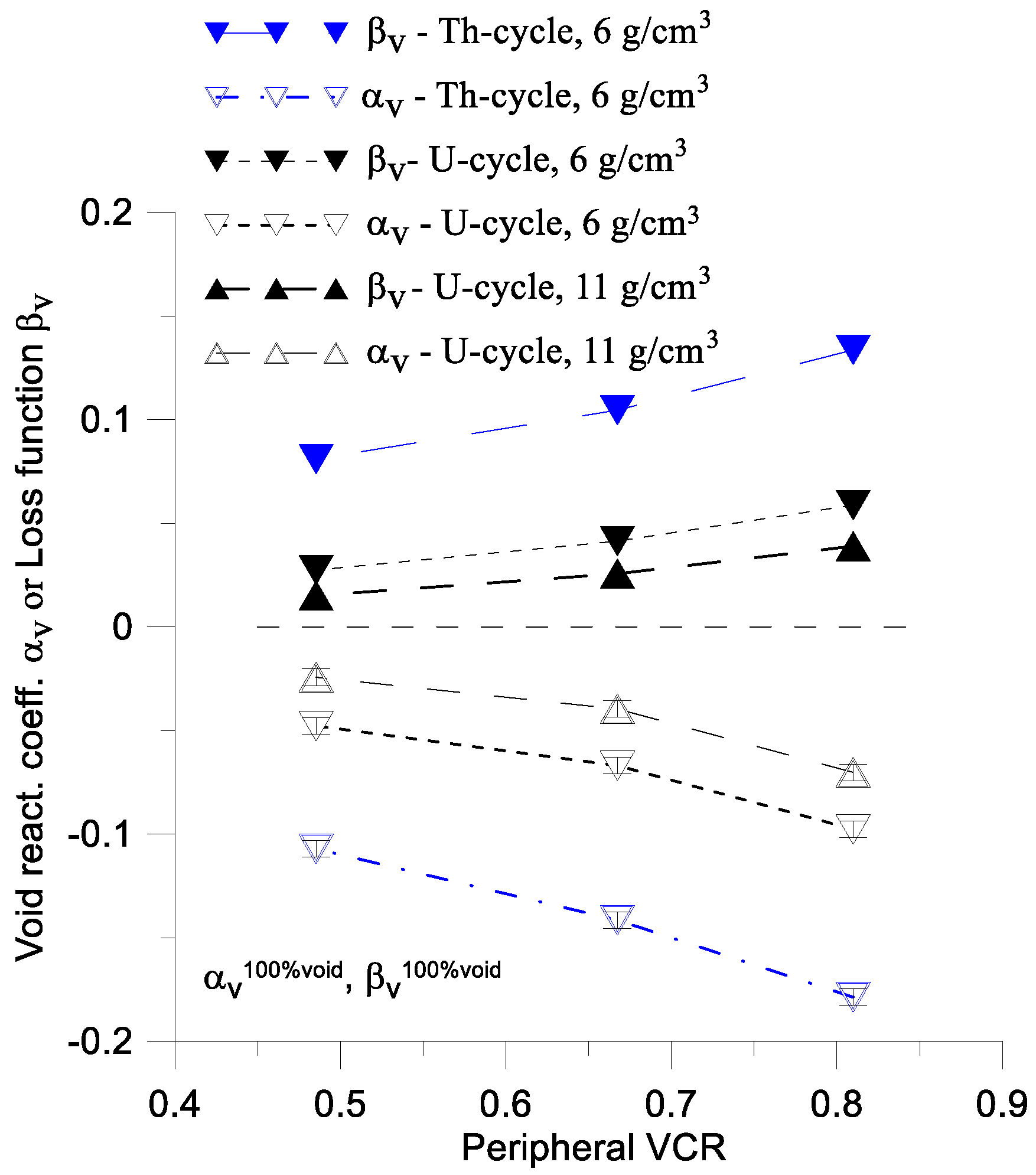
The negative value of ${\alpha }_V$ can be explained in another way. Note that the value of ${\beta }_V$ is positive for all the cases presented in this section (Figure 16); a positive value of ${\beta }_V$ always corresponds to negative value of ${\alpha }_V$ (Section 5). The primary reason of the positive value of ${\beta }_V$ is the high value of ΔEscape quantity, which indicates an increase of escaping neutrons in a voided reactor core; an increase in ΔEscape leads to a decrease in ΔIncore, that is, it reduces the fraction of neutrons in the core. 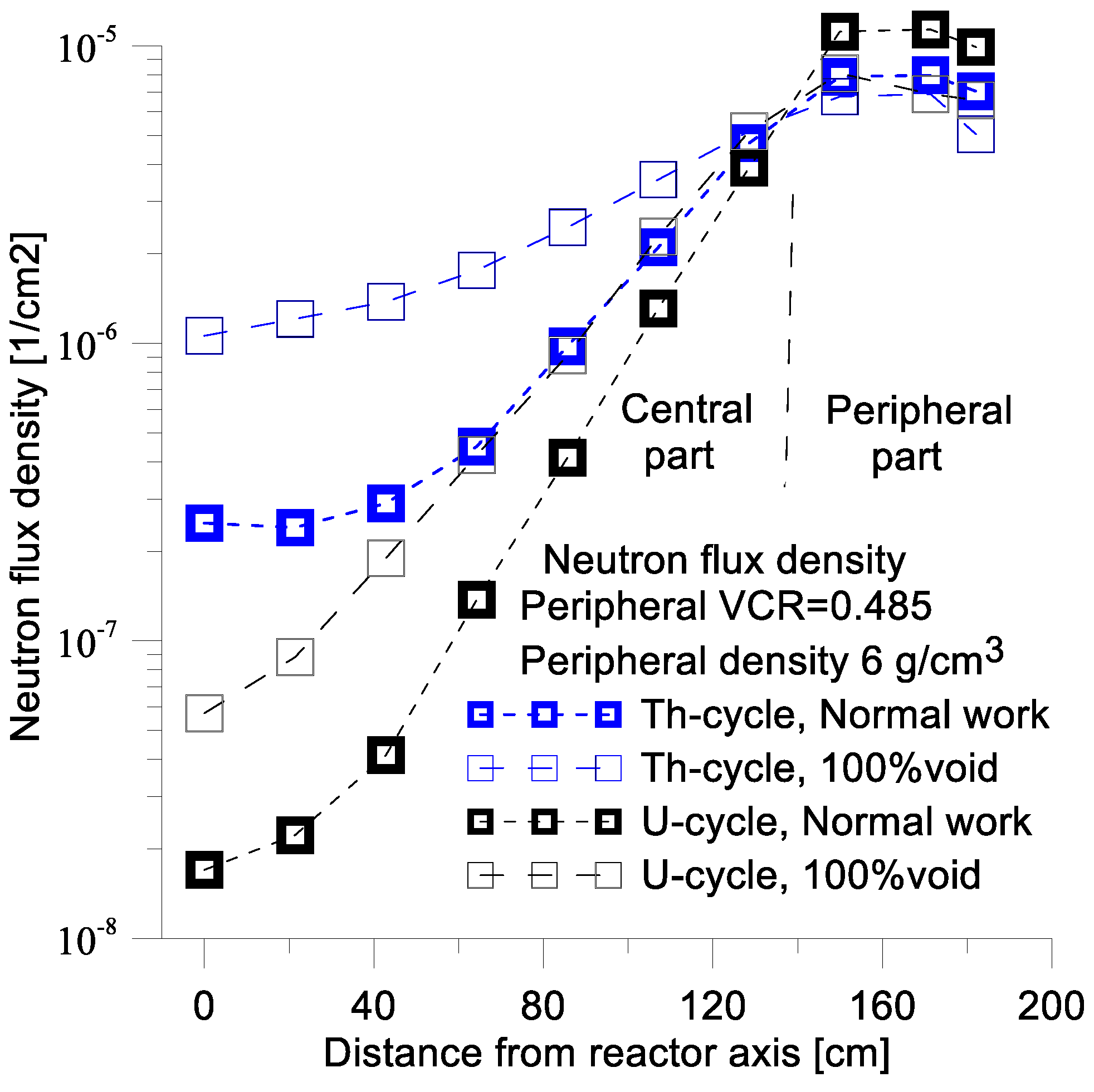The relative increase in ΔEscape exceeds 60% and the average energy of the escaping neutrons increases by more than 20%. This results in a reduction in the average value of neutron flux density in the peripheral part of the core (Figure 17), leading to a decrease in fission reaction within the core, as evidenced by the negative value of Δfission (Figure 18). The Δfission fraction is negative for all samples presented in this section.

Note that in cases of VCR = 0.485 with a normal fuel density value for both central and peripheral assemblies, a significant difference in fuel enrichment between the peripheral and center segments is sufficient to obtain a negative value of ${\alpha }_V$. This phenomenon occurs because the hybrid reactor undertakes high fuel enrichment in the peripheral region and reaches a high value of leakage neutrons under the condition of a voided reactor. Note also that an analogical large reactor Na-cooled U-cycle reactor based on a single type of assembly has ${VCR}_0^{100\%void}$ = 0.827 and ${\alpha }_V=0.03$.

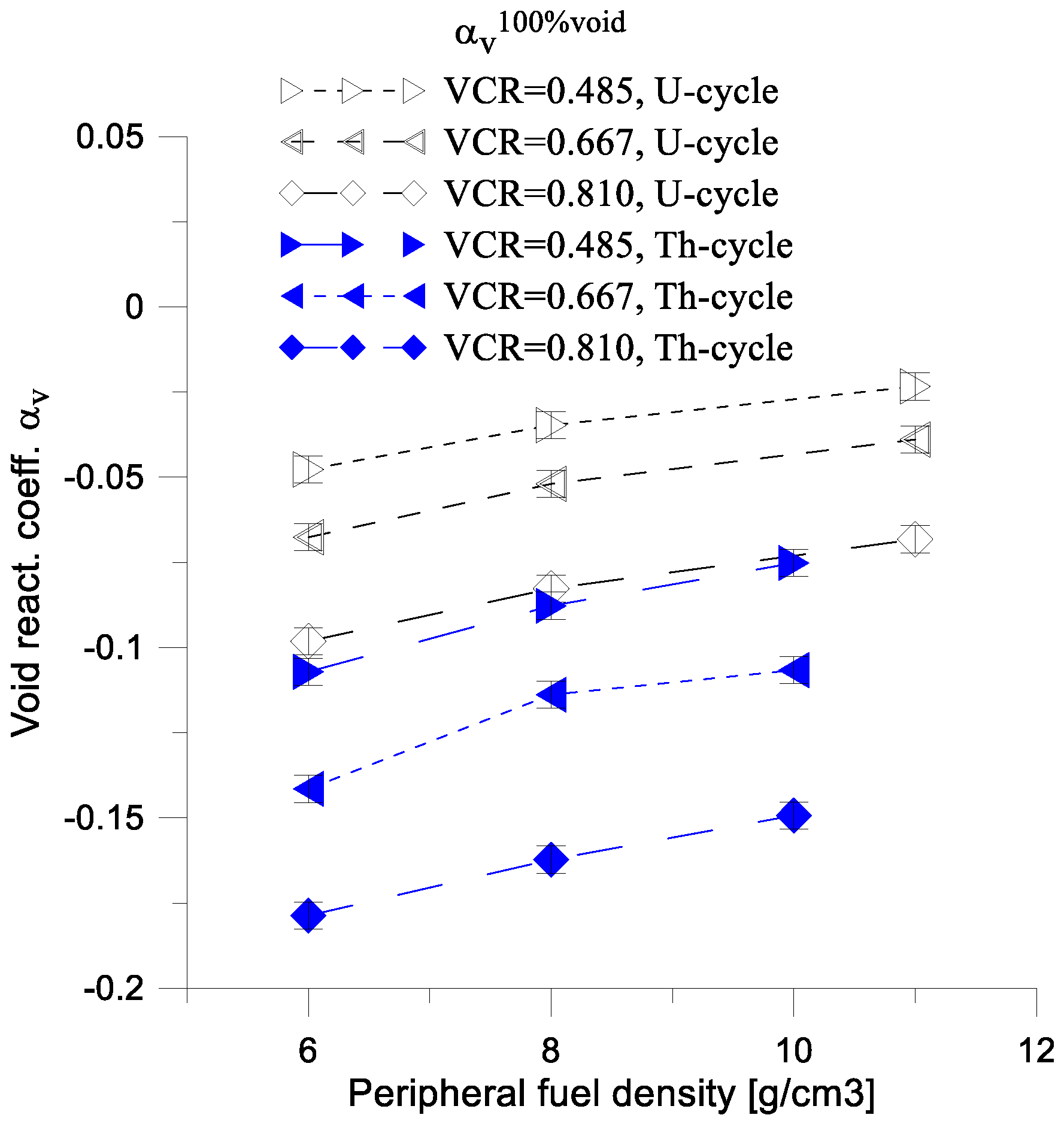
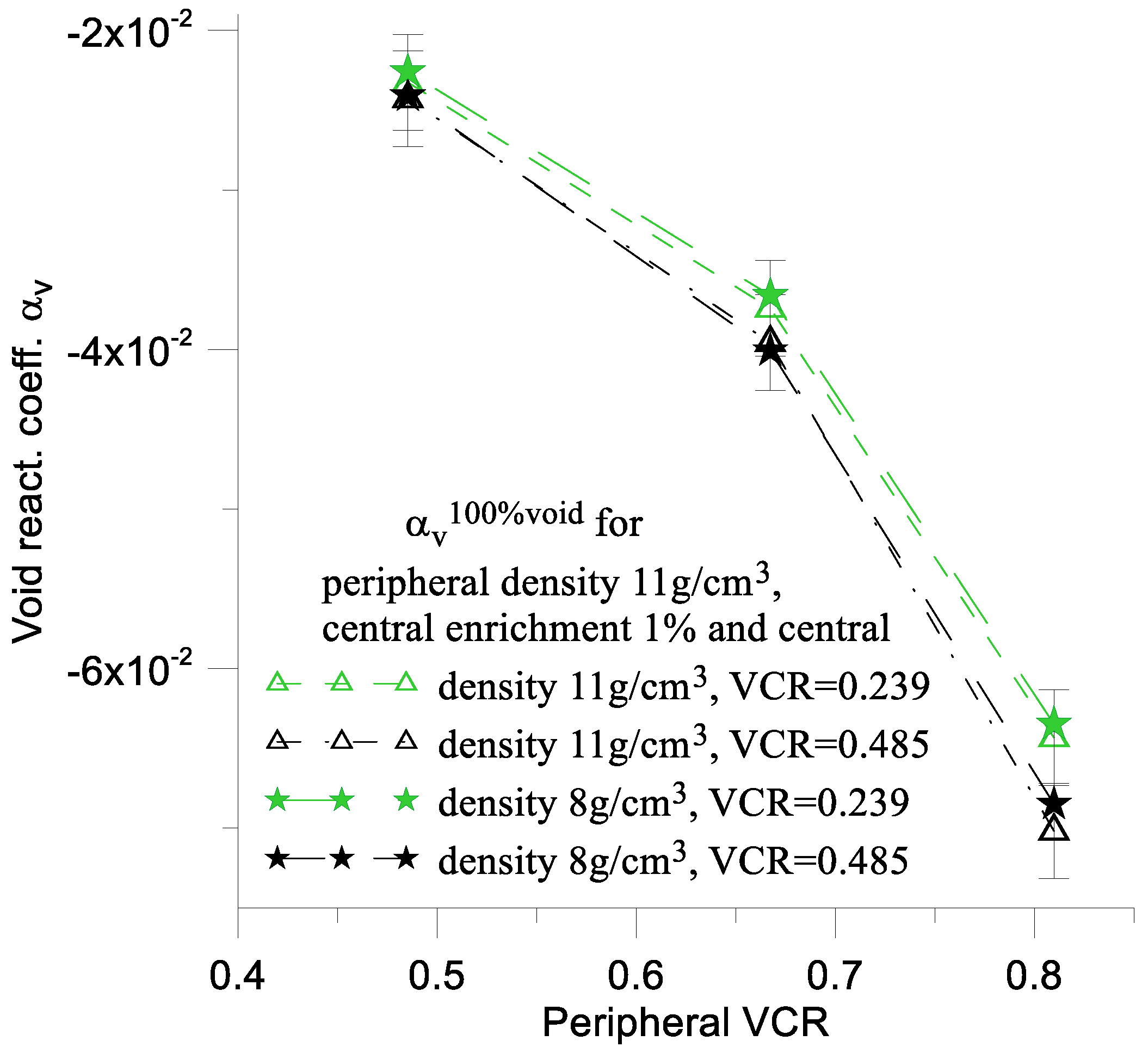
One can observe that ${\alpha }_V$ is a decreasing function of peripheral VCR (Figure 14) and an increasing function of peripheral fuel density (Figure 15). In other words, the negative value of ${\alpha }_V$ is a decreasing function of the difference in fuel enrichment and the fuel density, as well as the VCR between the central and peripheral parts (

Table 4. Base parameter of the hybrid reactor for the following set parameters: VCR^central = 0.485, fuel—(U-Pu-239) O₂, fuel density in central zone—11 g/cm³, and coolant—Na.

Peripheral VCR	Peripheral Fuel Density	${\mathit{\alpha }}_{\mathit{V}}^{100\%\mathit{v}\mathit{o}\mathit{i}\mathit{d}}$ Error < 0.004	Peripheral Enrichment	ANFE for Normal Work [MeV]	ANFE for 100% Void Core [MeV]
Central fuel enrichment 1 at.% of Pu-239
0.810	11	−0.07018	27	0.81	1.15
0.667	11	−0.03958	19	0.88	1.11
0.485	11	−0.02428	14	0.94	1.09
0.810	8	−0.08147	40	0.78	1.15
0.667	8	−0.05296	25	0.85	1.12
0.485	8	−0.0346	17	0.91	1.10
0.810	6	−0.0976	50	0.77	1.17
0.667	6	−0.06691	30	0.83	1.15
0.485	6	−0.04775	20	0.91	1.13
Central fuel enrichment 5 at. % of PU-239
0.810	11	−0.038	26	0.81	1.08
0.667	11	−0.015	17	0.87	1.07
0.485	11	−0.005	13	0.93	1.06
0.810	8	−0.052	33	0.79	1.09
0.667	8	−0.024	21	0.85	1.08
0.485	8	−0.011	15	0.91	1.08
0.810	6	−0.063	42	0.78	1.10
0.667	6	−0.033	24	0.84	1.09
0.485	6	−0.021	19	0.89	1.07

and

Table 5. Base parameter of the hybrid reactor for the following set parameters: VCR^central—0.485, fuel—(Th-U-233)O₂, fuel density in central zone—10 g/cm³, and coolant—Pb.

Peripheral VCR	Peripheral Fuel (Th-U-233) O2 Density [g/cm3]	${\mathit{\alpha }}_{\mathit{V}}^{100\%\mathit{v}\mathit{o}\mathit{i}\mathit{d}}$ Error < 0.004	Peripheral Enrichment	ANFE for Normal Work [MeV]	ANFE for 100% Void Core [MeV]
Central fuel enrichment 1at. % of U-233
0.810	10	−0.208	26	0.458	0.726
0.667	10	−0.152	19	0.481	0.678
0.485	10	−0.109	14	0.495	0.629
0.810	8	−0.225	30	0.455	0.746
0.667	8	−0.174	20	0.471	0.694
0.485	8	−0.126	16	0.502	0.652
0.810	6	−0.246	39	0.463	0.777
0.667	6	−0.194	28	0.487	0.732
0.485	6	−0.149	19	0.501	0.681
Central fuel enrichment 5 at. % of U-233
0.810	10	−0.149	24	0.425	0.627
0.667	10	−0.107	17	0.448	0.600
0.485	10	−0.070	14	0.475	0.587
0.810	8	−0.162	29	0.426	0.637
0.667	8	−0.114	17	0.448	0.616
0.485	8	−0.088	15	0.465	0.593
0.810	6	−0.179	37	0.427	0.650
0.667	6	−0.141	24	0.445	0.630
0.485	6	−0.107	18	0.468	0.608

, Figure 15).

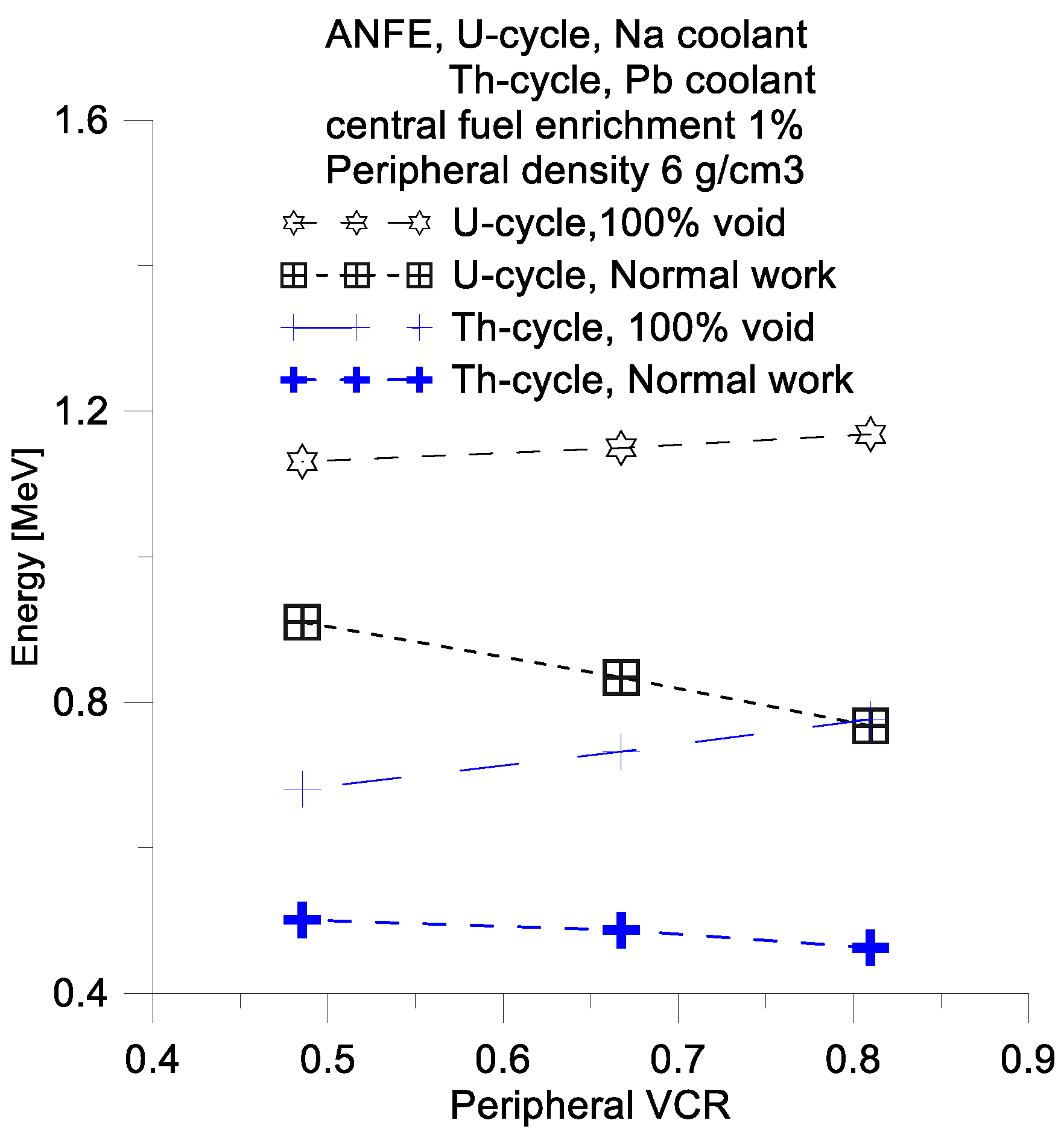
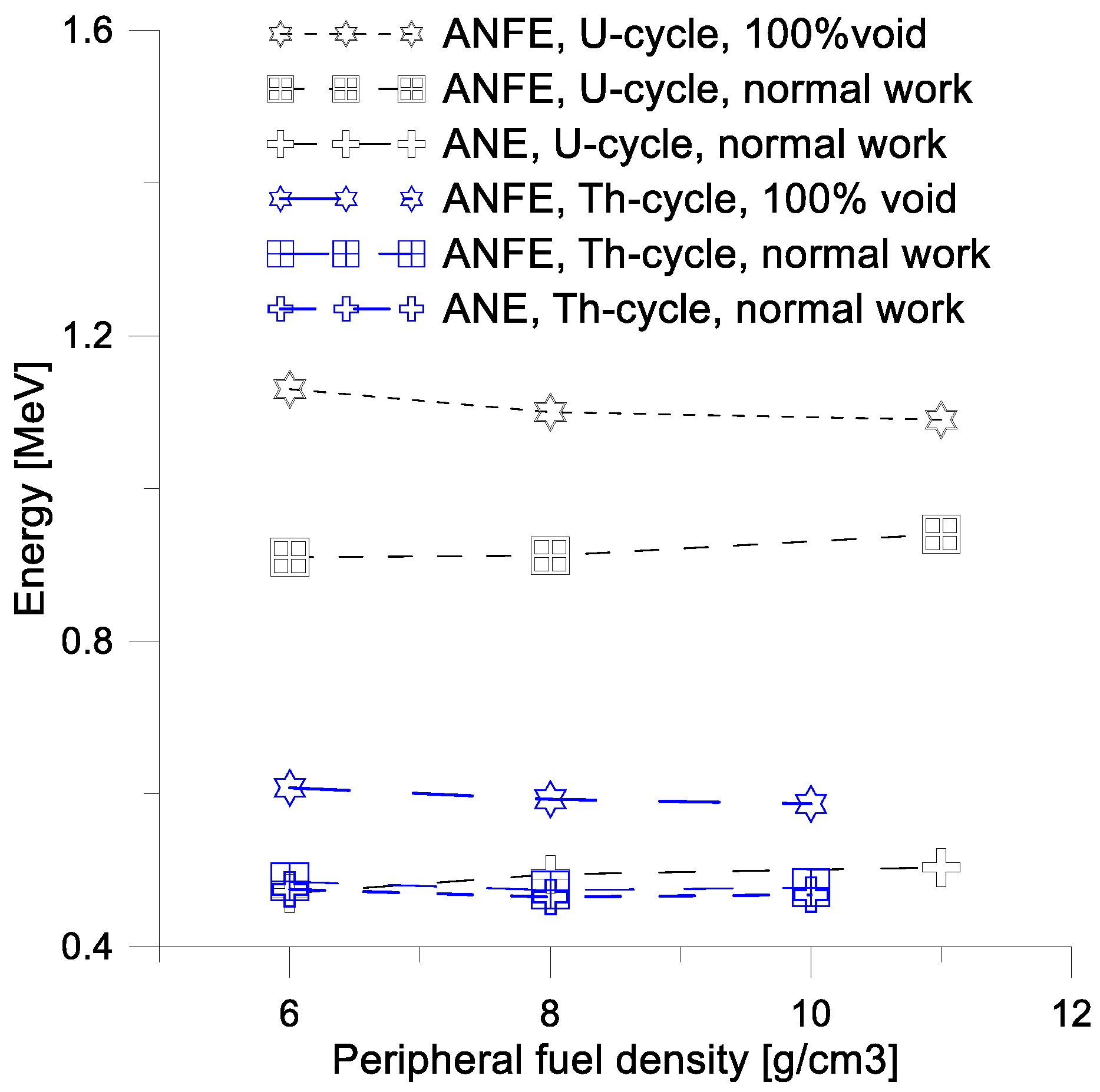
The ANE and ANFE have a weak dependence on the peripheral fuel density (Figure 16). However, ${\alpha }_V$ is an increasing function of peripheral fuel density. For these reasons, it is advantageous to reduce the peripheral fuel density.

The type of coolant and fuel has a significant impact on ${\alpha }_V$ value, i.e., a higher value for the cross section of the neutron absorption of the coolant increases of ${\alpha }_V$ value. An important factor contributing to an increase in ${\alpha }_V$ is the increase in the number of fission reactions induced by fast neutrons (

Table 6. Intermediate and fast fission fraction in Na-cooled U-cycle and Pb-cooled Th-cycle reactors; peripheral VCR = 0.485.

Peripheral Fuel Density [g/cm3]	Intermediate/Fast Fission Fraction, U-Cycle, Normal Work, Central Enrichment 1% [625 eV–0.1 MeV]/ [>0.1 MeV]	Intermediate/Fast Fission Fraction, U-Cycle, 100% Void Central Enrichment 1% [625 eV–0.1 MeV]/ [>0.1 MeV]	Intermediate/Fast Fission Fraction, Th-Cycle, Normal Work, Central Enrichment 5% [625 eV–0.1 MeV]/ [>0.1 MeV]	Intermediate/Fast Fission Fraction, Th-Cycle, 100% Void, Central Enrichment 5% [625 eV–0.1 MeV]/ [>0.1 MeV]
6	0.40/0.60	0.30/0.70	0.44/0.56	0.41/0.59
8	0.40/0.60	0.31/0.69	0.45/0.55	0.42/0.58
10 or 11	0.41/0.59	0.33/0.67	0.45/0.55	0.42/0.58

) and ANFE for a voided reactor core (Figure 19 and Figure 20). These magnitudes have significantly greater values for the U-cycle compared to the Th-cycle reactor. The reason for this is that the fission cross section (FCS) for U-233 is higher than that of Pu-239 in the intermediate neutron energy range (Table 6). Additionally, the FCS for Th-232 is lower than that of U-238 for neutron energies higher than 0.5 MeV. The number of directly fission events with U-238 is significantly greater than that with Th-232.

The geometry of the hybrid reactor presented in this section is not yet optimized. Furthermore, reducing of the value of ${\alpha }_V$ can be achieved by increasing the outer surface area of the peripheral part at the top and bottom of the core, for example.

Herein, is ${\alpha }_V^{100\%void}$, is calculated. However, neutron flux density, power density and the evaporation rate of the coolant in the peripheral region are significantly greater than in the central region. For these reasons, the rate of decrease in the coolant density in the peripheral region will be greater than in the central region. For this reason, the ${\alpha }_V\left(\mathrm{v}\mathrm{o}\mathrm{i}\mathrm{d}\right)$ functions are calculated for both total void and peripheral void. The α_v for the peripheral void is calculated for two cases: Partial Void-A and Partial Void-B.

Partial Void–A refers to the case in which the average coolant density is changed only in the peripheral assemblies. In this scenario, the thin layer of coolant between the fuel assemblies and core barrel has a constant normal density. This situation does not reflect a real case.

Partial Void–B, on the other hand, describes the case in which the average coolant density is modified in the peripheral region of the reactor, specifically in the peripheral assemblies and the thin layer of coolant between the fuel assemblies and the core barrel. This represents a more realistic scenario.

The difference between Partial Void-A and Partial Void-B predicts the significant impact of the peripheral thin layer of coolant on the α_v.

The results presented in this section indicate that the value of ${\alpha }_V$ is negative for all cases of the hybrid reactor (Table 4 and Table 5 and Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21).

The concept of a hybrid reactor allows for the construction of a large and efficient reactor with a negative ${\alpha }_V$ value. A low value for central fuel enrichment facilitates the use of natural uranium or thorium, as the criticality of the hybrid reactor is determined by the peripheral part of reactor. In other words the central region should contain blanket/fertile assemblies for the conversion of fuel. The fuel conversion ratio (CR) is a decreasing function of fuel enrichment. For this reason, the CR for peripheral region should be less than 1 [14,15].

Influence of the Central Region Parameters on α_v

In this section, we examine the influence of the central region parameters, i.e., the average fuel density and the central VCR parameter on α_v, while the central fuel enrichment is maintained at a stable level of 1%.

The peripheral fuel density is set to 11 g/cm³, and the peripheral VCR values are 0.485, 0.667 and 0.810.

We compare the ${\alpha }_V^{100\%void}\left(VCR\right)$ functions for central fuel densities of 11 g/cm³ and 8 g/cm³, as well as central VCR values of 0.239 and 0.485 (Figure 22).

The fuel density of the central core region does not influence α_v (Figure 22). However, the central VCR has a weak influence on α_v. Strictly speaking, a decrease in the central VCR parameter of about 50% induces an increase in the relative value of α_v of approximately 4–9%. A decrease in the value of the central VCR parameter decreases the absorption component of α_v, which should lead to a decrease in α_v. A slight increase in α_v suggests that the absolute value of the leakage component of α_v should simultaneously decrease. In other words, from the point of view of α_v, there is no need to employ very low values of central VCR in the a hybrid reactor; however, one could employ them to increase the average neutron energy.

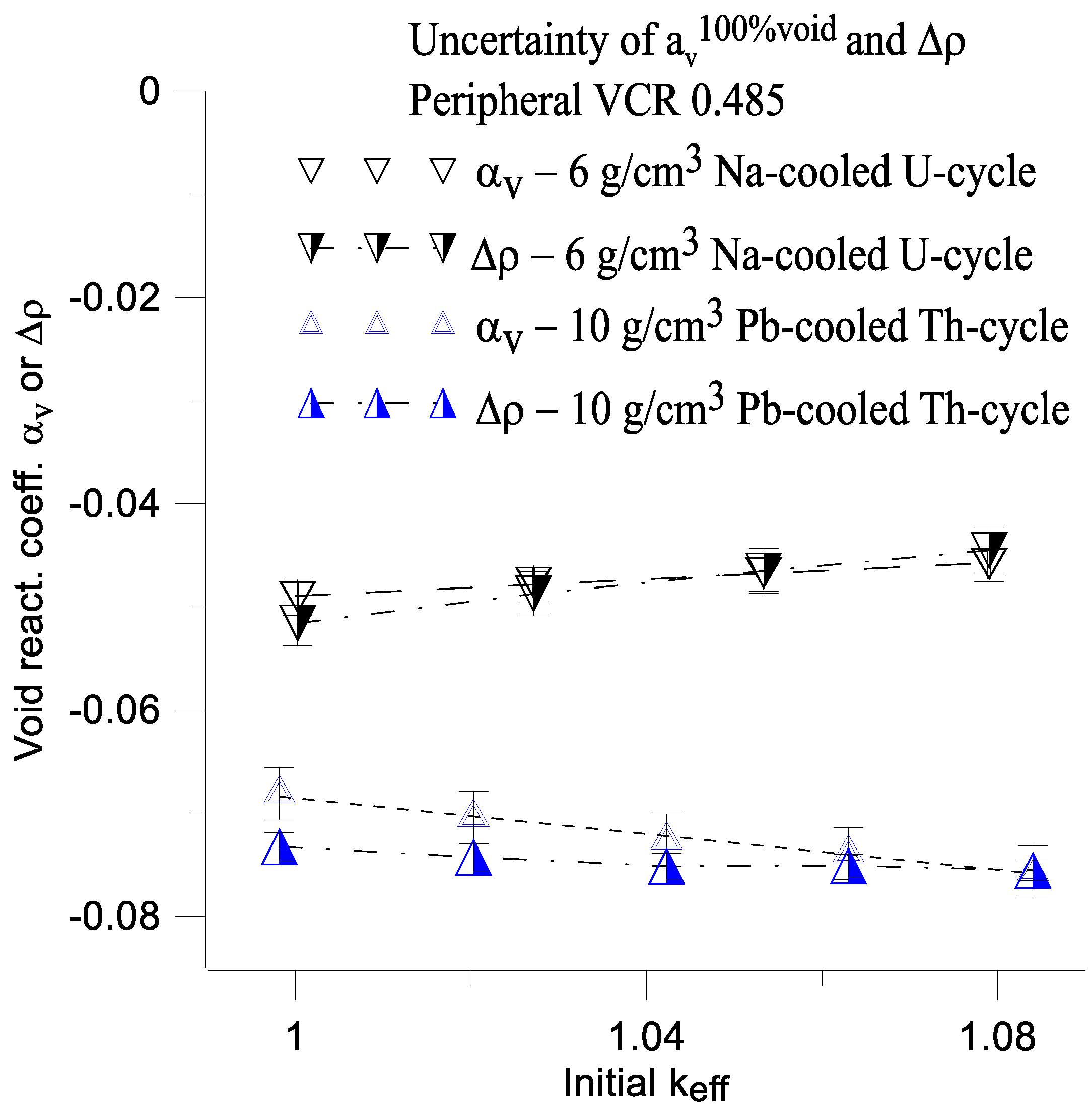
7. Calculation Uncertainties

This section presents the values of the uncertainties for both the α_v (Equation (4)) and the difference in reactivity defined by Δρ (Equation (5))_.

Here, Δρ and α_v are functions of the initial value of k_eff (Figure 23). The calculated uncertainties of α_v and Δρ include both the systematic error due to the uncertainty of the initial value of k_eff and standard deviation resulting from the statistical errors of the initial values of k_eff (Figure 23).

A value of the systematic error (MSE) in the range Δk_eff = 0.02 is calculated using the corresponding fitting function of α_V(k_eff) and Δρ(k_eff) for Na-coolled U-cycle and Pb-cooled Th-cycle reactors respectively.

The standard deviation of reactivity σ(ρ) was determined using the standard deviation σ_keff of k_eff and the following formula:

$$\mathsf{\sigma }(\mathsf{\rho })={\displaystyle \frac{\partial \mathsf{\rho }}{\partial {\mathrm{k}}_{\mathrm{e}\mathrm{f}\mathrm{f}}}}{\mathsf{\sigma }}_{\mathrm{k}\mathrm{e}\mathrm{f}\mathrm{f}}={\mathsf{\sigma }}_{\mathrm{k}\mathrm{e}\mathrm{f}\mathrm{f}}/{\mathrm{k}}_{\mathrm{e}\mathrm{f}\mathrm{f}}^2.$$

(12)

The standard deviation of Δρ is calculated using the following formula:

$$\sigma \left(∆\rho \right)=\sqrt{{\sigma (∆\rho )}_{norm}^2+\sigma ({∆\rho )}_{void}^2}.$$

(13)

The standard deviation of α_v is calculated from the following equation:

$$\sigma \left({\alpha }_v\right)=\sqrt{({{\displaystyle \frac{\partial {\alpha }_v}{\partial k_{norm}}}\sigma \left(k_{norm}\right))}^2+({{\displaystyle \frac{\partial {\alpha }_v}{\partial k_{void}}}\sigma \left(k_{void}\right))}^2}.$$

(14)

The total uncertainties of α_v and Δρ for 100% void are equal to the sum of the standard deviation and MSE. These are denoted as Δ^Tot(α_v) and Δ^Tot(Δρ), respectively (

Table 7. Uncertainties of α_v and Δρ for U-cycle and Th-cycle reactors.

	σ (αv)	MSE (αv)	ΔTot (αv)	σ (Δρ)	MSE (Δρ)	ΔTot (Δρ)
Na-cooled U-cycle	0.0008	0.001	0.0018	0.0002	0.0018	0.002
Pb-cooled Th-cycle	0.0008	0.0017	0.0025	0.0008	0.001	0.0018

).

The total uncertainties are significantly less than the absolute value of α_v and Δρ (Figure 14, Figure 15, Figure 16 and Figure 21).

The total uncertainty ${\Delta }_{pert}^{Tot}$ of the α_v(void) function (Figure 21) is determined by perturbation effective multiplicity factor $k_{eff}^{pert}$ and its standard deviation ${\sigma (k}_{eff}^{pert})$ and MSE. The perturbation error is calculated for 10% of the average coolant density using PERT command of MCP6.2 code. The maximal value of ${∆}_{pert}^{Tot}$ achieves is 0.004 for void = 20%.

8. FBR-IME Reactor Versus Hybrid Model

The main aim of this section is to compare the difference in reactivity Δρ of FBR-IME [9,10] and hybrid reactors with low average void values. The hybrid reactor is based on a VCR parameter of 0.485, a fuel density of 11 g/cm³, and a central fuel enrichment of 1%. Here, a hybrid-inverse reactor is presented. The geometry of this model is identical to that of the hybrid reactor, but assemblies with fuel enrichment of 1% are placed in peripheral region, while assemblies with high fuel enrichment are positioned in the central part of the reactor (likely as in FBR_IME, (see

Table 8. Comparison of the base parameters of FBR-IME, hybrid and hybrid-inverse reactors.

Reactor/Void [%]	ρ	σ (ρ)	Δρ	σ (Δρ)	Central Enrich. [%]	Peripheral Enrich. [%]
FBR-IME [9,10]	0.12209	0.001464			25–42	0.71
FBR IME/0.98	0.12455	0.001303	0.00246	0.00196	25–42	0.71
FBR IME/2.93	0.12319	0.001307	0.00110	0.001963	25–42	0.71
FBR IME/5.87	0.12219	0.001156	0.00010	0.001866	25–42	0.71
Hybrid	0.068285 0.180811	0.000182 0.000087			1 1	14 19
Hybrid/0.98	0.06812 0.18070	0.000165 0.000094	−0.00016 −0.00011	0.000246 0.000128	1 1	14 19
Hybrid/2.93	0.06778 0.18037	0.0002 0.000087	−0.0005 −0.00044	0.000289 0.000123	1 1	14 19
Hybrid/5.87	0.06741 0.18018	0.0002 0.000094	−0.00088 −0.00063	0.000271 0.000128	1 1	14 19
Hybrid/10.0	0.06676	0.000183	−0.00153	0.000258	1	14
Hybrid/20.0	0.05412	0.000143	−0.00327	0.000232	1	14
Hybrid-Inverse	0.03978 0.09558	0.000175 0.000204			8 9	1 1
Hybrid-Inverse/0.98	0.04010 0.09565	0.000599 0.000204	0.000030 0.000074	0.000624 0.000289	8 9	1 1
Hybrid Inverse/2.93	0.04126 0.09614	0.000626 0.000204	0.000608 0.000589	0.000880 0.000289	8 9	1 1
Hybrid Inverse/5.87	0.04204 0.09690	0.000616 0.000204	0.00147 0.00132	0.000646 0.000289	8 9	1 1
Hybrid-Inverse/10.0	0.04439	0.000633	0.002254	0.000662	8	1
Hybrid-Inverse/20.0	0.03983	0.000584	0.004606	0.000616	8	1

).

The FBR-IME reactor consists of a simple core with 91 fuel assemblies and an outer/fertile blanket with 295 assemblies. The fuel assemblies are designed based on the geometry of the assembly used in the Japanese experimental reactor named JOYO. The core consists of 75 fuel assemblies, nine control rods and seven inner blanket assemblies. The fuel assemblies are arrangement in special way: two inner layers are blanket assemblies, followed by two layers of MOX at 25% enrichment, one layer of MOX at 33% and one layer of MOX at 42%. In other words, the enrichment of the fuel assemblies increases with the distance from the center of the core. This specific arrangement of enrichment is a method involving decresing of α_v. A similary method was used in the LFR-ELSY reactor [6].

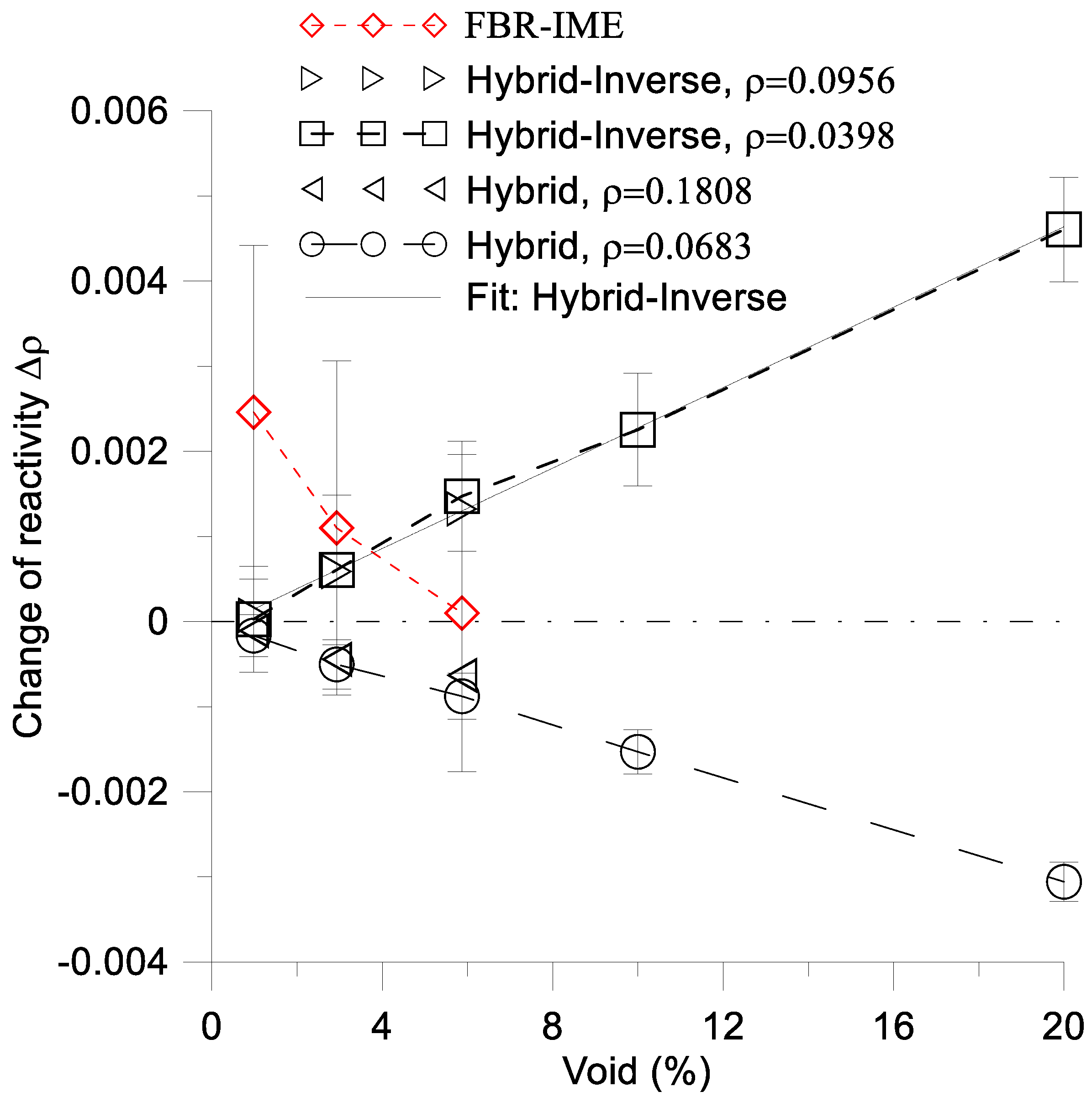
The Δρ for hybrid reactors are calculated for two different values of ρ. The difference between them is less than the corresponding standard deviation value (Figure 24 and Table 8).

The low void value indicates a low value of difference in reactivity Δρ and requires a high value of the corresponding statistics. For this reason, measurement of Δρ is a difficult task. The standard deviations of Δρ for voids of 2.93% and 5.87% for FBR_IME are significantly greater than the corresponding values of Δρ (Table 8, Figure 24) and exceed the corresponding values for the hybrid-inverse reactor. However, the results of Δρ are likely applicable to both FBR-IME and hybrid-inverse reactors. Despite the many differences between FBR-IME and hybrid-inverse reactors, the results are practically the same, i.e., with in the range of calculation errors. Strictly speaking, the differences between Δρ for voids of 2.93% and 5.87% are approximately to 0.0005 and 0.0014, respectively. These differences are both less than the corresponding standard deviation of FBR-IME. Meanwhile, the difference for a void of 0.98% is approximately 0.0024, which is less than the sum of the corresponding deviation of FBR-IME and hybrid-inverse reactors.

These reactors have a low value of fuel enrichment in the peripheral region (blanket/fertile) (Table 8, [9,10]).

Here, Δρ (void) is a decreasing function of the void for both the FBR-IME and hybrid reactors within the range of (0.98%, 5.87%) void. However, the FBR-IME exhibits a positive value of of Δρ, whereas the hybrid reactor shows a negative one. A special arrangement of high enrichment MOX fuel assemblies in the central part of the FBR-IME is insufficient to achieve a negative value of Δρ.

The hybrid model results in a negative value of Δρ in all cases. In this scenario the average coolant density is modified in the total peripheral region of reactor, which includes the peripheral assemblies and thin layer of coolant between the assemblies and the reactor barrel.

It is important to note, that blanket/fertile assemblies placed in central part of the reactor significantly decrease Δρ (Figure 24, Table 8), while those placed in the peripheral part acts as reflectors and increase Δρ (see Section 4).

This section is important, because it compares two methods of reducing α_v based on the distribution of high enrichment fuel assemblies in the reactor cores of significantly different reactors. The FBR-IME method involves increasing the enrichment of fuel assemblies with a distance from the center of the active zone, located in the central part reactor core. In contrast, the hybrid method uses a constant value of enrichment of the fuel assemblies within the active zone, positioned in the peripheral part of the reactor core. This section shows that the hybrid method is significantly more effective. Of course, these methods can be combined, and the results of such combination would be even more interesting.

The $\sigma \left(∆\rho \right)$ is calulated using Equation (13).

The standard deviation σ(α_v) of ${\alpha }_v={\displaystyle \frac{∆\rho }{∆v}}$ should may be determined from the following formula:

$$\sigma \left({\alpha }_v\right)={\displaystyle \frac{\partial {\alpha }_v}{\partial ∆\mathsf{\rho }}}\sigma \left(∆\mathsf{\rho }\right)+{\displaystyle \frac{\partial {\alpha }_v}{\partial ∆v}}\sigma \left(∆v\right)$$

(15)

If we assume that $\sigma \left(∆v\right)$ = 0 then $\sigma \left({\alpha }_v\right)=\sigma \left(∆\rho \right)/∆v$.

Using the above equations one can easy show that $\sigma \left({\alpha }_v\right)/{\alpha }_v=\sigma \left(∆\rho \right)/∆\rho$. This means that the relative values of $\sigma \left({\alpha }_v\right)$ of α_v and $\sigma \left(∆\rho \right)$ of for $∆\rho$ are the same. In a real reactor, the uncertainty of Δv can be significantly greater than 0. This implies, that the total relative uncertainty of α_V can be considerably greater than the total uncertainty of Δρ. For this reasons we compare Δρ in this section.

9. Discussion

The choice of the hybrid reactor geometry was made due to its large core without both a reflector and an upper sodium plenum (compare Ref. [24]). The hybrid reactor has all the features of fast reactor with negative α_v (see Section 6 and Section 8). Its core has a relatively simple geometry, and the special arrangement of the fuel assemblies are optimized for leakage neutron flux during void conditions.

The purpose of this section is to present the main differences between a fast reactor core and a PWR core, as well as to explain their influence on the value of α_v.

On top of that, the active fuel zone in SFRs and LFRs should only be about 1 m, due to significant concerns about the core void reactivity, which is much shorter than in conventional PWRs.

The high value of the active zone is intentional and is chosen to show that a negative value can still be achieved, even with an elevated core height.

Reducing the height of the active fuel zone to about 1 m is advantageous from the perspective of α_v and can be applied in a hybrid concept, as it increases the neutron leakage fraction and decreases α_v.

In the case of a sodium-cooled fast reactor (SFR), the fuel lattice should be very tight to minimize the void reactivity; all SFR designs are based on a hexagonal lattice.

The neutron flux spectrum and average value of neutron energy do not depend on the type of lattice. Instead, they are influenced mainly by the VCR or VCFR parameters. A hybrid reactor is designed based on the values of these parameters, i.e., central region VCR = 0.485 or 0.239 (Figure 22) and an average value of neutron energy of approximately 0.5 MeV. A square fuel lattice is used in a LFR-ELSY reactor in [6]. In other words, a hexagonal lattice can be used in a hybrid reactor without changing α_v. The minimal value of the VCR parameters for FBR-IME and hybrid reactor are 0.374 and 0.239, respectively.

In addition, there should be thick steel reflectors on both the radial and bottom sides of the core.

Excessive core height affects α_v in a manner similar to that of a thick bottom and top reflector. This means that the thick bottom reflector is included in the calculation results for the hybrid reactor. However, the thick radial side reflector presents a challenge that needs to be addressed; as such, this reflector should be removed. Additionally, the blanket/fertile should be positioned at the center of the core.

As such, there are significant differences in the core configurations between fast reactors and PWRs.

While there are many technical distinctions between the cores of fast reactors and PWRs, the neutron flux spectrum and neutron physics in the hybrid reactor in this study are similar to those in fast reactors. Many technical concepts from fast reactors, such as bending fuel assembly or upper gas plenum, can be applied in hybrid reactors. In other words, future fast reactors will integrate the hybrid concept based on the technology of present-day fast reactors.

10. Conclusions

The hybrid reactor concept offers a very effective passive and promising method for achieving a negative α_v value under a wide range of basic reactor parameters (Section 6).

The fuel density and VCR parameter are important reactor parameters in terms of reducing the value of α_v (Section 6); decreasing the average fuel density and increasing the VCR parameter in peripheral fuel assemblies induces a decrease of α_v. (Section 6, Figure 14 and Figure 15).

The ${VCR}_0^{100\%void}$ parameter is a very convenient parameter for determining the reduction value of α_v; reducing this parameter is crucial for decreasing the value of α_v. Additionally, this parameter can be used to compare different methods of reducing α_v. To achieve a negative α_v value, the reactor must have a VCR value exceeding ${VCR}_0^{100\%void}$ (Section 4). In other words, a positive value of the difference between VCR and ${VCR}_0^{100\%void}$ is the most important when seeking to achieve a negative value of α_v.

Particularly noteworthy is the low value of α_v for the Pb-cooled Th-cycle hybrid reactor in this study (Section 6).

Herein, only the calculated results for liquid Pb and Na cooled reactors are presented. However, the hybrid concept could be useful for obtaining a negative value of α_v in reactors cooled using other liquids.