Transmission of Mechanical Vibrations in an Electric Drive Unit with Scalar Control—Comparative Analysis with Evaluation Based on Experimental Studies
Abstract
1. Introduction
2. Materials and Methods
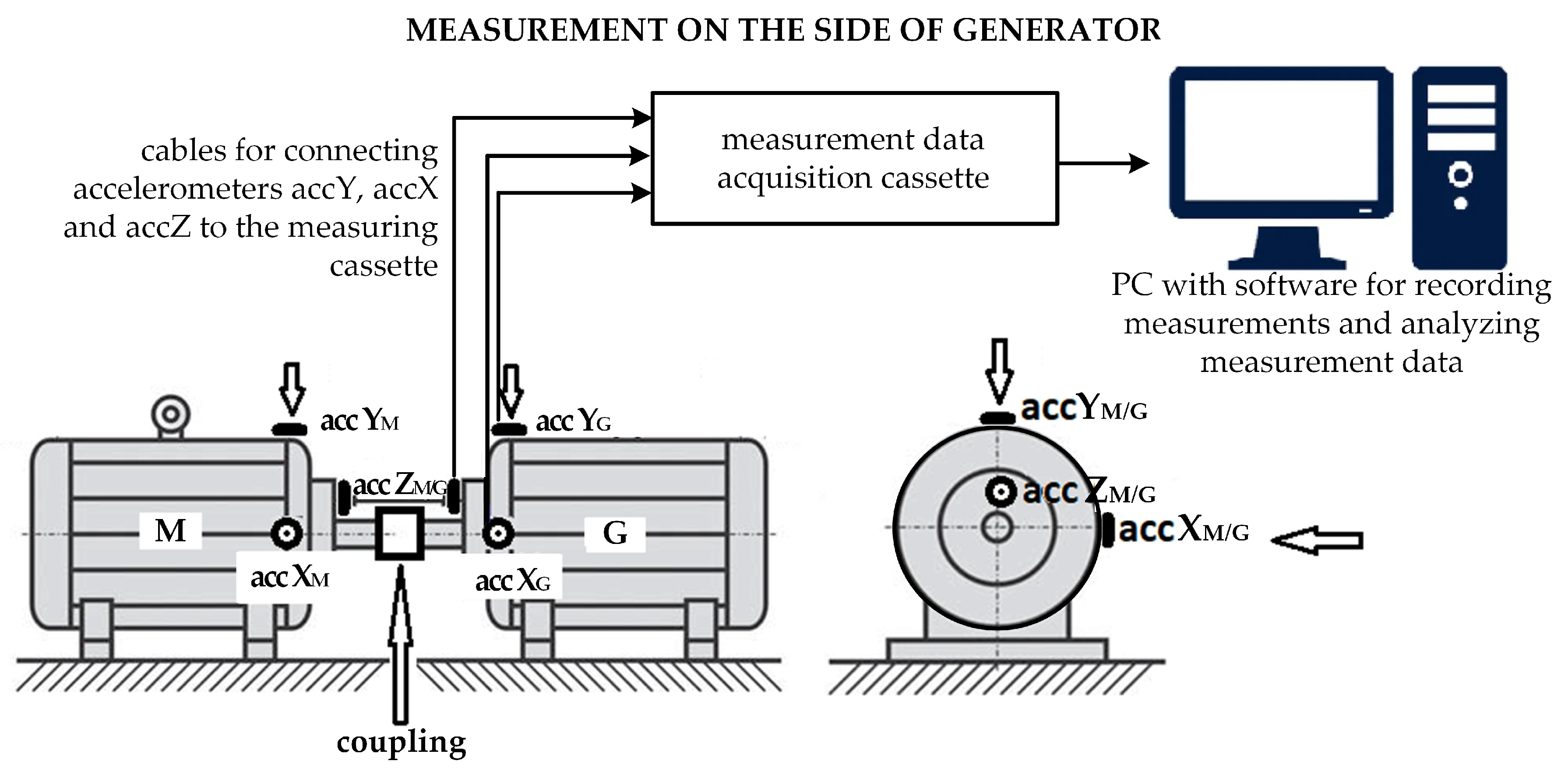
2.1. Description of Drive Unit Under Study
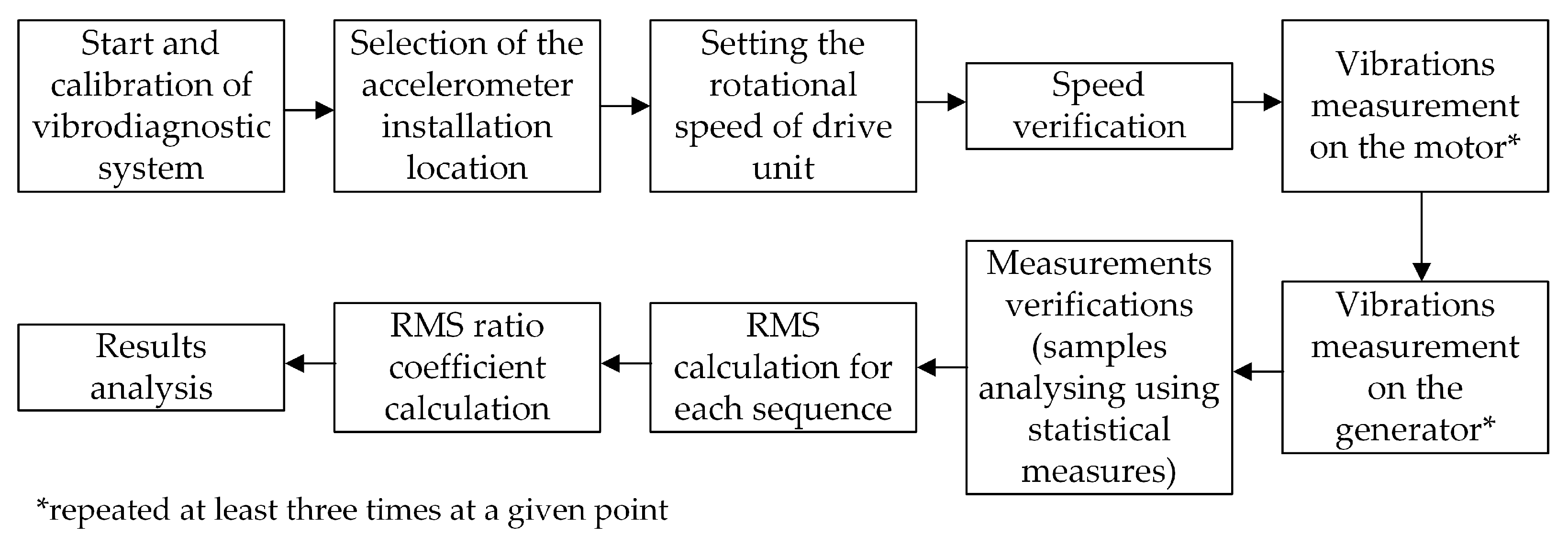
2.2. Description of the Vibrodiagnostic Testing System
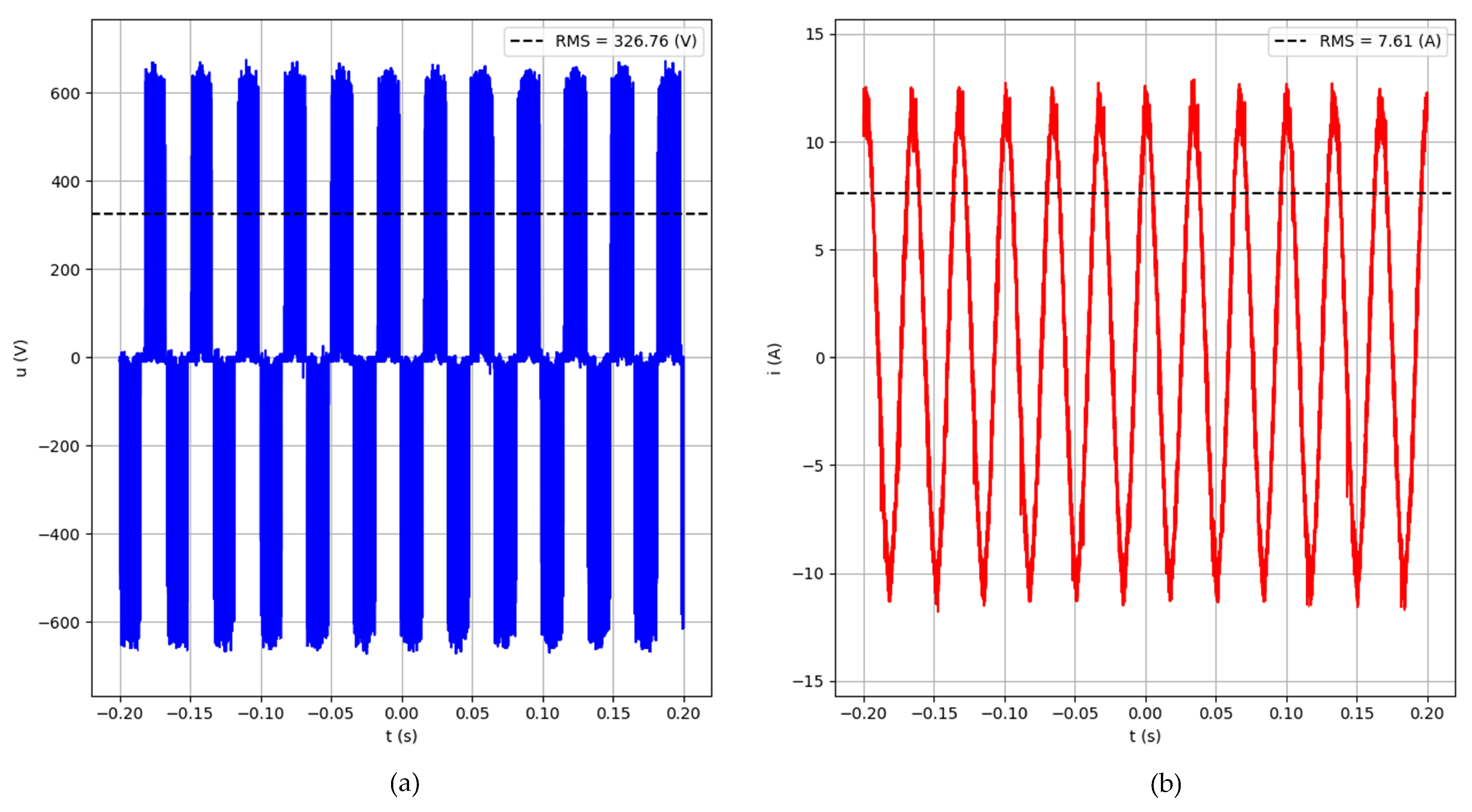
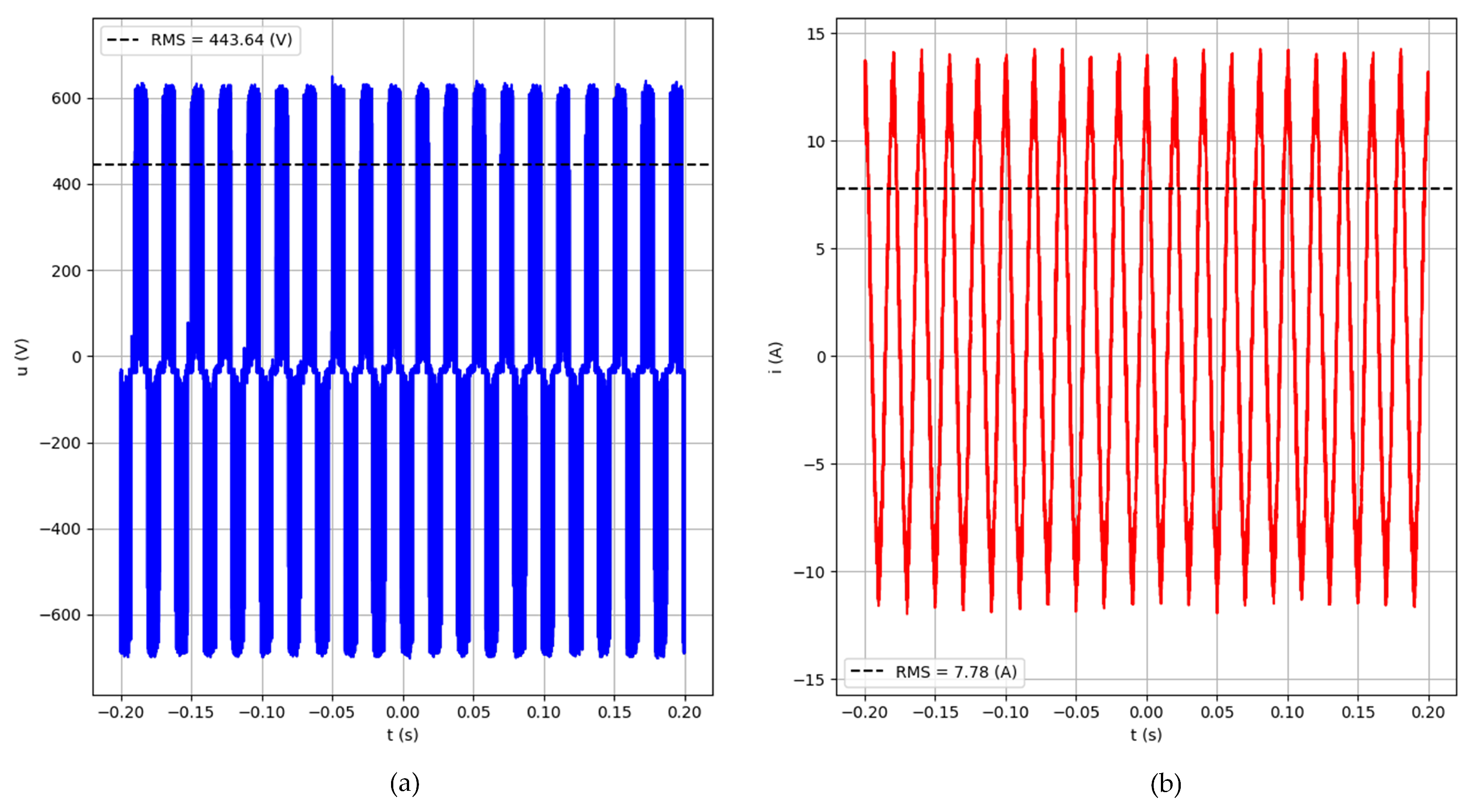
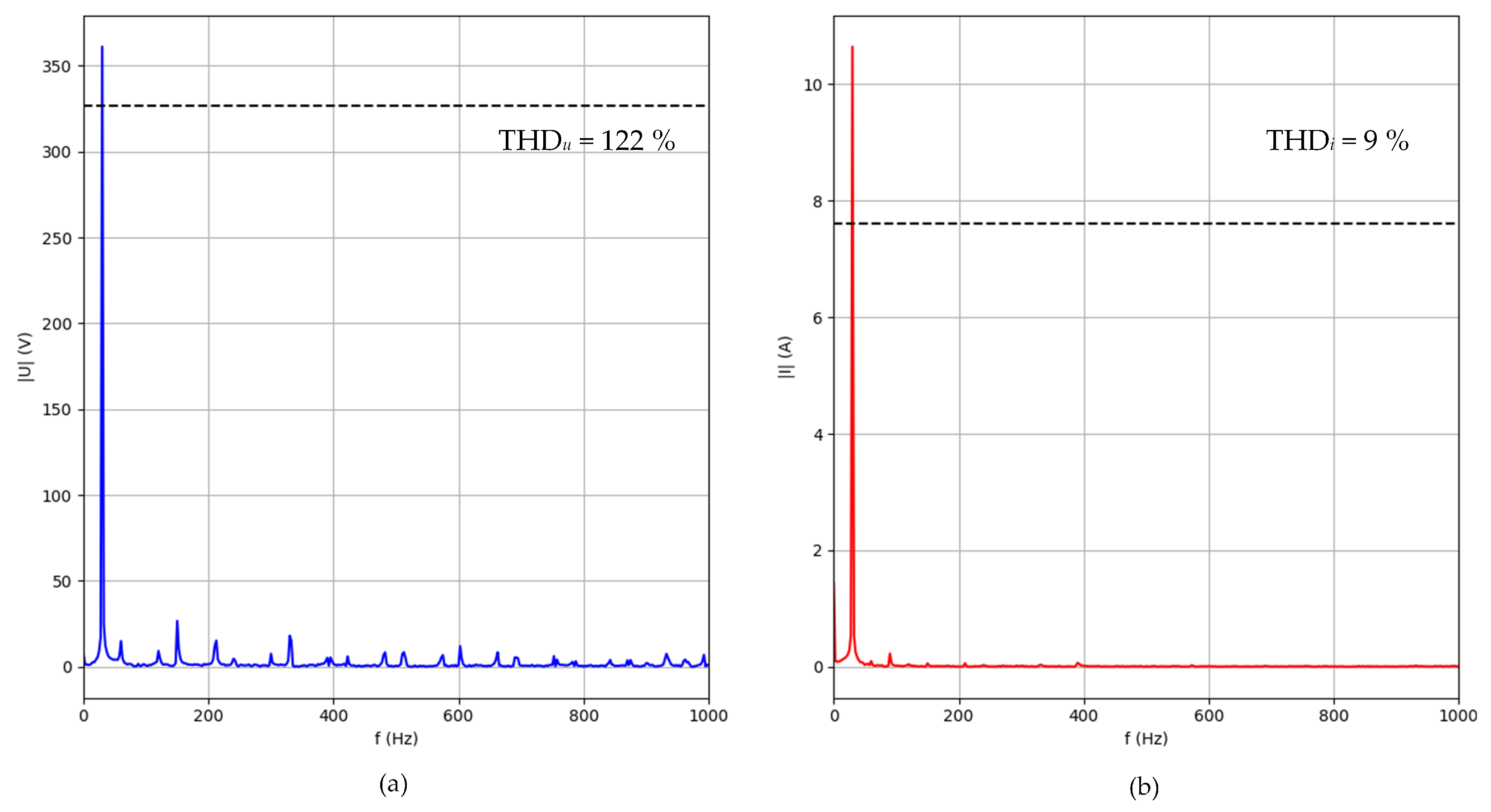
2.3. Methods of Analysis of Electrical and Vibrodiagnostic Measurements
- Results of electrical measurements;
- Results of vibration analysis measured in case of induction motor—induction generator drive unit set (measured with triaxial, and then three uniaxial accelerometers);
- Results of vibration analysis measured in case of induction motor—synchronous generator drive unit set (measured with triaxial, and then three uniaxial accelerometers).
| Measurement No. | Output Frequency of the Inverter [Hz] | Rotational Speed of the Unit [rpm] |
|---|---|---|
| 1 | 10 | 300 |
| 2 | 20 | 600 |
| 3 | 30 | 900 |
| 4 | 40 | 1200 |
| 5 | 50 | 1500 |
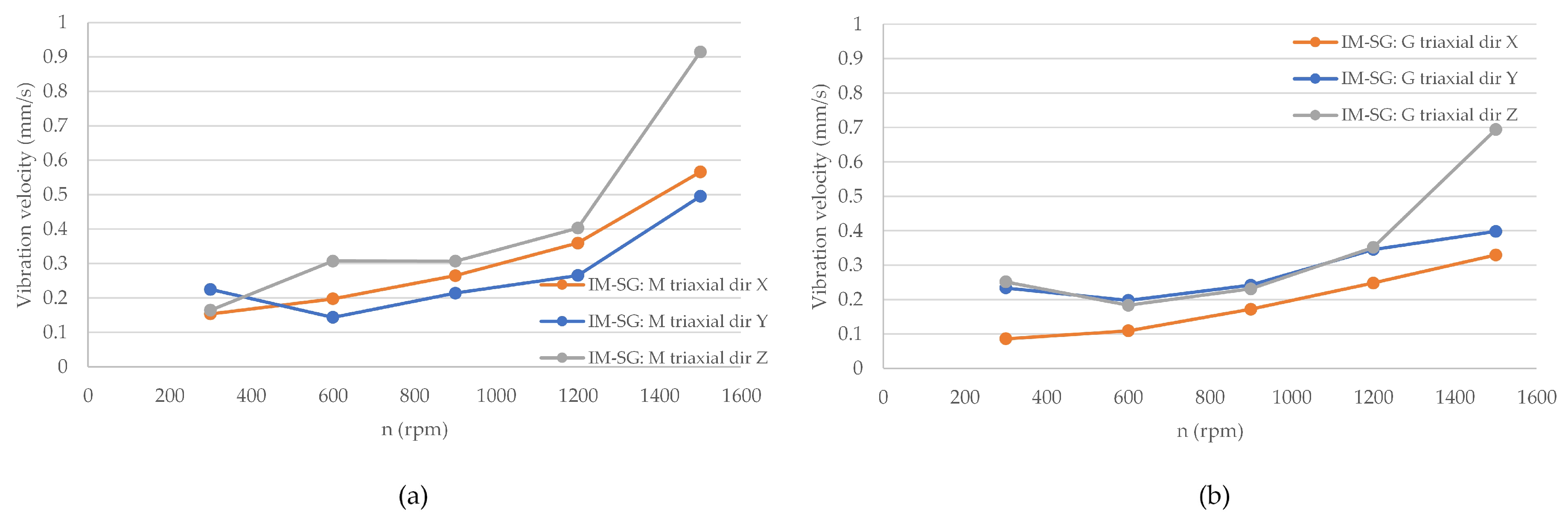
- Zone A: Vibrations generally correspond to newly commissioned machines;
- Zone B: Vibrations can be acceptable for the long-term, unrestricted operation of the machine;
- Zone C: Vibrations are permissible only for a limited time;
- Zone D: Vibrations are severe enough to cause damage to the machine.
- Zone A: Not greater than 0.71 mm/s;
- Zone B: Between 0.71 and 1.8 mm/s;
- Zone C: Between 1.8 and 4.5 mm/s;
- Zone D: Above 4.5 mm/s.
3. Experimental Results
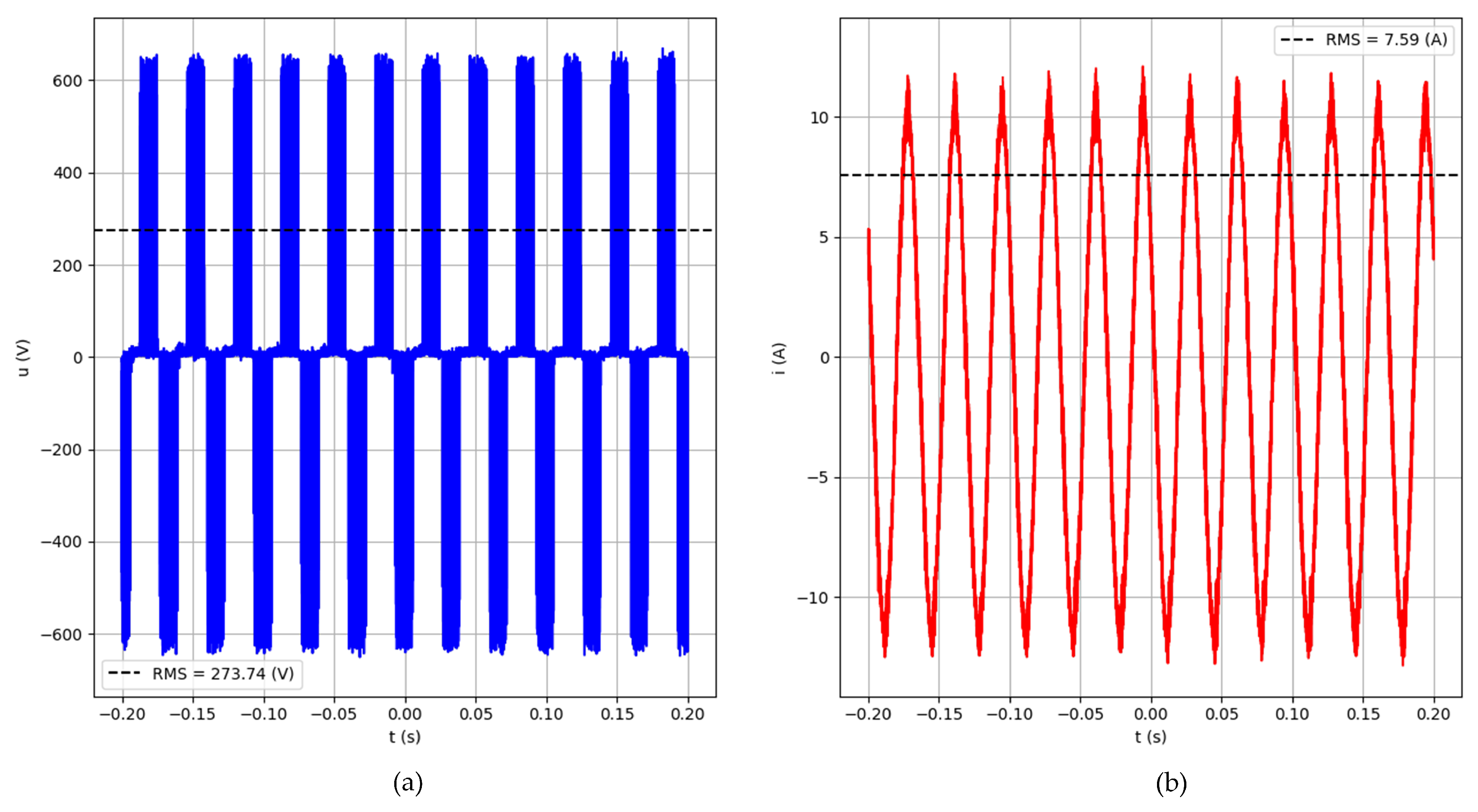
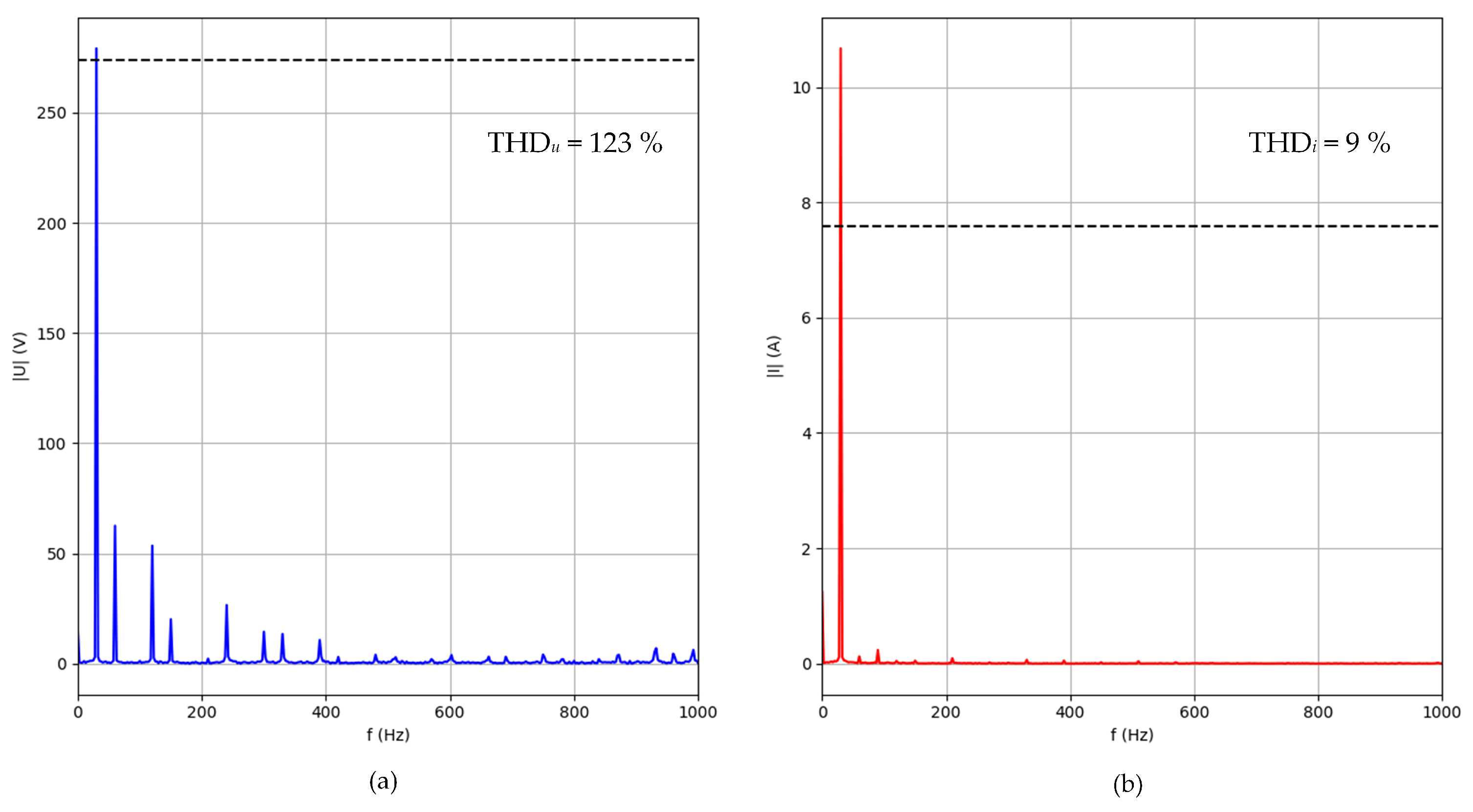
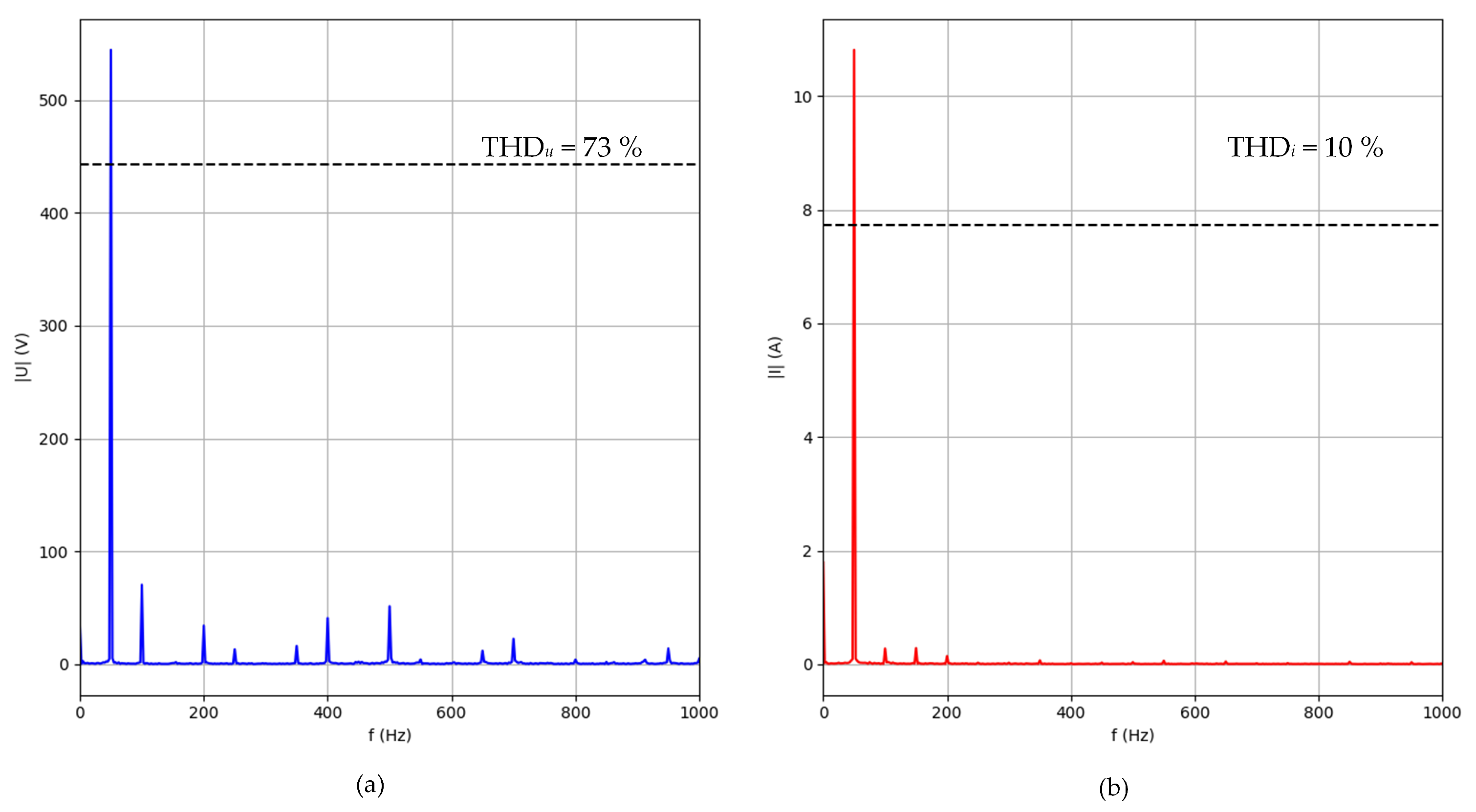
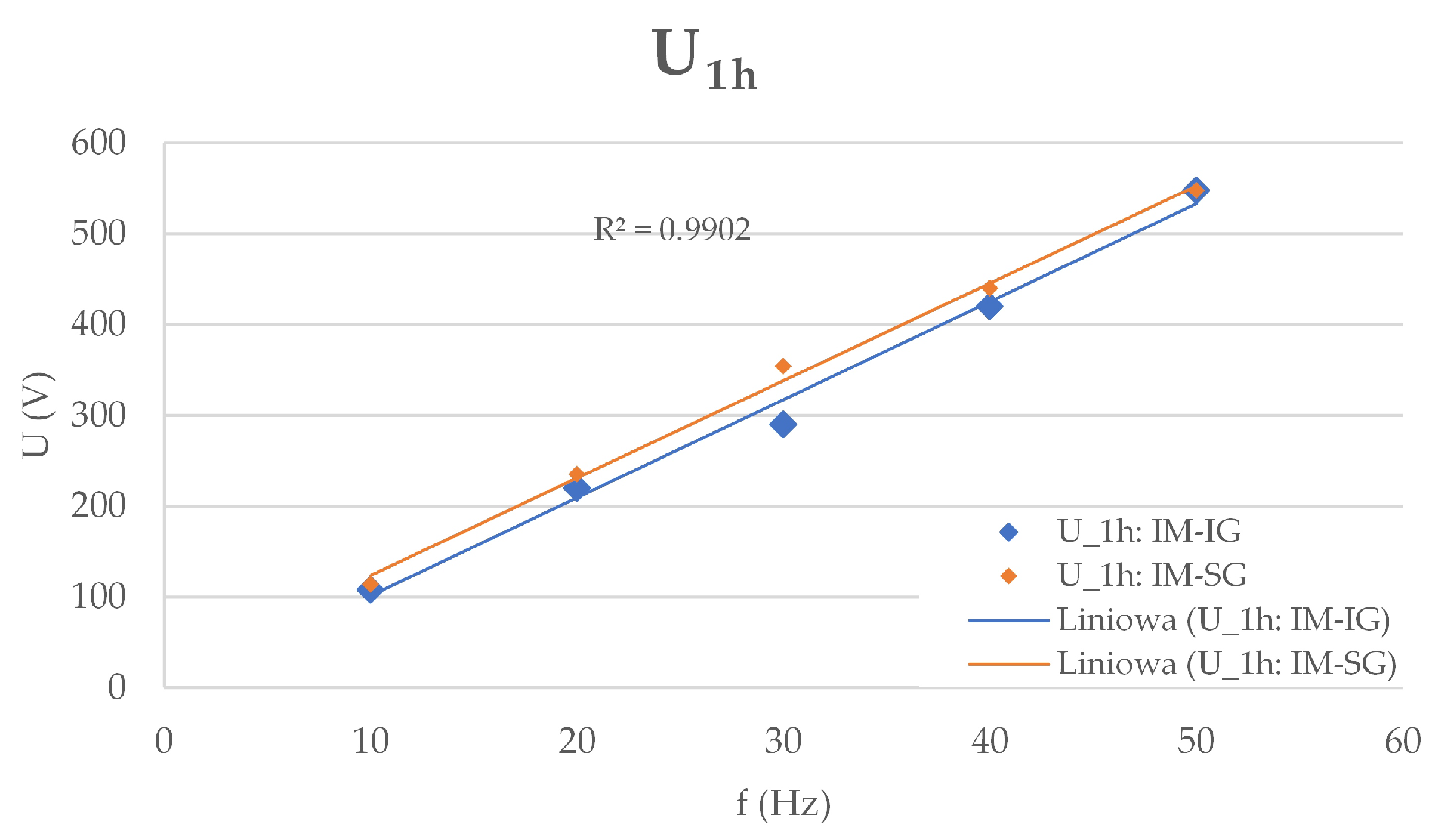
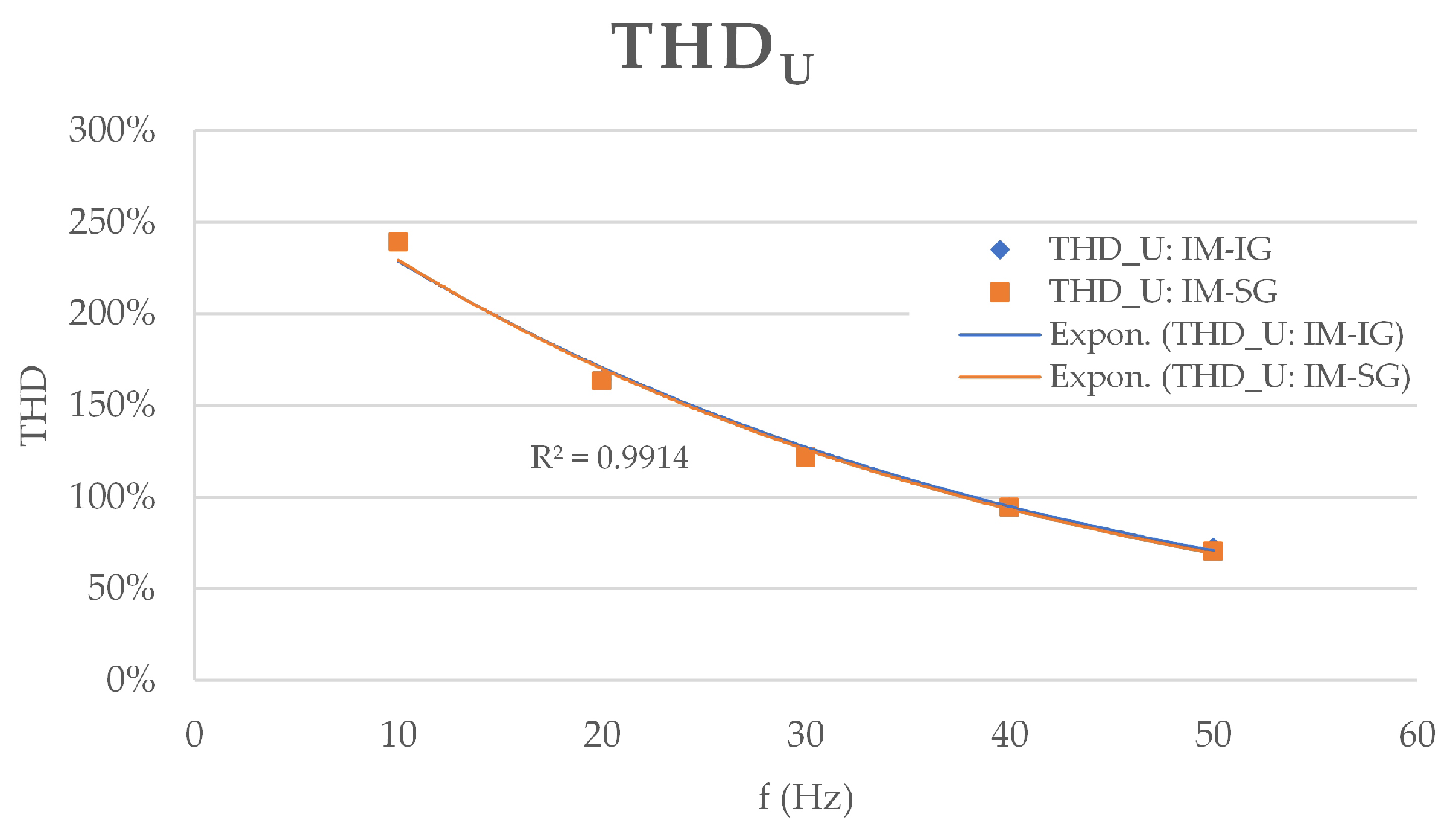
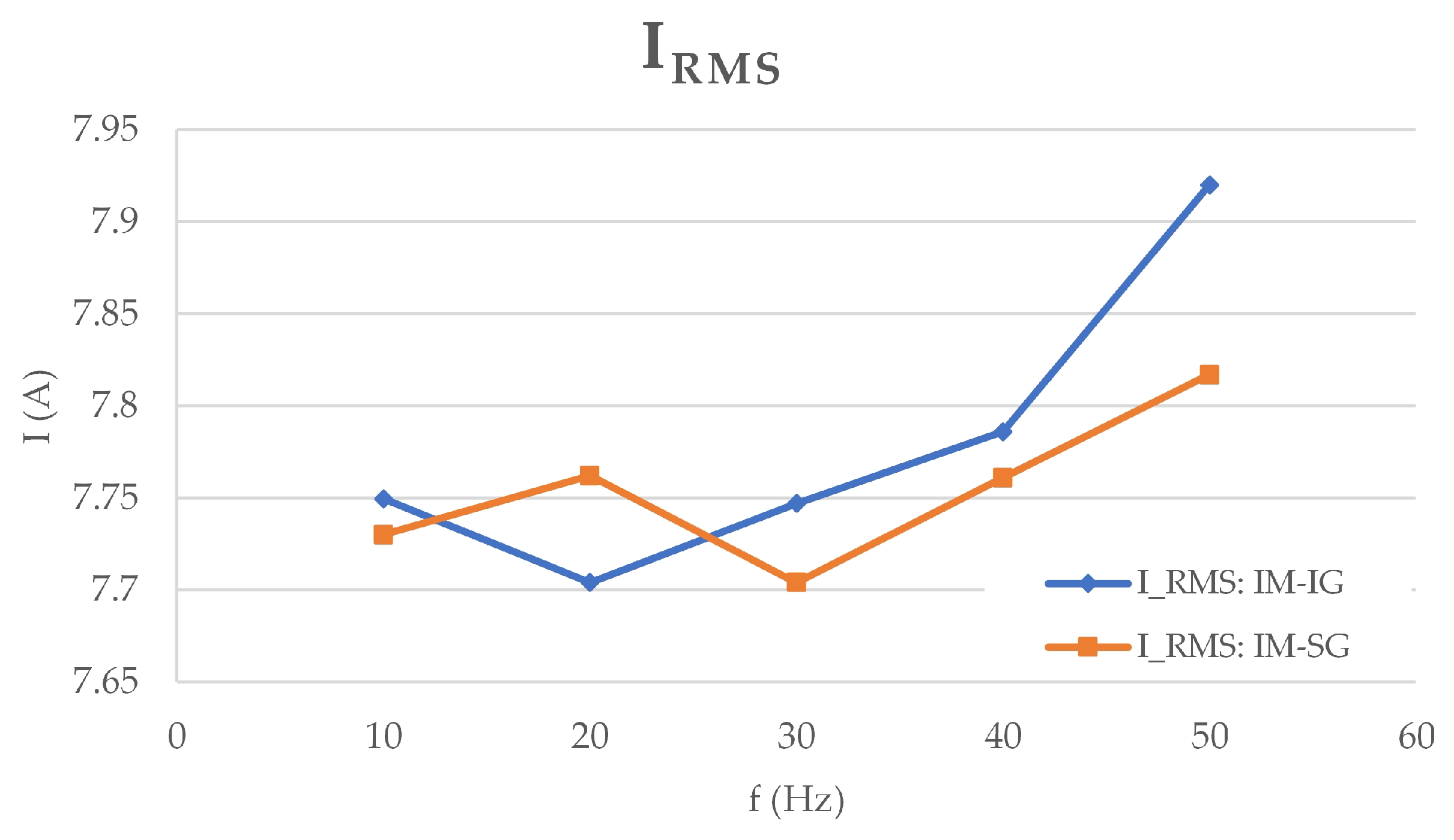
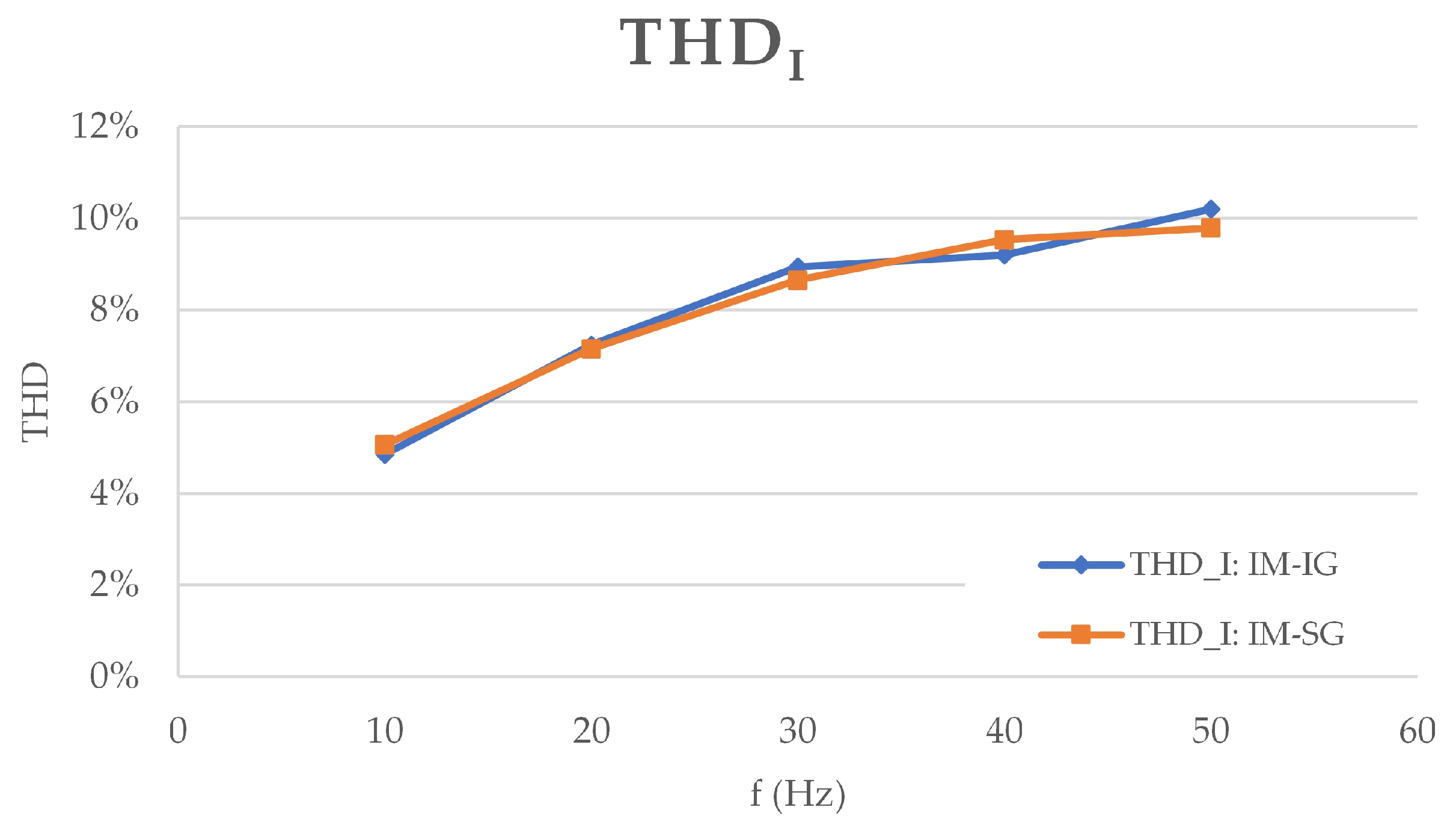
3.1. Analysis of Data Obtained from Electrical Measurements
3.2. Analysis of Data Obtained from Vibration Measurements
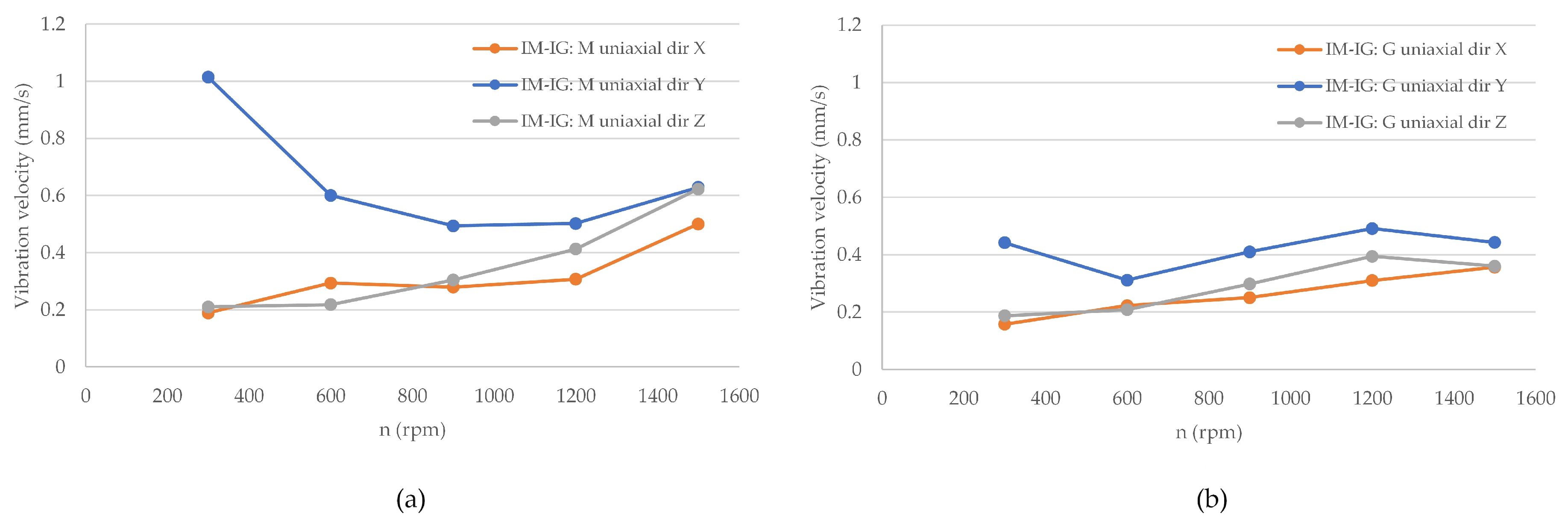
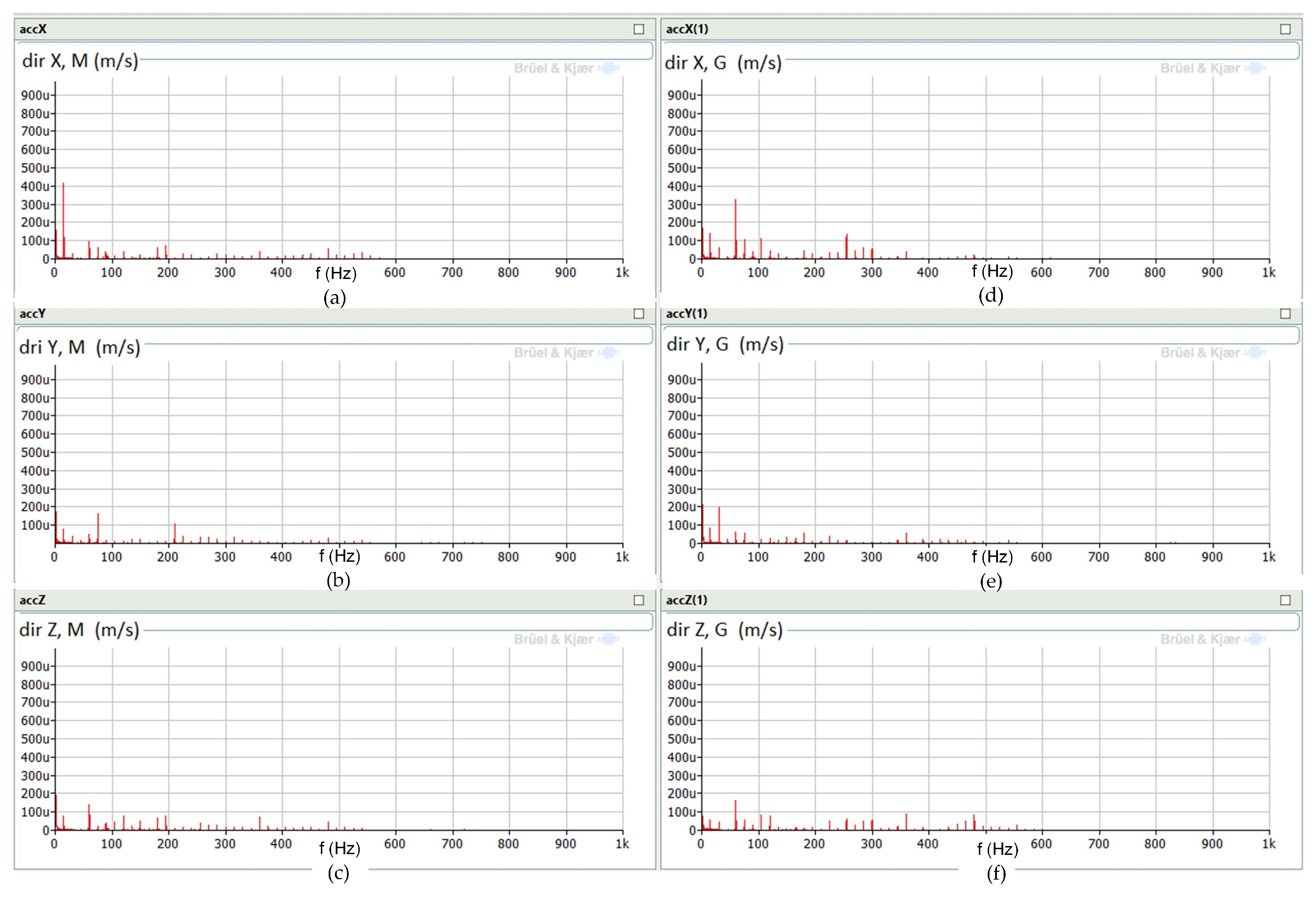
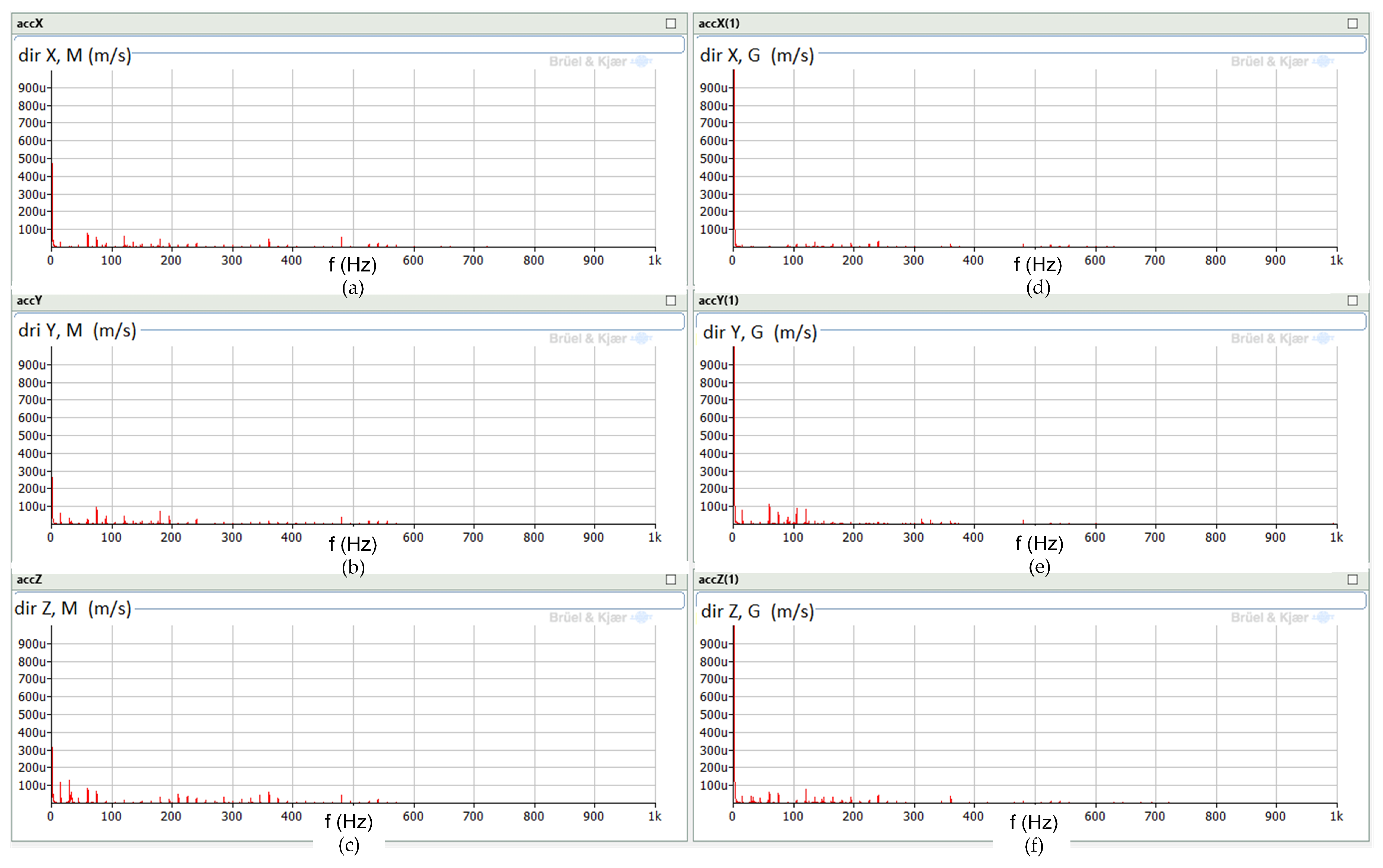
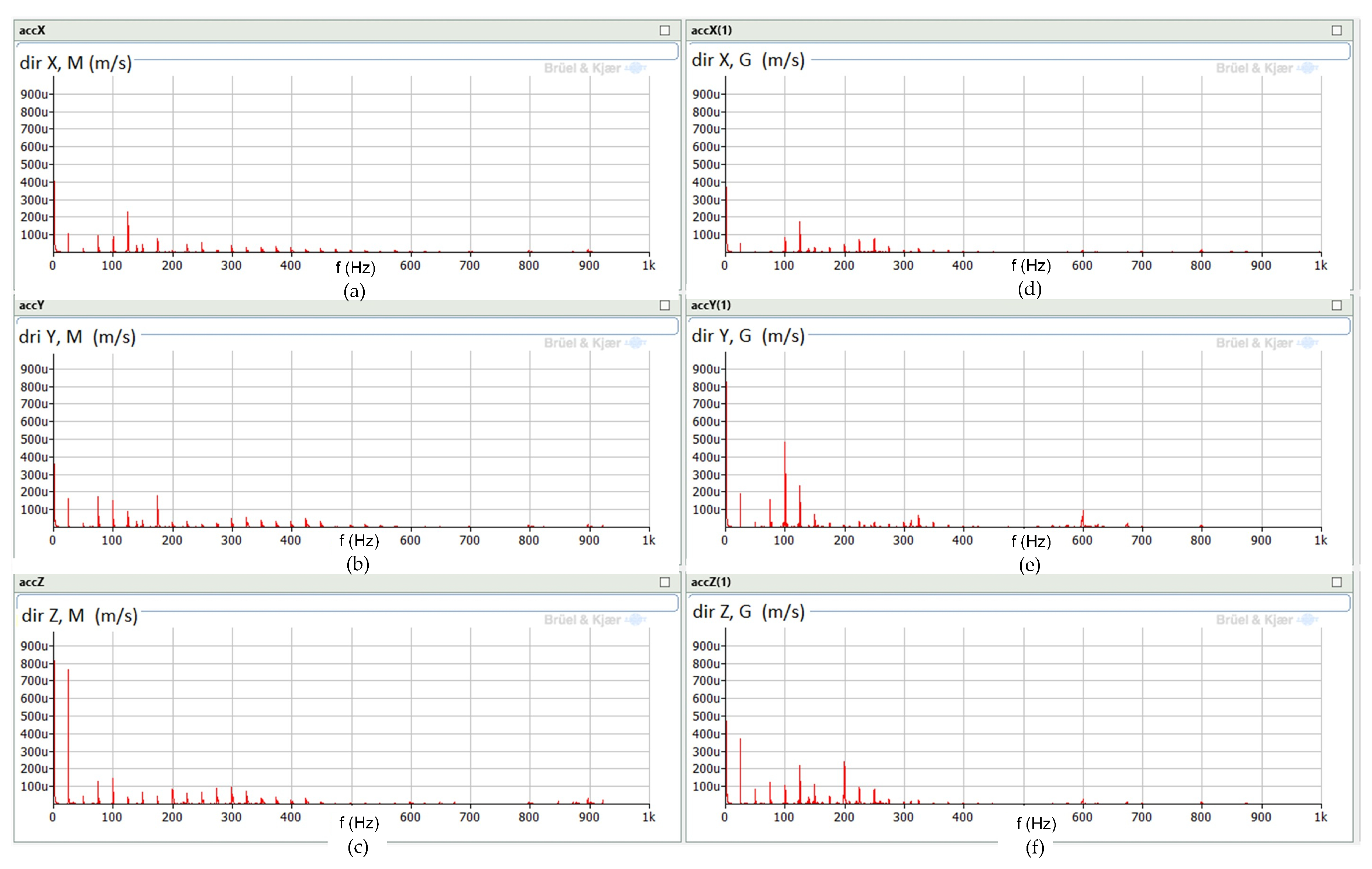
3.2.1. Analysis of the Drive Unit with an Induction Machine Operating as the Generator
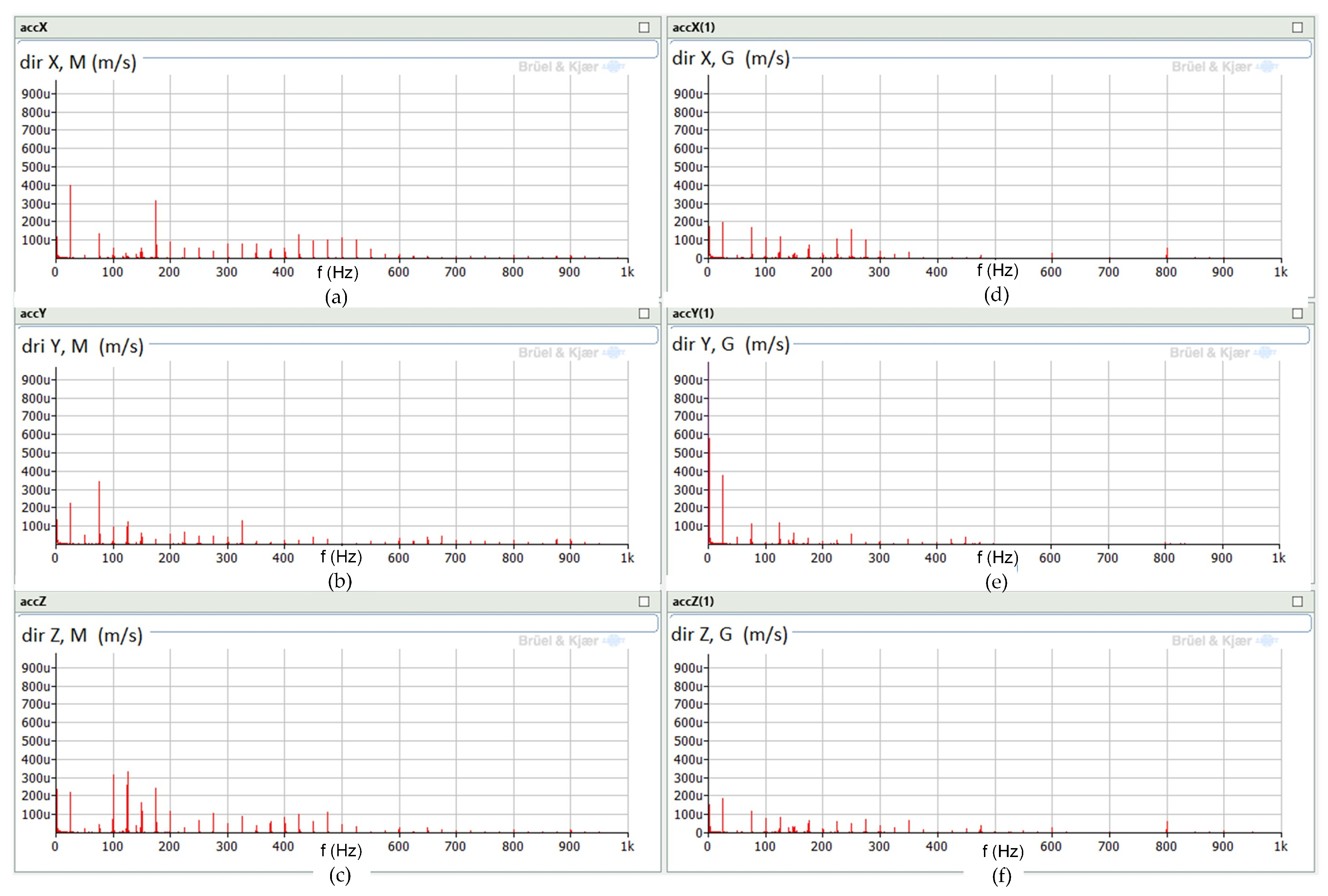
- IM—induction motor;
- IG—induction generator;
- SG—synchronous generator;
- M—measurements on the motor side;
- G—measurements on the generator side;
- dir—direction (X, Y, or Z).
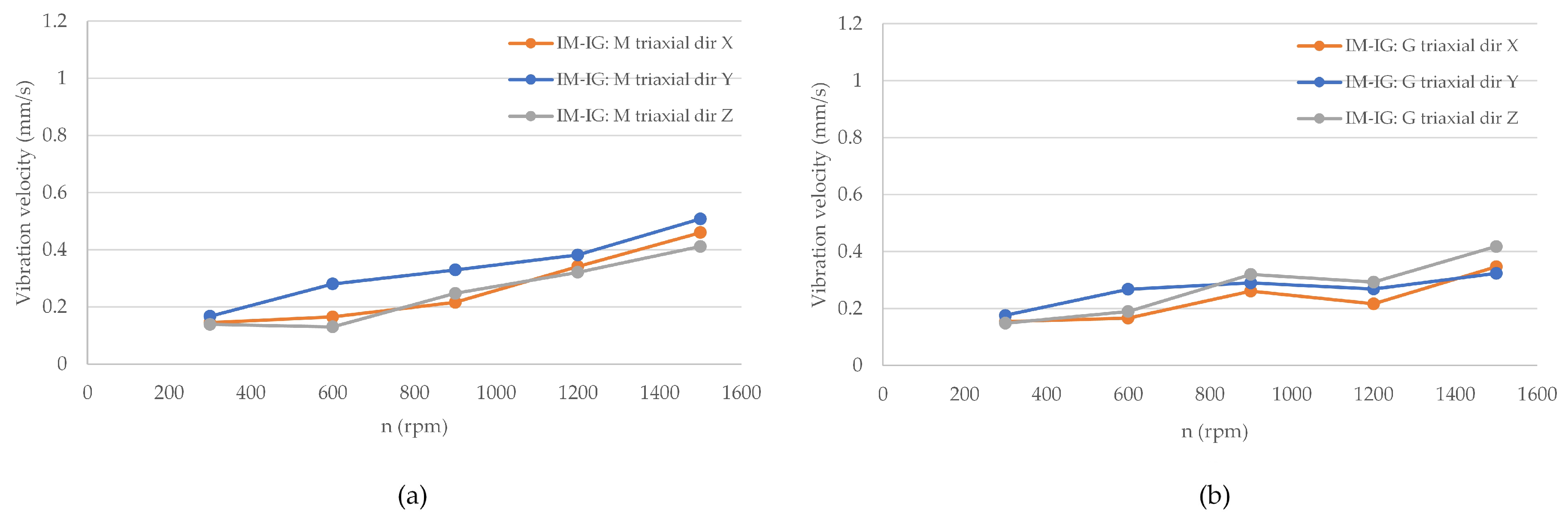

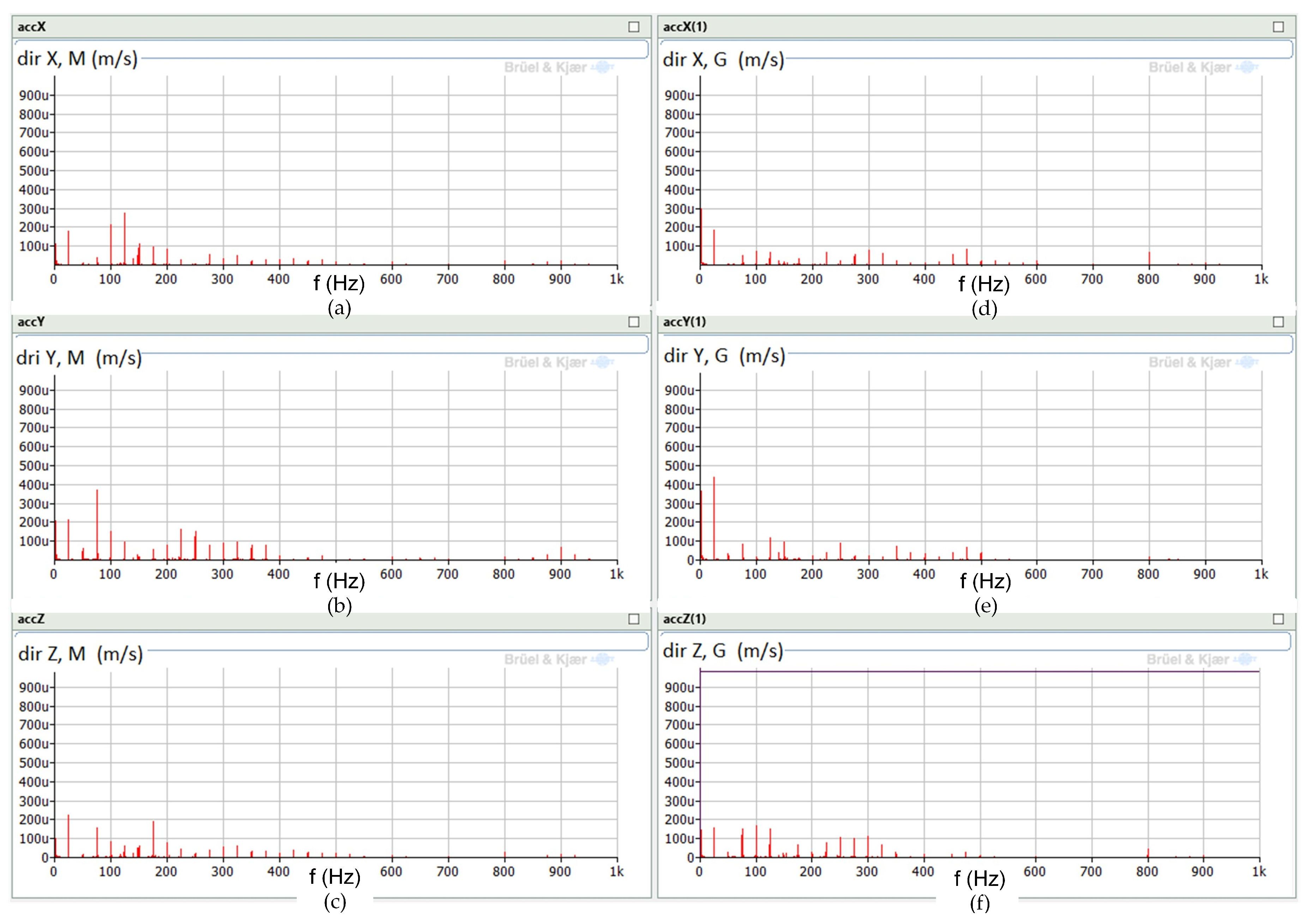
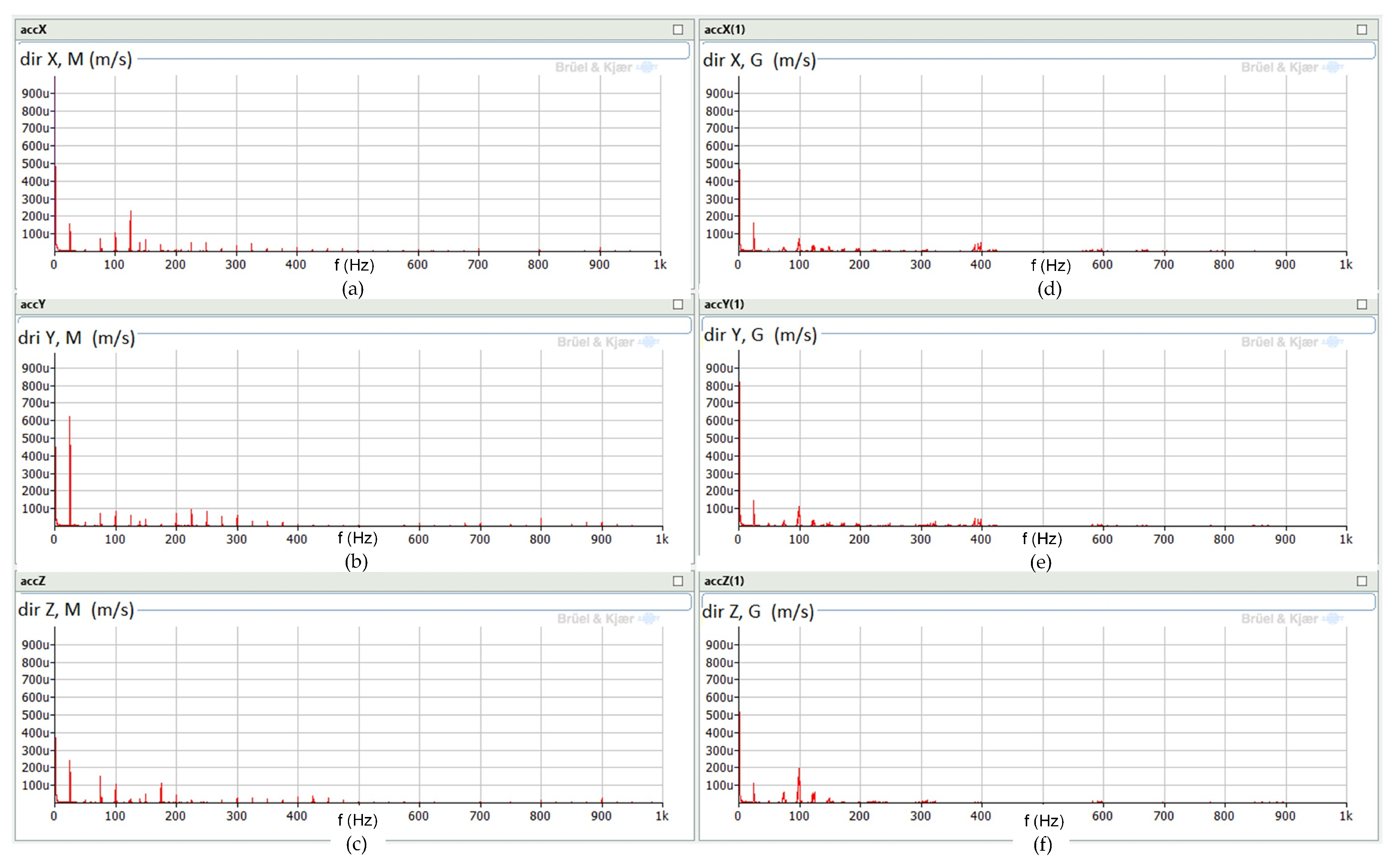
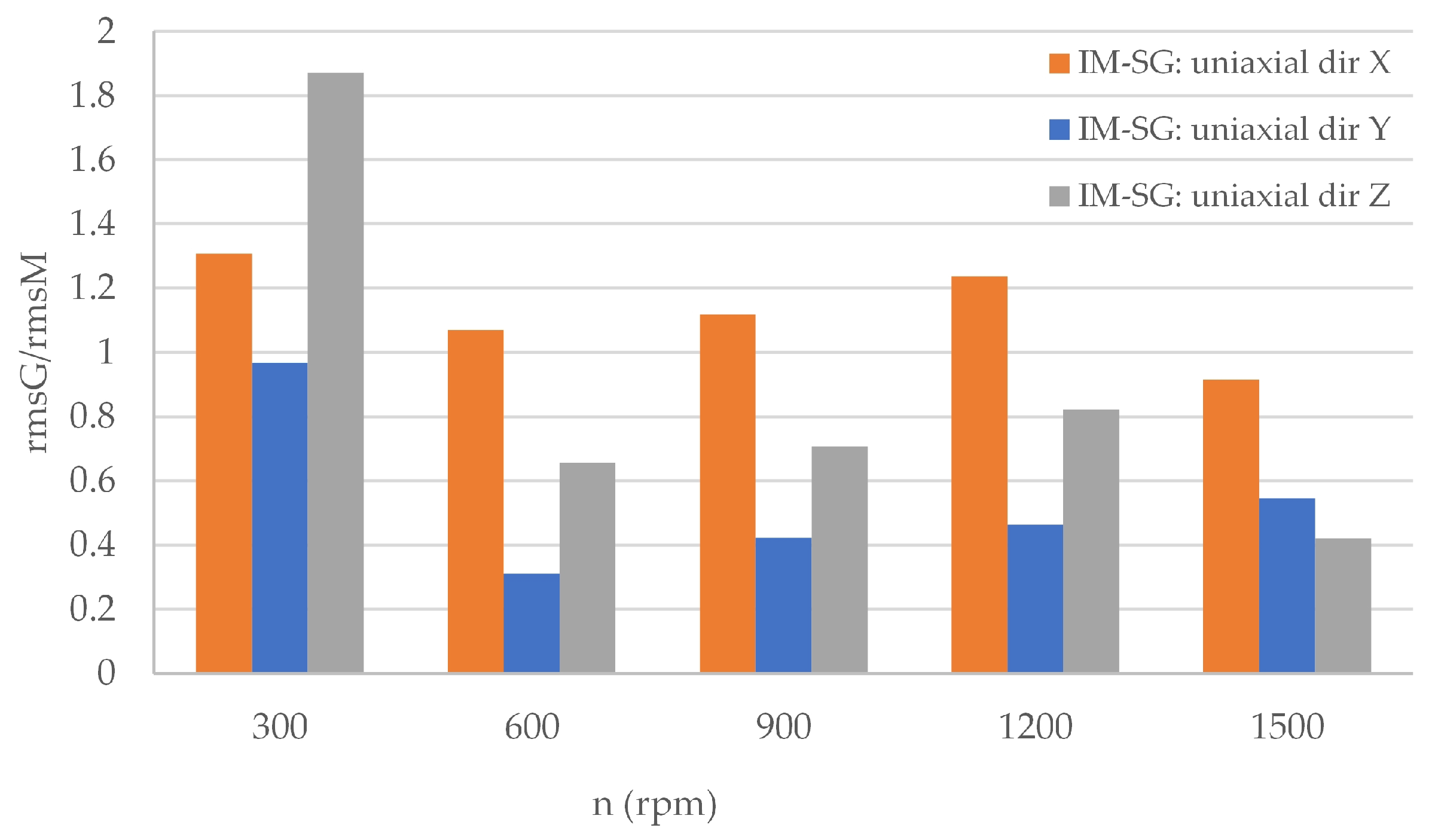
3.2.2. Analysis of the Drive Unit with a Synchronous Machine Operating as the Generator
3.3. Overview of Vibration Analysis Methods in Electrical Systems
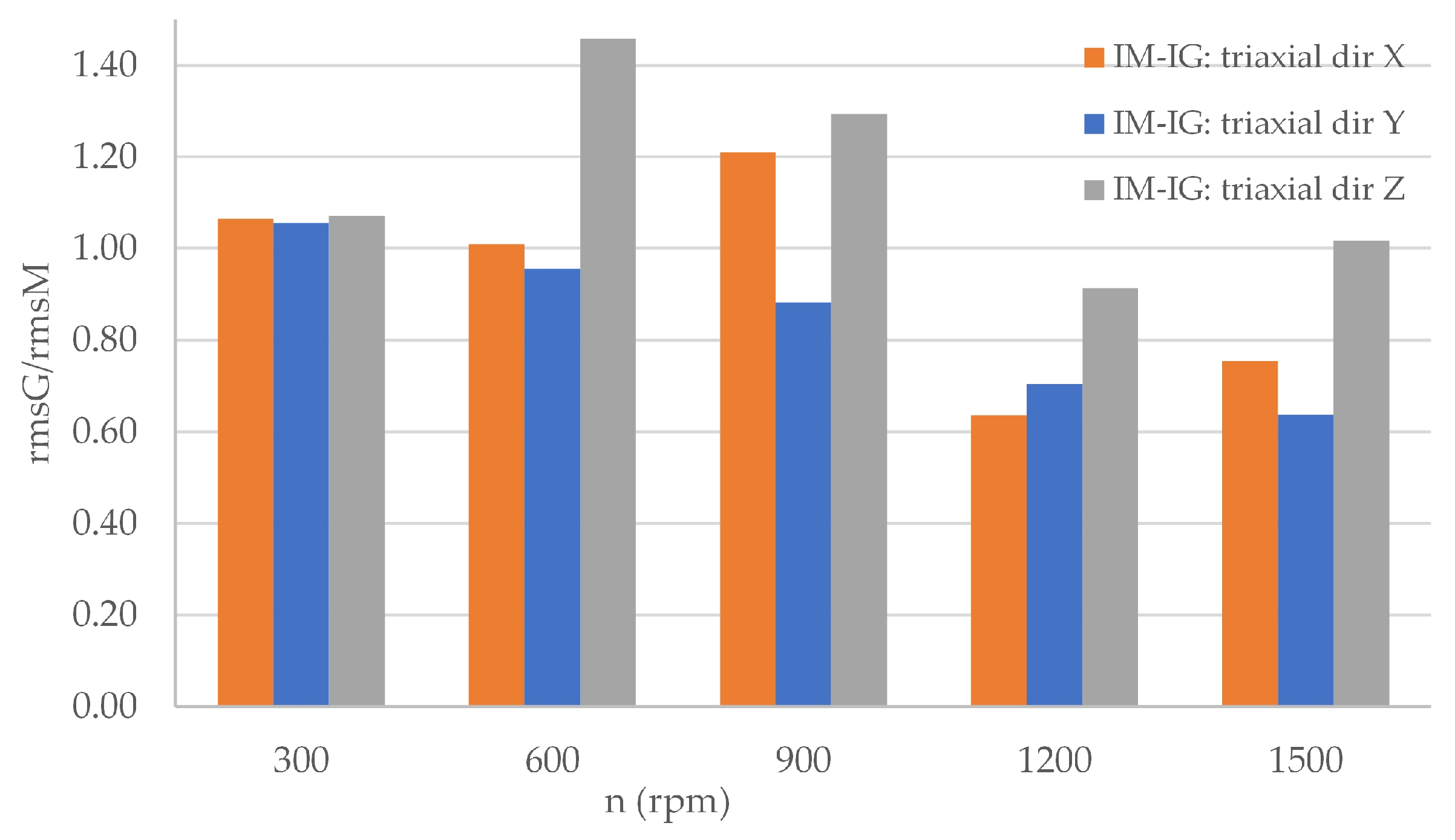
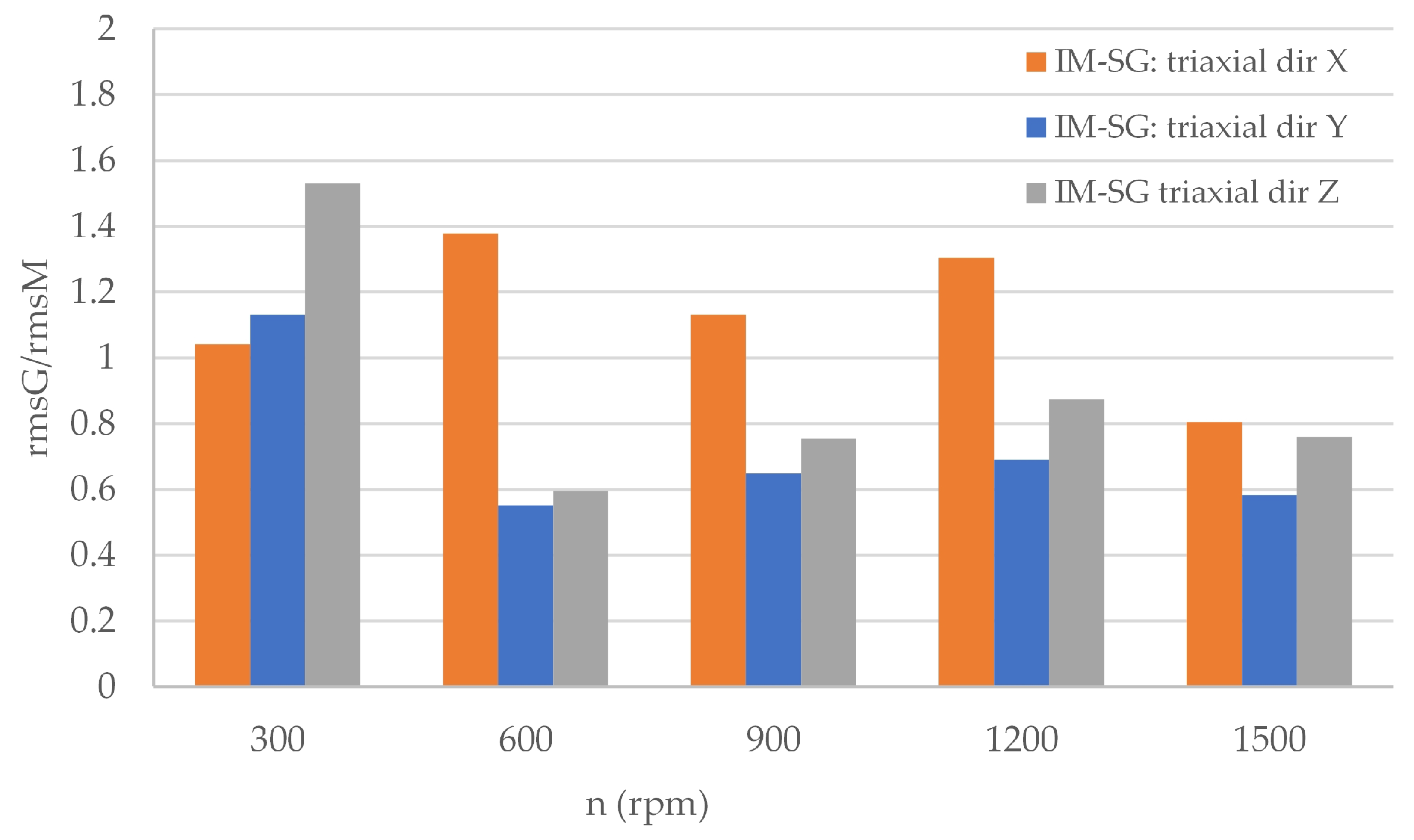
3.4. Analysis of Vibration Transmission Between Machines in the Tested Drive Unit
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Randall, R. Vibration-Based Condition Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Tavner, P.J.; Ran, L.; Penman, J.; Sedding, H. Condition Monitoring of Rotating Electrical Machines, 2nd ed.; Institution of Engineering and Technology (IET): Stevenage, UK, 2025. [Google Scholar]
- Harris, C.; Piersol, A. Harris’ Shock and Vibration Handbook; McGraw-Hill Handbooks; McGraw-Hill: Columbus, OH, USA, 2002. [Google Scholar]
- ISO 10816-3:2009; Mechanical Vibration—Evaluation of Machine Vibration by Measurements on Non-Rotating Parts. ISO: Geneva, Switzerland, 2009.
- Griffin, M. Handbook of Human Vibration; Academic Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Leonhard, W. Control of Electrical Drives, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Bose, B. Modern Power Electronics and AC Drives; Eastern Economy Edition; Prentice Hall PTR: Hoboken, NJ, USA, 2002. [Google Scholar]
- Rao, J. Vibratory Condition Monitoring of Machines; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Muszynska, A. Rotordynamics; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Yasuzawa, Y.; Morooka, A.; Tanimoto, K. Vibration Characteristics of Separated Superstructure of a Ship; Springer: Singapore, 2021; Volume 64, pp. 365–376. [Google Scholar] [CrossRef]
- Schmalhorst, J. Machine Elements for Mechanical Engineering; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Budynas, R.; Nisbett, K. Shigley’s Mechanical Engineering Design; McGraw-Hill Higher Education—VST E+p: Columbus, OH, USA, 2014. [Google Scholar]
- Chen, W.; Gunter, E. Introduction to Dynamics of Rotor-Bearing Systems; Trafford: Bloomington, IN, USA, 2007. [Google Scholar]
- Bonnett, A.H.; Soukup, G.C. Cause and analysis of stator and rotor failures in 3-phase squirrel cage induction motors. In Proceedings of the Conference Record of 1991 Annual Pulp and Paper Industry Technical Conference, Montreal, QC, Canada, 3–7 June 1991; pp. 22–42. [Google Scholar]
- Lalanne, M.; Ferraris, G. Rotordynamics Prediction in Engineering; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Romanssini, M.; de Aguirre, P.C.C.; Compassi-Severo, L.; Girardi, A.G. A Review on Vibration Monitoring Techniques for Predictive Maintenance of Rotating Machinery. Eng 2023, 4, 1797–1817. [Google Scholar] [CrossRef]
- Doorsamy, W. Condition Monitoring of Electric Machines: Modern Frameworks and Data-Driven Methodologies. Machines 2025, 13, 144. [Google Scholar] [CrossRef]
- Çalış, H. Vibration and motor current analysis of induction motors to diagnose mechanical faults. J. Meas. Eng. 2014, 2, 190–198. [Google Scholar]
- Mey, O.; Neudeck, W.; Schneider, A.; Enge-Rosenblatt, O. Machine Learning-Based Unbalance Detection of a Rotating Shaft Using Vibration Data. arXiv 2020, arXiv:2005.12742. [Google Scholar] [CrossRef]
- Ahmad, S.; Styp-Rekowski, K.; Nedelkoski, S.; Kao, O. Autoencoder-based Condition Monitoring and Anomaly Detection Method for Rotating Machines. arXiv 2021, arXiv:2101.11539. [Google Scholar] [CrossRef]
- Hua, X.; Gandee, E. Vibration and dynamics analysis of electric vehicle drivetrains. J. Low Freq. Noise Vib. Act. Control 2021, 40, 1241–1251. [Google Scholar] [CrossRef]
- Wu, B.; Qiao, M. A Review of the Research Progress of Motor Vibration and Noise. Int. Trans. Electr. Energy Syst. 2022, 2022, 5897198. [Google Scholar] [CrossRef]
- Gnaciński, P.; Pepliński, M.; Muc, A.; Hallmann, D. Induction Motors Under Voltage Unbalance Combined with Voltage Subharmonics. Energies 2024, 17, 6324. [Google Scholar] [CrossRef]
- Gnaciński, P.; Hallmann, D.; Muc, A.; Klimczak, P.; Pepliński, M. Induction Motor Supplied with Voltage Containing Symmetrical Subharmonics and Interharmonics. Energies 2022, 15, 7712. [Google Scholar] [CrossRef]
- Gnaciński, P.; Pepliński, M.; Muc, A.; Hallmann, D.; Klimczak, P. Induction Motors Under Voltage Fluctuations and Power Quality Standards. IEEE Trans. Energy Convers. 2024, 39, 1255–1264. [Google Scholar] [CrossRef]
- Muc, A.; Morawiec, M.; Wilczyński, F. Steady-State Vibration Level Measurement of the Five-Phase Induction Machine during Third Harmonic Injection or Open-Phase Faults. Energies 2023, 16, 838. [Google Scholar] [CrossRef]
- ISO Standard 10816-1; Mechanical Vibration—Evaluation of Machine Vibration by Measurements on Non-Rotating Parts—Part 1: General Guidelines. ISO: Genova, Switzerland, 1995.
- ISO Standard 20816-1; Mechanical Vibration—Measurement and Evaluation of Machine Vibration—Part 1: General Guidelines. ISO: Genova, Switzerland, 2016.
- EN 50160, 2010/A2:2019; Voltage Characteristics of Electricity Supplied by Public Distribution Network. CELENEC: Brussels, Belgium, 2019.
- de Klerk, D.; Rixen, D. Component transfer path analysis method with compensation for test bench dynamics. Mech. Syst. Signal Process. 2010, 24, 1693–1710. [Google Scholar] [CrossRef]
- de Klerk, D.; Ossipov, A. Operational transfer path analysis: Theory, guidelines and tire noise application. Mech. Syst. Signal Process. 2010, 24, 1950–1962. [Google Scholar] [CrossRef]
- Gajdatsy, P.; Desmet, W.; Gielen, L.; Janssens, K.; Van der Auweraer, H.; Mas, P. A Novel TPA Method Using Parametric Load Models: Validation on Experimental and Industrial Cases. In Proceedings of the SAE 2009 Noise and Vibration Conference and Exhibition, St. Charles, IL, USA, 19 May 2009; SAE International: Warrendale, PA, USA, 2009. [Google Scholar] [CrossRef]
- Janssens, K.; Gajdatsy, P.; Gielen, L.; Mas, P.; Britte, L.; Desmet, W.; Van der Auweraer, H. OPAX: A new transfer path analysis method based on parametric load models. Mech. Syst. Signal Process. 2011, 25, 1321–1338. [Google Scholar] [CrossRef]
- Lennström, D.; Johnsson, R.; Ågren, A.; Nykänen, A. The Influence of the Acoustic Transfer Functions on the Estimated Interior Noise from an Electric Rear Axle Drive. SAE Int. J. Passeng.-Cars-Mech. Syst. 2014, 7, 413–422. [Google Scholar] [CrossRef]
- Magrans, F.X. Method of Measuring Transmission Paths. J. Sound Vib. 1981, 74, 321–330. [Google Scholar] [CrossRef]
- Magrans, F. Definition and Calculation of Transmission Paths Within An S.E.A. Framework. J. Sound Vib. 1993, 165, 277–283. [Google Scholar] [CrossRef]
- Padilha, P.; Arruda, J. Comparison of Estimation Techniques for Vibro-Acoustic Transfer Path Analysis. Shock Vib. 2006, 13, 459–467. [Google Scholar] [CrossRef]
- De Sitter, G.; Devriendt, C.; Guillaume, P.; Pruyt, E. Operational transfer path analysis. Mech. Syst. Signal Process. 2010, 24, 416–431. [Google Scholar] [CrossRef]
- Gajdatsy, P.; Janssens, K.; Desmet, W.; Van der Auweraer, H. Application of the transmissibility concept in transfer path analysis. Mech. Syst. Signal Process. 2010, 24, 1963–1976. [Google Scholar] [CrossRef]
- Maia, N.; Silva, J.; Ribeiro, A. Transmissibility concept in multi-degree-of-freedom systems. Mech. Syst. Signal Process. 2001, 15, 129–137. [Google Scholar] [CrossRef]
- Diez-Ibarbia, A.; Battarra, M.; Palenzuela, J.; Cervantes, G.; Walsh, S.; De La Cruz, M.; Theodossiades, S.; Gagliardini, L. Comparison between transfer path analysis methods on an electric vehicle. Appl. Acoust. 2017, 118, 83–101. [Google Scholar] [CrossRef]
- Mohd Ghazali, M.H.; Rahiman, W. Vibration Analysis for Machine Monitoring and Diagnosis: A Systematic Review. Shock Vib. 2021, 2021, 9469318. [Google Scholar] [CrossRef]


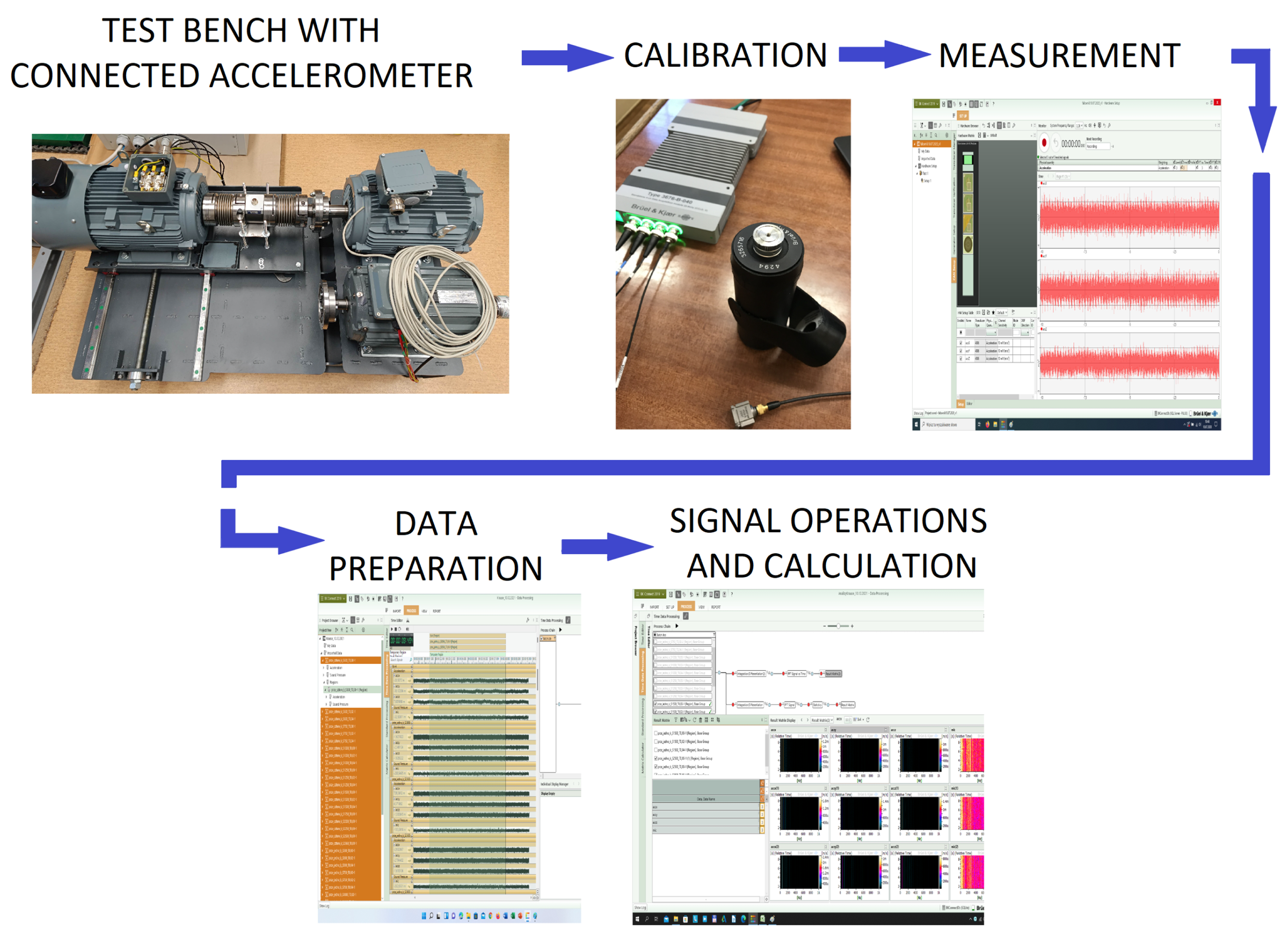







| Number | Name | Manufacturer, Model |
|---|---|---|
| 1 | Inverter | Twerd |
| 2 | Cage induction motor (11 kW, 50 Hz) | MFC Motors: OMT4–132MC–4 |
| 3 | Cage induction generator (7.5 kW, 50 Hz) | MFC Motors: OMT4–132M–4 |
| 5 | Permanent magnet synchronous generator (100 Hz) | Eura Drives: EVPM–752IN4Y–2D15S |
| 6 | Bellows coupling | - |
| 7 | Oscilloscope | Tektronix: MSO 4140 |
| 8 | Voltage probe | Tektronix: THDP0200 |
| 9 | Current probe | Tektronix: TCP0030 |
| 10 | Triaxial accelerometer | Bruel&Kjaer: 4529–B–31297 |
| 11 | Uniaxial accelerometer | Bruel&Kjaer: 4534–B–33927 |
| 12 | Data acquisition module | Bruel&Kjaer: 3676–B–040 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muc, A.; Bielecka, A. Transmission of Mechanical Vibrations in an Electric Drive Unit with Scalar Control—Comparative Analysis with Evaluation Based on Experimental Studies. Energies 2025, 18, 5140. https://doi.org/10.3390/en18195140
Muc A, Bielecka A. Transmission of Mechanical Vibrations in an Electric Drive Unit with Scalar Control—Comparative Analysis with Evaluation Based on Experimental Studies. Energies. 2025; 18(19):5140. https://doi.org/10.3390/en18195140
Chicago/Turabian StyleMuc, Adam, and Agata Bielecka. 2025. "Transmission of Mechanical Vibrations in an Electric Drive Unit with Scalar Control—Comparative Analysis with Evaluation Based on Experimental Studies" Energies 18, no. 19: 5140. https://doi.org/10.3390/en18195140
APA StyleMuc, A., & Bielecka, A. (2025). Transmission of Mechanical Vibrations in an Electric Drive Unit with Scalar Control—Comparative Analysis with Evaluation Based on Experimental Studies. Energies, 18(19), 5140. https://doi.org/10.3390/en18195140







