Transient Stability Control Method for Droop-Controlled Photovoltaics, Based on Power Angle Deviation Feedback †
Abstract
1. Introduction
2. Analysis of Transient Characteristics of Droop-Controlled Inverters
2.1. Basic Control of Droop-Controlled Inverters
2.2. Transient Power Angle Characteristics of Droop-Controlled Inverters
3. Qualitative Assessment of the Transient Stability Performance of Droop-Controlled Inverters
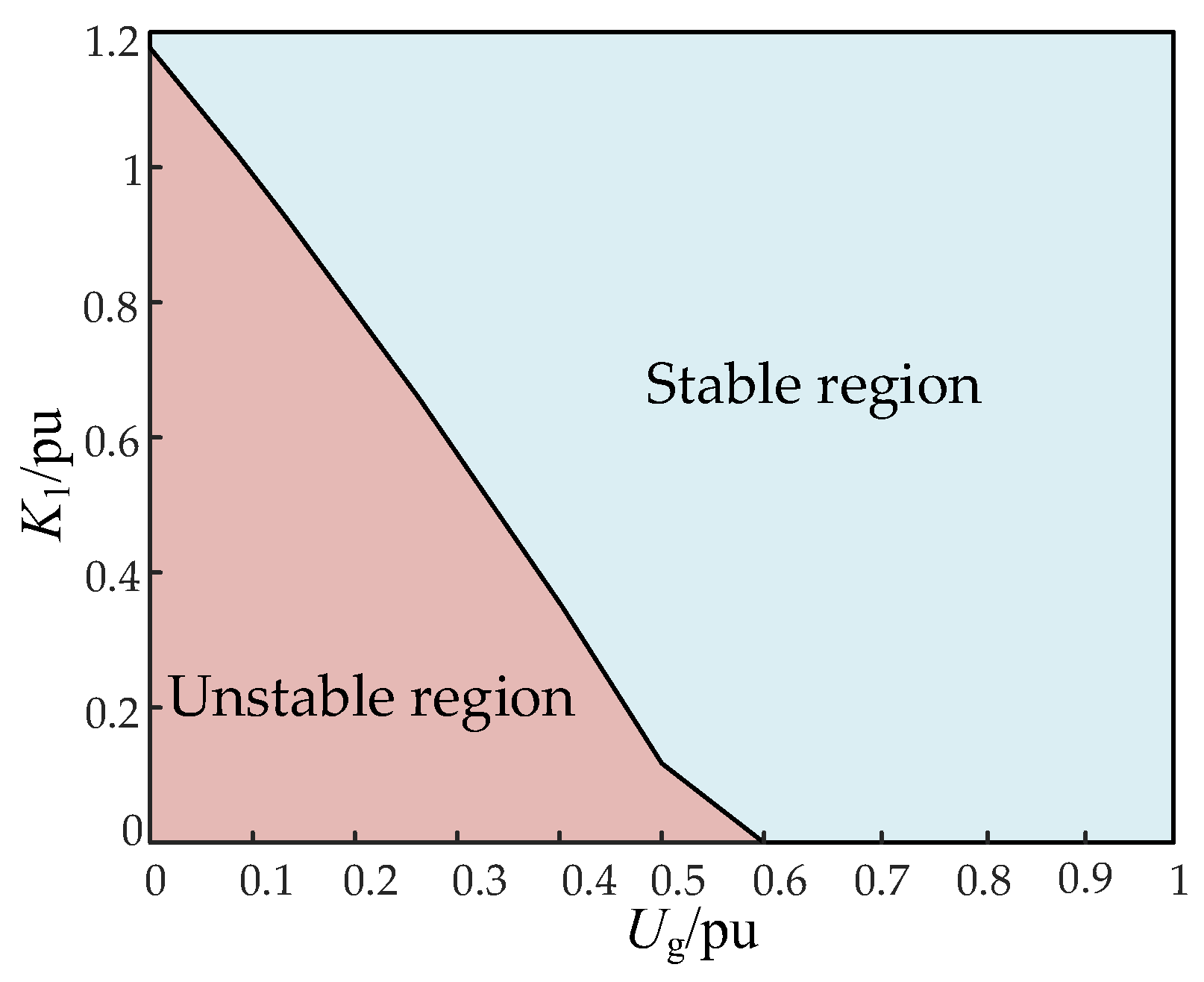
4. Quantitative Characterization of Transient Stable Operation Boundaries
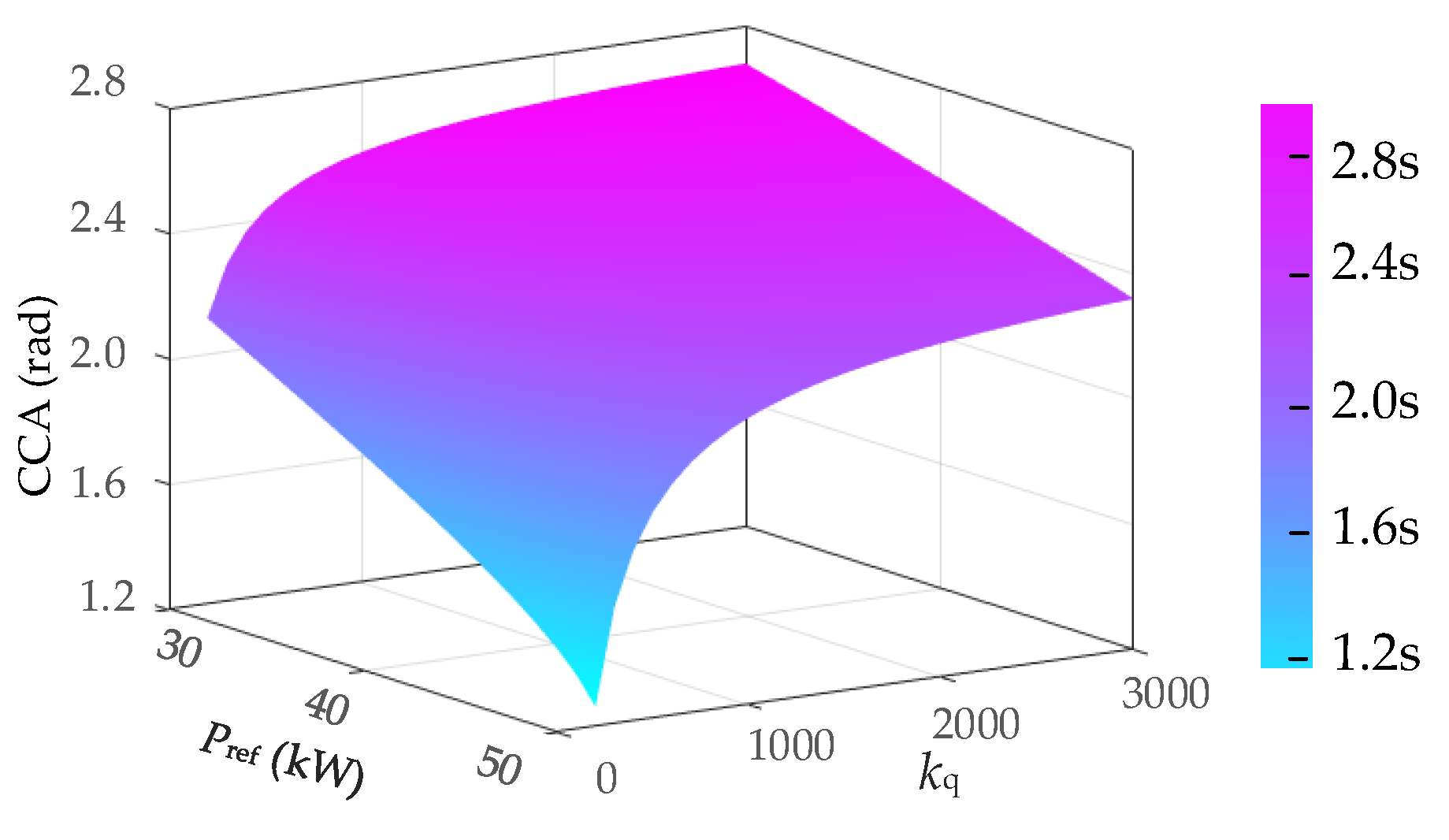
4.1. Quantitative Characterization of CCA
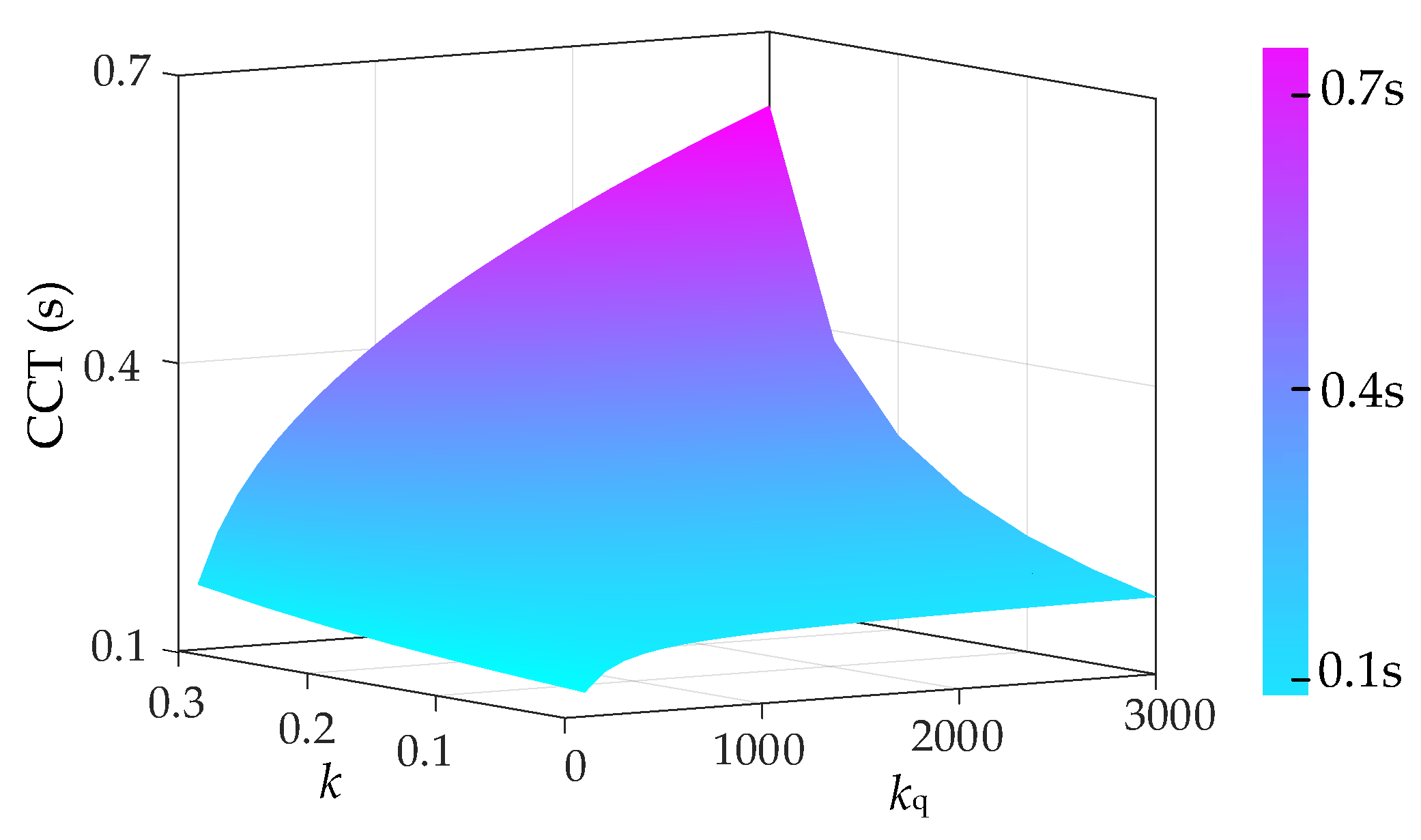
4.2. Quantitative Characterization of CCT
5. Power Angle Deviation Feedforward Control
5.1. Power Angle Deviation Feedforward Control Structure
5.2. Design of the Power Angle Deviation Feedforward Coefficient
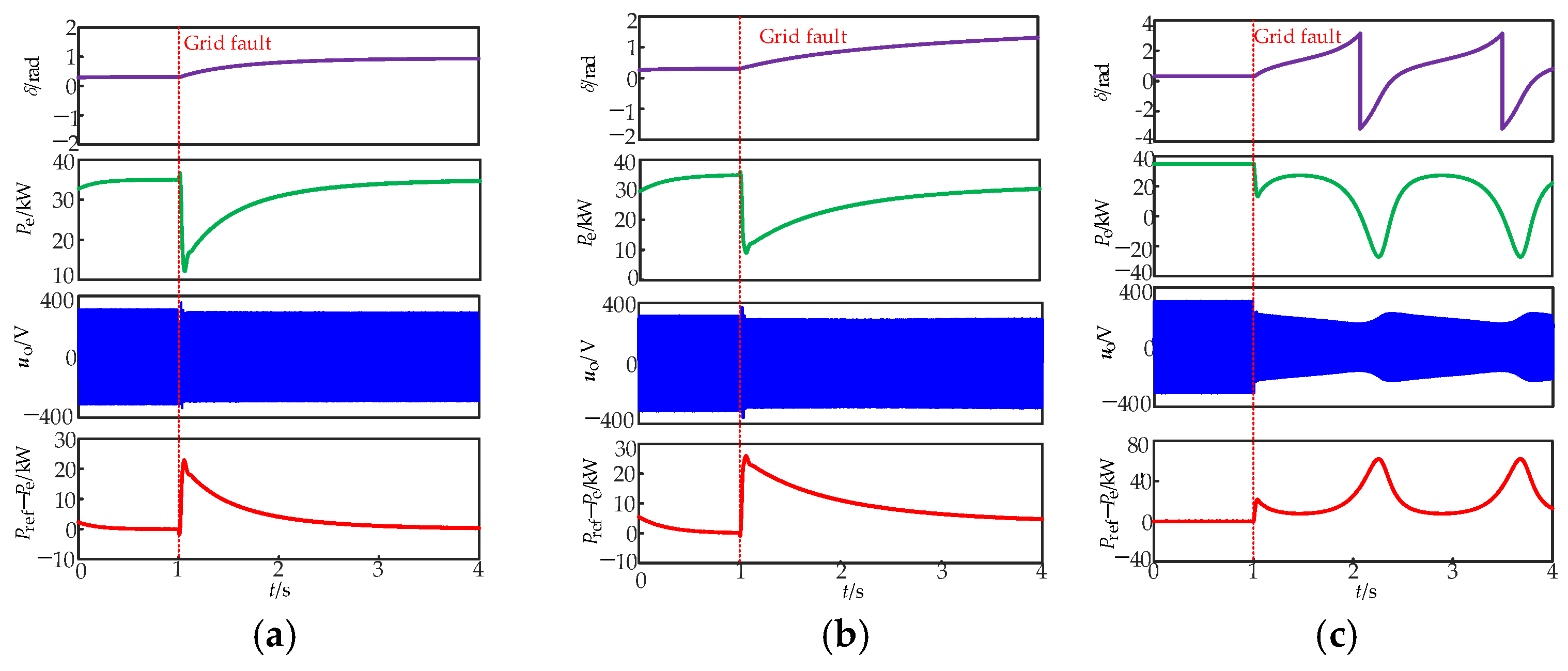
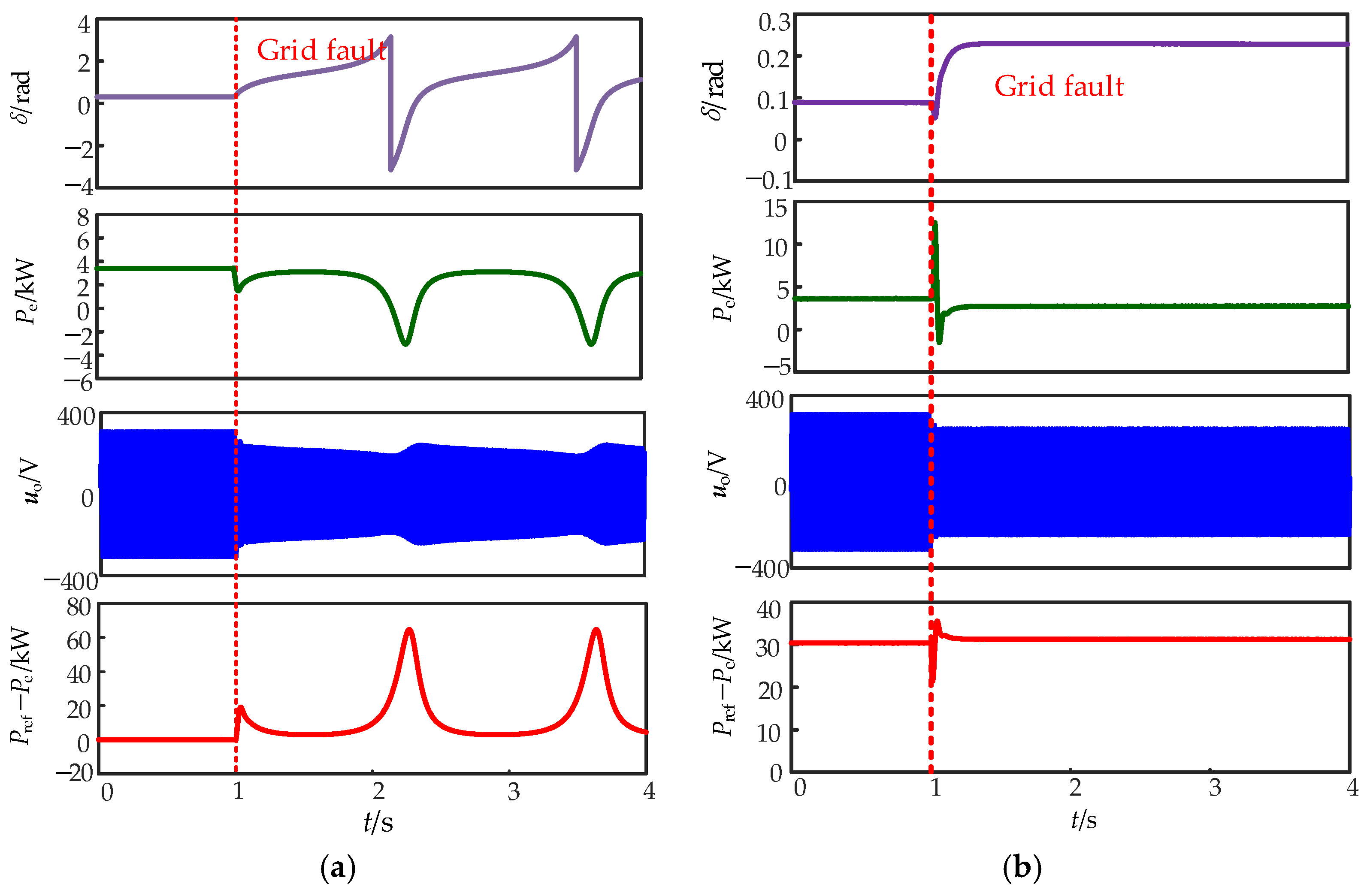
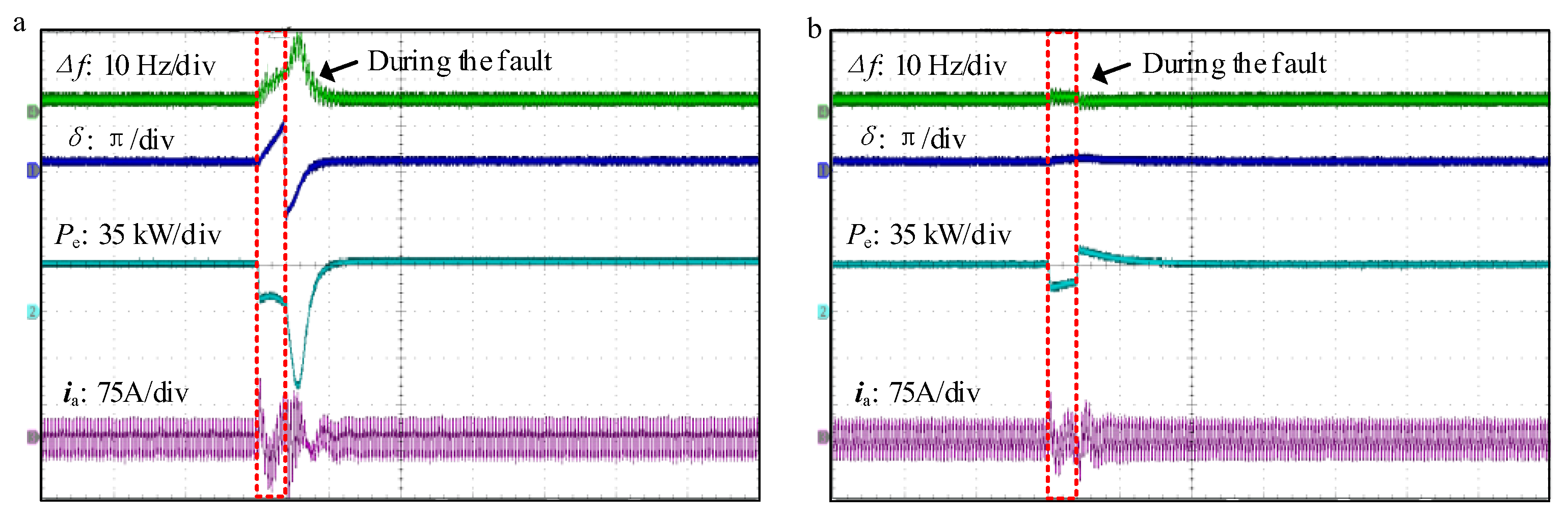
6. Simulation Results
7. Conclusions
- (1)
- Control parameters have significant impacts on the transient stability boundary of droop inverters. Increasing the active-power-frequency/voltage droop coefficient can improve the CCT of droop inverters, while increasing the reactive-power-voltage droop coefficient can simultaneously optimize both the CCA and CCT of droop inverters;
- (2)
- The control method for droop-controlled inverters, based on power angle deviation feedforward, proposed in this paper, can automatically feedback power angle deviation information and adaptively configure the feedforward coefficient according to fault depth, thereby ensuring the transient stable operation of the inverter at different grid fault depths;
- (3)
- The stability control strategy, based on power angle deviation, proposed in this paper, can reduce the impacts of grid disturbances on photovoltaic converters without the need for additional hardware equipment, solve the problem of frequent shutdowns of photovoltaic converters (caused by voltage disturbances), and improve the economy of new energy generation grid connections;
- (4)
- With an increase in the proportion of new energy grid connections, exploring the scalability of the power angle deviation feedforward control, proposed in this paper, in photovoltaic cluster systems and solving the stability problem in large-scale new energy generation scenarios will be the focus of the next work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, X.; Song, Y.; Wang, G.; Wang, W. A Comprehensive Review on the Development of Sustainable Energy Strategy and Implementation in China. IEEE Trans. Sustain. Energy 2010, 2, 57–65. [Google Scholar] [CrossRef]
- Yang, F.; Sun, Q.; Han, Q.-L.; Wu, Z. Cooperative Model Predictive Control for Distributed Photovoltaic Power Generation Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 2, 414–420. [Google Scholar] [CrossRef]
- Lv, X.; Qiao, F.; Sun, Y.; Dinavahi, V.; Liu, P.X. Improved Memory Event-Triggered Load Frequency Control in Multi-Area Power System with Renewable Energy. IEEE Trans. Circuits Syst. II Express Briefs 2024, 1, 311–315. [Google Scholar] [CrossRef]
- Zhang, W.; Li, T.; Wang, X.; Liu, Q.; Liu, S.; Luo, M.; Dai, Z. Protection Principle of DC Line Based on Fault Component of Line Mode Voltage with Current-Limiting Reactor. Energies 2025, 18, 4271. [Google Scholar] [CrossRef]
- Lee, S.; Kim, G.; Son, S.; Lee, J. Comparative Analysis of the Substitution Effect of Smart Inverter-Based Energy Storage Systems on the Improvement of Distribution System Hosting Capacity Using Vertical Photovoltaic Systems. Energies 2025, 18, 4307. [Google Scholar] [CrossRef]
- Mensah Akwasi, A.; Chen, H.; Liu, J.; Duku, O.-A. Hybrid Adaptive Learning-Based Control for Grid-Forming Inverters: Real-Time Adaptive Voltage Regulation, Multi-Level Disturbance Rejection, and Lyapunov-Based Stability. Energies 2025, 18, 4296. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Ding, Z.; Xie, W.; Li, C. Self-Adaptive Secondary Frequency Regulation Strategy of Micro-Grid with Multiple Virtual Synchronous Generators. IEEE Trans. Ind. Appl. 2020, 5, 6007–6018. [Google Scholar] [CrossRef]
- Najafabadi, S.R.K.; Fani, B.; Sadeghkhani, I. Optimal Determination of Photovoltaic Penetration Level Considering Protection Coordination. IEEE Syst. J. 2022, 2, 2121–2124. [Google Scholar] [CrossRef]
- Ghosh, S.; Bohra, A.; Dutta, S.; Verma, S. Integration Strategies for Large-Scale Renewable Interconnections with Grid Forming and Grid Following Inverters, Capacitor Banks, and Harmonic Filters. Energies 2025, 18, 3934. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Mijatovic, N.; Dragicevic, T. Frequency Stability Assessment of Grid-Forming VSG in Framework of MPME with Feedforward Decoupling Control Strategy. IEEE Trans. Ind. Electron. 2022, 7, 6903–6913. [Google Scholar] [CrossRef]
- Liu, C.; Chu, Z.; Duan, Z.; Zhang, Y. VSG-Based Adaptive Optimal Frequency Regulation for AC Microgrids with Nonlinear Dynamics. IEEE Trans. Autom. Sci. Eng. 2025, 22, 1471–1482. [Google Scholar] [CrossRef]
- Samanta, S.; Yang, B.; Seo, G.-S. Stability Analysis of Power Systems with High Penetration of State-of-the-Art Inverter Technologies. Energies 2025, 18, 3645. [Google Scholar] [CrossRef]
- Chen, S.; Sun, Y.; Hou, X.; Han, H.; Fu, S.; Su, M. Quantitative Parameters Design of VSG Oriented to Transient Synchronization Stability. IEEE Trans. Power Syst. 2023, 5, 4978–4981. [Google Scholar] [CrossRef]
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison Between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 6, 5416–5438. [Google Scholar] [CrossRef]
- Yu, J.; Lin, X.; Song, D.; Yu, R.; Li, Y.; Su, M. Harmonic Instability and Amplification for Grid-Connected Inverter with Voltage Harmonics Compensation Considering Phase-Locked Loop. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 4, 3944–3959. [Google Scholar] [CrossRef]
- Ding, Y.; Gao, F.; Khan, M.M. Transient Stability Analysis of Microgrid Considering Impact of Grid-Following Converter’s Current Controller. IEEE Trans. Power Electron. 2024, 8, 9100–9105. [Google Scholar] [CrossRef]
- Shuai, Z.; Shen, C.; Liu, X.; Li, Z.; Shen, Z.J. Transient Angle Stability of Virtual Synchronous Generators Using Lyapunov’s Direct Method. IEEE Trans. Smart Grid 2019, 4, 4648–4661. [Google Scholar] [CrossRef]
- Deng, Y.; Tao, Y.; Chen, G.; Li, G.; He, X. Enhanced Power Flow Control for Grid-Connected Droop-Controlled Inverters with Improved Stability. IEEE Trans. Ind. Electron. 2017, 7, 5919–5929. [Google Scholar] [CrossRef]
- Belgacem, M.; Khatir, M.; Djehaf, M.A.; Bouddou, R.; Behamida, F. Analysis and impacts of implementing droop control in Multi-Terminal VSC-HVDC under the steady state and Transient stability. In Proceedings of the 2020 International Conference on Electrical and Information Technologies (ICEIT), Rabat, Morocco, 4–7 March 2020; pp. 1–6. [Google Scholar]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. An Overview of Assessment Methods for Synchronization Stability of Grid-Connected Converters Under Severe Symmetrical Grid Faults. IEEE Trans. Power Electron. 2019, 10, 9655–9670. [Google Scholar] [CrossRef]
- Xin, H.; Huang, L.; Zhang, L.; Wang, Z.; Hu, J. Synchronous Instability Mechanism of P-f Droop-Controlled Voltage Source Converter Caused by Current Saturation. IEEE Trans. Power Syst. 2016, 6, 5206–5207. [Google Scholar] [CrossRef]
- Rouzbehi, K.; Miranian, A.; Candela, J.I.; Luna, A.; Rodriguez, P. A Generalized Voltage Droop Strategy for Control of Multiterminal DC Grids. IEEE Trans. Ind. Appl. 2015, 1, 607–618. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-Oriented Transient Stability Analysis of Grid-Connected Converters with Power Synchronization Control. IEEE Trans. Ind. Electron. 2019, 8, 6473–6482. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Transient angle stability analysis of grid-connected converters with the first-order active power loop. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Zhao, F.; Shuai, Z.; Shen, C.; Cheng, H.; Shen, Y.; Peng, Y. Comparison of transient angle stability between virtual synchronous generator and droop-controlled inverter. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020; IEEE: New York, NY, USA, 2020. [Google Scholar]
- Huang, L.; Xin, H.; Wang, Z.; Zhang, L.; Wu, K.; Hu, J. Transient Stability Analysis and Control Design of Droop-Controlled Voltage Source Converters Considering Current Limitation. IEEE Trans. Smart Grid 2019, 1, 578–591. [Google Scholar] [CrossRef]
- Fan, B.; Li, Q.; Wang, W.; Yao, G.; Ma, H.; Zeng, X. A Novel Droop Control Strategy of Reactive Power Sharing Based on Adaptive Virtual Impedance in Microgrids. IEEE Trans. Ind. Electron. 2022, 11, 11335–11347. [Google Scholar] [CrossRef]
- Mahmood, H.; Michaelson, D.; Jiang, J. Reactive Power Sharing in Islanded Microgrids Using Adaptive Voltage Droop Control. IEEE Trans. Smart Grid 2015, 6, 3052–3060. [Google Scholar] [CrossRef]
- Xiong, X.; Wu, C.; Blaabjerg, F. Effects of Virtual Resistance on Transient Stability of Virtual Synchronous Generators Under Grid Voltage Sag. IEEE Trans. Ind. Electron. 2021, 69, 4754–4764. [Google Scholar] [CrossRef]
- Peng, J.C.-H.; Raman, G.; Soon, J.L.; Hatziargyriou, N.D. Droop-Controlled Inverters as Educational Control Design Project. IEEE Trans. Power Syst. 2021, 37, 1623–1633. [Google Scholar] [CrossRef]
- Ge, P.; Xiao, F.; Tu, C.; Guo, Q.; Xiao, Z.; Xie, W. Transient power angle control for a droop-controlled voltage source converter considering fault current limitation. CSEE J. Power Energy Syst. 2022, 8, 968–970. [Google Scholar] [CrossRef]
- Ge, P.; Tu, C.; Xiao, F.; Xiao, Z.; Hou, Y.; Chen, L. Transient Stability Boundary of a Droop-Controlled Voltage Source Converter with Different Control Parameters. In Proceedings of the 2022 International Conference on Power Energy Systems and Applications (ICoPESA), Singapore, 25–27 February 2022; pp. 286–291. [Google Scholar]
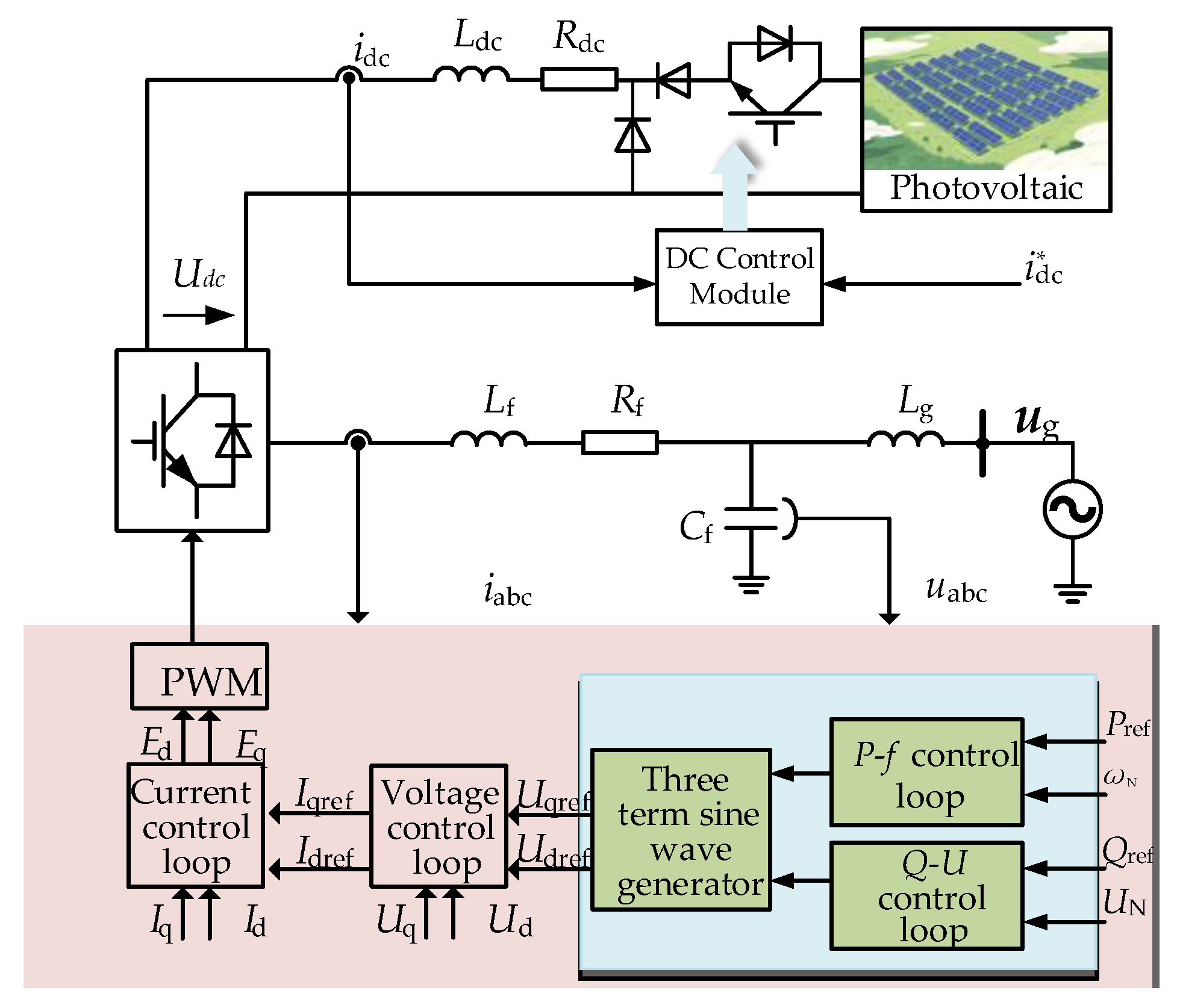
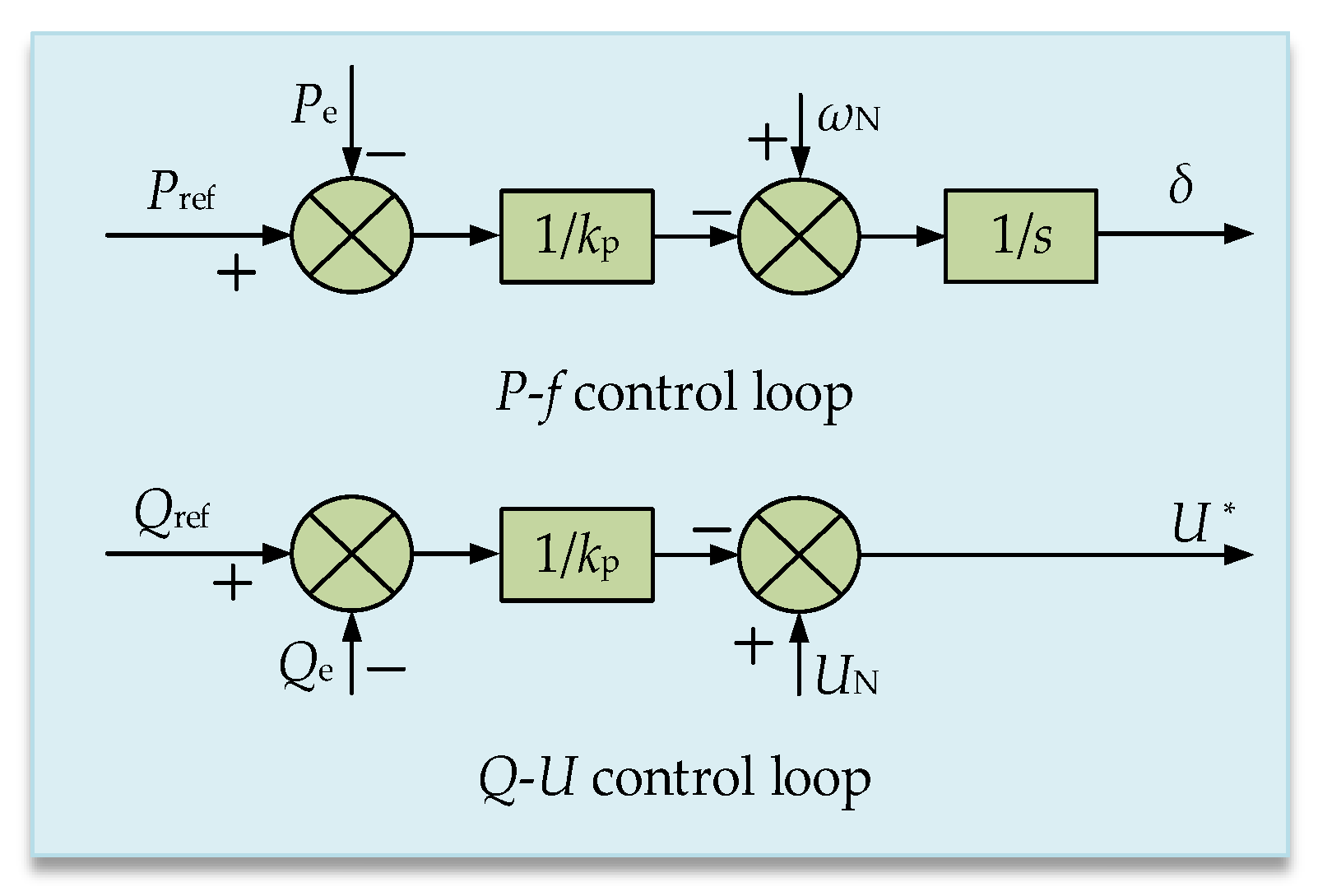
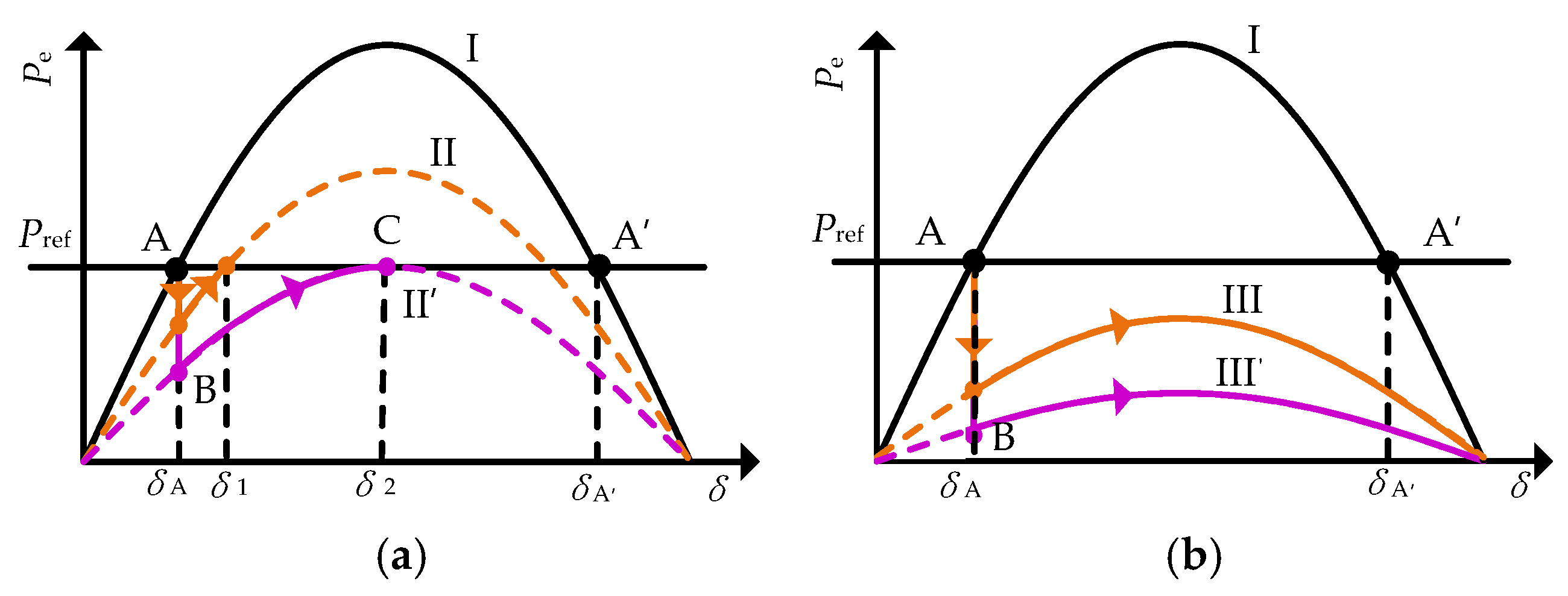
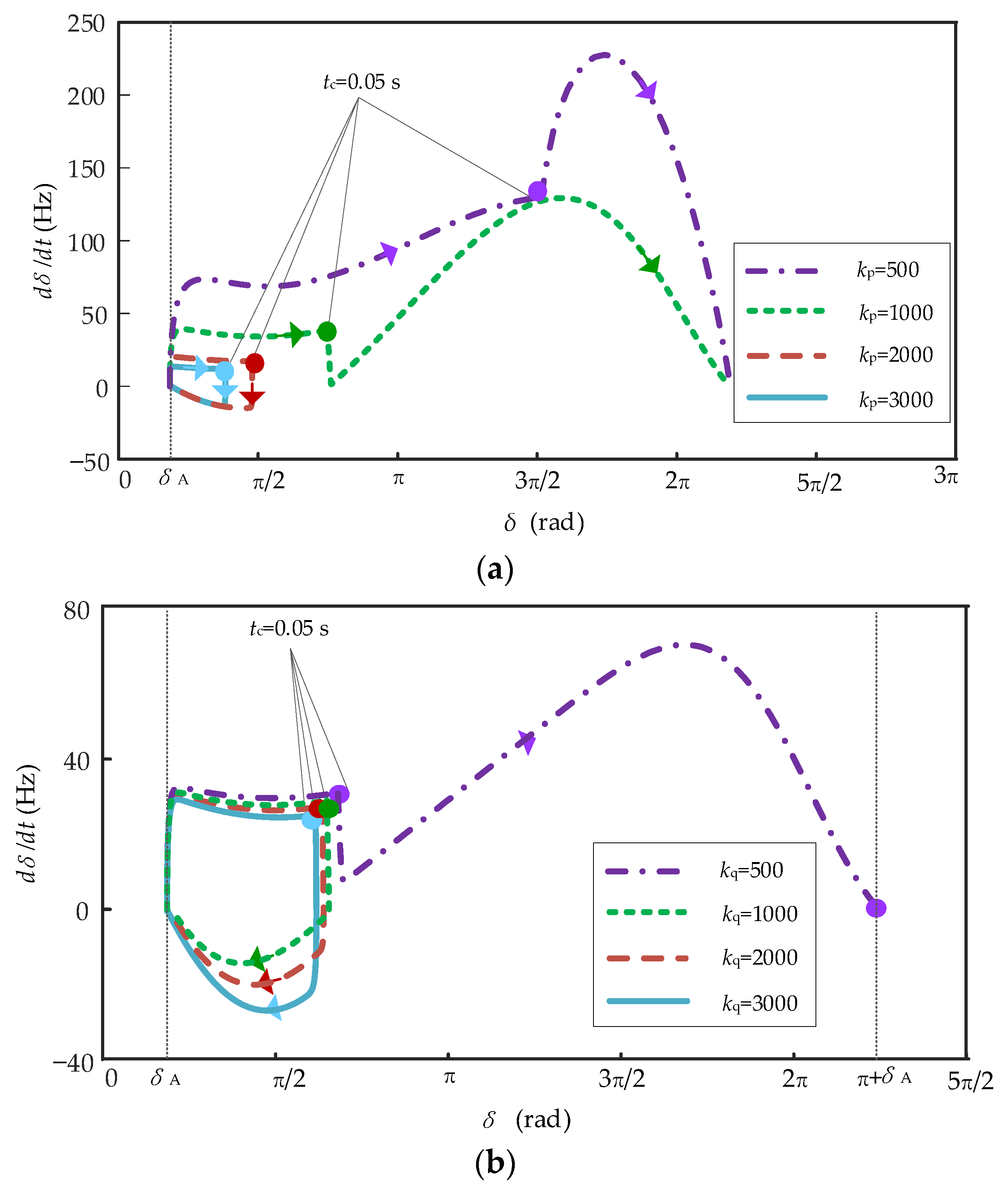





| Parameter | Meaning | Assignment |
|---|---|---|
| Udc/V | DC voltage | 800 |
| UgN/V | Grid nominal voltage | 311 |
| Cf/uF | Filter capacitor | 50 |
| Udc/V | DC voltage | 800 |
| UgN/V | Grid nominal voltage | 311 |
| Cf/uF | Filter capacitor | 50 |
| kip | Proportional coefficient of the current loop | 2 |
| kii | Integral coefficient of the current loop | 200 |
| kup | Proportional coefficient of the voltage loop | 0.55 |
| kui | Integral coefficient of the volt-age loop | 100 |
| kq | Reactive-power droop coefficient | 1500 |
| kp | Active-power droop coefficient | 3000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Xiao, Z.; Hua, L.; Guo, Q.; Li, C.; Chen, K. Transient Stability Control Method for Droop-Controlled Photovoltaics, Based on Power Angle Deviation Feedback. Energies 2025, 18, 5126. https://doi.org/10.3390/en18195126
Zheng Y, Xiao Z, Hua L, Guo Q, Li C, Chen K. Transient Stability Control Method for Droop-Controlled Photovoltaics, Based on Power Angle Deviation Feedback. Energies. 2025; 18(19):5126. https://doi.org/10.3390/en18195126
Chicago/Turabian StyleZheng, Youzhuo, Zekun Xiao, Long Hua, Qi Guo, Chun Li, and Kailei Chen. 2025. "Transient Stability Control Method for Droop-Controlled Photovoltaics, Based on Power Angle Deviation Feedback" Energies 18, no. 19: 5126. https://doi.org/10.3390/en18195126
APA StyleZheng, Y., Xiao, Z., Hua, L., Guo, Q., Li, C., & Chen, K. (2025). Transient Stability Control Method for Droop-Controlled Photovoltaics, Based on Power Angle Deviation Feedback. Energies, 18(19), 5126. https://doi.org/10.3390/en18195126






