Study on Low-Carbon Design Strategy of Block-Scale Science and Technology Industrial Park Based on Solar Energy Utilization Potential and Heat Island Effects
Abstract
1. Introduction
2. Simulation Methods
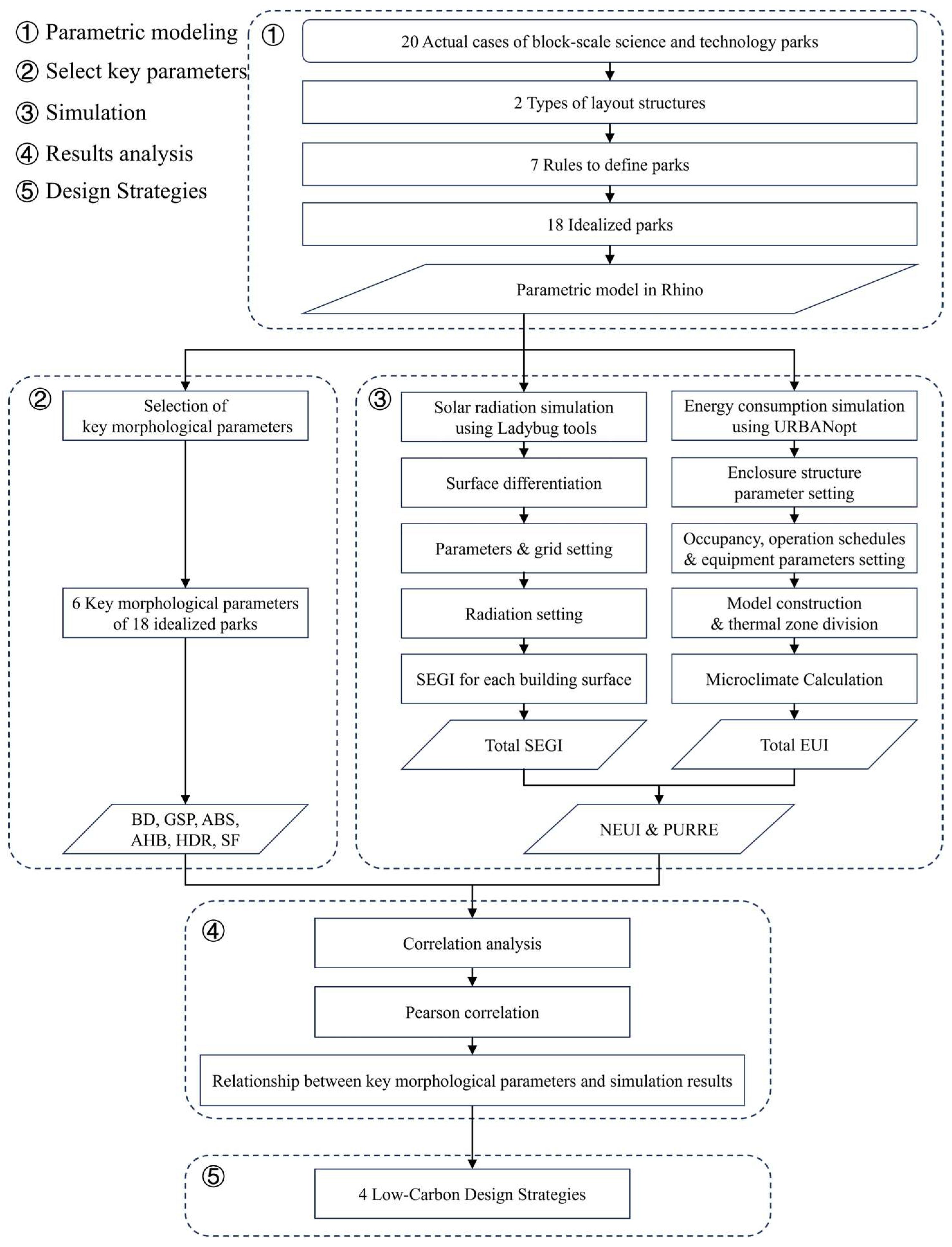
2.1. Integrated Energy Performance Evaluation System
- Parametric Modeling: By summarizing from twenty cases, two major types of park spatial forms were identified, and eighteen ideal park models were constructed based on seven established rules. Geometric attributes of the idealized models were translated into parametric modeling within Rhinoceros 7 and Grasshopper by extruding footprint polylines into volumetric building envelopes.
- Select Key Parameters: To systematically capture the spatial layout characteristics of science and technology industrial parks and to ensure broad applicability during early-stage planning and design, six key morphological parameters were identified as study variables.
- Simulation Workflow: The energy consumption simulation of parks was conducted using energy simulation software such as Ladybug 1.6.0, Radiance 5.4a, and URBANopt 0.9.2 to assess the photovoltaic power generation potential and the impact of the urban heat island effect. Based on the simulation results, the photovoltaic power generation intensity, energy use intensity, and integrated energy performance indicators were calculated.
- Results Analysis: By comparing the integrated energy performance of various idealized park models, the street patterns with superior energy performance were identified.
- Design Strategies: Based on the analysis results of the study, planning and design strategies for science and technology industrial parks were proposed, which focused on optimizing the integrated energy performance of the building complex.
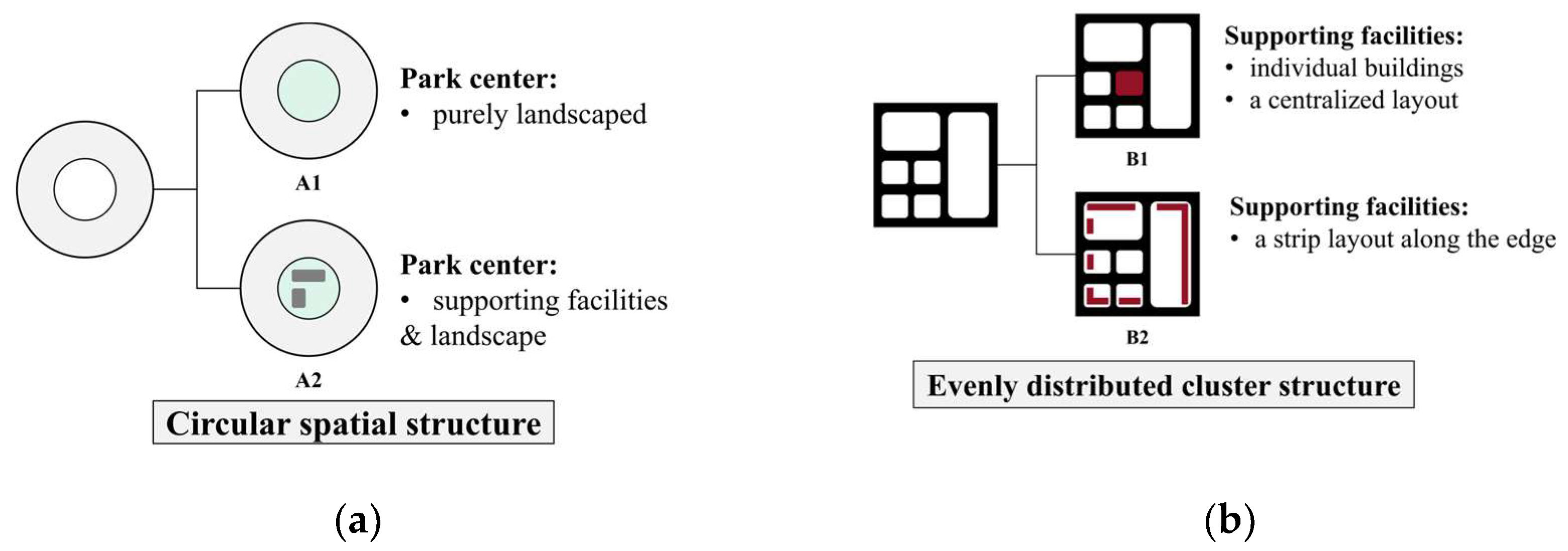
2.2. Idealized Models of Science and Technology Industrial Park
- Unified Park Plot and Floor Area Ratio: The model area is a rectangular plot measuring 300 m × 300 m (total area of 9 hm2), with urban roads surrounding the four boundaries of the plot. The FAR of the plot is set at 1.6.
- Building Density: The building density should be no less than 25% and no more than 50%.
- Functional Proportion: The proportion of building functions is approximately 80:15:5 for the study-and-development office area, commercial-and-catering supporting area, and cultural service supporting area, respectively. Other building functions are ignored.
- Building Form: The building form is simplified, with shapes mainly being rectangular, “L”-shaped, and “C”-shaped. All buildings have a due-south orientation. The buildings are primarily multi-story, with a maximum height of 50 m for any single building.
- Floor Height: The first floor of any building is 4.5 m high. For buildings with study-and-development office functions, the floor height is 4.2 m, while for those with supporting functions, it is 4.5 m.
- Building Layout Relationship: Building clusters are formed through three geometric operations of array, symmetry, and enclosure. The overall layout of the building cluster follows the principle of being lower in the south and higher in the north.
- Supporting Function Layout Principle: When supporting functions are centrally arranged, they are located in the center of the site. When they are dispersed, they are evenly distributed. When both arrangements are combined, the dispersed supporting functions are placed around the periphery of the site.
2.3. Quantification of Key Morphological Parameters
3. Simulation Results
3.1. Photovoltaic Potential Assessment and Simulation Results
3.1.1. Photovoltaic Potential Evaluation Metric
- EGT = annual total photovoltaic electricity output [kWh/a];
- AT = total gross floor area of the building cluster [m2].
3.1.2. Photovoltaic Potential Calculation
- EP = annual electricity yield of the photovoltaic system on the building surface [kWh/a];
- HA = annual solar irradiation on the corresponding building surface [kWh/(m2·a)];
- Apv = installable area of photovoltaic modules on the corresponding building surface [m2];
- η = photovoltaic conversion efficiency [%];
- K = integrated efficiency coefficient [%];
- Rd = degradation rate of the photovoltaic system [%];
- N = lifecycle of the photovoltaic system [a].
- Apv = installable area of photovoltaic modules on the corresponding building surface [m2];
- Arf = area of the roof or corresponding facade [m2];
- Crf = installation coefficient, equal to Cr for roof surfaces and 1.0 for facades;
- CT = proportion of the roof or corresponding facade area with solar irradiation exceeding the threshold [%].
- Cr = rooftop installation coefficient;
- Cra = rooftop area coefficient;
- Cf = equipment coefficient;
- Cst = solar thermal coefficient;
- Cs = shading coefficient;
- Crt = rooftop type coefficient;
- Cco = effective area coefficient.
- T = radiation threshold [kWh/(m2·a)];
- Csys = cost of per unit area for photovoltaic systems over entire life cycle [RMB/m2];
- η = photovoltaic conversion efficiency [%];
- K = integrated efficiency coefficient [%];
- Celec = feed-in tariff for photovoltaic power [RMB/kWh];
- Rd = degradation rate of the photovoltaic system [%];
- N = lifecycle of the photovoltaic system [a].
- Csys = cost of per unit area for photovoltaic systems over entire life cycle [RMB/m2];
- Cins = initial installation cost of the photovoltaic system [RMB/W];
- Pd = power density of photovoltaic modules [W/ m2];
- RAnn = annual system maintenance coefficient [%];
- N = lifecycle of the photovoltaic system [a].
3.1.3. Simulated Photovoltaic Potential
3.2. Energy Use Intensity Assessment and Simulation Results
3.2.1. Energy Use Intensity Evaluation Metric
- EUT = Total annual energy consumption of the building cluster [kWh/a];
- AT = Total floor area of the building cluster [m2].
3.2.2. Energy Use Intensity Evaluation Calculation
3.2.3. Simulated Energy Use Intensity
3.3. Integrated Energy Performance Assessment and Results
3.3.1. Integrated Energy Performance Metrics
- Net Energy Use Intensity (NEUI)
- 2.
- Potential Utilization Ratio of Renewable Energy (PURRE)
3.3.2. Integrated Energy Performance Calculation Results
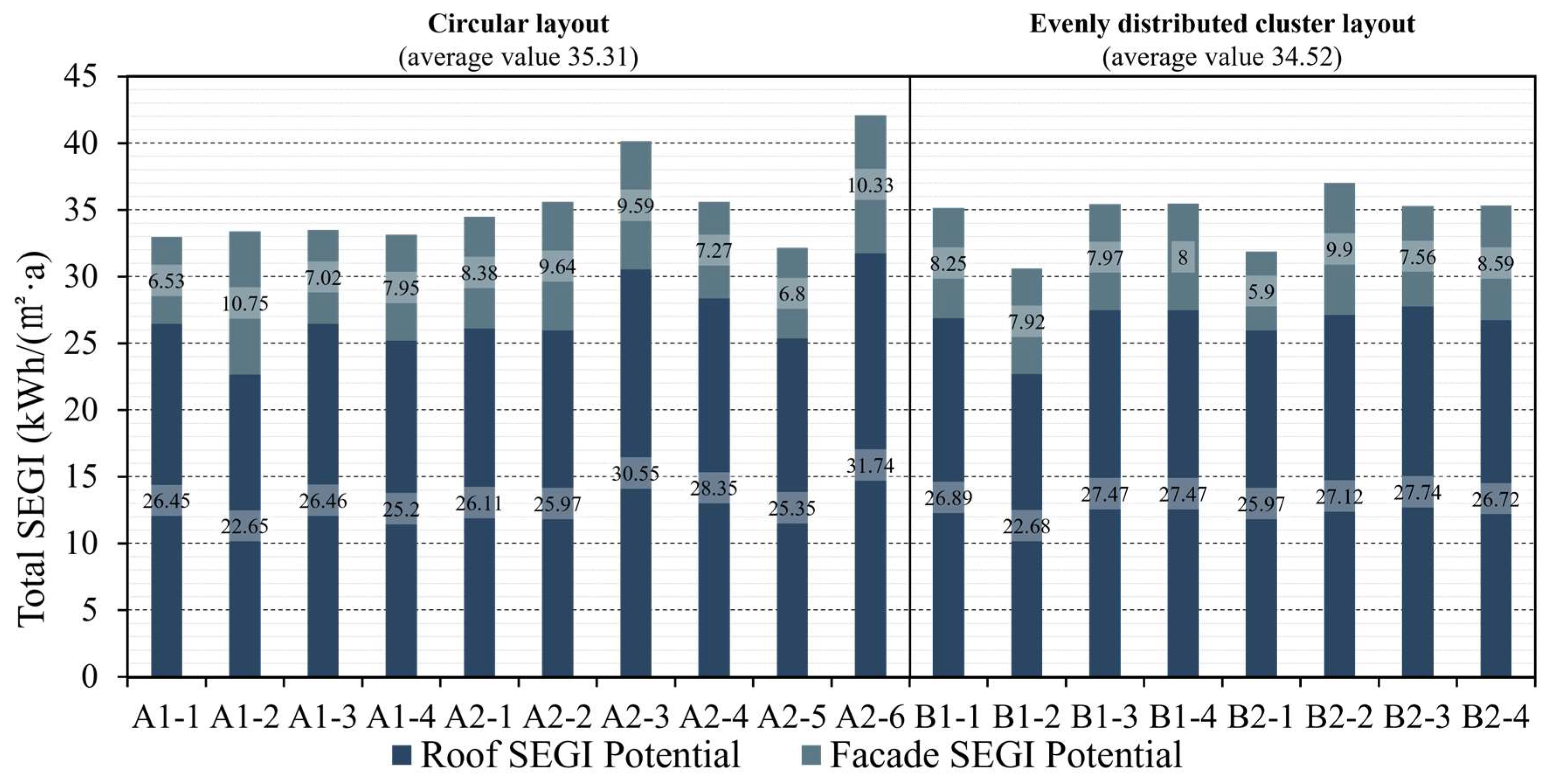
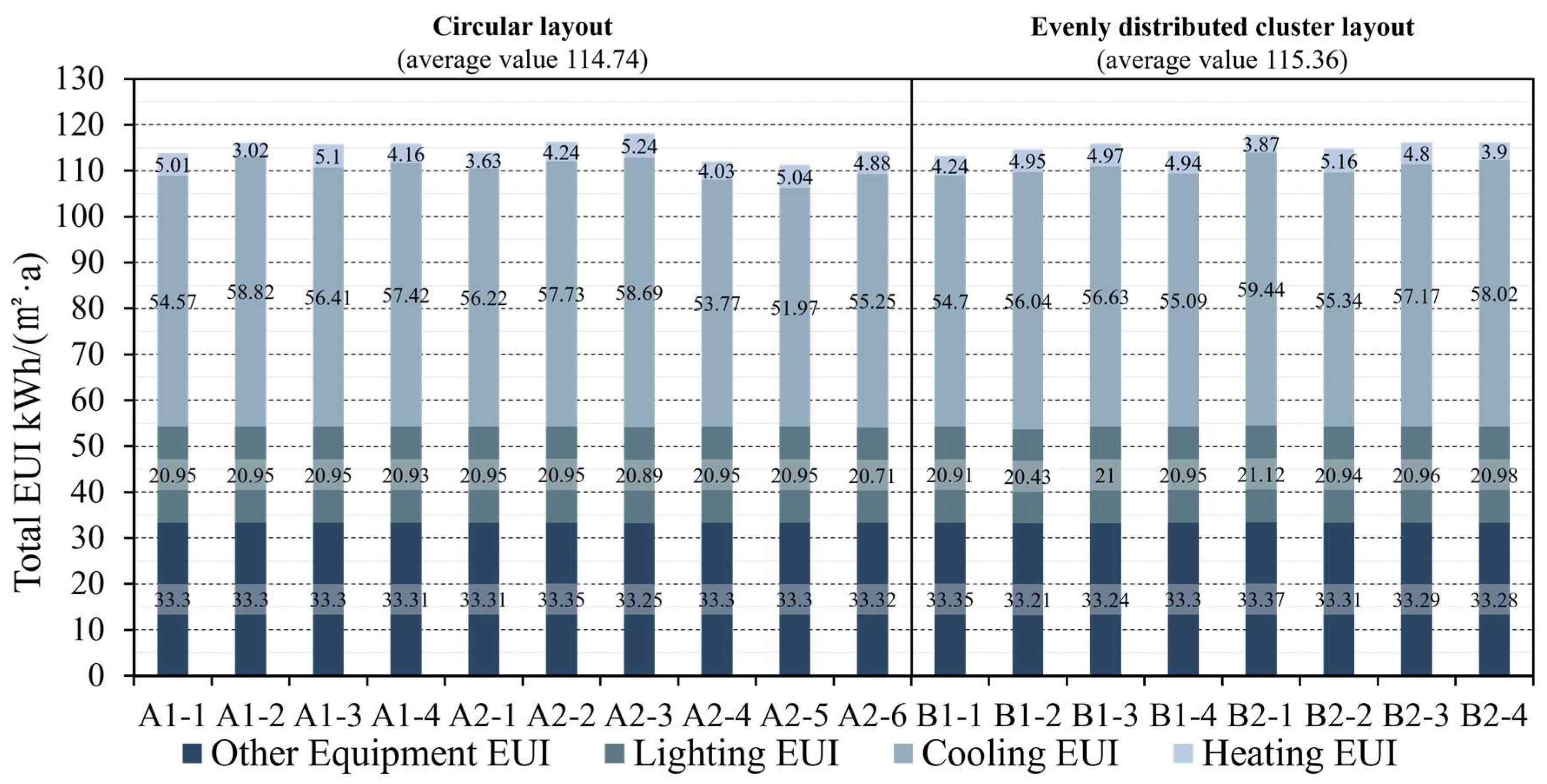
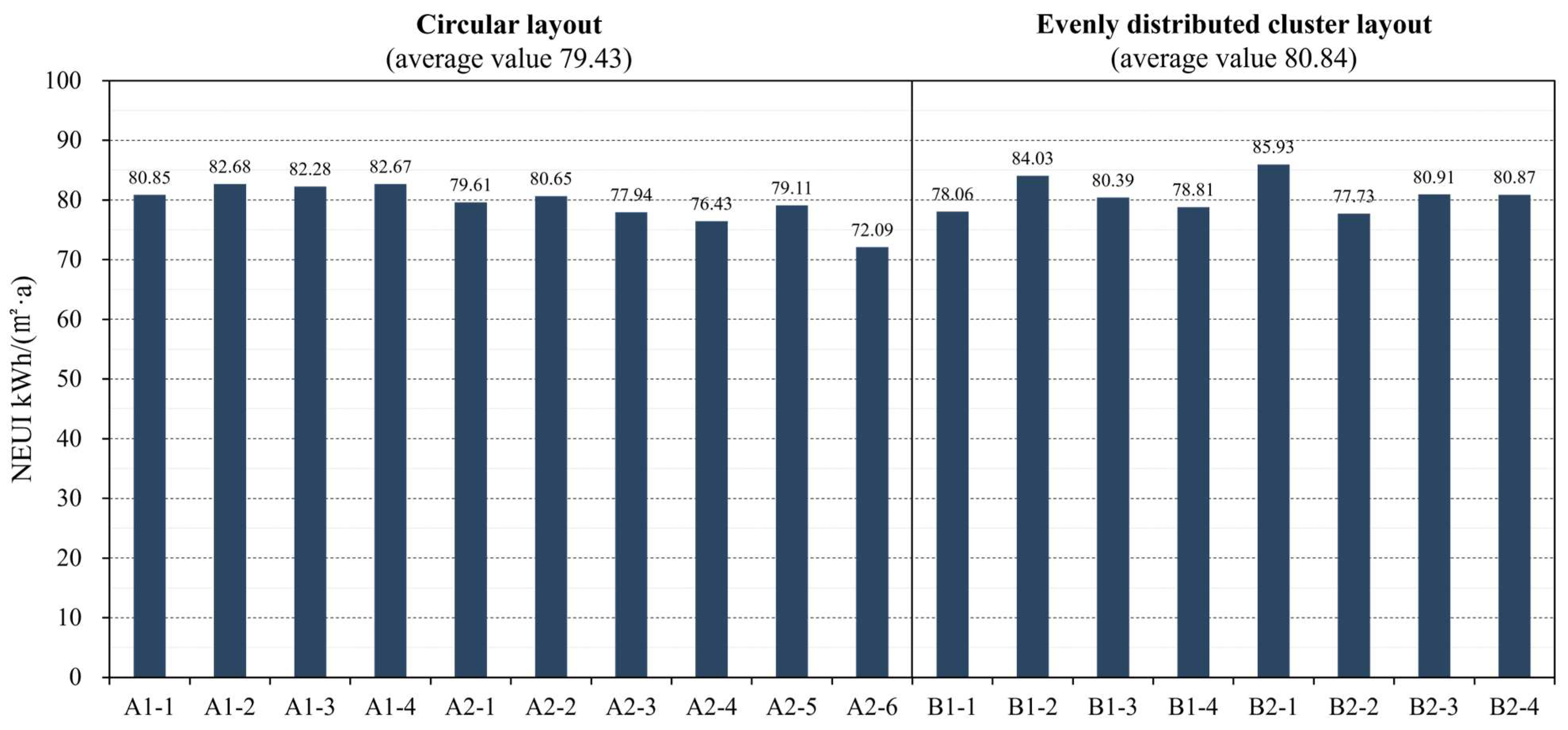
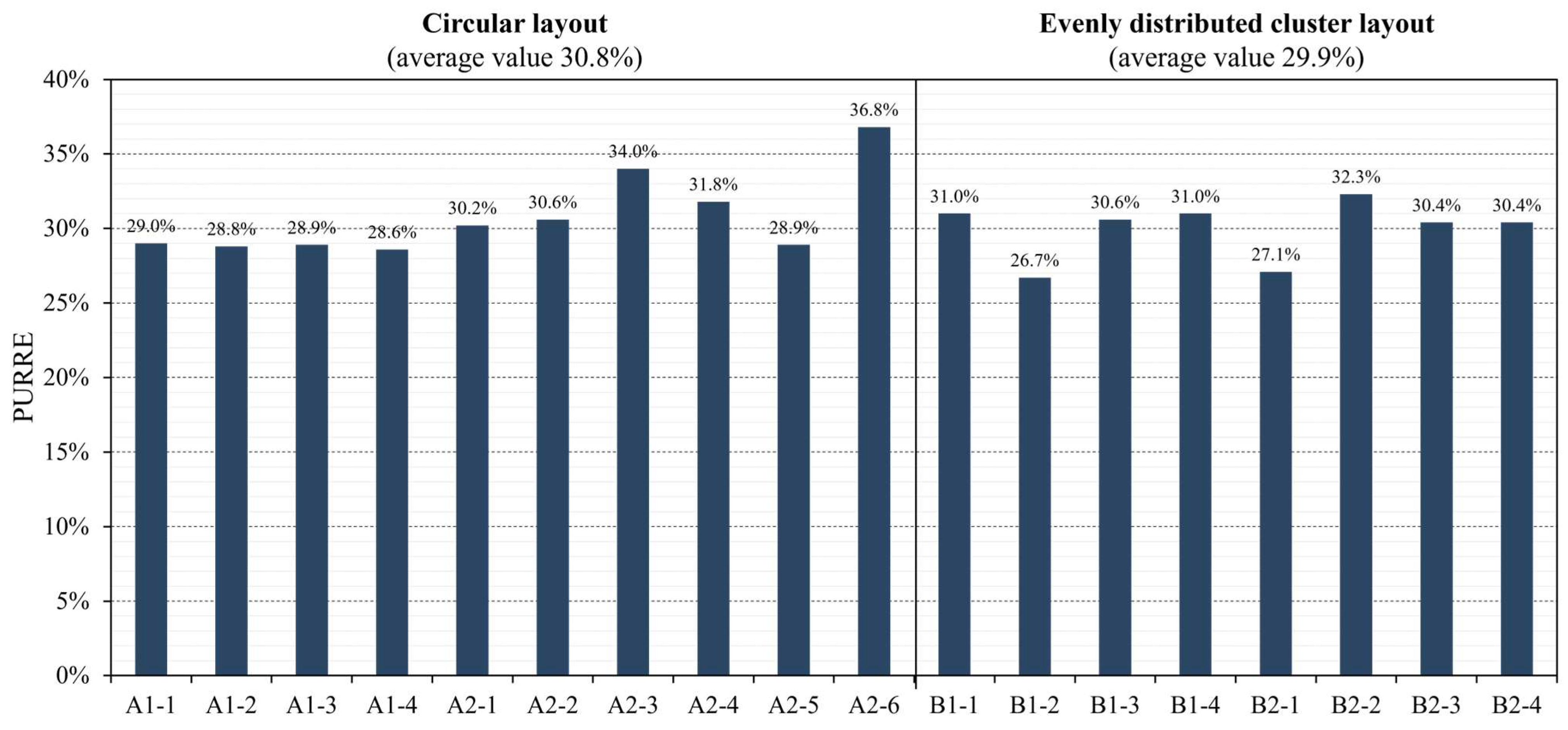
3.4. Summary of Simulation Results
4. Low-Carbon Design Strategies
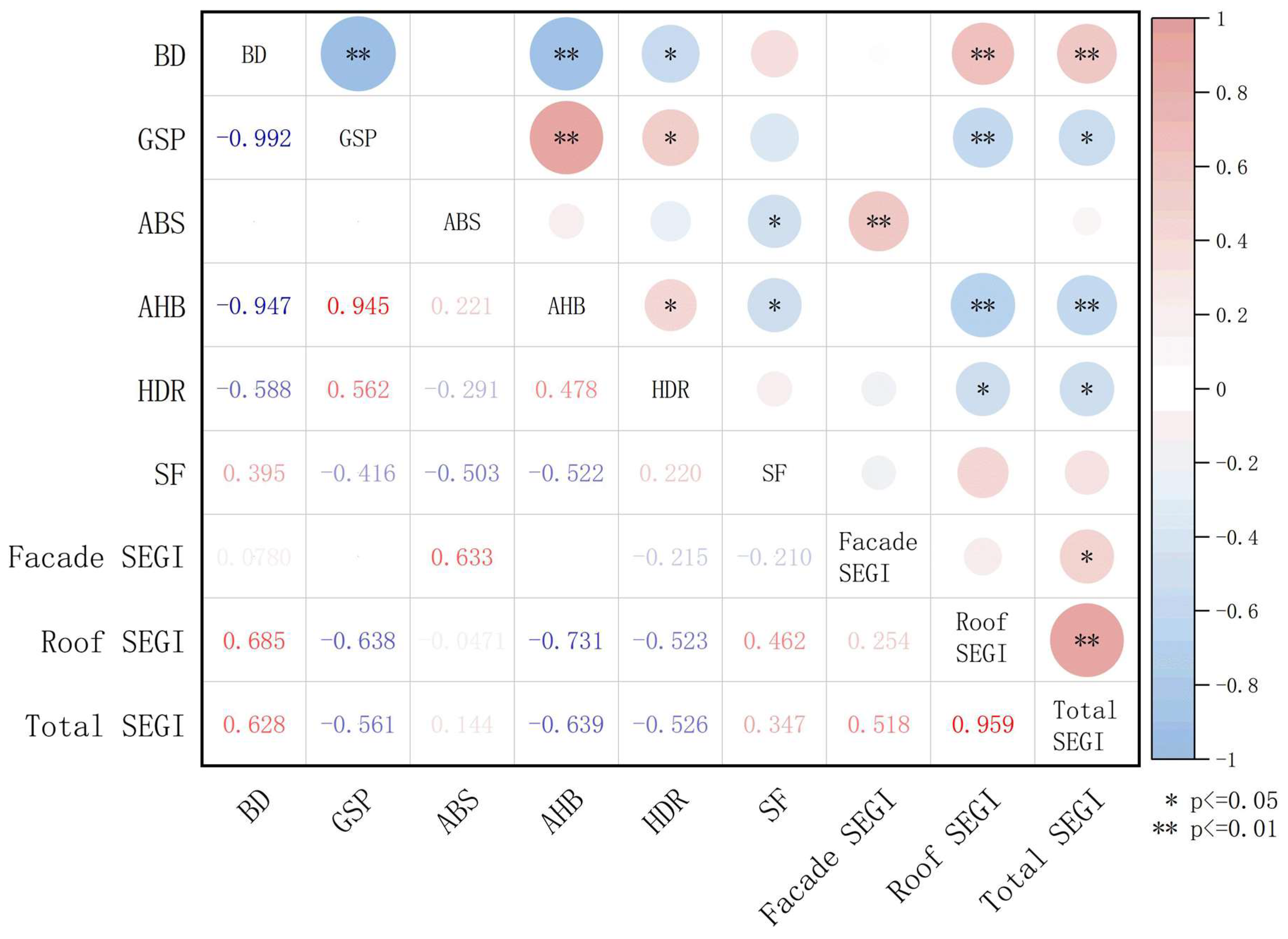
4.1. Morphological Characteristics of Superior Integrated Energy Performance
- Development intensity: Within allowable limits, maximize building density. As shown in Table 2 and Table 6, parks with superior integrated energy performance are all high-density developments. The building densities of A2-3, A2-4, A2-6, and B2-2 are 41.3%, 40.0%, 41.3%, and 39.0%, respectively, around 40%. For new developments, a target range of 35–40% is recommended.
- Spatial structure: Adopt a circular layout as the primary form. Among the top four parks with the best overall energy performance, the circular layout dominates. The highest-performing models, A2-6 and A2-3, combine supporting facilities with or within landscaping, while the outer circle integrates research and development clusters and ancillary functions (Figure 3).
- Morphological parameters: Under the study’s prescribed FAR of 1.6, an average building height of 16–18 m (four to five stories) is optimal; where multi-story height limits permit 20–24 m, the lower bound within this range yields improved energy performance. The building-cluster shape coefficient should be minimized—expected to fall between 0.15 and 0.20 after facade articulation. For predominantly mid-rise technology parks, long facades should be oriented north–south and the height-to-depth ratio should be kept to about 0.3. North–south inter-building spacing should generally not be less than 20 m for medium-intensity sites (FAR 1.0–3.0) and should be maximized beyond this threshold to reduce mutual shading.
- Building form: As shown in Figure 3, the four parks with the best integrated energy performance are dominated by simple, rectangular or square footprints and prefer rectangular or square footprints of 2000–4000 m2. Avoid complex multi-height assemblies, stagger blocks along the north–south axis, and limit continuous facade length to local code maxima to help integrated energy performance.
4.2. Energy-Performance-Driven Low-Carbon Design Strategies
4.2.1. High-Density Development Strategy
4.2.2. Circular Layout Strategy
4.2.3. Supporting-Function Centralized Layout Strategy
4.2.4. Carbon Sink Enhancement Strategy
5. Discussion and Conclusions
- Based on a survey of existing parks, science and technology industrial parks were classified into two spatial typologies—circular and evenly distributed clusters—from which 18 idealized models were generated to represent mid-rise, block-scale developments.
- An assessment methodology incorporating heat-island effects was established. First, six morphological parameters were selected to characterize each idealized model. Then, Ladybug Tools coupled with Radiance simulated surface irradiance and photovoltaic potential, while Dragonfly generated microclimate-adjusted weather files for URBANopt-driven energy simulations. Finally, Net Energy Use Intensity (NEUI) and Potential Utilization Ratio of Renewable Energy (PURRE) were adopted as composite performance indicators.
- Comparative analyses revealed that block-scale parks of circular layouts with high density (about 35–40%), low average building height (about 17–18 m), and a shape factor of about 0.15 generally achieve lower NEUI and higher PURRE than evenly distributed ones. Four low-carbon design strategies were therefore proposed: high-density development guided by morphological-parameter control, circular-based spatial layout, centralized placement of supporting facilities, and carbon-sink enhancement through green technologies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FAR | Floor Area Ratio |
| BD | Building Density |
| GSP | Green Space Ratio |
| ABS | Average North–South Building Spacing |
| ABH | Average Building Height |
| HDR | Height-to-Depth Ratio |
| SF | Building-Cluster Shape Factor |
| SEGI | Solar Energy Generation Intensity |
| EUI | Energy Use Intensity |
| UWG | Urban Weather Generator |
| SHGC | Solar Heat Gain Coefficient |
| NEUI | Net Energy Use Intensity |
| PURRE | Potential Renewable Energy Utilization Rate |
References
- Yin, H.; Zhou, X. Research on Low-Carbon Development Model of Domestic and Overseas Typical Cities and Parks. Shanghai Energy Conserv. 2022, 4, 363–369. (In Chinese) [Google Scholar]
- Li, J.; Liu, K. Theory and Practice of Industrial Park Master Planning; Science Press: Beijing, China, 2021. (In Chinese) [Google Scholar]
- Wu, Y.; Zhang, B.; Wu, C.; Zhang, T.; Liu, F. Optimal site selection for parabolic trough concentrating solar power plant using extended PROMETHEE method: A case in China. Renew. Energy 2019, 143, 1910–1927. [Google Scholar] [CrossRef]
- Izquierdo, S.; Rodrigues, M.; Fueyo, N. A method for estimating the geographical distribution of the available roof surface area for large-scale photovoltaic energy-potential evaluations. Sol. Energy 2008, 82, 929–939. [Google Scholar] [CrossRef]
- De Cristo, E.; Evangelisti, L.; Barbaro, L.; De Lieto Vollaro, R.; Asdrubali, F. A Systematic Review of Green Roofs’ Thermal and Energy Performance in the Mediterranean Region. Energies 2025, 18, 2517. [Google Scholar] [CrossRef]
- Liao, W.; Xu, S.; Lin, B. Prototype Study of the Solar Building Large-scale Application: Simulation Study of the Urban Form and Solar Availability. Cent. China Archit. 2013, 31, 64–66. (In Chinese) [Google Scholar]
- Xu, S. Discussion on the Assessment of Utilization Potential of Solar Energy. Dyn. (Ecol. City Green Build.) 2016, 2, 20–23. (In Chinese) [Google Scholar]
- Yang, X.; Peng, L.L.; Jiang, Z.; Chen, Y.; Yao, L.; He, Y.; Xu, T. Impact of urban heat island on energy demand in buildings: Local climate zones in Nanjing. Appl. Energy 2020, 260, 114279. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, J.; Yu, W.; Ren, J.; Xiao, X.; Xia, J.C. Relationship between urban spatial form and seasonal land surface temperature under different grid scales. Sustain. Cities Soc. 2023, 89, 104374. [Google Scholar] [CrossRef]
- Jiang, Z.; Yang, F. Simulation Analysis of the Impact of Urban Morphological Factors on Building Energy Consumption at the Block-scale. Build. Sci. 2022, 38, 140–149. (In Chinese) [Google Scholar]
- Gu, C. China’s High-Tech Industries and Parks; CITIC Press: Beijing, China, 1999; pp. 5–21. (In Chinese) [Google Scholar]
- Tang, X. Research on the Spatial Layout of Shanghai Industrial Parks and Their Integration with New Town Development. Ph.D. Thesis, East China Normal University, Shanghai, China, 2014. (In Chinese). [Google Scholar]
- Xu, J.; Zhang, X. Research and Planning Design of China’s Industrial Parks; Tongji University Press: Shanghai, China, 2015. (In Chinese) [Google Scholar]
- Zhang, H. Research for Public Space Systems Design of High-Density Science and Technology Park. Master’s Thesis, Shenzhen University, Shenzhen, China, 2019. (In Chinese). [Google Scholar]
- Yang, Z. Research on Three Dimensional Design of Public Space in High-Density Science and Technology Industrial Park. Master’s Thesis, South China University of Technology, Guangzhou, China, 2021. (In Chinese). [Google Scholar]
- Wu, Y.; Song, S. Comparative Study on the Spatial Form of “Internet +” Emerging Industrial Parks in Hangzhou West Innovation Corridor—Taking Xixi Park of Alibaba, the First Phase of ZOTP and Dream Town as Examples. Archit. Cult. 2018, 10, 83–85. (In Chinese) [Google Scholar]
- Xu, S. Current Situation and Prospect of Green Low Carbon Park. Shanghai Energy Conserv. 2019, 6, 438–440. (In Chinese) [Google Scholar]
- Liu, Y.; Wang, X.; Wang, J.; Zeng, X.; Wang, W. Exploration on the Construction Scheme of Near-zero Energy Consumption and Near-zero Carbon Smart Park. Intell. Build. Smart City 2023, 10, 12–15. (In Chinese) [Google Scholar]
- Quan, S.J.; Wu, J.; Wang, Y.; Shi, Z.; Yang, T.; Yang, P.P.-J. Urban Form and Building Energy Performance in Shanghai Neighborhoods. Energy Procedia 2016, 88, 126–132. [Google Scholar] [CrossRef]
- Lima, I.; Scalco, V.; Lamberts, R. Estimating the impact of urban densification on high-rise office building cooling loads in a hot and humid climate. Energy Build. 2019, 182, 30–44. [Google Scholar] [CrossRef]
- Charan, T.; Mackey, C.; Irani, A.; Polly, B.; Ray, S.; Fleming, K.; El Kontar, R.; Moore, N.; Elgindy, T.; Cutler, D.; et al. Integration of Open-Source URBANopt and Dragonfly Energy Modeling Capabilities into Practitioner Workflows for District-Scale Planning and Design. Energies 2021, 14, 5931. [Google Scholar] [CrossRef]
- Salvalai, G.; Zhu, Y.; Maria Sesana, M. From building energy modeling to urban building energy modeling: A review of recent research trend and simulation tools. Energy Build. 2024, 319, 114500. [Google Scholar] [CrossRef]
- Bande, L.; Afshari, A.; Al Masri, D.; Jha, M.; Norford, L.; Tsoupos, A.; Marpu, P.; Pasha, Y.; Armstrong, P. Validation of UWG and ENVI-Met Models in an Abu Dhabi District, Based on Site Measurements. Sustainability 2019, 11, 4378. [Google Scholar] [CrossRef]
- Wong, N.H.; Jusuf, S.K.; Syafii, N.I.; Chen, Y.; Hajadi, N.; Sathyanarayanan, H.; Manickavasagam, Y.V. Evaluation of the impact of the surrounding urban morphology on building energy consumption. Sol. Energy 2011, 85, 57–71. [Google Scholar] [CrossRef]
- TM Building Energy Demand Based on Urban Morphology Analysis. 2013. Available online: https://www.academia.edu/72590597/Building_Energy_Demand_Based_on_Urban_Morphology_Analysis (accessed on 10 January 2024).
- Zhu, D.; Song, D.; Shi, J.; Fang, J.; Zhou, Y. The Effect of Morphology on Solar Potential of High-Density Residential Area: A Case Study of Shanghai. Energies 2020, 13, 2215. [Google Scholar] [CrossRef]
- Wang, J. Research on the Distribution and Evaluation of Solar Photovoltaic Potential in Urban Block Scale. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2018. (In Chinese). [Google Scholar]
- Tian, J. Research on Solar Photovoltaic Potential of Urban Residential Areas. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2020. (In Chinese). [Google Scholar]
- National Development and Reform Commission; Ministry of Housing and Urban-Rural Development. Notice on Issuing the Development Plan for the Yangtze River Delta Urban Agglomeration [EB/OL]. 3 June 2016. Available online: https://www.ndrc.gov.cn/xxgk/zcfb/ghwb/201606/t20160603_962187.html (accessed on 15 August 2023). (In Chinese)
- Luo, X. Research on green building performance analysis method and application based on Ladybug tool set. J. Suzhou Univ. Sci. Technol. (Eng. Technol. Ed.) 2020, 33, 40–44. (In Chinese) [Google Scholar]
- China Photovoltaic Industry Association. Roadmap for the Development of China’s Photovoltaic Industry (2022–2023). 2023. Available online: https://www.chinapv.org.cn/Industry/resource_1137.html (accessed on 10 January 2024). (In Chinese).
- Bueno, B. Study and Prediction of the Energy Interactions Between Buildings and the Urban Climate. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2013. [Google Scholar]
- Salvati, A.; Monti, P.; Coch Roura, H.; Cecere, C. Climatic performance of urban textures: Analysis tools for a Mediterranean urban context. Energy Build. 2019, 185, 162–179. [Google Scholar] [CrossRef]
- Boccalatte, A.; Fossa, M.; Gaillard, L.; Menezo, C. Microclimate and urban morphology effects on building energy demand in different European cities. Energy Build. 2020, 224, 110129. [Google Scholar] [CrossRef]
- Zhang, H.; Cui, K. Design Guidelines for Green Public Buildings Adapted to Hot-Summer/Cold-Winter Climate; China Architecture & Building Press: Beijing, China, 2021. (In Chinese) [Google Scholar]
- Kanters, J.; Wall, M.; Dubois, M.-C. Typical Values for Active Solar Energy in Urban Planning. Energy Procedia 2014, 48, 1607–1616. [Google Scholar] [CrossRef]


| Morphological Parameters | Equations/Prescribed Limits | Definitions | Schematic Diagram |
|---|---|---|---|
| Building Density (BD) | The ratio (%) of the aggregate footprint area of all buildings to the gross site area within a given land parcel. It indicates the compactness of park development. |  | |
| Green Space Ratio (GSP) | The percentage of the total area of all green spaces to the gross site area within a given land parcel, indicating the degree of landscaping and vegetative coverage. | 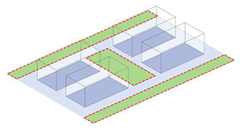 | |
| Average North–South Building Spacing (ABS) | The minimum perpendicular distance between the exterior facades of two adjacent buildings or structures measured along the north–south axis; distances exceeding 50 m are excluded from the calculation. This metric indicates the vertical morphology of the building cluster. |  | |
| Average Building Height (ABH) | The average height of all individual buildings within a given site, reflecting the overall vertical profile of the buildings. | 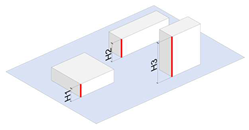 | |
| Height-to-Depth Ratio (HDR) | The volume-weighted average height of the building cluster divided by its volume-weighted average depth, quantifying the vertical-to-horizontal proportions of the park. |  | |
| Building-Cluster Shape Factor (SF) | The ratio of the external envelope area exposed to outdoor air to the enclosed volume of the building, indicating the geometric complexity of the built form and the extent of the heat-exchange surface. | 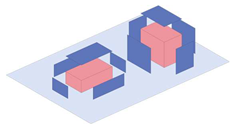 |
| Spatial Structure | Idealized Models | BD | GSP | ABS | ABH | HDR | SF |
|---|---|---|---|---|---|---|---|
| Circular layout | A1-1 | 37.3% | 32% | 20.00 m | 18.50 m | 0.347 | 0.131 |
| A1-2 | 32.0% | 38% | 40.00 m | 23.78 m | 0.396 | 0.114 | |
| A1-3 | 37.0% | 33% | 15.63 m | 18.50 m | 0.680 | 0.162 | |
| A1-4 | 35.6% | 34% | 20.00 m | 19.43 m | 0.547 | 0.140 | |
| A2-1 | 36.4% | 34% | 22.86 m | 18.75 m | 0.382 | 0.133 | |
| A2-2 | 36.7% | 33% | 20.00 m | 18.98 m | 0.622 | 0.149 | |
| A2-3 | 41.3% | 30% | 35.00 m | 16.79 m | 0.294 | 0.140 | |
| A2-4 | 40.0% | 30% | 25.56 m | 17.22 m | 0.316 | 0.131 | |
| A2-5 | 35.8% | 34% | 21.33 m | 19.37 m | 0.645 | 0.154 | |
| A2-6 | 41.3% | 30% | 26.92 m | 16.49 m | 0.231 | 0.150 | |
| Evenly distributed cluster layout | B1-1 | 39.2% | 31% | 26.67 m | 18.48 m | 0.394 | 0.137 |
| B1-2 | 32.0% | 38% | 15.00 m | 21.43 m | 0.714 | 0.138 | |
| B1-3 | 35.6% | 34% | 20.00 m | 19.55 m | 0.391 | 0.151 | |
| B1-4 | 40.0% | 30% | 23.82 m | 17.23 m | 0.278 | 0.153 | |
| B2-1 | 32.0% | 38% | 35.00 m | 21.81 m | 0.685 | 0.130 | |
| B2-2 | 39.0% | 31% | 28.00 m | 18.30 m | 0.654 | 0.160 | |
| B2-3 | 36.1% | 34% | 20.00 m | 19.22 m | 0.384 | 0.151 | |
| B2-4 | 37.0% | 33% | 28.63 m | 18.75 m | 0.412 | 0.151 |
| Envelope Component | K-Value [W/m2·K] | SHGC |
|---|---|---|
| roof | 0.4 | / |
| exterior wall | 0.8 | / |
| floor | 0.8 | / |
| exterior window | 2.2 | 0.4 |
| Functional Type | Orientation | Window-to-Wall Ratio | Sill Height | Window Height | Window Spacing | Floor-to-Floor Height |
|---|---|---|---|---|---|---|
| study-and- development office | South facade | 0.25 | 0.9 m | 2.4 m | 3 m | 4.2 m |
| North facade | 0.25 | |||||
| East facade | 0.2 | |||||
| West facade | 0.2 | |||||
| commercial-and- catering | South facade | 0.2 | 0.9 m | 2.4 m | 3 m | 4.5 m |
| North facade | 0.2 | |||||
| East facade | 0.1 | |||||
| West facade | 0.1 | |||||
| cultural services | South facade | 0.3 | 0.9 m | 2.7 m | 4.5 m | 4.2 m |
| North facade | 0.2 | |||||
| East facade | 0.15 | |||||
| West facade | 0.15 |
| Data Type | Value | Data Source/Basis |
|---|---|---|
| meteorological data | Shanghai Standard Weather Data | https://www.ladybug.tools/epwmap/, accessed on 28 November 2023 |
| sensible heat (excl. buildings) | 5 W/m2 | UWG recommended value |
| greenspace ratio | calculated from Table 1 | as determined in this study |
| road albedo | 0.05 | the study by Boccalatte et al. [34] |
| vegetation albedo | 0.25 | the study by Boccalatte et al. [34] |
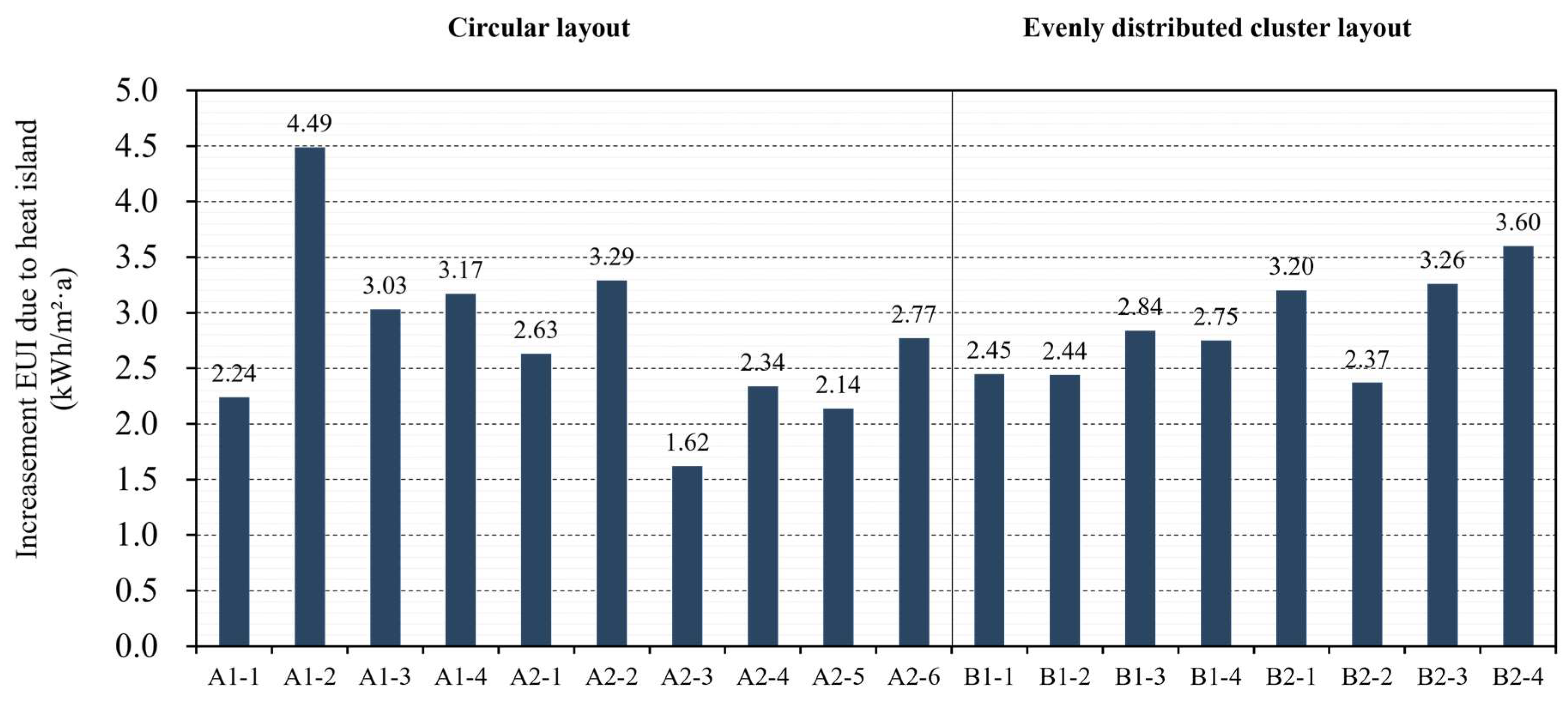
| Spatial Structure | Idealized Models | Total SEGI (kWh/(m2·a)) | Total EUI (kWh/(m2·a)) | NEUI (kWh/(m2·a)) | PURRE (%) | Increased EUI Due to Heat Island (kWh/m2·a) |
|---|---|---|---|---|---|---|
| Circular layout | A1-1 | 32.98 | 113.83 | 80.85 | 29.0 | 2.24 |
| A1-2 | 33.4 | 116.09 | 82.68 | 28.8 | 4.49 | |
| A1-3 | 33.48 | 115.76 | 82.28 | 28.9 | 3.03 | |
| A1-4 | 33.15 | 115.82 | 82.67 | 28.6 | 3.17 | |
| A2-1 | 34.49 | 114.11 | 79.61 | 30.2 | 2.63 | |
| A2-2 | 35.61 | 116.27 | 80.65 | 30.6 | 3.29 | |
| A2-3 | 40.14 | 118.07 | 77.94 | 34.0 | 1.62 | |
| A2-4 | 35.62 | 112.05 | 76.43 | 31.8 | 2.34 | |
| A2-5 | 32.15 | 111.26 | 79.11 | 28.9 | 2.14 | |
| A2-6 | 42.07 | 114.16 | 72.09 | 36.8 | 2.77 | |
| Evenly distributed cluster layout | B1-1 | 35.14 | 113.2 | 78.06 | 31.0 | 2.45 |
| B1-2 | 30.6 | 114.63 | 84.03 | 26.7 | 2.44 | |
| B1-3 | 35.44 | 115.84 | 80.39 | 30.6 | 2.84 | |
| B1-4 | 35.47 | 114.28 | 78.81 | 31.0 | 2.75 | |
| B2-1 | 31.87 | 117.8 | 85.93 | 27.1 | 3.20 | |
| B2-2 | 37.02 | 114.75 | 77.73 | 32.3 | 2.37 | |
| B2-3 | 35.3 | 116.22 | 80.91 | 30.4 | 3.26 | |
| B2-4 | 35.31 | 116.18 | 80.87 | 30.4 | 3.60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, H.; Cao, Y.; Ding, M. Study on Low-Carbon Design Strategy of Block-Scale Science and Technology Industrial Park Based on Solar Energy Utilization Potential and Heat Island Effects. Energies 2025, 18, 5127. https://doi.org/10.3390/en18195127
Ye H, Cao Y, Ding M. Study on Low-Carbon Design Strategy of Block-Scale Science and Technology Industrial Park Based on Solar Energy Utilization Potential and Heat Island Effects. Energies. 2025; 18(19):5127. https://doi.org/10.3390/en18195127
Chicago/Turabian StyleYe, Hai, Yiying Cao, and Mingqi Ding. 2025. "Study on Low-Carbon Design Strategy of Block-Scale Science and Technology Industrial Park Based on Solar Energy Utilization Potential and Heat Island Effects" Energies 18, no. 19: 5127. https://doi.org/10.3390/en18195127
APA StyleYe, H., Cao, Y., & Ding, M. (2025). Study on Low-Carbon Design Strategy of Block-Scale Science and Technology Industrial Park Based on Solar Energy Utilization Potential and Heat Island Effects. Energies, 18(19), 5127. https://doi.org/10.3390/en18195127







