Identification Method for Wideband Oscillation Parameters Caused by Grid-Forming Renewable Energy Sources Based on Multiple Matching Synchrosqueezing Transformation
Abstract
1. Introduction
- (1)
- An analysis of the mechanism by which the MMSST algorithm enhances the performance of traditional SST algorithms in processing oscillatory signals.
- (2)
- Extraction of multi-modal components of oscillatory signals to demonstrate the improved accuracy of parameter identification when combined with the Hilbert transform.
- (3)
- Improvement in the accuracy of wideband oscillation signal parameter estimation in grid-forming converter-based renewable energy systems, thereby supporting more effective suppression of oscillations in grid-forming converters.
2. Methods
2.1. SST
2.2. MMSST
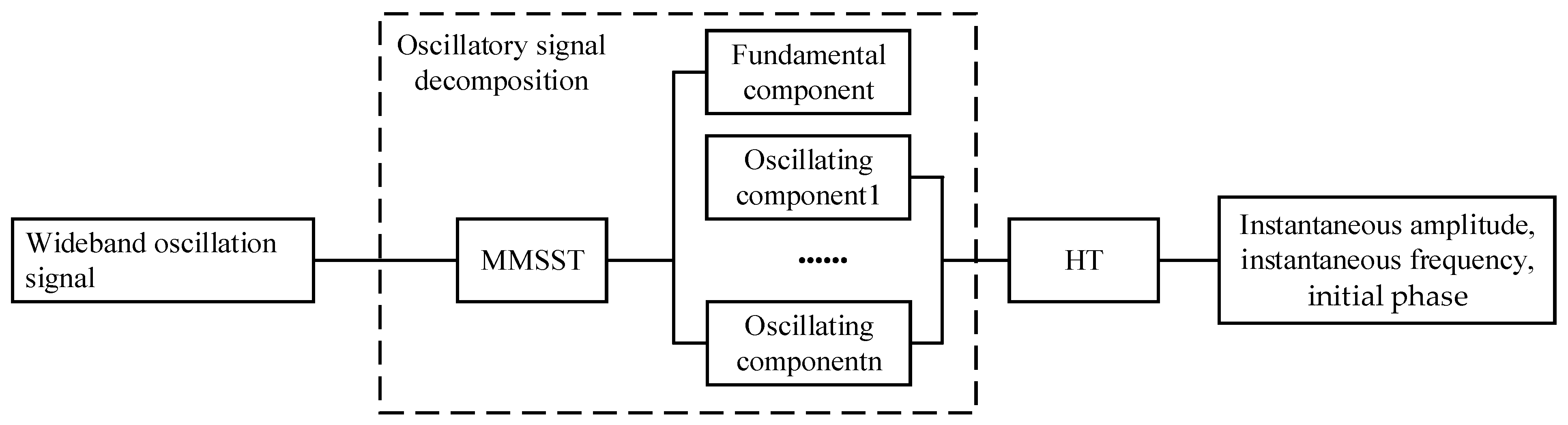
3. Identification Method for Wideband Oscillation Parameters
3.1. Mechanism of Wideband Oscillation Generation
3.2. Parameter Calculation
3.3. Parameter Identification Method
4. Validation Study
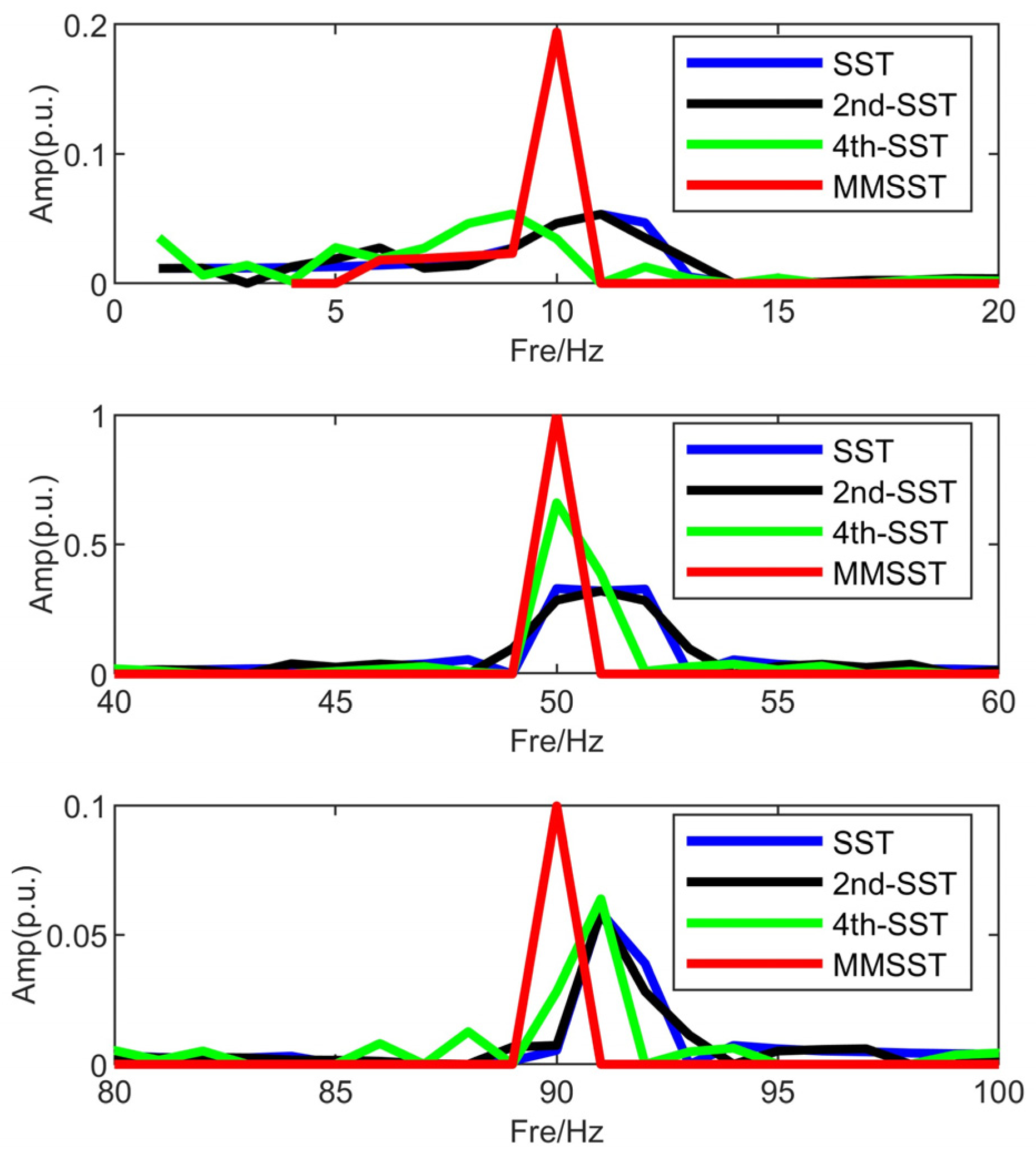
4.1. Synthetic Data Analysis
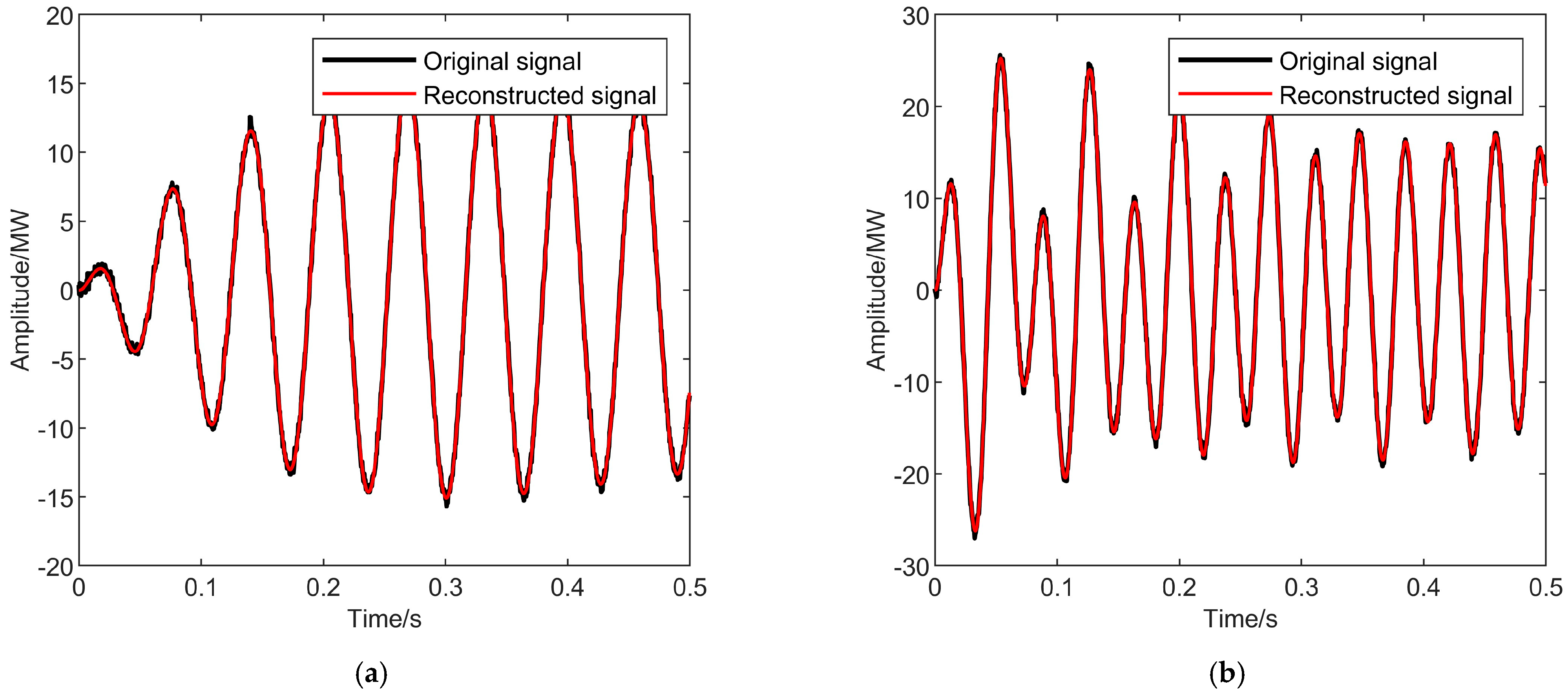
4.2. Simulation Oscillation Signal Analysis
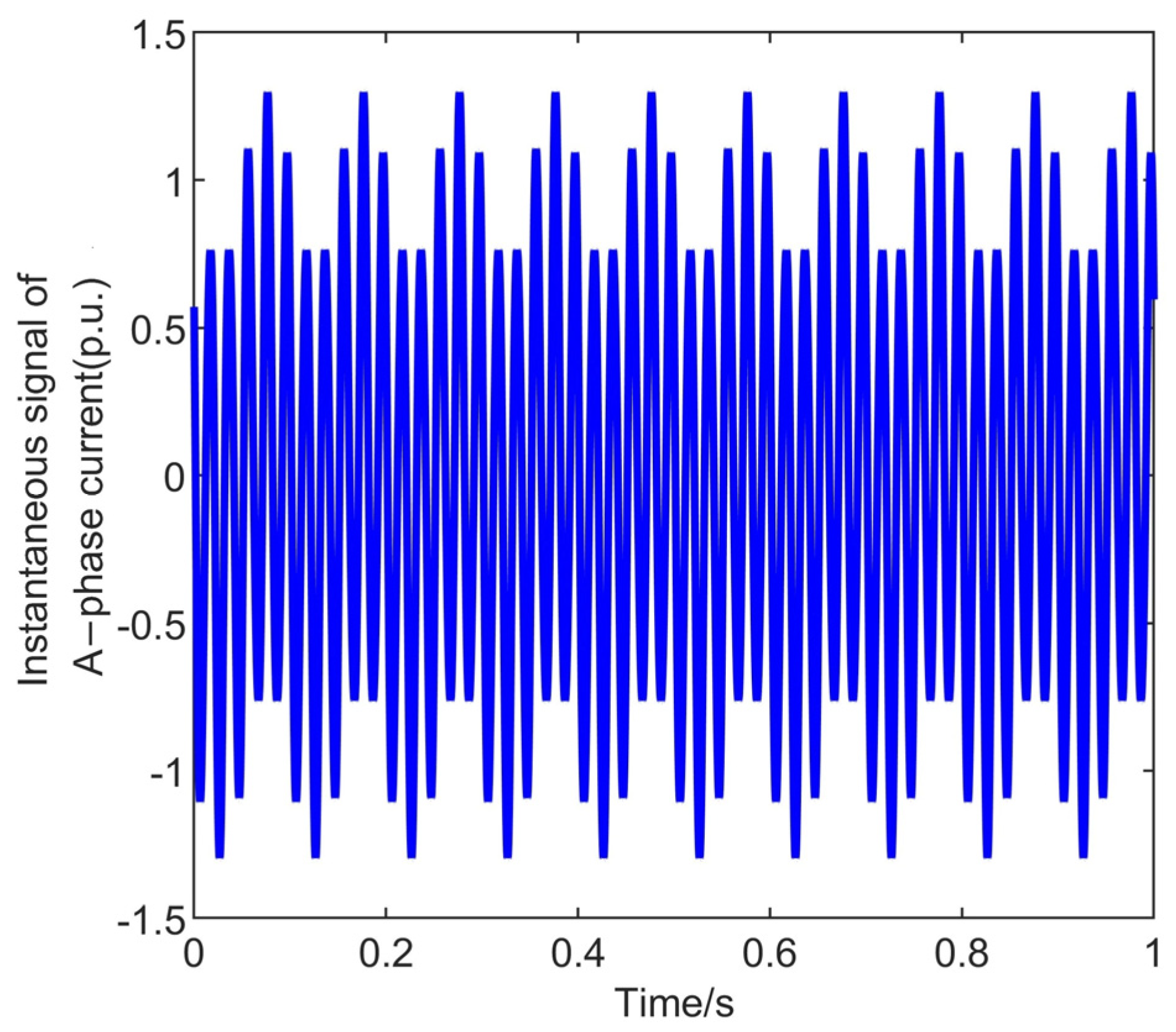
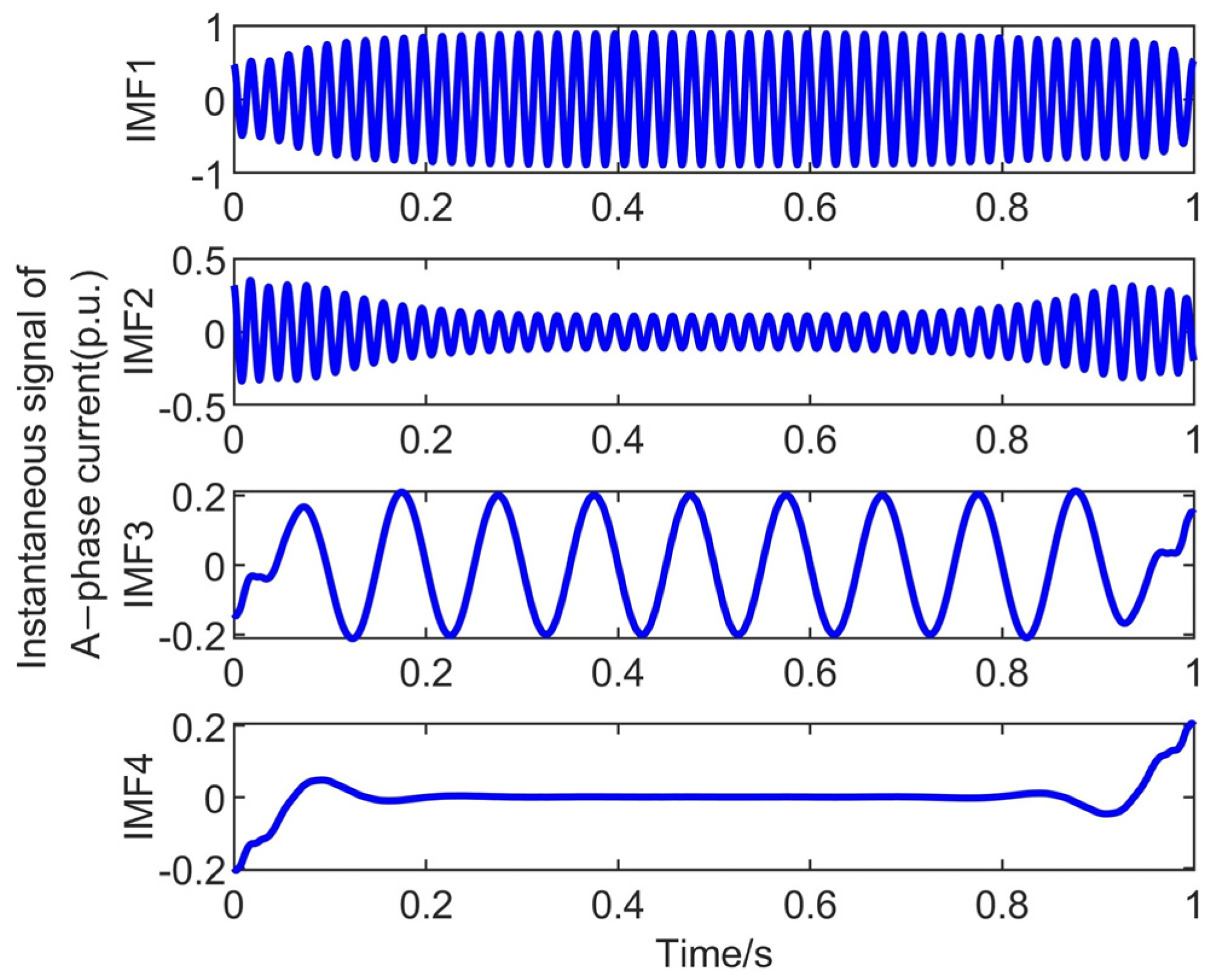
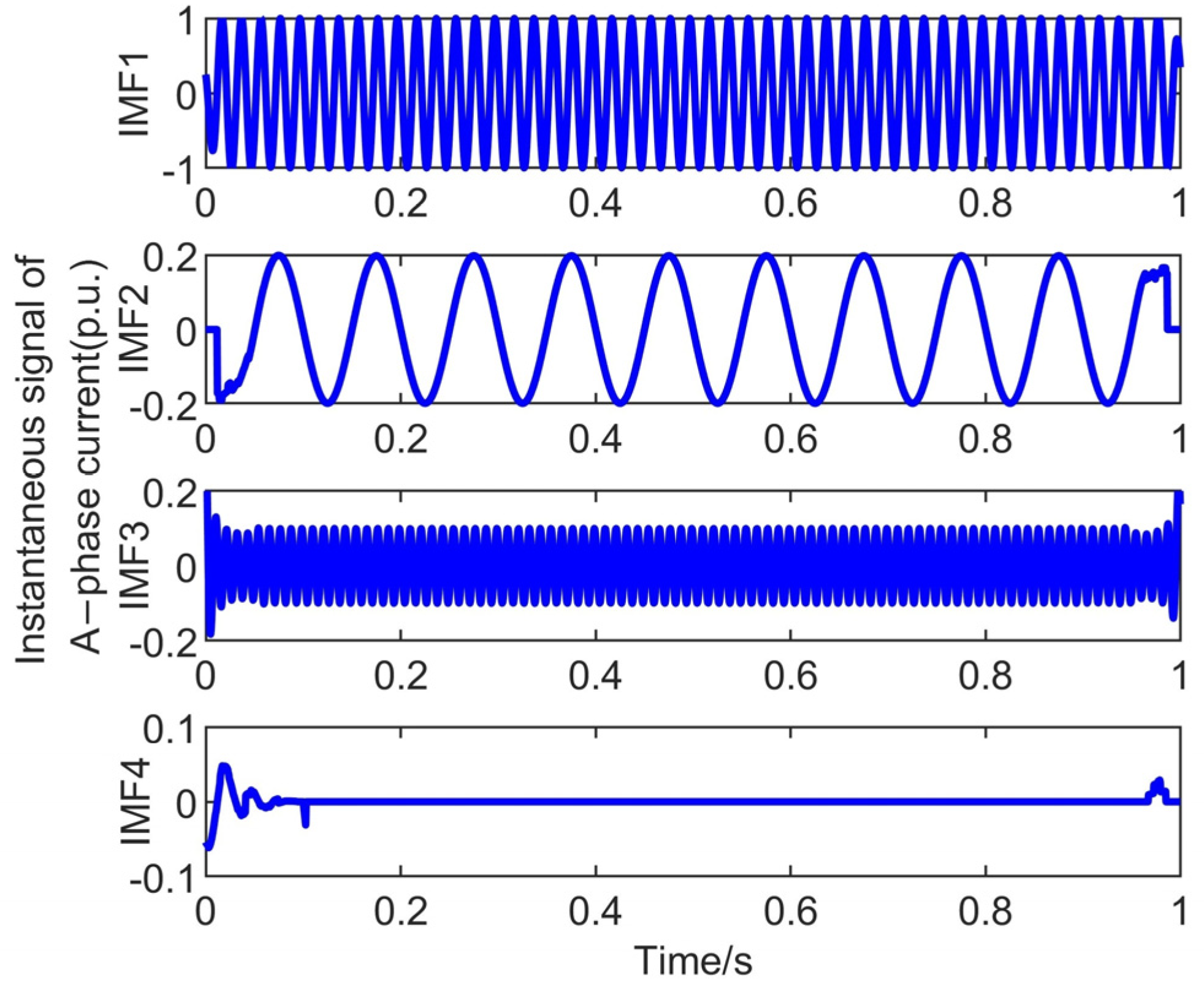
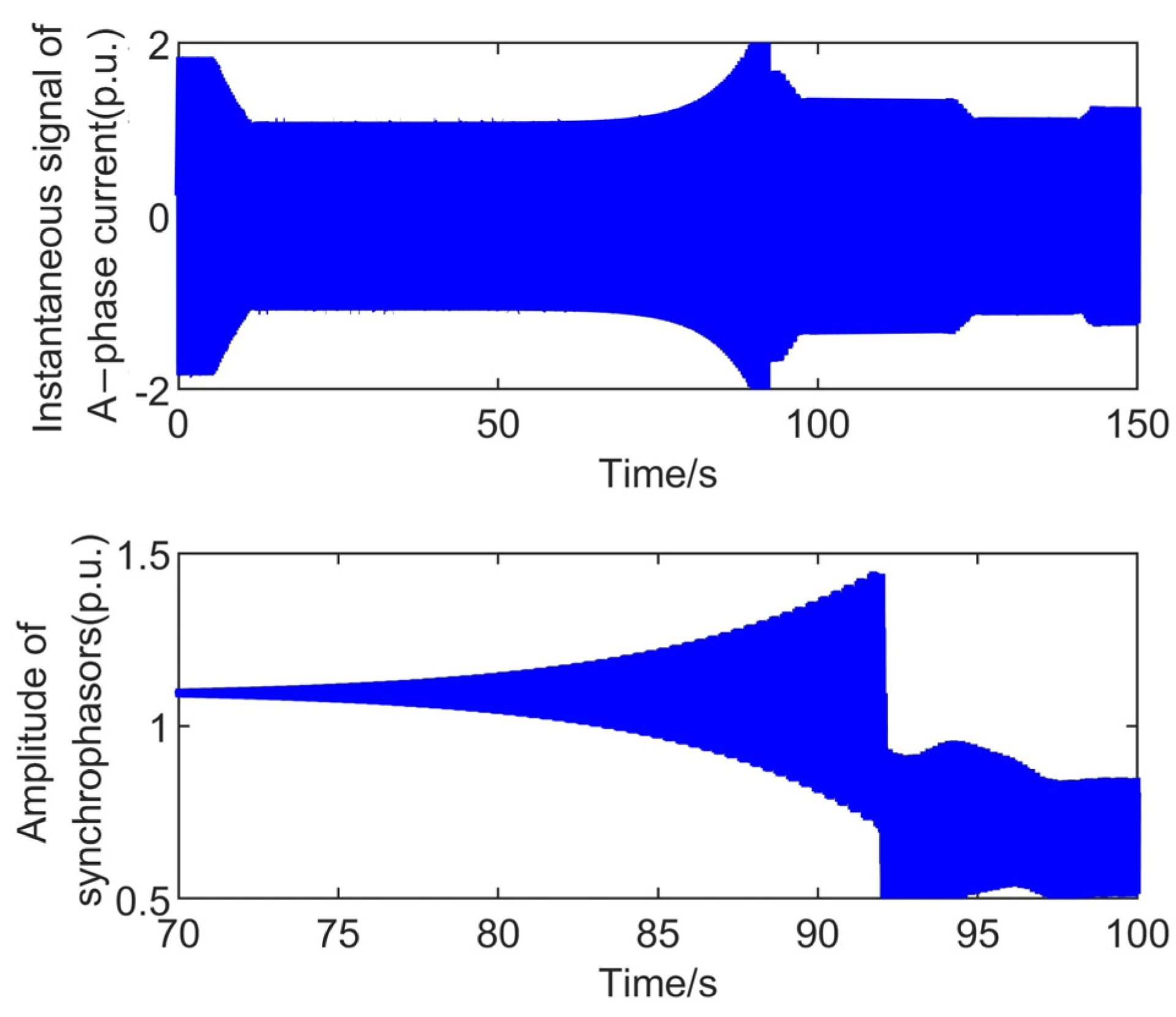
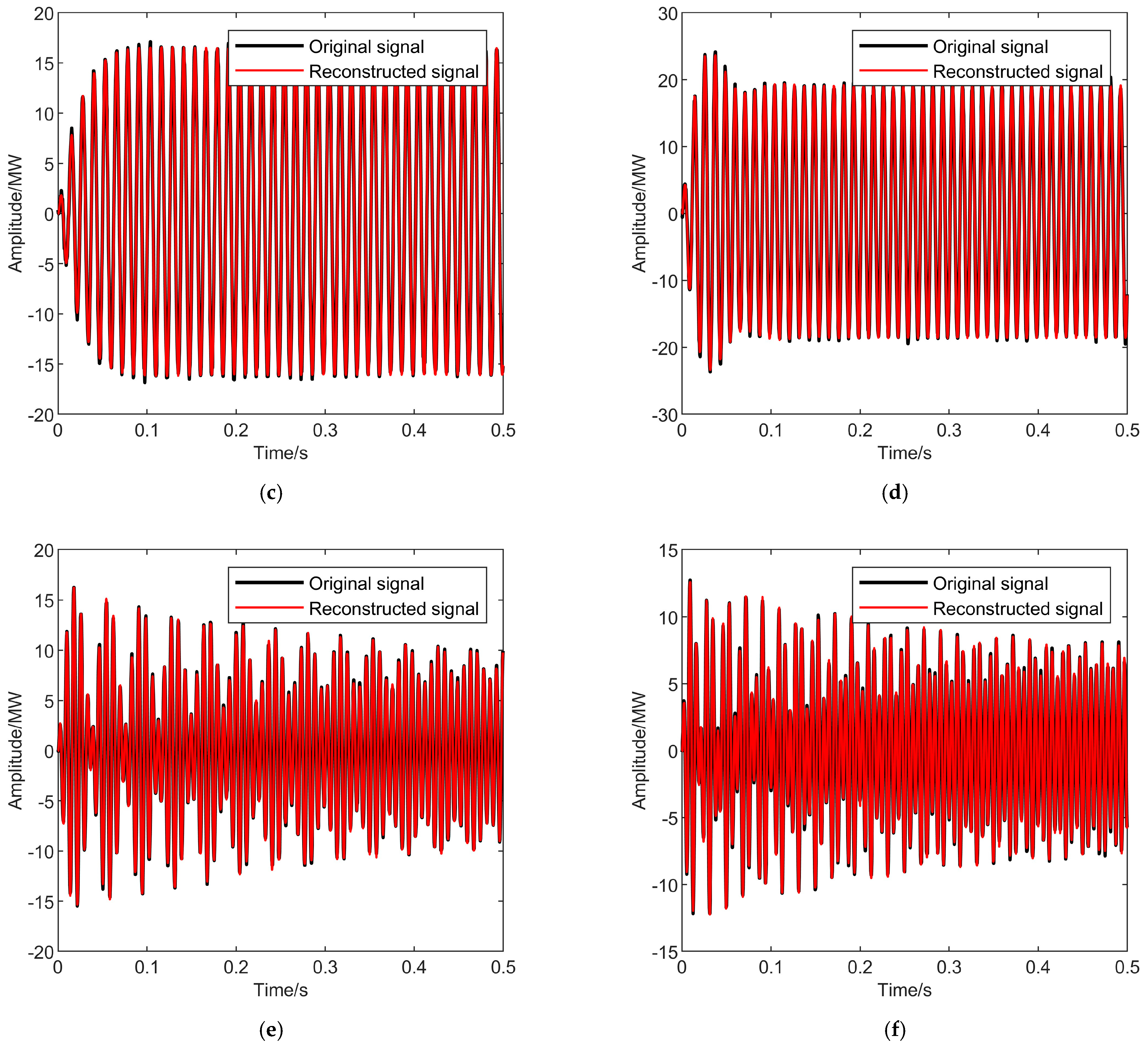
4.3. Actual System Signal Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Perera, U.; Oo, A.M.T.; Zamora, R. Sub synchronous oscillations under high penetration of renewables—A review of existing monitoring and damping methods, challenges, and research prospects. Energies 2022, 15, 8477. [Google Scholar] [CrossRef]
- Qiu, L.; Gu, M.; Chen, Z.; Du, Z.; Zhang, L.; Li, W.; Huang, J.; Fang, J. Oscillation suppression of grid-following converters by grid-forming converters with adaptive droop control. Energies 2024, 17, 5230. [Google Scholar] [CrossRef]
- Chen, L.; Xie, X.; He, J.; Xu, T.; Xu, D.; Ma, N. Wideband oscillationmonitoring in power systems with high-penetration ofrenewable energy sources and power electronics: A review. Renew. Sustain. Energy Rev. 2023, 175, 113148. [Google Scholar] [CrossRef]
- Verma, N.; Kumar, N.; Gupta, S.; Malik, H.; Márquez, F.P.G. Review of sub-synchronous interaction in wind integrated power systems: Classifcation, challenges, and mitigation techniques. Prot. Control Mod. Power Syst. 2023, 8, 17. [Google Scholar] [CrossRef]
- Cheng, Y.; Xie, J.; Zeng, C.; Yang, S.; Sun, H.; Qin, L. Comparison study of the wideband oscillation risk of MMC between grid-following and grid-forming control. Energies 2024, 17, 2507. [Google Scholar] [CrossRef]
- Carta, A.; Locci, N.; Muscas, C. A PMU for the measurement of synchronized harmonic phasors in three-phase distribution networks. IEEE Trans. Instrum. Meas. 2009, 58, 3723–3730. [Google Scholar] [CrossRef]
- Chakir, M.; Kamwa, I.; Le-Huy, H. Extended C37.118.1 PMU algorithms for joint tracking of fundamental and harmonic phasors in stressed power systems and microgrids. IEEE Trans. Power Deliv. 2014, 29, 1465–1480. [Google Scholar] [CrossRef]
- Liu, H.; Bi, T.; Xu, S.; Li, J.; Lin, J.; Zhao, Z.; Yang, F.; Ding, H.; Shang, J.; Liu, S. A full-view synchronized measurement system for the renewables, controls, loads, and waveforms of power-electronics-enabled power distribution grids. IEEE Trans. Smart Grid 2022, 13, 3879–3890. [Google Scholar] [CrossRef]
- Xie, X.; Zhan, Y.; Liu, H.; Liu, C. Improved synchrophasor measurement to capture sub/super-synchronous dynamics in power systems with renewable generation. IET Renew. Power Gener. 2019, 13, 49–56. [Google Scholar] [CrossRef]
- Macii, D.; Petri, D.; Zorat, A. Accuracy analysis and enhancement of DFT-based synchrophasor estimators in off-nominal conditions. IEEE Trans. Instrum. Meas. 2012, 61, 2653–2664. [Google Scholar] [CrossRef]
- Sun, B.; Wu, X.; Chen, X.; Zou, Z.; Li, Q.; Ren, B. Parameter estimation of sub-/super-synchronous oscillation based on interpolated all-phase fast Fourier transform with optimized window function. J. Mod. Power Syst. Clean Energy 2024, 12, 1031–1041. [Google Scholar] [CrossRef]
- Chen, C.I.; Chang, G.W. Virtual instrumentation and educational platform for time-varying harmonics and inter harmonics detection. IEEE Trans. Ind. Electron. 2010, 57, 3334–3342. [Google Scholar] [CrossRef]
- Zhou, N.; Trudnowski, D.J.; Pierre, J.W.; Mittelstadt, W.A. Electromechanical mode online estimation using regularized robust RLS methods. IEEE Trans. Power Syst. 2008, 23, 1670–1680. [Google Scholar] [CrossRef]
- Jain, S.K.; Singh, S.N. Exact model order ESPRIT technique for harmonics and interharmonics estimation. IEEE Trans. Instrum. Meas. 2012, 61, 1915–1923. [Google Scholar] [CrossRef]
- Laila, D.S.; Messina, A.R.; Pal, B.C. A refned Hilbert–Huang transform with applications to interarea oscillation monitoring. IEEE Trans. Power Syst. 2009, 24, 610–620. [Google Scholar] [CrossRef]
- Arrieta Paternina, M.R.; Tripathy, R.K.; Zamora-Mendez, A.; Dotta, D. Identifcation of electromechanical oscillatory modes based on variational mode decomposition. Electr. Power Syst. Res. 2019, 167, 71–85. [Google Scholar] [CrossRef]
- Du, D.; Guo, C.; Yang, S.; Peng, Y.; Zhao, C. Fast detection method of medium-high-frequency oscillations based on equal-band multi-channel signal tracking and screening. Proc. CSEE 2023, 43, 7030. [Google Scholar]
- Chen, L.; Xie, X.; Song, M.; Li, Y.; Zhang, Y. Estimation of high-frequency oscillation’s magnitude and frequency based on multi-tone FIR filter. IEEE Trans. Power Syst. 2023, 38, 528–536. [Google Scholar] [CrossRef]
- Oberlin, T.; Meignen, S.; Perrier, V. Second-order synchrosqueezing transform or invertible reassignment? towards ideal time-frequency representations. IEEE Trans. Signal Process. 2015, 63, 1335–1344. [Google Scholar]
- Thakur, G.; Brevdo, E.; Fučkar, N.S.; Wu, H.T. The synchrosqueezing algorithm for time-varying spectral analysis: Robustness properties and new paleoclimate applications. Signal Process. 2013, 93, 1079–1094. [Google Scholar] [CrossRef]
- Wang, H.; Long, J.; Deng, C.; Zhou, Y. Robust multisynchrosqueezing transform time frequency technologies with application to fault diagnosis. Int. J. Electr. Power Energy Syst. 2025, 170, 110849. [Google Scholar] [CrossRef]
- Liu, Y.; Wen, H.; Ding, Z.; Xu, L.; Chen, H.; Smulko, J. An instantaneous engine speed estimation method using multiple matching synchrosqueezing transform. J. Sens. 2021, 2021, 6650432. [Google Scholar] [CrossRef]
- Sun, B.; Wu, X.; Chen, X.; Zhou, J. An identification scheme for wideband oscillation parameters based on AR-EWT and interpolated DFT. IEEE Trans. Instrum. Meas. 2025, 74, 9001512. [Google Scholar] [CrossRef]
- Zeng, X.; Chen, G.; Liu, Y.; Zhang, F.; Shi, H. Parameter identification of power grid subsynchronous oscillations based on eigensystem realization algorithm. Energies 2024, 17, 2575. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Liu, J.; Gao, W.; He, J. An improved interpolated DFT-based parameter identification for sub-/super-synchronous oscillations with synchrophasors. IEEE Trans. Power Syst. 2023, 38, 1714–1727. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, J.; Xie, X.; Xiao, X.; Gao, B.; Wang, Y. Interpolated DFT-based identification of sub-synchronous oscillation parameters using synchrophasor data. IEEE Tran. Smart Grid 2025, 11, 2662–2675. [Google Scholar] [CrossRef]
- Wang, L.; Xie, X.; Jiang, Q.; Liu, H.; Li, Y.; Liu, H. Investigation of SSR in practical DFIG-based wind farms connected to a series-compensated power system. IEEE Trans. Power Syst. 2015, 30, 2772–2779. [Google Scholar] [CrossRef]
- Cui, H.; Feng, S.; Chen, J.; Ye, Y.; Tang, Y.; Lei, J. Wide-area location method of wide-band oscillations based on autoencoder and long short-term memory network. Autom. Electr. Power Syst. 2022, 46, 194–201. [Google Scholar]


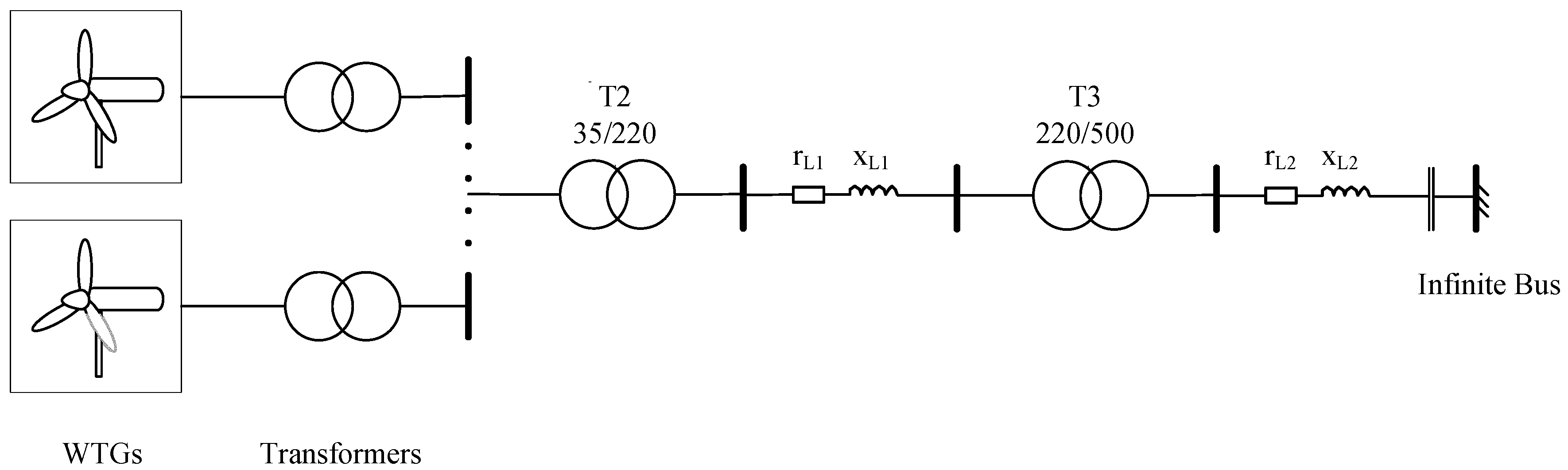

| Test Set | SNR (dB) | Method | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| EMD | 10−5 | 10−3 | 10−3 | / | / | / | / | / | / | ||
| VMD | 10−4 | 10−2 | 10−2 | 10−2 | 10−1 | 10−1 | 10−4 | 10−4 | 10−4 | ||
| MMSST | 10−7 | 10−6 | 10−6 | 10−5 | 10−5 | 10−5 | 10−5 | 10−5 | 10−5 | ||
| 40 | EMD | 1.0217 | 7.1035 | 9.0331 | / | / | / | / | / | / | |
| VMD | 1.1231 | 9.2434 | 10.7682 | 4.4851 | 17.1714 | 25.6782 | 1.4773 | 2.2354 | 4.9867 | ||
| MMSST | 0.5545 | 1.1170 | 2.1763 | 1.1825 | 1.7272 | 3.5768 | 1.1825 | 2.0316 | 4.7547 | ||
| EMD | 10−5 | 10−3 | 10−3 | / | / | / | / | / | / | ||
| VMD | 10−4 | 10−2 | 10−2 | 10−2 | 10−1 | 10−1 | 10−4 | 10−4 | 10−4 | ||
| MMSST | 10−7 | 10−6 | 10−6 | 10−5 | 10−5 | 10−5 | 10−5 | 10−5 | 10−5 | ||
| 40 | EMD | 0.9655 | 6.2678 | 8.6312 | / | / | / | / | / | / | |
| VMD | 1.1693 | 7.4463 | 9.3786 | 4.0571 | 16.8843 | 24.8756 | 1.3679 | 1.8164 | 4.2079 | ||
| MMSST | 0.4758 | 1.0937 | 1.7832 | 1.0465 | 1.5315 | 2.7544 | 1.0465 | 1.6450 | 3.9623 |
| Parameters | True Value | EMD | VMD | MMSST |
|---|---|---|---|---|
| 50.0000 | 50.0237 | 50.0322 | 50 | |
| 1.0956 | 1.1205 | 1.2372 | 1.1092 | |
| −1.4632 | −3.6316 | −3.7264 | −1.4960 | |
| 7.5125 | / | 8.3406 | 7.6032 | |
| 0.6926 | / | 0.9237 | 0.7055 | |
| −2.1112 | / | −2.4358 | −2.1916 | |
| 92.4871 | / | 95.3566 | 93.4676 | |
| 0.0275 | / | 0.1079 | 0.0281 | |
| 0.1772 | / | 0.1439 | 0.1692 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, P.; Sun, Y.; Li, L.; Zhao, Y.; Zhu, X.; He, S.; Zhang, M. Identification Method for Wideband Oscillation Parameters Caused by Grid-Forming Renewable Energy Sources Based on Multiple Matching Synchrosqueezing Transformation. Energies 2025, 18, 5123. https://doi.org/10.3390/en18195123
Xiong P, Sun Y, Li L, Zhao Y, Zhu X, He S, Zhang M. Identification Method for Wideband Oscillation Parameters Caused by Grid-Forming Renewable Energy Sources Based on Multiple Matching Synchrosqueezing Transformation. Energies. 2025; 18(19):5123. https://doi.org/10.3390/en18195123
Chicago/Turabian StyleXiong, Ping, Yu Sun, Lie Li, Yifan Zhao, Xiaoqian Zhu, Shunfan He, and Ming Zhang. 2025. "Identification Method for Wideband Oscillation Parameters Caused by Grid-Forming Renewable Energy Sources Based on Multiple Matching Synchrosqueezing Transformation" Energies 18, no. 19: 5123. https://doi.org/10.3390/en18195123
APA StyleXiong, P., Sun, Y., Li, L., Zhao, Y., Zhu, X., He, S., & Zhang, M. (2025). Identification Method for Wideband Oscillation Parameters Caused by Grid-Forming Renewable Energy Sources Based on Multiple Matching Synchrosqueezing Transformation. Energies, 18(19), 5123. https://doi.org/10.3390/en18195123





