Cutting-Edge Research: Artificial Intelligence Applications and Control Optimization in Advanced CO2 Cycles
Abstract
1. Introduction
- (a)
- Compatibility with a wider temperature range (up to 1000 °C);
- (b)
- Reduced irreversible losses in heat recovery exchangers due to improved temperature matching between waste heat and the working fluid [4];
- (c)
- Enhanced system performance even at temperatures below 400 °C [5];
- (d)
- Non-toxic, non-flammable, and non-corrosive characteristics;
- (e)
- Low global warming potential (GWP);
- (f)
- More compact system compared to SRC [6].
2. Advanced System Selection and Dynamic Performance Studies
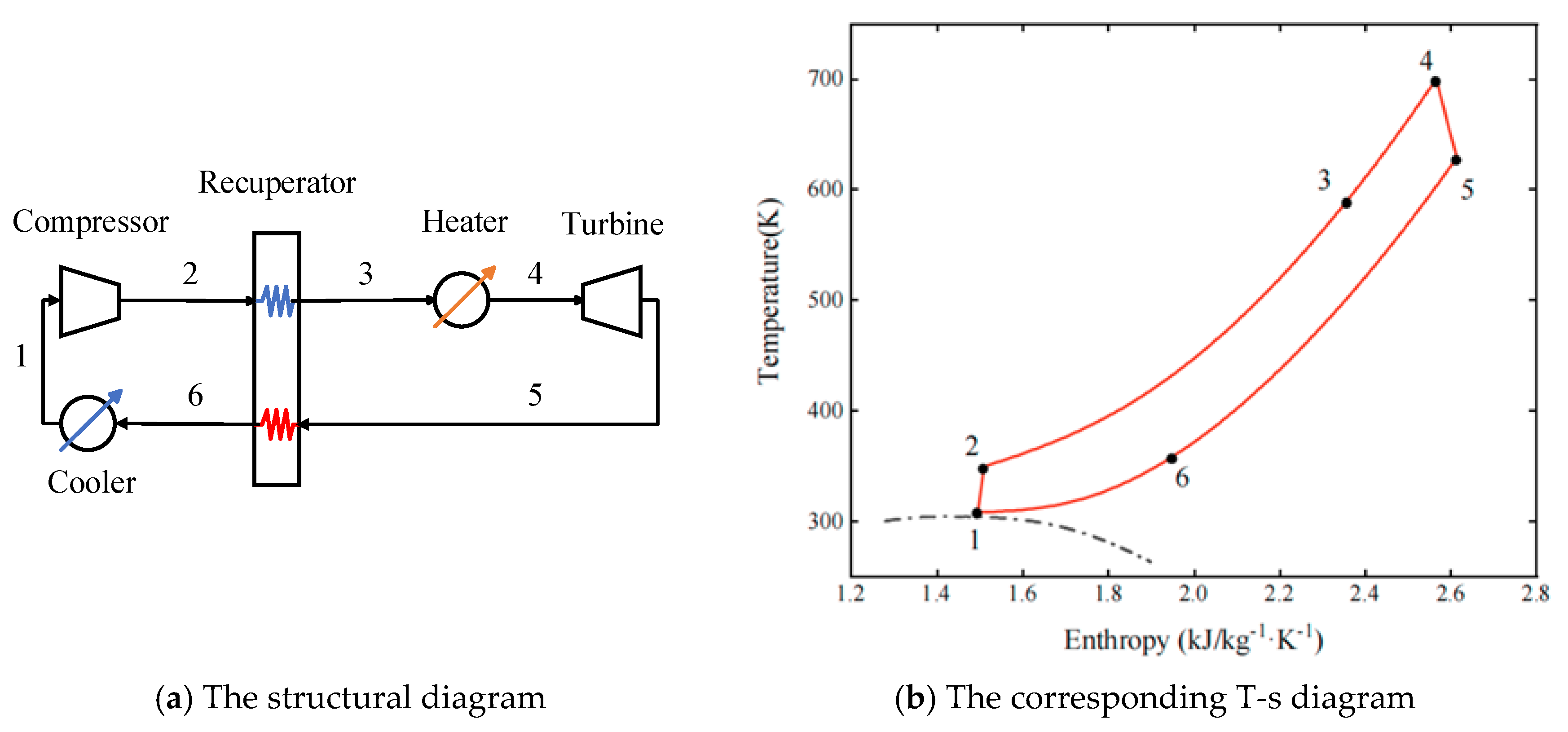
2.1. Simple Recuperative Cycle
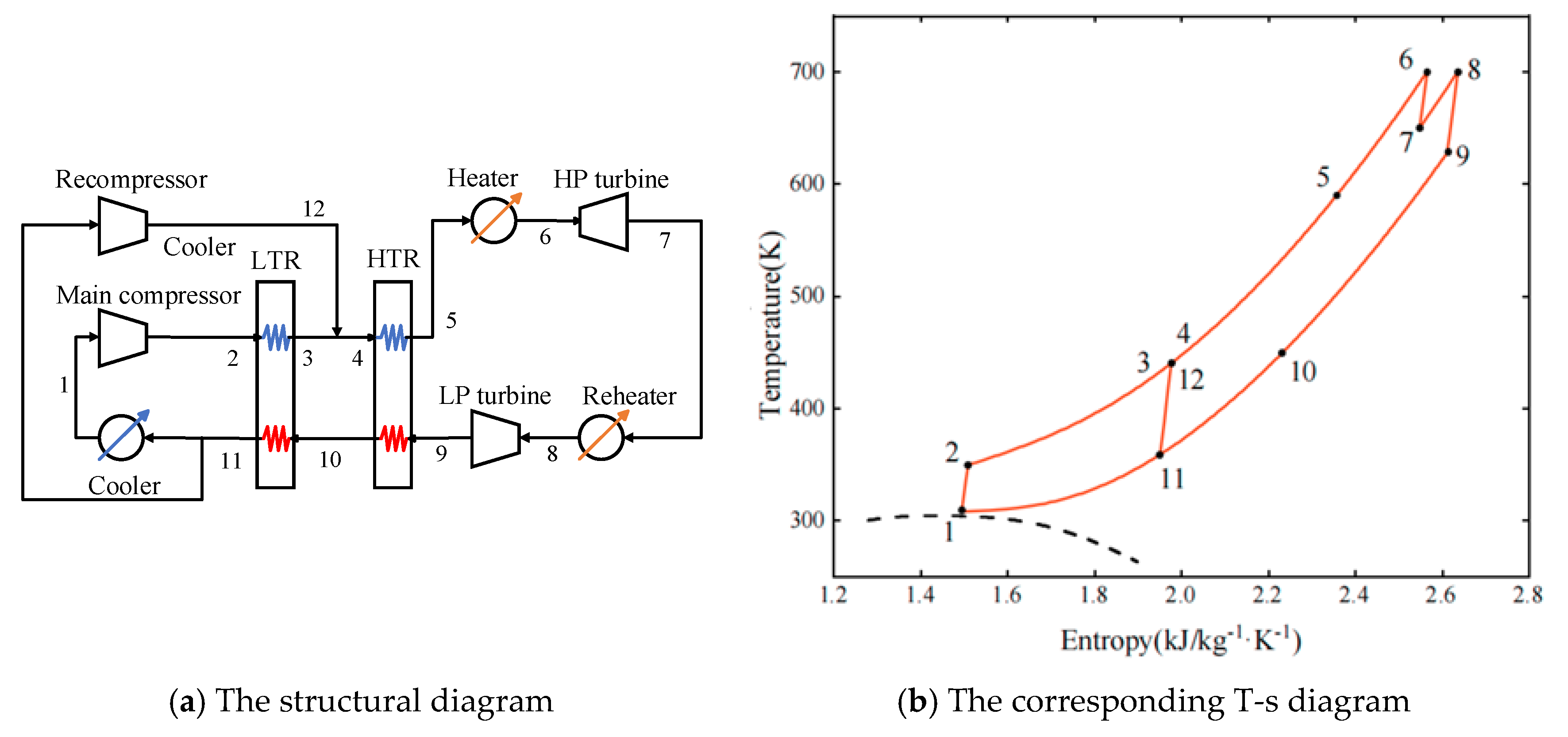
2.2. Recompression Cycle
2.3. Recompression Intercooling Cycle
2.4. Recompression Reheat Cycle
3. Control Strategies Applied to the CO2 Cycle and Comparative Analyses
3.1. Basic State Parameter Control Method
3.2. Control Strategy
3.3. Performance Comparison of Different Control Methods
3.4. Combined Control
3.4.1. Inventory Control-Dominated Combined Control
3.4.2. Bypass Control-Dominated Combined Control
3.5. Feedback Control Technology Based on PID Controllers
3.5.1. Introduction and Examples of Feedback Control Techniques
3.5.2. Limitations of Feedback Control Techniques
4. Novel AI Integrated Control Technology
4.1. Extremum Seeking Control
4.1.1. Research Background of ESC
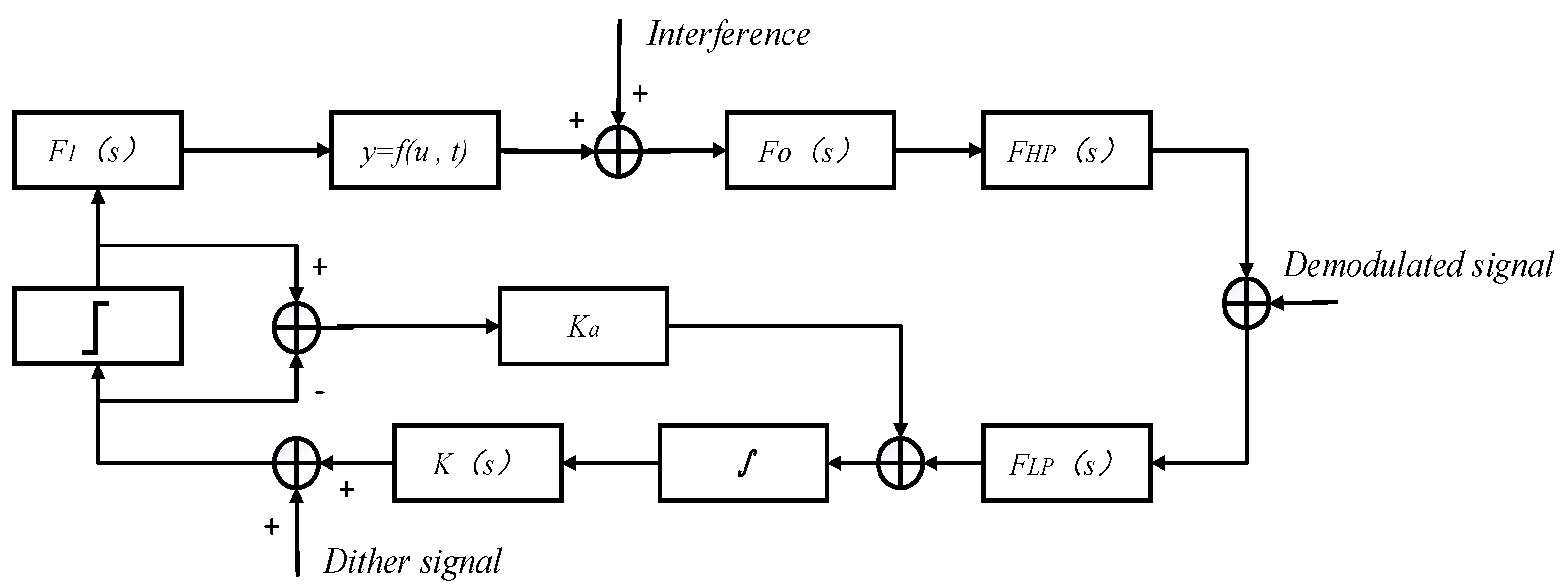
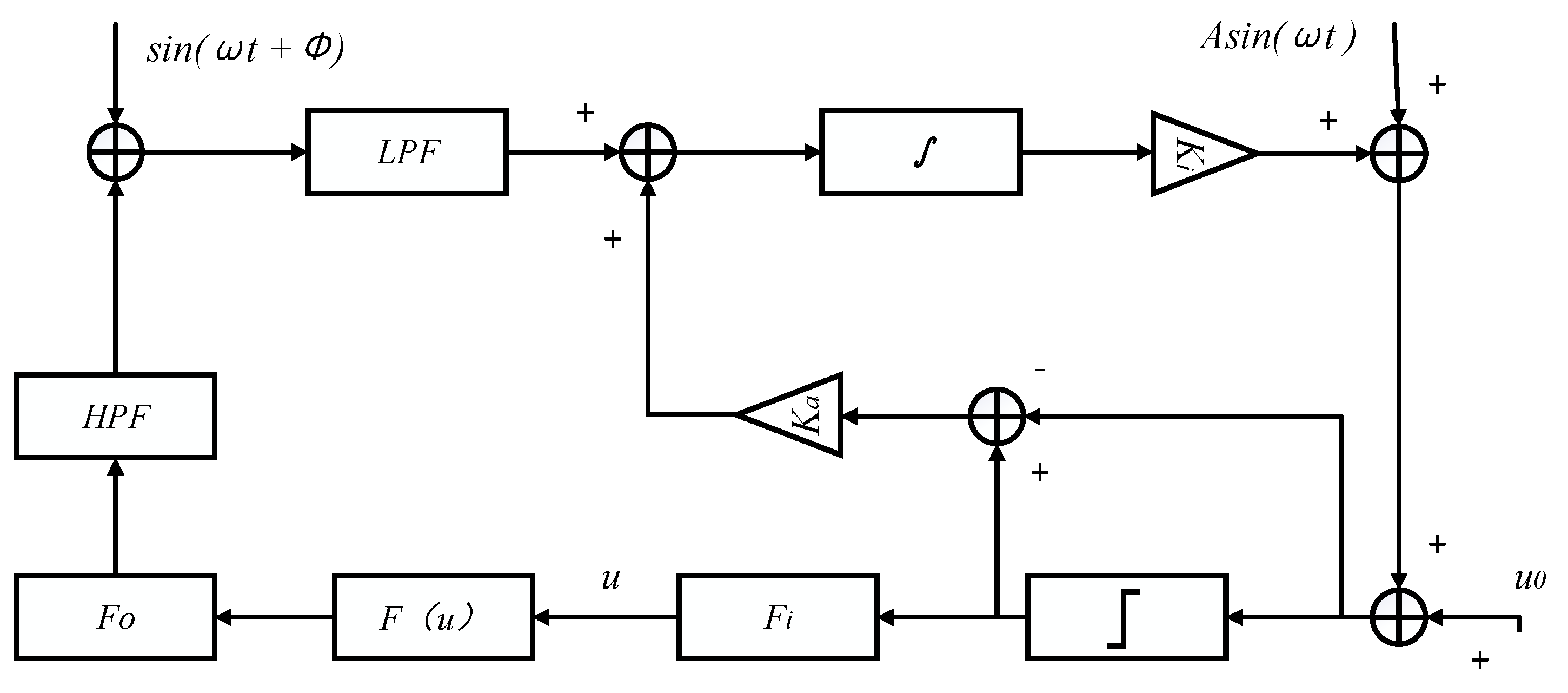
4.1.2. Principle of Operation of ESC
- 1.
- Input Perturbation
- 2.
- Output Gradient Information
- 3.
- High-pass Filter
- 4.
- Demodulation Process
- 5.
- Low-pass Filter
- 6.
- Integrator
- 7.
- System Stabilizer
4.1.3. Problems in the Practical Operation of ESC
4.2. Data-Driven MPC-Based Predictive Control Techniques
4.2.1. Overview of MPC Control
4.2.2. Multivariate Regression-Based Model Predictive Control
4.2.3. Support Vector Regression-Based Model Predictive Control
4.2.4. Artificial Intelligence-Based Model Predictive Control
- –
- vi(t): velocity of the i-th particle at moment t.
- –
- w: inertia weight, used to control the influence of the previous iteration value of the particle velocity.
- –
- c1: Individual learning factor, which indicates how much the particle is influenced by its own experience.
- –
- c2: social learning factor, indicating the extent to which the particle is influenced by the experience of the group.
- –
- r1 and r2: randomly generated numbers in the interval [0, 1].
- –
- pbest i: the historical best position of the i-th particle.
- –
- gbest: Historical best position of the whole population.
- –
- xi (t): the position of the i-th particle at moment t.
- –
- MaxIter: the maximum number of iterations of the algorithm.
4.3. Comparative Analysis of Different Control Technologies
Comparative Analysis
4.4. The Latest Progress and Challenges in the Application of AI-Based Model Predictive Control
4.4.1. Engineering Application Analysis
4.4.2. Limitations and Prospects of AI-Based Model Predictive Control in Applications
5. Analysis of the Application of New Control Technologies
5.1. Thermal Management of New Energy Vehicles
5.2. Solar Thermal Power Generation
5.3. Aerospace Field
6. Conclusions and Prospects
6.1. Conclusions
- (1)
- A multifaceted study has been conducted on the main variable load control strategies for CO2 cycles, including inventory control, bypass control, turbine speed control, and turbine throttling control. The first three control methods have been extensively studied and can serve as the primary variable load control strategies. Additionally, the safety characteristics of the system during startup and shutdown conditions should be controlled. Each control strategy has its own advantages and disadvantages, and their applicable ranges vary. Therefore, adopting different control strategies for different conditions or combining multiple control methods is necessary to ensure the safe, stable, efficient, and flexible operation of the unit.
- (2)
- After analyzing the existing problems in CO2 cycle control, various novel control technologies for CO2 cycles have been studied and analyzed, including extremum seeking control, MPC control based on ANN models, and MPC control optimized by PSO. A comparative analysis has been conducted on aspects such as the system’s model dependency, real-time optimization capability, and implementation difficulty. The results indicate that PID control is simple to establish and low in cost, but it is easily affected by environmental factors and changes in system components, leading to reduced control performance. Real-time control technologies represented by extremum seeking control can track system parameters such as maximum thermal efficiency in real-time, but the long optimization process results in extended convergence times for the control system. Model predictive control systems can achieve real-time optimization and rapid convergence, showing promising development prospects. Additionally, new-generation artificial intelligence model control technologies represented by PSO-optimized MPC control possess rapid convergence capabilities and a balance between global and local search capabilities, making them more suitable for new application scenarios with high real-time control requirements.
- (3)
- A comprehensive exposition of MPC control technology has been provided, including its control theory, methods, applicable scope, strengths, and weaknesses. The actual application status of control strategies in fields such as new energy vehicles, solar thermal power generation, and aerospace has been discussed. By integrating the development trends in the energy sector and artificial intelligence methods, the development direction of control strategies for advanced CO2 cycle has been explored, and ideas for the practical application of artificial intelligence model predictive control in these systems have been proposed.
- (4)
- In the existing research, the application of AI-Based Model Predictive Control still faces a series of widely recognized bottleneck problems, mainly including the following aspects: high dependence on data quality and scale; Relying on large-scale data sets for training; Lack of systematic model validation methodology; Network structure optimization still depends on a large number of trial and error operations; The supervision mechanism in the training process is not perfect.
6.2. Prospects
- (1)
- Integration of Advanced Control Algorithms: Develop hybrid control frameworks that combine multiple strategies, such as ESC and MPC, to enhance system adaptability and precision.
- (2)
- Reinforcement Learning-Based Adaptive MPC: Explore the application of artificial intelligence, particularly reinforcement learning, to create adaptive MPC frameworks that dynamically adjust to system changes and optimize performance in real time.
- (3)
- Digital Twin Integration: Combine digital twin technology with MPC to enable real-time optimization and predictive performance analysis of CO2 cycles, thereby improving operational efficiency and reliability under varying conditions.
- (4)
- AI-Driven Model Learning: Leverage advancements in AI to accurately learn CO2 cycle dynamics, enabling MPC-based control systems that achieve unprecedented levels of precision and efficiency.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| CO2 | Carbon Dioxide |
| sCO2 | Supercritical Carbon Dioxide |
| ORC | Organic Rankine Cycle |
| SRC | Steam Rankine Cycle |
| ODP | Ozone Depletion Potential |
| GWP | Global Warming Potential |
| T-s | Temperature-Entropy |
| HTR | High-Temperature Return Heaters |
| LTR | Low-Temperature Return Heaters |
| MCIT | Main Compressor Inlet Temperature |
| TIP | Turbine Inlet Pressure |
| TIT | Turbine Inlet Temperature |
| PID | Proportional-Integral-Derivative |
| IMC | Inventory Management Control |
| ESC | Extremum Seeking Control |
| COP | Coefficient of Performance |
| EEV | Electronic Expansion Valve |
| MPC | Model Predictive Control |
| SVR | Support Vector Regression |
| ANN | Artificial Neural Network |
| AI | Artificial Intelligence |
| PSO | Particle Swarm Optimization |
| GMDH | Group Method of Data Handling |
References
- Açıkkalp, E. Ecologic and sustainable objective thermodynamic evaluation of molten carbonate fuel cell–supercritical CO2 Brayton cycle hybrid system. Int. J. Hydrogen Energy 2016, 42, 6272–6280. [Google Scholar] [CrossRef]
- Kim, Y.M.; Kim, C.G.; Favrat, D. Transcritical or supercritical CO2 cycles using both low- and high-temperature heat sources. Energy 2012, 43, 402–415. [Google Scholar] [CrossRef]
- Li, L.; Ge, Y.; Luo, X.; Tassou, S.A. Experimental investigation on power generation with low grade waste heat and CO2 transcritical power cycle. Energy Procedia 2017, 123, 297–304. [Google Scholar] [CrossRef]
- Sarkar, J. Review and future trends of supercritical CO2 Rankine cycle for low-grade heat conversion. Renew. Sustain. Energy Rev. 2015, 48, 434–451. [Google Scholar] [CrossRef]
- Olumayegun, O.; Wang, M.; Kelsall, G. Closed-cycle gas turbine for power generation: A state-of-the-art review. Fuel 2016, 180, 694–717. [Google Scholar] [CrossRef]
- Olumayegun, O.; Wang, M.H. Dynamic modelling and control of supercritical CO2 power cycle using waste heat from industrial processes. Fuel 2019, 249, 89–102. [Google Scholar] [CrossRef]
- Lorentzen, G.; Pettersen, J. A new, efficient and environmentally benign system for car air-conditioning. Int. J. Refrig. 1993, 16, 4–12. [Google Scholar] [CrossRef]
- Qi, R.; Lu, L.; Huang, Y. Parameter analysis and optimization of the energy and economic performance of solar-assisted liquid desiccant cooling system under different climate conditions. Energy Convers. Manag. 2015, 106, 1387–1395. [Google Scholar] [CrossRef]
- Kim, J.H.; Nam, Y.B.; Ahn, M.J. Performance Analysis of Scroll Expander-Compressor Unit for CO2 Transcritical Cycles. Korean J. Air-Cond. Refrig. Eng. 2006, 18, 434–442. [Google Scholar]
- De la Calle, A.; Bayon, A.; Too, Y.C.S. Impact of ambient temperature on supercritical CO2 recompression Brayton cycle in arid locations: Finding the optimal design conditions. Energy 2018, 153, 1016–1027. [Google Scholar] [CrossRef]
- Marchionni, M.; Saravi, S.S.; Bianchi, G.; Tassou, S.A. Modelling and performance analysis of a supercritical CO2 system for high temperature industrial heat to power conversion at off-design conditions. In Proceedings of the 3rd European Supercritical CO2 Conference, Paris, France, 19–20 September 2019. [Google Scholar]
- Ma, Y.; Morozyuk, T.; Liu, J. Development of operation strategy for recompression supercritical CO2 cycle with intercooled main compressor under off-design condition. E3S Web Conf. 2019, 137, 01020. [Google Scholar] [CrossRef]
- Yang, J.; Yang, Z.; Duan, Y. Part-load performance analysis and comparison of supercritical CO2 Brayton cycles. Energy Convers. Manag. 2020, 214, 112832. [Google Scholar] [CrossRef]
- Xingyan, B.; Wang, X.; Wang, R.; Cai, J.; Tian, H.; Shu, G. Optimal selection of supercritical CO2 Brayton cycle layouts based on part-load performance. Energy 2022, 256, 124691. [Google Scholar] [CrossRef]
- Luu, M.T.; Milani, D.; McNaughton, R.; Abbas, A. Analysis for flexible operation of supercritical CO2 Brayton cycle integrated with solar thermal systems. Energy 2017, 124, 752–771. [Google Scholar] [CrossRef]
- Crespi, F.; Gavagnin, G.; Sánchez, D.; Martínez, G.S. Supercritical carbon dioxide cycles for power generation: A review. Appl. Energy 2017, 195, 152–183. [Google Scholar] [CrossRef]
- Cayer, E.; Galanis, N.; Desilets, M.; Nesreddine, H.; Roy, P. Analysis of a carbon dioxide transcritical power cycle using a low temperature source. Appl. Energy 2009, 86, 1055–1063. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Dai, Y.; Zhou, E. Thermodynamic analysis of a transcritical CO2 power cycle driven by solar energy with liquified natural gas as its heat sink. Appl. Energy 2011, 92, 194–203. [Google Scholar] [CrossRef]
- Padilla, R.V.; Benito, R.; Stein, W. An Exergy Analysis of Recompression Supercritical CO2 Cycles with and without Reheating. Energy Procedia 2015, 69, 1181–1191. [Google Scholar] [CrossRef]
- Milani, D.; Luu, M.T.; McNaughton, R.; Abbas, A. A comparative study of solar heliostat assisted supercritical CO2 recompression Brayton cycles: Dynamic modelling and control strategies. J. Supercrit. Fluids 2017, 120, 113–124. [Google Scholar] [CrossRef]
- Turchi, C.S.; Ma, Z.; Dyreby, J. Supercritical Carbon Dioxide Power Cycle Configurations for Use in Concentrating Solar Power Systems. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; pp. 967–973. [Google Scholar] [CrossRef]
- Dincer, I.; Ratlamwala, T. Importance of exergy for analysis, improvement, design, and assessment. WIREs Energy Environ. 2013, 2, 335–349. [Google Scholar] [CrossRef]
- Qin, T.; Yan, X.; Yuan, C.; Sun, Y. Review of system design and operation control technology of supercritical CO2 power cycle. Energy Convers. Manag. 2025, 326, 119462. [Google Scholar] [CrossRef]
- Liese, E.; Albright, J.; Zitney, S.A. Startup, shutdown, and load-following simulations of a 10 MWe supercritical CO2 recompression closed Brayton cycle. Appl. Energy 2020, 277, 115628. [Google Scholar] [CrossRef]
- Lock, A.; Bone, V. Off-design operation of the dry-cooled supercritical CO2 power cycle. Energy Convers. Manag. 2022, 251, 114903. [Google Scholar] [CrossRef]
- Wang, X.; Li, X.; Li, Q.; Liu, L.; Liu, C. Performance of a solar thermal power plant with direct air-cooled supercritical carbon dioxide Brayton cycle under off-design conditions. Appl. Energy 2020, 261, 114359. [Google Scholar] [CrossRef]
- Wang, X.; Wang, R.; Bian, X.; Cai, J.; Tian, H.; Shu, G.; Li, X.; Qin, Z. Review of dynamic performance and control strategy of supercritical CO2 Brayton cycle. Energy AI 2021, 5, 100078. [Google Scholar] [CrossRef]
- Oh, B.S.; Lee, J.-I. Study of autonomous control system for S-CO2 power cycle. In Proceedings of the 3rd European Supercritical CO2 Conference, Paris, France, 19–20 September 2019. [Google Scholar]
- Luu, M.T.; Milani, D.; McNaughton, R.; Abbas, A. Advanced control strategies for dynamic operation of a solar-assisted recompression supercritical CO2 Brayton power cycle. Appl. Therm. Eng. 2018, 136, 682–700. [Google Scholar] [CrossRef]
- Xiang, X.-Y.; Zhao, X.-C.; Jiang, P.-N.; Wang, J.; Gao, D.; Bai, F.-L.; An, M.-D.; Yi, L.-Y.; Wu, J.; Hu, J.-X. Scenario analysis of hydrofluorocarbons emission reduction in China’s mobile air-conditioning sector. Adv. Clim. Change Res. 2022, 13, 578–586. [Google Scholar] [CrossRef]
- Gao, C.; Wu, P.; Liu, W.; Ma, Y.; Shan, J. Development of a bypass control strategy for supercritical CO2 Brayton cycle cooled reactor system under load-following operation. Ann. Nucl. Energy 2021, 151, 107917. [Google Scholar] [CrossRef]
- Ma, X.; Jiang, P.; Zhu, Y. Performance analysis and dynamic optimization of integrated cooling and power generation system based on supercritical CO2 cycle for turbine-based combined cycle engine. Appl. Therm. Eng. 2022, 215, 118867. [Google Scholar] [CrossRef]
- Guo, H.; Xu, H.; Xu, C.; Xin, T. Off-design performance analysis and comparison of a coal-based semi-closed supercritical CO2 cycle under different operational strategies. Energy 2025, 315, 134441. [Google Scholar] [CrossRef]
- Ding, H.; Zhang, Y.; Hong, G.; Li, J. Comparative study of the supercritical carbon-dioxide recompression Brayton cycle with different control strategies. Prog. Nucl. Energy 2021, 137, 103770. [Google Scholar] [CrossRef]
- Chen, J.; Tan, S.; Jiaqiang, E.; Liao, G.; Zhang, F. Dynamic performance and control analysis of supercritical CO2 brayton cycle for solid oxide fuel cell waste heat recovery. Appl. Therm. Eng. 2024, 250, 123556. [Google Scholar] [CrossRef]
- Alsawy, T.; Mohammed, R.H.; Mesalhy, O.; Elsayed, M.L. Dynamic performance of supercritical CO2 Brayton cycle and its relationship to the correction of turbomachinery performance maps: A comparative analysis. Appl. Therm. Eng. 2024, 242, 122364. [Google Scholar] [CrossRef]
- Carstens, N. Control Strategies for Supercritical Carbon Dioxide Power Conversion Systems. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2007. [Google Scholar]
- Zhang, J.Y.; Yang, Z.J.; Moullec, Y.L. Dynamic modeling and transient analysis of a molten salt heated recompression supercritical CO2 Brayton cycle. In Proceedings of the 6th International Supercritical CO2 Power Cycles Symposium, Pittsburgh, PA, USA, 27–29 March 2018. [Google Scholar]
- Heifetz, A.; Vilim, R. Turbine Bypass, Mass Inventory, and Mixed-Mode Generator Power Control of S-CO2 Recompression Cycle. Nucl. Technol. 2015, 189, 268–277, 268e77. [Google Scholar] [CrossRef]
- Li, X.; Qin, Z.; Dong, K.; Wang, L.; Lin, Z. Experimental study of the startup of a supercritical CO2 recompression power system. Energy 2023, 284, 128538. [Google Scholar] [CrossRef]
- Conboy, T.; Pasch, J.; Fleming, D. Control of a Supercritical CO2 Recompression Brayton Cycle Demonstration Loop. J. Eng. Gas Turbines Power 2013, 135, 111701. [Google Scholar] [CrossRef]
- Bian, X.; Wang, X.; Wang, R.; Cai, J.; Tian, H.; Shu, G.; Lin, Z.; Yu, X.; Shi, L. A comprehensive evaluation of the effect of different control valves on the dynamic performance of a recompression supercritical CO2 Brayton cycle. Energy 2022, 248, 123630. [Google Scholar] [CrossRef]
- Wang, R.; Li, X.; Qin, Z.; Cai, J.; Bian, X.; Wang, X.; Tian, H.; Shu, G. Control strategy for actual constraints during the start–stop process of a supercritical CO2 Brayton cycle. Appl. Therm. Eng. 2023, 226, 120289. [Google Scholar] [CrossRef]
- Su, R.; Yu, Z.; Wang, D.; Sun, B.; Sun, J. Performance Analysis of an Integrated Supercritical CO2 Recompression/Absorption Refrigeration/Kalina Cycle Driven by Medium-Temperature Waste Heat. J. Therm. Sci. 2022, 31, 2051–2067. [Google Scholar] [CrossRef]
- Ma, Y.; Morosuk, T.; Liu, M.; Liu, J. Development and comparison of control schemes for the off-design operation of a recompression supercritical CO2 cycle with an intercooled main compressor. Energy 2020, 211, 119011. [Google Scholar] [CrossRef]
- Fan, G.; Du, Y.; Li, H.; Dai, Y. Off-design behavior investigation of the combined supercritical CO2 and organic Rankine cycle. Energy 2021, 237, 121529. [Google Scholar] [CrossRef]
- Li, H.; Fan, G.; Cao, L.; Yang, Y.; Yan, X.; Dai, Y.; Zhang, G.; Wang, J. A comprehensive investigation on the design and off-design performance of supercritical carbon dioxide power system based on the small-scale lead-cooled fast reactor. J. Clean. Prod. 2020, 256, 120720. [Google Scholar] [CrossRef]
- Liu, K.; Guo, Y.; Wang, L.; Fan, G.; Che, D. Control of supercritical CO2 Brayton cycle for fast and efficient load variation processes. Appl. Therm. Eng. 2024, 244, 122797. [Google Scholar] [CrossRef]
- Du, Y.; Yang, C.; Yu, Z.; Bao, W.; Hu, C.; He, X. Integrated design and off-design hybrid control strategy of supercritical CO2 recompression cycle for nuclear power. Appl. Therm. Eng. 2022, 217, 119194. [Google Scholar] [CrossRef]
- Ordys, A.J.; Pike, A.W.; Johnson, M.A.; Katebi, R.M.; Grimble, M.J. Modelling and Simulation of Power Generation Plants (Advances in Industrial Control); Springer: London, UK, 1994. [Google Scholar]
- Sakalis, G.N. Design and partial load operation optimization of integrated ship energy system based on supercritical CO2 waste heat recovery cycle. Sustain. Energy Technol. Assessments 2022, 51, 101965. [Google Scholar] [CrossRef]
- Zhiyuan, C.; Yu, Z.; Yuanyang, Z. Progress in the prediction and regulation of the performance of supercritical CO2 power systems under non-design conditions. Energy Conserv. Technol. (Chin.) 2024, 42, 327–334+344. [Google Scholar]
- Zhang, L.; Deng, T.; Klemeš, J.J.; Zeng, M.; Ma, T.; Wang, Q. Supercritical CO2 Brayton cycle at different heat source temperatures and its analysis under leakage and disturbance conditions. Energy 2021, 237, 121610. [Google Scholar] [CrossRef]
- Peñarrocha, I.; Llopis, R.; Tárrega, L.; Sánchez, D.; Cabello, R. A new approach to optimize the energy efficiency of CO2 transcritical refrigeration plants. Appl. Therm. Eng. 2014, 67, 137–146. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Bose, S.; Sarkar, J. Exergy maximization of cascade refrigeration cycles and its numerical verification for a transcritical CO2–C3H8 system. Int. J. Refrig. 2006, 30, 624–632. [Google Scholar] [CrossRef]
- Liao, S.; Zhao, T.; Jakobsen, A. A correlation of optimal heat rejection pressures in transcritical carbon dioxide cycles. Appl. Therm. Eng. 2000, 20, 831–841. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhattacharyya, S.; Gopal, M. Optimization of a transcritical CO2 heat pump cycle for simultaneous cooling and heating applications. Int. J. Refrig. 2004, 27, 830–838. [Google Scholar] [CrossRef]
- Cecchinato, L.; Corradi, M.; Minetto, S. A critical approach to the determination of optimal heat rejection pressure in transcritical systems. Appl. Therm. Eng. 2010, 30, 1812–1823. [Google Scholar] [CrossRef]
- Sharma, S.; Alleyne, A.G. Extremum seeking control of battery powered vapor compression systems for commercial vehicles. Int. J. Refrig. 2020, 115, 63–72. [Google Scholar] [CrossRef]
- Hu, B.; Li, Y.; Mu, B.; Wang, S.; Seem, J.E.; Cao, F. Extremum seeking control for efficient operation of hybrid ground source heat pump system. Renew. Energy 2016, 86, 332–346. [Google Scholar] [CrossRef]
- Hu, B.; Li, Y.; Wang, R.; Cao, F.; Xing, Z. Real-time minimization of power consumption for air-source transcritical CO2 heat pump water heater system. Int. J. Refrig. 2018, 85, 395–408. [Google Scholar] [CrossRef]
- Kim, M.S.; Shin, C.S.; Kim, M.S. A study on the real time optimal control method for heat rejection pressure of a CO2 refrigeration system with an internal heat exchanger. Int. J. Refrig. 2014, 48, 87–99. [Google Scholar] [CrossRef]
- Titica, M.; Dochain, D.; Guay, M. Real-Time Optimization of Fed-Batch Bioreactors via Adaptive Extremum-Seeking Control. Chem. Eng. Res. Des. 2003, 81, 1289–1295. [Google Scholar] [CrossRef]
- Krstić, M. Performance improvement and limitations in extremum seeking control. Syst. Control. Lett. 2000, 39, 313–326. [Google Scholar] [CrossRef]
- Hu, B.; Li, Y.Y.; Cao, F.; Ziwen, X. Extreme value search control of optimal exhaust pressure for transcritical CO2 heat pump system. J. Refrig. 2016, 37, 81–87. [Google Scholar]
- Dingbiao, W.; Hongxin, D.; Guanghui, W.; Shen, A.; Liu, H.; Qin, X. Research progress on control optimisation strategies for transcritical CO2 cycle systems. J. Zhengzhou Univ. 2024, 45, 1–11. [Google Scholar] [CrossRef]
- Hu, B.; Li, Y.; Cao, F.; Xing, Z. Extremum seeking control of COP optimization for air-source transcritical CO2 heat pump water heater system. Appl. Energy 2015, 147, 361–372. [Google Scholar] [CrossRef]
- Rampazzo, M.; Cervato, A.; Corazzol, C.; Mattiello, L.; Beghi, A.; Cecchinato, L.; Virzi, A. Energy-efficient operation of transcritical and subcritical CO2 inverse cycles via Extremum Seeking Control. J. Process. Control. 2019, 81, 87–97. [Google Scholar] [CrossRef]
- Ge, Y.; Tassou, S. Control optimisation of CO2 cycles for medium temperature retail food refrigeration systems. Int. J. Refrig. 2009, 32, 1376–1388. [Google Scholar] [CrossRef]
- Singh, R.; Kearney, M.P.; Manzie, C. Extremum-seeking control of a supercritical carbon-dioxide closed Brayton cycle in a direct-heated solar thermal power plant. Energy 2013, 60, 380–387. [Google Scholar] [CrossRef]
- Moase, W.H.; Manzie, C.; Brear, M.J. Newton-Like Extremum-Seeking for the Control of Thermoacoustic Instability. IEEE Trans. Autom. Control. 2010, 55, 2094–2105. [Google Scholar] [CrossRef]
- Sotiropoulos, F.E.; Asada, H.H. A Model-Free Extremum-Seeking Approach to Autonomous Excavator Control Based on Output Power Maximization. IEEE Robot. Autom. Lett. 2019, 4, 1005–1012. [Google Scholar] [CrossRef]
- Li, P.; Li, Y.; Seem, J.E. Efficient Operation of Air-Side Economizer Using Extremum Seeking Control. J. Dyn. Syst. Meas. Control. 2010, 132, 031009. [Google Scholar] [CrossRef]
- Ebegbulem, J.; Guay, M. Distributed Extremum Seeking Control for Wind Farm Power Maximization. IFAC-PapersOnLine 2017, 50, 147–152. [Google Scholar] [CrossRef]
- Krstić, M.; Wang, H.-H. Stability of extremum seeking feedback for general nonlinear dynamic systems. Automatica 2000, 36, 595–601. [Google Scholar] [CrossRef]
- Cui, C.; Ren, J.; Song, Y.; Yin, X.; Wang, W.; Yang, X.; Cao, F. Multi-variable extreme seeking control for efficient operation of sub-cooler vapor injection trans-critical CO2 heat pump water heater. Appl. Therm. Eng. 2021, 184, 116261. [Google Scholar] [CrossRef]
- Ye, S.; Long, Z.; Li, Y.; Zhao, H.; Li, X. An novel algorithm of vibration resonance control for power ultrasonic device via extremum seeking control based maximum conductance searching. Appl. Acoust. 2024, 230, 110409. [Google Scholar] [CrossRef]
- Li, X.; Li, Y.; Seem, J.E.; Li, P. Dynamic modeling and self-optimizing operation of chilled water systems using extremum seeking control. Energy Build. 2013, 58, 172–182. [Google Scholar] [CrossRef]
- Kim, M.S.; Kang, D.H.; Kim, M.S.; Kim, M. Investigation on the optimal control of gas cooler pressure for a CO2 refrigeration system with an internal heat exchanger. Int. J. Refrig. 2017, 77, 48–59. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y. Intermediate pressure optimization for two-stage air-source heat pump with flash tank cycle vapor injection via extremum seeking. Appl. Energy 2019, 238, 612–626. [Google Scholar] [CrossRef]
- Wang, W.; Li, Y.; Cao, F. Extremum seeking control for efficient operation of an air-source heat pump water heater with internal heat exchanger cycle vapor injection. Int. J. Refrig. 2019, 99, 153–165. [Google Scholar] [CrossRef]
- Malek, H.; Chen, Y. Fractional Order Extremum Seeking Control: Performance and Stability Analysis. IEEE/ASME Trans. Mechatron. 2016, 21, 1620–1628. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, K. Advanced model predictive control framework for autonomous intelligent mechatronic systems: A tutorial overview and perspectives. Annu. Rev. Control. 2021, 52, 170–196. [Google Scholar] [CrossRef]
- Rúa, J.; Hillestad, M.; Nord, L.O. Model predictive control for combined cycles integrated with CO2 capture plants. Comput. Chem. Eng. 2021, 146, 107217. [Google Scholar] [CrossRef]
- Rathod, D.; Xu, B.; Filipi, Z.; Hoffman, M. An experimentally validated, energy focused, optimal control strategy for an Organic Rankine Cycle waste heat recovery system. Appl. Energy 2019, 256, 113991. [Google Scholar] [CrossRef]
- Wei, Z.; Tien, P.W.; Calautit, J.; Darkwa, J.; Worall, M.; Boukhanouf, R. Investigation of a model predictive control (MPC) strategy for seasonal thermochemical energy storage systems in district heating networks. Appl. Energy 2024, 376, 124164. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, H.; Wang, T.; Zhang, B. Dynamic modeling and model predictive control for printed-circuit heat exchanger in supercritical CO2 power cycle. J. Clean. Prod. 2024, 472, 143495. [Google Scholar] [CrossRef]
- Park, J.H.; Bae, S.W.; Park, H.S.; Cha, J.E.; Kim, M.H. Transient analysis and validation with experimental data of supercritical CO2 integral experiment loop by using MARS. Energy 2018, 147, 1030–1043. [Google Scholar] [CrossRef]
- Catalina, T.; Iordache, V.; Caracaleanu, B. Multiple regression model for fast prediction of the heating energy demand. Energy Build. 2013, 57, 302–312. [Google Scholar] [CrossRef]
- Alobaid, F.; Mertens, N.; Starkloff, R.; Lanz, T.; Heinze, C.; Epple, B. Progress in dynamic simulation of thermal power plants. Prog. Energy Combust. Sci. 2017, 59, 79–162. [Google Scholar] [CrossRef]
- Drgoňa, J.; Arroyo, J.; Figueroa, I.C.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L.; et al. All you need to know about model predictive control for buildings. Annu. Rev. Control. 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Edwards, R.E.; New, J.; Parker, L.E. Predicting future hourly residential electrical consumption: A machine learning case study. Energy Build. 2012, 49, 591–603. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, Z.; Zhou, Q.; Qiao, Y.; Cao, F. Model predictive control for the operation of a transcritical CO2 air source heat pump water heater. Appl. Energy 2021, 30, 117339. [Google Scholar] [CrossRef]
- Efatinasab, E.; Irannezhad, N.; Rampazzo, M.; Diani, A. Machine and deep learning driven models for the design of heat exchangers with micro-finned tubes. Energy AI 2024, 16, 100370. [Google Scholar] [CrossRef]
- Son, S.; Heo, J.Y.; Lee, J.I. Prediction of inner pinch for supercritical CO2 heat exchanger using Artificial Neural Network and evaluation of its impact on cycle design. Energy Convers. Manag. 2018, 163, 66–73. [Google Scholar] [CrossRef]
- Mohanraj, M.; Jayaraj, S.; Muraleedharan, C. Applications of artificial neural networks for thermal analysis of heat exchangers—A review. Int. J. Therm. Sci. 2015, 90, 150–172. [Google Scholar] [CrossRef]
- Arat, H.; Arslan, O. Optimization of district heating system aided by geothermal heat pump: A novel multistage with multilevel ANN modelling. Appl. Therm. Eng. 2017, 111, 608–623. [Google Scholar] [CrossRef]
- He, J.; Shi, L.; Tian, H.; Wang, X.; Sun, X.; Zhang, M.; Yao, Y.; Shu, G. Applying artificial neural network to approximate and predict the transient dynamic behavior of CO2 combined cooling and power cycle. Energy 2023, 285, 129451. [Google Scholar] [CrossRef]
- Yang, F.; Cho, H.; Zhang, H.; Zhang, J.; Wu, Y. Artificial neural network (ANN) based prediction and optimization of an organic Rankine cycle (ORC) for diesel engine waste heat recovery. Energy Convers. Manag. 2018, 164, 15–26. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Y. Neural-Network-Based Nonlinear Model Predictive Control of Multiscale Crystallization Process. Processes 2022, 10, 2374. [Google Scholar] [CrossRef]
- Turja, A.I.; Hasan, M.; Ehsan, M.M.; Khan, Y. Multi-objective performance optimization & thermodynamic analysis of solar powered supercritical CO2 power cycles using machine learning methods & genetic algorithm. Energy AI 2023, 15, 100327. [Google Scholar] [CrossRef]
- Siddiqui, R.; Anwar, H.; Ullah, F.; Ullah, R.; Rehman, M.A.; Jan, N.; Zaman, F.; Prieto, J. Power Prediction of Combined Cycle Power Plant (CCPP) Using Machine Learning Algorithm-Based Paradigm. Wirel. Commun. Mob. Comput. 2021, 2021, 9966395. [Google Scholar] [CrossRef]
- Saeed, M.; Berrouk, A.S.; Al Wahedi, Y.F.; Singh, M.P.; Abu Dagga, I.; Afgan, I. Performance enhancement of a C-shaped printed circuit heat exchanger in supercritical CO2 Brayton cycle: A machine learning-based optimization study. Case Stud. Therm. Eng. 2022, 38, 102276. [Google Scholar] [CrossRef]
- Zhang, T.; Cao, F.; Song, Y.; Ren, J.; Bai, G.; Pang, X.; He, Y. The model predictive control strategy of the transcritical CO2 air conditioning system used in railway vehicles. Appl. Therm. Eng. 2022, 218, 119376. [Google Scholar] [CrossRef]
- Song, P.; An, Z.; Wei, M.; Sun, X.; Zhao, Y.; Dan, D.; Zhang, Y. Cooling performance and optimization of a thermal management system based on CO2 heat pump for electric vehicles. Energy Convers. Manag. 2024, 306, 118299. [Google Scholar] [CrossRef]
- Yin, X.; Cao, F.; Wang, J.; Li, M.; Wang, X. Investigations on optimal discharge pressure in CO2 heat pumps using the GMDH and PSO-BP type neural network—Part A: Theoretical modeling. Int. J. Refrig. 2019, 106, 549–557. [Google Scholar] [CrossRef]
- Song, Y.; Yang, D.; Li, M.; Cao, F. Investigations on optimal discharge pressure in CO2 heat pumps using the GMDH and PSO-BP type neural network—part B: Experimental study. Int. J. Refrig. 2019, 106, 248–257. [Google Scholar] [CrossRef]
- Wang, S.; Tuo, H.; Cao, F.; Xing, Z. Experimental investigation on air-source transcritical CO2 heat pump water heater system at a fixed water inlet temperature. Int. J. Refrig. 2013, 36, 701–716. [Google Scholar] [CrossRef]
- Guo, M.; Hao, Y.; Lu, Y.; Sun, L. Long-short term memory modeling and performance analysis of extended-state Kalman filter-based energy-saving model predictive control for supercritical unit. Appl. Therm. Eng. 2025, 272, 126202. [Google Scholar] [CrossRef]
- Fan, Q.; Zhang, J.; Li, R.; Fan, T. Review of Research on Hydrostatic Transmission Systems and Control Strategies. Processes 2025, 13, 317. [Google Scholar] [CrossRef]
- Vázquez-Aveledo, S.; Romero, R.J.; Montiel-González, M.; Cerezo, J. Control Strategy Based on Artificial Intelligence for a Double-Stage Absorption Heat Transformer. Processes 2023, 11, 1632. [Google Scholar] [CrossRef]
- Ahmed, N.; Assadi, M.; Ahmed, A.A.; Banihabib, R.; Zhang, Q. Assessing the impact of borehole field data on AI-based deep learning models for heating and cooling prediction. Geothermics 2023, 117, 102867. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, S.; Ding, Y.; Kim, M.K.; Yang, B.; Tian, Z.; Liu, J. Exploring the comprehensive integration of artificial intelligence in optimizing HVAC system operations: A review and future outlook. Results Eng. 2024, 25, 103765. [Google Scholar] [CrossRef]
- Adelekan, D.; Ohunakin, O.; Paul, B. Artificial intelligence models for refrigeration, air conditioning and heat pump systems. Energy Rep. 2022, 8, 8451–8466. [Google Scholar] [CrossRef]
- Ma, M.; Pektezel, O.; Ballerini, V.; Valdiserri, P.; di Schio, E.R. Performance Predictions of Solar-Assisted Heat Pumps: Methodological Approach and Comparison Between Various Artificial Intelligence Methods. Energies 2024, 17, 5607. [Google Scholar] [CrossRef]
- Song, D.; Shen, G.; Huang, C.; Huang, Q.; Yang, J.; Dong, M.; Joo, Y.H.; Duić, N. Review on the Application of Artificial Intelligence Methods in the Control and Design of Offshore Wind Power Systems. J. Mar. Sci. Eng. 2024, 12, 424. [Google Scholar] [CrossRef]
- Wang, K.; Li, M.-J.; Guo, J.-Q.; Li, P.; Liu, Z.-B. A systematic comparison of different S-CO2 Brayton cycle layouts based on multi-objective optimization for applications in solar power tower plants. Appl. Energy 2018, 212, 109–121. [Google Scholar] [CrossRef]
- Guo, J.-Q.; Li, M.-J.; He, Y.-L.; Jiang, T.; Ma, T.; Xu, J.-L.; Cao, F. A systematic review of supercritical carbon dioxide(S-CO2) power cycle for energy industries: Technologies, key issues, and potential prospects. Energy Convers. Manag. 2022, 258, 115437. [Google Scholar] [CrossRef]
- Qin, L.; Xie, G.; Ma, Y.; Li, S. Thermodynamic analysis and multi-objective optimization of a waste heat recovery system with a combined supercritical/transcritical CO2 cycle. Energy 2022, 265, 126332. [Google Scholar] [CrossRef]
- Huang, Y.; Jiang, P.; Zhu, Y. Analysis of a novel combined cooling and power system by integrating of supercritical CO2 Brayton cycle and transcritical ejector refrigeration cycle. Energy Convers. Manag. 2022, 269, 116081. [Google Scholar] [CrossRef]
- Alzuwayer, B.; Alhashem, A.; Albannaq, M.; Alawadhi, K. Advancements in Supercritical Carbon Dioxide Brayton Cycle for Marine Propulsion and Waste Heat Recovery. Processes 2024, 12, 1956. [Google Scholar] [CrossRef]
- Correa, F.; Barraza, R.; Too, Y.C.S.; Padilla, R.V.; Cardemil, J.M. Optimized operation of recompression sCO2 Brayton cycle based on adjustable recompression fraction under variable conditions. Energy 2021, 227, 120334. [Google Scholar] [CrossRef]
- He, Y.; Wang, L.; Dong, J.; Chen, Q. A Novel Fuel-Based CO2 Transcritical Cycle for Combined Cooling and Power Generation on Hypersonic Aircrafts. Energies 2024, 17, 4853. [Google Scholar] [CrossRef]






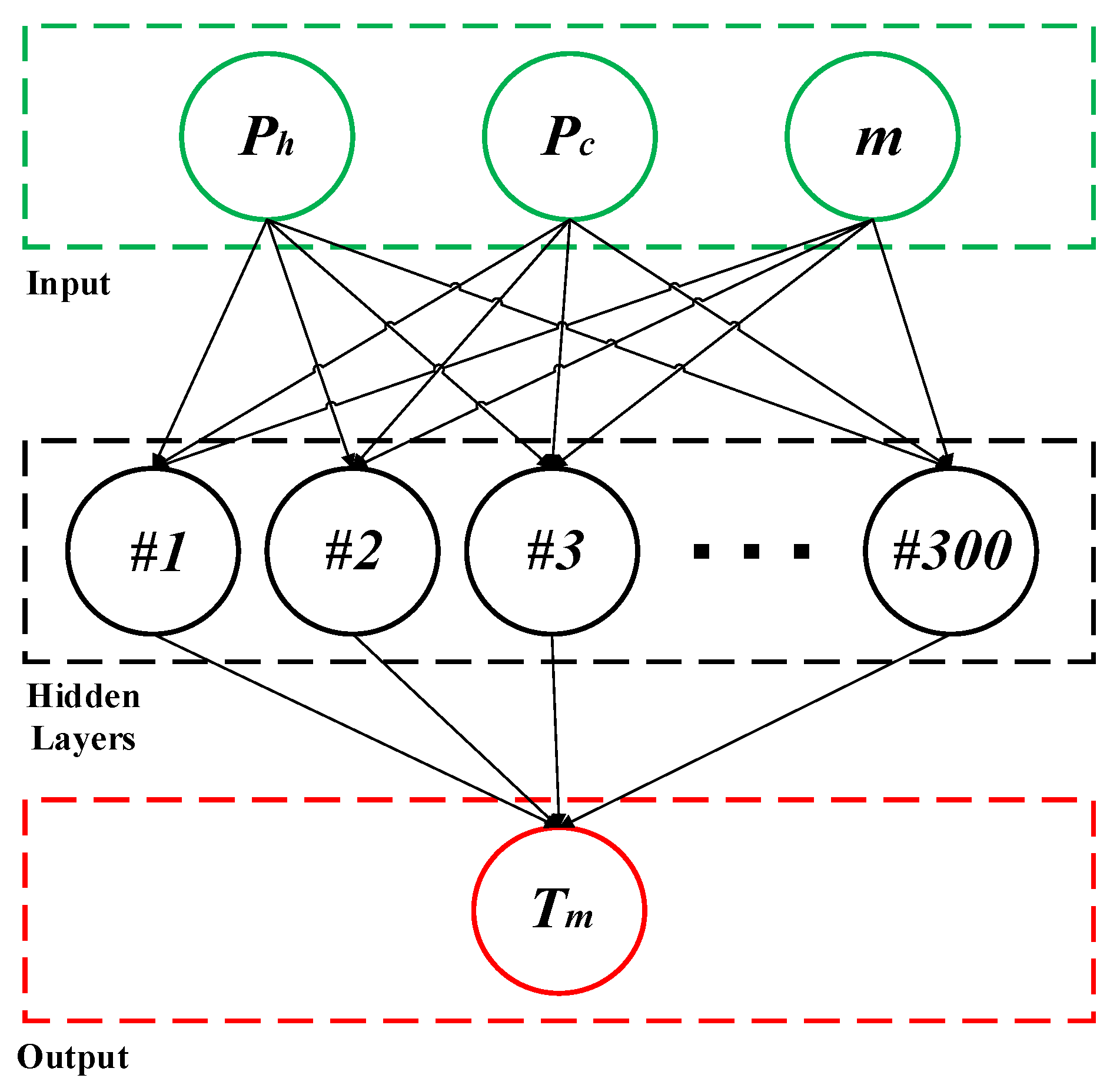
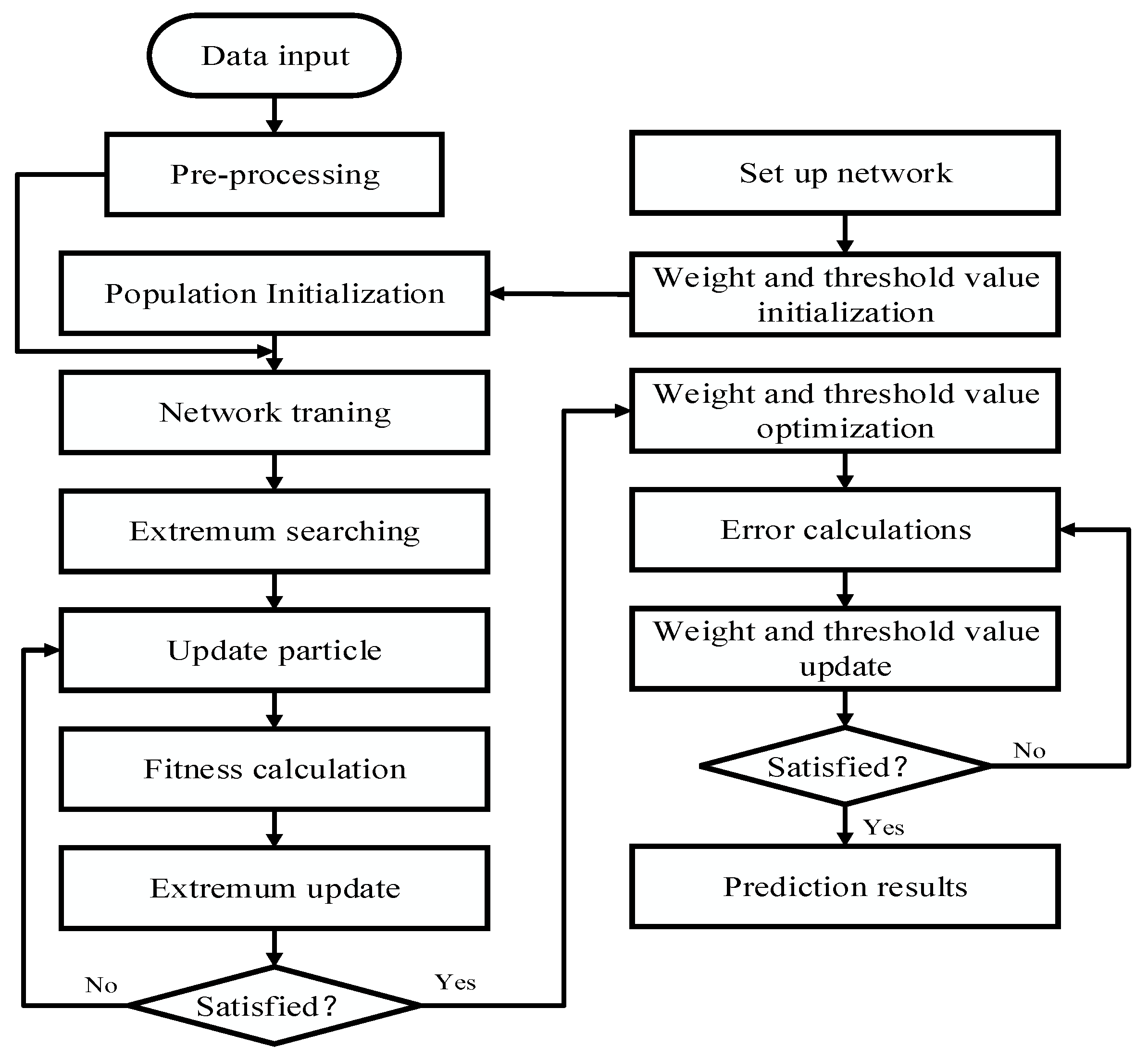
| Author | Control Strategies |
|---|---|
| Anton Moisseytsev et al. (Moisseytsev et al., 2009) (Moisseytsev and Sienicki, 2011a) (Moisseytsev and Sienicki, 2011b) (Moisseytsev and Sienicki, 2012) (Moisseytsev and Sienicki, 2018) | turbine throttle valve, turbine bypass valve, inventory control, compressor throttle valve, cooler bypass valve |
| Minh Tri Luu et al. (Luu et al., 2017a) | inventory control, cooler bypass valve, compressor throttle valve, compressor throttle valve |
| Felipe G. Battisti et al. (Battisti et al., 2018) | Heat source control |
| Eric M. Clementoni et al. (Clementoni et al., 2016) | Turbine bypass valve, turbine throttle valve, recuperator bypass valve |
| Control Method | Characteristics | Sensitivity to Operating Conditions | Impact of Ambient Temperature | Compatible Load Profile Characteristics |
|---|---|---|---|---|
| Inventory Control | Effectively improves cycle efficiency, but exhibits slow response to load changes; control range is limited by tank volume. Sole inventory control cannot maintain supercritical state at compressor inlet, requiring combined use with other methods. | Highly sensitive to system pressure variations; tank volume limitations become critical under extreme conditions. | Reduced pressure maintenance capability in low temperatures may compromise control stability. | Suitable for scenarios with gradual load variations and medium-to-long-term regulation needs. |
| Bypass Control | Enables rapid load adjustment, ideal for fast system response to load changes; regulation can be achieved solely via reliable valve control. | Performance depends heavily on valve response characteristics; high pressure differentials accelerate valve wear. | High temperatures may affect valve sealing and actuation reliability. | Appropriate for systems with frequent and sudden load changes requiring quick actuation. |
| Turbine Speed Control | Allows rapid load regulation while maintaining cycle efficiency; only applicable when compressor and turbine are arranged on separate shafts. | Requires high precision in speed control; split-shaft configuration is sensitive to system vibrations. | Low temperatures may impact lubrication and material contraction, affecting dynamic response. | Best suited for medium–high load ranges where both efficiency and dynamic performance are critical. |
| Turbine Throttling Control | Provides relatively fast load regulation but significantly reduces cycle efficiency; offers narrow control range under varying loads and cannot achieve low-load operation; may cause compressor choking. | Throttle valve position is highly sensitive to flow changes, potentially inducing surge under low pressure ratio conditions. | Efficiency losses worsen under high temperatures, with even poorer performance at low loads. | Recommended only for short-term, minor load adjustments or as a backup control strategy. |
| Control Technology | Advantages | Disadvantages | Suitable Application Scenarios |
|---|---|---|---|
| PID Control | Mature technology, simple structure easy to implement and maintain, suitable for many industrial processes | Performance may be insufficient for nonlinear and time-varying systems; requires an accurate system model to design controller parameters; poor adaptability and flexibility to environmental changes | Suitable for scenarios with relatively stable system dynamics and not extremely high control accuracy requirements |
| Extremum-Seeking Control | Can dynamically adjust control parameters to cope with external disturbances and system changes, reducing dependence on system models; suitable for dynamic optimization and real-time performance enhancement | May have long convergence times, not suitable for conditions with rapid environmental temperature changes; may only reach local optima; many parameters, complex design and implementation | Suitable for scenarios requiring real-time optimization and performance enhancement |
| ANN-based MPC Control | Strong nonlinear fitting capability, able to handle complex data relationships, capable of online output of control strategies | Existence of computational delay issues, relatively weak ability to control system dynamic performance; requires a large amount of data for training | Suitable for prediction and optimization problems, especially when there is abundant data and nonlinear relationships need to be processed |
| PSO-optimized MPC Control | Rapid convergence capability; ability to balance global and local search; suitable for real-time control | High dependence on data quality | Suitable for real-time control scenarios requiring fast response and optimization, especially in nonlinear and dynamically changing environments |
| Characteristic Dimension | Common Advantages | Common Challenges | Representative Performance Indicators |
|---|---|---|---|
| Performance Enhancement | >30% improvement in key performance indicators | Poor model interpretability | 20–60% energy efficiency improvement |
| Control Precision | Millisecond-level real-time control capability | Stringent real-time requirements | Latency requirement < 500 ms |
| Nonlinear Processing | Effective resolution of complex nonlinear relationships | High maintenance costs | Annual maintenance cost ~$15,000/system |
| Data Requirements | Multi-objective collaborative optimization | High-quality data dependency (“data hunger”) | Data acquisition cost $10K–15K/system |
| Computational Resources | Edge-cloud collaborative deployment architecture | Substantial computing power demands | BD-LSTM training time = 8 × CNN (NVIDIA T4 platform) |
| Breakthrough Direction | Core Concept | Technical Characteristics | Application Value | Development Goal |
|---|---|---|---|---|
| Physics-Embedded AI | Encoding physical laws as model prior knowledge | Integration of first principles & data-driven approaches | Enhance model extrapolation capability and generalizability | Reduce dependency on large training datasets |
| Self-Healing Systems | Automatic detection of data drift & triggered model updates | Online monitoring + adaptive adjustment | Reduce system maintenance costs and manual intervention | Achieve fully automated model lifecycle management |
| Energy Efficiency Optimization | Reducing energy consumption of AI control systems themselves | Lightweight models + efficient inference | Improve overall system energy efficiency ratio | Achieve self-energy consumption < 0.1% |
| Few-Shot Learning | Addressing scarce fault data problems | Meta-learning + transfer learning | Reduce data collection costs and annotation requirements | Train usable models with <100 samples |
| Physics-Informed Fusion | Encoding physical laws into neural network architectures | Combination of hard constraints + soft constraints | Enhance model interpretability and reliability | Improve cross-condition generalization by 20–30% |
| Self-Explaining AI | Developing interpretable fault diagnosis models | Visualized decision paths + uncertainty quantification | Meet industrial safety certification requirements | Pass SIL3/ISO certification |
| Lifelong Learning | Systems continuously adapt to equipment changes | Incremental learning + catastrophic forgetting avoidance | Adapt to equipment aging and environmental changes | Extend effective model lifecycle by 50% |
| Digital Twin | High-fidelity virtual models support AI training | Multi-physics simulation + real-time data interaction | Reduce field debugging time and risks | Reduce onsite debugging costs by 40–60% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, J.; Zheng, Y.; Zhao, J.; Luo, J.; He, Y. Cutting-Edge Research: Artificial Intelligence Applications and Control Optimization in Advanced CO2 Cycles. Energies 2025, 18, 5114. https://doi.org/10.3390/en18195114
Dong J, Zheng Y, Zhao J, Luo J, He Y. Cutting-Edge Research: Artificial Intelligence Applications and Control Optimization in Advanced CO2 Cycles. Energies. 2025; 18(19):5114. https://doi.org/10.3390/en18195114
Chicago/Turabian StyleDong, Jiaqi, Yufu Zheng, Jianguang Zhao, Jun Luo, and Yijian He. 2025. "Cutting-Edge Research: Artificial Intelligence Applications and Control Optimization in Advanced CO2 Cycles" Energies 18, no. 19: 5114. https://doi.org/10.3390/en18195114
APA StyleDong, J., Zheng, Y., Zhao, J., Luo, J., & He, Y. (2025). Cutting-Edge Research: Artificial Intelligence Applications and Control Optimization in Advanced CO2 Cycles. Energies, 18(19), 5114. https://doi.org/10.3390/en18195114




