MPC Design and Comparative Analysis of Single-Phase 7-Level PUC and 9-Level CSC Inverters for Grid Integration of PV Panels
Abstract
1. Introduction
2. Packed U-Cell Converter Topology
3. Crossover Switches Cell Converter Topology
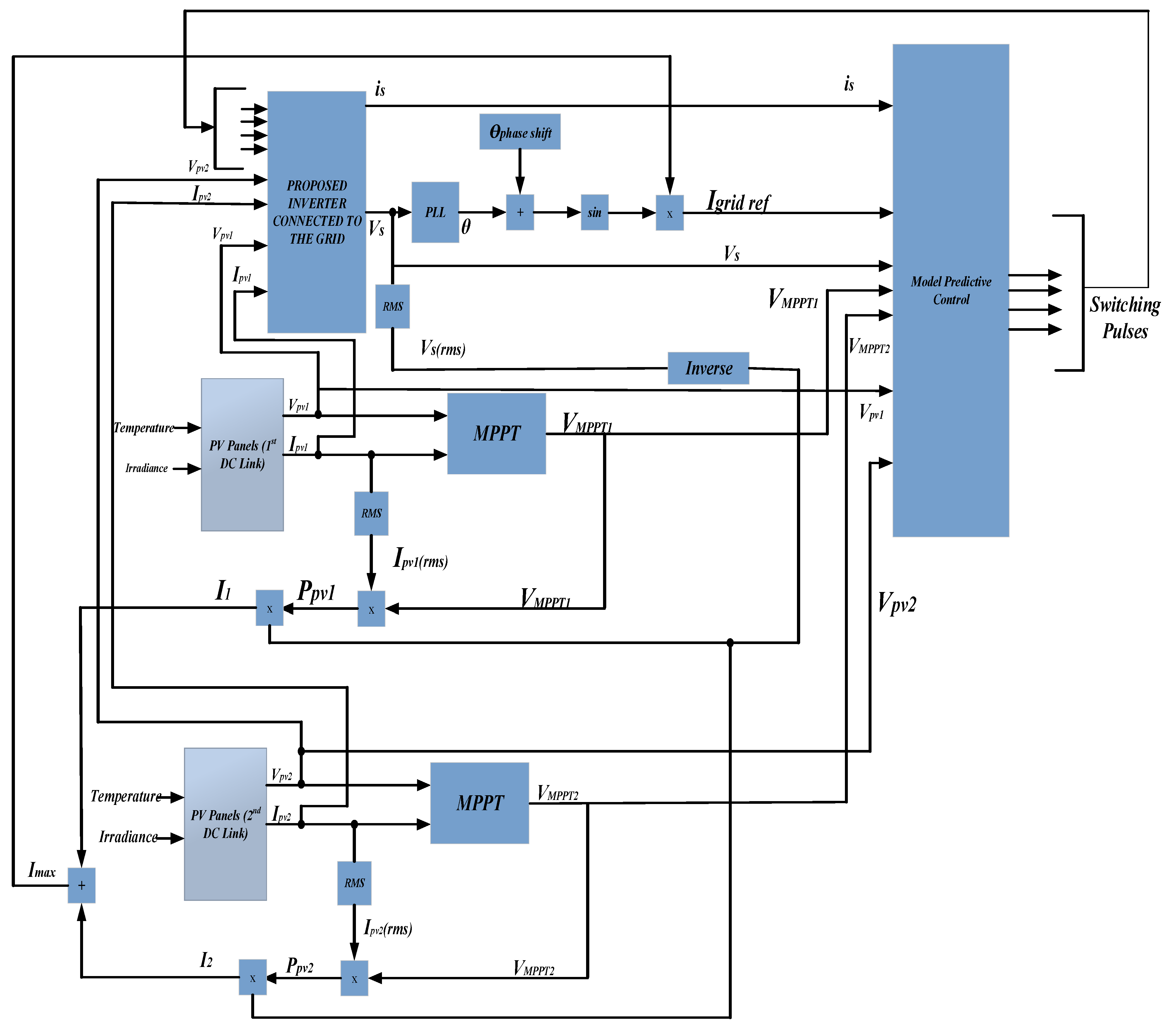
4. Model Predictive Control Design
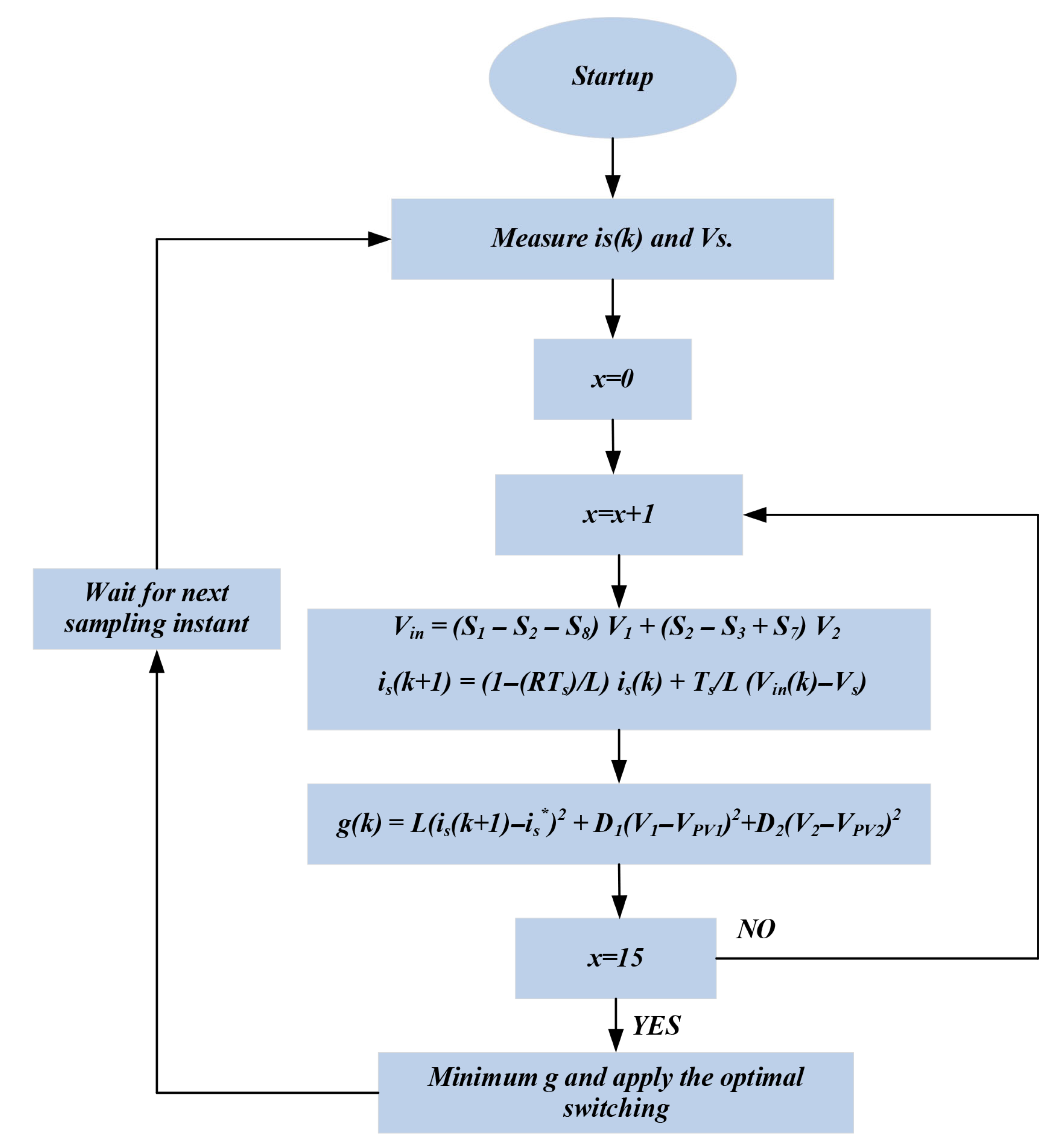
4.1. Model Predictive Control Design for PUC
4.2. Model Predictive Control Design for CSC
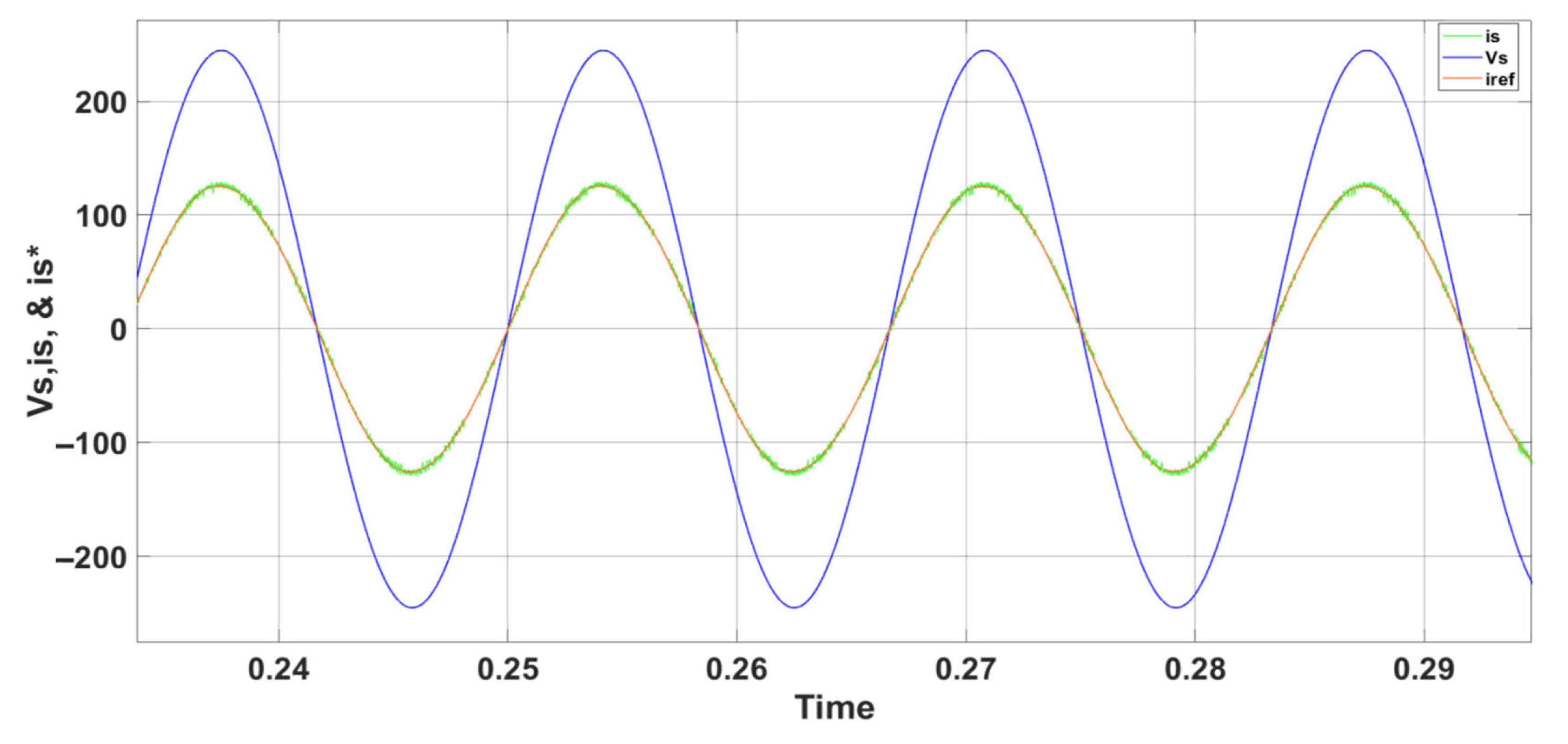
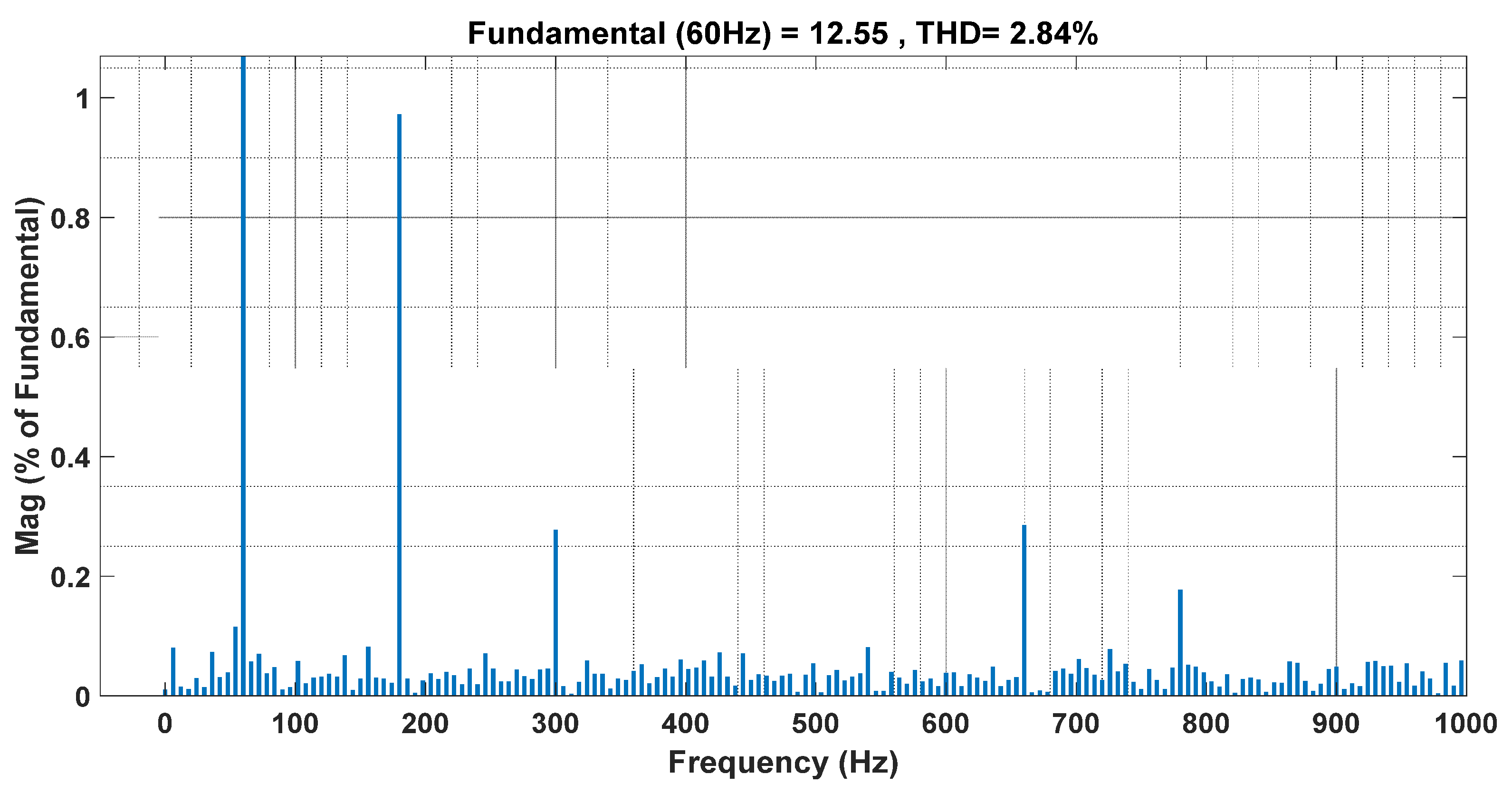
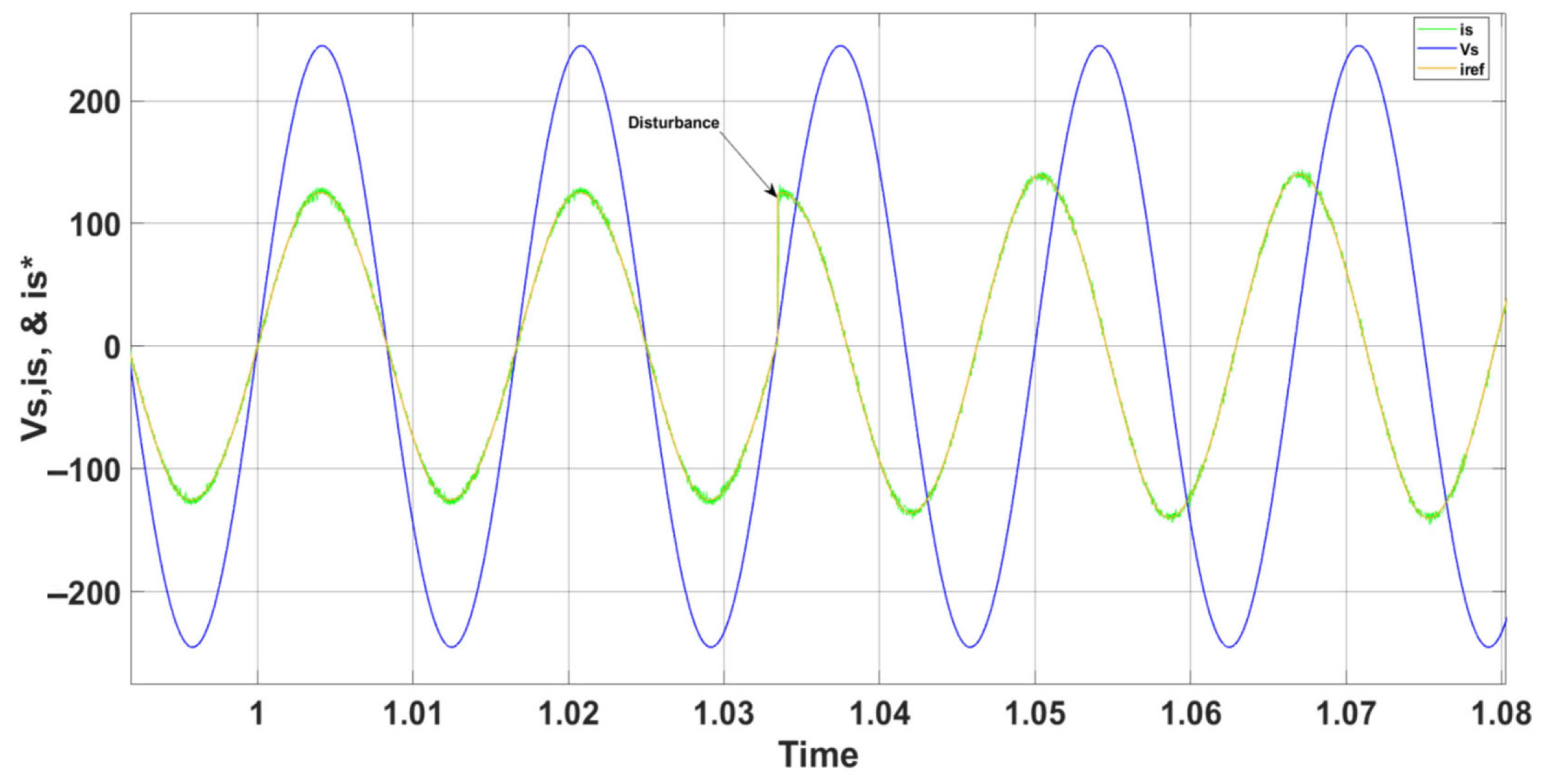
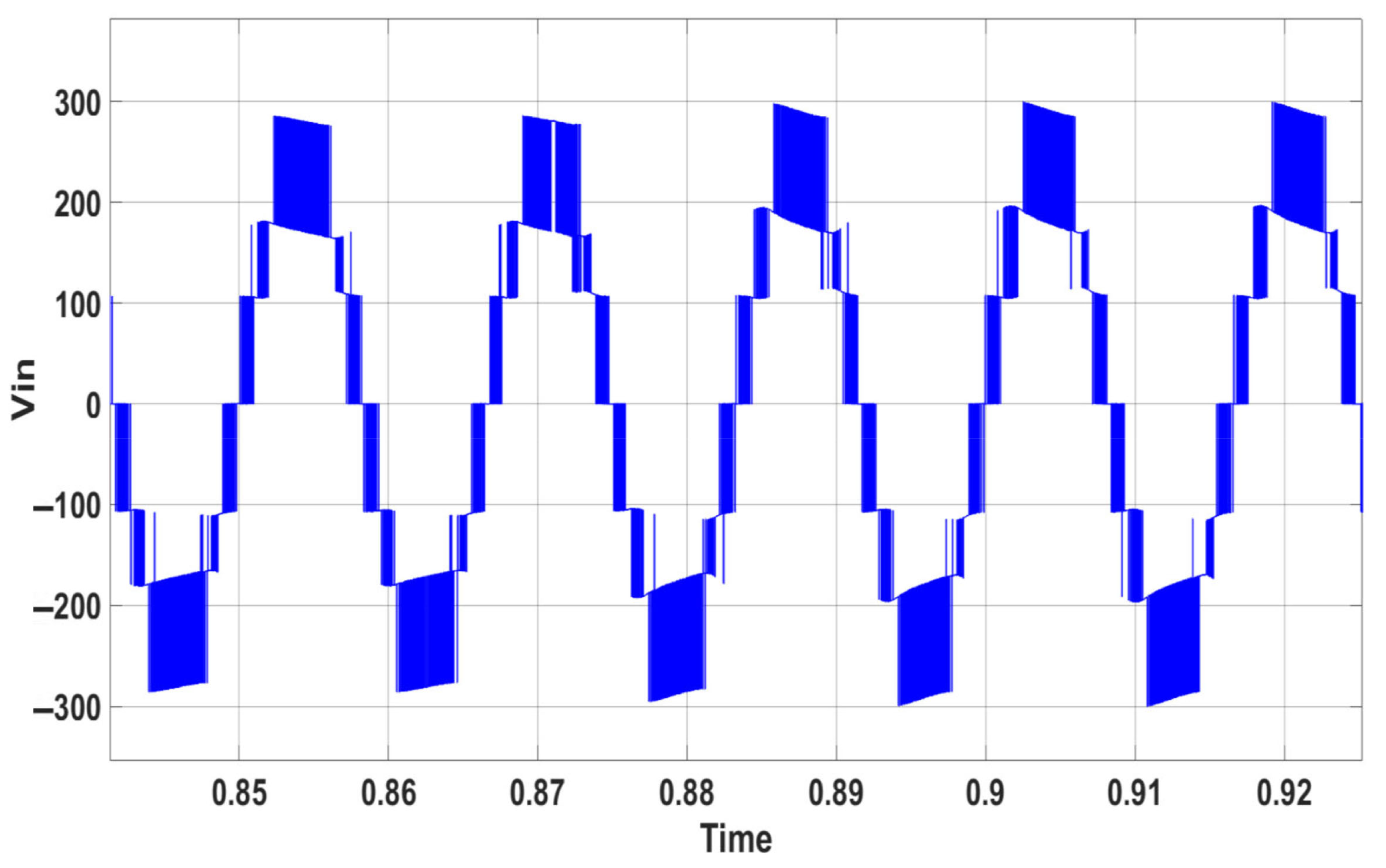
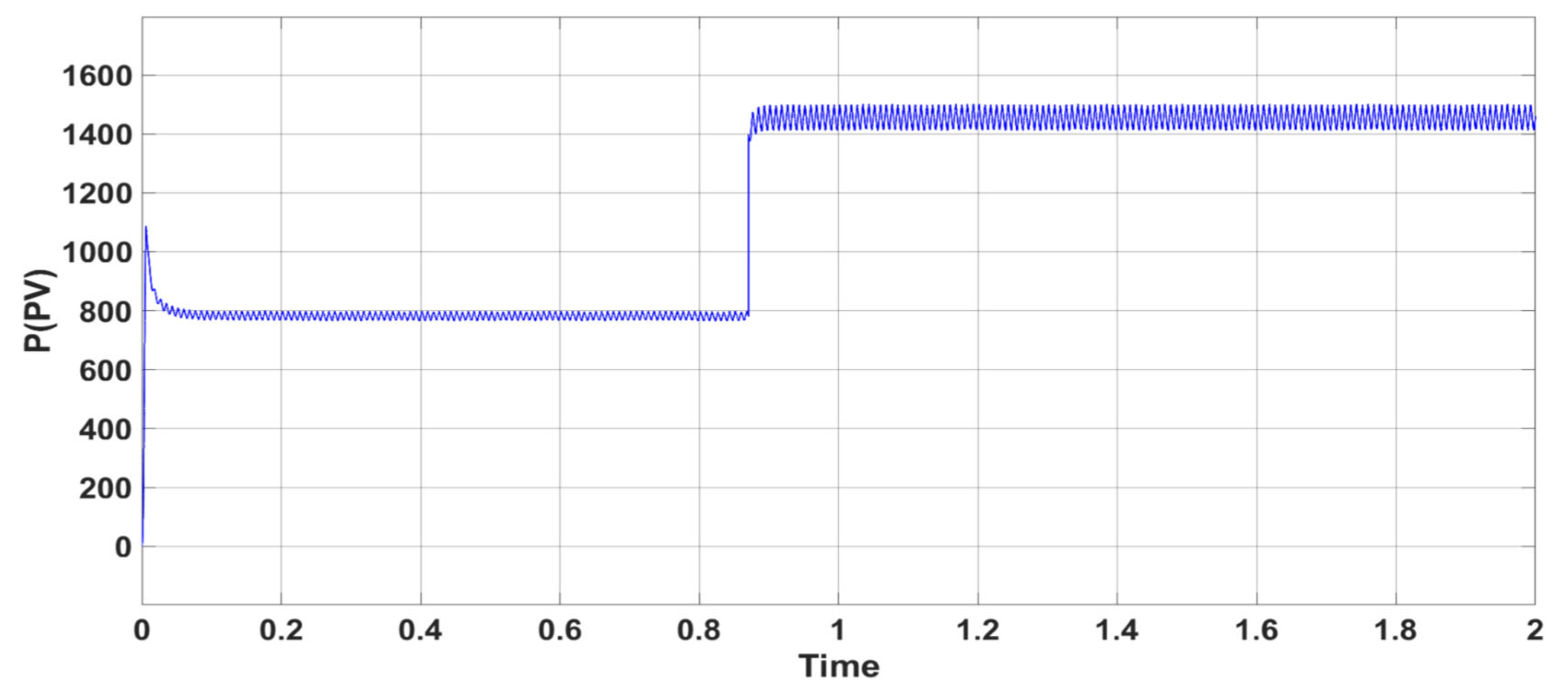
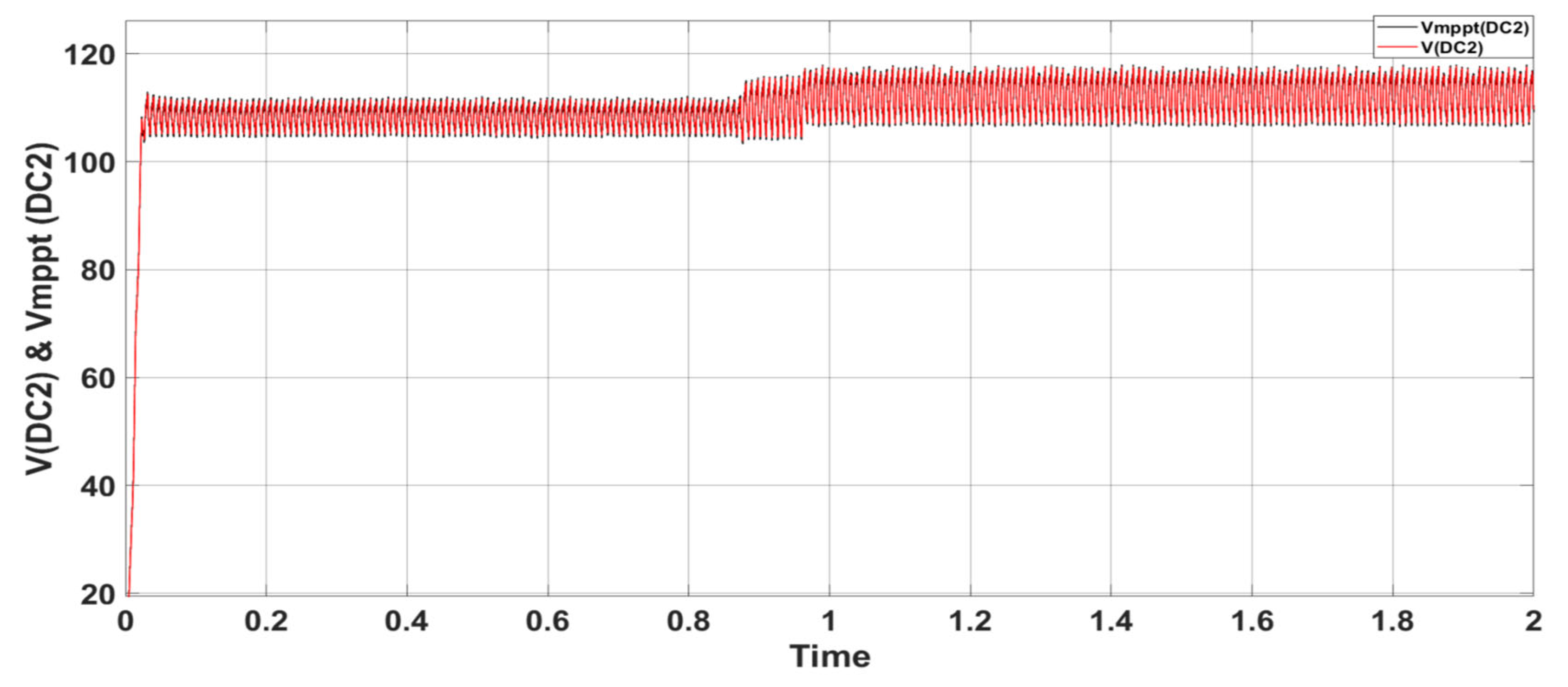
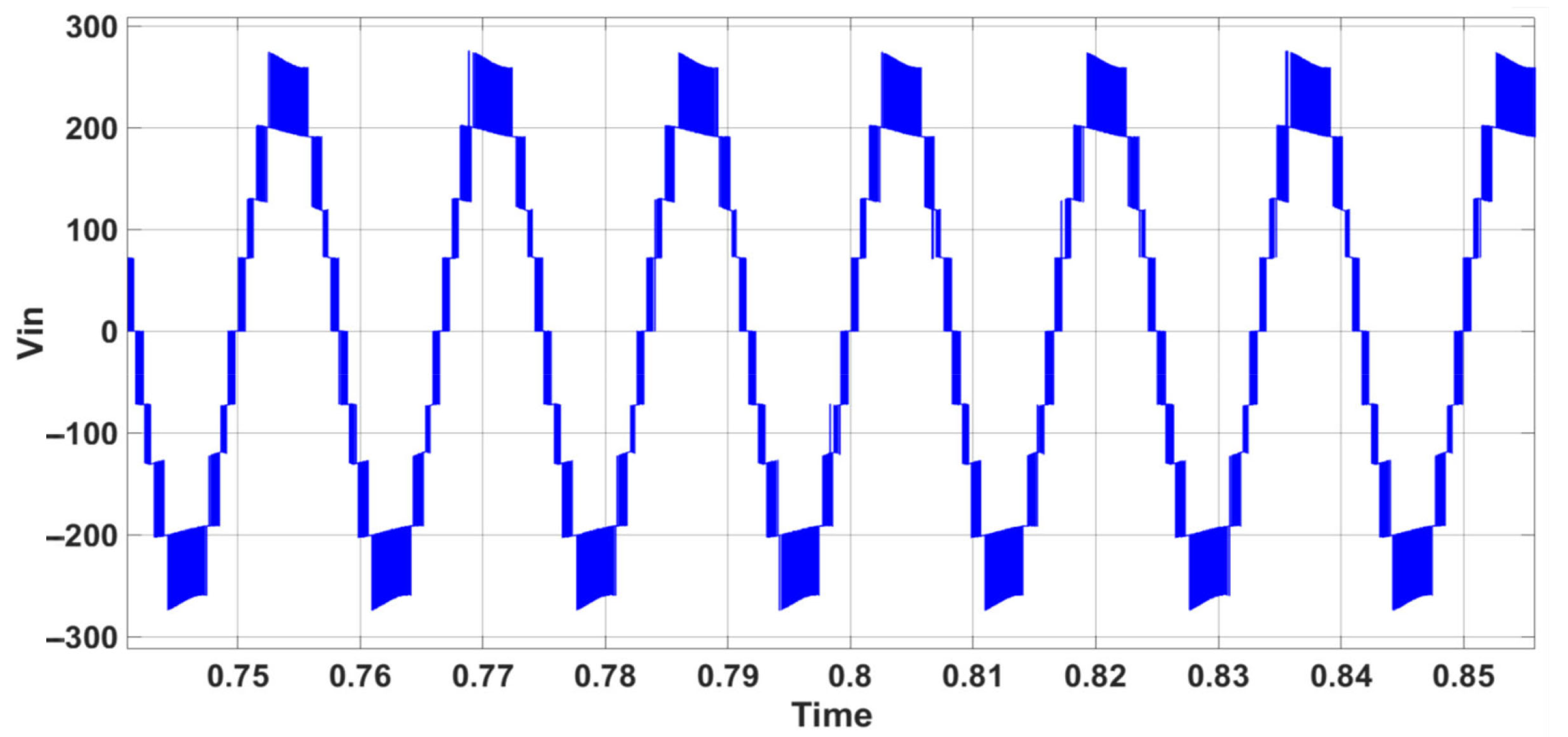
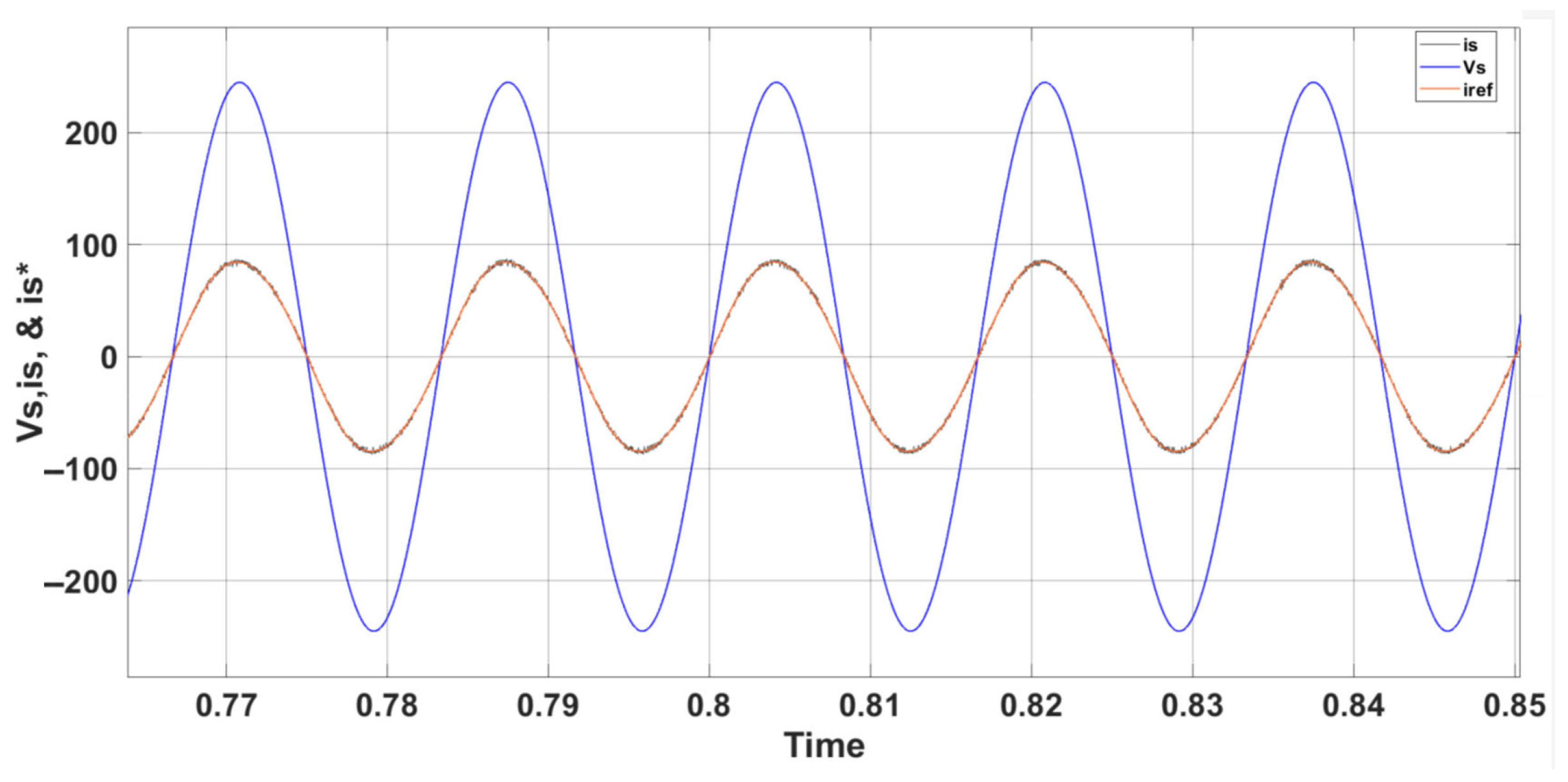
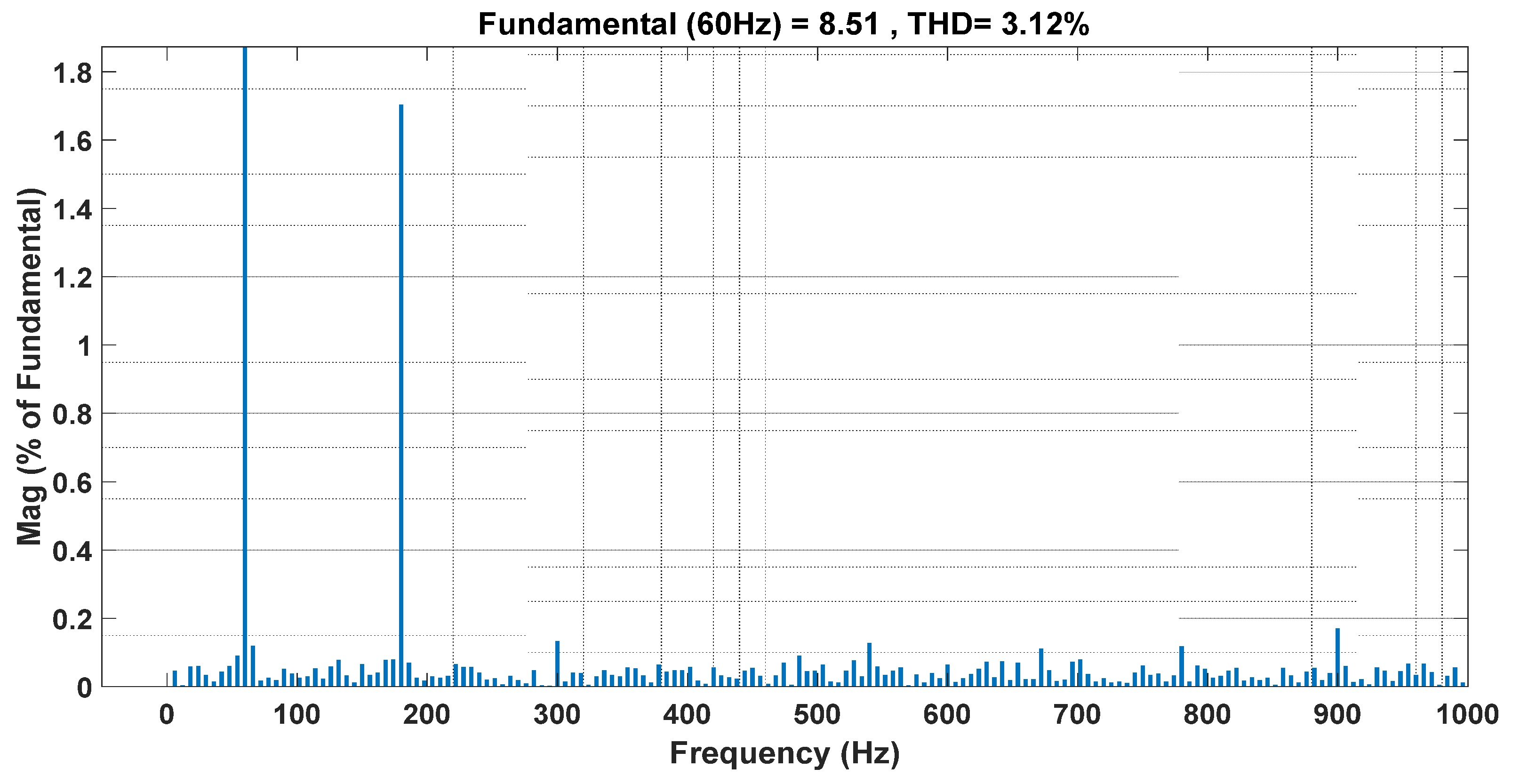
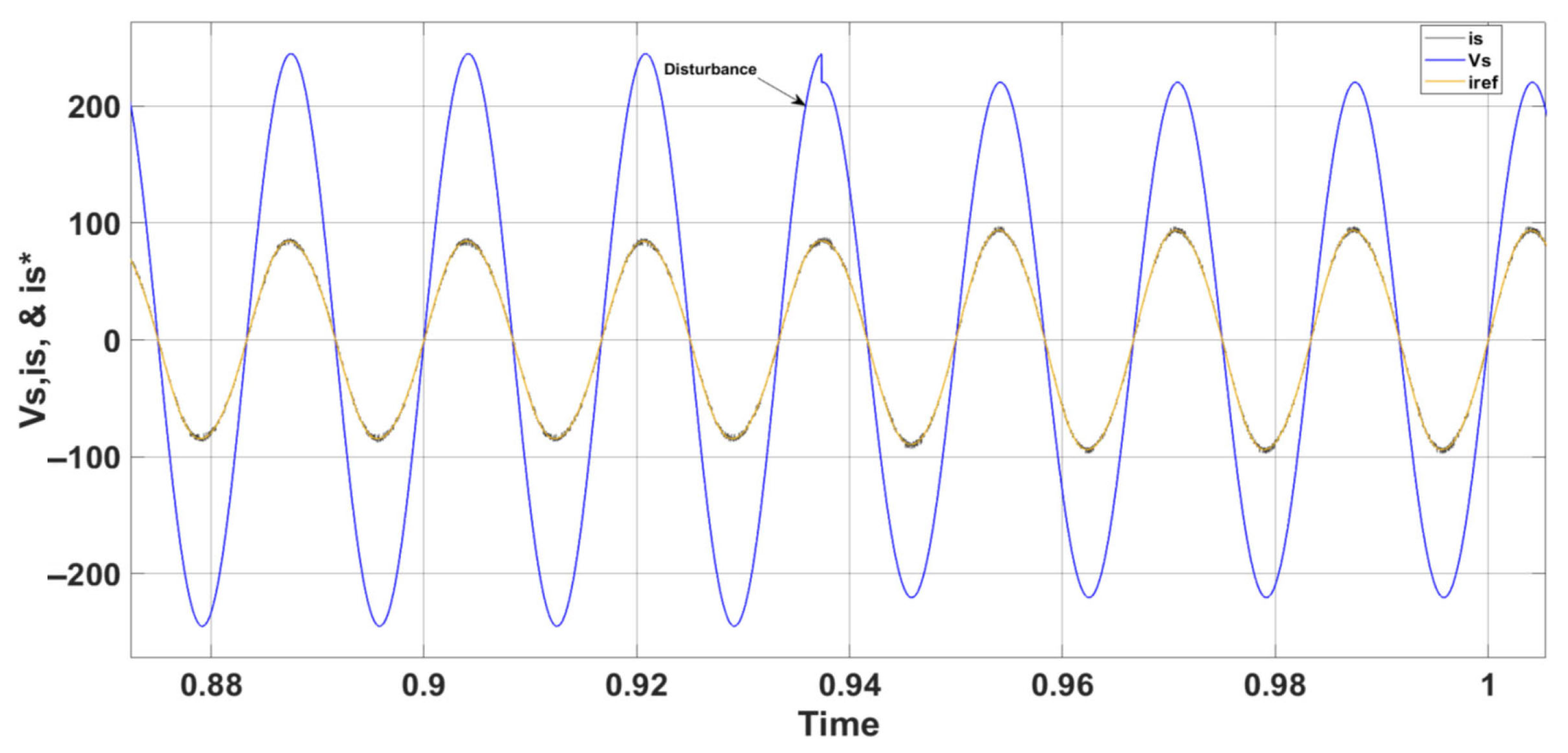
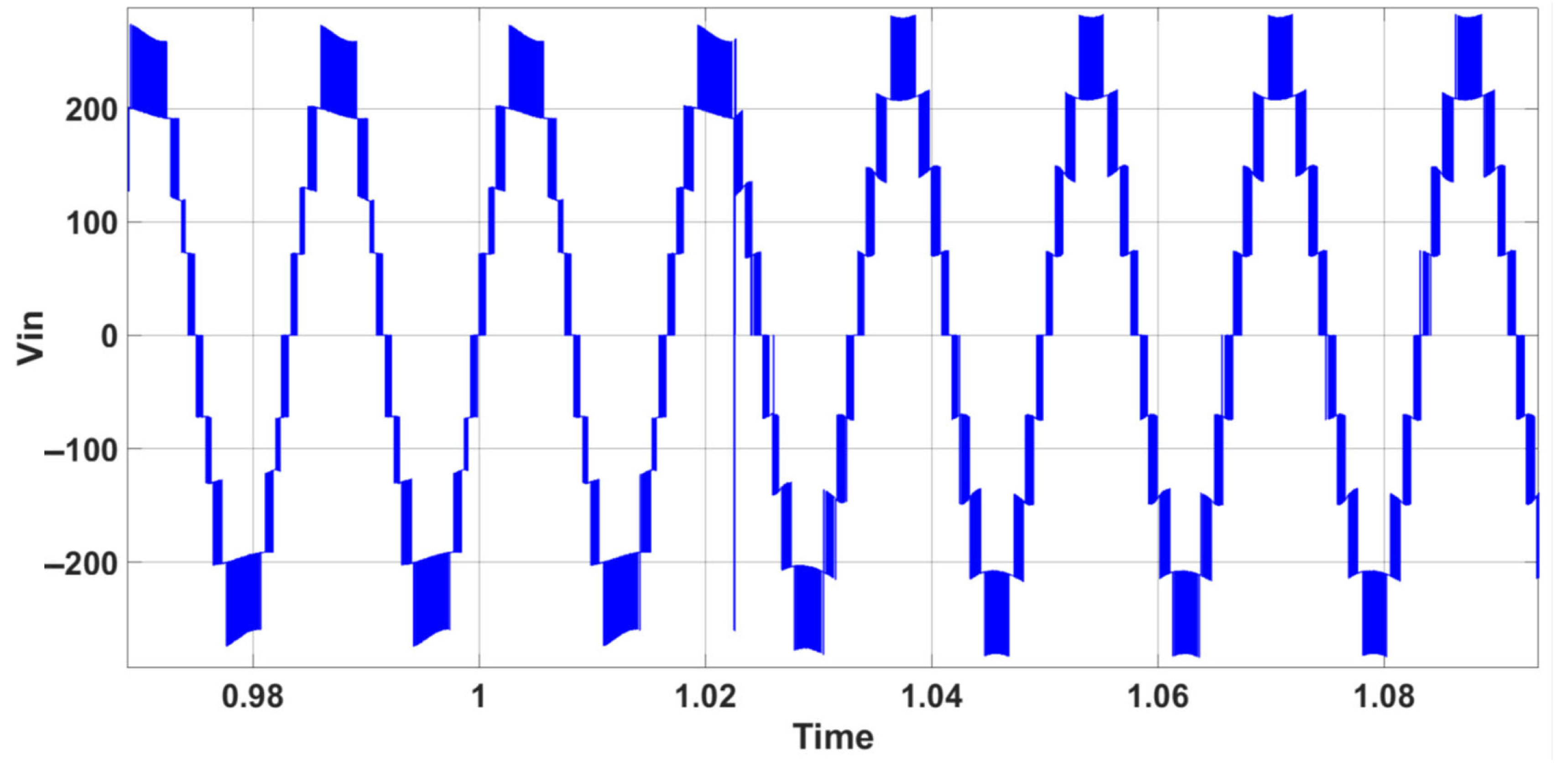
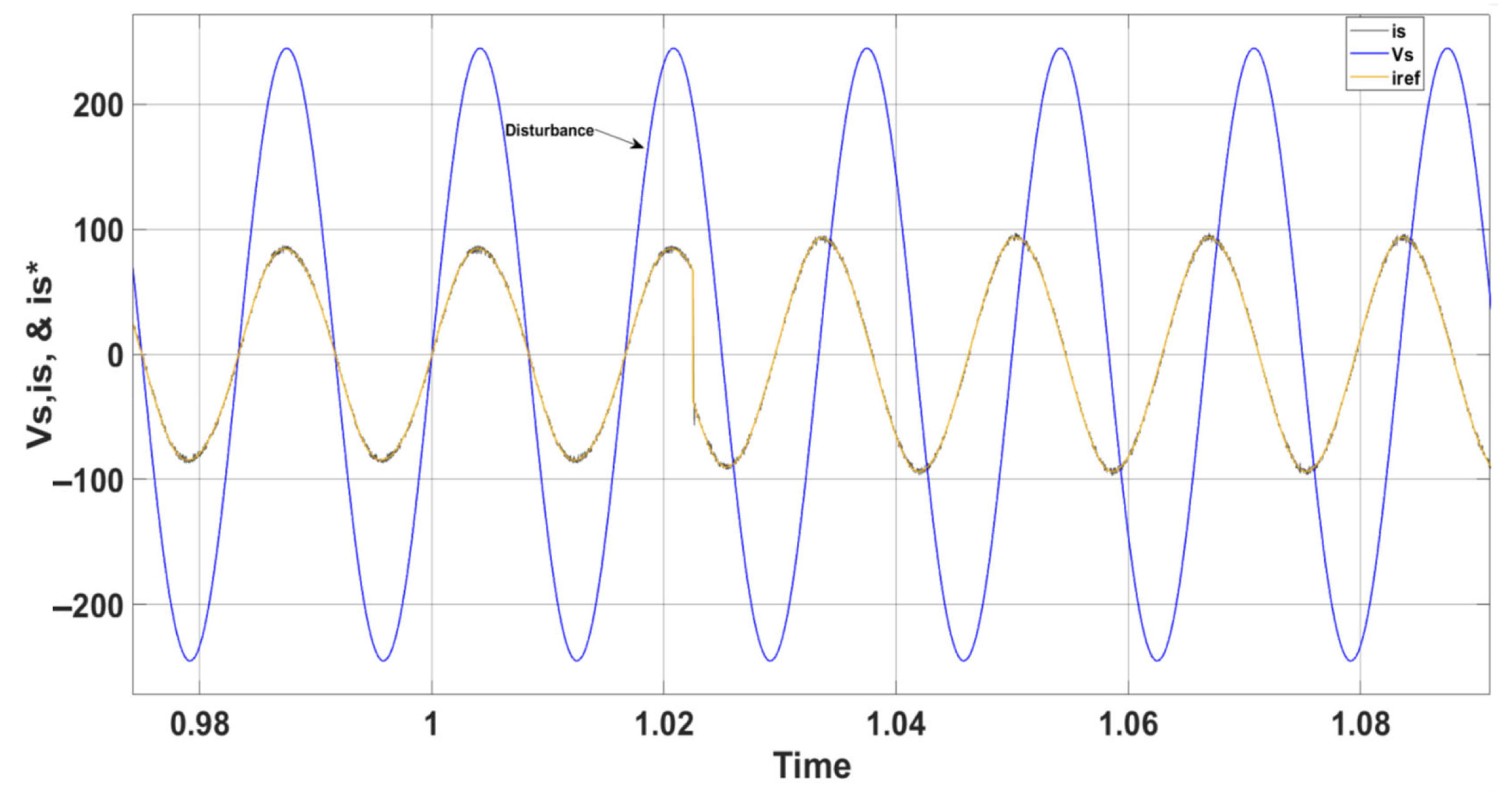
5. Simulation Results and Analysis for PUC
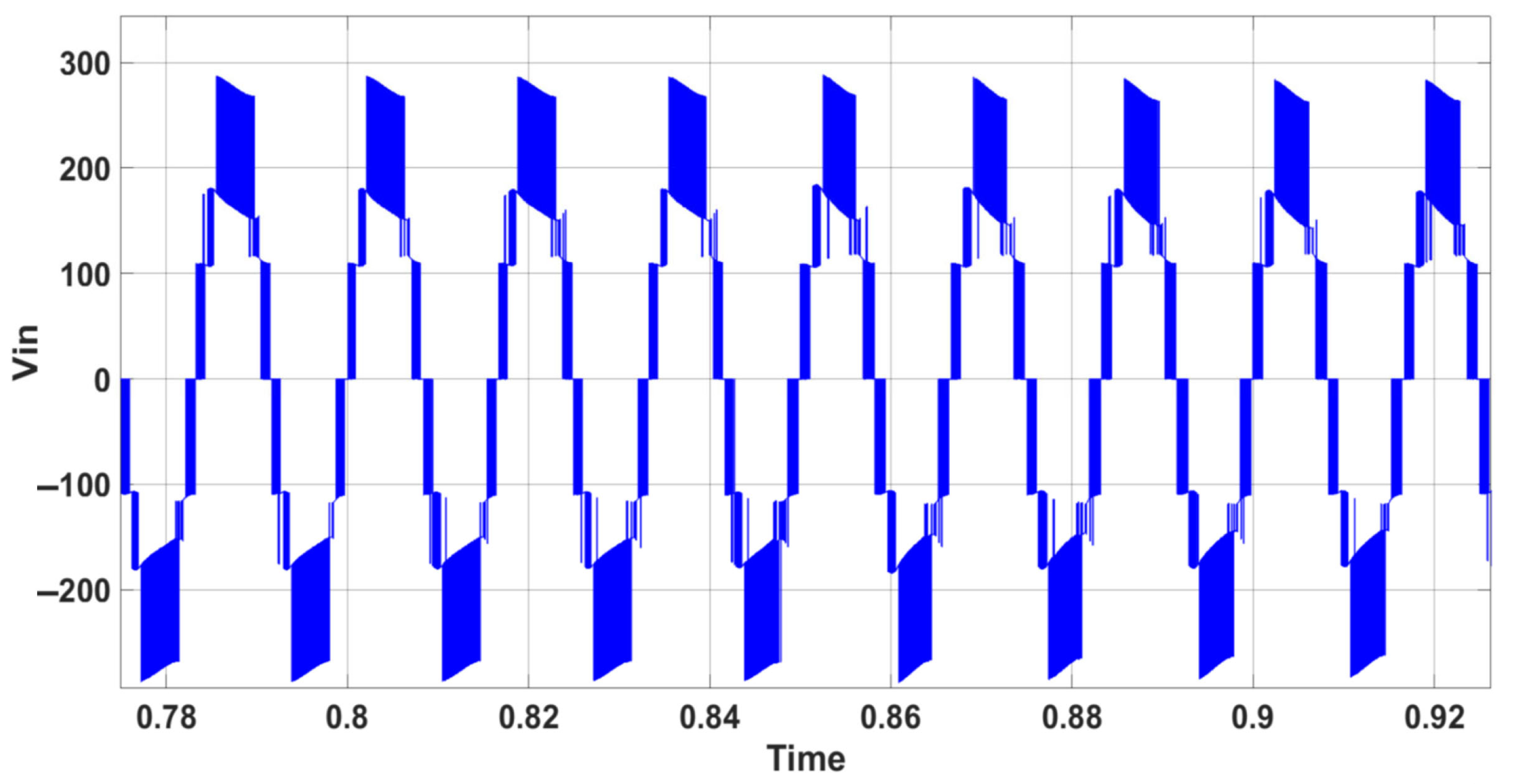
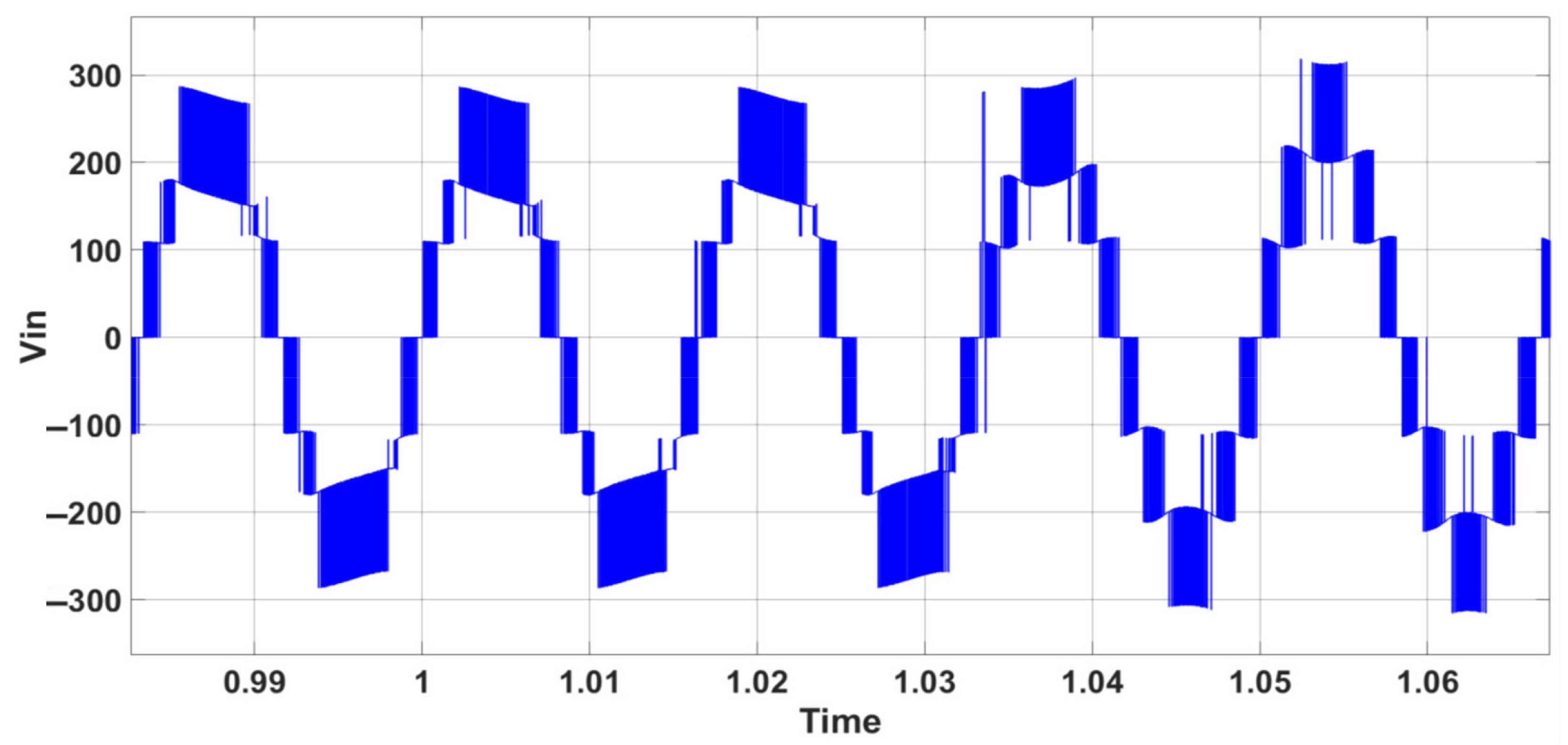
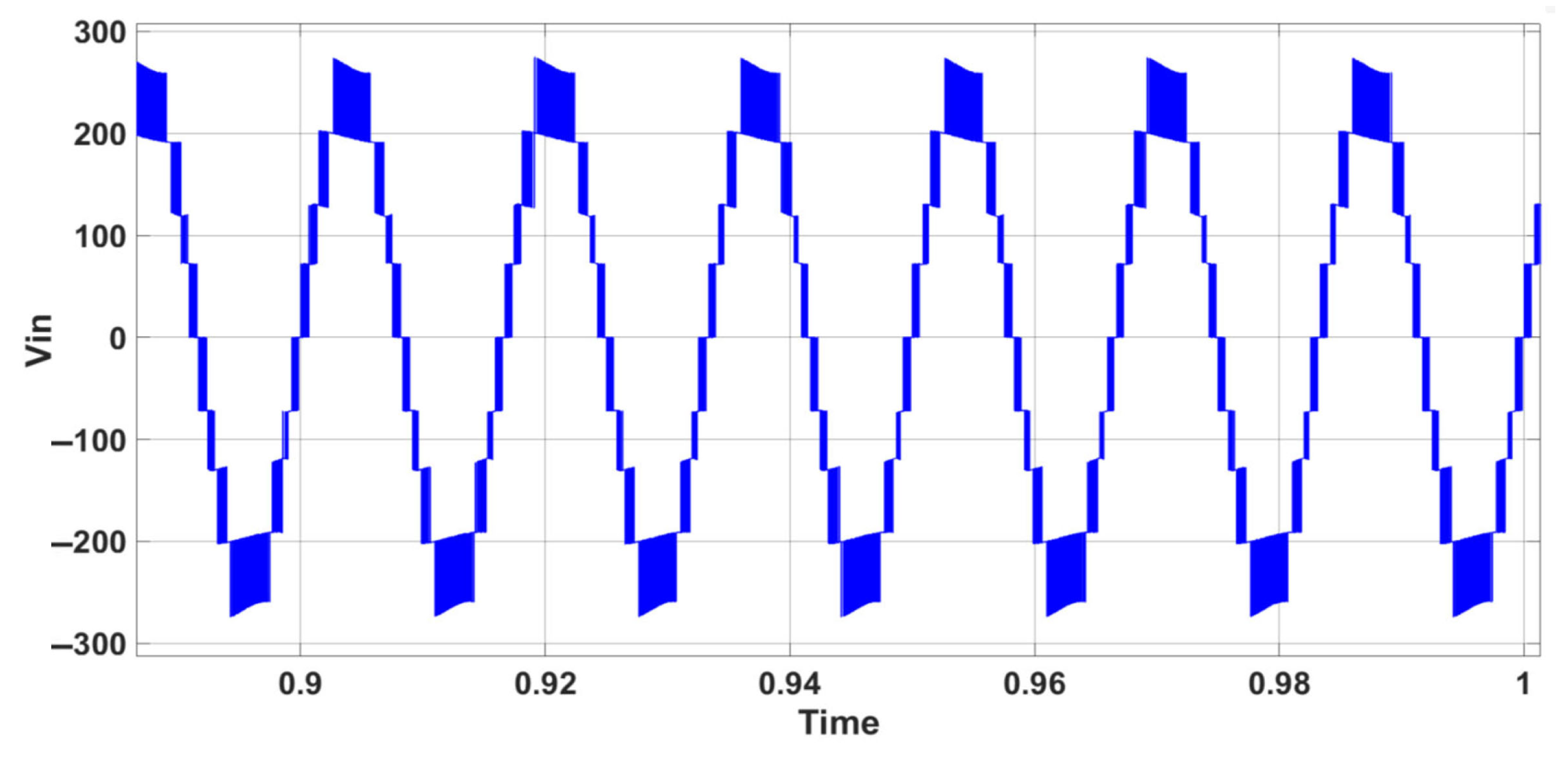
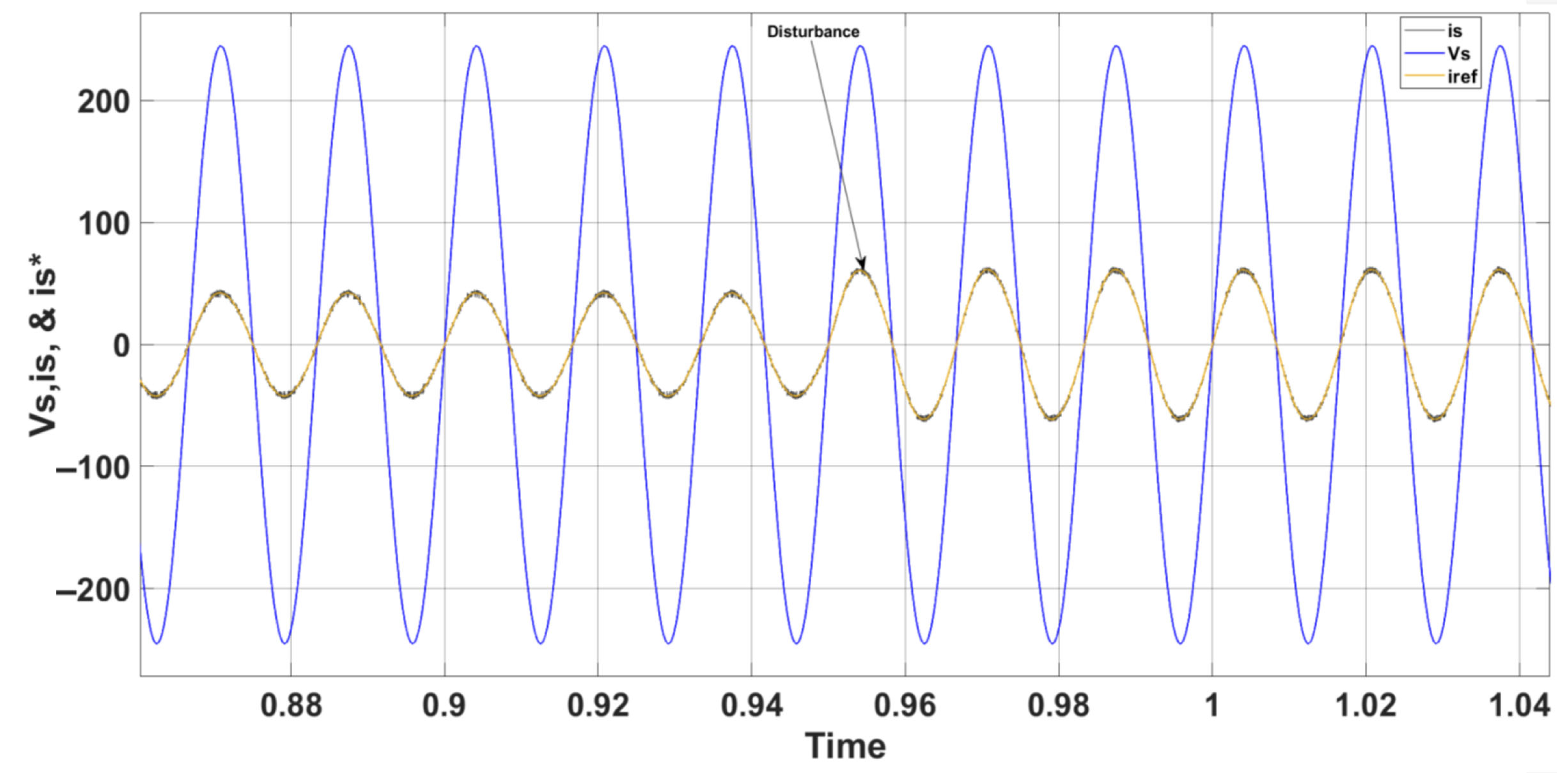
6. Simulation Results and Analysis for CSC
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feldman, D.; Zwerling, M.; Margolis, R. Q2/Q3 2019 Solar Industry Update; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2019. [Google Scholar]
- Lu, C.; Guan, S.; Yan, M.; Zhang, F.; Wu, K.; Wang, B. Grid Connected Photovoltaic Power Generation Station and it’s Influence on Dispatching Operation Mode. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–4. [Google Scholar]
- Gupta, K.K.; Jain, S. A Novel Multilevel Inverter Based on Switched DC Sources. IEEE Trans. Ind. Electron. 2014, 61, 3269–3278. [Google Scholar] [CrossRef]
- Vadizadeh, H.; Farokhniah, N.; Toodeji, H.; Kavousi, A. Formulation of line-to-line voltage total harmonic distortion of two-level inverter with low switching frequency. IET Power Electron. 2013, 6, 561–571. [Google Scholar] [CrossRef]
- Baker, R.H.; Bannister, L.H. Electric Power Converter. U.S. Patent 3,867,643, 18 February 1975. [Google Scholar]
- Hariri, R.; Sebaaly, F.; Kanaan, H.Y. A Review on Modulated Multilevel Converters in Electric Vehicles. In Proceedings of the IECON’20, Singapore, 18–21 October 2020; pp. 4987–4993. [Google Scholar]
- Qashqai, P.; Sheikholeslami, A.; Vahedi, H.; Haddad, K. A Review on Multilevel Converter Topologies for Electric Transportation Applications. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015. [Google Scholar]
- Meynard, T.; Foch, H. Multi-Level Conversion: High Voltage Choppers and Voltage-Source Inverters. In Proceedings of the PESC ’92 Record 23rd Annual Power Electronics Specialists Conference, Toledo, Spain, 29 June–3 July 1992; pp. 397–403. [Google Scholar]
- Lim, S.K.; Kim, J.H.; Nam, K. A DC-Link Voltage Balancing Algorithm for Three-Level Converter Using the Zero Sequence Current. In Proceedings of the Power Electronics Specialists Conference, Charleston, SC, USA, 1 July 1999; pp. 1083–1088. [Google Scholar]
- Mouton, H.D.T. Natural Balancing of Three-Level Neutral Point Clamped PWM Inverters. IEEE Trans. Ind. Electron. 2002, 49, 1017–1025. [Google Scholar] [CrossRef]
- John, J.; Jose, J.; Davis, P. A novel three phase three level step up multilevel inverter topology for aircraft applications. In Proceedings of the 2016 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Trivandrum, India, 14–17 December 2016; pp. 1–6. [Google Scholar]
- Arasteh, M.; Rahmati, A.; Abrishamifar, A.; Farhangi, S. DTC on multilevel inverters for pumping and ventilation applications. In Proceedings of the 2009 4th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 25–27 May 2009; pp. 2316–2320. [Google Scholar]
- Yamini, R.; Selvathai, T.; Reginald, R.; Sekar, K. Design of Multilevel Inverter for Hybrid Electric Vehicle System. In Proceedings of the 2018 International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 11–12 July 2018; pp. 966–971. [Google Scholar]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.; Wu, B.; Rodr, J.; Perez, M.A.; Leon, J. Recent Advances and Industrial Applications of Multilevel Converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Peng, F.Z.; Lai, J.-S.; McKeever, J.W.; VanCoevering, J. A Multilevel Voltage-Source Inverter with Separate DC Sources for Static VAR Generation. IEEE Trans. Ind. Appl. 1996, 32, 1130–1138. [Google Scholar] [CrossRef]
- Nabae, A.; Takahashi, I.; Akagi, H. A New Neutral-Point-Clamped PWM Inverter. IEEE Trans. Ind. Appl. 1981, IA-17, 518–523. [Google Scholar] [CrossRef]
- Ounejjar, Y.; Al-Haddad, K. A Novel High Energetic Efficiency Multilevel Topology with Reduced Impact on Supply Network. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; IECON: Piscataway, NJ, USA; pp. 489–494. [Google Scholar]
- Al-Haddad, K.; Ounejjar, Y.; Gregoire, L.A. Multilevel Electric Power Converter. U.S. Patent 20110280052, 17 November 2011. [Google Scholar]
- Sharifzadeh, M.; Al-Haddad, K. Packed E-Cell (PEC) Converter Topology Operation and Experimental Validation. IEEE Access 2019, 7, 93049–93061. [Google Scholar] [CrossRef]
- Ounejjar, Y.; Al-Haddad, K.; Gregoire, L. Packed U Cells Multilevel Converter Topology: Theoretical Study and Experimental Validation. IEEE Trans. Ind. Electron. 2011, 58, 1294–1306. [Google Scholar] [CrossRef]
- Vahedi, H.; Trabelsi, M. Single-DC-Source Multilevel Inverters; Springer Nature: Cham, Switzerland, 2019; ISBN 978-3-030-15252-9. [Google Scholar]
- Sheir, A.; Orabi, M.; Ahmed, M.E.; Iqbal, A.; Youssef, M. A High Efficiency Single-Phase Multilevel Packed U Cell Inverter for Photovoltaic Applications. In Proceedings of the 2014 IEEE 36th International Telecommunications Energy Conference (INTELEC), Vancouver, BC, Canada, 28 September 2014–2 October 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Trabelsi, M.; Bayhan, S.; Metry, M.; Abu-Rub, H.; Ben-Brahim, L.; Balog, R. An Effective Model Predictive Control for Grid Connected Packed U Cells Multilevel Inverter. In Proceedings of the 2016 IEEE Power and Energy Conference at Illinois (PECI), Urbana, IL, USA, 19–20 February 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Grigoletto, F.B.; Schuetz, D.; Junior, L.A.; de M. Carnielutti, F.; Pinheiro, H. Space Vector Modulation for Packed-U-Cell Converters (PUC). In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 4498–4503. [Google Scholar] [CrossRef]
- Azeem, A.; Tariq, M.; Lodi, K.A.; Bharatiraja, C. Performance Analysis of Discontinuous Pulse Width Modulation Schemes on PUC-5 Inverter. In Proceedings of the 2018 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 22–24 October 2018; pp. 636–641. [Google Scholar] [CrossRef]
- Seghir, M.M.; Krama, A.; Refaat, S.S.; Trabelsi, M.; Abu-Rub, H. Artificial Intelligence-Based Weighting Factor Autotuning for Model Predictive Control of Grid-Tied Packed U-Cell Inverter. Energies 2020, 13, 3107. [Google Scholar] [CrossRef]
- Iqbal, H.; Sarwat, A. Design and Implementation of Hybrid GA-PSO-Based Harmonic Mitigation Technique for Modified Packed U-Cell Inverters. Energies 2025, 18, 124. [Google Scholar] [CrossRef]
- Ebrahimi, J.; Babaei, E.; Gharehpetian, G.B. A New Topology of Cascaded Multilevel Converters With Reduced Number of Components for High-Voltage Applications. IEEE Trans. Power Electron. 2011, 26, 3109–3118. [Google Scholar] [CrossRef]
- Rodriguez, J.; Lai, J.-S.; Peng, F.Z. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef]
- Oskuee, M.R.J.; Salary, E.; Najafi-Ravadanegh, S. Creative design of symmetric multilevel converter to enhance the circuit’s performance. IET Power Electron. 2015, 8, 96–102. [Google Scholar] [CrossRef]
- Babaei, E.; Alilu, S.; Laali, S. A New General Topology for Cascaded Multilevel Inverters With Reduced Number of Components Based on Developed H-Bridge. IEEE Trans. Ind. Electron. 2014, 61, 3932–3939. [Google Scholar] [CrossRef]
- Vahedi, H.; Al-Haddad, K.; Ounejjar, Y.; Addoweesh, K. Crossover Switches Cell (CSC): A new multilevel inverter topology with maximum voltage levels and minimum DC sources. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 54–59. [Google Scholar]
- Niu, D.; Gao, F.; Wang, P.; Zhou, K.; Qin, F.; Ma, Z. A Nine-Level T Type Packed U-Cell Inverter. IEEE Trans. Power Electron. 2020, 35, 1171–1175. [Google Scholar] [CrossRef]
- Alquennah, N.; Trabelsi, M.; Krama, A.; Vahedi, H.; Mohamed-Seghir, M. ANN based Auto-Tuned Optimized FCS-MPC for Grid-Connected CSC Inverter. In Proceedings of the 2022 3rd International Conference on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 20–22 March 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Khan, S.A.; Sarwar, A.; Urooj, S.; Hossain, M.A. Open Circuit Fault Mitigation in a Nine-Level Modified Packed E-Cell Inverter. Energies 2022, 15, 7976. [Google Scholar] [CrossRef]
- Carrara, G.; Gardella, S.; Marchesoni, M.; Salutari, R.; Sciutto, G. A New Multilevel PWM Method: A Theoretical Analysis. IEEE Trans. Power Electron. 1992, 7, 497–505. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G. Multicarrier PWM Strategies for Multilevel Inverters. IEEE Trans. Ind. Electron. 2002, 49, 858–867. [Google Scholar] [CrossRef]
- Celanovic, N.; Boroyevich, D. A Fast Space-Vector Modulation Algorithm for Multilevel Three-Phase Converters. IEEE Trans. Ind. Appl. 2001, 37, 637–641. [Google Scholar] [CrossRef]
- Edpuganti, A.; Rathore, A.K. A Survey of Low Switching Frequency Modulation Techniques for Medium-Voltage Multilevel Converters. IEEE Trans. Ind. Appl. 2015, 51, 4212–4228. [Google Scholar] [CrossRef]
- Leon, J.; Kouro, S.; Franquelo, L.; Rodr, J.; Wu, B. The Essential Role and the Continuous Evolution of Modulation Techniques for Voltage Source Inverters in Past, Present and Future Power Electronics. IEEE Trans. Ind. Electron. 2016, 63, 2688–2701. [Google Scholar] [CrossRef]
- Ghias, A.; Pou, J.; Capella, G.J.; Agelidis, V.G.; Aguilera, R.P.; Meynard, T.A. Single-Carrier Phase-Disposition PWM Implementation for Multilevel Flying Capacitor Converters. IEEE Trans. Power Electron. 2015, 30, 5376–5380. [Google Scholar] [CrossRef]
- Ounejjar, Y.; Al-Haddad, K. A novel six-band hysteresis control of the packed U cells seven-level converter. In Proceedings of the 2010 IEEE International Symposium on Industrial Electronics, Bari, Italy, 4–7 July 2010; pp. 3199–3204. [Google Scholar]
- Memon, M.A.; Mekhilef, S.; Mubin, M.; Aamir, M. Selective harmonic elimination in inverters using bio-inspired intelligent algorithms for renewable energy conversion applications: A review. Renew. Sustain. Energy Rev. 2018, 82, 2235–2253. [Google Scholar] [CrossRef]
- Maswood, A.I.; Wei, S. Genetic-algorithm-based solution in PWM converter switching. IEEE Proc. Electr. Power Appl. 2005, 152, 473–478. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R.; Zanchetta, P.; Abu-Rub, H.; Young, H.A. State of the Art of Finite Control Set Model Predictive Control in Power Electronics. IEEE Trans. Ind. Inform. 2013, 9, 1003–1016. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, A.Q.; Song, W.; Bhattacharya, S.; Tan, G. Small-Signal Model-Based Control Strategy for Balancing Individual DC Capacitor Voltages in Cascade Multilevel Inverter-Based STATCOM. IEEE Trans. Ind. Electron. 2009, 56, 2259–2269. [Google Scholar] [CrossRef]
- Alquennah, A.N.; Trabelsi, M.; Vahedi, H. FCS-MPC of Grid-Connected 9-Level Crossover Switches Cell Inverter. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020. [Google Scholar]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kouro, S.; Cortés, P.; Vargas, R.; Ammann, U.; Rodríguez, J. Model predictive control—A simple and powerful method to control power converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Metri, J.; Vahedi, H.; Kanaan, H.Y.; Al Haddad, K. Real-Time Implementation of Model Predictive Control on 7-Level Packed U-Cell Inverter. IEEE Trans. Ind. Electron. 2016, 63, 4180–4186. [Google Scholar] [CrossRef]
- Khawaja, R.; Sebaaly, F.; Kanaan, H.Y. Design of a 7-Level Single-Stage/Phase PUC Grid Connected PV Inverter with FS-MPC Control. In Proceedings of the 2020 IEEE International Conference on Industrial Technology (ICIT), Buenos Aires, Argentina, 26–28 February 2020. [Google Scholar]
- Upreti, S.; Singh, B.; Kumar, N. A New Three-Phase Eleven Level Packed E-Cell Converter for Solar Grid-Tied Applications. E Prime Adv. Electr. Eng. Electron. Energy 2023, 4, 100152. [Google Scholar] [CrossRef]
- Hariri, R.; Sebaaly, F.; Al-Haddad, K.; Kanaan, H.Y. Modeling and Model Predictive Control of a 7-Level Packed U-Cell Converter for Grid-Tied PV Applications. In Proceedings of the IECON 2024-50th Annual Conference of the IEEE Industrial Elec-tronics Society, Chicago, IL, USA, 3–6 November 2024. [Google Scholar]
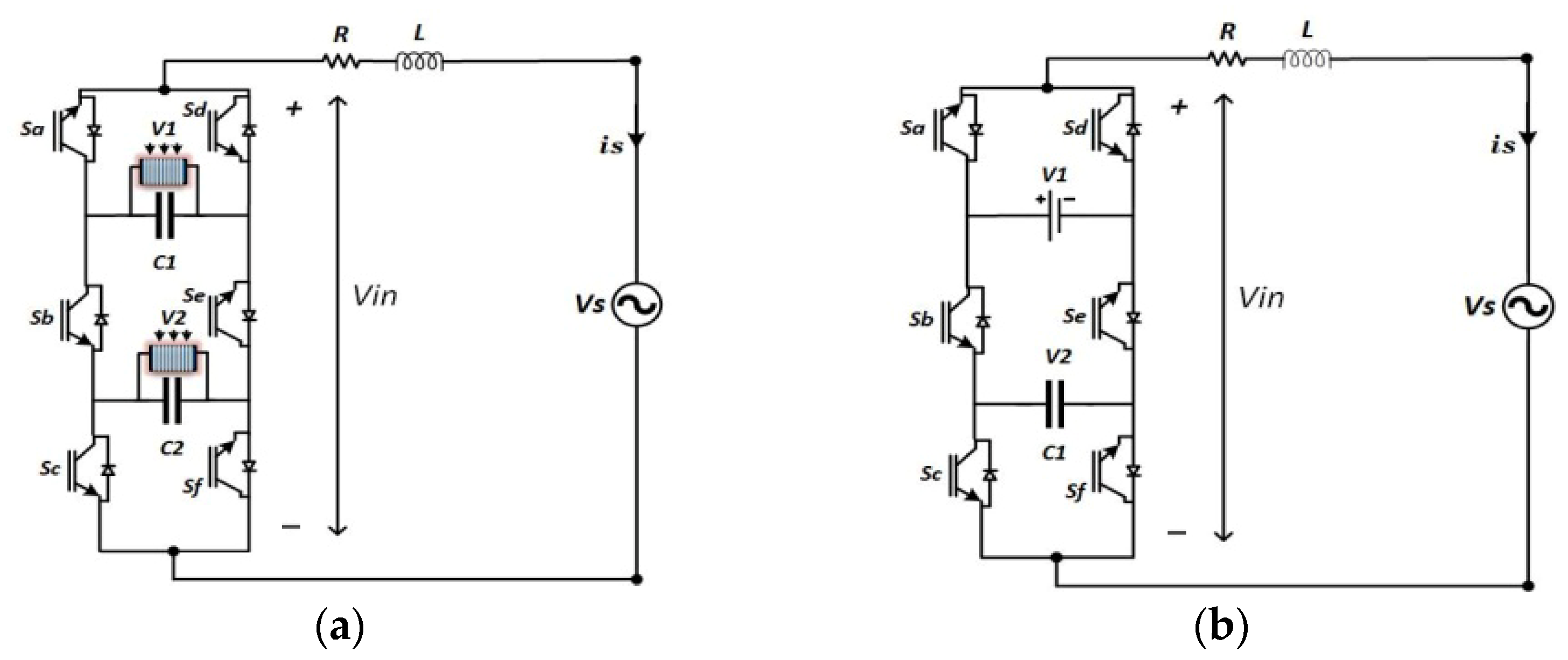
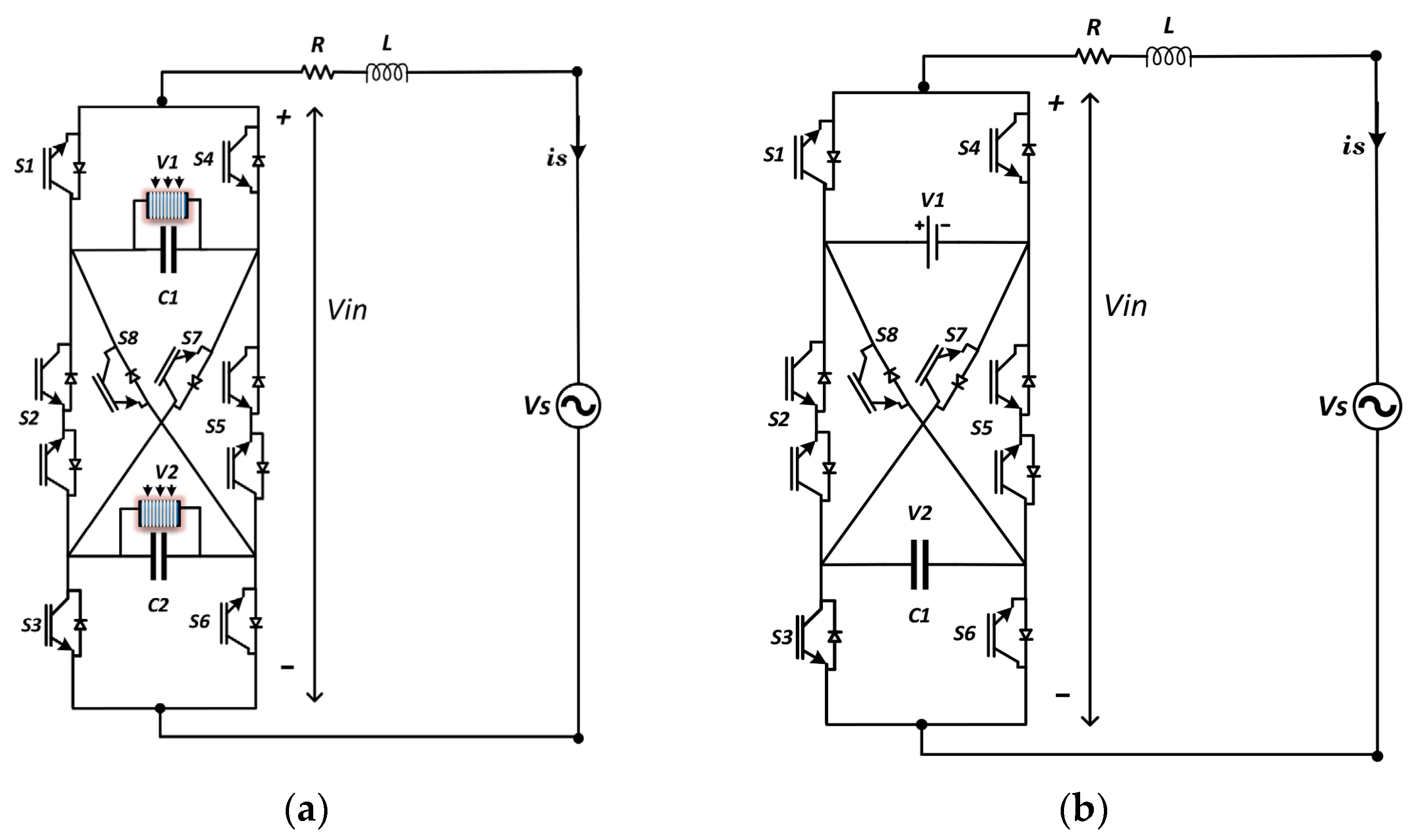









| States | Sa | Sb | Sc | Vin (Output Voltage) |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | V1 |
| 2 | 1 | 0 | 1 | V1 − V2 |
| 3 | 1 | 1 | 0 | V2 |
| 4 | 1 | 1 | 1 | 0 |
| 5 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 1 | −V2 |
| 7 | 0 | 1 | 0 | V2 − V1 |
| 8 | 0 | 1 | 1 | −V1 |
| States | Sa | Sb | Sc | Vin (Output Voltage) | Vin (Output Voltage Value) |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | V1 | +3E |
| 2 | 1 | 0 | 1 | V1 − V2 | 3E − E = +2E |
| 3 | 1 | 1 | 0 | V2 | +E |
| 4 | 1 | 1 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 1 | −V2 | −E |
| 7 | 0 | 1 | 0 | V2 − V1 | E − 3E = −2E |
| 8 | 0 | 1 | 1 | −V1 | −3E |
| States | Sa | Sb | Sc | Vin (Output Voltage) | Vin (Output Voltage Value) |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | V1 | +2E |
| 2 | 1 | 0 | 1 | V1 − V2 | 2E − E = +E |
| 3 | 1 | 1 | 0 | V2 | +E |
| 4 | 1 | 1 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 1 | −V2 | −E |
| 7 | 0 | 1 | 0 | V2 − V1 | E − 2E = −E |
| 8 | 0 | 1 | 1 | −V1 | −2E |
| States | Sa | Sb | Sc | Vin (Output Voltage) | Vin (Output Voltage Value) |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | V1 | +E |
| 2 | 1 | 0 | 1 | V1 − V2 | E − E = 0 |
| 3 | 1 | 1 | 0 | V2 | +E |
| 4 | 1 | 1 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 1 | −V2 | −E |
| 7 | 0 | 1 | 0 | V2 − V1 | E − E = 0 |
| 8 | 0 | 1 | 1 | −V1 | −E |
| States | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | Vin (Output Voltage) | Vin (Output Voltage Value) | Capacitor Charging State |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | V1 + V2 | 3E + E = 4E | Charged |
| 2 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | V1 | 3E | By passed |
| 3 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | V1 | 3E | By passed |
| 4 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | V1 − V2 | 3E − E = 2E | Discharged |
| 5 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | V2 | E | Charged |
| 6 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | V2 | E | Charged |
| 7 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | By passed |
| 8 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | By passed |
| 9 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | By passed |
| 10 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | By passed |
| 11 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | −V2 | −E | Discharged |
| 12 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | −V2 | −E | Discharged |
| 13 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | −V1 + V2 | −3E + E = −2E | Charged |
| 14 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | −V1 | −3E | By passed |
| 15 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | −V1 | −3E | By passed |
| 16 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | −V1 − V2 | −3E − E = −4E | Discharged |
| States | S1 | S2 | Vin (Output Voltage) |
|---|---|---|---|
| 1 | 1 | 0 | V1 |
| 2 | 1 | −1 | V1 − V2 |
| 3 | 0 | 1 | V2 |
| 4 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | −1 | −V2 |
| 7 | −1 | 1 | V2 − V1 |
| 8 | −1 | 0 | −V1 |
| Sampling Time | 20 µs |
|---|---|
| DC bus voltage (PV panels) | 300–315 V (9 panels in series) |
| DC link voltage (PV panels) | 99–105 V (3 panels in series) |
| DC capacitor C | 1000 µF |
| Line inductor L | 2.5 mH |
| Parasitic Resistor (r) | 0.1 Ω |
| AC grid voltage (Vrms) | 300 V |
| Frequency | 60 Hz |
| Sampling Time | 20 µs |
|---|---|
| DC bus voltage (PV panels) | 200–210 V (6 panels in series) |
| DC link voltage (PV panels) | 66–70 V (2 panels in series) |
| DC capacitor C | 1000 µF |
| Line inductor L | 2.5 mH |
| Parasitic Resistor (r) | 0.1 Ω |
| AC grid voltage (Vrms) | 300 V |
| Frequency | 60 Hz |
| Comparison Criteria | Packed U-Cell (PUC) Inverter | Cross Switches Cell (CSC) Inverter |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hariri, R.; Sebaaly, F.; Al-Haddad, K.; Kanaan, H.Y. MPC Design and Comparative Analysis of Single-Phase 7-Level PUC and 9-Level CSC Inverters for Grid Integration of PV Panels. Energies 2025, 18, 5116. https://doi.org/10.3390/en18195116
Hariri R, Sebaaly F, Al-Haddad K, Kanaan HY. MPC Design and Comparative Analysis of Single-Phase 7-Level PUC and 9-Level CSC Inverters for Grid Integration of PV Panels. Energies. 2025; 18(19):5116. https://doi.org/10.3390/en18195116
Chicago/Turabian StyleHariri, Raghda, Fadia Sebaaly, Kamal Al-Haddad, and Hadi Y. Kanaan. 2025. "MPC Design and Comparative Analysis of Single-Phase 7-Level PUC and 9-Level CSC Inverters for Grid Integration of PV Panels" Energies 18, no. 19: 5116. https://doi.org/10.3390/en18195116
APA StyleHariri, R., Sebaaly, F., Al-Haddad, K., & Kanaan, H. Y. (2025). MPC Design and Comparative Analysis of Single-Phase 7-Level PUC and 9-Level CSC Inverters for Grid Integration of PV Panels. Energies, 18(19), 5116. https://doi.org/10.3390/en18195116








