Experimental Assessment of a Passive Waste Heat Recovery System Using Thermosyphons and Thermoelectric Generators for Integration into District Heating Applications
Abstract
1. Introduction
| Reference (Year) | Configuration | Operating Temp. Range (Waste-Heat) [°C] | Reported Efficiency | Dual-Purpose Analysis (Electrical + Useful Thermal) |
|---|---|---|---|---|
| Jang et al. (2015) [29] | TEG + Loop Heat Pipe | 170–420 (simulated exhaust gas) | Not reported (focus on voltage output) | No |
| Remeli et al. (2015) [30] | TEG + Heat Pipes (for heating and cooling) | 108.5 (simulated low-grade waste heat) | Not reported (focus on heat transfer effectiveness) | No |
| Remeli et al. (2015) [31] | TEG + Heat Pipes (for heating and cooling) | 108 (simulated low-grade waste heat) | Not reported (focus on power output) | No |
| Remeli et al. (2016) [28] | TEG + Heat Pipes (for heating and cooling) | 82 (simulated low-grade waste heat) | 0.7% (thermal-to-electric conversion efficiency) | Yes (electricity and pre-heated air) |
| Kim et al. (2017) [18] | Direct Contact TEG (DCTEG) | Up to 200 (diesel engine exhaust) | 1.0–2.0% (energy conversion efficiency) | No |
| Remeli et al. (2017) [32] | TEG + Heat Pipes (for heating and cooling) | Not specified (simulated low-grade waste heat <150 °C) | Not reported (focus on power output and heat transfer effectiveness) | Yes (electricity and space heating) |
| Singh et al. (2017) [33] | TEG + In-pond heat exchanger (Solar Pond) | Up to 100 (simulated solar pond) | 1.5% (maximum conversion efficiency) | No |
| Mostafavi & Mahmoudi (2018) [34] | TEG + Heat Sinks | 125 (gasoline engine exhaust) | Not reported (focus on power output) | No |
| Fachini et al. (2019) [19] | TEG Only | Not specified (characterization study) | Focus on characteristic curves (P-V) | No |
| Wang et al. (2020) [25] | TEG + Potassium Heat Pipe | Up to 630 (electric heater) | 7.5% (maximum system conversion efficiency) | No |
| Kılkış et al. (2021) [35] | Solar PVT panel with integrated Heat Pipes, PCM, and TEG | Not specified (conceptual design) | Not reported | Yes (Solar PV + Thermal + additional TEG power) |
| Nadaf & Preethi (2021) [17] | TEG + Heat Sink | Not specified (T up to 105 °C reported) | Not reported | No |
| Dashevsky et al. (2022) [36] | Multilayer TEG (Bi2Te3 + PbTe based) | 50–600 | 15% (energy conversion efficiency) | Yes (electricity and domestic/water heating) |
| Gomaa et al. (2022) [21] | TEG Only (on coaxial shell of a cement kiln) | Up to 375 (cement kiln shell) | Up to 4.71% (conversion efficiency) | Yes (hot water production from cooling loop) |
| Pourrahmani et al. (2022) [23] | TEG + Water-to-water heat exchanger (from PEMFC) | 57.4 (PEMFC coolant) | Not reported (focus on recovered power) | No |
| Zhao et al. (2022) [27] | TEG + Copper-Ethanol Heat Pipe | Up to 210 (controlled heater) | 3.81% (maximum conversion efficiency) | No |
| Fernández-Yáñez et al. (2023) [20] | TEG + Squared heat exchanger with internal fins | 423.4 (diesel engine exhaust) | Not reported (focus on net power output) | No |
| Xiao et al. (2023) [22] | TEG + Arch bridge-shaped heat collector | 85–165 (simulated industrial pipe) | 2.67% (maximum conversion efficiency) | No |
| Zhang et al. (2023) [24] | TEG + Copper-Water Heat Pipe | 150–200 (simulated reactor waste heat) | 1.49% (maximum power generation efficiency) | No |
| Goswami et al. (2024) [37] | TEG-array with Salt Gradient Thermal Storage | Up to 437.55 (from biomass engine exhaust) | 4.63% (maximum conversion efficiency) | No |
| Wang et al. (2024) [38] | Heat Pipe Electric Generator (HPEG) using triboelectric effect | 60–137 (heated PTFE tube) | Not reported (focus on voltage output) | No |
| Zhang et al. (2024) [26] | TEG + Gravity Heat Pipe | 80–350 (controlled heater) | Up to 11.62% (power generation efficiency) | No |
| Jouhara et al. (2025) [39] | Multi-sink Heat Pipe Heat Exchanger (HPHE) | 340–360 (furnace exhaust gas) | 47% (average energy recovery) | No (Thermal only: preheated air and hot water) |
| Kubenova et al. (2025) [40] | TEG + Hexagonal heat exchanger with internal fins | up to 335 (simulated exhaust gas) | Up to 1.72% (conversion efficiency) | No |
| Muratçobanoğlu et al. (2025) [41] | TEG + Heat Pipes (for heating and cooling) | Up to 220 (PTC heater) | 2% (maximum conversion efficiency) | No (PUE analysis conducted) |
2. Materials and Methods
2.1. Experimental Setup
2.2. Wind Tunnel
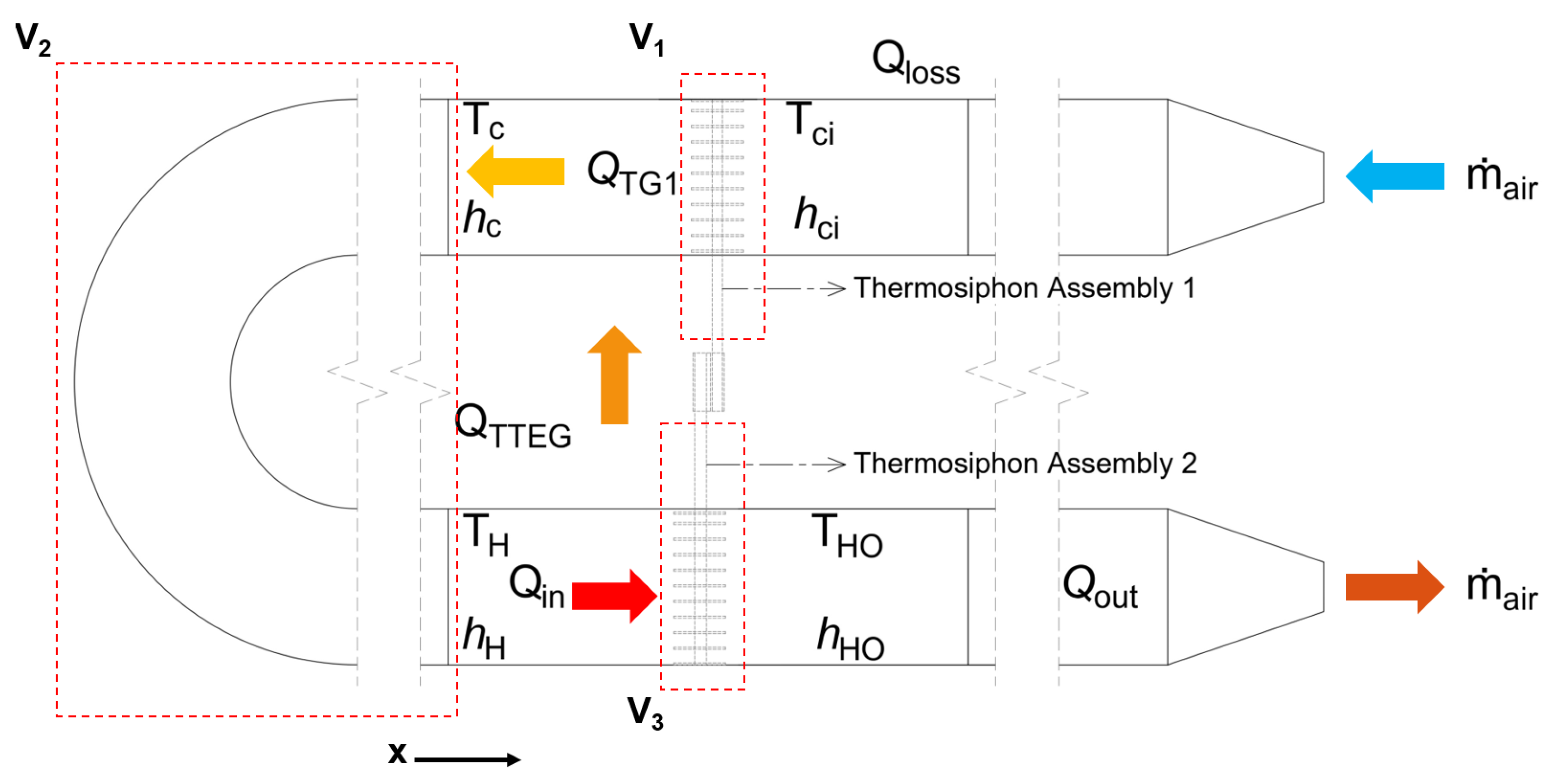
2.3. Waste Heat Recovery System
2.3.1. Thermoelectric Generators
2.3.2. Thermosyphons
2.4. Airflow Measurement and Control System
2.5. Air Heating System
2.6. Data Acquisition System for Thermoelectric Generators
2.7. Full Setup
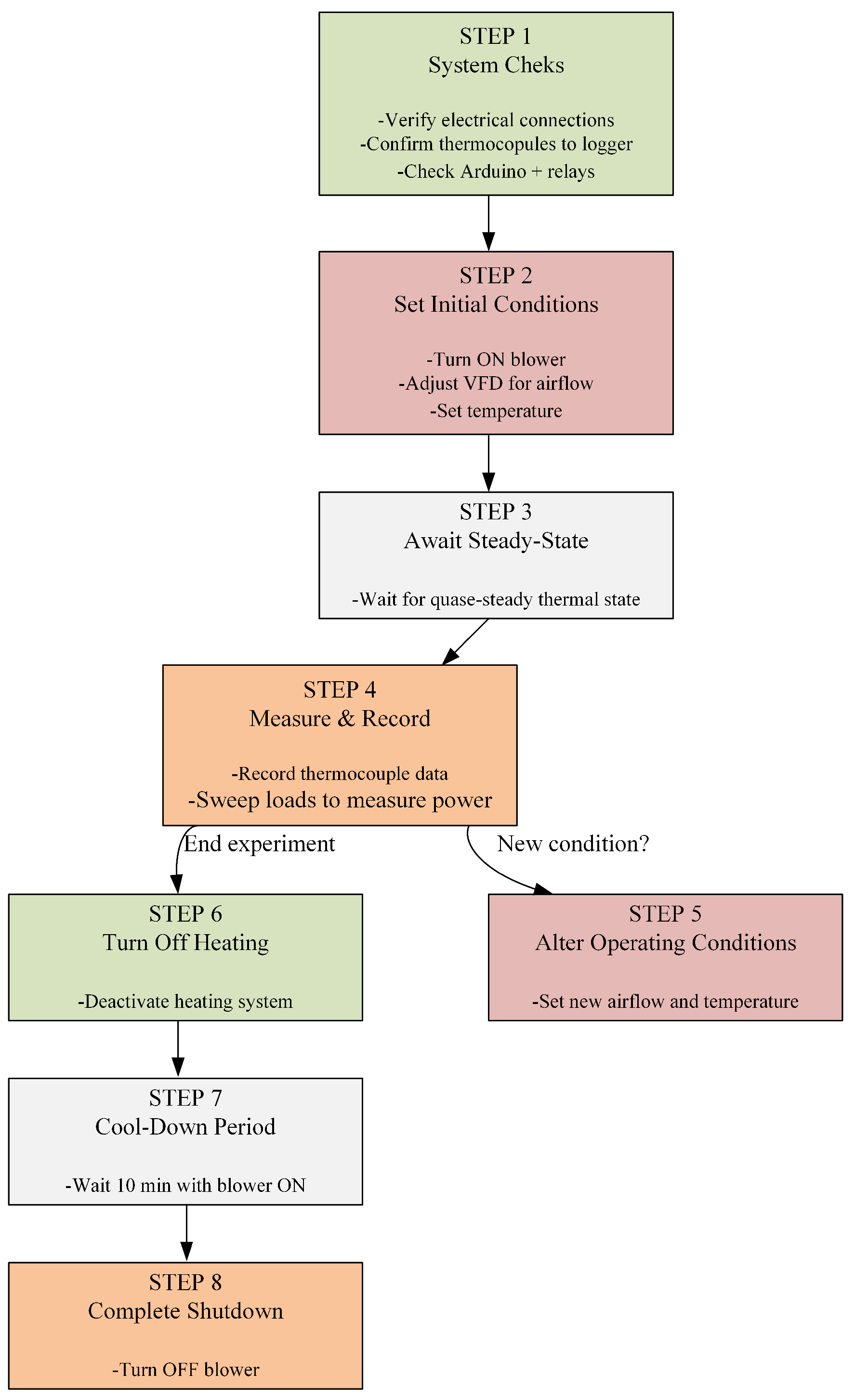
2.8. Experimental Procedure
2.9. Experimental Uncertainty
2.10. Data Reduction
3. Results and Discussion
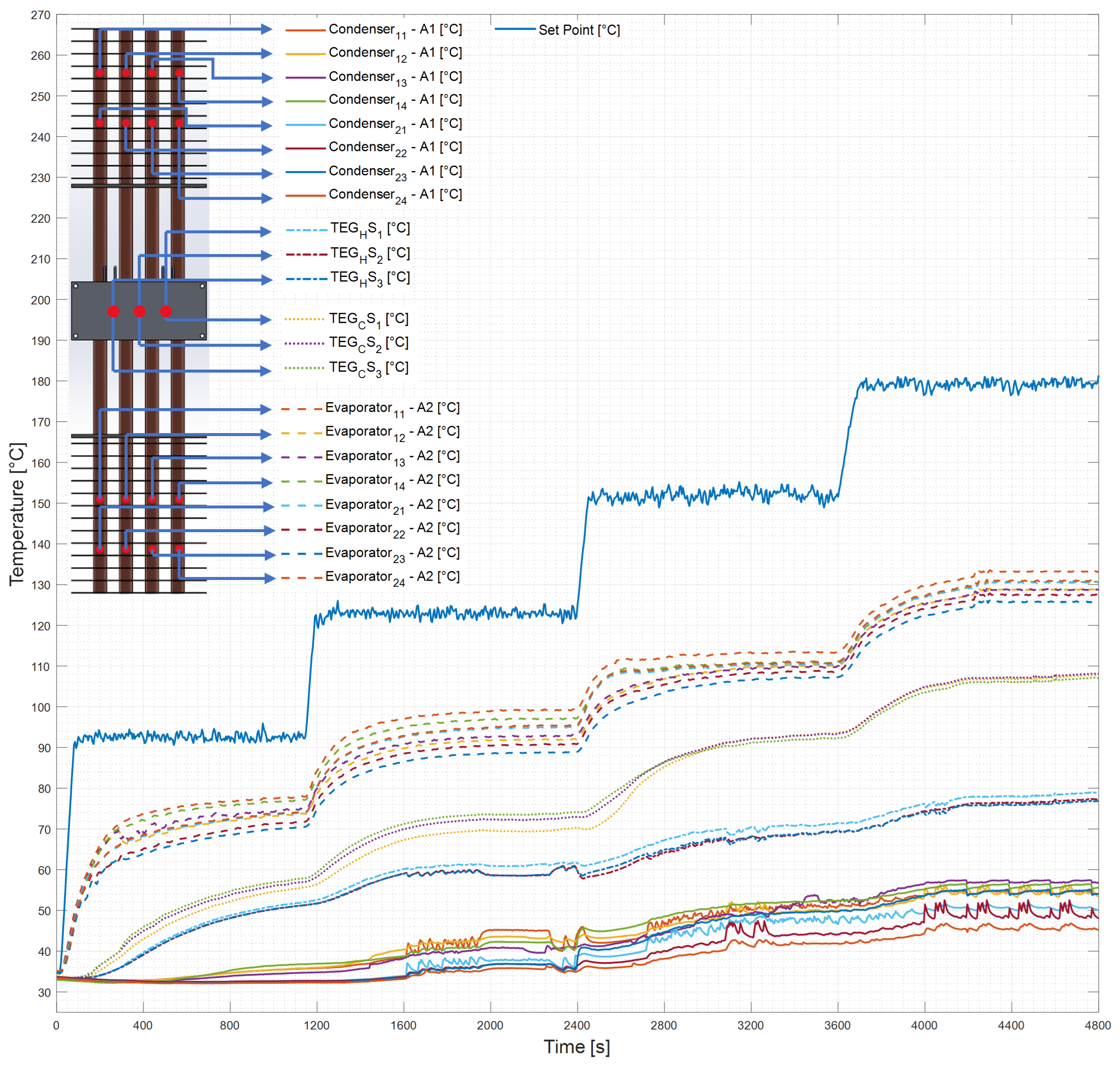
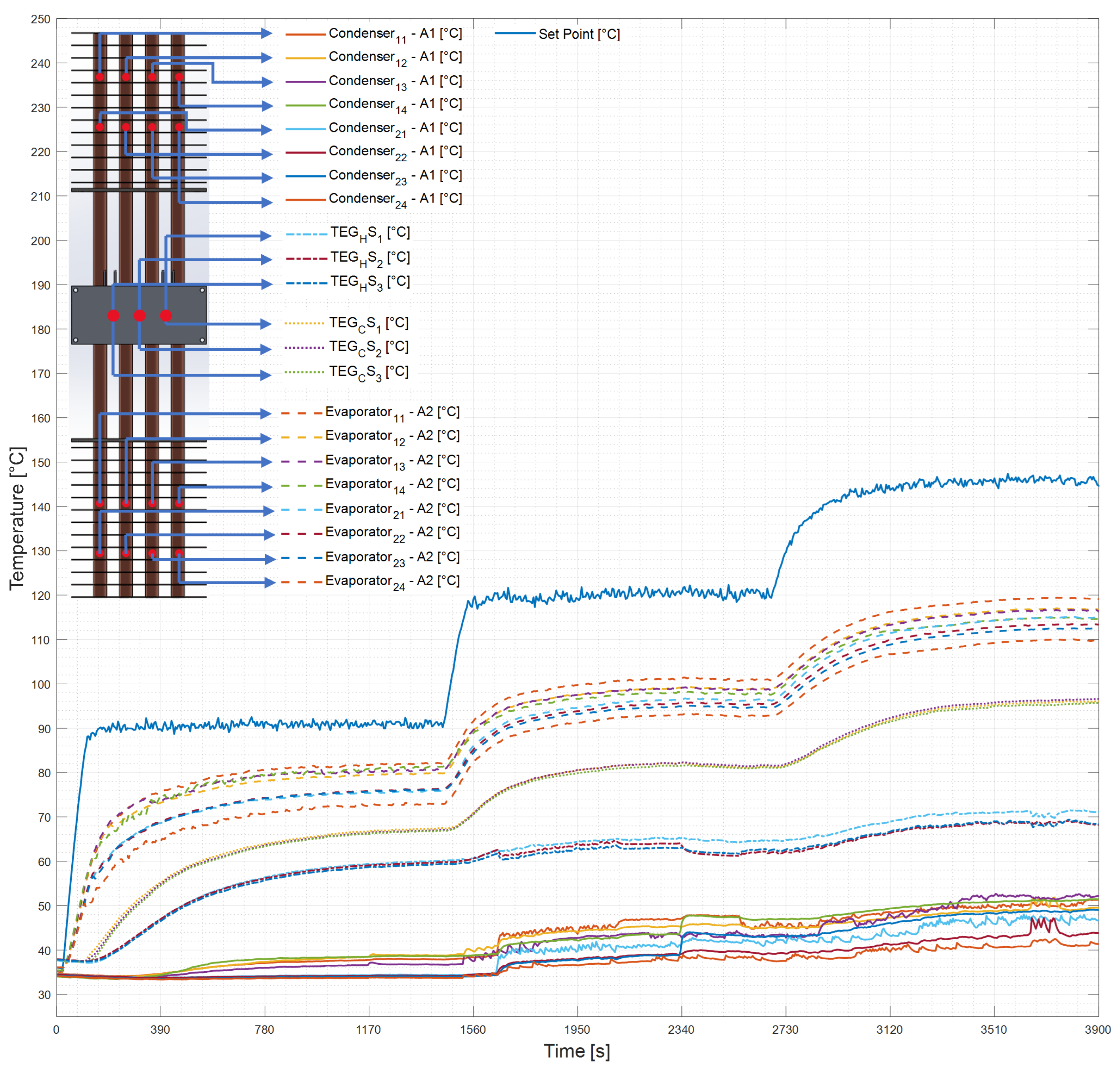
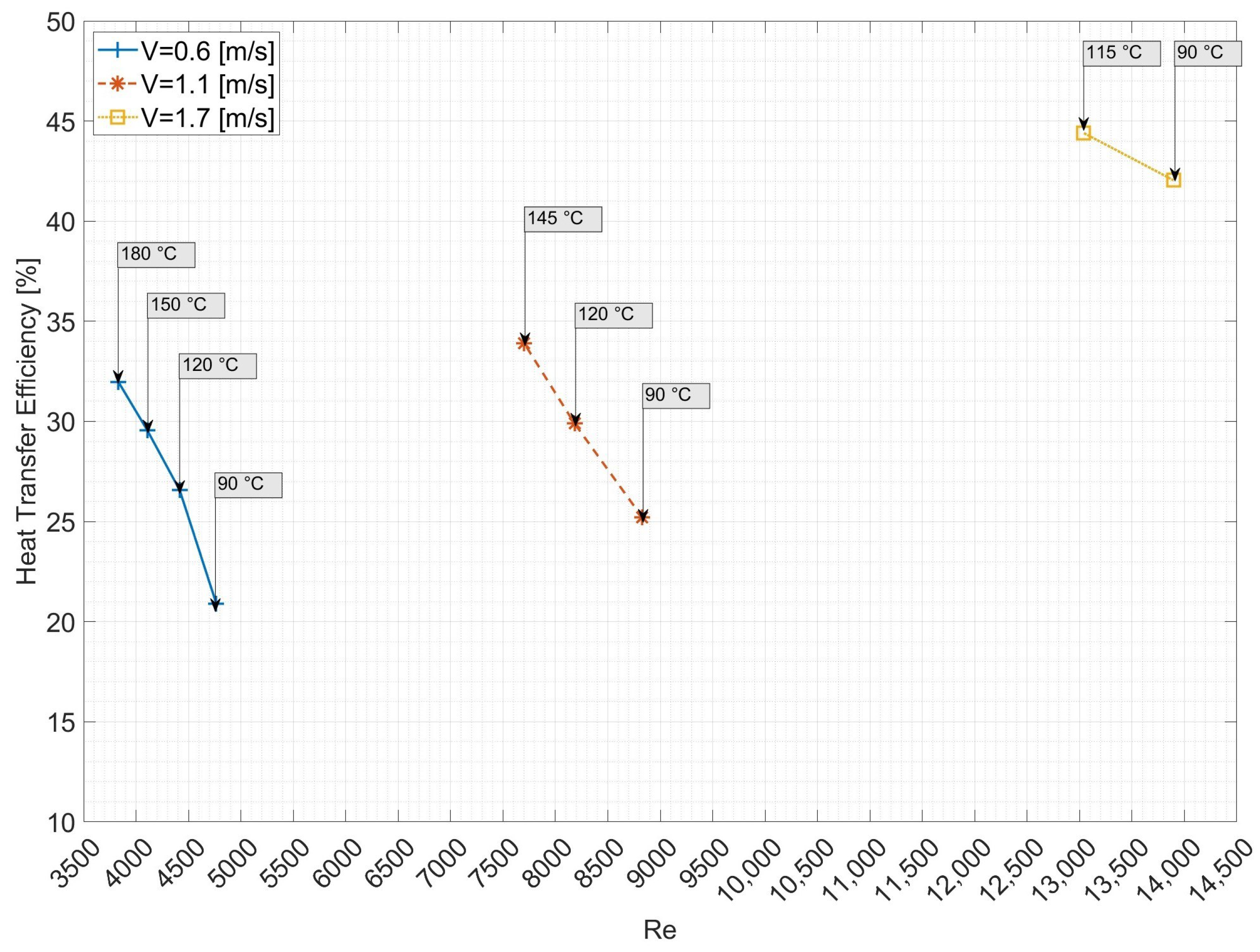
3.1. Thermal Performance
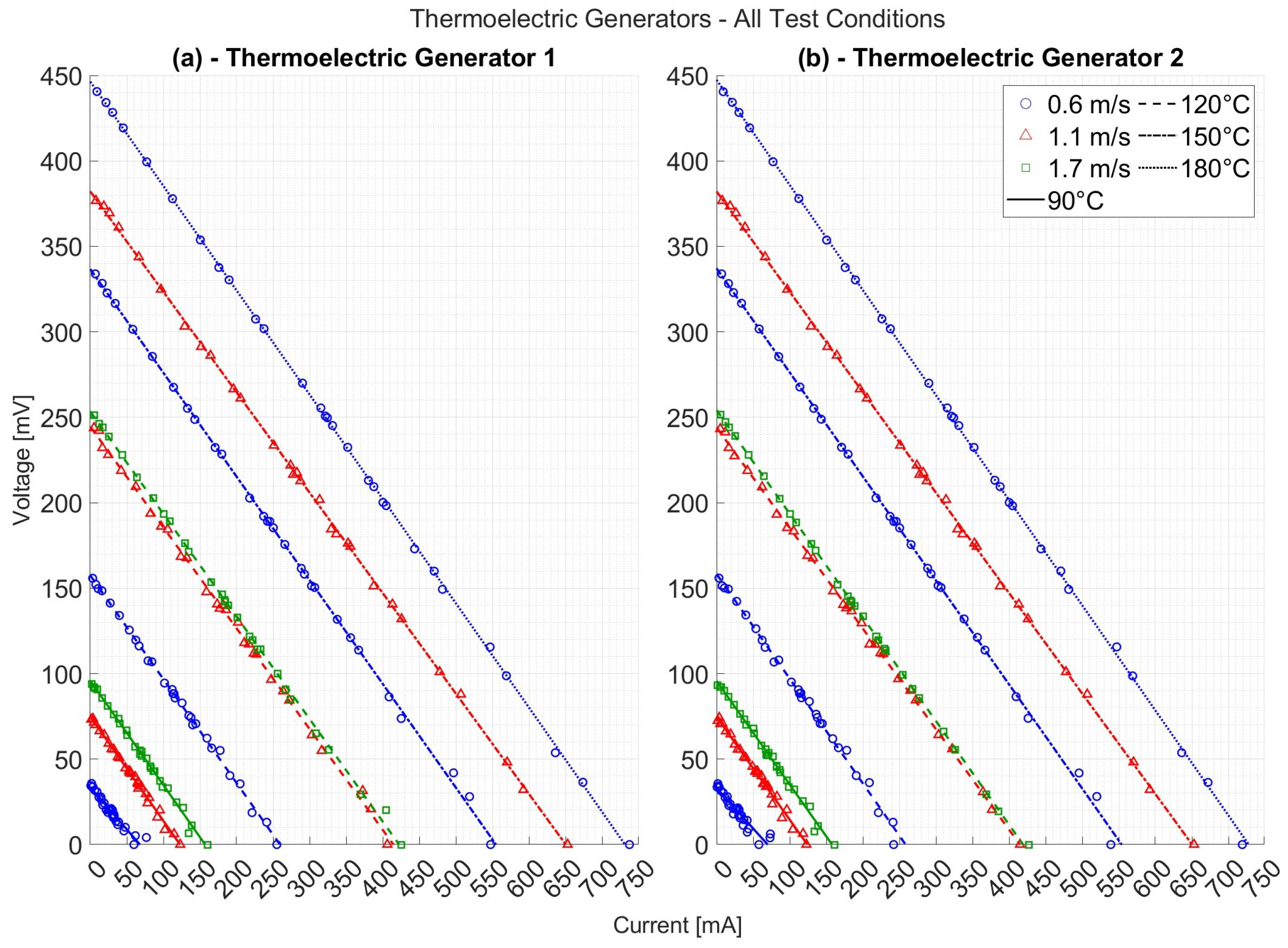
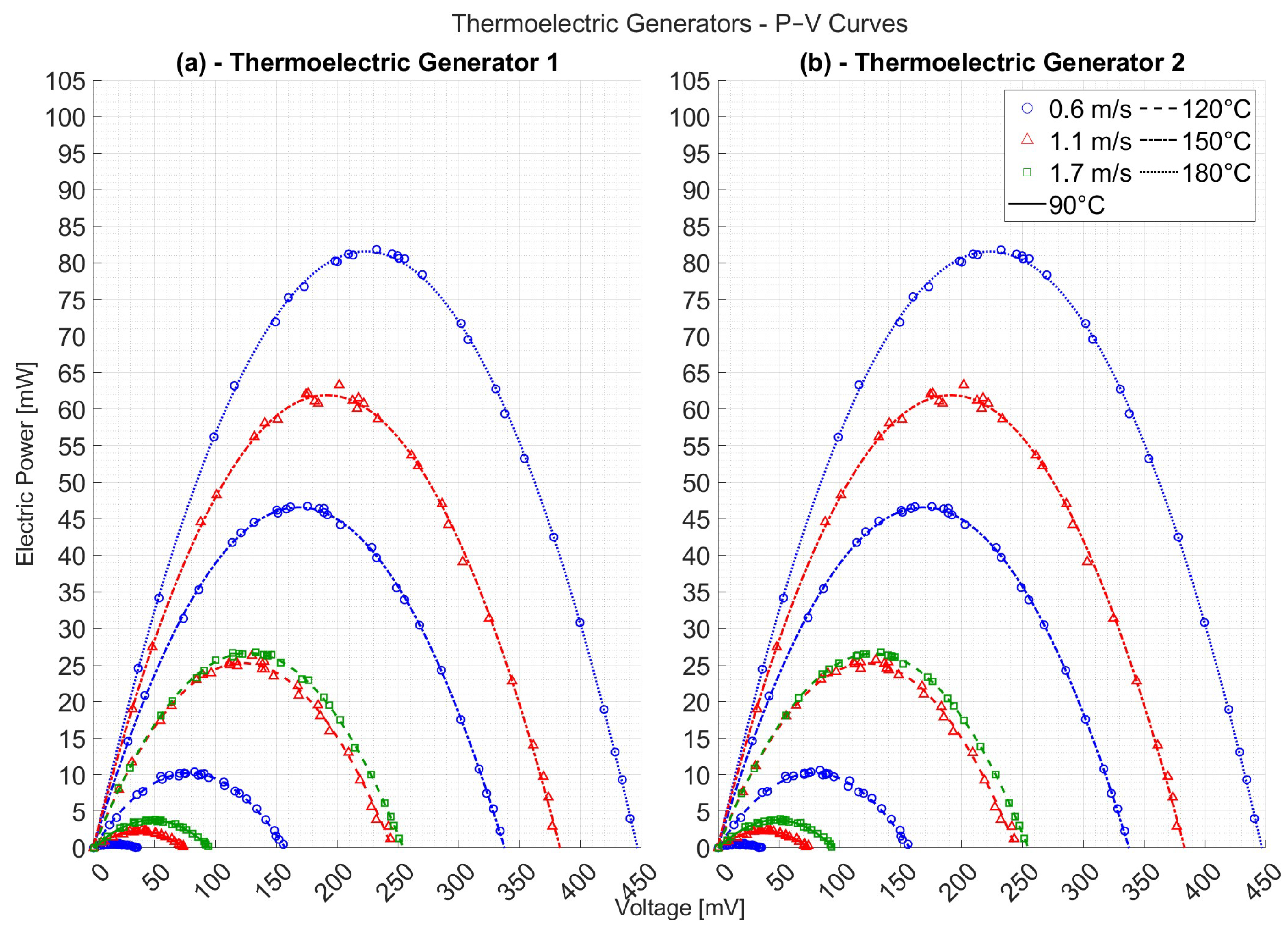
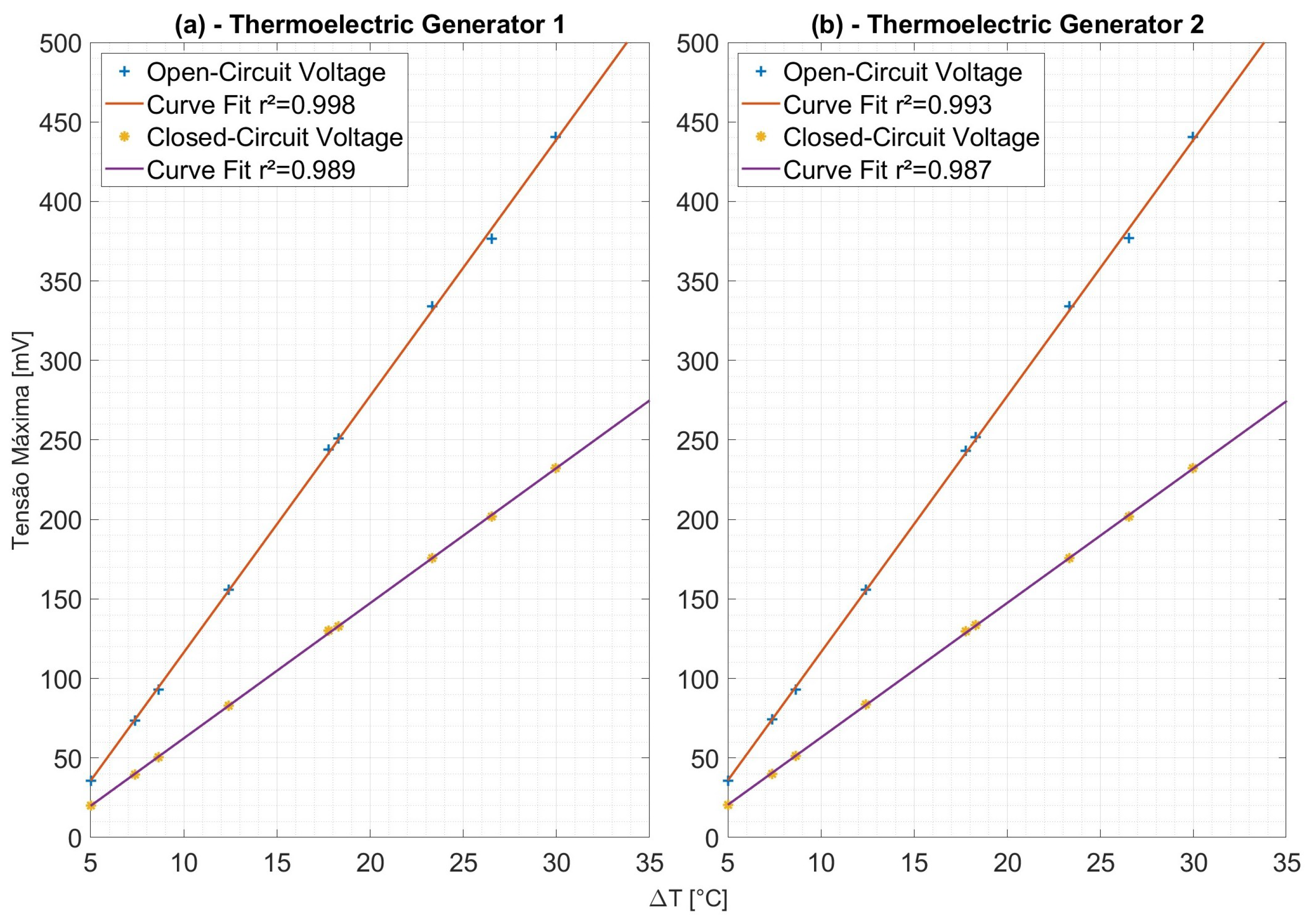
3.2. Electrical Performance
3.3. Overall System Performance
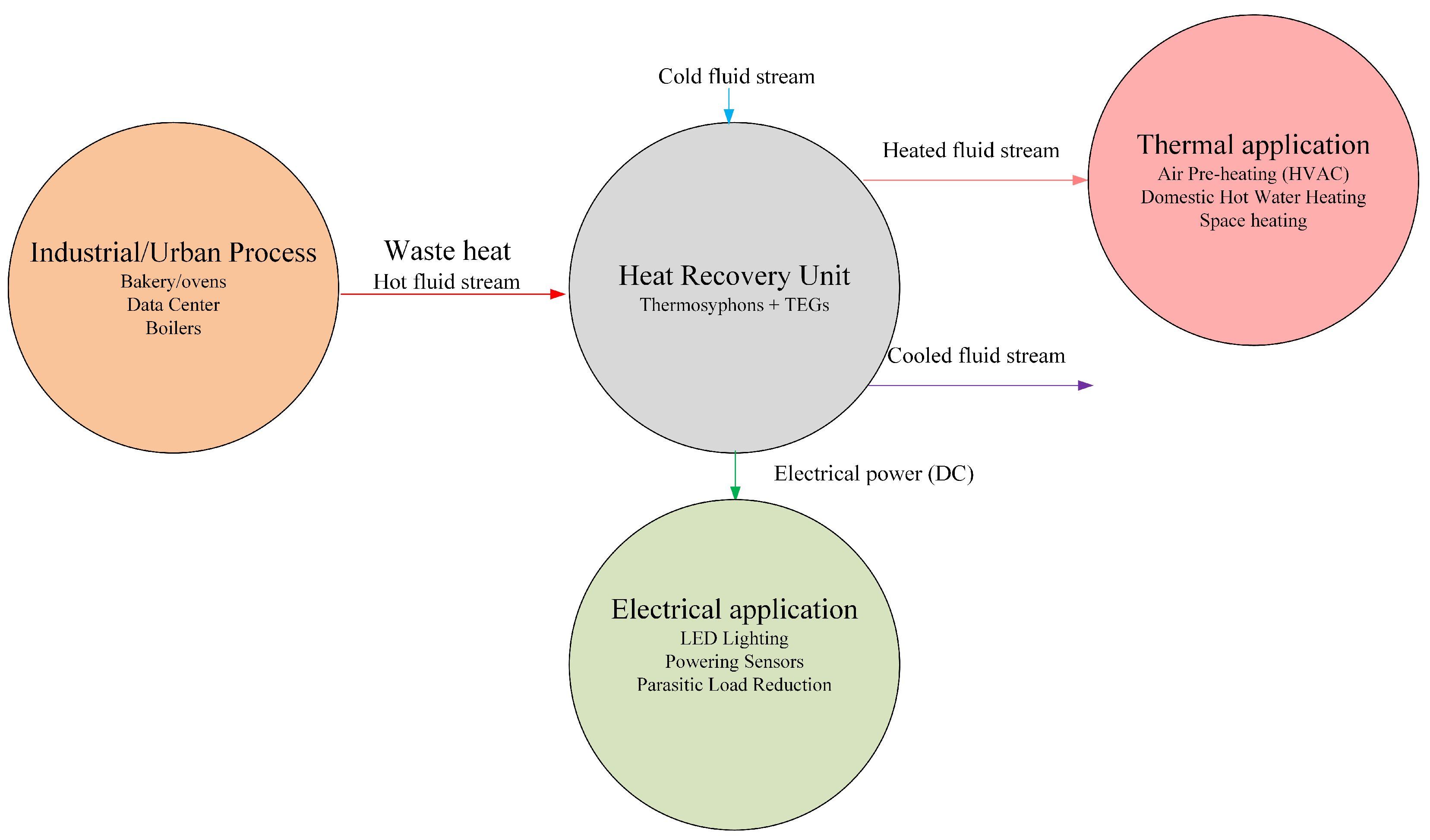
3.4. Practical Integration Scenarios
4. Conclusions
- The system successfully demonstrated its dual-function capability, achieving a maximum electrical power output of 81.84 mW per TEG (163.69 mW total) and simultaneously preheating the inlet air by up to 9.5 °C.
- The peak overall first-law efficiency of the system was 9.38%, achieved at an air velocity of 1.7 m/s and a hot side temperature of 90 °C, highlighting that the conditions for maximum efficiency and maximum power output do not coincide.
- The thermal behavior of the thermosyphons was influenced by instabilities consistent with the geyser boiling phenomenon, a factor to be considered in the dynamic modeling of such systems.
Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Latin Symbols | |
| A | Area [m2] |
| Specific heat at constant pressure [J·kg−1·K−1] | |
| Hydraulic diameter [m] | |
| h | Specific enthalpy [J·kg−1] |
| i | Electric current [A] |
| Mass flow rate [kg·s−1] | |
| P | Electrical Power [W] |
| Power Density [W·m−2] | |
| Q | Heat transfer rate [W] |
| R | Electrical Resistance [Ω] |
| Coefficient of determination [-] | |
| Re | Reynolds number [-] |
| T | Temperature [°C] |
| U | Voltage [V] |
| v | Velocity [m·s−1] |
| Greek Symbols | |
| Difference operator | |
| Heat transfer effectiveness [-] | |
| Efficiency [-] | |
| Dynamic viscosity [Pa·s] | |
| Density [kg·m−3] | |
| Abbreviations | |
| CCV | Closed-Circuit Voltage |
| CFD | Computational Fluid Dynamics |
| DAQ | Data Acquisition |
| EES | Engineering Equation Solver |
| MPP | Maximum Power Point |
| OCV | Open-Circuit Voltage |
| PV | Photovoltaic |
| TEG | Thermoelectric Generator |
| VFD | Variable Frequency Drive |
| WHR | Waste Heat Recovery |
References
- Brown, A.; Wayth, N. Statistical Review of World Energy. Energy Institute. 2025. Available online: https://www.energyinst.org/__data/assets/pdf_file/0007/1658077/Statistical-Review-of-World-Energy.pdf (accessed on 10 August 2025).
- Fleurial, J.P. Thermoelectric power generation materials: Technology and application opportunities. JOM 2009, 61, 79–85. [Google Scholar] [CrossRef]
- Papapetrou, M.; Kosmadakis, G.; Cipollina, A.; La Commare, U.; Micale, G. Industrial waste heat: Estimation of the technically available resource in the EU per industrial sector, temperature level and country. Appl. Therm. Eng. 2018, 138, 207–216. [Google Scholar] [CrossRef]
- Werner, S. International review of district heating and cooling. Energy 2017, 137, 617–631. [Google Scholar] [CrossRef]
- Savickas, R. Energy Efficiency in District Heating and Cooling, Waste Heat Utilisation. 2023. Available online: https://unece.org/sites/default/files/2024-04/UNEP%20CCC%2C%20CONFERENCE%2C%20UNECE%2C%20DC%20and%20WH%2C%202.pdf (accessed on 1 August 2025).
- Seebeck, T.J. Magnetische Polarisation der Metalle und Erregung Durch Temperatur-Differenz; Königlichen Akademie der Wissenschaften: Berlin, Germany, 1822; Available online: https://archive.org/details/magnetischepolar00seebuoft (accessed on 7 August 2025).
- Ismail, B.I.; Ahmed, W.H. Thermoelectric power generation using waste-heat energy as an alternative green technology. Recent Patents Electr. Electron. Eng. (Former. Recent Patents Electr. Eng.) 2009, 2, 27–39. [Google Scholar] [CrossRef]
- Singh, B.; Remeli, M.F.; Chet, D.L.; Oberoi, A.; Date, A.; Akbarzadeh, A. Experimental investigation on effect of adhesives on thermoelectric generator performance. J. Electron. Mater. 2015, 44, 1864–1869. [Google Scholar] [CrossRef]
- Wu, X.; Liu, W. An engineering roadmap for the thermoelectric interface materials. J. Mater. 2024, 10, 748–750. [Google Scholar] [CrossRef]
- Alves, T.A.; Krambeck, L.; Santos, P.d.; Aranguren, P. Heat pipe and thermosyphon for thermal management of thermoelectric cooling. In Bringing Thermoelectricity into Reality; IntechOpen: London, UK, 2018. [Google Scholar] [CrossRef]
- Jouhara, H.; Reay, D.; McGlen, R.; Kew, P.; McDonough, J. Heat Pipes: Theory, Design and Applications; Butterworth-Heinemann: Oxford, UK, 2023. [Google Scholar]
- Machado, P.L.; Pereira, T.S.; Trindade, M.G.; Biglia, F.M.; Santos, P.H.; Tadano, Y.S.; Siqueira, H.; Alves, T.A. Estimating thermal performance of thermosyphons by artificial neural networks. Alex. Eng. J. 2023, 79, 93–104. [Google Scholar] [CrossRef]
- Pereira, T.S.; Machado, P.L.O.; Veitia, B.D.R.; Biglia, F.M.; dos Santos, P.H.D.; Tadano, Y.d.S.; Siqueira, H.V.; Antonini Alves, T. Application of Artificial Neural Networks in Predicting the Thermal Performance of Heat Pipes. Energies 2024, 17, 5387. [Google Scholar] [CrossRef]
- Mantelli, M.B.H. Thermosyphons and Heat Pipes: Theory and Applications; Springer: Cham, Switzerland, 2021; Volume 1. [Google Scholar]
- Krambeck, L.; Baptista, N.F.; Marrone, V.d.A.; Dias, P.H.d.S.; Antonini Alves, T. Thermal Performance Evaluation of Different Passive Devices for Electronics Cooling. Therm. Sci. 2019, 23, 1151–1160. [Google Scholar] [CrossRef]
- Jaziri, N.; Boughamoura, A.; Müller, J.; Mezghani, B.; Tounsi, F.; Ismail, M. A comprehensive review of Thermoelectric Generators: Technologies and common applications. Energy Rep. 2020, 6, 264–287. [Google Scholar] [CrossRef]
- Nadaf, N.; Preethi, A. Review on waste heat energy harvesting using teg: Applications and enhancements. In Proceedings of the 2021 8th International Conference on Smart Computing and Communications (ICSCC), Kochi, Kerala, India, 1–3 July 2021; pp. 334–339. [Google Scholar] [CrossRef]
- Kim, T.Y.; Negash, A.; Cho, G. Experimental and numerical study of waste heat recovery characteristics of direct contact thermoelectric generator. Energy Convers. Manag. 2017, 140, 273–280. [Google Scholar] [CrossRef]
- Fachini, L.V.G.; Machado, P.L.O.; Krambeck, L.; Szmoski, R.M.; Alves, T.A. Heat Recovery and Power Generation Using Thermoelectric Generator. In Advanced Thermoelectric Materials for Energy Harvesting Applications; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Fernández-Yáñez, P.; Jarama, J.; Martos, F.J.; Armas, O. Heat transfer in thermoelectric generators for waste energy recovery in piston engines. Appl. Sci. 2023, 13, 5647. [Google Scholar] [CrossRef]
- Gomaa, M.R.; Murtadha, T.K.; Abu-jrai, A.; Rezk, H.; Altarawneh, M.A.; Marashli, A. Experimental investigation on waste heat recovery from a cement factory to enhance thermoelectric generation. Sustainability 2022, 14, 10146. [Google Scholar] [CrossRef]
- Xiao, D.; Sun, P.; Wu, J.; Zhang, Y.; Wu, J.; Liu, G.; Hu, H.; Hu, J.; Tan, X.; He, S.; et al. Thermoelectric generator design and characterization for industrial pipe waste heat recovery. Processes 2023, 11, 1714. [Google Scholar] [CrossRef]
- Pourrahmani, H.; Shakeri, H.; Van Herle, J. Thermoelectric generator as the waste heat recovery unit of proton exchange membrane fuel cell: A numerical study. Energies 2022, 15, 3018. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, Z.; Guo, K.; Dong, Z.; Wang, C.; Cui, S.; Tian, W.; Qiu, S.; Su, G. Investigations on thermoelectric characteristic of heat pipe thermoelectric generator waste heat utilization device in nuclear power system. Nucl. Eng. Des. 2023, 407, 112299. [Google Scholar] [CrossRef]
- Wang, C.; Tang, S.; Liu, X.; Su, G.; Tian, W.; Qiu, S. Experimental study on heat pipe thermoelectric generator for industrial high temperature waste heat recovery. Appl. Therm. Eng. 2020, 175, 115299. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Ge, S.; Zhang, B. Multi-criteria decision analysis and experimental study on heat pipe thermoelectric generator for waste heat recovery. Appl. Therm. Eng. 2024, 255, 123930. [Google Scholar] [CrossRef]
- Zhao, Y.; Fan, Y.; Li, W.; Li, Y.; Ge, M.; Xie, L. Experimental investigation of heat pipe thermoelectric generator. Energy Convers. Manag. 2022, 252, 115123. [Google Scholar] [CrossRef]
- Remeli, M.F.; Date, A.; Orr, B.; Ding, L.C.; Singh, B.; Affandi, N.D.N.; Akbarzadeh, A. Experimental investigation of combined heat recovery and power generation using a heat pipe assisted thermoelectric generator system. Energy Convers. Manag. 2016, 111, 147–157. [Google Scholar] [CrossRef]
- Jang, J.C.; Chi, R.G.; Rhi, S.H.; Lee, K.B.; Hwang, H.C.; Lee, J.S.; Lee, W.H. Heat pipe-assisted thermoelectric power generation technology for waste heat recovery. J. Electron. Mater. 2015, 44, 2039–2047. [Google Scholar] [CrossRef]
- Remeli, M.F.; Verojporn, K.; Singh, B.; Kiatbodin, L.; Date, A.; Akbarzadeh, A. Passive heat recovery system using combination of heat pipe and thermoelectric generator. Energy Procedia 2015, 75, 608–614. [Google Scholar] [CrossRef]
- Remeli, M.F.; Kiatbodin, L.; Singh, B.; Verojporn, K.; Date, A.; Akbarzadeh, A. Power generation from waste heat using heat pipe and thermoelectric generator. Energy Procedia 2015, 75, 645–650. [Google Scholar] [CrossRef]
- Remeli, M.F.; Singh, B.; Affandi, N.D.N.; Ding, L.C.; Date, A.; Akbarzadeh, A. Investigation of counter-flow in a heat pipe–thermoelectric generator (HPTEG). J. Electron. Mater. 2017, 46, 3115–3123. [Google Scholar] [CrossRef]
- Singh, B.; Baharin, N.A.; Remeli, M.F.; Oberoi, A.; Date, A.; Akbarzadeh, A. Experimental analysis of thermoelectric heat exchanger for power generation from salinity gradient solar pond using low-grade heat. J. Electron. Mater. 2017, 46, 2854–2859. [Google Scholar] [CrossRef]
- Mostafavi, S.A.; Mahmoudi, M. Modeling and fabricating a prototype of a thermoelectric generator system of heat energy recovery from hot exhaust gases and evaluating the effects of important system parameters. Appl. Therm. Eng. 2018, 132, 624–636. [Google Scholar] [CrossRef]
- Kılkıs, B.; Çağlar, M.; Sengül, M. Energy Benefits of Heat Pipe Technology for Achieving 100% Renewable Heating and Cooling for Fifth-Generation, Low-Temperature District Heating Systems. Energies 2021, 14, 5398. [Google Scholar] [CrossRef]
- Dashevsky, Z.; Jarashneli, A.; Unigovski, Y.; Dzunzda, B.; Gao, F.; Shneck, R.Z. Development of a High Perfomance Gas Thermoelectric Generator (TEG) with Possibible Use of Waste Heat. Energies 2022, 15, 3960. [Google Scholar] [CrossRef]
- Goswami, R.; Ganguly, S.; Das, R. Waste heat recovery from the biomass engine for effective power generation using a new array-based system. Sustain. Energy Technol. Assess. 2024, 63, 103630. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, H.; Qin, Y.; Liao, J.; Feng, Z.; Li, C. Heat pipe-based electric generator for waste heat harvesting. Appl. Therm. Eng. 2024, 242, 122482. [Google Scholar] [CrossRef]
- Jouhara, H.; Delpech, B.; Almahmoud, S.; Chauhan, A.; Al-Mansour, F.; Pusnik, M.; Buhvald, A.; Plesnik, K. Experimental investigation on an advanced thermosiphon-based heat exchanger for enhanced waste heat recovery in the steel industry. Energy 2025, 315, 134428. [Google Scholar] [CrossRef]
- Kubenova, M.; Kuterbekov, K.; Bekmyrza, K.; Kabyshev, A.; Kabdrakhimova, G.; Atamurotov, F.; Ibrahim, W. Exhaust waste heat recovery system using thermoelectric generator: A prospective of novel simulation technique toward low-carbon technology. Int. J. Low-Carbon Technol. 2025, 20, 8–24. [Google Scholar] [CrossRef]
- Muratçobanoğlu, B.; Akyürek, E.F.; Manay, E. Experimental evaluation and optimization of the heat pipes integrated thermoelectric generator using response surface methodology. Appl. Therm. Eng. 2025, 258, 124599. [Google Scholar] [CrossRef]
- Machado, P.L.O.; Fachini, L.V.G.; Tiuman, E.T.; Barchi, T.M.; Stevan, S.L., Jr.; Siqueira, H.V.; Szmoski, R.M.; Antonini Alves, T. A Low-Cost Arduino-Based I–V Curve Tracer with Automated Load Switching for PV Panel Characterization. Appl. Sci. 2025, 15, 8186. [Google Scholar] [CrossRef]
- Cavalcanti, E.J.; Carvalho, M.; Azevedo, J.L. Exergoenvironmental results of a eucalyptus biomass-fired power plant. Energy 2019, 189, 116188. [Google Scholar] [CrossRef]
- König, M.; Eisinger, K.; Hartmann, I.; Müller, M. Combined removal of particulate matter and nitrogen oxides from the exhaust gas of small-scale biomass combustion. Biomass Convers. Biorefinery 2019, 9, 201–212. [Google Scholar] [CrossRef]
- Oliveira, d.S.D.; Ochoski, M.P.L.; Chiarello, C.; Nunes, D.S.E.; da Silva, M.J.; Dias, D.S.P.H.; Antonini, A.T. Experimental study of hydrodynamic parameters regarding on geyser boiling phenomenon in glass thermosyphon using wire-mesh sensor. Therm. Sci. 2022, 26, 1391–1404. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Li, Y.; Kim, S.; Jiang, Y. Experimental investigation of geyser boiling in a two-phase closed loop thermosyphon with high filling ratios. Int. J. Heat Mass Transf. 2018, 127, 857–869. [Google Scholar] [CrossRef]
- Alexander, C.K.; Sadiku, M.N.; Sadiku, M. Fundamentals of Electric Circuits; McGraw-Hill Higher Education: Boston, MA, USA, 2007. [Google Scholar]
- Pakere, I.; Blumberga, D.; Volkova, A.; Lepiksaar, K.; Zirne, A. Valorisation of waste heat in existing and future district heating systems. Energies 2023, 16, 6796. [Google Scholar] [CrossRef]
- Akbarzadeh, A.; Dube, V. Industrial waste heat recovery, using a loop thermosyphon heat exchanger. In Proceedings of the ISES 2001 Solar World Congress, Adeleide, Australia, 25–30 November 2001. [Google Scholar]
- Remeli, M.F. Simultaneous Industrial Waste Heat Recovery and Power Generation Using Heat Pipe Assisted Thermoelectric Generator. Ph.D. Thesis, RMIT University, Melbourne, Australia, 2024. [Google Scholar]
- Yuan, X.; Liu, J.; Sun, S.; Lin, X.; Fan, X.; Zhao, W.; Kosonen, R. Data center waste heat for district heating networks: A review. Renew. Sustain. Energy Rev. 2025, 219, 115863. [Google Scholar] [CrossRef]
- Dorotić, H.; Čuljak, K.; Miškić, J.; Pukšec, T.; Duić, N. Technical and economic assessment of supermarket and power substation waste heat integration into existing district heating systems. Energies 2022, 15, 1666. [Google Scholar] [CrossRef]
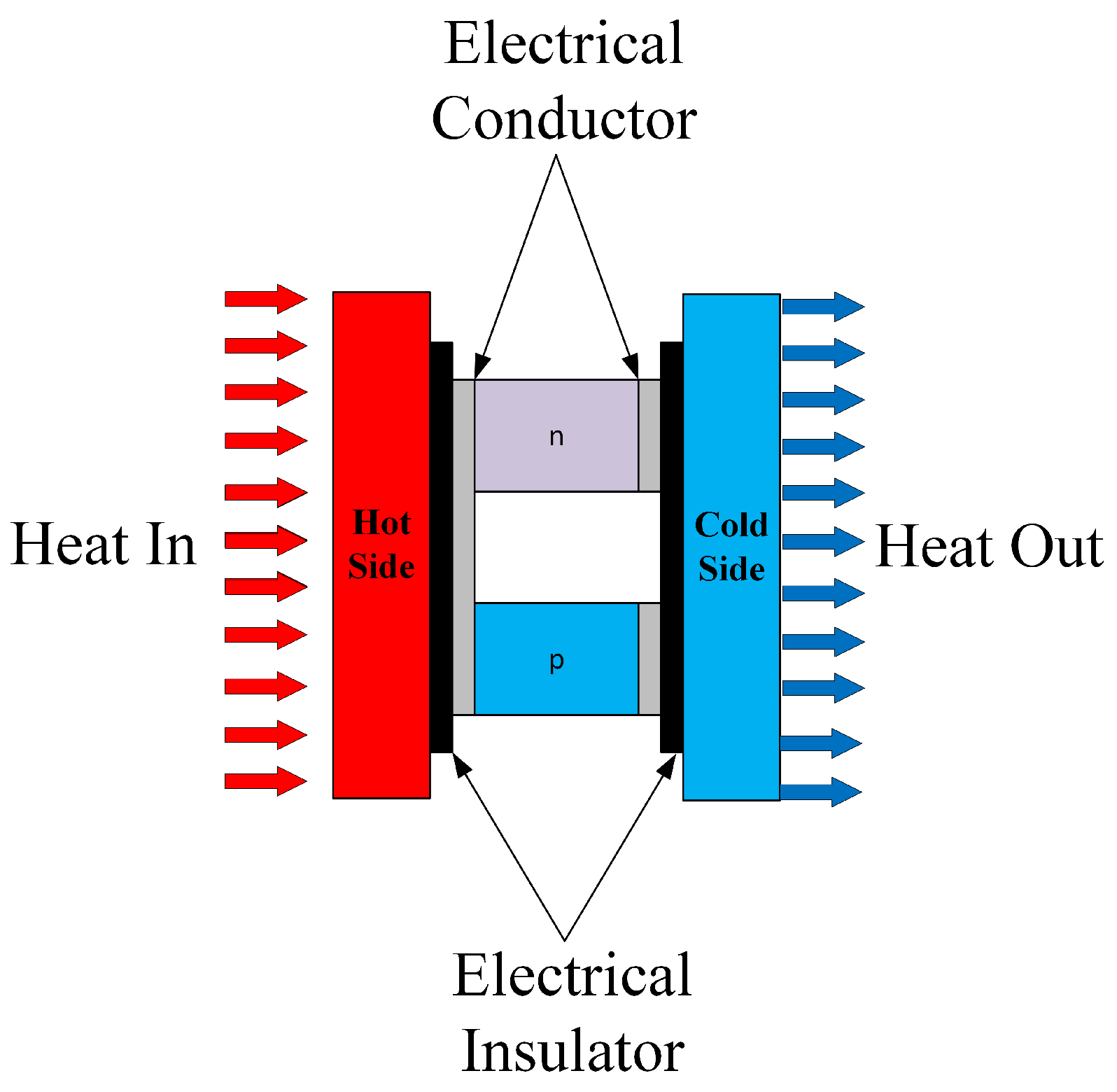
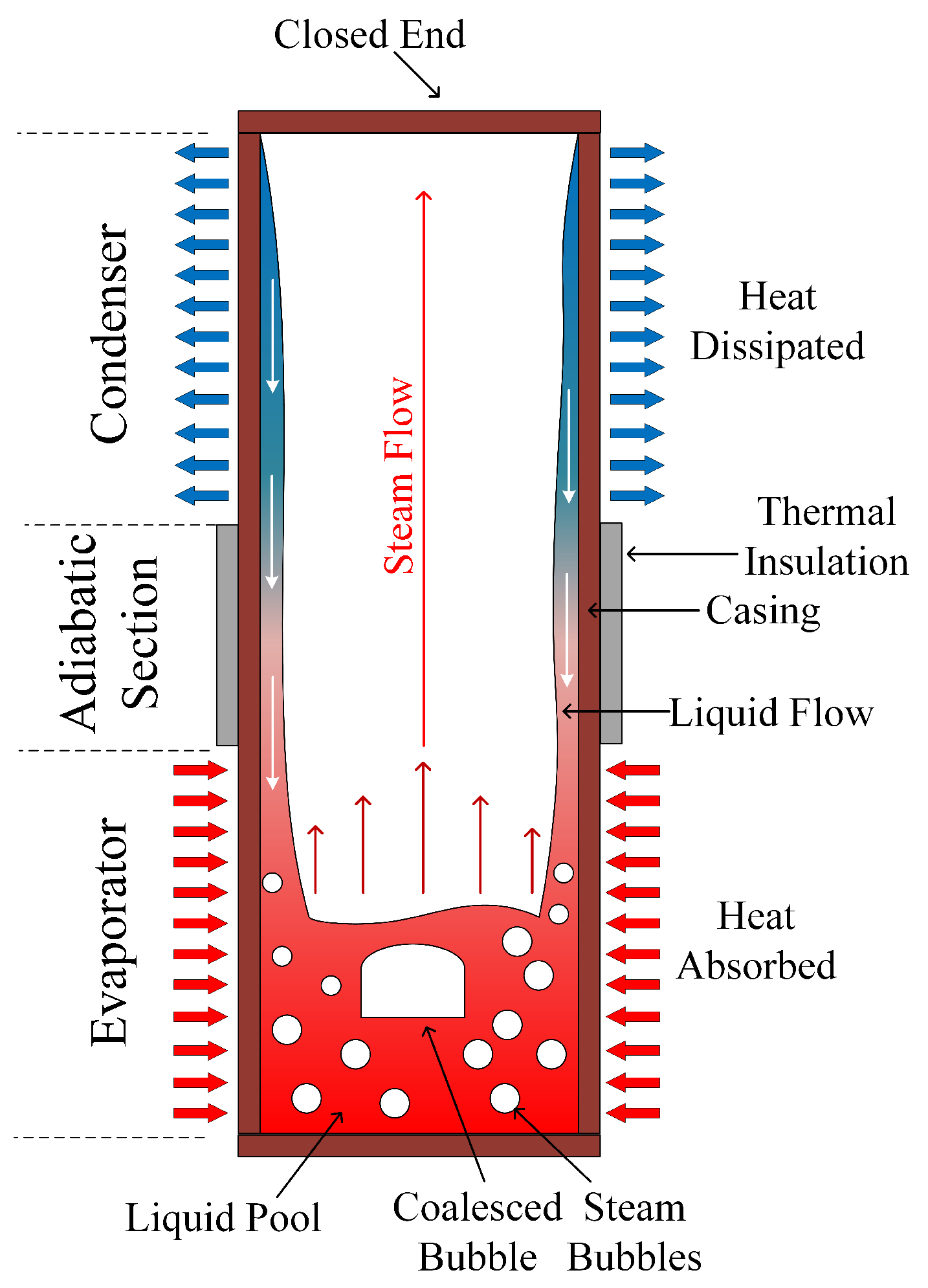
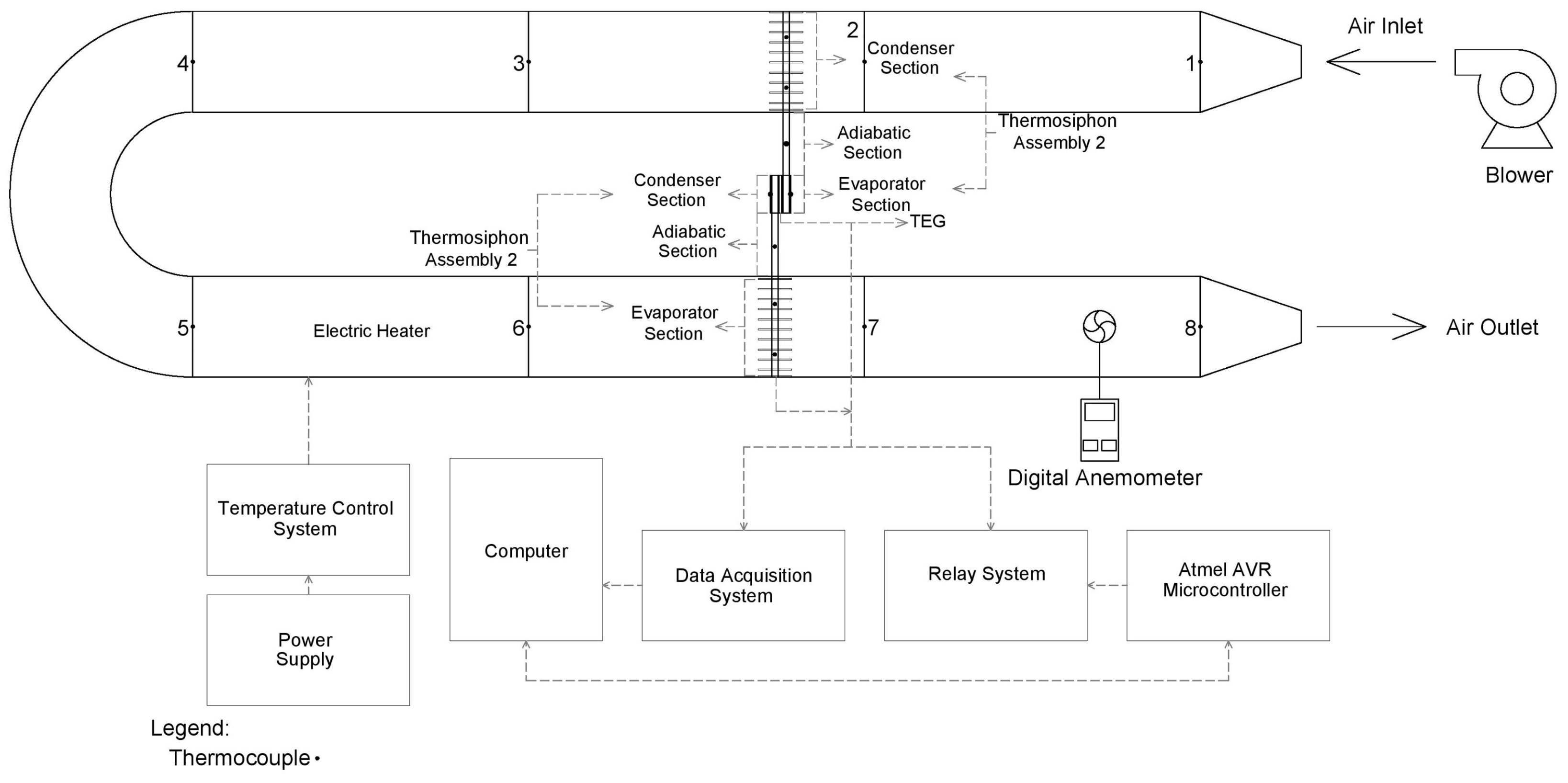

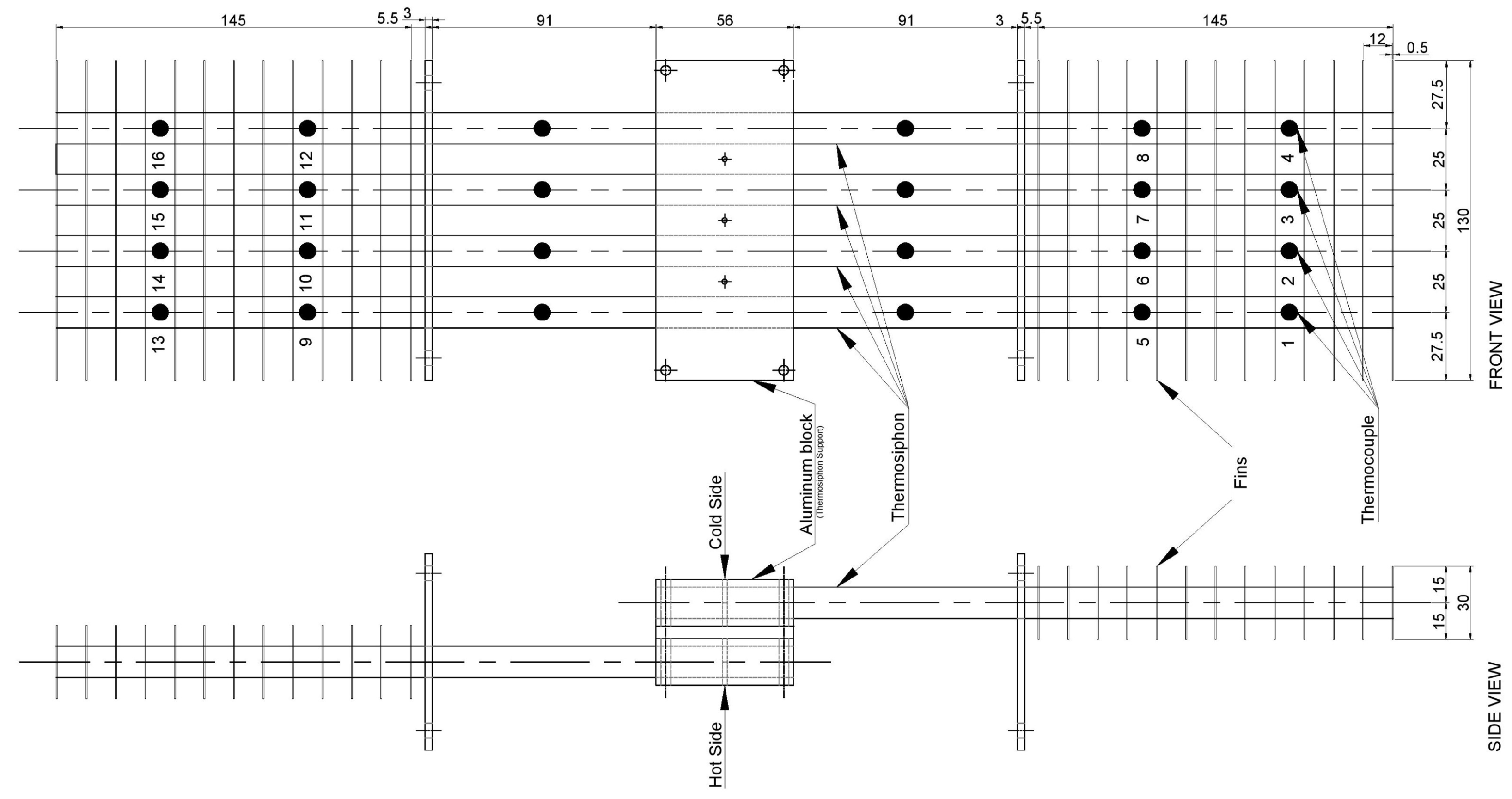






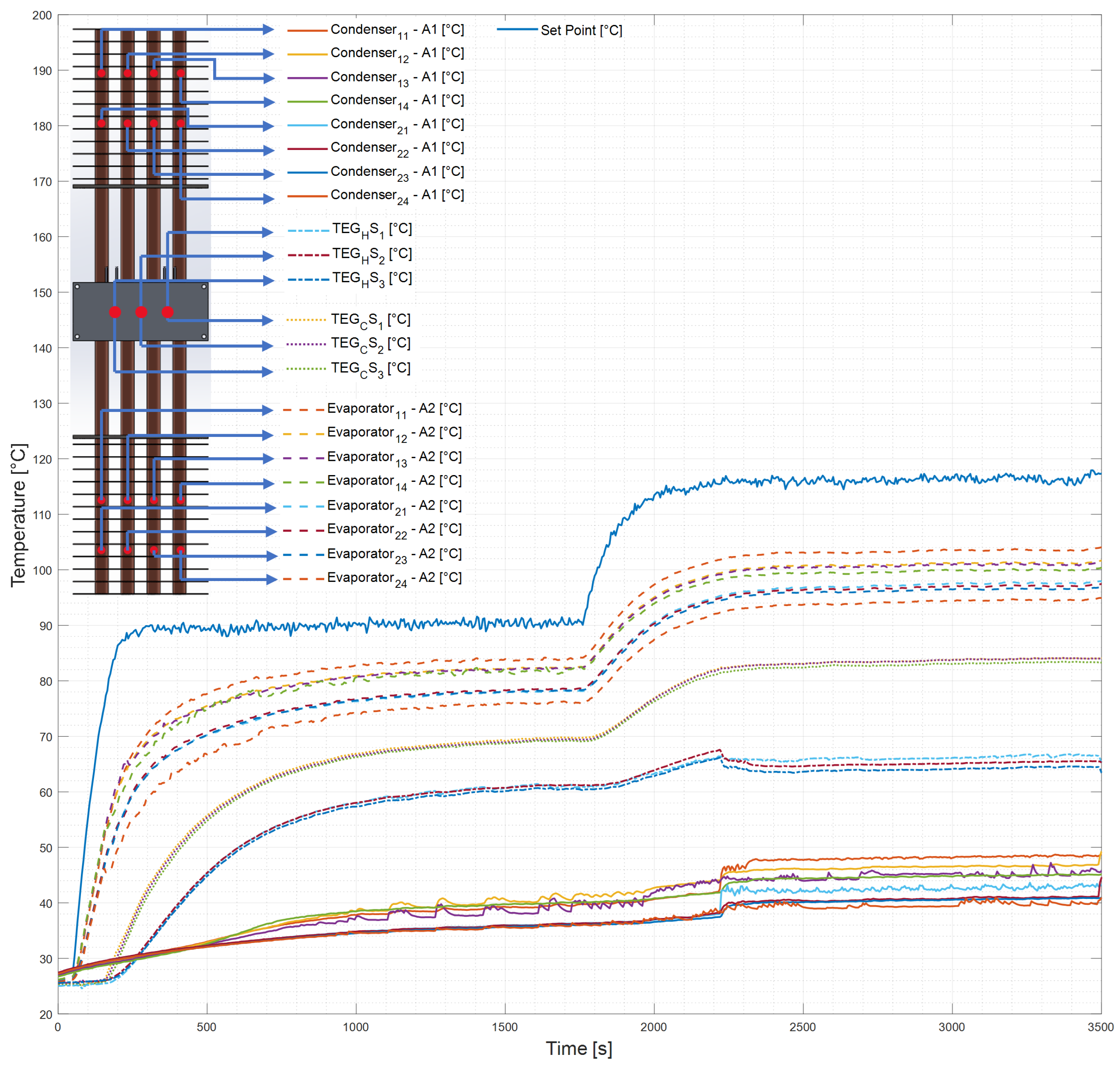
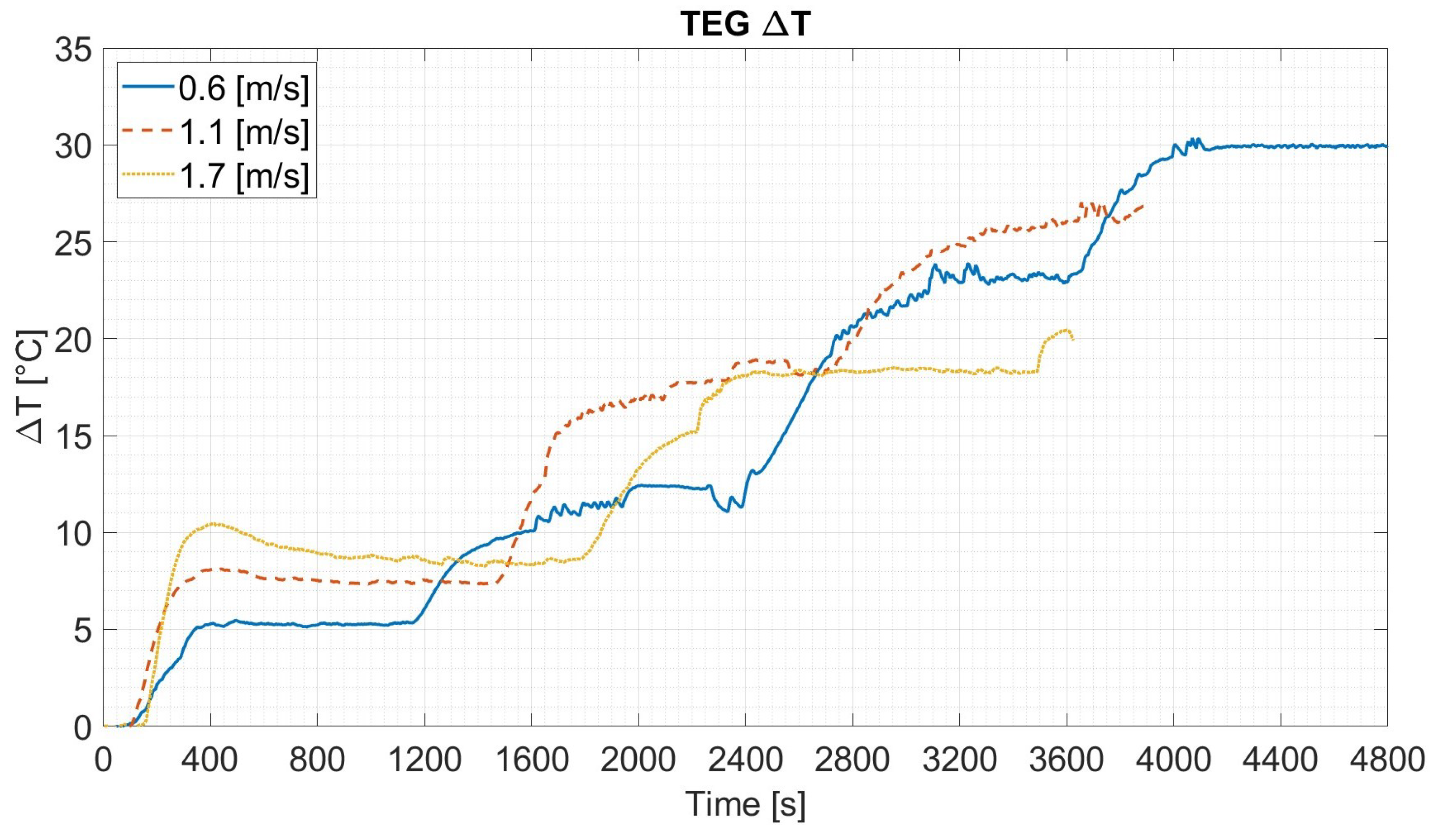
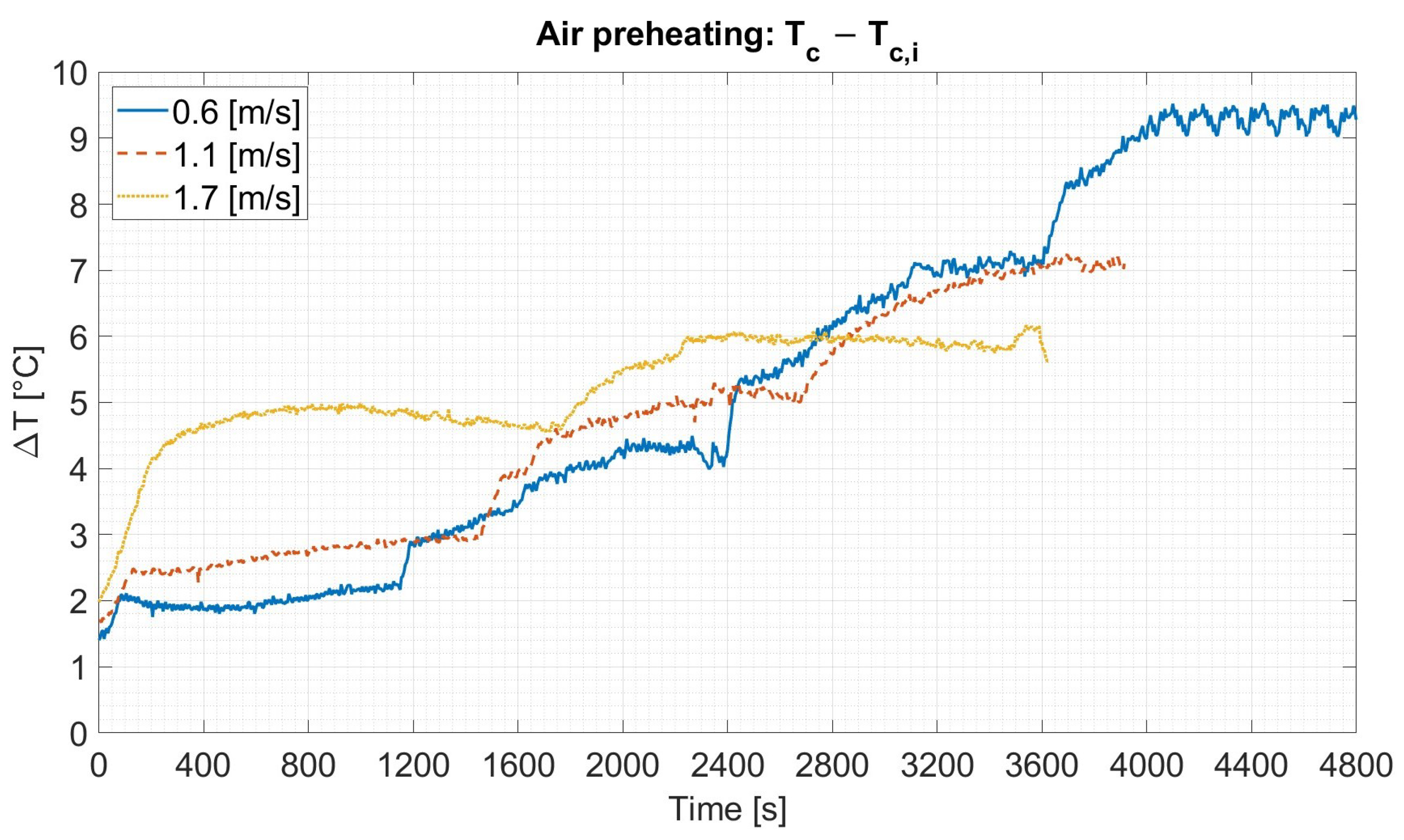
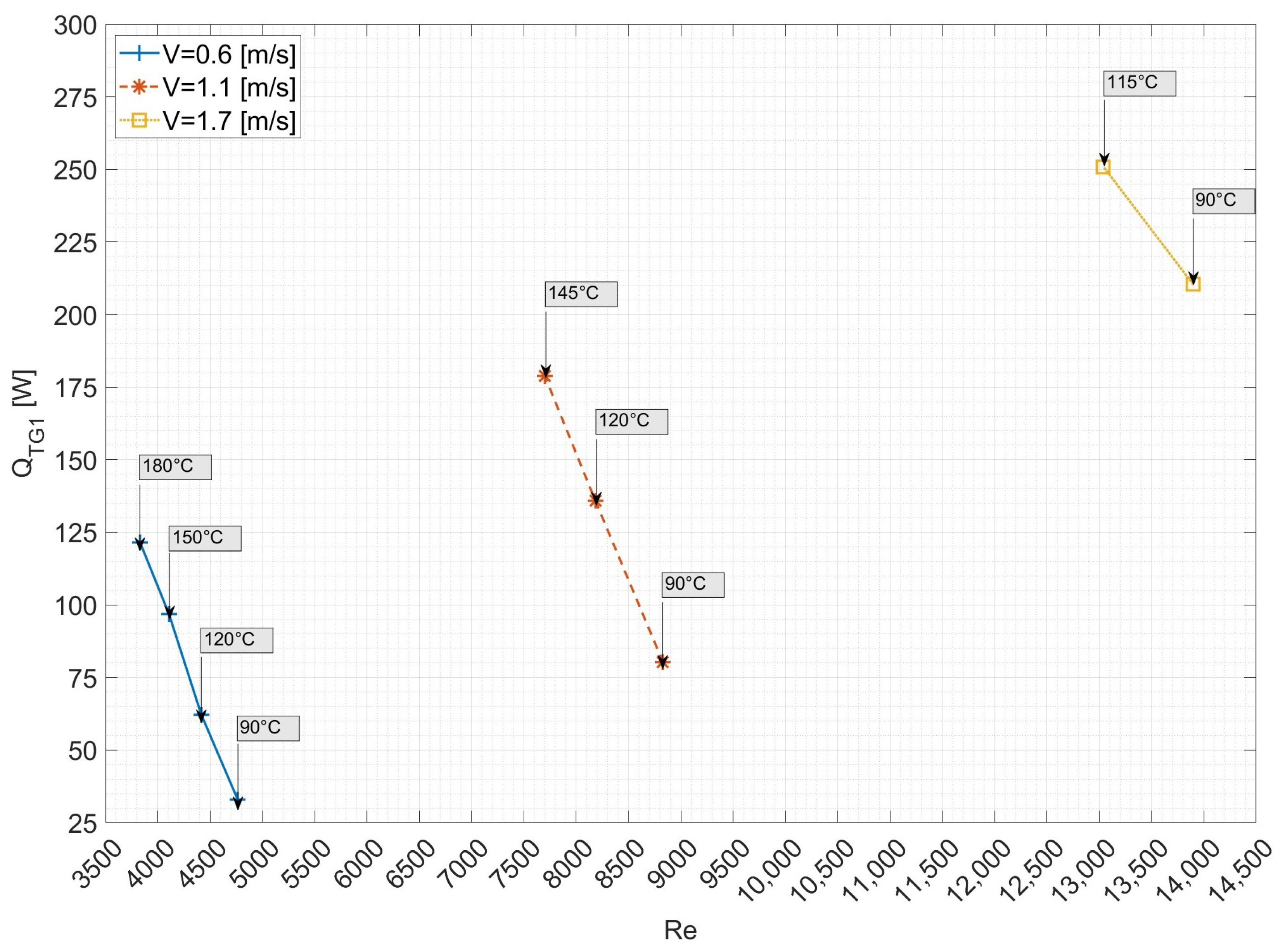

| Characteristic | Type 1 | Type 2 |
|---|---|---|
| Inner diameter [in] | 7/16 | 7/16 |
| Outer diameter [in] | 1/2 | 1/2 |
| Evaporator length [mm] | 56 | 150 |
| Adiabatic section length [mm] | 94 | 94 |
| Condenser length [mm] | 150 | 56 |
| Working fluid | Distilled water | Distilled water |
| Working fluid volume [mL] | 6.52 | 14.55 |
| Filling ratio [%] | 120 | 100 |
| Test | Air Velocity [m/s] | Reynolds Number | Air Temperature [°C] |
|---|---|---|---|
| 1 | 0.6 | 4765 | 90 |
| 2 | 0.6 | 4416 | 120 |
| 3 | 0.6 | 4107 | 150 |
| 4 | 0.6 | 3831 | 180 |
| 5 | 1.1 | 8830 | 90 |
| 6 | 1.1 | 8183 | 120 |
| 7 | 1.1 | 7701 | 145 |
| 8 | 1.7 | 13,897 | 90 |
| 9 | 1.7 | 13,040 | 115 |
| Parameter | Instrument | Uncertainty |
|---|---|---|
| Temperature | Type T thermocouples (Agilent™ 34970A) | ±0.25 °C |
| Air velocity | ITAN 720 Anemometer | m/s |
| Voltage (TEG output) | Arduino-based DAQ | V |
| Current (TEG output) | Arduino-based DAQ | A |
| Hydraulic diameter (test section) | Millimeter scale | mm |
| v [m/s] | Re | T [°C] | [kg/s] | [°C] | [°C] | [°C] | [°C] | [W] | [W] | [W] | [%] |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.60 | 4765 | 90 | 0.014 | 32.00 | 34.27 | 92.54 | 81.73 | 808.5 | 32.88 | 157.2 | 20.91 |
| 0.60 | 4416 | 120 | 0.014 | 32.00 | 36.49 | 122.87 | 106.10 | 1161 | 62.24 | 234.2 | 26.57 |
| 0.60 | 4107 | 150 | 0.013 | 32.00 | 39.29 | 151.94 | 127.50 | 1478 | 96.9 | 327.8 | 29.56 |
| 0.60 | 3831 | 180 | 0.013 | 32.00 | 41.52 | 179.21 | 149.80 | 1779 | 121.5 | 380.0 | 31.98 |
| 1.10 | 8830 | 90 | 0.030 | 32.00 | 34.99 | 90.69 | 78.86 | 1479 | 85.02 | 318.5 | 25.20 |
| 1.10 | 8183 | 120 | 0.020 | 32.00 | 37.29 | 120.06 | 102.50 | 2131 | 135.9 | 454.7 | 29.89 |
| 1.10 | 7701 | 145 | 0.020 | 32.00 | 39.21 | 145.73 | 124.60 | 2263 | 178.8 | 527.4 | 33.91 |
| 1.70 | 13897 | 90 | 0.040 | 32.00 | 36.99 | 89.96 | 78.15 | 2244 | 210.4 | 500.5 | 42.04 |
| 1.70 | 13040 | 115 | 0.040 | 32.00 | 38.16 | 116.29 | 102.50 | 3138 | 250.9 | 565.0 | 44.40 |
| ΔT [°C] | Power Density [W/m2] | Power [mW] | Total Power | Total Density | |||
|---|---|---|---|---|---|---|---|
| TG1 | TG2 | TG1 | TG2 | [mW] | [W/m2] | [%] | |
| 0.20 | 0.20 | 0.20 | 0.61 | 0.61 | 1.23 | 0.39 | 0.000078 |
| 0.78 | 0.78 | 0.78 | 2.44 | 2.44 | 4.88 | 1.56 | 0.002084 |
| 1.25 | 1.25 | 1.25 | 3.91 | 3.91 | 7.82 | 2.49 | 0.002383 |
| 3.32 | 3.32 | 3.32 | 10.40 | 10.40 | 20.80 | 6.63 | 0.005474 |
| 8.38 | 8.53 | 7.40 | 26.27 | 23.21 | 49.48 | 15.78 | 0.015536 |
| 8.53 | 8.53 | 8.53 | 26.75 | 26.75 | 53.50 | 17.06 | 0.011767 |
| 14.90 | 14.90 | 13.34 | 46.73 | 41.84 | 88.56 | 28.24 | 0.016792 |
| 20.19 | 20.19 | 20.19 | 63.30 | 63.30 | 126.60 | 40.37 | 0.025295 |
| 26.10 | 26.10 | 26.10 | 81.84 | 81.84 | 163.69 | 52.20 | 0.028971 |
| Flow Rate | ||||||||
|---|---|---|---|---|---|---|---|---|
| [m/s] | [°C] | [°C] | [W] | [mW] | [W] | [%] | [%] | [%] |
| 0.60 | 90 | 5.00 | 808.5 | 1.23 | 32.88 | 0.00015 | 4.07 | 4.07 |
| 0.60 | 120 | 12.41 | 1161 | 4.88 | 62.24 | 0.00042 | 5.36 | 5.36 |
| 0.60 | 150 | 23.33 | 1478 | 7.81 | 96.90 | 0.00053 | 6.56 | 6.56 |
| 0.60 | 180 | 29.96 | 1779 | 20.80 | 121.5 | 0.00117 | 6.83 | 6.83 |
| 1.10 | 90 | 7.37 | 1479 | 49.48 | 80.25 | 0.00335 | 5.43 | 5.43 |
| 1.10 | 120 | 17.77 | 2131 | 53.50 | 135.9 | 0.00251 | 6.38 | 6.38 |
| 1.10 | 145 | 26.53 | 2635 | 88.56 | 178.8 | 0.00336 | 6.79 | 6.79 |
| 1.70 | 90 | 8.65 | 2244 | 126.60 | 210.4 | 0.00564 | 9.38 | 9.38 |
| 1.70 | 115 | 18.31 | 3138 | 163.69 | 250.9 | 0.00522 | 8.00 | 8.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fachini, L.V.G.; Machado, P.L.O.; Ismail, K.A.R.; Biglia, F.M.; Vaz, A.J.C.; Szmoski, R.M.; Alves, T.A. Experimental Assessment of a Passive Waste Heat Recovery System Using Thermosyphons and Thermoelectric Generators for Integration into District Heating Applications. Energies 2025, 18, 5090. https://doi.org/10.3390/en18195090
Fachini LVG, Machado PLO, Ismail KAR, Biglia FM, Vaz AJC, Szmoski RM, Alves TA. Experimental Assessment of a Passive Waste Heat Recovery System Using Thermosyphons and Thermoelectric Generators for Integration into District Heating Applications. Energies. 2025; 18(19):5090. https://doi.org/10.3390/en18195090
Chicago/Turabian StyleFachini, Luis V. G., Pedro Leineker Ochoski Machado, Kamal A. R. Ismail, Felipe M. Biglia, Aleffe J. C. Vaz, Romeu M. Szmoski, and Thiago Antonini Alves. 2025. "Experimental Assessment of a Passive Waste Heat Recovery System Using Thermosyphons and Thermoelectric Generators for Integration into District Heating Applications" Energies 18, no. 19: 5090. https://doi.org/10.3390/en18195090
APA StyleFachini, L. V. G., Machado, P. L. O., Ismail, K. A. R., Biglia, F. M., Vaz, A. J. C., Szmoski, R. M., & Alves, T. A. (2025). Experimental Assessment of a Passive Waste Heat Recovery System Using Thermosyphons and Thermoelectric Generators for Integration into District Heating Applications. Energies, 18(19), 5090. https://doi.org/10.3390/en18195090








