Predicting the Temperature Rise in Oil-Immersed Transformers Based on the Identification of Thermal Circuit Model Parameters
Abstract
1. Introduction
2. Hot Circuit Model Parameter Identification and Winding Temperature Rise Prediction
2.1. Internal Heat Conduction Process of Transformers
2.2. Fifth-Order Thermal Circuit Modeling of Oil-Immersed Transformers
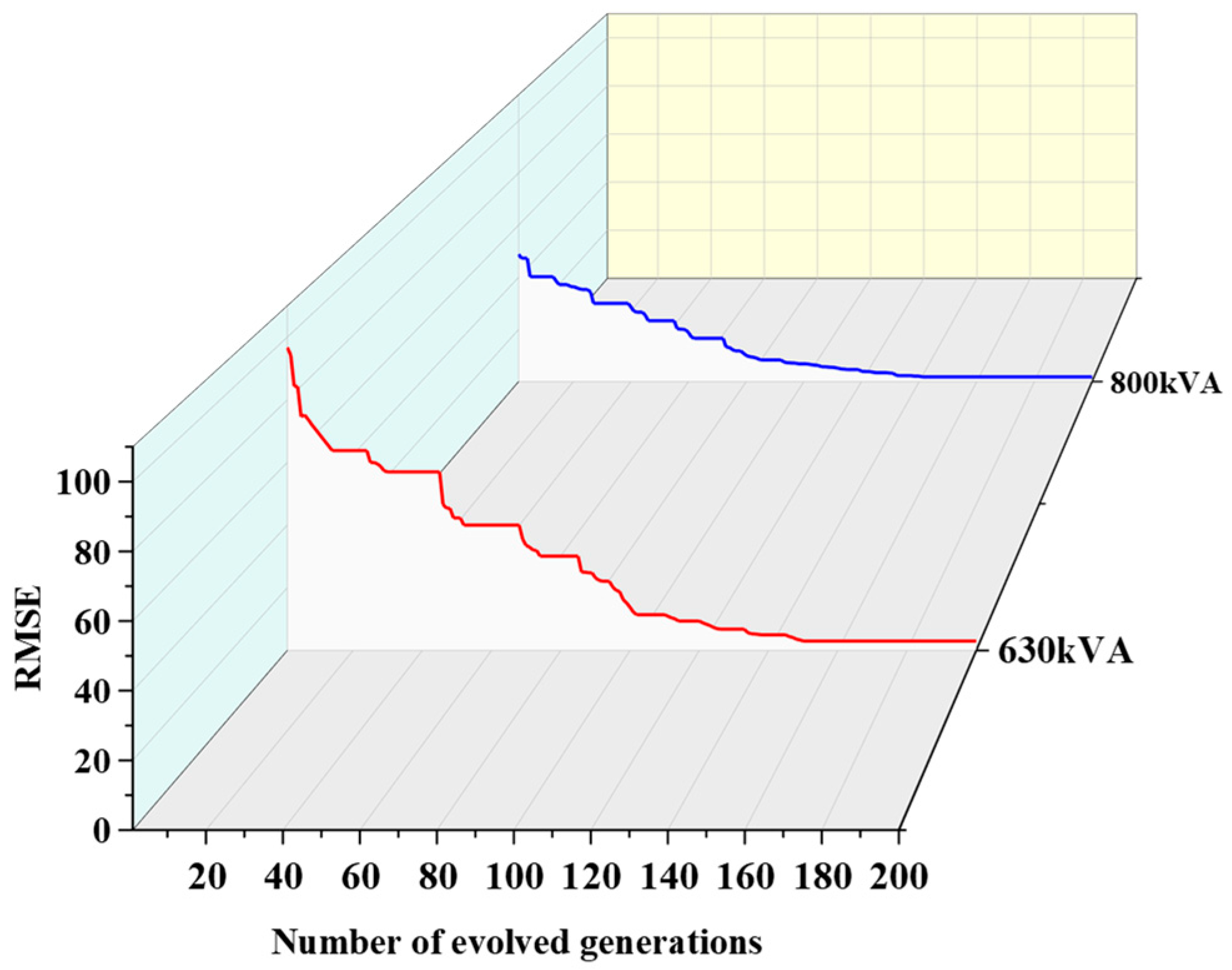
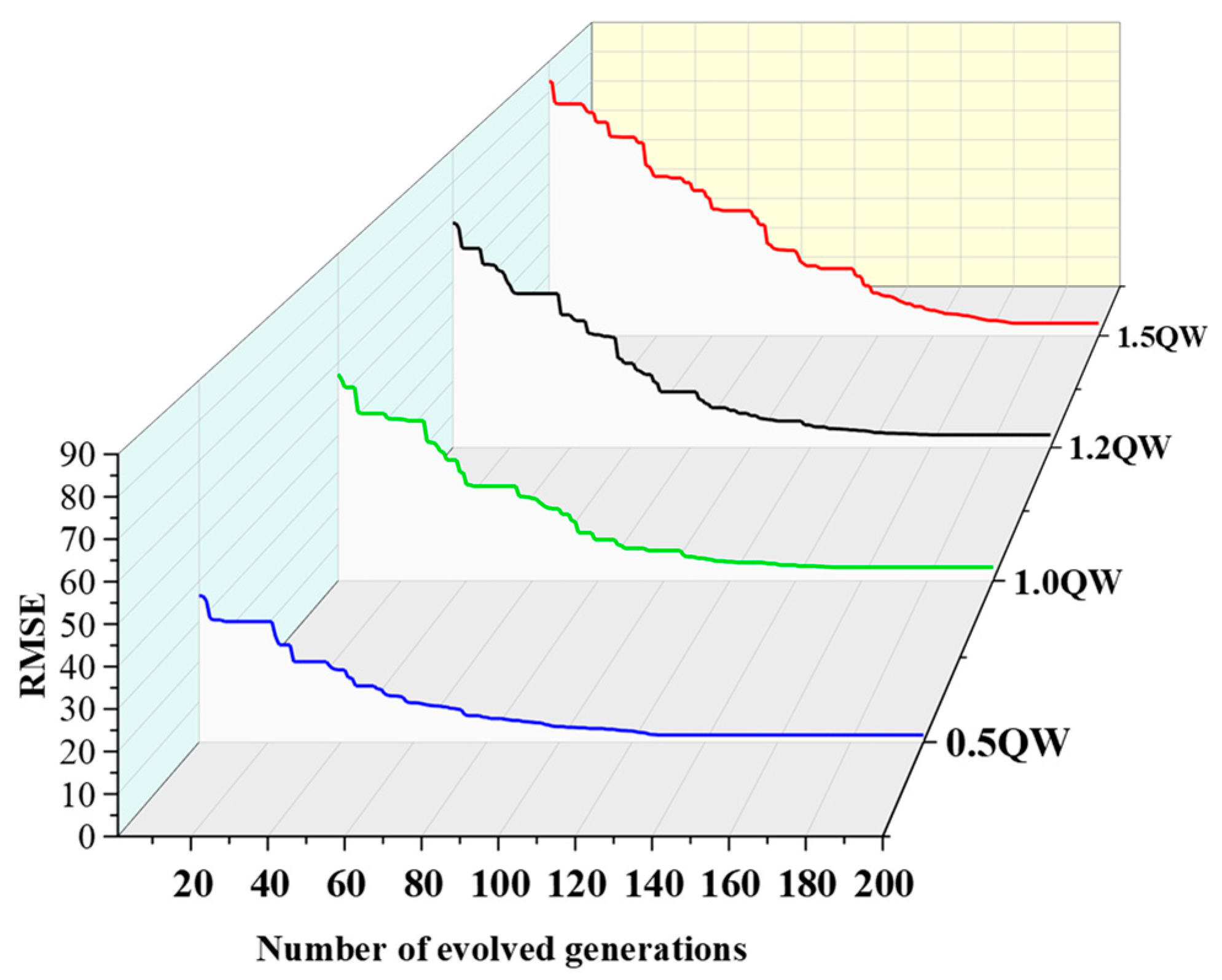
2.3. Parameter Identification Methods
2.4. Temperature Rise Calculation Method
3. Test Validation and Results
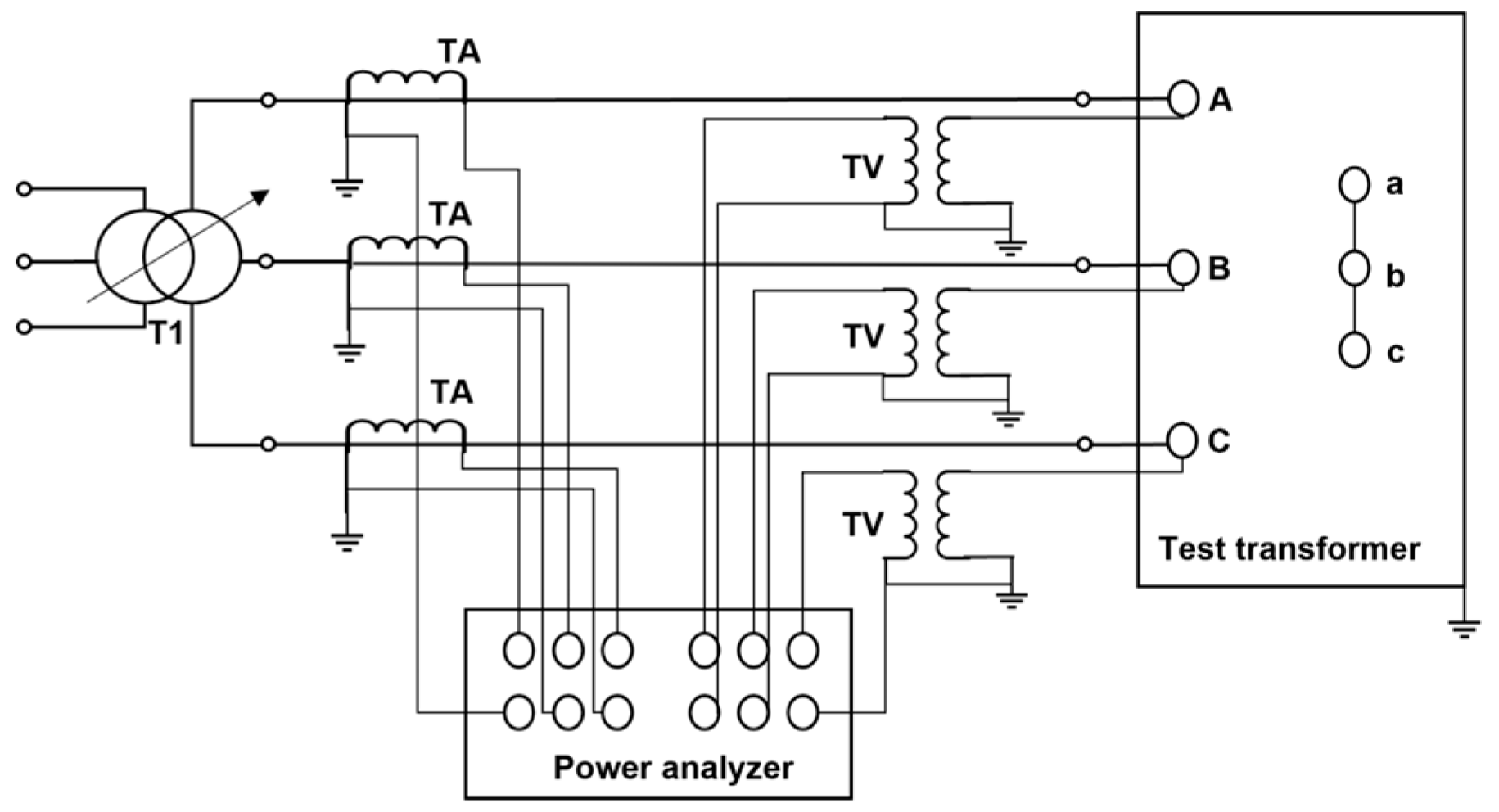
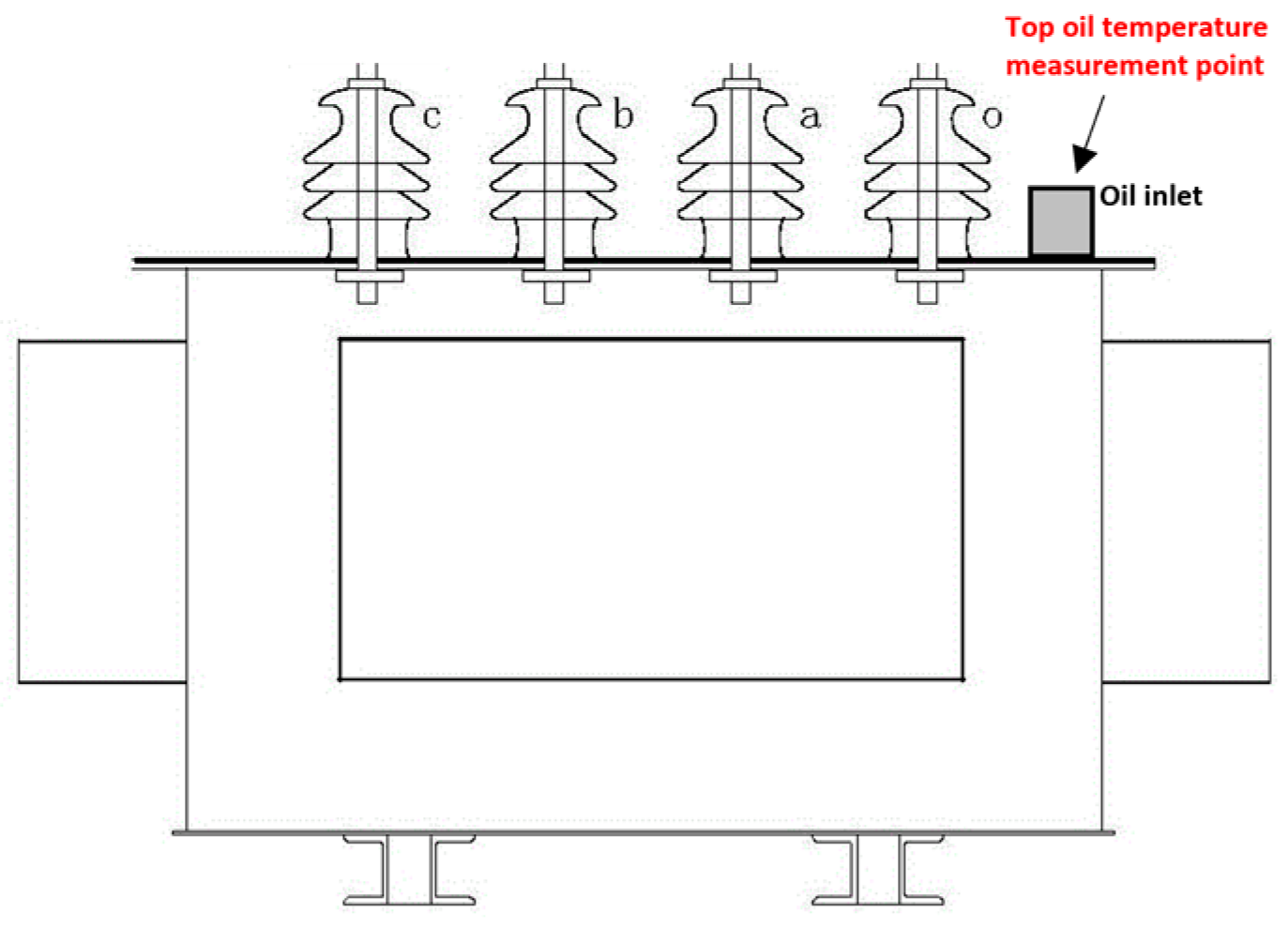
3.1. Temperature Rise Test Platform and Test Method
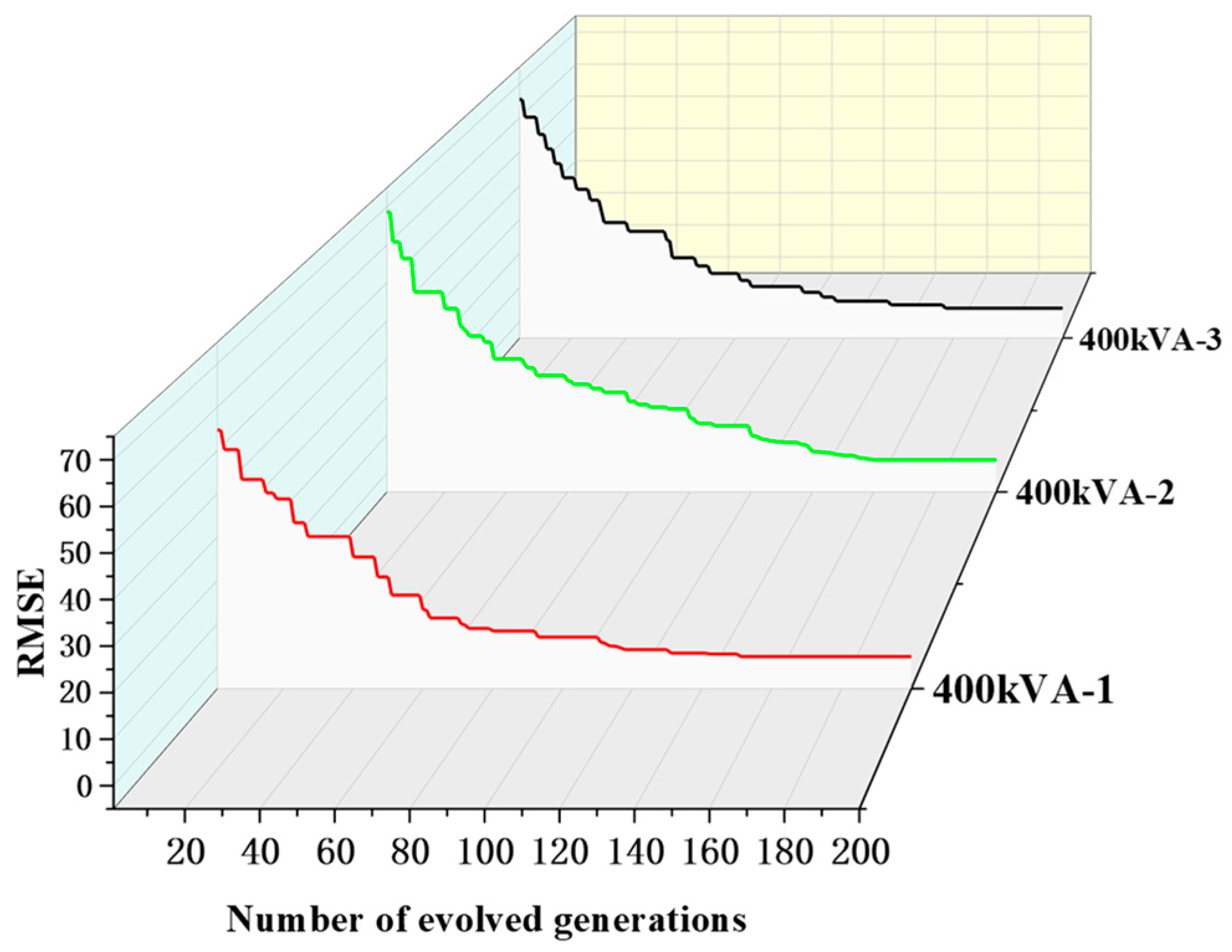
3.2. Model Parameter Identification Results
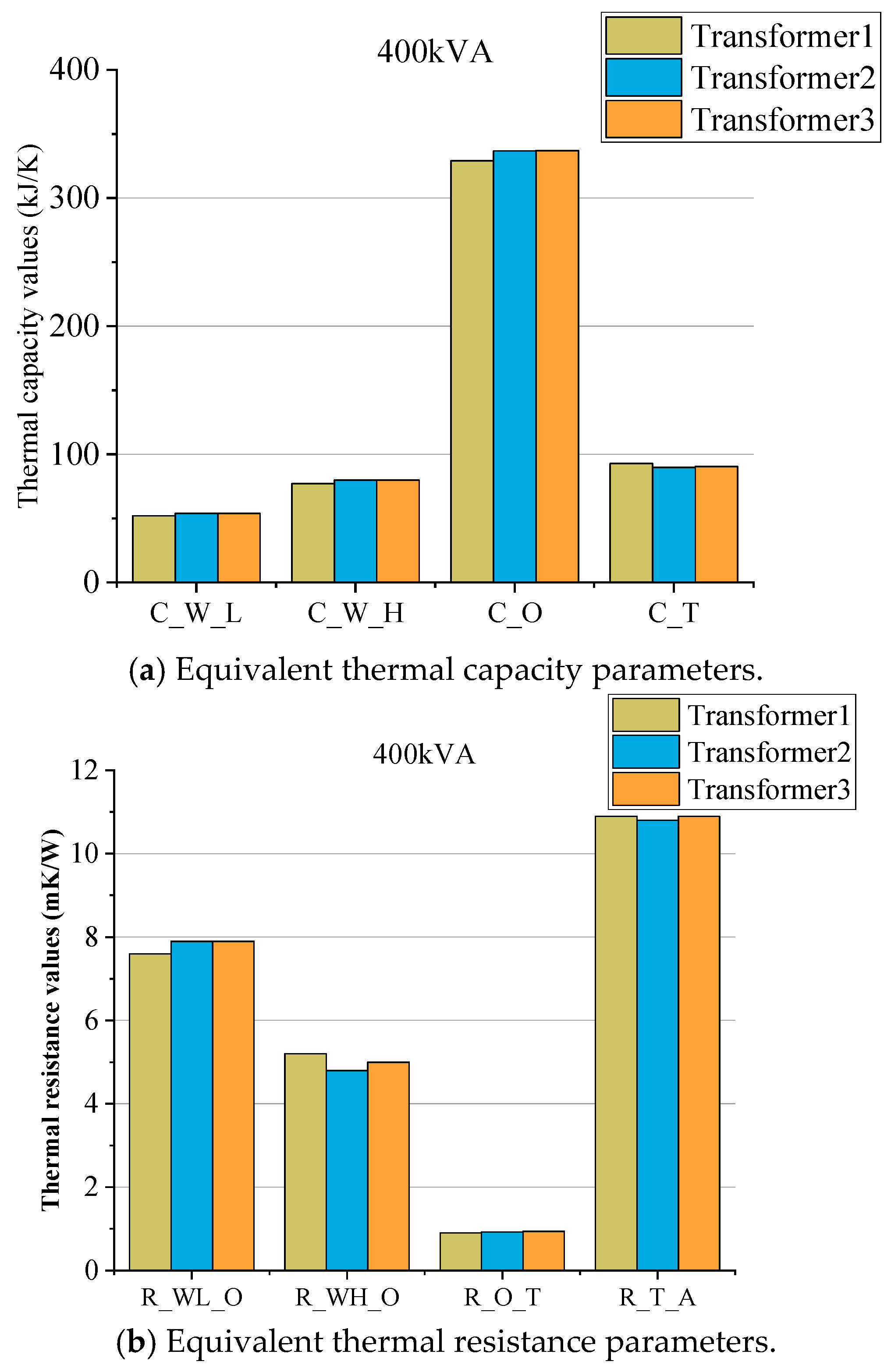
3.2.1. Thermal Capacity and Thermal Resistance of 400 kVA Transformers
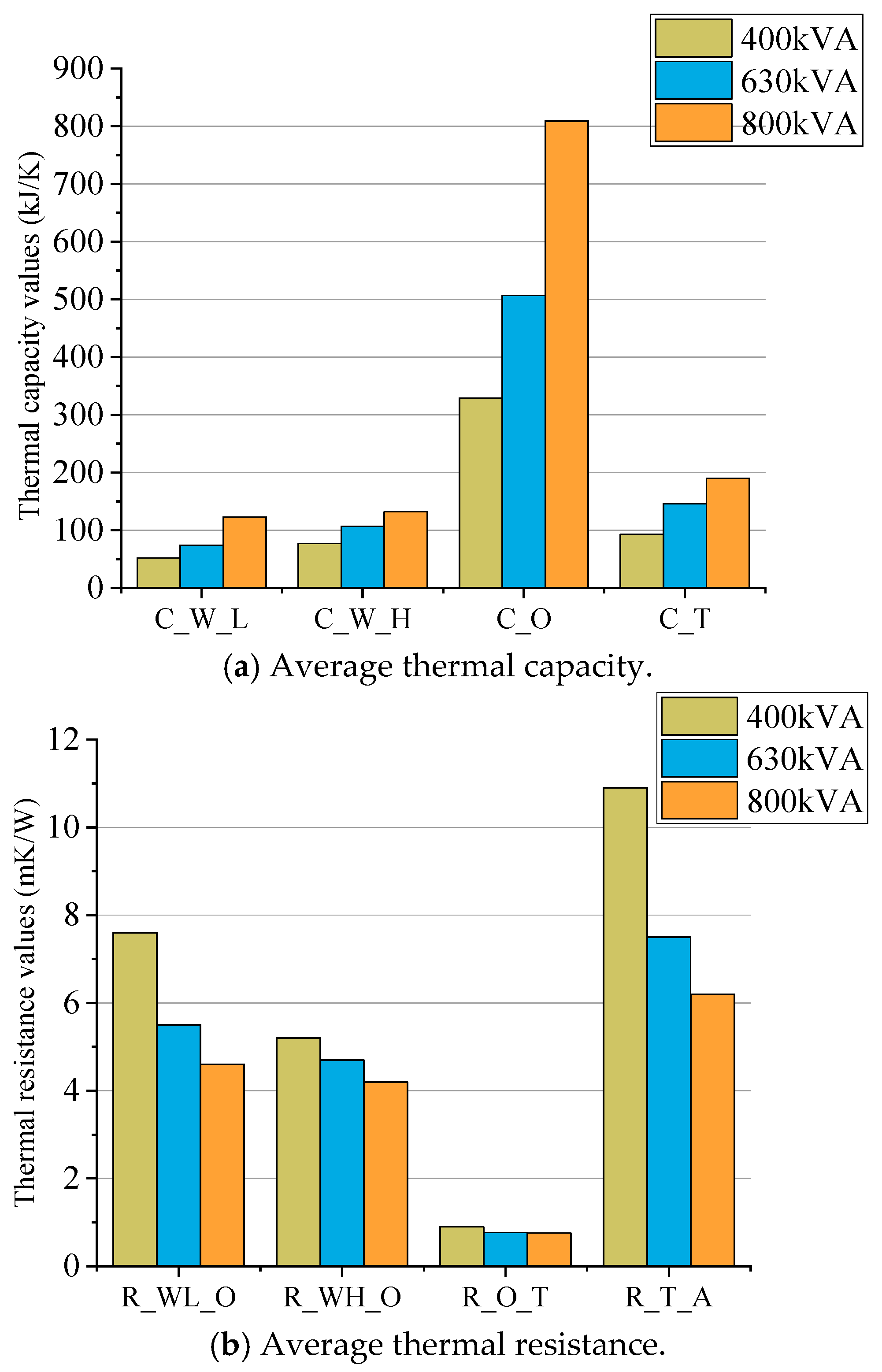
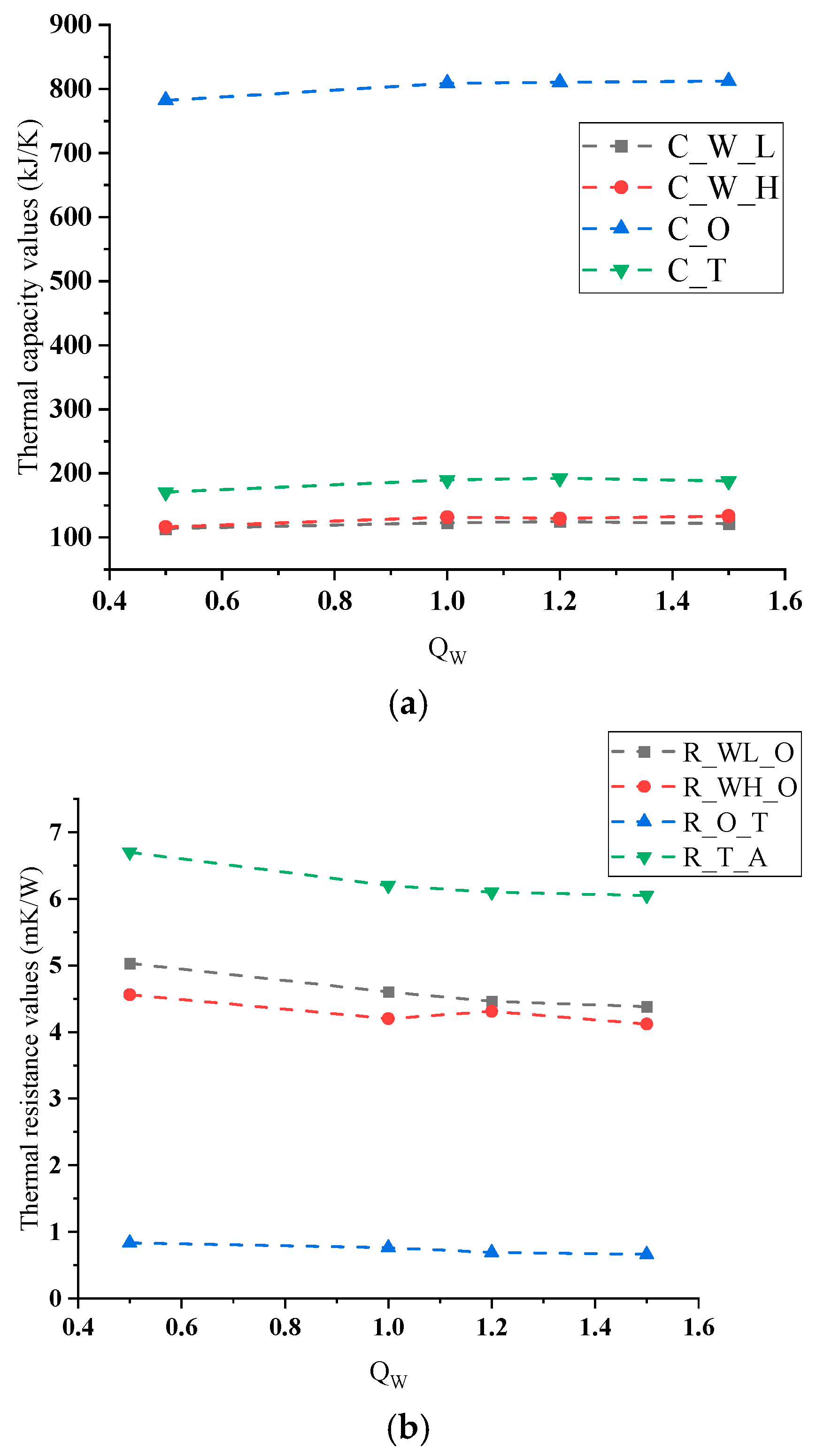
3.2.2. Thermal Capacitance and Thermal Resistance of Transformers of Different Capacities
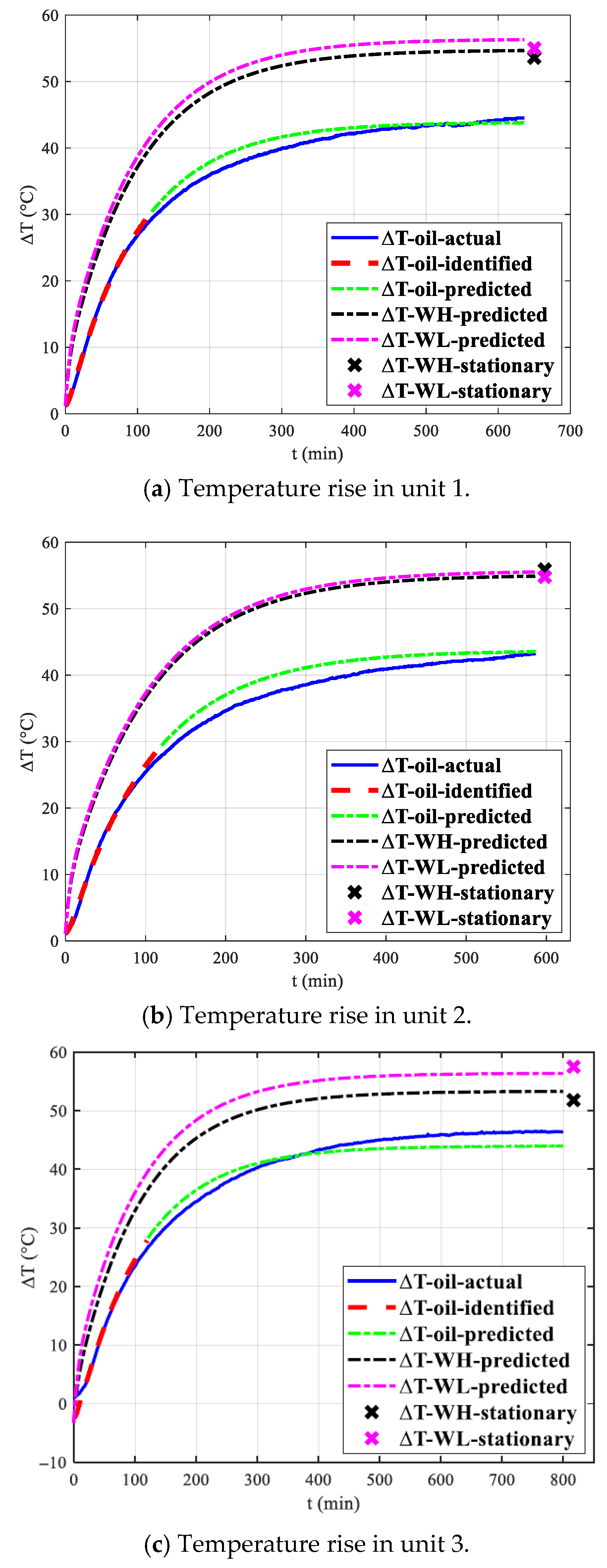
3.3. Temperature Rise Predictions with Different Transformers and Losses
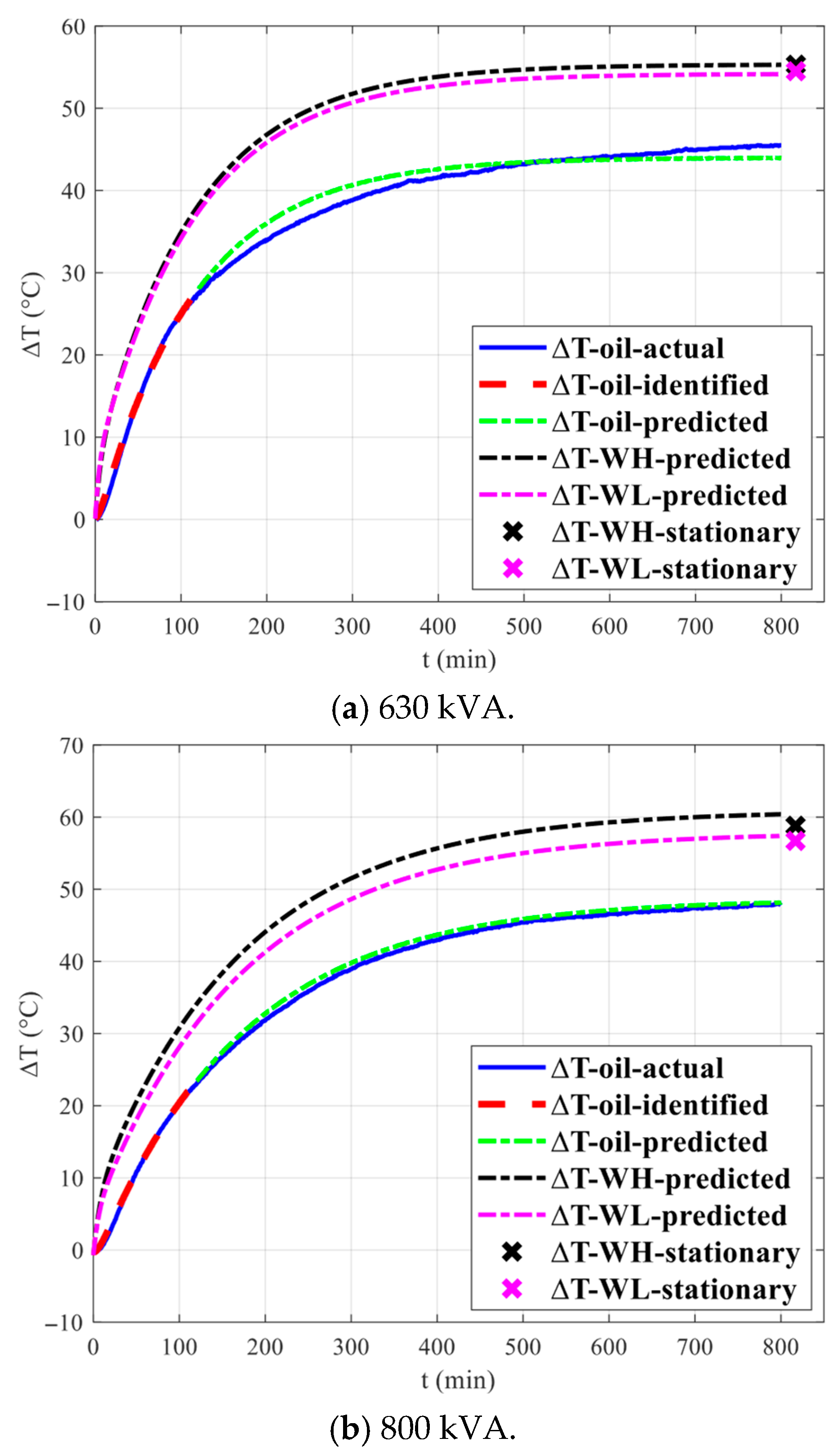
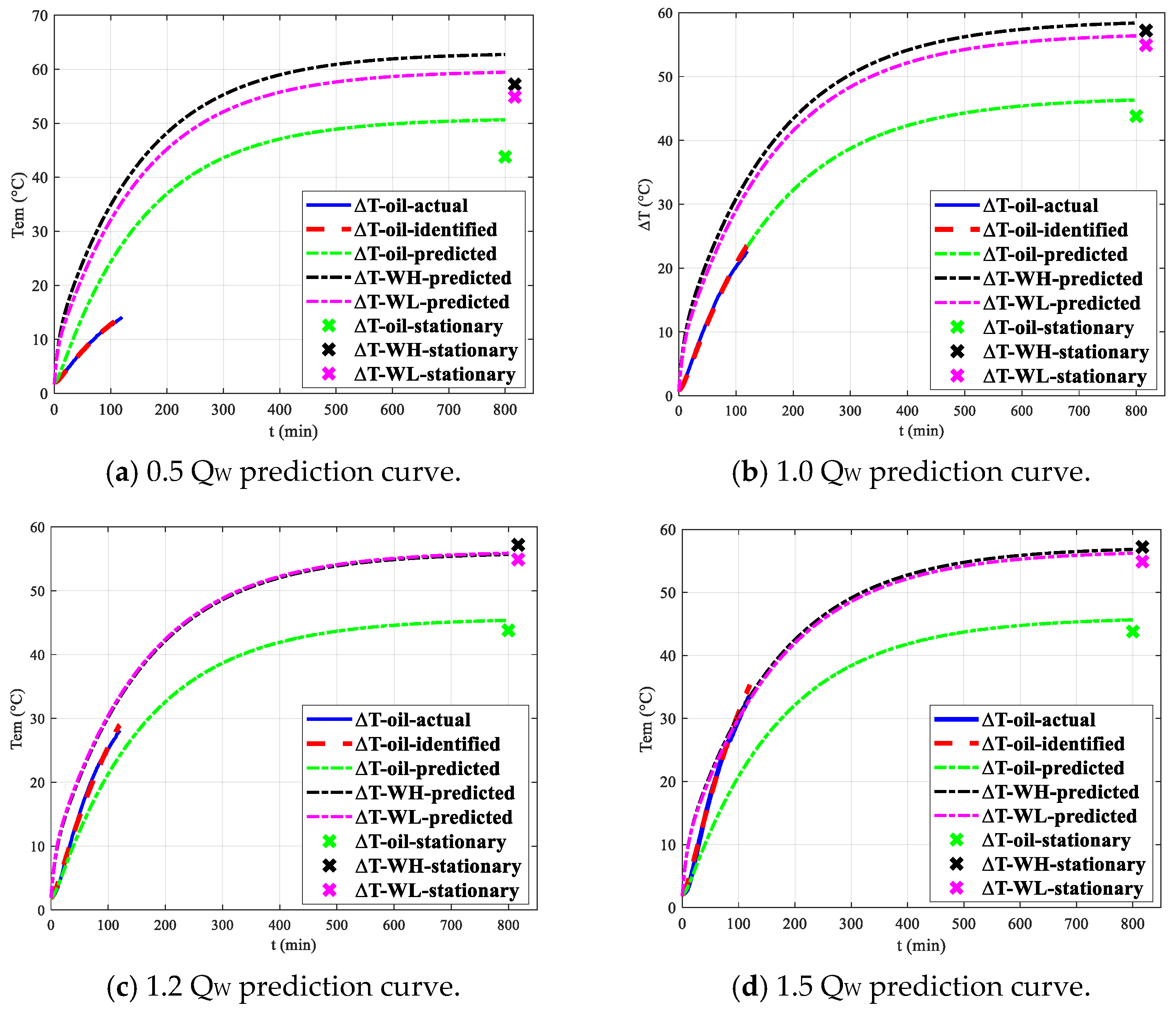
3.3.1. Prediction of Temperature Rise for Transformers with Different Capacities
3.3.2. Impact of Losses on Prediction Results
4. Discussion and Conclusions
- (1)
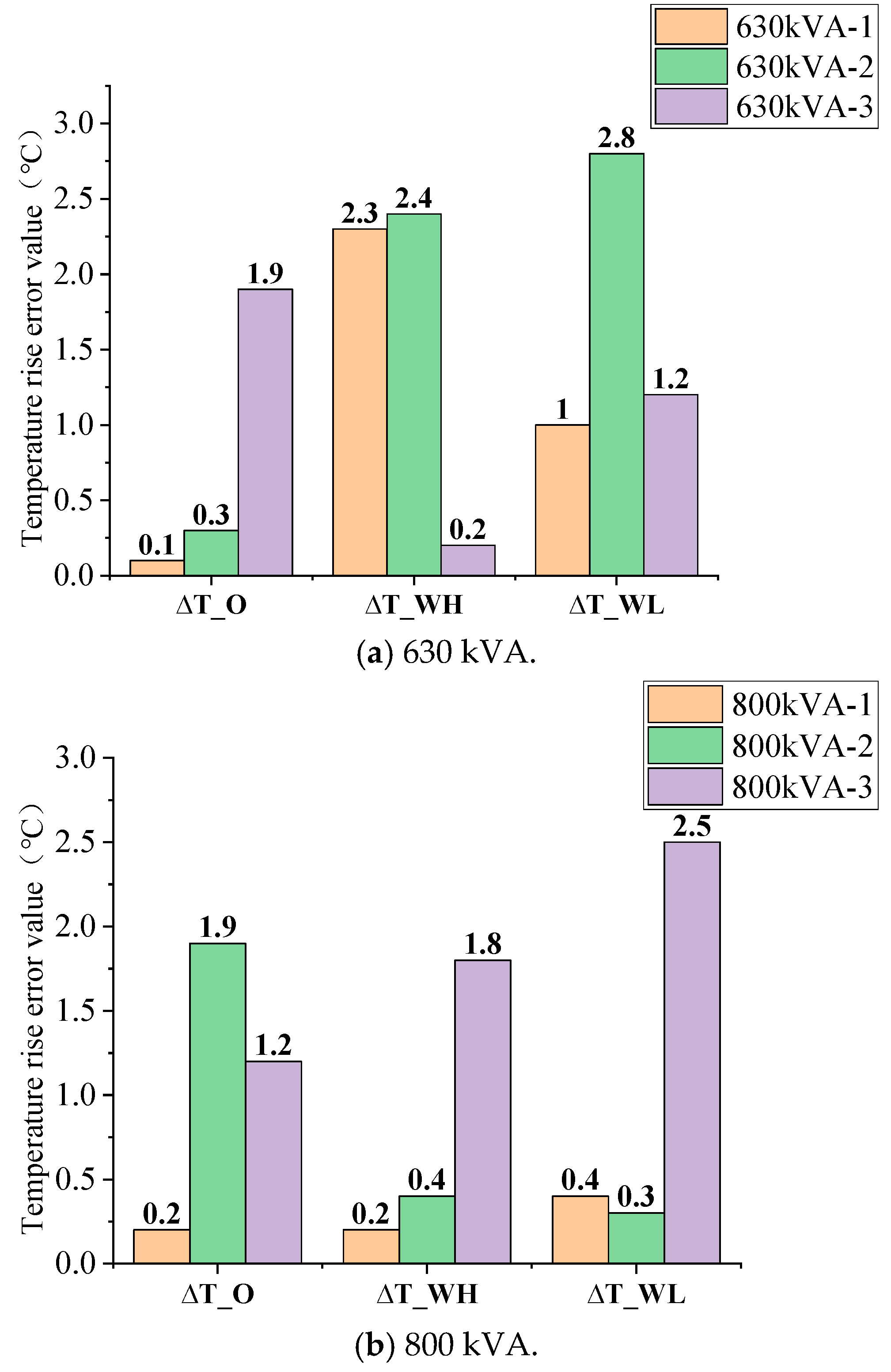
- The thermal resistance of the low-voltage winding is higher than that of the high-voltage winding. The oil–solid thermal resistance is significantly lower than the solid–gas thermal resistance. The parameter variation range for transformers of the same capacity, but different individuals, is lower than 10%;
- (2)
- The results indicate a positive correlation between thermal capacity and losses. A negative relationship was found between the thermal resistance and capacity. This coincides with the necessity to enhance the efficiency of heat dissipation in transformer design as the capacity increases;
- (3)
- The maximum absolute error of the calculated temperature is 2.9 °C. When the loss power is only half of the rated losses, the prediction error increases substantially, reaching a maximum of 6.9 °C. This can be attributed to the nonlinear characteristic shift exhibited by the transformer’s thermal system under low loss power conditions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wen, Q.; Baohui, Z.; Zhiguo, H.; Zhiqian, B. Simulation and analysis of oil-immersed transformer based on thermal-fluid coupled field. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014. [Google Scholar]
- Hao, Y.; Zhang, Z.; Xiao, J.; Zhao, H.; Yang, Y.; Dong, Z. Study on Thermal Characteristics of Winding Under Inter-Turn Fault of Oil-Immersed Transformer. Electronics 2024, 13, 2869. [Google Scholar] [CrossRef]
- Kalić, D.; Radaković, Z.; Lazarević, Z.; Radosavljević, R. On the determination of characteristic temperatures in power oil transformers during transient states. Arch. Für Elektrotechnik 1993, 76, 457–468. [Google Scholar] [CrossRef]
- Liao, C.; Ruan, J.; Liu, C.; Wen, W.; Du, Z. 3-D Coupled Electromagnetic-Fluid-Thermal Analysis of Oil-Immersed Triangular Wound Core Transformer. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, X.; Peng, Z.; Liu, P. 3D Coupled Electromagnetic-Thermal-Fluid Method for Computation of Temperature Field of Converter Transformer RIP Bushings. Proc. CSEE 2016, 36, 6269–6275. [Google Scholar] [CrossRef]
- Torriano, F.; Chaaban, M.; Picher, P. Numerical study of parameters affecting the temperature distribution in a disc-type transformer winding. Appl. Therm. Eng. 2010, 30, 2034–2044. [Google Scholar] [CrossRef]
- Susa, D.; Lehtonen, M.; Nordman, H. Dynamic thermal modelling of power transformers. IEEE Trans. Power Deliv. 2005, 20, 197–204. [Google Scholar] [CrossRef]
- Swift, G.; Molinski, T.S.; Lehn, W. A fundamental approach to transformer thermal modeling, I. Theory and equivalent circuit. IEEE Trans. Power Deliv. 2002, 16, 171–175. [Google Scholar] [CrossRef]
- Gerling, D.; Dajaku, G. Novel lumped-parameter thermal model for electrical systems. In Proceedings of the 2005 European Conference on Power Electronics and Applications, Dresden, Germany, 11–14 September 2005. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Zhuang, X.; Xiao, H.; Fan, X.; Wang, J.; Li, X.; Jiang, T. Test and Analysis on Extended Temperature Rise of 110 kV Transformer Based on Distributed Temperature Sensing. IEEE Trans. Power Deliv. 2023, 38, 1030–1041. [Google Scholar] [CrossRef]
- Tembo, F.; Bragone, F.; Laneryd, T.; Barreau, M.; Morozovska, K. Data-Driven vs Traditional Approaches to Power Transformers’ Top-Oil Temperature Estimation. arXiv 2025, arXiv:2501.16831. [Google Scholar]
- Wang, L.; Zhou, L.; Tang, H.; Wang, D.; Cui, Y. Numerical and experimental validation of variation of power transformers’ thermal time constants with load factor. Appl. Therm. Eng. 2017, 126, 939–948. [Google Scholar] [CrossRef]
- Córdoba, P.A.; Silin, N.; Osorio, D.; Dari, E. An experimental study of natural convection in a distribution transformer slice model. Int. J. Therm. Sci. 2018, 129, 94–105. [Google Scholar] [CrossRef]
- Picanço, A.F.; Martinez, M.L.; Rosa, P.C. Bragg system for temperature monitoring in distribution transformers—ScienceDirect. Electr. Power Syst. Res. 2010, 80, 77–83. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Li, H.; Wang, J.; Fan, X. Experimental and Numerical Investigation of the Internal Temperature of an Oil-Immersed Power Transformer with DOFS. Appl. Sci. 2020, 10, 5718. [Google Scholar] [CrossRef]
- Huang, Y.C.; Huang, C.M. Evolving wavelet networks for power transformer condition monitoring. IEEE Power Eng. Rev. 2007, 22, 63. [Google Scholar] [CrossRef]
- Feng, J.; Feng, Z.; Jiang, G.; Zhang, G.; Jin, W.; Zhu, H. A Prediction Method for the Average Winding Temperature of a Transformer Based on the Fully Connected Neural Network. Appl. Sci. 2024, 14, 6841. [Google Scholar] [CrossRef]
- Song, H.; Yao, H.; Wei, X.; Qin, H.; Li, Y.; Lv, K.; Chen, Q. Experimental Study on Fire Suppression of the Outdoor Oil-Immersed Transformer by High-Pressure Water Mist System. Fire 2023, 6, 238. [Google Scholar] [CrossRef]
- You, Y.; Shao, K.; Yi, Z. Dynamic Heat Dissipation Model of Distributed Parameters for Oil-Directed and Air-Forced Traction Transformers and Its Experimental Validation. Entropy 2023, 25, 457. [Google Scholar] [CrossRef]
- Liu, L.; Longfei, L.; Houguang, C.; Zhang, F.; Jin, M.; Zhang, W.; Zhijie, G.; Zhaoguang, D. Research of the Loss of Power Transformer Structure. IEEJ Trans. Electr. Electron. Eng. 2022, 2320, 012017. [Google Scholar]
- Wang, P.; Cao, H.; Xiao, J. Structure Design of a Four-Pillar Magnetically Integrated Fractional-Turn Planar Transformer and its Loss Analysis. IEEJ Trans. Electr. Electron. Eng. 2025, 20, 208–216. [Google Scholar] [CrossRef]
- Dou, M.; Zhao, W.; Zhang, L.; Sun, Y. Analysis of Parasitic Parameters and Winding Loss Characteristics of High-Frequency Transformer under Different Winding Structures. J. Phys. Conf. Ser. 2024, 2774, 012029. [Google Scholar] [CrossRef]
- Wei, B.; Huang, H.; Fu, C.; Li, H.; Liu, J. Algorithm for Transformer Top-Oil Temperature and Winding Hot-Point Temperature Based on Modified Thermal Circuit Model. East China Electr. Power 2012, 40, 444–447. [Google Scholar]
- Xu, W. Review of Studies on the Hot Spot Temperature of Oil-Immersed Transformers. Energies 2024, 18, 74. [Google Scholar] [CrossRef]
- Smolyanov, I.; Shmakov, E.; Butusov, D.; Khalyasmaa, A.I. Review of Modeling Approaches for Conjugate Heat Transfer Processes in Oil-Immersed Transformers. Computation 2024, 12, 97. [Google Scholar] [CrossRef]
- Taghikhani, M.A. Heat transfer modeling in a transformer using magneto-CFD analysis and GWO algorithm considering dynamic thermal model. Results Eng. 2024, 23, 102856. [Google Scholar] [CrossRef]
- Liang, J.; Liang, K.; Shao, Z.; Niu, Y.; Song, X.; Sun, P.; Feng, J. Research on Temperature-Rise Characteristics of Motor Based on Simplified Lumped-Parameter Thermal Network Model. Energies 2024, 17, 4717. [Google Scholar] [CrossRef]
- Jin, N.S.; Xu, X.P.; Wen, H.M.; Zhang, X. Thermal Behavior Calculation Model of Oil-immersed Transformer Winding Based on Thermoelectric Analogy Theory. Control Instrum. Chem. Ind. 2019, 725–730. [Google Scholar] [CrossRef]
- Tang, W.H.; Wu, Q.H. Thermoelectric Analogy Thermal Models of Power Transformers. In Condition Monitoring and Assessment of Power Transformers Using Computational Intelligence. Power Systems; Springer: London, UK, 2011; pp. 55–71. [Google Scholar] [CrossRef]
- Ding, Y.Q.; Zhang, Q.G.; Gao, M.; Li, Y.; Zhao, Y.; Yang, W.H. Distributed Thermal Circuit Model of Oil-immersed Distribution Transformers. High Volt. Eng. 2019, 45, 968–974. [Google Scholar] [CrossRef]
- Wang, F.W.; Zhou, X.; Gao, P.; Xi, X.G. Improved Thermal Circuit Model of Hot Spot Temperature in Oil-immersed Transformers Based on Heat Distribution of Winding. High Volt. Eng. 2015, 41, 895–901. [Google Scholar] [CrossRef]
- Weigen, C.; Chong, P.; Yuxin, Y. Power transformer top-oil temperature model based on thermal-electric analogy theory. Eur. Trans. Electr. Power Eng. 2009, 19, 341–354. [Google Scholar] [CrossRef]
- Mikhak-Beyranvand, M.; Faiz, J.; Rezaeealam, B. Thermal Analysis of Power Transformer Using an Improved Dynamic Thermal Equivalent Circuit Model. Electr. Power Compon. Syst. 2019, 47, 1598–1609. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M.A. Combination of Genetic Algorithm and Particle Swarm Optimization for Optimal Distributed Generation Location and Sizing in Distribution Systems with Fuzzy Optimal Theory. Int. J. Green Energy 2012, 9, 641–660. [Google Scholar] [CrossRef]
- Soltani, H.; Shafiei, S. Heat exchanger networks retrofit with considering pressure drop by coupling genetic algorithm with LP (linear programming) and ILP (integer linear programming) methods. Energy 2011, 36, 2381–2391. [Google Scholar] [CrossRef]
- IEC 60076-2-2011; Power Transformers—Part 2: Temperature Rise of Liquid-Immersed Transformers. IEC: Geneva, Switzerland, 2012.
- C57.91-2011; IEEE Guide for Loading Mineral-Oil-Immersed Transformers and Step-Voltage Regulators. IEEE: New York, NY, USA, 2012. [CrossRef]


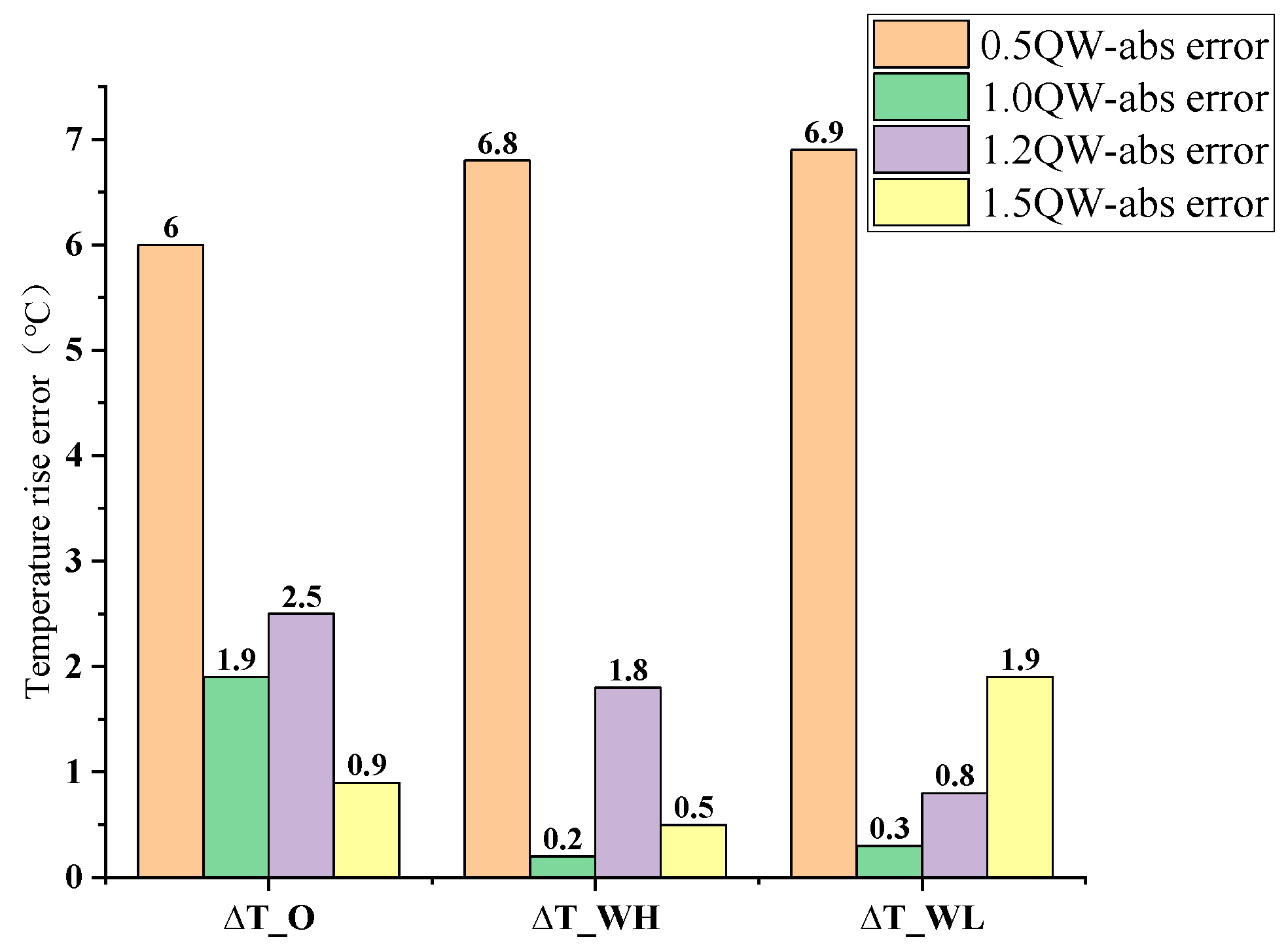
| Thermal Parameters | Electrical Parameters |
|---|---|
| Heat output q/W | Current i/A |
| Temperature T/K | Voltage u/V |
| Thermal resistance Rth/(K·W−1) | Resistor Rel/Ω |
| Thermal capacitor Cth/(J·K−1) | Capacitance Cel/F |
| Parameters | Notation | Unit |
|---|---|---|
| High-voltage winding loss | QWH | W |
| Low-voltage winding loss | QWL | W |
| Core loss | QC | W |
| Core thermal capacity | CC | J/K |
| High-voltage winding thermal capacity | CWH | J/K |
| Low-voltage winding thermal capacity | CWL | J/K |
| Oil thermal capacity | Co | J/K |
| Tank thermal capacity | CT | J/K |
| Core to oil thermal resistance | RC-O | K/W |
| High-voltage winding to oil thermal resistance | RWH-O | K/W |
| Low-voltage winding to oil thermal resistance | RWL-O | K/W |
| Oil to tank thermal resistance | RO-T | K/W |
| Tank to ambient thermal resistance | RT-A | K/W |
| Core average temperature | TC | K |
| High-voltage winding temperature | TWH | K |
| Low-voltage winding temperature | TWL | K |
| Top oil temperature | TO | K |
| Tank temperature | TT | K |
| Ambient temperature | TA | K |
| Parameter Type | Parameter Value/Method Name |
|---|---|
| Population size | 150 |
| Crossover probability | 0.6 |
| Mutation probability | 0.1 |
| Number of generations | 200 |
| Operator selection method | Roulette wheel selection |
| Operator crossover method | Uniform crossover |
| Operator mutation method | Adaptive mutation |
| Model | Capacity/kVA | Load Loss/kW | No-Load Loss/kW | HV/LV Winding DC Resistance (75 °C) |
|---|---|---|---|---|
| S20-M-400/10 | 400 | 3.615 | 0.37 | 3.312 Ω/1.494 mΩ |
| S20-M-630/10 | 630 | 4.96 | 0.6 | 1.771 Ω/0.809 mΩ |
| S20-M-800/10 | 800 | 6.0 | 0.63 | 1.483 Ω/0.464 mΩ |
| Number | TA_Final/TA_Set | Temperature Node | TActual/TPredicted | ∆TActual = TActual – TA_Final | ∆TPredicted = TPredicted – TA_Set | Error = |∆TPredicted − ∆TActual| |
|---|---|---|---|---|---|---|
| 400kVA-1 | 14.8/11.9 | TO | 58.8/55.1 | 44.1 | 45.0 | 0.9 |
| TWH | 68.4/64.7 | 53.6 | 54.1 | 0.5 | ||
| TWL | 69.8/66.8 | 55.0 | 57.9 | 2.9 | ||
| 400kVA-2 | 15.3/10.7 | TO | 57.9/53.7 | 42.6 | 43.0 | 0.4 |
| TWH | 71.2/63.8 | 55.9 | 53.1 | 2.8 | ||
| TWL | 70.1/67.3 | 54.8 | 56.6 | 0.8 | ||
| 400kVA-3 | 33.6/28.9 | TO | 79.8/73.1 | 46.2 | 44.2 | 2 |
| TWH | 85.4/81.7 | 51.8 | 52.8 | 1 | ||
| TWL | 92.5/85.7 | 58.9 | 56.8 | 2.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Wang, L.; Li, J.; Weng, H.; Zheng, Z.; Wen, G.; Zhang, F. Predicting the Temperature Rise in Oil-Immersed Transformers Based on the Identification of Thermal Circuit Model Parameters. Energies 2025, 18, 4707. https://doi.org/10.3390/en18174707
Hu Y, Wang L, Li J, Weng H, Zheng Z, Wen G, Zhang F. Predicting the Temperature Rise in Oil-Immersed Transformers Based on the Identification of Thermal Circuit Model Parameters. Energies. 2025; 18(17):4707. https://doi.org/10.3390/en18174707
Chicago/Turabian StyleHu, Yujia, Li Wang, Jialing Li, Huiying Weng, Zhiyao Zheng, Guohao Wen, and Fan Zhang. 2025. "Predicting the Temperature Rise in Oil-Immersed Transformers Based on the Identification of Thermal Circuit Model Parameters" Energies 18, no. 17: 4707. https://doi.org/10.3390/en18174707
APA StyleHu, Y., Wang, L., Li, J., Weng, H., Zheng, Z., Wen, G., & Zhang, F. (2025). Predicting the Temperature Rise in Oil-Immersed Transformers Based on the Identification of Thermal Circuit Model Parameters. Energies, 18(17), 4707. https://doi.org/10.3390/en18174707





