Applications of X-Ray Computed Tomography Technology to Solid–Liquid Phase Change Materials—A Review
Abstract
1. Introduction
1.1. PCM Challenges
1.2. PCM Characterization Techniques
2. Laboratory X-Ray Computed Tomography
2.1. XCT Workflow
2.2. Attenuation Contrast Imaging
2.3. Spatial Resolution
2.4. CT-Acquisition Parameters and Image Quality
2.5. Time-Lapse XCT Imaging
3. XCT Characterization of PCM Morphology
4. XCT Analysis of Solid–Liquid Phase Changes
4.1. Magnesium Chloride Hexahydrate MgCl2·6H2O
4.2. Calcium Chloride Hexahydrate CaCl2·6H2O
4.3. Ice as PCM
4.4. n-Eicosane C20H42
5. XCT as a Tool to Validate PCM Numerical Models
5.1. Melting of Ice
5.2. Solidification of n-Eicosane
5.3. Solidification of CaCl2·6H2O
6. XCT Challenges in PCM Research
6.1. X-Ray Attenuation Contrast
6.2. Spatial Resolution
6.3. Segmentation Algorithms
6.4. High Throughput
6.5. Non-Ambient Attachment
7. Conclusions
Funding
Conflicts of Interest
Abbreviations
| XCT | X-ray computed tomography |
| PCM | Phase change material |
| 3D | Three-dimensional |
| 2D | Two-dimensional |
| LHTES | Latent heat thermal energy storage system |
| DSC | Differential scanning calorimetry |
| TGA | Thermo-gravimetric analysis |
| FT-IR | Fourier-transform infrared |
| SEM | Scanning electron microscopy |
| XRPD | X-ray powder diffraction |
| SDD | Source-to-detector distance |
| SOD | Source-to-object distance |
| µ-CT | Microfocus computed tomography |
| SAT | Sodium acetate trihydrate |
| SA | Sodium acetate |
| XPS | Extruded polystyrene |
| CFD | Computational fluid dynamics |
| AI | Artificial Intelligence |
| LUASA | Lucerne University of Applied Science and Arts |
| LuCi | Lucerne CT Imaging |
| SXCT | Synchrotron X-ray computed tomography |
References
- Gilbert, T.; Menon, A.K.; Dames, C.; Prasher, R. Heat source and application-dependent levelized cost of decarbonized heat. Joule 2023, 7, 128–149. [Google Scholar] [CrossRef]
- Ang, T.-Z.; Salem, M.; Kamarol, M.; Das, H.S.; Nazari, M.A.; Prabaharan, N. A comprehensive study of renewable energy sources: Classifications, challenges and suggestions. Energy Strateg Rev. 2022, 143, 100939. [Google Scholar] [CrossRef]
- Hamzat, A.K.; Pasanaje, A.H.; Omisanya, M.I.; Sahin, A.Z.; Maselugbo, A.O.; Adediran, I.A.; Mudashiru, L.O.; Asmatulu, E.; Asmatulu, O.R.; Asmatülü, R. Phase change materials in solar energy storage: Recent progress, environmental impact, challenges, and perspectives. J. Energy Storage 2025, 114, 115762. [Google Scholar] [CrossRef]
- Mehta, P.; Patel, V.; Kumar, S.; Sharma, V.; Tejani, G.G.; Santhosh, A.J. Performance assessment of thermal energy storage system for solar thermal applications. Sci. Rep. 2025, 14, 13876. [Google Scholar] [CrossRef]
- Jayathunga, D.S.; Karunathilake, H.P.; Narayana, M.; Witharana, S. Phase change material (PCM) candidates for latent heat thermal energy storage (LHTES) in concentrated solar power (CSP) based thermal applications—A review. Renew. Sustain. Energy Rev. 2024, 189, 113904. [Google Scholar] [CrossRef]
- Stamatiou, A.; Maranda, S.; Fischer, L.J.; Worlitschek, J. Solid–Liquid Phase Change Materials for Energy Storage: Opportunities and Challenges. In Solid-Liquid Thermal Energy Storage: Modeling and Applications; Mobedi, M., Hooman, K., Tao, W.-Q., Eds.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2022; pp. 1–22. [Google Scholar]
- Zalba, B.; Marin, J.M.; Cabeza, L.F.; Mehling, H. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications. Appl. Therm. Eng. 2003, 23, 251–283. [Google Scholar] [CrossRef]
- Togun, H.; Sultan, H.S.; Mohammed, H.I.; Sadeq, A.M.; Biswas, N.; Hasan, H.A.; Homod, R.Z.; Abdulkadhim, A.H.; Yaseen, Z.M.; Talebizadehsardari, P. A critical review on phase change materials (PCM) based heat exchanger: Different hybrid techniques for the enhancement. J. Energy Storage 2024, 79, 109840. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Zsembinszki, G.; Martin, M. Evaluation of volume change in phase change materials during their phase transition. J. Energy Storage 2020, 28, 101206. [Google Scholar] [CrossRef]
- Sharshir, S.W.; Joseph, A.; Elsharkawy, M.; Hamada, M.A.K.; Kandeal, A.W.; Elkadeem, M.R.; Thakur, A.K.; Ma, Y.; Moustapha, M.E.; Rashad, M.; et al. Thermal energy storage using phase change materials in building applications: A review of the recent development. Energy Build. 2023, 285, 112908. [Google Scholar] [CrossRef]
- Babaharra, O.; Choukairy, K.; Faraji, H.; Khallaki, K.; Hamdaoui, S.; Bahammou, Y. Thermal performance analysis of hollow bricks integrated phase change materials for various climate zones. Heat Transf. 2024, 53, 2148–2172. [Google Scholar] [CrossRef]
- Lalau, Y.; Rigal, S.; Bedecarrats, J.P.; Haillot, D. Latent Thermal Energy Storage System for Heat Recovery between 120 and 150 °C: Material Stability and Corrosion. Energies 2024, 14, 787. [Google Scholar] [CrossRef]
- Yang, M.; Moghimi, M.A.; Loillier, R.; Markides, C.N.; Kadivar, M. Design of a latent heat thermal energy storage system under simultaneous charging and discharging for solar domestic hot water applications. Appl. Energy 2023, 336, 120848. [Google Scholar] [CrossRef]
- Farid, M.M.; Khudhair, A.M.; Razack, S.A.K.; Al-Hallaj, S. A review on phase change energy storage: Materials and applications. Energy Convers. Manag. 2004, 45, 1597–1615. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Castell, A.; Barreneche, C.; de Gracia, A.; Fernandez, A.I. Materials used as PCM in thermal energy storage in buildings: A review. Renew. Sustain. Energy Rev. 2011, 15, 1675–1695. [Google Scholar] [CrossRef]
- Reddy, K.S.; Mudgal, V.; Mallick, V.M. Review of latent heat thermal energy storage for improved material stability and effective load management. J. Energy Storage 2018, 15, 205–227. [Google Scholar] [CrossRef]
- Mehling, H. Review of classification of PCMs with a focus on the search for new suitable PCM candidates. Energies 2024, 17, 4455. [Google Scholar] [CrossRef]
- Shamseddine, I.; Pennec, F.; Biwole, P.; Fardoun, F. Supercooling of phase change materials: A review. Renew. Sustain. Energy Rev. 2022, 158, 112172. [Google Scholar] [CrossRef]
- Hua, W.; Xu, X.; Zhang, X.; Yan, H.; Zhang, J. Progress in corrosion and anti-corrosion measures of phase change materials in thermal storage and management systems. J. Energy Storage 2022, 56, 105883. [Google Scholar] [CrossRef]
- Aulakh, J.S.; Joshi, D.P. Thermal and Anti-Leakage Performance of PCM for Thermal Energy Storage Applications. In Recent Advances in Nanotechnology; Khan, Z.H., Jackson, M., Salah, N.A., Eds.; ICNOC 2022; Springer Proceedings in Materials: Singapore, 2023; Volume 28, pp. 235–241. [Google Scholar]
- Tan, P.; Lindberg, P.; Eichler, K.; Löveryd, P.; Johansson, P.; Kalagasidis, A.S. Effect of phase separation and supercooling on the storage capacity in a commercial latent heat thermal energy storage: Experimental cycling of a salt hydrate PCM. J. Energy Storage 2020, 29, 101266. [Google Scholar] [CrossRef]
- Anand, A.; Shukla, A.; Kumar, A.; Buddhi, D.; Sharma, A. Cycle test stability and corrosion evaluation of phase change materials used in thermal energy storage systems. J. Energy Storage 2021, 39, 102664. [Google Scholar] [CrossRef]
- Ferrer, F.; Solè, A.; Barreneche, C.; Martorell, I.; Cabeza, L.F. Review on the methodology used in thermal stability characterization of phase change materials. Renew. Sustain. Energy Rev. 2015, 50, 665–685. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, A.; Fang, G. Review on thermal conductivity improvement of phase change materials with enhanced additives for thermal energy storage. J. Energy Storage 2022, 51, 104568. [Google Scholar] [CrossRef]
- Oliver, D.E.; Bissell, A.J.; Liu, X.; Tang, C.C.; Pulham, C.R. Crystallisation studies of sodium acetate trihydrate— suppression of incongruent melting and sub-cooling to produce a reliable, high-performance phase-change material. CrystEngComm 2021, 23, 700. [Google Scholar] [CrossRef]
- Li, Y.; Kumar, N.; Hirschey, J.; Akamo, D.O.; Li, K.; Tugba, T.; Goswami, M.; Orlando, R.; LaClair, T.J.; Graham, S.; et al. Stable salt hydrate-based thermal energy storage materials. Compos. B Eng. 2022, 233, 109621. [Google Scholar] [CrossRef]
- Beaupere, N.; Soupremanien, U.; Zalewski, L. Nucleation triggering methods in supercooled phase change materials (PCM), a review. Thermochim. Acta 2018, 670, 184–201. [Google Scholar] [CrossRef]
- Nandan, R.; Arumuru, V.; Das, M. An experimental investigation into PCM-integrated heat sinks under varying duty cycles. J. Energy Storage 2024, 97, 112905. [Google Scholar] [CrossRef]
- Xia, C.; Chen, G.; Bao, X.; Shi, J.; Cui, H.; Chen, X. Thermal performance of heat storage-enhanced PCM energy pipe pile with heat conduction fin. Appl. Therm. Eng. 2025, 272, 1126407. [Google Scholar] [CrossRef]
- Alehosseini, E.; Jafari, S.M. Micro/nano-encapsulated phase change materials (PCMs) as emerging materials for the food industry. Trends Food Sci. Technol. 2019, 91, 116–128. [Google Scholar] [CrossRef]
- Chakraborty, A.; Noh, J.; Mach, R.; Schamberger, P.; Yu, C. Thermal energy storage composites with preformed expanded graphite matrix and paraffin wax for long-term cycling stability and tailored thermal properties. J. Energy Storage 2022, 52, 104856. [Google Scholar] [CrossRef]
- Said, Z.; Pandey, A.K.; Tiwuari, A.K.; Kalidasan, B.; Jamil, F.; Thakur, A.K.; Tyagi, V.V.; Sari, A.; Ali, H.M. Nano-enhanced phase change materials: Fundamentals and applications. Prog. Energy Combust. Sci. 2024, 104, 101162. [Google Scholar] [CrossRef]
- Shchegolkov, A.; Schegolkov, A.; Karpus, N.; Kovalenko, V.; Kotok, V. Investigation of charge and discharge regimes of nanomodified heat-accumulating materials. East.-Eur. J. Enterp. Technol. 2017, 3, 23–29. [Google Scholar] [CrossRef][Green Version]
- Akamo, D.O.; Kumar, N.; Li, Y.; Pekol, C.; Li, K.; Goswami, M.; Hirschey, J.; LaClair, T.J.; Keffer, D.J.; Rios, O.; et al. Stabilization of low-cost phase change materials for thermal energy storage applications. iScience 2023, 26, 107175. [Google Scholar] [CrossRef]
- Kant, K.; Bowole, P.H.; Shamseddine, I.; Tlaiji, G.; Pennec, F.; Fardoun, F. Recent advances in thermophysical properties enhancement of phase change materials for thermal energy storage. Energy Mater. Sol. Cells 2021, 231, 111309. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F.; Chabani, I. Review on Nano Enhanced PCMs: Insight on nePCM Application in Thermal Management/Storage Systems. Energies 2023, 16, 1066. [Google Scholar] [CrossRef]
- Cabeza, L.F.; Barreneche, C.; Martorell, I.; Miró, L.; Sari-Bey, S.; Fois, M.; Paksoy, H.O.; Sahan, N.; Weber, R.; Constantinescu, M.; et al. Unconventional experimental technologies available for phase change materials (PCM) characterization. Part 1. Thermophysical properties. Renew. Sustain. Energy Rev. 2015, 43, 1399–1414. [Google Scholar] [CrossRef]
- Müller, L.; Rubio-Pérez, G.; Bach, A.; Muñoz-Rujas, N.; Aguilar, F.; Worlitschek, J. Consistent DSC and TGA Methodology as Basis for the Measurement and Comparison of Thermo-Physical Properties of Phase Change Materials. Materials 2020, 13, 4486. [Google Scholar] [CrossRef]
- Fatahi, H.; Claverie, J.; Poncet, S. Thermal Characterization of Phase Change Materials by Differential Scanning Calorimetry: A Review. Appl. Sci. 2022, 12, 12019. [Google Scholar] [CrossRef]
- Martínez, A.; Carmona, M.; Cortés, C.; Arauzo, I. Characterization of Thermophysical Properties of Phase Change Materials Using Unconventional Experimental Technologies. Energies 2020, 18, 4687. [Google Scholar] [CrossRef]
- Solé, A.; Neumann, H.; Niedermaier, S.; Martorell, I.; Schossig, P.; Cabeza, L.F. Stability of sugar alcohols as PCM for thermal energy storage. Sol. Energy Mater. Sol. Cells 2014, 126, 125–134. [Google Scholar] [CrossRef]
- Fernandéz, A.I.; Solé, A.; Giró-Paloma, J.; Martínez, M.; Hadjieva, M.; Boudenne, A.; Constantinescu, M.; Anghel, E.M.; Malikova, M.; Krupa, I.; et al. Unconventional experimental technologies used for phase change materials (PCM) characterization: Part 2—Morphological and structural characterization, physico-chemical stability and mechanical properties. Renew. Sustain. Energy Rev. 2015, 43, 1415–1426. [Google Scholar] [CrossRef]
- Huang, X.; Alva, G.; Jia, Y.; Fang, G. Morphological characterization and applications of phase change materials in thermal energy storage: A review. Renew. Sustain. Energy Rev. 2017, 72, 1128–1145. [Google Scholar] [CrossRef]
- Carmignato, S.; Dewulf, W.; Leach, R. Industrial X-Ray Computed Tomography; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Withers, P.J.; Bouman, C.; Carmignato, S.; Cnudde, V.; Grimaldi, D.; Hagen, C.K.; Maire, E.; Manley, M.; Du Plessis, A.; Stock, S.R. X-ray computed tomography. Nat. Rev. Methods Prim. 2021, 1, 18. [Google Scholar] [CrossRef]
- Vǎvrík, D.; Jakøubek, J.; Kumpova, I.; Pichotka, M. Laboratory based study of dynamical processes by 4D X-ray CT with sub-second temporal resolution. J. Instrum. 2017, 12, C02010. [Google Scholar] [CrossRef]
- Yuki, R.; Ohtake, Y.; Suzuki, H. Acceleration of X-ray computed tomography scanning with high-quality reconstructed volume by deblurring transmission images using convolutional neural networks. Precis. Eng. 2022, 73, 153–165. [Google Scholar] [CrossRef]
- du Pleiss, A.; Yadroitsev, I.; Yadroitsava, I.; Le Roux, S.G. X-Ray Microcomputed Tomography in Additive Manufacturing: A Review of the Current Technology and Applications. 3D Print. Addit. Manuf. 2018, 5, 227–247. [Google Scholar] [CrossRef]
- Sun, X.; Huang, L.; Xiao, B.G.; Zhang, Q.; Li, J.Q.; Ding, Y.H.; Fang, Q.H.; He, W.; Xie, H.M. X-ray computed tomography in metal additive manufacturing: A review on prevention, diagnostic, and prediction of failure. Thin Walled Struct. 2025, 207, 112736. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.; Braginsky, L.; Shklover, V.; Lawson, J.W. Correlation function analysis of fiber networks: Implications for thermal conductivity. Phys. Rev. B 2011, 84, 054208. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.; Fenk, B.; Gwerder, D.; Schiffmann, D.; Delgado-Diaz, W.; Stamatiou, A.; Fischer, L.J.; Schuetz, P. Flow Field Simulation and Measurement in Packed Beds Based on 4D-X-Ray Computed Tomography. Chem. Ing. Tech. 2023, 95, 792–796. [Google Scholar] [CrossRef]
- Gebhard, M.; Schnucklake, M.; Hilger, A.; Röhe, M.; Osenberg, M.; Krewer, U.; Manke, I.; Roth, C. X-Ray-Computed Radiography and Tomography Study of Electrolyte Invasion and Distribution inside Pristine and Heat-Treated Carbon Felts for Redox Flow Batteries. Energy Technol. 2020, 8, 1901214. [Google Scholar] [CrossRef]
- Feldkamp, L.; Davis, L.C.; Kress, J. Practical cone-beam algorithm. J. Opt. Soc. Am. 1984, 1, 612–619. [Google Scholar] [CrossRef]
- Available online: https://x-aid.de (accessed on 30 June 2025).
- Maire, E.; Withers, P.J. Quantitative X-ray tomography. Int. Mater. Rev. 2014, 59, 1–43. [Google Scholar] [CrossRef]
- Available online: https://www.hslu.ch/luci (accessed on 30 June 2025).
- Endrizzi, M. Practical cone-beam algorithm. Nucl. Instrum. Methods Phys. Res. Sect. A 2018, 878, 88–98. [Google Scholar] [CrossRef]
- Liu, J.; Qiao, X.; Gong, K.; Meng, F.; Zhang, C.; Zhou, Z. Enhanced image contrast in laboratory X-ray computed tomography for additive manufacturing by optimizing voltage based on transmission. NDT&E Int. 2025, 156, 103462. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, H.; Huang, K. Cupping artifacts correction for polychromatic X-ray cone-beam computed tomography based on projection compensation and hardening behavior. Biomed. Signal Process. Control 2020, 57, 101823. [Google Scholar] [CrossRef]
- Di Schiavi Trotta, L.; Matenine, D.; Martini, M.; Stierstorfer, K.; Lemaréchal, Y.; Francus, P. Després, P. Beam-hardening corrections through a polychromatic projection model integrated to an iterative reconstruction algorithm. NDT&E Int. 2022, 126, 102594. [Google Scholar]
- Martinez-Garcia, J.; Gwerder, D.; Schiffmann, D.; Thuering, T.; Jung, D.S.; Gkoumas, S.; Schuetz, P. Energy-selective X-ray CT imaging with an EIGER2 hybrid photon counting detector in a Diondo d2 XCT system. e-J. Nondestruct. Test. 2024, 29, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Davis, R.G.; Elliot, J.C. Artefacts in X-ray microtomography of materials. Mater. Sci. Technol. 2006, 22, 1011–1016. [Google Scholar] [CrossRef]
- Eggert, A.; Müller, M.; Nachtrab, F.; Dombrowski, J.; Rack, A.; Zabler, S. High-speed in-situ tomography of liquid protein foams. Int. J. Mater. Res. 2014, 105, 632–639. [Google Scholar] [CrossRef]
- Dziȩciołl, K.; Durmus, Y.E.; Tempel, H.; Kungl, H.; Bauer, A.; Eichel, R.-A. Laboratory X-ray computed tomography imaging protocol allowing the operando investigation of electrode material evolution in various environments. iScience 2023, 26, 107097. [Google Scholar] [CrossRef] [PubMed]
- Zwanenburg, E.A.; Williams, M.A.; Warnett, J.M. Review of high-speed imaging with lab-based X-ray computed tomography. Meas. Sci. Technol. 2021, 33, 012003. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.; Guarda, D.; Gwerder, D.; Ayra, A.; Fenk, B.; Stamatiou, A.; Worlitschek, J.; Sahi, M.; Schuetz, P. X-ray computed tomography image processing of solid-liquid PCMs with Geodict. In Proceedings of the GeoDict Innovation Conference 2024, Ramstein, Germany, 6–7 February 2024. [Google Scholar]
- Stamatiou, A.; Martinez-Garcia, J.; Ravotti, R.; O’Neill, P.; Fenk, B.; Guarda, D.; Mancin, S.; Gwerder, D.; Fischer, L.J.; Worlitschek, J.; et al. Using in-situ X-ray computed tomography to study the crystallization of salt hydrates. In Proceedings of the Eurotherm Seminar #116 “Innovative Solutions for Thermal Energy Storage Deployment, Lleida, Spain, 24–26 May 2023. [Google Scholar]
- Fenk, B.; Stamatiou, A.; Guarda, D.; Martinez-Garcia, J.; Schuetz, P.; Gwerder, D.; O’Neill, P.; Ravotti, R.; Mancin, S.; Fischer, L.; et al. Characterization of hydration levels of salt hydrate using X-ray computed tomography. J. Phys. Conf. Ser. 2024, 2766, 012230. [Google Scholar] [CrossRef]
- Arya, A.; Martinez-Garcia, J.; Schuetz, P.; Mahmoudi, A.; Brem, G.; Donkers, P.A.J.; Shahi, M. Characterizing Changes in a Salt Hydrate Bed Using Micro X-Ray Computed Tomography. J. Nondestruct. Eval. 2024, 43, 177. [Google Scholar] [CrossRef]
- Dannemand, M.; Delgado, M.; Lazaro, A.; Penalosa, C.; Gundlach, C.; Trinderup, C.; Johansen, J.B.; Moser, C.; Schranzhofer, H.; Furbo, S. Porosity and density measurements of sodium acetate trihydrate for thermal energy storage. Appl. Therm. Eng. 2018, 131, 707–714. [Google Scholar] [CrossRef]
- Feng, G.; Feng, Y.; Qiu, L.; Zhang, X. Evaluation of thermal performance for bionic porous ceramic phase change material using micro-computed tomography and lattice Boltzmann method. Int. J. Therm. Sci. 2022, 179, 107621. [Google Scholar] [CrossRef]
- Bajnóczy, G.; Pálffy, G.; Prépostffy, E. Thermal properties of a heat storage device containing sodium acetate trihydrate. Period. Polytech. Chem. Eng. 1995, 39, 129–135. [Google Scholar]
- Ma, Z.; Bao, H.; Roskilly, A.P. Study on solidification process of sodium acetate trihydrate for seasonal solar thermal energy storage. Sol. Energy Mater. Sol. Cells 2017, 172, 99–107. [Google Scholar] [CrossRef]
- Sgreva, N.R.; Noel, J.; Métivier, C.; Marchal, P.; Chaynes, H.; Isaiev, M.; Jannot, Y. Thermo-physical characterization of Hexadecane during the solid–liquid phase change. Thermochim. Acta 2022, 710, 179180. [Google Scholar] [CrossRef]
- Wu, Y.; Bamgbade, B.; Liu, K.; McHugh, M.A.; Baled, H.; Enick, R.M.; Burgess, W.A.; Tapriyal, D.; Morreale, B.D. Experimental measurements and equation of state modeling of liquid densities for long-chain n-alkanes at pressures to 265 MPa and temperatures to 523 K. Fluid Phase Equilib. 2011, 311, 17–24. [Google Scholar] [CrossRef]
- Vélez, C.; Khayet, M.; Ortiz, J.M. Temperature-dependent thermal properties of solid–liquid phase change even-numbered n-alkanes: n-Hexadecane, n-octadecane and n-eicosane. Appl. Energy 2015, 143, 383–394. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.; Gwerder, D.; Wahli, F.; Guarda, D.; Fenk, B.; Stamatiou, A.; Worlitschek, J.; Schuetz, P. Volumetric quantification of melting and solidification of phase change materials by in-situ X-ray computed tomography. J. Energy Storage 2023, 61, 106726. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.; Gwerder, D.; Guarda, D.; Fenk, B.; Stamatiou, A.; Worlitschek, J.; Schuetz, P. Study of the solidification behaviour of calcium chloride hexahydrate by in-situ X-ray computed tomography. In Proceedings of the 13th European Conference on Non-Destructive Testing 2023, Lisbon, Portugal, 3–7 July 2023; Volume 1. [Google Scholar]
- Guarda, D.; Martinez-Garcia, J.; Fenk, B.; O’Neill, P.; Ravotti, R.; Gwerder, D.; Stamatiou, A.; Worlitschek, J.; Mancin, S.; Schuetz, P. Analysis of the solidification and phase separation of calcium chloride hexahydrate with different water content by means of X-ray computed tomography. Sci. Talks 2025, 15, 100475. [Google Scholar] [CrossRef]
- Liao, S.; Zhou, X.; Chen, X.; Li, Z.; Yamashita, S.; Zhang, C.; Kita, H. Development of Macro-Encapsulated Phase-Change Material Using Composite of NaCl-Al2O3 with Characteristics of Self-Standing. Processes 2024, 12, 1123. [Google Scholar] [CrossRef]
- Ji, H.; Sellan, D.P.; Pettes, M.T.; Kong, X.; Ji, J.; Shi, L.; Ruoff, R.S. Enhanced thermal conductivity of phase change materials with ultrathin-graphite foams for thermal energy storage. Energy Environ. Sci. 2014, 7, 1185. [Google Scholar] [CrossRef]
- Kohler, T.; Kögl, T. Study of the Crystallization and Melting Behavior of a Latent Heat Storage by Computed Tomography. Chem. Ing. Tech. 2018, 90, 366–371. [Google Scholar] [CrossRef]
- Guarda, D.; Martinez-Garcia, J.; Fenk, B.; O’Neill, P.; Ravotti, R.; Gwerder, D.; Stamatiou, A.; Worlitschek, J.; Mancin, S.; Schuetz, P. X-ray computed tomography analysis of calcium chloride hexahydrate solidification. Appl. Therm. Eng. 2024, 252, 123618. [Google Scholar] [CrossRef]
- Martinez-Garcia, J.; Gwerder, D.; Wahli, F. Fully volumetric tracking of melting processes in phase change materials with computed tomography. In Proceedings of the 11th Conference on Industrial Computed Tomography (ICT), Wels, Austria, 8–11 February 2022. [Google Scholar]
- Guarda, D.; Wahli, F.; Gwerder, D.; Martinez-Garcia, J.; Stamatiou, A.; Worlitschek, J.; Mancin, S.; Schuetz, P. Phase Change Material numerical simulation:enthalpy-porosity model validation against liquid fraction data from an X-ray computed tomography measurement/system. Nondestruct. Test. Eval. 2022, 37, 508–518. [Google Scholar] [CrossRef]
- Guarda, D.; Martinez-Garcia, J.; Fenk, B.; Schiffmann, D.; Gwerder, D.; Stamatiou, A.; Worlitschek, J.; Mancin, S.; Schuetz, P. New liquid fraction measurement methodology for phase change material analysis based on X-ray computed tomography. Int. J. Therm. Sci. 2023, 194, 108585. [Google Scholar] [CrossRef]
- Uzan, A.Y.; Kozak, Y.; Korin, Y.; Haray, I.; Mehling, G.; Ziskind, G. A novel multi-dimensional model for solidification process with supercooling. Int. J. Heat Mass Transf. 2017, 106, 91–102. [Google Scholar] [CrossRef]
- Khattari, Y.; El Rhafiki, T.; Choab, N.; Kousksou, T.; Alaphilippe, M.; Zeraouli, Y. Apparent heat capacity method to investigate heat transfer in a composite phase change material. J. Energy Storage 2020, 28, 101239. [Google Scholar] [CrossRef]
- Voller, V.R. An enthalpy method for convection/diffusion phase change. Int. J. Numer. Methods Eng. 1987, 24, 271–284. [Google Scholar] [CrossRef]
- Voller, V.R.; Swaminathan, C.R.; Thomas, B.G. General source-based method for solidification phase change. Numer. Heat Transf. Part B Fundam. 1991, 19, 175–189. [Google Scholar] [CrossRef]
- Guarda, D.; Martinez-Garcia, J.; Fenk, B.; Gwerder, D.; Stamatiou, A.; Worlitschek, J.; Mancin, S.; Schuetz, P. X-ray computed tomography tracking of the calcium chloride hexahydrate crystallisation process. J. Phys. Conf. Ser. 2024, 2766, 012082. [Google Scholar] [CrossRef]
- Shmueli, H.; Ziskind, G.; Letan, R. Melting in a vertical cylindrical tube: Numerical investigation and comparison with experiments. Int. J. Heat Mass Transf. 2010, 53, 4082–4091. [Google Scholar] [CrossRef]
- Fornarelli, F.; Camporeale, S.M.; Fortunato, B.; Torresi, M.; Oresta, P.; Magliocchetti, L.; Miliozzi, A.; Santo, G. CFD analysis of melting process in a shell- and-tube latent heat storage for concentrated solar power plants. Appl. Energy 2016, 164, 712–722. [Google Scholar] [CrossRef]
- Müller, D.; Graetz, J.; Balles, A.; Stier, S.; Hanke, R.; Fella, C. Laboratory-Based Nano-Computed Tomography and Examples of Its Application in the Field of Materials Research. Crystals 2021, 11, 677. [Google Scholar] [CrossRef]






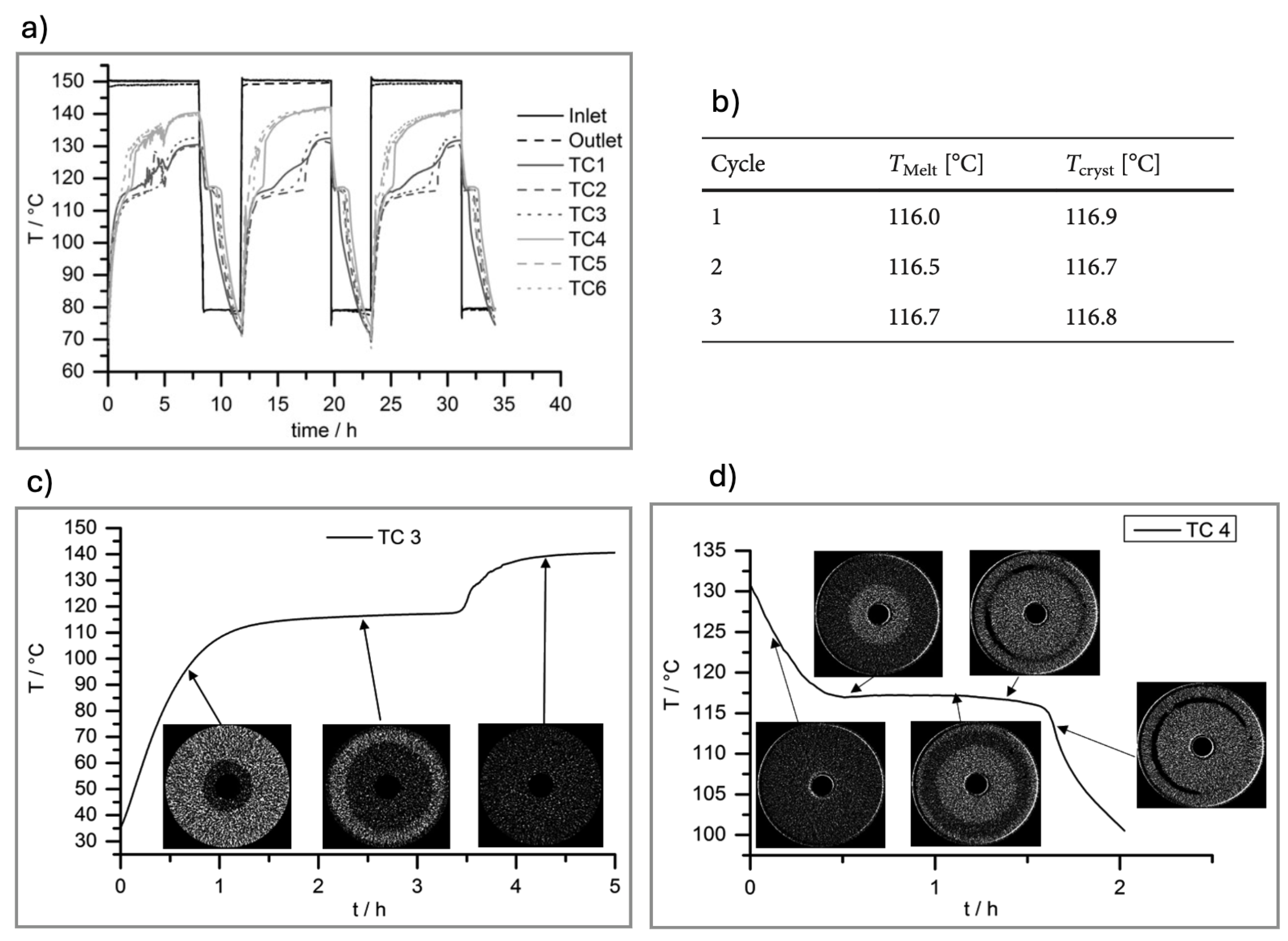







| PCM | * 100 (%) | Melting Point (°C) | Voltage (kV) | Tube Current (A) | Integration Time (s) | Frame Binning | No. Projections | SOD/SDD (mm/mm) | Voxel Size (µm) |
|---|---|---|---|---|---|---|---|---|---|
| CaCl2·6H2O [7,73] | 13.32 | 29 | 160 | 156 | 0.17 | 4 | 400 | 410/600 | 103 |
| SAT [73,74] | 11.72 | 58 | 160 | 156 | 0.13 | 6 | 2300 | 60/500 | 18 |
| Eicosane [75,76,77] | 10.25 | 36.4 | 120 | 270 | 0.12 | 3 | 330 | 155/462.6 | 103 |
| Hexadecane [75,76,77] | 7.78 | 18 | 120 | 270 | 0.11 | 3 | 400 | 155/463 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez-Garcia, J.; Guarda, D.; Gwerder, D.; Fenk, B.; Ravotti, R.; Mancin, S.; Stamatiou, A.; Worlitschek, J.; Fischer, L.J.; Schuetz, P. Applications of X-Ray Computed Tomography Technology to Solid–Liquid Phase Change Materials—A Review. Energies 2025, 18, 4704. https://doi.org/10.3390/en18174704
Martinez-Garcia J, Guarda D, Gwerder D, Fenk B, Ravotti R, Mancin S, Stamatiou A, Worlitschek J, Fischer LJ, Schuetz P. Applications of X-Ray Computed Tomography Technology to Solid–Liquid Phase Change Materials—A Review. Energies. 2025; 18(17):4704. https://doi.org/10.3390/en18174704
Chicago/Turabian StyleMartinez-Garcia, Jorge, Dario Guarda, Damian Gwerder, Benjamin Fenk, Rebecca Ravotti, Simone Mancin, Anastasia Stamatiou, Jörg Worlitschek, Ludger Josef Fischer, and Philipp Schuetz. 2025. "Applications of X-Ray Computed Tomography Technology to Solid–Liquid Phase Change Materials—A Review" Energies 18, no. 17: 4704. https://doi.org/10.3390/en18174704
APA StyleMartinez-Garcia, J., Guarda, D., Gwerder, D., Fenk, B., Ravotti, R., Mancin, S., Stamatiou, A., Worlitschek, J., Fischer, L. J., & Schuetz, P. (2025). Applications of X-Ray Computed Tomography Technology to Solid–Liquid Phase Change Materials—A Review. Energies, 18(17), 4704. https://doi.org/10.3390/en18174704









