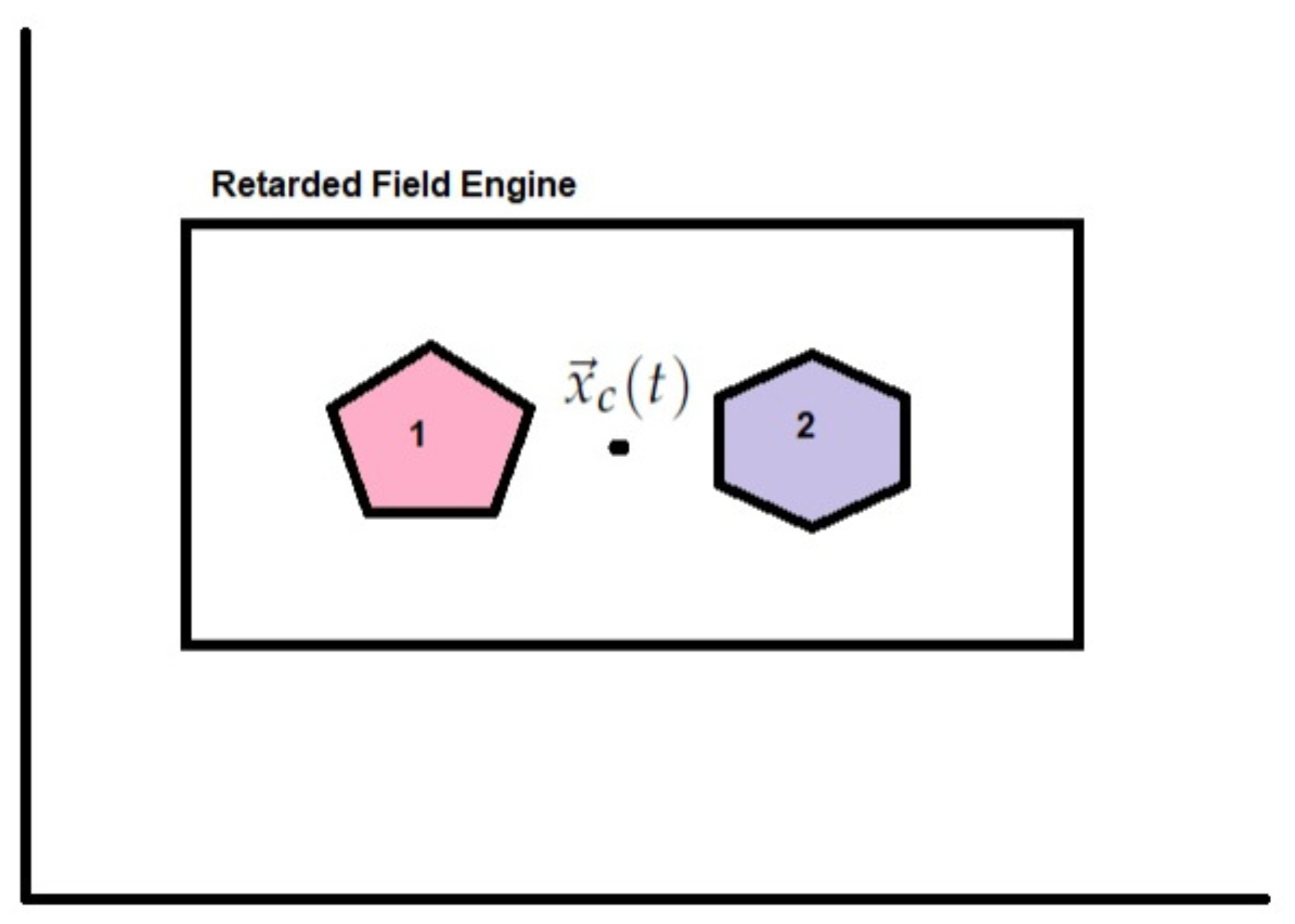
Appendix A
Equations (51) and (54) of [
13] provide detailed expressions for the zeroth-order term in the electric field expansion, which is just the Coulomb field:
Similarly,
where
and
define the relative position vectors:
By substituting Equations (A1) and (A2) into Equation (34), we obtain the following:
Applying the identities expressed as
the expression in Equation (A4) can be simplified as follows:
The same can be achieved by changing the order of integration in the following form:
Next, we compute the individual integral terms to simplify the above equation:
Using the Gaussian theorem and continuity equation, i.e.,
we obtain the following result:
The surface integral is applied over a surface encapsulating the volume of the volume integral. If the volume integral is applied over all space, the surface is at infinity. Provided that there are no currents at infinity. i.e.,
,
Substituting these identities into Equation (A7), we obtain the following:
Thus, the power contains two contributions:
and
We now make a change to the integration variable (
) in
; thus,
. We obtain the following:
We now present the complete expression for the power:
Appendix B
According to Equation (38), the field energy takes the following form:
Now, we separately solve the integral:
Using the identity expressed as
and taking into account the fact that [
3]
in which
is a three-dimensional delta function, we obtain the following:
The first term on the right is a divergence. Thus, using Gaussian theorem, its volume integral will become a surface integral, and the second term contains a delta function. This means that there is no contribution to the volume integral from the delta term unless
. Thus, Equation (A20) simplifies to
Let us look at the surface integral and assume that the system is contained inside an infinite sphere such that the surface integral is taken over a spherical surface of radius
:
where
, in which
is the solid angle. Furthermore,
,
, and
. It follows that
(see also Appendix A.1.2. of [
15] for a complete explanation of Equation (A25)). We simply conclude the following:
Hence, the expression for the field energy becomes the following:
Appendix C
We start by addressing the first integral in Equation (53):
According to Equations (51) and (54) of [
13], the second-order term in the electric field expansion is expressed as follows:
Inserting this in the
expression will result in the following:
We now change the integration variable (
) as before such that
Let us look at the following expression:
Based on the continuity (Equation (A9)) and taking into account the Gaussian theorem and the vanishing of current densities on a far-away encapsulating surface, it follows that
Thus, Equation (A33) takes the following form:
Upon substitution of Equation (A36) into Equation (A32), the resulting expression is
Exchanging indices 1 and 2, we obtain the second integral of Equation (53):
Combining Equations (A37) and (A38), we obtain the complete expression for the power:
Applying the product rule of derivatives, we obtain the following:
Appendix D
Equation (57) can be expressed as the sum of the following terms:
where
and
We now compute the integral of each term separately:
The relevant field expressions are provided in [
13] (as well as being previously mentioned in the current paper):
and
Substituting these field expressions into Equation (A45), we obtain the following:
which can also be expressed in the following form:
Let us look at the following expression:
Taking into account Equation (A229),
Substituting these integral forms into Equation (A51), we obtain the following:
Next, we simplify the second integral appearing in Equation (A49):
as is known from [
16]:
Subsequently, the required integral follows from a straightforward exchange of indices.
Inserting the evaluated integrals into Equation (A49) yields the following:
We now focus on the second term to enable further simplification:
In the above, we use Equations (A34) and (A35). By substituting this result into Equation (A60), we arrive at the following:
Notice that the following terms would be zero considering Equation (A9), the Gaussian theorem, and the null current densities at the convergence radius (
):
Hence, as the double integral in Equation (A62) decouples, it follows that
Analogously, the second integral in the field energy expression also nullifies:
Next, we calculate the third integral to finalize the field energy equation, employing Equation (61) of [
13]:
Applying the following vector identity expressed as
Equation (A68) can be rewritten as
Similar to Equation (A11), it can be shown that
Taking into account Equations (A27) and (A71), it follows that
Taking into account Equation (A235), we obtain the following:
The last equation sign is due to the fact that in the term containing , the volume integrals decouple; thus, according to Equation (A63), this term is null.
Appendix E
Following the approach used in the field energy analysis, the Poynting flux may, likewise, be represented as a sum of distinct terms, enabling the successive calculation of the corresponding integrals, i.e.,
such that
and
According to Equation (57) of [
13],
Let us now write an asymptotic expression for the second-order electric field:
According to Equation (A63), we have
Taking into account Equation (A243), we obtain the following:
The above expression decreases as
. According to Equation (62) of [
13],
Let us now write an asymptotic expression for the second-order magnetic field:
The above expression decreases as
. From Equations (A82) and (A84), it follows that the Poynting vector decays as
, and the associated surface integral over a large sphere with a radius of
, whose surface area grows as
, will decrease as
. Thus, provided
is large enough, we consider this contribution to be negligible, that is,
Next, we compute the third integral:
According to Equation (55) of [
13]:
Let us now write an asymptotic expression for the zeroth-order electric field:
As this vector is radially oriented, the cross product of the above with any other vector must be perpendicular to the radial direction. It follows that said cross product will have a zero scalar product with a radially oriented surface vector; thus,
Appendix F
Equations (51) and (54) of [
13] combine to yield the third-order terms in the electric field expansions:
We proceed to evaluate each integral individually.
Changing the order of integration, we obtain the following:
Let us look at the following expression:
in which we have changed the order of integrals and use the Einstein summation convention. Now, by continuity,
hence,
Inserting Equation (A100) into Equation (A97) and using the Gaussian theorem, we obtain the following:
Assuming a lack of currents on a far-away encapsulating surface, the above expression simplifies as follows:
Inserting Equation (A102) into Equation (A94), we obtain the following form:
We now change the integration variable (
). Thus,
, and also:
By switching the indices, we obtain the second integral:
Appendix G
As the first- and third-order electric field expression is given in Equation (A92), we now focus on the first integral in Equation (69):
By separating the terms, we obtain the following:
Using Equation (A5), we obtain the following:
since:
As
is a function of
and does not depend on
, it follows that
in which we use Gaussian theorem and assume, as usual, that there are no currents on the far-away encapsulating surface. Thus, it follows from Equation (A107) that
We now evaluate the following integral independently:
This can also be written in the following form:
Using Gaussian theorem, we can recast
in the following form:
Calculating the surface integral on a far-away spherical surface of radius
and assuming that all currents and charges are close to the origin of the axis with distances much smaller than
such that
and
, it follows that
Thus, Equation (A114) takes the following form:
At this point, we notice that up to rather small terms,
depends only on
and not on
; thus, we may partition the double integral given in Equation (A111) in the form of
because
(see Equation (A63)). Similarly,
Appendix H
For ease of computation, we divide the Poynting flux expression given in Equation (73) into four independent integrals:
We begin by evaluating the first integral:
Let us now write an asymptotic expression for the third-order electric field given in Equation (A92):
Using Equation (A63), we obtain
and an asymptotic expression for the second-order magnetic field:
In the above, we use the Einstein summation convention. Now, the radial unit vector can be written in Cartesian coordinates in the following form:
in which
is the azimuthal angle;
is the angle of latitude; and
, and
are unit vectors pointing in the direction of the Cartesian axes. Now,
As every non-diagonal element of
is calculated by integrating over a complete period, for a term containing either
or
, it follows that the non-diagonal elements of this matrix vanish. The remaining step is to calculate the diagonal elements:
Thus,
in which
is Kronecker’s delta. Inserting Equation (A130) into Equation (A124), it follows that
Analogously, the second integral of the Poynting flux takes the following form:
We now proceed to evaluate the third integral:
As referenced earlier, we adopt the electric and magnetic field expressions provided by [
13]:
and
Appendix I
For each of the terms appearing in Equation (83), we may write a Poynting flux; thus, we obtain the following:
Let us now calculate the first term (
):
Calculating the electric field on a far-away sphere, we may write Equation (77) in the following asymptotic form:
Taking into account Equation (A63), we obtain the following:
As current density integrals are related to charge density integrals through Equation (A243), it follows that
The asymptotic expression for
is given in Equation (A84). Using the asymptotic expressions, we are now in a position to calculate
. Taking into account the fact that radial components of neither the electric nor magnetic field contribute to the Poynting flux, we obtain the following expression:
Inserting Equation (A130) into Equation (A143), it follows that
Similarly, the second integral of the Poynting flux takes the following form:
We now proceed to calculate the following:
The fourth-order term of the magnetic field can be calculated using the asymptotic limit of Equation (61) of [
13]:
Using the asymptotic form of the second-order electric field given in Equation (A82) and recalling that the radial part of any field does not contribute to the Poynting flux, we now obtain the following:
Using Equation (A130), we obtain the following:
Subsequently, we calculate the fifth and sixth contributions appearing in Equation (A138):
The asymptotic form of the zeroth-order electric field is given in Equation (A89) and has only a radial component; hence, it follows that
Appendix J
Equation (87) can be separated into a sum of terms such that for each term, the integral is calculated separately, i.e.,
or in the following form:
The following simplifies the expression with the aid of Equation (A238):
Now, let us evaluate the following term:
which can also be written in the following form:
Using Gaussian theorem, we can recast
in the following form:
Calculating the surface integral on a far-away spherical surface of radius
and assuming that all currents and charges are close to the origin of the axis with distances much smaller than
such that
and
, we obtain the following:
Hence, using Equation (A238), it follows that
We now can write the triple volume integral given in Equation (A155) as a double volume integral:
Alternatively, it can be expressed more simply as
Now, for the
term, the double volume integrals decouple, and according to Equation (A63), we obtain the following:
Let us look at the following term:
This can be written in the following form:
Using Gaussian theorem and the continuity (Equation (A9)), this can be written as follows:
Assuming no currents at far-away surfaces, this reduces to the following:
Plugging
back into Equation (A164), we obtain the following:
In a similar fashion, the second integral of Equation (87) is obtained by interchanging the indices:
Next, using Equation (A30), we calculate the following:
which can be cast in the following form:
To reduce the above triple volume integral into a double volume integral, we notice that by using Equation (A238), it follows that
Exchanging the 1 and 2 indices, we obtain the following:
Taking into account Equation (A235), it follows that
The following integral can be computed using methods similar to those used in
Appendix L such that
Using Equations (A52) and (A53), we obtain the following:
Thus,
which can be slightly simplified as follows:
The
term decouples into a multiplication of two volume integrals and, thus, according to Equation (A63), vanishes; thus, we obtain the following:
The above can also be written in the following form:
Now:
in which we use Gaussian theorem and the continuity (Equation (A9)). Taking a far-away encapsulating surface in which no currents are to be found, it follows that
Plugging Equations (A183) and (A184) into Equation (A182), we obtain the following simplified expression:
In summary, the electric part of the fourth-order electromagnetic energy can be written in terms of the temporal derivatives of charge and current densities in the following form:
We remind the reader that
is the maximal radius for which Taylor-series expansion is applicable. The remaining step is to calculate the magnetic terms’ contributions, a task which we now attend to. First, we set
Now, according to Equation (61) of [
13],
Plugging Equations (A188) and (A189) into Equation (A187), it follows that
According to a well known vector identity, i.e.,
we may write Equation (A190) in the following form:
In the above, we have use the Gaussian theorem, assuming that there is no current density on far-away surfaces, and the continuity Equation (A9). Similarly,
Plugging Equations (A54), (A193) and (A194) into Equation (A192), we arrive at the following expression:
Taking into account Equation (A238), the above expression reduces as follows:
The term containing
decouples into a multiplication of two volume integrals. However, according to Equation (A63) and due to the fact that we assume no current density on the far-away encapsulating surface, it follows that
and
. Thus, we obtain a simplified form of Equation (A196):
Summing up Equations (A197) and (A198), we arrive at the fourth-order contribution to the magnetic field energy in terms of a double volume integral:
Appendix K
What follows is aimed at deriving the momentum (Equation (7)) as outline in [
13]. Using the expressions of the electric and magnetic fields given in [
13], we may now calculate the force that system 1 exerts on system 2 in the
order through the Lorentz force given in Equation (10) of [
13]:
It follows that for the zeroth order, we obtain the following:
Inserting Equation (55) of [
13], we obtain Coulomb’s force:
This type of force, which is just the quasi-static force, satisfies Newton’s third law; hence, the total force on the system is null:
The first-order force in
is null, since the first-order electric and magnetic fields are null; thus,
We now proceed with the calculation of the second-order force term; this will suffice, as
is a rather small number. To do this, we first divide the force given in Equation (A200) into electric and magnetic terms:
Inserting Equation (57) of [
13] into Equation (A205), we readily obtain the electric force as follows:
The magnetic force can be obtained by inserting Equation (62) of [
13] into Equation (A205):
However, given
it follows that
Let us look at the following integral:
Using Gaussian theorem and the continuity (Equation (A9)), we arrive at the following expression:
The surface integral is applied over a surface encapsulating the volume of the volume integral. If the volume integral is applied over all space, the surface is at infinity, provided there are no currents at infinity:
Inserting the result of Equation (A212) into Equation (A209), we arrive at the following expression for the second-order magnetic force:
We remark that for the magnetic field, the second order is the lowest order for the force, as the zeroth and first orders are null. Moreover, we observe that the force is the sum of two parts; the first one satisfies Newton’s third law, and the second does not. We can now calculate the total electromagnetic force by adding Equation (A206) to Equation (A213):
We now use the notation of
for clarity. Based on the above expressions, it is easy to calculate
by exchanging indices 1 and 2:
Combining Equations (A214) and (A215) and taking into account the fact that
, it follows that
Now, as
and since
it follows that
We remark that in some fast-changing systems, the second-order correction will not suffice and higher order terms will be needed. According to Newton’s second law, a system with a non-zero total force in its center of mass must have a change in its total linear momentum (
):
Assuming that
and that there are no current or charge densities at
, it follows from Equation (A218) that
which is the same as Equation (7).
Appendix L
We know that
, and as
is constant with respect to the
integration, it follows that
, so
Using spherical coordinates (
), i.e.,
we may write Equation (A221) in the following form:
We now recall the following definitions:
Using the above equation for
, we obtain the following:
Let us choose the
z axis in our spherical coordinates to be in the
direction.
Furthermore, let us expand as follows:
since
. We now introduce the dimensionless variable:
. Thus, Equation (A225) takes the following form:
Taking into account the solid angle expression given in Equation (A222), we finally obtain the following:
where
is the radius of a sphere whose surface is presumably far away from the charged systems and defines the limit when Taylor-series expansion is applicable.