High Fidelity 2-Way Dynamic Fluid-Structure-Interaction (FSI) Simulation of Wind Turbines Based on Arbitrary Hybrid Turbulence Model (AHTM)
Abstract
1. Introduction
2. Mathematical Formations and Numerical Methods
2.1. Fluid-Structure Interaction Approaches
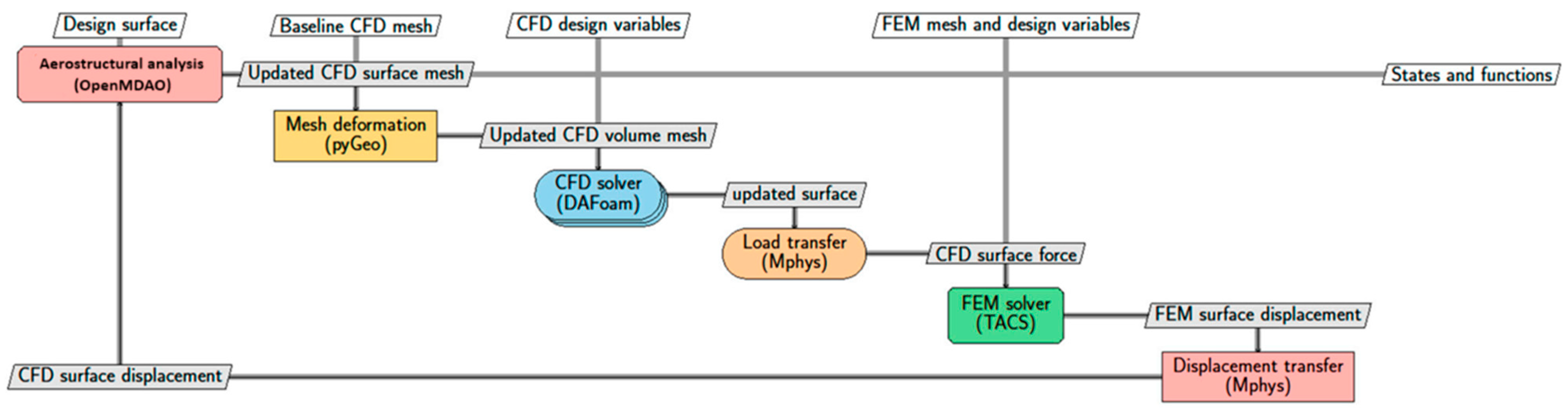
2.2. OpenMDAO/Mphys Coupling
2.3. Turbulence Models
2.3.1. RANS Model
2.3.2. LES Model
2.3.3. VLES Model
2.4. ALE Method for Dynamic FSI
2.5. PISO Algorithm
2.6. Shell Elements in TACS
Shell Volume Parametrization
3. Model Setup
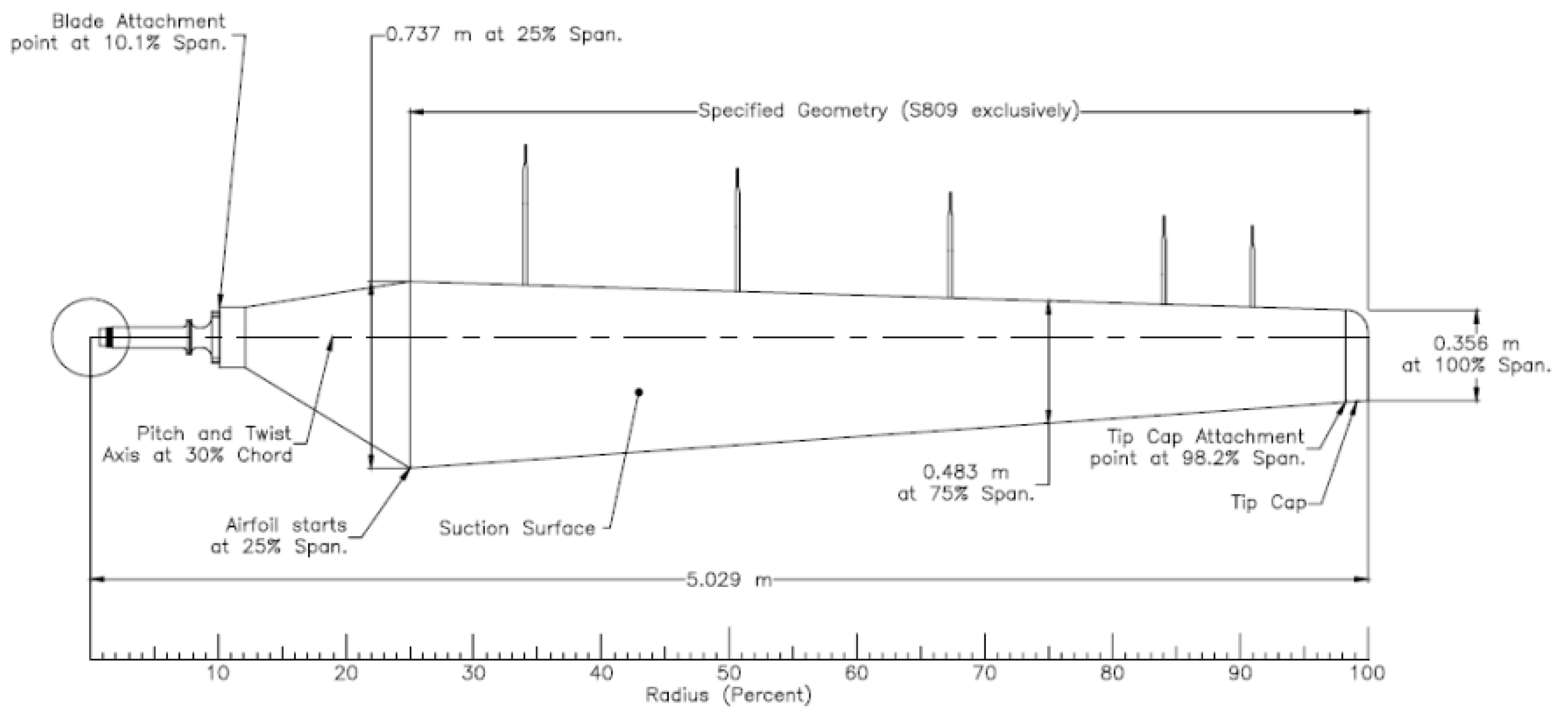
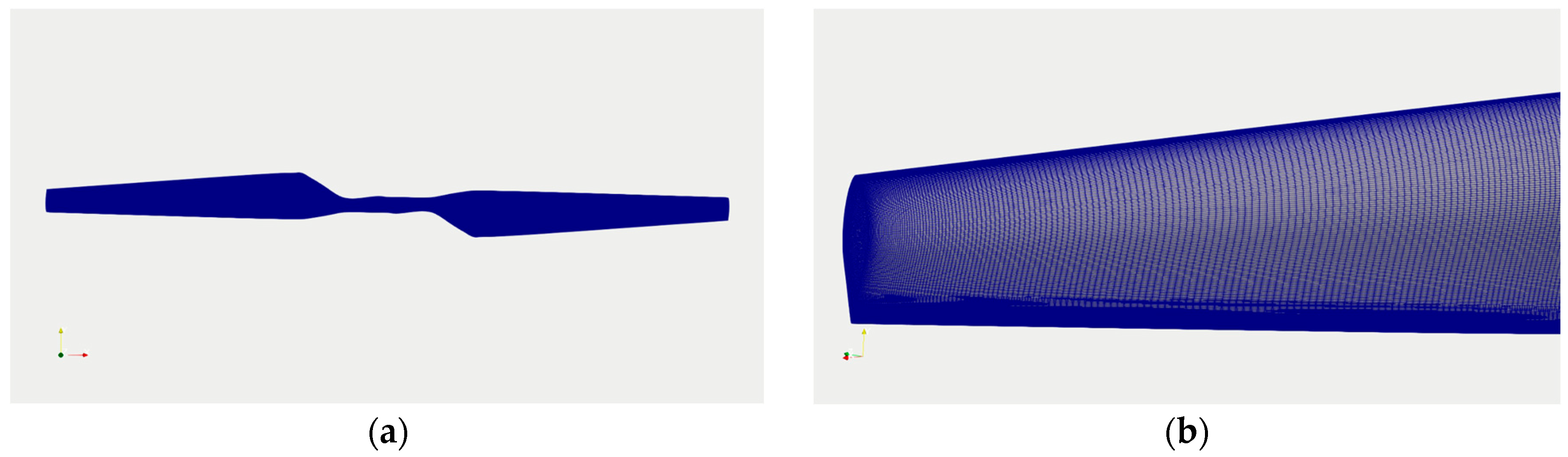
3.1. Fluid Model
3.2. Structural Model
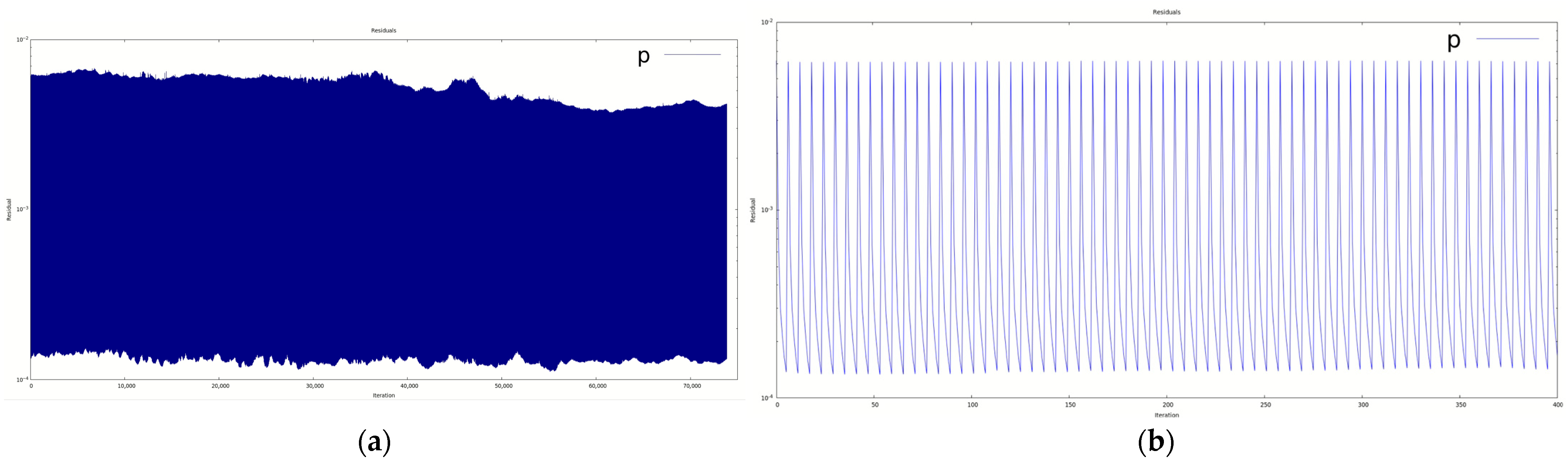
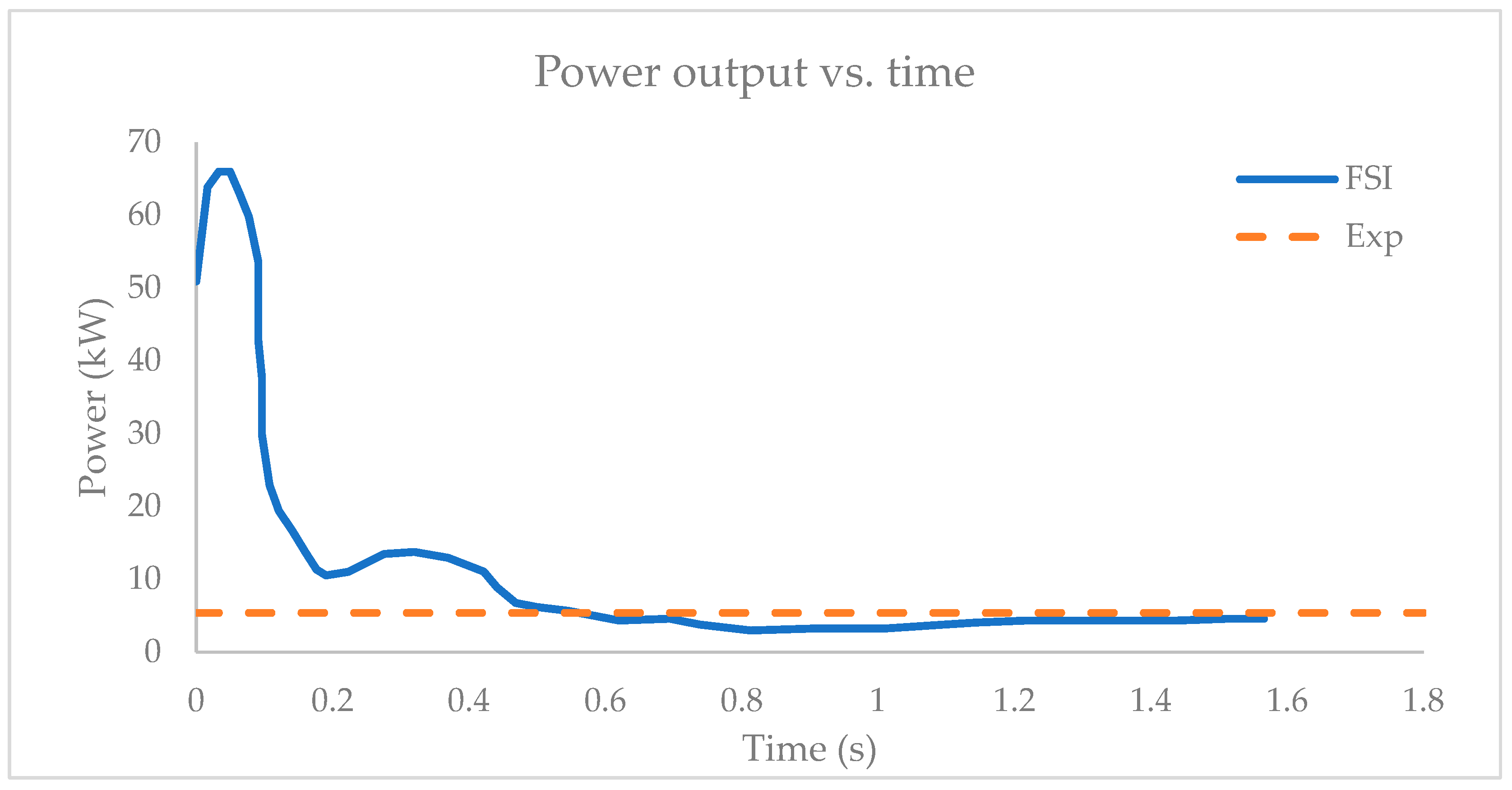
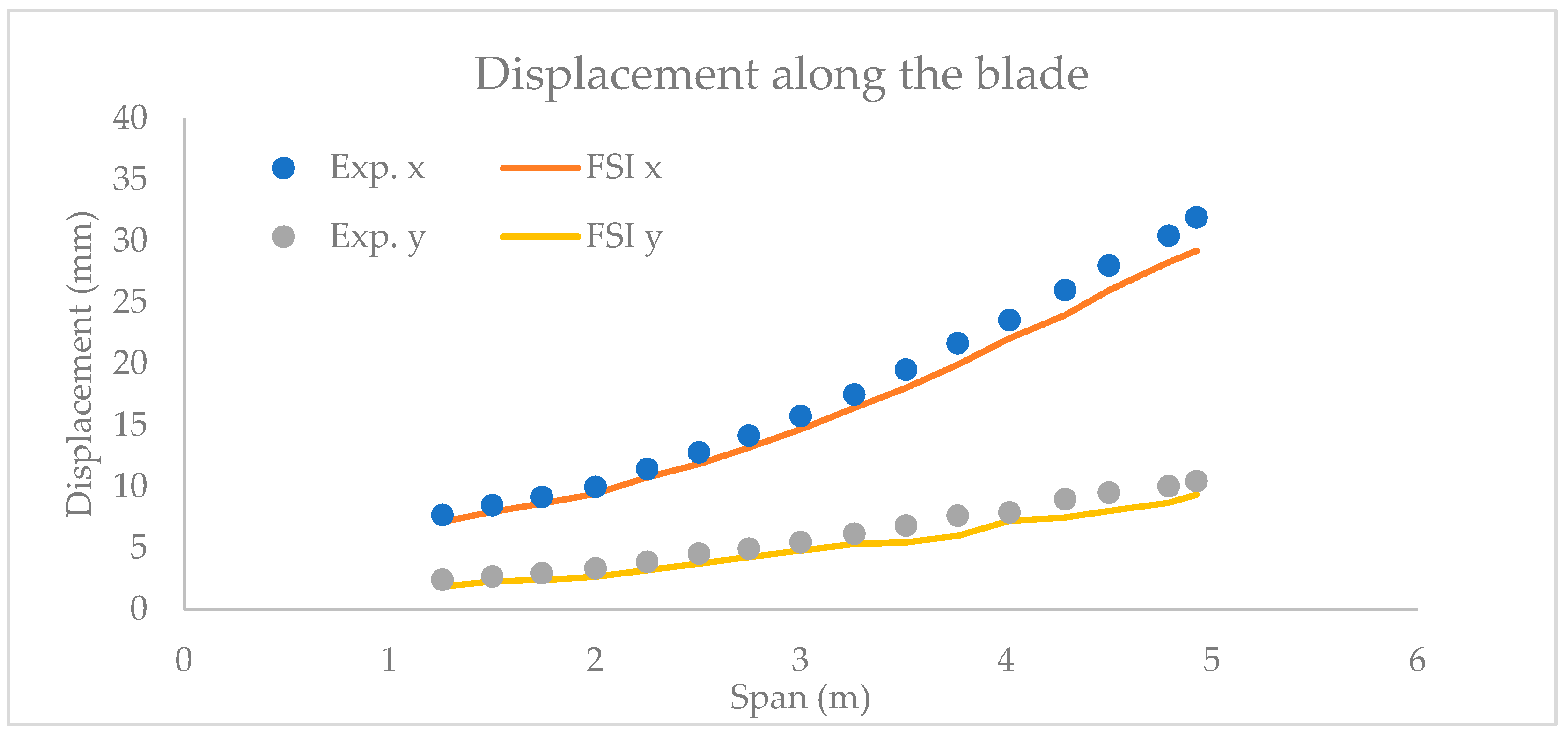
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Create a folder. For your convenience, use the same name everywhere.
- (In this case, it is named mykOmegaSST). Create file requires .H and .C files. (mykOmegaSST.H and my kOmegaSST.C)
- Use the following lines in your mykOmegaSST.H file.
- For mykOmegaSST.C file use the following lines.
- Then, it is required to create a makefile for this turbulence model. Name it makemykOmegaSSTIncompressible.C
- In the DAmykOmegaSST.C find change the following lines:
- Then, change these lines with the lines below:
- Add the following lines in section “Constructors”
- In DAmykOmegaSST.H file, add the lines below in section “SST parameters”
- Also, change the “TypeName” from “kOmegaSST”, to “mykOmegaSST”.
- Open the file_incompressible file and add the following lines:
- To recompile it run the “./Allmake incompressible” command in dafoam folder.
- After that, run the following commands in the terminal.
References
- Ren, Z.; Verma, A.S.; Li, Y.; Teuwen, J.J.; Jiang, Z. Offshore wind turbine operations and maintenance: A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 144, 110886. [Google Scholar] [CrossRef]
- Lee, Y.J.; Jhan, Y.T.; Chung, C.H. Fluid–structure interaction of FRP wind turbine blades under aerodynamic effect. Compos. Part B Eng. 2012, 43, 2180–2191. [Google Scholar] [CrossRef]
- Lee, K.; Huque, Z.; Kommalapati, R.; Han, S.E. Fluid-structure interaction analysis of NREL phase VI wind turbine: Aerodynamic force evaluation and structural analysis using FSI analysis. Renew. Energy 2017, 113, 512–531. [Google Scholar] [CrossRef]
- Hewitt, S.; Revell, A.; Margetts, L. A Novel Black-Box Massively Parallel Partitioned Approach to Fluid-Structure Interaction Problems. In Proceedings of the 24th UK Conference of the Association for Computational Mechanics in Engineering, Cardiff, UK, 31 March–1 April 2016. [Google Scholar]
- Xu, Z.; Wei, J.; Zhang, S.; Liu, Z.; Chen, X.; Yan, Q.; Guo, J. A state-of-the-art review of the vibration and noise of wind turbine drivetrains. Sustain. Energy Technol. Assess. 2021, 48, 101629. [Google Scholar] [CrossRef]
- Kim, D.H.; Lim, O.; Choi, E.H.; Noh, Y. Optimization of 5-MW wind turbine blade using fluid structure interaction analysis. J. Mech. Sci. Technol. 2017, 31, 725–732. [Google Scholar] [CrossRef]
- Zhangaskanov, D.; Batay, S.; Kamalov, B.; Zhao, Y.; Su, X.; Ng, E.Y.K. High-Fidelity 2-Way FSI Simulation of a Wind Turbine Using Fully Structured Multiblock Meshes in OpenFoam for Accurate Aero-Elastic Analysis. Fluids 2022, 7, 169. [Google Scholar] [CrossRef]
- Guma, G.; Bucher, P.; Letzgus, P.; Lutz, T.; Wüchner, R. High-fidelity aeroelastic analyses of wind turbines in complex terrain: FSI and aerodynamic modelling. Wind. Energy Sci. Discuss. 2022, 7, 1421–1439. [Google Scholar] [CrossRef]
- Kamalov, B.; Batay, S.; Zhangaskhanov, D.; Zhao, Y.; Ng, E.Y.K. Arbitrary Hybrid Turbulence Modeling (AHTM) Approach for High Fidelity NREL Phase VI Wind Turbine CFD Simulation. Fluids 2022, 7, 236. [Google Scholar] [CrossRef]
- Grinderslev, C.; González Horcas, S.; Sørensen, N.N. Fluid structure interaction simulation of a wind turbine rotor in complex flows, validated through field experiments. Wind Energy 2021, 24, 1426–1442. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Takizawa, K.; Tezduyar, T.E.; Hsu, M.C.; Kostov, N.; McIntyre, S. Aerodynamic and FSI analysis of wind turbines with the ALE-VMS and ST-VMS methods. Arch. Comput. Methods Eng. 2014, 21, 359–398. [Google Scholar] [CrossRef]
- Wang, L.; Quant, R.; Kolios, A. Fluid structure interaction modelling of horizontal-axis wind turbine blades based on CFD and FEA. J. Wind. Eng. Ind. Aerodyn. 2016, 158, 11–25. [Google Scholar] [CrossRef]
- Santo, G.; Peeters, M.; Van Paepegem, W.; Degroote, J. Fluid–structure interaction simulations of a wind gust impacting on the blades of a large horizontal axis wind turbine. Energies 2020, 13, 509. [Google Scholar] [CrossRef]
- Shi, F.; Wang, Z.; Zhang, J.; Gong, Z.; Guo, L. Influences of wind and rotating speed on the fluid-structure interaction vibration for the offshore wind turbine blade. J. Vibroeng. 2019, 21, 483–497. [Google Scholar] [CrossRef]
- Deng, Z.; Xiao, Q.; Huang, Y.; Yang, L.; Liu, Y. A general FSI framework for an effective stress analysis on composite wind turbine blades. Ocean. Eng. 2024, 291, 116412. [Google Scholar] [CrossRef]
- Gray, J.S.; Hwang, J.T.; Martins, J.R.R.A.; Moore, K.T.; Naylor, B.A. OpenMDAO: An open-source framework for multidisciplinary design, analysis, and optimization. Struct. Multidiscip. Optim. 2019, 59, 1075–1104. [Google Scholar] [CrossRef]
- Lafage, R.; Defoort, S.; Lefebvre, T. WhatsOpt: A web application for multidisciplinary design analysis and optimization. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019; p. 2990. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Springer: Cham, Switzerland, 2016; Volume 113. [Google Scholar] [CrossRef]
- Ridzuan, F.; Manshoor, B.; Omar, M.H.; Didane, D.H.; Abdelaal, M.A.; Amin, A. Aerodynamic Performance of NACA S809 Wind Turbine Blade Airfoil Using SST K-omega and K-epsilon Turbulence Models. J. Des. Sustain. Environ. 2024, 6, 36–42. [Google Scholar]
- Tachos, N.S.; Filios, A.E.; Margaris, D.P. A comparative numerical study of four turbulence models for the prediction of horizontal axis wind turbine flow. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 1973–1979. [Google Scholar] [CrossRef]
- Nichols, R. Applications of RANS/LES turbulence models. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003; p. 83. [Google Scholar]
- Taghinia, J.H.; Rahman, M.M.; Siikonen, T. A sub-grid scale model with natural near-wall damping. Aerosp. Sci. Technol. 2018, 74, 1–16. [Google Scholar] [CrossRef]
- Maulenkul, S.; Yerzhanov, K.; Kabidollayev, A.; Kamalov, B.; Batay, S.; Zhao, Y.; Wei, D. An Arbitrary Hybrid Turbulence Modeling Approach for Efficient and Accurate Automotive Aerodynamic Analysis and Design Optimization. Fluids 2021, 6, 407. [Google Scholar] [CrossRef]
- Stephens, D.; Sideroff, C.; Jemcov, A. A two equation VLES turbulence model with near-wall delayed behaviour. In Proceedings of the 7th Asia-Pacific International Symposium on Aerospace Technology, Cairns, QC, Australia, 25–27 November 2015; Volume 10. [Google Scholar]
- Tiwari, P.; Xia, Z.; Han, X. Comparison of VLES and LES turbulence modeling for swirling turbulent flow. J. Appl. Fluid Mech. 2020, 13, 1107–1116. [Google Scholar] [CrossRef]
- Liu, D.; Tang, W.; Wang, J.; Xue, H.; Wang, K. Comparison of laminar model, RANS, LES and VLES for simulation of liquid sloshing. Appl. Ocean. Res. 2016, 59, 638–649. [Google Scholar] [CrossRef]
- Mangani, L.; Buchmayr, M.; Darwish, M.; Moukalled, F. A fully coupled OpenFOAM® solver for transient incompressible turbulent flows in ALE formulation. Numer. Heat Transf. Part B Fundam. 2017, 71, 313–326. [Google Scholar] [CrossRef]
- Zhao, Y.; Su, X. Arbitrary Lagrangian–Eulerian (ALE) Method and Fluid-Structure Interaction. In Computational Fluid-Structure Interaction; Elsevier: Amsterdam, The Netherlands, 2019; pp. 127–144. [Google Scholar] [CrossRef]
- Issa, R. Solution of the implicit discretized fluid flow equations by operator splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Beam and Shell Elements in TACS—TACS Documentation. Available online: https://smdogroup.github.io/tacs/theory/shell_element.html (accessed on 25 May 2025).
- Abate, G.; Mavris, D.N.; Sankar, L.N. Performance effects of leading edge tubercles on the NREL Phase VI wind turbine blade. J. Energy Resour. Technol. 2019, 141, 051206. [Google Scholar] [CrossRef]
- Hsu, M.-C.; Akkerman, I.; Bazilevs, Y. Finite element simulation of wind turbine aerodynamics: Validation study using NREL Phase VI experiment. Wind. Energy 2014, 17, 461–481. [Google Scholar] [CrossRef]






| Boundary Conditions | k | nut | omega | P | U |
|---|---|---|---|---|---|
| Inlet | FixedValue | zeroGradient | FixedValue | zeroGradient | FixedValue |
| Outlet | zeroGradient | zeroGradient | zeroGradient | slip | zeroGradient |
| Cylinder | slip | nutkWallFunction | omegaWallFunction | zeroGradient | slip |
| Propeller MRF | kqRWallFunction | nutkWallFunction | omegaWallFunction | zeroGradient | fixedValue |
| Propeller AMI | cyclicAMI | cyclicAMI | cyclicAMI | cyclicAMI | cyclicAMI |
| AMI1 | cyclicAMI | cyclicAMI | cyclicAMI | cyclicAMI | cyclicAMI |
| AMI2 | cyclicAMI | cyclicAMI | cyclicAMI | cyclicAMI | cyclicAMI |
| Mesh | No. 1 | No. 2 | No. 3 | No. 4 |
|---|---|---|---|---|
| Number of cells | 17,131,110 | 24,078,878 | 36,932,383 | 54,937,248 |
| Error (%) | 10.1 | 8.22 | 3.86 | 0.9 |
| CPU time (h) | 254.6 | 365.2 | 602.5 | 950.3 |
| Property | Symbol | Value | Unit |
|---|---|---|---|
| Density | ρ | 2780.0 | kg/m3 |
| Elastic modulus | E | 73.1 × 109 | Pa |
| Poisson’s ratio | ν | 0.33 | — |
| Shear correction | k_corr | 5.0/6.0 | — |
| Yield stress | σ_y | 324.0 × 106 | Pa |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Nominal thickness | t | 0.010 | m |
| Minimum thickness | t_min | 0.002 | m |
| Maximum thickness | t_max | 0.050 | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarsenov, E.; Batay, S.; Baidullayeva, A.; Zhao, Y.; Wei, D.; Ng, E.Y.K. High Fidelity 2-Way Dynamic Fluid-Structure-Interaction (FSI) Simulation of Wind Turbines Based on Arbitrary Hybrid Turbulence Model (AHTM). Energies 2025, 18, 4401. https://doi.org/10.3390/en18164401
Sarsenov E, Batay S, Baidullayeva A, Zhao Y, Wei D, Ng EYK. High Fidelity 2-Way Dynamic Fluid-Structure-Interaction (FSI) Simulation of Wind Turbines Based on Arbitrary Hybrid Turbulence Model (AHTM). Energies. 2025; 18(16):4401. https://doi.org/10.3390/en18164401
Chicago/Turabian StyleSarsenov, Erkhan, Sagidolla Batay, Aigerim Baidullayeva, Yong Zhao, Dongming Wei, and Eddie Yin Kwee Ng. 2025. "High Fidelity 2-Way Dynamic Fluid-Structure-Interaction (FSI) Simulation of Wind Turbines Based on Arbitrary Hybrid Turbulence Model (AHTM)" Energies 18, no. 16: 4401. https://doi.org/10.3390/en18164401
APA StyleSarsenov, E., Batay, S., Baidullayeva, A., Zhao, Y., Wei, D., & Ng, E. Y. K. (2025). High Fidelity 2-Way Dynamic Fluid-Structure-Interaction (FSI) Simulation of Wind Turbines Based on Arbitrary Hybrid Turbulence Model (AHTM). Energies, 18(16), 4401. https://doi.org/10.3390/en18164401









