Distribution Network Situational Awareness Prediction Based on Spatio-Temporal Attention Dynamic Graph Neural Network
Abstract
1. Introduction
- Insufficient exploration of spatio-temporal dynamic correlations. Distribution networks are complex systems with spatio-temporal coupling, whose operation state not only changes over time but is also affected by spatial location. However, most existing methods [4,5,6,7] only consider the time-series dimension of distribution network data and fail to fully consider the spatial correlations of distribution networks. Neglecting the spatio-temporal dynamic correlations will result in the model being unable to comprehensively capture the operating patterns of distribution networks, thereby affecting the accuracy of the prediction.
- Insufficient adaptability of dynamic topology structures. Distribution networks are subject to complex and variable loads and faults, and dynamic changes in topology structures (such as fault disconnections, additional loads, equipment maintenance, etc.) may occur at any time [8]. It is difficult for traditional modeling methods based on fixed topology structures to adapt to such dynamic changes, and they cannot accurately reflect the actual operation state of distribution network.
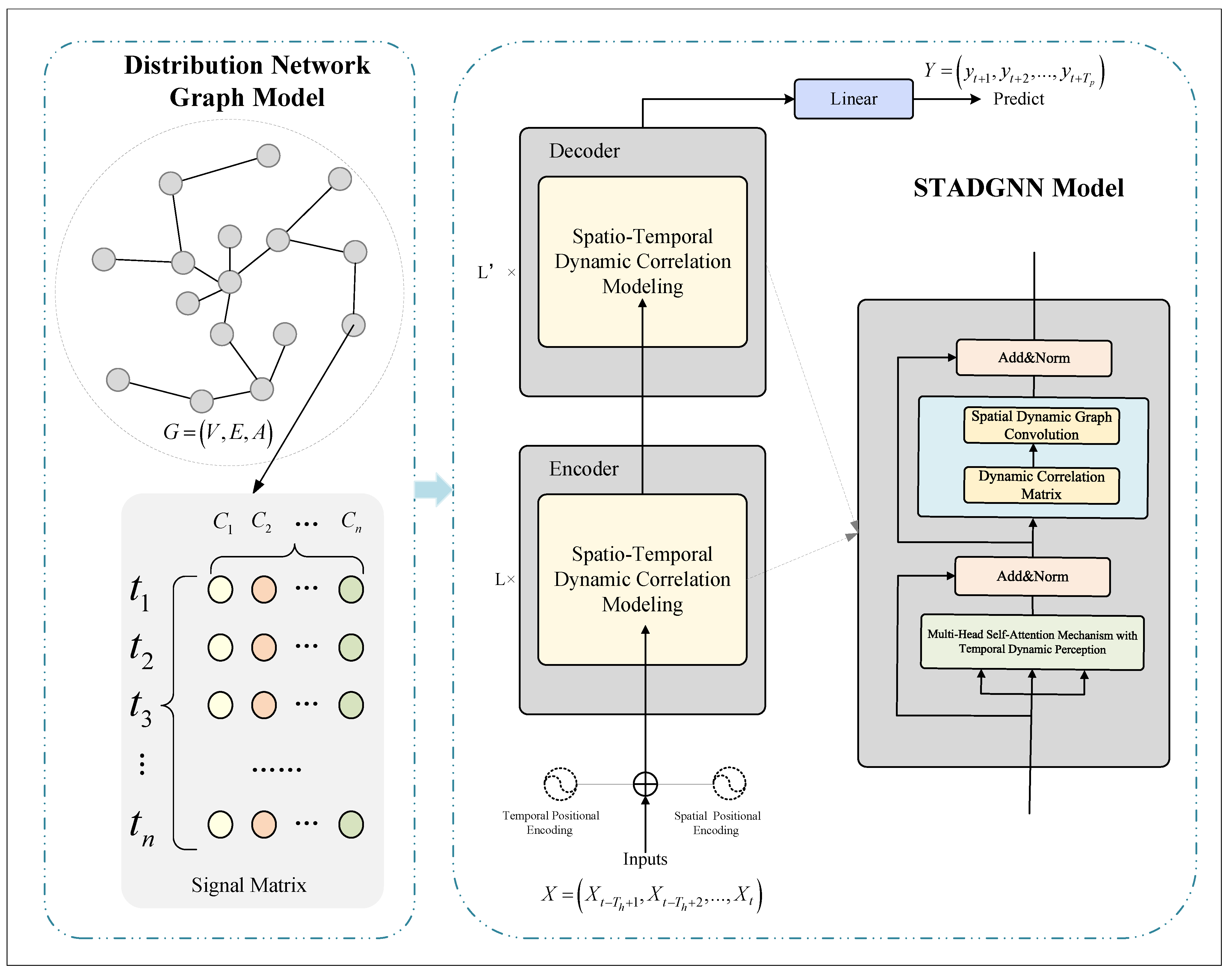
2. The Security Situational Awareness System Model
2.1. Distribution Network Graph Model
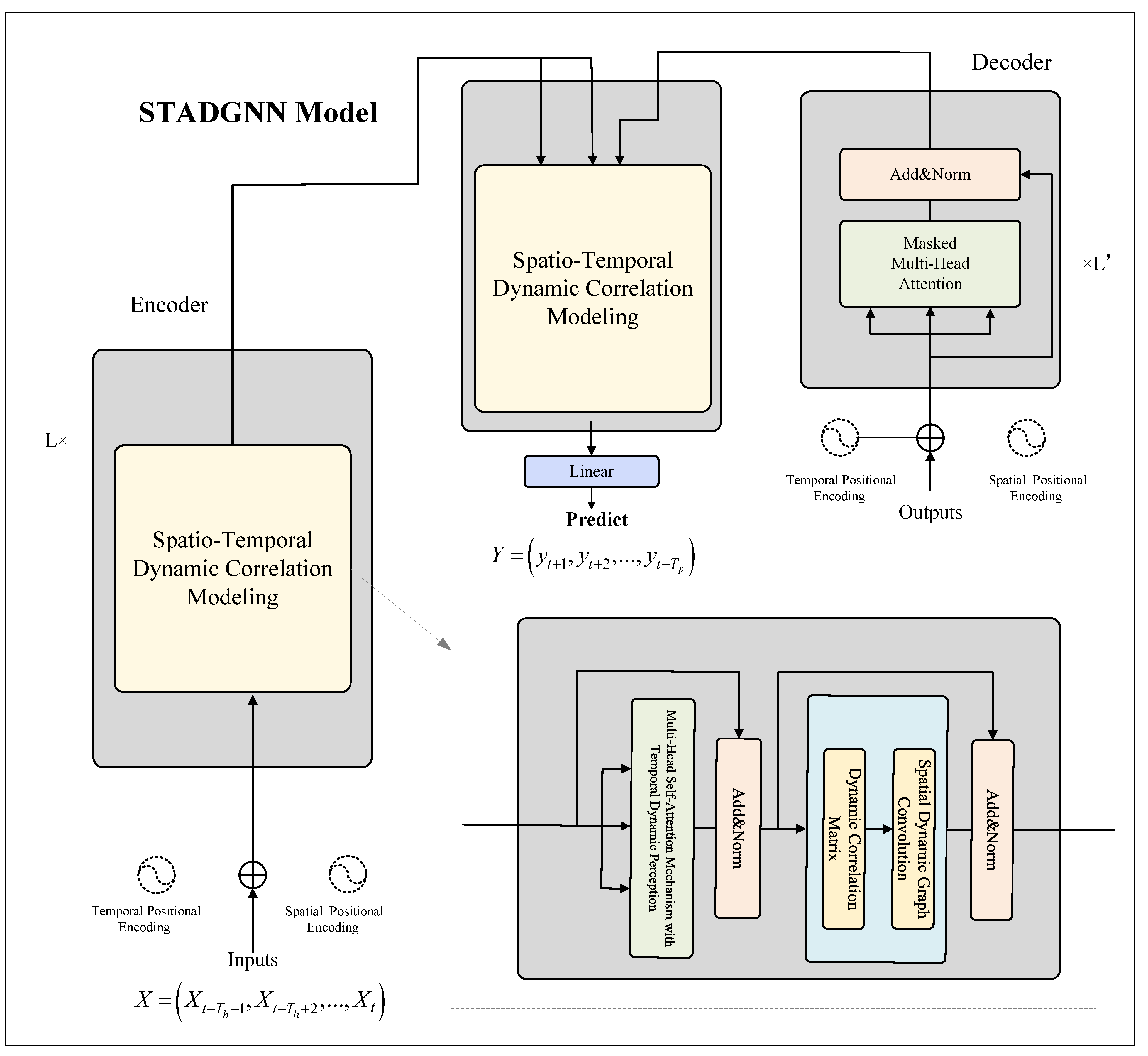
2.2. STADGNN Model
2.2.1. Multi-Head Self-Attention Mechanism with Temporal Dynamic Perception
2.2.2. Dynamic Correlation Matrix
2.2.3. Spatial Dynamic Graph Convolution
2.2.4. Spatio-Temporal Position Embedding Module
2.3. Distribution Network Situational Awareness Based on the STADGNN Model
2.3.1. Distribution Network Security Situational Assessment Indicators
2.3.2. Distribution Network Situational Awareness Process Based on the STADGNN Model
3. Experiments and Analysis
3.1. Datasets and Evaluation Metrics
3.2. Parameter Details and Baseline Methods
- (1)
- CNN: convolutional neural network.
- (2)
- LSTM [4]: long short-term memory network, a special type of RNN model.
- (3)
- LSTMGC [9]: a hybrid model combining long short-term memory networks and graph convolutional networks.
- (4)
- EMA-SVD-Elman [7]: Elman neural network combined with the EMD-SVD method.
- (5)
- MSTGCN [9]: multi-component spatio-temporal graph convolutional network.
- (6)
- ASTGCN [9]: attention-based spatio-temporal graph convolutional network. Adds spatio-temporal attention to the MSTGCN.
- (7)
- LSTMA [5]: a long short-term memory network combined with an attention mechanism.
- (8)
- TPA-BiLSTM [6]: a model based on temporal pattern attention mechanisms and a bidirectional long short-term memory network.
3.3. Analysis of Experimental Results
3.3.1. Prediction Effectiveness Testing
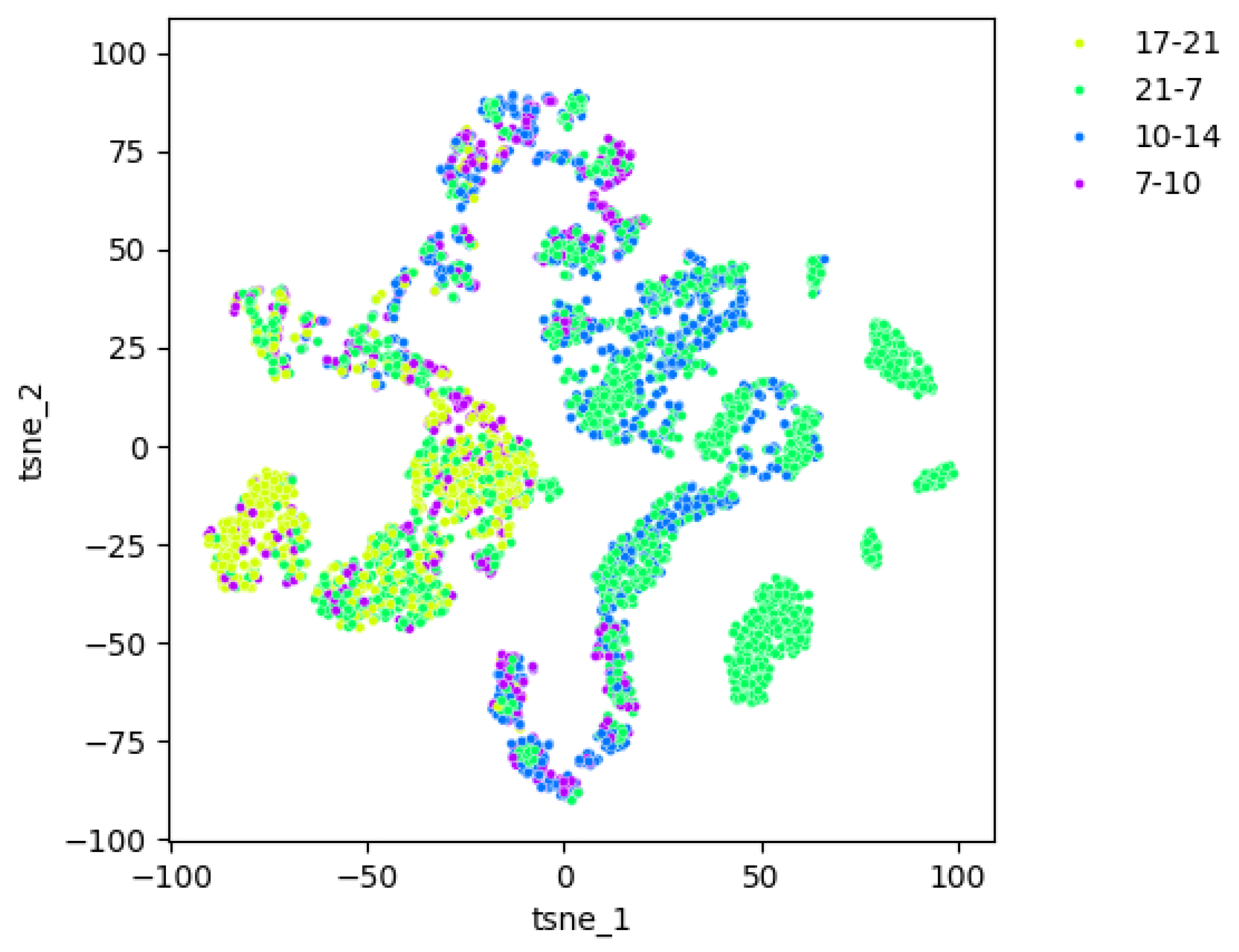
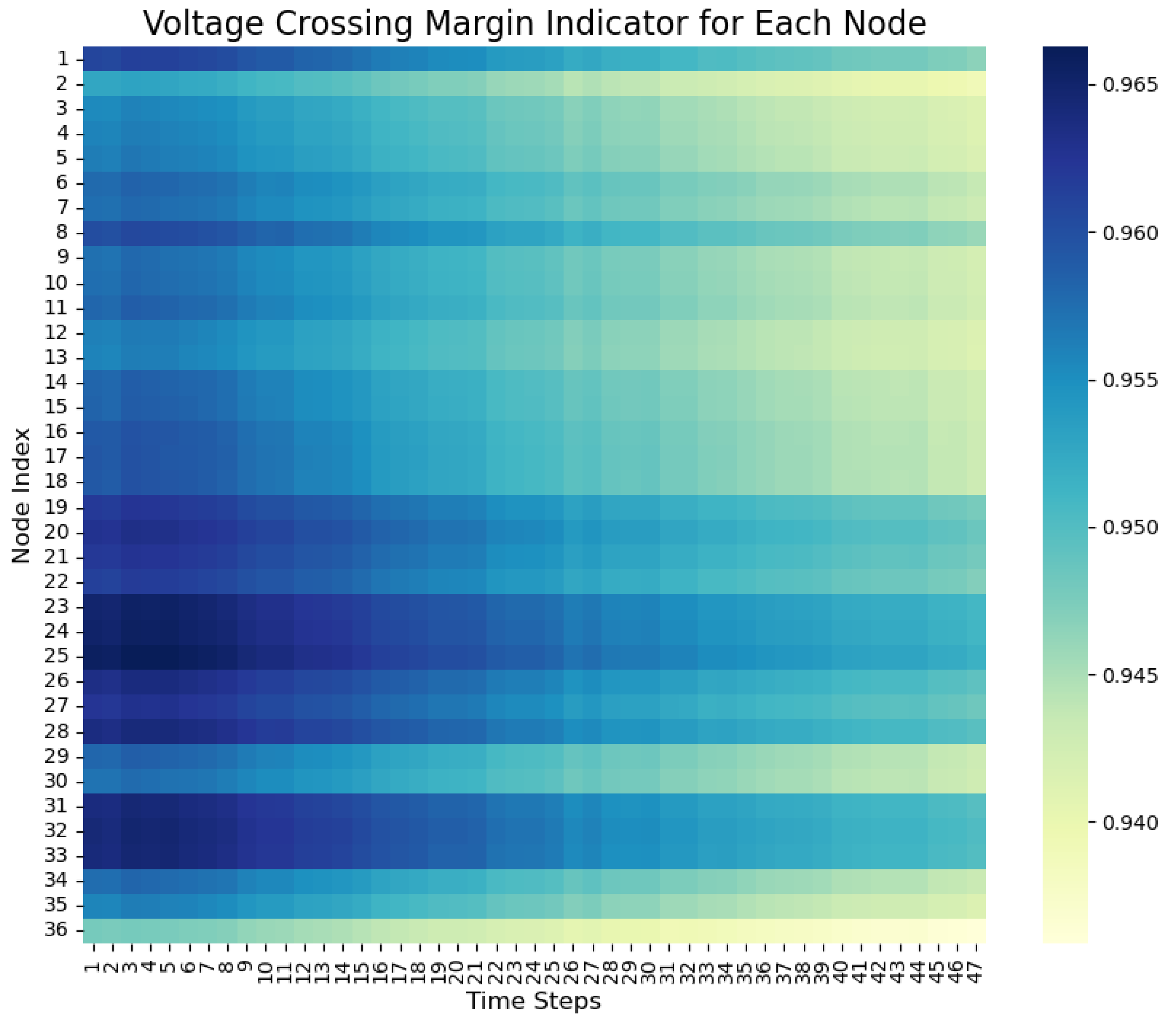
3.3.2. Situation Indicators Testing
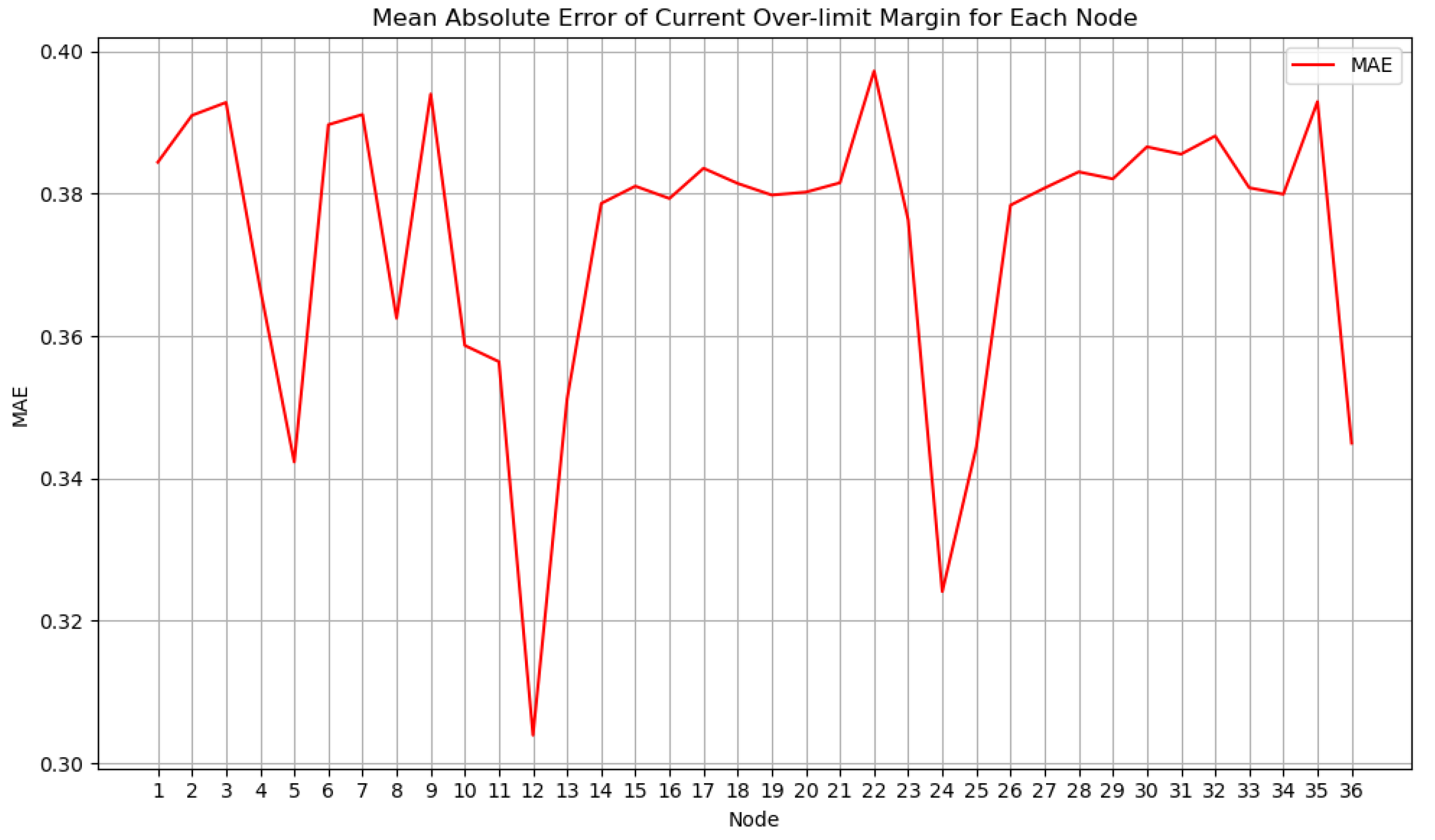
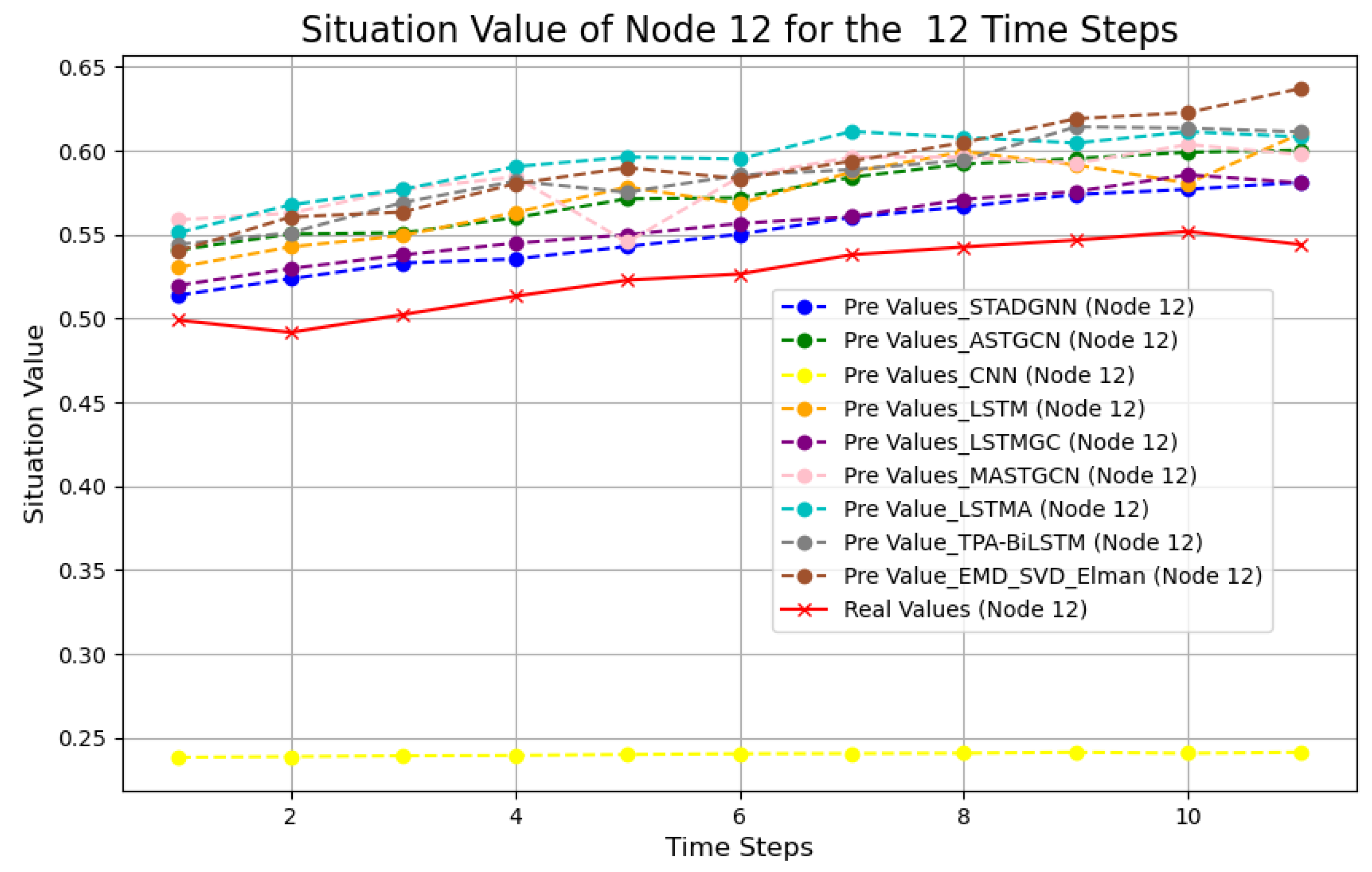
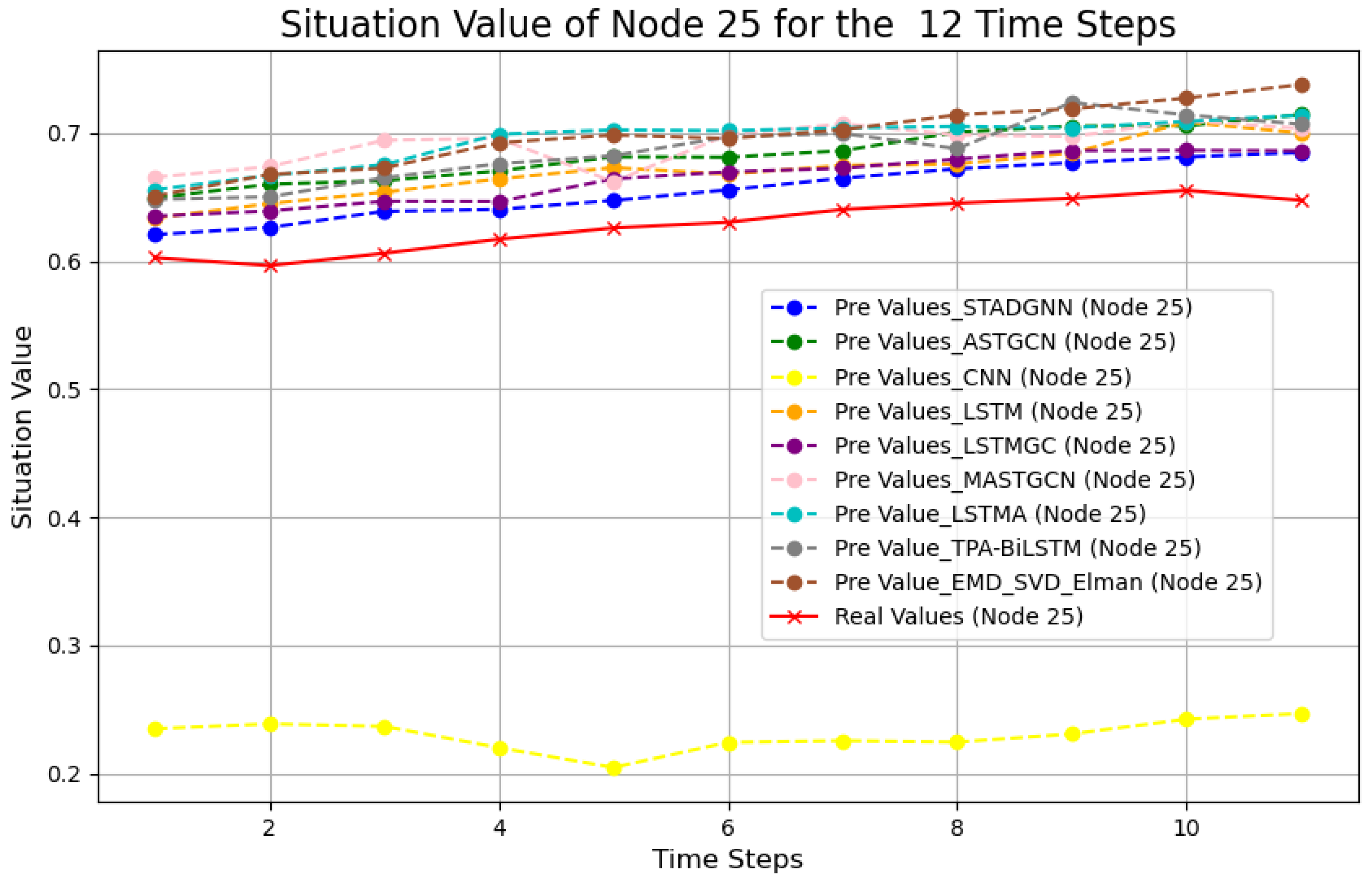
3.3.3. Node Assessment Values
3.3.4. The Ablation Experiments
- (1)
- No Temporal Position Embedding–STADGNN (noTE-STADGNN): It removes the role of temporal position embedding to study the modeling of sequential information of sequences;
- (2)
- No Temporal Dynamic Perception–STADGNN (noTDP-STADGNN): It replaces a multi-head self-attention module with temporal dynamic perception with a conventional multi-head self-attention module to investigate the role of taking dynamic perception into account in prediction.
- (3)
- No Spatial Position Embedding–STADGNN (noSE-STADGNN): It removes spatial position embedding to investigate the role of modeling the inherent static spatial features of distribution networks;
- (4)
- No Spatial Dynamic Correlation Matrix–STADGNN (noSDCM-STADGNN): It removes the spatial dynamic correlation matrix in order to study the role of dynamically adjusting the strength of the spatial correlation instead of basing it solely on static topological relations.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sonal; Ghosh, D. Impact of situational awareness attributes for resilience assessment of active distribution networks using hybrid dynamic Bayesian multi criteria decision-making approach. Reliab. Eng. Syst. Saf. 2022, 228, 108772. [Google Scholar] [CrossRef]
- Ge, L.J.; Li, Y.L.; Li, Y.L.; Yan, J.; Sun, Y.H. Smart Distribution Network Situation Awareness for High-Quality Operation and Maintenance: A Brief Review. Energies 2022, 15, 828. [Google Scholar] [CrossRef]
- Fang, Z.; Lin, Y.; Song, S.; Li, C.; Lin, X.; Chen, Y. State Estimation for Situational Awareness of Active Distribution System With Photovoltaic Power Plants. IEEE Trans. Smart Grid 2021, 12, 239–250. [Google Scholar] [CrossRef]
- Tian, S.X.; Li, K.P.; Wei, S.R.; Fu, Y.; Li, Z.K.; Liu, S. Security Situation Awareness Approach for Distribution Network Based onSynchronous Phasor Measurement Unit. Proc. CSEE 2021, 41, 617–632. (In Chinese) [Google Scholar] [CrossRef]
- Xie, Z.J.; Zhang, D.X.; Han, X.Q.; Hu, W. Research on Transient Stability Assessment Method of Power System Based on Improved Long Short Term Memory Network. Power Syst. Technol. 2024, 48, 998–1010. (In Chinese) [Google Scholar] [CrossRef]
- Xu, F.Q.; Li, Q.S.; Song, L.; Zheng, Z.X.; Chen, X.; Hu, Q. Situation Awareness of Distribution Network Based on TPA-BiLSTM. In Proceedings of the 2024 7th International Conference on Renewable Energy and Power Engineering (REPE), Beijing, China, 25–27 September 2024; pp. 80–84. [Google Scholar] [CrossRef]
- Luo, Y.H.; Cheng, Q.; Yan, S.J.; Yang, D.S. Situation awareness method of the distribution network based on EMD-SVD and Elman neural network. Energy Rep. 2022, 8, 632–639. [Google Scholar] [CrossRef]
- Huang, M.Y.; Guo, J.W.; Zang, H.X.; Fang, X.C.; Wei, Z.N.; Sun, G.Q. State Estimation of Power System Based on a Message Passing Neural Network. Power Syst. Technol. 2023, 47, 4396–4409. (In Chinese) [Google Scholar] [CrossRef]
- Guo, S.N.; Lin, Y.F.; Feng, N.; Song, C.; Wan, H.Y. Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting. Proc. AAAI Conf. Artif. Intell. 2019, 33, 922–929. [Google Scholar] [CrossRef]
- Khodayar, M.; Wang, J. Spatio-Temporal Graph Deep Neural Network for Short-Term Wind Speed Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 670–681. [Google Scholar] [CrossRef]
- Simeunović, J.; Schubnel, B.; Alet, P.J.; Carrillo, R.E.; Frossard, P. Interpretable temporal-spatial graph attention network for multi-site PV power forecasting. Appl. Energy 2022, 327, 120127. [Google Scholar] [CrossRef]
- Li, Z.; Ye, L.; Zhao, Y.; Pei, M.; Lu, P.; Li, Y.; Dai, B. A Spatiotemporal Directed Graph Convolution Network for Ultra-Short-Term Wind Power Prediction. IEEE Trans. Sustain. Energy 2023, 14, 39–54. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Ren, C.; Zhan, Z.; Wang, T.; Ma, D. Short-Term Load Forecasting Based on Spatial-Temporal Correlation for Virtual Power Plant. In Proceedings of the 2024 3rd International Conference on Power Systems and Electrical Technology (PSET), Tokyo, Japan, 5–8 August 2024; pp. 791–796. [Google Scholar] [CrossRef]
- Jiang, H.; Dong, Y.; Dong, Y.; Wang, J. Power load forecasting based on spatial–temporal fusion graph convolution network. Technol. Forecast. Soc. Change 2024, 204, 123435. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems—Volume 2 (NIPS’14), Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the Locality and Breaking the Memory Bottleneck of Transformer on Time Series Forecasting. In Proceedings of the Advances in Neural Information Processing Systems 33, Volume 7 of 20: 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Guo, S.N.; Lin, Y.F.; Wan, H.Y.; Li, X.C.; Cong, G. Learning dynamics and heterogeneity of spatial-temporal graph data for traffic forecasting. IEEE Trans. Knowl. Data Eng. 2021, 34, 5415–5428. [Google Scholar] [CrossRef]
- Li, Q.M.; Han, Z.C.; Wu, X.M. Deeper insights into graph convolutional networks for semi-supervised learning. Proc. AAAI Conf. Artif. Intell. 2018, 32. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, H.; Ge, Y.; Gao, W.; Li, J.; Su, B.; Cheng, K. Reliability Evaluation of Distribution Network Based on Situation Awareness. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 2043–2048. [Google Scholar] [CrossRef]
- Ge, L.; Li, Y.; Li, S.; Zhu, J.; Yan, J. Evaluation of the situational awareness effects for smart distribution networks under the novel design of indicator framework and hybrid weighting method. Front. Energy 2021, 15, 143–158. [Google Scholar] [CrossRef]
- Lin, Y.F.; Wang, X.Y. A Data-Driven Scheme Based on Sparse Projection Oblique Randomer Forests for Real-Time Dynamic Security Assessment. IEEE Access 2022, 10, 79469–79479. [Google Scholar] [CrossRef]
- Yang, H.Y.; Zeng, R.Y.; Xu, G.Q.; Zhang, L. A network security situation assessment method based on adversarial deep learning. Appl. Soft Comput. 2021, 102, 107096. [Google Scholar] [CrossRef]





| Parameters | Value |
|---|---|
| Model dimension () | 64 |
| Number of attention heads (h) | 8 |
| Learning rate () | 0.001 |
| Number of encoder layers (L) | 3 |
| Number of decoder layers () | 3 |
| Size of the convolution kernel (k) | 3 |
| Epochs | 100 |
| Batch size | 32 |
| Dropout rate () | 0.005 |
| Model | MAE | RMSE | MAPE |
|---|---|---|---|
| STADGNN | 0.0103 | 0.0247 | 3.4222 |
| ASTGCN | 0.0108 | 0.0249 | 3.6874 |
| CNN | 0.0118 | 0.0258 | 4.0773 |
| LSTM | 0.0179 | 0.0333 | 6.5887 |
| LSTMGC | 0.0108 | 0.0251 | 3.6142 |
| MSTGCN | 0.0165 | 0.0328 | 5.9383 |
| LSTMA | 0.0146 | 0.0289 | 5.2442 |
| TPA-BiLSTM | 0.0147 | 0.0293 | 5.2771 |
| EMD-SVD-Elman | 0.0158 | 0.03133 | 6.6274 |
| Model | MAE | RMSE | MAPE |
|---|---|---|---|
| STADGNN | 0.0005 | 0.0008 | 0.0557 |
| ASTGCN | 0.0009 | 0.0012 | 0.0893 |
| CNN | 0.0014 | 0.0041 | 0.1442 |
| LSTM | 0.0016 | 0.0024 | 0.1687 |
| LSTMGC | 0.0019 | 0.0033 | 0.2002 |
| MSTGCN | 0.0015 | 0.0024 | 0.1591 |
| LSTMA | 0.0016 | 0.0024 | 0.1615 |
| TPA-BiLSTM | 0.0015 | 0.0023 | 0.1573 |
| EMD-SVD-Elman | 0.0015 | 0.0022 | 0.1591 |
| Model | MAE | RMSE | MAPE |
|---|---|---|---|
| STADGNN | 0.2304 | 0.2993 | 7.3780 |
| ASTGCN | 0.2749 | 0.3377 | 11.3796 |
| CNN | 0.4607 | 1.3352 | 11.2167 |
| LSTM | 0.3349 | 0.4010 | 18.3343 |
| LSTMGC | 0.2891 | 0.3561 | 11.6696 |
| MSTGCN | 0.3185 | 0.3887 | 17.2258 |
| LSTMA | 0.3241 | 0.3932 | 17.5371 |
| TPA-BiLSTM | 0.3172 | 0.3810 | 17.1222 |
| EMD-SVD-Elman | 0.3215 | 0.3794 | 17.8959 |
| Model | MAE | RMSE | MAPE |
|---|---|---|---|
| STADGNN | 0.0103 | 0.0247 | 3.4222 |
| noTE-STADGNN | 0.0108 | 0.0252 | 3.6620 |
| noTDP-STADGNN | 0.0106 | 0.0252 | 3.5305 |
| noSE-STADGNN | 0.0106 | 0.0251 | 3.5152 |
| noSDCM-STADGNN | 0.0105 | 0.0247 | 3.5181 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, X.; Huang, Y.; Liu, G.; Yan, J.; Chen, S. Distribution Network Situational Awareness Prediction Based on Spatio-Temporal Attention Dynamic Graph Neural Network. Energies 2025, 18, 4402. https://doi.org/10.3390/en18164402
Qiu X, Huang Y, Liu G, Yan J, Chen S. Distribution Network Situational Awareness Prediction Based on Spatio-Temporal Attention Dynamic Graph Neural Network. Energies. 2025; 18(16):4402. https://doi.org/10.3390/en18164402
Chicago/Turabian StyleQiu, Xixi, Yuteng Huang, Guojin Liu, Jiaxiang Yan, and Shan Chen. 2025. "Distribution Network Situational Awareness Prediction Based on Spatio-Temporal Attention Dynamic Graph Neural Network" Energies 18, no. 16: 4402. https://doi.org/10.3390/en18164402
APA StyleQiu, X., Huang, Y., Liu, G., Yan, J., & Chen, S. (2025). Distribution Network Situational Awareness Prediction Based on Spatio-Temporal Attention Dynamic Graph Neural Network. Energies, 18(16), 4402. https://doi.org/10.3390/en18164402






