Structural Feasibility of a Wind Turbine Blade Inspired by an Owl Airfoil
Abstract
1. Introduction
2. Numerical Model
2.1. Model Geometry
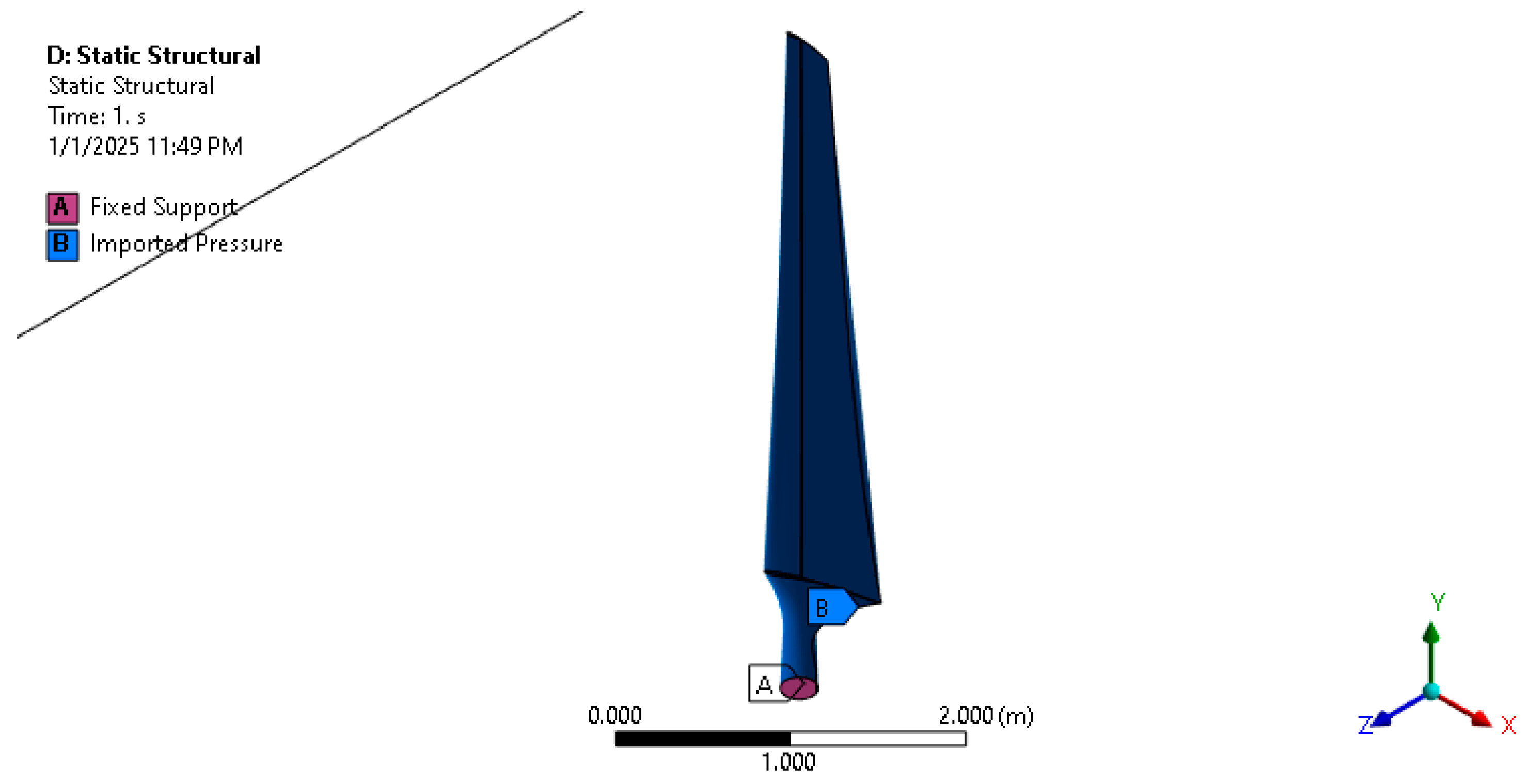
2.2. Boundary Conditions
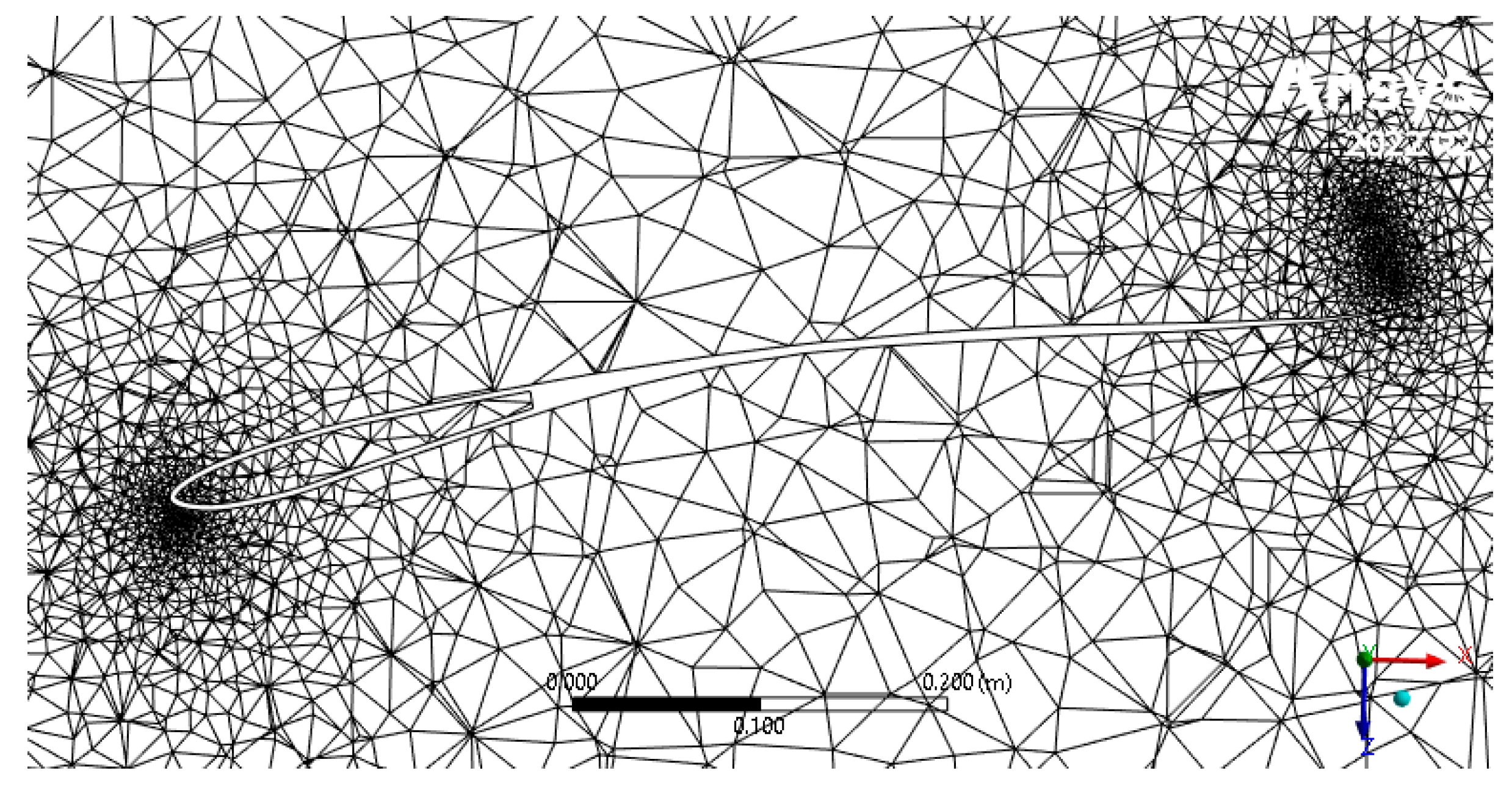
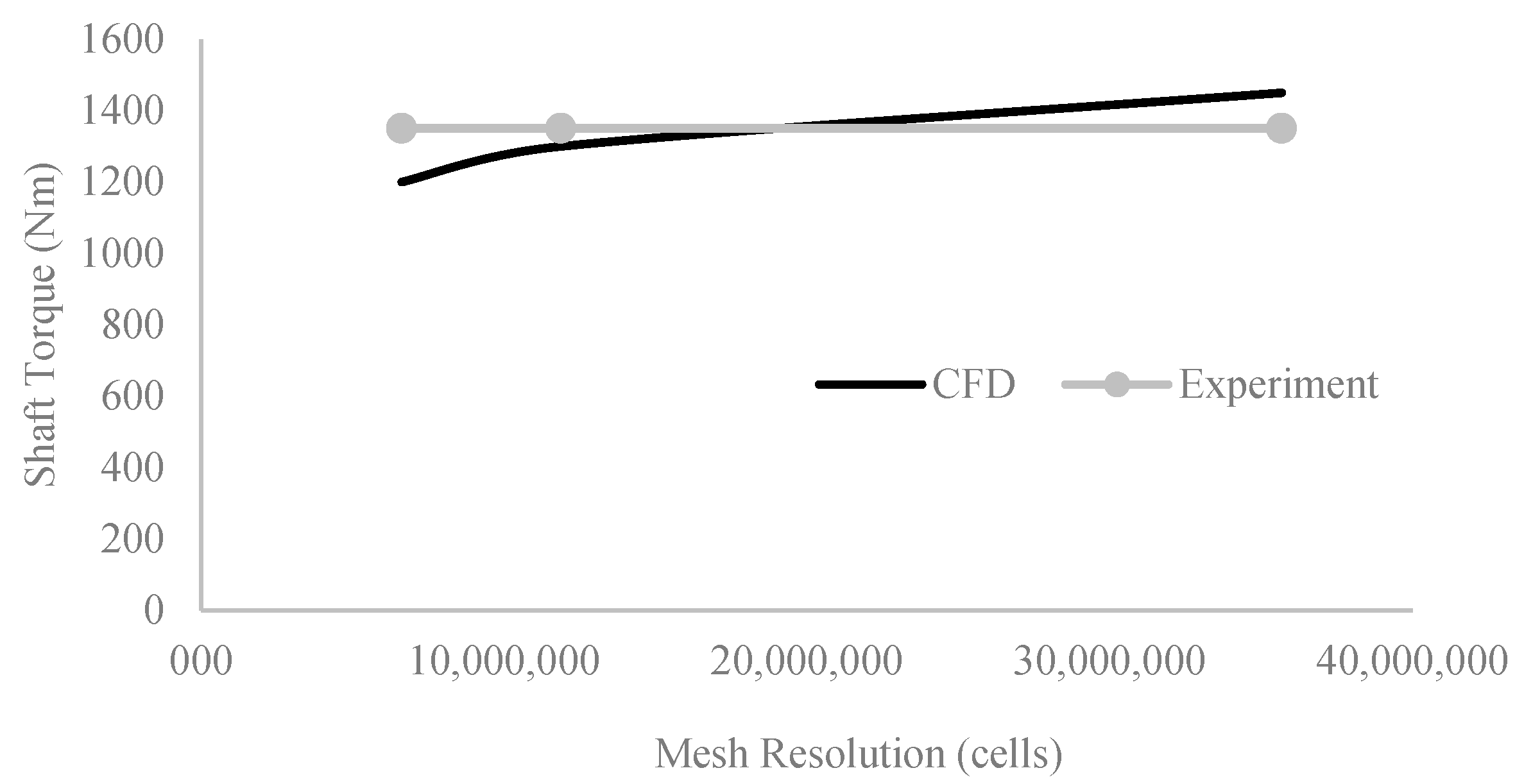
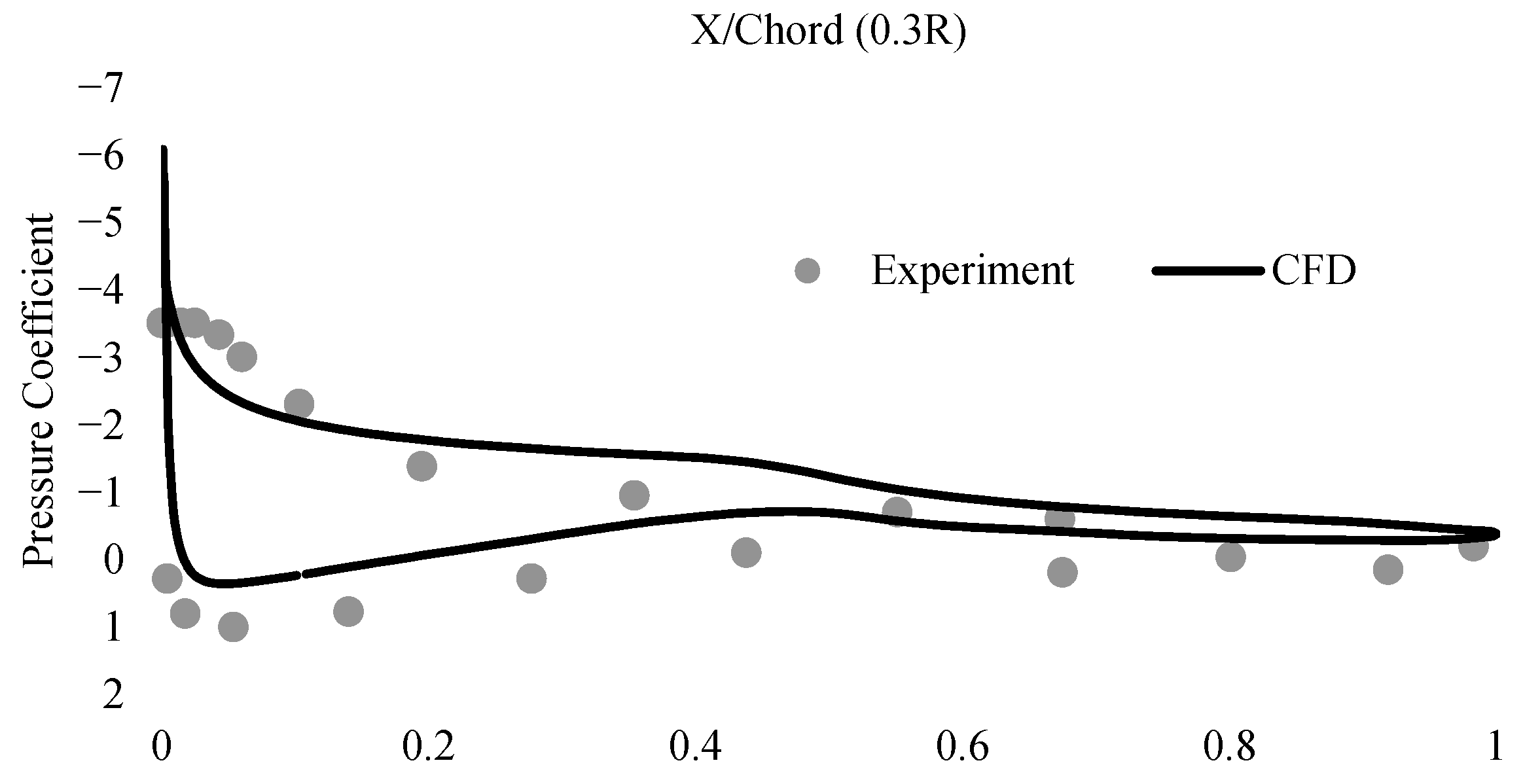
2.3. Mesh Refinement and Validation
3. Structural Analysis
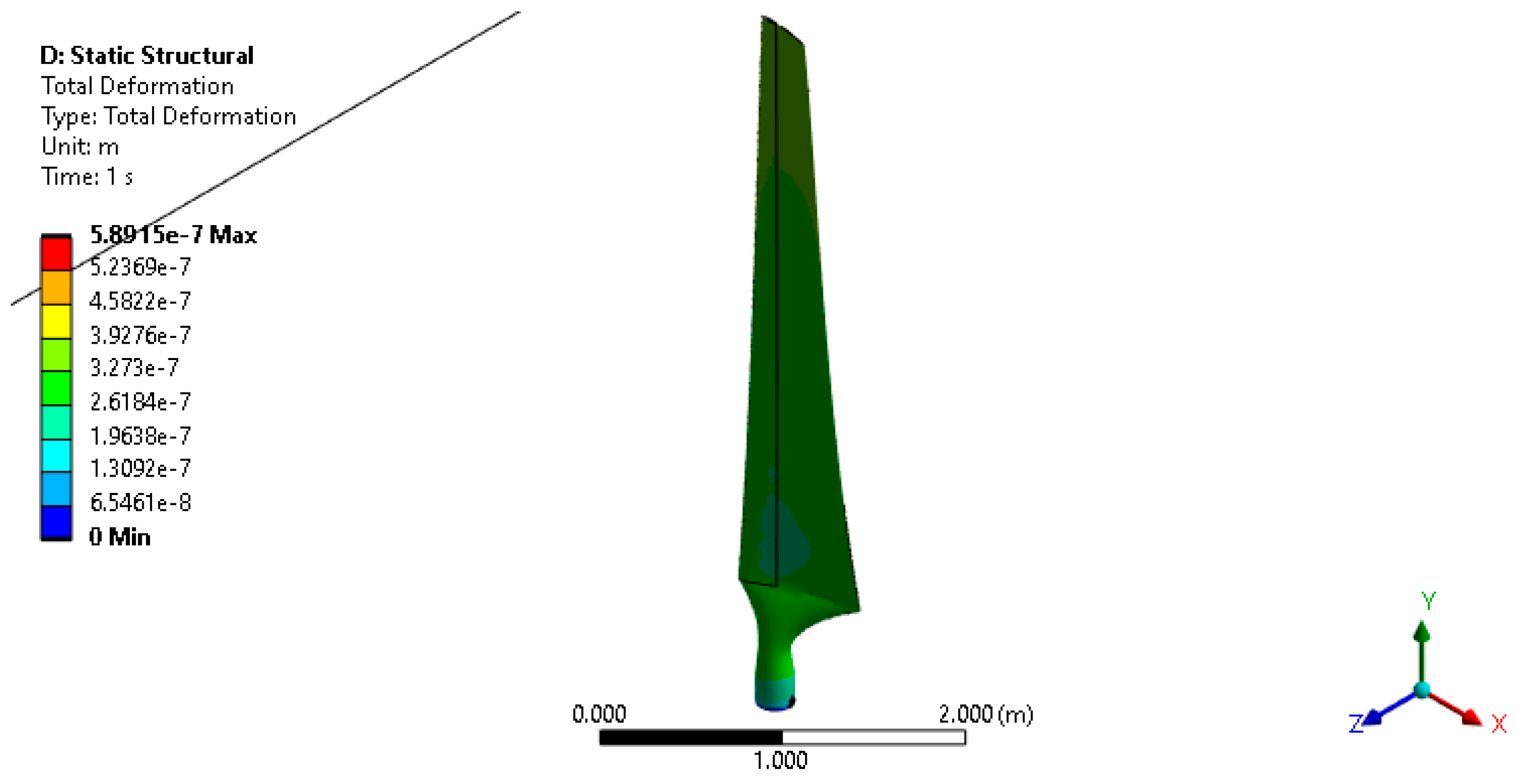
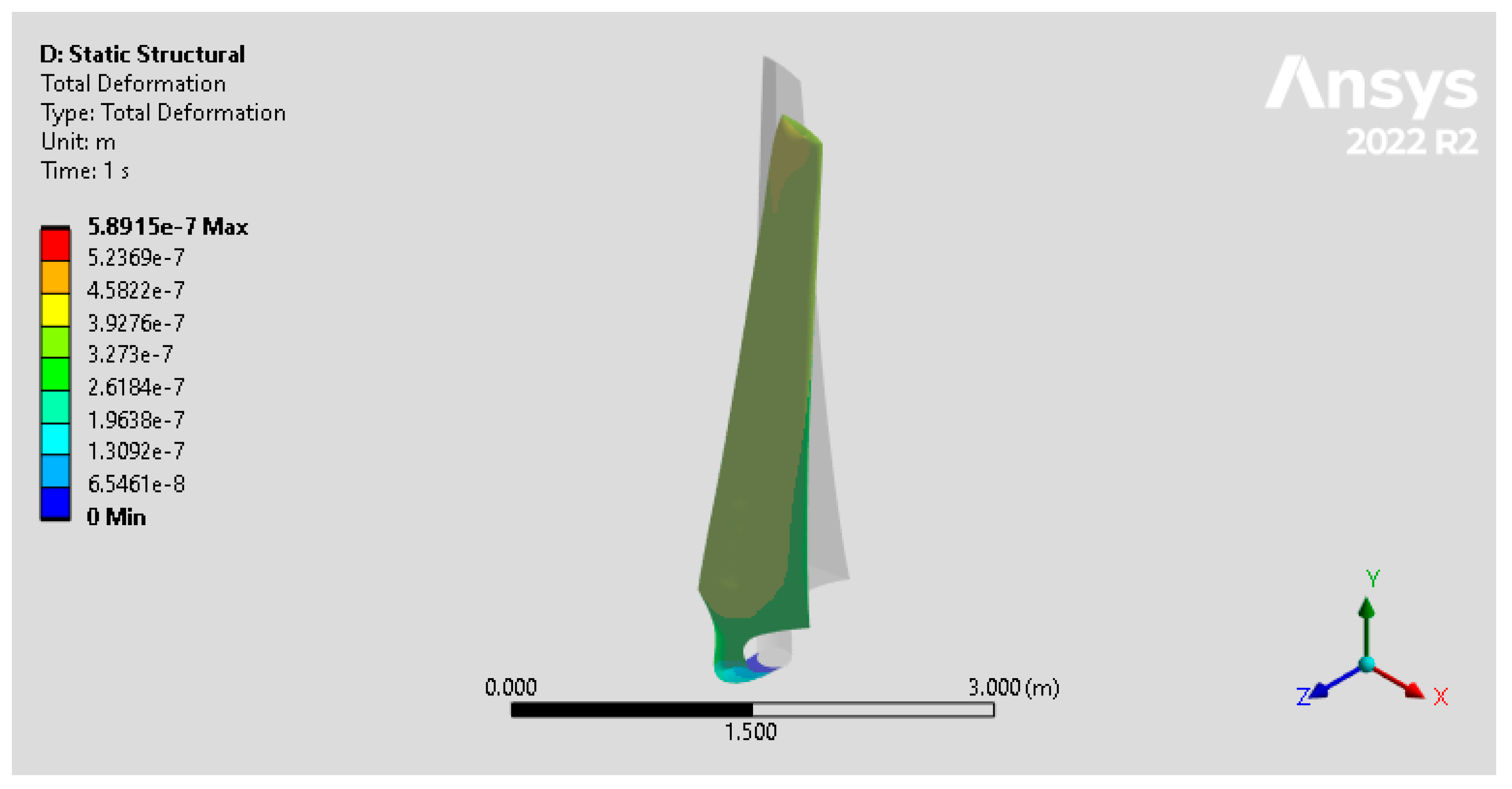
3.1. Deformation
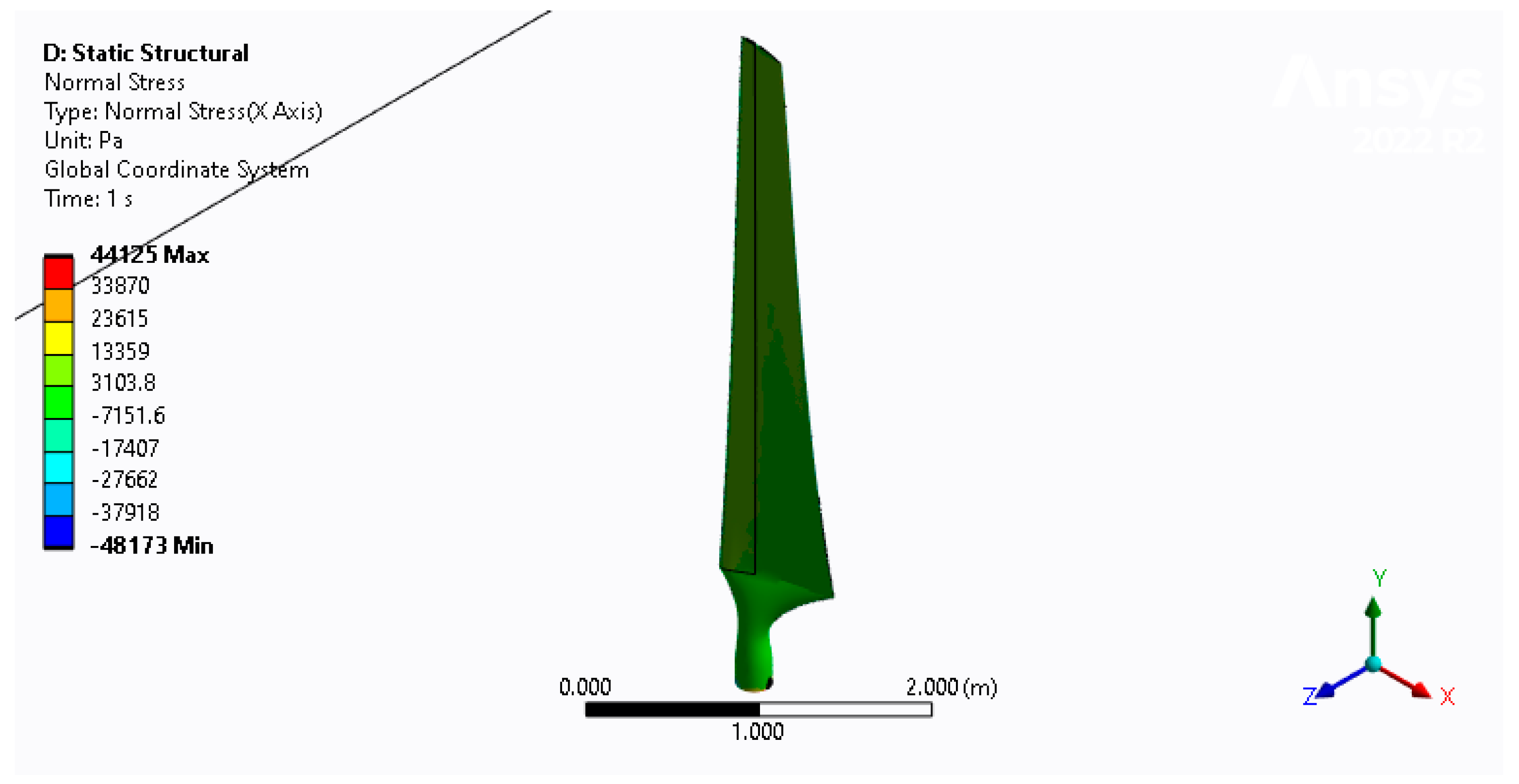
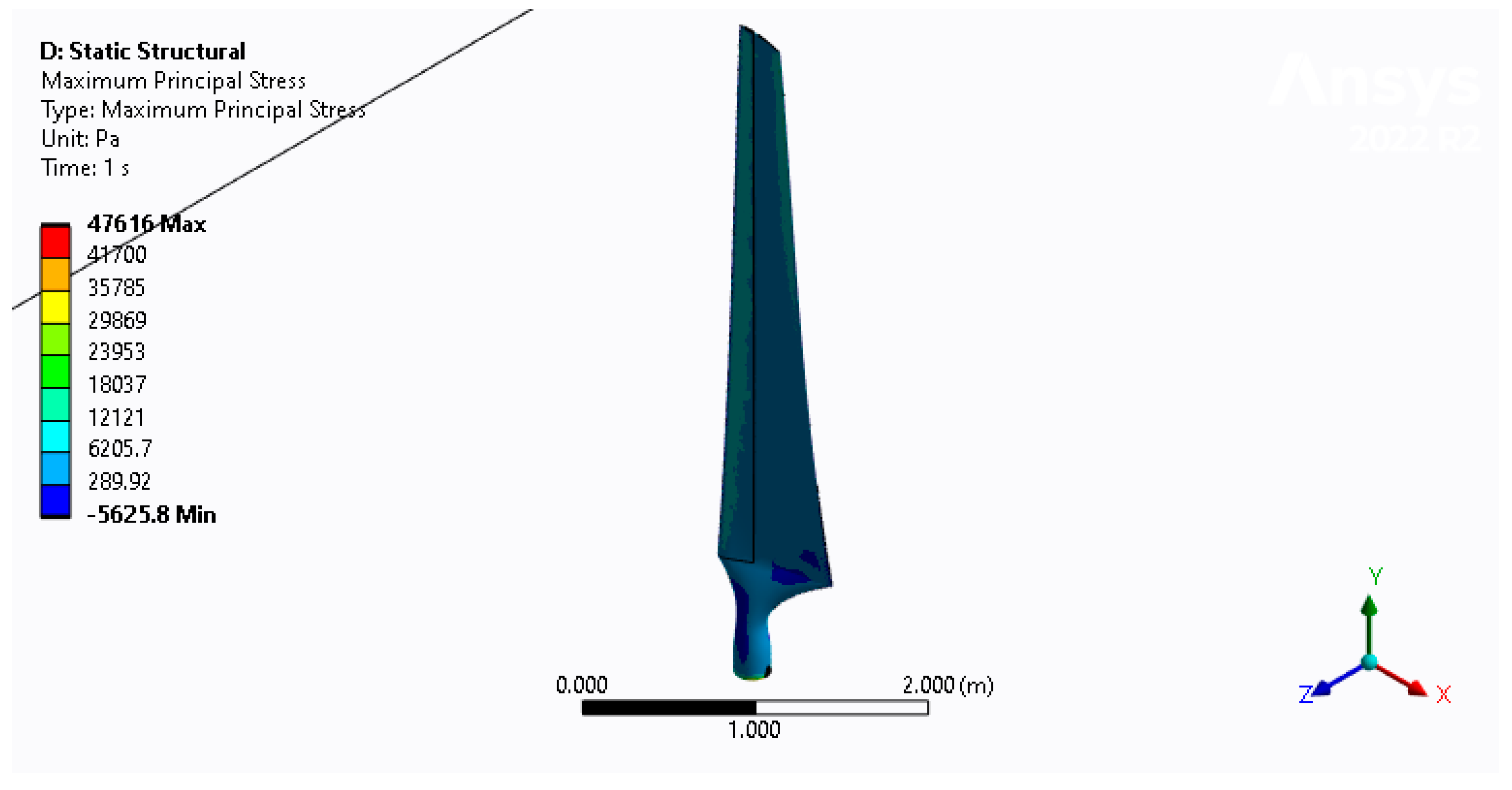
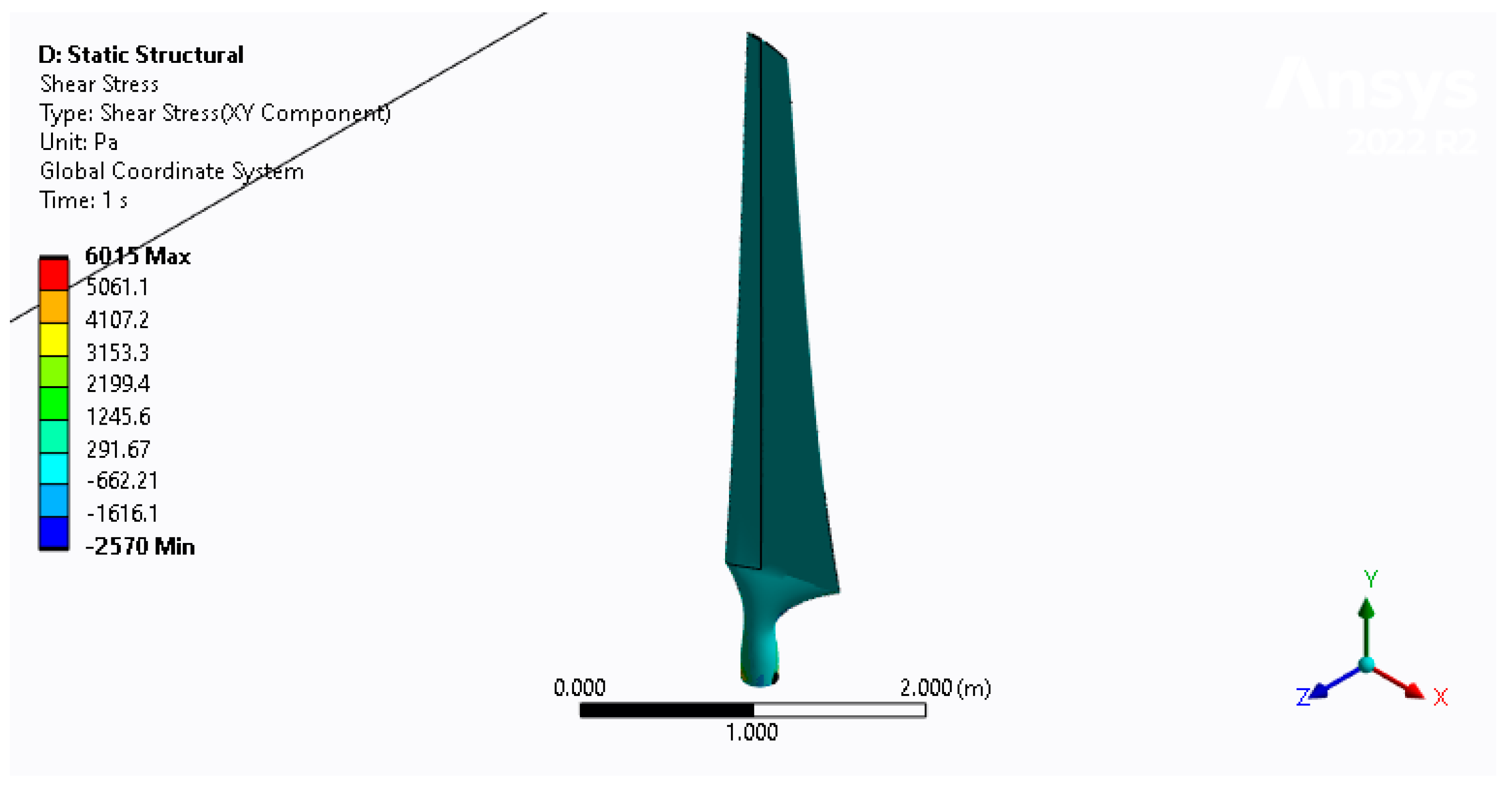
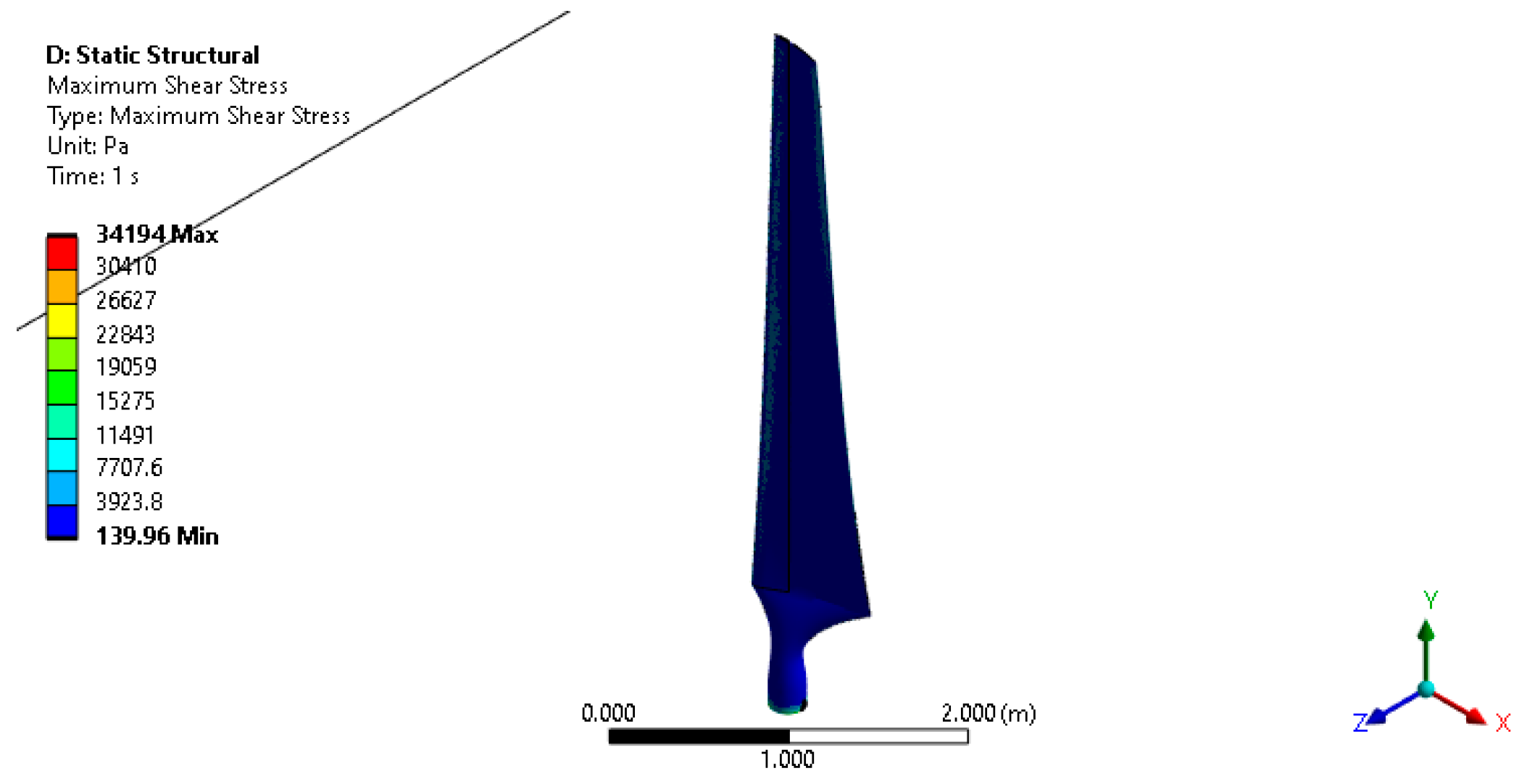
3.2. Sresses
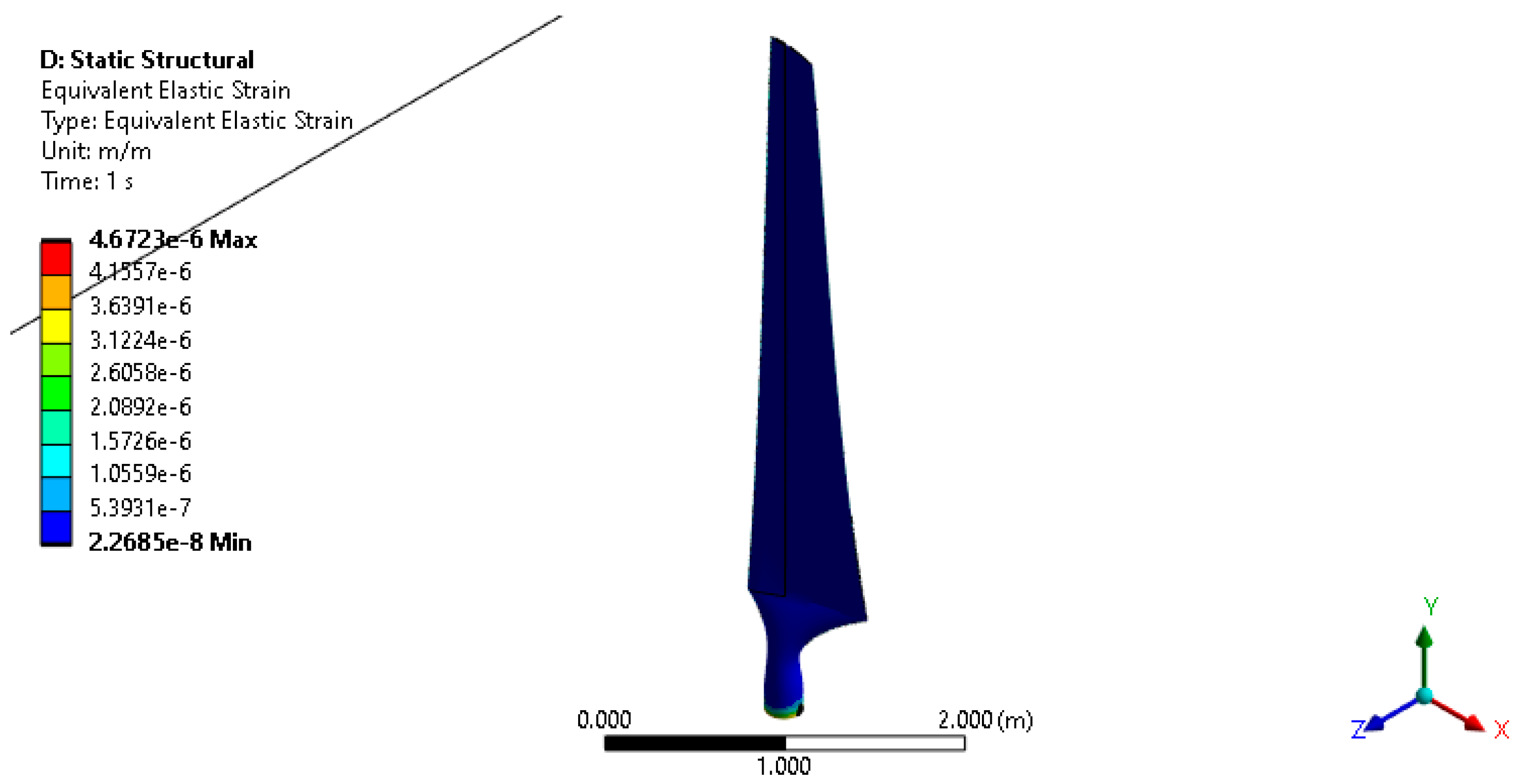
3.3. Srain
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sesalim, D.; Naser, J. The Effects of a Seagull Airfoil on the Aerodynamic Performance of a Small Wind Turbine. Energies 2024, 17, 2768. [Google Scholar] [CrossRef]
- Yossri, W.; Ayed, S.B.; Abdelkefi, A. Evaluation of the efficiency of bioinspired blade designs for low-speed small-scale wind turbines with the presence of inflow turbulence effects. Energy 2023, 273, 127210. [Google Scholar] [CrossRef]
- Coxworth, B. Seagull-Inspired Blades Could Give Small-Scale Wind Turbines a Power Boost. Energy, 24 June 2019. [Google Scholar]
- Seagull-Wing-Inspired Small-Scaled Wind Turbine to Deliver 15% More Power. TechNews, 5 July 2010.
- Qin, S.; Cheng, L.; He, Z. Bionic Fan Blade Shape Design Based on Owl Airfoil and Analysis of Its Effect on Noise. In Advances in Mechanical Design; Springer Nature Singapore Pte Ltd.: Singapore, 2022; pp. 665–672. [Google Scholar]
- Wang, M.; Liu, X. Numerical investigation of aerodynamic and acoustic characteristics of bionic airfoils inspired by bird wing. J. Aerosp. Eng. 2019, 233, 4004–4016. [Google Scholar] [CrossRef]
- Dean Sesalim, J.N. Effects of an Owl Airfoil on the Aeroacoustics of a Small Wind Turbine. Energies 2024, 17, 2254. [Google Scholar] [CrossRef]
- Beyene, D.W.M.A. Experimental and Fluid Structure Interaction analysis of a morphing wind turbine rotor. Energy 2015, 90, 1055–1065. [Google Scholar]
- Rajendra Roul, A.K. Fluid-Structure Interaction of Wind Turbine Blade Using Four Different Materials: Numerical Investigation. Symmetry 2020, 12, 1467. [Google Scholar] [CrossRef]
- Yassen El, S.Y.; Abdelhameed, A.S.; Elshorbagy, K.A. An examination of hub wind turbine utilizing fluid-structure interaction strategy. Alex. Eng. J. 2023, 64, 1–11. [Google Scholar] [CrossRef]
- Santo, G.; Peeters, M.; Van Paepegem, W.; Degroote, J. Dynamic load and stress analysis of a large horizontal axis wind turbine using full scale fluid-structure interaction simulation. Renew. Energy 2019, 140, 212–226. [Google Scholar] [CrossRef]
- Yan, J.; Korobenko, A.; Deng, X.; Bazilevs, Y. Computational free-surface fluid–structure interaction with application to floating offshore wind turbines. Comput. Fluids 2016, 141, 155–174. [Google Scholar] [CrossRef]
- Wiegard, B.; König, M.; Lund, J.; Radtke, L.; Netzband, S.; Abdel-Maksoud, M.; Düster, A. Fluid-structure interaction and stress analysis of a floating wind turbine. Mar. Struct. 2021, 78, 102970. [Google Scholar] [CrossRef]
- Adil Rasheeda, R.H.; Kvamsdala, T.; Åkervik, E. A Comprehensive Simulation Methodology for Fluid-Structure Interaction of Offshore Wind Turbines. Energy Procedia 2014, 53, 135–145. [Google Scholar] [CrossRef][Green Version]
- Christian Grinderslev, S.G.H.; Sørensen, N.N. Fluid–structure interaction simulations of a wind turbine rotor in complex flows, validated through field experiments. Wind Energy 2021, 24, 1426–1442. [Google Scholar] [CrossRef]
- Wang, L.; Quant, R.; Kolios, A. Fluid structure interaction modelling of horizontal-axis wind turbine blades based on CFD and FEA. J. Wind. Eng. Ind. Aerodyn. 2016, 158, 11–25. [Google Scholar] [CrossRef]
- Lee, K.; Huque, Z.; Kommalapati, R.; Han, S.E. The Evaluation of Aerodynamic Interaction of Wind Blade Using Fluid Structure Interaction Method. J. Clean Energy Technol. 2015, 3, 270–275. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Korobenko, A.; Deng, X.; Yan, J. Novel structural modeling and mesh moving techniques for advanced fluid–structure interaction simulation of wind turbines. Int. J. Numer. Methods Eng. 2015, 102, 766–783. [Google Scholar] [CrossRef]
- Lee, K.; Huque, Z.; Kommalapati, R.; Han, S.E. Fluid-structure interaction analysis of NREL phase VI wind turbine: Aerodynamic force evaluation and structural analysis using FSI analysis. Renew. Energy 2017, 113, 512–531. [Google Scholar] [CrossRef]
- Tu, J.; Yeoh, G.H.; Liu, C.; Tao, Y. Computational Fluid Dynamics: A Practical Approach; Butterworth-Heinemann: Oxford, UK, 2012. [Google Scholar]
- 40- BY 80-/80- BY 120-FOOT WIND TUNNELS. NASA Ames Research Center. Available online: https://rotorcraft.arc.nasa.gov/Research/Facilities/windtunnels.html (accessed on 25 November 2024).
- Hand, M.M.; Simms, D.A.; Fingersh, L.J.; Jager, D.W.; Cotrell, J.R.; Schreck, S.; Larwood, S.M. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; National Renewable Energy Laboratory: Golden, CO, USA, 2001. [Google Scholar]
- WebPlotDigitizer. Available online: https://apps.automeris.io/wpd/ (accessed on 15 January 2023).
- Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Navier–Stokes predictions of the NREL phase-VI rotor in the NASA Ames 80ft x 120ft wind tunnel. Wind Energy 2002, 5, 151–169. [Google Scholar] [CrossRef]
- Johansen, J.; Sørensen, N.N.; Michelsen, J.A.; Schreck, S. Detached-eddy simulation of flow around the NREL Phase VI blade. Wind Energy 2002, 5, 185–197. [Google Scholar] [CrossRef]
- Chao, D.D.; Van Dam, C.P. Computational aerodynamic analysis of a blunt trailing-edge airfoil modification to the NREL Phase VI rotor. Wind Energy 2007, 10, 529–550. [Google Scholar] [CrossRef]
- Zhang, R.K.; Wu, V.D. Aerodynamic characteristics of wind turbine blades with a sinusoidal leading edge. Wind Energy 2012, 15, 407–424. [Google Scholar] [CrossRef]
- Hsu, M.C.; Akkerman, I.; Bazilevs, Y. Finite element simulation of wind turbine aerodynamics: Validation study using NREL Phase VI experiment. Wind Energy 2014, 17, 461–481. [Google Scholar] [CrossRef]
- Elfarra, M.A.; Sezer-Uzol, N.; Akmandor, I.S. NREL VI rotor blade: Numerical investigation and winglet design and optimization using CFD. Wind Energy 2014, 17, 605–626. [Google Scholar] [CrossRef]
- Simms, D.; Schreck, S.; Hand, M.; Fingersh, L.J. NREL Unsteady Aerodynamics Experiment in the NASA-Ames Wind Tunnel: A Comparison of Predictions to Measurements; National Renewable Energy Laboratory: Golden, CO, USA, 2001. [Google Scholar]
- Spera, D.A. Wind Turbine Technology: Fundamental Concepts of Wind Turbine Engineering, 2nd ed.; ASME: Houston, TX, USA, 2009. [Google Scholar]
- Peijs, T.; Kirschbaum, R.; Lemstra, P.J. Chapter 5: A critical review of carbon fiber and related products from an industrial perspective. Adv. Ind. Eng. Polym. Res. 2022, 5, 90–106. [Google Scholar] [CrossRef]
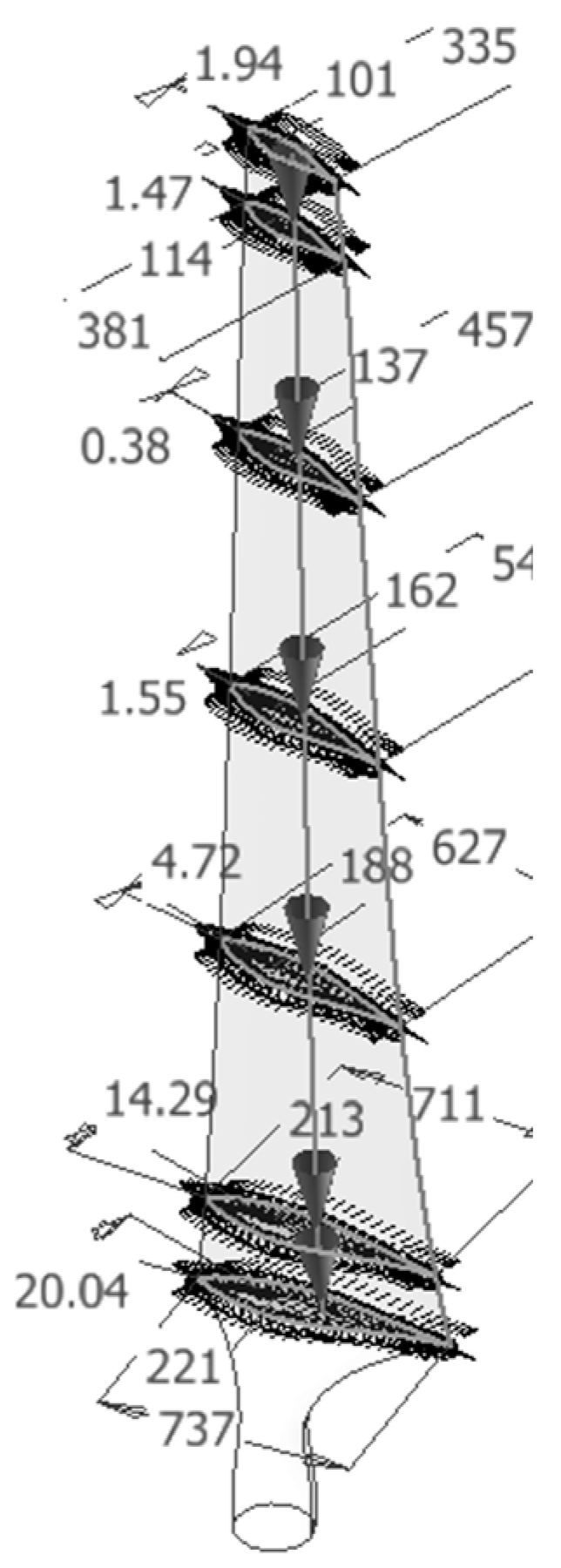



| Radial Distance R (m) | Span Station (R/5.029) | Chord Length (m) | Twist (Degrees) | Thickness (m) (20.95% Chord) | Twist Axis (% Chord), (m) |
|---|---|---|---|---|---|
| 0.0 | 0.0 | Hub center of rotation | Hub center of rotation | Hub center of rotation | Hub center of rotation |
| 0.508 | 0.101 | 218 (root hub adapter) | 0.0 (root hub adapter) | 0.218 (root hub adapter) | 50 (root hub adapter) |
| 0.660 | 0.131 | 0.218 | 0.0 | 0.218 | 50 |
| 0.883 | 0.176 | 0.183 | 0.0 | 0.183 | 50 |
| 1.257 | 0.250 | 0.737 | 20.040 | 0.154 | 30, (0.221) |
| 1.343 | 0.267 | 0.728 | 18.074 | 0.152 | 30, (0.218) |
| 1.510 | 0.300 | 0.711 | 14.292 | 0.149 | 30, (0.213) |
| 1.648 | 0.328 | 0.697 | 11.909 | 0.146 | 30, (0.209) |
| 1.952 | 0.388 | 0.666 | 7.979 | 0.139 | 30, (0.199) |
| 2.257 | 0.449 | 0.636 | 5.308 | 0.133 | 30, (0.190) |
| 2.343 | 0.466 | 0.627 | 4.715 | 0.131 | 30, (0.188) |
| 2.562 | 0.509 | 0.605 | 3.425 | 0.126 | 30, (0.181) |
| 2.867 | 0.570 | 0.574 | 2.083 | 0.120 | 30, (0.172) |
| 3.172 | 0.631 | 0.543 | 1.150 | 0.113 | 30, (0.162) |
| 3.185 | 0.633 | 0.542 | 1.115 | 0.113 | 30, (0.162) |
| 3.476 | 0.691 | 0.512 | 0.494 | 0.107 | 30, (0.153) |
| 3.781 | 0.752 | 0.482 | −0.015 | 0.100 | 30, (0.144) |
| 4.023 | 0.800 | 0.457 | −0.381 | 0.095 | 30, (0.137) |
| 4.086 | 0.812 | 0.451 | −0.475 | 0.094 | 30, (0.135) |
| 4.391 | 0.873 | 0.420 | −0.920 | 0.088 | 30, (0.162) |
| 4.696 | 0.934 | 0.389 | −1.352 | 0.081 | 30, (0.116) |
| 4.780 | 0.950 | 0.381 | −1.469 | 0.079 | 30, (0.114) |
| 5.000 | 0.994 | 0.358 | −1.775 | 0.075 | 30, (0.107) |
| 5.029 | 1 | 0.335 | −1.944 | 0.075 | 30, (0.101) |
| Carbon Fiber | 230 GPa |
|---|---|
| Density | 1800 kg/m3 |
| Young’s Modulus X direction | 2.3 × 1011 Pa |
| Young’s Modulus Y direction | 2.3 × 1010 Pa |
| Young’s Modulus Z direction | 2.3 × 1010 Pa |
| Poisson’s Ratio XY | 0.2 |
| Poisson’s Ratio YZ | 0.4 |
| Poisson’s Ratio XZ | 0.2 |
| Shear Modulus XY | 9 × 109 |
| Shear Modulus YZ | 8.2143 × 109 |
| Shear Modulus XZ | 9 × 109 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sesalim, D.; Naser, J. Structural Feasibility of a Wind Turbine Blade Inspired by an Owl Airfoil. Energies 2025, 18, 1288. https://doi.org/10.3390/en18051288
Sesalim D, Naser J. Structural Feasibility of a Wind Turbine Blade Inspired by an Owl Airfoil. Energies. 2025; 18(5):1288. https://doi.org/10.3390/en18051288
Chicago/Turabian StyleSesalim, Dean, and Jamal Naser. 2025. "Structural Feasibility of a Wind Turbine Blade Inspired by an Owl Airfoil" Energies 18, no. 5: 1288. https://doi.org/10.3390/en18051288
APA StyleSesalim, D., & Naser, J. (2025). Structural Feasibility of a Wind Turbine Blade Inspired by an Owl Airfoil. Energies, 18(5), 1288. https://doi.org/10.3390/en18051288







