Gramian Angular Field–Gramian Adversial Network–ResNet34: High-Accuracy Fault Diagnosis for Transformer Windings with Limited Samples
Abstract
1. Introduction
2. Obtaining the Winding Frequency Response Curve
2.1. Basic Principles of FRA
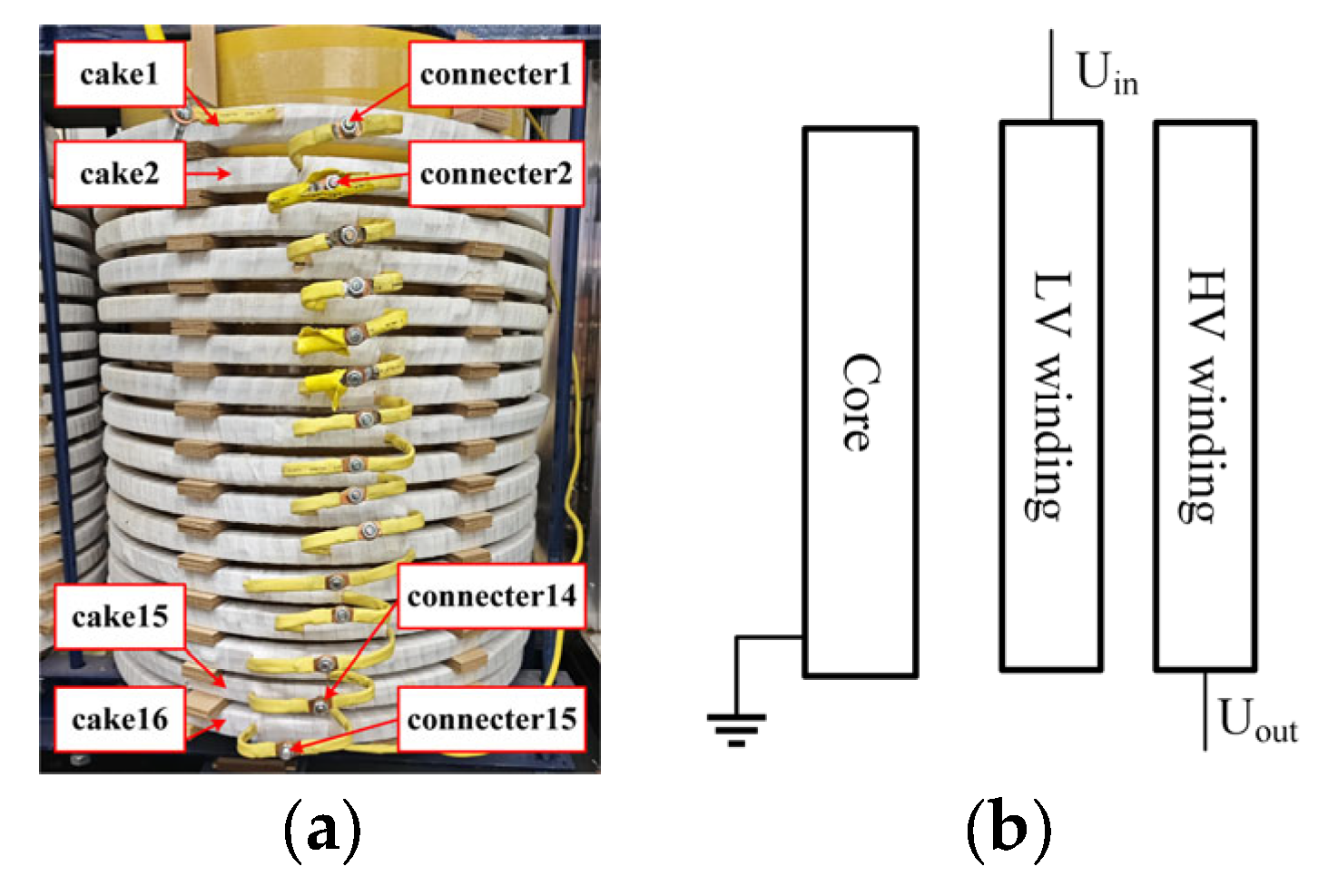
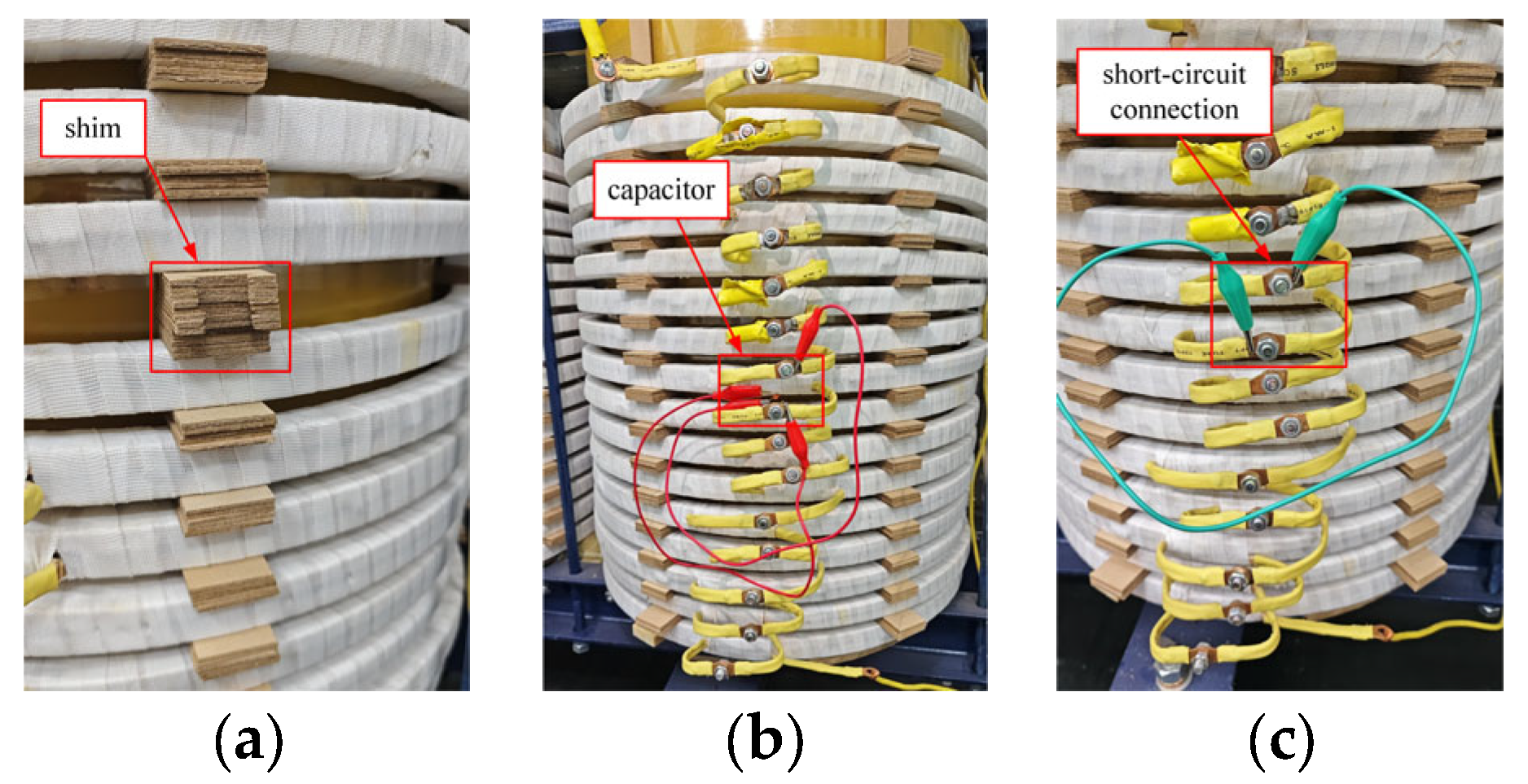
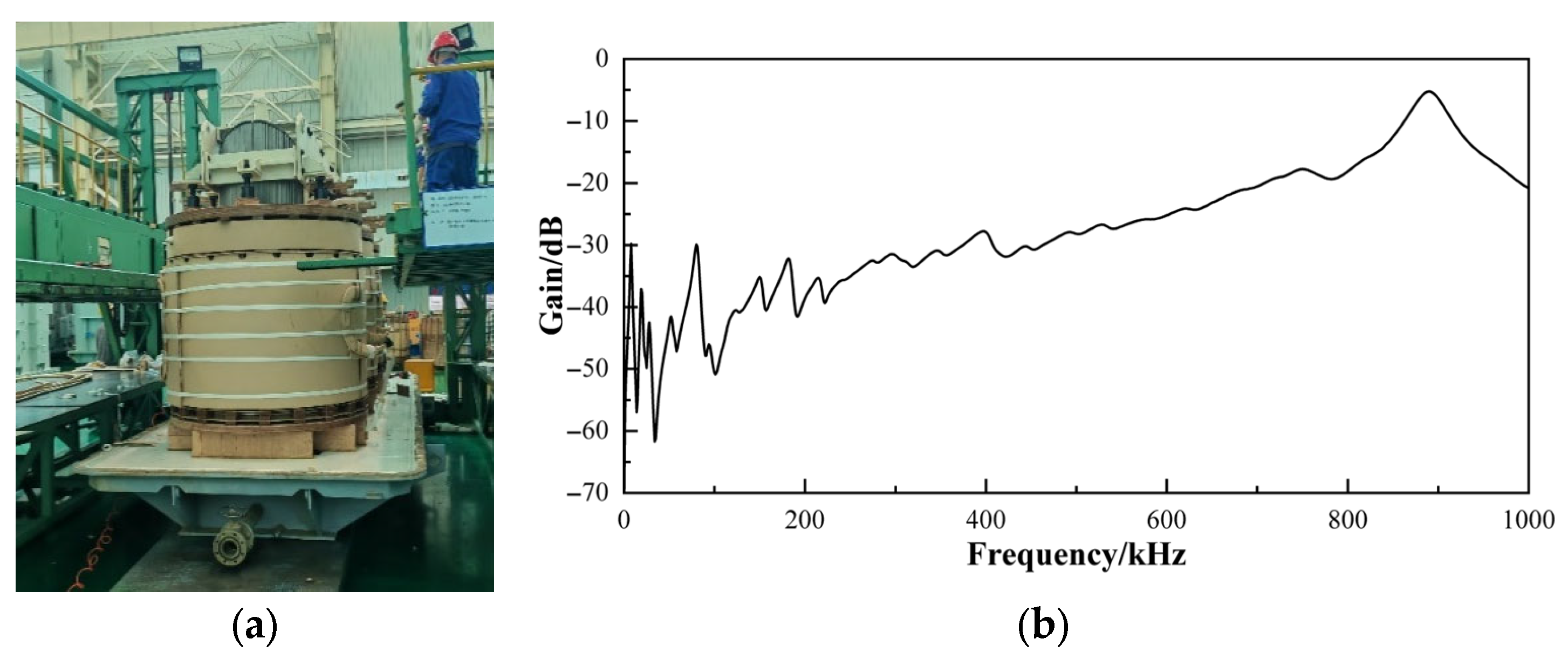
2.2. Test Platform Construction
- (1)
- AD
- (2)
- SCV
- (3)
- SC
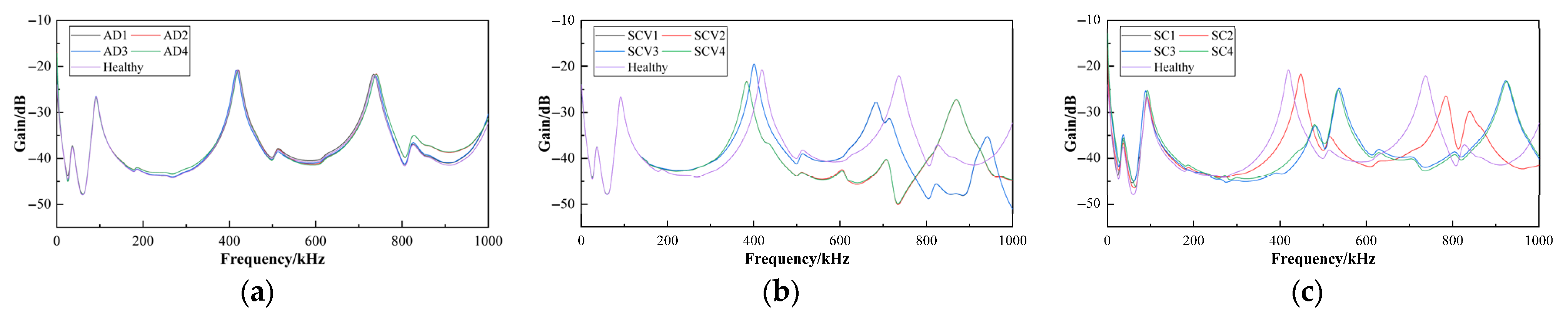
2.3. Frequency Response Curve Data Acquisition and Analysis
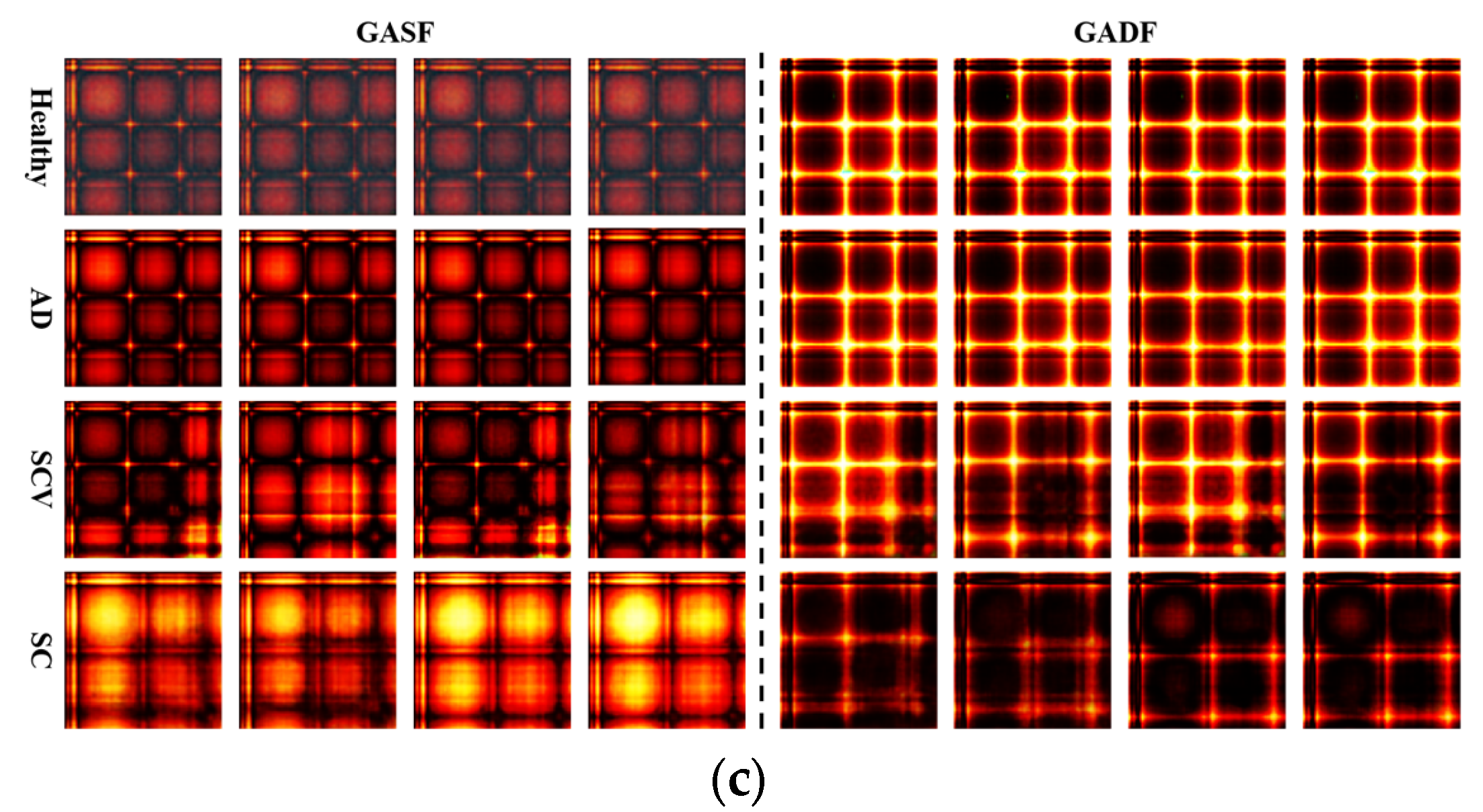
3. Visualisation and Analysis of Frequency Response Data Based on GAF
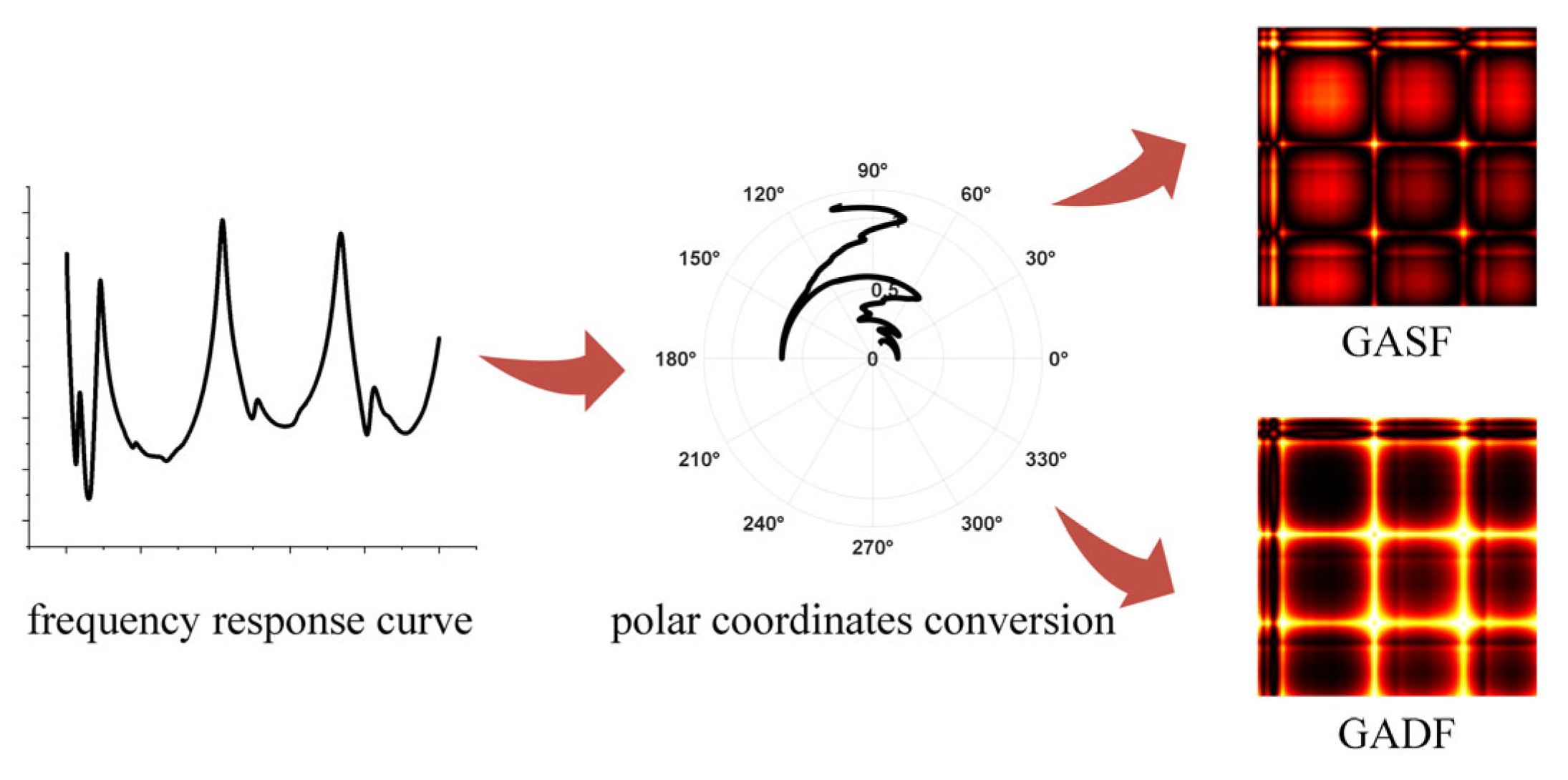
3.1. GAF Image Conversion Principle
- (1)
- Data normalisation: To ensure that the data are −1~1, normalise the data as shown in Equation (2).where X = {x1, x2, …, xN} is the original data, and is the normalised value.
- (2)
- Calculate angle encoding: Map the normalised one-dimensional data to the angle in the polar coordinate system. The value of each data point is converted to the angle in the polar coordinate system, as shown in Equation (3):
- (3)
- Calculate the GAF matrix: Based on the angle information, calculate the GASF and GADF values as shown in Equations (4) and (5):
- (4)
- Generate image: Generate GAF images based on the calculation results of GASF and GADF.
3.2. Steps for Converting GAF Images of Winding Frequency Response Curves
- (1)
- Using FRA, the frequency response curve of the transformer winding was tested, i.e., the original one-dimensional data sequence.
- (2)
- Scale the original one-dimensional data sequence to the range −1~1 for standardisation.
- (3)
- Convert the one-dimensional data sequence from the Cartesian coordinate system to the polar coordinate system.
- (4)
- Convert the one-dimensional data sequence into two-dimensional GASF and GADF images through trigonometric transformations of the angles and differences between each data point.
3.3. Results Analysis
4. Data Augmentation for Frequency Response Curves Based on GAF
4.1. Basic Principles and Improvements of GAN
- (1)
- WGAN-GP
- (2)
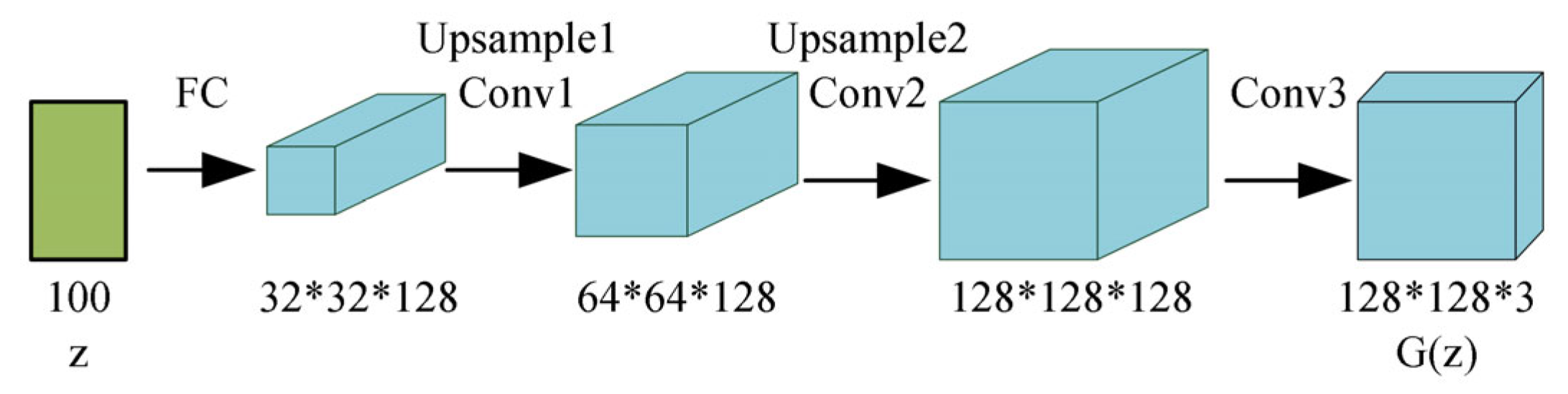
- DCGAN
- (3)
- BEGAN
4.2. Frequency Response Data Expansion
4.3. Quality Assessment of GAN-Generated Samples
5. Fault Diagnosis for Windings Based on GAF–GAN–ResNet34
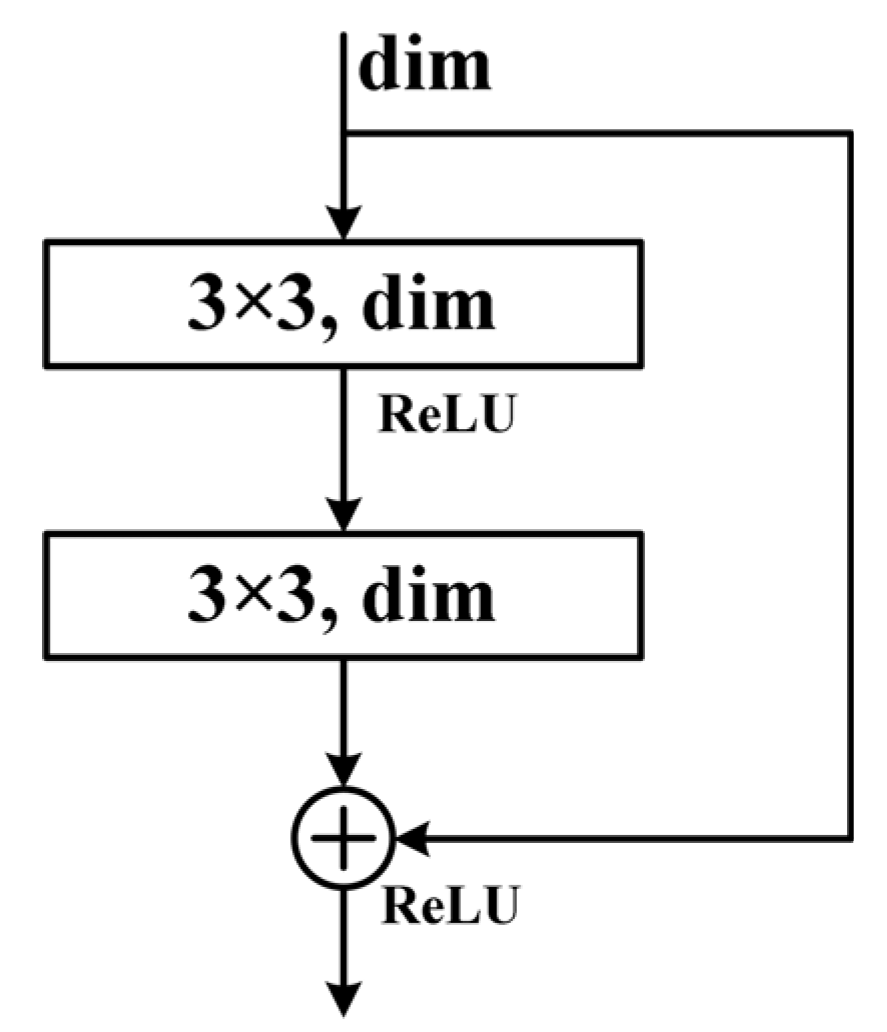
5.1. Residual Network
5.2. Research on Winding Fault Diagnosis
- (1)
- Dataset Construction: Based on the GASF images obtained from the frequency response data transformation described above, we constructed the original dataset (GASF image dataset) and the GAN-augmented datasets (WGAN-GP, DCGAN, and BEGAN-augmented GASF datasets). The GASF image dataset consists of a training set, a validation set, and a test set. Each dataset includes winding frequency response images under normal conditions and three typical fault conditions. Each category of frequency response data includes 16 images; the validation set includes 4 images per category of frequency response data; the test set includes 8 images per category of frequency response data, thereby constructing the GASF image dataset. The validation set and test set of the GAN-augmented dataset are augmented with 16 real images and 24 GAN-generated images. Different GANs were used to expand the training set, thereby constructing the WGAN-expanded GASF dataset, DCGAN-expanded GASF dataset, and BEGAN-expanded GASF dataset.
- (2)
- Classification network training: Train the ResNet34 network on the original dataset and the GAN-augmented dataset.
- (3)
- Comparison of recognition accuracy: Compare the classification accuracy of the ResNet34 network trained on the GASF image dataset, the WGAN-GP-augmented GASF dataset, the DCGAN augmented GASF dataset, and the BEGAN-augmented GASF dataset to evaluate the enhancement effects of different GANs.
5.3. On-Site Case Analysis
6. Conclusions
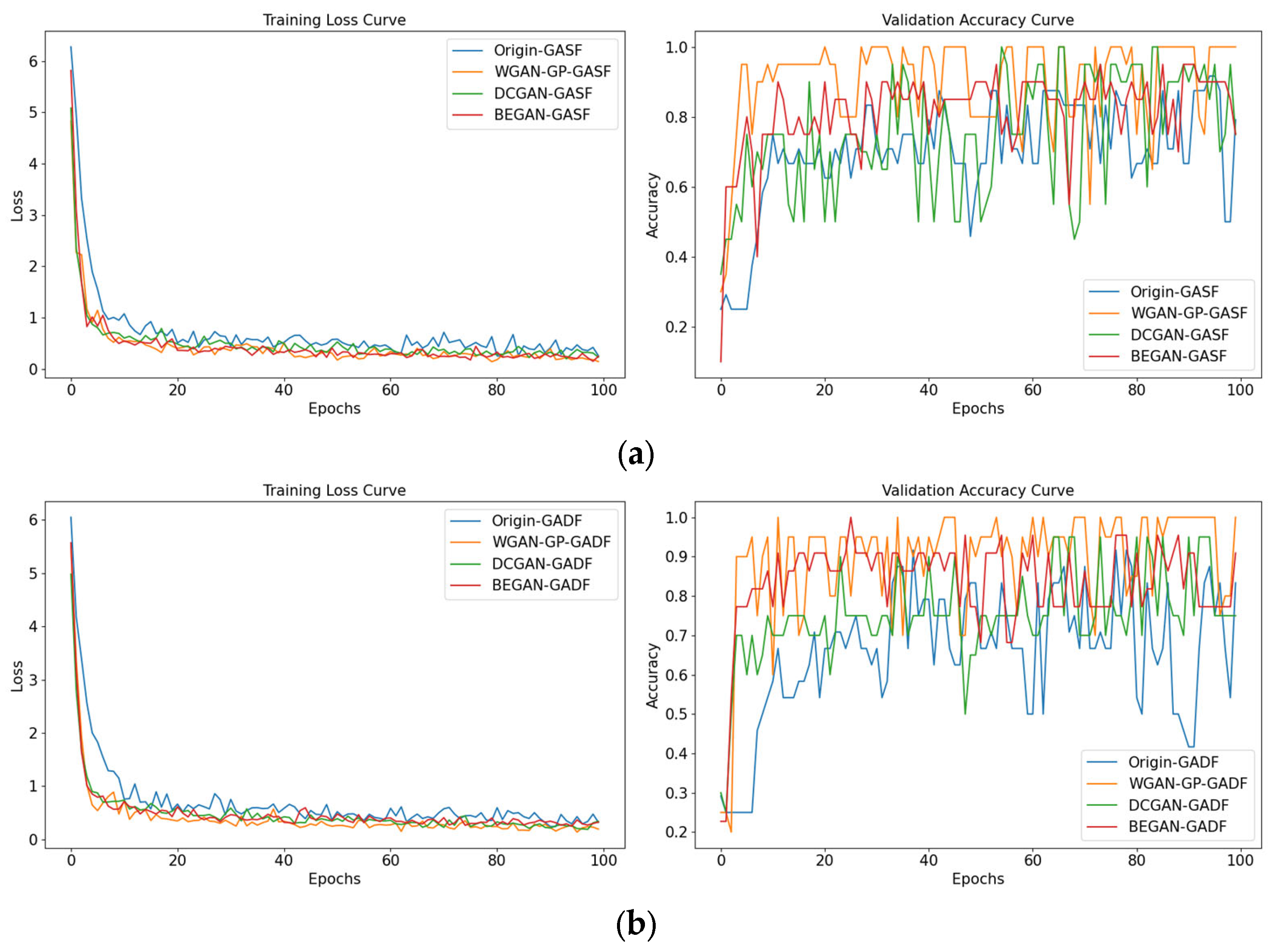
- Since the frequency response images of AD are quite similar to those of normal windings, the classification network performed poorly in distinguishing between normal winding images and AD images before using GAN to expand the training set. DCGAN, due to its poor image generation quality, lacks data augmentation capabilities and cannot effectively improve the classification network’s recognition accuracy.
- Both the BEGAN and WGAN-GP expanded datasets have the effect of improving the recognition accuracy of classification networks. The most effective combination is to use WGAN-GP to expand the GADF dataset. The classification network trained using this dataset achieved a recognition accuracy of 96.88%.
- Compared to diagnostic models trained on the original dataset, the GAF-WGAN-GP-ResNet34 diagnostic model consistently achieved an accuracy rate of over 93% in identifying transformer winding fault types. Through the analysis of actual transformer fault cases and comparison with maintenance results, the effectiveness of the analysis method proposed in this paper was validated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GAF | Gramian angular field |
| GAN | Generative adversarial networks |
| ResNet | Deep residual network |
| FRA | Frequency response analysis method |
| GASF | Gramian angular summation field |
| GADF | Gramian angular difference field |
| ANN | Artificial neural network |
| BP | Backpropagation |
| CNN | Convolutional neural network |
| BiGRU | Bidirectional gated recurrent unit |
| HV | High-voltage |
| AD | Axial displacement fault |
| SCV | Bulging and warping faulT |
| SC | Cake-to-cake short circuit fault |
| WGAN | Wasserstein GAN |
| GP | Gradient penalty term |
| BN | Batch normalisation |
| SSIM | Structural similarity |
| PSNR | Peak Signal-to-Noise Ratio |
| CS | Cosine similarity |
| FID | Fréchet Inception Distance |
| MSE | Mean squared error |
References
- Qian, G.; Yang, K.; Hu, J.; Liu, H.; He, S.; Zou, D.; Dai, W.; Wang, H.; Wang, D. Diagnosis Method for Transformer Winding Based on Differentiated M-Training Classification Optimized by White Shark Optimization Algorithm. Energies 2025, 18, 2290. [Google Scholar] [CrossRef]
- Yao, H.; Xu, Y.; Guo, Q.; Chen, S.; Lu, B.; Huang, Y. Study on Transformer Fault Diagnosisbased on Improved Deep Residual Shrinkage Network and Optimized Residual Variational Autoencoder. Energy Rep. 2025, 13, 1608–1619. [Google Scholar] [CrossRef]
- Zhao, X.; Yao, C.; Zhang, C.; Abu-Siada, A. Toward Reliable Interpretation of Power Transformer Sweep Frequency Impedance Signatures: Experimental Analysis. IEEE Electr. Insul. Mag. 2018, 34, 40–51. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, H.; Ma, Q.; Han, H.; Wang, S. Frequency Response Signature Analysis for Winding Mechanical Fault Detection of Power Transformer Using Sensitivity Method. Int. J. Appl. Electromagn. Mech. 2019, 61, 593–603. [Google Scholar] [CrossRef]
- Tahir, M.; Tenbohlen, S. Transformer Winding Condition Assessment Using Feedforward Artificial Neural Network and Frequency Response Measurements. Energies 2021, 14, 3227. [Google Scholar] [CrossRef]
- Luo, Y.; Ye, J.; Gao, J.; Chen, G.; Wang, G.; Liu, L.; Li, B. Recognition Technology of Winding Deformation Based on Principal Components of Transfer Function Characteristics and Artificial Neural Network. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3922–3932. [Google Scholar] [CrossRef]
- Jayasinghe, J.A.S.B.; Wang, Z.D.; Darwin, A.W. Winding Movement in Power Transformers: A Comparison of FRA Measurement Connection Methods. IEEE Trans. Dielectr. Electr. Insul. 2006, 13, 1342–1349. [Google Scholar] [CrossRef]
- Samimi, M.; Tenbohlen, S.; Akmal, A.; Mohseni, H. Power Transformer Fault Diagnosis Based on Improved BP Neural Network. Electronics 2023, 12, 3526. [Google Scholar] [CrossRef]
- Yang, S.; Li, Z.; Yang, X.; Wu, H. Fault Identification Method of Transformer Winding based on Gramian Angular Difference Field and Convolutional Neural Network. Recent Adv. Electr. Electron. Eng. 2024, 17, 837–847. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, X.; Xu, G.; Yang, S.; Duan, G. Transformer Fault Identification Method Based on Gramian Angle Difference Field and CNN-BiGRU. Electron. Sci. Technol. 2025, 38, 73–79. [Google Scholar] [CrossRef]
- Ma, X.; Tang, W.; Niu, Z.; Xin, Y. Deformation Fault Identification Method for Transformer Windings Based on Twin Convolutional Network Under Unbalanced Data Set. High Volt. Appar. 2023, 59, 120–128. [Google Scholar] [CrossRef]
- Duan, J.; Wu, X.; He, Y.; Song, W.; Yin, Y. Small Sample Fault Diagnosis of Transformer Windings Based on Virtual-real Feature Fusion and Data-mechanism Driven. Electr. Power Autom. Equip. 2024, 44, 212–218. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, Z.; Liu, J.; Tan, S.; Liu, C. Application of Generative AI-based Data Augmentation Technique in Transformer Winding Deformation Fault Diagnosis. Eng. Fail. Anal. 2024, 159, 108115. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, G.; Yang, D.; Xu, G.; Xing, Y.; Yao, C.; Abu-Siada, A. Enhanced Detection of Power Transformer Winding Faults Through 3D FRA Signatures and Image Processing Techniques. Electr. Pow. Syst. Res. 2025, 242, 111433. [Google Scholar] [CrossRef]
- Zhao, X.; Yao, C.; Li, C.; Zhang, C.; Dong, S.; Abu-Siada, A.; Liao, R. Experimental Evaluation of Detecting Power Transformer Internal faults Using FRA Polar Plot and Texture Analysis. Int. J. Electr. Power Energy Syst. 2019, 108, 1–8. [Google Scholar] [CrossRef]
- Zhao, X.; Yao, C.; Abu-Siada, A.; Liao, R. High Frequency Electric Circuit Modeling for Transformer Frequency Response Analysis Studies. Int. J. Electr. Power Energy Syst. 2019, 111, 351–368. [Google Scholar] [CrossRef]
- Tang, W.; Shintemirov, A.; Wu, Q. Detection of Minor Winding Deformation Fault in High Frequency Range for Power Transformer. In Proceedings of the IEEE Power & Energy Society General Meeting, Minneapolis, MN, USA, 25–29 July 2010. [Google Scholar]
- Usha, K.; Usa, S. Inter Disc Fault Location in Transformer Windings Using SFRA. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 3567–3573. [Google Scholar] [CrossRef]
- Bian, H.; Zhang, L. Gesture Recognition Based on Gramian Angular Difference Field and Multi-stream Fusion Methods. Signal Image Video Process. 2025, 19, 120. [Google Scholar] [CrossRef]
- Mohammadjafari, S.; Ozyegen, O.; Cevik, M.; Kavurmacioglu, E.; Ethier, J.; Basar, A. Designing Mm-wave Electromagnetic Engineered Surfaces Using Generative Adversarial Networks. Neural Comput. Appl. 2021, 33, 11309–11323. [Google Scholar] [CrossRef]
- Hong, I.; Ha, J. Generative Adversarial Networks for Solving Hand-Eye Calibration Without Data Correspondence. IEEE Robot. Autom. Lett. 2025, 10, 2494–2501. [Google Scholar] [CrossRef]
- Zhang, C.; Feng, Y.; Qiang, B.; Shang, J. Wasserstein Generative Recurrent Adversarial Networks for Image Generating. In Proceedings of the 24th International Conference on Pattern Recognition, Beijing, China, 20–24 August 2018. [Google Scholar]
- Mu, D.; Meng, W.; Zhao, S.; Wang, X.; Liu, W. Intelligent Optical Communication Based on Wasserstein Generative Adversarial Network. Chin. J. Lasers 2020, 47, 217–233. [Google Scholar] [CrossRef]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved Training of Wasserstein GANs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Tang, X.; Du, Y.; Liu, Y.; Li, J.; Jia, Y.; Ma, Y. Image Recognition With Conditional Deep Convolutional Generative Adversarial Networks. Acta. Autom. Sin. 2018, 44, 855–864. [Google Scholar] [CrossRef]
- Li, Y.; Du, Y.; Xiao, N.; Ouyang, W. Improved Boundary Equilibrium Generative Adversarial Networks. Acta IEEE Access 2018, 6, 11342–11348. [Google Scholar] [CrossRef]
- Park, S.W.; Huh, J.H.; Kim, J.C. BEGAN v3: Avoiding Mode Collapse in GANs Using Variational Inference. Electronics 2020, 9, 688. [Google Scholar] [CrossRef]
- Tang, Y. ECGAN: Translate Real World to Cartoon Style Using Enhanced Cartoon Generative Adversarial Network. Comput. Mater. Contin. 2023, 76, 1195–1212. [Google Scholar] [CrossRef]
- Wu, Z.; Li, M. ResNet-Swin Transformer Based Intrusion Detection System for In-vehicle Network. Expert Syst. Appl. 2025, 279, 127547. [Google Scholar] [CrossRef]
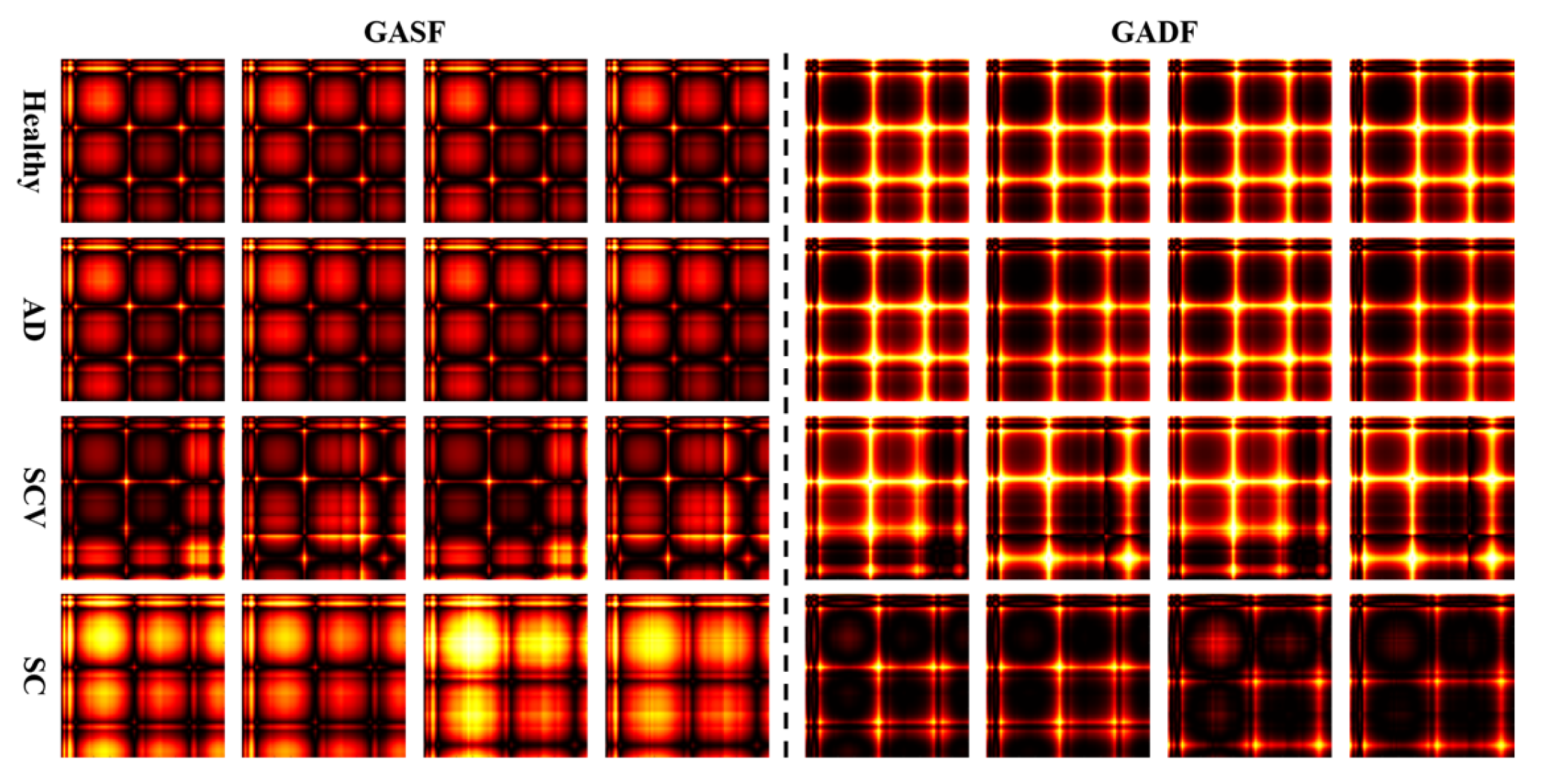

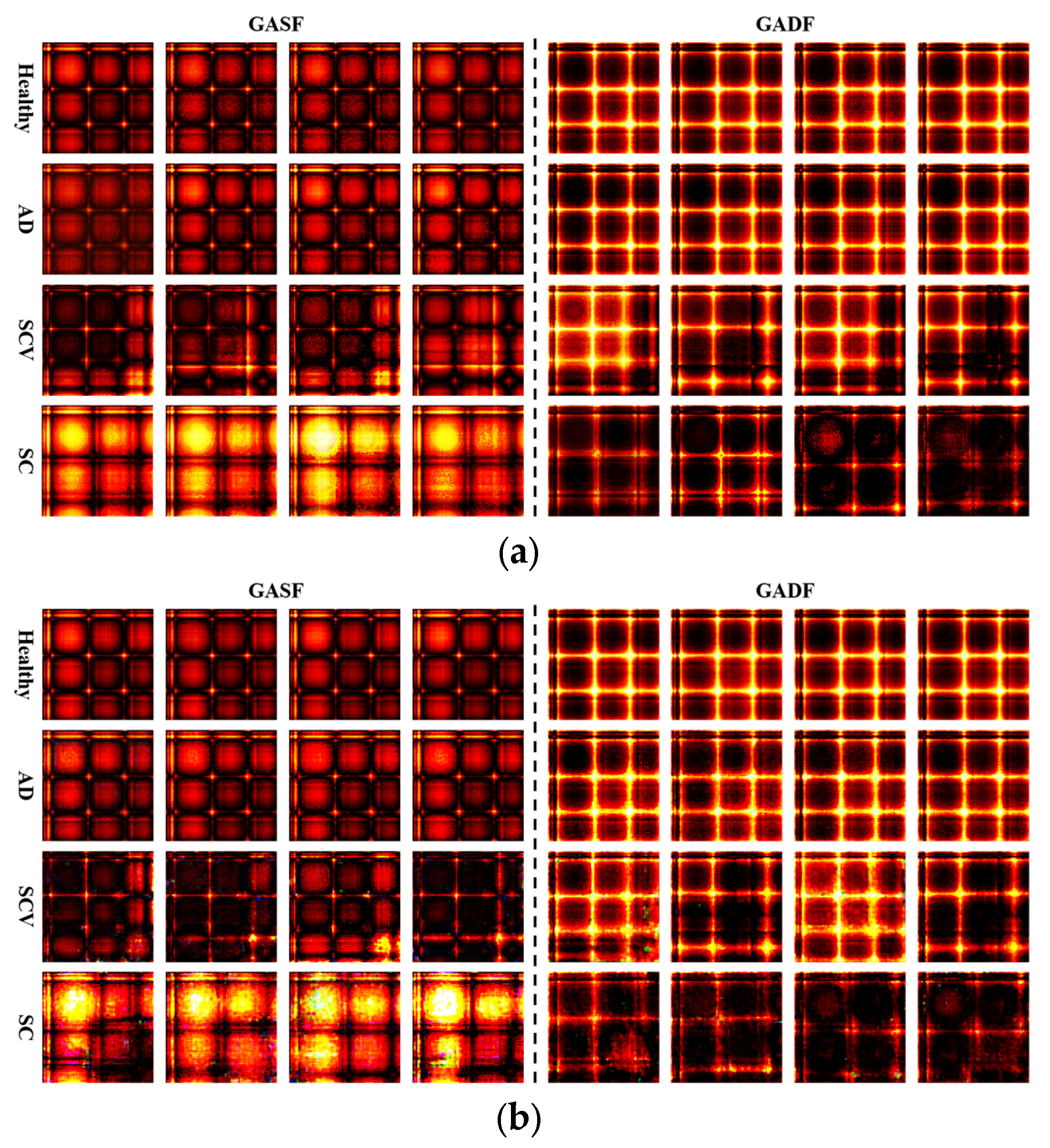



| Method | Accuracy | Sample Size | Limitations |
|---|---|---|---|
| BP Neural Network | 84.2% | 200+ | Slow convergence; manual features |
| CNN-BiGRU | 92.7% | 150 | Requires curve preprocessing |
| Twin CNN | 89.4% | 100 | Limited to binary faults |
| VAE Augmentation | 88.1% | 50 | Blurred high-frequency features |
| Proposed GAF–GAN–ResNet34 | 96.9% | 28 | Small sample-optimized |
| Structure | Parameter | Value |
|---|---|---|
| HV winding | Number of line cakes | 16 |
| Number of turns per coil | 16 | |
| Wire cake height/mm | 9 | |
| Wire cake width/mm | 34 | |
| Winding height/mm | 474 | |
| LV winding | Number of line cakes | 16 |
| Number of turns per coil | 8 | |
| Wire cake height/mm | 9 | |
| Wire cake width/mm | 17 | |
| Winding height/mm | 474 |
| Number | Faulty Line Cake Position | Fault Severity |
|---|---|---|
| 1 | 7 | 50% |
| 2 | 7 | 100% |
| 3 | 13 | 50% |
| 4 | 13 | 100% |
| Number | Faulty Joint Position | Fault Severity |
|---|---|---|
| 1 | 7, 8 | 200 pF |
| 2 | 7, 8 | 560 pF |
| 3 | 13, 14 | 200 pF |
| 4 | 13, 14 | 560 pF |
| Number | Faulty Line Cake Position |
|---|---|
| 1 | 5, 6 |
| 2 | 7, 8 |
| 3 | 13, 14 |
| 4 | 15, 16 |
| Structure | GAN Type | SSIM | PSNR | CS | FID |
|---|---|---|---|---|---|
| GASF | WGAN-GP | 0.8176 | 32.79 | 0.7394 | 92.73 |
| DCGAN | 0.6826 | 32.41 | 0.7026 | 192.43 | |
| BEGAN | 0.6734 | 31.16 | 0.8473 | 46.49 | |
| GDSF | WGAN-GP | 0.7896 | 32.65 | 0.838 | 62.32 |
| DCGAN | 0.76 | 32.54 | 0.7445 | 183.85 | |
| BEGAN | 0.7886 | 32.37 | 0.902 | 31.38 |
| Layer Type | Input Dimension | Output Dimension | Activation Function | Normalisation |
|---|---|---|---|---|
| Conv2d | (batch_size,3,img_size,img_size) | (batch_size,64,img_size/2,img_size/2) | ReLU | BatchNorm |
| MaxPool2d | (batch_size,64,img_size/2,img_size/2) | (batch_size,64,img_size/4,img_size/4) | ||
| Residual Block1 | (batch_size,64,img_size/4,img_size/4) | (batch_size,64,img_size/4,img_size/4) | ReLU | BatchNorm |
| Residual Block2 | (batch_size,64,img_size/4,img_size/4) | (batch_size,128,img_size/8,img_size/8) | ReLU | BatchNorm |
| Residual Block3 | (batch_size,128,img_size/8,img_size/8) | (batch_size,256,img_size/16,img_size/16) | ReLU | BatchNorm |
| Residual Block4 | (batch_size,256,img_size/16,img_size/16) | (batch_size,256,img_size/32,img_size/32) | ReLU | BatchNorm |
| Adaptive AvgPool2d | (batch_size,256,img_size/32,img_size/32) | (batch_size,512,1,1) | ||
| Reshape | (batch_size,512,1,1) | (batch_size,512) | ||
| Linear | (batch_size,512) | (batch_size,4) | ||
| Softmax | (batch_size,4) | (batch_size,1) | ReLU | BatchNorm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yang, K.; Qian, G.; Hu, J.; Dai, W.; Zhu, L.; Guo, T.; Shi, J.; Wang, D. Gramian Angular Field–Gramian Adversial Network–ResNet34: High-Accuracy Fault Diagnosis for Transformer Windings with Limited Samples. Energies 2025, 18, 4329. https://doi.org/10.3390/en18164329
Liu H, Yang K, Qian G, Hu J, Dai W, Zhu L, Guo T, Shi J, Wang D. Gramian Angular Field–Gramian Adversial Network–ResNet34: High-Accuracy Fault Diagnosis for Transformer Windings with Limited Samples. Energies. 2025; 18(16):4329. https://doi.org/10.3390/en18164329
Chicago/Turabian StyleLiu, Hongwen, Kun Yang, Guochao Qian, Jin Hu, Weiju Dai, Liang Zhu, Tao Guo, Jun Shi, and Dongyang Wang. 2025. "Gramian Angular Field–Gramian Adversial Network–ResNet34: High-Accuracy Fault Diagnosis for Transformer Windings with Limited Samples" Energies 18, no. 16: 4329. https://doi.org/10.3390/en18164329
APA StyleLiu, H., Yang, K., Qian, G., Hu, J., Dai, W., Zhu, L., Guo, T., Shi, J., & Wang, D. (2025). Gramian Angular Field–Gramian Adversial Network–ResNet34: High-Accuracy Fault Diagnosis for Transformer Windings with Limited Samples. Energies, 18(16), 4329. https://doi.org/10.3390/en18164329






