Study on the Width of a Narrow Coal Pillar for Gob-Side Entry Driving near an Advancing Working Face in a Shallow Coal Seam
Abstract
1. Introduction
2. Case Study
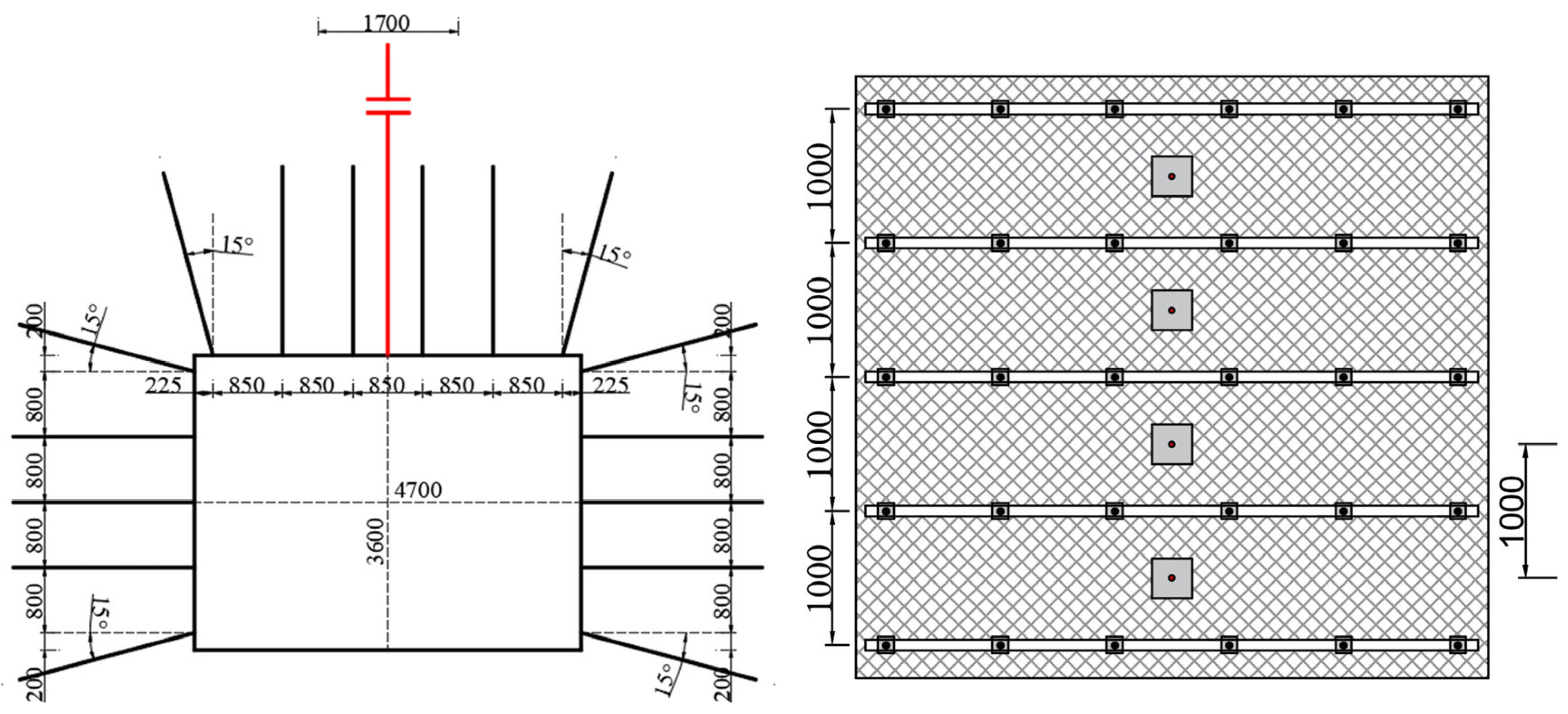
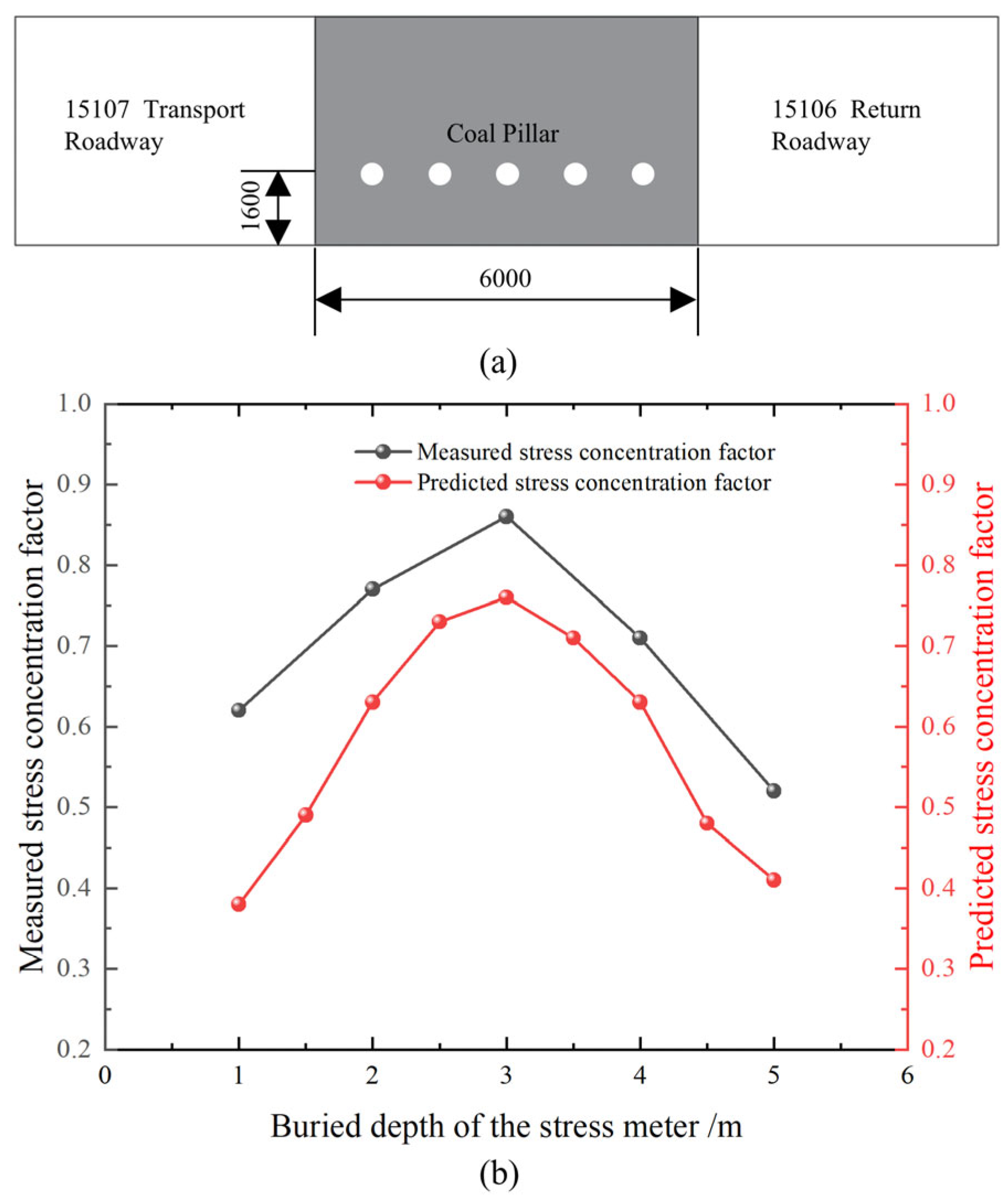
2.1. Field Background
2.2. Roadway Support
3. The Theoretical Determination of Coal Pillar Width
3.1. Coal Pillar Stress Analysis
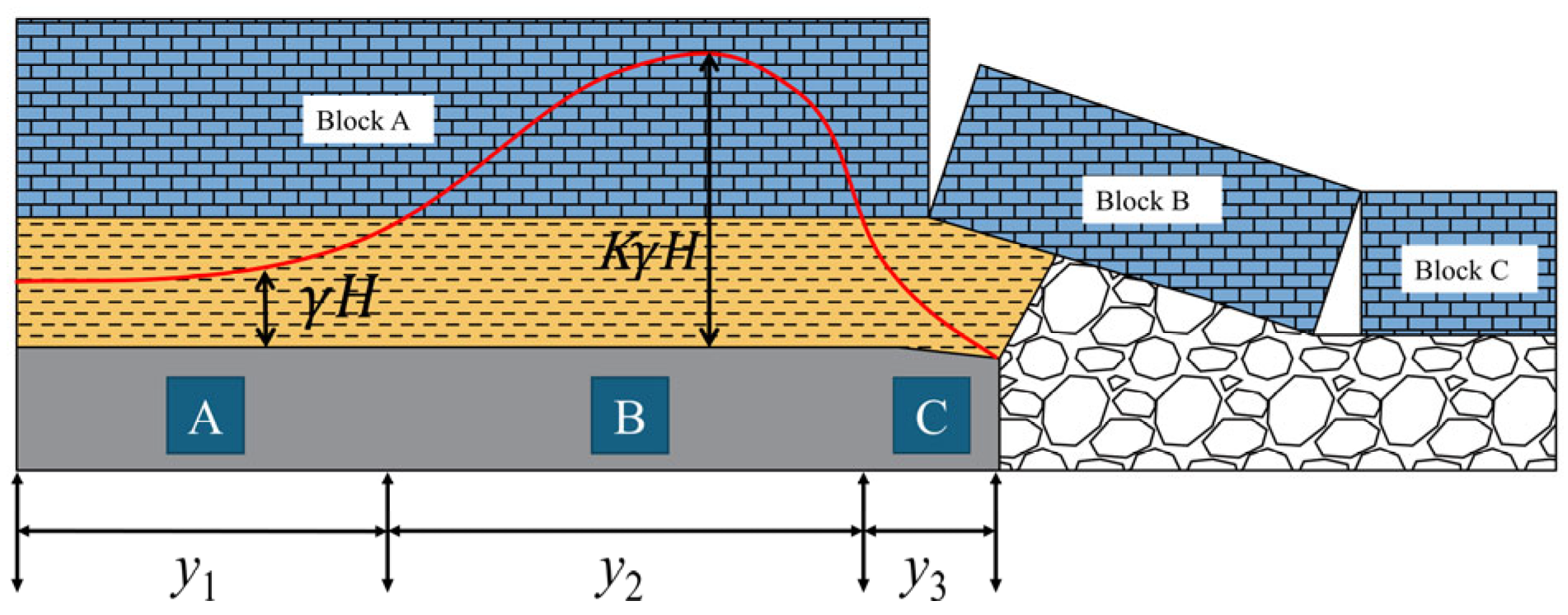
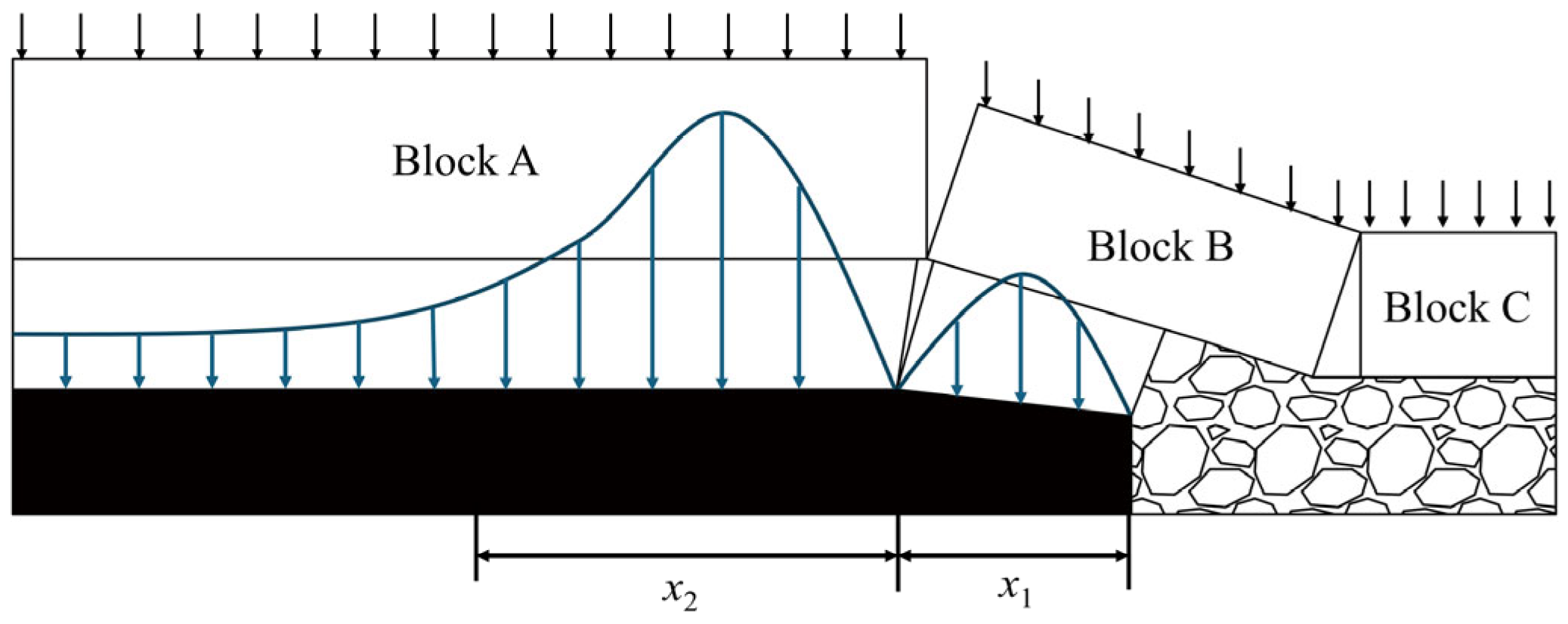
3.2. The Theory of Internal and External Stress Fields
3.3. Theoretical Calculation of Reasonable Coal Pillar Width
4. Establishment and Calibration of the Numerical Model
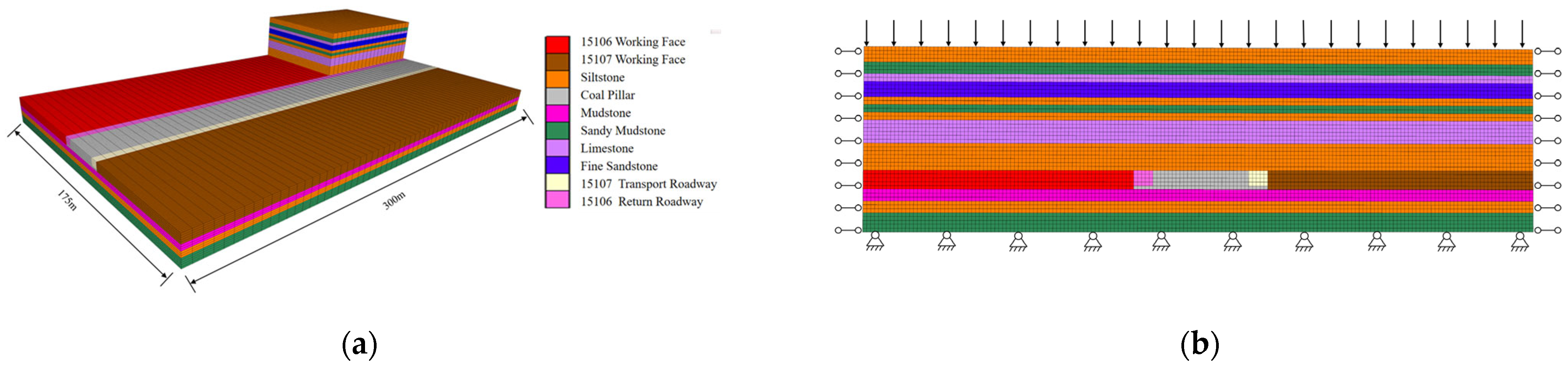
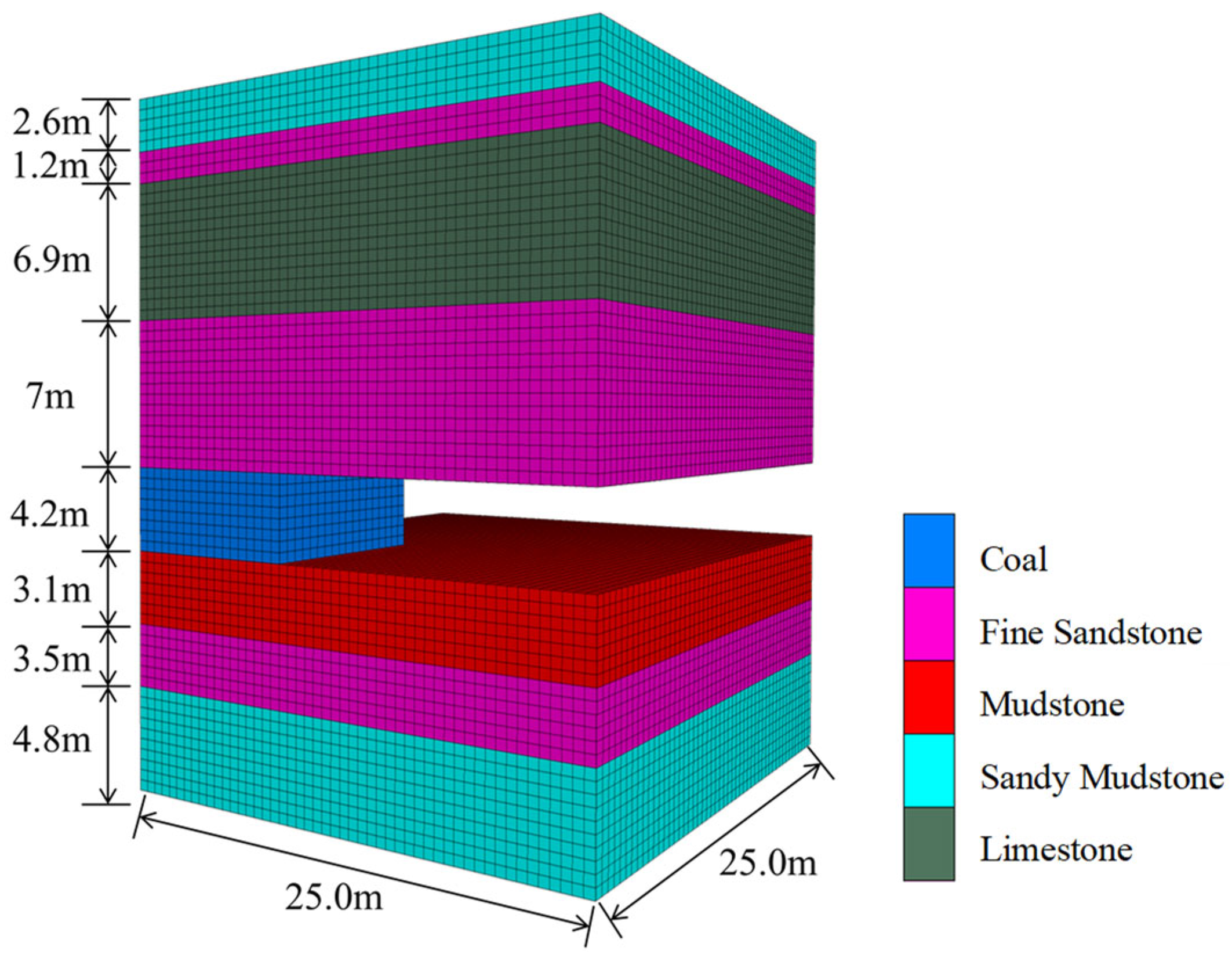
4.1. Numerical Model
4.2. Calibration of the Double-Yield Model for the Gob
4.2.1. Characteristics of Roof Rock
4.2.2. Determination of Model Parameters
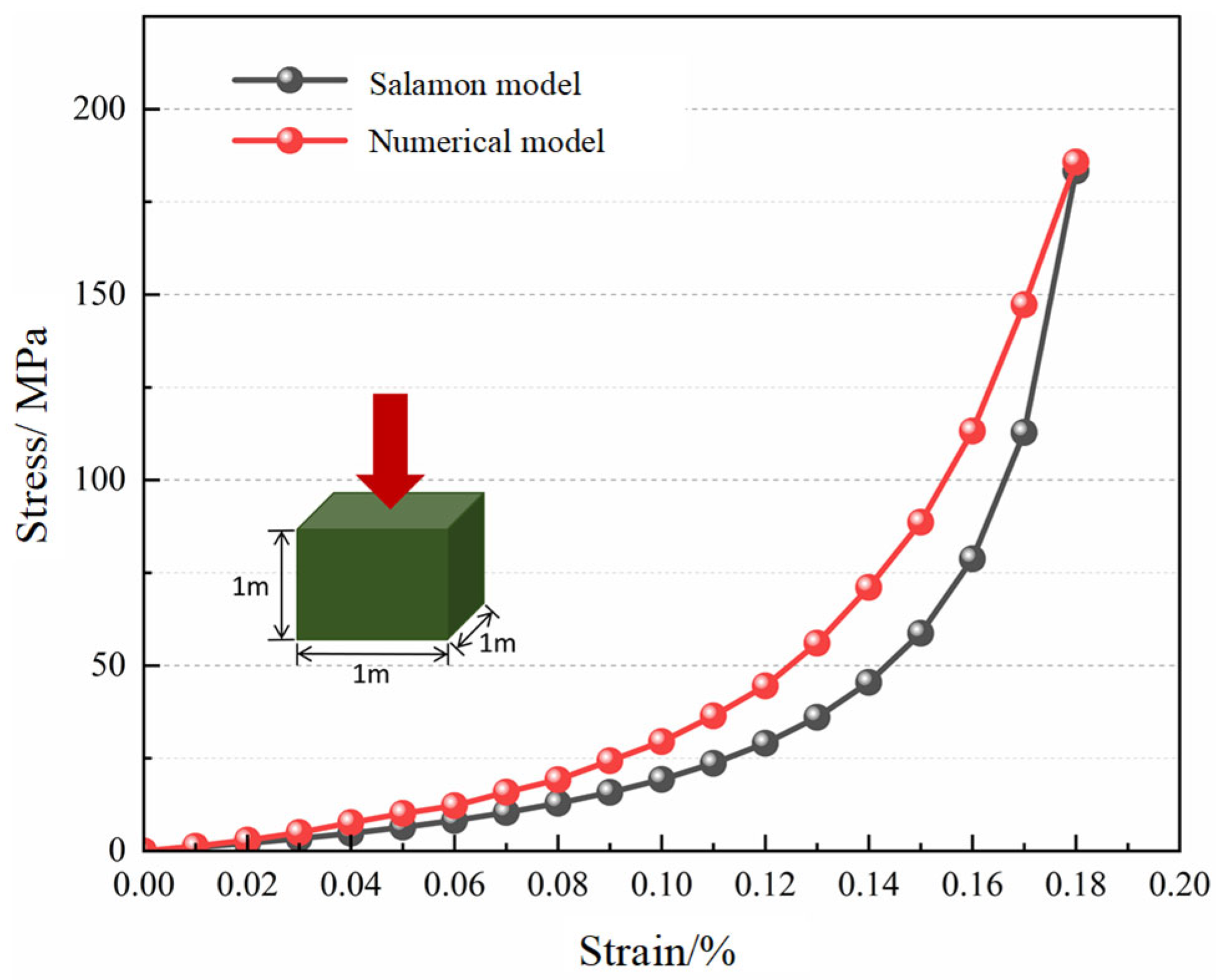
4.2.3. Validation of the Double-Yield Model for the Gob
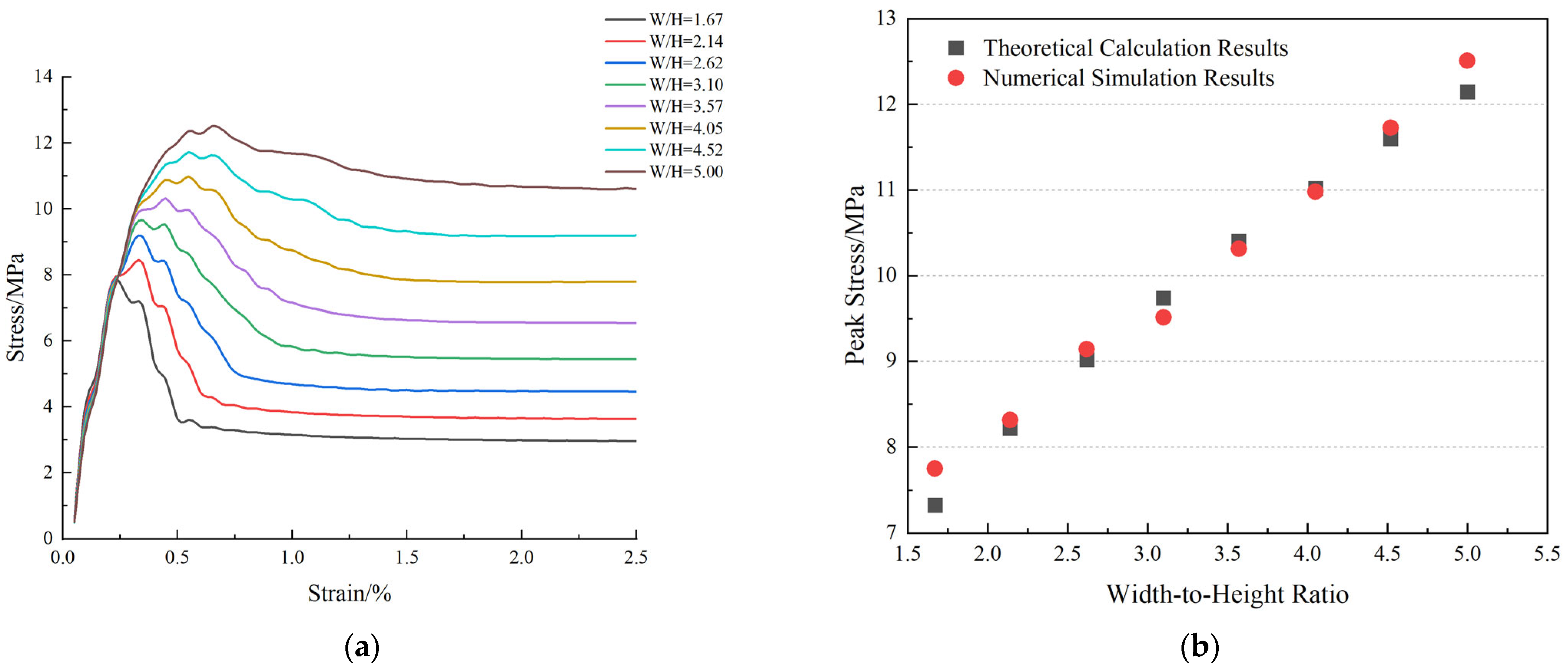
4.3. Calibration of the Strain-Softening Model for Coal Pillars
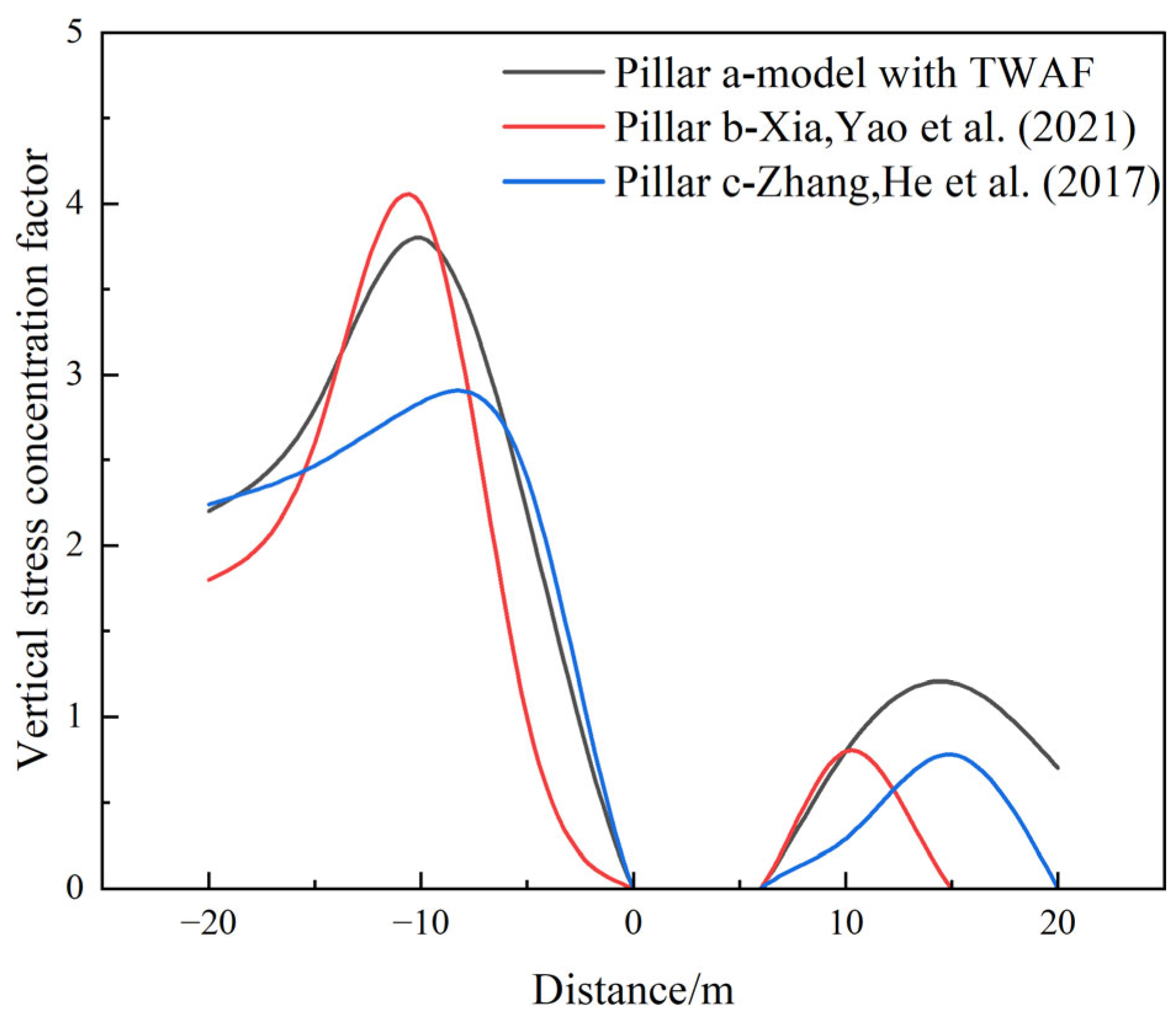
4.4. Validation of Global Model
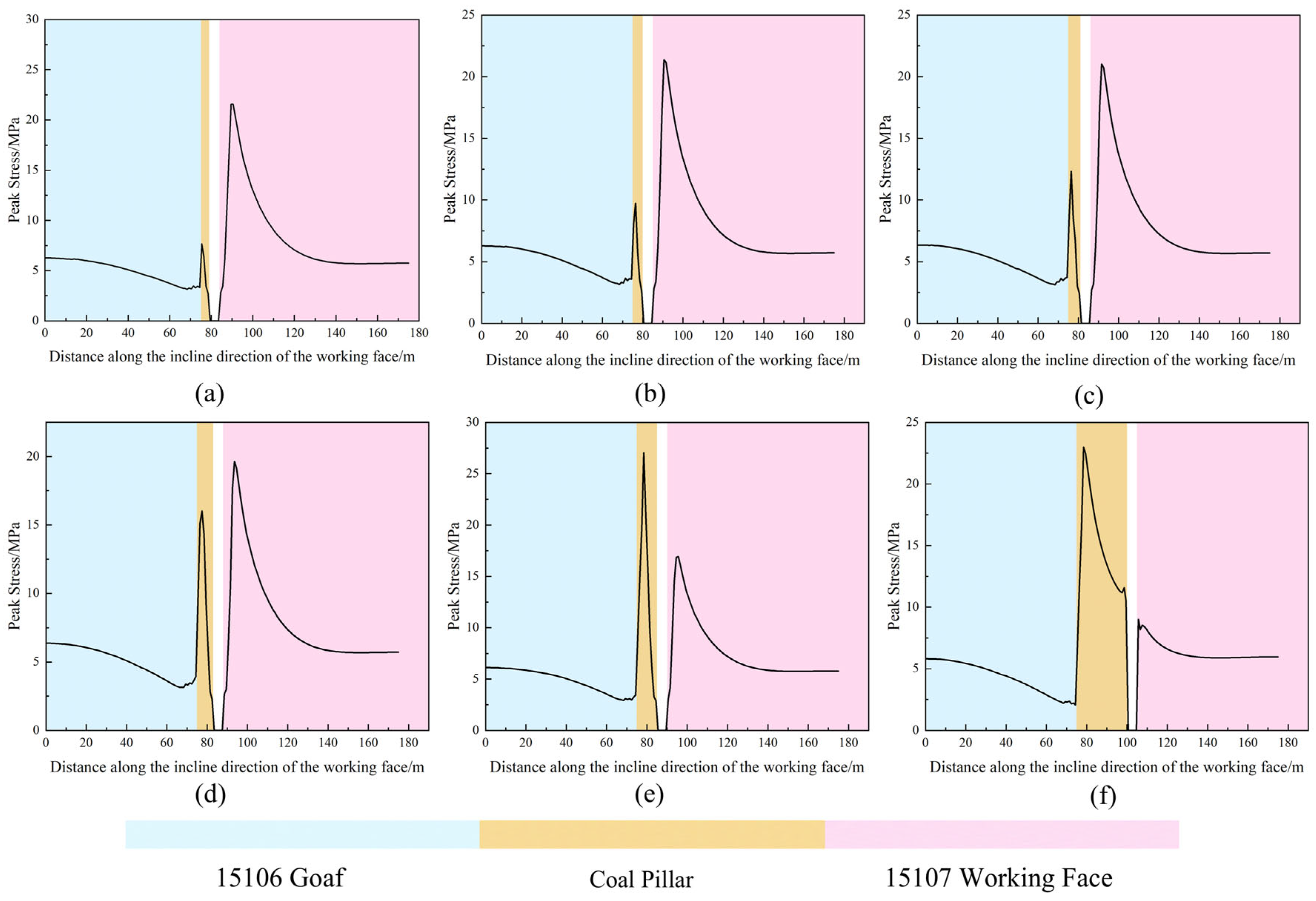
5. Simulation Results and Analysis
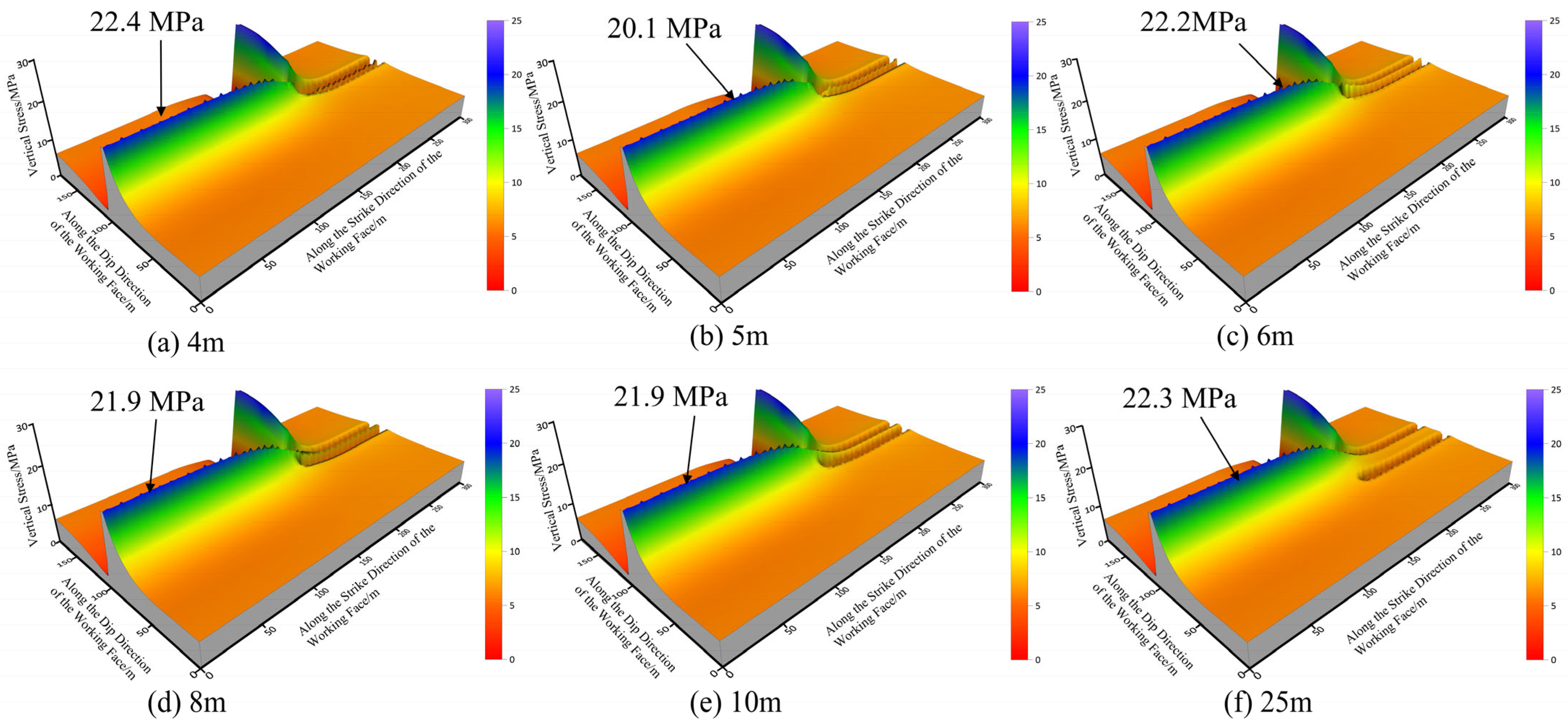
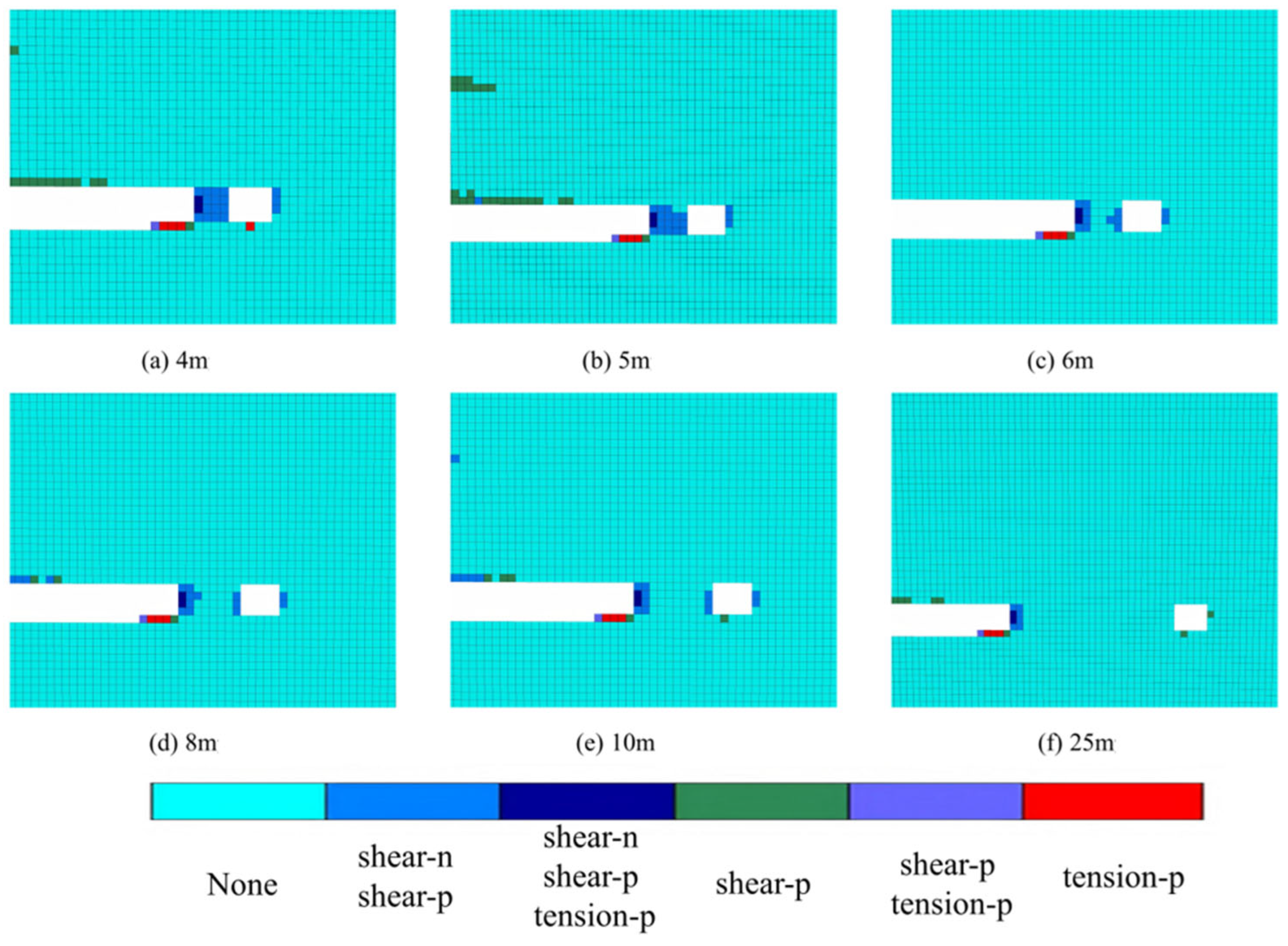
5.1. During the Roadway Driving near the Advancing 15106 Working Face
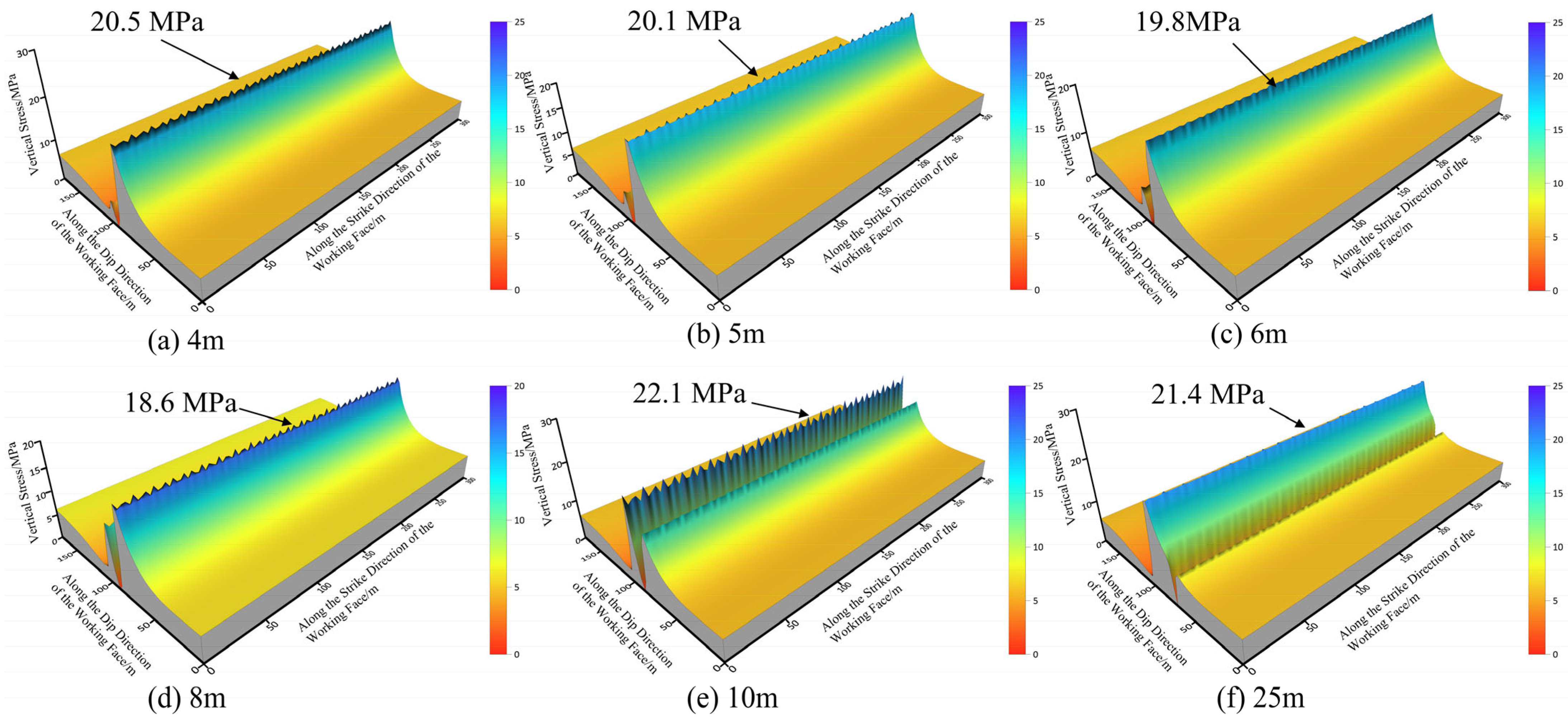
5.2. During the Tunneling Period Along the Gob
5.3. During the Mining of the 15107 Working Face
6. Field Test
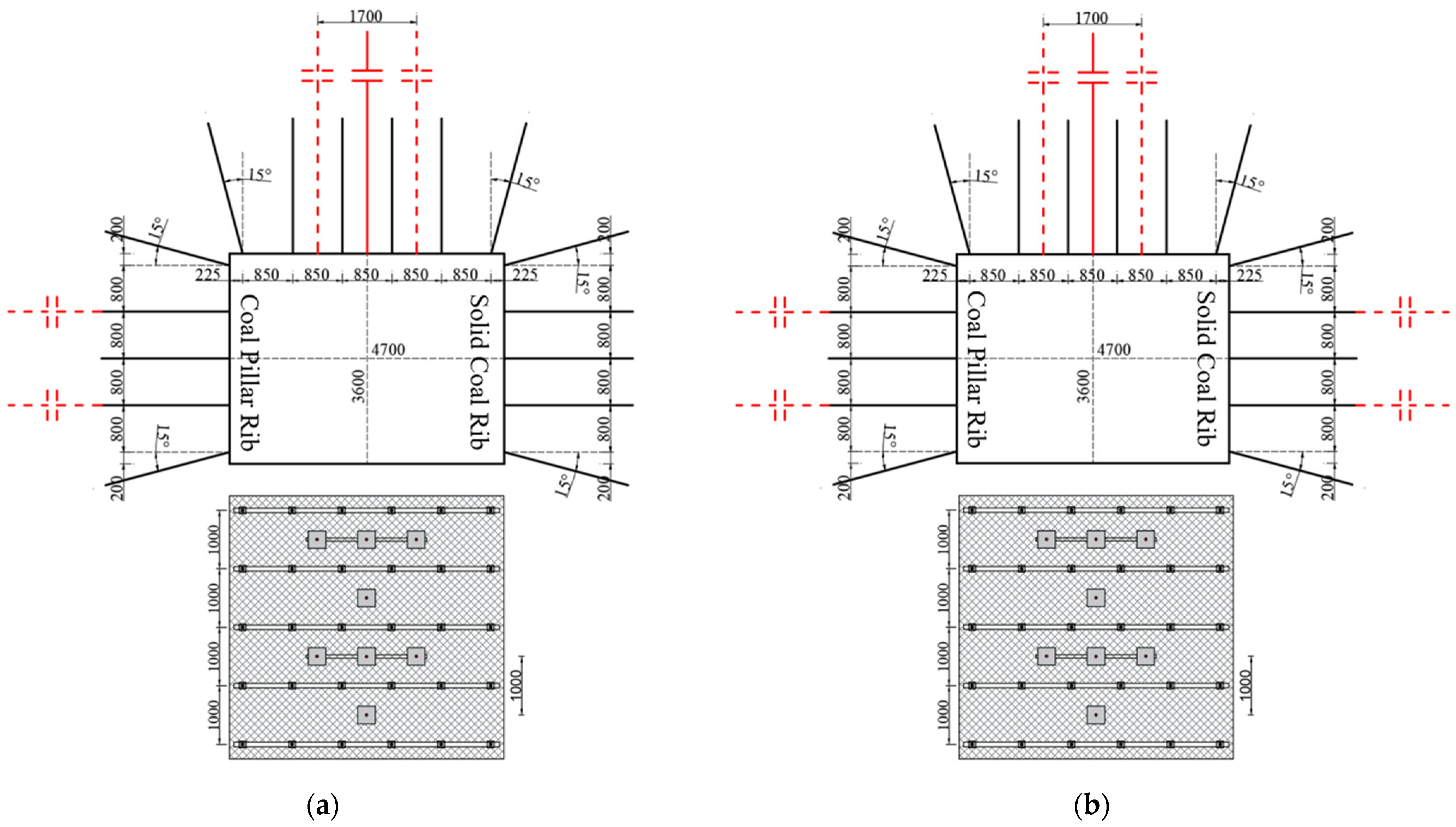
6.1. Optimization of Roadway Support Scheme
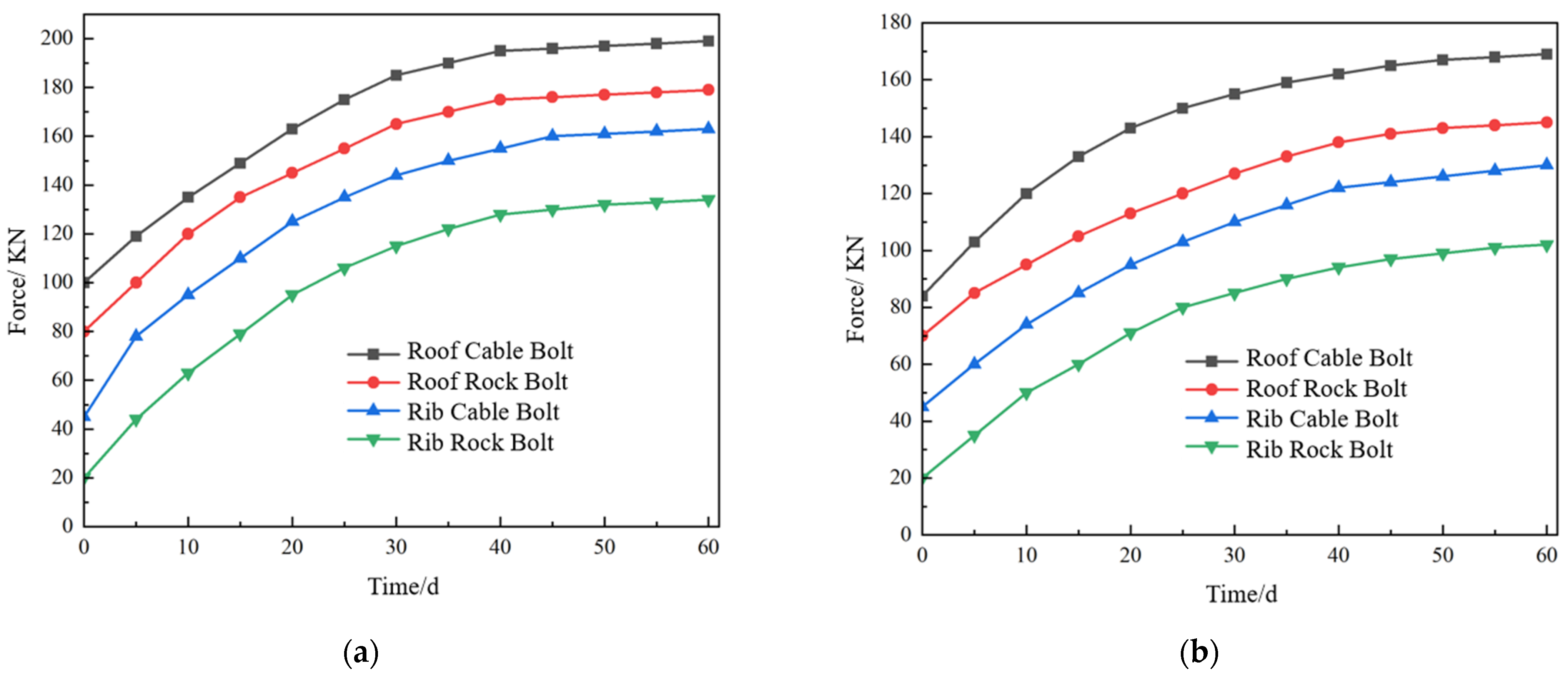
6.2. Ground Pressure Measurement
7. Discussion
8. Conclusions
- (1)
- Based on the internal–external stress field theory and limit equilibrium analysis, the optimal coal pillar width was determined to be 6 m, with an internal stress field extent of 9.83~11.43 m. Placing the roadway within this field locates it in a stress-reduction zone, ensuring stability and ease of maintenance.
- (2)
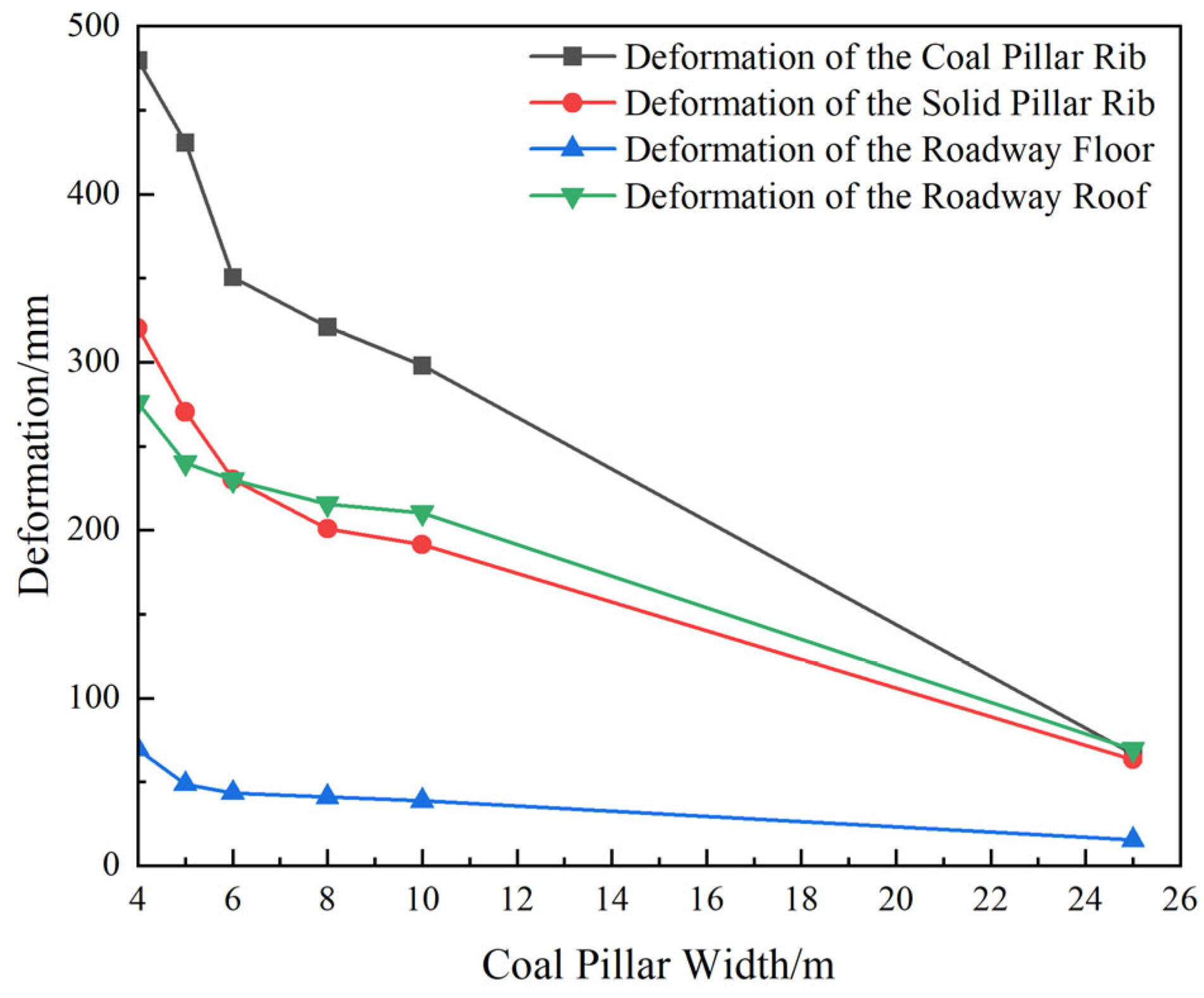
- During the gob-side entry driving near the advancing 15106 face, with pillar widths of 4 m and 5 m, the plastic zone penetrated the entire pillar, leaving minimal stress concentration zones and rendering the pillar almost incapable of bearing loads. For widths above 5 m, an elastic core formed within the pillar and the stress concentration area expanded. As the width increased, so did the elastic zone, resulting in an improved load-bearing capacity. The assessment during excavation along the gob showed that at a 25 m width, the pillar’s stress profile has two peaks, corresponding to peak support capacity and minimal face stress at 15107. For widths of 4, 5, 6, 8, and 10 m, the stress curve is single-peaked, and the peak stress increases with pillar width. During the 15107 face advance, with sectional pillars of 3~6 m, the pillar remains in a stress-reduction zone; however, the 4 m and 5 m pillars had already plastically failed during face-to-face driving, lacking adequate support strength. Therefore, a 6 m pillar width is recommended.
- (3)
- Based on these theoretical and numerical findings, support schemes were optimized for each roadway stage, the bolt and cable parameters were established, and real-time field monitoring was implemented. The monitoring results indicate that with a 6 m pillar and the roadway placed within the internal stress field, the surrounding rock deformation was effectively controlled, meeting project requirements.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.X.; Gao, M.S.; He, Y.L.; Yu, X.; Xu, D. Study of control technology about gob-side entry driving with top-coal caving in inclined extra-thick coal seam. J. China Univ. Ming Technol. 2021, 50, 1051–1059. [Google Scholar]
- Chen, D.; Wang, X.; Bai, J.; Li, M.; Lu, J.; Zhang, F.; Sun, S.; Zhao, X.; Yu, Y. Full cycle evolution law of energy-stress in the surrounding rock of the gob-side entry driving for adjacent advancing working face. Coal Sci. Technol. 2025, 53, 162–175. [Google Scholar]
- Cong, C.K.; Lim, R.W.; Sun, Y.C.; Gao, L.L. Stress evolution law and sectional control technology of surrounding rock in heading for adjacent advancing working face. J. Xi’an Univ. Sci. Technol. 2024, 44, 1071–1082. [Google Scholar]
- Di, X.F.; Zhang, B.S.; Guo, J.Q.; Chen, L.H.; Yang, Z.P.; Zhang, Z. Research on Law of Mine Pressure Behaviour of Roadway with Facing Large Mining Height and Roof-Slope Synergistic Reinforcement Support Technology. Coal Technol. 2022, 41, 44–48. [Google Scholar]
- Wu, W.D.; Wang, T.C.; Bai, J.B.; Liu, J.H.; Wang, X.Y.; Xu, H.Y.; Feng, G.R. Failure Characteristics and Cooperative Control Strategies for Gob-Side Entry Driving near an Advancing Working Face: A Case Study. Processes 2024, 12, 1398. [Google Scholar] [CrossRef]
- Chen, X.X.; Wang, Y.L.; Zhang, T. Deformation Law and Control Technique of Surrounding Rock in Gob-side Entry Driving Under Driven Heading for Adjacent Advancing Coal Face Conditions. Saf. Coal Mines 2020, 51, 66–71,76. [Google Scholar]
- Kang, J. Study on Surrounding Rock Deformation Rule and Sectional Control Technology of Roadway with Strong Dynamic Pressure. Min. Saf. Environ. Prot. 2017, 44, 74–78. [Google Scholar]
- Liu, J.H.; Cao, Y.Q.; Wei, Z.Q.; Shen, W. Research on reasonable width of partition pillar close to goaf heading mining in thick seam of deep shaft. Chin. J. Rock Mech. Eng. 2015, 34, 4269–4277. [Google Scholar]
- Zong, B.D.; Chen, L.H. Bearing characteristics and mine pressure behavior of wide coal pillars facing mining. Coal Eng. 2024, 56, 1–7. [Google Scholar]
- Yu, Y.; Wang, X.Y.; Xue, G.Z.; Zhong, D.Y. Dynamic sectional control technology of surrounding rock in gateway driving along goaf forward to mining face. Coal Sci. Technol. 2013, 41, 43–46. [Google Scholar]
- Hui, G.; Niu, S.; Jing, H. Physical simulation on deformation rules of god-side roadway subjected to dynamic pressure. J. Min. Saf. Eng. 2010, 27, 77–86. [Google Scholar]
- Wang, M.; Bai, J.-B.; Wang, X.-Y. The surrounding rock deformation rule and control technique of the roadway driven along goaf and heading for adjacent advancing coal face. J. Min. Saf. Eng. 2012, 29, 197–202. [Google Scholar]
- Zhang, N.; Li, X.H.; Gao, M.S. Pretensioned support of roadway driven along next gob and heading adjacent advancing coal face and its application. Chin. J. Rock Mech. Eng. 2004, 23, 2100–2105. [Google Scholar]
- Qi, F.; Zhou, Y.; Cao, Z.; Zhang, C.Q.; Li, N. Width optimization of narrow coal pillar of roadway driving along goaf in fully mechanized top coal caving face. J. Min. Saf. Eng. 2016, 33, 475–480. [Google Scholar]
- Zhang, G.; He, F.; Lai, Y.; Song, J.W.; Xiao, P. Reasonable width and control technique of segment coal pillar with high-intensity fully-mechanized caving mining. J. China Coal Soc. 2016, 41, 2188–2194. [Google Scholar]
- Sun, L.; Ding, B.; Li, W.; Chen, Z.; Shang, D.; Zhang, Y.; Song, J. Width optimization and application of narrow coal pillar in gob-side entry driven in thick coal seam in Luzigou Mine. J. Min. Saf. Eng. 2023, 40, 1151–1160. [Google Scholar]
- Ma, Z.Q.; Chen, C.; Liang, X.C.; Chen, A.M.; Song, W.X. Field and numerical investigation on the stability of coal pillars of gob-side entry driving with top coal. Arab. J. Geosci. 2020, 13, 1193. [Google Scholar] [CrossRef]
- Yu, Y.; Hong, X.; Chen, F. Study on load transmission mechanism and limit equilibrium zone of coal wall in extraction opening. J. China Coal Soc. 2012, 37, 1630–1636. [Google Scholar]
- Zhang, D.; Bai, J.B.; Tian, Z.J.; Zhang, Z.Z.; Guo, Y.H.; Wang, R.; Xu, Y.; Fu, H.; Yan, S.; Deng, M.; et al. Stability Mechanism and Control of the Pumpable Supports in Longwall Recovery Room. Int. J. Min. Sci. Technol. 2024, 34, 957–974. [Google Scholar] [CrossRef]
- Minneapolis, M.N.; Itasca Consulting Group (2023). FLAC3D (Version 9.0). Available online: https://www.itascacg.com/software/flac3d (accessed on 10 April 2025).
- Chen, D.C.; Wang, X.Y.; Bai, J.B.; Li, M.L. Correction: Characteristics of waterproof failure and optimal width of narrow coal pillars under the coupled effects of mining, excavation and seepage. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 190. [Google Scholar] [CrossRef]
- Zhu, G.; Liu, B.; Dou, L.; Wu, Y.P.; Ding, Z.W. Numerical simulation for whole process of longwall mining on the basis of goaf compaction effect. J. China Univ. Min. Technol. 2019, 48, 775–783. [Google Scholar]
- Whittles, D.N.; Lowndes, I.S.; Kingman, S.W.; Yates, C.; Jobling, S. Influence of geotechnical factors on gas flow experienced in a UK longwall coal mine panel. Int. J. Rock Mech. Min. Sci. 2006, 43, 369–387. [Google Scholar] [CrossRef]
- Wang, W.; Wang, S.; Liu, H.; Jiang, T.; Ren, M. The space and time characteristics of the cover stress re-establishment of the fractured rock mass in the goaf after coal mining. J. Min. Saf. Eng. 2017, 34, 127. [Google Scholar]
- Zhang, G.; Tao, G.; Cao, Z.; Zhao, Y.; Xu, Z.; Li, Y.; Zuo, H. Study on failure characteristics of stope overlying rock considering strain hardening characteristics of caved rock mass. Coal Sci. Technol. 2022, 50, 46–52. [Google Scholar]
- Yavuz, H. An estimation method for cover pressure re-establishment distance and pressure distribution in the goaf of longwall coal mines. Int. J. Rock Mech. Min. Sci. 2004, 41, 193–205. [Google Scholar] [CrossRef]
- Chen, D.C.; Wang, X.Y.; Wu, S.; Zhang, F.T.; Fan, Z.Z.; Wang, X.D.; Li, M.L. Study on stability mechanism and control techniques of surrounding rock in gob-side entry retaining with flexible formwork concrete wall. J. Cent. South Univ. 2023, 30, 2966–2982. [Google Scholar] [CrossRef]
- Chen, D.C.; Wang, X.Y.; Zhang, F.T.; Bai, J.B.; Zhao, X.Q.; Li, M.L.; Sun, S.Q. Study on the mechanism of progressive instability of special-shaped coal pillar and the stability control of roadway under the influence of mining. Rock Mech. Rock Eng. 2024, 57, 6461–6483. [Google Scholar] [CrossRef]
- Xia, Z.; Yao, Q.L.; Meng, G.S.; Xu, Q.; Tang, C.J.; Zhu, L.; Shen, Q. Numerical study of stability of mining roadways with 6.0-m section coal pillars under influence of repeated mining. Int. J. Rock Mech. Min. Sci. 2021, 138, 104641. [Google Scholar] [CrossRef]
- Shan, C.; Shang, H.; Zhang, Q.; Li, Y.; Liu, W.; Huang, P. Width and bearing strength check of “two hard” coal pillar in fully mechanized caving face. J. Min. Strat. Control Eng. 2024, 6, 023022. [Google Scholar]
- Xing, C.; Wang, J.; Ning, J.; Shen, Z. Instability failure mechanism of coal pillar in deep mine under dynamic disturbance. Coal Sci. Technol. 2023, 51, 29–36. [Google Scholar]
- Li, W.F.; Bai, J.B.; Peng, S.; Wang, X.Y.; Xu, Y. Numerical modeling for yield pillar design: A case study. Rock Mech. Rock Eng. 2015, 48, 305–318. [Google Scholar] [CrossRef]
- Wang, M.; Li, Z.; Shang, D.; Wei, S.; Shan, F.; Liu, H.; Zheng, K.; Li, Z. Study on energy characterization and control of unstable coal pillar in dynamic pressure gob-side entry. J. Min. Saf. Eng. 2024, 41, 958–970. [Google Scholar]
- Zhang, G.; He, F.L.; Jia, H.G.; Lai, Y.H. Analysis of Gateroad Stability in Relation to Yield Pillar Size: A Case Study. Rock Mech. Rock Eng. 2017, 50, 1263–1278. [Google Scholar] [CrossRef]









| Variable | Value | Variable | Value | Variable | Value |
|---|---|---|---|---|---|
| γ | 25 kN/m3 | L | 175 m | L0 | 18.3~22.3 m |
| hj | 8.1 m | B1 | 41.8~46.4 m | υ | 0.3 |
| ξ | 0.8 | E | 2.5 GPa | M | 4.2 m |
| h0 | 7 m | KP | 1.4 | A | 0.43 |
| φ0 | 32° | C0 | 1.78 MPa | k | 2.5 |
| H | 236 m | px | 0.2 MPa | σc | 43.7 MPa |
| Lithology | Thickness /m | Density /(kg/m3) | Bulk Modulus /GPa | Shear Modulus /GPa | Cohesion /MPa | Friction Angle /(°) | Tensile Strength /MPa |
|---|---|---|---|---|---|---|---|
| Siltstone | 4.5 | 2560 | 10.83 | 6.4 | 6.3 | 35 | 2.8 |
| Sandy Mudstone | 2.2 | 2597 | 7.4 | 5.47 | 3.29 | 32 | 1.69 |
| Limestone | 2.5 | 2610 | 11.72 | 9.11 | 6.61 | 37 | 3.72 |
| Fine Sandstone | 3.8 | 2650 | 6.94 | 3.97 | 3.5 | 30 | 2.8 |
| Siltstone | 1.9 | 2560 | 10.83 | 6.4 | 6.3 | 35 | 2.8 |
| Sandy Mudstone | 2.6 | 2597 | 7.4 | 5.47 | 3.29 | 32 | 1.69 |
| Siltstone | 1.2 | 2560 | 10.83 | 6.4 | 4.3 | 30 | 1.8 |
| Limestone | 6.9 | 2610 | 11.72 | 9.11 | 6.01 | 37 | 3.72 |
| Siltstone | 7 | 2560 | 10.83 | 6.4 | 6.3 | 35 | 2.8 |
| No. 15 Coal | 4.2 | 1407 | 1.93 | 1.38 | 1.78 | 32 | 0.45 |
| Mudstone | 3.1 | 2370 | 5.99 | 3.01 | 2.66 | 31 | 1.19 |
| Siltstone | 3.5 | 2560 | 10.83 | 6.4 | 6.3 | 35 | 2.8 |
| Sandy Mudstone | 4.8 | 2597 | 7.4 | 5.47 | 3.29 | 32 | 1.69 |
| Rock Type Category | Uniaxial Compressive Strength /MPa | Empirical Parameters | |
|---|---|---|---|
| S1 | S2 | ||
| Hard Rock Stratum | >40 | 2.1 | 16 |
| Medium-Strength Rock Stratum | 20~40 | 4.7 | 19 |
| Weak Rock Stratum | <20 | 6.2 | 32 |
| Strain | Stress /MPa | Strain | Stress /MPa | Strain | Stress /MPa |
|---|---|---|---|---|---|
| 0.01 | 1.01 | 0.07 | 10.36 | 0.13 | 36.06 |
| 0.02 | 2.13 | 0.08 | 12.84 | 0.14 | 45.44 |
| 0.03 | 3.39 | 0.09 | 15.78 | 0.15 | 58.68 |
| 0.04 | 4.80 | 0.10 | 19.31 | 0.16 | 78.76 |
| 0.05 | 6.41 | 0.11 | 23.63 | 0.17 | 112.82 |
| 0.06 | 8.24 | 0.12 | 29.05 | 0.18 | 183.28 |
| Density (kg/m3) | Bulk Modulus /GPa | Shear Modulus /GPa | Internal Friction Angle /(°) | Dilation Angle /(°) |
|---|---|---|---|---|
| 1710 | 4.51 | 3.08 | 17 | 10 |
| Density /(kg/m3) | Bulk Modulus /GPa | Shear Modulus /GPa | Tensile Strength /MPa | Cohesion /MPa | Internal Friction Angle /(°) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Initial Value | Softening Rate /% | Residual Value | Initial Value | Softening Rate /% | Residual Value | ||||
| 1407 | 1.93 | 1.38 | 0.45 | 1.78 | 1 | 0.68 | 32 | 1 | 19 |
| Width of Coal Pillar/m | 4 | 5 | 6 | 8 | 10 | 25 | |
|---|---|---|---|---|---|---|---|
| During the roadway driving near the advancing 15106 working face | Deformation of the Roadway Roof/mm | 331.48 | 288.40 | 276.38 | 258.89 | 252.45 | 83.28 |
| Deformation of the Roadway Floor/mm | 83.32 | 58.45 | 51.73 | 49.27 | 46.70 | 17.29 | |
| Deformation of the Solid Pillar Rib/mm | 383.85 | 324.63 | 276.31 | 241.03 | 229.67 | 73.12 | |
| Deformation of the Coal Pillar Rib/mm | 570.31 | 510.06 | 415.66 | 376.16 | 357.26 | 76.49 | |
| Peak Stress/MPa | 22.4 | 20.1 | 22.2 | 21.9 | 21.9 | 22.3 | |
| During the tunneling period along the gob | Deformation of the Roadway Roof/mm | 276.08 | 240.09 | 230.08 | 215.71 | 210.38 | 69.40 |
| Deformation of the Roadway Floor/mm | 69.41 | 48.71 | 43.41 | 41.06 | 38.70 | 15.29 | |
| Deformation of the Solid Pillar Rib/mm | 320.25 | 270.53 | 230.26 | 200.86 | 191.39 | 63.45 | |
| Deformation of the Coal Pillar Rib/mm | 479.56 | 430.86 | 350.56 | 320.96 | 298.04 | 66.64 | |
| Peak Stress/MPa | 20.5 | 20.1 | 19.8 | 18.6 | 22.1 | 21.4 | |
| During the mining of the 15107 working face | Deformation of the Roadway Roof/mm | 203.25 | 170.09 | 160.08 | 152.31 | 148.29 | 43.58 |
| Deformation of the Roadway Floor/mm | 49.25 | 38.29 | 33.41 | 28.56 | 26.92 | 10.56 | |
| Deformation of the Solid Pillar Rib/mm | 199.85 | 162.23 | 136.12 | 120.09 | 114.15 | 30.19 | |
| Deformation of the Coal Pillar Rib/mm | 276.19 | 257.16 | 197.26 | 190.24 | 177.98 | 36.84 | |
| Peak Stress/MPa | 29.8 | 27.5 | 26.8 | 27.2 | 33.7 | 24.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wen, Y.; Wu, W.; Wen, H.; Hu, Y.; Wang, B.; Shao, J.; Li, Z.; Niu, J. Study on the Width of a Narrow Coal Pillar for Gob-Side Entry Driving near an Advancing Working Face in a Shallow Coal Seam. Energies 2025, 18, 4303. https://doi.org/10.3390/en18164303
Zhang H, Wen Y, Wu W, Wen H, Hu Y, Wang B, Shao J, Li Z, Niu J. Study on the Width of a Narrow Coal Pillar for Gob-Side Entry Driving near an Advancing Working Face in a Shallow Coal Seam. Energies. 2025; 18(16):4303. https://doi.org/10.3390/en18164303
Chicago/Turabian StyleZhang, Hu, Yang Wen, Wenda Wu, Haipo Wen, Yaotong Hu, Bo Wang, Jianqiang Shao, Zhongwu Li, and Jianchun Niu. 2025. "Study on the Width of a Narrow Coal Pillar for Gob-Side Entry Driving near an Advancing Working Face in a Shallow Coal Seam" Energies 18, no. 16: 4303. https://doi.org/10.3390/en18164303
APA StyleZhang, H., Wen, Y., Wu, W., Wen, H., Hu, Y., Wang, B., Shao, J., Li, Z., & Niu, J. (2025). Study on the Width of a Narrow Coal Pillar for Gob-Side Entry Driving near an Advancing Working Face in a Shallow Coal Seam. Energies, 18(16), 4303. https://doi.org/10.3390/en18164303