Coordinated Electric Vehicle Demand Management in the Unit Commitment Problem Integrated with Transmission Constraints

Abstract

Advancements in battery technology, marked by reduced costs and enhanced efficiency, are steadily making electric vehicles (EVs) more accessible to consumers. This trend is fueling global growth in EV fleet sizes, allowing EVs to compete directly with internal combustion engine vehicles. However, this rapid growth in EV numbers is likely to introduce challenges to the power grid, necessitating effective load management strategies. This work proposes an optimization method where EV load management is integrated into the Transmission Constrained Unit Commitment Problem (TCUCP). A Differential Evolution (DE) variant, enhanced with heuristic repair sub-algorithms, is employed to address the TCUCP. The heuristic sub-algorithms, adapted from earlier approaches to the simpler Unit Commitment Problem (UCP), are updated to incorporate power flow constraints and ensure the elimination of transmission line violations. Additionally, new repair mechanisms are introduced that combine priority lists with grid information to minimize violation. The proposed formulation considers EVs as both flexible loads and energy sources in a large urban environment powered by two grid nodes, accounting for the vehicles’ daily movement patterns. The algorithm exhibits exceptionally fast convergence to a feasible solution in fewer than 150 generations, despite the nonlinearity of the problem. Depending on the scenario, the total production cost is reduced by up to 45% within these generations. Moreover, the results of the proposed model, when compared with a MILP algorithm, achieve values with a relative difference of approximately 1%.

1. Introduction

This work aims to introduce a novel method for solving the Transmission-Constrained Unit Commitment Problem (TCUCP) and investigates the integration of electric vehicles (EVs) as both flexible loads and power sources. Specifically, it examines EVs in the Grid-to-Vehicle (G2V) operation, where they function as adjustable loads, and the Vehicle-to-Grid (V2G) operation, where they inject power back into the electric grid. The problem is solved via a Differential Evolution (DE) variant that belongs to the family of evolutionary inspired algorithms.

1.1. Literature Review

The growing adoption of EVs in national fleets due to their significant advantages has raised legitimate concerns about the impact of uncoordinated charging on the power grid. The unscheduled charging of EVs can cause significant load peaks in daily electricity demand. This can lead to multiple consecutive or heightened existing peaks [1], resulting in increased electricity production costs. Other concerns include voltage dips, fluctuations, phase imbalances, and higher total harmonic distortion (THD). Such loads can also shorten the lifespan of power grid components like transformers and transmission lines, mainly due to excessive power loading from simultaneous EV charging at maximum capacity.

Several strategies have been proposed to mitigate the aforementioned problems while taking advantage of the existence of the EVs connected to the grid. All these strategies have in common the load management of the EVs. According to [2] the load management of EVs can be categorized as decentralized coordination and centralized coordination. Under centralized coordination, the following operations can be present: (1) the G2V operation, where EV load is handled as a flexible load under Demand-Side Management controls, and (2) the V2G operation, which involves EVs supplying electric power to the power grid. The coordinated charging strategy takes advantage of the flexibility of the EVs as a load in order to create a charging schedule that doesn’t hinder the smooth operation of the power grid. In addition, the stored energy of these EVs can be used for load management, power quality control, and power regulation [3].

In decentralized coordination, EV owners control their charging schedules, while EV aggregators incentivize beneficial charging for an independent system operator (ISO) through demand response programs (DRP). These programs use price signalling, reduced or increased pricing and tariffs to encourage charging during off-peak hours or times advantageous to the power network [4]. A DRP integrated with TCUCP reduces costs compared with uncoordinated charging [5]. DRPs can be utilized to prevent transformer saturation [6] and manage EVs to update daily demand curves [7]. Several DRPs with EVs approaches have been proposed. A DRP approach, strictly for residential complexes that considers the profitability of the V2G operation by comparing electricity price and multiple discharge costs is proposed by [8]. A decentralized approach using blockchain for secure smart charging is proposed in [9]. Furthermore Vehicle-to-Vehicle (V2V) operation can be fund under decentralized charging approaches such as in [10] where EVs coordinate with each other to facilitate V2G and V2V operation without relying on a centralized control system. In [11] a DRP is combined with frequency control in a system with high wind penetration. A decentralized approach to handling small EV fleets at the distribution network level via a DRP is proposed in [12]. Another price signal approach is proposed by [13] for type 3 charging (fast charging) in the day-ahead market. A DRP approach considering environmental constraints is suggested in [14]. The literature proves that the DRP is a very flexible management tool, however it might not operate as planed due to the customers risk aversion [15] leading to the need for direct load control and load shedding. In this section of the literature review, additional optimization approaches can be considered, such as energy management systems for individual vehicles. The presence of such vehicles in future fleets, especially those using hydrogen fuel cells, can help reduce the stress on the power grid by reducing the number of plug-in electric vehicles. Smart energy management systems that integrate both batteries and hydrogen fuel cells will be essential for improving driving efficiency. In [16], a real-time energy management system for fuel cell vehicles is proposed, combining GPS data with information from the vehicle’s DC bus system to regulate hydrogen consumption. In [17], an energy management system is enhanced by a reinforcement learning algorithm that leverages trip history data to predict hydrogen consumption needs, aiming to optimize both travel efficiency and cabin environment control. In decentralized coordination charger deployment problems such as [18] can be integrated into energy management problems.

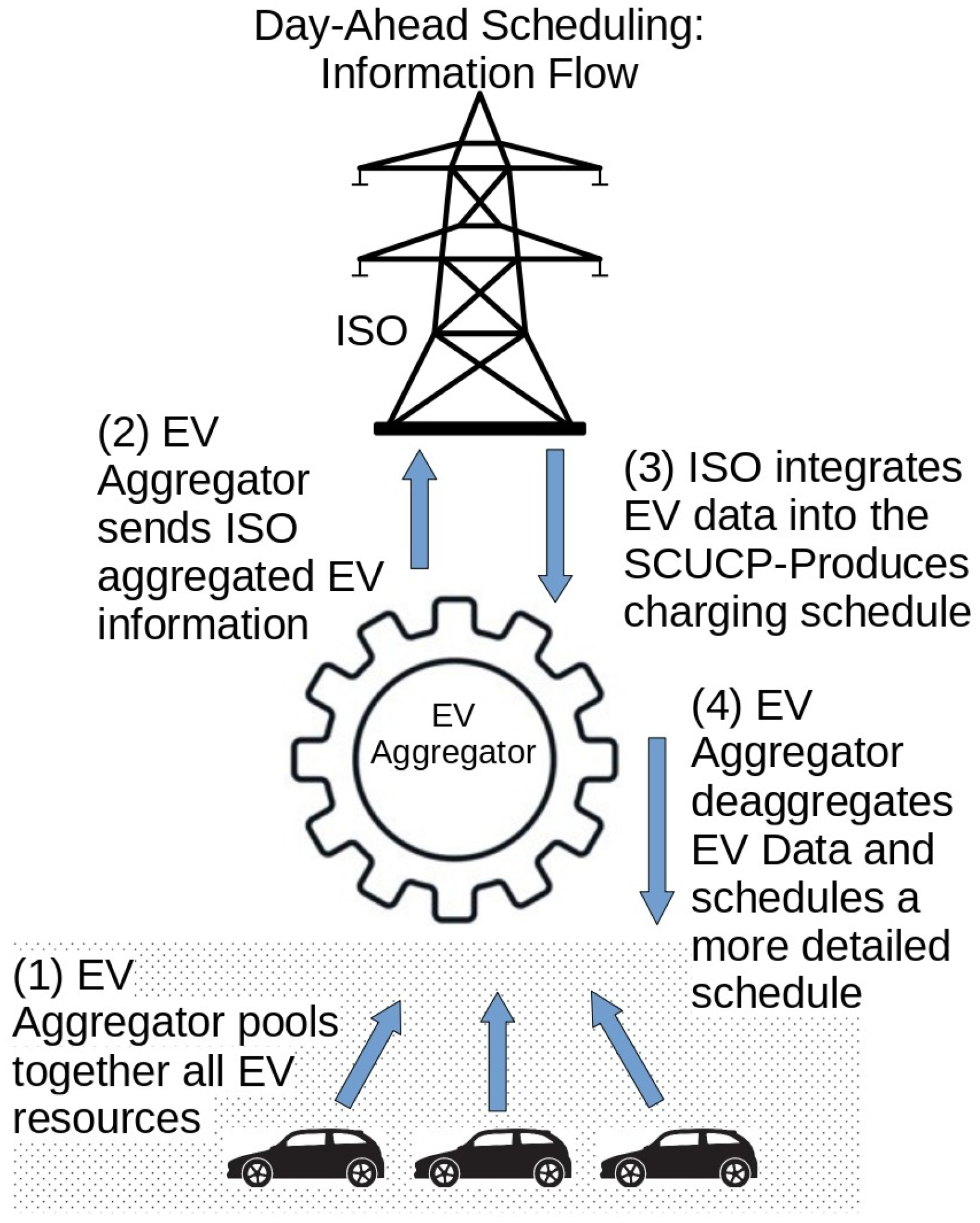
In centralized coordination, accountability for the EV charging lies mainly on the ISO, which, in cooperation with the EV aggregator, organizes the charging of the EV fleet attached to the system. The EV aggregator consolidates EV information, such as identification parameters, battery state of charge (SoC), customer priority profiles, and travel patterns. The EV data are processed for the creation of an effective charging schedule. The centralized coordinated charging schedule management may be a product of optimization from both the DSO and the aggregators, as depicted in Figure 1.

The centralized coordination problem may see a plethora of variations. For instance in [19], two different formulations of solving the centralized coordination problem are proposed. The first approach focuses on maximizing economic benefits by minimizing battery degradation and charging costs, while the second aims to reduce peak load and flatten the load curve by minimizing load deviations. Minimization of load deviation is also performed by [20] who also regulates EV charging power to stabilize voltage levels. In [21], three types of optimization are considered: (a) minimizing transmission line power loss and load variance, (b) minimizing charging cost for the EV owner, (c) maximizing aggregator profits. In [22], one of the EV charging criteria is customer satisfaction. Multi-objective optimization is employed by [23] to achieve economic benefits for charging station owners and EV users, as well as technological advantages for the power grid. Another criterion of centralized coordination is minimization of PV curtailment, as proposed by [24]. A distinct multi-objective algorithm is proposed by [25] to optimize electric vehicle (EV) load and enhance the voltage profile of the test system within an optimal power flow (OPF) optimization framework. Finally, the integration of EV charging scheduling into the UCP has been proposed as a means to facilitate the EV load management [26]. We refer to [27] for a part of the centralized coordination. This enables the establishment of realistic usage expectations and enhances the integration of the EV’s battery capacity across various energy markets, including day-ahead and regulation markets.

Table 1. Literature review contribution for coordinated and uncoordinated charging optimization.

Decentralized Coordination
Reference	Contribution
[5]	DRP integrated with TCUCP.
[4]	Price signaling and tariffs.
[6]	DRP for transformer saturation.
[7]	DRP for updates daily demand curves.
[8]	DRP for small residential complexes that enables V2G operation of residents.
[9]	Combines DRP with blockchain technology.
[10]	V2V (Vehicle to Vehicle) technology within DRP framework.
[12]	Small-scale EV fleet DRP in distribution network level.
[13]	Price signaling optimization for type 3 chargers for dayahead scheduling.
[14]	DRP with environmental constrains.
Centralized Coordination
Reference	Contribution
[19]	Minimizes battery degradation and charging costs and flattens the load curve by minimizing load deviations.
[20]	Minimization of charging load deviation and stabilization of voltage levels.
[21]	Comparison between 3 types of optimization: minimizing transmission line power loss and load variance, minimizing charging cost for the EV owner, maximizing aggregator profits.
[22]	Optimized charging considering customer satisfaction.
[23]	Multi-objective optimization to balance between economic benefits for EV owners and grid stabilization.
[24]	Optimizes charging schedule, reducing photovoltaic (PV) curtailment.
[26]	Optimized charging considering multiple infrastructure levels.

summarizes the main contributions of previous studies on centralized and decentralized charging coordination.

The TCUCP is a complex, nonlinear optimization problem solvable by deterministic or stochastic algorithms. Integrating EVs as flexible loads, especially in V2G mode, adds nonlinearities via battery degradation formulations, heightening optimization complexity, necessitating the use of more advanced and suitable computational tools such as stochastic algorithms.

Optimization algorithms can be categorized into deterministic and stochastic algorithms. The deterministic optimization algorithms utilize linear algebra and gradient methods in order to reach optimum solutions in an efficient manner. Stochastic algorithms or meta-heuristic algorithms utilize randomness in order to reach global near optimal solutions while managing to escape local optimal points by adopting nature inspired strategies.

Numerous deterministic algorithms have been employed in the literature to solve the UCP incorporating EVs, often utilizing various linearization techniques. Madzharov et al. [26] propose a MILP formulation that integrates EV charging into the UCP through load aggregation. However, the model excludes transmission constraints and V2G capabilities. The formulation focuses on optimizing valley-filling to achieve cost-efficient generation, without considering EVs as a potential energy source.

In [28], an MILP formulation is presented that engages in V2G operation, optimizing a 48 h UCP for greater flexibility than traditional 24 h schedules. This extended period better utilizes EV capacity to meet demand. However, EVs are evenly distributed across buses, preventing vehicle movement between them. Another deterministic formulation is proposed in [29], where a two-stage optimization approach was employed using Benders decomposition. In this formulation, EVs are modeled as a distributed battery storage system, where each network node represents a location at which stored energy can be injected into the power grid. Ref. [30] employs a second-order cone programming algorithm for TCUCP in distribution networks (DN), integrating natural gas, district heating, and EV constraints.

Stochastic algorithms have been employed in prior literature to address the TCUCP and the UCP incorporating EVs. In [31,32], a binary symmetric Particle Swarm Optimization (PSO) combined with a self-adaptive Differential Evolution algorithm is proposed to solve the UCP involving EVs. The two meta-heuristic algorithms were paired to determine the commitment schedule of the generators and their respective power generation, as well as the EV charging/discharging schedule. In their work, three constraint-handling mechanisms were used as suggested by [33]. DE has been utilized in [34] in order to reach near-optimal solutions to the optimal power flow problem, proving the versatility of the method. In [19], a Genetic Algorithm (GA) was utilized to minimize the charging cost of EVs aimed at charging cost reduction and battery degradation. A bat algorithm was used in [35] to solve the TCUCP with EVs while considering emission constraints in order to absorb considerable discharging energy from the EVs. A multi-objective optimization based on a Grey wolf algorithm that maximizes profits for the EV aggregator while minimizing the operating costs of the system by integrating the EV charging and discharging within the OPF is suggested in [36]. Meta-heuristic algorithms have proven highly effective in solving a wide range of optimization problems, particularly in energy applications [37].

Recent research has focused on improving meta-heuristic solvers for the UCP using specialized constraint handling algorithms (heuristic repair mechanisms) that led to improvements such as decreased convergence speed, reduced standard deviation, smaller convergence rates, and improved solutions. These gains are achieved by incorporating logical analyses of the real-world problem, which effectively create a filtering mechanism that guides the particles or agents of the meta-heuristic algorithm toward near-optimal global solutions. However, these methods have been successfully applied only to the UCP.

A prominent example of the application of heuristic methods is presented in [33], where a quantum binary Particle Swarm Optimization (PSO) algorithm is employed to solve the UCP. This approach has been adapted and extended in several subsequent studies. Three heuristic mechanisms were employed: the first addresses the minimum up and downtime constraints; the second ensures compliance with spinning reserve requirements by maintaining a sufficient number of generators in operation; and the third de-commits generator units to minimize the number of active generators, thereby reducing operational costs. These mechanisms were also integrated in the work of [27,38] who also introduced new mechanisms that repair the energy dispatch problem and the transmission line power flow violation. In [39] a hybrid optimization algorithm is employed that utilized a GA algorithm to solve the UCP using a priority list to initiate generators. Ref. [40] proposed a unit de-commitment and re-commitment module that is utilized in order to reduce voltage violation in a node. The module operates by manipulating the state of the generators, beginning from the closest ones to the furthest, until a result with no violation is obtained. A Lagrangian relaxation algorithm was proposed in [41] that utilized a spinning reserve handling technique to solve the UCP. Ref. [42] solves the UCP by including the reserve reduction heuristic repair mechanism in order to reduce the standard deviation of the solutions. On the operation of heuristic repair mechanisms rely other works such as [43], where the UCP with renewable energy production is solved via a PSO algorithm. In their work, the following three repair mechanisms are utilized: the Spinning reserve constraints repair mechanism, the minimum up/downtime repair mechanism, and the de-commitment of excess units repair mechanism. The same mechanisms are used in [44] where a priority list is integrated in the same mechanisms. A relevance matrix-inspired heuristic is introduced in [45] that increases the operational speed of their algorithm. Finally, a profit-based UCP is solved in [46] with the aid of the unit de-commitment repair mechanism and the ramp rate repair mechanism.

1.2. Motivation

As highlighted in the literature, most studies employing heuristic mechanisms primarily address the UCP. This focus arises from the fact that many widely used heuristics are effective at guiding solutions toward global optima in the UCP. However, when these heuristics are applied to the TCUCP, they often lead to solutions with transmission constraint violations, hindering convergence and compromising solution feasibility.

One commonly used heuristic involves the commitment of generators based on a priority list to ensure sufficient power reserve. While effective in the UCP, this approach can be problematic in the TCUCP. Specifically, when a generator essential for balancing the power network is ranked low on the priority list, it may not be committed, resulting in unaddressed transmission constraints. Consequently, the reliance on static priority-based commitment can impede the ability of the algorithm to maintain grid reliability under transmission constraints.

Another widely used heuristic is the enforcement of minimum up and minimum downtime constraints. Although this mechanism does not directly exacerbate power flow violations, it can hinder the optimization algorithm’s ability to find feasible schedules in the TCUCP. In particular, the inability to deactivate a generator at a specific hour, due to its minimum up time requirement, may prevent the mitigation of line overloads, thereby obstructing convergence to a feasible solution that satisfies both unit and transmission constraints.

A third popular heuristic is the de-commitment of generators to reduce excess reserve capacity. This approach is often employed to accelerate convergence in meta-heuristic algorithms by minimizing the number of active units. Typically, generators with lower capacity, often placed at the end of the priority list, are deactivated. While this strategy is effective in reducing operational costs and is frequently used to obtain cost-optimal schedules in the UCP, it poses significant challenges for the TCUCP. These smaller units often play a crucial role in reducing transmission violations. Their removal can destabilize power flow across the network, leading to severe violations of transmission constraints and undermining the performance of the optimization algorithm.

In many research studies, electric vehicles (EVs) are modeled as static loads or sources connected to fixed buses within the power network, without accounting for their mobility between different locations. This simplification is common across the referenced literature, including [5], where aggregated EV fleets are represented as virtual power plants centralized at a single node. Such approaches overlook the dynamic nature of EVs and their potential to impact multiple nodes within the network as they travel. However, only a limited number of works explore the possibility that EVs can move and connect to different buses over a 24 h period, thereby influencing multiple buses as they travel throughout the day. Additionally, while much of the literature posits that V2G operations can consistently reduce the system’s start-up, commitment, and unit commitment scheduling costs, some studies argue that EVs are less competitive compared with large-scale generators, especially when the system operator is required to replenish the energy utilized during V2G operations within the same 24 h period. This highlights the need for a tool that can optimize TCUCP while integrating EVs with V2G capabilities, accounting for complex nonlinearities such as battery degradation costs.

1.3. Contribution

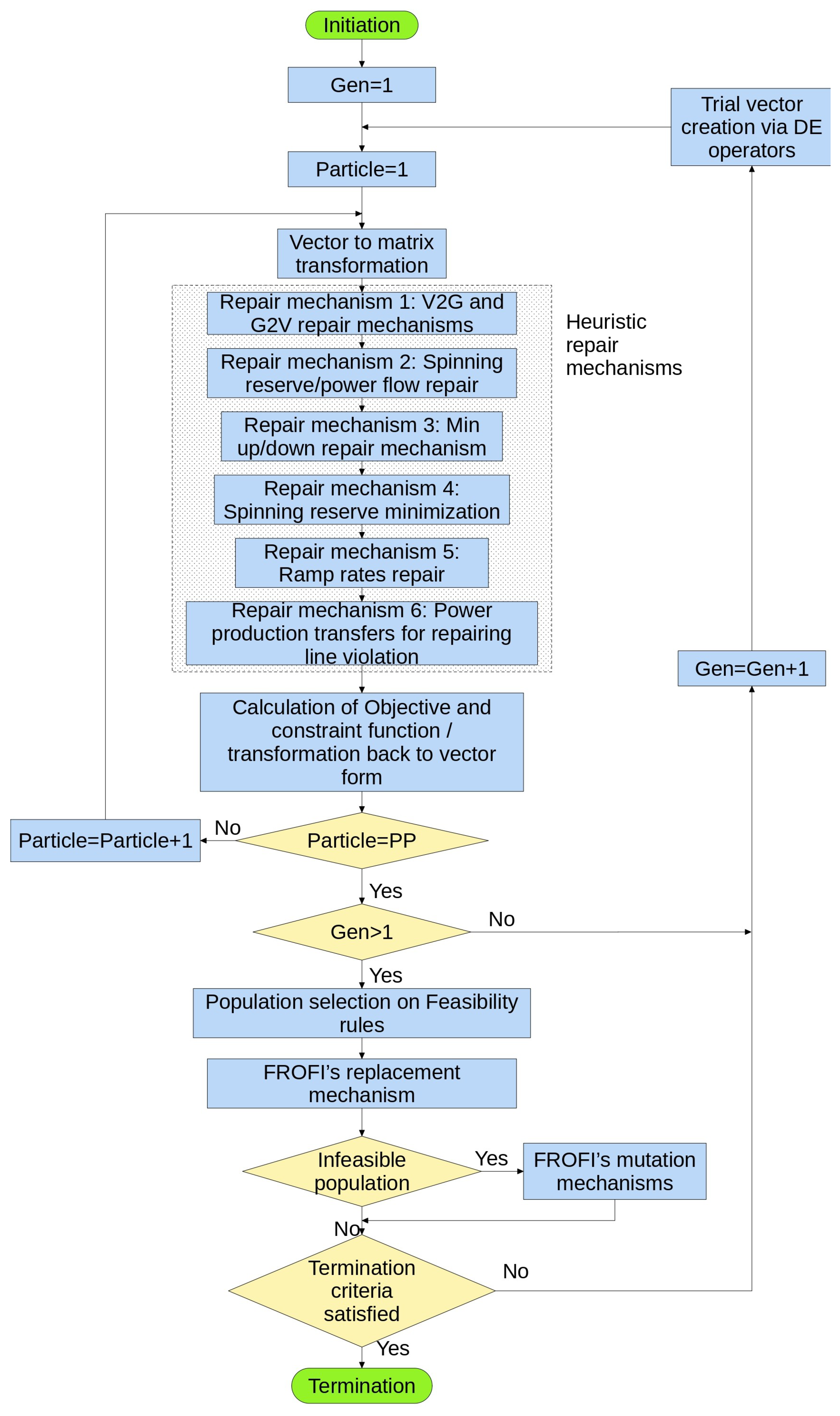
This work presents a novel formulation of integrating electric vehicles in the TCUCP, representing the coordinated charging and discharging of a large EV fleet. The fleet of EVs belongs to a large urban environment where the EVs travel within the day. The formulation accounts for the daily movement of EVs within two nodes (buses) that supply the city with power, allowing charging or discharging whenever vehicles are available. This is a complex problem solved via a variant of Differential Evolution. The algorithm is enhanced by a series of heuristic repair mechanisms that lead the solution to the feasible region by following problem-specific rules. Each repair mechanism handles a discrete set of constraints of the problem, repairing the variables of the problem so that both the constraint violation and the operational cost are reduced. This work incorporates several heuristic mechanisms previously used in the literature for the simpler UCP, adapted and updated here to accommodate transmission constraints. In addition to those heuristics that include the ramp-rate repair mechanism, the minimum up and downtime repair mechanism, the energy dispatch repair mechanism, and the minimization of reserve repair mechanism, three novel mechanisms are introduced. Two of them are assigned to the transmission power flow constraints, and a third one that handles the charging and discharging of EVs.

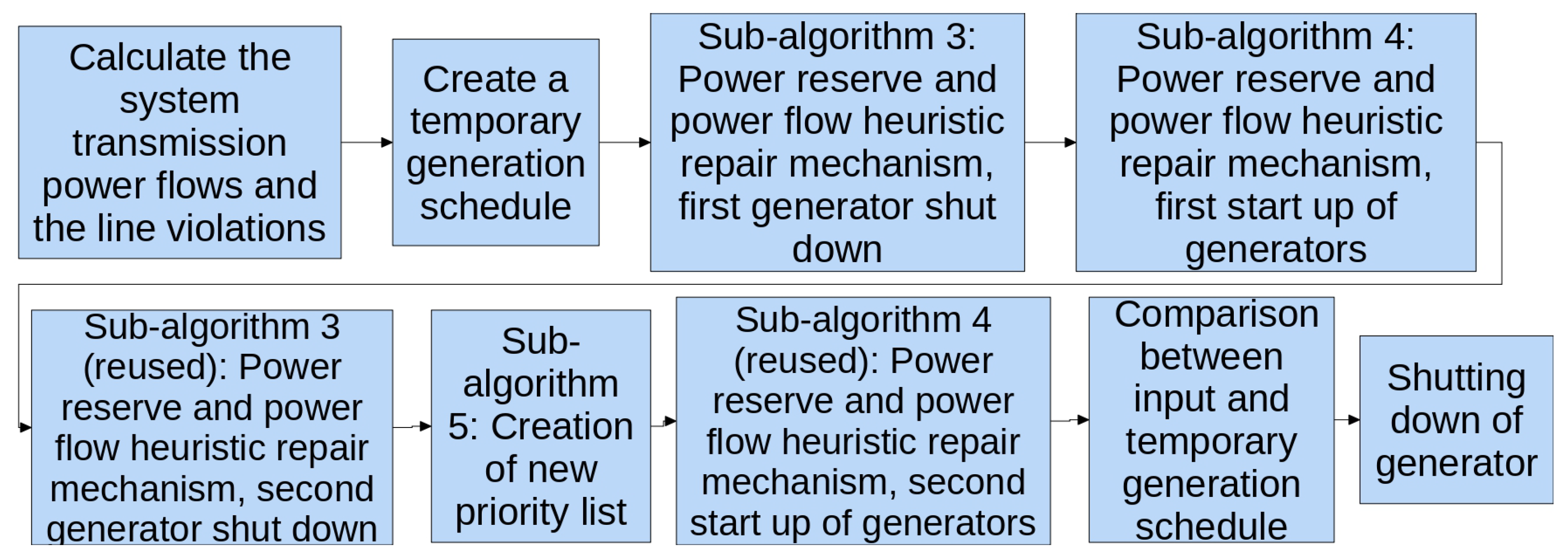
The transmission constraints are handled by two heuristic repair mechanisms. These heuristics utilize information from the PTDF matrix to identify the nodes (buses) that have the greatest impact on the overloaded transmission lines. By appropriately adjusting load and generation at these key nodes, either increasing or decreasing them, the power flow violations can be effectively mitigated. The approach is further enhanced with the use of priority lists, which guide the search toward feasible solutions more efficiently, despite the NP-hard nature of the problem. Although many meta-heuristic algorithms over the years have incorporated priority lists, none have successfully solved the Unit Commitment Problem (UCP) while accounting for transmission constraints.

The first transmission repair algorithm builds upon the average production priority list proposed in [38], which has been updated and expanded to incorporate power grid data using Power Transfer Distribution Factors (PTDFs). This enhancement enables the algorithm to systematically commit generators to resolve violations on transmission lines where power flow exceeds specified limits. The priority list determines the most cost-effective generator commitments until both energy reserve and dispatch constraints are met. Power Transfer Distribution Factors dictate the power flow within the transmission system. Each line’s power flow is determined by the PTDF values associated with each node (bus). By adjusting the demand or production at each node, the algorithm alters power flows across transmission lines. The second mechanism serves as a constraint handling mechanism, adjusting the production of committed generators based on PTDF information to minimize transmission violations without undoing previous repair efforts. A third proposed mechanism focuses on managing EV charging. By incorporating PTDFs, this mechanism adjusts EV loads at each node to mitigate transmission line violations effectively.

In addition to these contributions, the unit de-commitment constraint handling technique, aimed at minimizing reserve capacity, is enhanced by introducing a new variable into the optimization model. This variable defines the maximum acceptable level of reserve in the final solution, allowing the DE mechanisms to set the total number of operational generators in the system. Furthermore, all repair mechanisms, mainly the constraint handling techniques of minimum up to minimum downtime, unit de-commitment and energy dispatch constraints, are suggested mainly in [33,38] and numerous other literature works, which are utilized in this work, are appropriately modified and expanded so as to retain their original purpose and not hinder the optimization process that engages with power grid constraints.

The proposed optimization method solves all sub-problems of the TCUCP and EVs in a single DE convergence. The proposed method, despite aiming to optimize the operation of electrical generators, can be utilized for any available production method, including renewable energy sources. Thus, the primary objective of this work is to develop an effective heuristic mechanism that integrates power grid information to support an evolutionary-inspired algorithm in solving complex optimization problems, specifically the TCUCP. The proposed method for solving the TCUCP with EVs is evaluated utilizing a small, intermediate, and large test system, demonstrating the robustness of the proposed meta-heuristic algorithm.

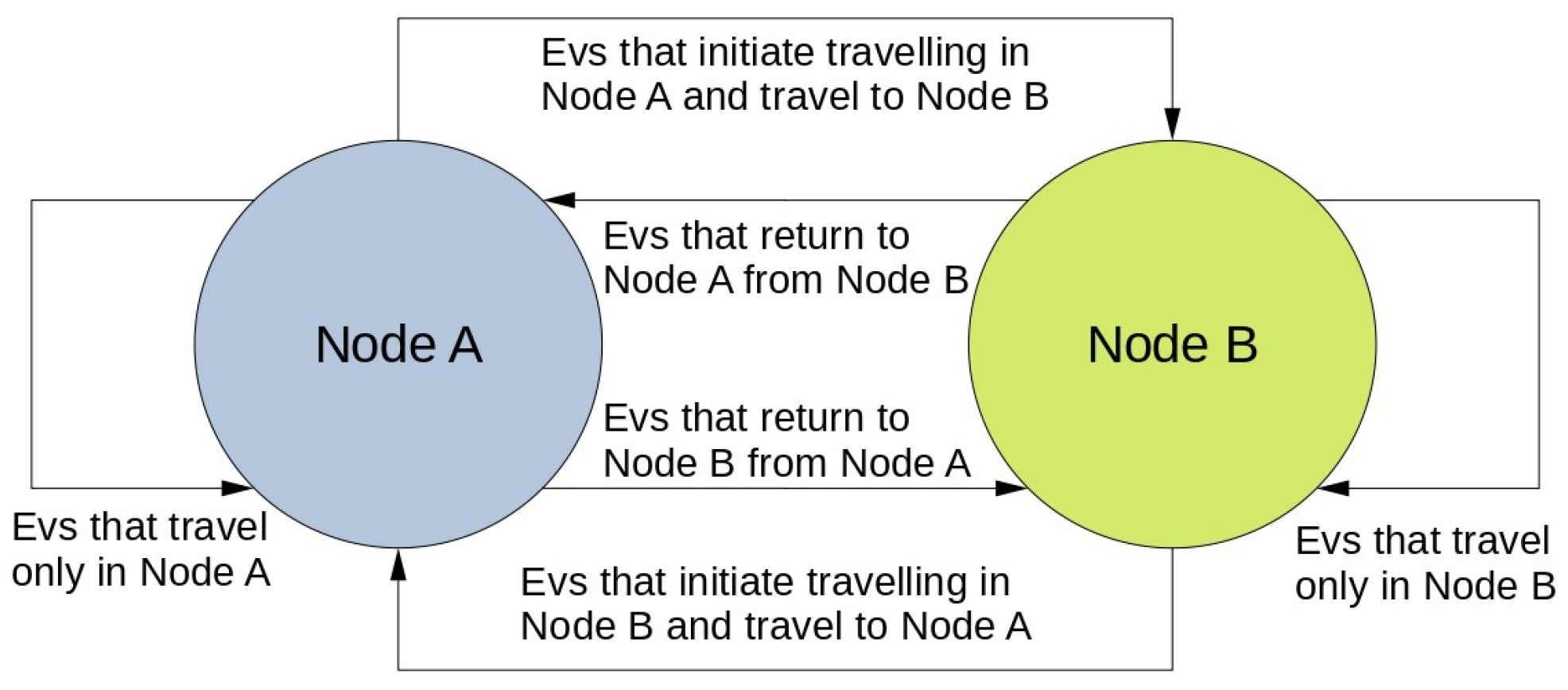
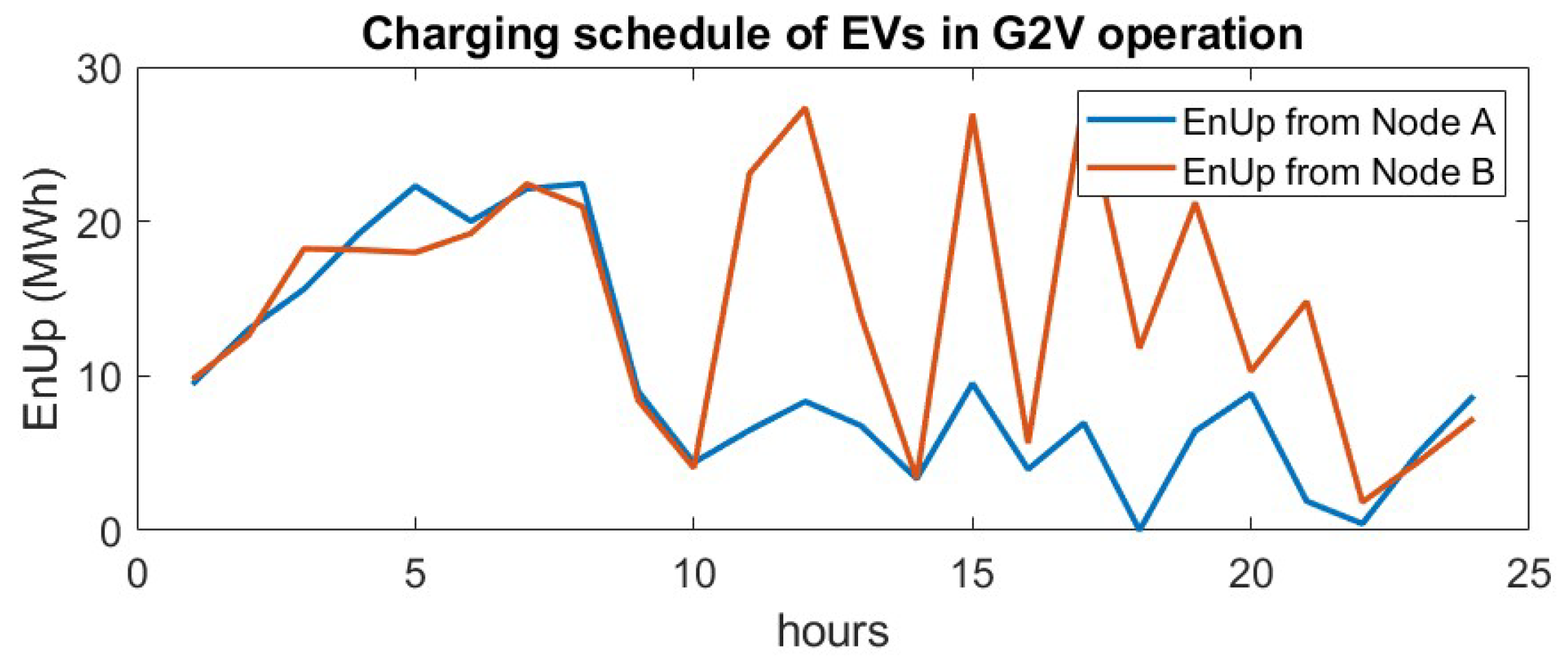
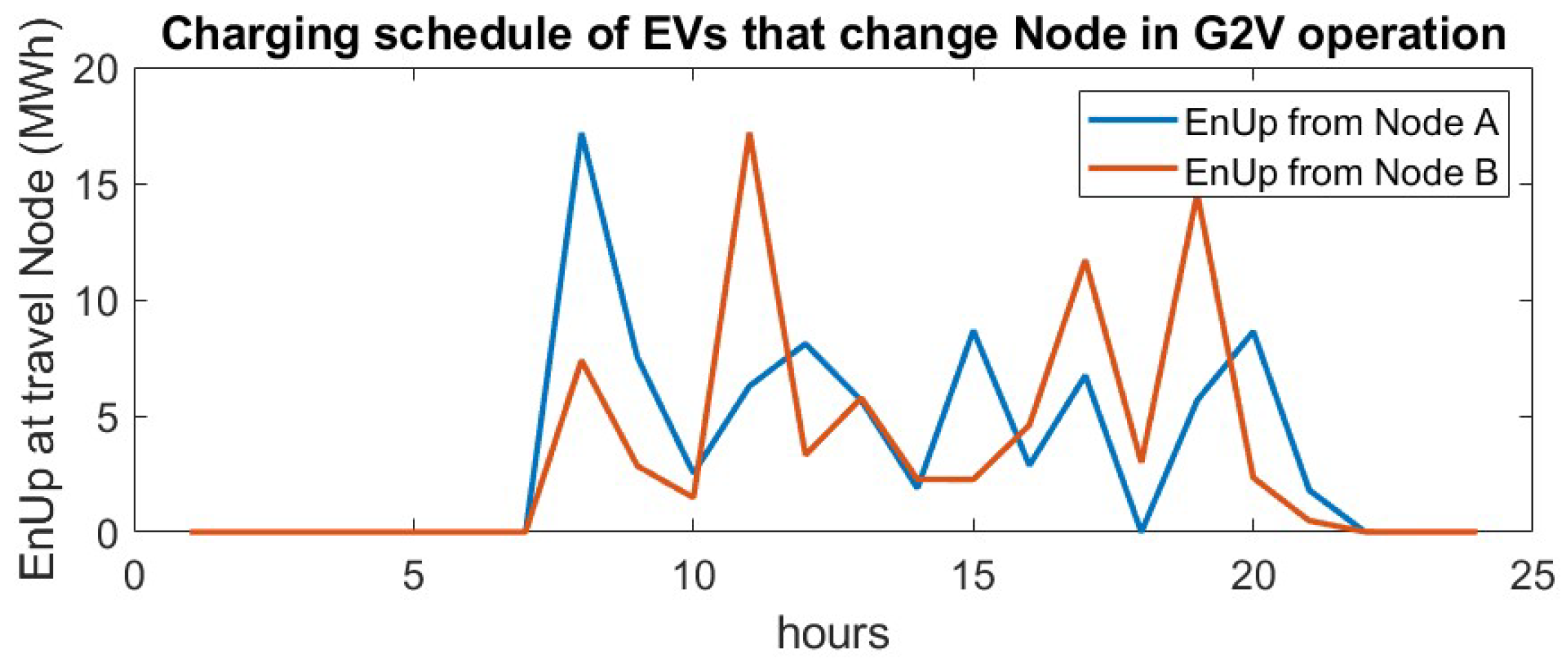
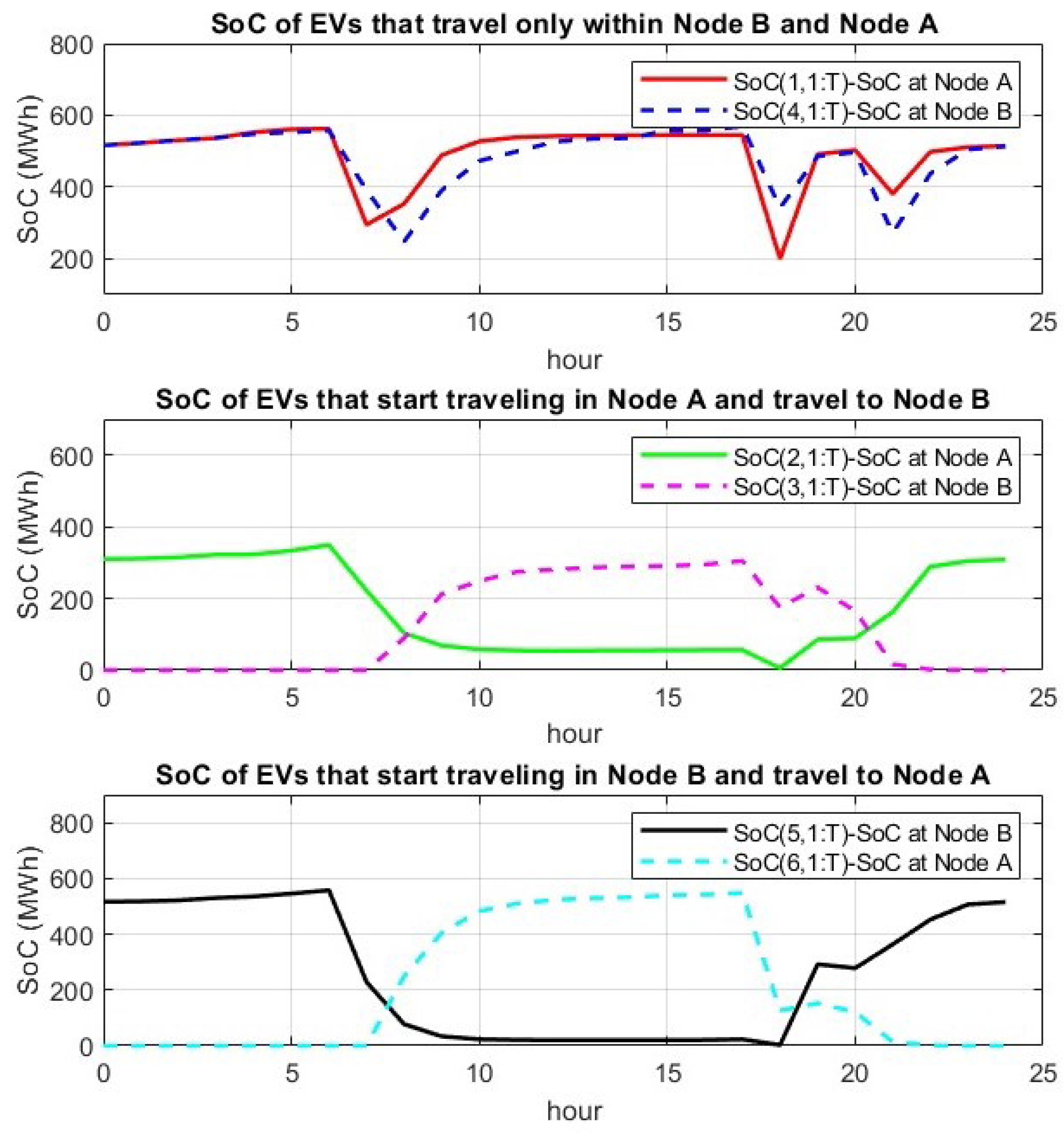
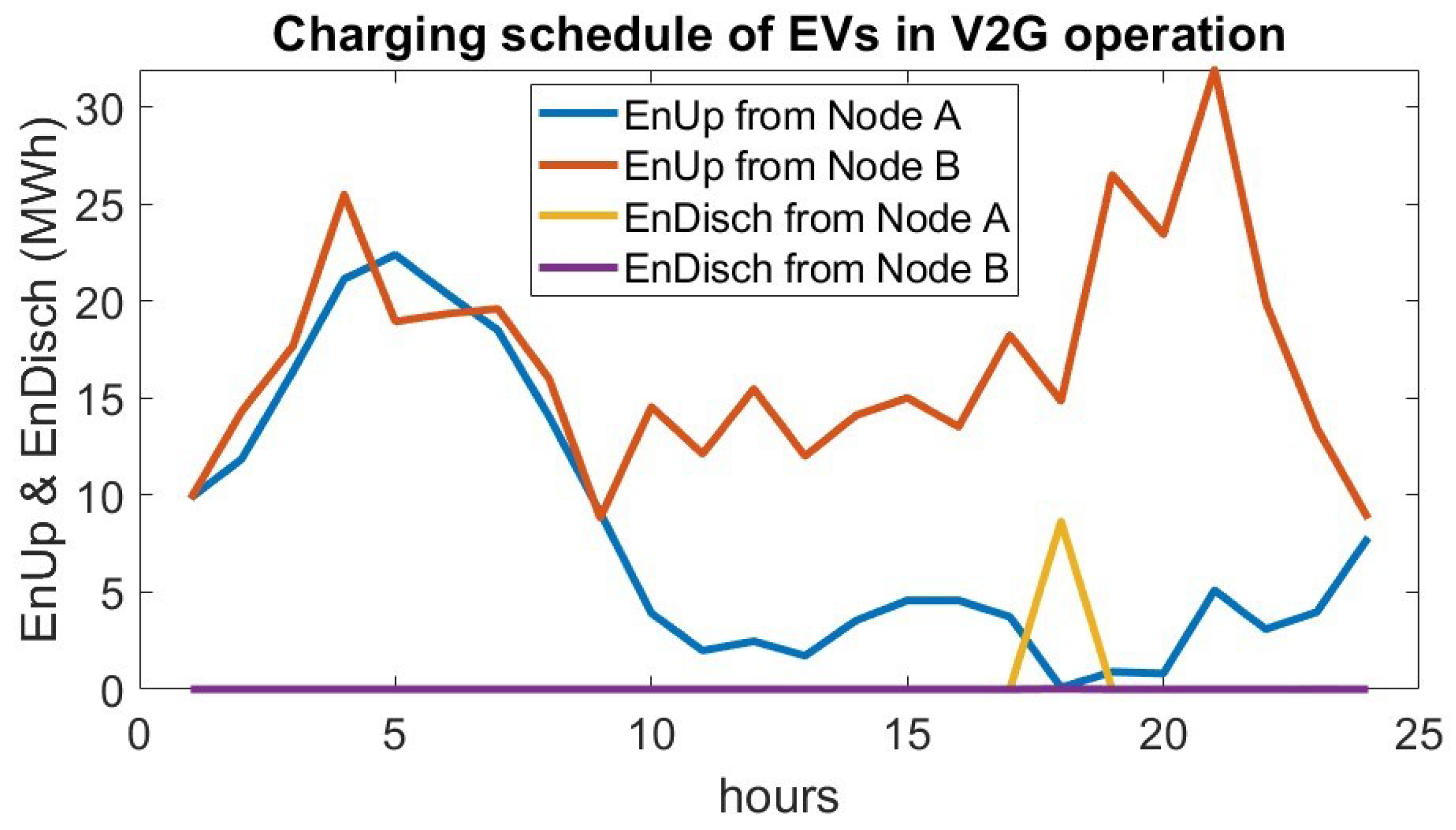
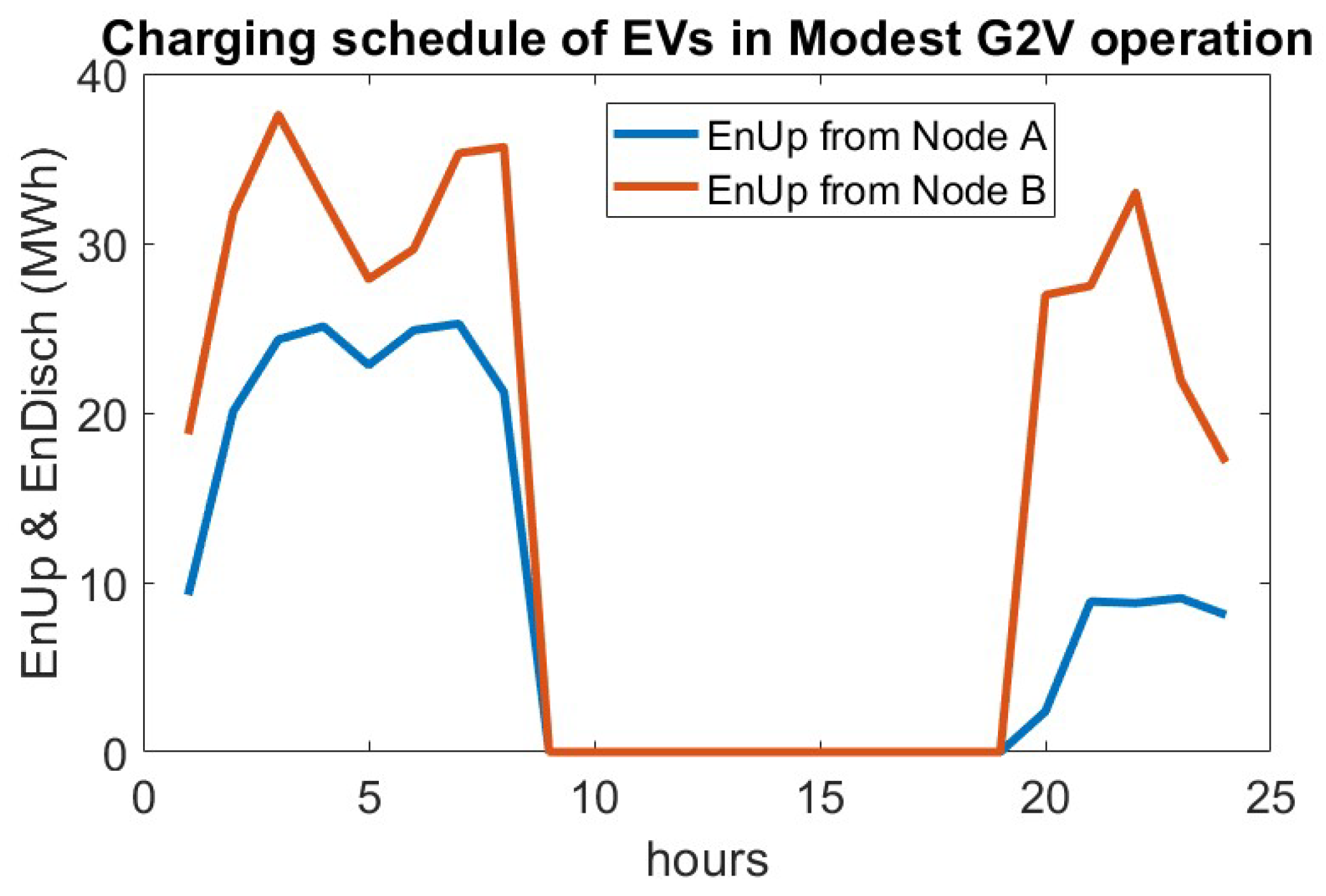
The EV formulation models a large urban area with two power nodes, allowing EVs to alternate their charging locations between the nodes over the course of the day. The charging of the EVs is coordinated and heavily constrained. This ensures that no negative effects such as power flow violations and peak loads affect the power grid and the energy production. To reduce the potential strain on the power network, each EV is restricted to a maximum charging rate of 3 kWh, which is considered as Level 1 charging [47]. Given the large number of vehicles, the charging process is managed in groups rather than individually, with the SoC of each group representing the average SoC of all vehicles within that group. It is further assumed that the SoC within each group is homogeneous. When a group of aggregated vehicles is combined with another group, it is assumed that the vehicles mix, and the new group’s SoC represents the average SoC of the combined vehicles. This approach allows for an estimation of vehicle movement throughout the day, which is essential because vehicles may change charging nodes as their schedule progresses. Previous studies have either considered EVs as part of the day-ahead demand without accounting for power network constraints or have modeled the entire fleet as charging at a single node. Additionally, some studies have assumed fixed EV populations at each node. In contrast, this work presents a formulation that accounts for spatial variability in the load.

The UCP primarily addresses the scheduling and operational cost of various network elements that impact the overall system cost in day-ahead planning and market operation. For this reason, the UCP typically uses a time resolution of one hour, aligning with the hourly scheduling intervals of the day-ahead market. One of the elements of the system can be considered to be EVs and their load, which could be optimized. In general, EVs are connected to the distribution system. However, in this work, all EVs and distribution system loads are aggregated into the system’s Nodes (buses) without causing significant differences in the total analysis.

The power production system interacts with EVs through two operations: G2V, where EVs are treated as flexible loads, and V2G, where EVs serve as power sources. The V2G operation accounts for battery degradation costs, a critical factor in many EV charging optimization models, as demonstrated by [48]. This consideration introduces significant nonlinearity into the optimization system.

2. Problem Formulation of the TCUCP with EVs

This work investigates three formulations of the TCUCP: (1) the TCUCP without the integration of EVs, (2) the TCUCP incorporating EVs as flexible loads under the G2V framework, and (3) the TCUCP with V2G integration, where EVs function both as flexible loads and as energy sources for the power system. The objective is to minimize the total operating cost of the generators, with the V2G formulation additionally considering the cost of EV battery degradation. The system is constrained by a set of generator and EV-specific constraints. The UCP formulation for generator costs is based on the works of [27,38], while the TCUCP integrates DC power flow modeling from [49], and the formulation follows closely the approach of [26].

2.1. Objective Function and Decision Variables

The objective function (Equation (1)) minimizes the system’s Total Cost (TC), including power production, start-up, and EV battery degradation costs. For L generators and EVF groups over K periods, production cost (Equation (2)) depends on $c{s}_{l,k}$, a decision variable indicating generator state (1 = on, 0 = off). Power output is $p{r}_{l,k}$. Start-up cost (Equation (3)) depends on prior offline duration (Equations (4) and (5)). Energy exchange variables are $EnC{h}_{evf,k}$ (G2V) and $EnDis{c}_{evd,k}$ (V2G). All Constants, Variables and Sets are presented in

Table 2. Constants.

Symbols	Description
Constants
$a_l$, $b_l$, $c_l$	Quadratic equation costs of gen l, USD/h, USD/MWh, USD/MWh2.
an, bn	EV aggregation category of EVs of the starting point Node a or b.
$b_{Diag}$	Diagonal matrix susceptance of transmission line ln.
$b_{ln}$	Susceptance of transmission line ln.
cna, cnb	EV aggregation category of EVs that travel within a single Node.
CED	Consumed energy of EV category evf in period k in MWh.
CoefGens	Matrix created utilizing the PTDF matrix, containing only the columns with nodes that receive power injections from generators.
$Co{B}_{evd,k}$	Cost of batteries of EVs connected to the node at hour k USD.
csc	Cold start-up cost of generator l in USD.
d0, d1, d2	Least square regression results.
EPV	Multiplier that determines the boundary of variable PPCV.
MaxTransf	Maximum allowable transfer of power to and from EVs in MWh.
$MT{D}_l$	Minimum operational time of generator l.
$MT{U}_l$	Minimum shutdown time of generator l.
ne	EV charging and discharging efficiency.
Pd	System day-ahead power demand of period k in MWh.
$Pma{x}_l$, $Pmi{n}_l$	Maximum and minimum generation limit of generator in MW.
SC	start-up cost of generator l in period k in USD.
SUC	start-up cost of generator l in period k in USD.
Td	Time down in hours.
Res	System day-ahead reserves of period k in MWh.
Est	Energy storage of EV battery.
TI	Time interval.
DE constants
ARC	External archive of the DE that stores all trial vectors that didn’t survive the feasibility rules.
CRR	Crossover rate of the DE.
lwv	Lines with violation.
n	DE particle index.
r1, r2, r3	Indexes of population vectors.
SF	DE scaling factor.
TDA	Temporary unit de-commitment archive.
w	Mutant vector of DE.
z	Population vector of DE.

,

Table 3. Variables.

Symbols	Description
anglND	Voltage angle at a node.
$B{D}_{evd,k}$	Battery degradation cost of EVs of period k in USD.
$BD{C}_{evd,k}$	Total battery degradation of EVs of cycle in period k in USD.
$C{l}_{evd,k}$	Cycle lifetime of EV battery.
$c{s}_{l,k}$	Generator commitment status of generator l in period k, binary variable.
$D{D}_{evd,k}$	Depth of discharge of EVs in period k.
$EnC{h}_{evf,k}$	Power received from the power grid by each evf EV group in period k in MWh.
$EnDisc{h}_{evd,k}$	Power sent to the power grid by each evd EV group in period k in MWh.
$G{C}_{l,k}$	Power production cost of generator l in period k in USD.
$P{f}_{ln,k}$	power flow in line ln in period k in WM.
PF nodal	Power injections at node nd including transmission power flow.
$pf{a}_{ln}$	power flow in line ln in period k in WM.
pfnodal	Power injections at node nd without transmission power flow.
Plavcost	Priority list of generators created by sorting all generators according to their average production cost.
Plmaxcost	Priority list of generators created by sorting all generators according to their maximum average production cost.
$PPC{V}_k$	Peak power control variable is an optimization variable that dictates the maximum available peak power of the system, for every hour k in MWh.
$p{r}_{l,k}$	Power production of generator l in period k in MW.
$Prma{x}_l$, $Prmi{n}_l$	Maximum and minimum allowable generation limit of generator l in period k in MW.
$So{C}_{evd,k}$	State of charge of the batteries of EVF groups of EVs in T total hours in MWh.
Tdecom	Consecutive time where generator is de-committed.
Ton	Total number of consecutive operational hours of generator l up to hour k.
$u_t$	Decision variable of G2V and V2G operation.
VND	Voltage at node (bus) ND.

and

Table 4. Sets.

Symbols	Description
L	Set of indexes of the generating units.
K	Set of indexes of the time periods.
EVD	Set of indexes of the EV groups in V2G operation.
EVF	Set of indexes of the EV groups during charging as a flexible load.
ND	Set of indexes of system’s nodes (buses).
LN	Set of indexes of the transmission lines.

.

$$\mathrm{minimize} \mathrm{TC}=\sum _{k=1}^K\sum _{l=1}^L[G{C}_{l,k}·TI+S{C}_{l,k}]+\sum _{k=1}^K\sum _{evd=1}^{EVD}BD{C}_{evd,k}$$

(1)

$$G{C}_{l,k}=(a_l+b_l·p{r}_{l,k}+c_l·{p{r}_{l,k}}^2)·c{s}_{l,k},x_{k,\ell }>0,\forall k\in K, \forall \ell \in L$$

(2)

$$S{C}_{l,k}=[SU{C}_{l,k}·(1-c{s}_{l,k-1})]·c{s}_{l,k},\forall k\in K, \forall \ell \in L$$

(3)

$$SU{C}_{l,k}=\left\{\begin{array}{c}hs{c}_l,\mathrm{if} T{d}_l\le Tdeco{m}_{l,k}\le T{d}_l+Tcl{d}_l\hfill \\ cs{c}_l,\mathrm{if} T{d}_l+Tcl{d}_l\le Tdeco{m}_{l,k}\hfill \end{array}\right.\forall k\in K, \forall \ell \in L$$

(4)

$$Tdeco{m}_{l,k}=\left\{\begin{array}{c}0,\mathrm{if} c{s}_{l,k}=1\hfill \\ 1+Tdeco{m}_{l,k-1},\mathrm{if} c{s}_{l,k}=0\hfill \end{array}\right.\forall k\in K, \forall \ell \in L$$

(5)

The battery life cycle is calculated according to Equation (6) [50]. In their work, the least square regression yields the following parameters in Equation (6), where $d0=2731.7$, $d1=0.679$, and $d2=1.614$. The type of battery considered is a lithium-ion battery, which is consistent with the one used in this work. The depth of discharge in the same equation is calculated in Equation (8). The battery degradation is estimated using Equation (7) according to [51]. The final cost of battery degradation, incorporated into the objective function, is computed using Equation (9). This equation calculates the cost of energy discharge during the discharging operation, as illustrated in Equation (10). It computes the total cost from the start ($t_S$) to the end ($t_E$) of the discharge cycle.

$$C{l}_{evd,k}=d0·D{D}_{evd,k}^{-d1}·exp(d2·(1-D{D}_{evd,k}))\forall k\in K, \forall evd\in EVD$$

(6)

$$B{d}_{evd,k}\left(So{C}_{evd,k}\right)={\displaystyle \frac{Co{B}_{evd,k}}{C{l}_{evd,k}}},\forall k\in K, \forall evd\in EVD$$

(7)

$$D{D}_{evd,k}=1-{\displaystyle \frac{So{C}_{evd,k}}{Ca{p}_{evd,k}}}\forall k\in K, \forall evd\in EVD$$

(8)

$$BD{C}_{evd,k}=B{d}_{evd,k}\left(So{C}_{evd,t_E}\right)-B{d}_{evd,k}\left(So{C}_{evd,t_S}\right)\forall k\in K, \forall evd\in EVD$$

(9)

$$BD{C}_{evd,k}=\left\{\begin{array}{cc}B{d}_{evd,k}\left(So{C}_{evd,t_E}\right)-B{d}_{evd,k}\left(So{C}_{evd,t_S}\right),\hfill & \mathrm{if} discharging\hfill \\ 0,\hfill & \mathrm{if} charging\hfill \end{array}\right.$$

(10)

$\forall k\in K, \forall evd\in EVD$

2.2. Constraints

The SCUC optimization problem incorporating EVs is constrained by several factors, including the operational limits of generators, the power flow through transmission lines, and the secure charging and discharging of the EVs. Additionally, the problem is constrained to ensure that its primary obligation, which is to meet the system’s power demand, is fulfilled. The power balance constraint is represented by Equation (11). The generator power production with the added discharge from the EVs must be equal to the day-ahead power demand ${Pd}_k$ of the system and the demand of the EVs. In Equation (12) the energy reserve of the system is denoted. The energy reserve ${Res}_k$ is set to be equal to 10 percent of the hourly system demand. EVs, due to their nature as flexible loads and the system’s capability to shed their loads, are not considered in the reserve calculation.

$$\sum _{l=1}^{L}c{s}_{l,k}·p{r}_{l,k}·TI+\sum _{evg=1}^{EVG}EnDisc{h}_{evg,k}=P{d}_k+\sum _{evf=1}^{EVF}EnC{h}_{evf,k}\forall k\in K$$

(11)

$$\sum _{l=1}^{L}c{s}_{l,k}·Prma{x}_l·TI\ge P{d}_k+Re{s}_k\forall k\in K$$

(12)

Equations (13)–(18) represent the electrical and mechanical characteristics of the power generators. Equation (13) represents the thermal limits of the generators where the power production of the generator is constrained between a minimum production level Prmin and a maximum Prmax. The power generators can increase or reduce their production level according to their ramp rate constraints that are shown in Equations (14) and (15). Once a generator is deactivated, it is required to remain offline for a specified number of periods in order to satisfy the minimum downtime constraint. Similarly, when a generator is activated, it must remain online for at least the minimum required period to comply with the minimum uptime constraint. The minimum up and minimum down constraints are expressed in Equations (18) and (16). The consecutive hours during which the generator remains operational are calculated using Equation (17).

$$Prmi{n}_{l,k}\le p{r}_{l,k}\le Prma{x}_{l,k}\forall k\in K, \forall \ell \in L$$

(13)

$$Prmi{n}_{l,k}=\left\{\begin{array}{cc}Pmi{n}_l,\hfill & \mathrm{if} c{s}_{l,k-1}=0\hfill \\ max(Pma{x}_l,p{r}_{l,k-1}-RD{n}_l),\hfill & \mathrm{if} c{s}_{l,k-1}=1\hfill \end{array}\right.$$

(14)

$$Prma{x}_{l,k}=\left\{\begin{array}{cc}Pma{x}_l,\hfill & \mathrm{if} c{s}_{l,k-1}=0\hfill \\ max(Pma{x}_l,p{r}_{l,k-1}+RU{n}_l),\hfill & \mathrm{if} c{s}_{l,k-1}=1\hfill \end{array}\right.$$

(15)

$\forall k\in K, \forall \ell \in L$

$$(To{n}_{l,k-1}-MT{U}_l)·(c{s}_{l,k-1}-c{s}_{l,k})\ge 0\forall k\in K, \forall \ell \in L$$

(16)

$$To{n}_{l,k}=(To{n}_{l,k-1}+1)·c{s}_{l,k}\forall k\in K, \forall \ell \in L$$

(17)

$$(Tof{f}_{l,k-1}-MT{D}_l)·(c{s}_{l,k}-c{s}_{l,k-1})\ge 0\forall k\in K, \forall \ell \in L$$

(18)

The transmission constraints are determined using a DC power flow formulation. Incorporating AC power flow calculations can be computationally intensive, particularly in the context of the UCP framework [49]. This issue is exacerbated in our research due to the inclusion of heuristic power flow repair mechanisms, necessitating repeated power flow calculations in the same period k within each particle of the DE-based algorithm. Equation (19) represents the power flow of a transmission line without any power losses. The problem can be simplified by considering the voltage of the buses equal to 1 pu and the difference between the angles of the nodes is close to zero. Following the work of [49], Equations (20)–(22) are obtained. The limits of the transmission lines are represented by Equation (23).

$$pf{a}_{ln}={\displaystyle \frac{|V_{NDM}|·|V_{NDN}|}{x_{ln}}}sin(anglNDM-anglNDN)$$

(19)

$$p{f}_{ln,k}=(b_{ln}·IMA)·{(IM{A}^T·b_{ln,k}·IMA)}^{-1}·pfnoda{l}_k$$

(20)

$\forall ln\in LN, \forall k\in K$

$$PTDF=(b_{ln}·IMA)·{(IM{A}^T·b_{ln}·IMA)}^{-1}$$

(21)

$$\sum _{node=1}^{ND}PFnodal=0$$

(22)

$$-Pf{l}_{ln}\le p{f}_{ln,k}\le Pf{l}_{ln}\forall ln\in LN, \forall k\in K$$

(23)

The EV charging and discharging problem in this work builds on the findings of Madzharov et al. [26], who suggest that electric vehicles (EVs) can be aggregated and managed as flexible loads, with an optimized charging schedule. The optimization of EV charging is based on the availability of aggregated EVs. This availability is primarily determined by the location of the EV’s connection to the power grid. EVs can either be in transit or parked and connected to one of two nodes. Consequently, the EV mix fluctuates as vehicles travel between nodes during the day. This approach enables the calculation of the SoC for all EVs at a given Node by classifying EV categories based on their travel patterns during the 24 h optimization period.

From this process, six 24 h SoC schedules are generated. Lines 1 and 4 of the SoC schedule represent the EV categories where all EVs remain connected throughout the day to bus A and bus B, respectively. Specifically, Line 1 of the EnCh variable represents the charging load of EVs added to the load of Node A, while Line 4 represents the charging load added to Node B. Lines 2 and 3 of the SoC variable reflect EVs that begin their travel at a location connected to Node A but reach at least one destination connected to Node B during the day. Line 2 of the EnCh variable represents the charging load connected to Node A before traveling to a location connected to Node B or after their return to a location connected to Node A, while Line 3 corresponds to the charging load added to Node B from EVs that initially traveled from Node A and are connected to Node B before traveling back to Node A. Similarly, Lines 5 and 6 represent EVs that begin their daily schedule connected to Node B but travel to at least one destination associated with Node A. Line 5 of the EnCh variable accounts for the charging load added to Node B from EVs connected to Node B, while Line 6 represents the load added to Node A by EVs that began their travel schedule at Node B. Figure 2 depicts the trip types of aggregated EVs. The formulation of trip schedules and EV numbers is generated as described in Appendix A.

The constants nt(x) from

Table 5. Multipliers representing EV movement between two nodes.

Multiplier	Node Traveling Category	Departure and Arrival Distinction	Trip Duration (hours)	Dependent SoC
nt1	Na to Na	departure from a	1	$So{C}_{a,k-1}$
nt2	Na to Na	arrival to a	1	$So{C}_{a,k-2}$
nt3	Na to Nb	departure from a	1	$So{C}_{a,k-1}$
nt4	Na to Nb	arrival to b	1	$So{C}_{a,k-2}$
nt5	Nb to Na	departure from b	1	$So{C}_{b,k-1}$
nt6	Nb to Na	arrival to a	1	$So{C}_{b,k-2}$
nt7	Nb to Nb	departure from b	1	$So{C}_{b,k-1}$
nt8	Nb to Nb	arrival to b	1	$So{C}_{b,k-2}$

were estimated from the existence of EVs at each Node by calculating the percentage of vehicles leaving a Node, as described in Appendix A. Table 5 explains the nt terms in Equations (35), (29), (28) and (39). In those equations, constants nt9 to nt16 serve the same purpose as constants nt1 to nt8; however, they represent trips with a duration of 2 h.

The following equations describe the charging and discharging behavior of EVs as well as the SoC of their batteries. Equations (24) through (35) define the dynamics of EVs traveling to a single Node only within their travels. Specifically, Equations (32) to (35) establish the constraints on the SoC for EVs that follow a 24 h charging schedule while traveling between nodes. In particular, Equations (24) to (31) represent the vehicles traveling from Node A to Node B. These same equations can also be applied to vehicles traveling from Node B to Node A within the 24 h period by reversing the variables an and bn within the equation.

$$So{C}_{an,k}=InS{t}_{an}+ne·EnC{h}_{an,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{an,k},k=1$$

(24)

$$So{C}_{bn,k}=InS{t}_{bn}+ne·EnC{h}_{bn,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{bn,k},k=1$$

(25)

$$So{C}_{an,k}=So{C}_{an,k-1}+ne·EnC{h}_{an,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{an,k},1<k\le 3$$

(26)

$$So{C}_{bn,k}=So{C}_{bn,k-1}+ne·EnC{h}_{bn,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{bn,k},1<k\le 3$$

(27)

$$\begin{array}{cc}So{C}_{an,k}\hfill & =So{C}_{an,k-1}+ne·EnC{h}_{an,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{an,k}\hfill \\ \hfill & -nt1·So{C}_{an,k-1}+nt2·So{C}_{an,k-2}-nt3·So{C}_{an,k-1}\hfill \\ \hfill & +nt6·So{C}_{bn,k-2}-nt9·So{C}_{an,k-1}+nt10·So{C}_{an,k-3}\hfill \\ \hfill & -nt11·So{C}_{an,k-1}+nt14·So{C}_{bn,k-3}-{\displaystyle \frac{1}{ne}}·CE{D}_{an},\hfill \\ \hfill & 3<k\le K\hfill \end{array}$$

(28)

$$\begin{array}{cc}So{C}_{bn,k}\hfill & =So{C}_{bn,k-1}+n·EnC{h}_{bn,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{bn,k}\hfill \\ \hfill & +nt4·So{C}_{an,k-2}-nt5·So{C}_{bn,k-1}-nt7·So{C}_{bn,k-1}\hfill \\ \hfill & +nt12·So{C}_{an,k-3}-nt13·So{C}_{bn,k-1}-nt15·So{C}_{bn,k-1}\hfill \\ \hfill & +nt16·So{C}_{bn,k-3}-{\displaystyle \frac{1}{ne}}·CE{D}_{bn},\hfill \\ \hfill & 3<k\le K\hfill \end{array}$$

(29)

When both indices $a_n$ and $b_n$ are used within the same equation, only the following two pairs are valid: (1) $a_n=2$, $b_n=3$, and (2) $a_n=5$, $b_n=6$.

$$So{C}_{an,k}\le Bca{p}_{an,k},1\le k\le K$$

(30)

$$So{C}_{bn,k}\le Bca{p}_{bn,k},1\le k\le K$$

(31)

$$So{C}_{cna,k}=InS{t}_{cna}+ne·EnC{h}_{cna,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{cna,k},k=1$$

(32)

$$So{C}_{cna,k}=So{C}_{cna,k-1}+ne·EnC{h}_{cna,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{cna,k},1<k\le 3$$

(33)

$$So{C}_{cna,k}\le Bca{p}_{cna,k},1\le k\le K$$

(34)

$$\begin{array}{cc}So{C}_{cna,k}\hfill & =So{C}_{cna,k-1}+ne·EnC{h}_{cna,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{cna,k}\hfill \\ \hfill & -nt1·So{C}_{cna,k-1}+nt2·So{C}_{cna,k-2}\hfill \\ \hfill & -nt9·So{C}_{cna,k-1}+nt10·So{C}_{cna,k-3}-{\displaystyle \frac{1}{ne}}·CE{D}_{cna},\hfill \\ \hfill & 3<k\le K\hfill \end{array}$$

(35)

$$So{C}_{cnb,k}=InS{t}_{cnb}+ne·EnC{h}_{cnb,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{cnb,k},k=1$$

(36)

$$So{C}_{cnb,k}=So{C}_{cnb,k-1}+ne·EnC{h}_{cnb,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{cnb,k},1<k\le 3$$

(37)

$$So{C}_{cnb,k}\le Bca{p}_{cnb,k},1\le k\le K$$

(38)

$$\begin{array}{cc}So{C}_{cnb,k}\hfill & =So{C}_{cnb,k-1}+ne·EnC{h}_{cnb,k}+{\displaystyle \frac{1}{ne}}·EnDisc{h}_{cnb,k}\hfill \\ \hfill & -nt7·So{C}_{cnb,k-1}+nt8·So{C}_{cnb,k-2}\hfill \\ \hfill & -nt15·So{C}_{cnb,k-1}+nt16·So{C}_{cnb,k-3}-{\displaystyle \frac{1}{ne}}·CE{D}_{cnb},\hfill \\ \hfill & 3<k\le K\hfill \end{array}$$

(39)

$$EnC{h}_{evf,k}\le MaxTrans{f}_{evf,k},1\le k\le K$$

(40)

$$EnDisc{h}_{evd,k}\le MaxTrans{f}_{evd,k},1\le k\le K$$

(41)

where $MaxTrans{f}_{evf,k}$ is defined, according to Equation (42), as the maximum allowed power that can be transferred to and from EVs and is calculated prior to the optimization process, taking into consideration that the chosen charging type is type 1, allowing for up to 3 kW charging per vehicle, and the hourly availability of EVs.

$$MaxTrans{f}_{evd,k}=EVsavai{l}_{evd,k}·ChargType,1\le k\le K$$

(42)

$$EnC{h}_{evf,k}\le Bca{p}_{evf,k}·u_t,$$

(43)

$$EnDisc{h}_{evd,k}\le Bca{p}_{evd,k}·(1-u_t)$$

(44)

$$u_t\in \{0,1\}$$

(45)

The charging loads of the electric vehicles (EVs) are incorporated into the nodal injections by adding the EV charging load to the respective nodal load and subtracting the EV discharging load accordingly. The charging loads represented by lines 1, 2, and 6 of the variable EnCh are added to the load at Node A, while the charging loads represented by lines 3, 4, and 5 are added to the load at Node B.

3. Description of the Optimization Algorithm

The suggested optimization algorithm is a variant of a DE optimization algorithm with the inclusion of feasibility rules and problem-specific heuristics that act as violation repair mechanisms. The TCUCP with EVs problem is a constrained, mixed integer, nonlinear optimization problem that, by utilizing repair mechanisms, can be transferred in continuous space, thus giving the capability to utilize DE mechanisms. The nonlinearities of the formulated problem are strong and originate in the terms of battery degradation costs, in addition to the generators’ quadratic production cost, and the presence of variables that only receive integer values. Due to the existence of constraints, the Feasibility Rules with incorporation of Objective Function Information (FROFI) [52] tool has been utilized, which is a variant of DE that can handle constrained optimization problems with strong nonlinearities.

The complexity of the proposed general computational problem is very complicated, given the fact that the general computational model contains the mechanisms of a stochastic algorithm. Stochastic algorithms are based on randomness to reach a solution close to the global optimum, and thus the complexity of the algorithm heavily depends on the stopping criterion set by the user and the complexity of the problem. In this case, the problem solved is the TCUCP, which is an NP-hard problem. The solution finding of the problem is improved by the use of heuristic repair mechanisms that utilize priority lists, leading to faster convergence to a near-optimum solution. A simplified calculation of the complexity of the general computational model can be given by the following relationship: O(G*P*(D + Cf + Ch)), where G are the selected number of generations, P is the selected number of particles, Cf is the cost of calculating the cost of the objective function, D is the dimension of the system, and Ch is the cost of the heuristic mechanisms.

The time complexity of the problem depends heavily on the purpose of the algorithm. One of the main goals of this work is to research charging patterns in a large urban environment, where EVs travel and charge across different nodes of the power grid that serve the city. Since this is an optimization of coordinated, centralized charging for a single EV fleet, solving systems with more than 100 generators, extending beyond the national level, would be impractical. The number of EVs does not affect the computational cost or time complexity, as the charging variables represent an aggregated fleet. What does impact complexity is whether multiple EV fleets, operating across different nodes, are included in the analysis.

3.1. Differential Evolution

In the event of constraint violations, the FROFI algorithm employs feasibility rules to manage the constraints of the optimization problem while simultaneously accounting for the cost of the objective function. The target vector of the population of the DE is expressed in Equation (46). Where gen is the generation counter, D represents the number of optimization variables, and PP as the total number of population particles. In the first generation, the values of the variables are randomly assigned within their lower and upper limits. Following the initialization process, three evolutionary mechanisms are applied.

$$z_n^{gen}=[z_{n,1}^{gen},z_{n,2}^{gen},\dots ,z_{n,D}^{gen}]$$

(46)

3.1.1. Differential Evolution Operators

The mutation mechanisms utilized in FROFI is expressed in Equations (47) and (48). In comparison with the DE originally proposed by [53], FROFI utilizes two mutation processes that are chosen with equal probability.

• DE/current-to-rand/1:

  $$w_n^{gen}=z_n^{gen}+U(0,1)·(z_{r1}^{gen}-z_n^{gen})+SF·(z_{r2}^{gen}-z_{r3}^{gen})$$

  (47)
• DE/rand-to-best/1:

  $$w_n^{gen}=z_{r1}^{gen}+U(0,1)·(z_{best}^{gen}-z_{r1}^{gen})+SF·(z_{r2}^{gen}-z_{r3}^{gen})$$

  (48)

where n is the DE particle index, $z_{r1}^{gen}$, $z_{r2}^{gen}$, $z_{r3}^{gen}$ are population vectors randomly sampled from the population from generation gen, and finally, $SF$ is the scaling factor that is applied on the differential variation and is chosen from the pool $S{F}_{pool}=[1.0,0.8,0.6]$.

The diversity of the solutions is increased with the crossover mechanism. The binomial crossover is implemented on the mutant vectors in order to create the trial vector $t{r}_{n,i}^{gen}$ according to Equation (49).

$$t{r}_{n,i}^{gen}=\left\{\begin{array}{cc}{w}_{n,i}^{gen},\hfill & \mathrm{if} ran{d}_i\le CRR \mathrm{or} i=irand\hfill \\ z_{n,i}^{gen},\hfill & \mathrm{otherwise} \hfill \end{array}\right.$$

(49)

where i = 1, …, D, $ran{d}_i\sim \mathcal{U}(0,1)$ generated for every variable in the population, irand is a random index from [1, D], and finally, CRR is the crossover rate of the DE.

3.1.2. Feasibility Rules

Feasibility rules, as established by [54], are sequentially applied to the population. These rules involve a comparison between the trial vector and the parent vector in the following manner:

• If both compared vectors produce infeasible solutions, the solution with the least violation is preferred.
• If one vector produces a feasible solution and one an infeasible solution, the feasible solution is chosen.
• If both vectors produce feasible solutions, then the vector that produces the solution with the lowest objective function cost is chosen.

In case of a trial vector not surviving to the next generation, it is stored in an archive ARC for usage in the selection mechanism.

3.1.3. FROFI Mechanisms

After creating the target vector, the greediness of the feasibility rules is mitigated by the selection mechanism. This mechanism leverages the vectors stored in ARC. The population of target vectors is sorted in descending order according to their objective function values. Subsequently, this population is divided into as many parts as the cardinality of ARC. For each division, the vector that produces the solution with the maximum violation is compared with the vector with the minimum constraint violation in the archive ARC. If the objective function value of the vector from the target vector exceeds that of the archive ARC, then the vector from the archive replaces the vector from the target vector and is removed from the archive. This process continues until either the archive is empty or all divided parts of the target vector have been updated.

If all vectors in the population are found to be infeasible, a final mutation is applied. In this process, a randomly selected population member, $z_r^{gen}$, undergoes mutation by randomly altering one of its dimensions, assigning it a new value within the specified upper and lower bounds. If for this mutant vector $m_r^{gen}$ the cost of the objective function is lower than the objective function of the vector with the highest constrained violation of the next generation $f\left(m_r^{gen}\right)\le f\left(z_r^{gen+1}\right)$, then $m_r^{gen}$ replaces $z_r^{gen+1}$.

3.1.4. Implementation of the Method

The optimization method is implemented with the following steps and is summarized in Figure 3:

• Trial vectors equal to the chosen population number PP are created with the engagement of the FROFI mechanisms
• Each vector is transformed into a matrix, with one matrix generated for each group of variables. The on/off schedule is determined as a by-product of the power production schedule ($p{r}_{l,k}$). These matrices are subsequently processed using the heuristic mechanisms described in Section 3.3. The objective function and constraint violation for each particle are then evaluated. Finally, the matrices are converted back to their vector form.
• The feasibility rules are then applied and the target vector of the next generation (gen + 1) is created.The trial vectors that did not survive but have a lower objective function value than the respective target vectors are stored in an auxiliary archive ARC.
• The replacement process is engaged.
• The FROFI mutation mechanism for dealing with a population of only infeasible solutions is engaged.
• The termination condition is evaluated, specifically to check whether the predetermined number of function evaluations has been reached.

3.2. Structure of Solution Vector

The optimization algorithm solves a system of L generators in a time horizon of K hours. The system offers energy to 6 categories of EVs that can also provide energy back to the system in V2G operation. In addition, a variable is introduced in the system that dictates the operation of two repair mechanisms, one for every hour k, as depicted in the last term of the Equation (50). Thus, the solution of the TCUCP with V2G is a vector with the following dimensions:

$$Dim=L·K+EVF·K+EVD·K+1·K$$

(50)

The population vector size that is calculated according to Equation (50) changes with the engagement of different EV operations. With the engagement of only the power flow constraints and the UCP, $EVF$ and $EVD$ are set to zero. For the strict G2V operation of the EV charging, $EVD$ is set to zero. The initial vector receives initial values randomly within the limits of each variable. The limit of variable $PPC{V}_k$ is dependent on the constant EPV. The constant EPV, which is determined experimentally, is multiplied by the maximum limit of the generator with the largest production capacity ($[0, EPV·max\left(Prma{x}_l\right)]$). This approach enables the repair algorithm to activate either a single large generator or multiple smaller generators as needed to balance transmission power flow constraints effectively. The DE is able to handle this integer problem in linear space by utilizing the following transformation function: if the generator production $p{r}_{l,k}$ is smaller than $Prmi{n}_l$, then the decision variable $c{s}_{l,k}$ becomes 0, and if it is larger than $Prmi{n}_l$, it takes value 1.

3.3. Description of Heuristic Repair Mechanisms

3.3.1. Repair Mechanism 1—Electric Vehicle Constraint Repair Mechanism

The proposed general computational model is built upon a variant of Differential Evolution (DE) that operates in continuous space. To address the mixed-integer nature of the V2G problem, the discrete variables are mapped to continuous space through the application of Algorithm 1. In this mechanism, if the charging energy exceeds the energy provided by the EVs, the discharged energy is set to zero; conversely, if the discharged energy is greater, the charging energy is set to zero.

After the transfer of the problem to continuous space, the SoC is handled by two repair mechanisms. Initially, Algorithm 2 calculates the total power required by the EVs to replenish all the energy consumed over a 24 h period. This energy includes both the trips’ energy consumption and, in the case of V2G operations, the power supplied to the energy grid. A ratio is then calculated, representing the power provided by the power network, as determined by the heuristic mechanisms and the DE mechanisms, relative to the total energy consumed. This ratio is used to adjust the power supplied to the EVs, ensuring that by the end of the 24 h period, the EVs have stored the same amount of energy as they had at the beginning. According to Equations (30), (31), (34), and (38), the SoC for each category must not exceed the capacity of the EV batteries connected to the power network at each hour. If this occurs, the excess energy, divided by the EV charging efficiency, is subtracted from the power provided by the network by Algorithm 3, and the SoC is recalculated for use in the subsequent hour.

The demand of EVs during hours with line violations is reduced using Algorithm 3, which applies the PTDF method to decrease EV demand and consequently alleviate power flow on overloaded transmission lines. Unlike the approach in repair mechanism 6, which focuses on power generation, this method addresses demand. Thus, applying the opposite signs from those of the PTDF matrix will result in reduced power flow due to the inverse impact of demand in relation to production on line flow. This repair mechanism compares the PTDF of the nodes that the EVs are connected to, for the lines that are deemed problematic. These factors are the $PTD{F}_{NODE:1,2,6}$ for EVs connected to Node A and $PTD{F}_{NODE:3,4,5}$ for EVs connected to Node B. In the case that the power flow is positive and either one PTDF of Node A or B is negative, then when the demand connected to that Node is reduced, the power flow in that line is decreased.

Algorithm 1: Electric Vehicle heuristic repair mechanism that transfer the mixed integer V2G problem into linear space.

Algorithm 2: Electric Vehicle heuristic repair mechanism load reduction.

Algorithm 3: Electric Vehicle heuristic repair mechanism, total load repair, and SoC calculation.

3.3.2. Repair Mechanism 2—Spinning Reserve and Power Flow Repair Mechanism

This heuristic repair mechanism is the first to engage with the TCUCP problem. Its primary function is to activate generators sequentially until the spinning reserve requirement is satisfied. The spinning reserve and power flow repair mechanisms generate schedules based on priority list methods from contemporary literature and the unique insights of the PTDF matrix. The heuristic mechanism initially creates a mirror schedule that is identical to the schedule received from the DE mechanisms. Algorithm 4 receives the DE mechanisms’ schedule and shuts down costly generators until the hourly demand to peak-power ratio (TR) equals 2 in a temporary variable. Algorithm 5 reopens generators until the system’s peak-power (sum of maximum production limits of all open generators) meets or exceeds the hourly demand plus required reserves. Algorithm 4 is called and shuts down generators until TR is less than 1. The second shutdown process aims to shut down all generators that were opened in previous generations by the proposed dynamic priority list, keeping open only generators from the Plavcost priority list (that is based on the average production cost of the generators, read [38] for the Plavcost). This approach aims to allocate sufficient capacity for the priority list containing grid information, ensuring it can accommodate the additional required reserve increased by the newly introduced variable PPCV while reducing power flow violation.

Algorithm 4: Power reserve and power flow heuristic repair mechanism, first shut down of generators.

Algorithm 5: Power reserve and power flow heuristic repair mechanism, first start-up of generators.

The Algorithm 6 creates the new priority list that consists of the Plavcost priority list in combination with the coefficients of the PTDF matrix. At first, the violation of every line within the 24 h schedule is calculated. Then the lines where the power flow exceeds the power transfer limit are utilized in order to sort the system’s generators. This is achieved by adding the absolute values of the PTDF coefficients of those lines. The lowest values end up at the bottom of the priority list since the effect of the generator on the violated lines is minimal, and turning those generators off or on will not significantly affect the power flow violation of the targeted lines. A value is assigned to every generator as shown in Algorithm 7, which consists of the sum of the absolute values of all violated transmission lines increased by 1 over $PLweigh{t}_{k,l}$. This variable, as per Algorithm 6, receives a lower value the less expensive a generator is. Thus, a generator with a high $PLweigh{t}_{k,l}$ value (meaning the more expensive it is) with a small contribution of PTDF will be placed lower in the new priority list than a generator with small $PLweigh{t}_{k,l}$ value and with a large contribution to the violated lines. Thus, the further down a generator is in the FinalPL, the worse it is considered for the system, both due to cost and line violation. Upon the establishment of the updated priority list, a new phase of generator activation is initiated by Algorithm 8 using the new priority list “FinalPL” until the sum of the Prmax of all open generators is equal to the hourly demand added by the necessary reserves and the variable PPCV. After the execution of Algorithm 8, a comparison is performed between the schedule received by the DE mechanisms and the temporary schedule that resulted from Algorithms 4–8. If a generator is active in both schedules, its production in the temporary schedule is adjusted to match the output generated by the DE mechanisms. If more generators were open in the schedule provided by the DE and are closed in the temporary schedule, then those generators are turned on in the temporary schedule. The temporary schedule then becomes the new regular schedule. This way, information provided by the DE is retained.

Algorithm 6: Creation of dynamic priority list.

Following the comparison between the two schedules, a generator might shut down. This generator is the open generator that lies furthest down the FinalPL priority list. After the shutdown of this generator at hour k, the schedule of the same generator is altered in adjacent hours in a stochastic manner, in order to repair the minimum downtime constraint of the generator. This shutting down is performed under the following conditions: (1) the total line violation of the hour k is larger than 0.05 MW, (2) the peak power of the open generators divided by the pick power of all generators of the system (both opened and closed) is larger than 0.9, and $P=U(0,1)>0.4$. The repair of the minimum downtime of the generator follows some simple rules after counting the consecutive hours the generator is open before and after the hour k:

• In a stochastic manner, pick an hour close to hour k from the range $k-MT{D}_l+1$ till k and shut down all consecutive generators from the randomly selected hour until the minimum down constraint is satisfied.
• If the shutdown of the previous step causes the minimum uptime to be disturbed, extend the operating hours of the generators.
• If the shutting down of the generators creates conflict with the initial state of the system or the energy reserves of the system, then do not shut the generator down and perform the previous steps with the next generator from the FinalPL priority list.
• If the power reserve is not satisfied by the shutdown of any generator, do not shut down a generator.

Algorithm 7: Algorithm of 6, calculation of the characterization number of every generator considering their PTDF coefficient and position on average cost priority list.

The complete flowchart of this heuristic is shown in Figure 4.

Algorithm 8: Power reserve and power flow heuristic repair mechanism, second start-up of generators.

3.3.3. Repair Mechanism 3—Minimum Up and Minimum Down Repair Mechanism

This mechanism is adopted from the work of [38], and readers are encouraged to consult this article for further details.

3.3.4. Repair Mechanism 4—Spinning Reserve Minimization/Shutdown of Excess Reserve

The mechanism employed in this work is adapted from [27,38] and others. The mechanism is presented in Algorithm 9 and aims to reduce the excessive reserve produced by the system by decreasing the number of operational generators. This minimizes the constant costs of generators, resulting in a more economical system. The process is only interrupted when the minimum up and minimum downtime constraints are violated.

Despite the reduction in operational time, the sub-algorithm’s design conflicts with the integration of transmission constraints, as, in many cases, generators would need to operate in greater numbers to satisfy these constraints. To address this issue, the optimization variable $PPC{V}_k$ is introduced as a control mechanism for the operation of several heuristics within the proposed general computational model. This variable $PPC{V}_k$ as used in Algorithm 9 decreases the amount of power that is perceived by the sub-algorithm as excessive reserve, reducing the number of generators that need to be shut down for achieving minimum reserve level, thus regulating the amount of excess peak power available each hour.

Algorithm 9: Power reserve minimization via shutdown of generators.

3.3.5. Repair Mechanism 5—Ramp Rates Repair

This mechanism is adopted from the work of [38], and readers are encouraged to consult their study for further details.

3.3.6. Repair Mechanism 6—Power Production Transfers for Repairing Line Violation

The operation of this mechanism uses information from the coefficients of the PTDF matrix to repair power flow constraint violations, and every action involves operational generators only. In this step, two generators at a time are paired, and an equal amount of power production is transferred from generator i to generator j. This trade is dictated by the sign of the power flow of the transmission line and the sign of the coefficient of the PTDF matrix of the corresponding node to which each generator is connected. The basic principle of the sub-algorithm is that an increase in production of a generator with a positive PTDF coefficient will reduce the power flow of a line with negative power flow and vice versa. The amount of power production that is traded is calculated by Equation (53). This equation is produced by Equation (51) if equal power production is transferred from generator i to generator j.

The process follows the steps in Algorithm 10: Initially, a demand constraint repair mechanism, used in [38], adjusts generator production to match day-ahead demand. This ensures energy dispatch meets the demand, preventing power flow violations in transmission lines. Next, power flows are computed, identifying lines with violations. The line with the highest violation guides subsequent energy trades. After each trade, power flows are recalculated, choosing trades that minimize the sum of violations across all lines. During the search for the optimal trade, the generators are classified into two distinct groups. The first group, referred to as the “Best group”, consists of generators whose PTDF coefficients have an opposite sign to the power flow on the transmission line exhibiting the highest violation. Conversely, the second group, termed the “Worst group”, includes generators whose PTDF coefficients share the same sign as the power flow on the most violated line. Algorithm 11 prioritizes trades to minimize energy exchange. Trades first occur between Worst and Best groups; if one is empty, then all generators are considered for trade within the same group. This way, evaluations are significantly reduced. If Best is empty, trades shift from higher to lower negative impact generators. If Worst is empty, trades move from positive to more positive impact generators.

Algorithm 10: Power generation and power flow heuristic repair mechanism, generation trades between open generators.

Trades are executed as long as the total sum of power flow violations across all transmission lines remains positive. The reason for evaluating the impact of each trade on the entire transmission network, rather than on individual lines, is that while a trade may reduce the violation on a specific line, it could simultaneously exacerbate violations on other lines. Therefore, it is crucial to prioritize trades that optimize the overall network performance, even if they do not fully eliminate the violation on the target transmission line. This holistic approach ensures that the overall power system operation is improved.

$$PoweFlow=const+PTD{F}_i·p{r}_i+PTD{F}_j·p{r}_j$$

(51)

Reduce the production from generator i by $p{r}_t$ MW and increase the production of generator j by the same amount:

$$(PTD{F}_i-PTD{F}_j)·p{r}_t\ge Violation$$

(52)

$$p{r}_t\ge {\displaystyle \frac{\left|Violation\right|}{\left(\right|\left|PTD{F}_i\right|-\left|PTD{F}_j\right|\left|\right)}}$$

(53)

Algorithm 11: Power generation and power flow heuristic repair mechanism, generation trades between open generators—Algorithm of 10, cases depending on the existence of generators in “Best” and “Worst” archives.

4. Results

The TCUCP with EVs was solved using a variant of DE and is a real-coded approach implemented in MATLAB (2024a). All MILP formulations were optimized with MATLAB’s intlinprog algorithm. The simulations were executed on an Intel^®$Cor{e}^{TM}$ i5-6402P CPU @ 2.80 GHz with 8.00 GB of RAM.

4.1. Objectives of the Experiments

This work set out to address six key objectives related to the integration of EVs into the TCUCP using a DE framework. First, a computational model was developed to allow DE, traditionally suited for continuous spaces, to handle mixed-integer variables. This was achieved by implementing heuristic repair mechanisms that transform solutions into a continuous domain. To validate the accuracy of this approach, results were compared with those from a MILP benchmark under the same linear problem formulation, specifically in scenarios without EVs and with G2V operation only. Despite DE being a stochastic metaheuristic and MILP a deterministic optimization method, the DE-based approach delivered results within 1% of the MILP solutions, demonstrating high solution quality in linear cases.

Second, the model introduced a novel variable to guide heuristic repairs under transmission constraints, allowing the algorithm to control the number of generators remaining online and ensuring feasibility. This was supported by sensitivity analysis showing improved convergence when the variable was active. Third, EV charging was modeled as a flexible load to smooth the system’s load profile, successfully preventing constraint violations and distributing demand more evenly throughout the day.

Fourth, the economic viability of EV discharging was explored; results show that it could reduce costs and prevent generator shutdowns when generator startup costs were considered, making it a competitive option under certain conditions. Fifth, the study accounted for EV fleet movement across multiple urban nodes, revealing that nearly half of EV charging occurred at destination nodes, an insight critical for planning charger placement and aggregation strategies. Finally, EV travel behavior and energy consumption were modeled using a stochastic trip chain approach. Despite introducing variability and increasing system costs, the algorithm effectively optimized schedules, demonstrating robustness under uncertainty. Together, these contributions offer a realistic and flexible framework for integrating EVs into short-term power system planning.

4.2. Results of the TCUCP Without EVs

The preliminary evaluation of the proposed general computational model was conducted in the absence of flexible loads. The proposed general computational model with its heuristic sub-algorithms was tested on three distinct power networks: a small-scale network with three generators, a medium-scale network with sixteen generators, and a large-scale system with fifty-four generators. This range of network sizes allows for a comprehensive assessment of the general computational model’s capacity to achieve near-optimal solutions across various scales of power systems. The input data for the power systems were obtained from [55] and were also used in [56,57] among other mentioned in the literature review. These networks and variations of them have been heavily used as test cases in many works. The total demand of every power system is presented in Appendix B.

The boundaries of the PPCV variable were established experimentally and define the maximum allowable reserve within the system. The upper limit of the PPCV variable, represented by the EPV, was varied from 0 to 2.5. Each system demonstrated a distinct EPV threshold where the optimization algorithm produced optimal results. When the EPV exceeded this threshold, there was no further improvement in solution quality or convergence rate. The chosen EPV values are 0.8, 1, and 1.6 for the three power systems, respectively. The DE formulation’s termination criterion is the total function evaluations (FES) and was also determined experimentally, aiming for the DE solution to reach within approximately a 1% relative difference from the MILP solution. The results of the DE-based optimization algorithm are compared with the results of the MILP algorithm with the same formulation. The system’s hourly reserve is set at 10% of the hourly demand, with EV loads excluded from reserve calculations. The cost function was linearised in four segments. The schedule presented in

Table 6. Generator 24 h operation schedule for the 3-unit system without the presence of EVs. (A value of 1 indicates that the generator is operational, and 0 indicates that it is shut down).

Hour
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
Generator
G1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
G2	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	1	1	1	1	0
G3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	0	0	0

can be confirmed by [55] for the results of the classical DC power flow, with the same operating cost. In

Table 7. Results and stochastic algorithm statistics of the proposed general computational model for all three cases with DC power flow, without EVs, and comparison with the TCUCP MILP formulation.

Power System	3 Units—6 Bus	16 Units—31 Bus	54 Units—118 Bus
min	77.797 k USD	1.295 M USD	1.367 M USD
mean	77.858 k USD	1.296 M USD	1.367 M USD
max	78.125 k USD	1.296 M USD	1.368 M USD
std	116.073 USD	466.154 USD	313.684 USD
average time (min)	24.319	24.077	56.288
runs	20	15	15
FES	50 k	160 k	300 k
relative difference with MILP	0	0.00073	0.01144

, the results of all the examined power systems are showcased. The results demonstrate that the total costs for the 3-unit and 16-unit systems are approximately the same when using the MILP formulation, while the 54-unit system shows a relative difference of slightly over 1%. All the following results depict the solution up to three decimals. The real solution contains eight decimals for a solution without violation.

4.3. Results of the TCUCP with EVs in G2V Operation

The G2V formulation was developed by integrating EVs at two Nodes of each system with significant load that represent an urban environment. The chosen Nodes are close to each other and are not directly connected via a transmission line. The chosen Nodes were the following: (1) Nodes 5 and 6 for the 3-unit system, (2) Nodes 3 and 10 for the 16-Unit system and (3) Nodes 86 and 90 for the 54-Unit system. The number of EVs assigned to each Node was determined based on the load profiles of these Nodes. The corresponding numbers of EVs are 100k, 1 mil, and 200k, respectively.

The selected numbers of EVs represent realistic scenarios of EV penetration in power generation systems. Fleet sizes were chosen to ensure that EV loads are comparable to the existing load at each node. These nodes represent large urban centers, with EV loads designed not to exceed the established load of the particular node of the test system.

In the 3-unit system, the total load connected to the node is 1125.7 MWh. An additional EV load, amounting to approximately one-fourth of this value, was assigned to the node, but it is not included in the connected load. In the 16-unit system, which has a connected load of 46,790.654 MWh, the assigned EV load was set to ten times that of the 3-unit system, while ensuring the total number of EVs remained below one million. In the 54-unit system, although the connected node load is similar to that of the 3-unit system, the EV load assigned was doubled due to the system’s larger scale. The charging schedule of the 3-unit system in G2V operation is presented in

Table 8. Generator 24 h operation schedule for the 3-unit system with G2V operation. (A value of 1 indicates that the generator is operational, and 0 indicates that it is shut down).

Hour
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
Generator
G1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
G2	1	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	1	1	1	1	1	1
G3	0	0	0	0	0	0	1	1	0	0	1	1	1	0	1	0	1	1	1	1	1	0	0	0

.

From the results presented in Table 8 and Figure 5, we observe the following:

• EV Charging Patterns: EV charging is distributed evenly throughout the day, with no significant peaks as seen in Figure 5.
• Charging at Travel Nodes: EVs traveling to different Nodes receive substantial charging power while parked at these locations as showcased in Figure 6. This highlights the importance of charging station availability across all travel destinations to support a smooth charging process.
• EVs as Flexible Load: Utilizing EVs as a flexible load enables a considerable amount of power to be added to the hourly nodal load without causing power flow violations in the transmission lines.

Some notable aspects of the results can be observed in Table 7 and

Table 9. Results and stochastic algorithm statistics of the proposed general computational model for all three cases of the TCUCP with G2V operation with DE variant and comparison with MILP formulation.

Power System	3 Units—6 Bus	16 Units—31 Bus	54 Units—118 Bus
min	93.710 k USD	1.357 M USD	1.379 M USD
mean	94.495 k USD	1.359 M USD	1.381 M USD
max	95.986 k USD	1.361 M USD	1.383 M USD
std (USD)	532.780	1259.416	706.000
average time (min)	68.859	44.813	57.531
runs	100	15	15
FES	300 k	200 k	300 k
relative difference with MILP	0.01691	0.00466	0.01144

. Initially, the computation times for the 3-unit and 16-unit systems are comparable. This occurs due to the operation of the spinning reserve and power flow repair mechanism. In the 3-unit system, specifically in cases with EV inclusion, repair mechanism two frequently attempts to shut down generators nearly every hour, following the four rules presented in Section 3.3.2. The reason for this originates in the hourly fluctuations in demand due to the variability of the EV load. This forces the general computational model to explore shutting down generators in search of a solution without violations. In the test case without EVs, the complete algorithm infrequently initiates generator shutdowns, with exceptions occurring primarily during hours 17 to 20. However, with the inclusion of EVs, computational times increase substantially for the 3-unit system, as the general computational model expands the hours during which it attempts generator shutdowns. Notably, this instability in hourly demand due to the presence of EVs led to increased computational times across all systems.

Figure 7 illustrates the SoC of the EVs for the day-ahead schedule. At hour 0, the initial state of the EVs is depicted, which is equal to the state at the end of the 24 h period for all three diagrams. The first diagram in the figure illustrates the SoC of EVs that remain within the range of a single node throughout the day. On the other hand, the second and third diagrams represent the categories of EVs that travel to different Nodes within the day. At the beginning of the 24 h schedule, EVs are not considered to be fully charged, nor are they required to reach a state where their batteries are fully charged. However, by the end of the 24 h schedule, they are forced to recover all the energy they discharged within the day. The same systems were optimized with a basic PSO algorithm, including the proposed heuristic repair algorithms. The results are presented in

Table 10. Results and stochastic algorithm statistics of basic PSO for all three cases of the TCUCP with G2V operation.

Power System	3 Units—6 Bus	16 Units—31 Bus	54 Units—118 Bus
min	99.3 k USD	1.4169 M USD	1.479 M USD
mean	100.24 k USD	1.4303 M USD	1.4876 M USD
max	100.997 k USD	1.438 M USD	1.4953 M USD
std (USD)	645.52	6616.1	5430.481
time (min)	79.18	54.67	64.14

.

4.4. Results of the TCUCP with EVs in V2G Operation

This subsection presents the results for all three power systems in the V2G operation, with the overall results summarized in

Table 11. Results and stochastic algorithm statistics of the proposed general computational model for all three cases of the TCUCP with V2G operation.

Power System	3 Units—6 Bus	16 Units—31 Bus	54 Units—118 Bus
min	92.523 k USD	1.354 M USD	1.379 M USD
Mean	92.946 k USD	1.357 M USD	1.380 M USD
Max	93.782 k USD	1.358 M USD	1.382 M USD
Std (USD)	571.951	1190.587	643.518
average time (min)	57.531	59.796	89.915
runs	100	15	15
FES	200 k	200 k	300 k
relative difference with MILP	NA	NA	NA

. By observing the general computational model’s behavior, it is clear (see

Table 12. Generator 24 h operation schedule for the 3-unit system with V2G operation. (A value of 1 indicates that the generator is operational, and 0 indicates that it is shut down).

Hour
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24
Generator
G1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
G2	1	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
G3	0	0	0	1	0	0	0	0	0	1	1	1	1	1	1	1	1	1	1	1	1	1	1	0

) that V2G operation is utilized at hour 18, enabling all generators to remain active. In contrast, in the G2V schedule, as observed in Table 8, the second generator is shut down at hour 18 to meet power flow constraints. The V2G power injection, despite being minimal, effectively mitigates power flow violations, allowing generator 2 to stay online, as shown in Table 6, Table 8, and Table 12.

Despite maintaining a higher number of active generators, the generation schedule associated with the V2G formulation achieves a lower operational cost compared with the G2V configuration. The charging schedule of the V2G operation is presented in Figure 8. As observed at hour 18, charging and discharging cannot occur simultaneously at the same Node, and no power was extracted from EVs in Node B.

During the solution process of the 16-unit system under G2V operation (excluding V2G operation) using the DE-based algorithm, the activation of two additional generators for most hours produced a solution nearly identical to that achieved by the MILP algorithm. Notably, the DE-based algorithm bypassed one of the primary priority list generators for the entire time horizon, opting instead to activate generators further down the original priority list sequence. Unlike in the three-unit system, V2G operation was insufficient to counteract this bypass. This outcome is likely due to the larger scale of the system, which reduces the impact of EV discharge power on the scheduling process. Thus, the V2G power in the larger systems was close to zero MWh as showcased in Table 11. The relative difference between the MILP algorithm and the proposed computational method is unavailable (NA in Table 11) due to the absence of MILP results, attributed to significant model nonlinearities.

The results of the 16- and 54-unit power systems show that the system opts not to utilize power from EVs to meet the demand. This happens due to the degradation cost of the EVs’ batteries. More specifically:

The degradation cost of EV batteries in this study ranged from USD 33 to USD 110 per MWh, while the average production cost of the test case systems was below USD 19 per MWh. This significant cost gap, combined with the requirement to recharge the discharged energy within the same 24 h period, increases the overall system load and makes power from EVs less economical.

Although V2G operation can potentially help reduce extreme demand peaks, the coordinated charging of EVs already contributes to a flattened demand profile, often outperforming the benefits of V2G power injections. Under coordinated charging, the average power production cost was calculated at USD 9.87 per MWh for the 16-unit system and USD 14.02 per MWh for the 52-unit system, making EV discharging economically uncompetitive in these cases.

In contrast, in the 3-unit system, EV power injections led to a reduction in total production cost, primarily due to relief in power flow constraints. This was achieved through Generator 2 remaining online for two consecutive hours (avoiding shutdown and startup costs), reduced output from the most expensive generator, and the elimination of Generator 2’s startup events. These factors were sufficient to offset the additional battery degradation cost. In summary, V2G can provide economic benefit by eliminating start-up costs, and increased penetration could be achieved mainly by significantly reducing battery costs and by adding economic constraints via RES curtailment costs and emissions penalties.

4.5. Convergence of Proposed General Computational Model

The proposed heuristic repair mechanisms result in an algorithm with rapid convergence. Notably, the experimental results in

Table 13. Convergence of the proposed general computational model for all cases of the TCUCP. * RD stands for Relative Difference.

Power System	3 Units—6 Bus	16 Units—31 Bus	54 Units—118 Bus
No Evs Operation
Cost of Initial Vector	143.73 k USD	2.20685 M USD	1.50342 M USD
Violation of Initial Vector	5.375 k	174.61 k	60.686 k
Generation until Feasible	7	55	10
Cost of feasible solution	81.440 k USD	1.3092 M USD	1.37357 M USD
RD * of Initial Vector (%)	43.34	40.67	8.64
RD of min value (%)	4.47	1.11	0.48
Particles	80	80	80
G2V operation
Cost of Initial Vector	122.081 k USD	2.1433 M USD	1.5311 M USD
Violation of Initial Vector	3.628 k	170.090 k	52.833 k
Generation until Feasible	381	137	3
Cost of Feasible Solution	97.021 k USD	1.3757 M USD	1.3937 M USD
RD of Initial Vector (%)	20.53	35.81	8.98
RD of min value (%)	3.41	1.39	0.99
Particles	80	80	80
V2G operation
Cost of Initial Vector	177.817 k USD	2.4908 M USD	1.5951 k USD
Violation of Initial Vector	3.42 k	133.420 k	49.303 k
Generation until Feasible	415	125	8
Cost of Feasible Solution	96.26 k USD	1.3750 M USD	1.3917 M USD
RD of Initial Vector (%)	45.86	44.8	12.75
RD of min value (%)	3.09	1.52	0.86
Particles	80	80	80

demonstrate that the general computational model converges quickly, yielding a feasible solution in most cases within 150 generations. The reduction in the objective function value from the initial random vector to the first feasible solution reaches up to 45%. Moreover, the first feasible solution is, in most cases, within 1.5% of the near-optimal solution.

In scenarios with stable demand, where no flexible demand from EVs is present, the general computational model exhibits exceptionally fast convergence, achieving a feasible solution in under 100 generations. Furthermore, the algorithm scales effectively with increasing system size. As shown in Table 7, Table 9 and Table 11, the standard deviation of the solutions remains below 1% of the mean value, indicating that the results are highly consistent and tightly clustered.

In Table 13, information about the operation of the general computational model is presented for all three systems and the three main operations (no EVs, G2V, and V2G) described in this work. When a meta-heuristic algorithm initiates its operation, a random vector is created, which is named the initial vector. The initial vector contains a cost and a degree of violation that are presented in this Table in the first two rows. For the 3-unit system, in the operation without EVs, the cost of the initial vector exceeds 5k in violation. The initial cost exceeds 143k in USD. The general computational model operates by proceeding through multiple generations. For the 3-unit system operating without EVs, a feasible solution, defined as one that satisfies all constraints, is found after seven generations, as shown in the corresponding Table. The cost for that first viable generation is USD 81.440 k, as shown in the following row. The relative difference (RD) between the initial vector and the first feasible solution is presented in the following row of the Table. The cost decreases by more than 43%, and the violation is entirely eliminated (100% reduction), marking a substantial improvement within only seven generations. Following the RD of the cost between the initial vector and the first feasible solution, the RD between the feasible solution and the lowest value recorded in the experiments is presented in the following row. This is a comparison between the lowest feasible solution presented in Table 13 and of the min value presented in Table 7. Finally, the chosen number of particles that process every generation is presented. All systems and operations use the same number of test cases. In

Table 14. Number of constraints.

Power System	3 Units—6 Bus	16 Units—31 Bus	54 Units—118 Bus
Constraints	2911	13,436	43,594

, the total number of constraints is presented.

4.6. PPCV Control Variable Effect on General Computational System’s Operation and Convergence

In this section, a sensitivity analysis is conducted to depict the effect of the PPCV control variable and its upper value, EPV, on the operation of the general computational model. This variable controls the highest amount of reserve that can be considered as minimum reserve for the purposes of controlling the behavior of two heuristic mechanisms. The selected EPV value has a significant impact on the results. When it exceeds a certain threshold, the general computational model is able to optimize the problem without any issues.

In the case of the 3-unit system, for EPV values less than 0.8, the algorithm consistently fails to converge to a violation-free solution. This is evident in the violation diagram, as seen in Figure 9, where the blue and red lines never reach zero, and in the cost diagram, where the cost continuously increases as the DE mechanisms search unsuccessfully for a feasible solution. The selected EPV value of 0.8 demonstrates convergence behavior similar to that of higher values in terms of violations, while achieving faster cost reduction, as shown by the yellow lines in the cost diagram. Therefore, an EPV of 0.8 was chosen.

For the 16-unit system, which exhibits behavior very similar to the 54-unit system, an EPV value of 1 was selected. EPV values below 0.4 resulted in solutions with persistent constraint violations, as indicated by the blue line of the violation figure in Figure 10, while values between 0.4 and 1 led to suboptimal solutions, as shown by the yellow and red lines. EPV values of 1 and above produced the best results. The cost and violation values of the first generation for both systems were removed, as they were excessively high and disrupted the visual quality of the graphs.

4.7. V2G Traveling Schedule with Stochastic Inputs

This subsection presents the analysis of V2G operation under stochastic inputs. The optimization schedules that were produced in previous sub-sections were based on simulated patterns as described in Appendix A. These travel patterns are based on the daily routines of workers in a large urban environment, where vehicle movements are driven by departure times from home to work, and subsequently from work either to commercial areas or back home. However, it is also important to evaluate the algorithm’s performance under conditions of increased uncertainty. To simulate this uncertainty, a Monte Carlo analysis was conducted, treating departure time, energy consumption, and travel duration as stochastic EV inputs. The following stochastic inputs were considered: The departure times from home to work initiated at 07:00 and followed the Weibull distribution as described in [58] with scale parameter of 1 and shape parameter of 1.2. Same with the departure times from the commercial area. As far as the trip duration is concerned, it follows a normal distribution with a mean travel duration of 45 min (as was determined from the calculations in Appendix A) and a standard deviation of 15 min. Finally, the consumed energy during the trip also follows a normal distribution with a mean of 3kWh and with a standard deviation of 2kWh per trip. The results are presented in

Table 15. Results for the three test systems for V2G operation with stochastic inputs.

Power System	3 Units—6 Bus	16 Units—31 Bus	54 Units—118 Bus
min	95.209 k USD	1.37615 k USD	1.3849 M USD
mean	95.298 k USD	1.37758 M USD	1.38694 M USD
max	95.47 k USD	1.37921 M USD	1.38906 M USD
std	111.02	750.235	1169.032

.

The power production cost of the system has increased noticeably, as the stochastic inputs led to higher energy consumption from EVs and reduced their availability during certain hours. Still, the results show only small deviations, mainly for two reasons. First, the optimization inherently shifts charging to hours when EVs are available, which leads to similar outcomes. Second, the large number of EVs being aggregated reduces the impact of variations in individual input data.

4.8. Modest Infrastructure and Delayed Charging

In the transition to EV fleets, it is likely that charging infrastructure will not be available at all of the destinations visited by EV owners. As a result, EVs may be forced to delay charging until they return to their home location. To reflect this limitation, a test case was created in which EVs are only allowed to charge when they are present at their home destination. This operation is formulated by setting the EnCh variable (the charging of the EVs) equal to zero in hours 08:00 to 19:00. This mode of charging is referenced as modest infrastructure [26,27] in contrast to the formulation that allows for charging within the entire 24 h system, which is referenced as perfect infrastructure. The results of the Perfect infrastructure are presented in Table 9. The results for the modest infrastructure are presented in

Table 16. Results for the three test systems for the Modest infrastructure.

Power System	3 Units—6 Bus	16 Units—31 Bus	54 Units—118 Bus
min	95.12 k USD	1.35613 M USD	1.380033 M USD
mean	95.63 k USD	1.35719 M USD	1.380432 M USD
max	96.72 k USD	1.35799 M USD	1.38105 M USD
std	566.602	814.321	444.5187

. The charging schedule is presented in Figure 11. In the 3-unit system, the results are worse than those of Table 9, as anticipated due to increased load density. On the contrary, in the 16-unit and 54-unit systems, the results are almost the same. The explanation for this phenomenon lies in computational reasons rather than in the physical state itself. More specifically, since the final FES number was imposed to be the same in both cases (Perfect and Modest infrastructure), in the first case (G2V-Perfect infrastructure) the model was struggling to obtain the optimal state whilst in the second case (Modest infrastructure) it was much easier computationally for the model to achieve optimal state since the charging in a lot of hours was imposed to be zero.

4.9. Stochastic Heterogeneous Charging

The homogeneity in the formulation is represented by the coefficients in Table 5. These coefficients (nt1 to nt16) capture the movement of EVs between the two grid nodes that model the urban environment in which EVs charge and travel (see Figure 2). Each transfer coefficient is calculated by dividing the number of trips per hour by the number of EVs present at the departure node prior to the trip, specifically, one hour before for trips lasting less than one hour, and two hours before for trips lasting between one and two hours. Thus, each nt coefficient represents the proportion of EVs departing from a node and quantifies the corresponding transfer of power capacity between nodes.

To account for potential heterogeneity in EV load transfer between the two nodes, the transfer coefficient nt can be modeled as a stochastic variable. This variable follows a normal distribution with a mean defined by Equation (54) and a standard deviation from Equation (55), where Capfull represents the full battery capacity of the traveling EVs and Cap25p denotes the battery capacity at 25% charge for the same vehicles. This adjustment results in a power capacity transfer from Node A to Node B that is no longer strictly proportional to the EV population.

Despite this variation, other parameters, such as the maximum battery capacity of EVs remaining at the node and the maximum allowable power transfer (maximum allowable charging), remain unchanged. This introduces pressure on the optimized charging schedule. The impact of this heterogeneity is evident in the results obtained for the three power systems analyzed (

Table 17. Results for the three test systems for the stochastic heterogeneous charging.

Power System	3 Units—6 Bus	16 Units—31 Bus	54 Units—118 Bus
min	94.226 k USD	1.3772 M USD	1.38683 M USD
mean	94.94 k USD	1.3794 M USD	1.38782 M USD
max	95.675 k USD	1.3827 M USD	1.38984 M USD
std	745.914	1528.67	787.21

), compared with the results under homogeneous G2V operation (Table 8). Under heterogeneous conditions, the total system cost increases by 0.5% due to the above-mentioned reasons.

$$mean=(Capfull+Cap25p)/2$$

(54)

$$std=(Capfull-Cap25p)/6$$

(55)

5. Conclusions

The method presented in this research analyzes an approach for enhancing TCUCP through the integration of novel heuristics, a novel EV modeling, and V2G mechanisms.

This work developed an encompassing set of heuristics that consolidate commonly used heuristic repair mechanisms in the UCP, adapting them effectively for resolving the TCUCP with EVs. It is demonstrated that multiple heuristics may interfere with the seamless transition from UCP to TCUCP, severely impacting convergence. The analysis of the proposed repair mechanisms and their results, particularly the sensitivity analysis on the EVP (the upper limit of the PPCV variable), demonstrates that when the EVP approaches zero, no system is capable of converging to a violation-free solution. This confirms that heuristics commonly found in the literature, originally designed to solve the simpler Unit Commitment Problem (UCP), are insufficient to handle power flow constraints, underscoring the necessity of the proposed modifications.

Furthermore, two heuristic repair mechanisms for addressing transmission line violations were introduced. The proposed general computational model was tested in three distinct power systems (small, medium, and large-scale), confirming the flexibility of the new heuristics across varying scales, thus justifying the effort to construct a computational model that would not be case-specific. Finally, a third repair mechanism was suggested that repairs the EV constraint equations. The general computational algorithm demonstrates notably fast convergence, particularly in medium- and large-scale power systems, with the first feasible solution typically found within 150 generations as presented in Table 13. In addition, the general computational model reduces the objective function value by a large margin, of up to 40%, during the generations it takes for the proposed model to reach a feasible solution.

To evaluate the performance of the proposed general computational model, the corresponding mathematical formulation was also solved using an MILP algorithm. This comparison was feasible only for the linear cases, specifically, the scenario without EVs and the novel TCUCP formulation with EVs under G2V operation in the two-node system. The results from the general computational model closely matched those of the MILP algorithm, with relative differences close to 1% and in many cases under 1%.

This comparison is particularly important because MILP optimization methods are deterministic methods that solve mixed-integer problems through linear programming techniques and systematic procedures such as branch-and-bound, which can guarantee the global optimum. In contrast, DE is a stochastic, population-based meta-heuristic that operates in continuous space. Due to its reliance on randomness and heuristic search, DE cannot guarantee the exact global optimum but typically converges to high-quality, near-optimal solutions. Achieving results within 1% of the MILP benchmark demonstrates the ability of the DE-based method to deliver solutions very close to the global optimum, validating its effectiveness for complex, nonlinear cases.

In the case of the TCUCP with V2G operation, the formulation becomes nonlinear, making it incompatible with MILP-based solvers and therefore not suitable for direct comparison. However, comparing the results of G2V and V2G operation revealed that, in the 3-unit system, a slight discharge of EV batteries led to a lower-cost solution, approximately 1.7% less, by keeping a generator online and preventing a shutdown, as shown in Table 8 and Table 12. Nevertheless, in scenarios where generator startup costs were excluded, EV discharging proved less competitive than conventional generator power.

The optimization results of the TCUCP with G2V operation demonstrated that the EV load was distributed more evenly across the 24 h period, leading to optimized solutions that satisfied all constraints without violations. The experimental results in Section 4.3, illustrated in Figure 6, show that vehicles traveling between nodes charge nearly 50% of their energy at the destination node (rather than the origin node). This is a significant finding for aggregation strategies and should be carefully considered in both aggregator business models and the planning of EV chargers’ location (e.g., workplace, commercial places, etc.). More specifically, in the G2V case with modest infrastructure, the absence of chargers at travel destinations in the 3-unit system led to a 1.19% increase in system cost. Finally, the algorithm’s performance under stochastic inputs was evaluated. Specifically, travel duration, departure time, and energy consumption were modeled as stochastic variables, along with increased heterogeneity in the state of charge (SoC) among EVs. While the introduction of uncertainty led to a rise in overall system costs, ranging from 0.5% to 1.6%, the algorithm consistently generated optimized charging schedules that effectively minimized production costs despite the variability of inputs.

The problem that was solved is a fairly complicated problem with a large number of constraints. The MILP formulation contains 2911 constraints in the 3-unit-6-bus system, 13,436 constraints in the 16-unit-31-bus system, and 43,594 constraints in the 54-unit-118-bus system. These systems contain only thermal generators. Most test cases are solved with both MILP and DE algorithm, reaching solutions without violating any constraints while 100% satisfying the hourly demand.

The statistical analysis of the results for the three scenarios, of no EVs (Table 6), G2V operation (Table 9), and V2G operation (Table 11), showed very small dispersion, typically under 0.5%, proving the robustness of the algorithm.

Concerning the applicability of the model: The EV formulation developed in this work has shown potential for urban environments applicable in varying-sized systems. This formulation incorporates EV travel patterns, allowing for more precise generator scheduling. This approach also provides an improved perspective on battery state-of-charge distribution beyond simple node-based aggregation, offering valuable insights for EV aggregators when managing EV discharge availability and other discharging services across different energy markets. The results of this model can also provide a more secure and comprehensive guide for EV aggregators when scheduling the day-ahead charging and discharging of the EVs.

It is true that the DC power flow model has inherent limitations compared with the full AC power flow formulation. Specifically, it neglects voltage magnitude variations, reactive power flows, and transmission losses. In networks with significant voltage deviations or a high X/R ratio, these simplifications can result in non-negligible deviations between DC power flow and AC power flow solutions. Therefore, for improved accuracy, either an AC power flow analysis should accompany economic evaluations such as this, or the DC power flow model should be applied only to networks where its underlying assumptions are reasonably satisfied [59].

Future work includes two important aspects of the problem: One of the most important aspects of integrating EVs into national fleets, and replacing internal combustion engine (ICE) vehicles with fully electric, hydrogen, or biofuel-powered alternatives, is the reduction in ${\mathrm{CO}}_2$ emissions. In this work, the test cases considered only thermal generation units. The proposed model estimates a net increase of approximately 6,000 tons of ${\mathrm{CO}}_2$ emissions when transitioning from uncoordinated to coordinated EV charging. This increase is partially offset by an estimated 1,400 tons of ${\mathrm{CO}}_2$ emissions avoided through the replacement of conventional vehicles with electric ones. However, it is important to note that the present work does not assess environmental impacts, as the IEEE test systems employed consist exclusively of conventional thermal power plants and do not incorporate Renewable Energy Sources (RES). In a real-world scenario, where EV charging would be powered by RES, the associated emissions would be significantly lower. If charging is predominantly sourced from renewable generation, as envisioned in modern grid planning, ${\mathrm{CO}}_2$ emissions could even approach zero. Furthermore, integrating RES into such models would allow surplus renewable generation (i.e., production exceeding local demand) to be effectively used for EV charging. This would not only minimize renewable curtailment but also enhance grid flexibility, system efficiency, and overall sustainability. However, given the high complexity of modeling such interactions, a dedicated investigation is needed and is therefore identified as a promising direction for future research.

Another key aspect of the general computational model is the aggregation of EVs into a small number of decision variables. However, this aggregation could potentially lead to an overestimation of the state of charge across the fleet. For this reason, future work should incorporate a de-aggregation step, where the energy provided by the system is distributed more precisely to smaller EV groups, improving the accuracy of the charging representation.