Abstract
This study evaluates the environmental benefits of retrofitting conventional diesel-powered waterbuses in Venice with a series hybrid electric powertrain comprising three generator sets and dual electric propulsion motors. Using real-world operational profiles recorded during typical passenger service, a quasi-static simulation model was developed to assess energy and emission performance. Real-world speed and torque data were collected from a conventional waterbus during regular passenger service to accurately reflect real operational conditions, including driver behavior and the sea state. These profiles were used as inputs to a quasi-static simulation model to assess the hybrid system’s energy efficiency and emission performance. Dynamic programming was applied to derive emissions-optimal control strategies, targeting trade-offs between nitrogen oxides (NOx) and unburned hydrocarbons (HC). The results demonstrate emission reductions of up to 31% in NOx and 15% in HC, confirming the strong potential of hybridization for urban maritime transport. The paper also examines component-level behavior under optimal control and discusses practical considerations for implementing these strategies in real-time applications. These findings support the strategic value of hybrid retrofitting and fleet renewal for reducing the environmental footprint of passenger ferries and improving air quality in sensitive coastal urban environments.
1. Introduction
The shipping industry is a major contributor to global emissions, impacting both with greenhouse gas (GHG) emissions that accelerate global warming and with health-endangering agents, including sulfur oxides (SOx), nitrogen oxides (NOx), particulate matter (PM), and hydrocarbons (HC) [1]. Stricter emissions regulations [2] pushed technological improvements such as synthetic fuels, exhaust gas post-treatment, and hybrid electric powertrains. The latter seems to be a promising solution, especially for short-sea passenger ships. However, the effectiveness of hybrids relies heavily on a properly designed control strategy which in turn requires a deep understanding of the vessel’s powertrain and its operational requirements.
This study focuses on a new hybrid electric powertrain architecture for a waterbus used in Venice, one of the busiest coastal areas in the world in terms of passengers. The potential reduction in pollutant emissions is evaluated through simulation and optimal control methods.
1.1. Air Pollution in Venice
Nearly 70% of maritime emissions are estimated to occur within 400 km of land [3]. For this reason, the impact of these substances is more evident on the air quality of densely populated port cities, raising significant concern for the health of local inhabitants. On average, shipping emissions contributed to 8% of the population exposure to primary PM2.5, 16.5% to NOx, and 11% to SOx in Europe [4]. Venice and its lagoon, a UNESCO World Heritage Site since 1987, faces similar environmental challenges. Pollutant emissions, particularly PM10 and NOx emissions, have exceeded the annual limit value multiple times in recent years [5]. This situation has drawn increasing attention from local authorities and the international regulatory framework. In particular, the International Maritime Organization (IMO) has adopted progressively stricter emission limits under MARPOL Annex VI, including the designation of Emission Control Areas (ECAs). The Mediterranean Sea was recently approved as a Sulphur ECA (SECA), with enforcement beginning in 2025, setting a maximum sulfur content of 0.1% in marine fuels [6]. While NOx limits vary depending on engine tier and ship construction date, proposals for the creation of a Mediterranean NOx ECA are gaining traction. These developments highlight the strategic importance of hybrid retrofitting as a proactive compliance measure for passenger fleets operating in this sensitive region.
Because of its characteristics, boats are the primary means of transportation in Venice for the local inhabitants as well as around 4.5 million tourists every year [7]. Furthermore, recent studies have confirmed that the local public transport network is responsible for a large part of all emissions in the city [8]. This large impact is not surprising as the public transport authority, ACTV Spa, operates a large fleet of both water and land buses, owning around 570 buses, 20 trams, 150 boats, and 150 floating pontoons. The waterborne transport service alone has 27 routes with a total length of approximately 230 km and serves 145 million passengers per year for a total of 535,000 h of navigation. In order to reduce its impact on air quality, the company is planning to renovate its fleet with new hybrid electric vessels. This transition will also enable the company to comply with regulations and adapt to technological advancements, enhancing long-term viability and competitiveness.
1.2. Overview of Waterbus Hybridization
Contrary to popular belief, electric ship propulsion has been widely adopted since at least the 1990s, mainly in cruise ships and capital naval ships [9]. These ships, which still rely on internal combustion engines as the primary source of power, are in effect hybrid ships. However, these propulsion systems are primarily aimed at better maneuverability in ports, thanks to the rapid response characteristic of electric motors and the ability to use Azimuth thrusters with in-hub motors.
Recent developments in high-power density batteries and improved power electronics in the transport industry have led to new forms of hybridization being applied to tugs, offshore vessels, and ferries. However, the industry’s ability to respond quickly to these new trends is hindered by the limited research available in the open literature.
A modern ship with a conventional architecture typically consists of a prime mover which drives the propeller through a mechanical transmission. These prime movers are typically diesel or gas engines, optimized for the highest fuel efficiency when the vessel’s speed is between 80% and 100% of its top speed, or during 90% of the ship mission. For this reason, mechanical propulsion with internal combustion engines remains the preferred architecture for ships that sail at a consistent cruise speed most of the time, such as cargo ships, cruises, and tankers. This is because a purely mechanical transmission has the lowest transmission losses since there is no power conversion involved.
However, conventional boats have drawbacks such as limited maneuverability, high dynamic engine loading, and very low efficiency at less than 70% of design speed, which also results in high emissions [10]. Electrification can be useful for missions with highly varying speeds, frequent maneuvering, and those that must operate in low-emissions zones. A hybrid electric vessel uses a combination of diesel engines and batteries.
A parallel hybrid configuration uses hybrid mechanical-electric propulsion, composed of an electrical motor/generator coupled to the same mechanical propulsion system of the conventional architecture. This is also referred to as hybrid propulsion with a hybrid power supply. The series hybrid architecture, also known as electrical propulsion with a hybrid power supply, uses electrical propulsion with an electric motor that drives the propeller and a generator unit powered by a diesel engine.
The main advantage of using a hybrid powertrain is load leveling: engines operate at constant, efficient working points most of the time, while batteries handle power peaks and fluctuations. This results in lower emissions and fuel consumption. Series hybrids enable greater flexibility than parallel hybrids because the speed of the engine is not tied to the speed of the propeller. Therefore, the operating point of the engine can be optimized and stabilized independently of the vessel’s propulsion.
Hybrid ships also benefit from reduced maintenance, enhanced responsiveness, and improved control, especially in critical situations such as docking and maneuvering in congested waterways. Many municipalities are implementing green policies and demanding cleaner vessels, and nowadays around 200 electric or hybrid ferries are operating in Europe. Significant examples are summarized in Table 1. However, fully electric architectures were discarded by the company due to the need for long charging sessions and the lack of available space for the installation of the charging infrastructure.

Table 1.
Examples of hybrid and fully electric ferries.
1.3. Energy Management Strategies for Hybrid Ships
One of the most important aspects that determine whether the full potential of a hybrid ship can be achieved in practice is the control strategy. Unfortunately, while a wide body of research was published covering the control of hybrid vehicles for automotive applications, works related to marine applications are still limited in number.
The goal of an energy management strategy (EMS) is to manage the power sources, such as diesel engines and batteries, to meet the total instantaneous load most effectively. It is also referred to as supervisory control because it processes information from the ship and outputs set-points for the individual components to their primary control layers. The EMS typically defines the set-points for the engine, electrical machine, and battery. Then, each component has its own primary or low-level control layer, which is responsible for realizing these operating points (for example, in the case of diesel engines, by controlling the injection system). In essence, for a series hybrid powertrain, the EMS is responsible for setting the speed and torque (or power) of the engines and generators, the torque of the electric motors, and the battery current [15,16,17].
The EMS is the core of a hybrid powertrain, and only recently has its design been investigated and applied in maritime applications. Many approaches and techniques are being used in the automotive industry. They are typically divided into rule-based methods (relying on expertise and intuition) and model-based optimization methods (relying on global optimization algorithms) [15]. EMS design is a very broad research topic and many optimization-based techniques have been proposed that are suitable for on-line implementation, including equivalent consumption minimization strategies (ECMS) [18,19,20,21], reinforcement learning-based solutions [22,23,24,25], and model predictive control [26,27,28]. In addition to these, off-line methods such as dynamic programming (DP) and Pontryagin’s minimum principle [15,16] are typically employed to obtain design-optimal EMSs, which can be used to benchmark real-time strategies and for powertrain optimization.
There are several examples in the literature related to the design of optimization-based EMSs for marine vessels. Kalitzakis et al. [29] developed an ECMS for a series-parallel hybrid tugboat in order to minimize fuel consumption and found that it performs 5% to 10% better than a charge-sustaining rule-based controller and only 1–2% worse than the global optimum, which was obtained with dynamic programming. Dedes et al. [20] investigated the use of an ECMS for slow-speed, ocean-going ships with different series-parallel hybrid concepts and found that a fuel consumption reduction of up to 5.8% could be obtained. Considering a more sophisticated energy storage system, Ref. [30] presents a fuel-optimal ECMS for a series hybrid with diesel generators, batteries, and ultracapacitors.
Other studies also include economic considerations in defining the optimization target. For example, Ref. [31] used a dynamic programming algorithm to minimize operating costs, including both the fuel cost and other variable costs related to the utilization of the diesel generators (such as lubrication and maintenance). Similar approaches for EMS design have also been used for hybrid powertrains using fuel cells. Wu et al. [32] developed a dynamic programming-based algorithm to control a plug-in fuel cell/battery ferry in order to minimize the voyage cost, including hydrogen cost and shore electricity costs as well as fuel cell and battery degradation costs. In a similar approach, a co-design framework is developed in [33], where the EMS layer uses mixed-integer linear programming (MILP) to obtain control strategies that minimize both hydrogen consumption and degradation costs for the fuel cell and battery.
All the aforementioned works address fuel consumption and, possibly, considerations related to operational costs. Unfortunately, little to no research has been published related to EMS design for pollutant abatement of diesel-powered hybrids. In [28], MPC was applied to control the e-machine in a parallel hybrid test-bed in order to reduce pollutant emissions during transients. One notable contribution is the work by [34], where a nonlinear MPC framework is developed to minimize fuel consumption and NOx emissions for a parallel hybrid powertrain. The framework also includes a prediction model for the operators’ command and a propeller observer to estimate load disturbance, and is thus highly suitable for online implementation.
Regarding the case of Venice, our previous work in [35] confirmed the benefits of using a series hybrid architecture rather than a parallel one to reduce emissions for a small waterbus operating mostly within the city’s narrow canals; this is significantly different from the vessel investigated in this study, which is a larger waterbus (comparable to a small-sized passenger ferry) to be used in the open waters of the lagoon to connect different islands. This difference in operational requirements has an impact on the performance of the hybrid architectures.
In summary, while the potential for a reduction of greenhouse gas emissions with marine hybrid powertrains has been addressed by many works, there is currently a lack of published research about their potential for pollutant abatement. It appears that almost all published works rely on energy management strategies that are only focused on fuel consumption (and therefore CO2) or operating costs, without considering other pollutants. Furthermore, the application of hybrid powertrains for improving the air quality in short-sea passenger transport has been explored little.
1.4. Main Contributions
This study aims to assess the environmental benefits of replacing the conventional diesel-powered foraneo waterbuses with a series hybrid architecture, whose preliminary design was developed by ACTV. A simulation model was developed using a quasi-static approach for a series hybrid powertrain featuring two electric motors coupled to two propellers, three diesel-powered generator sets, and an LFP battery pack. The simulation model includes component-level submodels and allows for evaluating battery usage, fuel consumption, and pollutant emissions given an operating mission and a hybrid control strategy. With this model, a dynamic programming algorithm was used to design the energy management strategy.
The main contributions of this article can be summarized as follows:
- Simulation of a complex series hybrid waterbus for emissions abatement. Hybrid powertrains have a high potential for improving the air quality of coastal areas and inland waterways. This study relies on state-of-the-art modeling techniques and experimental operational profiles to assess these benefits in the context of a public transportation network in the Venice Lagoon, a densely populated urban area.
- Assessment of a hybrid architecture with different emission-optimal control strategies. The simulation model was coupled with a dynamic programming algorithm to obtain global optimal control strategies. Different control strategies targeting different trade-offs of HC and NOx emissions were obtained; at the same time, fuel consumption was also evaluated. The results provide performance limits for the hybrid architecture with respect to different pollutant-reducing objectives.
- Recommendations for EMS implementation. Analyzing the behavior of the gen-sets and of the battery pack, valuable insight is gathered from optimal control trajectories on how to design an effective real-time EMS to reduce emissions. Also, some computational aspects are discussed related to the formulation of the control variables of the system. The discussion has practical implications for similar applications of optimal control methods to series-hybrid powertrains and for the development of real-time control strategies.
The rest of the article is organized as follows. First, the operational requirements and the architecture of the current conventional waterbus are analyzed. Next, the simulation model that was developed for the hybrid architecture is presented, and the implementation of the dynamic programming algorithm is detailed. Finally, simulation results with different emission-reducing strategies are presented and discussed.
2. Current Waterbus and Experimental Mission Analysis
The vessel under consideration in this work is a waterbus operating on line 12 within the Venice Lagoon’s transportation network. The service connects Venice’s main island with a peninsula (litorale del Cavallino) which divides the Venetian lagoon from the Adriatic Sea, through the islands of Murano and Burano, as shown in Figure 1. The line includes seven stops and covers 16 km in about 1 h. The service is active every day from about 04:00 to 23:41, with exceptions due to festivities and seasonal variations; the trip from Treporti to Punta Sabbioni is only served on selected runs. Currently, the service is operated with conventional foraneo waterbuses, powered by two diesel engines. The foranei are relatively large waterbuses, with an overall length of 30.4 m, a gross tonnage of 100, and carrying up to 400 passengers. One such vessel is depicted in Figure 2 and its main characteristics are summarized in Table 2.

Figure 1.
The route covered by line 12 with selected stops.

Figure 2.
Drawing of a foraneo waterbus [36].

Table 2.
Main characteristics of the conventional waterbus.
Time profiles of the speed and power output for the two engines were available for two missions: a whole day of operation from 7:00 to 19:50, and a second one lasting 1 h from the Fondamente Nove stop to Treporti, which represents the typical route the waterbus performs most frequently in a round-trip. During 12 h of operation, the waterbus is docked with the engine idling for 16% of the time. Moreover, 40% of the time is spent cruising with the engines providing 80% of their rated power (Figure 3). The availability of experimentally acquired profiles represents a significant advantage for the modeling and simulation of the marine hybrid powertrains. Unlike theoretical or assumed duty cycles, these profiles ensure a high level of realism in system-level analyses by capturing the influence of external factors such as sea conditions and operator behavior. The resulting fuel consumption and emissions for the conventional waterbus are listed in Table 3.
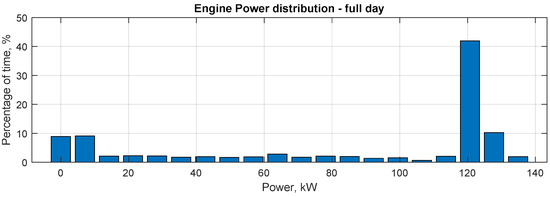
Figure 3.
Frequency distribution of the engine power output (for one engine) within a full day of operation.

Table 3.
Average fuel consumption and emissions for a conventional waterbus.
In order to simulate the behavior of the hybrid powertrain, the propeller speed and torque profiles were derived from the experimental engine speed and torque profiles. These profiles represent the expected loads and will be used as inputs of the hybrid waterbus simulation model. The profiles were derived by accounting for losses at the gearbox () and an auxiliary load of 5 kW. Furthermore, we observed that the difference between the two propellers’ profiles, from an energetic point of view, was minimal. Hence, to simplify the simulation model, we allocated equal speed and torque to each propeller, averaging the two. The resulting profiles (for a single propeller) can be seen in Figure 4 along with the recorded boat speed profile.
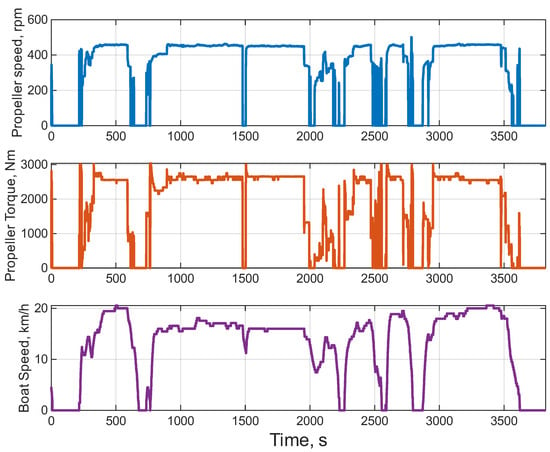
Figure 4.
Operational profiles for the Murano–Treporti trip.
3. Hybrid Waterbus Model
The proposed hybrid waterbus is a series hybrid architecture with three diesel generator sets with a rated power of 125 kW, a 150 kWh lithium-iron-phosphate battery pack, and two 147 kW electric motors. A schematic of the powertrain can be seen in Figure 5, while a summary of the main parameters can be found in Table 4.
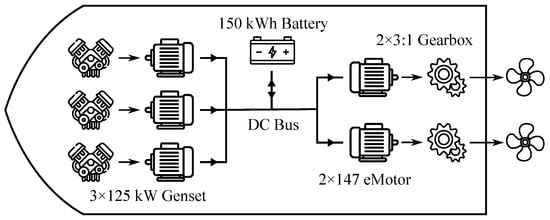
Figure 5.
Hybrid waterbus powertrain schematic.

Table 4.
Main parameters of the hybrid powertrain.
The generator sets have variable-speed drives and they deliver electrical power to a 700 V DC bus, using suitable AC/DC and boost converters. The battery is also connected to the DC bus through a boost converter. The rated power of the electric motors was set to match the rated power of the conventional architecture’s thermal engines to ensure that the same mission could be performed. This means that the series hybrid architecture is slightly better performing at low speed, due to the capability of e-motors to deliver high torque at a low speed. The propellers are connected to a reversing gearbox, which can act as a motion inverter when reverse thrust is needed in docking and maneuvering. The electrical power demand of the electric motors must be met by the battery and the three generator sets.
3.1. Reversing Gearbox
First, the propeller speed and torque are processed by the gearbox model, which has a reduction ratio of . Frictional losses were modeled with a constant efficiency . Moreover, the contribution of inertia, with the moment of inertia = 1.15 kg m2, was considered. Thus, the gearbox rotational speed, acceleration, and torque were evaluated as follows:
Notice that was defined to be always positive or null because when braking power is needed, the gearbox also reverses the propeller’s speed.
3.2. Electric Motor
The electric motors used are asynchronous permanent magnet induction motors with a rated power of 147 kW. An efficiency map was used to model losses, defining the electro-mechanical conversion efficiency as a function of the e-machine’s speed and torque. Additionally, maximum speed and upper and lower torque limit curves were used to limit the operational envelope. For each motor, the speed and torque and were evaluated as follows:
After obtaining efficiency by the linear interpolation of the efficiency map , the electrical power demand was computed as follows:
The model also makes sure that the motor speed does not exceed its maximum speed,
and that the torque does not exceed the limit torque curve:
3.3. Battery
The battery pack was modeled with an equivalent circuit model [37], which was used to evaluate the evolution of the SOC (denoted here as ) as a function of the battery power. The model is characterized by an open circuit voltage characteristic and an equivalent resistance characteristic, which were obtained by scaling the cell characteristics.
The battery was modeled with an equivalent circuit model [37], as shown in Figure 6, which was used to evaluate the evolution of the SOC (denoted here as ) as a function of the battery power.
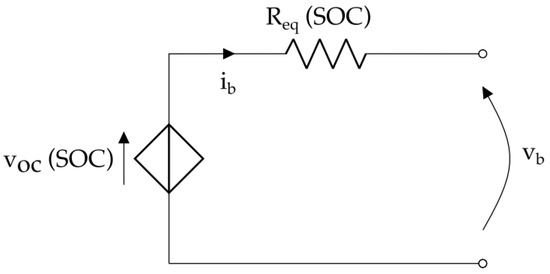
Figure 6.
Battery equivalent resistance model.
The battery current was evaluated as follows:
where the battery power was evaluated as follows:
where is a constant power consumption (set to 5 kW) that accounts for the electrical power demand from the control panels and various minor electrical appliances connected to the DC bus.
By definition, when the battery is charging while when the battery is discharging; finally, if the battery power is exactly zero, the propeller and the auxiliaries’ power demands are fully satisfied by the gen-sets.
After evaluating the battery current with Equation (9), the SOC dynamics were defined by the following equation:
where the Coulombic efficiency of the battery was set to . Furthermore, the model ensures that does not exceed the charge and discharge limit currents imposed by the battery characteristic, i.e., = 1190 A and = −833 A. To avoid a deep charge/discharge on the battery, which would reduce its lifetime, the SOC was limited to a range of 0.4–0.8.
The battery is a key component in a hybrid vessel. For the waterbus model subject of the case study, data from an LFP battery pack was used [38]. A preliminary design has been done regarding the correct sizing and packaging. The total capacity is 150 kWh which is more than a normal hybrid vessel of this size would have. While this size is larger than is strictly needed in terms of energy requirements, it was considered necessary in terms of power requirements to ensure the feasibility of full-electric operations as well as to ensure battery durability.
3.4. Engine
The engine model was used to evaluate fuel consumption and emissions at each instant, by linear interpolation of look-up tables that characterize the engine fuel consumption and emissions as a function of speed and torque. For this work, engine maps were available for fuel consumption as well as NOx and HC emissions. Thus, their flow rates were evaluated as follows:
In principle, each engine can be set to work at its own speed and torque, independently of the other engines and of the propeller load; the EMS is responsible for controlling the working point of all three engines in order to satisfy operational constraints (such as keeping the battery SOC in its allowed range) while minimizing fuel consumption and emissions. This means that the EMS must select six control variables (the speed and torque of the three engines). In practice, it might be more convenient to define a reduced number of control variables and use some heuristics to set all speeds and torques, as will be explained in Section 4.
The model also ensures that each engine’s speed does not exceed the torque limit curve:
and that it stays within the idle and maximum speed (when providing torque):
3.5. Generator
Each thermal engine is mechanically coupled to an induction generator to form a gen-set. The generators are permanent magnet synchronous machines with a peak power of 125 kW and an output voltage of 400 V three-phase AC at 50 Hz. Losses in the power electronics are taken into account as well. As for the electric motors, the generator efficiency was evaluated through an efficiency map. The generator speed and torque were determined by the engine operating point, and a constraint was enforced on the maximum torque.
4. Energy Management Strategy
As previously mentioned, the energy management strategy plays a critical role in realizing the full potential of hybrid powertrains. For the series hybrid architecture presented in this work, the EMS is responsible for setting the operating points of the three gen-sets; this in turn will determine the amount of power that needs to be drawn from or charged into the battery in order to meet the propulsive and auxiliaries’ power demand.
Dynamic programming is a widely used technique in EMS design because it provides the optimal global control trajectory solution to complex control problems regardless of their non-linearity; moreover, it is not subject to calibration as other techniques are, and it can handle conflicting multiple optimization objectives. However, this technique is not suitable for online implementation because it requires prior knowledge of the operating mission. The DP algorithm is also computationally demanding and simulation time rises exponentially as the number of states and control variables increases. Nevertheless, because of its advantages, dynamic programming is highly popular in the context of the preliminary design and energy analysis of hybrid powertrains. Furthermore, the optimal control trajectories obtained with dynamic programming can also be used to design an online EMS.
To this end, a dynamic programming algorithm was used to obtain the optimal control strategy with respect to NOx and HC emissions, similar to the approach followed in [35] to compare a series and a parallel architecture for a smaller waterbus. Dynamic programming is based on Bellman’s principle of optimality [39] which implies that the solution to an optimal control problem over a multi-stage, finite horizon can be built starting from the last stage and proceeding backward, solving at each stage the tail sub-problem from that stage to the end [40]. In particular, the algorithm was implemented by developing a simulation model as described in Section 3 in MATLAB R2024a and by coupling it with an optimal control tool called DynaProg v1.6.5 [41]. This is an open-source MATLAB toolbox that is able to solve deterministic, finite horizon multi-stage decision problems.
4.1. Optimal Control Problem Setup
In order to apply dynamic programming, the energy management strategy must be formulated as an optimal control problem, comprising a total cost (to be minimized over the operational mission), a set of state and control variables, and a model describing the state dynamics. In addition, we define as exogenous inputs all those time-varying quantities that cannot be controlled and that affect the state dynamics, in other words, the operational mission.
For the control variables, we decided to select two controls to set the engine speed and torque for all engines that are turned on, and a third control variable to decide how many gen-sets should be on.
The stage cost is the cost associated with performing a control action at a given stage (time interval) and which affects the total cost J for the whole mission:
where is the control sequence . The optimal control sequence is the one that minimizes J.
In order to minimize the total emissions of NOx and HC over a mission, the stage cost was defined as a trade-off between NOx and HC flow rates:
where and are the maximum flow rates of HC and NOx that can be obtained with all three engines working together, and is a trade-off factor. In addition, an engine shut-down penalty term was used to prevent the gen-sets from switching states too frequently [42], formulated as follows:
where represents the on/off state of the engine at the previous stage . It is worth noticing that this EMS design problem is a multi-objective problem with conflicting objectives since the engine’s NOx and HC brake-specific consumption maps have significantly different shapes.
The state variables represent all those variables whose value evolves in time as a function of the controls and which influence the stage cost, in our case pollutant emissions. Therefore, the battery’s state of charge must obviously be a state as we want to set a charge-sustaining constraint () and we also want to ensure that the SOC stays within the prescribed bounds. Furthermore, must also be a state as it influences the stage cost and it cannot be purely determined by the current stage’s states, controls, and exogenous inputs.
For all states, the state dynamics must be formulated in the form of to evaluate their evolution from one stage to the next as a function of the current states, controls, and exogenous inputs. For the SOC, this is carried out using the equations given in Section 3. For , it is sufficient to store the current value of the control variable for the next stage.
Summarizing, the states, controls, and exogenous inputs are as follows:
| State variables: | , battery SOC |
| , number of engines on at previous stage | |
| Control variables: | , engine speed rad/s |
| , engine torque Nm | |
| , number of engines on | |
| Exogenous inputs: | , propeller speed, rad/s |
| , propeller torque, Nm |
Finally, dynamic programming requires the definition of discrete computational grids for state and control variables [41], as well as initial conditions and terminal constraints for the state variable. A finer discretization for the state and control grid leads to increased computational time, but coarser grids introduce more approximations in the DP algorithm which can cause the solution to deviate from the optimal solution.
Notably, the computational complexity of dynamic programming scales rapidly with the number of states and controls. For a system with n states and m controls, denote with N, , and the number of stages (time intervals) and the number of elements in the state grid i and in the control grid j. Then, the computational time is proportional to the following equation:
Memory requirements for the algorithm scale similarly. This consideration, amongst others, drove the selection of the control sets for our simulations, as will be discussed in Section 5.3.
4.2. Dynamic Programming Algorithm
The algorithm finds the optimal control sequence in two phases: the backward phase and the forward phase. In the backward phase, the algorithm generates a sequence of value functions . First, is initialized to some terminal cost , which can be used to penalize undesired values for the terminal states or, alternatively, can be set to zero for all . Then, the algorithm proceeds iteratively from stage to 0 to construct the value functions as follows:
The value function, also called cost-to-go, quantifies the minimum cost incurred in controlling the system, starting from stage k with state to stage N. Note that the value function is only a function of the current state, which is a reflection of Bellman’s principle of optimality. Thus, these value functions can be used in the forward phase to construct the optimal control sequence. In the hybrid powertrain context, this backward phase systematically evaluates all admissible engine operating points (speed, torque, on/off state) and the resulting state of charge trajectories, identifying the least-emissions paths over the full mission.
In the forward phase, the algorithm starts from state at stage 0 and proceeds iteratively in two steps: evaluate as
and advance the simulation by one timestep, evaluating . This forward pass effectively constructs the optimal engine speed, torque, and on/off state profiles across the mission, given the initial SOC.
Together, the two phases translate the emission minimization problem into a globally optimal control trajectory for the hybrid waterbus, using real operational profiles as input.
Among these two phases, the most time-consuming is the backward phase. At each iteration, the state dynamics must be evaluated for all values of in a defined computational grid and for all possible values of the control variables. Furthermore, must be evaluated by interpolation on the known values, which can also be a time-consuming operation. To see why this interpolation is needed, note that according to Equation (25) the value function is only computed and stored for the values of x that belong to the SV computational grid. Nonetheless, the value function update itself requires evaluating for values of the state that result from the state dynamics and may not belong to the computational grid.
5. Results and Discussion
In this section, we analyze the simulation results that were obtained by applying dynamic programming to the simulation models presented in Section 3. First, we discuss the effect of the NOx–HC trade-off factor on the emissions of the hybrid waterbus. Then, we select one specific value for the trade-off factor and analyze the behavior of the powertrain component under the obtained optimal control strategy. Furthermore, we discuss some numerical and practical aspects related to the choice of the control architecture that was presented in the previous section. Finally, we discuss some limitations of the employed methods.
5.1. Impact of the Trade-Off Factor
In Section 4.1, we introduced a cost function for the EMS design problem that considers a trade-off of HC and NOx emissions, through a trade-off factor . By acting on this value, it is effectively possible to steer the optimization between the selective minimization of these two pollutants. In order to assess the emission-abatement capabilities of the hybrid architecture under different objectives, we ran several optimizations with varying values. Figure 7 shows the obtained emissions and fuel consumption, normalized to the values obtained with the conventional architecture.
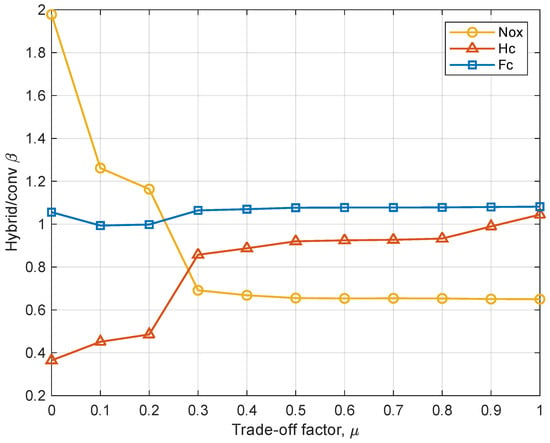
Figure 7.
Ratio of fuel consumption, NOx and HC from the hybrid with respect to the conventional architecture, as a function of the trade-off factor .
As previously mentioned, minimizing the two pollutant species creates conflicting objectives: this is clearly visible for the HC-oriented case (), where the HC emissions are reduced by more than 60% with respect to the conventional waterbus, but the NOx emissions are almost doubled. In the opposite case (), the NOx emissions are reduced by slightly more than 35% while the HC emissions are increased by about 5%.
Another fact that is clearly visible from the plot is that the relationship between the trade-off factor and the emission flow rates is highly non-linear. The NOx emissions fall rapidly as the trade-off factor ranges from 0 to 0.3, and change very little beyond . The HC emissions increase quite regularly throughout the whole range except for values of the trade-off factor from 0.2 to 0.3, where there is a sharp increase. This region was also identified as the most interesting in terms of trade-off results.
In terms of fuel consumption, Figure 7 shows a modest increase across the entire range of the trade-off factor . This trend reflects the energy conversion losses that are inherent to the hybrid powertrain and the tendency of emissions-optimal operating points to deviate slightly from fuel-optimal ones. Nonetheless, the overall increase remains limited (approximately 6.5%) and must be weighed against the significant pollutant reductions achieved.
Based on the observed trends in Figure 7, the interval was identified as particularly promising in terms of achieving a favorable trade-off between NOx and HC emissions. Therefore, a focused sweep of control simulations was conducted in this range. Among these, the value emerged as the most balanced compromise, offering significant reductions in both pollutant species. This case was therefore selected to be analyzed in further detail. The corresponding results are reported in Table 5 and further analyzed in the following sections. While the selected value was optimized for the analyzed mission, the same methodology can be applied to other routes to determine mission-specific trade-offs.

Table 5.
Emissions and fuel consumption results for the conventional and hybrid waterbuses, with trade-off factor .
5.2. Analysis of the Components Behavior
Clearly, the results obtained with the selected trade-off factor of show a significant pollutant emission reduction potential for the hybrid waterbus. The main reason for this reduction is that the hybrid powertrain allows the DP algorithm to set the engine operating point at a very low level of specific emissions, as is clearly visible in Figure 8. In particular, Figure 8b–d illustrate engine operating points as scattered data points, for each simulation time step, overlaid to the engine’s brake-specific fuel consumption, and NOx and HC emission maps; while Figure 8a represents the electric motor operating points on the motor’s efficiency map.
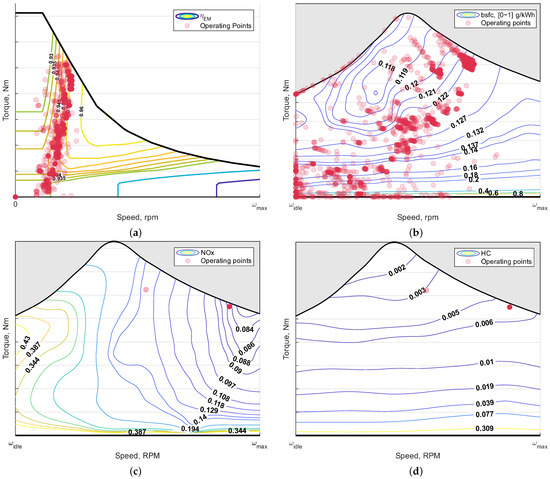
Figure 8.
Operating point distribution on the engine and e-motor maps. The brake-specific fuel consumption, and NOx and HC maps are normalized. (a) Electric motor efficiency and operating points (hybrid waterbus). (b) Engine brake-specific fuel consumption and engine operating points (conventional waterbus). (c) Specific NOx emission maps and engine 1 operating points (hybrid waterbus). (d) Specific HC emission maps and engine 1 operating points (hybrid waterbus).
In the conventional architecture, each working point is directly related to the propeller speed and torque, while in the series hybrid architecture, the load is satisfied by the electric machines (Figure 8a) and the engines work independently. The system can benefit from high control flexibility since the engines can be turned on independently from each other. This allows the algorithm to find an optimal power output point and then take advantage of the control variable to start and stop engines, delivering a similar amount of power to the DC bus.
This is also well illustrated in Figure 9, where power profiles along the missions are presented. More specifically, engines 1, 2, and 3 run 75.2%, 60.8%, and 14.6% of the total mission time, respectively, with an average power of 120 kW. This also corresponds to 80% of the maximum power of a single thermal engine. These results suggest that removing one generator set from the architecture could be possible. Simulations with two generator sets led to similar results in terms of emissions; the saved weight and lower complexity of the powertrain would be an advantage.
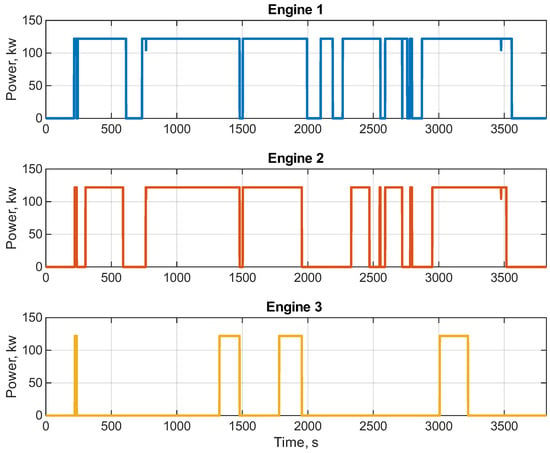
Figure 9.
Power output profiles of the three engines of the hybrid waterbus model.
Going back to Table 5, it is evident that the hybrid architecture, if an emissions-optimal strategy is adopted, is less fuel-efficient than the conventional one. We attributed this mainly to two reasons. First, the operational mission has a rather consistent power demand, and the vessel spends most of the time cruising at its design speed. Therefore, the engine often operates close to its design operating point which is typically selected to minimize bsfc. This stands in contrast with the application presented in [35], where the highly dynamic and frequent part-load operation of the conventional powertrain meant that a higher bsfc was obtainable with a series hybrid even when targeting emissions instead of fuel consumption. Second, the hybrid architecture introduces new transmission losses, due to the electro-mechanical conversion losses at the motors and generators and due to the electric losses in the power converters, all of which ultimately contribute to energy dissipation. After an energy analysis, we found that about 12% of the total energy produced by the engines is lost in this way.
Considering the battery pack, Figure 10 shows how it essentially acts as a load leveler, enabling stable operation of the engines. During stops and maneuvering, the waterbus operates in full electric mode, turning the engines off. In the cruising phases, part of the trip is spent with two engines turned on at their emissions-optimal operating points and the battery discharges to cover the difference with the power demand. Then, a smaller part of the trip is spent with three engines on at their emissions-optimal operating point and the battery is charged.
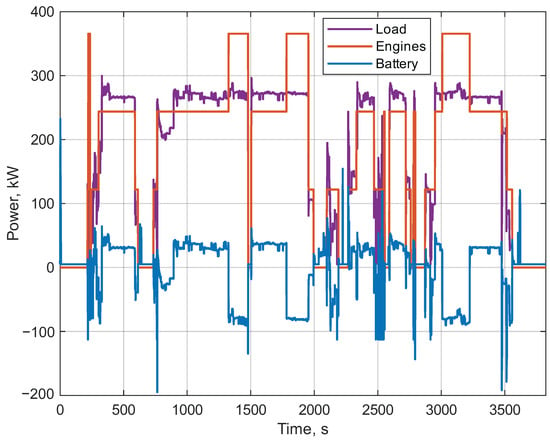
Figure 10.
Load, battery, and total engine power along the operational mission.
Throughout the mission, the SOC swings to a minimum of 57% and a maximum of 61%; also, its final value is 60%, thus a charge-sustaining mission is accomplished. Overall the battery can charge and discharge a total of around 48 kWh of energy. Notably, the battery’s usable SOC window is not fully exploited. The reason for this is due to the large capacity of the battery, and the constraint that the mission is charge-sustaining. Therefore, the battery pack appears to be oversized in terms of energy content. Unfortunately, due to the limited power density of LFP batteries, this sizing was deemed necessary by ACTV in order to reach a power rating that would enable fully electric sailing, which is particularly desirable in the proximity of stops.
5.3. Notes on the Selected Control Set
Before performing our extensive set of simulations with the setup presented in Section 4.1, other choices for the control set were investigated. In our architecture, it is possible in principle to control each engine independently; this would require three control variables for the engine’s speed and three for the engine torques , with , for a total of six control variables.
However, this inevitably results in significant complexity for the EMS, which must be justified by improved performance with respect to simpler control sets [43]. In particular, as explained in Section 4.1, this would require a significantly higher computational cost when compared with the model with the three control variables , , and . The more complex model replaces the control set for (made of four inherently discrete values) with four control sets related to engine speeds and torques that must be discretized into finite sets that cover the whole engine map. As Equation (24) shows, this would greatly increase both simulation time and the memory requirement for the processing hardware.
For example, a simulation was performed with the complex model with six controls. In this case, the definition of the computational grids was limited by the available RAM of 32 GB, using and , . This discretization is still not satisfactory because many points on the maps are discarded and the results are underestimated; furthermore, the execution time of the algorithm would be around two days. The so-called curse of dimensionality compelled us to consider other control models.
The model introduced in Section 4.1, using three control variables, , , , was deemed more effective as it is far less computationally demanding while producing good results. As is clear from the results presented in Section 5.2, the flexibility given by the ability to select the number of engines to be used for this architecture is already enough that the engine operating points can be set at their optimal operating point.
While the above considerations on computational complexity and memory requirements refer to dynamic programming specifically, similar considerations of controller complexity can be made for other EMS techniques. One important takeaway of our results is that the optimal control strategy obtained with the presented control scheme is highly effective; therefore, this choice would also be appropriate for a real-time EMS, which would be designed to reproduce this optimal strategy as much as possible.
5.4. Limitations
When considering the results discussed so far, a few limitations that are inherent to the employed methods must be addressed. First, the simulations were performed with a quasi-static model, neglecting the transient behavior of engine operating points. Thus, emission results for both the conventional and hybrid architecture are underestimated to some extent. While this can be considered negligible for the hybrid architecture, due to the very stable operation of the thermal engines, this is certainly not the case for the conventional powertrain.
Furthermore, the modeling approach that we presented is effective for the purpose of energy consumption and emissions and for control strategy design. However, there are other benefits to waterbus hybridization that cannot be captured by this approach. For example, hybrid waterbuses require reduced engine maintenance requirements due to their having a more stable operation. Furthermore, a hybrid waterbus produces less vibration, leading to an improved experience for passengers and lower noise, which is beneficial both for the passengers and for the citizens living in the proximity of stops.
Nonetheless, the simulation results presented in the previous sections provide a significant amount of practical insight for the preliminary design of both the hybrid powertrain and its energy management strategy, highlighting the potential for significant reductions in pollutant emissions. Additionally, environmental factors such as tidal conditions, weather, and seasonal passenger loads could influence power demand and hybrid performance; these effects can be accommodated in future simulations by updating the operational profiles accordingly.
6. Conclusions
This study estimates the air quality improvement that can be achieved by retrofitting a fleet of conventional diesel-powered waterbuses currently in use in the Venice transportation network with a new series hybrid powertrain. A simulation model for the hybrid waterbus was presented and a dynamic programming algorithm was used to obtain optimal control strategies that minimize a trade-off of NOx and HC emissions. The hybrid architecture shows good abatement potential with up to 31% and 15% NOx and HC reductions, respectively.
The battery’s role as a load leveler proved to be effective: it charged and discharged a total of approximately 48 kWh of energy swing during the mission, maintaining the state of charge within a narrow 57% to 61% window. The gen-sets operated predominantly at a stable average load of 120 kW, and notably, the third engine was used only 14.6% of the time. These findings suggest the potential simplification of the powertrain architecture without compromising emission performance. In future work, alternative component sizing strategies will be explored not only for this specific line, but also for other representative routes within the network.
This system-level analysis also provided important suggestions for implementing real-time controllers and design improvements. First, we discussed how a relatively simple control architecture that forces all engines that are currently on to operate at the same speed and torque is almost as effective as more complex strategies that attempt to control the operating points of the three engines independently. Second, our results show that it is possible to identify a specific operating point for the engines to operate at for most of the time, therefore using the gen-sets to provide three discrete power levels (one for each engine). The battery pack can then be used as a buffer to cover the difference between the electric loads and the power generated by the engines. Furthermore, it should be noted that this engine operating point is mission-specific, and it can be identified using the dynamic programming algorithm presented in this work.
More generally, this case study can foster new ideas for further studies on the advantages of small hybrid ferries, which are still relatively little explored technologies. Finally, the encouraging results provide a strong indication of the benefits of increased investment in fleet renewals and retro-fitting, in order to meet emission regulations, improve the citizens’ quality of life, and demonstrate a commitment to innovation and sustainability.
Author Contributions
Conceptualization, F.M. and D.A.M.; methodology, F.M.; software, F.M. and A.N.; validation, F.M.; formal analysis, F.M. and A.N.; investigation, A.N.; resources, D.A.M. and A.F.; data curation, A.N.; writing—original draft preparation, F.M. and A.N.; writing—review and editing, D.A.M.; visualization, F.M. and A.N.; supervision, D.A.M. and A.F.; project administration, D.A.M.; funding acquisition, D.A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
Author Antonio Ferrari was employed by the company ACTV SpA. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NOx | Nitrogen oxides |
| HC | Unburned hydrocarbons |
| GHG | Greenhouse gases |
| SOx | Sulfur oxides |
| PM | Particulate matter |
| EMS | Energy management strategy |
| ECMS | Equivalent consumption minimization strategy |
| DP | Dynamic programming |
| LFP | Lithium-iron-phosphate |
| SOC | State of charge |
References
- Contini, D.; Merico, E. Recent Advances in Studying Air Quality and Health Effects of Shipping Emissions. Atmosphere 2021, 12, 92. [Google Scholar] [CrossRef]
- Faber, J.; Hanayama, S.; Zhang, S.; Pereda, P.; Comer, B.; Hauerhof, E.; van der Loeff, W.S.; Smith, T.; Zhang, Y.; Kosaka, H.; et al. Fourth Greenhouse Gas Study 2020; Technical report; International Maritime Organization: London, UK, 2021. [Google Scholar]
- Viana, M.; Hammingh, P.; Colette, A.; Querol, X.; Degraeuwe, B.; de Vlieger, I.; van Aardenne, J. Impact of maritime transport emissions on coastal air quality in Europe. Atmos. Environ. 2014, 90, 96–105. [Google Scholar] [CrossRef]
- Cohen, A.J.; Brauer, M.; Burnett, R.; Anderson, H.R.; Frostad, J.; Estep, K.; Balakrishnan, K.; Brunekreef, B.; Dandona, L.; Dandona, R.; et al. Estimates and 25-year trends of the global burden of disease attributable to ambient air pollution: An analysis of data from the Global Burden of Diseases Study 2015. Lancet 2017, 389, 1907–1918. [Google Scholar] [CrossRef]
- Arpa Direzione Generale. La qualità dell’aria nel Comune di Venezia. Technical report, Agenzia Regionale per la Prevenzione e Protezione Ambientale del Veneto, 2022. (In Italian). Available online: https://web.archive.org/web/20250522040632/https://www.comune.venezia.it/sites/comune.venezia.it/files/documenti/Ambiente/Relazione%20qualita%20aria_2022_comune%20VE.pdf (accessed on 22 May 2025).
- International Maritime Organization. New Sulphur Emission Limits Enter into Effect in the Mediterranean. 2025. Available online: https://www.imo.org/en/mediacentre/pages/whatsnew-2254.aspx (accessed on 7 August 2025).
- Vezzà, M.; Venturini, S.; Carlin, M.; Marini, E. Annuario del Turismo DATI 2019. Technical report, Città di Venezia. 2020. Available online: https://web.archive.org/web/20250319155305/https://www.comune.venezia.it/sites/comune.venezia.it/files/immagini/Turismo/Annuario%20del%20turismo%202019.pdf (accessed on 22 May 2025).
- Pecorari, E.; Menegaldo, M.; Innocente, E.; Ferrari, A.; Giuponi, G.; Cuzzolin, G.; Rampazzo, G. On which grounds a decision is taken in waterborne transport technology to reduce air pollution? Atmos. Pollut. Res. 2020, 11, 2088–2099. [Google Scholar] [CrossRef]
- Sáiz, V.M.M.; López, A.P. Future trends in electric propulsion systems for commercial vessels. J. Marit. Res. 2007, 4, 81–100. [Google Scholar]
- Geertsma, R.D.; Negenborn, R.R.; Visser, K.; Hopman, J.J. Design and control of hybrid power and propulsion systems for smart ships: A review of developments. Appl. Energy 2017, 194, 30–54. [Google Scholar] [CrossRef]
- Damen Shipyards Group. Damen Hybrid Waterbus 2907. Available online: https://www.damen.com/vessels/ferries/city-ferries/waterbus-2907-e3-hybrid (accessed on 22 May 2025).
- Danfoss Drives. Hybrid Ferries Connect the City of Amsterdam Nonstop. 2017. Available online: https://files.danfoss.com/download/Drives/DKDDPC939A402_IJFerry_LR.pdf (accessed on 22 May 2025).
- Fjellstrand Shipyard. NB 1700 Medstraum. 2023. Available online: https://fjellstrand.no/projects/nb-1700-medstraum/ (accessed on 22 May 2025).
- Siemens Energy AG. Siemens Energy & Bellona Foundation: Decarbonizing Maritime Transport—A Study on the Electrification of the European Ferry Fleet; Technical report; Siemens Energy AG: Munich, Germany, 2022. [Google Scholar]
- Onori, S.; Serrao, L.; Rizzoni, G. Hybrid Electric Vehicles: Energy Management Strategies; SpringerBriefs in Control, Automation and Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1–112. [Google Scholar] [CrossRef]
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems: Introduction to Modeling and Optimization; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- de Jager, B.; van Keulen, T.; Kessels, J. Optimal Control of Hybrid Vehicles; Springer: London, UK, 2013. [Google Scholar] [CrossRef]
- Musardo, C.; Rizzoni, G.; Guezennec, Y.; Staccia, B. A-ECMS: An Adaptive Algorithm for Hybrid Electric Vehicle Energy Management. Eur. J. Control 2005, 11, 509–524. [Google Scholar] [CrossRef]
- Kim, N.; Cha, S.; Peng, H. Optimal Control of Hybrid Electric Vehicles Based on Pontryagin’s Minimum Principle. IEEE Trans. Control Syst. Technol. 2011, 19, 1279–1287. [Google Scholar] [CrossRef]
- Dedes, E.K.; Hudson, D.A.; Turnock, S.R. Investigation of Diesel Hybrid Systems for Fuel Oil Reduction in Slow Speed Ocean Going Ships. Energy 2016, 114, 444–456. [Google Scholar] [CrossRef]
- Acquarone, M.; Miretti, F.; Anselma, P.G.; Misul, D.A. Online Temperature-aware Equivalent Consumption Minimization Strategy for Mild Hybrid Electric Powertrains. IEEE Trans. Veh. Technol. 2024, 73, 4646–4658. [Google Scholar] [CrossRef]
- Liu, T.; Hu, X.; Li, S.E.; Cao, D. Reinforcement Learning Optimized Look-Ahead Energy Management of a Parallel Hybrid Electric Vehicle. IEEE/ASME Trans. Mechatronics 2017, 22, 1497–1507. [Google Scholar] [CrossRef]
- Liu, C.; Murphey, Y.L. Optimal Power Management Based on Q-Learning and Neuro-Dynamic Programming for Plug-in Hybrid Electric Vehicles. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1942–1954. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Partridge, J.; Anderlini, E.; Liu, Y.; Bucknall, R. Near-optimal energy management for plug-in hybrid fuel cell and battery propulsion using deep reinforcement learning. Int. J. Hydrogen Energy 2021, 46, 40022–40040. [Google Scholar] [CrossRef]
- Biswas, A.; Acquarone, M.; Wang, H.; Miretti, F.; Misul, D.A.; Emadi, A. Safe Reinforcement Learning for Energy Management of Electrified Vehicle with Novel Physics-Informed Exploration Strategy. IEEE Trans. Transp. Electrif. 2024, 10, 9814–9828. [Google Scholar] [CrossRef]
- Borhan, H.; Vahidi, A.; Phillips, A.M.; Kuang, M.L.; Kolmanovsky, I.V.; Di Cairano, S. MPC-Based Energy Management of a Power-Split Hybrid Electric Vehicle. IEEE Trans. Control Syst. Technol. 2012, 20, 593–603. [Google Scholar] [CrossRef]
- Haseltalab, A.; Negenborn, R.R.; Lodewijks, G. Multi-Level Predictive Control for Energy Management of Hybrid Ships in the Presence of Uncertainty and Environmental Disturbances. IFAC-PapersOnLine 2016, 49, 90–95. [Google Scholar] [CrossRef]
- Papalambrou, G.; Samokhin, S.; Topaloglou, S.; Planakis, N.; Kyrtatos, N.; Zenger, K. Model Predictive Control for Hybrid Diesel-Electric Marine Propulsion. IFAC-Pap. 2017, 50, 11064–11069. [Google Scholar] [CrossRef]
- Kalikatzarakis, M.; Geertsma, R.D.; Boonen, E.J.; Visser, K.; Negenborn, R.R. Ship energy management for hybrid propulsion and power supply with shore charging. Control Eng. Pract. 2018, 76, 133–154. [Google Scholar] [CrossRef]
- Xie, P.; Tan, S.; Guerrero, J.M.; Vasquez, J.C. MPC-informed ECMS based real-time power management strategy for hybrid electric ship. Energy Rep. 2021, 7, 126–133. [Google Scholar] [CrossRef]
- Kanellos, F.D.; Tsekouras, G.J.; Hatziargyriou, N.D. Optimal Demand-Side Management and Power Generation Scheduling in an All-Electric Ship. IEEE Trans. Sustain. Energy 2014, 5, 1166–1175. [Google Scholar] [CrossRef]
- Wu, P.; Bucknall, R. Hybrid fuel cell and battery propulsion system modelling and multi-objective optimisation for a coastal ferry. Int. J. Hydrogen Energy 2020, 45, 3193–3208. [Google Scholar] [CrossRef]
- Dall’Armi, C.; Pivetta, D.; Taccani, R. Uncertainty analysis of the optimal health-conscious operation of a hybrid PEMFC coastal ferry. Int. J. Hydrogen Energy 2022, 47, 11428–11440. [Google Scholar] [CrossRef]
- Planakis, N.; Papalambrou, G.; Kyrtatos, N. Predictive power-split system of hybrid ship propulsion for energy management and emissions reduction. Control Eng. Pract. 2021, 111, 104795. [Google Scholar] [CrossRef]
- Miretti, F.; Misul, D.; Gennaro, G.; Ferrari, A. Hybridizing waterborne transport: Modeling and simulation of low-emissions hybrid waterbuses for the city of Venice. Energy 2022, 244, 123183. [Google Scholar] [CrossRef]
- Azienda del Consorzio Trasporti Veneziano (ACTV). Ai Cantiere Navale Vittoria la costruzione di due Nuovi Motobattelli Foranei con Motorizzazione Ibrida, 2023. (In Italian). Available online: https://avm.avmspa.it/en/node/7724 (accessed on 22 May 2025).
- Plett, G.L. Battery Management Systems, Volume I: Battery Modeling; Artech House: London, UK, 2015; Volume 1. [Google Scholar]
- RELiON. 12V 35Ah X-Series 35Ah Lithium Battery for Renewable Energy and Mobility Applications. Available online: https://www.relionbattery.com/products/lithium/rb35-x (accessed on 22 May 2025).
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Bertsekas, D. Dynamic Programming and Optimal Control: Volume I; Athena Scientific: Nashua, NH, USA, 2012; Volume 4. [Google Scholar]
- Miretti, F.; Misul, D.; Spessa, E. DynaProg: Deterministic Dynamic Programming solver for finite horizon multi-stage decision problems. SoftwareX 2021, 14, 100690. [Google Scholar] [CrossRef]
- Miretti, F.; Misul, D. Driveability Constrained Models for Optimal Control of Hybrid Electric Vehicles. In Proceedings of the I4SDG Workshop 2023, Bilbao, Spain, 22–23 June 2023; Petuya, V., Quaglia, G., Parikyan, T., Carbone, G., Eds.; Springer: Cham, Switzerland, 2023; pp. 430–440. [Google Scholar] [CrossRef]
- Miretti, F.; Misul, D. Robust Modeling for Optimal Control of Parallel Hybrids with Dynamic Programming. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; pp. 1015–1020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).