Wake Losses, Productivity, and Cost Analysis of a Polish Offshore Wind Farm in the Baltic Sea

Abstract

This study presents a comprehensive analysis of the long-term energy performance and economic viability of offshore wind farms planned for locations within the Polish Exclusive Economic Zone of the Baltic Sea. It focuses on the impact of wind farm layout, aerodynamic wake effects, and rotor blade surface degradation. Using the Jensen wake model, modified Weibull wind speed distributions are computed for various turbine spacing configurations (5D, 8D, and 10D) and wake decay constants $k_w\in \{0.02;0.03;0.05\}$. The results reveal a trade-off between turbine density and individual turbine efficiency: tighter spacing increases the total annual energy production (AEP) but also intensifies wake-induced losses. The study shows that cumulative losses due to wake effects can range from 16.5% to 38%, depending on the scenario considered. This corresponds to capacity factors ranging from 33.4% to 45.2%. Finally, lifetime productivity scenarios over 20 and 25 years are analyzed, and the levelized cost of electricity (LCOE) is calculated to assess the economic implications of design choices. The analysis reveals that, depending on the values of the considered parameters, the LCOE can range from USD 116.3 to 175.7 per MWh produced. The study highlights the importance of early stage optimization in maximizing both the energy yield and cost-efficiency in offshore wind farm developments.

1. Introduction

The ongoing energy transition in the countries of the European Union requires the adoption of increasingly ambitious plans for the development of renewable energy sources (RES). Recent changes in the geopolitical landscape have underscored the critical importance of minimizing dependence on fossil fuels, particularly for countries that lack significant domestic natural resources. Among the renewable technologies that contribute to this shift, offshore wind energy has emerged as a rapidly developing and strategically important sector in the European energy landscape. Since the commissioning of the Vindeby Offshore Wind Farm in 1991, approximately 37 GW of the offshore wind capacity was installed throughout Europe by 2024 [1], including around 3.5 GW located in the Baltic Sea [2]. In Poland, national plans foresee that the installed capacity of offshore wind farms (OWFs) will reach 5.9 GW by 2030 and approximately 11 GW by 2040 [3], which would enable offshore wind to account for nearly one-fifth of the country’s electricity generation [4]. However, it is important to note that capital expenditures associated with offshore investments remain high and that the success of current projects still relies on the financial security provided by state support schemes. Ensuring the diversification of energy sources is essential for the security of the country’s energy, but it must also align with the need to maintain the competitiveness of the Polish economy, which is directly influenced by electricity prices. Consequently, thorough planning, critical productivity assessment, and detailed economic analysis of projects undertaken by Polish companies are indispensable.

One of the critical stages in wind farm design is layout optimization, which involves positioning turbines to minimize wake effects and thereby maximize energy yield. A wide range of models have been developed to represent wake losses, among which the Jensen analytical model and its variants are the most widely used [5]. The study of wake-related phenomena employs various methods, including mathematical modeling, computational fluid dynamics (CFD), remote sensing techniques, and in situ turbulence measurements. While the Jensen model is appreciated for its computational efficiency and simplicity, it is widely acknowledged to oversimplify the complex nature of wake interactions. However, it remains a valuable tool in the optimization of preliminary design and layout, particularly under conditions characterized by homogeneous flow fields, such as those commonly found in offshore environments [6]. Its rapid computation makes it especially useful in iterative optimization processes, where the use of more sophisticated models would be computationally prohibitive. As the demand for more accurate representations of wake behavior increases, particularly in more complex or heterogeneous flow conditions, advanced modeling approaches become necessary.

Computational fluid dynamics (CFD) simulations, for instance, offer high-fidelity insights into the intricate turbulent flow structures within a wind farm, capturing nonlinear wake interactions and recovery mechanisms with greater precision. This increased accuracy comes at a significantly higher computational cost, limiting its application to detailed analyses of smaller sections of a wind farm or validation studies [7]. Actuator line models (ALM), often coupled with large-eddy simulations (LES), bridge the gap between simplified analytical models and full-scale CFD. They represent turbine blades as force distributions, providing a more realistic depiction of turbine wake generation and evolution than analytical models, while remaining more computationally feasible than full CFD for large arrays [8].

Despite advances in wake modeling techniques, a persistent challenge lies in accurately capturing wake-induced energy losses. It is well established that many models tend to underestimate these effects, leading to significant discrepancies in energy production forecasts. For example, an analysis of SCADA data from the Anholt Offshore Wind farm in Denmark revealed a median wake modeling error of nearly 9% [9]. Similarly, studies conducted off the U.S. East Coast estimate that wake-related energy losses in offshore wind farms could reach between 15 and 49 TWh annually, representing 11–28% of the expected energy output [10]. This discrepancy can significantly affect the projected return on investment and lead to higher-than-anticipated capital expenditures. According to [11], the total costs can exceed those of a reference scenario by as much as 21.6%. As wind energy technologies continue to advance, particularly through the installation of larger turbines in increasingly diverse geographical conditions, achieving a thorough understanding and accurate modeling of wake effects remains a fundamental research challenge with significant implications for both industry and the academic community.

Based on the observed underestimations of wake losses during wind farm layout planning, a distinct branch of engineering is emerging that focuses on optimizing the energy production of existing wind farms. These efforts mainly focus on the management and control of turbine operation in various wind conditions.

One such technique is the development of wake steering methods. Implementing appropriate control algorithms in wind farms can increase their annual energy production by up to 1% [12,13], providing substantial financial benefits for large-scale installations. Furthermore, wake steering can reduce the variability in wind farm power production by as much as 72% [14].

Equally promising is wake mixing, a strategy designed to accelerate wind speed recovery within the wake region behind a turbine. These techniques, often achieved through dynamic induction control or methods such as the “helix approach,” involve deliberately disturbing the aerodynamic wake by varying the turbine’s thrust force over time. This enhanced mixing of the free-stream air with the turbine wake leads to an overall improvement in wind farm performance, increasing power generation for downstream turbines. Although wake mixing strategies may introduce increased structural loads on turbines, including blades and towers, their potential to reduce energy losses and improve production is significant. This is particularly relevant for floating wind turbines, where platform motion can influence wake stability, as highlighted in research such as [15].

The aim of this study is to analyze the impact of turbine spacing on the energy yield of the offshore wind farm located in the Baltic Sea. Specifically, three inter-row spacing scenarios are considered in the prevailing wind direction: 5D, 8D, and 10D. The analysis includes a comparison of results under varying wake decay constants, underscoring the importance of appropriately tuning critical parameters within the chosen Jensen model for accurate wake loss predictions. The study is based on the area boundary of the most advanced offshore wind project currently under development in the exclusive economic zone of Poland of the Baltic Sea, for which a lifecycle economic assessment is performed. Furthermore, the investigation accounts for the potential reduction in annual energy production due to blade surface degradation caused by leading edge erosion, ice accretion, or other types of contamination commonly occurring in the marine environment, and includes an estimation of the average capacity factor for 20- and 25-year operational periods.

2. Materials and Methods

2.1. Wake Loss Model

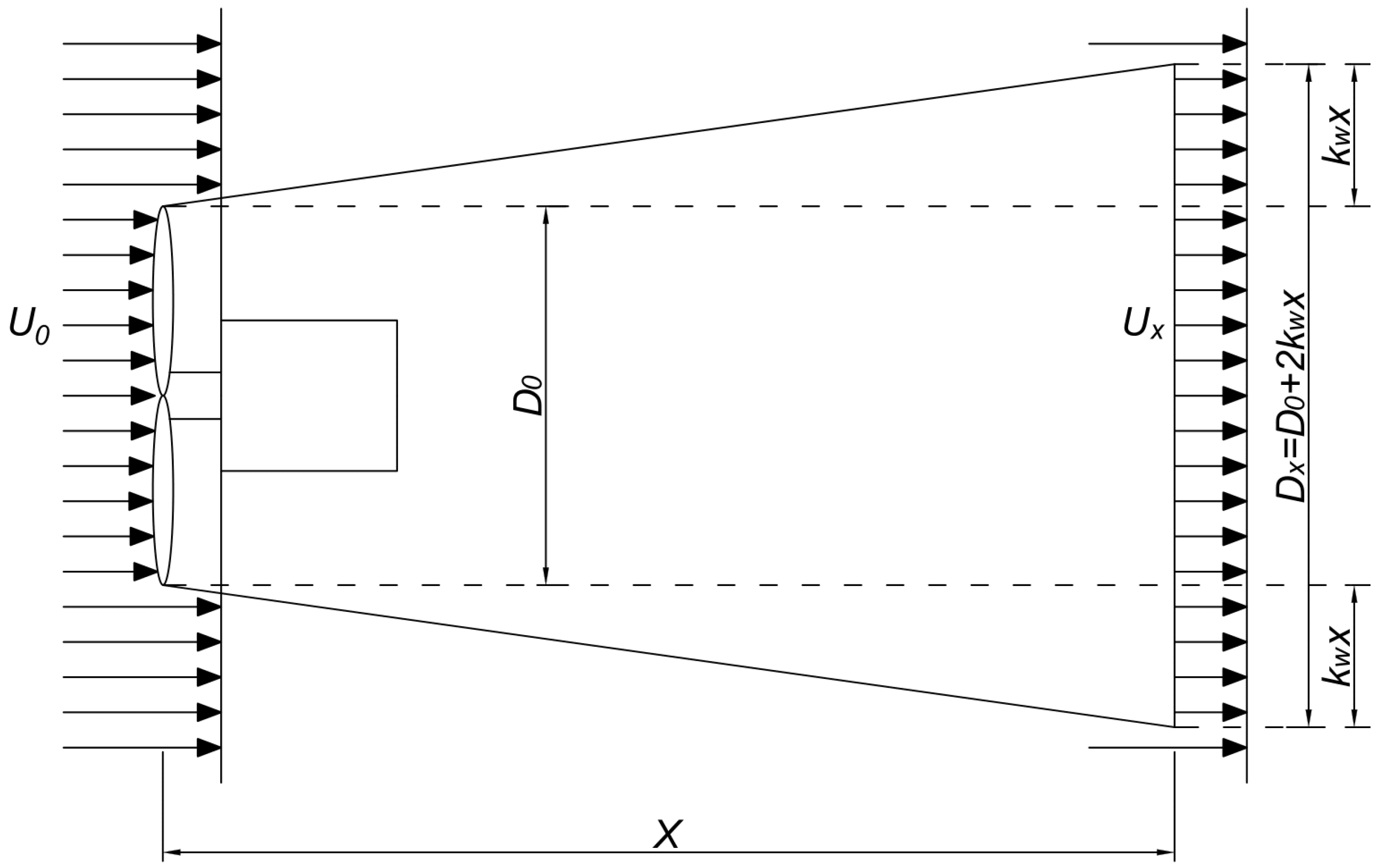
To evaluate wake-induced energy losses in the wind farm, the semi-empirical Jensen model was applied. While the model’s initial formulation was introduced in a 1983 technical report [16], the present study utilizes a more widely adopted modification [17]. Despite its simplifications and the assumption of linear wake propagation, this pioneering analytical model has demonstrated sufficient accuracy for large-scale wind farm applications, as confirmed in [18]. It is also considered a baseline approach under appropriately defined atmospheric conditions, and its use for offshore wind energy yield predictions is recommended in [19]. The conceptual framework of the Jensen model is illustrated in Figure 1.

The model assumes that the wind velocity has a single component perpendicular to the rotor plane of the turbine, and that the aerodynamic wake expands uniformly. This implies that the wake decay constant, $k_w$, governs the rate at which the wake spreads with distance and ultimately determines its final width. This parameter plays a crucial role in modeling wake-induced losses resulting from turbine interactions, which in turn affects the estimation of power output in downstream rows of the wind farm.

In the scientific literature, various approaches have been developed to determine this key constant. Broadly, these methods can be categorized as either dependent or independent of the turbulence intensity, $I_t$. Equation (1) reflects the latter case, considering only the terrain roughness length $z_0$ and the hub height of the turbine H [20].

$$k_w={\displaystyle \frac{0.5}{ln\left(H/z_0\right)}}.$$

(1)

A more advanced formulation (Equation (2)) includes the von Kármán constant $\kappa \approx 0.4$ and the atmospheric stability correction factor ${\psi }_m(H/L)$ [21]:

$$k_w=\kappa ·{\left[ln\left({\displaystyle \frac{H}{z_0}}\right)-{\psi }_m\left({\displaystyle \frac{H}{L}}\right)\right]}^{-1}.$$

(2)

The components listed above can be simplified to the concept of turbulence intensity at a given height, $I_t^H$, and are represented by the following expression:

$$k_w\approx 0.4·I_t^H.$$

(3)

According to fluid mechanics theory, a higher intensity of turbulence contributes to a faster recovery of the wind speed in the wake zone behind a turbine. Therefore, accurate estimation of the wake decay constant ($k_w$) is critical for forecasting wind farm productivity. This constant directly reflects the prevailing atmospheric conditions and therefore the operating environment of wind turbines.

As established, $k_w$ is fundamentally influenced both by the roughness of the terrain (Equation (1)) and the intensity of air turbulence (Equation (3)). In particular, the intensity of the turbulence itself strongly depends on the roughness of the terrain. Consequently, higher terrain roughness, characteristic of onshore wind farms, typically leads to increased turbulence intensity, and, in turn, to a larger wake decay constant. In contrast, offshore environments are generally associated with lower terrain roughness and reduced turbulence intensity.

In this study, three distinct values of the wake decay constant, $k_w\in \{0.02;0.03;0.05\}$, are applied. This range specifically corresponds to values representative of offshore conditions, consistent with the findings of [22,23]. This approach emphasizes the influence of $k_w$ on wake losses and consequently on annual energy production (AEP).

Using Equation (4), the wind speed $U_x$ can be calculated at a distance of x behind the turbine [17]. It is also important to note that the thrust coefficient $C_T$ is a value dependent on wind speed and specific turbine characteristics:

$$1-{\displaystyle \frac{U_x}{U_0}}={\displaystyle \frac{\left(1-\sqrt{1-C_T}\right)}{{\left(1+2k_{w}x/D\right)}^2}}.$$

(4)

In cases where the aerodynamic wakes of multiple turbines interact, it can be assumed that the loss of kinetic energy in the overlapping wake regions corresponds to the sum of losses generated by the individual turbine wakes. As a result, the wind speed reduction in the region of overlapping wakes from two turbines can be computed using the following relation:

$${\left(1-{\displaystyle \frac{U_x}{U_0}}\right)}^2={\left(1-{\displaystyle \frac{U_{x,1}}{U_0}}\right)}^2+{\left(1-{\displaystyle \frac{U_{x,2}}{U_0}}\right)}^2,$$

(5)

where $U_{x,i}$ is the wind speed in the aerodynamic wake of the i-th turbine at a distance of x.

Based on Equation (5), the overall wind speed reduction for the n-th turbine can be expressed as follows:

$${\delta }_n={\left(\sum _{i=1}^n{\delta }_i^2\right)}^{1/2},$$

(6)

where ${\delta }_n=1-(U_n/U_0)$. The above equations allow for the estimation of the wind speed in subsequent turbine rows, thereby facilitating the calculation of energy yield and power output.

2.2. Wind Turbines and Meteorological Conditions

To reflect the concepts of an actual offshore wind project in the Polish Exclusive Economic Zone, turbines with a rated capacity of 15 MW are assumed. The model turbine used in this study is the IEA Wind 15-MW reference turbine, developed by the National Renewable Energy Laboratory (NREL) [24].

It is important to note that the reference turbine can theoretically yield more favorable results than commercial models in the real world, such as Vestas V236-15.0 MW [25]. Figure 2 presents data provided by NREL [26], showing the electrical power output, thrust coefficient $C_T$, and power coefficient $C_P$ as functions of wind speed, including their interpolations over the entire operational range of the turbine.

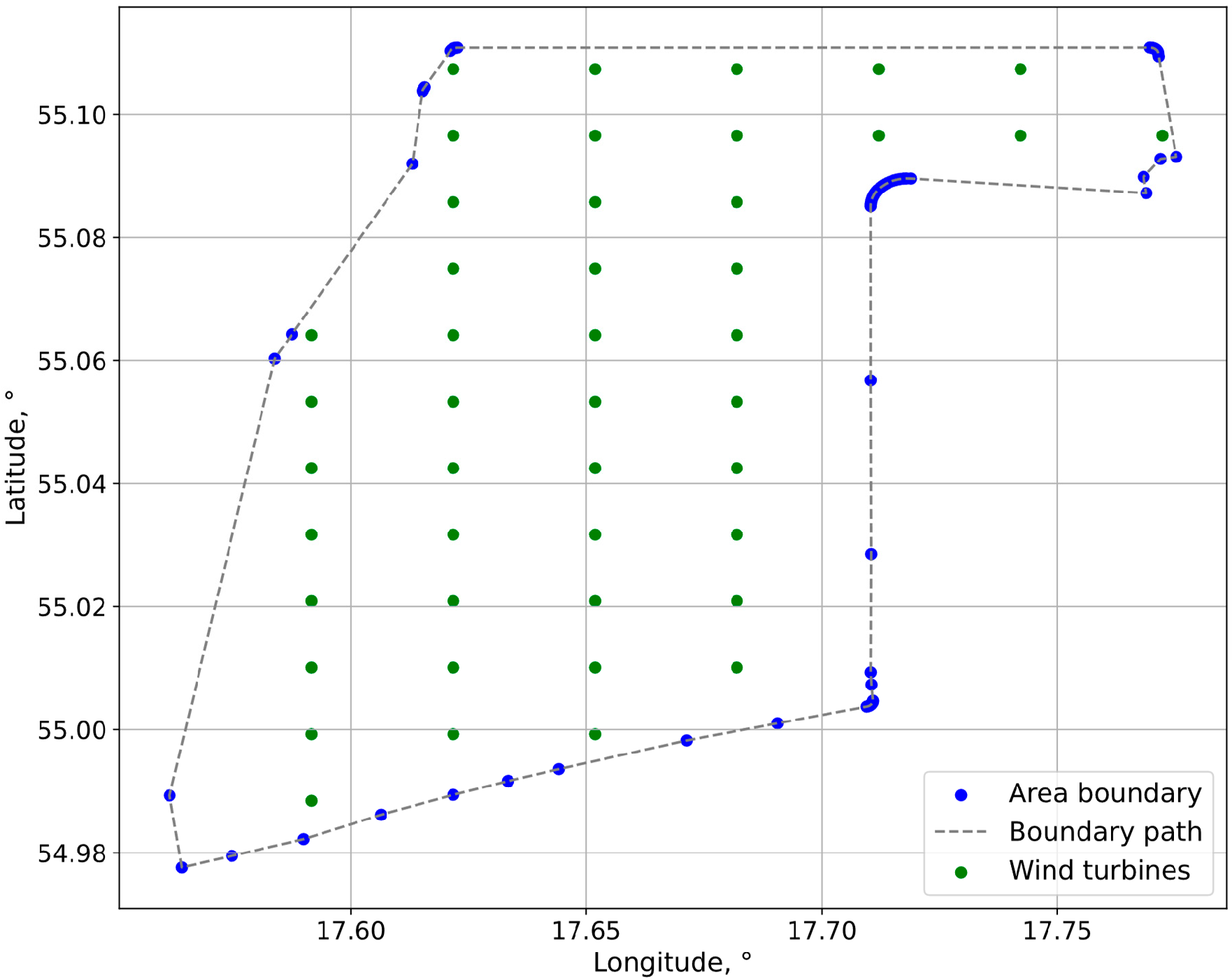
To analyze wind conditions, specifically wind speed and direction, within the Polish Exclusive Economic Zone of the Baltic Sea, data are obtained from the FINO 2 research platform, located 33 km north of the German island of Rügen [27]. The platform’s latitude closely corresponds to that of the planned location of the Baltic Power offshore wind farm, which constitutes the focus of the present study on wake losses, productivity, and cost analysis.

Notably, FINO 2 is the only platform in the southern Baltic region that provides measured wind data at heights comparable to those relevant for offshore wind energy applications. This makes it an invaluable source of information for the accurate modeling and optimization of offshore wind energy projects in the region. It is worth noting that the highest cup anemometer on the platform is located at an elevation of 102.5 m, while the wind vane is mounted at 91.8 m. Data from these instruments are used to visualize wind conditions in the form of a wind rose, as presented in Figure 3.

Annual wind speed distribution can be characterized by a suitable probability density function. Among various models, the Weibull distribution has gained broad acceptance for representing wind behavior at most geographical sites [28]:

$$f\left(U\right)=k{\displaystyle \frac{U^{k-1}}{{\lambda }^k}}exp\left(-{\left({\displaystyle \frac{U}{\lambda }}\right)}^k\right),$$

(7)

where k denotes the shape parameter, and $\lambda$ represents the scale parameter.

Table 1. Wind conditions at the FINO 2 platform at 102.5 m above sea level, based on measurements from 2007–2018 [27].

Description	Symbol	Value
Mean wind speed	$U_{\mathrm{FINO}}$	9.6 m/s
Scale parameter	$\lambda$	10.84 m/s
Shape parameter	k	2.33

summarizes the results of the data analysis obtained from the FINO 2 research platform, based on 11 years of operational measurements. It includes the average wind speed and the parameters characterizing the Weibull probability distribution, which is commonly used to describe the frequency distribution of wind speeds. It is important to note that the reported wind speed represents a direction-independent mean value. This estimate is closely aligned with the data provided by the Global Wind Atlas [29] for the geographic coordinates corresponding to the Baltic Power project. However, the analysis of wind direction based on measurements from the FINO 2 platform, as illustrated in Figure 3, clearly indicates the predominance of westerly winds.

To refine the analysis of wind farm productivity, a directional frequency study is conducted based on four quadrants: 315°–45°, 45°–135°, 135°–225°, and 225°–315°. The results reveal that winds from the west and east (i.e., 225°–315° and 45°–135°) account for approximately 60% of annual occurrences. The remaining 40% is attributable to winds from the north and south (i.e., 315°–45° and 135°–225°), with the majority of this contribution driven by southern winds.

Furthermore, the wind directions falling exactly on the quadrant boundaries are evenly distributed between the two adjacent sectors. The resulting 60/40 directional distribution is later incorporated into the energy yield and wake loss estimations to ensure greater accuracy under realistic wind conditions.

To accurately reflect wind conditions at the hub height of the IEA Wind 15-MW reference turbine, the wind speed is extrapolated using the logarithmic law expressed in Equation (8), which accounts for the change in height above sea level [30]:

$$U_0=U_{\mathrm{FINO}}·{\displaystyle \frac{ln\left(\frac{h_{\mathrm{FINO}}}{z_0}\right)}{ln\left(\frac{H}{z_0}\right)}},$$

(8)

where $U_0$ is the wind speed at the turbine’s hub height H, $U_{\mathrm{FINO}}$ is the measured wind speed at the FINO 2 platform, $h_{\mathrm{FINO}}$ is the measurement height (102.5 m), and $z_0$ is the surface roughness length (0.0002 m) [31]. In the calculations, a mean wind speed of $U_0=9.88$ m/s is assumed at the hub height of the turbines. This value corresponds to the undisturbed wind velocity reaching the first row of the wind farm, prior to the onset of aerodynamic wake effects.

2.3. Proposed Turbine Layout Configurations

In order to analyze the impact of offshore wind farm layout on energy productivity and aerodynamic losses, three configurations are proposed (Figure 4, Figure 5 and Figure 6). These differ in the spacing between turbine rows along the prevailing wind direction. A constant lateral spacing of 5 rotor diameters of the IEA Wind 15MW turbine ($D=240\mathrm{m}$) is maintained perpendicular to the dominant westerly wind.

Based on these assumptions, the number of wind turbines within the boundaries of the OWF Baltic Power area is maximized, resulting in three distinct installed capacity scenarios. Despite the simplified rectangular arrangement, the 5D variant corresponds to the actual planned capacity of the case study project, i.e., 76 wind turbines, yielding a total installed capacity of 1140 MW. The subsequent 8D and 10D layouts contain 45 and 35 turbines, respectively, which are expected to reduce wake interaction losses, albeit at the cost of lower total energy production due to fewer generating units.

2.4. Calculation of the Annual Energy Production

Wind farm layout optimization often aims to maximize the wind farm efficiency, which is defined as follows:

$${\eta }_{WF}={\displaystyle \frac{\mathrm{AEP}\mathrm{of}\mathrm{the}\mathrm{wind}\mathrm{farm}}{\left(\mathrm{AEP}\mathrm{of}\mathrm{a}\mathrm{standalone}\mathrm{turbine}\right)·(\mathrm{number}\mathrm{of}\mathrm{turbines})}}.$$

(9)

Using Equation (9), wake losses can be calculated as follows [32]:

$${\zeta }_{WF}=1-{\eta }_{WF}.$$

(10)

This estimation enables the quantification of the percentage of energy lost due to mutual turbine interference. Furthermore, the current study distinguishes aerodynamic losses associated with westerly and easterly winds (${\zeta }_{\mathrm{W}\text{-}\mathrm{E}}$), as well as those resulting from less frequent northerly and southerly winds (${\zeta }_{\mathrm{N}\text{-}\mathrm{S}}$). The turbine layout configurations analyzed (5D, 8D, and 10D) differ in terms of inter-row spacing along the longitudinal axis, implying that the arrangement is optimized to reduce losses from winds aligned with the east–west direction. However, the influence of winds aligned with the latitudinal (north–south) axis is not disregarded, as the spacing between turbines in the N–S direction is consistently set to five rotor diameters. Therefore, the total aerodynamic losses (${\zeta }_{total}$) must be calculated based on the wind direction frequency distribution defined in Section 2.2. This relationship can be interpreted as follows:

$${\zeta }_{total}=1-{\eta }_{WF(60/40)}.$$

(11)

An equally important component of the analysis is the determination of the overall capacity factor for the wind farm, denoted as $C_F^{WF}$, along with the estimation of its annual energy production (AEP). The capacity factor can be expressed by the following:

$$C_F^{WF}={\displaystyle \frac{E_{year}^{WF}}{P_z^{WF}·365·24}},$$

(12)

where $E_{year}^{WF}$ is the total annual energy output of the wind farm in megawatt-hours (MWh), and $P_z^{WF}$ represents its total installed capacity, calculated as the product of the rated power of a single turbine, $P_z^{WT}$, and the total number of turbines, N.

The energy yield for an isolated wind turbine, $E_{year}^{WT}$, is computed by integrating the product of the turbine’s power curve $P\left(U\right)$ and the wind speed probability distribution $f\left(U\right)$, as described by the Weibull function (Equation (7)), over a range of operating wind speeds:

$$E_{year}^{WT}={\int }_{U_{in}}^{U_{out}}f\left(U\right)P\left(U\right)\mathrm{d}U.$$

(13)

To obtain the total energy production for the entire wind farm, it is necessary to account for the aerodynamic wake effects that influence the wind speed experienced by downstream turbines. This is carried out by adjusting the Weibull distribution for each row of turbines to reflect the reduced wind velocity [33]:

$$E_{year}^{WF}=0.6R\sum _{n=1}^{N_i}{\int }_{U_{in}}^{U_{out}}{f}_n\left(U\right)P\left(U\right)\mathrm{d}U+0.4C\sum _{n=1}^{N_j}{\int }_{U_{in}}^{U_{out}}{f}_n\left(U\right)P\left(U\right)\mathrm{d}U.$$

(14)

In this expression, $N_i$ is the number of turbines in the i-th row, $N_j$ is the number of turbines in the j-th column, R is the number of rows, C is the number of columns in the farm layout, and $f_n\left(U\right)$ is the modified Weibull distribution accounting for the wind conditions in the n-th row. Importantly, Equation (14) assumes that turbines in different columns operate independently without aerodynamic interaction. In Equation (14), it is assumed that the aerodynamic wake does not negatively affect the electricity production of turbines in adjacent rows. This implies that the aerodynamic wakes from individual rows do not overlap. This assumption is justified because the aerodynamic wake reaching a turbine from an adjacent row is already very weak.

2.5. Reduction in AEP

The operational lifetime of offshore wind farms is typically planned for 25 years. During this period, rotor blades are exposed to numerous environmental factors that may alter their shape and surface roughness, consequently reducing the generated lift force and increasing drag. Among the key contributors to the reduction of annual energy production (AEP) are leading-edge erosion, surface contamination (e.g., sea salt), and blade icing.

Leading-edge erosion is one of the most thoroughly studied factors contributing to the degradation of the aerodynamic profile of rotor blades. This phenomenon involves the progressive deterioration of the blade’s leading edge surface due to mechanical interactions with small particles such as dust, sand, sea salt, or raindrops. This leads to increased surface roughness and decreased aerodynamic efficiency. Field studies conducted on wind farms such as Horns Rev 1 have shown that the average AEP loss due to this effect is approximately 1.4% during the first 10 years of operation, potentially increasing to 2.7% after a decade [34].

Estimating losses caused by biological contamination is considerably more challenging. Analyses suggest that the presence of dead insects on blade surfaces can lead to power losses of up to 25% under high wind conditions [35]. The marine environment facilitates the deposition of contaminants on blade surfaces, which, similarly to insect remains, increases aerodynamic roughness. It is assumed that AEP losses due to surface contamination may range from 5% in the early years of operation to as much as 8% over time, depending on the frequency of contamination, which may occur on 10–40% of days annually [36].

Blade icing presents a considerable challenge during the winter months, particularly in the southern Baltic region. Icing not only increases blade mass but also alters their aerodynamic shape, significantly reducing turbine efficiency. According to the analysis presented in [36], in extreme cases, icing may cause a drop in generated power of over 50%. In this study, AEP losses due to blade icing are estimated at approximately 2% annually, both during the initial operational period and after 10 years of service.

In summary, all these factors are cumulative in nature, leading to significant reductions in energy production. The assumptions regarding AEP reduction are presented in

Table 2. Assumed AEP reduction in offshore wind farms due to external impacts on rotor blade surface conditions.

AEP Reduction Factor	Average AEP Loss First 10 Years	Average AEP Loss After 10 Years
Blade Erosion	1.4%	2.7%
Contamination (e.g., salt)	5%	8%
Icing	2%	2%
Cumulative Impact	8.4%	12.7%

.

3. Results and Discussion

3.1. Weibull Distribution

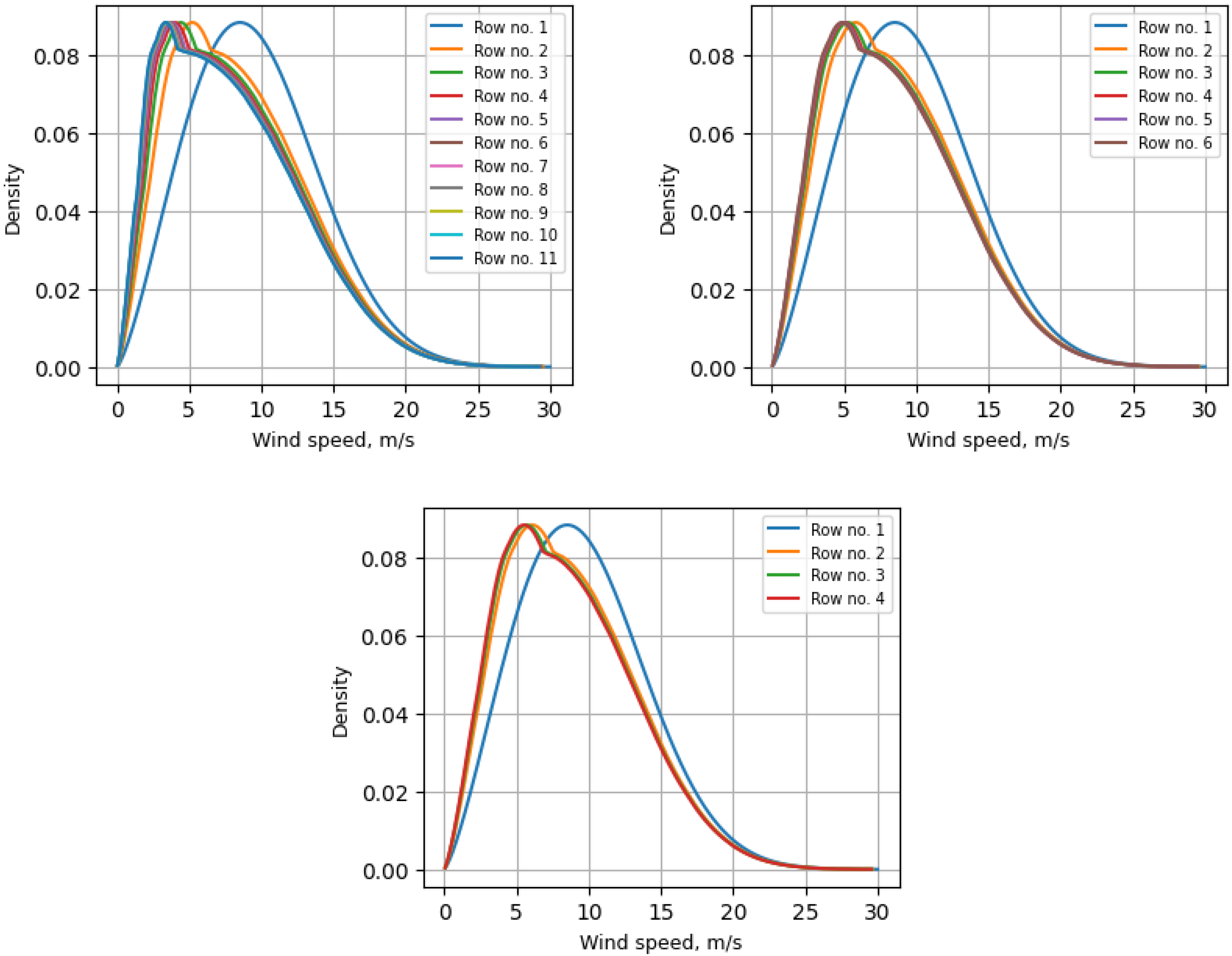
In order to estimate the wind conditions for individual rows of the offshore wind farm, the probability density distributions of wind speed must be modified according to the wind speed deficit calculated using the Jensen wake model. Figure 7 presents the Weibull distributions for the investigated turbine layout configurations for a wake decay constant of $k_w=0.02$.

The local minimum observed in the modified Weibull distribution curves (starting from row 2 onward) is caused by the shape of the thrust coefficient function $C_T\left(U\right)$, which is a component of Equation (4) used to calculate the wind speed behind a turbine.

Moreover, the comparison of the Weibull distributions for the three turbine spacing configurations illustrates a noticeable shift of the probability density function toward lower wind speeds, particularly more rapidly when the inter-row spacing is smaller, as in the 5D configuration.

In contrast, the 10D configuration shows that the curves for subsequent rows almost overlap and are significantly closer to the undisturbed Weibull distribution representing the first row. This indicates a strong ability of the wind flow to recover behind a turbine only at a distance of approximately 10 rotor diameters, i.e., 2.4 km.

Although Figure 7 only presents the case for $k_w=0.02$, additional analyses performed for higher wake decay constants ($k_w=0.03$ and $k_w=0.05$) reveal consistent trends. Increasing $k_w$ results in a weaker and more rapidly dissipating wake, which leads to reduced wind speed deficits in downstream rows. For $k_w=0.05$, the Weibull curves for all rows, regardless of configuration, are nearly overlapping. This indicates that under such favorable conditions, wake effects are substantially mitigated, and the wind speed recovers effectively even with tight spacing, such as 5D.

3.2. Annual Energy Production and Wake Losses

Initially, results are presented that exclude the reduction factors discussed in Section 2.5. Figure 8 summarizes the annual energy production (AEP) and estimates of capacity factors ($C_F$) as a function of the wake decay constant. These results should be interpreted as the theoretical maximum values, attainable under the investigated site conditions and the three analyzed scenarios of turbine spacing in the prevailing wind direction. It is important to note that westerly winds dominate at the site, and the layout configurations were oriented accordingly: the spacing of the turbines increases along the longitudinal axis (west–east). However, to account for the full wind rose, a directional weighting factor of 60/40 was applied, reflecting the annual frequency ratio between winds aligned with the longitudinal axis (W–E) and those from the latitudinal (N–S) direction.

The total annual energy production (AEP) is highest for the 5D configuration, which is primarily attributable to the greater number of installed wind turbines. In contrast, the capacity factor (CF) reaches its maximum values in the 10D configuration. This illustrates a fundamental design trade-off: increasing turbine density enhances energy output per unit area, but simultaneously reduces the operational efficiency of individual turbines due to intensified wake losses.

Table 3. Wake losses (${\zeta }_{\mathrm{W}\text{-}\mathrm{E}}$) for each turbine row under different inter-row spacings (5D, 8D, and 10D) and wake decay constants. Dash (–) indicates the undisturbed first row. Results under the assumption of westerly/easterly winds, i.e., occurring on 60% of days in a year.

Row no.	$\mathit{\zeta }$ 5D			$\mathit{\zeta }$ 8D			$\mathit{\zeta }$ 10D
	0.02	0.03	0.05	0.02	0.03	0.05	0.02	0.03	0.05
1	–	–	–	–	–	–	–	–	–
2	18.4%	16.3%	12.8%	15.2%	12.5%	8.8%	13.8%	10.9%	7.3%
3	26.1%	22.9%	17.8%	22.0%	18.0%	12.5%	19.5%	15.3%	10.1%
4	30.7%	26.8%	20.7%	25.1%	20.4%	14.1%	20.4%	16.0%	10.5%
5	33.8%	29.4%	22.6%	25.8%	20.9%	14.5%
6	35.9%	31.2%	23.8%	26.1%	21.2%	14.6%
7	36.9%	32.0%	24.4%
8	37.2%	32.2%	24.6%
9	37.4%	32.4%	24.7%

presents the estimated wake losses in each row of the wind farm for the assumed spatial configurations and various values of the wake decay constant $k_w$, considering wind directions aligned with the longitudinal axis of the farm (i.e., westerly or easterly winds). The aerodynamic losses decrease with increasing inter-row spacing, from 5D to 10D, as well as with higher values of $k_w$. For the three analyzed wind farm scenarios, the average difference in losses between the lowest and highest $k_w$ values is 11.4%.

The results in Table 3 indicate that the increase in wake losses between successive turbine rows is most pronounced in the initial part of the array. For instance, in the 5D spacing scenario with $k_w=0.02$, losses rise sharply from 18.4% in the second row to 30.7% in the fourth row, while the subsequent increase is significantly smaller, reaching only 37.4% in the ninth row. This trend supports the findings of Frandsen [37], who noted that as turbulence intensifies downstream, it tends to reach a quasi-equilibrium state. In this regime, additional wake effects from upstream turbines have diminishing influence, leading to a slower accumulation of losses in the deeper part of the wind farm. Similar trends are observed in

Table 4. Wake losses (${\zeta }_{\mathrm{N}\text{-}\mathrm{S}}$) for each turbine row under different inter-row spacings (5D, 8D, and 10D) and wake decay constants. Dash (–) indicates the undisturbed first row. Results under the assumption of northerly/southerly winds, i.e., occurring on 40% of days in a year.

Row no.	$\mathit{\zeta }$ 5D			$\mathit{\zeta }$ 8D			$\mathit{\zeta }$ 10D
	0.02	0.03	0.05	0.02	0.03	0.05	0.02	0.03	0.05
1	–	–	–	–	–	–	–	–	–
2	18.4%	16.3%	12.8%	17.0%	15.0%	11.8%	18.4%	16.3%	12.8%
3	24.3%	21.4%	16.7%	23.1%	20.3%	15.8%	24.0%	21.1%	16.5%
4	28.4%	24.9%	19.2%	27.3%	23.9%	18.5%	28.1%	24.5%	19.0%
5	31.4%	27.4%	21.1%	30.5%	26.5%	20.4%	31.0%	27.0%	20.8%
6	33.7%	29.3%	22.4%	32.8%	28.5%	21.8%	33.3%	28.9%	22.2%
7	35.3%	30.6%	23.3%	34.7%	30.1%	22.9%	35.1%	30.4%	23.2%
8	36.6%	31.6%	24.1%	36.2%	31.3%	23.8%	36.5%	31.6%	24.1%
9	37.6%	32.5%	24.7%	37.2%	32.1%	24.3%	37.7%	32.6%	24.7%
10	38.4%	33.1%	25.1%	38.0%	32.8%	24.8%	38.4%	33.1%	25.1%
11	38.8%	33.5%	25.4%	38.5%	33.2%	25.1%	39.0%	33.6%	25.5%

, which presents the aerodynamic losses for wind coming from the north or south (i.e., along the latitudinal axis, where the spacing between turbines remains constant across all examined layouts). When analyzing turbine arrangements with respect to the less frequent northerly or southerly winds, the number of rows affected by wake losses increases accordingly.

Table 5. Weighted total aerodynamic wake losses (${\zeta }_{total}$) for each wind farm layout configuration, based on a 60/40 directional wind distribution between the longitudinal (W–E) and latitudinal (N–S) axes.

Scenario	$\mathit{\zeta }$ 5D			$\mathit{\zeta }$ 8D			$\mathit{\zeta }$ 10D
	0.02	0.03	0.05	0.02	0.03	0.05	0.02	0.03	0.05
Total wake losses	38.0%	32.8%	24.9%	31.0%	26.0%	18.8%	27.8%	23.0%	16.5%

accounts for wind occurrence frequency, based on the assumption that 60% of winds blow along the longitudinal axis and 40% along the latitudinal axis. For the 5D configuration, the differences in wake losses between scenarios considering only dominant wind directions and those applying the 60/40 distribution are relatively small. More pronounced differences, however, are observed for the 10D configuration, which is typically designed with the prevailing westerly winds over the Baltic Sea in mind. When northerly and southerly winds, representing 40% of annual wind occurrences, are also considered, wake losses may increase from 20.4% to 27.8% for a wake decay constant of $k_w=0.02$.

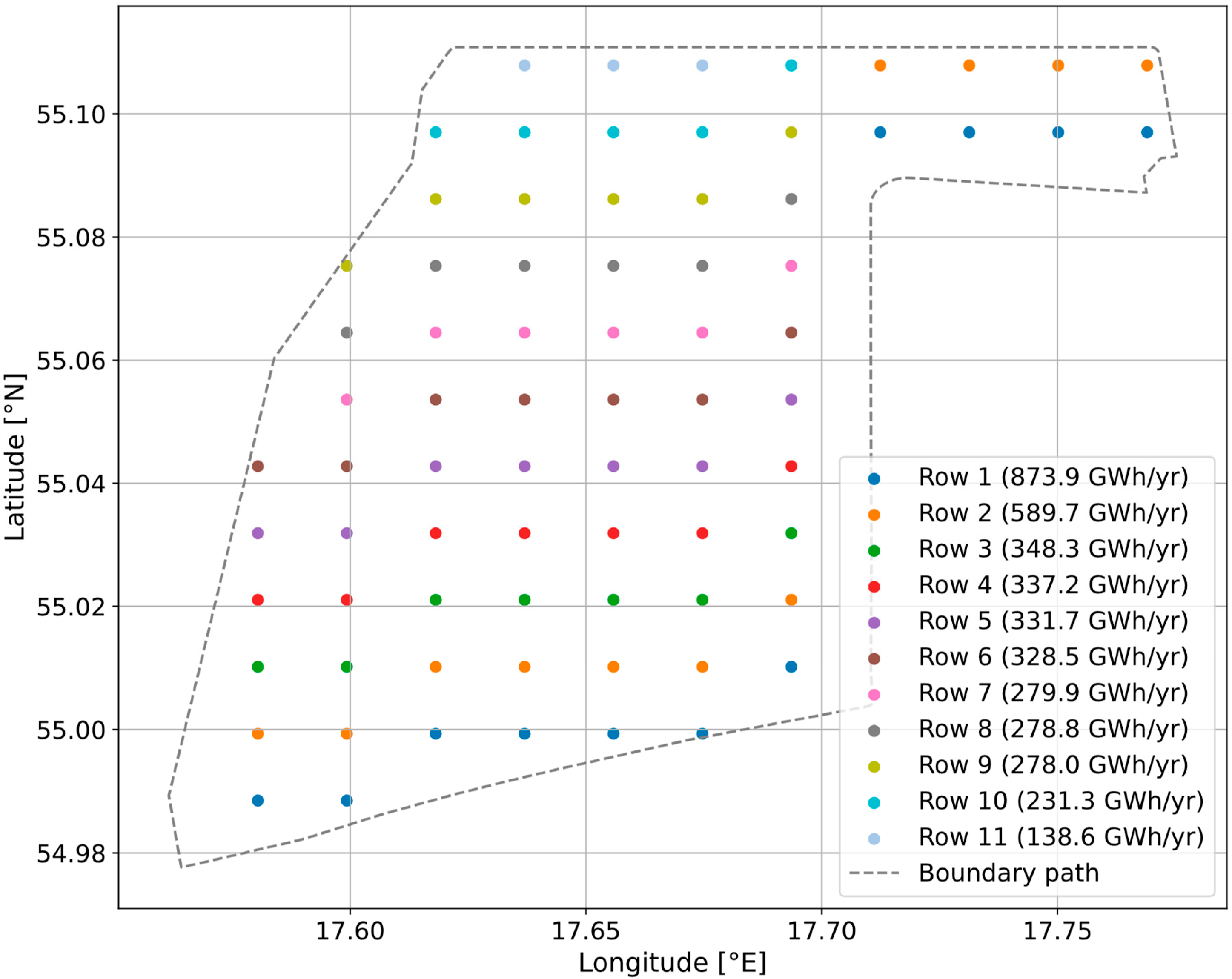
To illustrate the row-wise productivity of the investigated wind farm configurations, Figure 9 and Figure 10 present the results for the intermediate value of the wake decay constant, $k_w=0.03$. The analysis shown in Figure 9 is based on the hypothetical case of wind exclusively from the west, while Figure 10 illustrates a corresponding scenario with wind solely from the south.

Combining these directional cases in a weighted ratio of 60/40, as described earlier, enabled a more accurate estimation of wake losses. This composite result serves as a baseline for evaluating the idealized performance of an offshore wind farm under realistic wind distribution conditions.

To estimate the lifetime productivity of the wind farm, the assumptions listed in Table 2 were applied.

Table 6. Summary of estimated energy production and capacity factors ($C_F$) for a wind farm over 20 and 25 years of operation. The results account for AEP reduction factors (erosion, soiling, and icing) and are shown for various wake decay constants ($k_w$) and turbine spacing configurations (5D, 8D, and 10D).

Turbine Spacing	5D			8D			10D
${\mathbf{k}}_{\mathbf{w}}$	0.02	0.03	0.05	0.02	0.03	0.05	0.02	0.03	0.05
AEP avg. [GWh]	3334	3611	4034	2195	2356	2584	1787	1905	2068
Total prod. 25y [TWh]	83.4	90.3	100.9	54.9	58.9	64.6	44.7	47.6	51.7
Total prod. 20y [TWh]	67.0	72.6	81.1	44.1	47.3	51.9	35.9	38.3	41.6
$C_F$ 25y [%]	33.4	36.2	40.4	37.1	39.8	43.7	38.8	41.4	45.0
$C_F$ 20y [%]	33.5	36.3	40.6	37.3	40.0	43.9	39.0	41.6	45.2

summarizes the projected energy output and capacity factors ($C_F$) for two operational scenarios: 25 years, typical for offshore wind projects, and 20 years, accounting for potential early repowering. The results show a clear dependence on both the inter-row spacing and the wake decay constant $k_w$, with higher AEP and $C_F$ values achieved for wider spacing and greater $k_w$.

These findings align with the observations of Lorentzen et al. [38], who emphasize the sensitivity of $C_F$ to wind farm layout and wake mitigation, particularly in offshore settings where developing technologies intensify wake effects. The capacity factors range from 33.7% to 48.4%, with the highest performance seen in the 10D/$k_w=0.05$ configuration, with values comparable to the upper bounds reported in [38]. This highlights the critical role of early stage layout optimization in maximizing long-term energy yield and economic viability.

The above results align with the data observed from real-world wind farms. In Europe, onshore wind farms typically exhibit an average capacity factor of about 21%, while offshore installations generally achieve a higher average of 32% [39]. Specific instances illustrate this, such as the Margonin onshore wind farm’s 26% capacity factor, the North Hoyle offshore wind farm’s 25%, and the Scroby Sands offshore wind farm’s 35% [40,41,42]. It is crucial to acknowledge that the losses in power output from a wind farm are significantly affected by its geographical location and the predominant wind conditions. Suboptimal planning can result in losses that reach 23%, while optimized designs can effectively limit these losses to a minimum of 12.5% [43,44,45].

3.3. Levelized Cost of Electricity

To evaluate the profitability of the proposed offshore wind farm configuration within the Baltic Power (BLP) project boundaries, the levelized cost of electricity (LCOE) was used, following the methodology presented in [46]. LCOE is defined as the ratio of the total lifetime costs, including both capital expenditures (CAPEX) and operational expenditures (OPEX), to the total amount of electricity generated over the entire operational period of the installation. This indicator enables a direct and consistent comparison of different energy generation technologies, regardless of their technical characteristics or operational lifespans:

$$\mathrm{LCOE}={\displaystyle \frac{\mathrm{FCR}·\mathrm{CAPEX}+\mathrm{OPEX}}{{\mathrm{AEP}}_{\mathrm{net}}}},$$

(15)

where

• CAPEX is the total capital investment cost (USD/kW);
• OPEX is the total annual operational expenditures, consisting of fixed costs (USD/kW/year) and variable costs (USD/kWh), dependent on annual energy production;
• ${\mathrm{AEP}}_{\mathrm{net}}$ is the annual energy production of the offshore wind farm [MWh];
• FCR is the fixed charge rate, also known as the cost recovery factor, representing the annualized share of the investment cost.

The fixed charge rate (FCR) expresses the annual equivalent cost of the initial capital investment, considering the time value of money. It is assumed to be a fixed rate based on the project’s financing terms and can be calculated as follows:

$$\mathrm{FDR}={\displaystyle \frac{i}{1-{(1+i)}^{-N}}},$$

(16)

where

• i is the interest or discount rate;
• N is the project lifetime in years.

This formulation enables a uniform cost comparison between different energy projects by converting upfront capital investments into equivalent annual payments, which are then divided by the annual energy output.

In this study, the interest rate and operational expenditures (OPEX) for offshore wind farms were adopted based on data provided in the Fraunhofer Institute report [47]. The baseline interest rate was assumed to be $i=7\%$. Operational costs were divided as follows:

• Fixed annual costs: USD 41.9/kW/year;
• Variable costs: USD 0.009/kWh, dependent on the annual energy output.

Additionally, a sensitivity analysis will be conducted for a lower interest rate of $i=5\%$, in line with the value applied in the study by [46]. This reduced rate is considered justified in the context of Polish offshore wind projects, particularly due to the involvement of public financing instruments. Specifically, funding is expected to be partially sourced from the National Recovery and Resilience Plan through a loan mechanism provided by Bank Gospodarstwa Krajowego S.A., which typically offers more favorable financial conditions.

The capital expenditures were estimated based on public information disclosed by offshore wind developers in Poland after reaching the final investment decision (FID) [48,49,50].

Table 7. Estimated CAPEX and unit investment cost for selected Polish offshore wind farm projects.

OWF	CAPEX [USD]	CAPACITY [kW]	COSTS PER kW [USD]	AVERAGE [USD/kW]
Baltic Power	5,080,966,000	1,140,000	4457	4734
Baltica 2	7,539,270,023	1,498,000	5033
Bałtyk 2 and 3	6,785,345,021	1,440,000	4712

presents the assumed investment costs per installed kilowatt. All currency values presented in this study were converted to USD using the average exchange rate from April 2024 to April 2025 based on data from the National Bank of Poland (USD 1 = PLN 3.9792) and the European Central Bank (EUR 1 = USD 1.0742) [51,52].

An analysis of costs for offshore wind projects within Poland’s exclusive economic zone reveals that the reported investment costs are significantly higher than the estimates provided by leading international research institutions. For instance, the International Renewable Energy Agency (IRENA) reports average capital expenditures for European offshore wind projects at approximately USD 3138/kW [53], while the Fraunhofer Institute estimates a range between USD 2363 and 3652/kW [47]. These discrepancies suggest that Polish project estimates may be inflated relative to broader European benchmarks.

The levelized cost of electricity results for a discount rate of 7% are presented in

Table 8. Levelized cost of electricity (USD/MWh) for different inter-row spacings (10D, 8D, and 5D) and wake decay constants $k_w\in \{0.02,0.03,0.05\}$. Results are shown for project lifetimes of 25 and 20 years. The interest rate is assumed to be $i=7\%$.

Scenario	Years	10D			8D			5D
		0.02	0.03	0.05	0.02	0.03	0.05	0.02	0.03	0.05
LCOE (USD/MWh) based on BLP costs	25	133.3	125.5	116.3	139.1	130.2	119.4	153.7	142.6	128.5
	20	144.5	136.1	126.0	150.9	141.1	129.4	166.8	154.6	139.3
LCOE (USD/MWh) based on an average	25	140.3	132.1	122.4	146.4	137.0	125.7	161.8	150.1	135.2
	20	152.2	143.3	132.7	158.9	148.6	136.3	175.7	162.9	146.7

. These outcomes reveal a rather stringent economic outlook for the profitability of the hypothetical offshore wind farm configurations considered within the analyzed Baltic Sea area. More importantly, they underscore the critical role of assumptions related to aerodynamic wake modeling, in particular, the wake decay constant $k_w$, in shaping the economic viability of offshore wind energy projects.

The subsequent

Table 9. Levelized cost of electricity (USD/MWh) for different inter-row spacings (10D, 8D, and 5D) and wake decay constants $k_w\in \{0.02,0.03,0.05\}$. Results are shown for project lifetimes of 25 and 20 years. The interest rate is assumed to be $i=5\%$.

Scenario	Years	10D			8D			5D
		0.02	0.03	0.05	0.02	0.03	0.05	0.02	0.03	0.05
LCOE (USD/MWh) based on BLP costs	25	113.8	107.3	99.5	118.7	111.2	102.1	131.0	121.6	109.8
	20	126.0	118.7	110.0	131.5	123.1	113.0	145.2	134.7	121.5
LCOE (USD/MWh) based on average	25	119.6	112.7	104.5	124.8	116.8	107.3	137.8	127.9	115.3
	20	132.5	124.8	115.7	138.3	129.4	118.8	152.8	141.7	127.8

, based on a reduced project discount rate of 5%, offers a more optimistic outlook regarding the economic feasibility of the analyzed offshore wind farm layouts. Notably, a greater number of configurations yield LCOE values below the volume-weighted average electricity price on the Polish Day-Ahead Market in 2024, which amounted to USD 106.8/MWh [54].

It should be emphasized that the calculated LCOE values generally lie near the upper boundary or slightly exceed the range of USD 59–110/MWh reported in [47]. This may suggest that, despite the favorable site conditions of the projects listed in Table 7, such as relatively shallow water depths and close proximity to shore, certain assumptions regarding inter-row spacing, AEP reduction factors, or the wake decay constant could substantially prolong the return on investment (ROI) period beyond the expectations typically held by project developers.

Furthermore, the integration of a high share of wind energy into national power grids presents complex operational challenges, as observed in countries such as Germany and Denmark. A notable issue is the frequent curtailment of wind farms due to overproduction. This phenomenon significantly influences the annual average capacity factor (AACF) of wind installations, which consequently increases their LCOE. Specifically, highly wind-penetrated energy systems, even those that incorporate offshore wind, tend to exhibit a lower or comparable AACF in contrast to countries that have a lower overall penetration of wind energy and no offshore installations [55,56].

3.4. Limitations of the Analysis

The limitations of the presented analysis primarily stem from the application of a relatively simple method for calculating the velocity deficit, the Jensen model. The main constraints of this method include the following:

• The assumption of only one velocity component.
• The lack of mutual influence between neighboring wind farm columns.
• Other simplifications in modeling the wake phenomenon.

However, it should be noted that the incorporation of more complex wake models generally has a secondary impact on the overall results. Such models might become significant in locations with a more "diverse" aerodynamic airflow characteristics and in cases of more irregular wind turbine layouts within the farm.

Furthermore, the obtained LCOE results pertain exclusively to the wind farms themselves and do not account for the system services that are indispensable for their operation. This includes aspects such as merit order pricing, maintaining power reserves during periods of no wind, or the necessity of additional energy storage facilities. All these elements are crucial for the energy system precisely because of the presence of wind farms, yet their costs are not factored into the LCOE but instead impose an additional burden on end-users of energy.

4. Conclusions

This study demonstrates the significant influence of wind farm layout design, wake effects, and rotor blade degradation on long-term energy performance and economic viability of offshore wind farms in the exclusive economic zone of the Polish Baltic Sea. Key findings can be summarized as follows:

1.

Wake effects and turbine spacing: The analysis confirms that tighter turbine spacing increases total annual energy production (AEP) but also leads to substantial wake-induced losses. Depending on the wake decay constant and the layout configuration, cumulative wake-related losses can range from 16.5% to 38%.

2.

Capacity factor variation: The impact of layout design on the capacity factor is pronounced, with values ranging from 33.4% to 45.2% across scenarios. This underlines the critical role of aerodynamic interactions in determining wind farm efficiency.

3.

Economic implications: The levelized cost of electricity (LCOE) analysis over 20- and 25-year operational lifespans shows that economic outcomes are highly sensitive to both technical and design parameters. LCOE values range from 116.3 to 175.7 USD/MWh, highlighting the importance of optimized design in achieving cost-effective energy production.

4.

Design optimization: The results emphasize that the early stage optimization of the wind farm layout, balancing turbine density with wake loss mitigation, is essential to maximize both energy yield and cost efficiency over the project’s lifetime.

In general, this study reinforces the necessity for integrated energy and economic modeling in offshore wind farm planning and supports the use of wake modeling tools such as the Jensen model for scenario-based optimization. Future work should include validation with real-world wind farm data and consideration of maintenance costs, environmental constraints, and evolving turbine technologies.