Shuffled Puma Optimizer for Parameter Extraction and Sensitivity Analysis in Photovoltaic Models
Abstract
1. Introduction
2. Methodology
2.1. Contribution
- Proposed a novel algorithm called SPO with a shuffle-mutation strategy to improve the global search capability of PO while maintaining population diversity.
- Applied SPO to accurately extract parameters for four photovoltaic models: SDM, DDM, TDM, and PMM.
- A comparative performance analysis of SPO against multiple advanced algorithms using metrics including best fitness, mean fitness, and standard deviation.
- Performed OFAT sensitivity analysis to identify the influence of individual parameters and determine the key factors in each PV model.
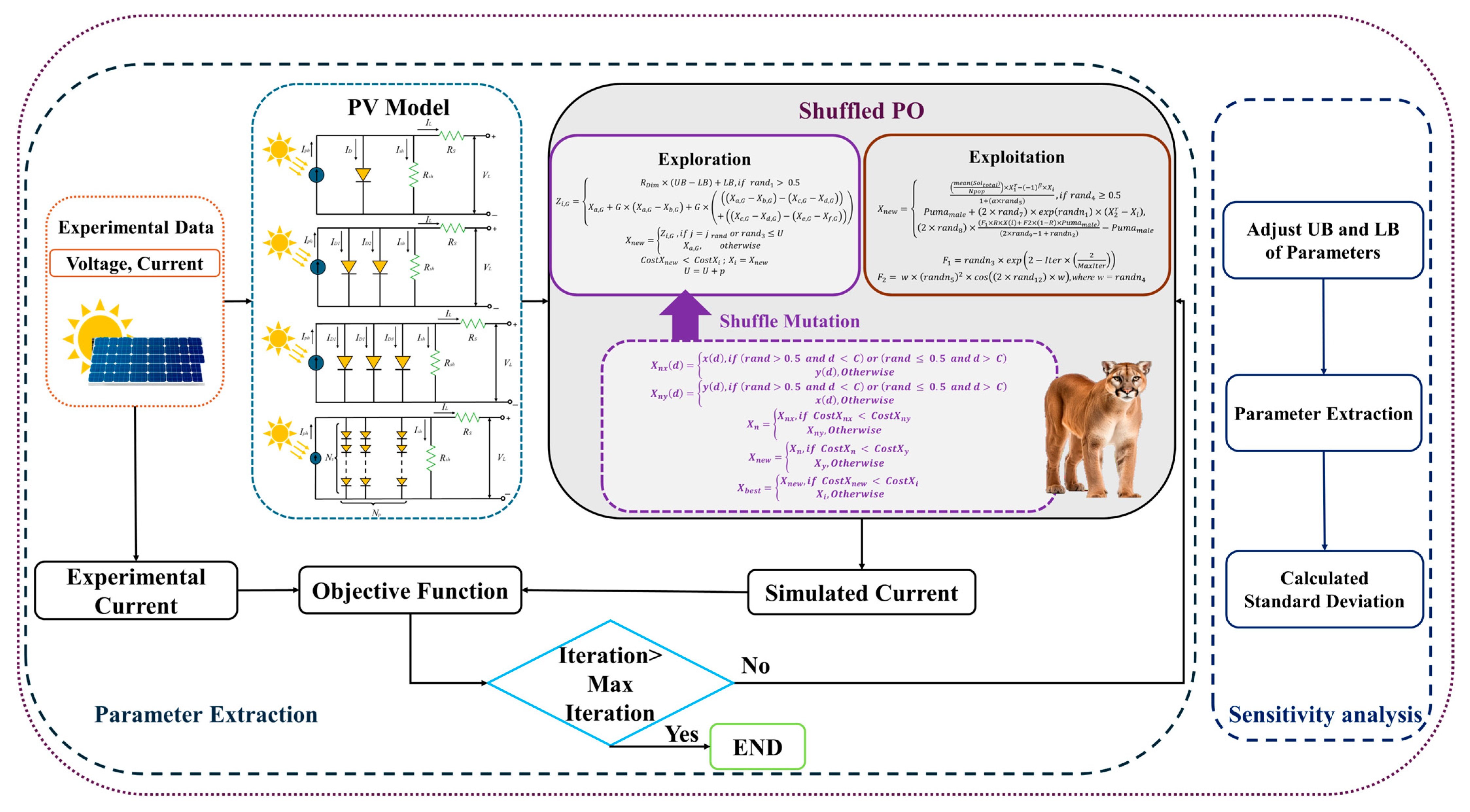
2.2. Research Framework
- Detailed experimental data collected from the PV system.
- Built multi-diode models to represent the behavior of the PV system.
- Enhanced Puma Optimizer with mutation-shuffle strategy.
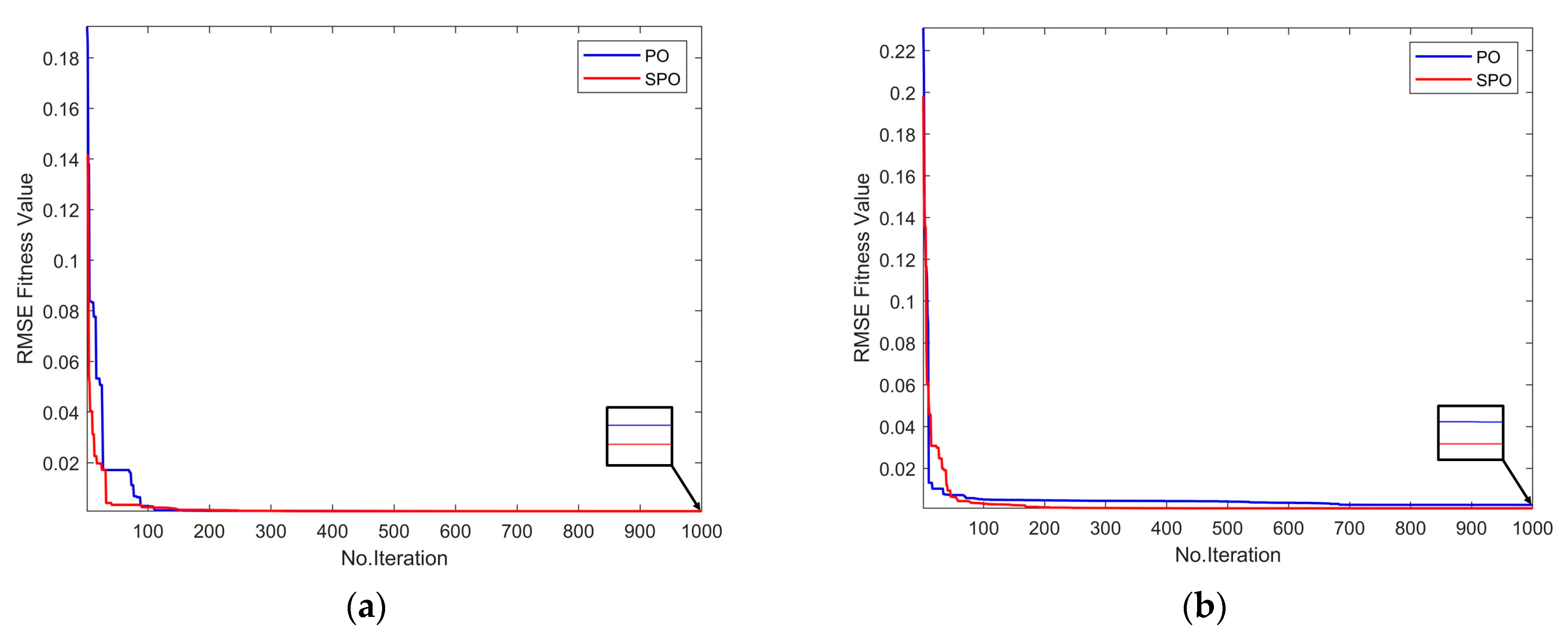
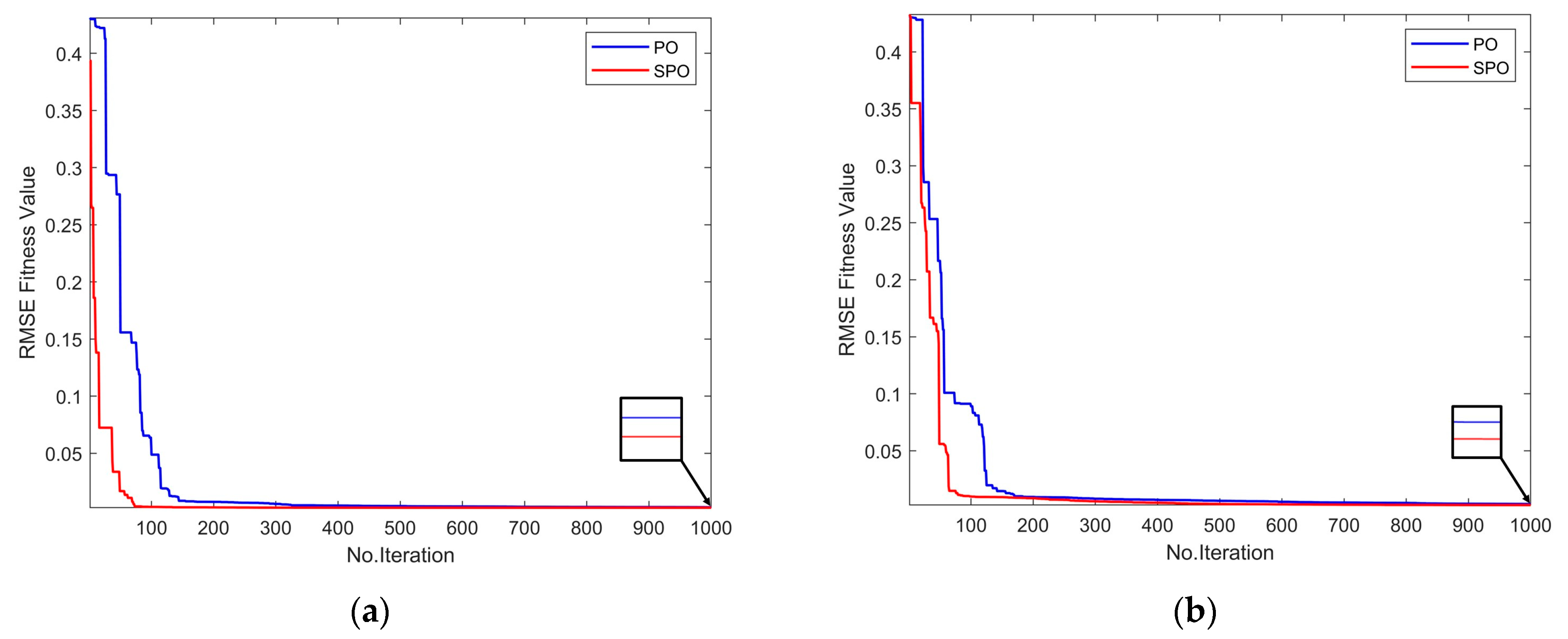
- Using SPO to extract PV model parameters and analyze the algorithm’s robustness in RMSE.
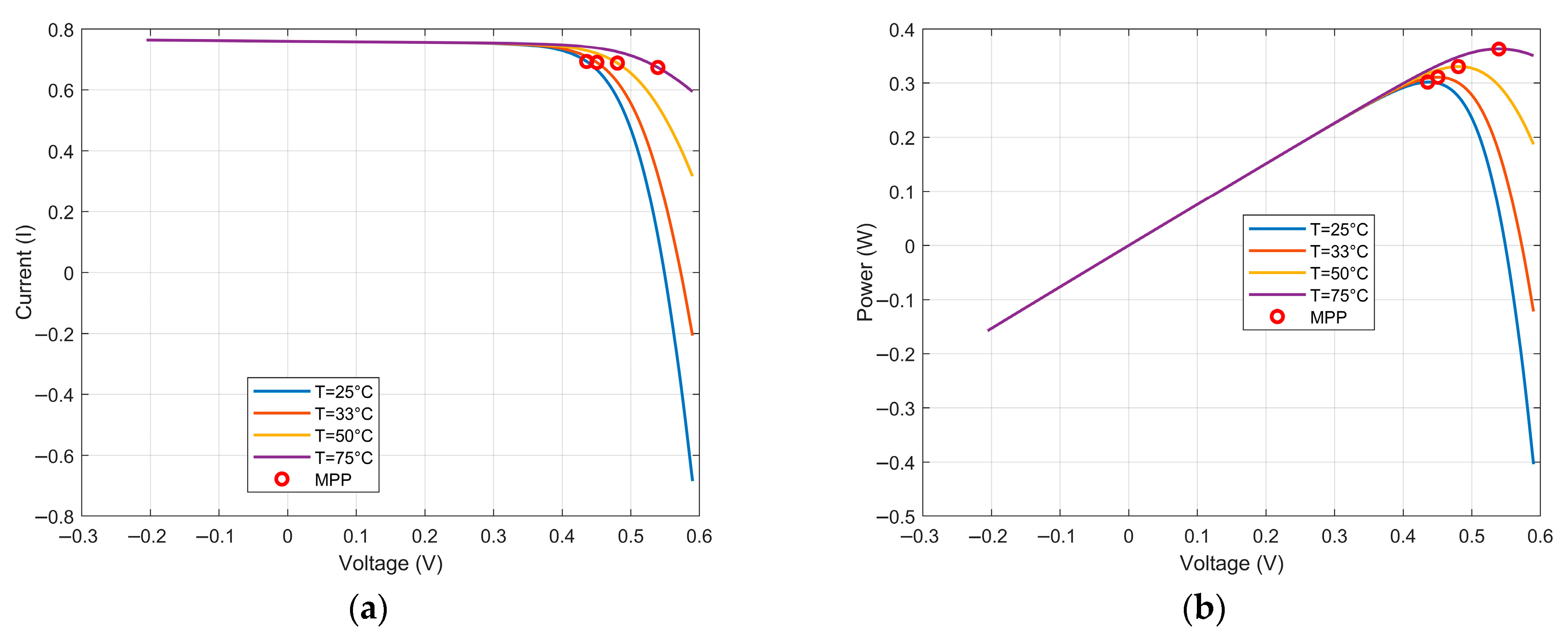
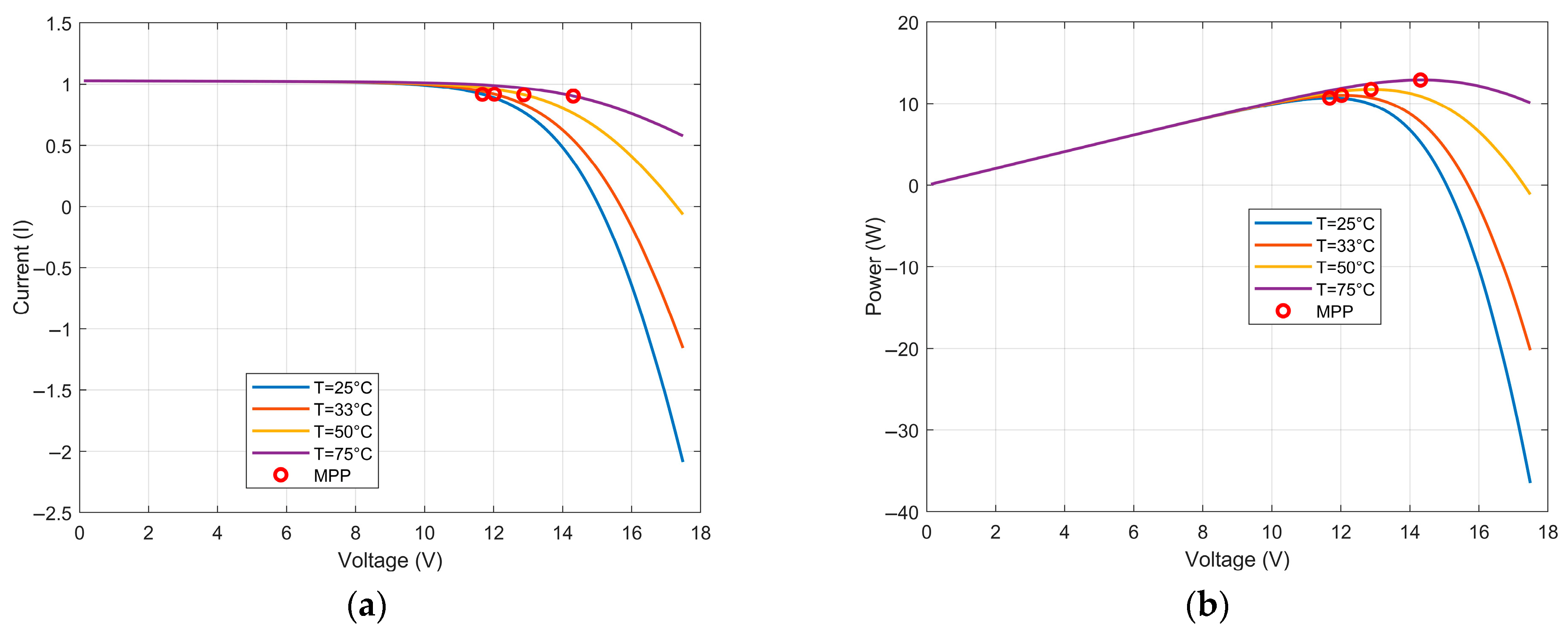
- Predict PV system performance and maximum power point under four different temperature conditions.
- Use the OFAT method to analyze key parameters in PV models.
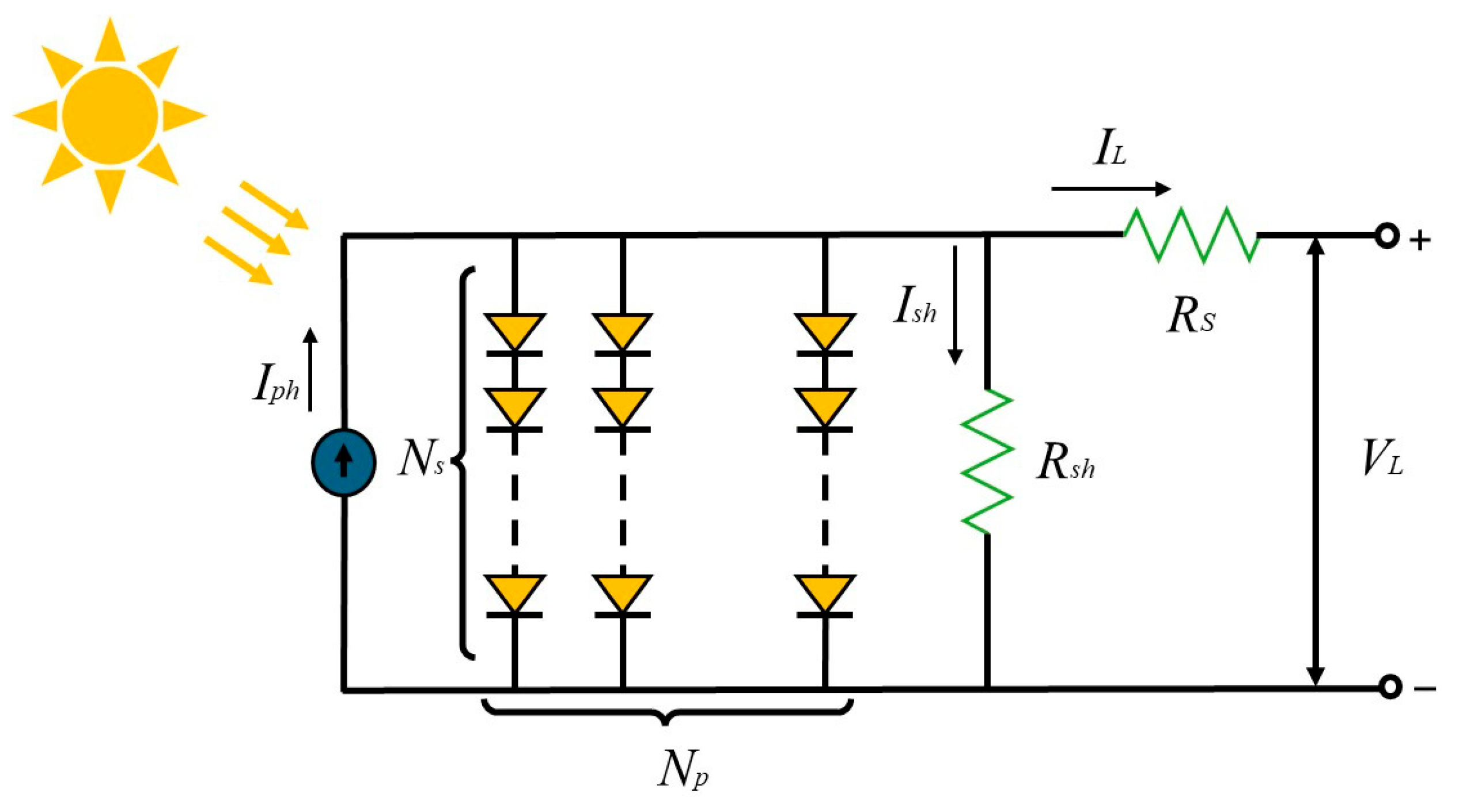
2.3. Photovoltaic System Modeling
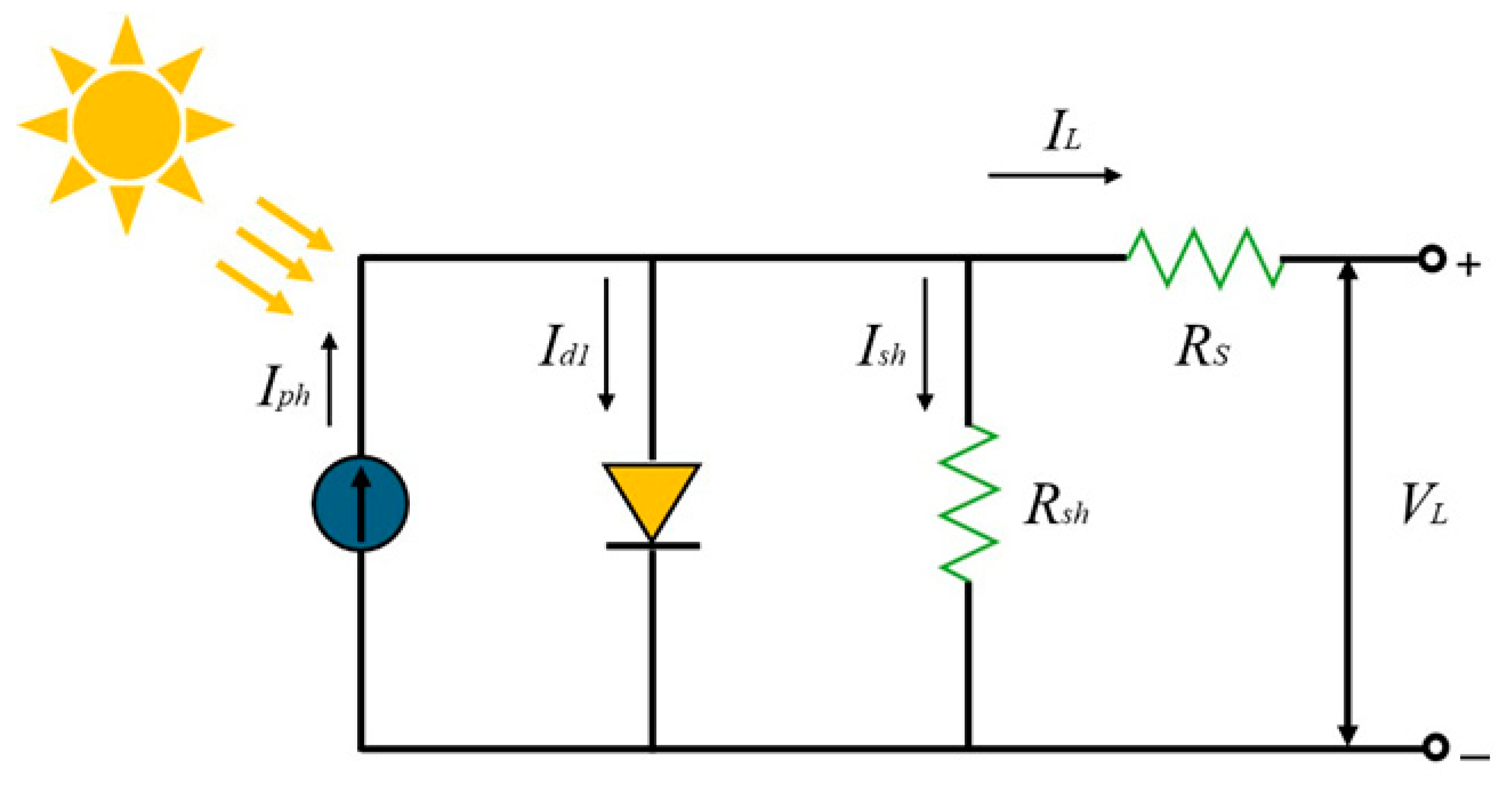
2.3.1. Single Diode Model
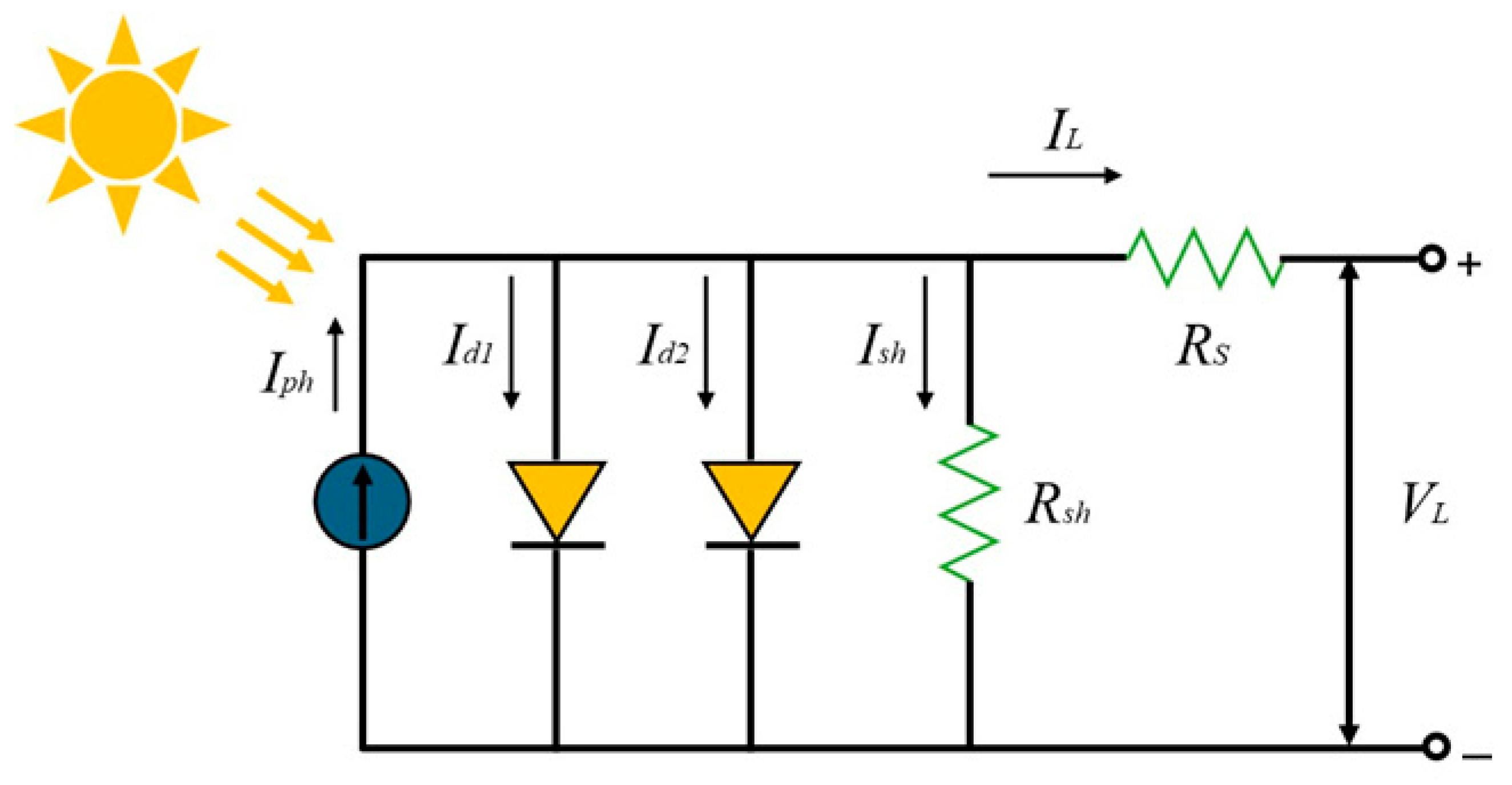
2.3.2. Double Diode Model
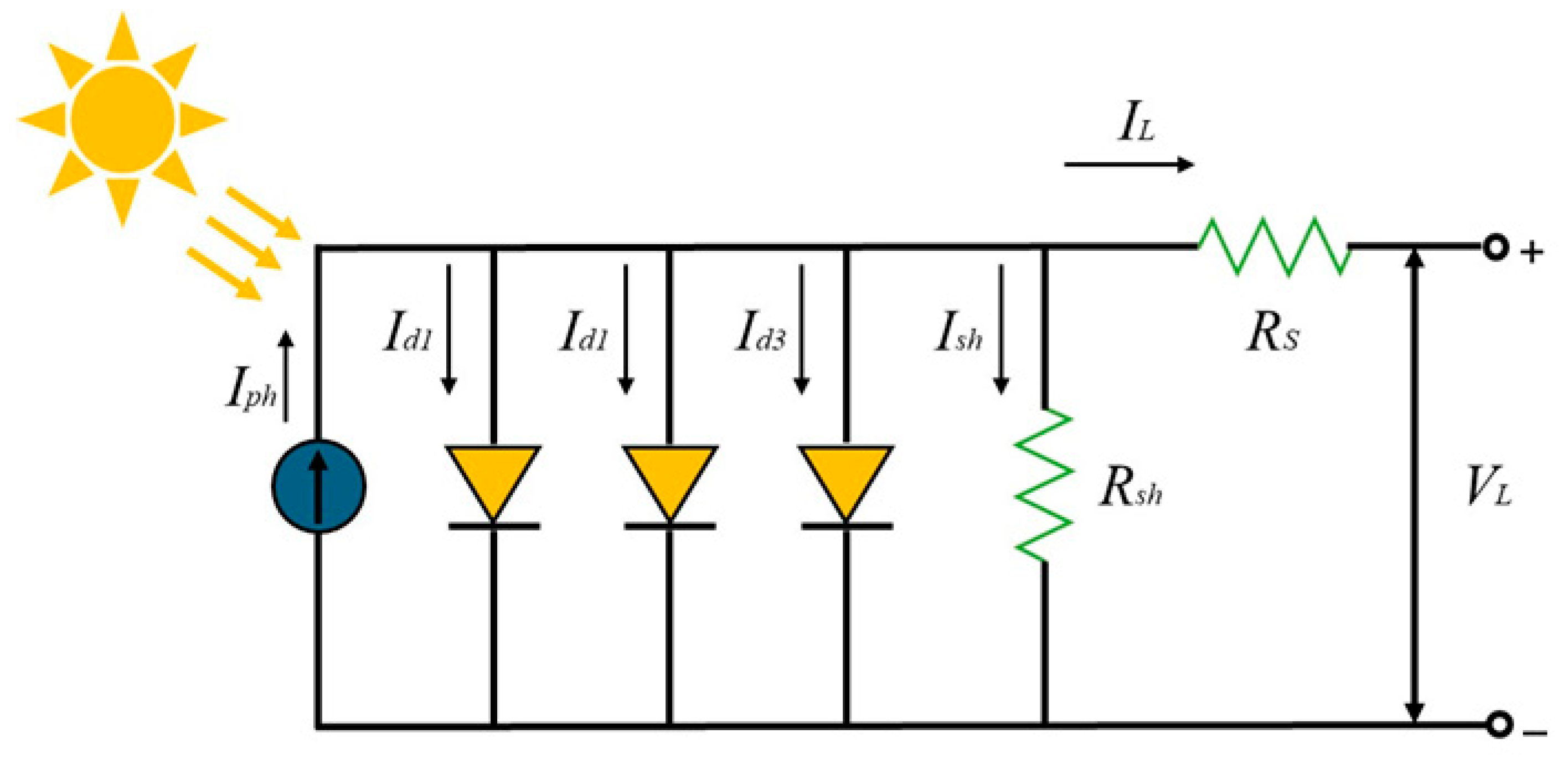
2.3.3. Triple Diode Model
2.3.4. Photovoltaic Module Model
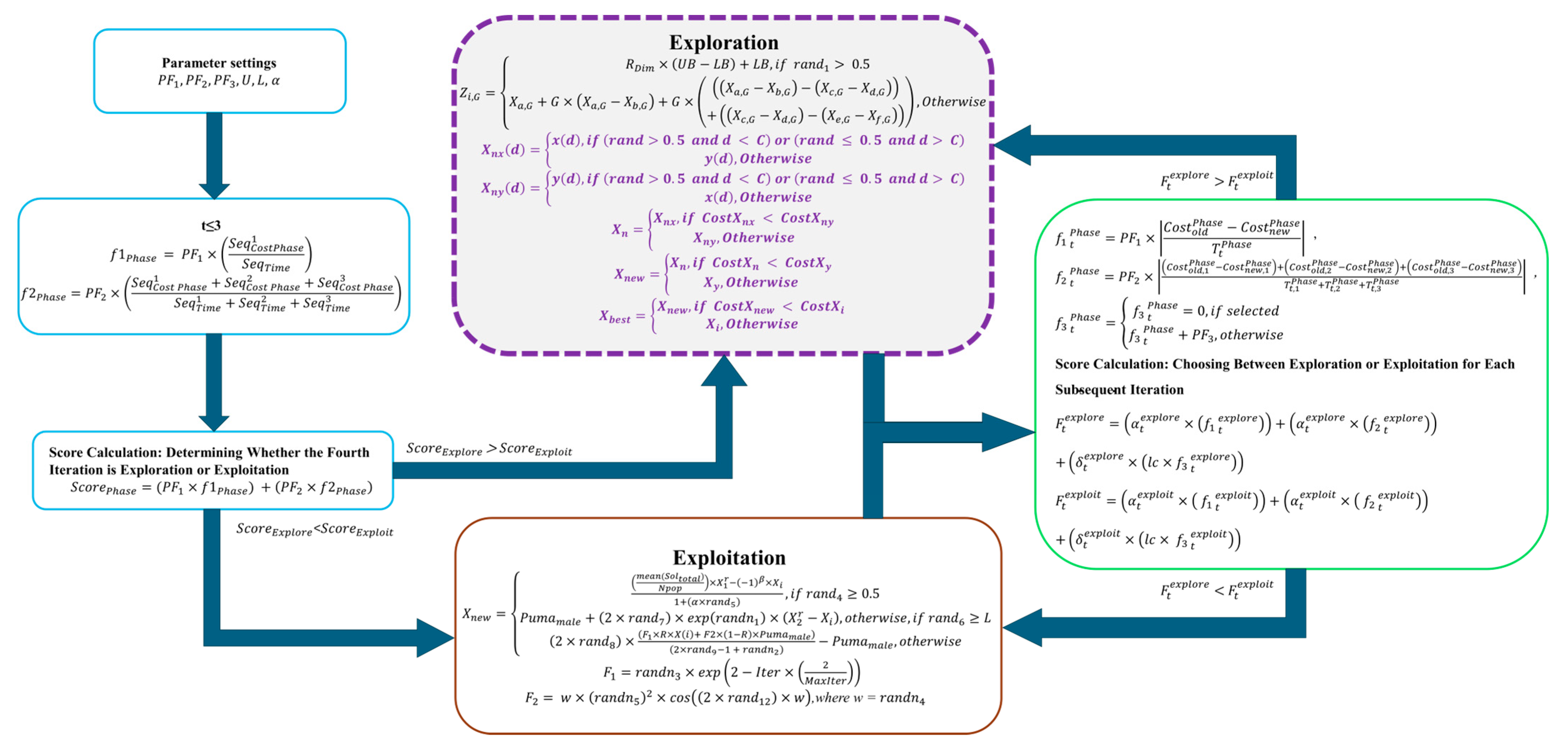
2.4. Shuffled Puma Optimizer
2.4.1. Initialization
2.4.2. Unexperienced Phase
2.4.3. Experienced Phase
2.4.4. Exploration Phase
2.4.5. Exploitation Phase
2.4.6. A Shuffle Mutation Strategy for Global Optimization
2.5. Objective Function and Parameter Setting
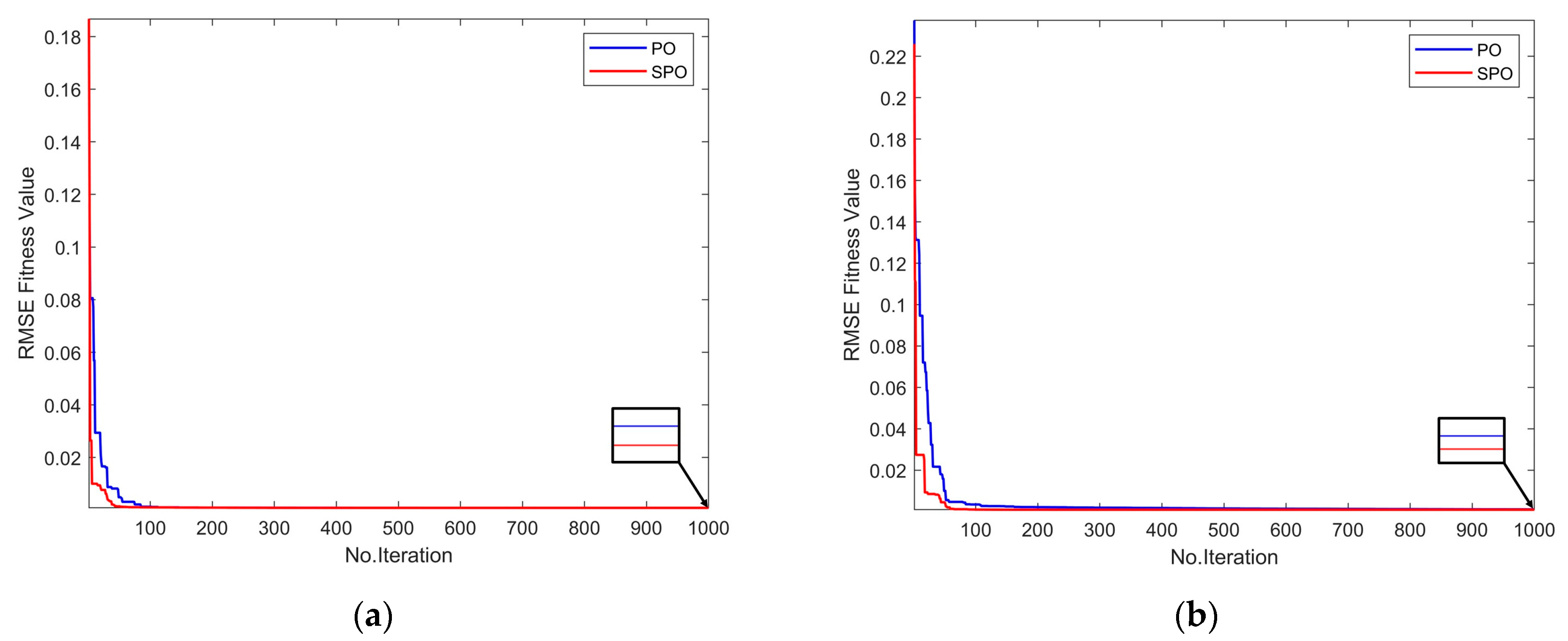
3. Results and Discussion
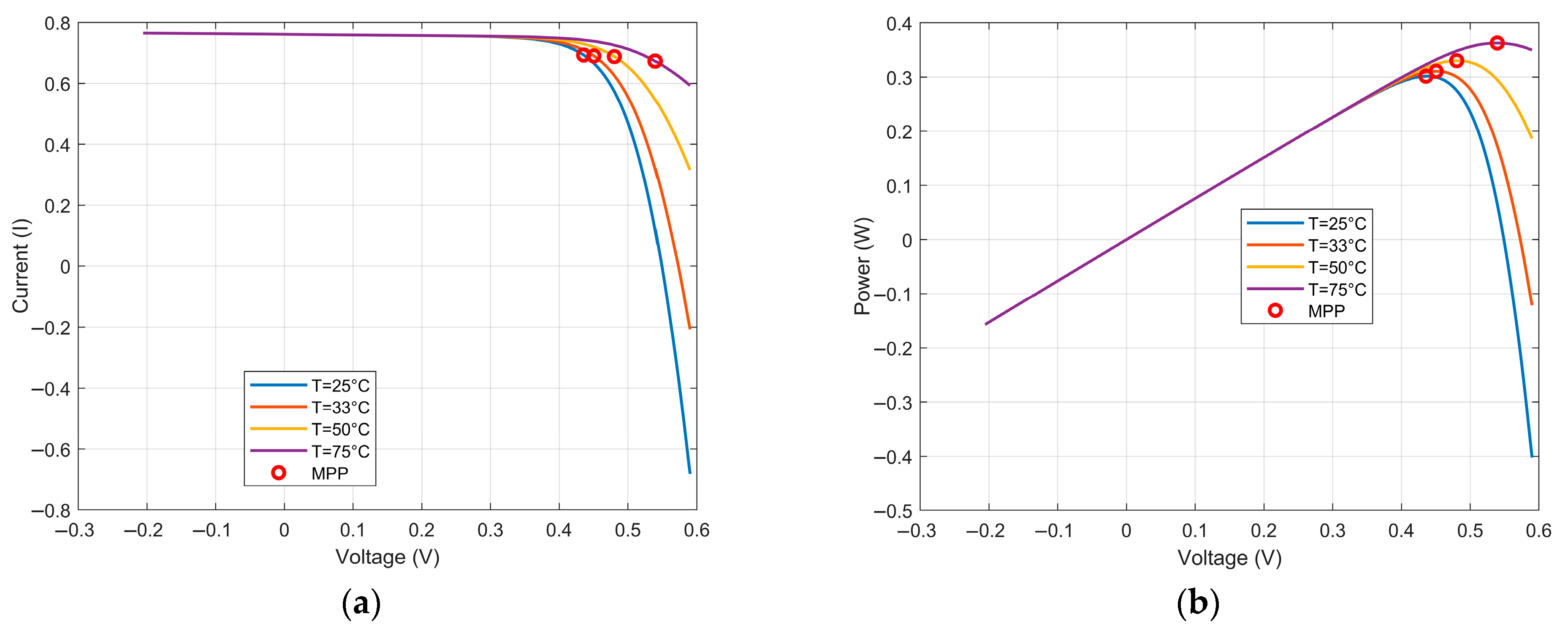
3.1. SDM
3.2. Double Diode Model
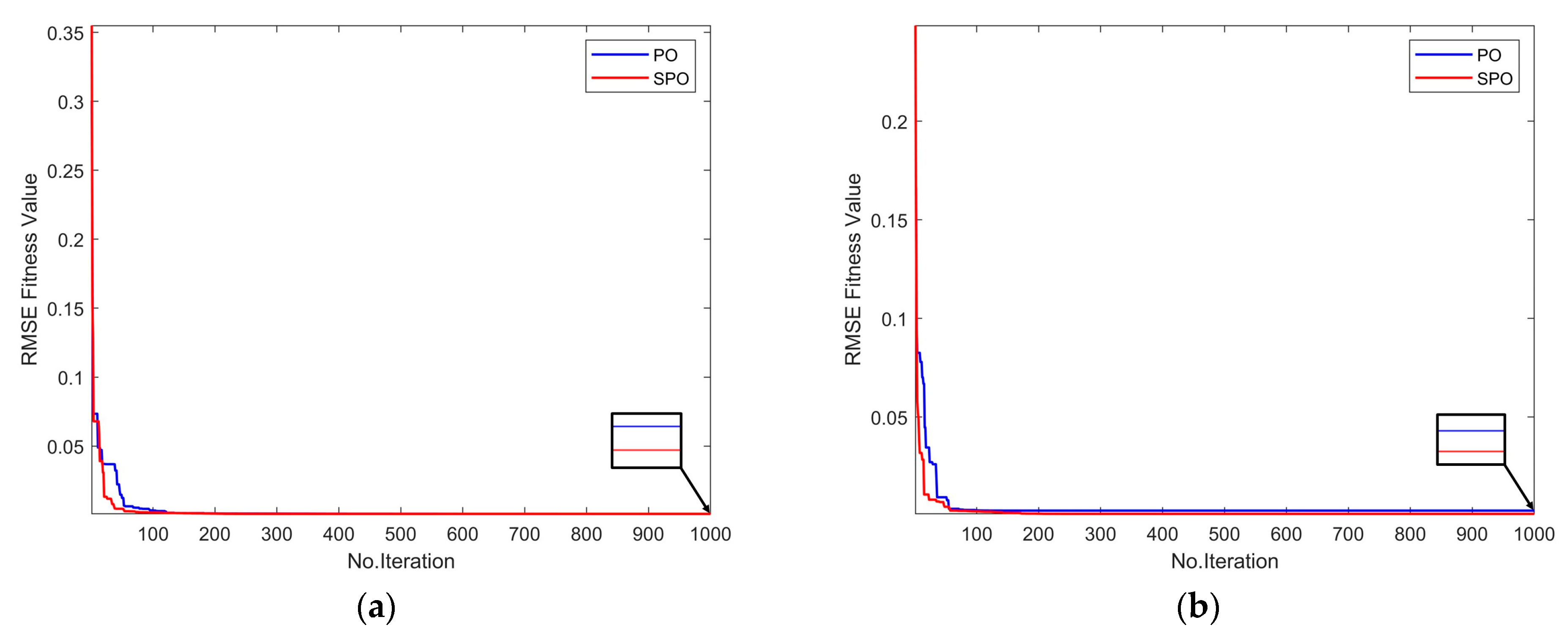
3.3. Triple Diode Model
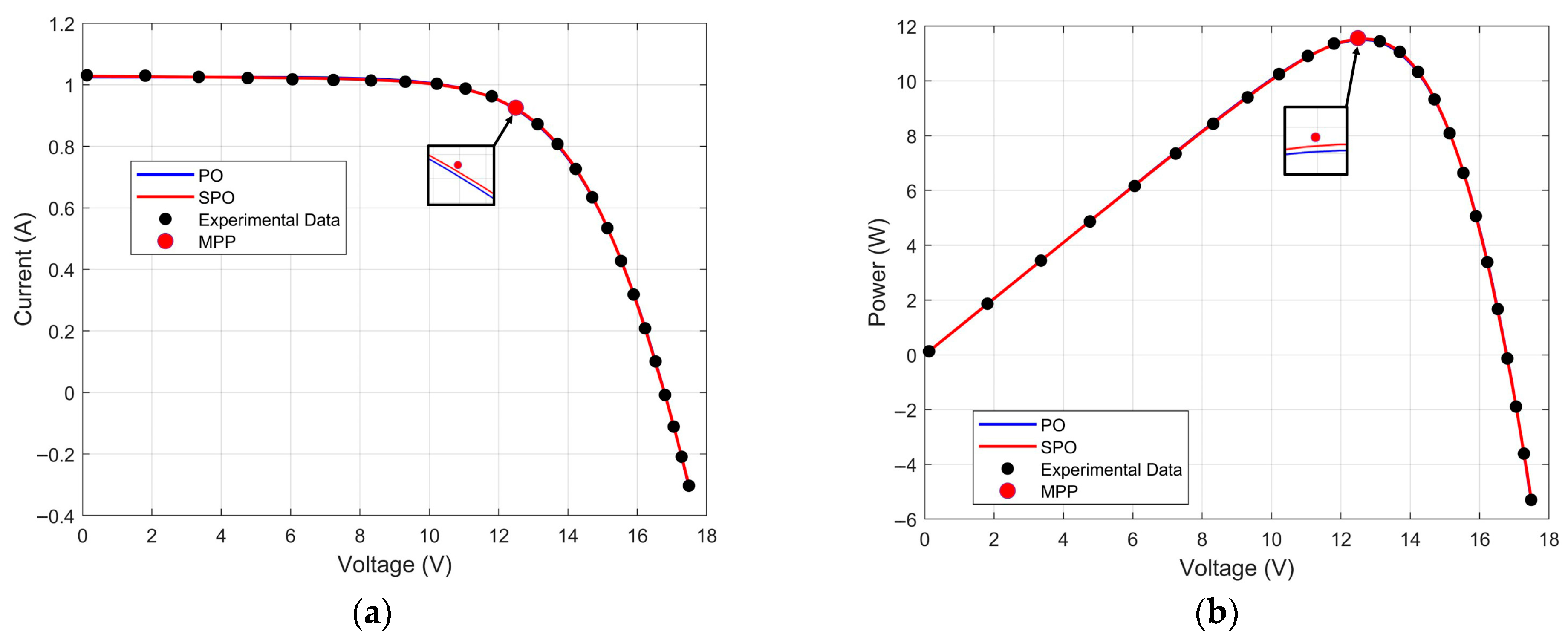
3.4. Photovolataic Module Model
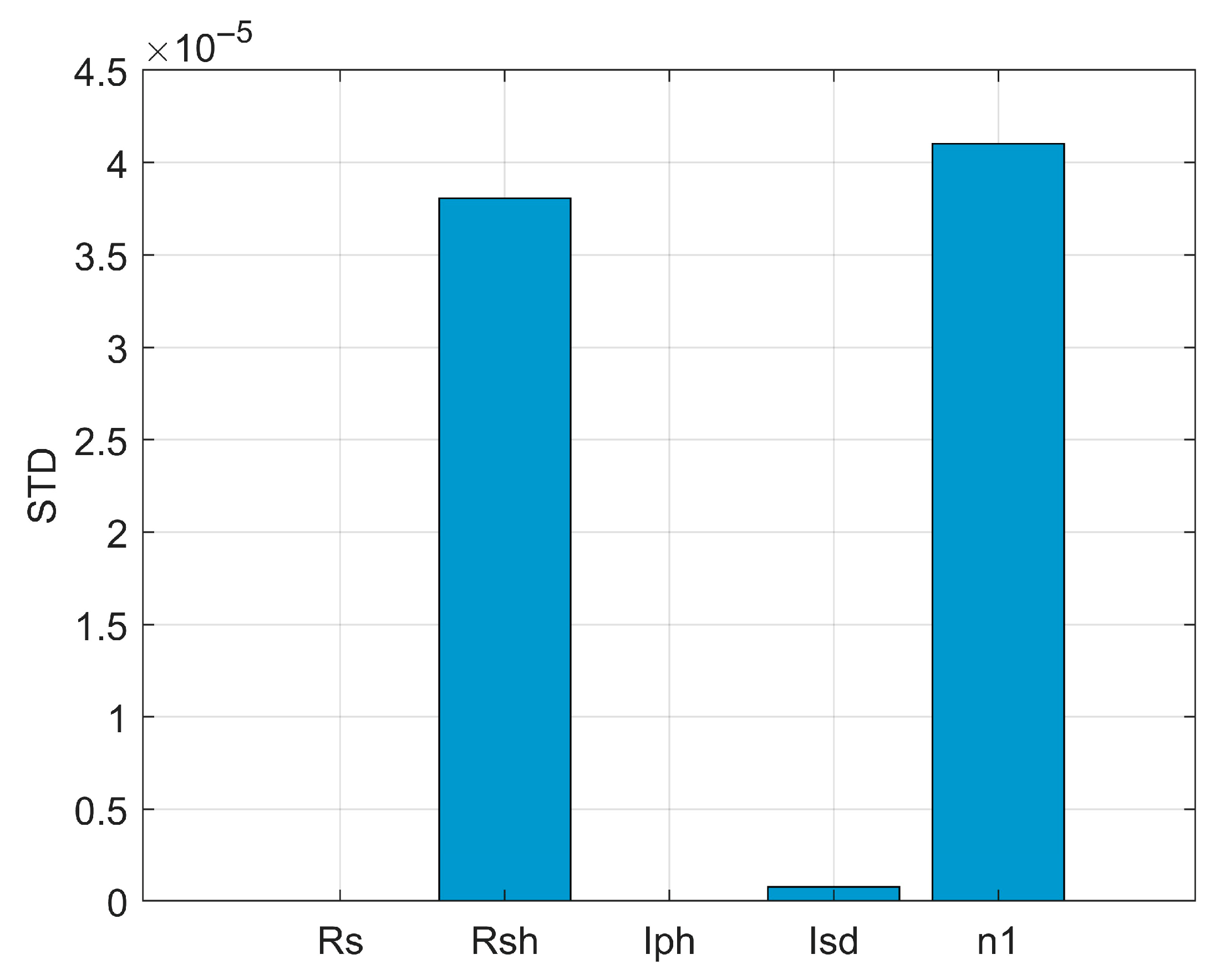
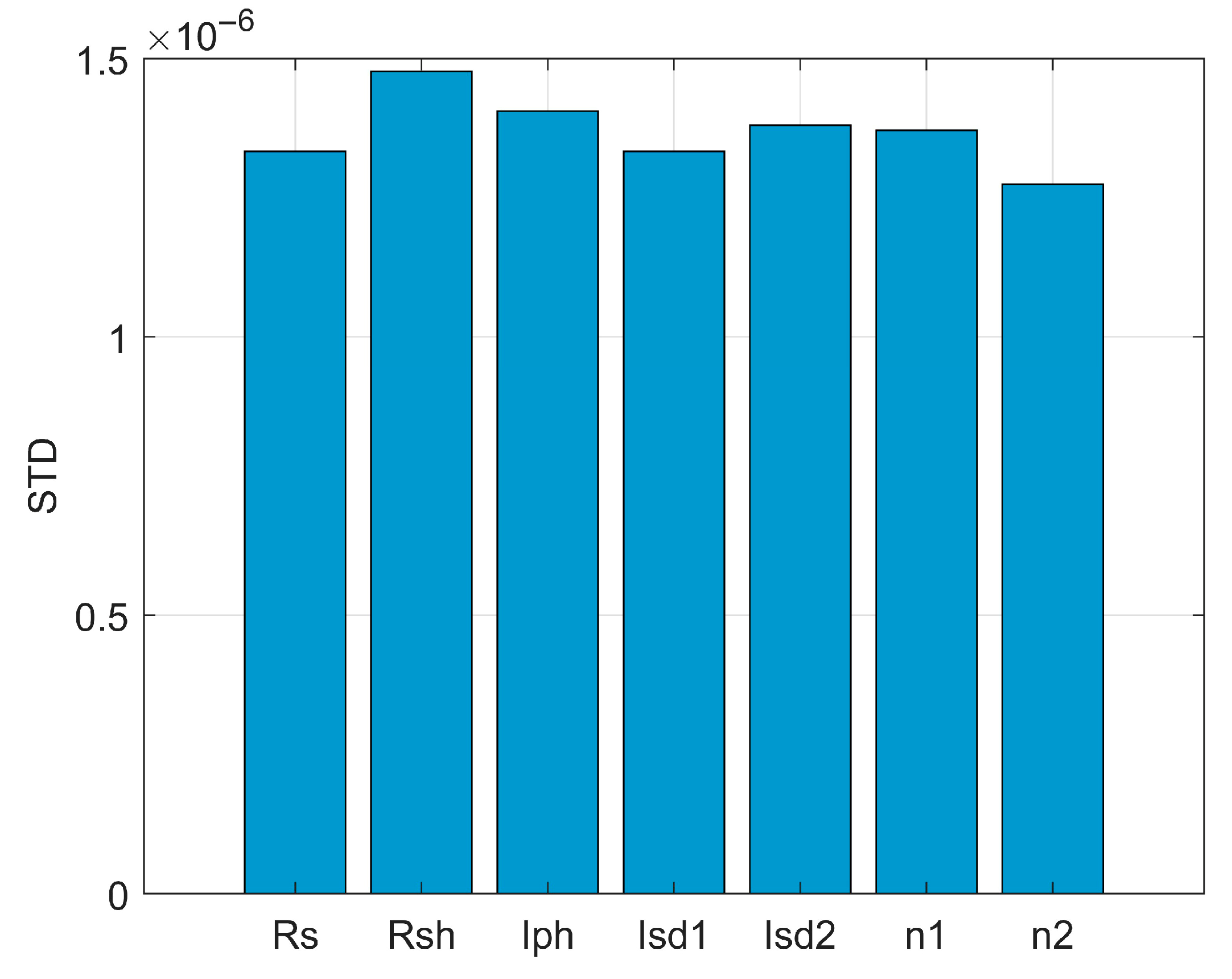
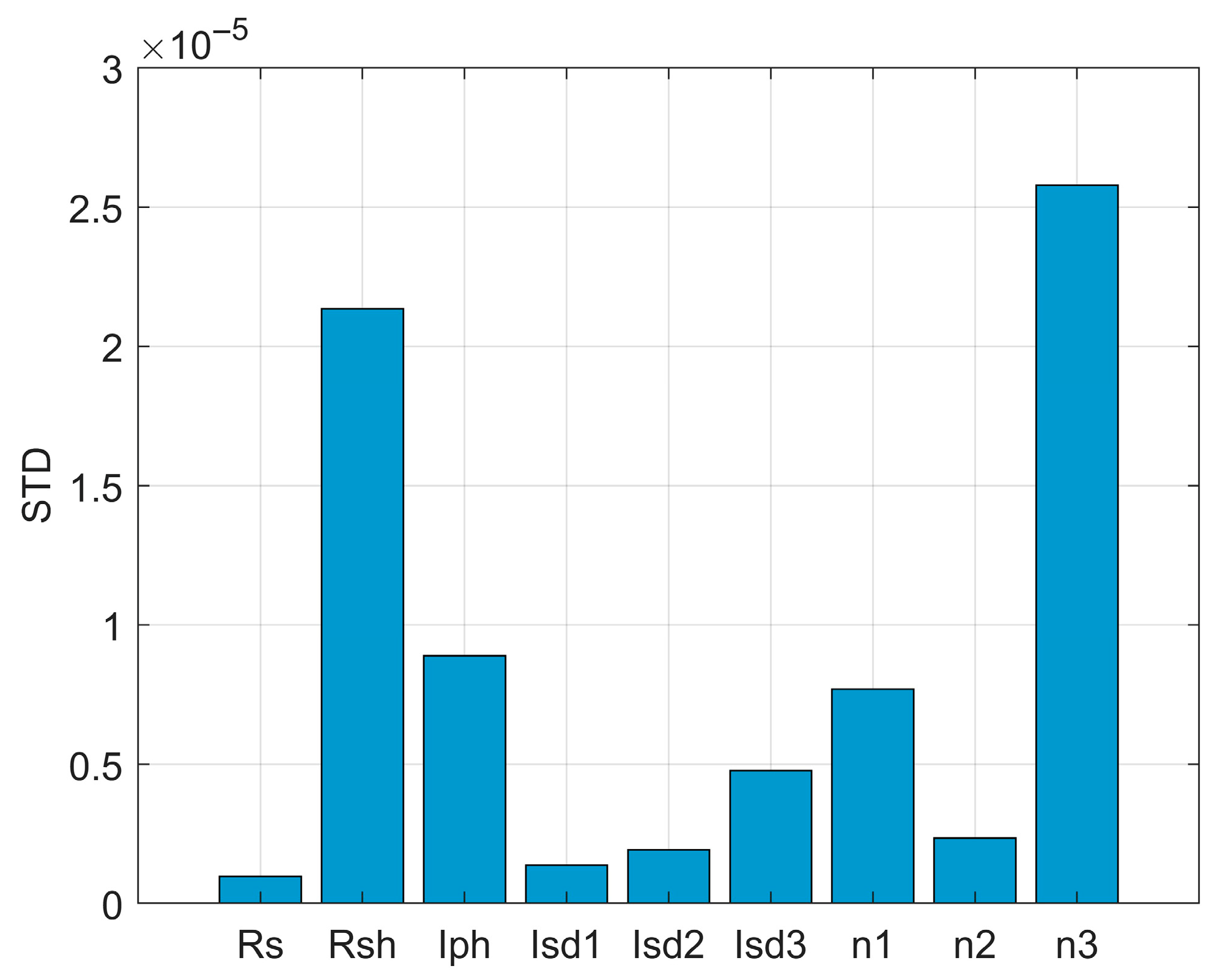
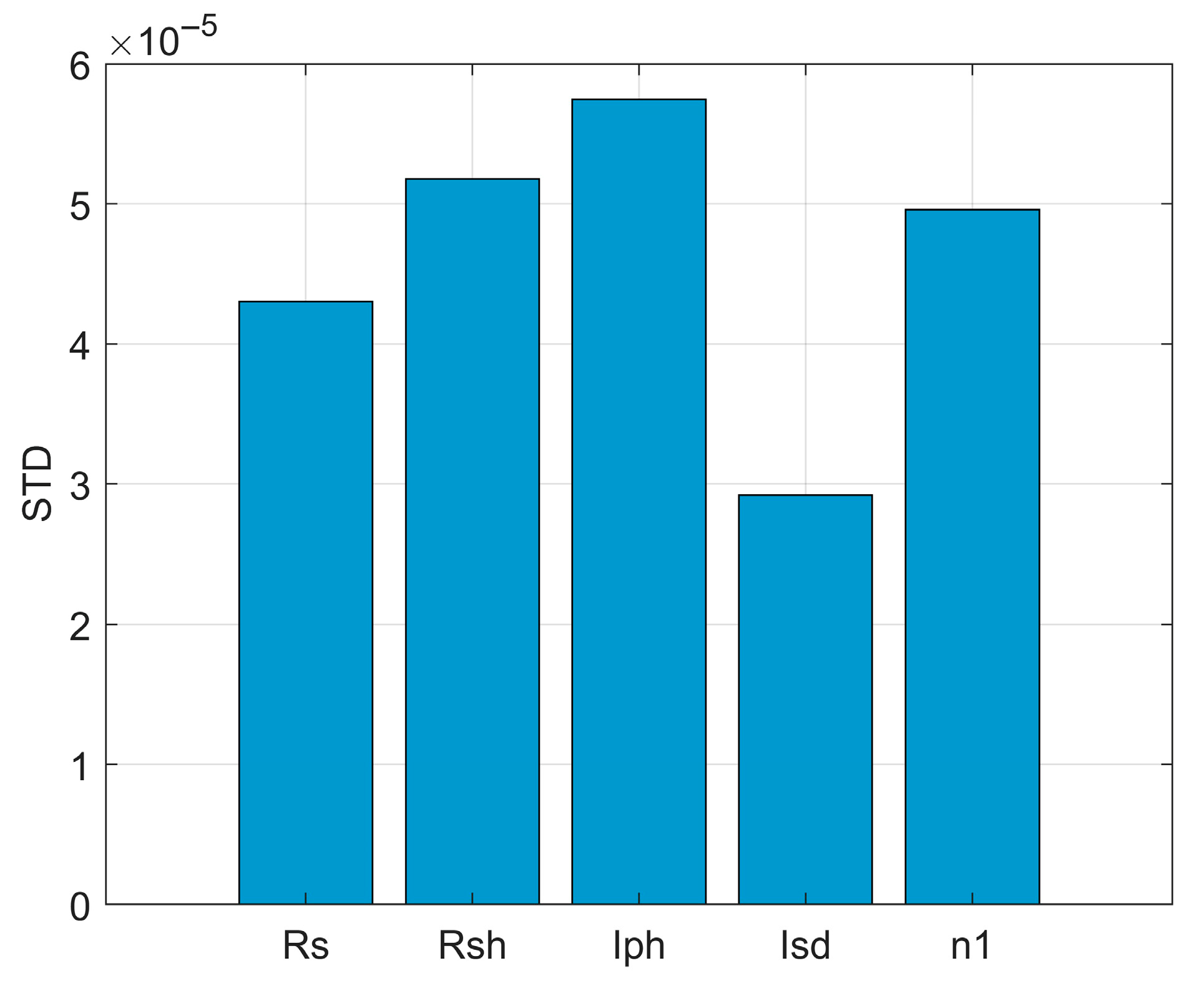
3.5. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Küfeoğlu, S. Net Zero: Decarbonizing the Global Economies; Springer Nature: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Liu, Y.; Ding, K.; Zhang, J.; Li, Y.; Yang, Z.; Zheng, W.; Chen, X. Fault diagnosis approach for photovoltaic array based on the stacked auto-encoder and clustering with IV curves. Energy Convers. Manag. 2021, 245, 114603. [Google Scholar] [CrossRef]
- Fahim, S.R.; Hasanien, H.M.; Turky, R.A.; Aleem, S.H.A.; Ćalasan, M. A comprehensive review of photovoltaic modules models and algorithms used in parameter extraction. Energies 2022, 15, 8941. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Zhang, X.; Yu, T.; Yao, W.; Shu, H.; Zeng, F.; Sun, L. Comprehensive overview of meta-heuristic algorithm applications on PV cell parameter identification. Energy Convers. Manag. 2020, 208, 112595. [Google Scholar] [CrossRef]
- Reis, L.; Camacho, J.R.; Novacki, D. The Newton Raphson method in the extraction of parameters of PV modules. Renew. Energy Power Qual. J. 2017, 1, 634–639. [Google Scholar]
- Et-Torabi, K.; Nassar-Eddine, I.; Obbadi, A.; Errami, Y.; Rmaily, R.; Sahnoun, S.; Agunaou, M. Parameters estimation of the single and double diode photovoltaic models using a Gauss–Seidel algorithm and analytical method: A comparative study. Energy Convers. Manag. 2017, 148, 1041–1054. [Google Scholar] [CrossRef]
- Maouhoub, N. Photovoltaic module parameter estimation using an analytical approach and least squares method. J. Comput. Electron. 2018, 17, 784–790. [Google Scholar] [CrossRef]
- Di Piazza, M.C.; Luna, M.; Vitale, G. Dynamic PV model parameter identification by least-squares regression. IEEE J. Photovolt. 2013, 3, 799–806. [Google Scholar] [CrossRef]
- Toledo, F.J.; Galiano, V.; Herranz, V.; Blanes, J.M. Efficient computation of the photovoltaic single-diode model curve by means of a piecewise linear self-adaptive representation. J. Comput. Sci. 2024, 75, 102199. [Google Scholar] [CrossRef]
- Rezk, H.; Olabi, A.; Wilberforce, T.; Sayed, E.T. A comprehensive review and application of metaheuristics in solving the optimal parameter identification problems. Sustainability 2023, 15, 5732. [Google Scholar] [CrossRef]
- Houssein, E.H.; Zaki, G.N.; Abualigah, L.; Younis, E.M. Metaheuristics for parameter estimation of solar photovoltaic cells: A comprehensive review. In Integrating Meta-Heuristics and Machine Learning for Real-World Optimization Problems; Springer Nature: Berlin/Heidelberg, Germany, 2022; pp. 149–179. [Google Scholar]
- Yesilbudak, M. A comparative study on accurate parameter estimation of solar photovoltaic models using metaheuristic optimization algorithms. Electr. Power Compon. Syst. 2024, 52, 1001–1021. [Google Scholar] [CrossRef]
- Fathi, H.; Alsekait, D.M.; Tawil, A.A.; Kamal, I.W.; Aloun, M.S.; Manhrawy, I.I. Enhancing sustainability in renewable energy: Comparative analysis of optimization algorithms for accurate pv parameter estimation. Sustainability 2025, 17, 2718. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 2002, 1, 67–82. [Google Scholar] [CrossRef]
- Gao, S.; Wang, K.; Tao, S.; Jin, T.; Dai, H.; Cheng, J. A state-of-the-art differential evolution algorithm for parameter estimation of solar photovoltaic models. Energy Convers. Manag. 2021, 230, 113784. [Google Scholar] [CrossRef]
- Liu, E.-J.; Hung, Y.-H.; Hong, C.-W. Improved metaheuristic optimization algorithm applied to hydrogen fuel cell and photovoltaic cell parameter extraction. Energies 2021, 14, 619. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Shi, D.; He, Y. Parameter extraction of solar photovoltaic models using an improved whale optimization algorithm. Energy Convers. Manag. 2018, 174, 388–405. [Google Scholar] [CrossRef]
- Rawat, N.; Thakur, P.; Singh, A.K.; Bhatt, A.; Sangwan, V.; Manivannan, A. A new grey wolf optimization-based parameter estimation technique of solar photovoltaic. Sustain. Energy Technol. Assess. 2023, 57, 103240. [Google Scholar] [CrossRef]
- Lei, W.; He, Q.; Yang, L.; Jiao, H. Solar photovoltaic cell parameter identification based on improved honey badger algorithm. Sustainability 2022, 14, 8897. [Google Scholar] [CrossRef]
- Elshara, R.; Hançerlioğullari, A.; Rahebi, J.; Lopez-Guede, J.M. PV cells and modules parameter estimation using coati optimization algorithm. Energies 2024, 17, 1716. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Khodadadi, N.; Barshandeh, S.; Trojovský, P.; Gharehchopogh, F.S.; El-kenawy, E.-S.M.; Abualigah, L.; Mirjalili, S. Puma optimizer (PO): A novel metaheuristic optimization algorithm and its application in machine learning. Clust. Comput. 2024, 27, 5235–5283. [Google Scholar] [CrossRef]
- Easwarakhanthan, T.; Bottin, J.; Bouhouch, I.; Boutrit, C. Nonlinear minimization algorithm for determining the solar cell parameters with microcomputers. Int. J. Sol. Energy 1986, 4, 1–12. [Google Scholar] [CrossRef]
- Bouali, Y.; Alamri, B. Parameter Extraction for Photovoltaic Models with Flood-Algorithm-Based Optimization. Mathematics 2024, 13, 19. [Google Scholar] [CrossRef]
- Qaraad, M.; Amjad, S.; Hussein, N.K.; Farag, M.; Mirjalili, S.; Elhosseini, M.A. Quadratic interpolation and a new local search approach to improve particle swarm optimization: Solar photovoltaic parameter estimation. Expert Syst. Appl. 2024, 236, 121417. [Google Scholar] [CrossRef]
- Yuan, S.; Ji, Y.; Chen, Y.; Liu, X.; Zhang, W. An improved differential evolution for parameter identification of photovoltaic models. Sustainability 2023, 15, 13916. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, S.; Ouyang, H.; Li, S.; Wang, G.-g. Hybrid multi-group stochastic cooperative particle swarm optimization algorithm and its application to the photovoltaic parameter identification problem. Energy Rep. 2023, 9, 4654–4681. [Google Scholar] [CrossRef]
- Kullampalayam Murugaiyan, N.; Chandrasekaran, K.; Manoharan, P.; Derebew, B. Leveraging opposition-based learning for solar photovoltaic model parameter estimation with exponential distribution optimization algorithm. Sci. Rep. 2024, 14, 528. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Kuang, F.; Yu, S.; Cai, Z.; Chen, H. Static photovoltaic models’ parameter extraction using reinforcement learning strategy adapted local gradient Nelder-Mead Runge Kutta method. Appl. Intell. 2023, 53, 24106–24141. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Elavarasan, R.M.; Sowmya, R. Opposition decided gradient-based optimizer with balance analysis and diversity maintenance for parameter identification of solar photovoltaic models. J. Ambient. Intell. Humaniz. Comput. 2023, 14, 7109–7131. [Google Scholar] [CrossRef]
- Izci, D.; Ekinci, S.; Ma’arif, A. Parameter Extraction of Triple-diode Photovoltaic Model via RIME Optimizer with Neighborhood Centroid Opposite Solution. J. Robot. Control. (JRC) 2024, 5, 1098–1103. [Google Scholar]
- Arıkan, B.; Koçkanat, S. Estimation and Analysis of the Characteristic Parameters of Photovoltaic Cells by Mayfly Algorithm. Avrupa Bilim Ve Teknol. Derg. 2022, 33, 223–235. [Google Scholar] [CrossRef]
- Ji, Y.; Yuan, S.; Zhang, W.; Chen, Y.; Liu, X. Parameters Estimation of Photovoltaic Models via an Improved Differential Evolution Algorithm. In Proceedings of the 4th International Conference on Artificial Intelligence and Computer Engineering, Dalian, China, 17–19 November 2023; pp. 9–16. [Google Scholar]
- Temurtaş, H.; Yavuz, G.; Özyön, S.; Ünlü, A. Estimating equivalent circuit parameters in various photovoltaic models and modules using the dingo optimization algorithm. J. Comput. Electron. 2024, 23, 1049–1090. [Google Scholar] [CrossRef]
- İzCi, D.; EkinCi, S.; Güleydin, M. Improved reptile search algorithm for optimal design of solar photovoltaic module. Comput. Sci. 2023, 172–179. [Google Scholar] [CrossRef]
- Yu, X.; Duan, Y.; Cai, Z. Sub-population improved grey wolf optimizer with Gaussian mutation and Lévy flight for parameters identification of photovoltaic models. Expert Syst. Appl. 2023, 232, 120827. [Google Scholar] [CrossRef]
- Zhou, T.t.; Shang, C. Parameter identification of solar photovoltaic models by multi strategy sine–cosine algorithm. Energy Sci. Eng. 2024, 12, 1422–1445. [Google Scholar] [CrossRef]
- Słowik, A.; Cpałka, K.; Xue, Y.; Hapka, A. An efficient approach to parameter extraction of photovoltaic cell models using a new population-based algorithm. Appl. Energy 2024, 364, 123208. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, Z.; Mohamed, A.W. A novel hybrid algorithm based on improved marine predators algorithm and equilibrium optimizer for parameter extraction of solar photovoltaic models. Heliyon 2024, 10, e38412. [Google Scholar] [CrossRef] [PubMed]



| Function | Parameter Vector |
|---|---|
| ] | |
| ] | |
| ] | |
| ] |
| SDM, DDM, TDM | |||||
|---|---|---|---|---|---|
| Parameter | Range | Parameter | Range | ||
| 1 | Iph (A) | [0, 1] | 6 | Isd2 (μA) | [0, 1] |
| 2 | Rs (Ω) | [0, 0.5] | 7 | n2 | [1, 2] |
| 3 | Rsh (Ω) | [0, 100] | 8 | Isd3 (μA) | [0, 1] |
| 4 | Isd1 (μA) | [0, 1] | 9 | n3 | [1, 2] |
| 5 | n1 | [1, 2] | - | - | - |
| PMM | |||||
| 1 | Iph (A) | [0, 2] | 4 | Isd1 (μA) | [0, 50] |
| 2 | Rs (Ω) | [0, 2] | 5 | n1 | [1, 50] |
| 3 | Rsh (Ω) | [0, 2000] | - | - | - |
| Algorithm Setting | |
|---|---|
| Independent run time | 30 |
| Population size | 30 |
| Iteration time | 1000 |
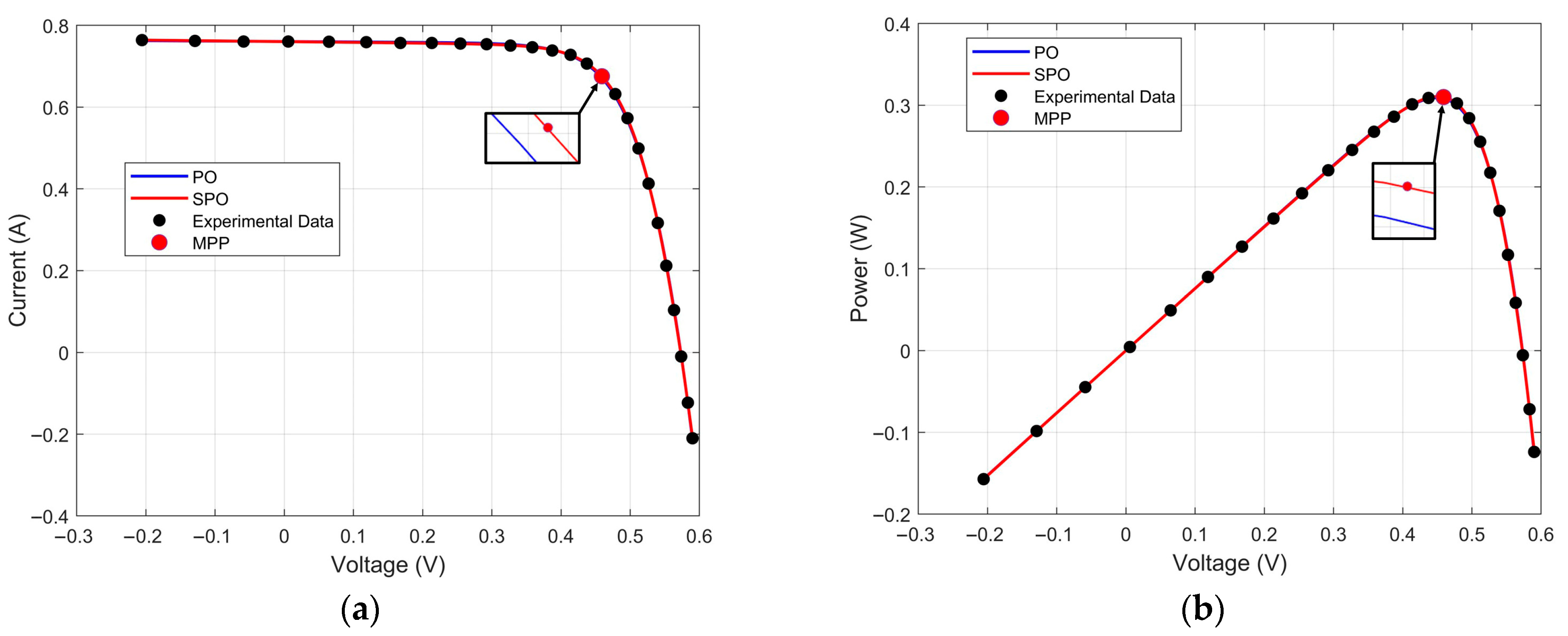
| Experimental Data [22] | SPO | PO | |
|---|---|---|---|
| Vt (V) | It (A) | Computed It (A) | |
| −0.2057 | 0.764 | 0.764221 | 0.763816 |
| −0.1291 | 0.762 | 0.762752 | 0.762509 |
| −0.0588 | 0.7605 | 0.761404 | 0.761308 |
| 0.0057 | 0.7605 | 0.760166 | 0.760206 |
| 0.0646 | 0.76 | 0.759033 | 0.759197 |
| 0.1185 | 0.759 | 0.75799 | 0.758265 |
| 0.1678 | 0.757 | 0.757013 | 0.757385 |
| 0.2132 | 0.757 | 0.756041 | 0.756493 |
| 0.2545 | 0.7555 | 0.754973 | 0.755477 |
| 0.2924 | 0.754 | 0.753549 | 0.754059 |
| 0.3269 | 0.7505 | 0.751295 | 0.751743 |
| 0.3585 | 0.7465 | 0.747302 | 0.747593 |
| 0.3873 | 0.7385 | 0.740135 | 0.740164 |
| 0.4137 | 0.728 | 0.727489 | 0.72716 |
| 0.4373 | 0.7065 | 0.707163 | 0.706447 |
| 0.459 | 0.6755 | 0.675516 | 0.67448 |
| 0.4784 | 0.632 | 0.630965 | 0.629802 |
| 0.496 | 0.573 | 0.572026 | 0.570992 |
| 0.5119 | 0.499 | 0.499543 | 0.498877 |
| 0.5265 | 0.413 | 0.41341 | 0.413295 |
| 0.5398 | 0.3165 | 0.317167 | 0.317613 |
| 0.5521 | 0.212 | 0.211844 | 0.212718 |
| 0.5633 | 0.1035 | 0.102174 | 0.103172 |
| 0.5736 | −0.01 | −0.00828 | −0.00768 |
| 0.5833 | −0.123 | −0.12431 | −0.1245 |
| 0.59 | −0.21 | −0.20647 | −0.20777 |
| RMSE | |||
| PARAM/ALGO | FLA [23] | QPSOL [24] | DODE [25] | HMSCPSO [26] | OBEDO [27] | RLGNMRUN [28] | OBGOA [29] | PO | SPO |
|---|---|---|---|---|---|---|---|---|---|
| Rs (Ω) | 0.036377 | 0.03637709 | 0.036377093 | 0.0364 | 0.0364 | 0.0356 | 0.0370 | ||
| Rsh (Ω) | 53.7189 | 53.71852345 | 53.71852054 | 53.7185 | 53.72 | 58.5336 | 52.1064 | ||
| Iph (A) | 0.76078 | 0.76077553 | 0.760775531 | 0.7608 | 0.7608 | 0.7608 | 0.7608 | ||
| Isd1 (μA) | 0.32302 | 0.32302080 | 0.3991 | 0.2918 | |||||
| n1 | 1.4812 | 1.48118360 | 1.48118358 | 1.481183588 | 1.4812 | 1.481 | 1.4812 | 1.5042 | 1.4723 |
| Best | |||||||||
| Mean | 8.8180 | ||||||||
| Std. |
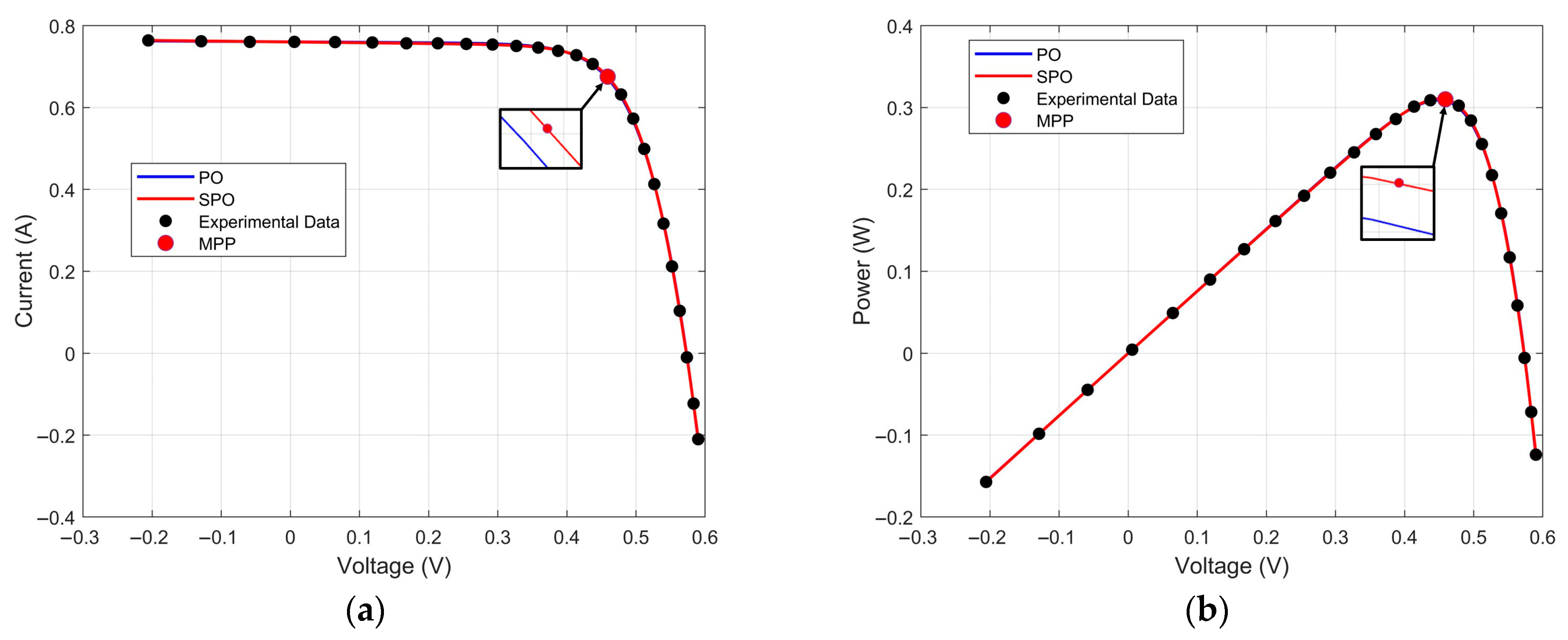
| Experimental Data [22] | SPO | PO | |
|---|---|---|---|
| Vt (V) | It (A) | Computed It (A) | |
| −0.2057 | 0.764 | 0.764104 | 0.762619 |
| −0.1291 | 0.762 | 0.762678 | 0.761854 |
| −0.0588 | 0.7605 | 0.761368 | 0.761151 |
| 0.0057 | 0.7605 | 0.760164 | 0.760504 |
| 0.0646 | 0.76 | 0.759063 | 0.759909 |
| 0.1185 | 0.759 | 0.758046 | 0.75935 |
| 0.1678 | 0.757 | 0.757089 | 0.758794 |
| 0.2132 | 0.757 | 0.756129 | 0.758162 |
| 0.2545 | 0.7555 | 0.755059 | 0.757305 |
| 0.2924 | 0.754 | 0.753617 | 0.755893 |
| 0.3269 | 0.7505 | 0.751327 | 0.753357 |
| 0.3585 | 0.7465 | 0.747286 | 0.748696 |
| 0.3873 | 0.7385 | 0.740071 | 0.740431 |
| 0.4137 | 0.728 | 0.72739 | 0.726323 |
| 0.4373 | 0.7065 | 0.707058 | 0.704452 |
| 0.459 | 0.6755 | 0.675437 | 0.671549 |
| 0.4784 | 0.632 | 0.630935 | 0.62651 |
| 0.496 | 0.573 | 0.572046 | 0.568077 |
| 0.5119 | 0.499 | 0.499596 | 0.497005 |
| 0.5265 | 0.413 | 0.413466 | 0.412962 |
| 0.5398 | 0.3165 | 0.3172 | 0.31882 |
| 0.5521 | 0.212 | 0.211837 | 0.215068 |
| 0.5633 | 0.1035 | 0.102132 | 0.105784 |
| 0.5736 | −0.01 | −0.0083 | −0.00632 |
| 0.5833 | −0.123 | −0.12432 | −0.12551 |
| 0.59 | −0.21 | −0.20638 | −0.21211 |
| RMSE | |||
| PARAM/ALGO | FLA [23] | QPSOL [24] | DODE [25] | HMSCPSO [26] | OBEDO [27] | RLGNMRUN [28] | OBGOA [29] | PO | SPO |
|---|---|---|---|---|---|---|---|---|---|
| Rs (Ω) | 0.036739 | 0.03674043 | 0.036754273 | 0.0367 | 0.0368 | 0.0314 | 0.0372 | ||
| Rsh (Ω) | 55.477 | 1.99999179 | 55.48544435 | 55.5555001 | 55.3995 | 55.8326 | 100 | 53.6401 | |
| Iph (A) | 0.76078 | 0.76078107 | 0.76078126 | 0.7608 | 0.7608 | 0.7608 | 0.7608 | ||
| Isd1 (μA) | 0.22635 | 0.74934831 | 1 | 0.1871 | |||||
| Isd2 (μA) | 0.74607 | 0.22597418 | 0 | 0.3718 | |||||
| n1 | 1.4512 | 2.00000000 | 2 | 1.4529 | 1.448 | 1.4489 | 1.6059 | 1.4385 | |
| n2 | 2 | 1.45114969 | 1.45101673 | 1.44988432 | 2.0000 | 1.999 | 2.0000 | 1.7440 | 1.7895 |
| Best | |||||||||
| Mean | |||||||||
| Std. |
| Experimental Data [22] | SPO | PO | |
|---|---|---|---|
| Vt (V) | It (A) | Computed It (A) | |
| −0.2057 | 0.764 | 0.764211 | 0.76265 |
| −0.1291 | 0.762 | 0.762749 | 0.761884 |
| −0.0588 | 0.7605 | 0.761407 | 0.761182 |
| 0.0057 | 0.7605 | 0.760174 | 0.760535 |
| 0.0646 | 0.76 | 0.759047 | 0.75994 |
| 0.1185 | 0.759 | 0.758008 | 0.759381 |
| 0.1678 | 0.757 | 0.757034 | 0.758825 |
| 0.2132 | 0.757 | 0.756065 | 0.758194 |
| 0.2545 | 0.7555 | 0.754997 | 0.757337 |
| 0.2924 | 0.754 | 0.75357 | 0.755926 |
| 0.3269 | 0.7505 | 0.751308 | 0.753393 |
| 0.3585 | 0.7465 | 0.747304 | 0.748735 |
| 0.3873 | 0.7385 | 0.740124 | 0.740473 |
| 0.4137 | 0.728 | 0.727463 | 0.726369 |
| 0.4373 | 0.7065 | 0.707128 | 0.704499 |
| 0.459 | 0.6755 | 0.675479 | 0.671595 |
| 0.4784 | 0.632 | 0.630936 | 0.62655 |
| 0.496 | 0.573 | 0.57201 | 0.568107 |
| 0.5119 | 0.499 | 0.499543 | 0.497028 |
| 0.5265 | 0.413 | 0.413424 | 0.412982 |
| 0.5398 | 0.3165 | 0.317189 | 0.318851 |
| 0.5521 | 0.212 | 0.211866 | 0.215129 |
| 0.5633 | 0.1035 | 0.102191 | 0.105897 |
| 0.5736 | −0.01 | −0.00827 | −0.00612 |
| 0.5833 | −0.123 | −0.12432 | −0.12521 |
| 0.59 | −0.21 | −0.20648 | −0.21171 |
| RMSE | |||
| PARAM/ALGO | FLA [23] | DODE [25] | HMSCPSO [26] | OBEDO [27] | RLGNMRUN [28] | NCO-RIME [30] | PO | SPO |
|---|---|---|---|---|---|---|---|---|
| Rs (Ω) | 0.036736 | 0.03674042 | 0.03673646 | 0.0367 | 0.036728 | 0.0314 | 0.0370 | |
| Rsh (Ω) | 55.752 | 55.48544324 | 55.45775792 | 55.7780 | 55.36 | 100 | 52.3502 | |
| Iph (A) | 0.76078 | 0.76078107 | 0.76078168 | 0.7608 | 0.76078 | 0.7608 | 0.7608 | |
| Isd1 (μA) | 0.37926 | 0.22597432 | 0.37909 | 0.9938 | 0.0170 | |||
| Isd2 (μA) | 0.23913 | 0.25789585 | 0.22898 | 0.0065 | ||||
| Isd3 (μA) | 1 | 0.49145138 | 0.34284 | 0.2850 | ||||
| n1 | 1.9999 | 1.45101678 | 1.99999989 | 1.9995 | 1.594 | 2 | 1.6052 | 1.5409 |
| n2 | 1.4551 | 2.00000000 | 1.45134072 | 1.4537 | 1.999 | 1.4521 | 2.0000 | 1.3433 |
| n3 | 2.3982 | 2.00000000 | 1.99999989 | 2.7316 | 1.452 | 2 | 1.9858 | 1.4845 |
| Best | ||||||||
| Mean | ||||||||
| Std. |
| Experimental Data [22] | SPO | PO | |
|---|---|---|---|
| Vt (V) | It (A) | Computed It (A) | |
| 0.1248 | 1.0315 | 1.028621 | 1.025411 |
| 1.8093 | 1.03 | 1.027049 | 1.025334 |
| 3.3511 | 1.026 | 1.025561 | 1.025182 |
| 4.7622 | 1.022 | 1.02406 | 1.024843 |
| 6.0538 | 1.018 | 1.022359 | 1.024087 |
| 7.2364 | 1.0155 | 1.020089 | 1.022484 |
| 8.3189 | 1.014 | 1.016583 | 1.019281 |
| 9.3097 | 1.01 | 1.010738 | 1.013293 |
| 10.2163 | 1.0035 | 1.000848 | 1.002775 |
| 11.0449 | 0.988 | 0.984698 | 0.985561 |
| 11.8018 | 0.963 | 0.959565 | 0.9591 |
| 12.4929 | 0.9255 | 0.922755 | 0.920988 |
| 13.1231 | 0.8725 | 0.872394 | 0.869663 |
| 13.6983 | 0.8075 | 0.806978 | 0.803917 |
| 14.2221 | 0.7265 | 0.727998 | 0.725269 |
| 14.6995 | 0.6345 | 0.636812 | 0.635023 |
| 15.1346 | 0.5345 | 0.535951 | 0.535496 |
| 15.5311 | 0.4275 | 0.429348 | 0.430223 |
| 15.8929 | 0.3185 | 0.318733 | 0.320777 |
| 16.2229 | 0.2085 | 0.207475 | 0.210208 |
| 16.5241 | 0.101 | 0.096381 | 0.099323 |
| 16.7987 | −0.008 | −0.00803 | −0.00603 |
| 17.0499 | −0.111 | −0.11056 | −0.10996 |
| 17.2793 | −0.209 | −0.20881 | −0.21022 |
| 17.4885 | −0.303 | −0.3004 | −0.30456 |
| RMSE | |||
| PARAM/ALGO | MA [31] | DPDE-SIRM [32] | DOA [33] | RSALF [34] | SPGWO [35] | ESCA [36] | μAFCSO [37] | IMPAEO [38] | PO | SPO |
|---|---|---|---|---|---|---|---|---|---|---|
| Rs (Ω) | 1.2013 | 0.0334 | 1.2013 | 1.2012710 | 1.20127101 | 0.03337 | 1.20127 | 0.0308 | 0.0333 | |
| Rsh (Ω) | 981.9870 | 27.2773 | 981.98 | 981.9822009 | 981.98230604 | 27.27673 | 981.98238 | 1450.9807 | 30.2393 | |
| Iph (A) | 1.0305 | 1.0305 | 1.030362 | 1.0305 | 1.0305143 | 1.03051430 | 1.03051 | 1.03051 | 1.0254 | 1.0299 |
| Isd1 (μA) | 3.4823 | 3.4823 | 3.4823 | 3.48226293 | 3.48211 | 3.48226 | 8.0327 | 3.6837 | ||
| n1 | 48.6428 | 1.3512 | 1.354652 | 48.643 | 48.6428346 | 48.64283488 | 1.35118 | 48.64284 | 1.4473 | 1.3583 |
| Best | ||||||||||
| Mean | ||||||||||
| Std. |
| PV Model | Algorithm | Exploration (%) | Exploitation (%) | Total Iteration |
|---|---|---|---|---|
| SDM | SPO | 62.09 | 37.91 | 1000 |
| PO | 57.17 | 42.83 | 1000 | |
| DDM | SPO | 73.72 | 26.28 | 1000 |
| PO | 52.06 | 47.94 | 1000 | |
| TDM | SPO | 71.82 | 28.18 | 1000 |
| PO | 50.05 | 49.95 | 1000 | |
| PMM | SPO | 70.21 | 29.79 | 1000 |
| PO | 53.46 | 46.54 | 1000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, E.-J.; Chen, R.-W.; Wang, Q.-A.; Lu, W.-L. Shuffled Puma Optimizer for Parameter Extraction and Sensitivity Analysis in Photovoltaic Models. Energies 2025, 18, 4008. https://doi.org/10.3390/en18154008
Liu E-J, Chen R-W, Wang Q-A, Lu W-L. Shuffled Puma Optimizer for Parameter Extraction and Sensitivity Analysis in Photovoltaic Models. Energies. 2025; 18(15):4008. https://doi.org/10.3390/en18154008
Chicago/Turabian StyleLiu, En-Jui, Rou-Wen Chen, Qing-An Wang, and Wan-Ling Lu. 2025. "Shuffled Puma Optimizer for Parameter Extraction and Sensitivity Analysis in Photovoltaic Models" Energies 18, no. 15: 4008. https://doi.org/10.3390/en18154008
APA StyleLiu, E.-J., Chen, R.-W., Wang, Q.-A., & Lu, W.-L. (2025). Shuffled Puma Optimizer for Parameter Extraction and Sensitivity Analysis in Photovoltaic Models. Energies, 18(15), 4008. https://doi.org/10.3390/en18154008






