Multi-Criteria Optimization and Techno-Economic Assessment of a Wind–Solar–Hydrogen Hybrid System for a Plateau Tourist City Using HOMER and Shannon Entropy-EDAS Models
Abstract
1. Introduction
2. Geographical Location and Meteorological Data
2.1. Selection of the Study Area
2.2. Introduction to Load Demand in the Study Area
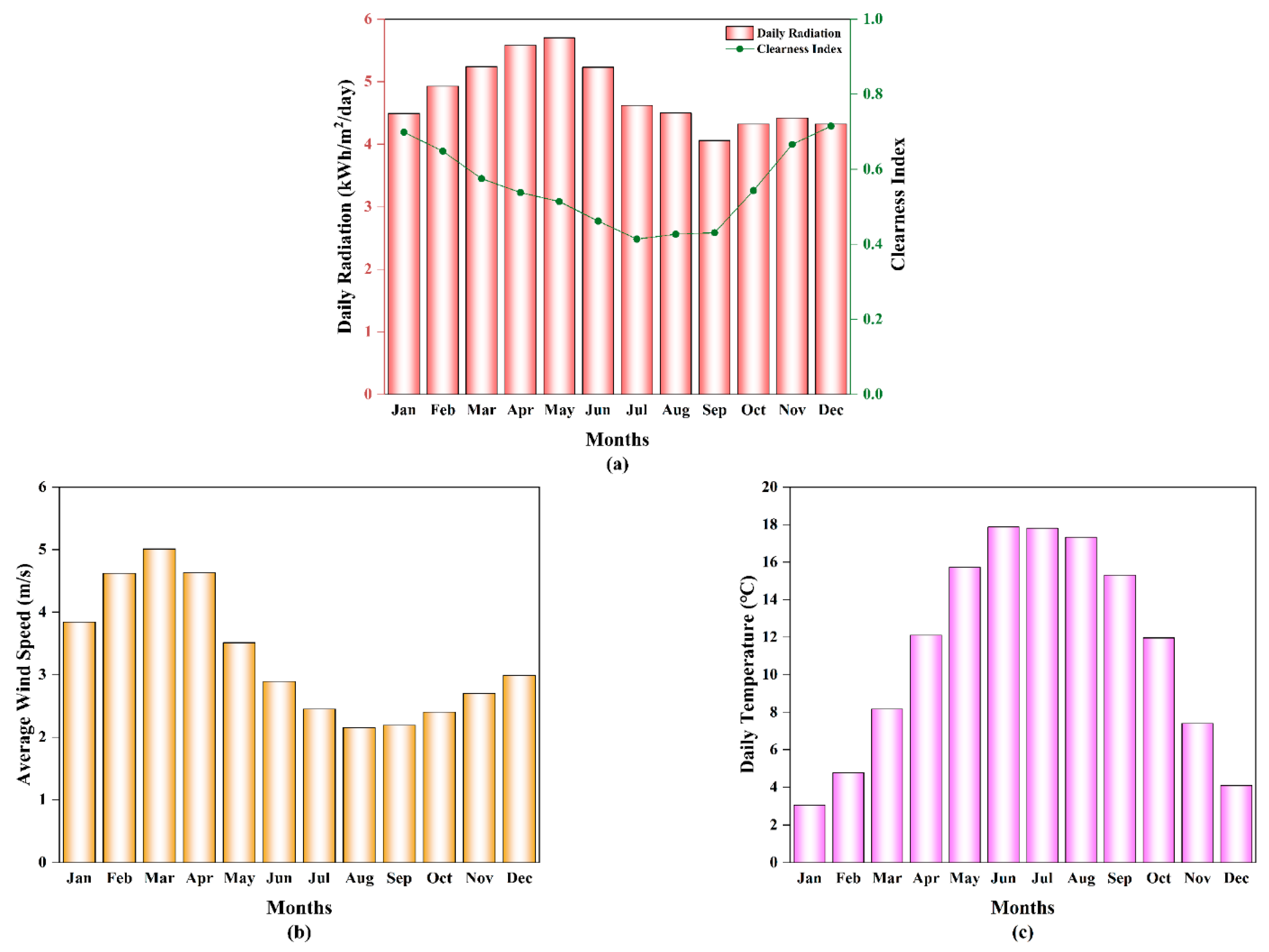
2.3. Introduction to Resources in the Study Area
3. Methodology
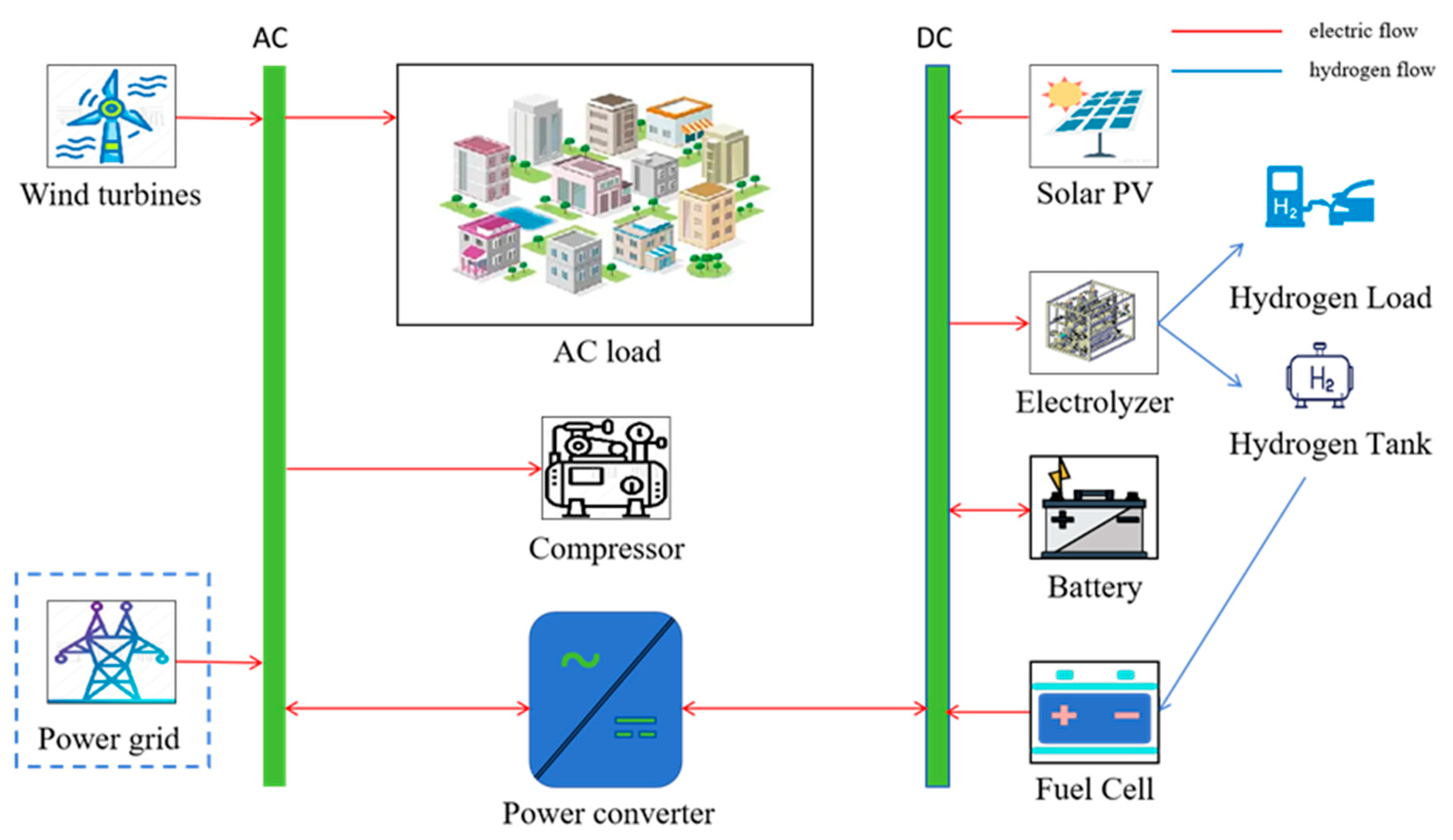
3.1. System Modeling
3.1.1. Wind Turbine Components
3.1.2. Photovoltaic Components
3.1.3. Battery Components
3.1.4. Converter Components
3.1.5. Electrolyzer Components
3.1.6. Fuel Cell Components
3.1.7. Hydrogen Storage Tank Components
3.1.8. Compressor Components
3.2. Analysis and Optimization
3.2.1. Economic Analysis Parameters
- (1)
- (2)
- Levelized costs of energy (LCOE) [50]:
- (3)
- Levelized costs of hydrogen (LCOH) [7]:
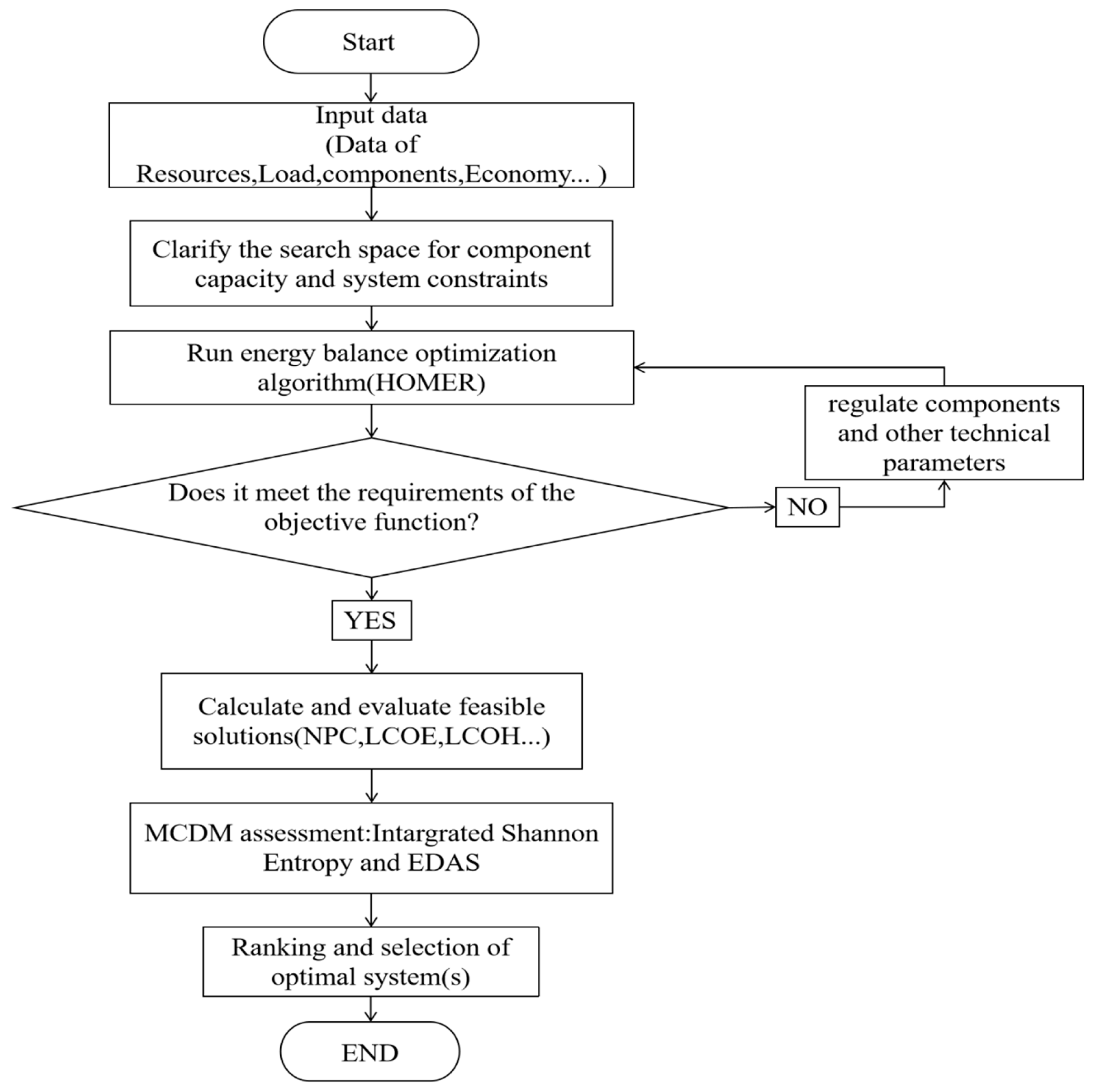
3.2.2. Optimization Processes
3.2.3. Sensitivity Analysis Overview
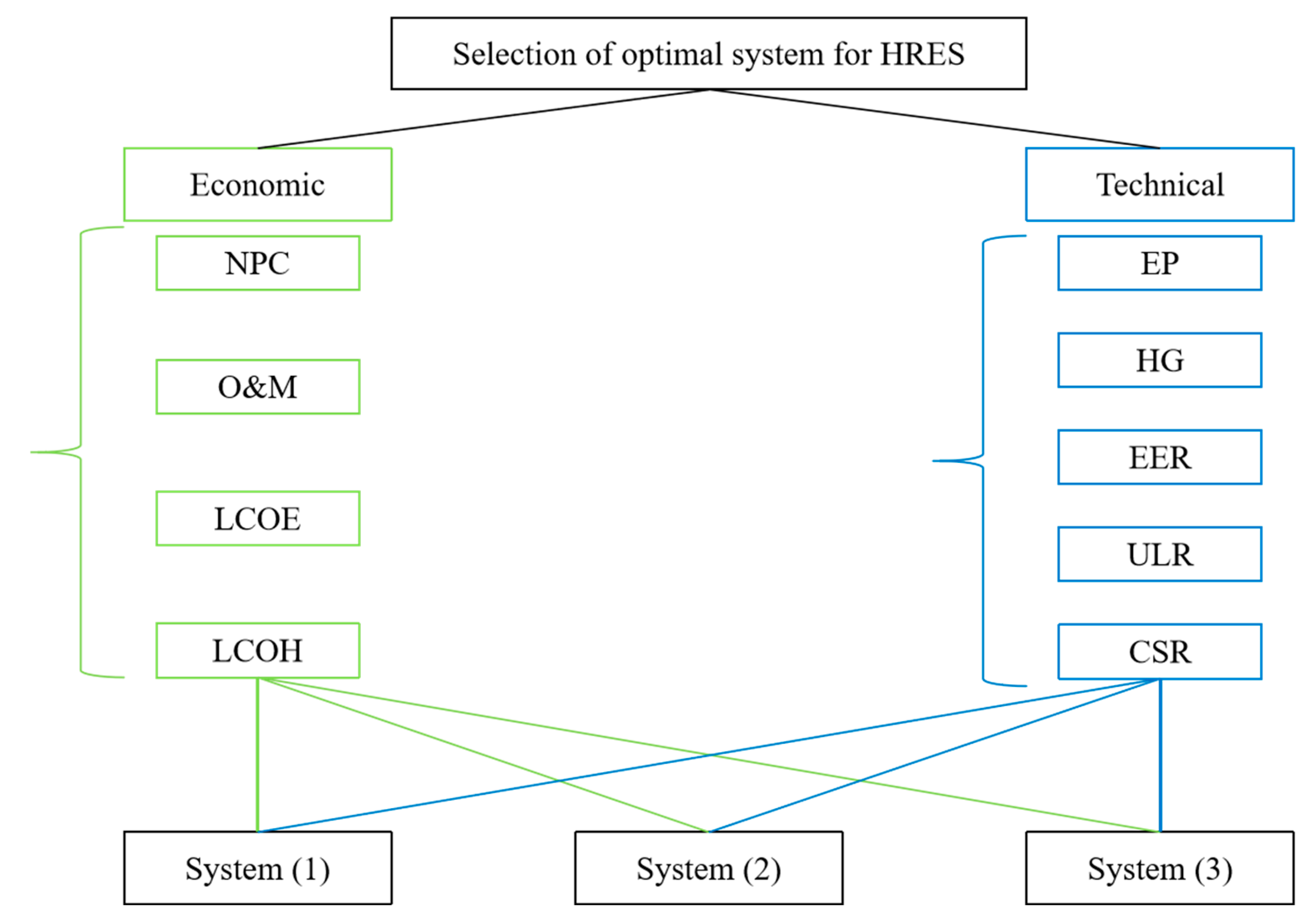
4. Multi-Criteria Decision Assessment
4.1. Shannon Entropy
4.2. EDAS
5. Results and Discussion
5.1. Software Optimization Results
5.2. Economic Analysis
5.3. Technical Analyses
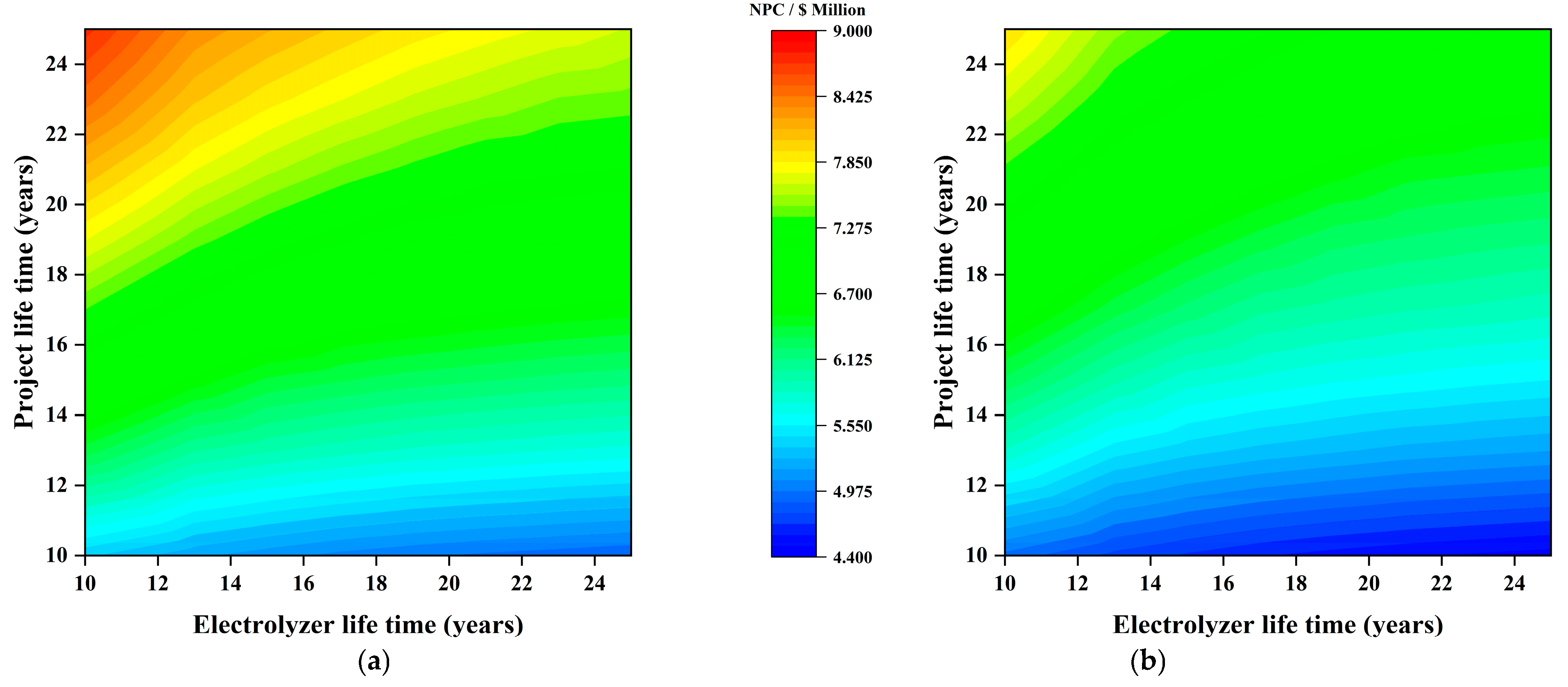
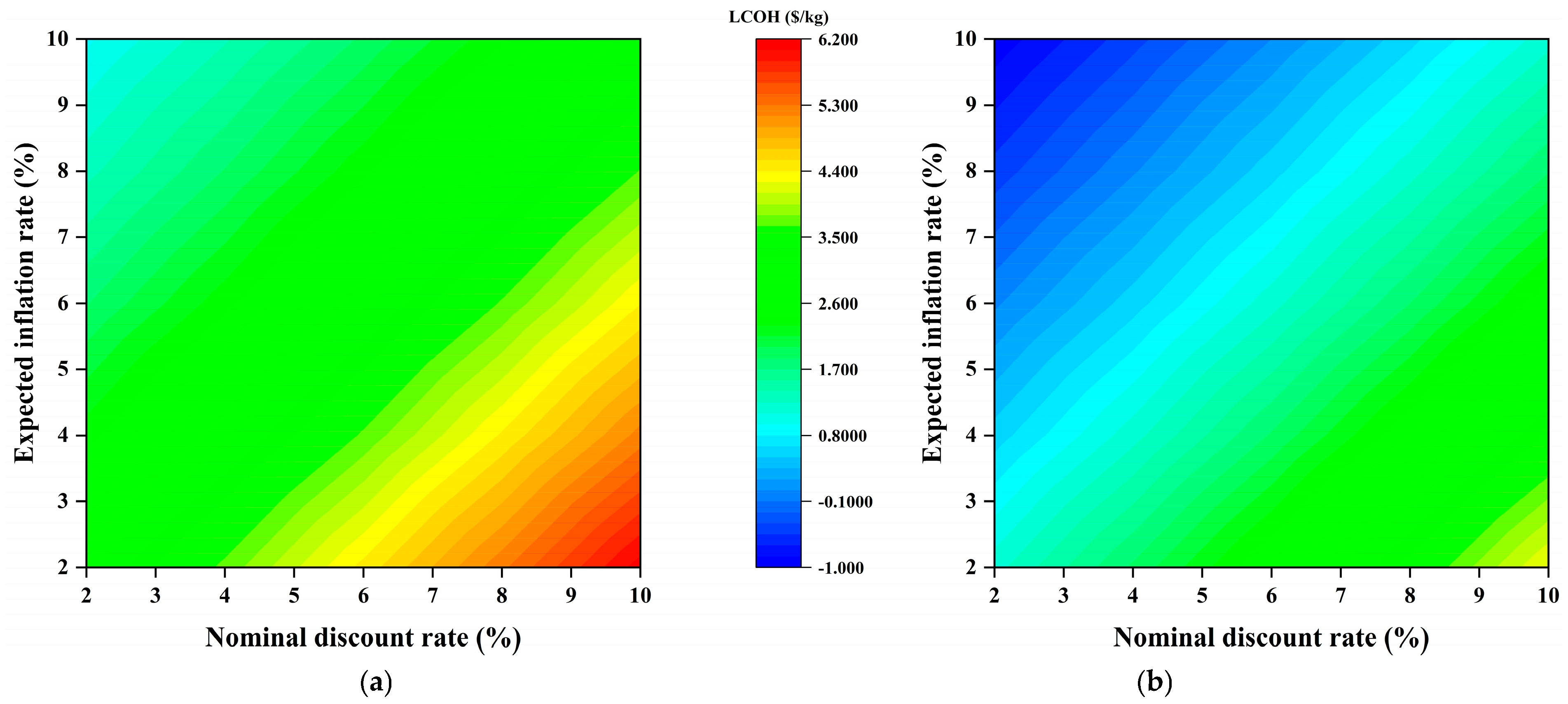
5.4. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AHP | Analytic Hierarchy Process |
| CSR | Capacity Shortage Rate |
| EDAS | Evaluation based on Distance from Average Solution |
| EER | Excess Electricity Rate |
| EP | Electricity Production |
| GRA | Grey Relational Analysis |
| HG | Hydrogen Generation |
| HOMER Pro | Hybrid Optimization of Multiple Energy Resources |
| HRESs | Hybrid Renewable Energy Systems |
| LCOE | Levelized Cost of Energy |
| LCOH | Levelized Cost of Hydrogen |
| NPC | Net Present Cost |
| O&M | Operation and Maintenance |
| PROMETHEE | Preference Ranking Organization Method for Enrichment Evaluations |
| PV | Photovoltaic |
| TOPSIS | Technique for Order Preference by Similarity to Ideal Solution |
| ULR | Unmet Load Rate |
References
- Krishna, K.S.; Kumar, K.S. A review on hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2015, 52, 907–916. [Google Scholar] [CrossRef]
- Ang, T.Z.; Salem, M.; Kamarol, M.; Das, H.S.; Nazari, M.A.; Prabaharan, N. A comprehensive study of renewable energy sources: Classifications, challenges and suggestions. Energy Strategy Rev. 2022, 43, 100939. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Sawle, Y.; Lala, H. A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renew. Sustain. Energy Rev. 2023, 176, 113192. [Google Scholar] [CrossRef]
- Basnet, S.; Deschinkel, K.; Le Moyne, L.; Cécile Péra, M. A review on recent standalone and grid integrated hybrid renewable energy systems: System optimization and energy management strategies. Renew. Energy Focus 2023, 46, 103–125. [Google Scholar] [CrossRef]
- Manoo, M.U.; Shaikh, F.; Kumar, L.; Arıcı, M. Comparative techno-economic analysis of various stand-alone and grid connected (solar/wind/fuel cell) renewable energy systems. Int. J. Hydrogen Energy 2024, 52, 397–414. [Google Scholar] [CrossRef]
- Agyekum, E.B.; Ampah, J.D.; Afrane, S.; Adebayo, T.S.; Agbozo, E. A 3E, hydrogen production, irrigation, and employment potential assessment of a hybrid energy system for tropical weather conditions—Combination of HOMER software, shannon entropy, and TOPSIS. Int. J. Hydrogen Energy 2022, 47, 31073–31097. [Google Scholar] [CrossRef]
- Chen, Q.; Gu, Y.; Tang, Z.; Wang, D.; Wu, Q. Optimal design and techno-economic assessment of low-carbon hydrogen supply pathways for a refueling station located in Shanghai. Energy 2021, 237, 121584. [Google Scholar] [CrossRef]
- Türkay, B.E.; Telli, A.Y. Economic analysis of standalone and grid connected hybrid energy systems. Renew. Energy 2011, 36, 1931–1943. [Google Scholar] [CrossRef]
- Abdin, Z.; Al Khafaf, N.; McGrath, B. Feasibility of hydrogen hybrid energy systems for sustainable on- and off-grid integration: An Australian REZs case study. Int. J. Hydrogen Energy 2024, 57, 1197–1207. [Google Scholar] [CrossRef]
- Shahzad, M.K.; Zahid, A.; ur Rashid, T.; Rehan, M.A.; Ali, M.; Ahmad, M. Techno-economic feasibility analysis of a solar-biomass off grid system for the electrification of remote rural areas in Pakistan using HOMER software. Renew. Energy 2017, 106, 264–273. [Google Scholar] [CrossRef]
- Miao, H.; Yu, Y.; Kharrazi, A.; Ma, T. Multi-criteria decision analysis for the planning of island microgrid system: A case study of Yongxing island, China. Energy 2023, 284, 129264. [Google Scholar] [CrossRef]
- Gonzalez, A.; Riba, J.-R.; Esteban, B.; Rius, A. Environmental and cost optimal design of a biomass–Wind–PV electricity generation system. Renew. Energy 2018, 126, 420–430. [Google Scholar] [CrossRef]
- Abdin, Z.; Mérida, W. Hybrid energy systems for off-grid power supply and hydrogen production based on renewable energy: A techno-economic analysis. Energy Convers. Manag. 2019, 196, 1068–1079. [Google Scholar] [CrossRef]
- HassanzadehFard, H.; Tooryan, F.; Collins, E.R.; Jin, S.; Ramezani, B. Design and optimum energy management of a hybrid renewable energy system based on efficient various hydrogen production. Int. J. Hydrogen Energy 2020, 45, 30113–30128. [Google Scholar] [CrossRef]
- Li, Y.; Liu, F.; Chen, K.; Liu, Y. Technical and economic analysis of a hybrid PV/wind energy system for hydrogen refueling stations. Energy 2024, 303, 131899. [Google Scholar] [CrossRef]
- Yue, M.; Lambert, H.; Pahon, E.; Roche, R.; Jemei, S.; Hissel, D. Hydrogen energy systems: A critical review of technologies, applications, trends and challenges. Renew. Sustain. Energy Rev. 2021, 146, 111180. [Google Scholar] [CrossRef]
- Ishaq, H.; Dincer, I.; Crawford, C. A review on hydrogen production and utilization: Challenges and opportunities. Int. J. Hydrogen Energy 2022, 47, 26238–26264. [Google Scholar] [CrossRef]
- Allakhverdiev, S.I. Artificial photosynthesis: Powering a green new deal for sustainable energy. Int. J. Hydrogen Energy 2024, 90, 199–209. [Google Scholar] [CrossRef]
- Bozieva, A.M.; Khasimov, M.K.; Voloshin, R.A.; Sinetova, M.A.; Kupriyanova, E.V.; Zharmukhamedov, S.K.; Dunikov, O.O.; Tsygankov, A.A.; Tomo, T.; Allakhverdiev, S.I. New cyanobacterial strains for biohydrogen production. Int. J. Hydrogen Energy 2023, 48, 7569–7581. [Google Scholar] [CrossRef]
- Kamshybayeva, G.K.; Kossalbayev, B.D.; Sadvakasova, A.K.; Bauenova, M.O.; Zayadan, B.K.; Bozieva, A.M.; Alharby, H.F.; Tomo, T.; Allakhverdiev, S.I. Screening and optimisation of hydrogen production by newly isolated nitrogen-fixing cyanobacterial strains. Int. J. Hydrogen Energy 2023, 48, 16649–16662. [Google Scholar] [CrossRef]
- Kamshybayeva, G.K.; Kossalbayev, B.D.; Sadvakasova, A.K.; Zayadan, B.K.; Bozieva, A.M.; Dunikov, D.; Alwasel, S.; Allakhverdiev, S.I. Strategies and economic feasibilities in cyanobacterial hydrogen production. Int. J. Hydrogen Energy 2022, 47, 29661–29684. [Google Scholar] [CrossRef]
- Kossalbayev, B.D.; Tomo, T.; Zayadan, B.K.; Sadvakasova, A.K.; Bolatkhan, K.; Alwasel, S.; Allakhverdiev, S.I. Determination of the potential of cyanobacterial strains for hydrogen production. Int. J. Hydrogen Energy 2020, 45, 2627–2639. [Google Scholar] [CrossRef]
- Kossalbayev, B.D.; Yilmaz, G.; Sadvakasova, A.K.; Zayadan, B.K.; Belkozhayev, A.M.; Kamshybayeva, G.K.; Sainova, G.A.; Bozieva, A.M.; Alharby, H.F.; Tomo, T.; et al. Biotechnological production of hydrogen: Design features of photobioreactors and improvement of conditions for cultivating cyanobacteria. Int. J. Hydrogen Energy 2024, 49, 413–432. [Google Scholar] [CrossRef]
- Irham, A.; Roslan, M.F.; Jern, K.P.; Hannan, M.A.; Mahlia, T.M.I. Hydrogen energy storage integrated grid: A bibliometric analysis for sustainable enrgy production. Int. J. Hydrogen Energy 2024, 63, 1044–1087. [Google Scholar] [CrossRef]
- Sdanghi, G.; Maranzana, G.; Celzard, A.; Fierro, V. Review of the current technologies and performances of hydrogen compression for stationary and automotive applications. Renew. Sustain. Energy Rev. 2019, 102, 150–170. [Google Scholar] [CrossRef]
- Ajanovic, A.; Haas, R. Prospects and impediments for hydrogen and fuel cell vehicles in the transport sector. Int. J. Hydrogen Energy 2021, 46, 10049–10058. [Google Scholar] [CrossRef]
- Moradi, R.; Growth, K.M. Hydrogen storage and delivery: Review of the state of the art technologies and risk and reliability analysis. Int. J. Hydrogen Energy 2019, 44, 12254–12269. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, Q.; Xue, J.; Tang, Z.; Sun, Y.; Wu, Q. Comparative techno-economic study of solar energy integrated hydrogen supply pathways for hydrogen refueling stations in China. Energy Convers. Manag. 2020, 223, 113240. [Google Scholar] [CrossRef]
- Pareek, A.; Dom, R.; Gupta, J.; Chandran, J.; Adepu, V.; Borse, P.H. Insights into renewable hydrogen energy: Recent advances and prospects. Mater. Sci. Energy Technol. 2020, 3, 319–327. [Google Scholar] [CrossRef]
- Khan, T.; Yu, M.; Waseem, M. Review on recent optimization strategies for hybrid renewable energy system with hydrogen technologies: State of the art, trends and future directions. Int. J. Hydrogen Energy 2022, 47, 25155–25201. [Google Scholar] [CrossRef]
- Bahramara, S.; Moghaddam, M.P.; Haghifam, M.R. Optimal planning of hybrid renewable energy systems using HOMER: A review. Renew. Sustain. Energy Rev. 2016, 62, 609–620. [Google Scholar] [CrossRef]
- Emrani, A.; Berrada, A. A comprehensive review on techno-economic assessment of hybrid energy storage systems integrated with renewable energy. J. Energy Storage 2024, 84, 111010. [Google Scholar] [CrossRef]
- Upadhyay, S.; Sharma, M.P. A review on configurations, control and sizing methodologies of hybrid energy systems. Renew. Sustain. Energy Rev. 2014, 38, 47–63. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Leahy, M. A review of computer tools for analysing the integration of renewable energy into various energy systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Caliskan, A.; Percin, H.B. Techno-economic analysis of a campus-based hydrogen-producing hybrid system. Int. J. Hydrogen Energy 2024, 75, 428–437. [Google Scholar] [CrossRef]
- Tiar, B.; Fadlallah, S.O.; Benhadji Serradj, D.E.; Graham, P.; Aagela, H. Navigating Algeria towards a sustainable green hydrogen future to empower North Africa and Europe’s clean hydrogen transition. Int. J. Hydrogen Energy 2024, 61, 783–802. [Google Scholar] [CrossRef]
- Elomari, Y.; Mateu, C.; Marín-Genescà, M.; Boer, D. A data-driven framework for designing a renewable energy community based on the integration of machine learning model with life cycle assessment and life cycle cost parameters. Appl. Energy 2024, 358, 122619. [Google Scholar] [CrossRef]
- Zghaibeh, M.; Ben Belgacem, I.; Barhoumi, E.M.; Baloch, M.H.; Chauhdary, S.T.; Kumar, L.; Arıcı, M. Optimization of green hydrogen production in hydroelectric-photovoltaic grid connected power station. Int. J. Hydrogen Energy 2024, 52, 440–453. [Google Scholar] [CrossRef]
- Kumar, L.; Manoo, M.U.; Ahmed, J.; Arıcı, M.; Awad, M.M. Comparative techno-economic investigation of hybrid energy systems for sustainable energy solution. Int. J. Hydrogen Energy 2024, 104, 513–526. [Google Scholar] [CrossRef]
- Lai, Y.Y.; Yang, S.; Fan, L.W. Analysis and optimization of the performance of a solar PV/T system integrated with seasonal latent heat storage for decarbonized heating and hot water supply. Energy 2025, 331, 137069. [Google Scholar] [CrossRef]
- Yang, J.; Yang, Z.; Duan, Y. Capacity optimization and feasibility assessment of solar-wind hybrid renewable energy systems in China. J. Clean. Prod. 2022, 368, 133139. [Google Scholar] [CrossRef]
- Ampah, J.D.; Afrane, S.; Agyekum, E.B.; Adun, H.; Yusuf, A.A.; Bamisile, O. Electric vehicles development in Sub-Saharan Africa: Performance assessment of standalone renewable energy systems for hydrogen refuelling and electricity charging stations (HRECS). J. Clean. Prod. 2022, 376, 134238. [Google Scholar] [CrossRef]
- Hussam, W.K.; Barhoumi, E.M.; Abdul-Niby, M.; Sheard, G.J. Techno-economic analysis and optimization of hydrogen production from renewable hybrid energy systems: Shagaya renewable power plant-Kuwait. Int. J. Hydrogen Energy 2024, 58, 56–68. [Google Scholar] [CrossRef]
- province TdarcoY. Notice of the Yunnan Provincial Development and Reform Commission on Further Improving the Time-of-Use Electricity Pricing Policy. Available online: https://yndrc.yn.gov.cn/html/2023/qitawenjian_1115/13903.html (accessed on 2 April 2024).
- Network PES. 16 Provinces and Cities with Peak and Valley Price Differences of More Than ¥0.7!2024 Summary of Peak and Valley Electricity Prices Across the Country in April! Available online: https://news.bjx.com.cn/html/20240401/1369193-3.shtml (accessed on 2 April 2024).
- Hassan, Q.; Algburi, S.; Sameen, A.Z.; Salman, H.M.; Jaszczur, M. A review of hybrid renewable energy systems: Solar and wind-powered solutions: Challenges, opportunities, and policy implications. Results Eng. 2023, 20, 101621. [Google Scholar] [CrossRef]
- Okundamiya, M.S.; Wara, S.T.; Obakhena, H.I. Optimization and techno-economic analysis of a mixed power system for sustainable operation of cellular sites in 5G era. Int. J. Hydrogen Energy 2022, 47, 17351–17366. [Google Scholar] [CrossRef]
- Bhatt, A.; Ongsakul, W.; Madhu, M.N. Optimal techno-economic feasibility study of net-zero carbon emission microgrid integrating second-life battery energy storage system. Energy Convers. Manag. 2022, 266, 115825. [Google Scholar] [CrossRef]
- Maisanam, A.K.S.; Biswas, A.; Sharma, K.K. Integrated socio-environmental and techno-economic factors for designing and sizing of a sustainable hybrid renewable energy system. Energy Convers. Manag. 2021, 247, 114709. [Google Scholar] [CrossRef]
- Barhoumi, E.M.; Okonkwo, P.C.; Ben Belgacem, I.; Zghaibeh, M.; Tlili, I. Optimal sizing of photovoltaic systems based green hydrogen refueling stations case study Oman. Int. J. Hydrogen Energy 2022, 47, 31964–31973. [Google Scholar] [CrossRef]
- Li, C.; Ge, X.; Zheng, Y.; Xu, C.; Ren, Y.; Song, C.; Yang, C. Techno-economic feasibility study of autonomous hybrid wind/PV/battery power system for a household in Urumqi, China. Energy 2013, 55, 263–272. [Google Scholar] [CrossRef]
- Thakkar, N.; Paliwal, P. Data driven MCDM models for reliability-economic-environmental analysis of energy storage based autonomous micro-grid. J. Energy Storage 2024, 81, 110408. [Google Scholar] [CrossRef]
- Yazdani, M.; Torkayesh, A.E.; Santibanez-Gonzalez, E.D.; Otaghsara, S.K. Evaluation of renewable energy resources using integrated Shannon Entropy—EDAS model. Sustain. Oper. Comput. 2020, 1, 35–42. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-Criteria Inventory Classification Using a New Method of Evaluation Based on Distance from Average Solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Torkayesh, A.E.; Deveci, M.; Karagoz, S.; Antucheviciene, J. A state-of-the-art survey of evaluation based on distance from average solution (EDAS): Developments and applications. Expert Syst. Appl. 2023, 221, 119724. [Google Scholar] [CrossRef]
- Kumar, N.; Karmakar, S. Techno-economic optimization of hydrogen generation through hybrid energy system: A step towards sustainable development. Int. J. Hydrogen Energy 2024, 55, 400–413. [Google Scholar] [CrossRef]
- Kandel, M.R.; Pan, U.N.; Dhakal, P.P.; Ghising, R.B.; Sidra, S.; Kim, D.H.; Kim, N.H.; Lee, J.H. Manganese-Doped Bimetallic (Co,Ni)2P Integrated CoP in N;S Co-Doped Carbon: Unveiling a Compatible Hybrid Electrocatalyst for Overall Water Splitting. Small 2024, 20, 2307241. [Google Scholar] [CrossRef]


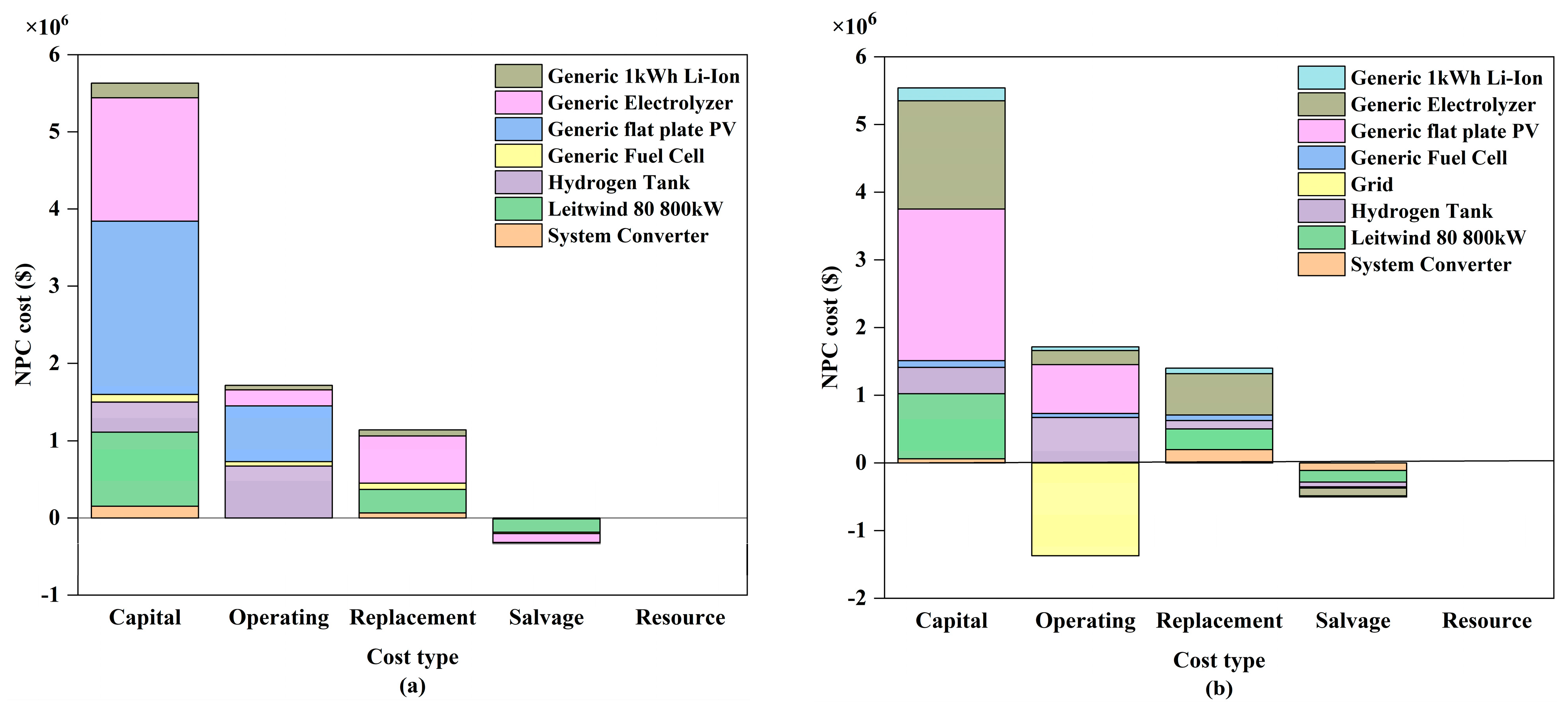
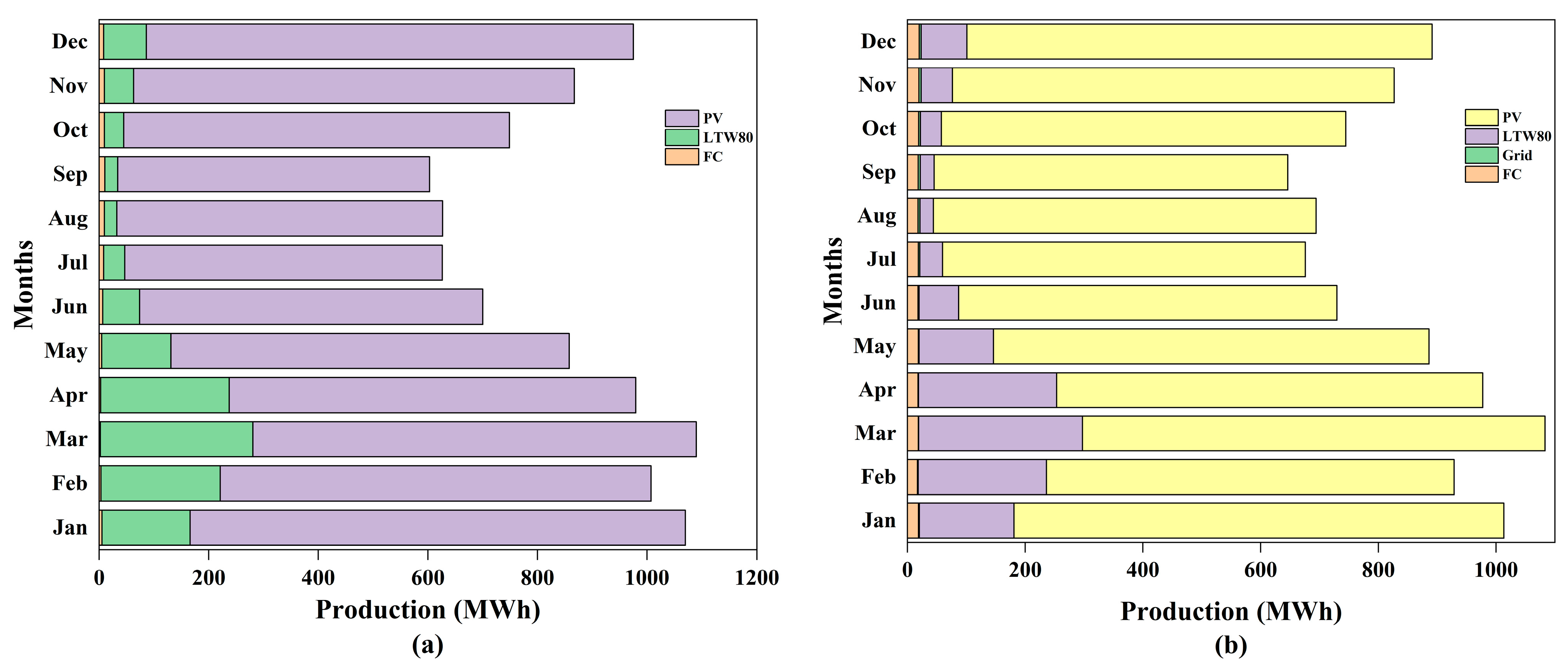
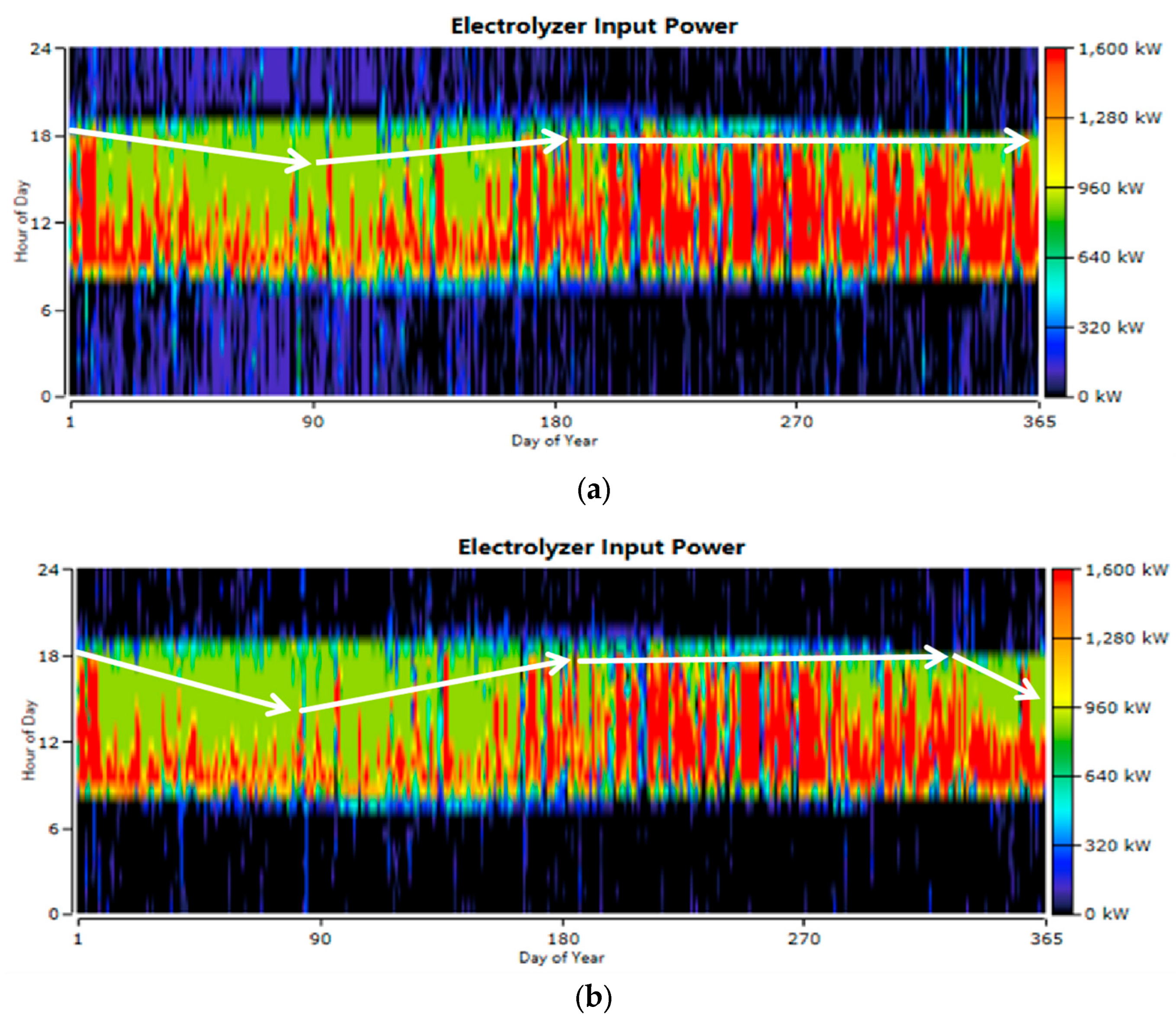
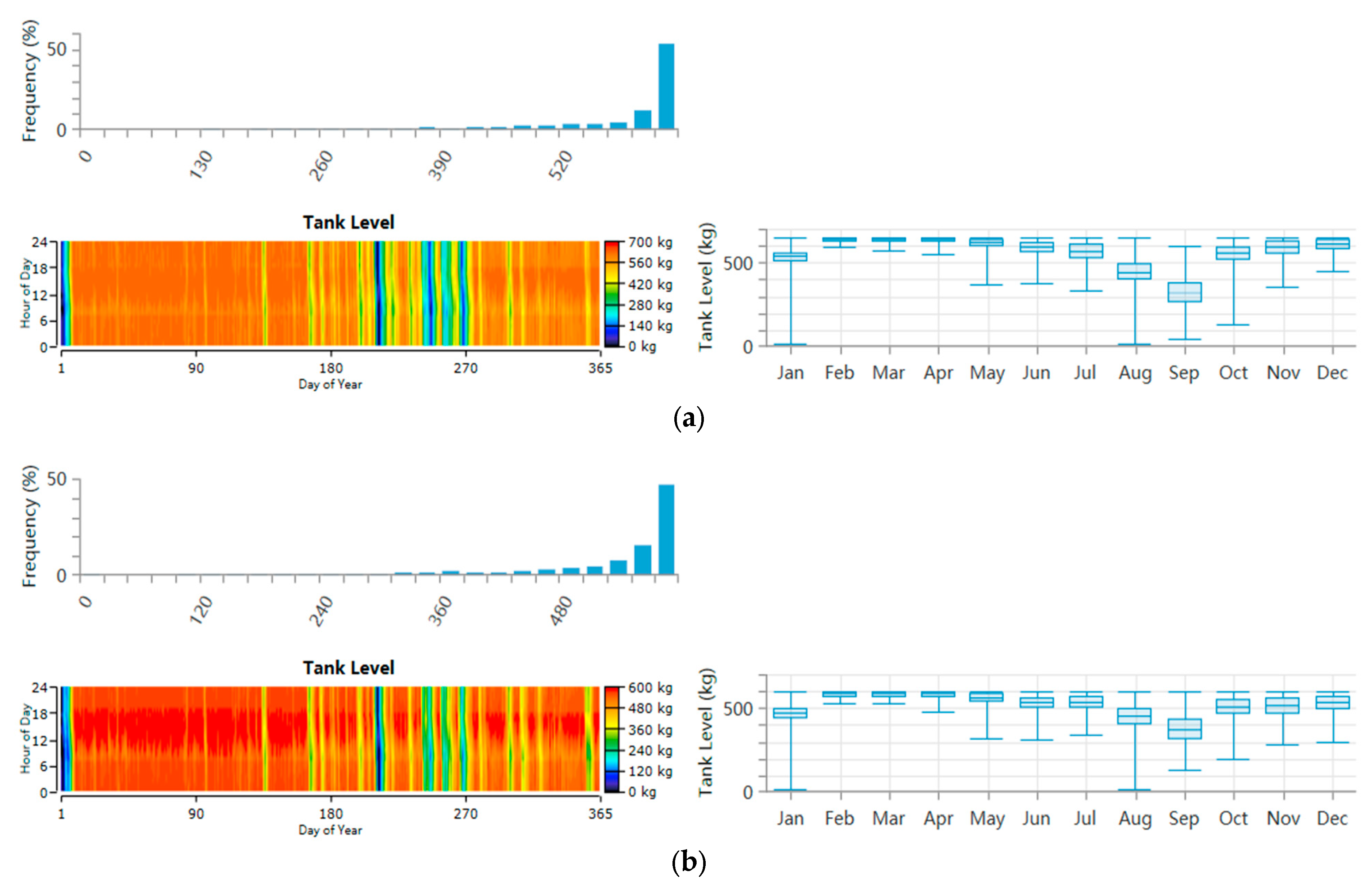
| Country | System Components | NPC | LCOE | LCOH | Reference |
|---|---|---|---|---|---|
| Pakistan | Wind Turbine, PV, Fuel Cell, Hydrogen Tank, Electrolyzer, Battery, Converter | M USD 1.54–6.82 | USD 0.16/kWh–USD 0.37/kWh | - | [5] |
| Ghana | PV, Hydrokinetic Turbine, PSIM, Converter, Electrolyzer, Hydrogen Tank, Battery | Scenario I: M USD 0.51, scenario II: M USD 1.14 | Scenario I: USD 0.06/kWh, scenario II: 0.14/kWh | Scenario I: 4.47 USD/kg, scenario II: 9.81 USD/kg | [6] |
| China | PV, Wind Turbine, Battery, Converter, Electrolyzer, Compressor, Hydrogen Tank, Liquefier, Liquid H2 Pump, Evaporator, Cooling, Dispenser | No specific numerical specifications provided | CNY 0.28/kWh, CNY 0.49/kWh, CNY 0.58/kWh, CNY 0.83/kWh | No specific numerical specifications provided | [7] |
| Australia | PV, Wind Turbine, Fuel Cell, Battery, Converter, Electrolyzer, Hydrogen Tank, Compressor | Off-grid systems: M USD 19.6, M USD 20.1, M USD 21.2, M USD 20.7, M USD 23.5. On-grid systems: M USD 6.86, M USD 6.77, M USD 7.33, M USD 6.95, M USD 8.25. | Off-grid systems: USD 0.32/kWh, USD 0.33/kWh, USD 0.34/kWh, USD 0.34/kWh, USD 0.38/kWh. On-grid systems: USD 0.033/kWh, USD 0.030/kWh, USD 0.032/kWh, USD 0.031/kWh, USD 0.034/kWh. | Off-grid systems: USD 3.62/kg, USD 3.91/kg, USD 4.49/kg, USD 4.17/kg, USD 5.72/kg. On-grid systems: USD −17.5/kg, USD −19.3/kg, USD −19.8/kg, USD −19.3/kg, USD −20/kg. | [9] |
| Pakistan | PV, Biogas-Fueled Generator, Battery, Converter | M PKR 4.48 | PKR 5.51/kWh | - | [10] |
| China | PV, Wind Turbine, Hydrokinetic Turbines, Diesel Generators, Power Grid, Battery, Converter, Electrolyzer, Hydrogen Tank, Thermal Load Controller, Boiler, Diesel Reformer | M CNY 101.39 | CNY 0.18/kWh | CNY 51.83/kg | [11] |
| Türkiye | PV, Wind Turbine, Electrolyzer, Hydrogen Tank, Power Grid, Converter | M USD 7.67 | USD 0.02/kWh | No specific numerical specifications provided | [35] |
| Time | Note | Purchase Price (USD/kWh) | Sale Price (USD/kWh) | |||
|---|---|---|---|---|---|---|
| Rush | Peak | Shoulder | Off-Peak | |||
| 7:00–9:00 | 0.07 | |||||
| 9:00–10:30 | 0.09 | 0.04 | ||||
| 10:30–11:30 | Implemented in January, March, April, and December only. | 0.11 | 0.09 | |||
| 11:30–12:00 | 0.09 | |||||
| 12:00–17:00 | 0.07 | |||||
| 17:00–17:30 | 0.09 | |||||
| 17:30–18:30 | Implemented in January, March, April, and December only. | 0.11 | 0.09 | |||
| 18:30–22:00 | 0.09 | |||||
| 22:00–23:00 | 0.07 | |||||
| 23:00–7:00 | 0.05 | |||||
| Components | Parameters | Value | References |
|---|---|---|---|
| Wind turbine (LTW80) | Capital cost (USD/kW) | 1200 | [7] |
| Replacement cost (USD/kW) | 1200 | ||
| O&M cost (USD/y) | 24 | ||
| Rated capacity (kW) | 800 | ||
| Hub height (m) | 80 | ||
| Cut-in wind speed (m/s) | 3 | ||
| Cut-out wind speed (m/s) | 25 | ||
| Life (y) | 20 | ||
| Generic flat-plate PV | Capital cost (USD/kW) | 400 | [5] |
| Replacement cost (USD/kW) | 400 | ||
| O&M cost (USD/y) | 10 | ||
| Rated capacity (kW) | 1 | ||
| Efficiency | 20% | ||
| Life (y) | 25 | ||
| Generic 1 kWh Li-ion battery | Efficiency | 90% | [15] |
| Capital cost (USD/kW) | 450 | ||
| Replacement cost (USD/kW) | 450 | ||
| O&M cost (USD/y) | 10 | ||
| Maximum capacity | 167 | ||
| Nominal voltage | 6 | ||
| Life (y) | 15 | ||
| Converter | Capital cost (USD/kW) | 500 | [34] |
| Replacement cost (USD/kW) | 500 | ||
| O&M cost (USD/y) | 0 | ||
| Life (y) | 15 | ||
| Generic electrolyzer | Model | AWE | [7] |
| Efficiency | 85% | ||
| Capital cost (USD/kW) | 1000 | ||
| Replacement cost (USD/kW) | 900 | ||
| O&M cost (USD/y) | 10 | ||
| Life (y) | 15 | ||
| Efficiency (%) | 85 | ||
| Generic fuel cell | Efficiency | 50% | [47] |
| Capital cost (USD/kW) | 2000 | ||
| Replacement cost (USD/kW) | 2000 | ||
| O&M cost (USD/op. hr) | 0.02 | ||
| Life (h) | 50,000 | ||
| Hydrogen storage tank | Capital cost (USD/kW) | 600 | [42] |
| Replacement cost (USD/kW) | 600 | ||
| O&M cost (USD/y) | 80 | ||
| Life (y) | 25 | ||
| Grid | Max exchange capacity (kW) | 1000 | [7] |
| Sell back prices | Table 1 | ||
| Purchase prices | Table 1 |
| System | Grid (kW) | Wind Turbine (kW) | Solar Panel (kW) | Battery (Li-Ion, kWh) | Fuel Cell (kW) | Electrolyzer (kW) | Hydrogen Tank (kg) | Converter (kW) |
|---|---|---|---|---|---|---|---|---|
| (1) | - | 800 | 5588 | 421 | 50 | 1600 | 650 | 303 |
| (2) | - | 6042 | 621 | 50 | 1700 | 750 | 281 | |
| (3) | - | 800 | 5482 | 200 | 1700 | 750 | 285 |
| System | NPC/106 (USD) | Initial Capital/106 (USD) | O&M Cost/106 (USD) | Replacement Cost/106 (USD) | LCOE (USD/kWh) | LCOH (USD/kg) |
|---|---|---|---|---|---|---|
| (1) | 8.15 | 5.63 | 1.71 | 1.14 | 0.43 | 5.26 |
| (2) | 8.24 | 5.49 | 1.75 | 1.21 | 0.48 | 5.65 |
| (3) | 8.50 | 5.75 | 1.81 | 1.36 | 0.51 | 6.01 |
| System | EP (kWh/yr) | HG (ton/yr) | EER (%) | ULR (%) | CSR(%) |
|---|---|---|---|---|---|
| (1) | 10.15 × 106 | 93.44 | 42.50 | 0.02 | 0.08 |
| (2) | 9.68 × 106 | 94.67 | 43.10 | 0.04 | 0.09 |
| (3) | 10.04 × 106 | 95.40 | 45.40 | 0.03 | 0.09 |
| NPC | LCOE | O&M | LCOH | EP | EER | HG | ULR | CSR | |
|---|---|---|---|---|---|---|---|---|---|
| Weight (%) | 8.529 | 10.501 | 8.952 | 9.597 | 6.486 | 13.119 | 8.847 | 9.465 | 24.504 |
| Rank | 8 | 3 | 6 | 4 | 9 | 2 | 7 | 5 | 1 |
| Hybrid System | PDA | NDA | Score | Ranking |
|---|---|---|---|---|
| (1) | 7.504 | 2.000 | 3.252 | 1 |
| (2) | 0.560 | 3.695 | −0.685 | 3 |
| (3) | 2.630 | 5.000 | −1.067 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Xu, R.; Li, D.; Zhu, T.; Fan, N.; Hong, Z.; Wang, G.; Han, Y.; Zhu, X. Multi-Criteria Optimization and Techno-Economic Assessment of a Wind–Solar–Hydrogen Hybrid System for a Plateau Tourist City Using HOMER and Shannon Entropy-EDAS Models. Energies 2025, 18, 4183. https://doi.org/10.3390/en18154183
Shi J, Xu R, Li D, Zhu T, Fan N, Hong Z, Wang G, Han Y, Zhu X. Multi-Criteria Optimization and Techno-Economic Assessment of a Wind–Solar–Hydrogen Hybrid System for a Plateau Tourist City Using HOMER and Shannon Entropy-EDAS Models. Energies. 2025; 18(15):4183. https://doi.org/10.3390/en18154183
Chicago/Turabian StyleShi, Jingyu, Ran Xu, Dongfang Li, Tao Zhu, Nanyu Fan, Zhanghua Hong, Guohua Wang, Yong Han, and Xing Zhu. 2025. "Multi-Criteria Optimization and Techno-Economic Assessment of a Wind–Solar–Hydrogen Hybrid System for a Plateau Tourist City Using HOMER and Shannon Entropy-EDAS Models" Energies 18, no. 15: 4183. https://doi.org/10.3390/en18154183
APA StyleShi, J., Xu, R., Li, D., Zhu, T., Fan, N., Hong, Z., Wang, G., Han, Y., & Zhu, X. (2025). Multi-Criteria Optimization and Techno-Economic Assessment of a Wind–Solar–Hydrogen Hybrid System for a Plateau Tourist City Using HOMER and Shannon Entropy-EDAS Models. Energies, 18(15), 4183. https://doi.org/10.3390/en18154183






