A Multi-Stage Feature Selection and Explainable Machine Learning Framework for Forecasting Transportation CO2 Emissions
Abstract
1. Introduction
1.1. Background
1.2. Research Novelty
- This research proposed a sophisticated multi-stage ML framework for an accurate forecasting of transportation CO2 emission in the U.S. potential factors were selected based on a comprehensive literature review, including energy usage, economic and demo-graphic parameters like population, unemployment rate, Gross Domestic Product (GDP), urban population, total fossil fuels consumed, etc. This broad and varying information allows the model to comprehend driving contributors to CO2 emissions in the transport field, which also provides a comprehensive method in comparison with conventional methods that concentrate exclusively on energy metrics.
- Given the extremely multicollinear features like total primary energy production, GDP, fossil fuel consumption, population, air transport freight, road mileage, and so on, conventional forecasting usually faces issues associated with decreased precision. To this, a main concentrate of the study was a two-stage FS procedure starting with time series clustering to determine groups of correlated factors, accompanied by an advanced FS voting mechanism based on Boruta FS and Spearman correlation analysis to identify the best appropriate features. This arranged method ensured the robustness and reliability of forecasting results.
- Four different ML models, like SVR, eXtreme Gradient Boosting (Xgboost), ElasticNet, and Multilayer perceptron (MLP), were employed to improve the accuracy of CO2 emissions forecasting in the transportation field. The SHAP method was then applied to uncover the black box of ML, identifying the global and local relationship between input features and CO2 emissions. The explainable ML methods ensured offering valuable insights for policymakers to support efficient techniques regarding decreasing CO2 emissions in the USA. Figure 2 depicts the conceptual framework for forecasting transportation CO2 emissions based on the above procedure. All machine learning coding was implemented based on python 3.11.9, scikit-learn 1.5.1, xgboost 2.1.0 and shap 0.47.0.
2. Literature Review
2.1. Machine Learning for CO2 Prediction
2.2. Feature Selection for the CO2 Prediction
| Article | Country | Time Period | Feature Selection | Machine Learning | Applied Models | ||
|---|---|---|---|---|---|---|---|
| ML | Hybrid | Others | |||||
| Qiao et al. [22] | UK | 1990–2019 | Yes | Yes | LSTM | SVR-RBF | --- |
| Javanmard et al. [16] | Canada | No | Yes | --- | multi-objective mathematical model with data-driven ML | --- | |
| Ahmed et al. [20] | China, India, the USA, and Russia | 1992–2018 | No | Yes | SVM, ANN, LSTM | --- | --- |
| Qin and Gong [28] | China | 2000–2019 | No | Yes | RF, decision tree | --- | --- |
| Ulussever et al. [24] | USA | 1973–2021 | No | Yes | MLP, SVM, RF, MARS, k-NN | --- | Time Series Econometric |
| Li et al. [25] | 30 Countries | 1960–2020 | No | Yes | OLS, SVM, GBR | --- | --- |
| Ağbulut [5] | Turkey | 1970–2016 | No | Yes | DL, SVM, ANN | --- | --- |
| Li and Sun [31] | China | 2010 | Yes | Yes | GBM, SVM, RF, and XGBoost | --- | --- |
| Chukwunonso et al. [19] | USA | 1973–2022 | No | Yes | RNN, FFNN, CNN | --- | --- |
| Wang and Jixian [26] | China | 2000–2012 | No | Yes | --- | MRFO-ELM | --- |
| Alfaseeh et al. [27] | Canada | N/A | No | Yes | LSTM | --- | ARIMA |
| Yin et al. [4] | China | N/A | No | Yes | Decision Tree, MLR, ANN | --- | MLR |
| Fu et al. [23] | worldwide | 2021 | No | Yes | GNN, CNN | --- | --- |
| Wang et al. [29] | China | 1980–2014 | Yes | Yes | SVM, GPR, BPNN | PSO-SVM | --- |
| Peng et al. [36] | China | N/A | No | Yes | --- | GAPSO-SVR | --- |
| Chadha et al. [37] | India | N/A | No | Yes | XGBoost, (SVR), RF, and Ridge Regression | --- | --- |
| Anonna et al. [38] | USA | 1970–2020 | No | Yes | RF, Support Vector Classifier, and Logistic Regression | --- | --- |
| Jha et al. [39] | USA | 2004–2023 | No | Yes | 11 AI algorithms | --- | --- |
| Li et al. [40] | USA | N/A | No | Yes | DL-LSTM | --- | --- |
| Tian et al. [41] | USA | 1973–2022 | No | Yes | k-nearest neighbors (KNN), RF, MLR, gradient boosting, decision tree and SVR | --- | --- |
| Ajala et al. [42] | China, India, the USA, and the EU27&UK | 2022–2023 | No | Yes | 14 AI algorithms | --- | --- |
| Current Research | USA | 1990–2023 | Yes | Yes | XGBoost, MLP, SVR, Elastic Net | ---- | ---- |
3. Materials and Methods
3.1. Data Collection
3.2. Feature Selection Methods
3.2.1. Hierarchical Clustering
3.2.2. Boruta Feature Selection (BFS) and Spearman Correlation
- Add randomness to the variables by generating shuffled copies (shadow variables) of the whole variables and then combine the shadow variables using original variables to create extended variables.
- Set up an RF procedure for the extended variables as well as calculate the significance variable (the mean decreased precision Z value). The greater the Z value, the more significant the variable; the greatest Z value of the shadow variable is determined as Zmax.
- Throughout every iteration, if the Z value of the variable is greater than Zmax, after that, the variable is taken into account as significant and will be retained. Otherwise, the variable is considered highly insignificant as well as will be eliminated through the variables.
- The earlier mentioned procedure stops whenever either all variables are generally rejected or verified, or BFS gets to the highest range of iterations [42].
- If multiple variables are tested to be relevant in a cluster, the variable that has the highest correlation score with statistical significance is determined as the best candidate variable for this cluster. In case no variable indicates statistical significance, a compromise is that the variable that has the highest correlation score is still regarded as the best one.
- If only one variable is either tested to be relevant or indicates the highest correlation score with statistical significance in a cluster, then this variable is the chosen variable for this cluster.
- If variables in a cluster show neither relevancy nor statistical significance in Spearman correlation, then this cluster is discarded and no variable will be selected for the next step of ML.
3.3. Machine Learning Models
3.3.1. eXtreme Gradient Boosting (Xgboost)
3.3.2. Multilayer Perceptron (MLP)
3.3.3. Support Vector Regression (SVR)
3.3.4. Elastic Net
- L2 as ridge regression reduces coefficients in the direction of zero through penalizing their squared degree. It performs properly when variables are extremely correlated, however, it does not carry out FS.
- L1 as Lasso promotes sparsity through penalizing the total magnitudes of coefficients, frequently establishing some coefficients to zero as well as carrying out FS. Nevertheless, this method is challenged when predictors are usually extremely correlated, as it randomly chooses one and neglects some others.
3.4. Model Evaluation
3.5. Shapley Analysis
4. Results and Discussion
4.1. Multicollinearity Analysis and FS Method
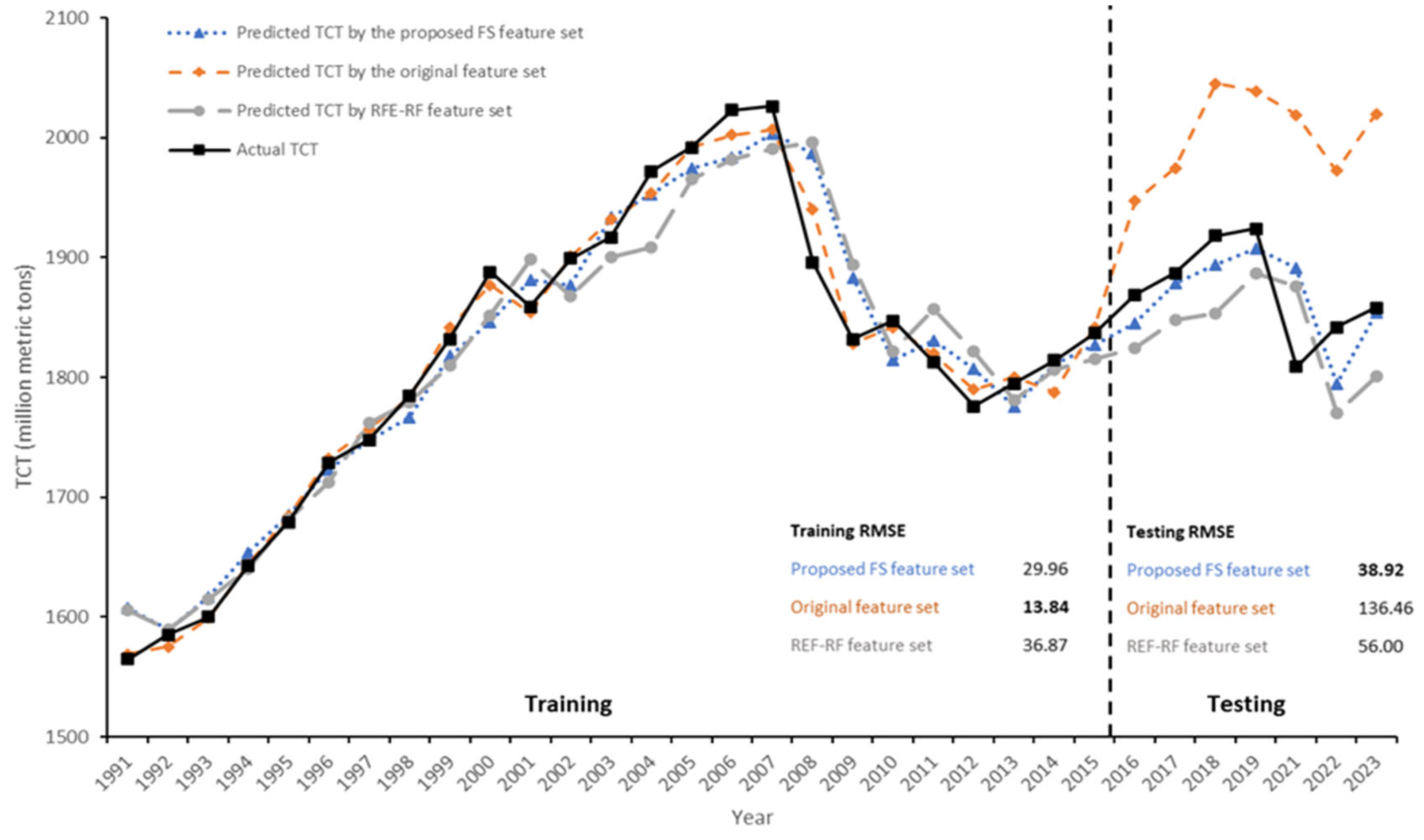
4.2. Modeling and Evaluation
4.3. SHAP Analysis
5. Policy Recommendations and Limitations
5.1. Policy Recommendations
5.2. Limitations
6. Conclusions and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEA. Energy Technology Perspectives. 2020. Available online: https://www.iea.org/reports/energy-technology-perspectives-2020 (accessed on 1 September 2020).
- Our World in Data. Cars, Planes, Trains: Where Do CO2 Emissions from Transport Come from? Available online: https://ourworldindata.org/co2-emissions-from-transport (accessed on 6 October 2020).
- EIA. U.S. Energy-Related Carbon Dioxide Emissions. 2023. Available online: https://www.eia.gov/environment/emissions/carbon/ (accessed on 29 May 2025).
- Yin, C.; Wu, J.; Sun, X.; Meng, Z.; Lee, C. Road transportation emission prediction and policy formulation: Machine learning model analysis. Transp. Res. Part D Transp. Environ. 2024, 135, 104390. [Google Scholar] [CrossRef]
- Ağbulut, Ü. Forecasting of transportation-related energy demand and CO2 emissions in Turkey with different machine learning algorithms. Sustain. Prod. Consum. 2022, 29, 141–157. [Google Scholar] [CrossRef]
- Janhuaton, T.; Ratanavaraha, V.; Jomnonkwao, S. Forecasting Thailand’s Transportation CO2 Emissions: A Comparison among Artificial Intelligent Models. Forecasting 2024, 6, 462–484. [Google Scholar] [CrossRef]
- Bamrungwong, N.; Vongmanee, V.; Rattanawong, W. The development of a CO2 emission coefficient for medium-and heavy-duty vehicles with different road slope conditions using multiple linear regression, and considering the health effects. Sustainability 2020, 12, 6994. [Google Scholar] [CrossRef]
- Huang, S.; Xiao, X.; Guo, H. A novel method for carbon emission forecasting based on EKC hypothesis and nonlinear multivariate grey model: Evidence from transportation sector. Environ. Sci. Pollut. Res. 2022, 29, 60687–60711. [Google Scholar] [CrossRef]
- Sangeetha, A.; Amudha, T. A novel bio-inspired framework for CO2 emission forecast in India. Procedia Comput. Sci. 2018, 125, 367–375. [Google Scholar] [CrossRef]
- Singh, P.K.; Pandey, A.K.; Ahuja, S.; Kiran, R. Multiple forecasting approach: A prediction of CO2 emission from the paddy crop in India. Environ. Sci. Pollut. Res. 2022, 29, 25461–25472. [Google Scholar] [CrossRef]
- Xu, B.; Lin, B. Factors affecting carbon dioxide (CO2) emissions in China’s transport sector: A dynamic nonparametric additive regression model. J. Clean. Prod. 2015, 101, 311–322. [Google Scholar] [CrossRef]
- Solaymani, S. CO2 emissions patterns in 7 top carbon emitter economies: The case of transport sector. Energy 2019, 168, 989–1001. [Google Scholar] [CrossRef]
- Saboori, B.; Sapri, M.; bin Baba, M. Economic growth, energy consumption and CO2 emissions in OECD (Organization for Economic Co-operation and Development)’s transport sector: A fully modified bi-directional relationship approach. Energy 2014, 66, 150–161. [Google Scholar] [CrossRef]
- Jabali, O.; Van Woensel, T.; De Kok, A. Analysis of travel times and CO2 emissions in time-dependent vehicle routing. Prod. Oper. Manag. 2012, 21, 1060–1074. [Google Scholar] [CrossRef]
- Zagow, M.; Elbany, M.; Darwish, A.M. Identifying urban, transportation, and socioeconomic characteristics across US zip codes affecting CO2 emissions: A decision tree analysis. Energy Built Environ. 2024, 6, 484–494. [Google Scholar] [CrossRef]
- Javanmard, M.E.; Tang, Y.; Wang, Z.; Tontiwachwuthikul, P. Forecast energy demand, CO2 emissions and energy resource impacts for the transportation sector. Appl. Energy 2023, 338, 120830. [Google Scholar] [CrossRef]
- Sun, W.; Wang, C.; Zhang, C. Factor analysis and forecasting of CO2 emissions in Hebei, using extreme learning machine based on particle swarm optimization. J. Clean. Prod. 2017, 162, 1095–1101. [Google Scholar] [CrossRef]
- Xu, G.; Schwarz, P.; Yang, H. Determining China’s CO2 emissions peak with a dynamic nonlinear artificial neural network approach and scenario analysis. Energy Policy 2019, 128, 752–762. [Google Scholar] [CrossRef]
- Chukwunonso, B.P.; Al-Wesabi, I.; Shixiang, L.; AlSharabi, K.; Al-Shamma’a, A.A.; Farh, H.M.H.; Saeed, F.; Kandil, T.; Al-Shaalan, A.M. Predicting carbon dioxide emissions in the United States of America using machine learning algorithms. Environ. Sci. Pollut. Res. 2024, 31, 33685–33707. [Google Scholar] [CrossRef]
- Ahmed, M.; Shuai, C.; Ahmed, M. Analysis of energy consumption and greenhouse gas emissions trend in China, India, the USA, and Russia. Int. J. Environ. Sci. Technol. 2023, 20, 2683–2698. [Google Scholar] [CrossRef]
- Mishra, S.; Sinha, A.; Sharif, A.; Suki, N.M. Dynamic linkages between tourism, transportation, growth and carbon emission in the USA: Evidence from partial and multiple wavelet coherence. Curr. Issues Tour. 2020, 23, 2733–2755. [Google Scholar] [CrossRef]
- Qiao, Q.; Eskandari, H.; Saadatmand, H.; Sahraei, M.A. An interpretable multi-stage forecasting framework for energy consumption and CO2 emissions for the transportation sector. Energy 2024, 286, 129499. [Google Scholar] [CrossRef]
- Fu, H.; Li, H.; Fu, A.; Wang, X.; Wang, Q. Transportation emissions monitoring and policy research: Integrating machine learning and satellite imaging. Transp. Res. Part D Transp. Environ. 2024, 136, 104421. [Google Scholar] [CrossRef]
- Ulussever, T.; Kılıç Depren, S.; Kartal, M.T.; Depren, Ö. Estimation performance comparison of machine learning approaches and time series econometric models: Evidence from the effect of sector-based energy consumption on CO2 emissions in the USA. Environ. Sci. Pollut. Res. 2023, 30, 52576–52592. [Google Scholar] [CrossRef]
- Li, X.; Ren, A.; Li, Q. Exploring patterns of transportation-related CO2 emissions using machine learning methods. Sustainability 2022, 14, 4588. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J. Determinants investigation and peak prediction of CO2 emissions in China’s transport sector utilizing bio-inspired extreme learning machine. Environ. Sci. Pollut. Res. 2021, 28, 55535–55553. [Google Scholar] [CrossRef]
- Alfaseeh, L.; Tu, R.; Farooq, B.; Hatzopoulou, M. Greenhouse gas emission prediction on road network using deep sequence learning. Transp. Res. Part D Transp. Environ. 2020, 88, 102593. [Google Scholar] [CrossRef]
- Qin, J.; Gong, N. The estimation of the carbon dioxide emission and driving factors in China based on machine learning methods. Sustain. Prod. Consum. 2022, 33, 218–229. [Google Scholar] [CrossRef]
- Wang, L.; Xue, X.; Zhao, Z.; Wang, Y.; Zeng, Z. Finding the de-carbonization potentials in the transport sector: Application of scenario analysis with a hybrid prediction model. Environ. Sci. Pollut. Res. 2020, 27, 21762–21776. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Ding, Y.; Cheng, J.C.; Jiang, F.; Tan, Y.; Gan, V.J.; Wan, Z. Identification of high impact factors of air quality on a national scale using big data and machine learning techniques. J. Clean. Prod. 2020, 244, 118955. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Y. Modeling and predicting city-level CO2 emissions using open access data and machine learning. Environ. Sci. Pollut. Res. 2021, 28, 19260–19271. [Google Scholar] [CrossRef]
- Van Zyl, C.; Ye, X.; Naidoo, R. Harnessing eXplainable artificial intelligence for feature selection in time series energy forecasting: A comparative analysis of Grad-CAM and SHAP. Appl. Energy 2024, 353, 122079. [Google Scholar] [CrossRef]
- Amiri, S.S.; Mostafavi, N.; Lee, E.R.; Hoque, S. Machine learning approaches for predicting household transportation energy use. City Environ. Interact. 2020, 7, 100044. [Google Scholar] [CrossRef]
- Karasu, S.; Altan, A.; Bekiros, S.; Ahmad, W. A new forecasting model with wrapper-based feature selection approach using multi-objective optimization technique for chaotic crude oil time series. Energy 2020, 212, 118750. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, S.; Li, Y. Dynamic NOX emission concentration prediction based on the combined feature selection algorithm and deep neural network. Energy 2024, 292, 130608. [Google Scholar] [CrossRef]
- Peng, T.; Yang, X.; Xu, Z.; Liang, Y. Constructing an environmental friendly low-carbon-emission intelligent transportation system based on big data and machine learning methods. Sustainability 2020, 12, 8118. [Google Scholar] [CrossRef]
- Chadha, A.S.; Shinde, Y.; Sharma, N.; De, P.K. Predicting CO2 emissions by vehicles using machine learning. In Proceedings of the International Conference on Data Management, Analytics & Innovation, Virtual Conference, 14–16 January 2022; pp. 197–207. [Google Scholar]
- Anonna, F.R.; Mohaimin, M.R.; Ahmed, A.; Nayeem, M.B.; Akter, R.; Alam, S.; Nasiruddin, M.; Hossain, M.S. Machine Learning-Based Prediction of US CO2 Emissions: Developing Models for Forecasting and Sustainable Policy Formulation. J. Environ. Agric. Stud. 2023, 4, 85–99. [Google Scholar]
- Jha, R.; Jha, R.; Islam, M. Forecasting US data center CO2 emissions using AI models: Emissions reduction strategies and policy recommendations. Front. Sustain. 2025, 5, 1507030. [Google Scholar] [CrossRef]
- Li, S.; Tong, Z.; Haroon, M. Estimation of transport CO2 emissions using machine learning algorithm. Transp. Res. Part D Transp. Environ. 2024, 133, 104276. [Google Scholar] [CrossRef]
- Tian, L.; Zhang, Z.; He, Z.; Yuan, C.; Xie, Y.; Zhang, K.; Jing, R. Predicting Energy-Based CO2 Emissions in the United States Using Machine Learning: A Path Toward Mitigating Climate Change. Sustainability 2025, 17, 2843. [Google Scholar] [CrossRef]
- Ajala, A.A.; Adeoye, O.L.; Salami, O.M.; Jimoh, A.Y. An examination of daily CO2 emissions prediction through a comparative analysis of machine learning, deep learning, and statistical models. Environ. Sci. Pollut. Res. 2025, 32, 2510–2535. [Google Scholar] [CrossRef]
- Monath, N.; Dubey, K.A.; Guruganesh, G.; Zaheer, M.; Ahmed, A.; McCallum, A.; Mergen, G.; Najork, M.; Terzihan, M.; Tjanaka, B. Scalable hierarchical agglomerative clustering. In Proceedings of the Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; pp. 1245–1255. [Google Scholar]
- Tang, R.; Zhang, X. CART decision tree combined with Boruta feature selection for medical data classification. In Proceedings of the 2020 5th IEEE International Conference on Big Data Analytics (ICBDA), Xiamen, China, 8–11 May 2020; pp. 80–84. [Google Scholar]
- Hu, L.; Wang, C.; Ye, Z.; Wang, S. Estimating gaseous pollutants from bus emissions: A hybrid model based on GRU and XGBoost. Sci. Total Environ. 2021, 783, 146870. [Google Scholar] [CrossRef]
- Adegboye, O.R.; Ülker, E.D.; Feda, A.K.; Agyekum, E.B.; Mbasso, W.F.; Kamel, S. Enhanced multi-layer perceptron for CO2 emission prediction with worst moth disrupted moth fly optimization (WMFO). Heliyon 2024, 10, e31850. [Google Scholar] [CrossRef]
- Afzal, S.; Ziapour, B.M.; Shokri, A.; Shakibi, H.; Sobhani, B. Building energy consumption prediction using multilayer perceptron neural network-assisted models; comparison of different optimization algorithms. Energy 2023, 282, 128446. [Google Scholar] [CrossRef]
- Vapnik, V.N. The support vector method. In Proceedings of the International Conference on Artificial Neural Networks, Lausanne, Switzerland, 12 June 1997; pp. 261–271. [Google Scholar]
- Burges, C.J. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Cao, C.; Liao, J.; Hou, Z.; Wang, G.; Feng, W.; Fang, Y. Parametric uncertainty analysis for CO2 sequestration based on distance correlation and support vector regression. J. Nat. Gas Sci. Eng. 2020, 77, 103237. [Google Scholar] [CrossRef]
- Otten, N.V. What is Elastic Net Regression? Available online: https://spotintelligence.com/2024/11/20/elastic-net/ (accessed on 20 November 2024).
- Štrumbelj, E.; Kononenko, I. Explaining prediction models and individual predictions with feature contributions. Knowl. Inf. Syst. 2014, 41, 647–665. [Google Scholar] [CrossRef]
- Datta, A.; Sen, S.; Zick, Y. Algorithmic transparency via quantitative input influence: Theory and experiments with learning systems. In Proceedings of the 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 23–25 May 2016; pp. 598–617. [Google Scholar]
- Wen, X.; Xie, Y.; Wu, L.; Jiang, L. Quantifying and comparing the effects of key risk factors on various types of roadway segment crashes with LightGBM and SHAP. Accid. Anal. Prev. 2021, 159, 106261. [Google Scholar] [CrossRef]
- Li, Z. Extracting spatial effects from machine learning model using local interpretation method: An example of SHAP and XGBoost. Comput. Environ. Urban Syst. 2022, 96, 101845. [Google Scholar] [CrossRef]
- Shapley, L.S. A value for n-person games. Contrib. Theory Games 1953, 2, 307–317. [Google Scholar]
- Webb, G.I. Occam’s Razor. In Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2010; p. 735. [Google Scholar]




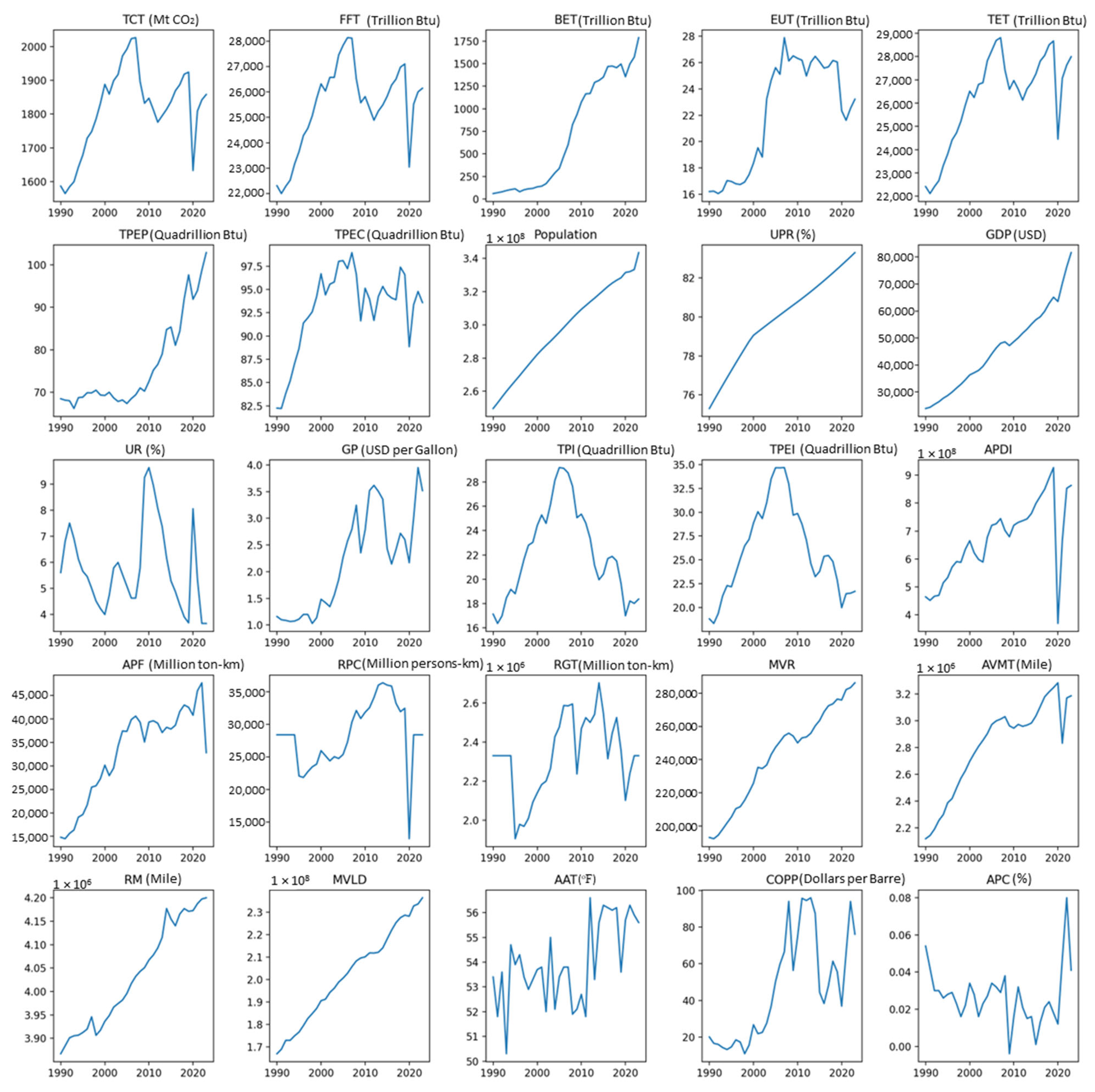




| Variables | Abbr. | Unit | Mean | Std | Min | Max |
|---|---|---|---|---|---|---|
| Total CO2 by Transportation | TCT | MtCO2 | 1814.09 | 125.51 | 1565.00 | 2026.00 |
| Total Fossil Fuels Consumed (transportation field) | FFT | Trillion Btu | 25,439.21 | 1691.27 | 21,994.76 | 28,142.77 |
| Biomass Energy Consumed (transportation field) | BET | Trillion Btu | 722.10 | 612.08 | 60.42 | 1788.41 |
| Electricity Sales to Ultimate Customers (transportation field) | EUT | Trillion Btu | 22.11 | 4.18 | 16.06 | 27.89 |
| Total Energy Consumed (Transportation field) | TET | Trillion Btu | 26,224.57 | 1982.71 | 22,114.32 | 28,810.91 |
| Total Primary Energy Production | TPEP | Quadrillion Btu | 76.31 | 10.78 | 66.20 | 102.85 |
| Total Primary Energy Consumption | TPEC | Quadrillion Btu | 92.94 | 4.47 | 82.21 | 98.97 |
| Population | --- | --- | 297,726,251.53 | 26,600,955.72 | 249,623,000.00 | 343,477,335.00 |
| Urban Population rate | UPR | % | 79.90 | 2.24 | 75.30 | 83.30 |
| GDP Per Capita | GDP | USD | 46,036.55 | 15,435.30 | 23,888.60 | 81,632.25 |
| Total Unemployment rate | UR | % | 5.77 | 1.63 | 3.65 | 9.63 |
| Retail Gasoline Prices | GP | USD per Gallon | 2.17 | 0.94 | 1.03 | 3.95 |
| Total Petroleum, Excluding Biofuels, Imports | TPI | Quadrillion Btu | 22.18 | 3.84 | 16.35 | 29.20 |
| Total Primary Energy Imports | TPEI | Quadrillion Btu | 26.02 | 4.81 | 18.33 | 34.68 |
| Air Passengers-Domestic and international | APDI | Million | 668,920,157.79 | 138,802,316.46 | 369,501,000.00 | 926,737,000.00 |
| Air transport, freight | APF | million ton-km | 32,826.18 | 9782.80 | 14,486.20 | 47,716.00 |
| Railways Passengers | RPC | million passenger-km | 28,411.97 | 5851.35 | 12,460.00 | 36,393.11 |
| Railways, goods transported | RGT | million ton-km | 2,330,457.76 | 227,003.11 | 1,906,206.0 | 2,702,736.0 |
| Number of motor vehicles registered | MVR | 1000 s | 242,272.71 | 28,968.71 | 192,314.00 | 286,300.00 |
| Annual Vehicle Miles Traveled | AVMT | Miles | 2,811,389.09 | 342,132.55 | 2,117,716.00 | 3,284,596.00 |
| Road Milage | RM | Mile | 4,032,513.13 | 111,366.49 | 3,866,926.00 | 4,200,000.00 |
| Motor vehicle licensed drivers | MVLD | Number | 202,325,783.05 | 20,679,848.46 | 167,015,250.00 | 236,404,000.00 |
| Average annual temperature | AAT | °F | 53.97 | 1.64 | 50.30 | 56.60 |
| Crude Oil First Purchase Price | COPP | Dollars per Barre | 46.70 | 29.21 | 10.87 | 95.99 |
| Annual Percent Change | APC | % | 0.03 | 0.02 | 0.00 | 0.08 |
| Model | Hyperparameter |
| Xgboost |
|
| MLP |
|
| SVR |
|
| Elastic Net |
|
| Variable | Correlation | p-Value | Boruta Ranking | Cluster | Decision |
|---|---|---|---|---|---|
| TPI | 0.684 | <0.001 | 2 | 1 | ○ |
| TPEI | 0.711 | <0.001 | 1 | 1 | ● |
| FFT | 0.881 | <0.001 | 1 | 2 | ● |
| TPEC | 0.789 | <0.001 | 1 | 2 | ○ |
| BET | 0.44 | <0.05 | 1 | 3 | ○ |
| TPEP | 0.075 | 0.68 | 1 | 3 | ○ |
| Population | 0.449 | <0.01 | 1 | 3 | ○ |
| UPR | 0.449 | <0.01 | 1 | 3 | ○ |
| GDP | 0.45 | <0.01 | 1 | 3 | ○ |
| APF | 0.517 | <0.01 | 1 | 3 | ○ |
| MVR | 0.486 | <0.01 | 1 | 3 | ○ |
| AVMT | 0.572 | <0.001 | 1 | 3 | ● |
| RM | 0.418 | <0.05 | 2 | 3 | ○ |
| MVLD | 0.448 | <0.05 | 1 | 3 | ○ |
| AAT | 0.245 | 0.18 | 7 | 4 | ○ |
| RPC | −0.056 | 0.76 | 9 | 5 | ○ |
| RGT | 0.194 | 0.29 | 10 | 5 | ○ |
| EUT | 0.459 | <0.05 | 3 | 6 | ○ |
| GP | 0.295 | 0.1 | 4 | 6 | ○ |
| APDI | 0.503 | <0.01 | 1 | 6 | ● |
| COPP | 0.272 | 0.13 | 5 | 6 | ○ |
| UR | −0.483 | <0.01 | 6 | 7 | ● |
| APC | −0.18 | 0.32 | 8 | 8 | ○ |
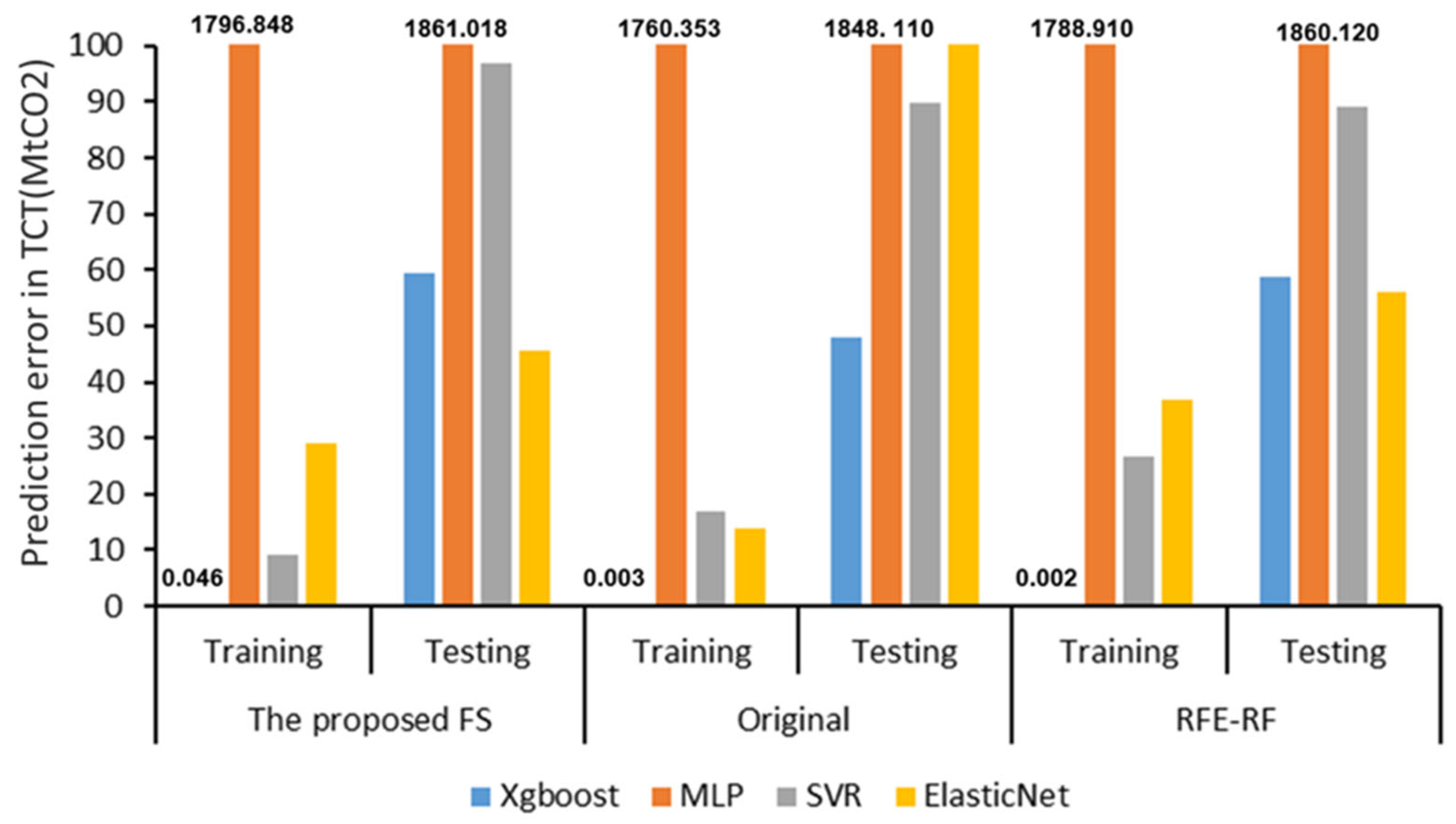
| ML | Metrics | The Proposed FS | Original | RFE-RF | |||
|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | ||
| Xgboost | StD | 0.045 | 58.823 | 0.003 | 39.562 | 0.002 | 39.334 |
| RMSE | 0.046 | 59.280 | 0.003 | 47.849 | 0.002 | 58.574 | |
| MAE | 0.046 | 45.227 | 0.002 | 44.540 | 0.002 | 52.498 | |
| MAPE | 1.99 × 10−5 | 0.0243 | 1.32 × 10−6 | 0.023 | 1.22 × 10−6 | 0.027 | |
| MLP | StD | 135.220 | 37.638 | 169.130 | 37.408 | 143.540 | 38.363 |
| RMSE | 1796.848 | 1861.018 | 1760.353 | 1848.11 | 1788.91 | 1860.122 | |
| MAE | 1792.046 | 1860.637 | 1752.73 | 1847.738 | 1783.030 | 1859.74 | |
| MAPE | 0.987 | 0.993 | 0.964 | 0.986 | 0.982 | 0.993 | |
| SVR | StD | 8.880 | 94.998 | 16.890 | 63.669 | 20.707 | 170.830 |
| RMSE | 8.992 | 96.994 | 16.978 | 89.629 | 26.676 | 89.045 | |
| MAE | 5.433 | 79.123 | 8.346 | 63.084 | 17.325 | 64.5 | |
| MAPE | 0.002 | 0.042 | 0.004 | 0.034 | 0.009 | 0.035 | |
| Elastic Net | StD | 28.977 | 45.257 | 13.837 | 41.652 | 35.404 | 48.434 |
| RMSE | 28.977 | 45.533 | 13.837 | 136.464 | 36.873 | 55.999 | |
| MAE | 22.462 | 30.6 | 9.821 | 129.952 | 29.393 | 54.405 | |
| MAPE | 0.012 | 0.016 | 0.005 | 0.069 | 0.015 | 0.029 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahraei, M.A.; Li, K.; Qiao, Q. A Multi-Stage Feature Selection and Explainable Machine Learning Framework for Forecasting Transportation CO2 Emissions. Energies 2025, 18, 4184. https://doi.org/10.3390/en18154184
Sahraei MA, Li K, Qiao Q. A Multi-Stage Feature Selection and Explainable Machine Learning Framework for Forecasting Transportation CO2 Emissions. Energies. 2025; 18(15):4184. https://doi.org/10.3390/en18154184
Chicago/Turabian StyleSahraei, Mohammad Ali, Keren Li, and Qingyao Qiao. 2025. "A Multi-Stage Feature Selection and Explainable Machine Learning Framework for Forecasting Transportation CO2 Emissions" Energies 18, no. 15: 4184. https://doi.org/10.3390/en18154184
APA StyleSahraei, M. A., Li, K., & Qiao, Q. (2025). A Multi-Stage Feature Selection and Explainable Machine Learning Framework for Forecasting Transportation CO2 Emissions. Energies, 18(15), 4184. https://doi.org/10.3390/en18154184







