Study on Thermal Conductivity Prediction of Granites Using Data Augmentation and Machine Learning
Abstract
1. Introduction
2. Methodology and Materials
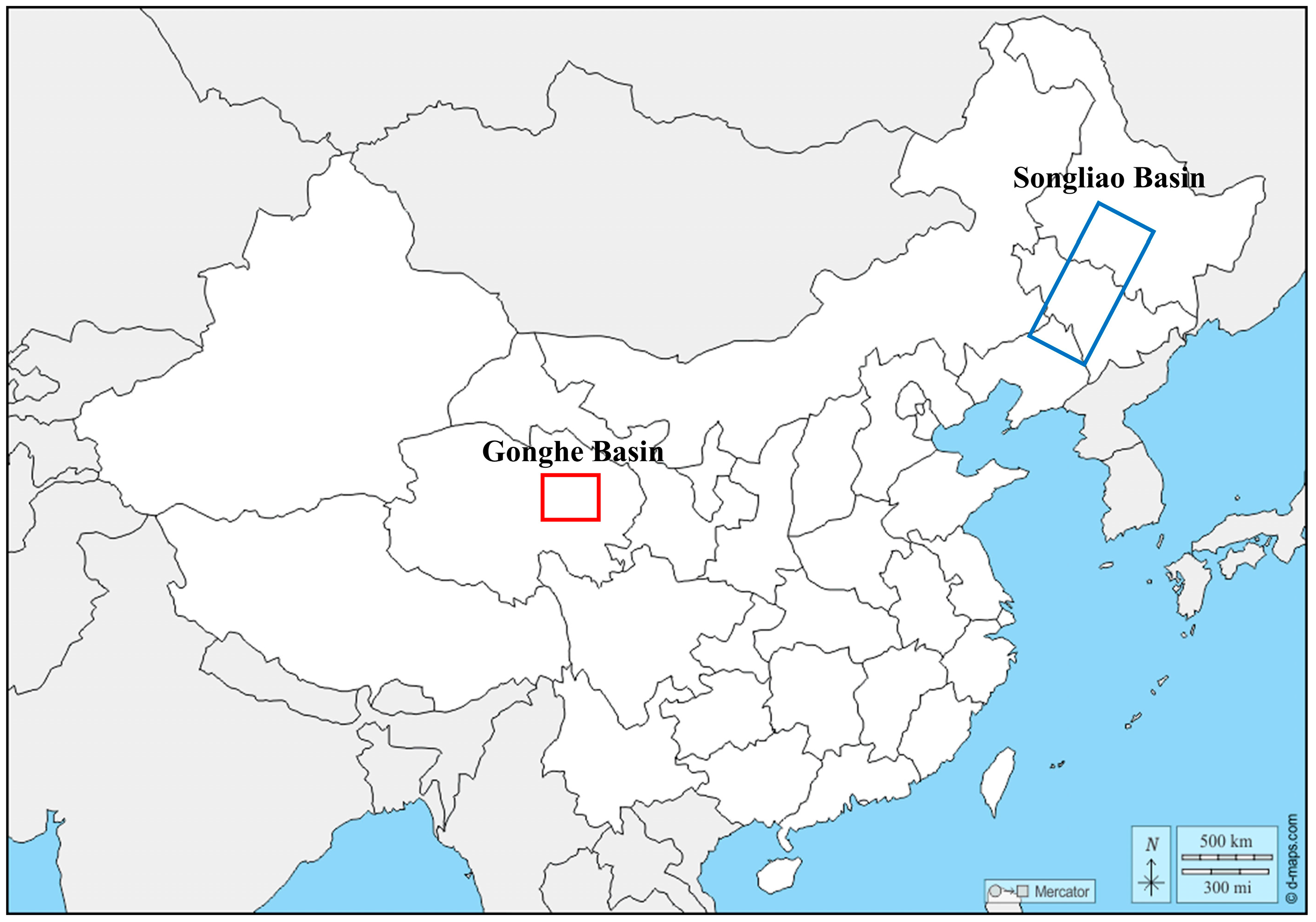
2.1. Geologic Background
2.2. Laboratory Test
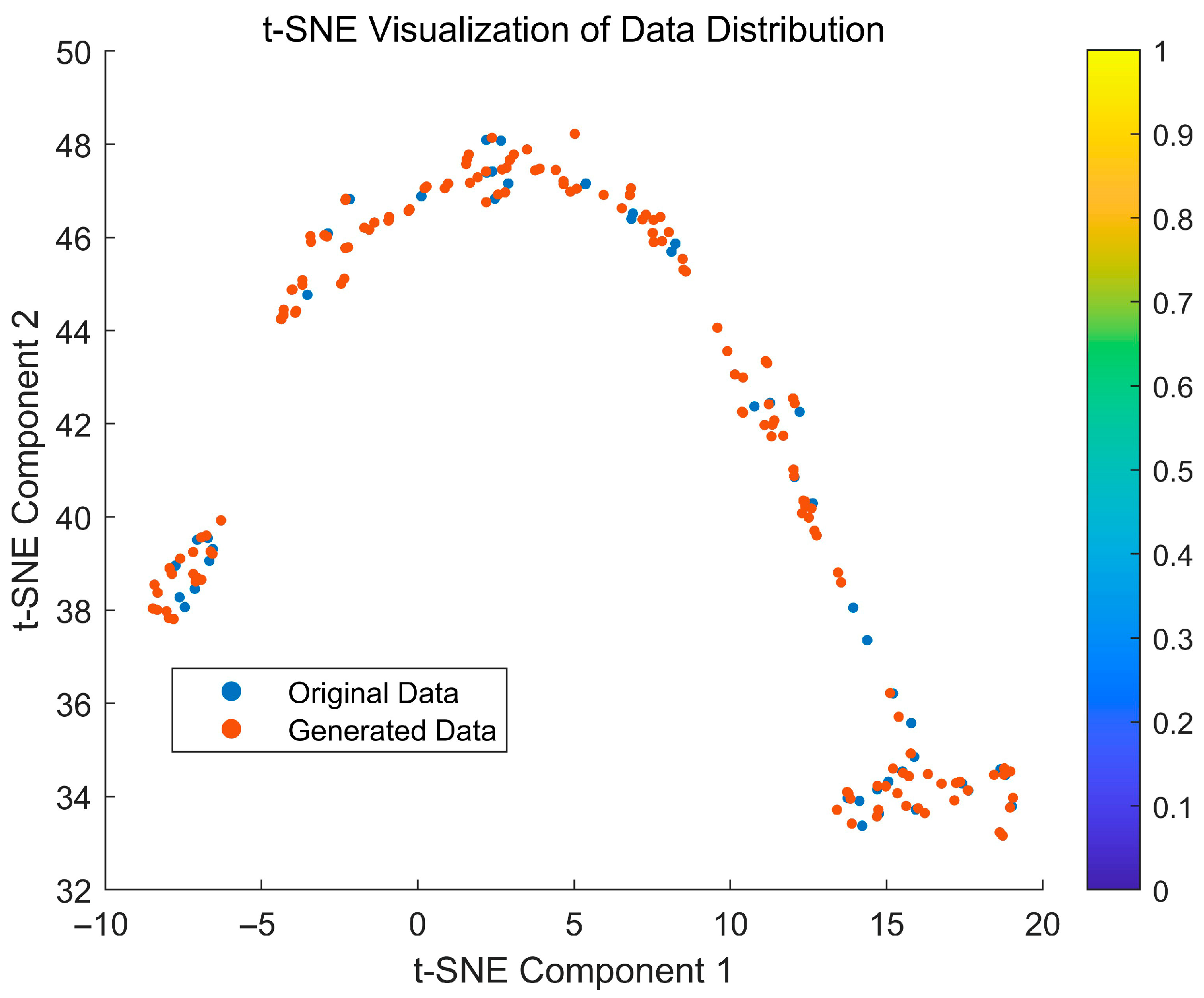
2.3. Data Enhancement
2.4. Machine Learning Models
2.4.1. Support Vector Machine (SVM)
2.4.2. Random Forest (RF)
2.4.3. Backpropagation Neural Network (BPNN)
2.5. Model Parameter Setting, Training, Validation, and Evaluation
2.5.1. Parameter Settings
2.5.2. Model Training
2.5.3. Model Validation and Evaluation
3. Results and Discussion
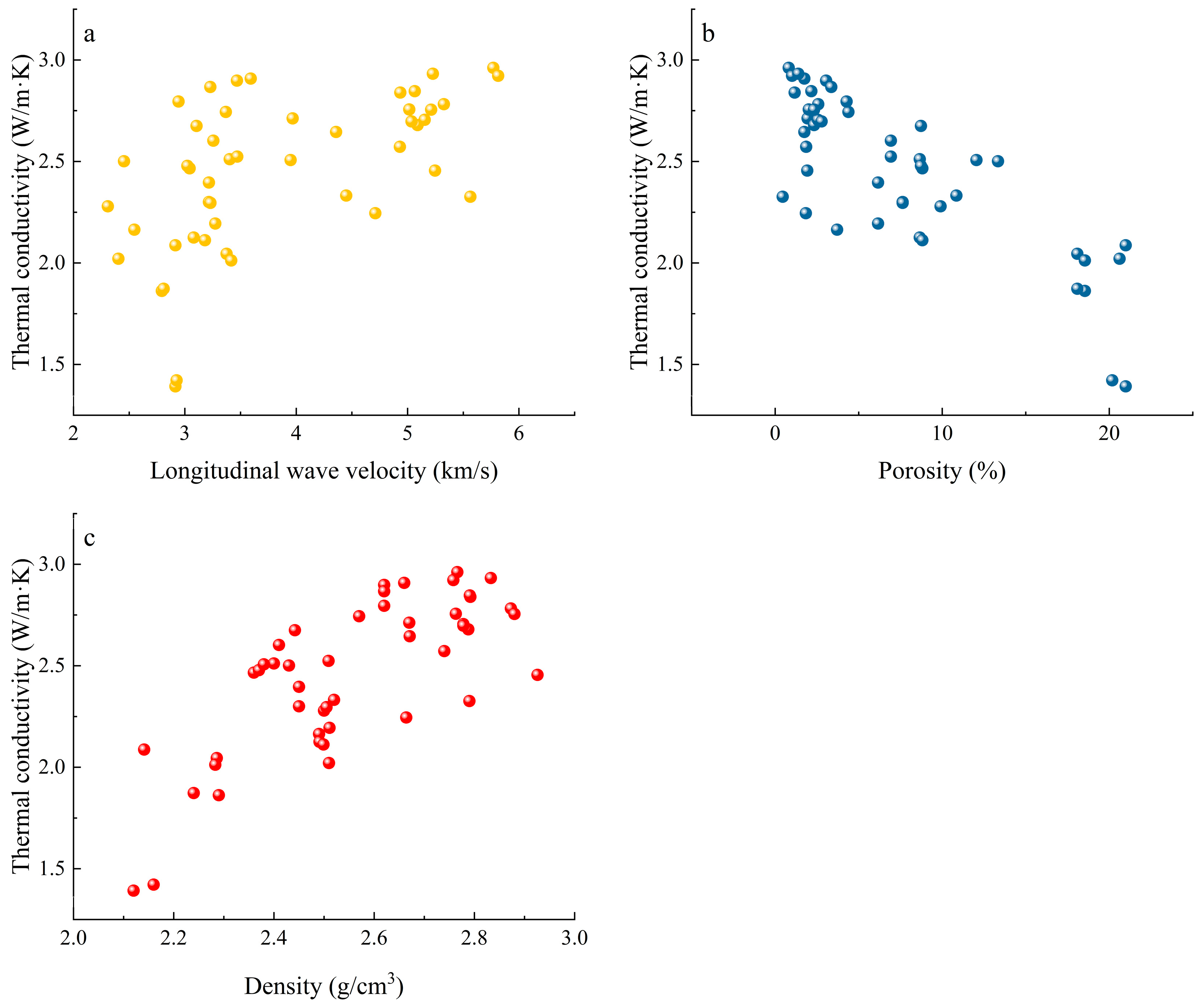
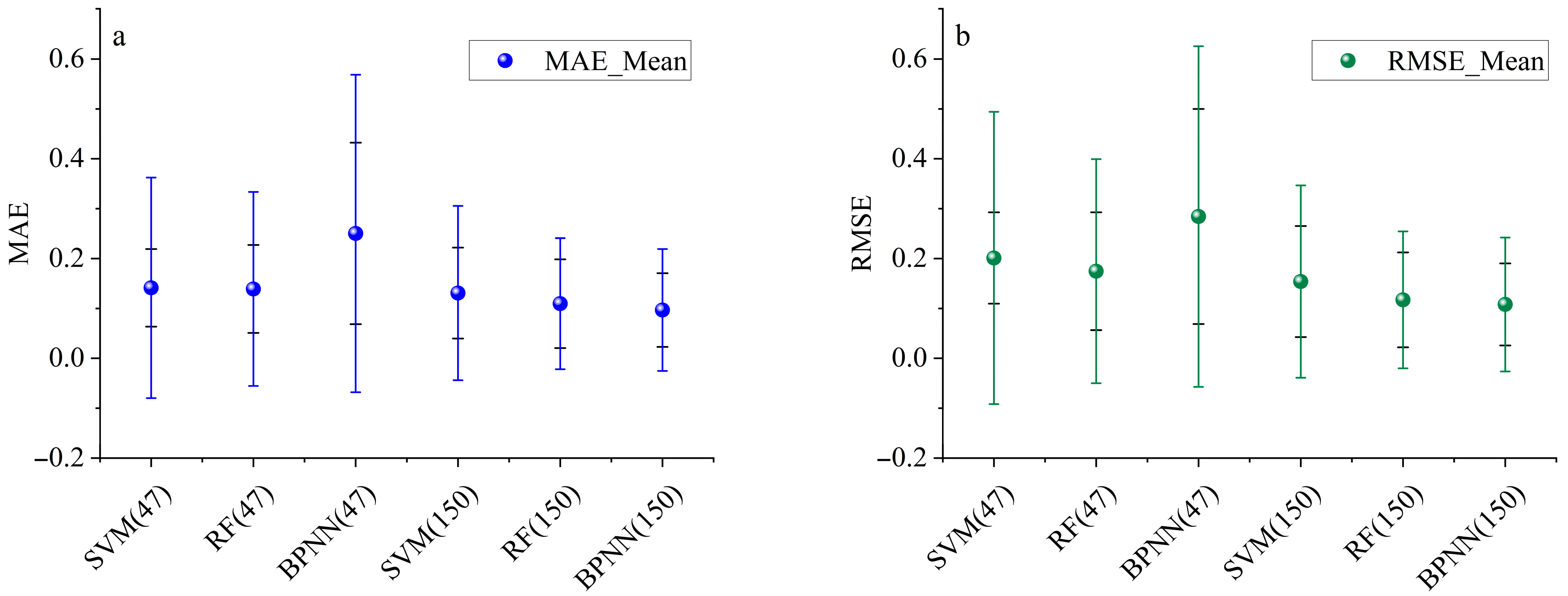
3.1. Analysis of Test Results and Enhancement Analysis
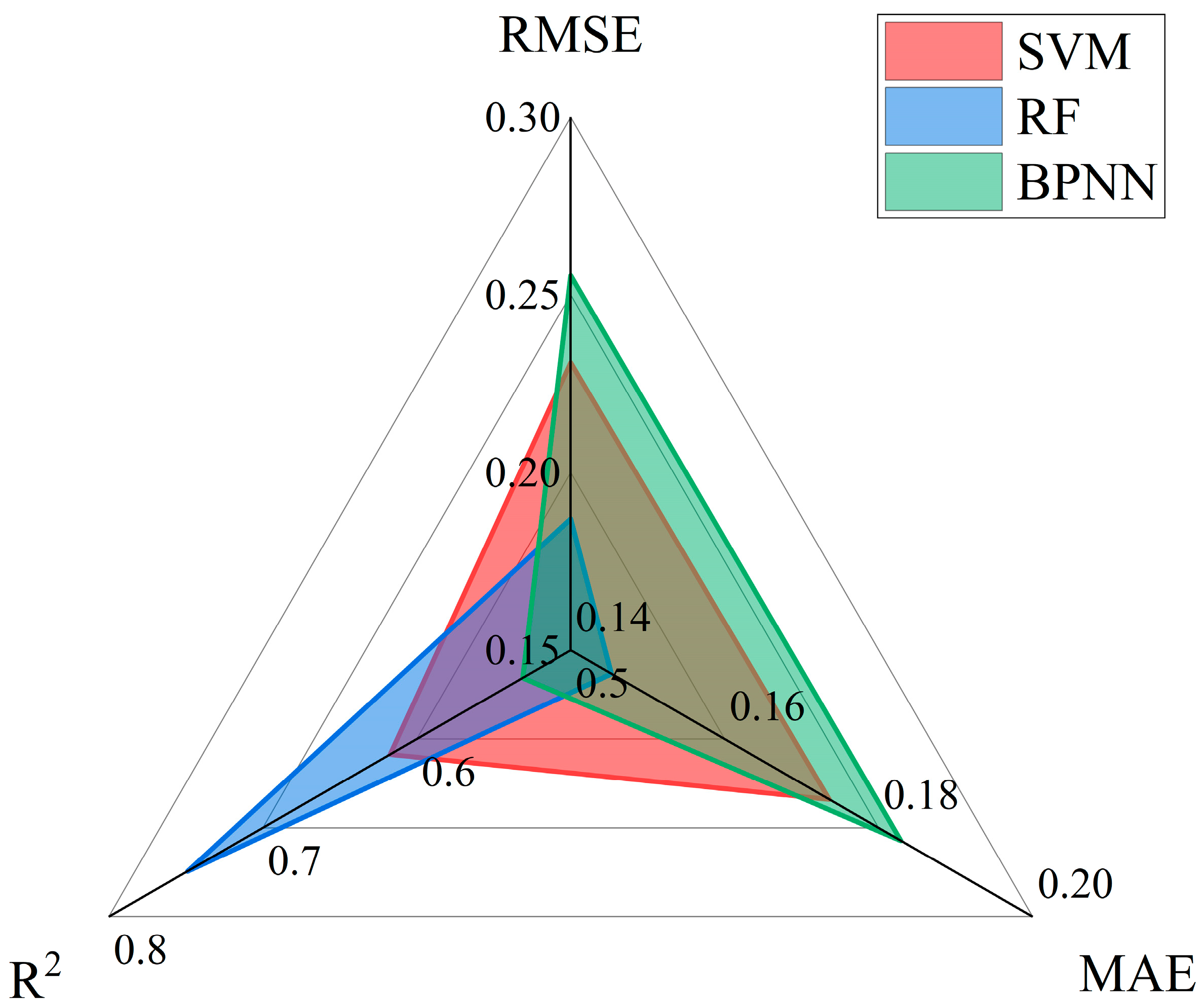
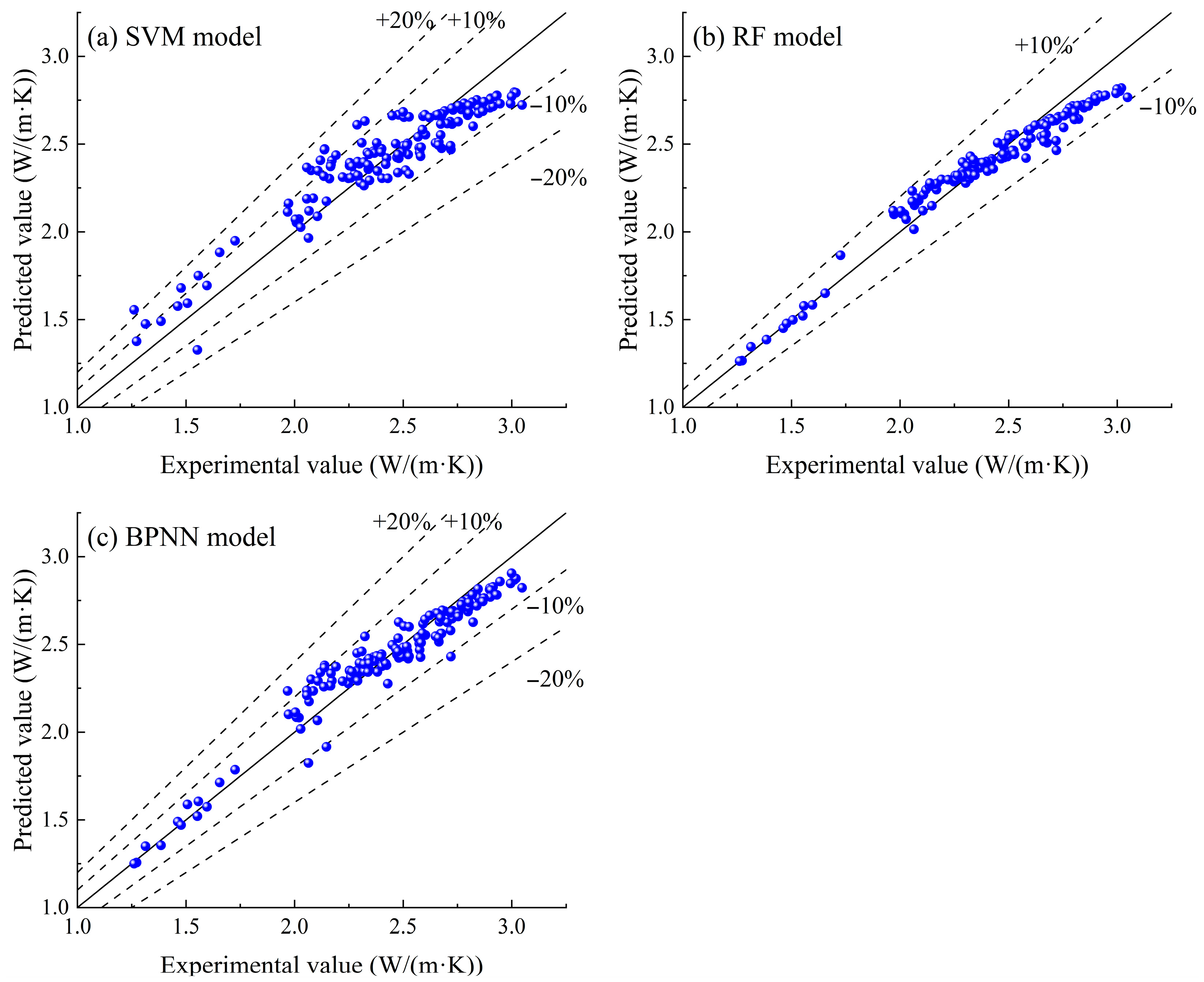
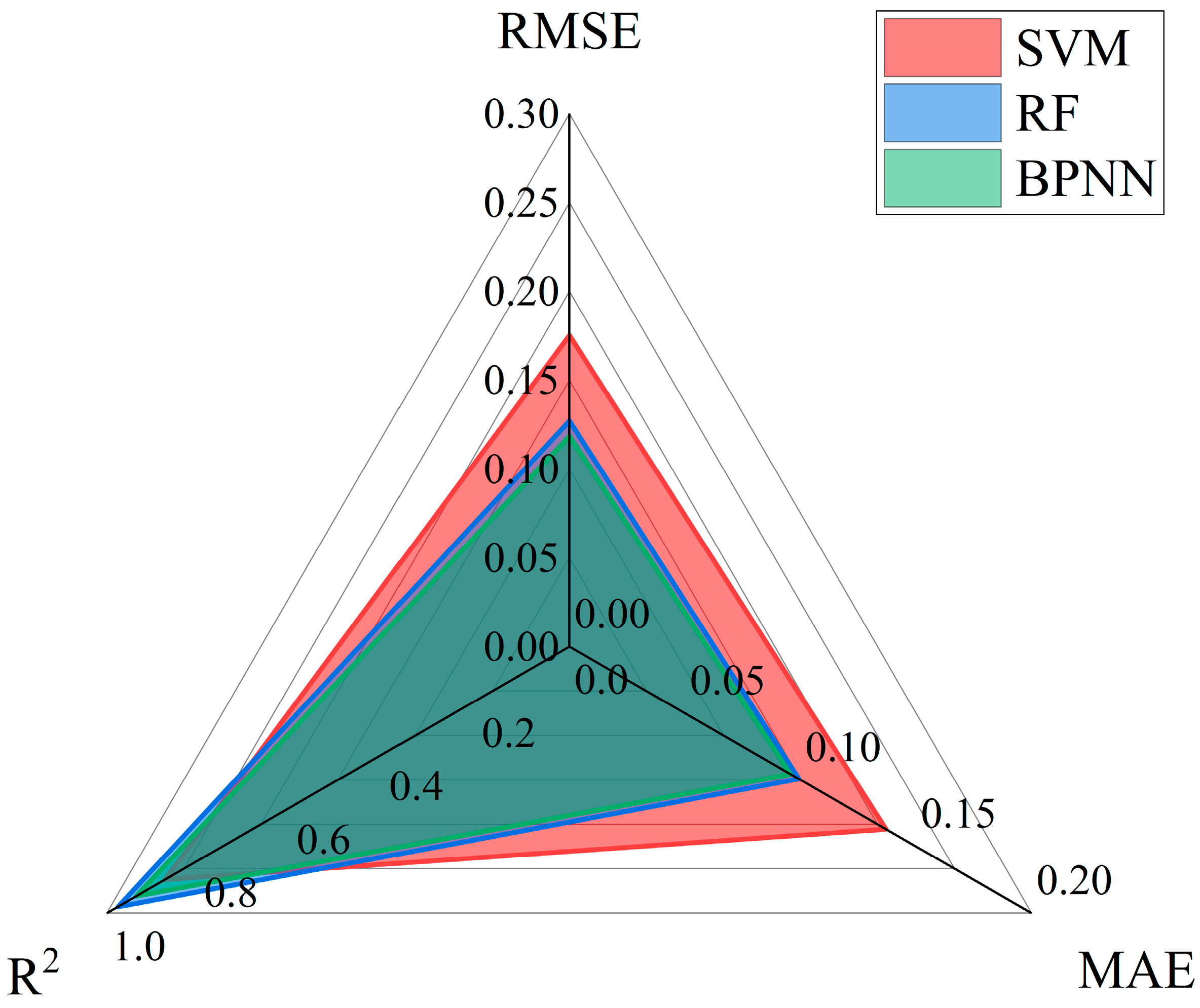
3.2. Comparison of Model Prediction Performance
3.3. Analysis of Relative Importance of Input Features
4. Conclusions
Research Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, F.; Lin, J.; He, G.; Wang, S.; Huang, X.; Zhao, B.; Wang, S.; Han, Y.; Qi, S. Analysis of geothermal resources in the northeast margin of the Pamir plateau. Geothermics 2025, 127, 103254. [Google Scholar] [CrossRef]
- Spichak, V.V.; Nenyukova, A.I. Delineating crustal domains favorable for exploring enhanced geothermal resources based on temperature, petro- and thermophysical properties of rocks: A case study of the Soultz-sous-Forêts geothermal site, France. Renew. Energy 2025, 246, 122902. [Google Scholar] [CrossRef]
- Yu, Z.; Ye, X.; Zhang, Y.; Gao, P.; Huang, Y. Experimental research on the thermal conductivity of unsaturated rocks in geothermal engineering. Energy 2023, 282, 129019. [Google Scholar] [CrossRef]
- Dong, S.; Yu, Y.; Li, B.; Ni, L. Thermal analysis of medium-depth borehole heat exchanger coupled layered stratum thermal conductivity. Renew. Energy 2025, 246, 122880. [Google Scholar] [CrossRef]
- Sowiżdżał, A.; Machowski, G.; Krzyżak, A.; Puskarczyk, E.; Krakowska-Madejska, P.; Chmielowska, A. Petrophysical evaluation of the Lower Permian formation as a potential reservoir for CO2-EGS—Case study from NW Poland. J. Clean. Prod. 2022, 379, 134768. [Google Scholar] [CrossRef]
- Oh, H.-R.; Baek, J.-Y.; Park, B.-H.; Kim, S.-K.; Lee, K.-K. Influence of borehole characteristics on thermal response test analysis using analytical models. Appl. Therm. Eng. 2025, 268, 125892. [Google Scholar] [CrossRef]
- García-Noval, C.; Álvarez, R.; García-Cortés, S.; García, C.; Alberquilla, F.; Ordóñez, A. Definition of a thermal conductivity map for geothermal purposes. Geotherm. Energy 2024, 12, 17. [Google Scholar] [CrossRef]
- Priarone, A.; Morchio, S.; Fossa, M.; Memme, S. Low-Cost Distributed Thermal Response Test for the Estimation of Thermal Ground and Grout Conductivities in Geothermal Heat Pump Applications. Energies 2023, 16, 7393. [Google Scholar] [CrossRef]
- Wilke, S.; Menberg, K.; Steger, H.; Blum, P. Advanced thermal response tests: A review. Renew. Sustain. Energy Rev. 2020, 119, 109575. [Google Scholar] [CrossRef]
- Kang, J.; Yu, Z.; Wu, S.; Zhang, Y.; Gao, P. Feasibility analysis of extreme learning machine for predicting thermal conductivity of rocks. Environ. Earth Sci. 2021, 80, 455. [Google Scholar] [CrossRef]
- Mahmoodzadeh, A.; Mohammadi, M.; Salim, S.G.; Ali, H.F.H.; Ibrahim, H.H.; Abdulhamid, S.N.; Nejati, H.R.; Rashidi, S. Machine Learning Techniques to Predict Rock Strength Parameters. Rock Mech. Rock Eng. 2022, 55, 1721–1741. [Google Scholar] [CrossRef]
- Zamanzadeh Talkhouncheh, M.; Davoodi, S.; Wood, D.A.; Mehrad, M.; Rukavishnikov, V.S.; Bakhshi, R. Robust Machine Learning Predictive Models for Real-Time Determination of Confined Compressive Strength of Rock Using Mudlogging Data. Rock Mech. Rock Eng. 2024, 57, 6881–6907. [Google Scholar] [CrossRef]
- Xu, H.; Yan, J.; Feng, G.; Jia, Z.; Jing, P. Rock Layer Classification and Identification in Ground-Penetrating Radar via Machine Learning. Remote Sens. 2024, 16, 1310. [Google Scholar] [CrossRef]
- Ali, N.; Fu, X.; Chen, J.; Hussain, J.; Hussain, W.; Rahman, N.; Iqbal, S.M.; Altalbe, A. Advancing Reservoir Evaluation: Machine Learning Approaches for Predicting Porosity Curves. Energies 2024, 17, 3768. [Google Scholar] [CrossRef]
- Bu, M.; Fang, C.; Guo, P.; Jin, X.; Wang, J. Predicting thermal conductivity of granite subjected to high temperature using machine learning techniques. Environ. Earth Sci. 2025, 84, 219. [Google Scholar] [CrossRef]
- Luo, P.; Fang, X.; Li, D.; Yu, Y.; Li, H.; Cui, P.; Ma, J. Evaluation of excavation method on point load strength of rocks with poor geological conditions in a deep metal mine. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 90. [Google Scholar] [CrossRef]
- Zhang, C.-h.; Wang, Y.; Wu, L.-j.; Dong, Z.-k.; Li, X. Physics-informed and data-driven machine learning of rock mass classification using prior geological knowledge and TBM operational data. Tunn. Undergr. Space Technol. 2024, 152, 105923. [Google Scholar] [CrossRef]
- Chen, M.; Kang, X.; Ma, X. Deep Learning-Based Enhancement of Small Sample Liquefaction Data. Int. J. Geomech. 2023, 23, 04023140. [Google Scholar] [CrossRef]
- Mehdi, S.; Smith, Z.; Herron, L.; Zou, Z.; Tiwary, P. Enhanced Sampling with Machine Learning. Annu. Rev. Phys. Chem. 2024, 75, 347–370. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Yu, X.; Wang, X.; Wang, Z.; Chao, G. Enhanced transfer learning with data augmentation. Eng. Appl. Artif. Intell. 2024, 129, 107602. [Google Scholar] [CrossRef]
- Li, X.; Ao, Y.; Guo, S.; Zhu, L. Combining Regression Kriging With Machine Learning Mapping for Spatial Variable Estimation. IEEE Geosci. Remote Sens. Lett. 2020, 17, 27–31. [Google Scholar] [CrossRef]
- Wang, T.; Trugman, D.; Lin, Y. SeismoGen: Seismic Waveform Synthesis Using GAN With Application to Seismic Data Augmentation. JGR Solid Earth 2021, 126, e2020JB020077. [Google Scholar] [CrossRef]
- Bai, L.; Li, J.; Zeng, Z.; Tao, D. Prediction of Terrestrial Heat Flow in Songliao Basin Based on Deep Neural Network. Earth Space Sci. 2023, 10, e2023EA003186. [Google Scholar] [CrossRef]
- Huang, J.; Lu, C.; Huang, D.; Qin, Y.; Xin, F.; Sheng, H. A Spatial Interpolation Method for Meteorological Data Based on a Hybrid Kriging and Machine Learning Approach. Int. J. Climatol. 2024, 44, 5371–5380. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, J.; Wang, X.; Liang, M.; Li, D.; Liang, M.; Ou, Y.; Jia, D.; Tang, X.; Li, X. Deep structure and geothermal resource effects of the Gonghe basin revealed by 3D magnetotelluric. Geotherm. Energy 2024, 12, 6. [Google Scholar] [CrossRef]
- Niu, P.; Han, J.; Zeng, Z.; Hou, H.; Liu, L.; Ma, G.; Guan, Y. Deep controlling factors of the geothermal field in the northern Songliao basin derived from magnetotelluric survey. Chin. J. Geophys. 2021, 64, 4060–4074. [Google Scholar] [CrossRef]
- Rao, G.; Pujari, D.G.; Khalkar, R.G.; Medhe, V.A. Study on Software Defect Prediction Based on SVM and Decision Tree Algorithm. Int. J. Recent Innov. Trends Comput. Commun. 2023, 11, 90–95. [Google Scholar] [CrossRef]
- Liu, G. Tropical climate prediction method combining random forest and feature fusion. Int. J. Low-Carbon Technol. 2025, 20, 154–166. [Google Scholar] [CrossRef]
- Shao, J.-J.; Li, L.-B.; Yin, G.-J.; Wen, X.-D.; Zou, Y.-X.; Zuo, X.-B.; Gao, X.-J.; Cheng, S.-S. Prediction of Compressive Strength of Fly Ash-Recycled Mortar Based on Grey Wolf Optimizer–Backpropagation Neural Network. Materials 2025, 18, 139. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, Y.; Yu, Z.; Yang, Y. Reservoir temperature prediction based on characterization of water chemistry data—Case study of western Anatolia, Turkey. Sci. Rep. 2024, 14, 10339. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Zhang, Y.; Cheng, Y.; Guo, J.; Zheng, J.; Zhang, X.; Lei, Y.; Ma, Y.; Bai, L. A novel machine learning approach for reservoir temperature prediction. Geothermics 2025, 125, 103204. [Google Scholar] [CrossRef]
- Altindag, R. Correlation between P-wave velocity and some mechanical properties for sedimentary rocks(Article). J. S. Afr. Inst. Min. Metall. 2012, 112, 229–237. [Google Scholar]

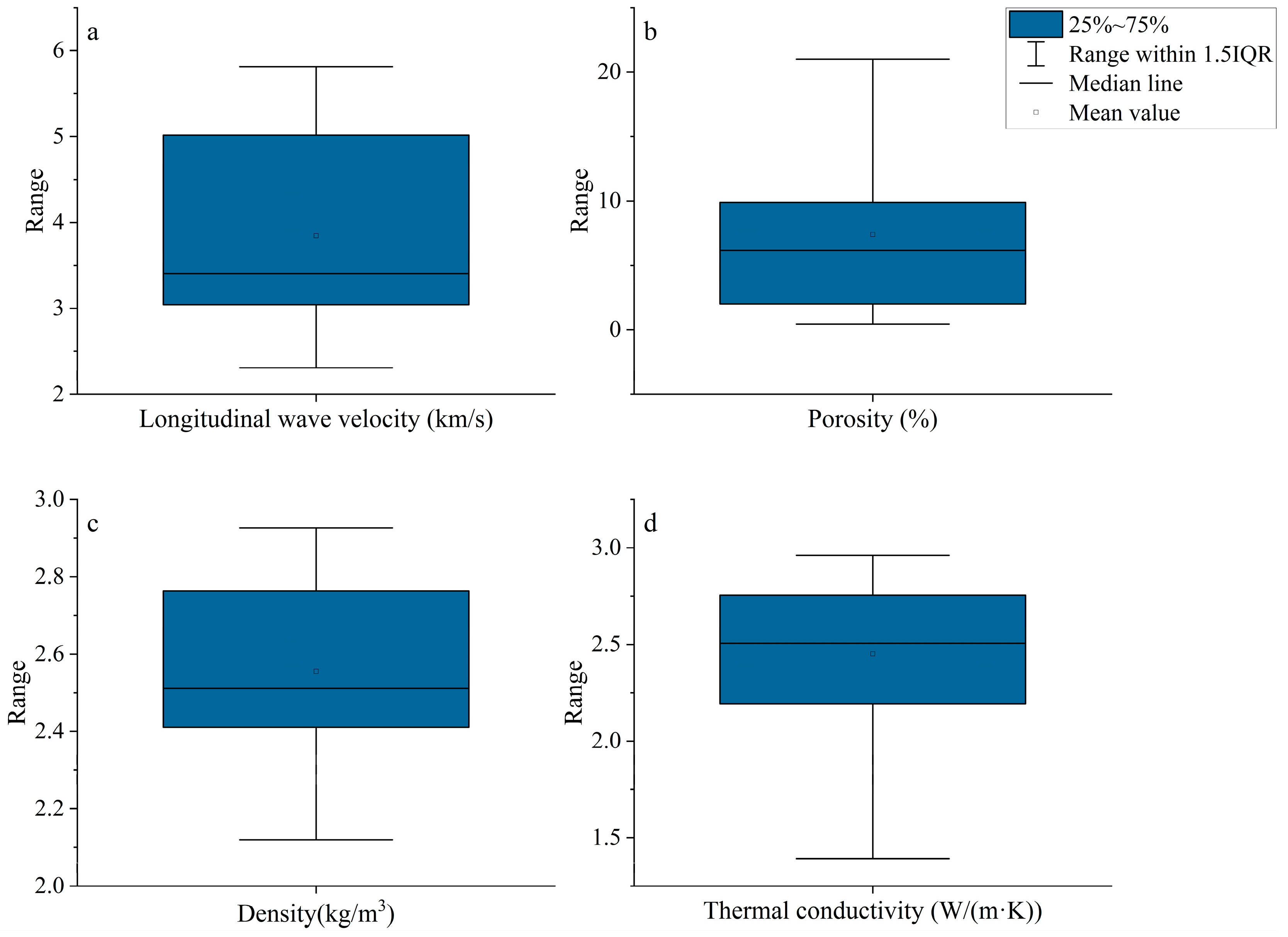


| Parameter | Longitudinal Wave Velocity (km/s) | Porosity (%) | Density (kg/m3) | Thermal Conductivity (W/(m·K)) |
|---|---|---|---|---|
| Symbol | Vp | n | ρ | λ |
| Average value | 3.847 | 7.392 | 2.556 | 2.451 |
| Maximum value | 5.814 | 20.99 | 2.926 | 2.961 |
| Minimum value | 2.309 | 0.45 | 2.120 | 1.392 |
| Standard deviation | 1.039 | 6.443 | 0.209 | 0.377 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Tian, L.; Hu, F.; Wang, J.; Yan, E.; Zhang, Y. Study on Thermal Conductivity Prediction of Granites Using Data Augmentation and Machine Learning. Energies 2025, 18, 4175. https://doi.org/10.3390/en18154175
Ma Y, Tian L, Hu F, Wang J, Yan E, Zhang Y. Study on Thermal Conductivity Prediction of Granites Using Data Augmentation and Machine Learning. Energies. 2025; 18(15):4175. https://doi.org/10.3390/en18154175
Chicago/Turabian StyleMa, Yongjie, Lin Tian, Fuhang Hu, Jingyong Wang, Echuan Yan, and Yanjun Zhang. 2025. "Study on Thermal Conductivity Prediction of Granites Using Data Augmentation and Machine Learning" Energies 18, no. 15: 4175. https://doi.org/10.3390/en18154175
APA StyleMa, Y., Tian, L., Hu, F., Wang, J., Yan, E., & Zhang, Y. (2025). Study on Thermal Conductivity Prediction of Granites Using Data Augmentation and Machine Learning. Energies, 18(15), 4175. https://doi.org/10.3390/en18154175






