Flexibility Resource Planning and Stability Optimization Methods for Power Systems with High Penetration of Renewable Energy
Abstract
1. Introduction
- A virtual network coupling modeling method has been implemented to address topological constraints during network reconfiguration. In the planning stage, this method effectively resolves radiality constraints, facilitates truthful topology optimization, and improves operational efficiency. Moreover, accurate topology modeling contributes to the stable operation of the distribution network.
- A CVaR-based risk quantification framework has been established to manage uncertainties arising from extreme weather and fault risks. By integrating CVaR into the bi-level optimization model, an effective balance between investment costs and operational risks is achieved. Compared to traditional deterministic methods, this approach handles uncertainties more effectively, thereby enhancing system robustness and economic efficiency.
- A coordinated planning model for multiple flexibility resources has been developed to enable the integrated configuration of micro gas turbines, ESSs, intelligent soft switches, and other resources. Through a bi-level optimization framework that coordinates planning and operational decisions, and with the aid of a hybrid SA-PSO algorithm, the solution performance is significantly improved. Compared with single-resource configuration methods, this approach markedly enhances overall system benefits and operational resilience.
2. Modeling Methods for Multi-Type Flexibility Resources
2.1. Microturbine Model
2.2. Soft Open Point Model
2.3. On-Load Tap Changer Model
2.4. Capacitor Bank Model
2.5. Demand Response Model
2.5.1. Price-Based Demand Response
2.5.2. Incentive-Based Demand Response
2.6. Energy Storage System Model
3. Planning Method for Power System Flexibility Resources Considering Network Reconfiguration and Fault Risk
3.1. Virtual Network Coupling-Based Reconfiguration
- The network topology must not contain closed loops.
- All buses must remain connected to the power source.
3.2. CVaR-Based Fault Risk Quantification and Planning
- Planning Layer
- 2.
- Operation Layer
4. Model Solution
| Algorithm 1: SA-PSO for Solving the Bi-Level Flexibility Resource Planning Model |
Input:
2: Set current temperature , iteration 3: while k < MaxIter do 4: for each particle i = 1 to N do 5: Input current particle into the lower-level model 6: Solve lower-level operation problem via SOCP to get cost 7: Evaluate fitness of particle i using upper-level objective 8: Update and if needed 9: end for 10: for each particle i = 1 to N do 11: Update velocity using PSO update rule 12: Update position 13: Calculate 14: if then 15: Accept new solution 16: else 17: Accept with probability 18: end if 19: end for 20: //Simulated annealing cooling 21: 22: end while 23: Return optimal solution |
5. Case Study
5.1. Parameter Settings
5.2. Impact Analysis of Coordinated Planning of Multiple Flexible Resources
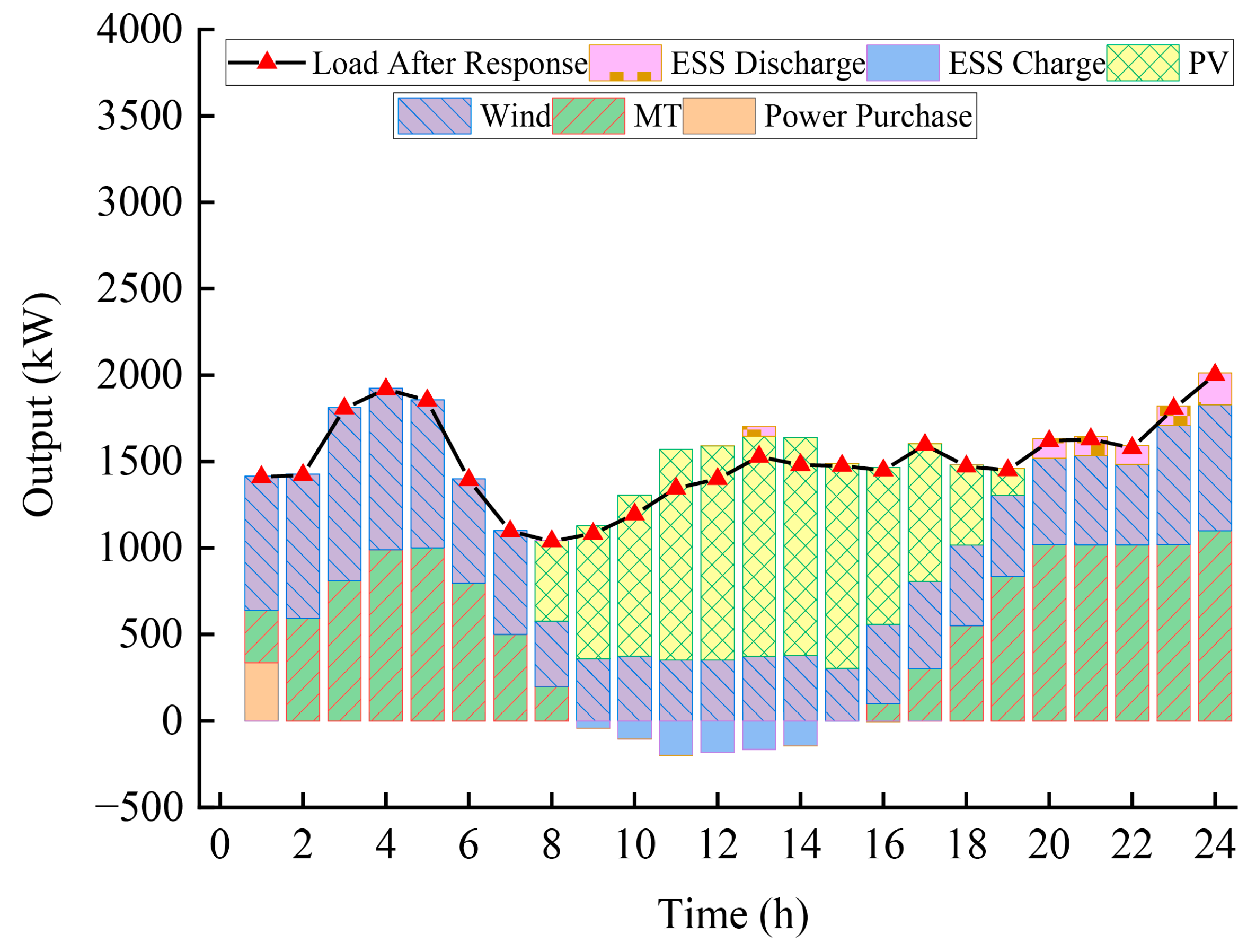
5.3. Analysis of System Operation Results Under Multiple Flexibility Resource Deployment
5.4. Comparison of Planning Outcomes
5.5. Parameter Analysis of the CVaR Model
5.6. Performance Analysis of the Algorithm
5.7. Voltage Quality Analysis
6. Conclusions
- By introducing the virtual network coupling modeling method to handle topological constraints in network reconfiguration, the proposed approach significantly improves computational efficiency while ensuring radial operation requirements. This method effectively resolves the complexity challenges in traditional network reconfiguration modeling and provides rapid topology adjustment capabilities for fault isolation and power restoration, enhancing both the accuracy of topological decision-making and the overall system operational flexibility.
- The proposed CVaR-based risk quantification framework offers a comprehensive approach to managing extreme weather uncertainties and fault risks by incorporating conditional value-at-risk into the bi-level optimization model. By tuning risk preference parameters, system planners can effectively balance investment costs and operational risks under uncertain conditions, improving system robustness and economic performance while enhancing the system’s resilience against extreme events.
- The coordinated multi-type flexibility resource planning model significantly increases system operational efficiency and resilience. By integrating microturbines, energy storage systems, and soft open points through the bi-level optimization framework combined with the SA-PSO hybrid algorithm, the proposed method achieves superior overall benefits compared to single-resource configuration approaches, demonstrating substantial improvements in both system reliability and economic viability while contributing to the sustainable development of modern power systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| CVaR | Conditional Value-at-Risk | / | Shiftable load transferred in and out |
| SA-PSO | Simulated Annealing–Particle Swarm Optimization | Whether load is reduced | |
| PV | Photovoltaic | / | Whether load is shifted in/out |
| PSO | Particle Swarm Optimization | / | Charging and discharging power |
| SA | Simulated Annealing | / | Binary about charging/discharging state |
| MT | Microturbine | Energy level of ESS | |
| SOP | Soft Open Point | State of charge of ESS | |
| OLTC | On-Load Tap Changer | Parameters | |
| CB | Capacitor Bank | Initial state of microturbine | |
| DR | Demand Response | Initial output power of microturbine | |
| VaR | Value at Risk | / | Upward/Downward ramp rates |
| SOCP | Second-Order Cone Programming | / | Maximum upward/downward ramping power |
| ESS | Energy Storage System | Converter capacity of the SOP | |
| Indices | / | Loss coefficients of SOP converters | |
| i/j | Index of distribution network bus | / | Absolute values of sine of power factor angles |
| t | Index of time | / | Resistance and reactance of branch ij |
| s | Index of scenario | Maximum tap position of the OLTC | |
| Variables | Tap adjustment step size for OLTC | ||
| On/off status | Reactive power compensation of a single capacitor unit | ||
| / | microturbine start-up/shutdown | Maximum number of capacitor units available at bus i | |
| / | Active/reactive power injected by SOP | / | Time-of-use electricity prices |
| Active power loss of the SOP | Cooling load | ||
| / | Active and reactive power flow on branch ij | Time periods for TOU prices | |
| Voltage magnitude at bus i | DR cycle period | ||
| Current on branch ij | Maximum reducible load | ||
| Tap position of OLTC at time t, scenario s | / | Maximum load shift-in/out | |
| Reactive power compensation of CB at bus i | / | Start/end times of load reduction | |
| Number of capacitor units switched in at bus i | / | Start/end times of load shift-in | |
| Change in demand after DR | / | Start/end times of load shift-out | |
| Change in electricity price after DR | Maximum reduction duration | ||
| / | Load before/after DR implementation | / | Max charging/discharging power |
| / | Electricity price before/after DR | / | Charging/discharging efficiency |
| Reducible load amount | / | Min/max energy storage level |
References
- Wan, Y.; Kober, T.; Schildhauer, T.; Schmidt, T.J.; McKenna, R.; Densing, M. Conditions for Profitable Operation of P2X Energy Hubs to Meet Local Demand with Energy Market Access. Adv. Appl. Energy 2023, 10, 100127. [Google Scholar] [CrossRef]
- Wei, Z.; Xu, H.; Chen, S.; Sun, G.; Zhou, Y. Learning-Aided Distributionally Robust Optimization of DC Distribution Network with Buildings to the Grid. Sustain. Cities Soc. 2024, 113, 105649. [Google Scholar] [CrossRef]
- Kumpalavalee, S.; Suwanasri, T.; Suwanasri, C.; Phadungthin, R. Risk Assessment Framework for Power Circuit Breakers Based on Condition, Replacement, and Criticality Indices. Energies 2025, 18, 3298. [Google Scholar] [CrossRef]
- Huang, H.; Sun, G.; Chen, S.; Wei, Z.; Zang, H. Peer-to-Peer Energy Trading of Hydrogen-Producing Prosumers in Power Distribution Network. Sustain. Energy Technol. Assess. 2025, 75, 104221. [Google Scholar] [CrossRef]
- Wang, D.; Wen, Y.; Zhang, J.; Chen, Q.; Gu, Y.; Chen, X.; Tang, Z. Potential Solution to Wheat Straw-to-Methanol for Marine Fuel under Carbon Emission Restrictions: A Comparative Energy, Exergy, Economic, and Environmental Analysis. Appl. Energy 2025, 397, 126338. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Q.; Chen, S.; Wei, Z.; Zang, H. Look-Ahead Dispatch of Power Systems Based on Linear Alternating Current Optimal Power Flow Framework with Nonlinear Frequency Constraints Using Physics-Informed Neural Networks. J. Mod. Power Syst. Clean Energy 2024, 13, 778–790. [Google Scholar] [CrossRef]
- Wang, J.; El Kontar, R.; Jin, X.; King, J. Decarbonizing All-Electric Communities via Carbon-Responsive Control of behind-the-Meter Resources. Adv. Appl. Energy 2023, 10, 100139. [Google Scholar] [CrossRef]
- Wu, C.; Wei, Z.; Jiang, X.; Huang, Y.; Fan, D. Optimization Decomposition of Monthly Contracts for Integrated Energy Service Provider Considering Spot Market Bidding Equilibria. Electronics 2024, 13, 1945. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Xu, D. Source-Load Scenario Generation Based on Weakly Supervised Adversarial Learning and Its Data-Driven Application in Energy Storage Capacity Sizing. IEEE Trans. Sustain. Energy 2023, 14, 1918–1932. [Google Scholar] [CrossRef]
- Zhao, C.; Li, X. Microgrid Optimal Energy Scheduling Considering Neural Network Based Battery Degradation. IEEE Trans. Power Syst. 2024, 39, 1594–1606. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Q.; Chen, S.; Li, Q.; Zhang, N.; Wei, Z.; Zang, H. Using Machine Learning to Achieve Highly Efficient Solutions of Frequency-Constrained Unit Commitment Models. Energy 2025, 328, 136223. [Google Scholar] [CrossRef]
- Zeng, Y.; Qiu, Y.; Zhu, J.; Chen, S.; Zang, T.; Zhou, B.; He, G.; Ji, X. Planning of Off-Grid Renewable Power to Ammonia Systems with Heterogeneous Flexibility: A Multistakeholder Equilibrium Perspective. IEEE Trans. Power Syst. 2025. early access. [Google Scholar] [CrossRef]
- Putratama, M.A.; Rigo-Mariani, R.; Mustika, A.D.; Debusschere, V.; Pachurka, A.; Besanger, Y. A Three-Stage Strategy with Settlement for an Energy Community Management under Grid Constraints. IEEE Trans. Smart Grid 2023, 14, 1505–1514. [Google Scholar] [CrossRef]
- Li, G.; Li, Q.; Liu, Y.; Liu, H.; Song, W.; Ding, R. A Cooperative Stackelberg Game Based Energy Management Considering Price Discrimination and Risk Assessment. Int. J. Electr. Power Energy Syst. 2022, 135, 107461. [Google Scholar] [CrossRef]
- Liu, J.; Tang, Z.; Liu, Y.; Zhou, Y.; Zeng, P.P.; Wu, Q. Region-Inspired Distributed Optimal Dispatch of Flexibility Providers in Coordinated Transmission-Distribution Framework. Energy 2025, 319, 134985. [Google Scholar] [CrossRef]
- Zhou, M.; Chen, S.; Huang, K.; Liang, J.; Fu, M.; Sun, G. Coordination of Medium-Voltage Distribution Networks and Microgrids Based on an Aggregate Flexibility Region Approach. Sustain. Energy Grids Netw. 2024, 39, 101485. [Google Scholar] [CrossRef]
- Wu, Y.; Lin, Z.; Chen, Z.; Chen, R.; Chen, Y. Vickrey-Clark-Groves-Based Method for Eradicating Deceptive Behaviors in Demand Response Transactions. J. Mod. Power Syst. Clean Energy 2024, 12, 1260–1271. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, H.; Li, F.; Sun, B. Bi-Level Optimal Design of Integrated Energy System with Synergy of Renewables, Conversion, Storage, and Demand. IEEE Trans. Ind. Appl. 2025, 61, 2170–2181. [Google Scholar] [CrossRef]
- Zhang, Q.; Leng, S.; Ma, X.; Liu, Q.; Wang, X.; Liang, B.; Liu, Y.; Yang, J. CVaR-Constrained Policy Optimization for Safe Reinforcement Learning. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 830–841. [Google Scholar] [CrossRef]
- Han, H.; Jiang, X.; Zhang, S.; Wu, C.; Cao, S.; Zang, H.; Sun, G.; Wei, Z. A Risk-Based Scheduling Optimization Strategy with Explainability Enhanced Multi-Scenario Photovoltaic Forecasting. Electr. Power Syst. Res. 2025, 246, 111729. [Google Scholar] [CrossRef]
- Belles-Sampera, J.; Guillén, M.; Santolino, M. Beyond Value-at-risk: GlueVaR Distortion Risk Measures. Risk Anal. 2014, 34, 121–134. [Google Scholar] [CrossRef]
- Xiong, L.; Goyal, A.; Bhattacharya, K.; Tang, Y.; Dong, Z.; Qian, F.; Thummalacherla, V.B. DRL-Based Distributed Coordination of ISO and DSOs in Bi-Level Electricity Markets. IEEE Trans. Ind. Inf. 2025, 21, 6422–6432. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.; Peng, C.; Zhou, H.; Xu, S. Distributed Optimization for EVs Integrated Power System Considering Flexible Ramping Requirement. Int. J. Electr. Power Energy Syst. 2024, 160, 110104. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, Y.; Wu, J. Two-Layer Data-Driven Robust Scheduling for Industrial Heat Loads. J. Mod. Power Syst. Clean Energy 2024, 13, 265–275. [Google Scholar] [CrossRef]
- Kouba, N.; Menaa, M.; Tehrani, K.; Boudour, M. Optimal Tuning for Load Frequency Control Using Ant Lion Algorithm in Multi-Area Interconnected Power System. Intell. Autom. Soft Comput. 2019, 25, 279–294. [Google Scholar] [CrossRef]
- Qiu, D.; Dong, Z.; Ruan, G.; Zhong, H.; Strbac, G.; Kang, C. Strategic Retail Pricing and Demand Bidding of Retailers in Electricity Market: A Data-Driven Chance-Constrained Programming. Adv. Appl. Energy 2022, 7, 100100. [Google Scholar] [CrossRef]
- Ji, H.; Jian, J.; Yu, H.; Ji, J.; Wei, M.; Zhang, X.; Li, P.; Yan, J.; Wang, C. Peer-to-Peer Electricity Trading of Interconnected Flexible Distribution Networks Based on Distributed Ledger. IEEE Trans. Ind. Inf. 2022, 18, 5949–5960. [Google Scholar] [CrossRef]
- Han, H.; Yu, L.; Zhou, Y.; Zang, H.; Cao, Y.; Chen, S.; Sun, G.; Wei, Z. Two-Stage Robust Co-Optimization of Energy and Reserve Scheduling for Resilient Distribution Systems Considering Line Reinforcement. Energy 2025, 316, 134600. [Google Scholar] [CrossRef]
- Chen, S.; Conejo, A.J.; Wei, Z. Gas-Power Coordination: From Day-Ahead Scheduling to Actual Operation. IEEE Trans. Power Syst. 2022, 37, 1532–1542. [Google Scholar] [CrossRef]
- Ji, D.; Wei, Z.; Zhou, Y.; Chen, S.; Sun, G.; Zang, H. Distributionally Robust Co-Optimization of Energy and Reserve Dispatch for Integrated Electricity-Gas-Heating Systems. Sustain. Energy Technol. Assess. 2025, 73, 104125. [Google Scholar] [CrossRef]
- Chu, Y.; Wei, Z.; Sun, G.; Zang, H.; Chen, S.; Zhou, Y. Optimal Home Energy Management Strategy: A Reinforcement Learning Method with Actor-Critic Using Kronecker-Factored Trust Region. Electr. Power Syst. Res. 2022, 212, 108617. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z. A Novel Risk-Averse Multi-Energy Management for Effective Offering Strategy of Integrated Energy Production Units in a Real-Time Electricity Market. Appl. Energy 2025, 377, 124380. [Google Scholar] [CrossRef]
- Chen, S.; Zhu, L.; Wei, Z.; Sun, G.; Zhou, Y. Application of a Graph Convolutional Network for Predicting the Feasible Operating Regions of Power to Hydrogen Facilities in Integrated Electricity and Hydrogen-Gas Systems. Energy 2025, 326, 136107. [Google Scholar] [CrossRef]
- Wynn, S.L.L.; Boonraksa, T.; Boonraksa, P.; Pinthurat, W.; Marungsri, B. Decentralized Energy Management System in Microgrid Considering Uncertainty and Demand Response. Electronics 2023, 12, 237. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, Y.; Tang, P. Uncertain Mean-CVaR Model for Portfolio Selection with Transaction Cost and Investors’ Preferences. N. Am. J. Econ. Financ. 2024, 69, 102028. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Ji, X.; Ye, P.; Yu, D.; Zhang, B. Optimal Dispatching of Electric-heat-hydrogen Integrated Energy System Based on Stackelberg Game. Energy Convers. Econ. 2023, 4, 267–275. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, Y.; Zhang, Q.; Jia, Y. Berth Allocation and Energy Scheduling for All-Electric Ships in Seaport Microgrid: A Stackelberg Game Approach. Energy 2025, 322, 135640. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, J.; Dong, H.; Zeng, C.; Pan, Z. Knowledge-Augmented Population-Based Deep Reinforcement Learning for Real-Time Network-Constrained Economic Dispatch of Large-Scale Power Grid. IEEE Trans. Power Syst. 2025. early access. [Google Scholar] [CrossRef]










| Reference | Resource Types | Risk Model | Network Reconfiguration | Optimization | Solution Method |
|---|---|---|---|---|---|
| [11] | ESS, DR | No | No | Coordinated Planning | MIP |
| [12] | ESS, DR, SOP | No | Yes | Three-stage dispatch under constraints | Heuristic |
| [13] | ESS | No | Big-M linearization | Deterministic Optimization | MILP |
| [15] | ESS | No | Virtual Network | Graph-based Topology Optimization | MILP |
| [16] | ESS, DR | No | Yes | Incentive-integrated Modeling | Game-based |
| [17] | ESS | No | No | Basic Planning | MIP |
| [18] | ESS | CVaR | No | Multi-objective Scheduling | Stochastic Programming |
| [19] | DR | CVaR | No | Bi-level Energy Management | Mixed Integer |
| [20] | ESS | VaR | No | Risk-constrained Optimization | MILP |
| [21] | ESS, DR | No | No | Classical Bi-level | MILP |
| [22] | ESS | No | Yes | Bi-level (with topology) | MILP |
| This paper | MT, ESS, SOP, DR | CVaR | Virtual Network Coupling | Bi-level (Planning + Operation) | SA–PSO + SOCP |
| Parameter | Wind Turbines | PV Systems | ||||
|---|---|---|---|---|---|---|
| Access Location | 9 | 25 | 32 | 7 | 17 | 22 |
| Capacity (kW) | 400 | 400 | 400 | 400 | 400 | 400 |
| Scheme | Configuration Object | ||
|---|---|---|---|
| MT/kW (Location) | ESS/kWh (Location) | SOP/kVA (Location) | |
| 1 | 800 (5), 800 (10), 300 (18) | 500 (9), 700 (22), 500 (25) | / |
| 2 | 300 (10), 300 (18), 500 (28) | 700 (9), 300 (17), 400 (22) | / |
| 3 | 700 (5), 800 (10), 400 (28) | 600 (17), 600 (22), 600 (25) | 300 (9–15), 300 (25–29) |
| 4 | 500 (5), 300 (16), 500 (28) | 200 (7), 800 (17), 400 (22) | 200 (9–15), 100 (12–22) |
| Scheme | Cost Distribution (CNY) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MT | ESS | SOP | Power Purchase | Wind & Solar Curtailment | Network Loss | SOP Loss | Carbon Emission | O&M Cost | Annual Total | |
| 1 | 415,192 | 193,355 | / | 237,659 | 12,977 | 159,748 | / | 13,433 | 70,446 | 1,102,810 |
| 2 | 240,374 | 165,733 | / | 203,781 | 4791 | 125,236 | / | 12,512 | 55,046 | 807,473 |
| 3 | 415,192 | 202,563 | 65,557 | 170,739 | 0 | 31,526 | 71,178 | 13,506 | 68,382 | 1,038,643 |
| 4 | 284,079 | 165,733 | 32,778 | 167,609 | 0 | 32,935 | 28,602 | 12,282 | 54,438 | 778,456 |
| Scenario Number | Operating Cost (CNY) | |||
|---|---|---|---|---|
| Network Loss Cost | SOP Loss Cost | Power Purchase Cost | Carbon Emission | |
| Typical Scenario 1 | 60 | 187 | 0 | 17 |
| Typical Scenario 2 | 239 | 30 | 2975 | 93 |
| Typical Scenario 3 | 68 | 12 | 86 | 28 |
| Category | Peak Load (kW) | Valley Load (kW) | Peak-Valley Difference (kW) | Peak-Valley Ratio |
|---|---|---|---|---|
| Original Load Curve | 2988 | 763 | 2225 | 0.745 |
| After DR | 2199 | 888 | 1311 | 0.596 |
| After ESS + DR | 1929 | 888 | 1041 | 0.540 |
| Method | Configuration Scheme Capacity (Location) | Total Planning Cost (CNY) | Total Operating Cost (CNY) | Total Cost (CNY) |
|---|---|---|---|---|
| Risk-neutral | ESS: 400 (9), 1400 (25), 900 (32) MT: 300 (5), 600 (10), 500 (18) SOP: 200 (12–22), 200 (18–33) | 483,805 | 353,386 | 837,191 |
| CVaR | ESS: 1000 (22), 500 (25), 1900 (32) MT: 700 (5), 800 (10), 900 (28) SOP: 200 (9–15), 300 (12–22) | 738,626 | 274,158 | 1,012,784 |
| Method | Risk-Neutral | CVaR | ||||||
|---|---|---|---|---|---|---|---|---|
| Cost Distribution (CNY) | Load Shedding | External Purchase | Other Costs | Total Cost | Load Shedding | External Purchase | Other Costs | Total Cost |
| Typical Scenario 1 | 0 | 0 | 895 | 895 | 0 | 0 | 572 | 572 |
| Typical Scenario 2 | 75 | 0 | 690 | 765 | 0 | 0 | 647 | 647 |
| Typical Scenario 3 | 2254 | 2188 | 2080 | 6522 | 1594 | 526 | 1890 | 4010 |
| Fault Scenario 1 | 4821 | 2097 | 1977 | 8896 | 1920 | 627 | 2074 | 4621 |
| Fault Scenario 2 | 5023 | 2725 | 1992 | 9740 | 2415 | 763 | 2199 | 5377 |
| Fault Scenario 3 | 2366 | 2328 | 2289 | 6983 | 1694 | 585 | 1960 | 4239 |
| Fault Scenario 4 | 5255 | 2593 | 2058 | 9907 | 2093 | 823 | 2276 | 5192 |
| L | Investment Cost (CNY) | Annual Total Cost (CNY) | CVaR (CNY) |
|---|---|---|---|
| 0.01 | 619,139 | 902,948 | 3,191,488 |
| 0.05 | 625,077 | 933,782 | 2,711,396 |
| 0.1 | 639,662 | 952,633 | 2,135,347 |
| 0.2 | 648,312 | 979,901 | 2,054,545 |
| 0.5 | 697,351 | 992,768 | 1,913,240 |
| 1 | 738,626 | 1,012,784 | 1,853,854 |
| 2 | 782,195 | 1,064,974 | 1,838,959 |
| 3 | 837,459 | 1,144,030 | 1,831,561 |
| Algorithm | Best Solution (CNY) | Average Solution (CNY) | Standard Deviation | Average Computation Time (s) | Convergence Iterations |
|---|---|---|---|---|---|
| SA-PSO | 778,456 | 780,832 | 2156 | 45.2 | 152 |
| PSO | 812,347 | 817,529 | 4287 | 38.7 | 245 |
| SA | 785,692 | 791,276 | 3825 | 52.8 | 298 |
| GA | 823,571 | 832,184 | 5967 | 41.3 | 320 |
| M | Solution Time (S) | Average Solution (CNY) | Constraint Violation |
|---|---|---|---|
| N | 45.2 | 778,456 | No |
| 2 N | 47.6 | 778,460 | No |
| 0.5 N | Error | - | Yes |
| 0.7 N | 46.3 | 778,457 | No |
| Network Size | Objective Value | Computation Time | Convergence Iterations |
|---|---|---|---|
| 33 | 778,456 | 45.2 | 152 |
| 69 | 1,083,920 | 98.7 | 214 |
| 118 | 1,626,370 | 183.5 | 289 |
| 150 | 1,975,280 | 265.4 | 327 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Jiang, X.; Cao, Y.; Luo, X.; Liu, S.; Yang, B. Flexibility Resource Planning and Stability Optimization Methods for Power Systems with High Penetration of Renewable Energy. Energies 2025, 18, 4139. https://doi.org/10.3390/en18154139
Han H, Jiang X, Cao Y, Luo X, Liu S, Yang B. Flexibility Resource Planning and Stability Optimization Methods for Power Systems with High Penetration of Renewable Energy. Energies. 2025; 18(15):4139. https://doi.org/10.3390/en18154139
Chicago/Turabian StyleHan, Haiteng, Xiangchen Jiang, Yang Cao, Xuanyao Luo, Sheng Liu, and Bei Yang. 2025. "Flexibility Resource Planning and Stability Optimization Methods for Power Systems with High Penetration of Renewable Energy" Energies 18, no. 15: 4139. https://doi.org/10.3390/en18154139
APA StyleHan, H., Jiang, X., Cao, Y., Luo, X., Liu, S., & Yang, B. (2025). Flexibility Resource Planning and Stability Optimization Methods for Power Systems with High Penetration of Renewable Energy. Energies, 18(15), 4139. https://doi.org/10.3390/en18154139








