A Comparative Study of Statistical and Machine Learning Methods for Solar Irradiance Forecasting Using the Folsom PLC Dataset
Abstract
1. Introduction
- RQ1: Are ML methods more accurate than traditional methods?
- RQ2: Can the use of time series enhance forecast accuracy?
2. Related Literature
3. Materials and Methods
3.1. Dataset
3.2. Machine Learning Methods
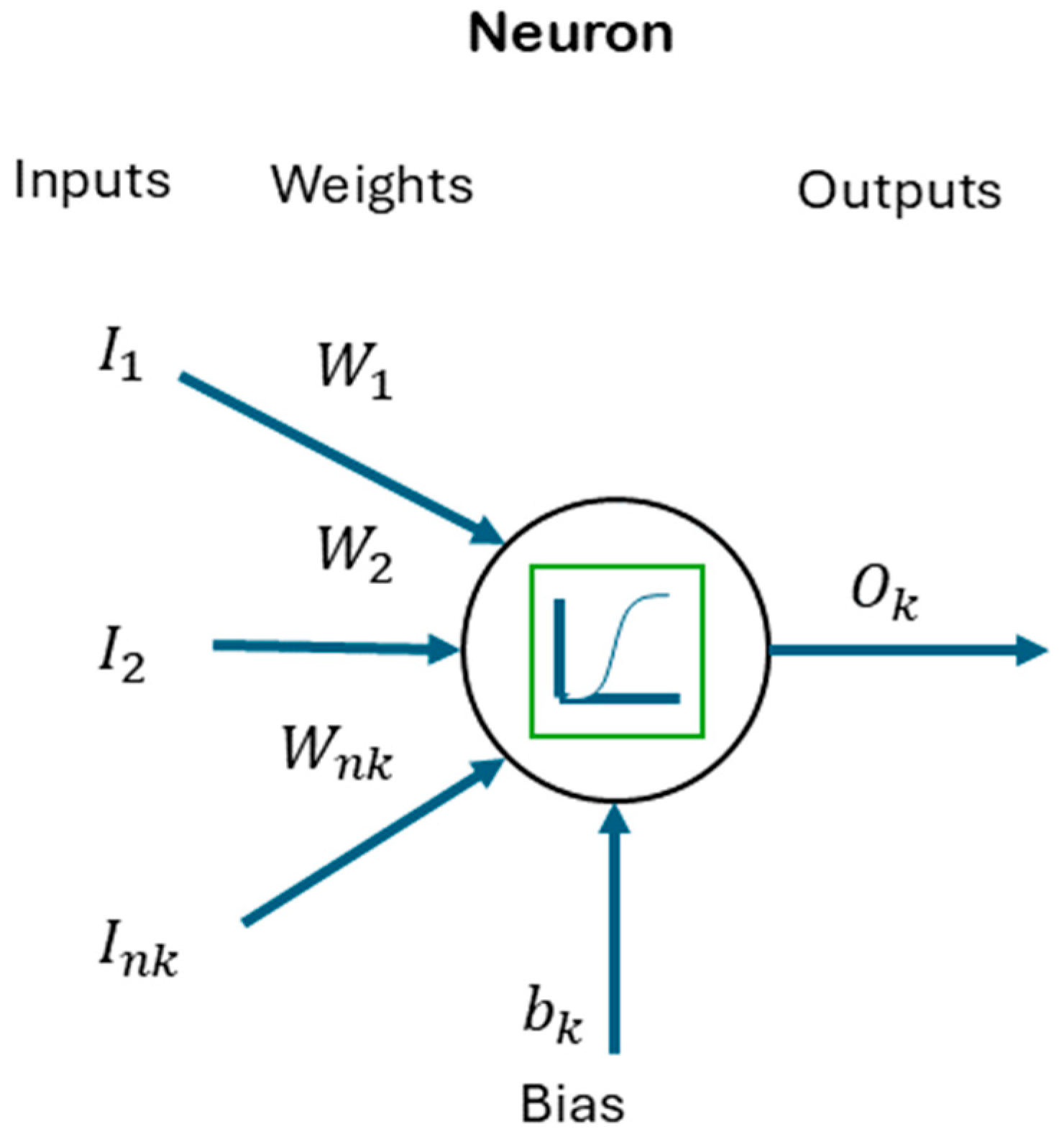
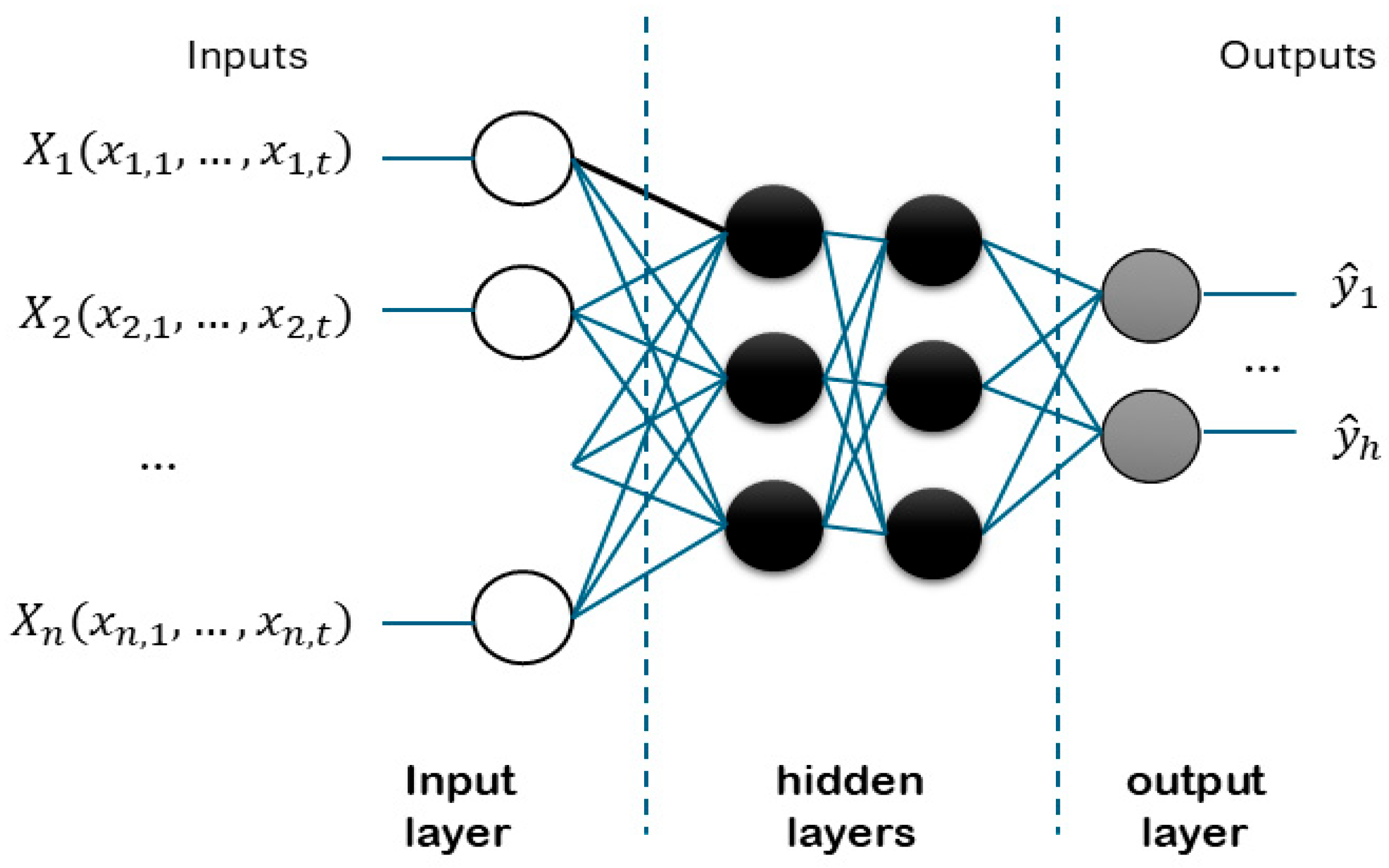
3.2.1. Neural Networks
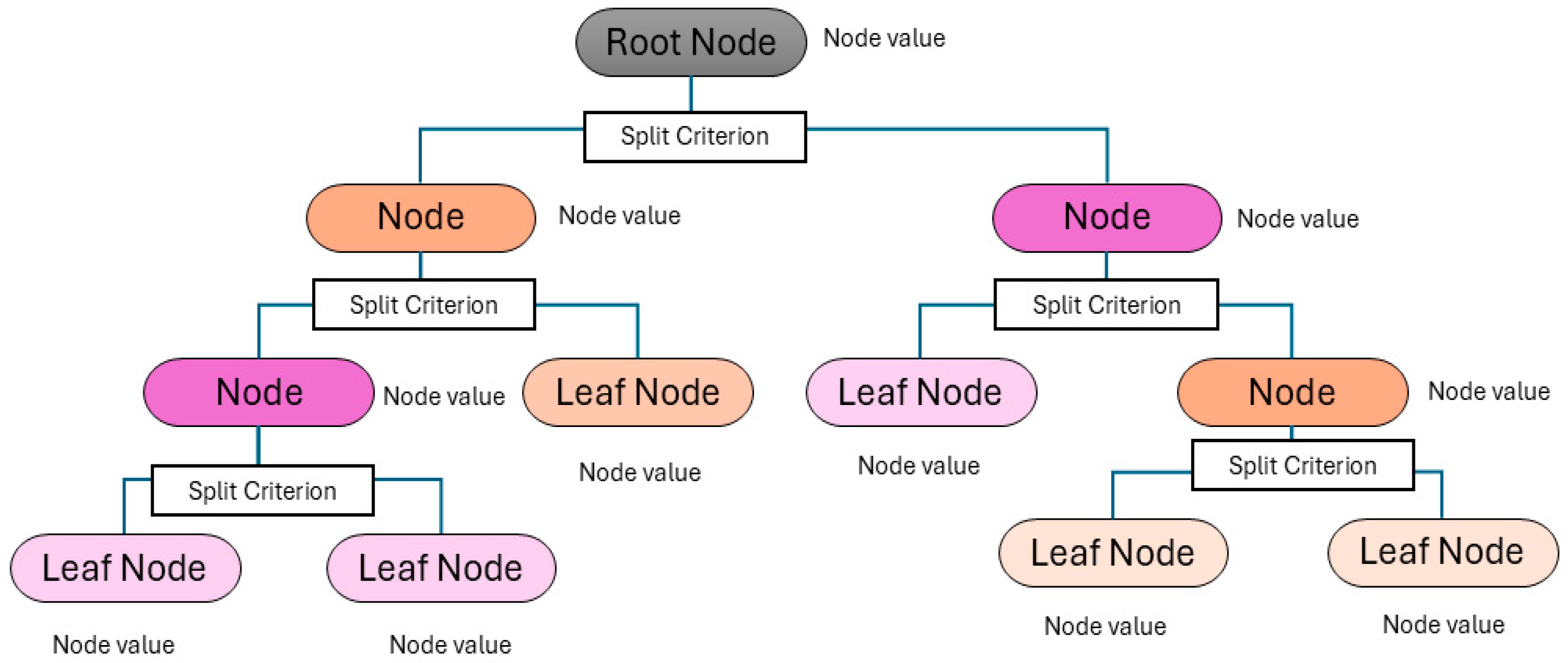
3.2.2. Regression Trees
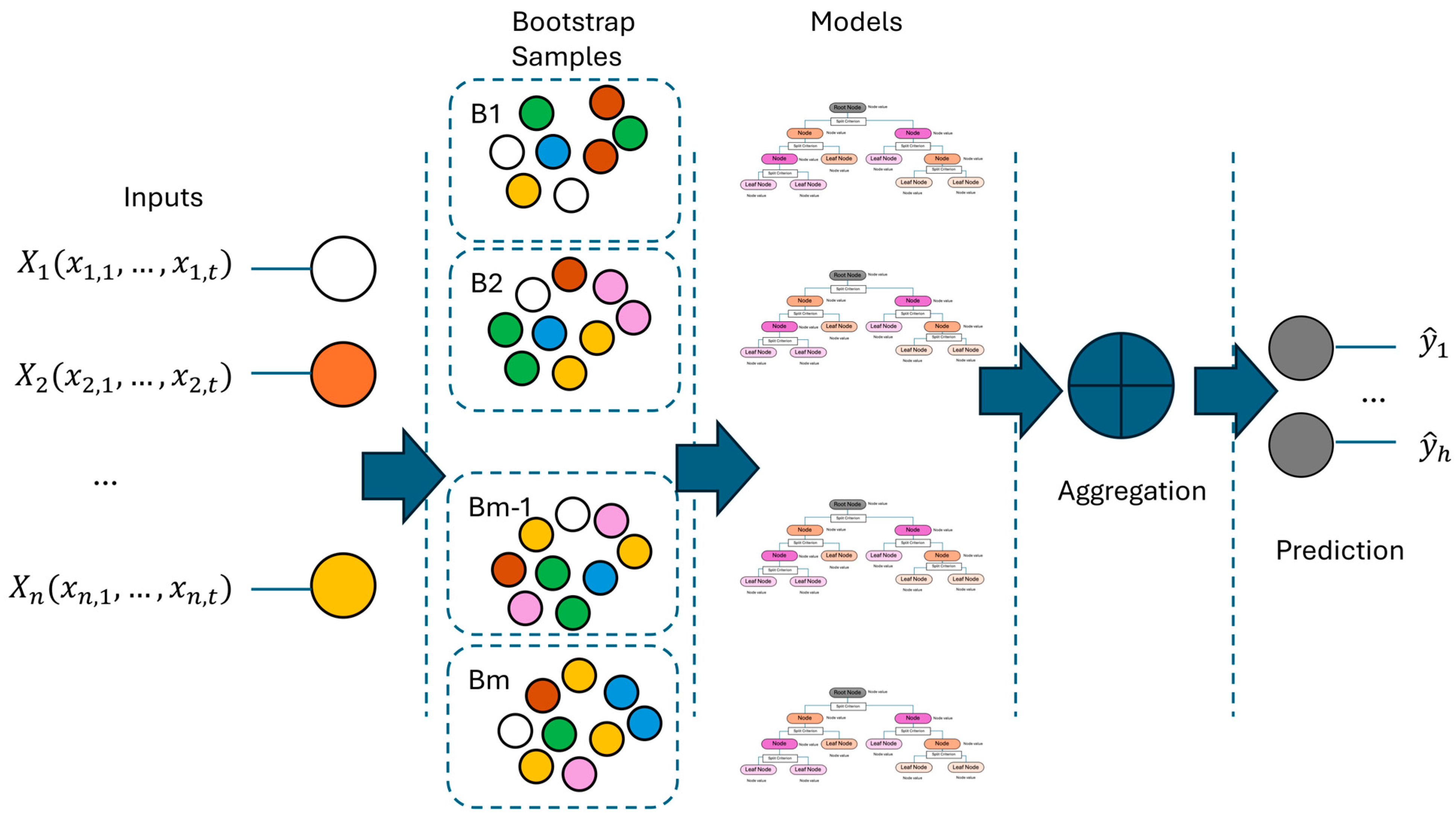
3.2.3. Random Forest Ensemble
3.2.4. LSTM Networks
3.3. Analysis
3.3.1. Physical Modelling Approach
3.3.2. Time Series Approach
3.3.3. Hybrid Approach
3.3.4. Metrics
3.3.5. Model Development, Hyperparameter Optimisation, and Validation Strategy
- For models based on physical variables, k-fold cross-validation was applied to assess generalisation.
- For time series models, a holdout validation approach was used to preserve the temporal structure and avoid data leakage.
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mathiesen, B.V.; Lund, H.; Connolly, D.; Wenzel, H.; Ostergaard, P.A.; Möller, B.; Nielsen, S.; Ridjan, I.; KarnOe, P.; Sperling, K.; et al. Smart Energy Systems for Coherent 100% Renewable Energy and Transport Solutions. Appl. Energy 2015, 145, 139–154. [Google Scholar] [CrossRef]
- Albadi, M.H.; El-Saadany, E.F. A Summary of Demand Response in Electricity Markets. Electr. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar] [CrossRef]
- IEA. Renewables 2023. Analysis and Forecasts to 2028; IEA: Paris, France, 2024. [Google Scholar]
- REN21. Renewables 2024 Global Status Report Collection; REN21: Paris, France, 2024. [Google Scholar]
- Pedro, H.T.C.; Larson, D.P.; Coimbra, C.F.M. A Comprehensive Dataset for the Accelerated Development and Benchmarking of Solar Forecasting Methods. J. Renew. Sustain. Energy 2019, 11, 036102. [Google Scholar] [CrossRef]
- Prema, V.; Bhaskar, M.S.; Almakhles, D.; Gowtham, N.; Rao, K.U. Critical Review of Data, Models and Performance Metrics for Wind and Solar Power Forecast. IEEE Access 2022, 10, 667–688. [Google Scholar] [CrossRef]
- Zsiborács, H.; Pintér, G.; Vincze, A.; Baranyai, N.H.; Mayer, M.J. The Reliability of Photovoltaic Power Generation Scheduling in Seventeen European Countries. Energy Convers. Manag. 2022, 260, 115641. [Google Scholar] [CrossRef]
- Brusco, G.; Burgio, A.; Menniti, D.; Pinnarelli, A.; Sorrentino, N.; Vizza, P. Quantification of Forecast Error Costs of Photovoltaic Prosumers in Italy. Energies 2017, 10, 1754. [Google Scholar] [CrossRef]
- Gandhi, O.; Zhang, W.; Kumar, D.S.; Rodríguez-Gallegos, C.D.; Yagli, G.M.; Yang, D.; Reindl, T.; Srinivasan, D. The Value of Solar Forecasts and the Cost of Their Errors: A Review. Renew. Sustain. Energy Rev. 2024, 189, 113915. [Google Scholar] [CrossRef]
- Polasek, T.; Čadík, M. Predicting Photovoltaic Power Production Using High-Uncertainty Weather Forecasts. Appl. Energy 2023, 339, 120989. [Google Scholar] [CrossRef]
- Iheanetu, K.J. Solar Photovoltaic Power Forecasting: A Review. Sustainability 2022, 14, 17005. [Google Scholar] [CrossRef]
- Koehl, M.; Heck, M.; Wiesmeier, S.; Wirth, J. Modeling of the Nominal Operating Cell Temperature Based on Outdoor Weathering. Sol. Energy Mater. Sol. Cells 2011, 95, 1638–1646. [Google Scholar] [CrossRef]
- Fuentes, M.K. A Simplified Thermal Model for Flat-Plate Photovoltaic Arrays; Sandia National Labs: Albuquerque, NM, USA, 1987. Available online: https://www.osti.gov/biblio/6802914 (accessed on 10 June 2025).
- Dolara, A.; Leva, S.; Manzolini, G. Comparison of Different Physical Models for PV Power Output Prediction. Sol. Energy 2015, 119, 83–99. [Google Scholar] [CrossRef]
- Brecl, K.; Topic, M. Photovoltaics (PV) System Energy Forecast on the Basis of the Local Weather Forecast: Problems, Uncertainties and Solutions. Energies 2018, 11, 1143. [Google Scholar] [CrossRef]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.C.; Coimbra, C.F.M. History and Trends in Solar Irradiance and PV Power Forecasting: A Preliminary Assessment and Review Using Text Mining. Sol. Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Aryaputera, A.W.; Yang, D.; Zhao, L.; Walsh, W.M. Very Short-Term Irradiance Forecasting at Unobserved Locations Using Spatio-Temporal Kriging. Sol. Energy 2015, 122, 1266–1278. [Google Scholar] [CrossRef]
- Gupta, A.K.; Singh, R.K. A Review of the State of the Art in Solar Photovoltaic Output Power Forecasting Using Data-Driven Models. Electr. Eng. 2025, 107, 4727–4770. [Google Scholar] [CrossRef]
- Singh, C.; Garg, A.R. Enhancing Solar Power Output Predictions: Analyzing ARIMA and S-ARIMA Models for Short-Term Forecasting. In Proceedings of the 2024 IEEE 11th Power India International Conference (PIICON), JAIPUR, India, 11–12 December 2024; pp. 1–5. [Google Scholar]
- Sapundzhi, F.; Chikalov, A.; Georgiev, S.; Georgiev, I. Predictive Modeling of Photovoltaic Energy Yield Using an ARIMA Approach. Appl. Sci. 2024, 14, 11192. [Google Scholar] [CrossRef]
- Despotovic, M.; Voyant, C.; Garcia-Gutierrez, L.; Almorox, J.; Notton, G. Solar Irradiance Time Series Forecasting Using Auto-Regressive and Extreme Learning Methods: Influence of Transfer Learning and Clustering. Appl. Energy 2024, 365, 123215. [Google Scholar] [CrossRef]
- Torres, J.F.; Troncoso, A.; Koprinska, I.; Wang, Z.; Martínez-Álvarez, F. Big Data Solar Power Forecasting Based on Deep Learning and Multiple Data Sources. Expert Syst. 2019, 36, e12394. [Google Scholar] [CrossRef]
- Torres, J.F.; Troncoso, A.; Koprinska, I.; Wang, Z.; Martínez-Álvarez, F. Deep Learning for Big Data Time Series Forecasting Applied to Solar Power. In Proceedings of the International Joint Conference SOCO’18-CISIS’18-ICEUTE’18, San Sebastián, Spain, 6–8 June 2018; Proceedings 13. Springer: Berlin/Heidelberg, Germany, 2019; pp. 123–133. [Google Scholar]
- Qing, X.; Niu, Y. Hourly Day-Ahead Solar Irradiance Prediction Using Weather Forecasts by LSTM. Energy 2018, 148, 461–468. [Google Scholar] [CrossRef]
- Xu, W.; Wang, Z.; Wang, W.; Zhao, J.; Wang, M.; Wang, Q. Short-Term Photovoltaic Output Prediction Based on Decomposition and Reconstruction and XGBoost under Two Base Learners. Energies 2024, 17, 906. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J.; Batlles, F.J.; Portillo, C. Solar Irradiance Forecasting at One-Minute Intervals for Different Sky Conditions Using Sky Camera Images. Energy Convers. Manag. 2015, 105, 1166–1177. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, H.; Wang, H.; Zhu, T.; Zhang, K. 3D-CNN-Based Feature Extraction of Ground-Based Cloud Images for Direct Normal Irradiance Prediction. Sol. Energy 2019, 181, 510–518. [Google Scholar] [CrossRef]
- Bu, Q.; Zhuang, S.; Luo, F.; Ye, Z.; Yuan, Y.; Ma, T.; Da, T. Improving Solar Radiation Forecasting in Cloudy Conditions by Integrating Satellite Observations. Energies 2024, 17, 6222. [Google Scholar] [CrossRef]
- Paulescu, M.; Blaga, R.; Dughir, C.; Stefu, N.; Sabadus, A.; Calinoiu, D.; Badescu, V. Intra-Hour Pv Power Forecasting Based on Sky Imagery. Energy 2023, 279, 128135. [Google Scholar] [CrossRef]
- Chen, G.; Qi, X.; Wang, Y.; Du, W. ARIMA-LSTM Model-Based Siting Study of Photovoltaic Power Generation Technology. In Proceedings of the 2024 4th Asia-Pacific Conference on Communications Technology and Computer Science (ACCTCS), Shenyang, China, 24–26 February 2024; pp. 557–562. [Google Scholar]
- Nie, Y.; Li, X.; Paletta, Q.; Aragon, M.; Scott, A.; Brandt, A. Open-Source Sky Image Datasets for Solar Forecasting with Deep Learning: A Comprehensive Survey. Renew. Sustain. Energy Rev. 2024, 189, 113977. [Google Scholar] [CrossRef]
- Sengupta, M.; Xie, Y.; Lopez, A.; Habte, A.; Maclaurin, G.; Shelby, J. The National Solar Radiation Data Base (NSRDB). Renew. Sustain. Energy Rev. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- Vignola, F.; Grover, C.; Lemon, N.; McMahan, A. Building a Bankable Solar Radiation Dataset. Sol. Energy 2012, 86, 2218–2229. [Google Scholar] [CrossRef]
- Barhmi, K.; Heynen, C.; Golroodbari, S.; van Sark, W. A Review of Solar Forecasting Techniques and the Role of Artificial Intelligence. Solar 2024, 4, 99–135. [Google Scholar] [CrossRef]
- Marinho, F.P.; Rocha, P.A.C.; Neto, A.R.R.; Bezerra, F.D. V Short-Term Solar Irradiance Forecasting Using CNN-1D, LSTM, and CNN-LSTM Deep Neural Networks: A Case Study with the Folsom (USA) Dataset. J. Sol. Energy Eng. 2022, 145, 041002. [Google Scholar] [CrossRef]
- Oliveira Santos, V.; Marinho, F.P.; Costa Rocha, P.A.; Thé, J.V.G.; Gharabaghi, B. Application of Quantum Neural Network for Solar Irradiance Forecasting: A Case Study Using the Folsom Dataset, California. Energies 2024, 17, 3580. [Google Scholar] [CrossRef]
- Zhang, L.; Wilson, R.; Sumner, M.; Wu, Y. Advanced Multimodal Fusion Method for Very Short-Term Solar Irradiance Forecasting Using Sky Images and Meteorological Data: A Gate and Transformer Mechanism Approach. Renew. Energy 2023, 216, 118952. [Google Scholar] [CrossRef]
- Yang, D.; van der Meer, D.; Munkhammar, J. Probabilistic Solar Forecasting Benchmarks on a Standardized Dataset at Folsom, California. Sol. Energy 2020, 206, 628–639. [Google Scholar] [CrossRef]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of Solar Irradiance Forecasting Methods and a Proposition for Small-Scale Insular Grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Loh, W. Classification and Regression Trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yang, D. Choice of Clear-Sky Model in Solar Forecasting. J. Renew. Sustain. Energy 2020, 12, 026101. [Google Scholar] [CrossRef]
- Haupt, T.; Trull, O.; Moog, M. PV Production Forecast Using Hybrid Models of Time Series with Machine Learning Methods. Energies 2025, 18, 2692. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R.; Taylor, J. Springer Texts in Statistics An Introduction to Statistical Learning with Applications in Python; Springer: New York, NY, USA, 2017. [Google Scholar]
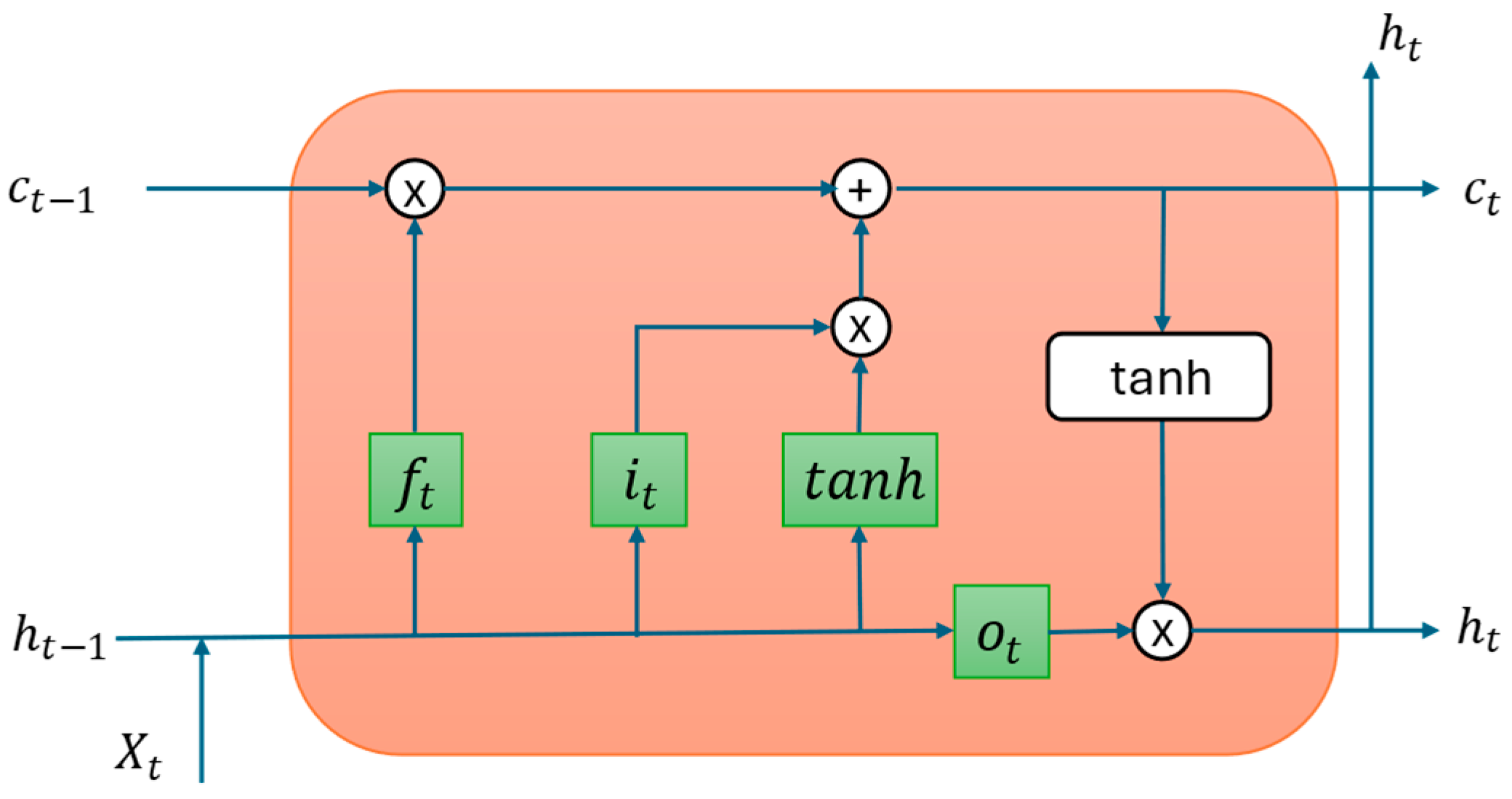
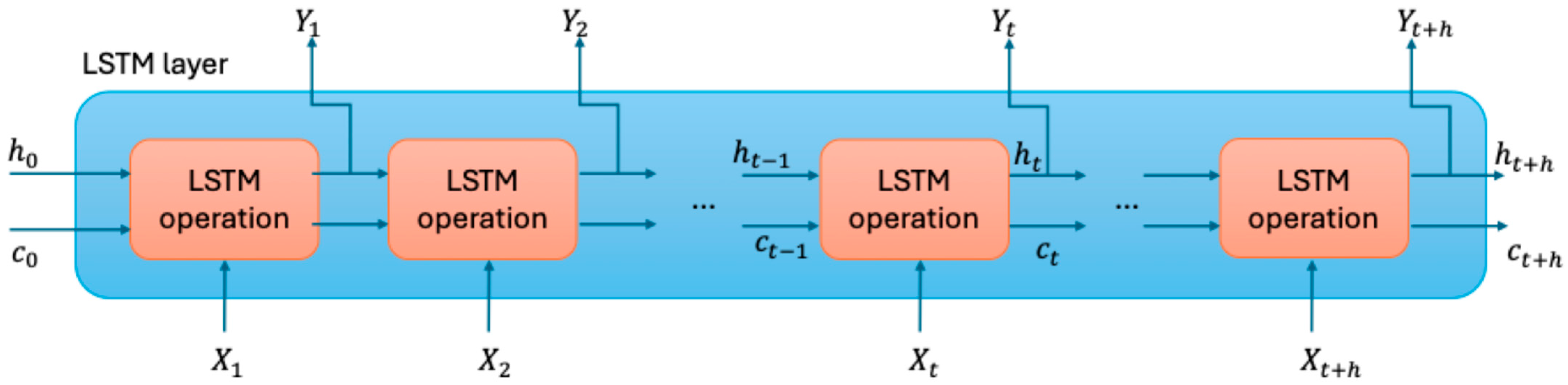
| Reference | Authors | Methods Used | Forecast Horizon | Reported Results |
|---|---|---|---|---|
| [19] | Singh & Garg | ARIMA and S-ARIMA | Short-term on Power Production | nRMSE 3.4% on a 24 MW power station |
| [21] | Despotovic et al. | Autoregressive + Transfer Learning for Spanish PV | Short-term | nRMSE ≈ 19% for 30 min, 31% for 180 min and 34% for 6h for GHI |
| [22,23] | Torres et al. | CNN + LSTM with meteorological, historical, and satellite data for Queensland (AUS) | Short-term (intra-day) | RMSE ≈ 148 MW for PV power in a 70 MW PV plant |
| [24] | Qing & Niu | LSTM + weather forecasts for Cape Verde | Day-ahead (hourly) | RMSE ≈ 76 W/m2 for GHI |
| [25] | Xu et al. | Signal decomposition + XGBoost | Short-term | eRMSE ≈ 1.19 for Power (MW) |
| [26] | Alonso-Montesinos et al. | Sky images + cloud cross-correlation | Minute-level | RMSE ≈ 17% for GHI under partly cloudy conditions |
| [27] | Zhao et al. | 3D-CNN vs. 2D-CNN and LSTM | Short-term (DNI) | nRMSE ≈ 30% for DNI |
| [28] | Bu et al. | CNN + LSTM on satellite images for several PV Stations in China | Short-term | RMSE ≈ 60–80 W/m2 |
| [29] | Paulescu et al. | PV2-state + sky imagery | Intra-hour (15–30 min) | nRMSE ≈ 23% |
| [35] | Marinho et al. | CNN-1D, LSTM, CNN-LSTM | Short-term | RMSE ≈ 75 W/m2 (GHI, Folsom dataset) |
| [36] | Oliveira et al. | XGBoost, SVR, GMDH, QNN | Intra-hour and intra-day | RMSE for GHI: 39–48.5 W/m2 for DNI: 86.8–109.9 W/m2 |
| [37] | Zhang et al. | AutoML, CNN, ViT, SPM | Ultra short-term (2, 6, 10 min) | RMSE for GHI ≈ 95 W/m2 |
| Model | Hyperparameters | Optimisation Space |
|---|---|---|
| NN | Number of hidden layers Number of hidden layers | [1, 3] [10, 300] |
| Activation functions | [ReLU, tanh, sigmoid] | |
| DT | Minimum leaf size | [1, 7500] |
| RF | Number of learning cycles Learning rate Minimum leaf size | [100, 3000] [0, 1] [1, 7500] |
| LSTM | Number of hidden units Learning rate Dropout rate | [50, 300] [0, 0.1] [0, 0.6] |
| Intra-Hour | Intra-Day | Day-Ahead | |||||
|---|---|---|---|---|---|---|---|
| GHI | RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| Statistical methods | lasso | 68.4 | 34.2 | 88.0 | 47.8 | 101.1 | 59.4 |
| lasso + weather | 67.2 | 35.1 | 93.1 | 53.3 | 70.5 | 43.0 | |
| ols | 67.7 | 35.9 | 89.2 | 50.1 | 98.5 | 35.9 | |
| ols + weather | 66.4 | 37.5 | 83.1 | 47.8 | 75.1 | 37.5 | |
| ridge | 68.5 | 34.2 | 87.7 | 47.6 | 100.5 | 34.2 | |
| ridge + weather | 67.3 | 35.0 | 99.5 | 55.8 | 74.1 | 35.0 | |
| ML Methods | Random Forest | 66.8 | 35.3 | 86.9 | 48.0 | 98.0 | 35.3 |
| Random Forest + weather | 63.8 | 34.3 | 78.9 | 43.8 | 68.6 | 34.3 | |
| Neural network | 66.3 | 35.1 | 91.5 | 51.7 | 152.2 | 35.1 | |
| Neural network + weather | 64.8 | 36.6 | 92.9 | 52.9 | 107.1 | 36.6 | |
| Regression Tree | 81.5 | 41.7 | 103.5 | 55.8 | 120.6 | 41.7 | |
| Regression Tree + weather | 81.1 | 41.7 | 95.8 | 52.7 | 84.0 | 41.7 | |
| LSTM | 66.2 | 36.0 | 89.2 | 51.2 | 140.4 | 94.3 | |
| LSTM + weather | 70.7 | 39.5 | 87.0 | 49.5 | 107.9 | 73.9 |
| Intra-Hour | Intra-Day | Day-Ahead | |||||
|---|---|---|---|---|---|---|---|
| DNI | RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| Statistical methods | lasso | 130.5 | 75.9 | 183.0 | 110.7 | 261.4 | 188.3 |
| lasso + weather | 128.8 | 35.1 | 188.9 | 123.2 | 177.7 | 121.0 | |
| ols | 130.1 | 35.9 | 189.2 | 125.3 | 258.0 | 208.3 | |
| ols + weather | 127.5 | 37.5 | 178.1 | 117.3 | 184.2 | 131.1 | |
| ridge | 131.5 | 34.2 | 182.6 | 110.0 | 262.6 | 189.3 | |
| ridge + weather | 128.7 | 35.0 | 200.5 | 128.2 | 178.5 | 121.6 | |
| ML methods | Random Forest | 129.2 | 35.3 | 185.6 | 120.5 | 256.2 | 206.0 |
| Random Forest + weather | 125.0 | 34.3 | 172.4 | 111.3 | 173.9 | 122.0 | |
| Neural network | 128.2 | 35.1 | 194.2 | 126.2 | 334.4 | 246.1 | |
| Neural network + weather | 126.1 | 36.6 | 202.1 | 128.0 | 247.5 | 170.2 | |
| Regression Tree | 157.6 | 41.7 | 220.9 | 136.1 | 316.6 | 233.2 | |
| Regression Tree + weather | 158.4 | 41.7 | 214.8 | 129.5 | 211.9 | 141.5 | |
| LSTM | 127.9 | 79.9 | 191.4 | 125.9 | 376.3 | 299.3 | |
| LSTM + weather | 125.5 | 79.7 | 183.1 | 116.0 | 222.8 | 161.9 |
| Intra-Hour | Intra-Day | Day-Ahead | ||||||
|---|---|---|---|---|---|---|---|---|
| GHI | RMSE | MAE | RMSE | MAE | RMSE | MAE | ||
| TS | Random Forest | 206.9 | 206.2 | 214.3 | 206.2 | 329.7 | 207.1 | |
| Random Forest + features | 207.0 | 206.2 | 214.3 | 206.2 | 329.7 | 207.1 | ||
| Neural network | 207.0 | 206.3 | 215.2 | 206.3 | 329.6 | 207.1 | ||
| Neural network + feat | 207.0 | 206.3 | 214.5 | 206.4 | 329.6 | 207.1 | ||
| Regression Tree | 206.9 | 206.2 | 215.0 | 206.2 | 329.7 | 207.1 | ||
| Regression Tree + features | 206.9 | 206.2 | 214.3 | 206.2 | 329.7 | 207.1 | ||
| LSTM | 211.8 | 206.2 | 270.5 | 206.3 | 318.2 | 210.7 | ||
| LSTM+features | 211.8 | 206.3 | 270.5 | 206.3 | 318.5 | 210.6 | ||
| TS | Random Forest | 41.3 | 39.2 | 46.3 | 39.2 | 82.2 | 43.0 | |
| hybrid | Random Forest + features | 40.7 | 38.9 | 45.8 | 39.1 | 78.8 | 41.3 | |
| Neural network | 41.1 | 39.0 | 45.6 | 39.3 | 74.4 | 40.2 | ||
| Neural network + feat | 41.7 | 39.5 | 46.1 | 39.6 | 76.5 | 40.9 | ||
| Regression Tree | 44.9 | 41.3 | 51.0 | 41.8 | 90.4 | 45.4 | ||
| Regression Tree + features | 46.0 | 42.2 | 54.8 | 42.9 | 92.6 | 44.9 | ||
| LSTM | 108.5 | 89.0 | 86.6 | 51.6 | 89.0 | 41.3 | ||
| LSTM+features | 102.9 | 84.0 | 82.5 | 50.0 | 88.8 | 41.5 | ||
| Intra-Hour | Intra-Day | Day-Ahead | ||||||
|---|---|---|---|---|---|---|---|---|
| DNI | RMSE | MAE | RMSE | MAE | RMSE | MAE | ||
| TS | Random Forest | 260.7 | 258.0 | 274.8 | 258.0 | 403.6 | 258.9 | |
| Random Forest + features | 260.6 | 257.9 | 274.8 | 258.0 | 403.5 | 258.9 | ||
| Neural network | 261.3 | 258.1 | 275.0 | 258.1 | 403.4 | 259.0 | ||
| Neural network + feat | 260.9 | 258.1 | 275.0 | 258.1 | 403.5 | 259.0 | ||
| Regression Tree | 261.2 | 258.0 | 274.8 | 257.9 | 403.5 | 258.8 | ||
| Regression Tree + features | 260.6 | 257.9 | 274.8 | 257.9 | 403.6 | 258.9 | ||
| LSTM | 265.5 | 269.62 | 320.6 | 258.0 | 407.5 | 269.6 | ||
| LSTM + features | 266.2 | 269.83 | 320.6 | 258.0 | 407.1 | 269.8 | ||
| TS | Random Forest | 116.9 | 112.6 | 128.4 | 112.9 | 210.8 | 119.0 | |
| hybrid | Random Forest + features | 113.4 | 109.0 | 125.6 | 109.2 | 209.0 | 118.8 | |
| Neural network | 116.5 | 112.7 | 124.6 | 113.2 | 198.9 | 115.4 | ||
| Neural network + feat | 113.4 | 109.4 | 124.8 | 110.6 | 205.0 | 118.4 | ||
| Regression Tree | 121.4 | 114.9 | 134.6 | 116.0 | 225.5 | 123.1 | ||
| Regression Tree + features | 120.2 | 112.2 | 140.6 | 114.6 | 239.1 | 125.7 | ||
| LSTM | 179.0 | 151.0 | 165.7 | 113.9 | 218.3 | 116.3 | ||
| LSTM + features | 186.5 | 160.6 | 170.0 | 115.9 | 218.8 | 115.9 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trull, O.; García-Díaz, J.C.; Peiró-Signes, A. A Comparative Study of Statistical and Machine Learning Methods for Solar Irradiance Forecasting Using the Folsom PLC Dataset. Energies 2025, 18, 4122. https://doi.org/10.3390/en18154122
Trull O, García-Díaz JC, Peiró-Signes A. A Comparative Study of Statistical and Machine Learning Methods for Solar Irradiance Forecasting Using the Folsom PLC Dataset. Energies. 2025; 18(15):4122. https://doi.org/10.3390/en18154122
Chicago/Turabian StyleTrull, Oscar, Juan Carlos García-Díaz, and Angel Peiró-Signes. 2025. "A Comparative Study of Statistical and Machine Learning Methods for Solar Irradiance Forecasting Using the Folsom PLC Dataset" Energies 18, no. 15: 4122. https://doi.org/10.3390/en18154122
APA StyleTrull, O., García-Díaz, J. C., & Peiró-Signes, A. (2025). A Comparative Study of Statistical and Machine Learning Methods for Solar Irradiance Forecasting Using the Folsom PLC Dataset. Energies, 18(15), 4122. https://doi.org/10.3390/en18154122







