An Automated Method of Parametric Thermal Shaping of Complex Buildings with Buffer Spaces in a Moderate Climate
Abstract
1. Introduction
- To develop a parametric description of the relationships appearing between the form of passive buildings and the geometry of the attached or built-in buffer spaces, especially in the case of complex envelopes;
- To create qualitative and quantitative parametric models describing the geometric, physical and thermal features of buildings with buffer spaces;
- To analyze the thermal performance of buildings with built-in buffer spaces using the invented models;
- To develop various research, test and simulation plans to obtain the expected universality and accuracy of the configured quantitative models (it is reasonable to use statistical methods to minimize the number of the independent variables necessary to obtain the universality and accuracy of the developed models);
- To develop a new method to assist the invented quantitative parametric model, the algorithm of which makes it possible (a) to define the input and output variables of the models, (b) to develop research plans, (c) to perform simulations of the thermal performance of buildings with buffer spaces in a temperate climate of the Central Europe Plane, (d) to describe the relationships found during tests and simulations and (e) to search for new solutions in terms of the effective thermal operation of a building with a buffer space;
- To support the search for optimal solutions using artificial intelligence, including parametric artificial neural networks and optimizing genetic algorithms, due to the large number of independent and dependent variables and the complexity of the observed relationships between the properties of the models used;
- To automate the activities in the field of simulations, analysis and description of the existing relationships as well as predictions of the thermal operation of buildings with buffer spaces using computer techniques.
2. Methodology
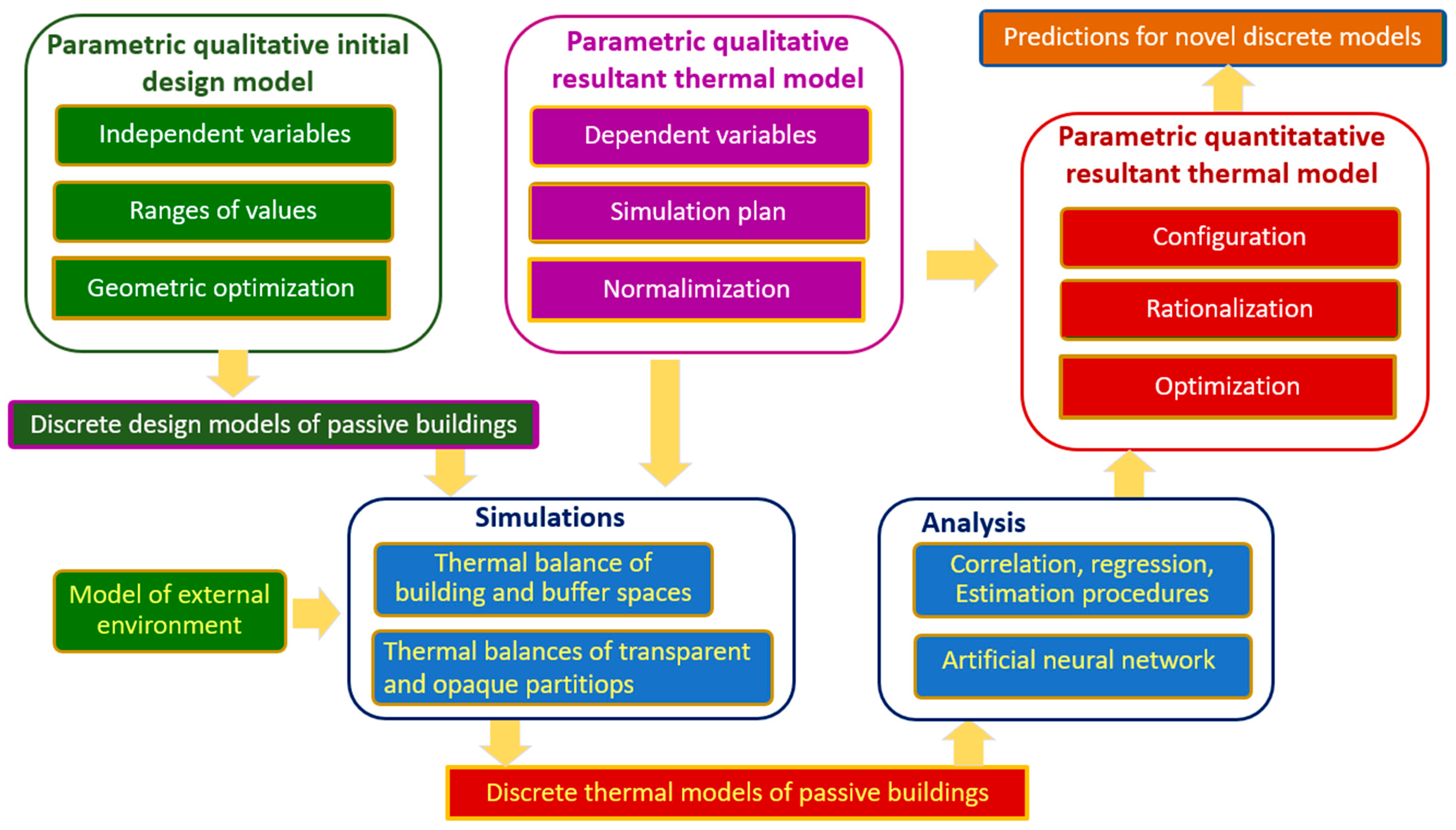
2.1. The Method’s Algorithm
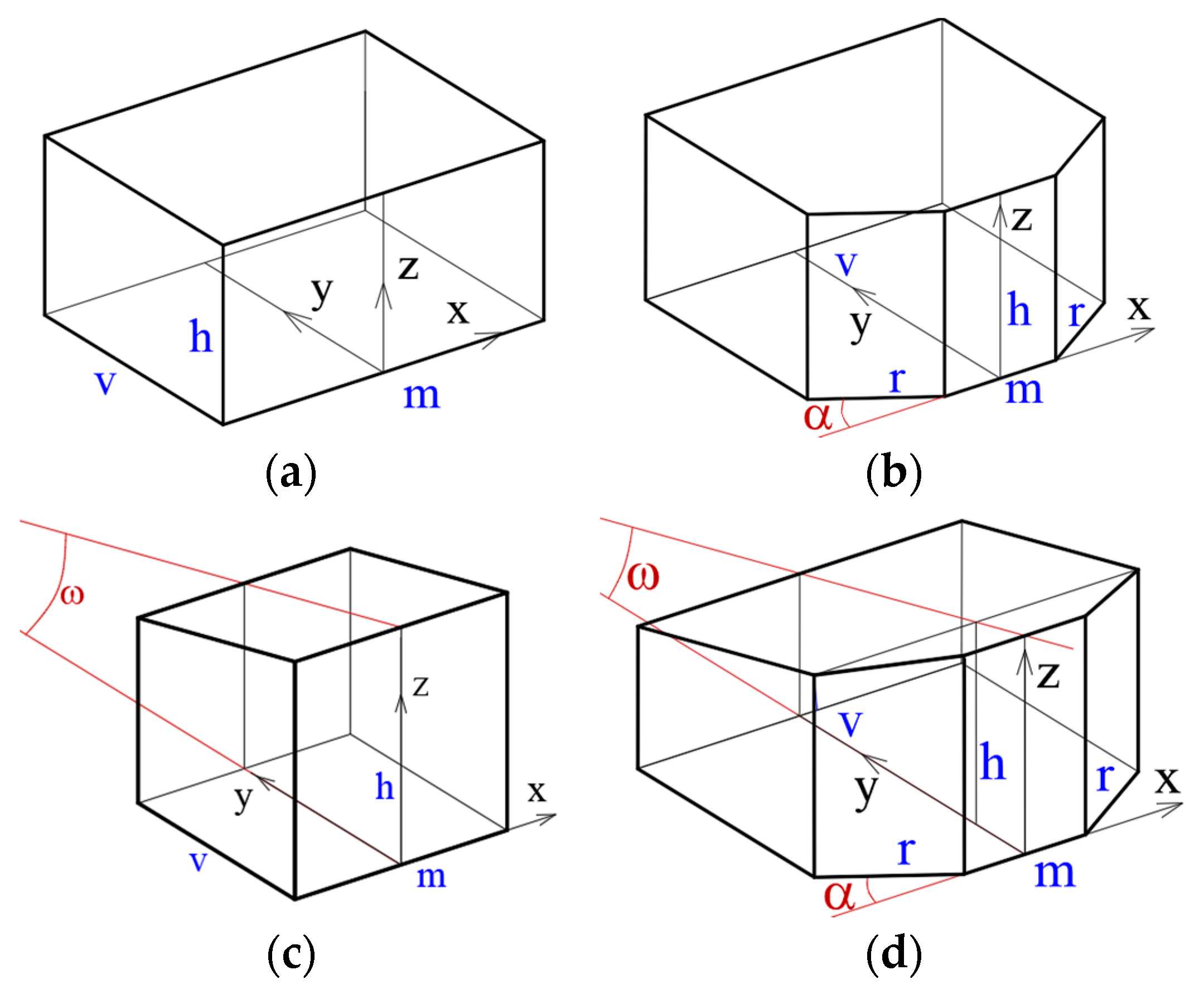
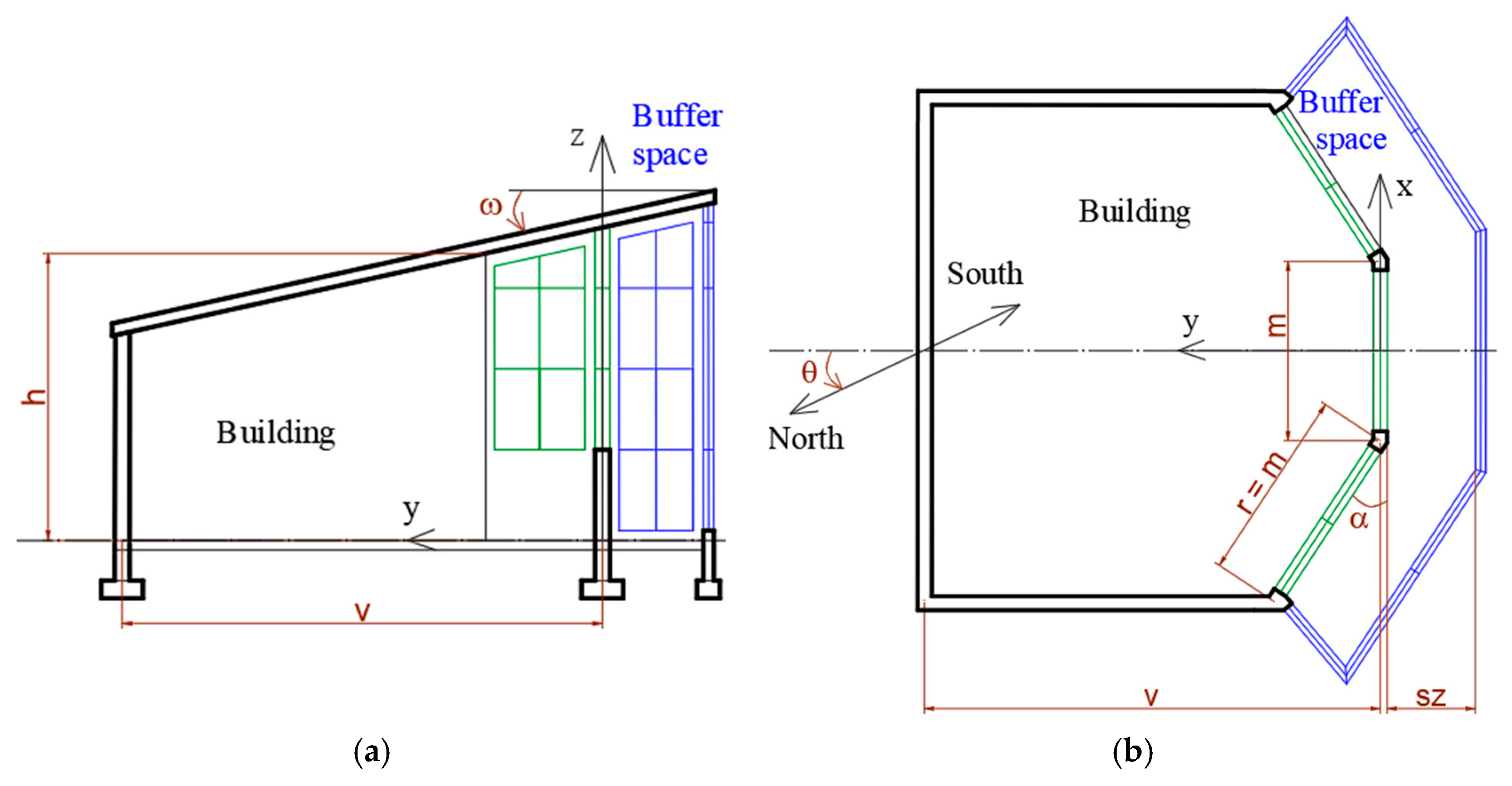
2.2. Geometric Models
2.3. Physical Design Model
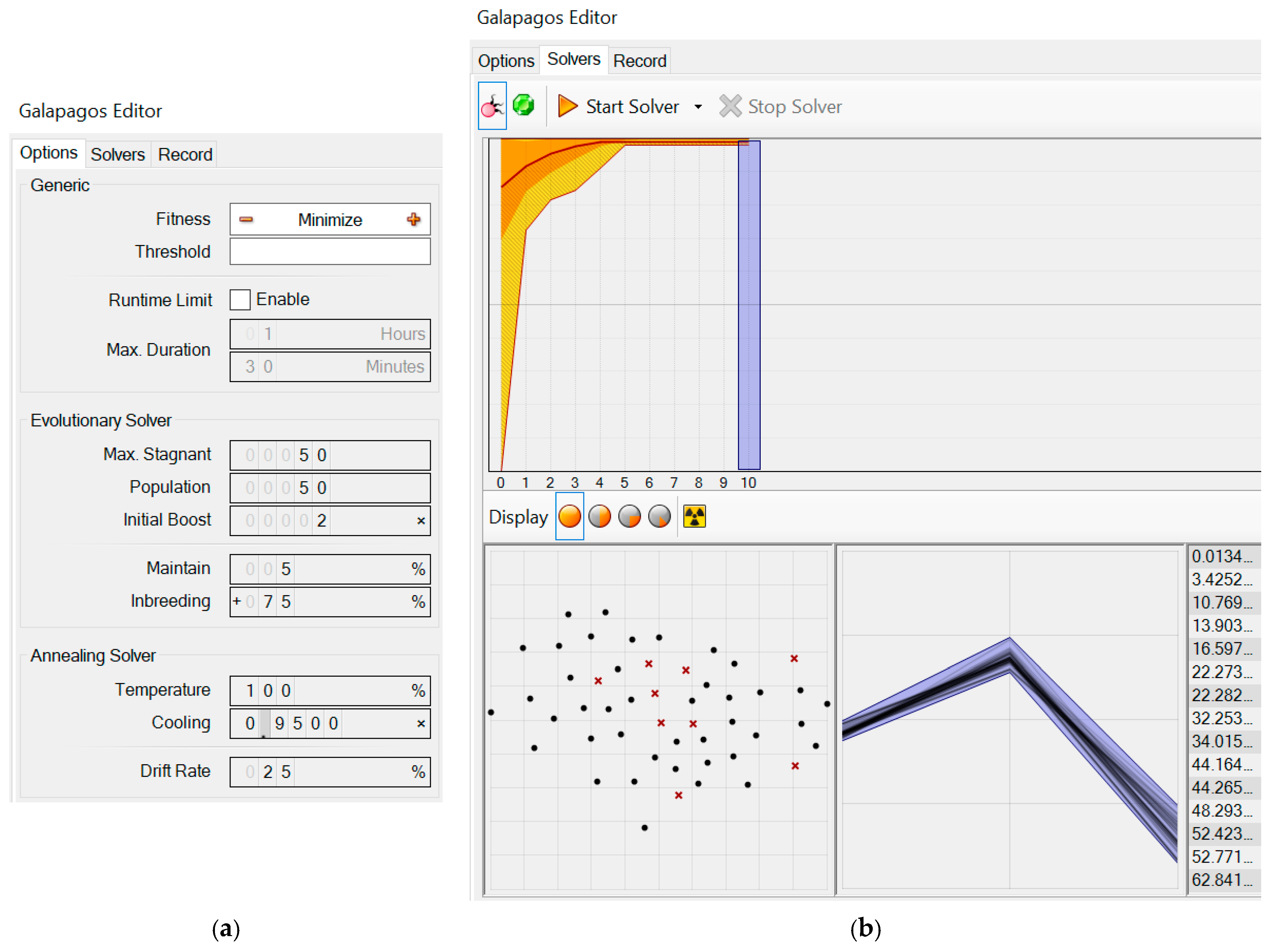
2.4. The Research Plan
2.5. Parametric Thermal Model
3. Simulation Results
4. The Analysis of the Simulation Results
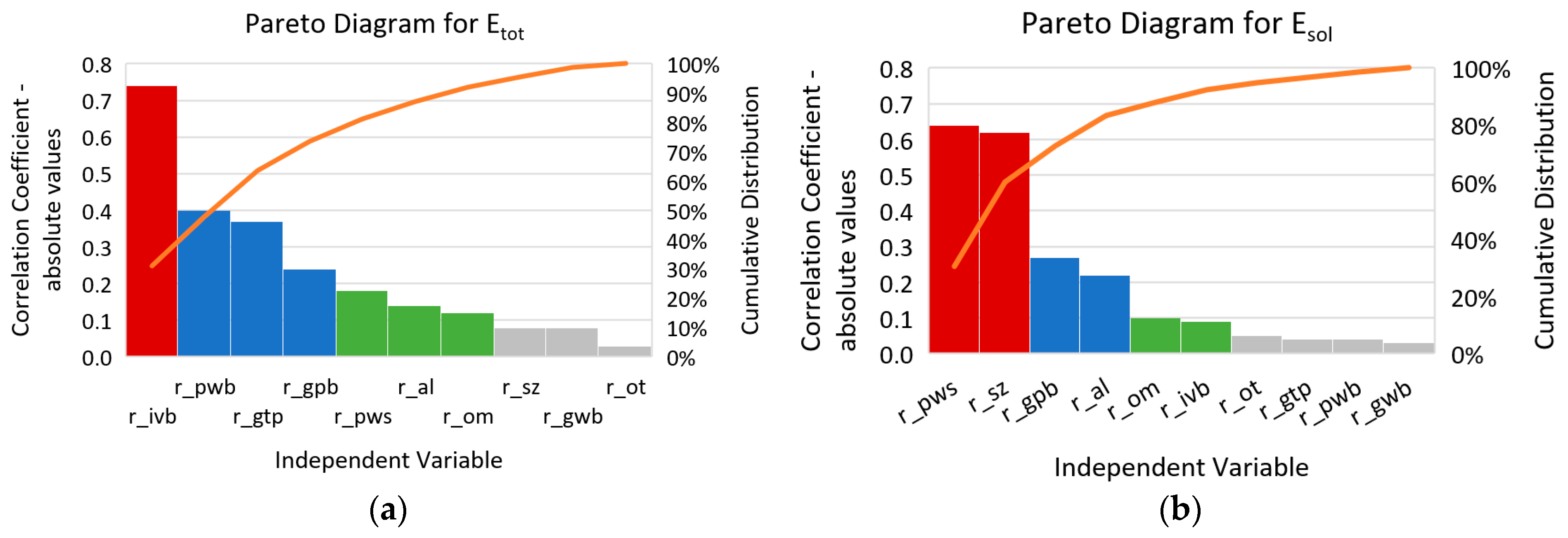
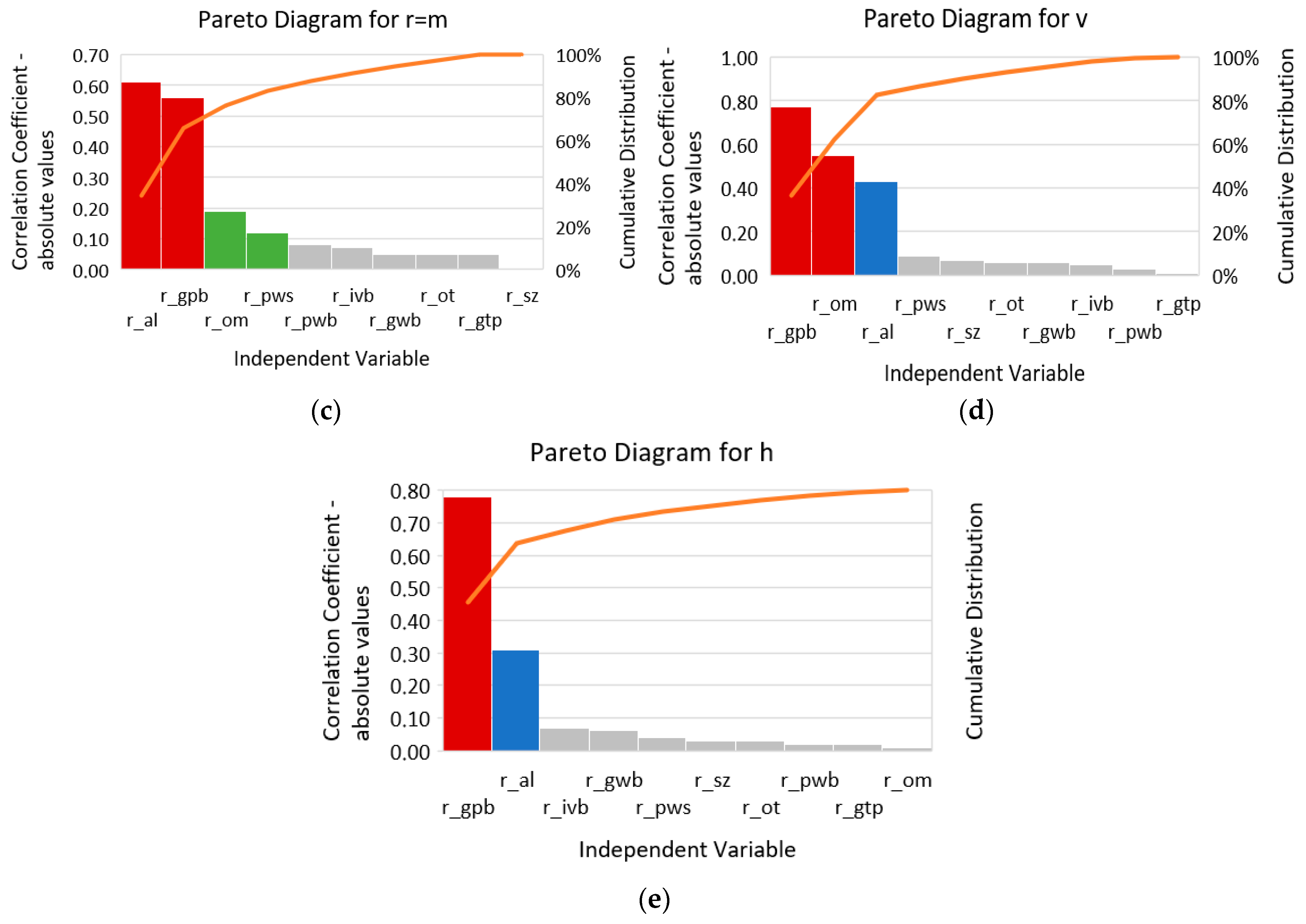
4.1. Correlation Analysis
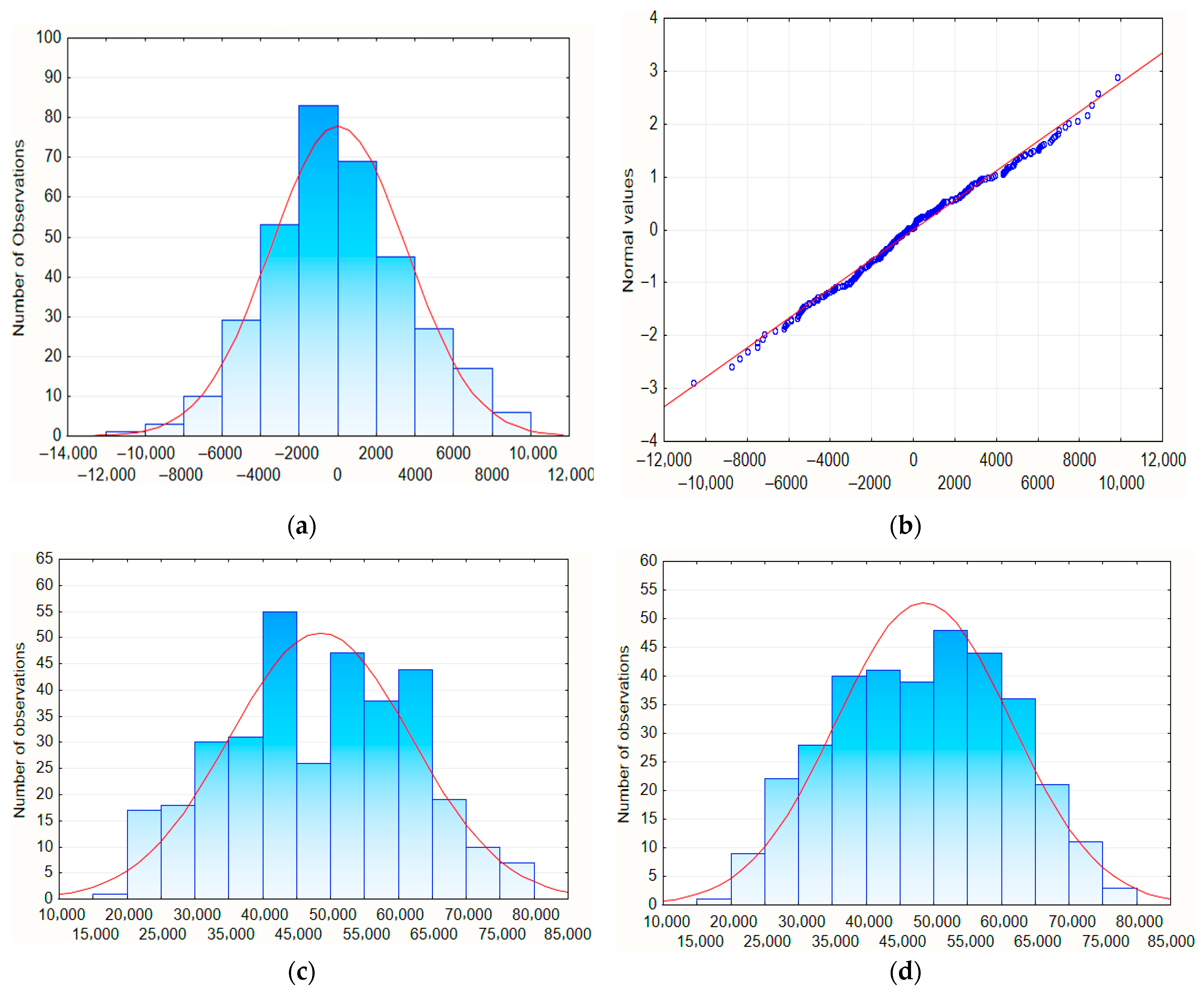
4.2. Regression Analysis
4.3. The Parametric Neural Network Describing the Relations Found During the Simulations
5. Discussion
5.1. The Impact of Each Independent Variable on the Thermal Model of Buildings with Buffer Spaces
5.2. A Comparison of the Obtained Results with the Available Results from Other Studies
5.3. New Effective Configurations of Buildings with Buffer Spaces Based on the Parametric Quantitative Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Cubature of building | |
| Surface area of building envelope | |
| Surface area of south-facing fall | |
| Width of each strip of south-facing fall | |
| α | Folding angle of south-facing fall |
| ω | Angle of inclination of roof |
| Reference height of building | |
| Length of building | |
| g_al | Normalized value of α |
| g_om | Normalized value of ω |
| g_sz | Normalized value of buffer space’s width |
| Etot | Total heating and cooling energy |
| Esol | Solar gains |
| Cfgi | i-th configuration of building with buffer space |
Appendix A
| Type | Personnel Density [People/m2] | Lighting Power Density [W/m2] | Power Density of Equipment [W/m2] |
|---|---|---|---|
| 0.108 | 4.6 | 10.8 |
| External Wall | Layer | Value [mm] |
|---|---|---|
| South-facing external wall | Plaster | 10 |
| Thermal insulation | Variable | |
| Concrete | 400 | |
| Cement–lime mortar | 15 | |
| External wall (east-facing, north-facing, west-facing) | Plaster | 10 |
| Thermal insulation | Variable | |
| Concrete | 200 | |
| Cement–lime mortar | 15 | |
| Roof | Steel trapezial sheets | 0.1 Variable 350 15 |
| Thermal insulation | ||
| Reinforced concrete beam-slab cement–lime mortar | ||
| Floor | Concrete | 100 |
| Thermal insulation | Variable | |
| Cement mortar | 30 | |
| Triple-glazed windows | Pane1 | Variable |
| Argon | 13 | |
| Pane2 | Variable | |
| Air | 13 | |
| Pane3 | Variable |
| Element | Layer | Value |
|---|---|---|
| South-facing external wall | Plaster | 10 [mm] |
| Thermal insulation | Variable | |
| Concrete | 200 [mm] | |
| Cement–lime mortar | 15 [mm] | |
| Single-glazed windows | Thickness | 4 [mm] |
| U-value | [W/m·K] | |
| Solar transmittance | 0.95 | |
| Solar reflectance | 0.04 | |
| Emissivity | 0.25 | |
| Solar diffuse | No |
References
- EU. Directive (EU) 2018/844 of the European Parliament and of the Council of 30 May 2018 Amending Directive 2010/31/EU on the Energy Performance of Buildings and Directive 2012/27/EU on Energy Efficiency, Brussels: J. Eur. Communities L 156/75 from 19.6.2019 EU. 2016, European Commission—Environment-Sustainable Buildings; EU: Maastricht, The Netherlands, 2018; Available online: http://ec.europa.eu/environment/eussd/buildings.htm (accessed on 10 January 2025).
- EU. Directive (EU) 2024/1275 of the European Parliament and of the Council of 24 April 2024 Amending Directive 2010/31/EU on the Energy Performance of Buildings; EU: Maastricht, The Netherlands, 2024; Available online: http://data.europa.eu/eli/dir/2024/1275/oj (accessed on 10 January 2025).
- Cai, K.; Wu, L. Grey prediction of carbon emission and carbon peak in several developing countries. Eng. Appl. Artif. Intell. 2024, 133, 108210. [Google Scholar] [CrossRef]
- D’Agostino, D.; Daraio, L.; Marino, C.; Minichiello, F. Cost-optimal methodology and passive strategies for building energy efficiency: A case-study. Archit. Sci. Rev. 2018, 61, 400–409. [Google Scholar] [CrossRef]
- Jiang, W.; Jin, Y.; Liu, G.; Li, Q.; Li, D. Passive nearly zero energy retrofits of rammed earth rural residential buildings based on energy efficiency and cost effectiveness analysis. Renew. Sustain. Energy Rev. 2023, 180, 113300. [Google Scholar] [CrossRef]
- Young-Sub, A.; Jongkyu, K.; Hong-Jin, J.; Gwang-Woo, H.; Haneul, K.; Wangje, L.; Min-Hwi, K. Retrofit of renewable energy systems in existing community for positive energy community. Energy Rep. 2023, 9, 3733–3744. [Google Scholar] [CrossRef]
- Shekar, V.; Abraham, V.; Calo, A.; Pongracz, E. Determining the optimal azimuth for solar-ready buildings: Simulating for maximising the economic value of solar PV installations in Lapland, Finland. Renew. Energy 2025, 241, 122357. [Google Scholar] [CrossRef]
- Liu, J.; Zang, H.; Zhang, F.; Cheng, L.; Ding, T.; Wei, Z.; Sun, G. A hybrid meteorological data simulation framework based on time-series generative adversarial network for global daily solar radiation estimation. Renew. Energy 2023, 219, 119374. [Google Scholar] [CrossRef]
- European Commission Science Hub PVGIS. Available online: https://ec.europa.eu/jrc/en/PVGIS/docs/methods (accessed on 10 May 2025).
- Xi, H.; Zhang, Q.; Ren, Z.; Li, G.; Chen, Y. Urban Building Energy Modeling with Parameterized Geometry and Detailed Thermal Zones for Complex Building Types. Buildings 2023, 13, 2675. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, R.J.; Liu, C.; Sun, C. Solar building envelope potential in urban environments: A state-of-the-art review of assessment methods and framework. Build. Environ. 2023, 244, 110831. [Google Scholar] [CrossRef]
- Desthieux, G.; Carneiro, C.; Camponovo, R.; Ineichen, P.; Morello, E.; Boulmier, A.; Abdennadher, N.; Dervey, S.; Ellert, C. Solar Energy Potential Assessment on Rooftops and Façades in Large Built Environments Based on LiDAR Data, Image Processing, and Cloud Computing. Methodological Background, Application, and Validation in Geneva (Solar Cadaster). Front. Built Environ. 2018, 4, 14. [Google Scholar] [CrossRef]
- Abramczyk, J. Parametric building forms rationalizing the incident direct solar irradiation. Build. Environ. 2022, 215, 108963. [Google Scholar] [CrossRef]
- Abramczyk, J.; Bielak, W. Parametric Building Envelopes Rationalized in Terms of Their Solar Performance in a Temperate Climate. Energies 2025, 18, 2479. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Processes and Systems. In Solar Energy Engineering, 2nd ed.; ScienceDirect, Academic Press: Oxford, UK, 2013. [Google Scholar] [CrossRef]
- A, Y.; Li, N.; Long, J.; He, Y. Thermal performance of a novel solar thermal facade system in a hot summer and cold-winter zone. Sol. Energy 2020, 204, 106–114. [Google Scholar] [CrossRef]
- Chwieduk, D. Solar Energy in Buildings, 1st ed.; Elsevier Science & Technology: Oxford, UK, 2014. [Google Scholar] [CrossRef]
- Maturo, A.; Buonomano, A.; Athienitis, A. Design for energy flexibility in smart buildings through solar based and thermal storage systems: Modelling, simulation and control for the system optimization. Energy 2022, 260, 125024. [Google Scholar] [CrossRef]
- Bushra, N. A comprehensive analysis of parametric design approaches for solar integration with buildings: A literature review. Renew. Sustain. Energy Rev. 2022, 168, 112849. [Google Scholar] [CrossRef]
- Kistelegdi, I.; Horváth, K.R.; Storcz, T.; Ercsey, Z. Building Geometry as a Variable in Energy, Comfort. and Environmental Design Optimization—A Review from the Perspective of Architects. Buildings 2022, 12, 69. [Google Scholar] [CrossRef]
- Chorak, A.; Mahdaoui, M.; Taher, M.A.B.; Kaitouni, S.I.; Afass, A.; Ouardouz, M.; Ahachad, M. Integrating active and passive solar strategies in modular residential positive energy building in semi-arid climates: Insights from the TDART project. Energy Rep. 2025, 13, 1239–1265. [Google Scholar] [CrossRef]
- Feng, J.; Luo, X.; Gao, M.; Abbas, A.; Xu, Y.P.; Pouramini, S. Minimization of energy consumption by building shape optimization using an improved Manta-Ray Foraging Optimization algorithm. Energy Rep. 2021, 7, 1068–1078. [Google Scholar] [CrossRef]
- Jiao, Y.; Yu, Y.; Yu, H.; Wang, F. The impact of thermal environment of transition spaces in elderly-care buildings on thermal adaptation and thermal behavior of the elderly. Build. Environ. 2023, 228, 109871. [Google Scholar] [CrossRef]
- Juan, X.; Wenjing, M.; Wenting, Y.; Ziliang, L.; Gengfang, X.; Xiaomin, W. Impact of transition spaces on the indoor thermal environment: A case study of traditional dwellings in Southern Shaanxi, China. J. Build. Eng. 2024, 95, 110283. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, D.; Li, J.; Yu, H.; He, B. Optimizing building envelope dimensions for passive solar houses in the Qinghai-Tibetan region: Window to wall ratio and depth of sunspace. J. Therm. Sci. 2019, 28, 1115–1128. [Google Scholar] [CrossRef]
- Luo, S.; Yuan, P.F.; Zhao, M.; Yao, J.; Yang, F. Developing a framework for sustainable retrofit of residential buildings based on ensemble learning algorithm: A case study of Shanghai. Build. Environ. 2025, 282, 113311. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y. Shape optimization of free-form buildings based on solar radiation gain and space efficiency using a multi-objective genetic algorithm in the severe cold zones of China. Sol. Energy 2016, 132, 38–50. [Google Scholar] [CrossRef]
- Uniyal, S.; Lodhi, M.S.; Pawar, Y.; Thakral, S.; Garg, P.K.; Mukherjee, S.; Nautiyal, S. Passive solar heated buildings for enhancing sustainability in the Indian Himalayas. Renew. Sustain. Energy Rev. 2024, 200, 114586. [Google Scholar] [CrossRef]
- Gainza-Barrencua, J.; Odriozola-Maritorena, M.; Hernandez-Minguillon, R.; Gomez-Arriaran, I. Energy savings using sunspaces to preheat ventilation intake air: Experimental and simulation study. J. Build. Eng. 2021, 40, 102343. [Google Scholar] [CrossRef]
- Liua, Z.; Wua, D.; Heb, B.-J.; Wanga, Q.; Yuc, H.; Mad, W.; Jina, G. Evaluating potentials of passive solar heating renovation for the energy poverty alleviation of plateau areas in developing countries: A case study in rural Qinghai-Tibet Plateau, China. Sol. Energy 2019, 187, 95–107. [Google Scholar] [CrossRef]
- Chiesa, G.; Simonetti, M.; Ballada, G. Potential of Attached Sunspaces in Winter Season Comparing Different Technological Choices in Central and Southern Europe. Energy Build. 2017, 138, 377–395. [Google Scholar] [CrossRef]
- Zhang, L.; Dong, Z.; Liu, F.; Li, H.; Zhang, X.; Wang, K.; Chen, C.; Tian, C. Passive solar sunspace in a Tibetan buddhist house in Gannan cold areas: Sensitivity analysis. J. Build. Eng. 2023, 67, 105960. [Google Scholar] [CrossRef]
- Bataineh, K.M.; Fayez, N. Analysis of thermal performance of building attached sunspace. Energy Build. 2011, 43, 1863–1868. [Google Scholar] [CrossRef]
- Yao, G.; Guo, X.; Qian, Z.; Pang, Y.; Zhang, Y.; Xie, C. Application of thermal buffer spaces in the renovation of rural dwellings for nearly zero energy consumption in severe cold regions of China. J. Build. Eng. 2025, 99, 111543. [Google Scholar] [CrossRef]
- Monge-Barrio, A.; Sanchez-Ostiz, A. Energy efficiency and thermal behaviour of attached sunspaces, in the residential architecture in Spain, Summer Conditions. Energy Build. 2015, 108, 244–256. [Google Scholar] [CrossRef]
- Ignjatovic, D.; Popovic, M.J.; Kavran, J. Application of sunspaces in fostering energy efficiency and economic viability of residential buildings in Serbia. Energy Build. 2015, 98, 3–9. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, X.; Li, D.; Arıcı, M.; Yıldız, Ç.; Li, Q.; Zhang, S.; Jiang, W. Influence of sunspace on energy consumption of rural residential buildings. Sol. Energy 2020, 211, 336–344. [Google Scholar] [CrossRef]
- Hilliahoa, K.; Mäkitalob, E.; Lahdensivu, J. Energy saving potential of glazed space: Sensitivity analysis. Energy Build. 2015, 99, 87–97. [Google Scholar] [CrossRef]
- Alzamil, A.; Hamed, M. Prediction of thermal buffer zone effectiveness in real-size buildings—An experimental and analytical study. Int. J. Energy Res. 2019, 43, 5284–5300. [Google Scholar] [CrossRef]
- Ma, Q.S.; Fukuda, H.; Lee, M.; Kobatake, T.; Kuma, Y.; Ozaki, A.; Wei, X.D. Experimental analysis of the thermal performance of a sunspace attached to a house with a central air conditioning system. Sustainability 2018, 10, 1428. [Google Scholar] [CrossRef]
- Fernandes, J.; Malheiro, R.; de Fátima Castro, M.; Gerv’asio, H.; Silva, S.M.; Mateus, R. Thermal performance and comfort condition analysis in a vernacular building with a glazed balcony. Energies 2020, 13, 624. [Google Scholar] [CrossRef]
- Kurnitski, J.; Guasco, M.; Orlanno, M.; Piccardo, C.; Giachetta, A.; Dodoo, A.; Kalamees, T. Design optimization of a building attached sunspace through experimental monitoring and dynamic modelling. In Proceedings of the 12th Nordic Symposium on Building Physics (NSB 2020), Tallinn, Estonia, 6–9 September 2020; Volume 172, p. 03010. [Google Scholar] [CrossRef]
- Gao, Y.; Meng, X.; Shi, X.; Wang, Z.; Long, E.; Gao, W. Optimization on non-transparent envelopes of the typical office rooms with air-conditioning under intermittent operation. Sol. Energy 2020, 201, 798–809. [Google Scholar] [CrossRef]
- Kang, X.; Yan, D.; Xie, X.; An, J.; Liu, Z. Co-simulation of dynamic underground heat transfer with building energy modeling based on equivalent slab method. Energy Build. 2022, 256, 111728. [Google Scholar] [CrossRef]
- Huang, Z.; Sun, Y.; Gan, L.; Liu, G.; Zhang, Y.; Zhou, T. Durability Analysis of Building Exterior Thermal Insulation, System in Hot Summer and Cold Winter Area Based on ANSYS. Sustainability 2022, 14, 5702. [Google Scholar] [CrossRef]
- Twidell, J.; Weir, T. Renewable Energy Resources, 3rd ed.; Taylor & Francis: London, UK, 2015. [Google Scholar] [CrossRef]
- Walton, G.N. The Thermal Analysis Research Program Reference Manual Program (TARP); National Bureau of Standards (Now National Institute of Standards and Technology): Washington, DC, USA, 1983.
- Bauer, H.-G.; Nembrini, J.; Samberger, S.; Gengnagel, C. Assessing Renovation Interventions Towards “Energy Plus” Buildings Through Parametric Exploration—The Case Of Glazed Buffer Spaces. In Proceedings of the Building Simulation 2013: 13th Conference of IBPSA, Chambery, France, 26–28 August 2013. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, D.H.; Lu, S.L. Research on the indoor thermal environment of attached sunspace passive solar heating system based on zero-state response control strategy. Appl. Sci. 2022, 12, 855. [Google Scholar] [CrossRef]
- Rahiminejad, M.; Khovalyg, D. Thermal resistance of ventilated air-spaces behind external claddings; definitions and challenges (ASHRAE 1759-RP). Sci. Technol. Built Environ. 2021, 27, 788–805. [Google Scholar] [CrossRef]
- Wang, X.; Lei, B.; Bi, H.; Yu, T. Study on the Thermal Performance of a Hybrid Heat Collecting Facade Used for Passive Solar Buildings in Cold Region. Energies 2019, 12, 1038. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, M.; Li, Y.-Z.; Li, C. Numerical investigation on the impact of an on-top sunspace passive heating approach for typical rural buildings in northern China. Sol. Energy 2019, 186, 300–310. [Google Scholar] [CrossRef]
- Vukadinović, A.; Radosavljević, J.; Đorđević, A.; Protić, M.; Petrović, N. Multi-objective optimization of energy performance for a detached residential building with a sunspace using the NSGA-II genetic algorithm. Sol. Energy 2021, 224, 1426–1444. [Google Scholar] [CrossRef]
- Vukadinović, A.; Radosavljević, J.; Đorđević, A.; Petrović, N. Effects of the geometry of residential buildings with a sunspace on their energy performance. Facta Univ. Ser. Archit. Civ. Eng. 2019, 17, 105–118. [Google Scholar] [CrossRef]
- Hosamo, H.H.; Tingstveit, M.S.; Nielsen, H.K.; Svennevig, P.R.; Svidt, K. Multiobjective optimization of building energy consumption and thermal comfort based on integrated BIM framework with machine learning—NSGA II. Energy Build. 2022, 277, 112479. [Google Scholar] [CrossRef]
- Rhinoceros. Rhino; Rhinoceros: Seattle, WA, USA, 2024; Available online: https://www.rhino3d.com/ (accessed on 10 May 2025).
- StatSoft. Statistica; StatSoft: Tulsa, OK, USA, 2024; Available online: https://www.statsoft.pl/ (accessed on 10 May 2025).
- Office. Excel; Microsoft: Redmond, MA, USA, 2019; Available online: https://chromewebstore.google.com/ (accessed on 10 May 2025).
- European Commission Science Hub PVGIS. Available online: https://re.jrc.ec.europa.eu/pvg_tools/ (accessed on 10 May 2025).
- SAT23.COM—The Meteo Company. Available online: https://www.sat24.com/en-gb (accessed on 29 July 2025).
- ASHRAE. ASHRAE Handbook of Fundamentals; ASHRAE: Peachtree Corners, GA, USA, 2017; Available online: https://www.ashrae.org/technical-resources/ashrae-handbook (accessed on 29 July 2025).
- ASHRAE. ASHRAE Handbook of Fundamentals; ASHRAE: Peachtree Corners, GA, USA, 2021; Available online: https://www.ashrae.org/technical-resources/ashrae-handbook (accessed on 29 July 2025).
- Ding, J.; Su, J.; Tang, H.-K.; Yu, W.C. Efficient sampling using macrocanonical Monte Carlo and density of states mapping. Phys. Rev. Res. 2024, 6, 043070. [Google Scholar] [CrossRef]

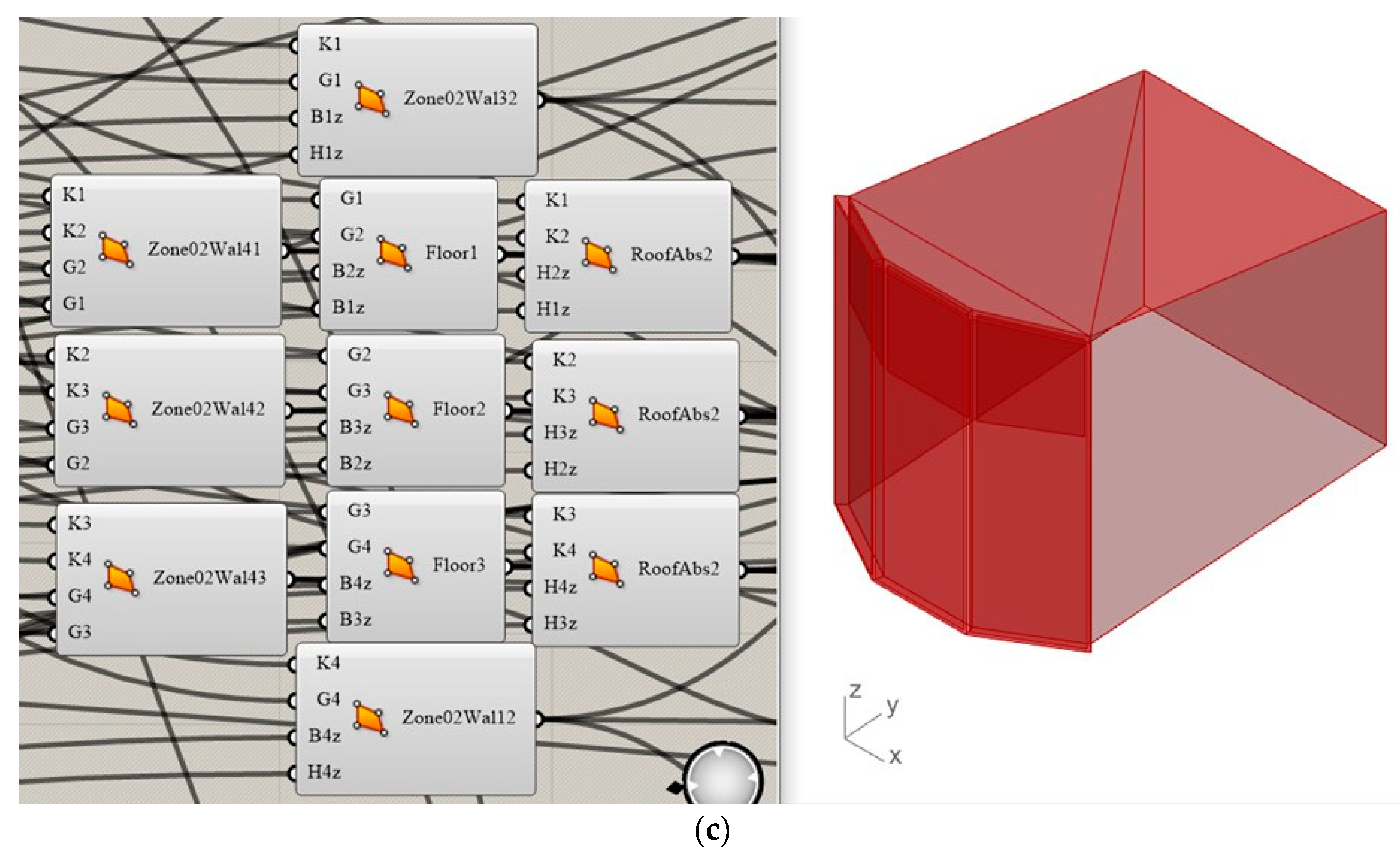

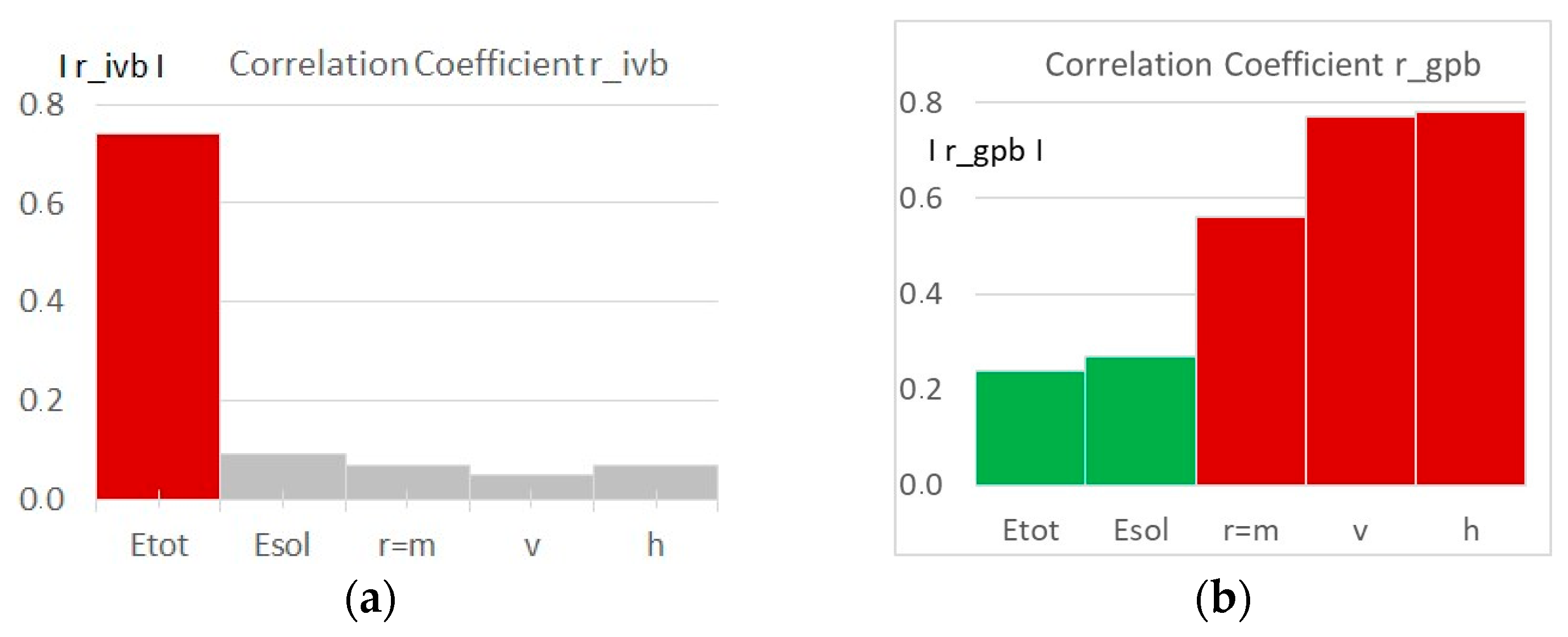
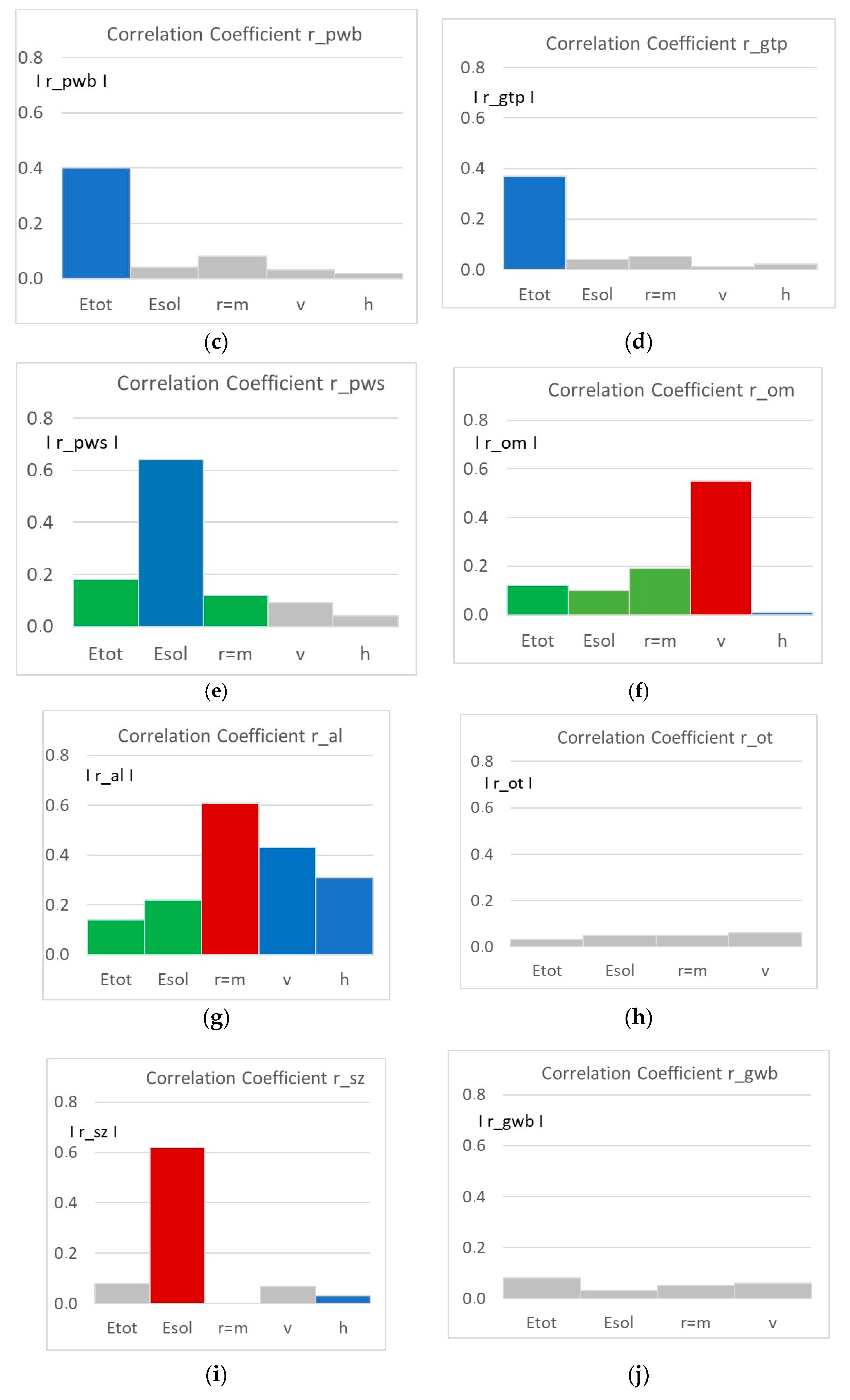
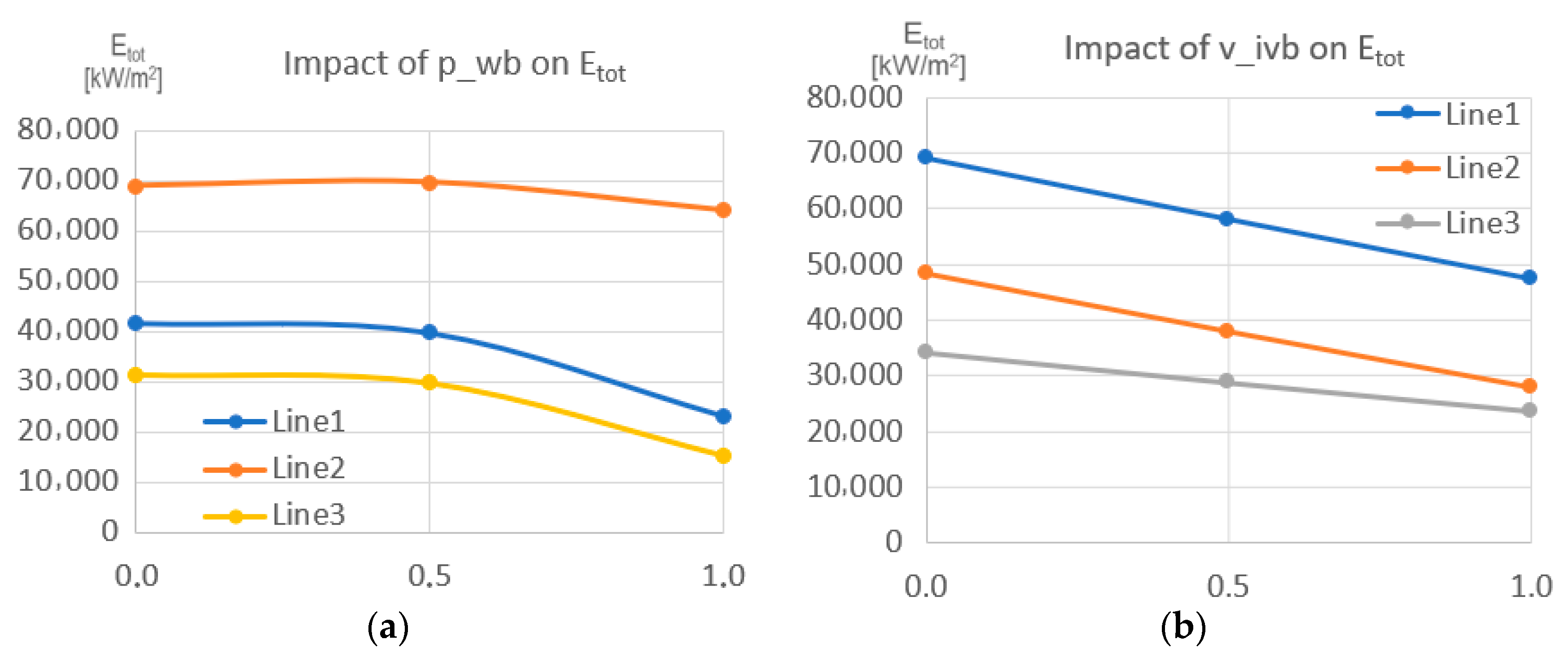
| Type | Independent Variable | Set1 | Set2 |
|---|---|---|---|
| Geometric Model | ω | 0° | 12° |
| α | 0° | 30° | |
| pb | 168 m2 | 210 m2 | |
| gwb | 0.3 | 0.885 | |
| Material Model | tp | 25 cm | 35 cm—roof |
| 15 cm | 25 cm—walls | ||
| 10 cm | 30 cm—floor | ||
| pwb | 0.003 m | 0.004 m—pane thickness | |
| 0.88 W/m-K | 0.88 W/m-K—transmittance | ||
| 0.85 W/m-K | 0.88 W/m-K—emissivity | ||
| 1.0 W/m-K | 0.70 W/m-K conductivity | ||
| Buffer Space Model | sz | 3 m | 0.5 m |
| pws | 0.003 m | 0.004 m—pane thickness | |
| 0.70 W/m-K | 0.95 W/m-K—transmittance | ||
| 0.50 W/m-K | 0.25 W/m-K—emissivity front | ||
| 0.50 W/m-K | 0.25 W/m-K—emissivity back | ||
| Physical Model | ivb | 0.00236/person | 0.001180/person—ventilation |
| 0.00030/m2 | 0.000152/m2—ventilation | ||
| 0.000226/m2 | 0.000113/m2—infiltration | ||
| ot | 0° | −40° |
| Config. | g_al | g_om | g_sz | g_tp | g_ot | g_pb | g_wb | v_ivb | p_wb | p_ws |
|---|---|---|---|---|---|---|---|---|---|---|
| Cfg1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| Cfg2 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| Cfg3 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| Cfg4 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| Cfg5 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| Cfg6 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| Cfg7 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| Cfg8 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Cfg9 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Cfg10 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| Config. | Etot kWh/m2 | Esol kWh/m2 | r = m [m] | v [m] | h [m] |
|---|---|---|---|---|---|
| Cfg1 | 35,237 | 151,907 | 4.59 | 18.80 | 14.94 |
| Cfg2 | 44,605 | 125,467 | 5.69 | 14.40 | 12.30 |
| Cfg3 | 44,686 | 125,457 | 5.69 | 14.40 | 12.30 |
| Cfg4 | 34,211 | 108,652 | 4.84 | 16.58 | 14.47 |
| Cfg5 | 23,455 | 103,295 | 5.09 | 16.51 | 13.74 |
| Cfg6 | 44,071 | 813,989 | 4.67 | 18.00 | 12.00 |
| Cfg7 | 65,172 | 131,427 | 4.71 | 26.35 | 11.55 |
| Cfg8 | 68,890 | 109,515 | 4.59 | 18.80 | 14.94 |
| Cfg9 | 66,304 | 131,427 | 4.71 | 26.35 | 11.55 |
| Cfg10 | 65,035 | 103,295 | 5.09 | 16.51 | 13.74 |
| Dependent Variable | Correlations | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| r_al | r_om | r_sz | r_gtp | r_ot | r_gpb | r_gwb | r_ivb | r_pwb | r_pws | |
| Etot | 0.14 | 0.12 | −0.08 | −0.37 | 0.03 | −0.24 | −0.08 | −0.74 | −0.40 | −0.18 |
| Esol | 0.22 | 0.10 | −0.62 | −0.04 | −0.05 | 0.27 | 0.03 | 0.09 | 0.04 | 0.64 |
| r = m | −0.61 | −0.19 | 0.00 | 0.05 | 0.05 | 0.56 | 0.05 | 0.07 | −0.08 | −0.12 |
| v | 0.43 | 0.55 | −0.07 | 0.01 | −0.06 | −0.77 | 0.06 | −0.05 | 0.03 | 0.09 |
| h | 0.31 | −0.01 | 0.03 | −0.02 | 0.03 | 0.78 | −0.06 | 0.07 | 0.02 | −0.04 |
| Coefficients Calculated for Etot, pc = 0.000, R = 0.96, R2 = 0.93 | ||||||||||
| b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | b9 | b10 |
| 69,566 | 3271 | 46,678 | −1666 | −10,573 | 695 | −4105 | −3150 | −19,001 | −10,273 | −40,079 |
| Coefficients calculated for Esol, pc = 0.000, R = 0.96, R2 = 0.93 | ||||||||||
| b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | b9 | b10 |
| 112,833 | 17,342 | 4213 | −4286 | −984 | −4501 | 29,453 | −1482 | −493 | 1127 | 49,965 |
| Coefficients calculated for r = m, pc = 0.000, R = 0.81, R2 = 0.65 | ||||||||||
| b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | b9 | b10 |
| 4.984 | −0.420 | −0.100 | −0.042 | 0.0354 | 0.002 | 0.354 | 0.047 | 0.021 | −0.028 | −0.059 |
| Coefficients calculated for v, pc = 0.000, R = 0.98, R2 = 0.95 | ||||||||||
| b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | b9 | b10 |
| 18.826 | 2.681 | 3.799 | −0.177 | 0.155 | 0.017 | −5.446 | 0.213 | 0.072 | −0.158 | −0.145 |
| Coefficients calculated for h, pc = 0.000, R = 0.87, R2 = 0.76 | ||||||||||
| b0 | b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 | b9 | b10 |
| 11.251 | 0.952 | 0.096 | 0.108 | −0.100 | 0.006 | 2.022 | −0.122 | −0.077 | 0.083 | 0.150 |
| Configuration | Calculated Values of Etot kWh/m2 | Predicted Values of Esol Linear Regression kWh/m2 | Residuals | Predicted Values of Esol Neural Network kWh/m2 | Residuals |
|---|---|---|---|---|---|
| Cfg1 | 35,237 | 35,708 | −471 | 35,439 | −203 |
| Cfg2 | 44,605 | 47,138 | −2533 | 44,635 | −30 |
| Cfg3 | 44,686 | 44,041 | 645 | 44,775 | −89 |
| Cfg4 | 34,211 | 27,142 | 7069 | 34,349 | −138 |
| Cfg5 | 23,455 | 26,104 | −2649 | 22,771 | 685 |
| Cfg6 | 44,071 | 44,684 | −613 | 43,834 | 238 |
| Cfg7 | 65,172 | 63,905 | 1267 | 65,189 | −17 |
| Cfg8 | 68,890 | 71,639 | −2751 | 68,893 | −3 |
| Cfg9 | 66,304 | 64,108 | 2196 | 66,613 | −309 |
| Cfg10 | 65,035 | 65,980 | −945 | 65,065 | −30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abramczyk, J.; Bielak, W.; Gotkowska, E. An Automated Method of Parametric Thermal Shaping of Complex Buildings with Buffer Spaces in a Moderate Climate. Energies 2025, 18, 4050. https://doi.org/10.3390/en18154050
Abramczyk J, Bielak W, Gotkowska E. An Automated Method of Parametric Thermal Shaping of Complex Buildings with Buffer Spaces in a Moderate Climate. Energies. 2025; 18(15):4050. https://doi.org/10.3390/en18154050
Chicago/Turabian StyleAbramczyk, Jacek, Wiesław Bielak, and Ewelina Gotkowska. 2025. "An Automated Method of Parametric Thermal Shaping of Complex Buildings with Buffer Spaces in a Moderate Climate" Energies 18, no. 15: 4050. https://doi.org/10.3390/en18154050
APA StyleAbramczyk, J., Bielak, W., & Gotkowska, E. (2025). An Automated Method of Parametric Thermal Shaping of Complex Buildings with Buffer Spaces in a Moderate Climate. Energies, 18(15), 4050. https://doi.org/10.3390/en18154050





