Multi-Energy Flow Optimal Dispatch of a Building Integrated Energy System Based on Thermal Comfort and Network Flexibility
Abstract
1. Introduction
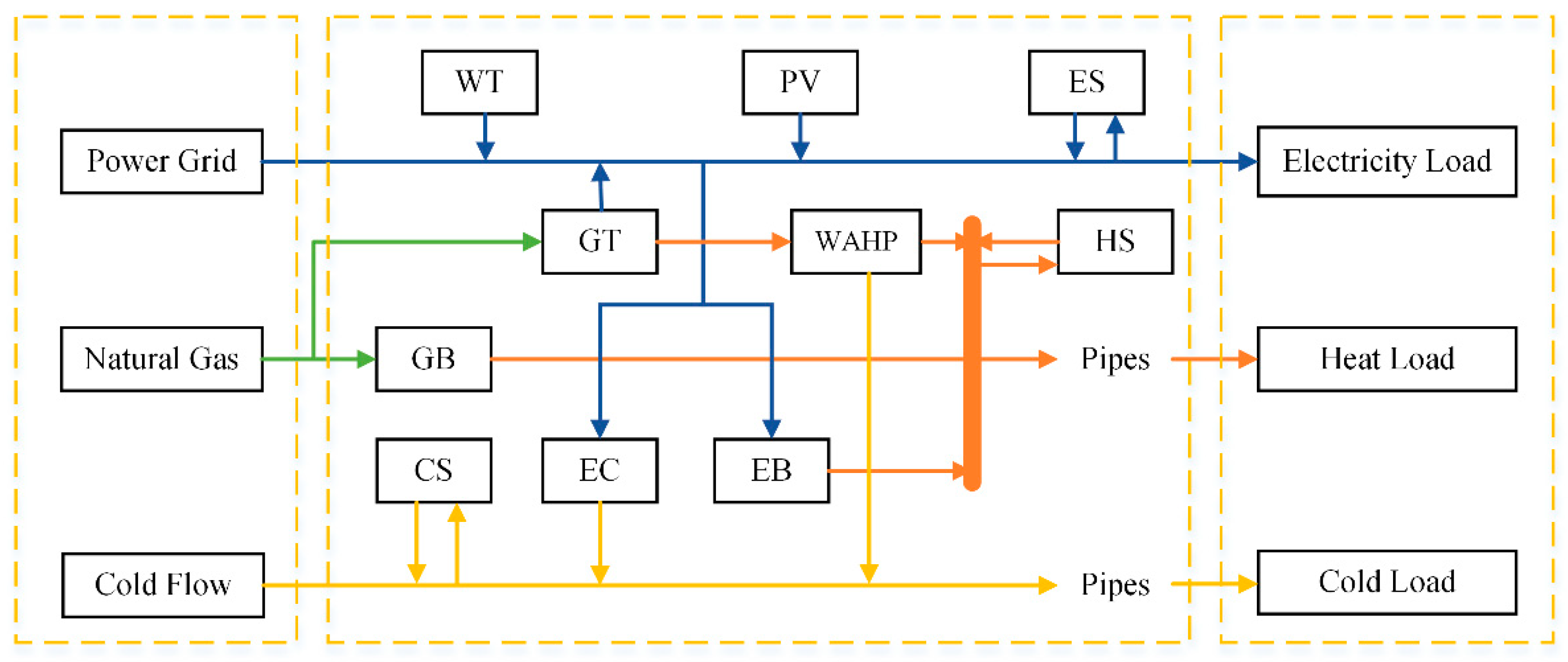
2. Mathematical Modeling of IES
2.1. IES Description
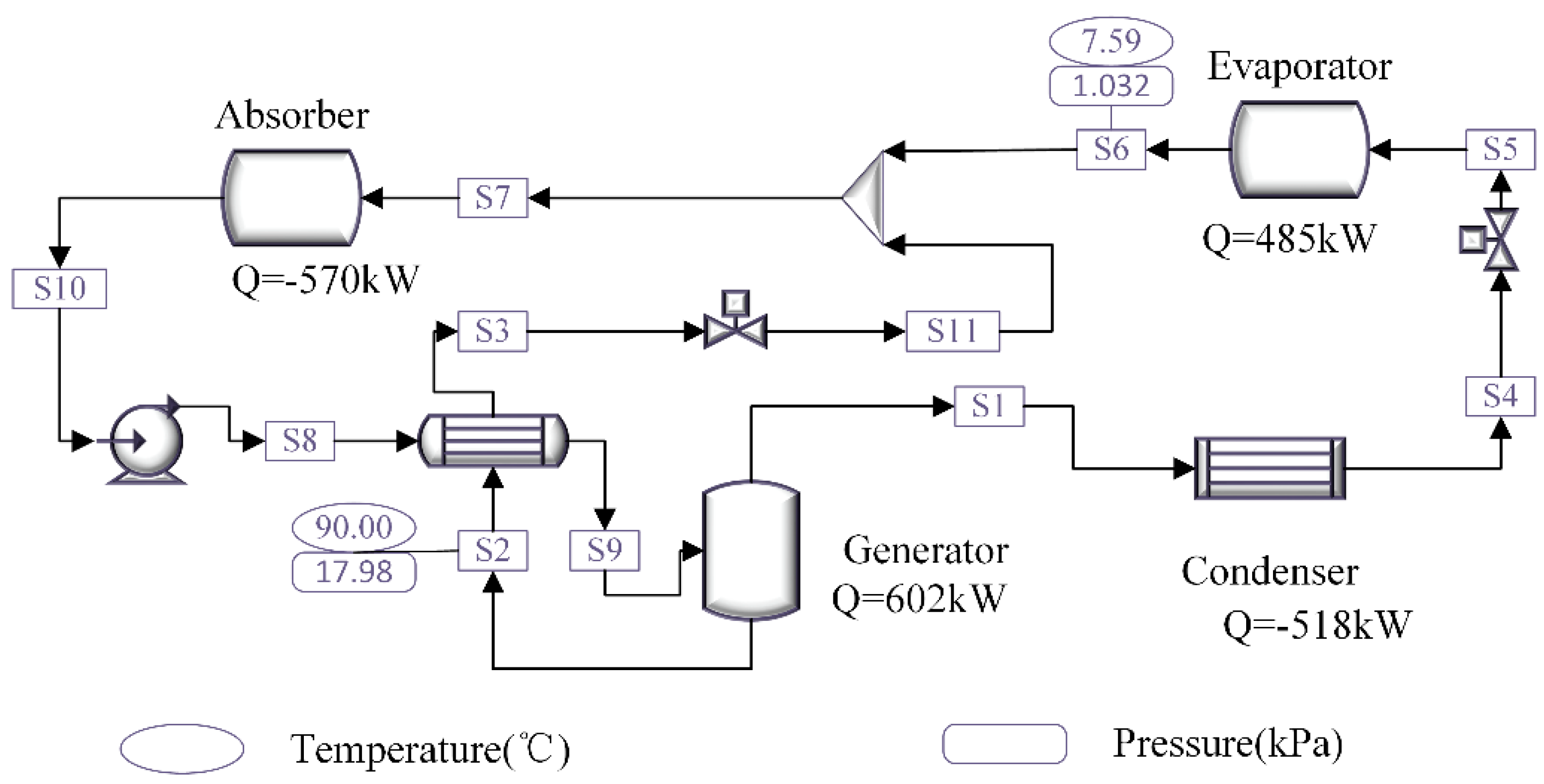
2.2. WAHP Model
2.2.1. Mixed Operation Mode
2.2.2. Heating Mode
2.2.3. Cooling Mode
2.3. Energy Storage System Model
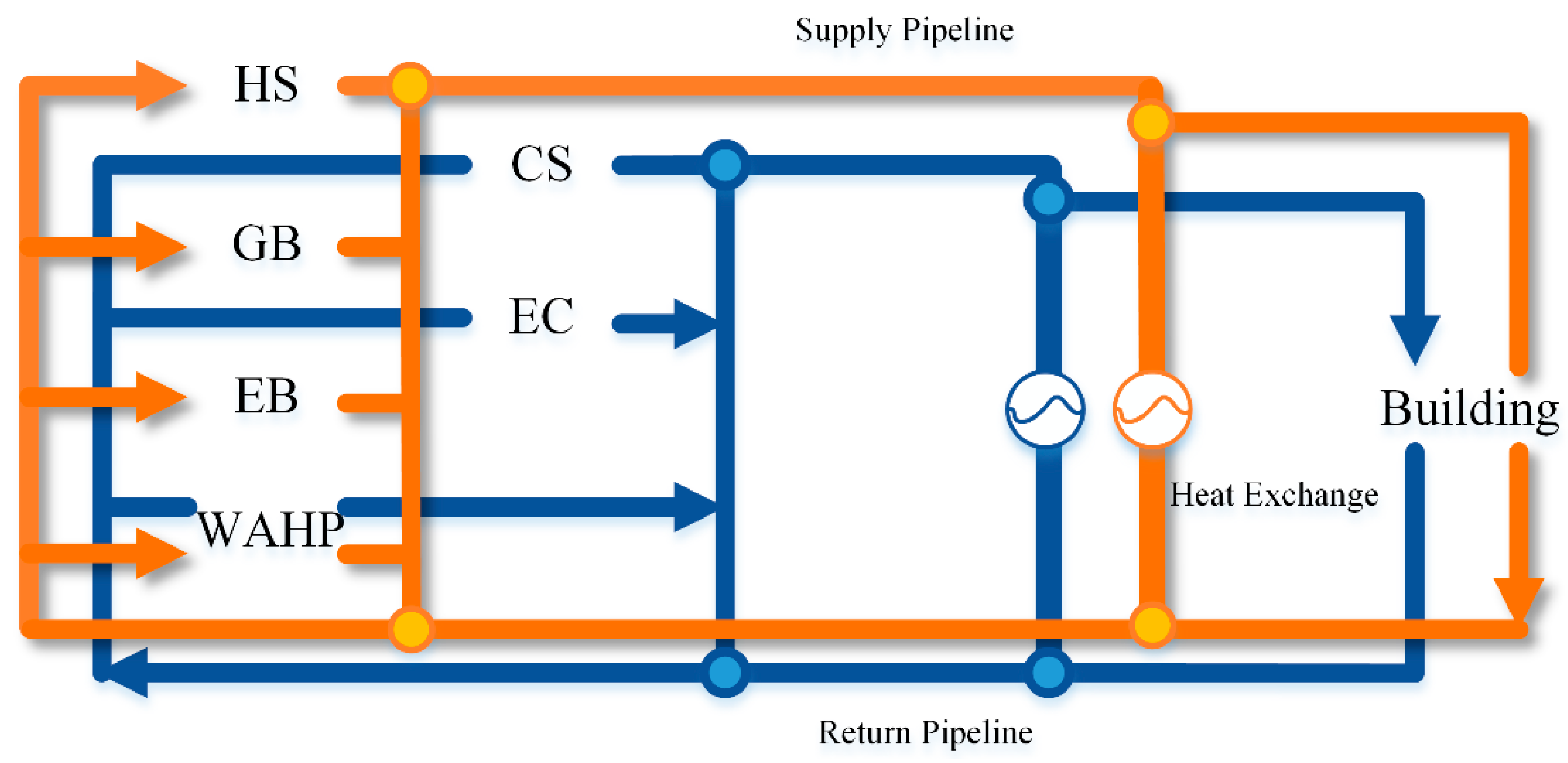
2.4. Temperature-Flow Model
2.5. Building Thermal Comfort and Inertia of Pipeline
2.5.1. Thermal Comfort
2.5.2. Thermal Inertia
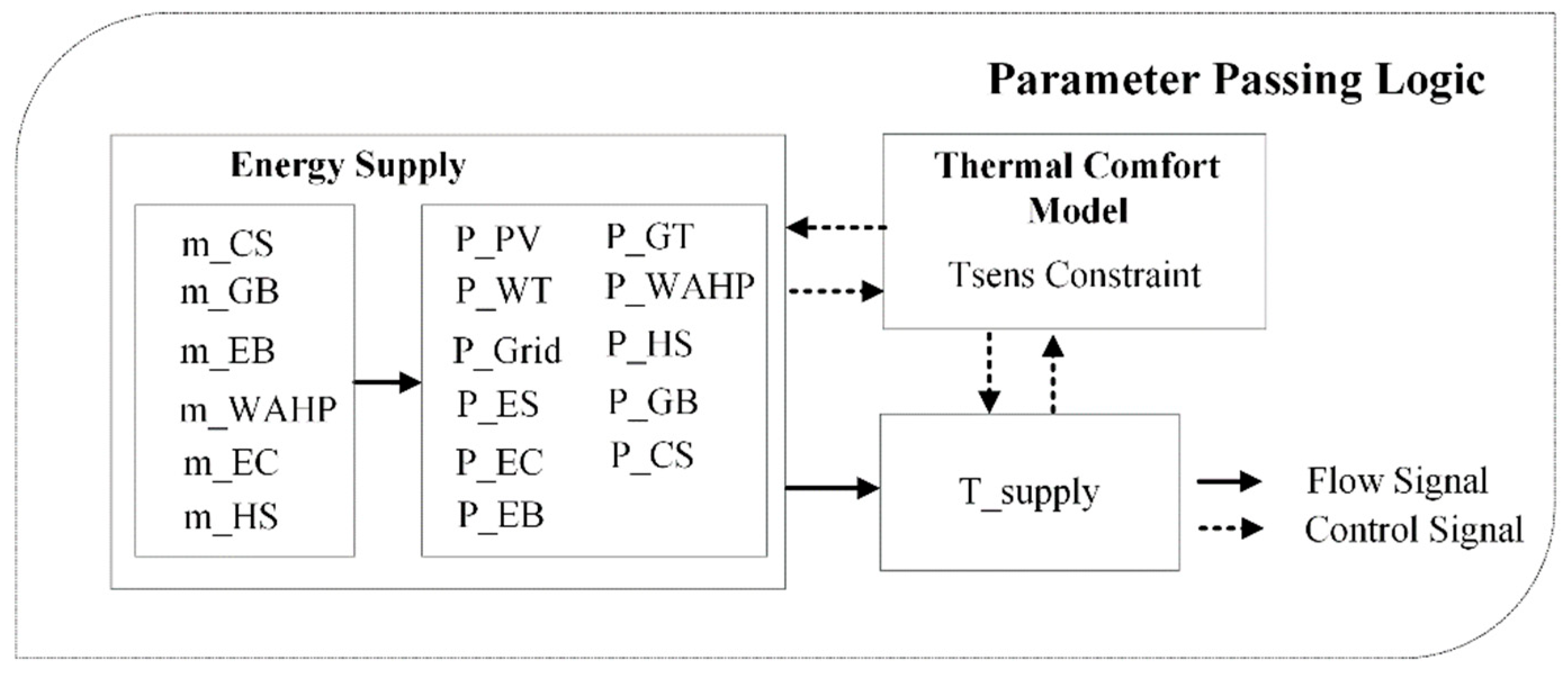
3. Optimal Scheduling Modeling of IES
3.1. Constraints
3.1.1. Energy Balance Constraints
3.1.2. Device Operation Constraints
3.2. Objective Function
3.3. Optimization Algorithm
4. Results and Discussion
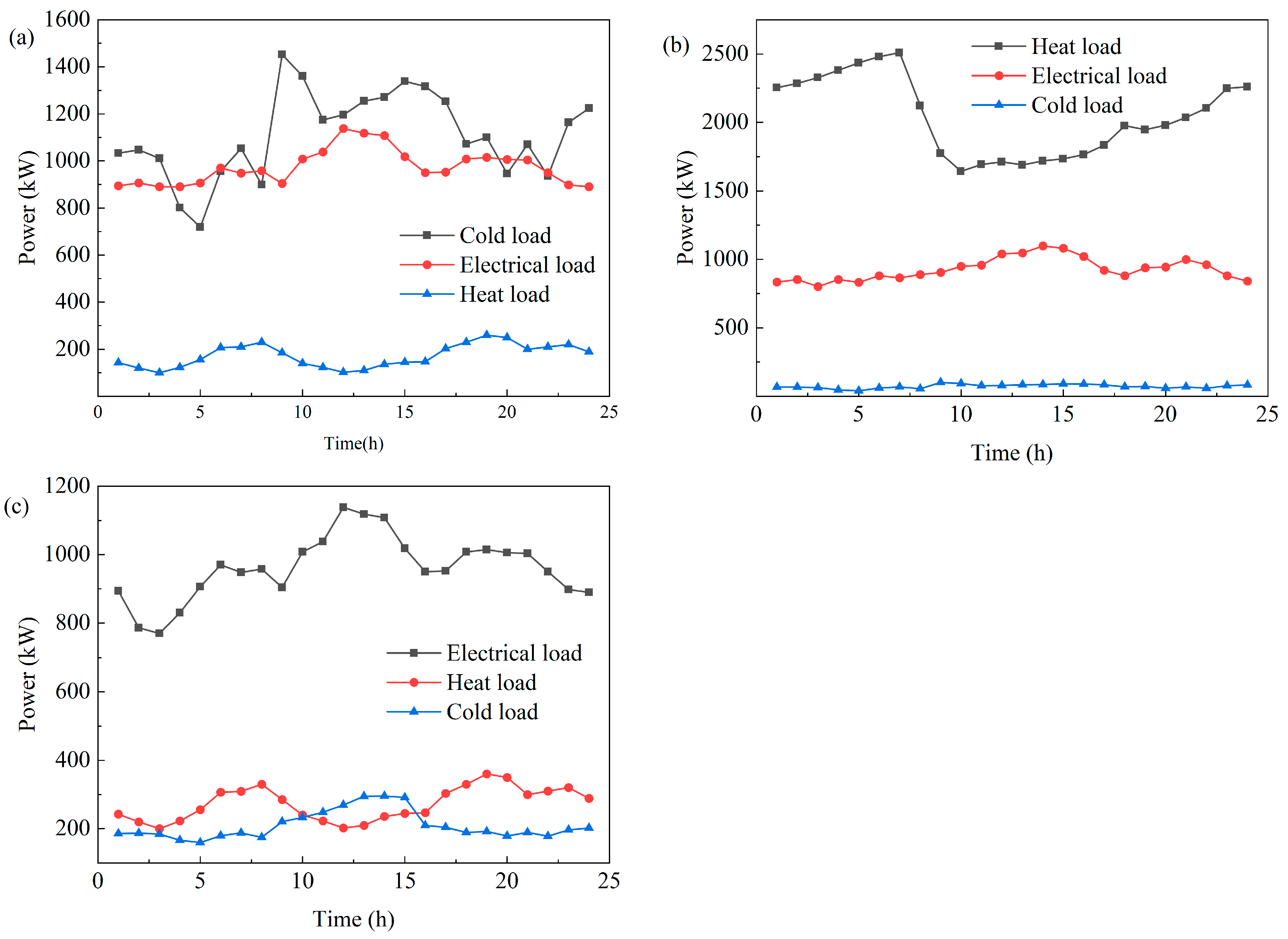
4.1. Basic Parameter Settings of the IES Model
4.2. Comparisons of Case Study
4.2.1. Energy Storage System Analysis
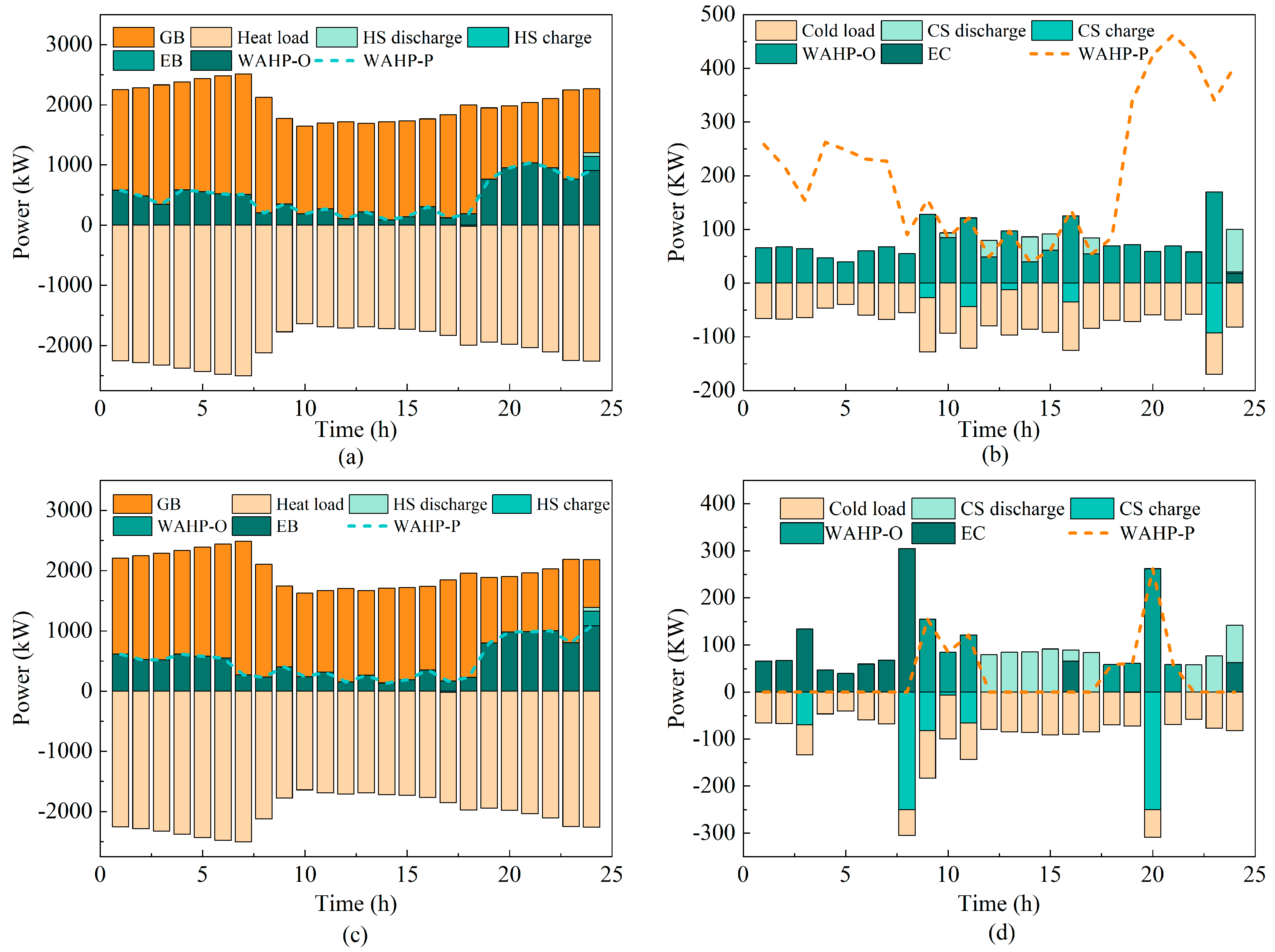
4.2.2. Effect of Thermal Comfort Control
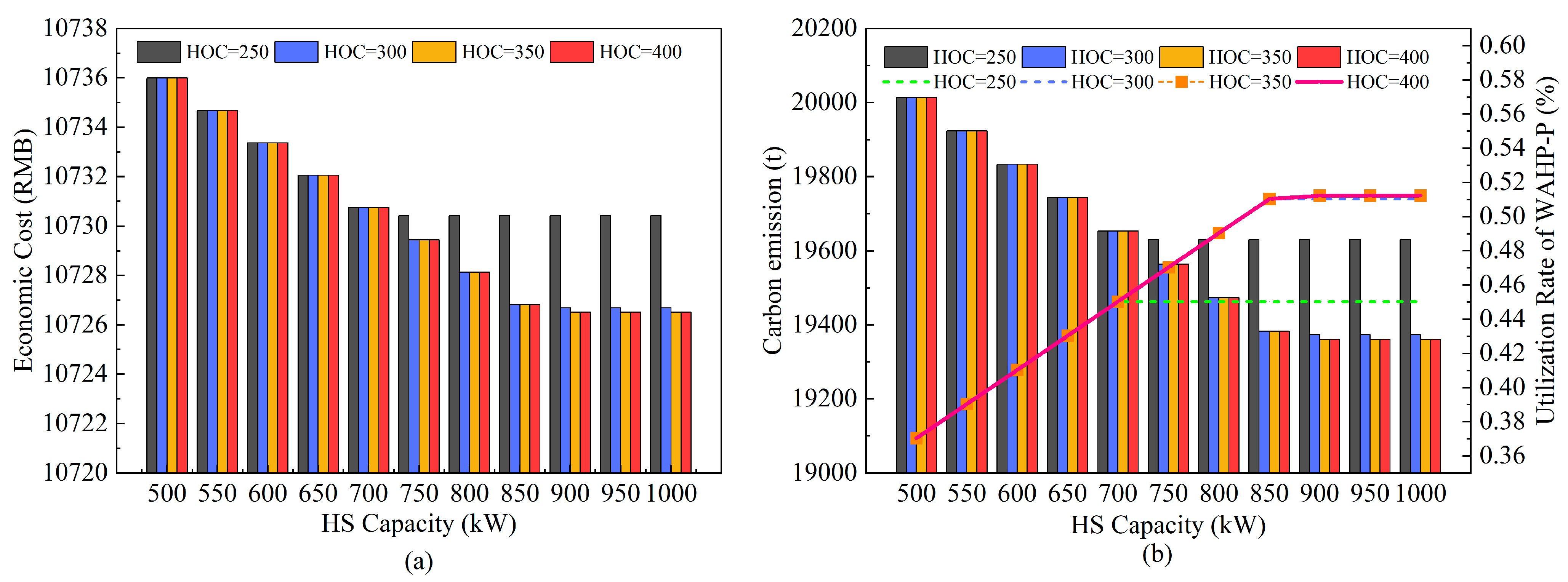
4.2.3. Effect of Pipeline Thermal Inertia
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| IES, Integrated energy system | PV, Photovoltaic |
| WT, Wind turbine | GT, Gas turbine |
| EC, Electric chiller | WAHP, Waste heat absorption heat pump |
| GB, Gas boiler | EB, Electric boiler |
| ES, Electricity storage | HS, Heat storage |
| CS, Cold storage | PMV, Predicted mean vote |
| TSENS, Thermal sensation | TSC, Thermal comfort constraints |
| Symbols | |
| rate of metabolic heat production, W/m2 | grid purchase power, kWh |
| metabolic level required for shivering W/m2 | state of charge of ES |
| rate of mechanical work accomplished, W/m2 | state of charge of HS |
| total rate of heat loss through respiration, W/m2 | state of charge of CS |
| skin heat transfer coefficient, 5.28 W/(m2·K) | ES capacity, kW |
| dry (sensible) heat loss from the skin, W/m2 | HS capacity, kW |
| wet (sensible) heat loss from the skin, W/m2 | CS capacity, kW |
| specific heats of core, 3500 J/(kg·K) | electricity purchase cost, RMB |
| specific heats of skin, 3500 J/(kg·K) | gas purchase cost, RMB |
| specific heats of skin, 4190 J/(kg·K) | equipment maintenance cost RMB |
| body core weight, kg | evaporative efficiency (0.85) |
| body skin weight, kg | heat capacity of fluid, MJ/kg °C |
| peripheral blood mass flow, kg/s | , HS charging and discharging state, only 0 or 1. |
| , battery charging and discharging status, only 0 or 1. | , HS charging and discharging state, only 0 or 1. |
References
- Zhu, Y.; Xu, Y.; Chen, H.; Guo, H.; Zhang, H.; Zhou, X.; Shen, H. Optimal dispatch of a novel integrated energy system combined with multi-output organic Rankine cycle and hybrid energy storage. Appl. Energy 2023, 343, 121113. [Google Scholar] [CrossRef]
- Ma, M.; Zhou, N.; Feng, W.; Yan, J. Challenges and opportunities in the global net-zero building sector. Cell Rep. Sustain. 2024, 1, 100154. [Google Scholar] [CrossRef]
- Yu, M.G.; Huang, B.; Ma, X.; Devaprasad, K. Multi-objective sizing and dispatch for building thermal and battery storage towards economic and environmental synergy. Appl. Energy 2024, 372, 123819. [Google Scholar] [CrossRef]
- Rosales-Asensio, E.; Icaza, D.; González-Cobos, N.; Borge-Diez, D. Peak load reduction and resilience benefits through optimized dispatch, heating and cooling strategies in buildings with critical microgrids. J. Build. Eng. 2023, 68, 106096. [Google Scholar] [CrossRef]
- Lou, J.; Wang, Y.; Wang, H.; Wang, J.; Chen, L.; Zhang, J.; Islam, M.; Chua, K. Operation characteristics analysis and optimal dispatch of solar thermal-photovoltaic hybrid microgrid for building. Energy Build. 2024, 315, 114340. [Google Scholar] [CrossRef]
- Zhou, B.; Huang, Y.; Nie, J.; Ding, L.; Sun, C.; Chen, B. Modification and verification of the PMV model to improve thermal comfort prediction at low pressure. J. Therm. Biol. 2023, 117, 103722. [Google Scholar] [CrossRef]
- Qi, T.; Hui, H.; Song, Y. Chance constrained economic dispatch of central air conditionings in large-scale commercial buildings considering demand response. Energy Build. 2024, 320, 114607. [Google Scholar] [CrossRef]
- Tang, H.; Wang, S. A model-based predictive dispatch strategy for unlocking and optimizing the building energy flexibilities of multiple resources in electricity markets of multiple services. Appl. Energy 2022, 305, 117889. [Google Scholar] [CrossRef]
- Feng, W.; Wei, Z.; Sun, G.; Zhou, Y.; Zang, H.; Chen, S. A conditional value-at-risk-based dispatch approach for the energy management of smart buildings with HVAC systems. Electr. Power Syst. Res. 2020, 188, 106535. [Google Scholar] [CrossRef]
- Zhang, J.; Kong, X.; Shen, J.; Sun, L. Day-ahead optimal scheduling of a standalone solar-wind-gas based integrated energy system with and without considering thermal inertia and user comfort. J. Energy Storage 2023, 57, 106187. [Google Scholar] [CrossRef]
- Tan, X.; Wang, Y.; Wu, L.; Yu, Y.; Yu, Q.; Sun, G. An ANFIS-Based indirect control strategy for solar heating system: Exploring PMV approach. Energy Build. 2024, 309, 114056. [Google Scholar] [CrossRef]
- Li, X.; Wang, H. Integrated energy system model with multi-time scale optimal dispatch method based on a demand response mechanism. J. Clean. Prod. 2024, 445, 141321. [Google Scholar] [CrossRef]
- Yi, Z.-K.; Li, Z.-M. Combined Heat and Power Dispatching Strategy Considering Heat Storage Characteristics of Heating Network and Thermal Inertia in Heating Area. Power Syst. Technol. 2018, 42, 1378–1384. Available online: https://kns.cnki.net/kcms2/article/abstract?v=liLFU49ICVu9Z9Lwdgbmlu0QtEJydFeL0dpnWJs5wGzLw4VEm0gHVMliesrE4irTJxd_CHo5AqoxVUABFY3Yo4GI6_9oPUKrBHx_fQRTeW5YSKCe3ov6TrmzGpRKcL7llvS8_4f8HMmRdoTBAAt1riMDAuMa6piTVqLIyCKmp2V_08h1R-1OuA==&uniplatform=NZKPT&language=CHS (accessed on 29 July 2025).
- Li, B.; Niu, H.-H.; Yu, F.; Chen, P.; Lou, Q.-H. Research on Optimized Model of IES Integrated with Building. Process Autom. Instrum. 2020, 41, 85–88. Available online: https://kns.cnki.net/kcms2/article/abstract?v=liLFU49ICVvPrbyLfVRJ0c4-ZE5FIY9lOG7Yqt1pacq-a7C0sFJCFgTznk-Wy1QkiGatK9ykbjinUr7GeL5lfnFIKqIPccertKjOYg4L84t7tA9tT3o2p5PvE03J00MIq5VdrqcSaIIXe4l_Dq6267AcLHtVY4Oa0uXpV6UpTARmv6oBBoNdg==&uniplatform=NZKPT&language=CHS (accessed on 29 July 2025).
- Klyapovskiy, S.; You, S.; Cai, H.; Bindner, H.W. Integrated Planning of a Large-Scale Heat Pump in View of Heat and Power Networks. IEEE Trans. Ind. Appl. 2019, 55, 5–15. [Google Scholar] [CrossRef]
- Zhang, S.; Wen, M.; Cheng, H.; Hu, X.; Xu, G. Reliability Evaluation of Electricity-Heat Integrated Energy System with Heat Pump. CSEE J. Power Energy Syst. 2018, 4, 425–433. [Google Scholar] [CrossRef]
- Zhang, Z.-L.; Zhang, H.-J.; Xie, B.; Zhang, X.-T. Energy scheduling optimization of the integrated energy system with ground source heat pumps. J. Clean. Prod. 2022, 365, 132758. [Google Scholar] [CrossRef]
- Wu, D.; Liu, Z.; Han, Z.; Zhang, H.; Ma, F.; Zhang, S.; Yang, X.; Ge, H. Thermodynamic performance analyses and collaborative optimization for a novel integrated energy system coupled with organic Rankine cycle. Energy Convers. Manag. 2020, 225, 113484. [Google Scholar] [CrossRef]
- Tao, J.; Xu, W.X.; Li, Y.L.L.; Huo, Y.W.H.; Zhang, Y.M. Optimal operation of integrated energy system combined cooling heating and power based on multi-objective algorithm. Sci. Technol. Eng. 2019, 19, 200–205. Available online: https://kns.cnki.net/kcms2/article/abstract?v=liLFU49ICVt4TfYQ_oFLZ8GPKm-nXF4R6uD14QGJemqmfu-pTk_ELZJoX4LL0FRrdPSZimEz5NPpaorAugZrf69BRtaAxLYTylflNadpbUZKKutNqtS3Q5xY6kOM6dj3VHxnSBYA-ZV_fv2b0iT5TBhjiP_D1md7dhzQEepbj5IzEPni8RLkng==&uniplatform=NZKPT&language=CHS (accessed on 29 July 2025).
- Yu, L.G. A study on Human Thermal Comfort and Dynamic Thermal Comfort in Outdoor Shaded Environments. Master’s thesis, Dalian University of Technology, Dalian, China, 2004. Available online: https://kns.cnki.net/kcms2/article/abstract?v=liLFU49ICVu8fhMTz2dZxNPB1eVXUIiLXXf8TySCMPiZvsEhKGWJbCDSY31HDuO1ToBGcm92EUL2bfbRDfhkdnXaOWIkWyRlnfB6r9WQkIPP0m3ZABzu1ALUa35ZRCsK24QSy2YZplGo97Ji9JsPIdQLAyC6TpL-BhiCCfsUL1ts8sy0j0bbqT5rvt8Z8qGQ&uniplatform=NZKPT&language=CHS (accessed on 29 July 2025).
- Yang, S.; Wu, H.; Song, J.; Li, H.; Chen, H. Two-stage robust optimization scheduling for integrated energy systems considering ammonia energy and waste heat utilization. Energy Convers. Manag. 2024, 319, 118922. [Google Scholar] [CrossRef]
- Han, Z.; Zhang, X.; Wu, D.; Liu, A.; Han, S.; Liu, Z.; Wu, X. Cascaded utilization of heat energy and coordinated optimization of quantity and quality in an integrated energy system. Energy Convers. Manag. 2025, 342, 120108. [Google Scholar] [CrossRef]
- Lyu, Z.; Huang, M.; Liu, B.; Liu, Y. Robust optimization of regional integrated energy systems considering thermal comfort and uncertainty in heat networks. Appl. Therm. Eng. 2025, 275, 126895. [Google Scholar] [CrossRef]
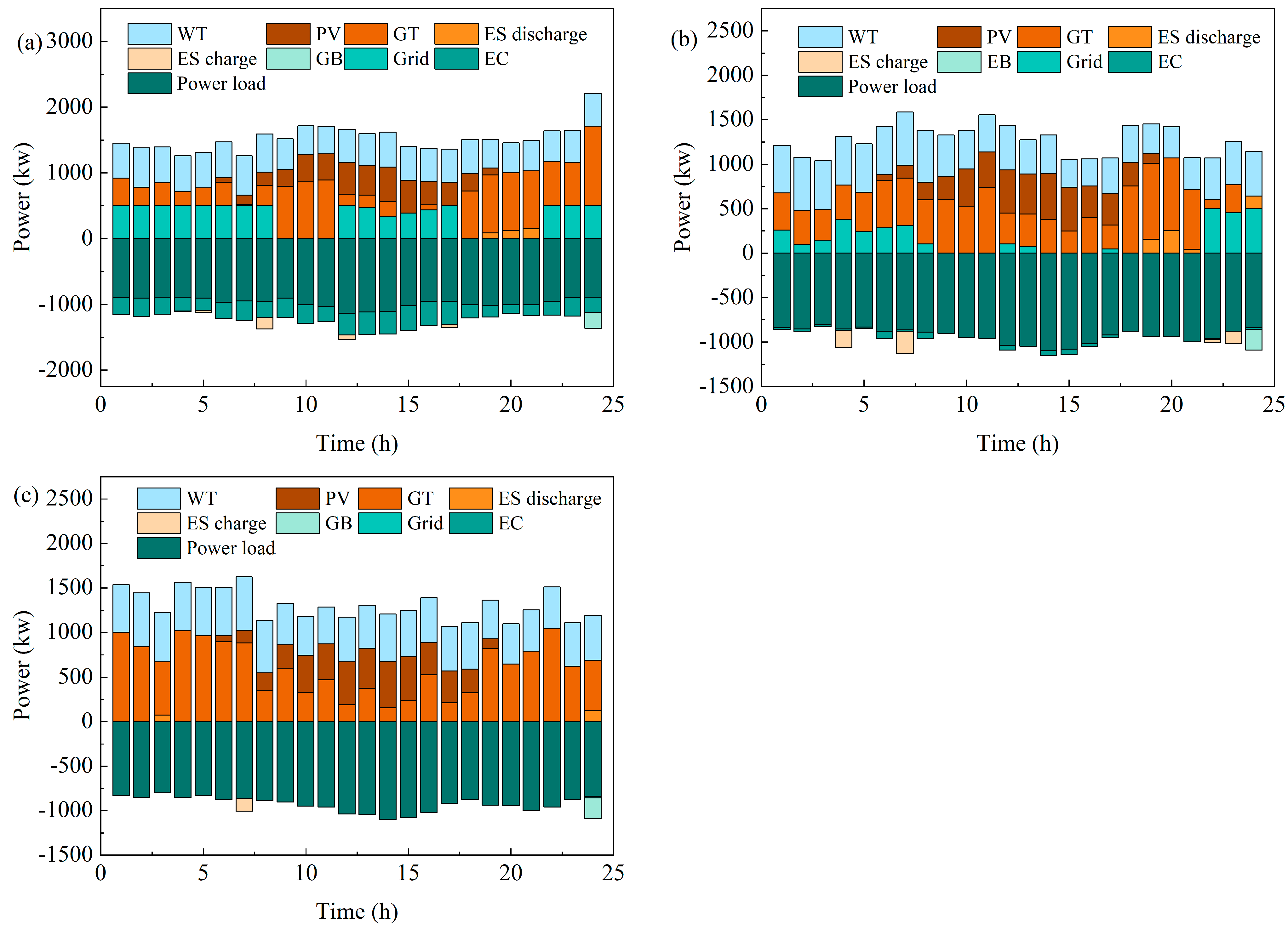


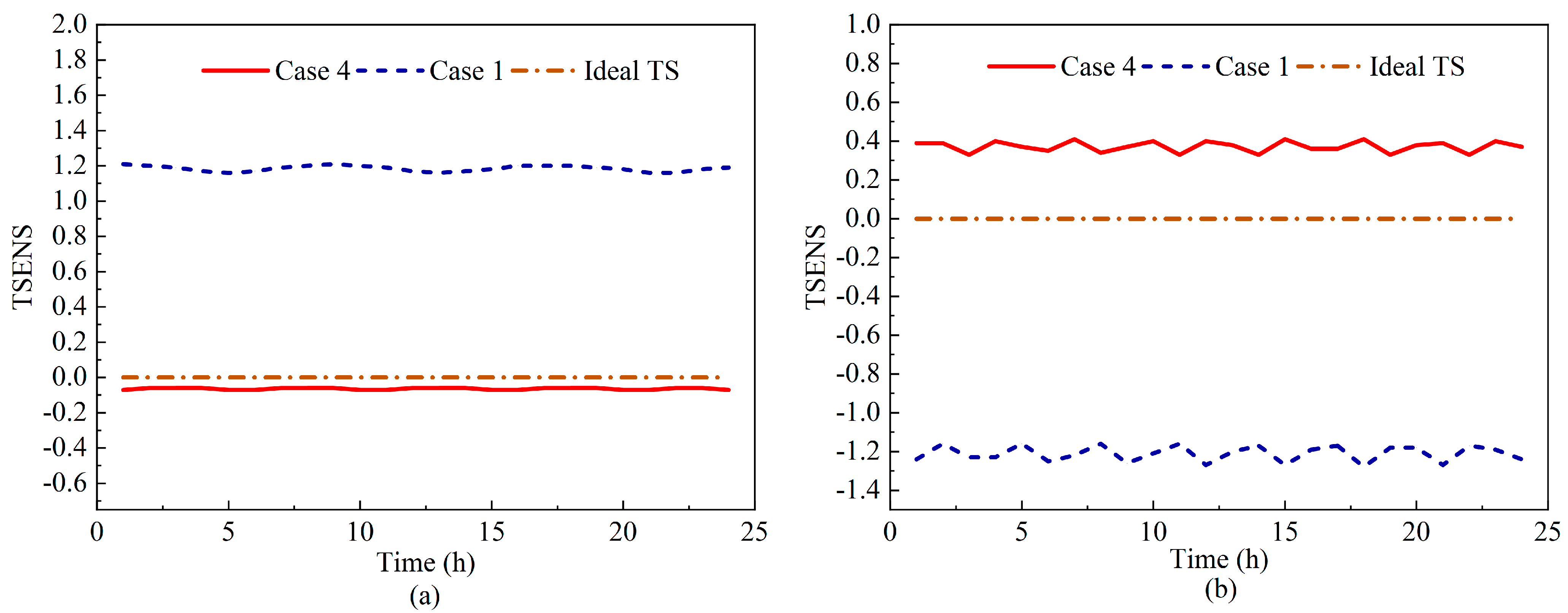
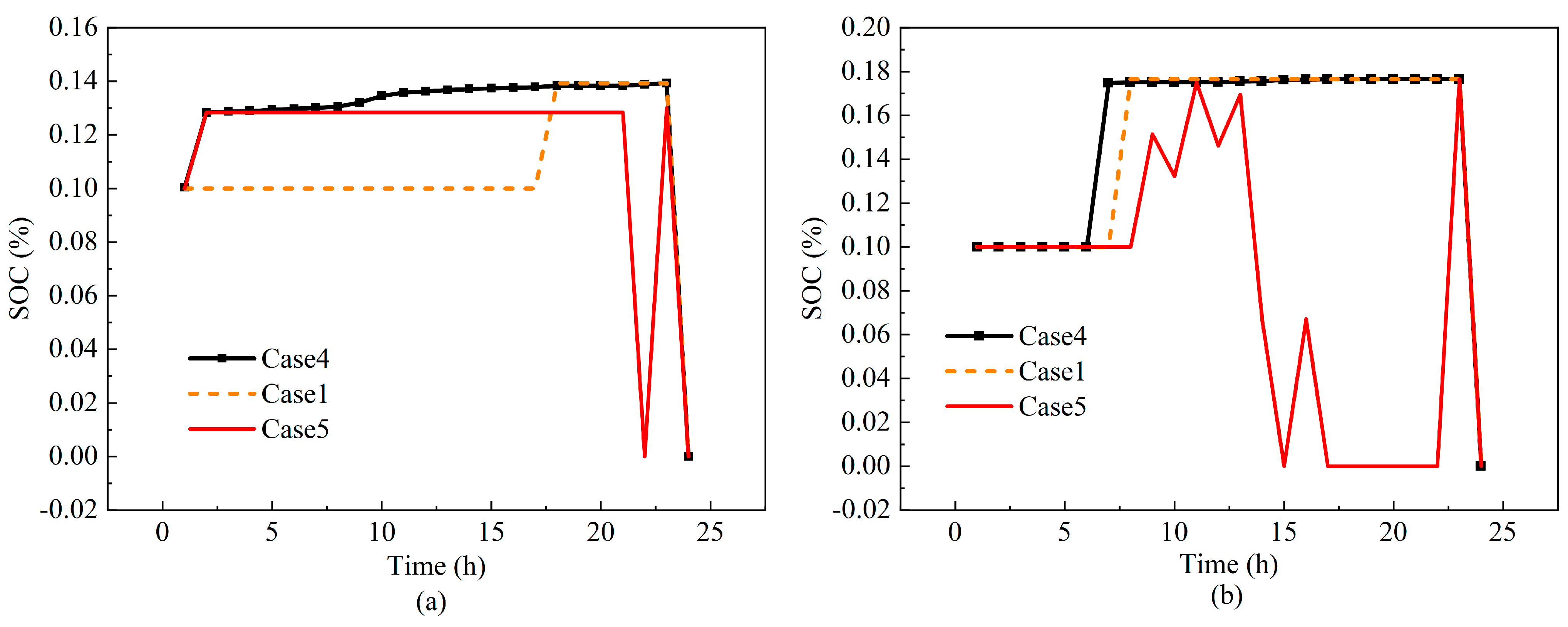
| Degree | Sensation |
|---|---|
| ±5 | intolerable hot/cold |
| ±4 | limited tolerance |
| ±3 | very hot/cold |
| ±2 | uncomfortable and unpleasant |
| ±1 | slightly hot/cold but acceptable |
| 0 | comfortable |
| Device | Installed Capacity | Performance Coefficient and Parameter/Time |
|---|---|---|
| GB(kW) | 1000 | 0.9 |
| EB(kW) | 1000 | 0.98 |
| EC(kW) | 1000 | 3.50 |
| GT(kW) | 2000 | 0.30(power)/0.40(heat) |
| ES(kW) | 500 | 0.01(loss)/0.95(char)/0.9(discharge) |
| HS(kW) | 500 | 0.01/0.95/0.90 |
| CS(kW) | 500 | 0.01/0.95/0.90 |
| Main pipe(kg/s) | 200 | / |
| Gas price (¥/m3) | 2.55 | / |
| Electricity price (¥/kWh) | 1.1 | 9:00–13:00 |
| 0.75 | 14:00–17:00 | |
| 0.5 | 0:00–9:00, 18:00–24:00 |
| Case | WAHP | TSENS Constraint | Pipeline Thermal Inertia and Loss | |
|---|---|---|---|---|
| Heating | Cooling | |||
| Case 1 | √ | √ | × | × |
| Case 2 | √ | × | × | × |
| Case 3 | × | √ | × | × |
| Case 4 | √ | √ | √ | × |
| Case 5 | √ | √ | √ | √ |
| Case | Economic Cost | ||
|---|---|---|---|
| Summer | Winter | Transition Season | |
| Case 1 | 10,735.99 | 17,949.28 | 6196.95 |
| Case 2 | 11,726.72 | 18,783.29 | 6708.11 |
| Case 3 | 11,706.81 | 19,248.39 | 7395.42 |
| Case 4 | 10,737.58 | 17,961.12 | 6200.11 |
| Case 5 | 10,736.00 | 17,961.12 | 6200.11 |
| Case | Utilization Ratio of Energy Storage Device | |||||
|---|---|---|---|---|---|---|
| ES | HS | CS | ||||
| Summer | Winter | Summer | Winter | Summer | Winter | |
| Case 1 | 41.67% | 12.5% | 54.17% | 8.33% | 8.33% | 54.17% |
| Case 4 | 58.33% | 4.17% | 54.17% | 45.83% | 29.17% | 75% |
| Case 5 | 33.33% | 4.17% | 54.17% | 8.33% | 8.33% | 33.33% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, J.; Sun, B.; Cai, X.; Liu, D.; Yang, Y. Multi-Energy Flow Optimal Dispatch of a Building Integrated Energy System Based on Thermal Comfort and Network Flexibility. Energies 2025, 18, 4051. https://doi.org/10.3390/en18154051
Sun J, Sun B, Cai X, Liu D, Yang Y. Multi-Energy Flow Optimal Dispatch of a Building Integrated Energy System Based on Thermal Comfort and Network Flexibility. Energies. 2025; 18(15):4051. https://doi.org/10.3390/en18154051
Chicago/Turabian StyleSun, Jian, Bingrui Sun, Xiaolong Cai, Dingqun Liu, and Yongping Yang. 2025. "Multi-Energy Flow Optimal Dispatch of a Building Integrated Energy System Based on Thermal Comfort and Network Flexibility" Energies 18, no. 15: 4051. https://doi.org/10.3390/en18154051
APA StyleSun, J., Sun, B., Cai, X., Liu, D., & Yang, Y. (2025). Multi-Energy Flow Optimal Dispatch of a Building Integrated Energy System Based on Thermal Comfort and Network Flexibility. Energies, 18(15), 4051. https://doi.org/10.3390/en18154051





