Fault-Tolerant Control of Non-Phase-Shifted Dual Three-Phase PMSM Joint Motor for Open Phase Fault with Minimized Copper Loss and Reduced Torque Ripple

Abstract

Dual three-phase PMSMs (DTP-PMSMs) have attracted increasing attention in the field of robotics industry for their higher power density and enhanced fault-tolerant ability. The non-phase-shifted DTP-PMSM (NPSDTP-PMSM), which shows naturally prevailed performance on zero-sequence current (ZSC) suppression, necessitates the investigation on the control method with improved fault-tolerant performance. In this paper, a novel fault-tolerant control (FTC) method for NPSDTP-PMSM is proposed, which concurrently simultaneously reduces copper loss and suppresses torque ripple under single and dual open phase fault. Firstly, the mathematical model of NPSDTP-PMSM is established, where the ZSC self-suppressing mechanism is revealed. Based on which, investigations on open phase fault and the copper loss characteristics for NPSDTP-PMSM are conducted. Subsequently, a novel fault-tolerant control method is proposed for NPSDTP-PMSM, where the torque ripple is reduced by mutual cancellation of harmonic torques from two winding sets and minimized copper loss is achieved based on the convex characteristic of copper loss. Experimental validation on an integrated robotic joint motor platform confirms the effectiveness of the proposed method.

1. Introduction

Joint motors, the core components in the rapidly growing robotics industry field, have gathered significant attention [1,2]. Contemporary advancements in joint motor design necessitate enhanced output torque, increased power density, and improved reliability [3,4]. With enhanced fault-tolerant performance and higher power density compared with the traditional three phase PMSM [5], multi-phase permanent magnet synchronous motors attract increasing interest. In the meantime, pursuing higher output power increases the likelihood of faults in power switch devices [6]. Studies [7] attribute 38% of motor faults in variable-speed ac drives to the power switch failure. Instantaneous overcurrent typically causes switch failures [8], leading protection protocols to disable the faulty bridge arm and induce open-phase faults. Consequently, fault-tolerant control (FTC) for multiphase motors is critical. To improve the fault-tolerant performance, various fault-tolerant control (FTC) methods of open-phase-fault strategies have been proposed.

In the study of open-phase faults, the common optimized target is the reduction in output torque ripple. In the early applications, a simple approach to maintain the smooth output torque is to deactivate the faulted three-phase [9]. With the remaining healthy three-phase winding set, the motor is able to maintain the torque output in low load, but the maximum output torque capability is reduced by half. In the recent studies, the mainstream method to maintain the torque capability is to fully use all the remaining healthy windings, and various control strategies are proposed. In [10], an improved direct torque control (DTC) based on virtual vector is proposed for a five phase induction motor. The space vector is reconstructed under open-phase-fault. Then a modified lookup table is designed to improve the fault-tolerant performance. In the study of [11], virtual vector-DTC and rotor-field-oriented control are compared in a five phase induction motor, and the obtained results show that the virtual vector-DTC has a lower capability of maximum torque and higher harmonic phase current content than rotor field-oriented control (RFOC). In [12,13], an adaptive fault control and diagnosis strategy is proposed for dual three-phase PMSM (DTP-PMSM). This work resolves the conflict between the x-y current closed-loop control and the desired after-fault x-y current control. To tackle this problem, x-y reference is updated by a half-sine phase locked loop to generate smooth output torque under open -phase fault without diagnosis. Ref. [14] proposed a deadbeat-predictive-current-control-based FTC strategy combined with a T type three level inverter for DTP-PMSM. This paper introduced the voltage vector in T type three level inverter, and proposed multi-FTC strategies for different fault types, including open switch and open-phase fault. In [15,16], different maximum torque per ampere (MTPA) control strategies are proposed to enhance the output torque capability.

Beyond torque ripple, copper loss minimization is equally critical. Due to the absence of faulty phase, the output power is supported by the remaining healthy phase, which leads to higher copper loss [17]. Under a heavy load condition, the increased copper loss may break the heat balance and leads to overheating [18]. In [19], current references are derived for the minimized copper loss control for DTP-PMSM under open-phase fault. However, the sinusoidal phase current condition reduces the optimization level of copper loss. Ref. [20] proposed a FTC scheme with full range minimum-loss under open phase for DTP PMSM. The reference x-y current is derived from the trajectories of torque and harmonic subspace under open-phase fault and this control method is equipped with adaptive fault-tolerant capability. Nevertheless, the optimization is yet limited by the sinusoidal current, leading to incomplete copper loss reduction. In [21], the harmonic disturbance induced by open-phase fault and dead time in torque and harmonic subspace are extensively studied. By redesigning the loop controller, copper loss is reduced by suppressing the harmonic current. Though, the harmonic-induced copper loss is minimized, the sinusoidal current does not reach the optimal minimized copper loss condition. In [22], by controlling the copper loss power rate to minimum, the copper loss of DTP-PMSM is further optimized. However, the introduced zero-sequence current (ZSC) in connected neutral point DTP-PMSM causes torque ripple and degrades the operation performance [23].

As among the most popular multi-phase motors [24], DTP-PMSMs are classified into phase-shift type and non-phase-shift type according to the spatial distribution of two winding sets. For phase-shift DTP-PMSM (PSDTP-PMSM), low impedance in the 5th and 7th harmonic loop leads to the heavy harmonic disturbance. Thus, in the common control framework for PSDTP-PMSM, vector space decomposition method (VSD) [25] is applied to decouple variables into torque subspace and harmonic subspace. However, the non-phase-shift DTP-PMSM (NPSDTP-PMSM) has no such impedance characteristic. Dual independent current control (DICC) is widely applied for NPSDTP-PMSM, considering the two sets of windings as two independent virtual motors [26]. Compared with the VSD method, DICC offers lower complexity and reduces the controller’s computational burden.

However, the current studies focus on single open-phase fault (SOPF), and few studies on dual open-phase fault (DOPF) are conducted. In addition, current methods on torque ripple reduction are through DTC or harmonic tracking by VSD [9,10,11,12,13,14,15,16], and copper loss optimization remains limited by sinusoidal current constraints [19,20,21,22] and ZSC complications [23]. These existing FTC methods prioritize PSDTP-PMSMs using VSD control. Despite simpler DICC implementation, NPSDTP-PMSMs lack dedicated FTC strategies.

This paper bridges this gap by proposing a novel FTC strategy for NPSDTP-PMSMs that simultaneously minimizes copper loss and torque ripple under SOPF and DOPF. This work presents three key advances:

(1)

Analytical proof of the ZSC self-suppressing mechanism in NPSDTP-PMSMs and immunity to ZSC-induced torque ripple;

(2)

A copper-loss-optimized FTC strategy for SOPF and DOPF leveraging the advantages in (1);

(3)

Experimental validation on a robotic integrated motor drive (IMD) platform.

The rest of the content of this paper is organized as follows. The mathematical model of NPSDTP-PMSM and zero-sequence loop analysis are presented in Section 2. Then, in Section 3, the copper loss model of NPSDTP-PMSM is derived and maximum-constraint-free conditions are constructed for single and dual open-phase fault in one winding set, and the proposed FTC strategy is established. In Section 4, the proposed FTC strategy is performed on a joint IMD platform and experimental results validate the proposed method. Finally, the conclusions of this paper are drawn in Section 5.

2. Mathematical Model of NPSDTP-PMSM

DTP-PMSMs are classified into two types: connected neutral point and isolated neutral point. The difference is the zero-sequence loop (ZSL) is blocked in the isolated neutral point type but remains unblocked in the connected type. ZSL provides an additional control dimension for enhanced FTC performance. However, the induced ZSC causes more power loss in healthy condition. In this section, the general model of DTP-PMSM with connected neutral point is established. Based on which, ZSC self-suppressing mechanism and immunity to ZSC-induced torque ripple in NPSDTP-PMSM are extensively analyzed.

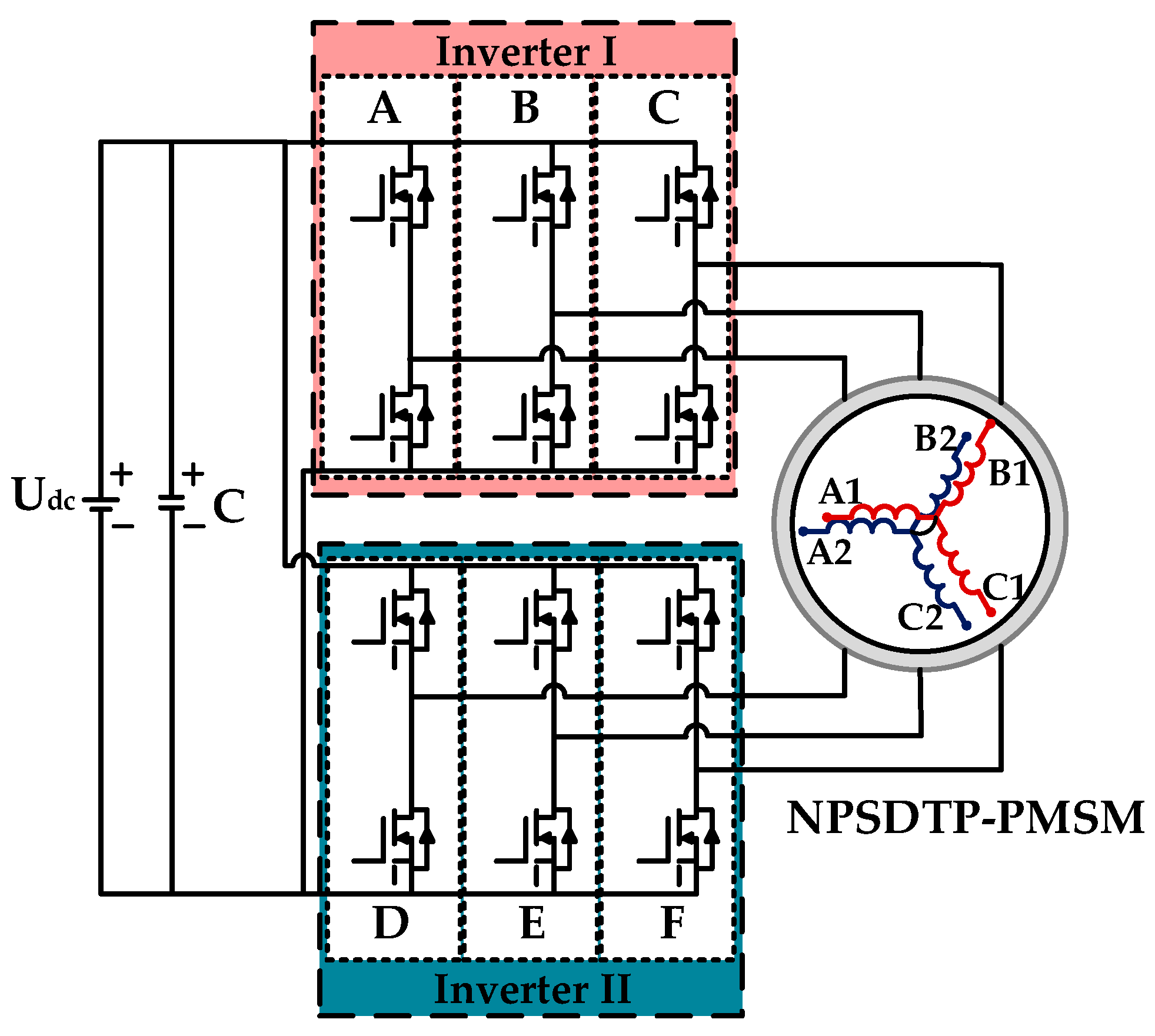
NPSDTP-PMSMs have two sets of windings fed by two inverters connected to the same DC power, as shown in Figure 1. The two winding sets have no spatial phase shift. In the stationary coordinate, named as ABC-axis, the phase voltage, flux linkage and torque equations can be written as

$$u_s=R_s{i}_s+d{\psi }_s/dt$$

(1)

$${\psi }_s=L_{\mathrm{s}}{i}_s+{\psi }_f$$

(2)

$$T_e=0.5n_{\mathrm{p}}\partial (i_s^T{\psi }_s)/\partial \theta$$

(3)

where u_s is the phase voltage vector, i_s the phase current vector, ${\psi }_s$ is the linkage flux vector, R_s is the stator resistance, L_s is the inductance matrix, and ${\psi }_f$ is the permanent magnet flux linkage matrix. T_e is the electromagnetic torque. n_p is the pole pair number.

In the ZSL, the harmonics of permanent magnet flux linkage should be considered. Since the 3rd-harmonic is the main content, the permanent magnet flux linkages can be written as

$${\psi }_f=\left[\begin{array}{c}{\psi }_a\\ {\psi }_b\\ {\psi }_c\\ {\psi }_d\\ {\psi }_e\\ {\psi }_f\end{array}\right]={\psi }_{f1}\left[\begin{array}{c}\cos ({\theta }_e)\\ \cos ({\theta }_e-2\pi /3)\\ \cos ({\theta }_e+2\pi /3)\\ \cos ({\theta }_e)\\ \cos ({\theta }_e-2\pi /3)\\ \cos ({\theta }_e+2\pi /3)\end{array}\right]+{\psi }_{f3}\left[\begin{array}{c}\cos (3{\theta }_e)\\ \cos (3{\theta }_e)\\ \cos (3{\theta }_e)\\ \cos (3{\theta }_e)\\ \cos (3{\theta }_e)\\ \cos (3{\theta }_e)\end{array}\right]$$

(4)

where ψ_f1 is amplitude of fundamental permanent magnet flux linkage, ψ_f3 is amplitude of the 3rd-harmonic permanent magnet flux linkage, and θ_e is the electrical angle.

$$\mathrm{T}=\left[\begin{array}{cccccc}\cos ({\theta }_e)& \cos ({\theta }_e-2\pi /3)& \cos ({\theta }_e+2\pi /3)& 0& 0& 0\\ -\sin ({\theta }_e)& -\sin ({\theta }_e-2\pi /3)& -\sin ({\theta }_e+2\pi /3)& 0& 0& 0\\ 0.5& 0.5& 0.5& 0& 0& 0\\ 0& 0& 0& \cos ({\theta }_e)& \cos ({\theta }_e-2\pi /3)& \cos ({\theta }_e+2\pi /3)\\ 0& 0& 0& -\sin ({\theta }_e)& -\sin ({\theta }_e-2\pi /3)& -\sin ({\theta }_e+2\pi /3)\\ 0& 0& 0& 0.5& 0.5& 0.5\end{array}\right]$$

(5)

The variables under A-B-C axis are strongly coupled, making the analysis difficult. Applying coordinate transformation (5) to (1) yields voltage equations in the synchronous d-q-z axis. It should be noted that to shorten the end of stator for the limited space, common joint motors adopt concentrated winding configuration. The mutual inductance between two sets of windings is small and can be neglected in the modeling. Thus, the voltage equations and electromagnetic torque in d-q-z axis can be written as

$$\left[\begin{array}{c}{u}_{d1}\\ u_{q1}\\ u_{z1}\\ u_{d2}\\ u_{q2}\\ u_{z2}\end{array}\right]=R_s\left[\begin{array}{c}{i}_{d1}\\ i_{q1}\\ i_{z1}\\ i_{d2}\\ i_{q2}\\ i_{z2}\end{array}\right]+p\left[\begin{array}{c}{\psi }_{d1}\\ {\psi }_{q1}\\ {\psi }_{z1}\\ {\psi }_{d2}\\ {\psi }_{q2}\\ {\psi }_{z2}\end{array}\right]+\omega \left[\begin{array}{c}-{\psi }_{q1}\\ {\psi }_{d1}\\ 0\\ -{\psi }_{q2}\\ {\psi }_{d2}\\ 0\end{array}\right]$$

(6)

$$\left[\begin{array}{c}{\psi }_{d1}\\ {\psi }_{q1}\\ {\psi }_{z1}\\ {\psi }_{d2}\\ {\psi }_{q2}\\ {\psi }_{z2}\end{array}\right]=\left[\begin{array}{cccccc}{L}_d& 0& 0& 0& 0& 0\\ 0& L_q& 0& 0& 0& 0\\ 0& 0& L_z& 0& 0& 0\\ 0& 0& 0& L_d& 0& 0\\ 0& 0& 0& 0& L_q& 0\\ 0& 0& 0& 0& 0& L_z\end{array}\right]\left[\begin{array}{c}{i}_{d1}\\ i_{q1}\\ i_{z1}\\ i_{d2}\\ i_{q2}\\ i_{z2}\end{array}\right]+\left[\begin{array}{c}{\psi }_{f1}\\ 0\\ {\psi }_{f3}\cos (3{\theta }_e)\\ {\psi }_{f1}\\ 0\\ {\psi }_{f3}\cos (3{\theta }_e)\end{array}\right]$$

(7)

$$T_e=1.5{\mathrm{n}}_{\mathrm{p}}[{\psi }_{f1}(i_{q1}+i_{q2})+e_{31}{i}_{z1}+e_{32}{i}_{z2}]$$

(8)

where u_dx, u_qx, and u_zx are the d-q-z voltage. i_dx, i_qx, and i_zx are the d-q-z axis current. ψ_dx, ψ_qx, and ψ_zx represent the d-q-z axis flux linkage, and e_3x is the 3rd-harmonic back electromotive force (3rd BMF). The subscript represents the winding set. And L_d, L_q, and L_z are the d-axis, q-axis, and zero-axis inductance separately.

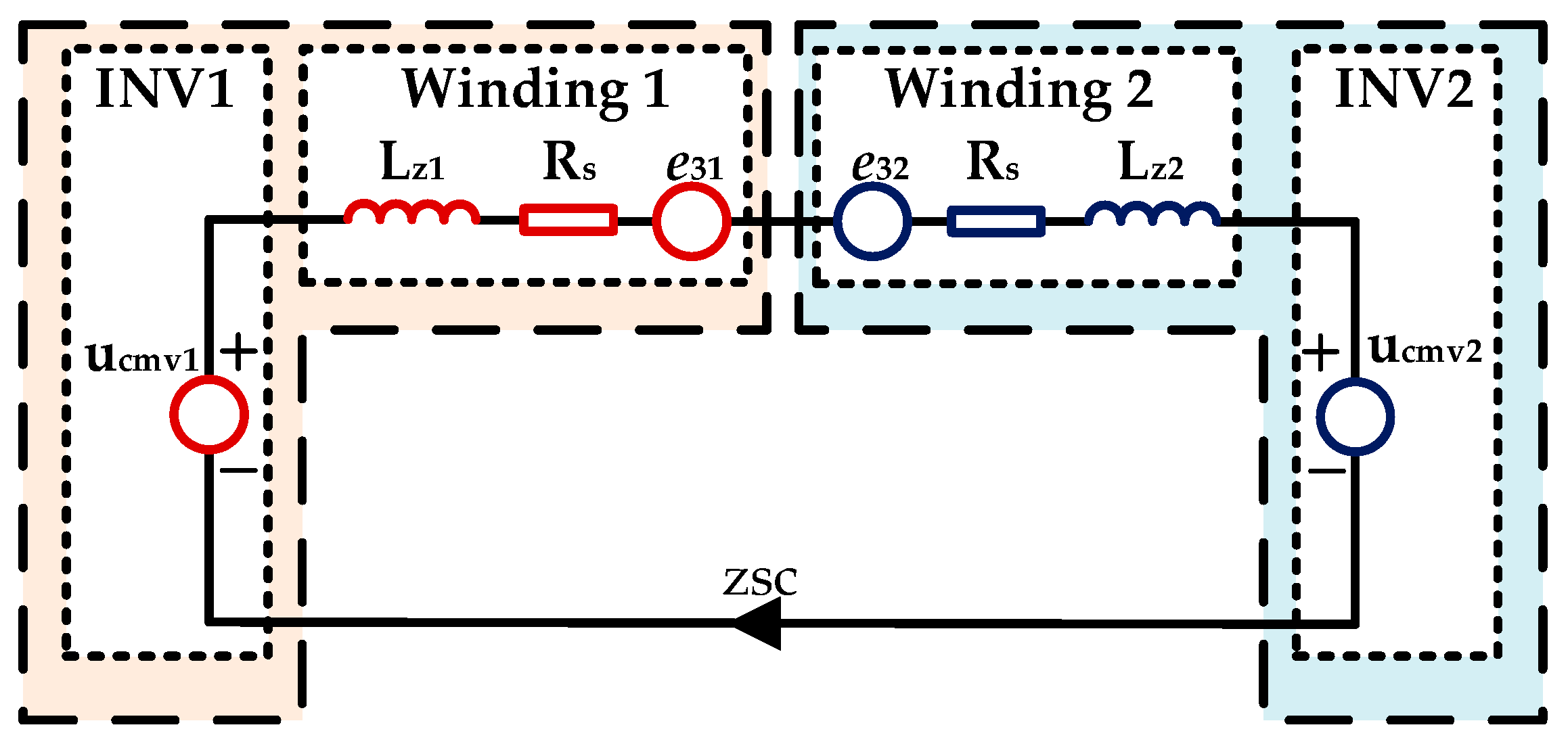
From (6), in DTP-PMSM, the two winding sets have independent d-q axis variables but share the same current path in z-axis. Consequently, the ZSL becomes the sole coupling path. The ZSC of each winding set has the connection of i_z = i_z1 = −i_z2. Thus, the ZSL is illustrated in Figure 2, which consists of common-mode voltage (CMV) from each inverter, zero-sequence inductance and resistance, and the 3rd BEMF from each winding set. Then the voltage equation can be written as

$$(u_{z1}-u_{z2})=R_s{i}_z+L_z{\displaystyle \frac{d{i}_z}{dt}}+(e_{31}-e_{32})$$

(9)

The key difference between PSDTP-PMSM and NPSDTP-PMSM lies in the phase shift angle between two winding sets. Under healthy condition, ZSC in PSDTP-PMSM causes torque ripple and additional copper loss, shown in (8), where e₃₁i_z1+ e₃₁i_z1 ≠ 0. Thus, high bandwidth current controller is required to suppress the ZSC. Moreover, the existence of 3rd BEMF, being an AC component, requires high-bandwidth ZSC controllers [27]. However, in NPSDTP-PMSMs, the symmetric spatial and electrical characteristics inherently suppress ZSC: CMVs and the 3rd BMFs mutually counteract between winding sets. Critically, ZSC induces zero torque ripple for harmonic torques cancel out e₃₁i_z1+ e₃₁i_z1 = 0. Consequently, under fault-tolerant operation, ZSC can be actively regulated without concern of inducing torque ripple. Moreover, due to the cancellation of 3rd BMF harmonics, the ZSL behaves as a purely resistive-inductive (R-L) load, simplifying ZSC controller design to a standard RL load regulation problem. Theoretically, these properties grant NPSDTP-PMSMs superior current and torque performance under both healthy and fault conditions.

The control framework of NPSDTP-PMSM is shown in Figure 3. In the DICC strategy, NPSDTP-PMSM is considered as two separate virtual motors with the same rotor position, and each virtual motor is controlled by individual current loops in d-q-z axis. In the z axis, ZSC is controlled by regulating the CMVs from two inverters. To avoid the disturbance on effective voltage vector, 000 and 111 voltage vectors are used for the regulation. Moreover, to reduce the influence of scattered signal error, the average of ZSC from two winding sets is adopted and a PI regulator with saturation of 0–1 is implemented in the z-axis closed-up current control.

3. Minimum Copper Loss Fault-Tolerant Control of NPSDTP-PMSM Under Single and Two Open Phase

3.1. Copper Loss Model of NPSDTP-PMSM

To simplify the analysis of NPSDTP-SPMSM, the transformation matrix in (5) is applied to decouple the phase currents in A-B-C axis into d-q-z axis, namely d₁-q₁-z₁ and d₂-q₂-z₂ for each winding set. The current relation between A-B-C axis and d-q-z axis can be expressed in (10) and (11). As analyzed in Section 2, under d-q-z axis, the phase currents are completely decoupled into d-q-z axis. For NPSDTP-PMSM, the current in d-axis generates the component affecting the flux linkage, q-axis current bears the ability of torque output and the ZSC in zero-axis generates copper loss. Thus, DICC can be performed, and each axis current can be regulated independently.

$$\left[\begin{array}{c}{i}_{d1}\\ i_{q1}\\ i_{\mathrm{z}1}\\ i_{d2}\\ i_{q2}\\ i_{z2}\end{array}\right]={\displaystyle \frac{2}{3}}\left[\begin{array}{cccccc}\cos ({\theta }_e)& \cos ({\theta }_e-2\pi /3)& \cos ({\theta }_e+2\pi /3)& 0& 0& 0\\ -\sin ({\theta }_e)& -\sin ({\theta }_e-2\pi /3)& -\sin ({\theta }_e+2\pi /3)& 0& 0& 0\\ 0.5& 0.5& 0.5& 0& 0& 0\\ 0& 0& 0& \cos ({\theta }_e)& \cos ({\theta }_e-2\pi /3)& \cos ({\theta }_e+2\pi /3)\\ 0& 0& 0& -\sin ({\theta }_e)& -\sin ({\theta }_e-2\pi /3)& -\sin ({\theta }_e+2\pi /3)\\ 0& 0& 0& 0.5& 0.5& 0.5\end{array}\right]\left[\begin{array}{c}{i}_A\\ i_B\\ i_C\\ i_D\\ i_E\\ i_F\end{array}\right]$$

(10)

$$\left[\begin{array}{c}{i}_A\\ i_B\\ i_C\\ i_D\\ i_E\\ i_F\end{array}\right]=\left[\begin{array}{cccccc}\cos ({\theta }_e)& -\sin ({\theta }_e)& 1& 0& 0& 0\\ \cos ({\theta }_e-2\pi /3)& \cos ({\theta }_e-2\pi /3)& 1& 0& 0& 0\\ \cos ({\theta }_e+2\pi /3)& \cos ({\theta }_e+2\pi /3)& 1& 0& 0& 0\\ 0& 0& 0& \cos ({\theta }_e)& -\sin ({\theta }_e)& 1\\ 0& 0& 0& \cos ({\theta }_e-2\pi /3)& \cos ({\theta }_e-2\pi /3)& 1\\ 0& 0& 0& \cos ({\theta }_e+2\pi /3)& \cos ({\theta }_e+2\pi /3)& 1\end{array}\right]\left[\begin{array}{c}{i}_{d1}\\ i_{q1}\\ i_{z1}\\ i_{d2}\\ i_{q2}\\ i_{z2}\end{array}\right]$$

(11)

As studied in [22], neglecting magnetic saturation effects and temperature-induced resistive variations in the model, the theoretical average copper loss power (ACLP) can be calculated by the integration of the six-phase instant copper loss power (ICLP). Thus, the total ACLP can be expressed as

$$P_{Cu\_average}={\displaystyle \frac{R_s}{2\pi }}\int (i_A^2+i_B^2+i_C^2+i_D^2+i_E^2+i_F^2)d{\theta }_e$$

(12)

By performing the transformation in (10), the phase currents in A-B-C axis can be transferred into d-q-z axis. Thus, the ACLP can be expressed in d-q-z axis as

$$P_{Cu\_average}={\displaystyle \frac{3R_s}{4\pi }}\int (i_{d1}^2+i_{q1}^2+2i_{z1}^2+i_{d2}^2+i_{q2}^2+2i_{z2}^2)d{\theta }_e$$

(13)

To reach the minimized copper loss, ICLP should be minimized at all positions. Thus, the ICLP and minimized constraints can be expressed as (14). The ICLP is simplified as the sum of squared currents under d-q-z axis. The partial derivative of each current forming the constraints to achieve the minimized copper loss.

$$\left\{\begin{array}{l}{P}_{Cu}=i_{d1}^2+i_{q1}^2+2i_{z1}^2+i_{d2}^2+i_{q2}^2+2i_{z2}^2\\ {\displaystyle \frac{d{P}_{Cu}}{d{i}_{d1}}}=0, {\displaystyle \frac{d{P}_{Cu}}{d{i}_{q1}}}=0, {\displaystyle \frac{d{P}_{Cu}}{d{i}_{d2}}}=0, {\displaystyle \frac{d{P}_{Cu}}{d{i}_{q2}}}=0, {\displaystyle \frac{d{P}_{Cu}}{d{i}_{o1}}}=0, {\displaystyle \frac{d{P}_{Cu}}{d{i}_{o2}}}=0\end{array}\right.$$

(14)

3.2. Single Open-Phase Fault

As SOPF occurs to NPSDTP-PMSM, the current in the open phase is forced to zero. And the basic FTC strategy is to regulate the space voltage vectors, maintaining the rotating magnetic field without the faulty phase current. Taking phase-A as the faulty phase in Figure 4a, by performing the inverse transformation in (11), the current constraint in d-q-z axis can be expressed as (15). As the constraint is satisfied, the current in phase A is actively controlled to zero.

$$i_{d1}\cos ({\theta }_e)-i_{q1}\sin ({\theta }_e)+i_{z1}=0$$

(15)

To maintain the smooth torque output, the sum of torque output from each winding set should meet the load torque at all position. For surface-mounted NPSDTP-PMSM, the torque output of each winding set has a linear relation with q-axis current. As DICC is performed for NPSDTP-PMSM, the demanding torque is regulated by the PI controller through the closed-loop speed control, and is transformed into the current reference i_{q_ref}. Then, the current reference is allocated to each winding set as i_q1 and i_q2. Thus, the constraint can be simplified as

$$i_{q1}+i_{q2}=i_{q\_ref}$$

(16)

Copper loss minimization requires setting i_d2 = 0. For ZSCs, the single current path constrains i_z1 = −i_z2.

$$\left\{\begin{array}{l}{i}_{d2}=0\\ i_{z1}+i_{z2}=0\end{array}\right.$$

(17)

By substituting (15)–(17) into (14), the ICLP can be expressed by i_d1 and i_q1 as

$$P_{Cu}=(3+2\cos (2{\theta }_e))i_{d1}^2+(4-2\cos (2{\theta }_e))i_{q1}^2-4\sin (2{\theta }_e)i_{d1}{i}_{q1}-2i_{q\_ref}{i}_{q1}+i_{q\_ref}^2$$

(18)

In (18), the ICLP is a function of i_d1 and i_q1. The extreme point must be the minimum value, for the maximum is infinity with increasing current. The extreme point can be derived by the partial derivative of i_d1 and i_q1. Thus, the current references in d-q-z axis with minimized copper loss under SOPF can be expressed as

$$\left\{\begin{array}{l}{i}_{d1}^{\ast }={\displaystyle \frac{2\sin (2{\theta }_e)}{8+2\cos (2{\theta }_e)}}{i}_{q\_ref}\\ i_{q1}^{\ast }={\displaystyle \frac{3+2\cos (2{\theta }_e)}{8+2\cos (2{\theta }_e)}}{i}_{q\_ref}\\ i_{z1}^{\ast }={\displaystyle \frac{\sin ({\theta }_e)}{8+2\cos (2{\theta }_e)}}{i}_{q\_ref}\\ i_{d2}^{\ast }=0\\ i_{q2}^{\ast }={\displaystyle \frac{5}{8+2\cos (2{\theta }_e)}}{i}_{q\_ref}\\ i_{z2}^{\ast }={\displaystyle \frac{-\sin ({\theta }_e)}{8+2\cos (2{\theta }_e)}}{i}_{q\_ref}\end{array}\right.$$

(19)

According to (19), taken i_{q_ref} = 5 as the base value, the waveforms of current references under d-q-z axis are shown in Figure 5a. The sum of q-axis current is a fixed value equal to i_{q_ref}, representing smooth torque output. The phase current waveforms and ICLP are derived and illustrated in Figure 5b. The ACLP increased 32% under SOPF. In the regulation process, the ZSL functions as a regulator path between the faulty and healthy winding sets, and provide an additional current path for phase E and F. Thus, the phase angle and amplitude of E and F can be adjusted, instead of forming a single-phase machine in the traditional three phase PMSM. This mechanism enables the faulty winding of outputting non-zero torque at all positions, further reducing the burden of the healthy winding set and achieving deeper optimization on copper loss.

Moreover, the FFT analysis of current references is conducted and shown in Figure 5c. Harmonic orders in d-q axis are 2nd and 4th, and that in z-axis are 1st, 3rd, and 5th. Critically, the harmonics in q-axis are phase reversed for the two winding sets, standing the dynamic torque regulation. It should be noted that, in the joint motor applications, the current loop bandwidth can be modified to 1 kHz or higher, with 20 kHz sampling frequency and is capable of tracking the obtained AC references component by universal PID controller.

3.3. Dual-Open-Phase Fault

As DOPF occurs to a winding set, taking phase A and phase B as the faulty phase in Figure 4b, both phase currents are forced to zero as i_A = i_B = 0. To maintain the rotating magnetic field, transformation in (10) is conducted and the current references in d-q-z axis are regulated, with sufficient of the first two equations in (20). And the smooth output torque is ensured by the third equation. The fourth equation is the ZSC relation between two winding sets.

$$\left\{\begin{array}{l}{i}_{d1}\cos ({\theta }_e)-i_{q1}\sin ({\theta }_e)+i_{z1}=0\\ i_{d1}\cos ({\theta }_e-2\pi /3)-i_{q1}\sin ({\theta }_e-2\pi /3)+i_{z1}=0\\ i_{q1}+i_{q2}=i_{q\_ref}\\ i_{z1}+i_{z2}=0\end{array}\right.$$

(20)

Through (20), all the current references in d-q-z axis can be expressed by i_q1. Then, the ICLP in (14) can be expressed by a single variable and the minimum point can be derived by the derivative of i_q1. The copper loss minimization constraint can be expressed as

$$\left\{\begin{array}{l}{P}_{cu}=2i_{q1}^2/{\sin }^2({\theta }_e-\pi /3)+{(i_{q\_ref}-i_{q1})}^2\\ d{P}_{cu}/d{i}_{q1}=0\end{array}\right.$$

(21)

With the constraints in (20) and (21). The current references under DOPF can be obtained as (22).

$$\left\{\begin{array}{l}{i}_{d1}^{\ast }=-i_{q\_ref}{\displaystyle \frac{\sin (2{\theta }_e-2\pi /3)}{5-\cos (2{\theta }_e-2\pi /3)}}\\ i_{q1}^{\ast }=i_{q\_ref}{\displaystyle \frac{1-\cos (2{\theta }_e-2\pi /3)}{5-\cos (2{\theta }_e-2\pi /3)}}\\ i_{z1}^{\ast }=i_{q\_ref}{\displaystyle \frac{\sin ({\theta }_e-\pi /3)}{5-\cos (2{\theta }_e-2\pi /3)}}\\ i_{d2}^{\ast }=0\\ i_{q2}^{\ast }=i_{q\_ref}{\displaystyle \frac{4}{5-\cos (2{\theta }_e-2\pi /3)}}\\ i_{z2}^{\ast }=-i_{q\_ref}{\displaystyle \frac{\sin ({\theta }_e-\pi /3)}{5-\cos (2{\theta }_e-2\pi /3)}}\end{array}\right.$$

(22)

The current references in d-q-z and A-B-C axis are shown in Figure 6a,b. Different from SOPF, there exists points where the faulty winding set has no contribution on torque output. And the healthy winding set bears more torque output, bringing higher phase current amplitude and copper loss compared with SOPF. The ACLP is increased by 68.5% and the peak value reaches 2 times on the points where phase current C is zero.

The FFT analysis of d-q-z current references is carried out in Figure 6c. The main harmonic orders are the same with single-open-phase fault, but the content is different. In d-axis, 2nd order harmonic is decreased by 5%. In q-axis, the 2nd order harmonic remains the same, indicating the optimal output torque regulation mode under minimum copper loss constraint. And in z-axis, 1st order component is increased by 4%, for ZSL is the only current path in the faulty winding set, and phase C current becomes the ZSC.

4. Experimental Verification

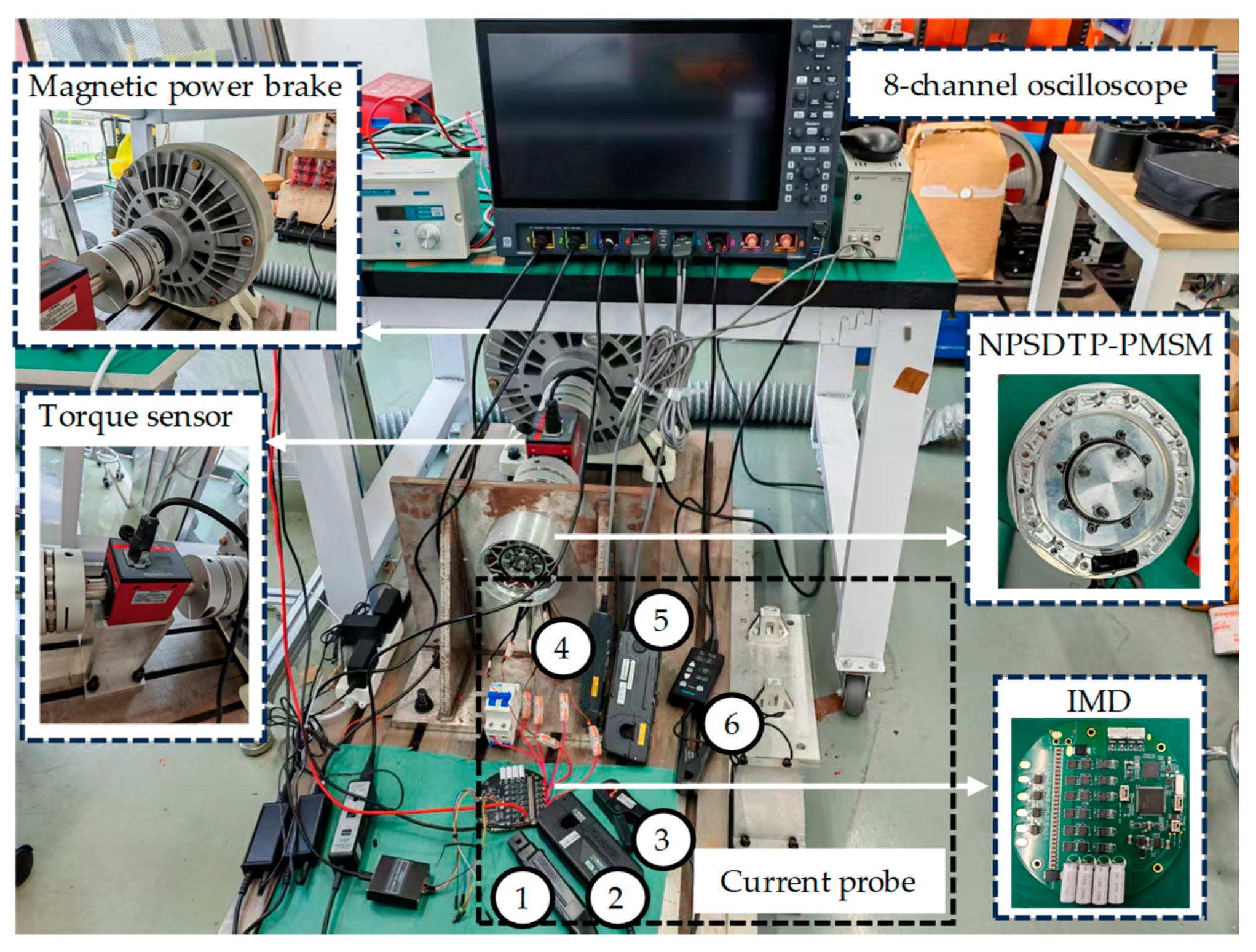
Experiments were conducted on a joint motor powered by an integrated machine drive (IMD). The experiment platform is shown in Figure 7. The key parameters of the joint motor are listed in

Table 1. Parameters of the experiment platform.

Name	Value
Pole	28
Slot	24
d-q axis inductance	125 uH
Phase resistance	0.0125 ohm
Flux linkage	0.00445 Wb
DC voltage	100 v
Reduction ratio	25:1
Load	30 Nm
Speed reference	24 rpm
Sampling frequency	20 kHz
Switching frequency	40 kHz
Sampling frequency for Uart	20 kHz
Sampling frequency for oscilloscope	50 kHz
ambient temperature	25 °C
MPB max-load	300 Nm
MPB max-speed	100 rpm

. In the IMD, the MCU (GD32F470VGT6) and the drive circuit are on the same PCB board. The proposed FTC algorithm is performed by MCU. PWM signals are sent to the gate-driver IC. The on-board magnetic encoder comprises two magnetic sensors with 90° phase shifted, where the magnetic ring is sensed. In the experiment, a magnetic powder brake (MPB) is adopted as the load. By adjusting the input current of MPB, the load torque can be adjusted. Open-phase faults were emulated by disconnecting phases via air switches. In the experiment, the control performance is decided by the current traction. Thus, the actual and reference currents in d-q-z axis are collected and transmitted to computer, where a high speed universal asynchronous receiver/transmitter (UART) with 6M bps is used to improve the data quality. Moreover, to precisely calculate the copper loss, 6 current probes are used for the phase current and Data was recorded via an 8-channel oscilloscope.

All the experiments are carried out under 30 Nm load and 24 rpm speed. To simplify the description, winding set of ABC and DEF are named as M0 and M1. The initial d-z axis current references of M0 and M1 are zero, and q axis current reference is equally dispatched. In SOPF, phase D is disconnected, and in DOPF, phase D and E are blocked. Furthermore, consistent with the Nyquist-Shannon sampling theorem, signal components exceeding 25 kHz (where fs = 50 kHz) are inherently attenuated and thus omitted from analysis. This 50 kHz sampling configuration remains invariant for all operational scenarios during oscilloscope measurements.

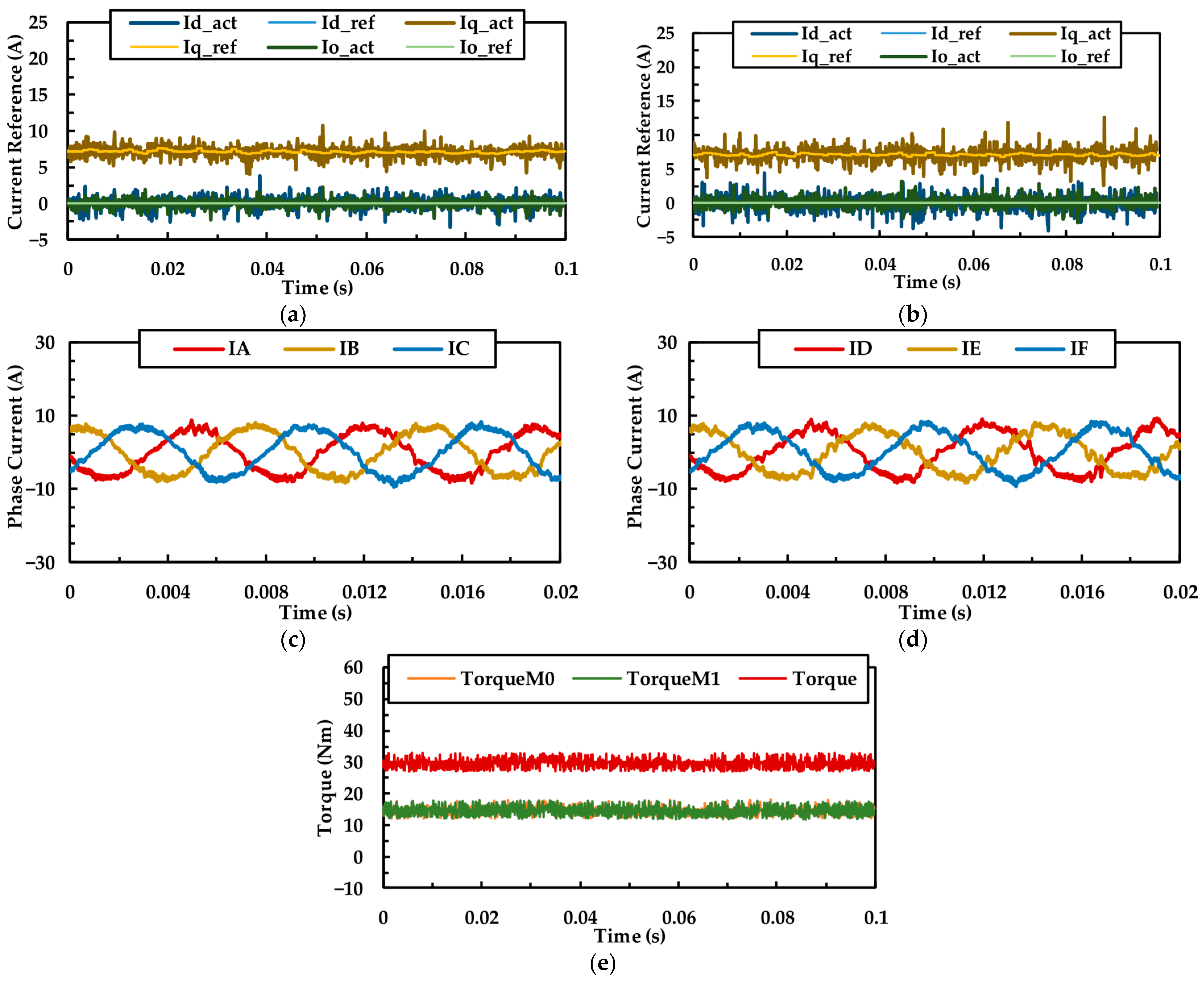
The steady-state performance of the NPSDTP-PMSM joint motor under healthy condition is shown in Figure 8. In Figure 8a,b,e, the d-q-z current references of M0 and M1 are the same, and the load torque is equally allocated to each winding set. For the same electrical phase, mutual cancellation of CMVs and 3rd BEMFs between winding sets minimizes ZSC.

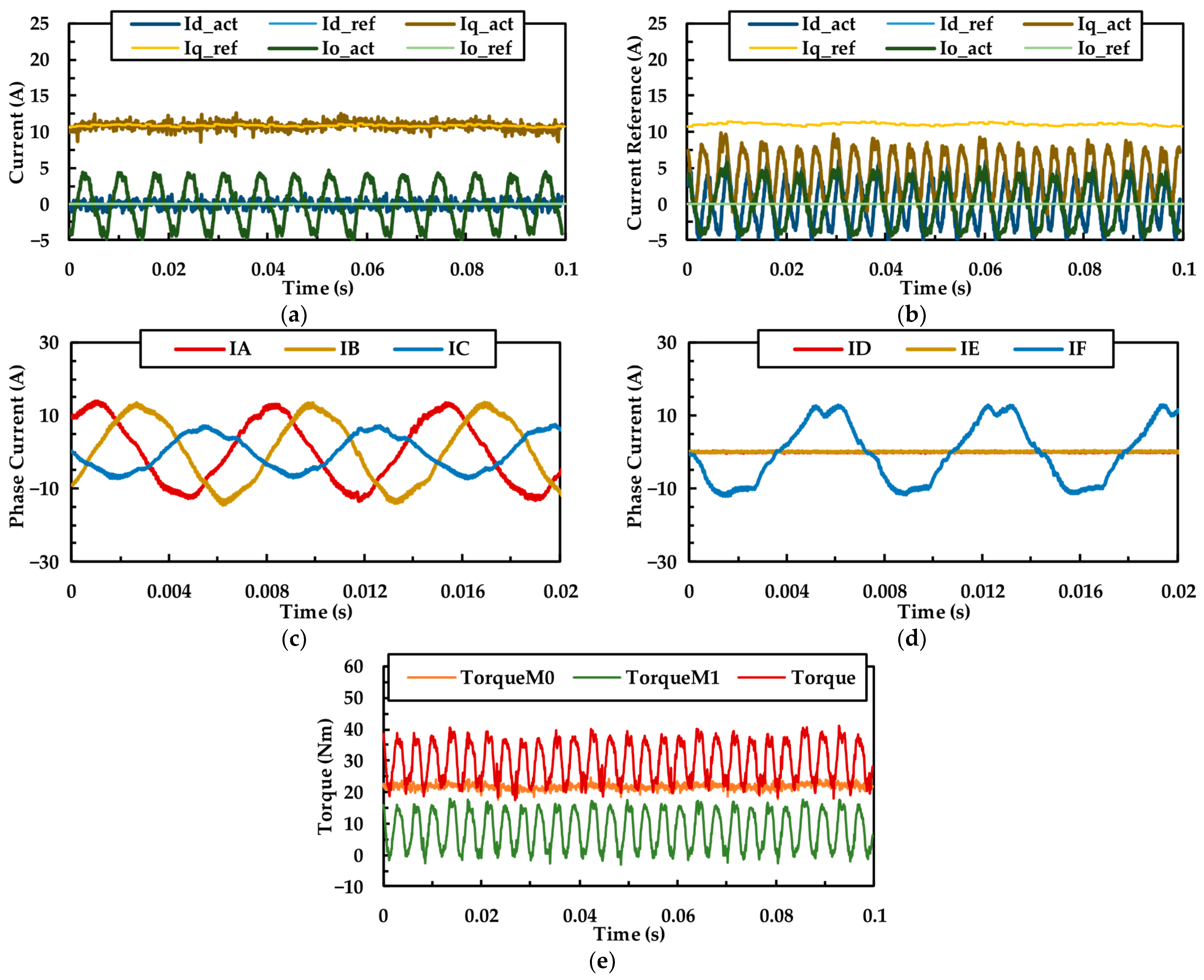
Figure 9 shows the performance of NPSDTP-PMSM under SOPF with no FTC strategy. From Figure 9a,b, in d-q axis, M0 is capable of tracking the current references and generates steady output torque. However, with two phases remaining, M1 fails to track reference commands, and the 2nd order frequency ripple occurs in the d-q currents and fundamental frequency ripple is induced in the z-axis. In Figure 9e, the output torque of NPSDTP-PMSM manifests 2nd order frequency torque ripple under single-open-phase fault.

In Figure 9c,d, for the additional current path in ZSL, fundamental currents of phase E and F can be regulated independently instead of forming a single-phase loop. ZSL enables continuous torque production in the faulted set (M1) by independent phase E/F current regulation. Moreover, the load torque is still equally allocated to M0 and M1, and the average q axis current of M1 is equal to the reference. This characteristic shows the outstanding fault-tolerant performance of NPSDTP-PMSM with connected neutral point. However, the 2nd order frequency torque ripple brings vibration and noise, which is vital in the joint motor applications.

To suppress the torque ripple under the constraint of minimized copper loss, the proposed FTC strategy under SOPF is implemented and the performance is shown in Figure 10. From Figure 10a,b, d-q-z currents are well tracked with the references and are matched with the theoretical waveforms in Figure 5a. By regulating the current references under d-q-z axis, the q axis current ripples of M0 and M1 have the same amplitude but reversed phase angle. For the linearity relation between torque and q axis current, as Figure 10e shows, the torque ripples from M0 and M1 are reversed. In the torque sensor, output torque fluctuation is reduced, compared with Figure 9e. The experimental results in Figure 10 demonstrate the effectiveness of the proposed fault-tolerant control strategy under SOPF.

Figure 11 shows the performance of NPSDTP-PMSM under DOPF (D, E) without FTC strategy. For the healthy winding set, the M0 closed-up current control is well performed in d-q axis. However, in M1, the single healthy phase is not sufficient of tracking current references. The harmonic orders in d-q-z axis are the same with Figure 9b: 2nd order frequency ripples in d-q axis and 1st frequency ripple in z-axis. However, compared with Figure 9b, the average q-axis current in M1 is unable to meet the reference, and zero torque output happens at points where phase current C is zero. In the meantime, through the closed-up speed loop, the q-axis reference is regulated till the average output torque is sufficient for the load. Thus, the current amplitude in M0 increases compared with Figure 9c.

As observed in Figure 9b and Figure 11b, the currents of the faulted three-phase winding exhibit significant oscillations in the d-q-z axis when no fault-tolerant control strategy is implemented. These oscillations manifest predominantly as second-order harmonics. This phenomenon occurs because the altered current paths during faults cannot satisfy the original reference currents in the d-q-z axis. Moreover, according to (8), oscillations in the q-axis current directly induce electromagnetic torque ripple. Consequently, while the healthy winding set maintains steady torque output (Figure 9e and Figure 11e), the faulted set develops second-order torque oscillations. This results in output torque exhibiting second-harmonic ripple. In robotic joint applications, particularly during low-speed operation, this torque oscillation causes significant mechanical vibration and audible noise. These effects compromise joint positioning accuracy and accelerate mechanical wear.

Figure 12 shows performance of the proposed FTC strategy under DOPF (D, E). In Figure 12a,b, the closed-up current loop is well performed in M0 and M1 and the currents are consistent with the theoretical waveforms in Figure 6a. The 2nd order ripples in q axis current in M0 and M1 are phase reversed. In Figure 12e, the torque ripples in M0 and M1 are counteracted, and the ripples in output torque are reduced, compared with Figure 11e. The phase currents in Figure 12c,d are also well matched with the theoretical waveforms in Figure 6b. Thus, the experimental results in Figure 12 verify the validation of the proposed fault-tolerant control strategy under DOPF.

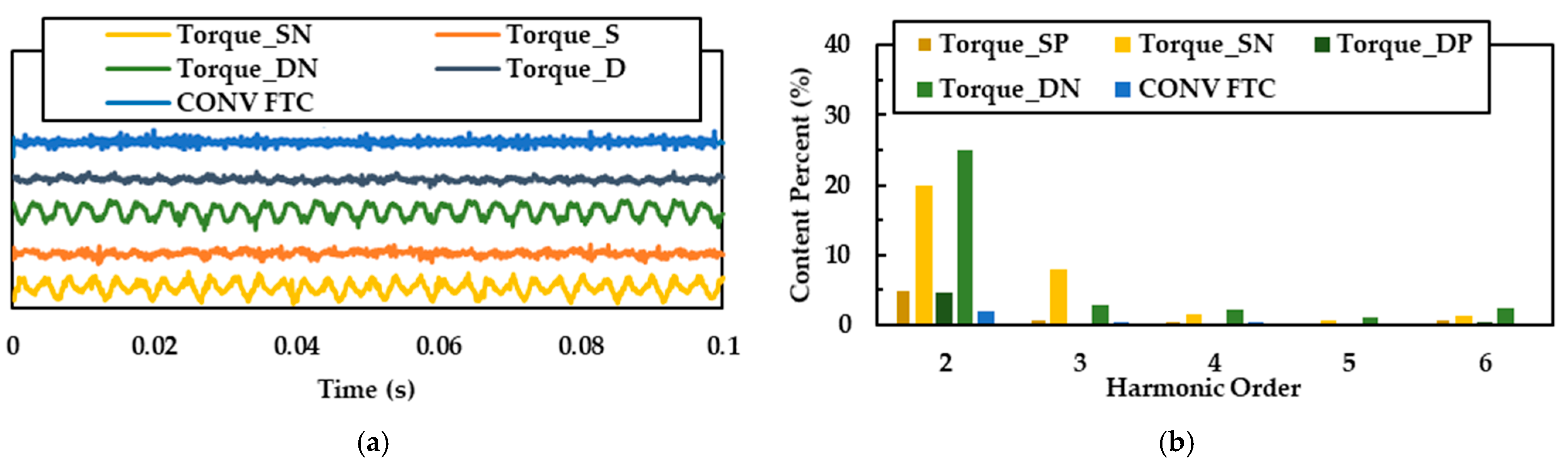
Explicit comparisons of post-fault torque performance are presented in Figure 13. Figure 13a superimposes output torque waveforms across conditions, while Figure 13b provides FFT analysis demonstrating harmonic suppression under both SOPF and DOPF using the proposed strategy.

Table 2. Output torque ripple under different condition.

Condition	Peak to Peak Ripple (Nm)	Per Unit Value
Healthy condition	7.8	1.00
SOP-N	21.2	2.71
SOP-P	13.3	1.70
DOP-N	20.1	2.57
DOP-P	12.0	1.53
FTC [9]	14.3	1.83

quantifies peak-to-peak torque ripple, revealing reduction rates of 37.2% (SOPF) and 40.4% (DOPF) versus FTC-free operation. These results validate the FTC strategy’s effectiveness in torque ripple mitigation.

Notably, Reference [9] exhibits higher peak-to-peak ripple dominated by 2 × PWM-frequency harmonics. This stems from single-winding-set operation where elevated phase currents induce magnetic saturation and amplify PWM-induced current ripple.

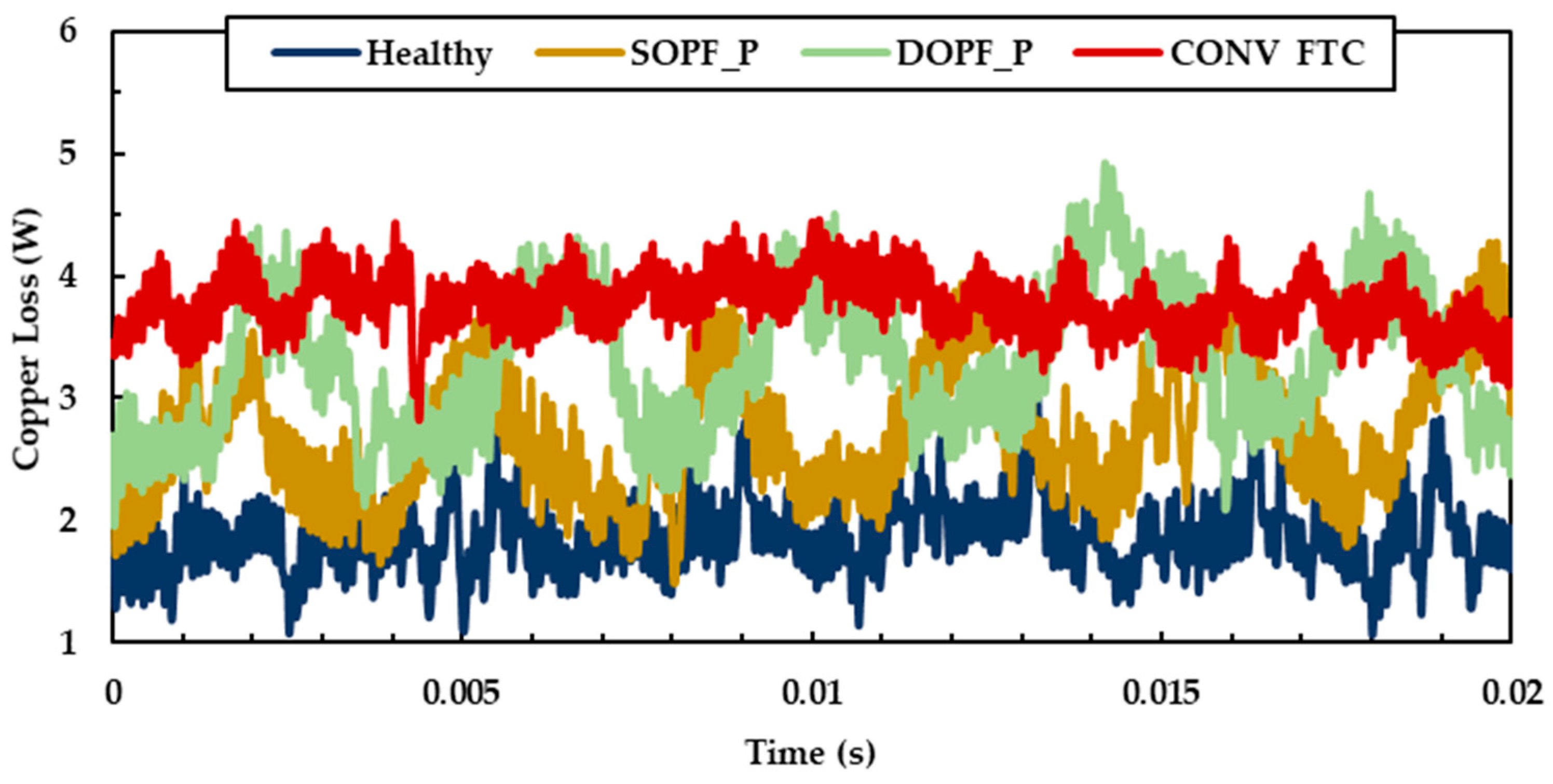
The ICPL waveforms under different working conditions are shown in Figure 14. And the ACPL of each working condition is illustrated in

Table 3. ACLP under different condition.

Condition	Average Copper Loss (W)	Per Unit Value
Healthy	1.7512	1.00
SOPF-P	2.4761	1.41
DOPF-P	3.0672	1.75
FTC [11]	3.6254	2.07

. Under healthy conditions, both sets of windings share the load torque equally. The resulting copper loss is calculated by summing the squares of the six-phase currents and multiplying by the resistance, yielding an average copper loss of 1.7512 W in the healthy state and this value serves as the baseline. Under SOPF, the generated ICPL waveform matches the theoretical waveform shown in Figure 5b, with an average copper loss of 2.4761 W, which represents an increase of 41% compared to the healthy state. Under DOPF, the copper loss waveform matches the theoretical waveform shown in Figure 6b, resulting in an average copper loss of 3.0672 W, which is an increase of 75% compared to the healthy state. Furthermore, compared with the FTC method presented in [9], which produced a copper loss of 3.6254 W (an increase of 107% over the healthy state), the copper loss performance shown in Figure 14 demonstrates the effectiveness of the proposed fault-tolerant control strategy in suppressing copper loss. Figure 15 shows the temperature after thermal balance. As observed in Figure 15, the proposed FTC strategy effectively suppresses both the average temperature rise (overall winding temperature) and hotspot temperature compared to the FTC method in [9], owing to optimized utilization of the remaining healthy windings. Given the enclosed structure of joint motors, reducing overall copper loss significantly mitigates internal temperature rise within the motor housing. Under these conditions, the enhanced thermal gradient facilitates heat dissipation from hotspot regions. Under SOPF operation, while Phase A current amplitude under proposed strategy remains identical to that in [9] (twice the healthy-state current), the hotspot temperature is reduced by nearly 40 °C compared to [9].

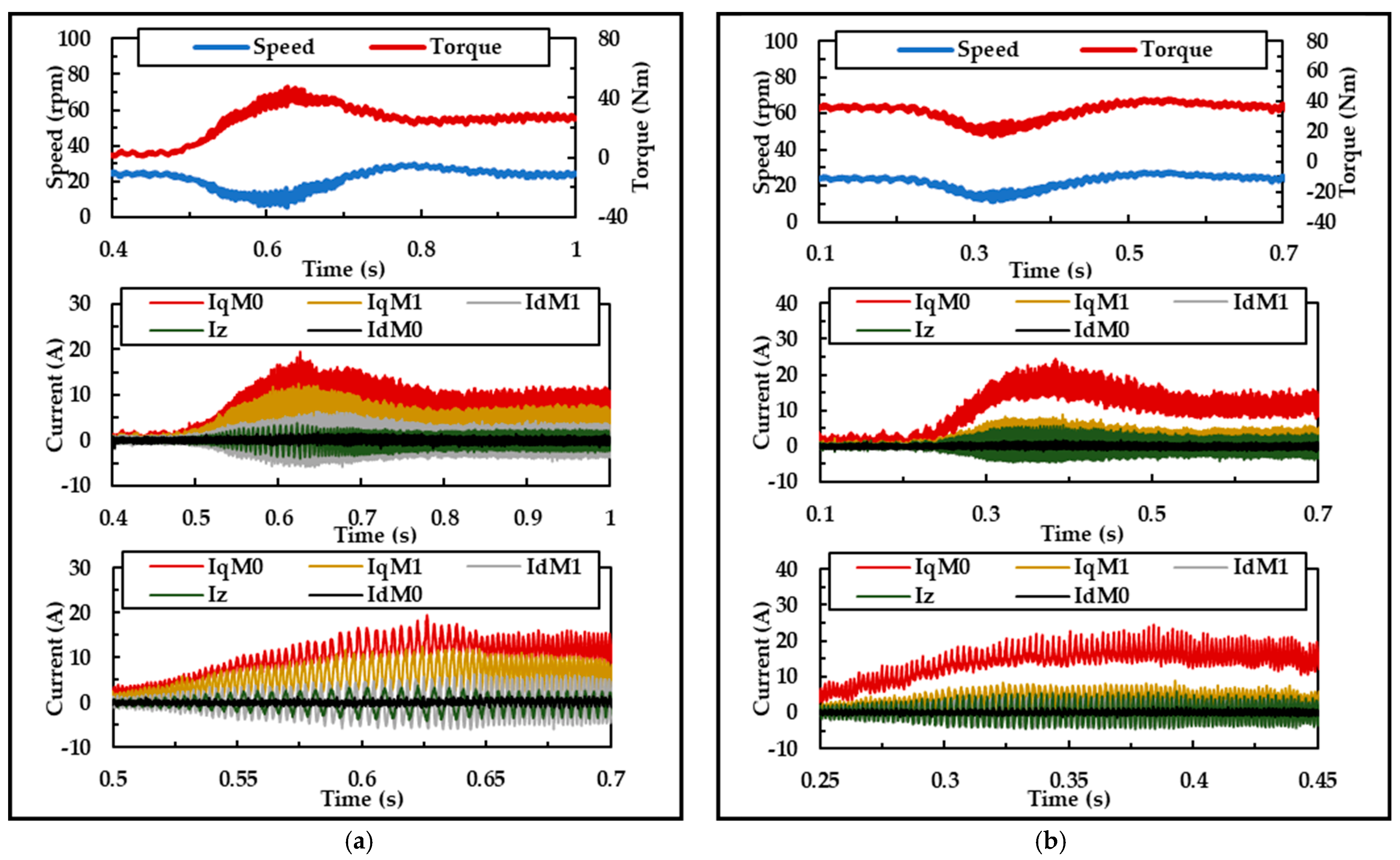
Figure 16 demonstrates the dynamic performance of the proposed fault-tolerant control strategy under step speed variations. In Figure 16a, operating under a single-phase open-circuit fault, the speed command increases from 24 rpm to 48 rpm at 0.22 s and subsequently decreases back to 24 rpm at 0.46 s. As observed in Figure 16a, the phase currents remain well-regulated throughout the adjustment period, closely adhering to their reference commands. Similarly, Figure 16b illustrates the speed regulation performance under a two-phase open-circuit fault, where the currents maintain precise tracking of their references during the speed change.

Figure 17 presents the dynamic performance of the proposed fault-tolerant strategy under high-slop load changes (0–30 Nm within 10 ms, by starting the output of controlled current source connected to the MPB). In Figure 17a, under SOPF, the load torque changes from 0 Nm to 30 Nm at 0.5 s. Throughout the torque regulation process, the currents consistently follow the references. Figure 17b shows operation under DOPF, where the load torque changes to 30 Nm at 0.3 s. During this adjustment, the currents continuously track their reference commands.

Collectively, Figure 16 and Figure 17 validate the effectiveness of the proposed fault-tolerant strategy in handling both speed variations and load transients.

5. Conclusions

A fault-tolerant control strategy for non-phase-shifted dual three-phase permanent magnet synchronous motors (NPSDTP-PMSMs) is developed to simultaneously improve copper loss and torque ripple performance under single and dual open-phase faults. The established mathematical model revealed the inherent zero-sequence current (ZSC) self-suppression mechanism in NPSDTP-PMSMs, while analysis confirmed the mutual cancellation characteristic of ZSC-induced torque components. This property enables full utilization of ZSC regulation, particularly during fault conditions. The proposed methodology constructs fault-tolerant strategies for both fault types based on torque smoothness and copper loss minimization constraints. Through position-dependent regulation of d-q-z axis current references, smooth output torque and minimized instantaneous copper loss power (ICLP) are achieved. Experimental validation demonstrated 37% torque ripple reduction in single open-phase fault (SOPF) and 40% reduction in dual open-phase fault (DOPF) operation versus baseline non-FTC conditions, representing a 16.3% improvement over existing FTC method [9]. Concurrently, relative to healthy operation, copper loss was limited to 1.41 p.u. (SOPF) and 1.75 p.u. (DOPF), significantly lower than the 2.07 p.u. attained by method [9].

This work provides the first dedicated FTC strategy exploiting NPSDTP-PMSMs’ intrinsic ZSC advantages. The strategy’s position-dependent current regulation enables direct deployment in robotic applications where torque stability and thermal management are critical. In future work, two key extensions emerge from this research:

• Fault-induced dynamics characterization: Detailed analysis of post-fault current oscillations and harmonic propagation paths to quantify impacts on control loop bandwidth and stability margins.
• Zero-sequence circuit utilization: Development of model-based fault detection algorithms leveraging the ZSC pathway’s sensitivity to phase imbalances for rapid open-phase diagnosis.