A Multi-Objective Decision-Making Method for Optimal Scheduling Operating Points in Integrated Main-Distribution Networks with Static Security Region Constraints
Abstract
1. Introduction
2. Establishment of Risk Indicators for IMDN
2.1. Risk of Insufficient Reserve
2.2. Risk of Power Factor Violation
2.3. Risk of Feeder Power Overload
2.4. Risks of Wind and Solar Curtailment
3. Integrated Operation Scheduling Model for IMDN
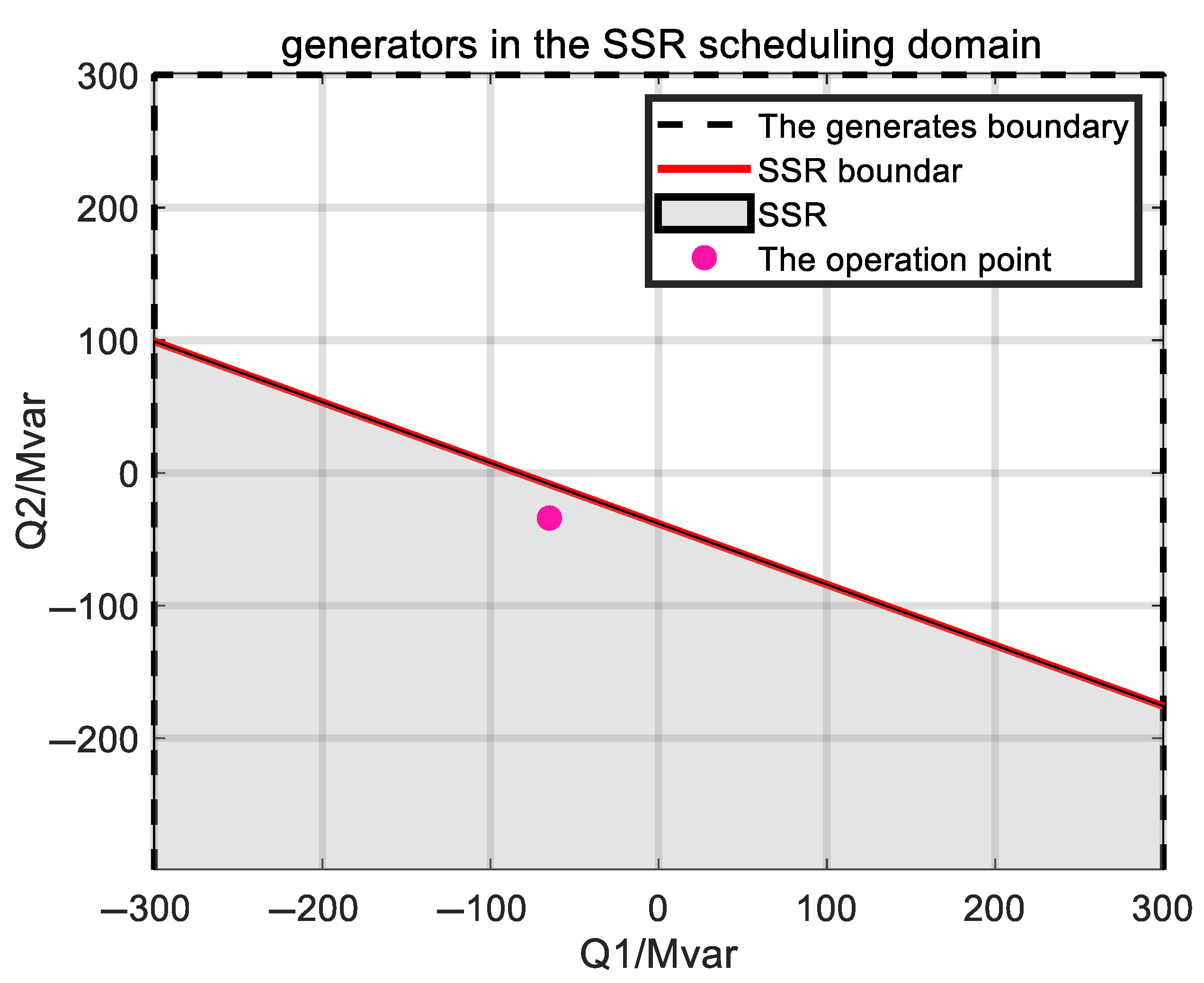
3.1. SSR Constraint Model
3.2. Multi-Objective Model Construction Based on SSR
3.2.1. Objective Function
3.2.2. Constraints
3.3. Model Solution
- (1)
- IMDN operation data are input, and AG-MOPSO parameters are initialized.
- (2)
- After determining each particle’s position based on base-case constraints, the objective function values are calculated as particle fitness. Personal best solutions for particles are initialized, followed by evaluating the Pareto dominance relationships among the particles to construct the initial non-dominated solution set.
- (3)
- Using the adaptive grid method and roulette wheel selection, the global optimal solution is extracted from the non-dominated set, and the particle positions are updated accordingly.
- (4)
- Penalty functions are applied to each objective function under base-case constraints to compute the modified objective values. The personal best solutions are then updated, with synchronous maintenance of the non-dominated solution set.
- (5)
- While the size of the non-dominated set exceeds its capacity, redundant solutions are pruned based on the grid density.
- (6)
- The iteration count is accumulated. If the maximum iteration number is reached, the non-dominated solution set is output; otherwise, the process returns to Step 3 for further iteration.
4. Optimal Operating Point Decision-Making Based on Fuzzy Comprehensive Evaluation
4.1. Weight Determination of Evaluation Indicators
Determination of Weights for Each Indicator
4.2. Construction of Fuzzy Evaluation Model
5. Simulation and Result Analysis
5.1. Basic Information of Simulation
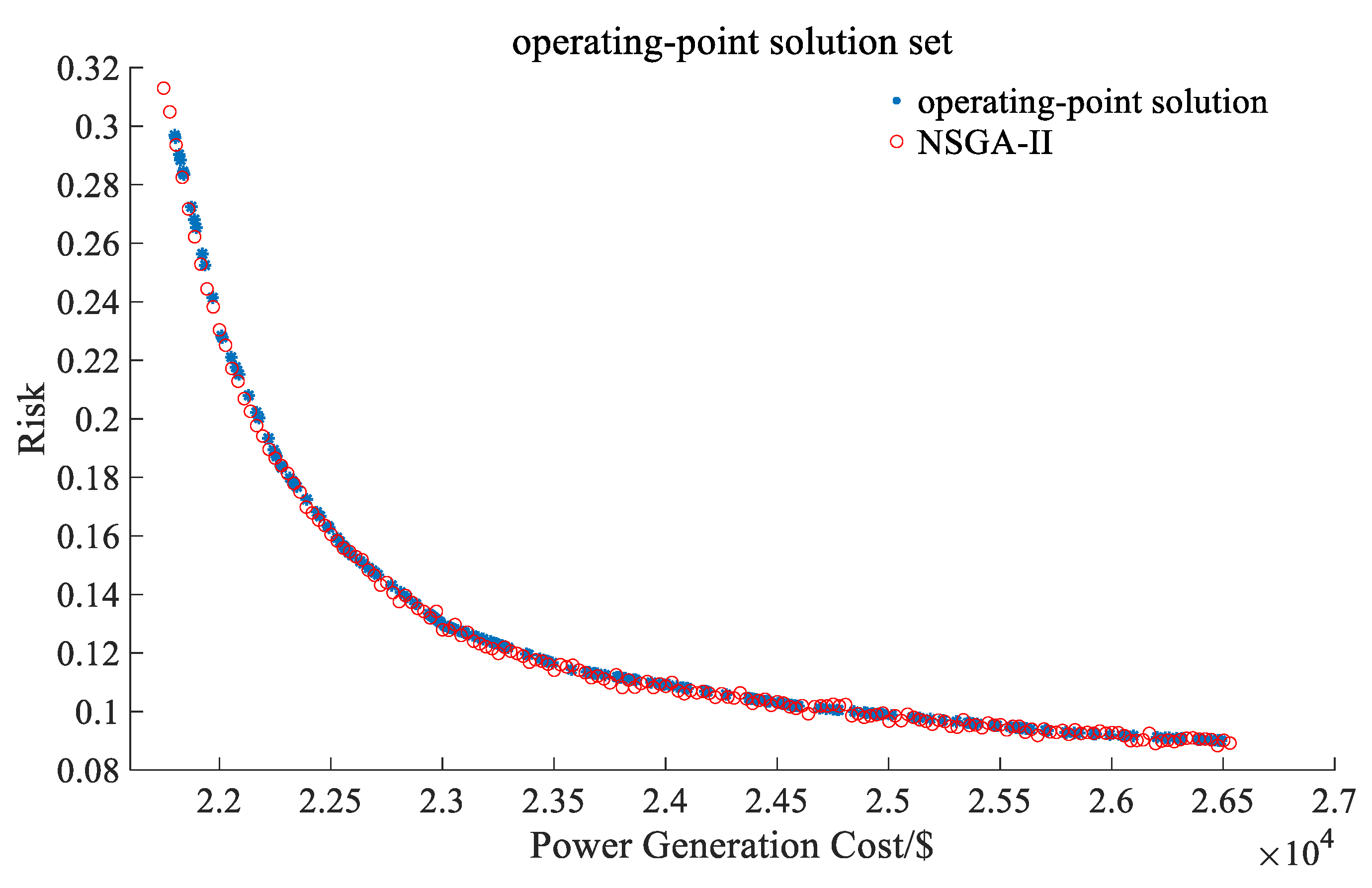
5.2. Simulation Result
5.3. Optimal Decision Making Based on Fuzzy Comprehensive Analysis
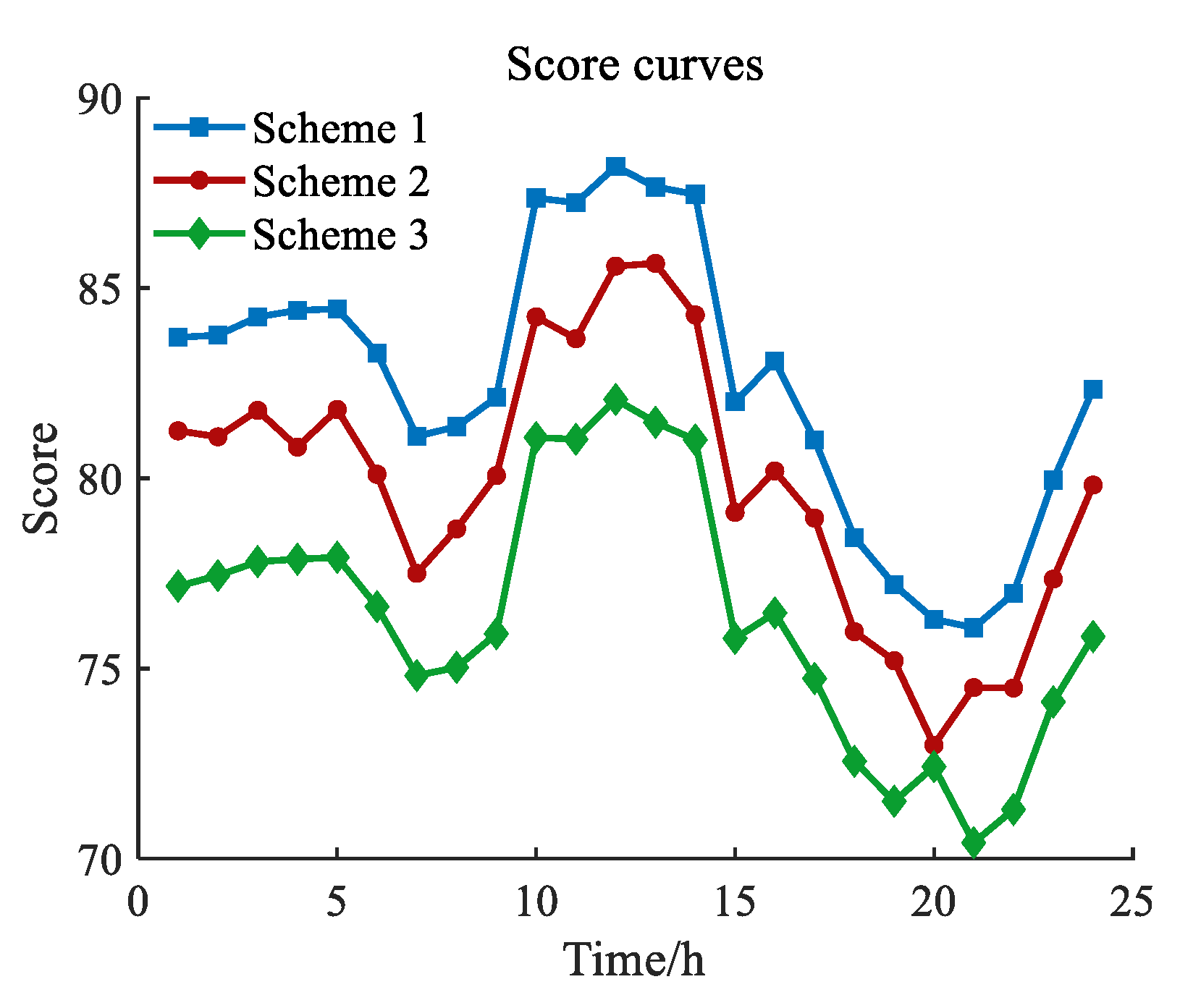
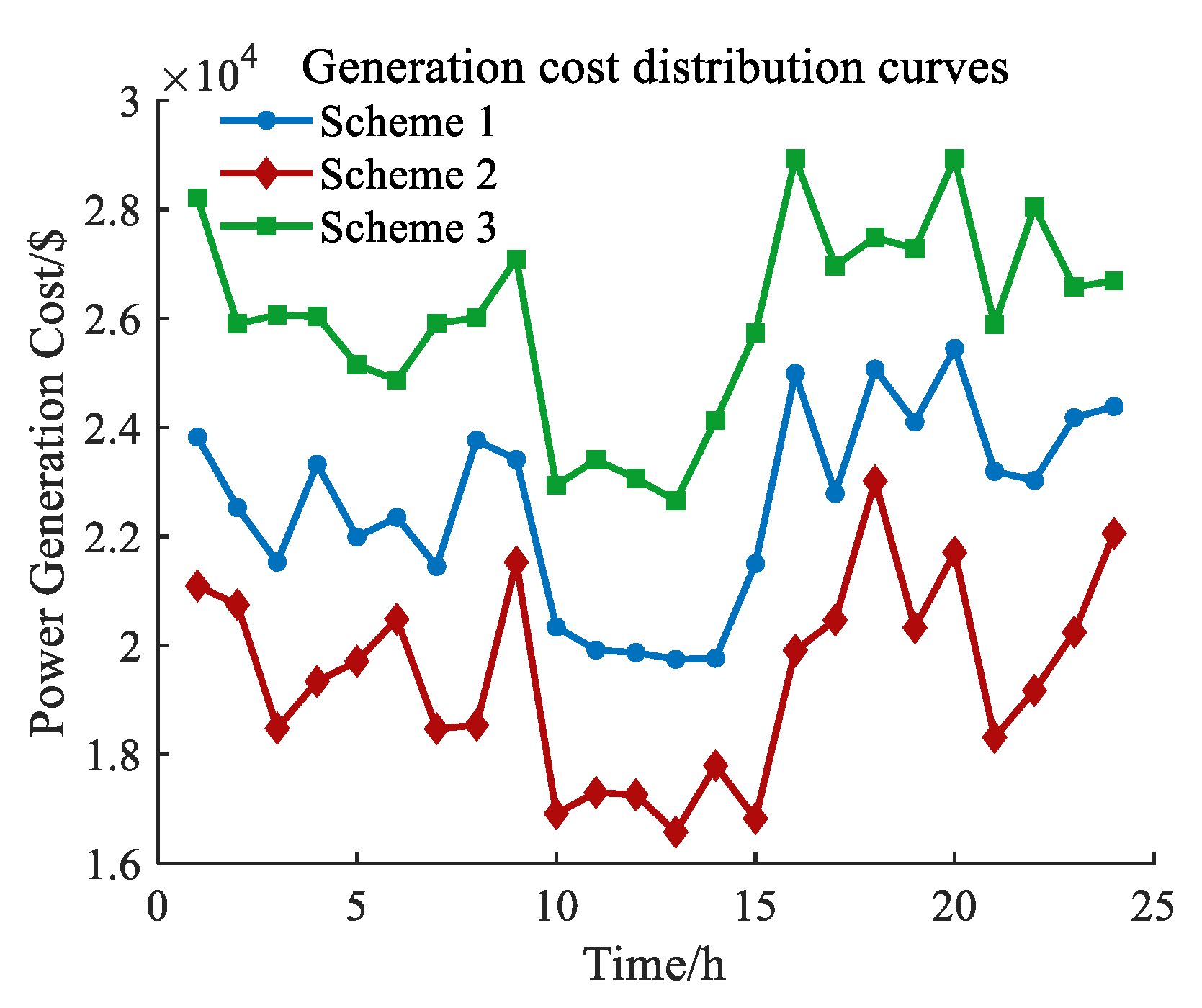
5.4. Comparative Analysis of Different Scheduling Schemes
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
Appendix A.2
Appendix A.2.1. Subjective Weight Determination Based on AHP [21]
Appendix A.2.2. Objective Weight Determination Based on Entropy Weight Method [22]
Appendix A.2.3. Determination of Synthetic Weights
References
- Zhao, Y.; Zhang, G.; Hu, W.; Huang, Q.; Chen, Z.; Blaabjerg, F. Meta-Learning Based Voltage Control for Renewable Energy Integrated Active Distribution Network Against Topology Change. IEEE Trans. Power Syst. 2023, 38, 5937–5940. [Google Scholar] [CrossRef]
- Poudyal, A.; Poudel, S.; Dubey, A. Risk-Based Active Distribution System Planning for Resilience Against Extreme Weather Events. IEEE Trans. Sustain. Energy 2023, 14, 1178–1192. [Google Scholar] [CrossRef]
- Tao, Y.; Qiu, J.; Lai, S.; Sun, X.; Liu, H.; Zhao, J. Distributed Adaptive Robust Restoration Scheme of Cyber-Physical Active Distribution System With Voltage Control. IEEE Trans. Power Syst. 2024, 39, 2170–2184. [Google Scholar] [CrossRef]
- Wang, G.; Wang, C.; Feng, T.; Wang, K.; Yao, W.; Zhang, Z. Day-Ahead and Intraday Joint Optimal Dispatch in Active Distribution Network Considering Centralized and Distributed Energy Storage Coordination. IEEE Trans. Ind. Appl. 2024, 60, 4832–4842. [Google Scholar] [CrossRef]
- Fan, G.; Lin, S.; Feng, X.; Wang, Q.; Liu, M. Stochastic Economic Dispatch of Integrated Transmission and Distribution Networks Using Distributed Approximate Dynamic Programming. IEEE Syst. J. 2022, 16, 5985–5996. [Google Scholar] [CrossRef]
- Tang, K.; Dong, S.; Huang, J.; Ma, X. Operational Risk Assessment for Integrated Transmission and Distribution Networks. CSEE J. Power Energy Syst. 2023, 9, 2109–2120. [Google Scholar]
- Li, X.; Han, X.; Yang, M. Risk-Based Reserve Scheduling for Active Distribution Networks Based on an Improved Proximal Policy Optimization Algorithm. IEEE Access 2023, 11, 15211–15228. [Google Scholar] [CrossRef]
- Liang, Z.; Kang, C.; Sui, L.; Yu, R.; Jia, Y.; Du, Y.; Chen, W. Research on operation risk assessment and prevention and control strategy of main distribution network with high proportion of distributed photovoltaic. J. Tsinghua Univ. (Nat. Sci. Ed.) 2024, 64, 1964–1978. (In Chinese) [Google Scholar]
- Tang, Y.; Sun, D.; Zhou, Y.; Zhou, L. Research on day-ahead-real-time coordinated risk scheduling method for integrated main distribution network with distributed generation. Smart Power 2020, 48, 8–14+23. (In Chinese) [Google Scholar]
- Yu, Y.; Liu, Y.; Qin, C.; Yang, T. Theory and Method of Power System Integrated Security Region Irrelevant to Operation States: An Introduction. Engineering 2020, 6, 754–777. [Google Scholar] [CrossRef]
- Shi, X.; Qiu, R.; Mi, T.; He, X.; Zhu, Y. Adversarial Feature Learning of Online Monitoring Data for Operational Risk Assessment in Distribution Networks. IEEE Trans. Power Syst. 2020, 35, 975–985. [Google Scholar] [CrossRef]
- Dechgummarn, Y.; Fuangfoo, P.; Kampeerawat, W. Reliability Assessment and Improvement of Electrical Distribution Systems by Using Multinomial Monte Carlo Simulations and a Component Risk Priority Index. IEEE Access 2022, 10, 111923–111935. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Liang, Z.; Huo, X.; Yu, R.; Bian, J. Multi-timescale risk scheduling for transmission and distribution networks for highly proportional distributed energy access. Int. J. Electr. Power Energy Syst. 2024, 155, 109598. [Google Scholar] [CrossRef]
- Tang, M.; Li, R.; Zhang, R.; Yang, S. Research on New Electric Power System Risk Assessment Based on Cloud Model. Sustainability 2024, 16, 2014. [Google Scholar] [CrossRef]
- Yang, T.; Yu, Y. Static Voltage Security Region-Based Coordinated Voltage Control in Smart Distribution Grids. IEEE Trans. Smart Grid 2018, 9, 5494–5502. [Google Scholar] [CrossRef]
- Cai, L.; Thornhill, N.F.; Kuenzel, S.; Pal, B.C. Wide-Area Monitoring of Power Systems Using Principal Component Analysis and k-Nearest Neighbor Analysis. IEEE Trans. Power Syst. 2018, 33, 4913–4923. [Google Scholar] [CrossRef]
- Han, H.; Lu, W.; Zhang, L.; Qiao, J. Adaptive Gradient Multiobjective Particle Swarm Optimization. IEEE Trans. Cybern. 2018, 48, 3067–3079. [Google Scholar] [CrossRef]
- Wu, J.; Wang, H.; Wang, W.; Zhang, Q. Performance evaluation for sustainability of wind energy project using improved multi-criteria decision-making method. J. Mod. Power Syst. Clean Energy 2019, 7, 1165–1176. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Z.; Han, L.; Mei, N. Fuzzy Comprehensive Evaluation Method for Energy Management Systems Based on an Internet of Things. IEEE Access 2017, 5, 21312–21322. [Google Scholar] [CrossRef]
- Sun, D.; Yu, Y. Accurate Identification of Critical Boundary Hyperplanes of Practical Steady-State Security Region in Distribution Grids. IEEE Trans. Smart Grid 2023, 14, 4312–4321. [Google Scholar] [CrossRef]
- Wang, C.; Chu, S.; Ying, Y.; Wang, A.; Chen, R.; Xu, H.; Zhu, B. Underfrequency Load Shedding Scheme for Islanded Microgrids Considering Objective and Subjective Weight of Loads. IEEE Trans. Smart Grid 2023, 14, 899–913. [Google Scholar] [CrossRef]
- Liu, R.; Yang, T.; Sun, G.; Lin, S.; Li, F.; Wang, X. Multi-Objective Optimal Scheduling of Community Integrated Energy System Considering Comprehensive Customer Dissatisfaction Model. IEEE Trans. Power Syst. 2023, 38, 4328–4340. [Google Scholar] [CrossRef]
- Hua, H.; Shi, J.; Chen, X.; Yu, K.; Qin, Y.; Shen, J.; Ding, Y.; He, D. Low-carbon economic energy routing strategy based on adaptive shape estimation multi-objective evolutionary algorithm. Chin. J. Electr. Eng. 2025, 45, 1394–1409. (In Chinese) [Google Scholar]




| Objective Layer | Criterion Layer | Index Layer |
| Main-Distribution Integration | Riskiness | Insufficient Reserve Risk |
| Power Factor Violation Risk | ||
| Feeder Power Overload risk | ||
| Wind and Solar Curtailment Risk | ||
| Economy | Power Generation Cost |
| Risk Index | Weight |
|---|---|
| 0.31 | |
| 0.19 | |
| 0.23 | |
| 0.27 |
| Time/h | AG-MOPSO | NSGA-II | Time/h | AG-MOPSO | NSGA-II | ||||
|---|---|---|---|---|---|---|---|---|---|
| Operating Point | Score | Operating Point | Score | Operating Point | Score | Operating Point | Score | ||
| 1 | 106 | 83.7 | 110 | 83.1 | 13 | 100 | 87.5 | 132 | 86.5 |
| 2 | 16 | 83.8 | 25 | 82.9 | 14 | 10 | 87.5 | 34 | 86.8 |
| 3 | 23 | 84.2 | 26 | 83.6 | 15 | 82 | 82.0 | 156 | 81.2 |
| 4 | 28 | 84.4 | 18 | 84.6 | 16 | 67 | 83.1 | 89 | 81.1 |
| 5 | 19 | 84.5 | 35 | 83.6 | 17 | 160 | 81.0 | 152 | 81.0 |
| 6 | 9 | 83.3 | 23 | 82.8 | 18 | 174 | 78.5 | 157 | 77.5 |
| 7 | 115 | 81.1 | 65 | 80.5 | 19 | 81 | 77.2 | 65 | 76.4 |
| 8 | 139 | 81.4 | 113 | 80.1 | 20 | 45 | 76.3 | 63 | 76.0 |
| 9 | 20 | 82.1 | 31 | 81.8 | 21 | 144 | 76.0 | 158 | 75.3 |
| 10 | 54 | 87.4 | 64 | 87.4 | 22 | 31 | 77.0 | 43 | 76.1 |
| 11 | 78 | 87.2 | 85 | 86.9 | 23 | 151 | 80.0 | 187 | 80.3 |
| 12 | 155 | 88.2 | 143 | 87.7 | 24 | 73 | 82.3 | 96 | 81.4 |
| Algorithm | Swarm Size/ Population Size | Number of Iterations | Running Time/s |
|---|---|---|---|
| AG-MOPSO | 150 | 2000 | 545.4 |
| NSGA-II | 150 | 2000 | 685.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Liu, Z.; Li, S. A Multi-Objective Decision-Making Method for Optimal Scheduling Operating Points in Integrated Main-Distribution Networks with Static Security Region Constraints. Energies 2025, 18, 4018. https://doi.org/10.3390/en18154018
Xu K, Liu Z, Li S. A Multi-Objective Decision-Making Method for Optimal Scheduling Operating Points in Integrated Main-Distribution Networks with Static Security Region Constraints. Energies. 2025; 18(15):4018. https://doi.org/10.3390/en18154018
Chicago/Turabian StyleXu, Kang, Zhaopeng Liu, and Shuaihu Li. 2025. "A Multi-Objective Decision-Making Method for Optimal Scheduling Operating Points in Integrated Main-Distribution Networks with Static Security Region Constraints" Energies 18, no. 15: 4018. https://doi.org/10.3390/en18154018
APA StyleXu, K., Liu, Z., & Li, S. (2025). A Multi-Objective Decision-Making Method for Optimal Scheduling Operating Points in Integrated Main-Distribution Networks with Static Security Region Constraints. Energies, 18(15), 4018. https://doi.org/10.3390/en18154018






