Power Transformer Short-Circuit Force Calculation Using Three and Two-Dimensional Finite-Element Analysis
Abstract
1. Introduction
- While previous studies have primarily employed 2D and 3D finite element models to analyze short-circuit forces in small transformers, this study focuses on large power transformers, which have significantly different structures and operating conditions.
- This research systematically calculates and analyzes short-circuit forces in large transformers, contributing to enhanced design reliability and operational safety in transmission and distribution networks.
- This study presents a novel investigation into the differences in short-circuit forces inside and outside the winding, as well as the effects of winding displacement. These insights offer a new perspective for optimizing the design of large power transformers.
2. Calculation of Electromechanical Field
2.1. Maxwell’s Equations and Boundary Conditions
2.2. Short-Circuit Current
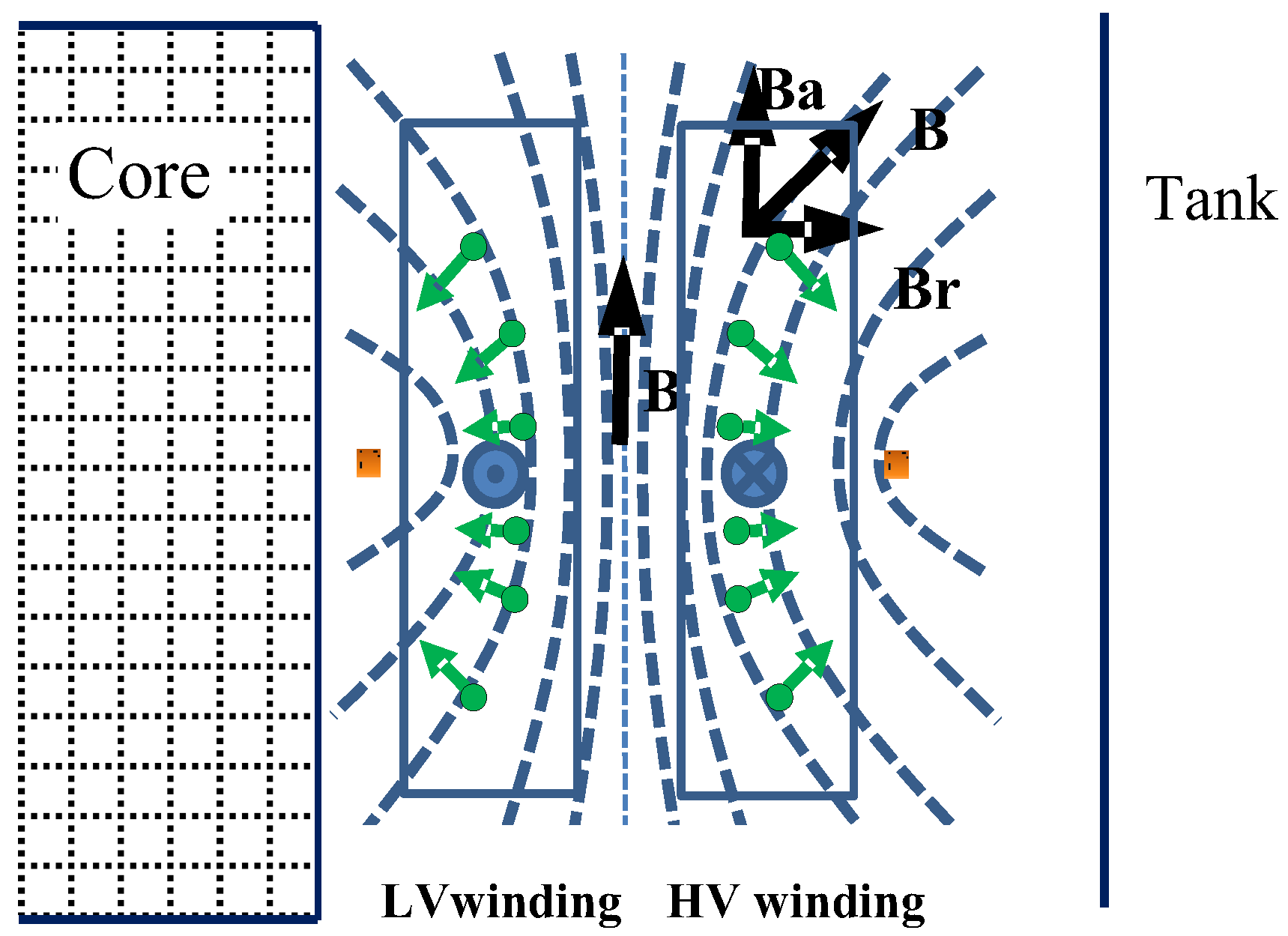
2.3. The Density of Leakage Magnetic Flux and Short-Circuit Force
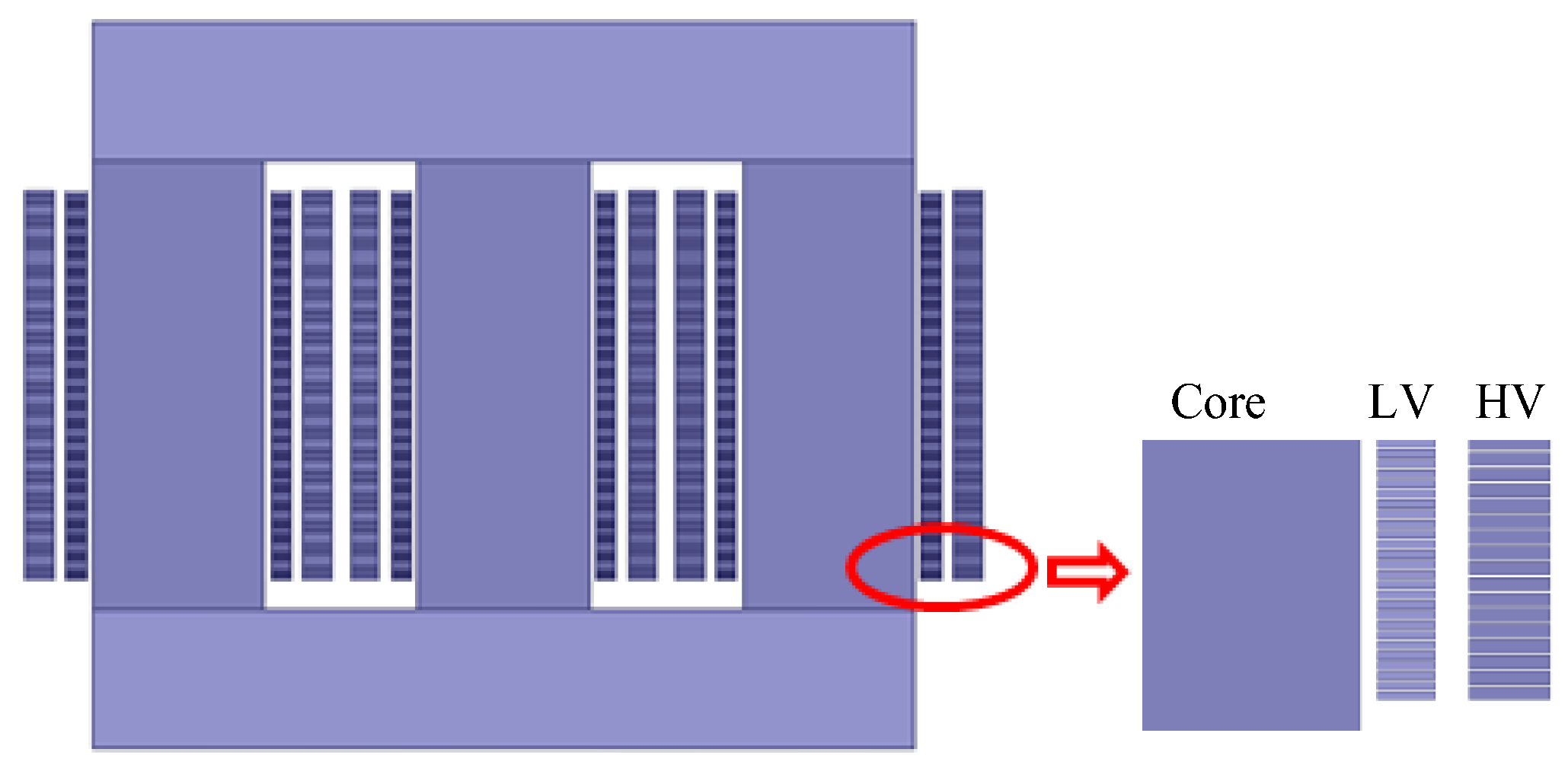
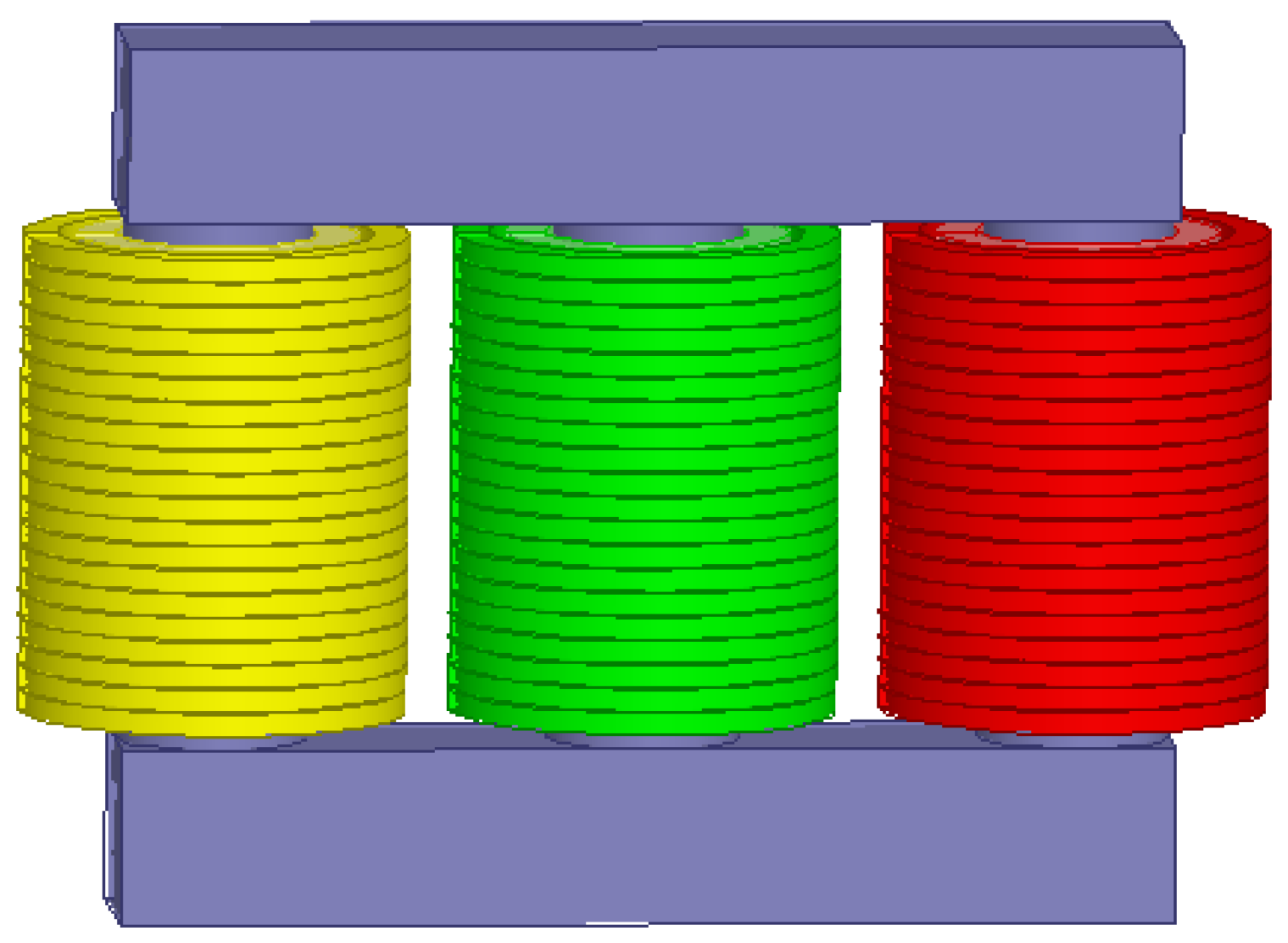
3. Transformer Model
4. Results and Discussion
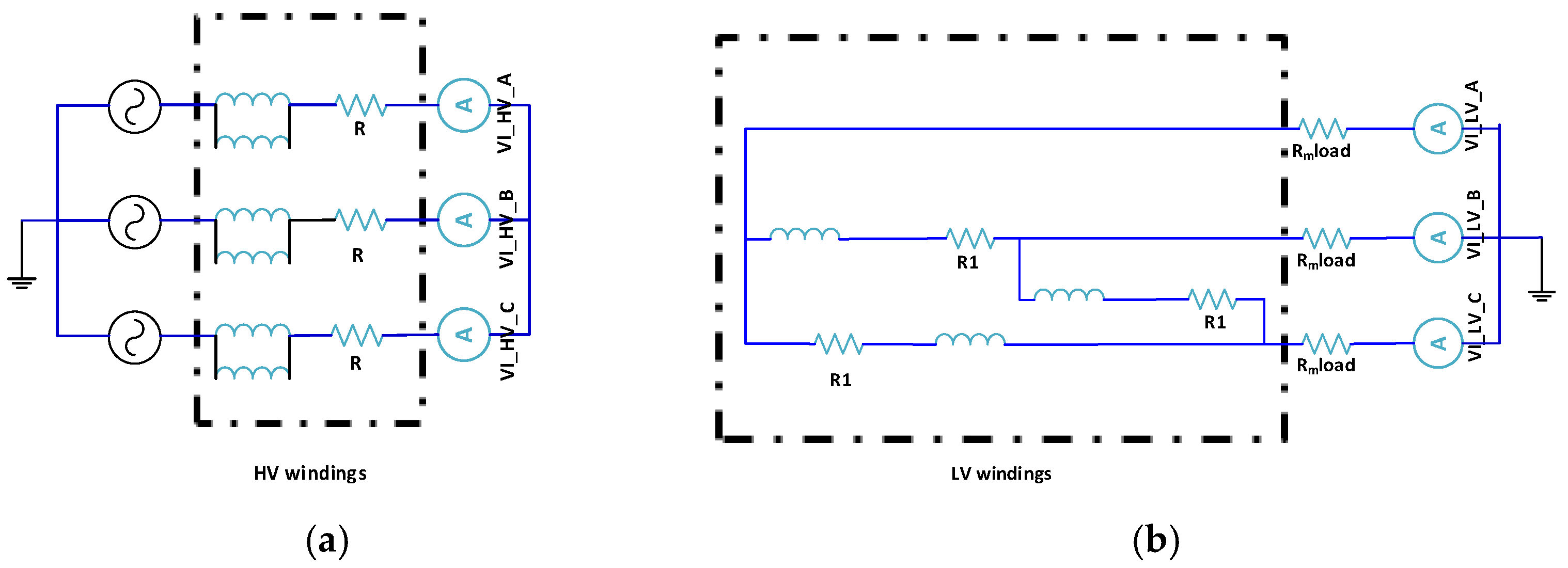
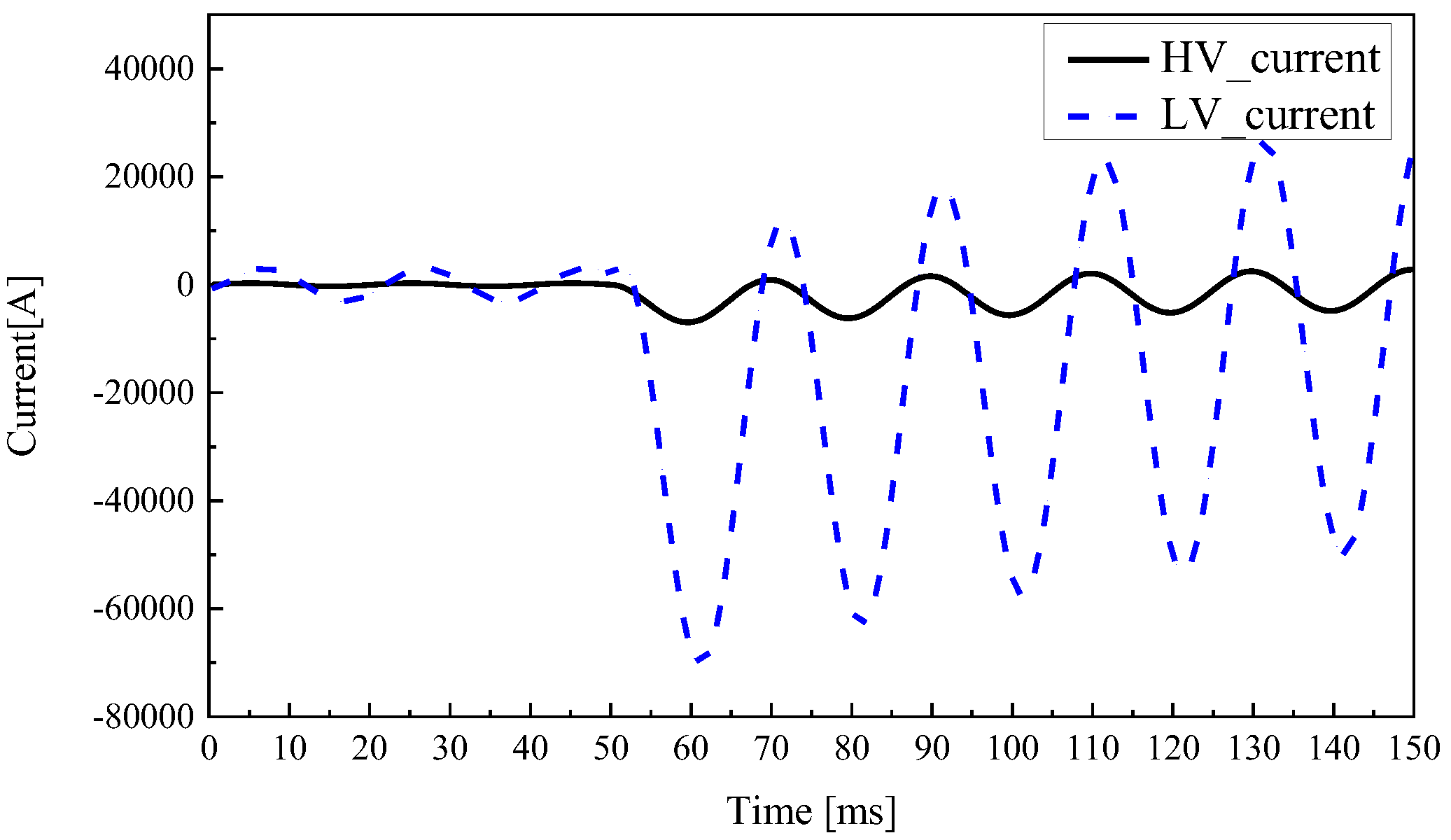
4.1. Short-Circuit Current of Three-Phase Transformer
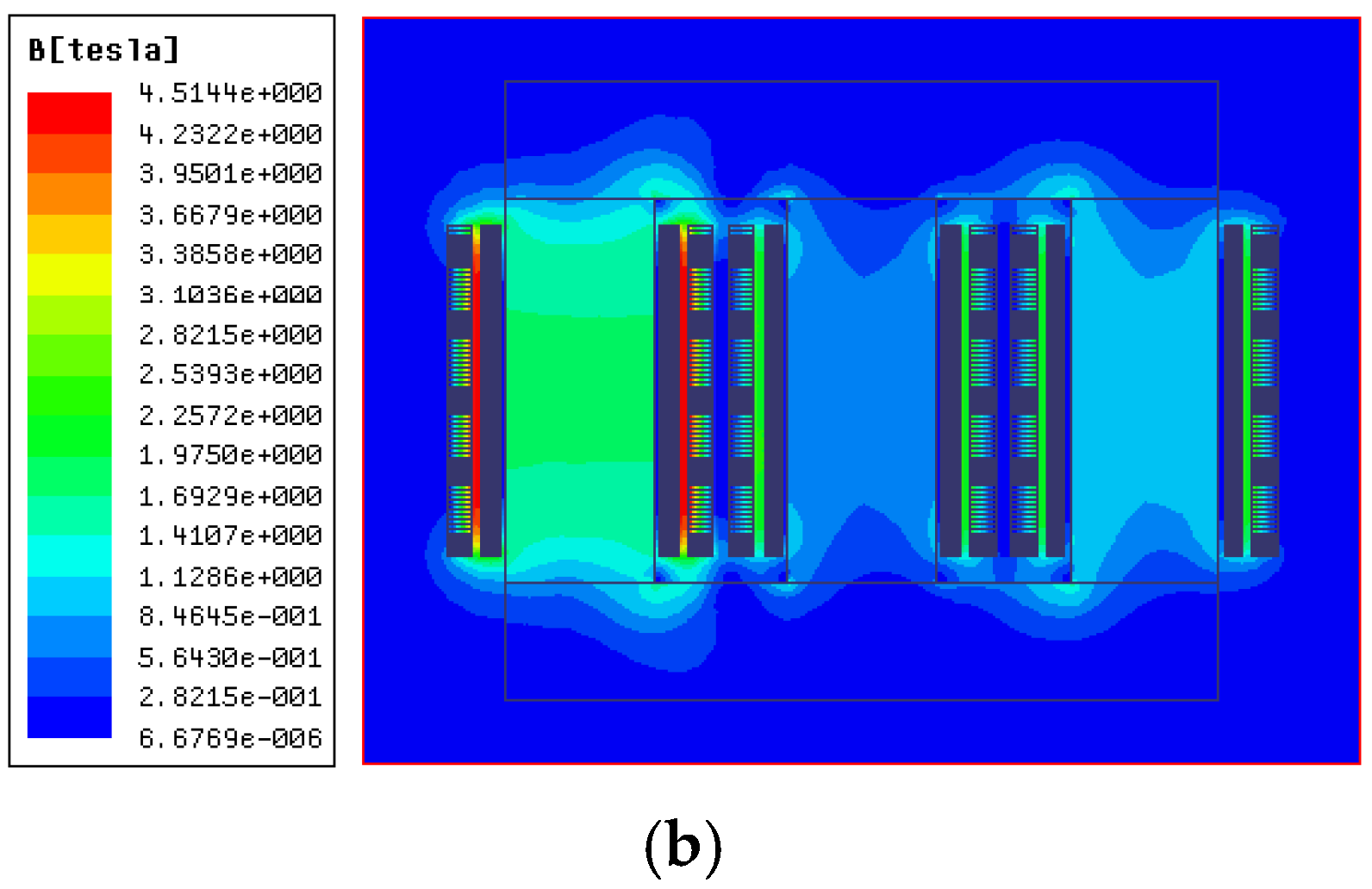
4.2. Magnetic Flux Density
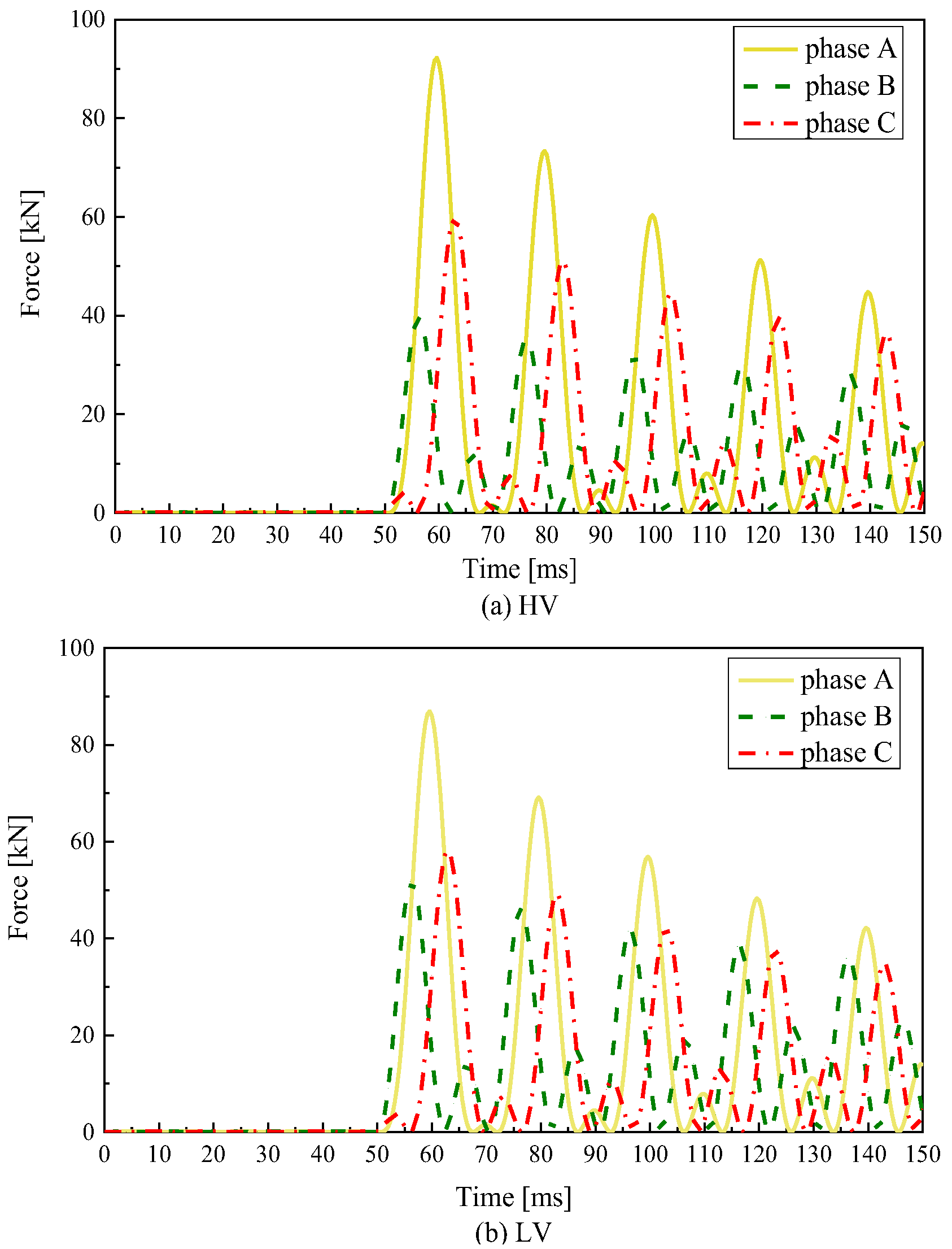
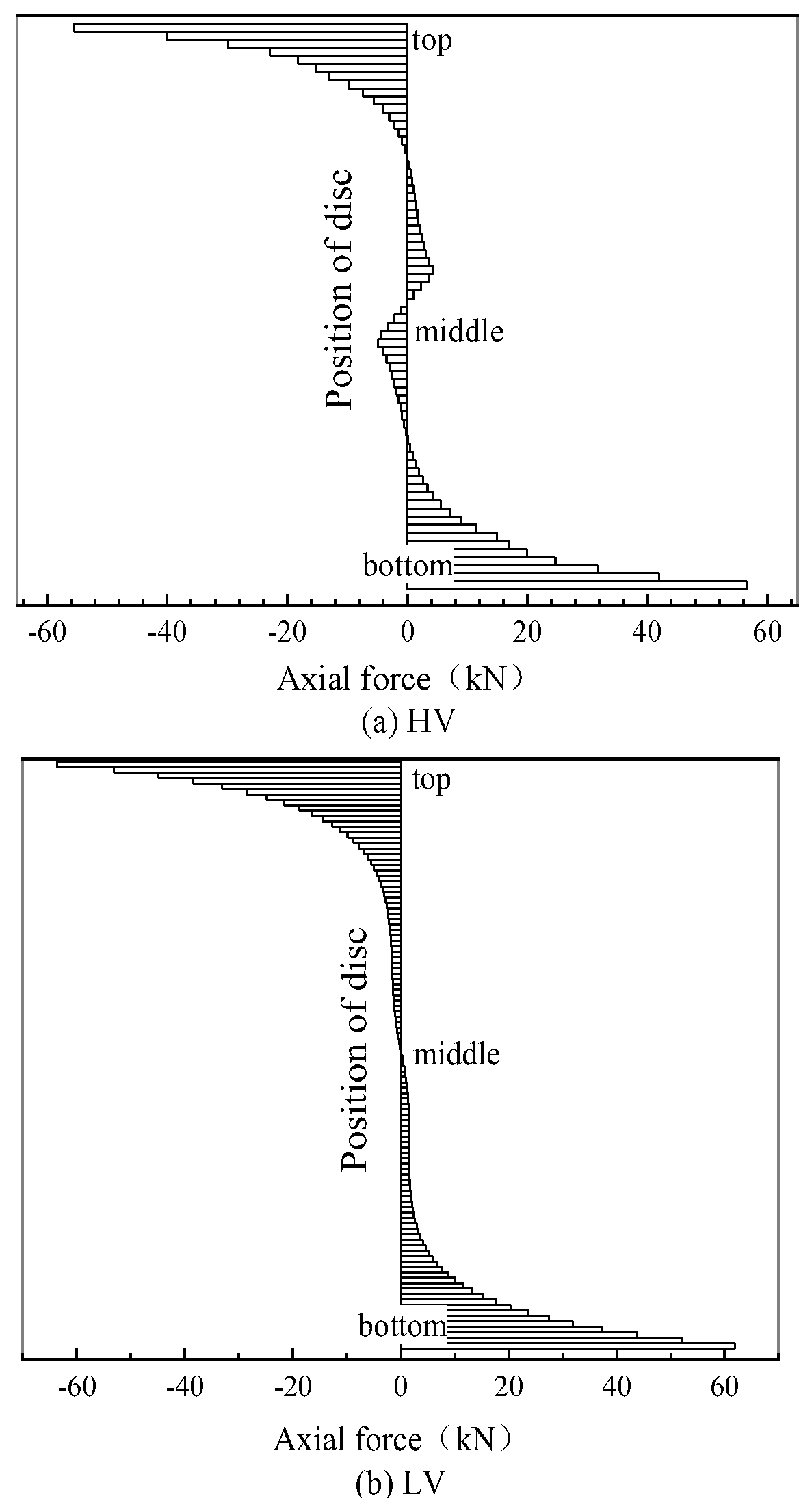
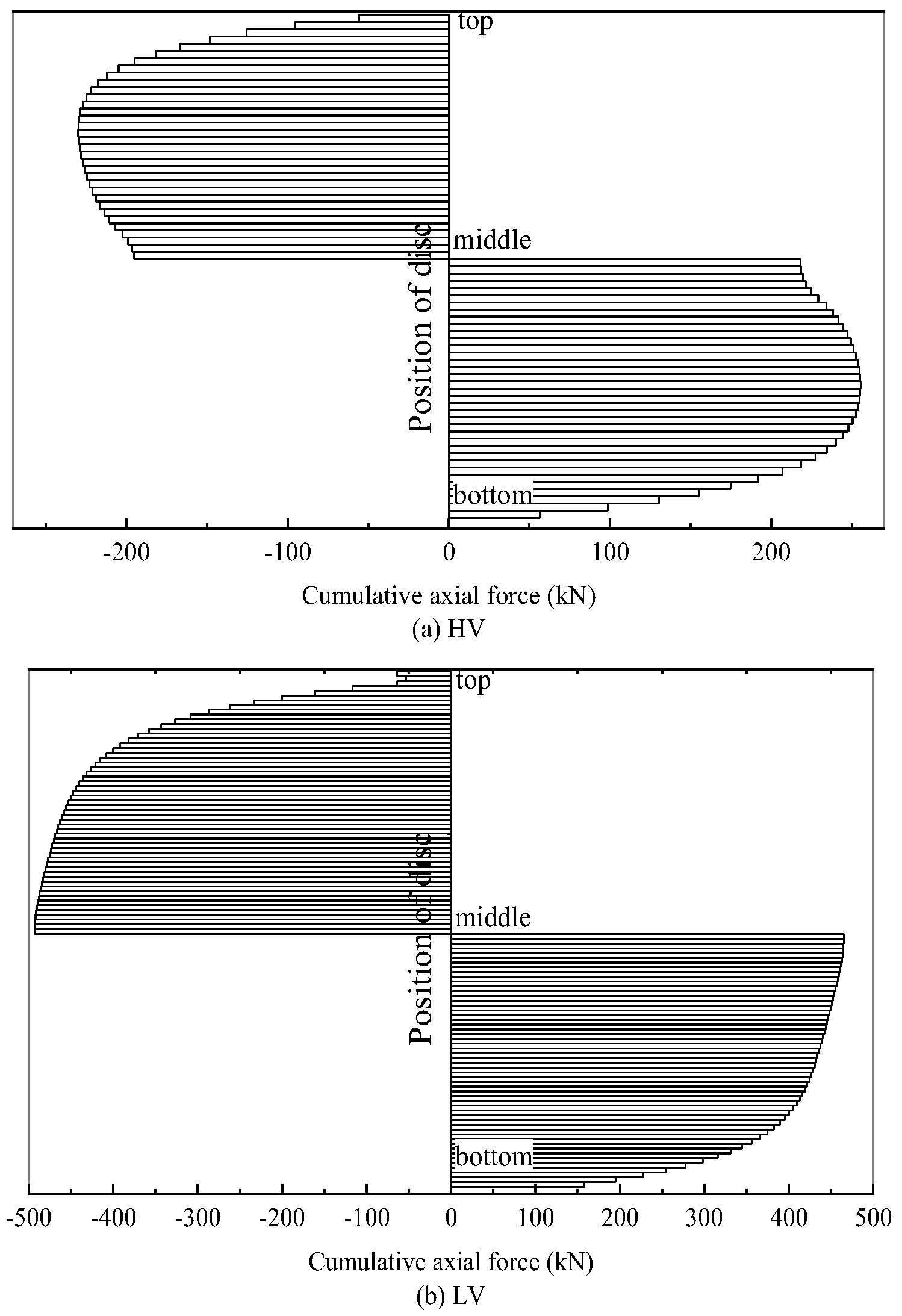
4.3. Electromagnetic Force
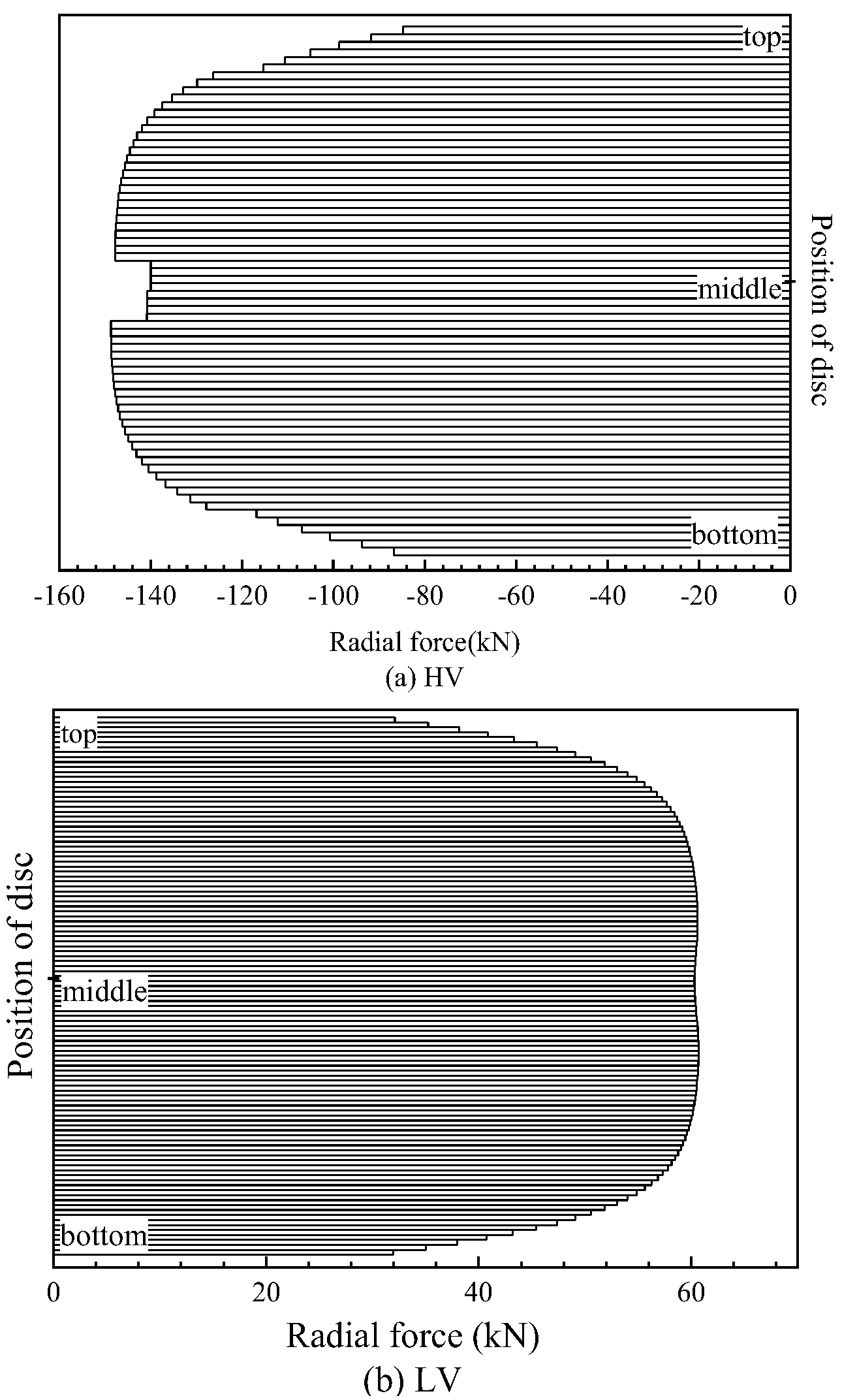
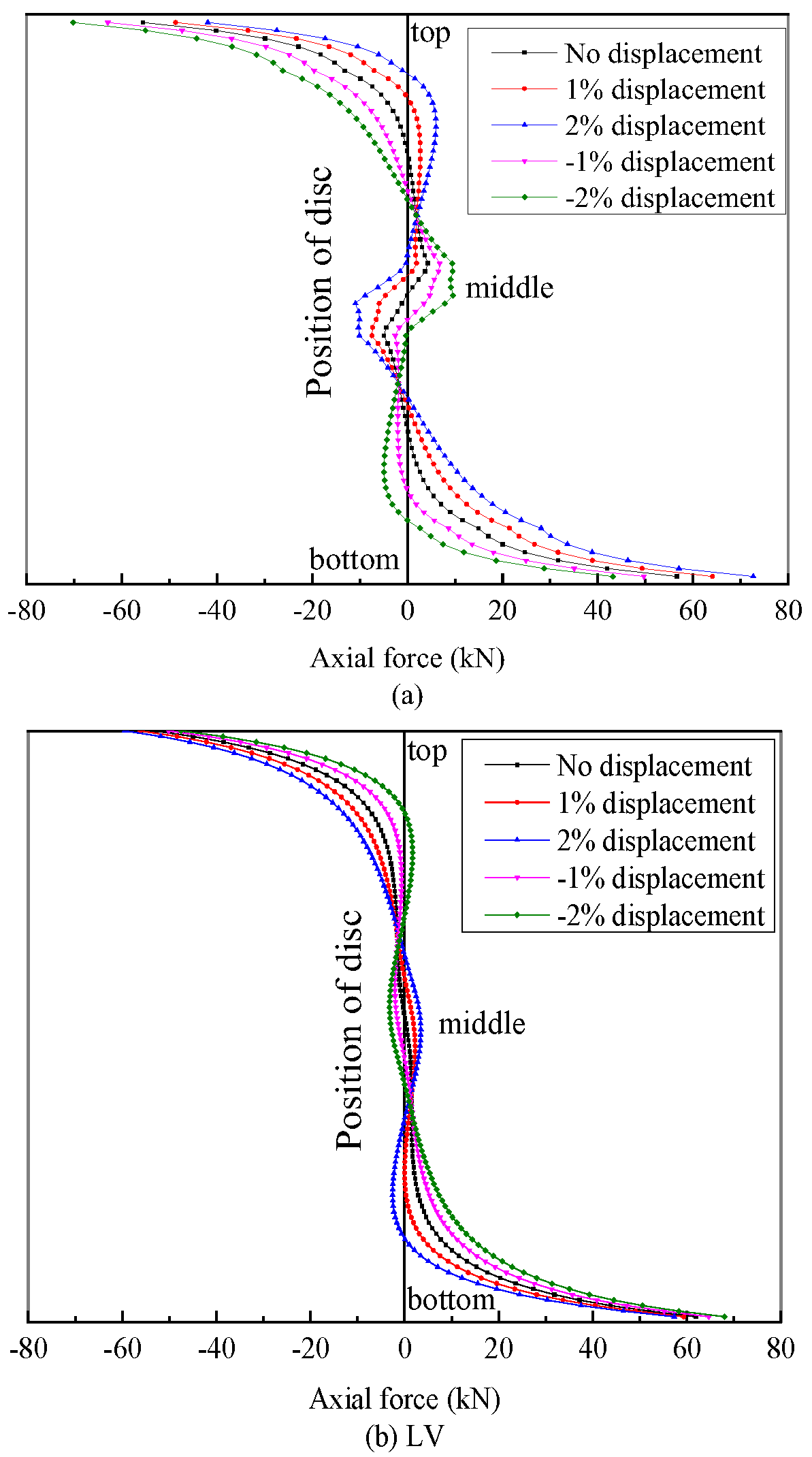
4.4. Winding Displacement
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hameed, K.R.; Suraiji, A.L.; Hanfesh, A.O. Comparative the effect of distribution transformer coil shape on electromagnetic forces and their distribution using the fem. Open Eng. 2024, 14, 20220503. [Google Scholar] [CrossRef]
- Dawood, K.; Komurgoz, G.; Isik, F. Investigating the effect of axial displacement of transformer winding on the electromagnetic forces. In Proceedings of the 2020 7th International Conference on Electrical and Electronics Engineering (ICEEE), Antalya, Turkey, 14–16 April 2020; IEEE: Los Alamitos, CA, USA; pp. 360–364. [Google Scholar]
- Bigdeli, M.; Azizian, D.; Gharehpetian, G.B. Detection of probability of occurrence, type and severity of faults in transformer using frequency response analysis based numerical indices. Measurement 2021, 168, 108322. [Google Scholar] [CrossRef]
- Andrade, A.F.; Costa, E.G.; Souza, J.P.; Andrade, F.L.; Araujo, J.F. Evaluation of computational models for electromagnetic force calculation in transformer windings using finite-element method. Int. J. Electr. Power Energy Syst. 2024, 156, 109744. [Google Scholar] [CrossRef]
- Dawood, K.; Komurgoz, G.; Isik, F. Computation of the axial and radial forces in the windings of the power transformer. In Proceedings of the 2019 4th International Conference on Power Electronics and their Applications (ICPEA), Elazig, Turkey, 25–27 September 2019; IEEE: Los Alamitos, CA, USA; pp. 1–6. [Google Scholar]
- Rao, T.M.; Mitra, S.; Pramanik, S. A novel estimation methodology for multi-resonance equivalent inductance of transformer winding for inter-turn short-circuit fault detection. Electr. Power Syst. Res. 2024, 231, 110359. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Moayyed, H.; Mohammadi-Ivatloo, B.; Ghareh-petian, G.B.; Aguiar, A.P. Turn-to-turn short circuit fault localization in transformer winding via image processing and deep learning method. IEEE Trans. Ind. Inform. 2022, 18, 4417–4426. [Google Scholar] [CrossRef]
- Cheng, Q.; Zhao, Z.; Tang, C.; Qian, G.; Islam, S. Diagnostic of transformer winding deformation fault types using continuous wavelet transform of pulse response. Measurement 2019, 140, 197–206. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, H.; Tang, J.; Zhang, W.; Zang, T.; Xiao, X. Fault location based on voltage measurement at secondary side of low-voltage transformer in distribution network. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Akhmetov, Y.; Nurmanova, V.; Bagheri, M.; Zollanvari, A.; Gharehpetian, G.B. A new diagnostic technique for reliable decision-making on transformer fra data in interturn short-circuit condition. IEEE Trans. Ind. Inform. 2021, 17, 3020–3031. [Google Scholar] [CrossRef]
- Ahmadzadeh-Shooshtari, B.; Rezaei-Zare, A. Advanced transformer differential protection under gic conditions. IEEE Trans. Power Deliv. 2022, 37, 1433–1444. [Google Scholar] [CrossRef]
- IEC 60076-5:2006; Power Transformers—Part 5: Ability to Withstand Short-Circuit. International Electrotechnical Commission: Geneva, Switzerland, 2006.
- IEEE C57.164-2021; IEEE Guide for Establishing Short-Circuit Withstand Capabilities of Liquid-Filled Power Transformers, Regulators, and Reac-tors. IEEE Power and Energy Society: Piscataway, NJ, USA, 2021.
- Hashemnia, N.; Abu-Siada, A.; Islam, S. Improved Power Transformer Winding Fault Detection using FRA Diagnostics—Part 1: Axial Displacement Simulation. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 556–563. [Google Scholar] [CrossRef]
- Hashemnia, N.; Abu-Siada, A.; Islam, S. Improved Power Transformer Winding Fault Detection using FRA Diagnostics—Part 2: Radial Deformation Simulation. IEEE Trans. Dielectr. Electr. Insul. 2015, 22, 564–570. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, W.; Jin, M.; Wen, T.; Xue, J.; Zhang, Q.; Chen, M. Short-circuit electromagnetic force distribution characteristics in transformer winding transposition structures. IEEE Trans. Magn. 2020, 56, 1–8. [Google Scholar] [CrossRef]
- Tarimoradi, H.; Karami, H.; Gharehpetian, G.B.; Tenbohlen, S. Sensitivity analysis of different components of transfer function for detection and classification of type, location and extent of transformer faults. Measurement 2022, 187, 110292. [Google Scholar] [CrossRef]
- Dawood, K.; Komurgoz, G.; Isik, F. Effect of tapping position on the electromagnetic forces of the tap-winding transformer. J. Electr. Eng. Technol. 2024, 19, 1–12. [Google Scholar] [CrossRef]
- Yang, W.; Pan, Y.; Qiu, Z.; Zhai, G. Electromagnetic transient model and field-circuit coupling numerical calculation of sen transformer based 25 on finite-element method. Electr. Power Syst. Res. 2023, 214, 108941. [Google Scholar] [CrossRef]
- Dawood, K.; Tursun, S.; Kömürgöz, G. Optimized gap positions for improved electromagnetic forces in dry-type transformer design. In Proceedings of the 2024 6th Global Power, Energy and Communication Conference (GPECOM), Budapest, Hungary, 4–7 June 2024; IEEE: Los Alamitos, CA, USA; pp. 211–215. [Google Scholar]
- Ahn, H.-M.; Oh, Y.-H.; Kim, J.-K.; Song, J.-S.; Hahn, S.-C. Experimental verification and finite element analysis of short-circuit electromagnetic force for dry-type transformer. IEEE Trans. Magn. 2012, 48, 819–822. [Google Scholar] [CrossRef]
- Jin, M.; Chen, W.; Zhao, Y.; Wen, T.; Wu, J.; Wu, X.; Zhang, Q. Coupled magnetic-structural modeling of power transformer for axial vibration analysis under short-circuit condition. IEEE Trans. Magn. 2022, 58, 1–9. [Google Scholar] [CrossRef]
- Salon, S.; LaMattina, B.; Sivasubramaniam, K. Comparison of assumptions in computation of short circuit forces in transformers. IEEE Trans. Magn. 2000, 36, 3521–3523. [Google Scholar] [CrossRef]
- Faiz, J.; Ebrahimi, B.M.; Noori, T. Three and two-dimensional finite-element computation of inrush current and short-circuit electromagnetic forces on windings of a three-phase core-type power transformer. IEEE Trans. Magn. 2008, 44, 590–597. [Google Scholar] [CrossRef]
- Liu, J.; Chen, S.; Wang, F.; Zhu, D.; Xu, K.; Chen, P. Theoretical Evaluation of Transformer Short-Circuit Withstand Capability and Identification Method of Winding Cumulative Deformation. IEEE Trans. Power Deliv. 2025, 1–12. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Yu, Z.; Li, P.; Xu, Z. A methodology to evaluate the radial bending stress of transformer inner windings based on the turn-to-turn model. IEEE Trans. Appl. Supercond. 2024, 34, 1–4. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Yu, Z.; Miao, Y.; Li, P.; Xu, Z. Analysis method of transformer fatigue life and damage under multiple short-circuit conditions. IEEE Trans. Appl. Supercond. 2024, 34, 1–4. [Google Scholar] [CrossRef]
- Ou, Q.; Luo, L.; Li, Y.; Han, R.; Peng, Y. An Improved Radial Buckling Analysis Method and Test Investigation for Power Transformer Under Short Circuit Impact. IEEE Trans. Power Deliv. 2023, 38, 2854–2863. [Google Scholar] [CrossRef]
- Ibrahima, S. Electromagnetic Waves 1: Maxwell’s Equations, Wave Propagation; Wiley: Hoboken, NJ, USA, 2020; p. 26. [Google Scholar]
- Hewitt, D.A.; Sundeep, S.; Wang, J.; Griffo, A. High frequency modeling of electric machines using finite element analysis derived data. IEEE Trans. Ind. Electron. 2024, 71, 1432–1442. [Google Scholar] [CrossRef]
- John, C.; Aaron, C. Transformer protection, in: Power System Protection: Fundamentals and Applications; IEEE: Los Alamitos, CA, USA, 2022; pp. 185–235. [Google Scholar]
- Li, Y.; Xu, Q.; Lu, Y. Electromagnetic force analysis of a power transformer under the short-circuit condition. IEEE Trans. Appl. Supercond. 2021, 31, 1–3. [Google Scholar] [CrossRef]
- Adly, A. Computation of inrush current forces on transformer windings. IEEE Trans. Magn. 2001, 37, 2855–2857. [Google Scholar] [CrossRef]
- Mikhak-Beyranvand, M.; Rezaeealam, B.; Faiz, J.; Rezaei-Zare, A. Impacts of ferroresonance and inrush current forces on transformer windings. IET Electr. Power Appl. 2019, 13, 914–921. [Google Scholar] [CrossRef]
- Xian, R.; Wang, L.; Zhang, B.; Li, J.; Xian, R.; Li, J. Identification method of interturn short circuit fault for distribution transformer based on power loss variation. IEEE Trans. Ind. Inform. 2024, 20, 2444–2454. [Google Scholar] [CrossRef]
- Wang, S.; Wang, S.; Zhang, N.; Yuan, D.; Qiu, H. Calculation and analysis of mechanical characteristics of transformer windings under short-circuit condition. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Cardenas-Cornejo, J.-J.; Ibarra-Manzano, M.-A.; Gonz’alez-Parada, A.; Castro-Sanchez, R.; Almanza-Ojeda, D.-L. Classification of inter-turn short-circuit faults in induction motors based on quaternion analysis. Measurement 2023, 222, 113680. [Google Scholar] [CrossRef]
- MacLeman, C. Transformer and Inductor Design Handbook; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Li, L.; Liu, X.; Zhu, G.; Chen, H.; Gao, S. Research of short-circuit performance of a split-winding transformer with stabilizing windings. IEEE Trans. Appl. Supercond. 2019, 29, 1–6. [Google Scholar] [CrossRef]
- Jurkovi’c, M.; ˇZarko, D. Calculation of current distribution in parallel-connected transformer winding sections in the case of asymmetric magnetic field during short-circuit test. Electr. Power Syst. Res. 2022, 210, 108141. [Google Scholar] [CrossRef]
- Mejia-Barron, A.; Valtierra-Rodriguez, M.; Granados-Lieberman, D.; Olivares-Galvan, J.C.; Escarela-Perez, R. The application of emdbased methods for diagnosis of winding faults in a transformer using transient and steady state currents. Measurement 2018, 117, 371–379. [Google Scholar] [CrossRef]
- Zhao, X.; Wu, G.; Yang, D.; Xu, G.; Xing, Y.; Yao, C.; Abu-Siada, A. Enhanced detection of power transformer winding faults through 3D FRA signatures and image processing techniques. Electr. Power Syst. Res. 2025, 242, 111433. [Google Scholar] [CrossRef]




| Classification | Quantify |
|---|---|
| Phase | Three |
| Structure | Core type |
| Frequency [Hz] | 50 |
| Rated Power [MVA] | 40 |
| Winding configuration | YN, dll |
| Primary/secondary turns [Turn] | 200/1200 |
| Voltage rating [kV] | 110/10.5 |
| Current rating [A] | 209.95/1269.84 |
| Distance of 1st/2nd row taps to yoke [mm] | 187/226 |
| Distance of HV/LV winding to upper yoke [mm] | 106/75 |
| Distance of HV/LV winding to lower yoke [mm] | 86/55 |
| Core cross-section diameter [mm] | 560 |
| Insulated core cross-section diameter [mm] | 579 |
| Inner diameter of HV/LV winding/taps [mm] | 826/613/1071 |
| Mineral Oil | Value |
|---|---|
| Dielectric Breakdown [kV] | 30/85 |
| Relative Permittivity at 25 °C | 2.1/2.5 |
| Viscosity at 0, 40, 100 C [mm2·s−1] | <76, 3/16, 2/2.5 |
| Pour Flash Fire Point [°C] | −30/−60, 100/170, 110/185 |
| Density at 20 °C [kg·m3] | 0.83/0.89 |
| Thermal Conductivity [W.m−1·K−1] | 0.11/0.16 |
| Expansion Coefficient [10−4·K−1] | 7/9 |
| Electrical Conductivity [S·m−1] | 1.5 × 10−10 |
| Kraft Paper | Value |
| Relative Permittivity at 25 °C | 4.4 |
| Electrical Conductivity [S· m−1] | 24 × 10−15 |
| Parameters | HV | LV | |
|---|---|---|---|
| Ls [µH] | 10 | 10.5 | |
| Rs [Ω] | 1 | 0.25 | |
| Csw [pF] | 393.4 | 127.67 | |
| Gsw [µS] | 196.7 | 63.835 | |
| Co [pF] | 61.192 | 115.53 | |
| Co [µS] | 30.596 | 57.765 | |
| CHL [pF] | 89.283 | ||
| GµS [µS] | 44.65 |
| HV Winding (A) | LV Winding (A) | |
|---|---|---|
| Analysis data | 6963.43 | 70,411.12 |
| Numerical data | 6971.76 | 70,269.87 |
| HV Winding (A) | LV Winding (A) | |||
|---|---|---|---|---|
| Edges | Middle | Edges | Middle | |
| Axial force (kN) | 56.050 | 0.063 | 62.805 | 0.096 |
| Radial force (kN) | 85.688 | 140.735 | 32.022 | 60.312 |
| Total force (kN) | 102.391 | 140.735 | 70.498 | 60.313 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; He, J.; Chen, X.; Tian, T.; Yao, C.; Abu-Siada, A. Power Transformer Short-Circuit Force Calculation Using Three and Two-Dimensional Finite-Element Analysis. Energies 2025, 18, 3898. https://doi.org/10.3390/en18153898
Wang J, He J, Chen X, Tian T, Yao C, Abu-Siada A. Power Transformer Short-Circuit Force Calculation Using Three and Two-Dimensional Finite-Element Analysis. Energies. 2025; 18(15):3898. https://doi.org/10.3390/en18153898
Chicago/Turabian StyleWang, Jian, Junchi He, Xiaohan Chen, Tian Tian, Chenguo Yao, and Ahmed Abu-Siada. 2025. "Power Transformer Short-Circuit Force Calculation Using Three and Two-Dimensional Finite-Element Analysis" Energies 18, no. 15: 3898. https://doi.org/10.3390/en18153898
APA StyleWang, J., He, J., Chen, X., Tian, T., Yao, C., & Abu-Siada, A. (2025). Power Transformer Short-Circuit Force Calculation Using Three and Two-Dimensional Finite-Element Analysis. Energies, 18(15), 3898. https://doi.org/10.3390/en18153898







