Abstract
Precise evaluation of risk and reliability is crucial for decision making and predicting the outcome of investment in a photovoltaic power system (PVPS) due to its intermittent source. This paper explores different methodologies for risk evaluation and reliability assessment, which can be categorized into qualitative, quantitative, and hybrid qualitative and quantitative (HQQ) approaches. Qualitative methods include failure mode analysis, graphical analysis, and hazard analysis, while quantitative methods include analytical methods, stochastic methods, Bayes’ theorem, reliability optimization, multi-criteria analysis, and data utilization. HQQ methodology combines table-based and visual analysis methods. Currently, reliability assessment techniques such as mean time between failures (MTBF), system average interruption frequency index (SAIFI), and system average interruption duration index (SAIDI) are commonly used to predict PVPS performance. However, alternative methods such as economical metrics like the levelized cost of energy (LCOE) and net present value (NPV) can also be used. Therefore, a risk and reliability approach should be applied together to improve the accuracy of predicting significant aspects in the photovoltaic industry.
1. Introduction
Solar power generation expected to be the largest source of low-carbon capacity by 2040, with 40% of total power expected to be generated by renewable energy sources [1]. The photovoltaic (PV) system is a popular choice as one of the clean energy sources because it does not produce any greenhouse gases during power generation. Solar photovoltaic systems are admired for being noiseless, low maintenance, and emitting no greenhouse gases in their operational phase because the clean energy came from the sun’s irradiation [2].
The major concern regarding solar photovoltaic power generation is the source intermittence [3] and complex nature of PV systems [4]. Therefore, precise risk and reliability assessment are important to evaluate the optimum generation output and for risk-informed decision-making purposes [5]. The source intermittence is not only caused by solar irradiation and cell temperature [6] but includes weather condition at a particular location. Reliability is defined as the probability that a system will accomplish its required function without failure for a specified time interval under specified operating conditions [7]. It also includes the probability and capability of the parts, components, products, and systems to accomplish their required functions in specified environments for the desired period of operation without failure [8].
Reliability failure can be seen as an intense failure that obviously leads to the deprivation of the photovoltaic devices before the warranty threshold. The risk is defined as the effect of uncertainty and any such uncertainty can have positive or negative effects [9]. Hence, assessing the risk and reliability of a PV (photovoltaic) system is crucial, as it has a significant impact on investments. The objective of this paper is to examine and deliberate on the analysis of risk and reliability in the PV sector and classify it into three categories: qualitative, quantitative, and hybrid.
The objective of this paper is to provide a comprehensive review and systematic classification of methodologies employed in the risk evaluation and reliability assessment of photovoltaic (PV) power generation systems. Considering the inherent intermittency and uncertainty associated with solar energy, this review aims to identify effective analytical strategies that support both performance assurance and informed investment decision making. To this end, the study is guided by the following research questions:
- RQ1: What are the principal qualitative, quantitative, and hybrid methodologies utilized in assessing risk and reliability in PV systems?
- RQ2: In what ways have these methodologies been implemented within practical, real-world PV power generation applications?
- RQ3: Which technical and financial performance indicators are most frequently applied in the evaluation of risk and reliability for PV systems?
The structure of this paper is as follows: Section 2 presents the background and outlines key challenges associated with the reliability of photovoltaic (PV) systems. Section 3 describes the principal methodologies for risk and reliability assessment, categorized into qualitative, quantitative, and hybrid approaches. Section 4 explores the practical implementation of these methodologies in real-world PV applications. Section 5 reviews the technical and economic performance indicators commonly employed to evaluate PV system reliability and viability. Section 6 discusses the key findings and insights derived from the analysis, and Section 7 concludes the paper with a summary and recommendations for the integration of comprehensive risk and reliability frameworks in PV power generation systems.
2. Background of the Research
Photovoltaic (PV) power generation has become one of the leading renewable energy technologies, attributed to its low environmental footprint and widespread resource availability [1,2]. Despite its global proliferation, the reliability and risk challenges associated with PV systems remain critical concerns [3,4]. Due to their reliance on solar irradiance and meteorological conditions, PV systems inherently exhibit intermittent behavior, resulting in variable power output that necessitates careful management in both grid-connected and standalone configurations [6,10].
To address these challenges, a range of methodologies has been developed to evaluate and mitigate risk in PV systems. These include qualitative techniques such as failure mode and effects analysis (FMEA) [11,12,13], and hazard and operability study (HAZOP) [14,15,16,17], as well as quantitative methods including Monte Carlo simulation (MCS) [18,19], Bayesian networks (BBN) [20], and reliability block diagrams (RBD) [21,22]. Recent literature highlights a growing emphasis on hybrid approaches, which integrate qualitative and quantitative techniques to better capture the complex, real-world behavior of PV systems [20,23,24,25].
Beyond equipment-level risks, systemic inefficiencies are increasingly recognized as a barrier to PV system optimization—particularly in high-penetration markets such as the European Union. Grid saturation during peak solar generation hours has led to the curtailment of available energy, where surplus clean energy is discarded due to infrastructure, storage, or regulatory constraints. This curtailment not only undermines the environmental benefits of solar deployment but also introduces financial inefficiencies. Without adequate demand-side management and flexible grid infrastructure, the risk of energy waste may rise in parallel with continued PV expansion [10,26,27].
These emerging issues underscore the necessity for comprehensive risk and reliability assessment frameworks that extend beyond component failure analysis to encompass broader operational and policy-level considerations. Integrating such macro-level factors enhances the predictive capacity of reliability models and supports more resilient and sustainable planning for PV infrastructure [3,4,10].
Building on this context, the present study aims to systematically classify existing risk and reliability assessment methodologies and evaluate their applicability to PV power generation. The objective is to identify the most effective strategies for supporting data-driven investment decisions and optimizing long-term performance in both mature and developing solar energy markets.
3. Risk and Reliability Methods
The risk and reliability analysis can be executed towards components, systems or process [28] through the methodology of qualitative, quantitative or combination of both [29]. Risk and reliability analysis could be a useful systematic assessment of uncertainties and their impact, providing useful information for decisions making process input. Many methods of risk and reliability exist; nevertheless, not every technique is suitable [30] to be implemented in evaluating the PV power systems. The risk and reliability analysis may improve the quality of the components and system by minimizing the failure cost [31].
3.1. Qualitative Methodology
The qualitative methodology using subjective and criteria-based evaluation. This includes failure mode analysis, graphical analysis, and hazard analysis. A variety of failure modes depending on the weather condition, system design, topology type, and electrical tuning. Failure mode analysis includes FMEA [11] where the likelihood of detection and severity of failure effect is decided by design control and normally used as a failure-preventive approach. Diverse sources can give rise to failure modes that can affect photovoltaic devices in various ways. The purpose of conducting a failure mode analysis is to appraise the likelihood of system function or equipment failure and determine measures to reduce the associated risks. FMEA is applicable in numerous industries, including military, aerospace, automotive, medical, electronics, and software. Normally, FMEA is tailored specifically to the respective industry in which it is being used [12]. The indicator represented in the FMEA is the risk priority number (RPN) as in Equation (1).
The risk priority number (RPN) is a risk ranking metric and the input variables based on DOS (likelihood of detection (D), probability of occurrence (O), and severity of effects (S)) to determine the priority ranking of risks in the FMEA approach. The RPN provides insights into the primary risk and its level of impact on the product. A higher RPN indicates a greater degree of effect or risk on the product. Regarding likelihood (D), conducting an assessment to determine the probability of potential defects is recommended to reduce the uncertainty of the collected data and outcomes [32].
Some criticism of RPN metric is that sometimes a similar RPN value shows difference root causes and different failure effects and it is difficult to make a prioritization [33]. RPN ambiguity could be addressed by the fuzzy-based analysis, grey theory, and cost-based analysis [34]. Furthermore, the DOS variables can be replaced by cost-based analysis with two ratio scales for probability of failure and cost of failure to address the ambiguity of the RPN prioritization metric [35]. It is also possible to add cost-based analysis to DOS to solve the ambiguity issues of the RPN and give a clear insight into the impact.
The RPN deployment method can be used to rate the severity of failure modes, with the most highly ranked RPN representing the worst possible failure scenario. By identifying major failure modes that are associated with specific weather conditions or system designs, PV plant developers can improve module designs to better withstand those particular failure modes. FMEA analysis provides useful insights into the performance of individual system elements and devices.
Newer versions of FMEAs have been developed, including DFMEA (design FMEA) and PFMEA (process FMEA). DFMEA is used during the initial design phase of a product and focuses on identifying potential design failures. On the other hand, PFMEA is used during the manufacturing process and concentrates on detecting any possible defects that may occur during production [12]
Some available commercial software includes Reliasoft XFMEA Version 2, Isograph Reliability Workbench 10.1 and Relex Reliability Studio 2007 V2. The use of FMEA enables the identification and assessment of the impact of each failure mode and the factors that cause them. In the case of manufacturers, the most significant failure modes typically result from design or manufacturing errors. Consequently, the production of a dependable photovoltaic product could result in fewer warranty claims [13].
Another way in which failures can occur is through the analysis of hazards, including hazard identification, risk assessment, and risk control (HIRARC), as well as hazard and operability studies (HAZOP). These two analyses focus on safety risks. The HAZOP procedure involves an investigation into all potential ways in which deviations from normal operation may occur. Subsequent inquiries aim to identify the most effective defensive measures, taking into account any necessary modifications to operating procedures or designs [14]. HAZOP is achieved by the efforts of a dedicated HAZOP team that produces documented recommendations [15]. The HAZOP study objective is to comprehensively document the hazard causes and consequences of the operation deviations and devise recommended actions [16]. HAZOP is considered to be a beneficial approach for hazard identification, as it can help to increase safety, prevent accidents, and improve system reliability [17].
The HIRARC model presents a comprehensive series of steps for identifying hazards, evaluating risks, and making informed decisions regarding control measures to ensure safety and health in operational settings [36]. The HIRARC analysis consists of hazard identification, risk assessment, and determination of risk rating [37].
Firstly, hazard identification is based on hazard during the operation of the specific process, production, function, etc. Next is the risk assessment phase, which is based on the likelihood of risk occurrence and severity of the risk. This risk can be calculated using Equation (2).
The final step involves assessing the level of risk and identifying any risks that require immediate attention based on the risk assessment. This assessment is made using a risk assessment matrix that classifies risks as low, medium, or high. To analyze the system’s reliability graphically, a variety of tools such as a fish bone diagram, fault tree analysis (FTA), event tree analysis (ETA), and bow-tie tree analysis (BTA) are utilized. FTA predicts potential incidents that can lead to an unwanted effect or outcome by analyzing the causes of failure events and their chain reactions. In contrast to FMEA, FTA examines the sequence of events leading up to the risk event rather than individual system failures, helping to identify the root cause of the risk event [38].
An illustration of a basic fault tree analysis (FTA) is presented in Figure 1, where the top event is represented by Block T. Block T often refers to system failures or risks. Intermediate events are depicted by Blocks J and K. Basic events that typically occur are indicated by the circles, A, B, C, and E, while the diamond-shaped D is an undeveloped event. Event D is not really a basic event; the information is not sufficient [39] and an event is not further developed or does not need further resolution [12]. This type of event does not require further development due to inadequate information, low consequence, or common elements in the environment.
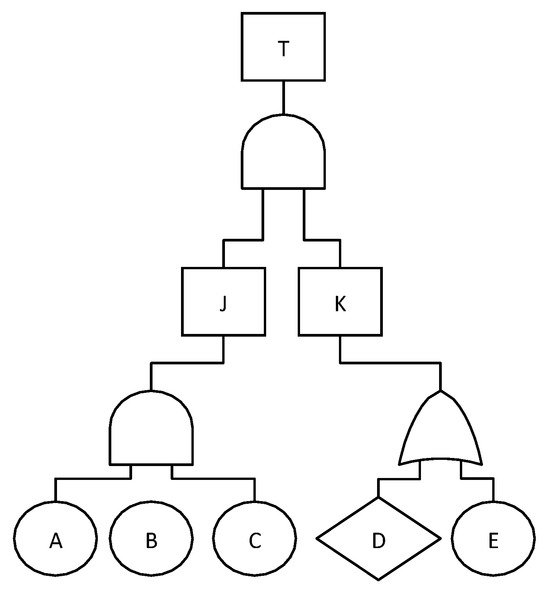
Figure 1.
Fault tree analysis (FTA).
The structure function can be simplified as follows:
ℙ(T) = ℙ(J) ∩ ℙ(K)
ℙ(T) = ℙ(A ∩ B ∩ C) ∩ ℙ(D + E)
Table 1 presents the logical breakdown of the fault tree components in Figure 1, which models the top-level failure event T using standard Boolean logic gates. Each row in the table maps a hierarchical fault event (i.e., T, J, K) to its underlying basic events and the corresponding logic gate used in the structure.

Table 1.
Logical decomposition of Fault Tree Analysis (FTA) events through Boolean expressions.
The structure function is then derived by recursive substitution of intermediate events (J and K) into the expression for T. This yields the simplified Boolean form:
ℙ(T) = ℙ((A ∩ B ∩ C) ∩ (D ∪ E))
This function defines the minimum cut set necessary for the top-level failure, identifying critical combinations of lower-level faults that propagate upward in the system failure hierarchy.
The size of the FTA structure can increase exponentially with the number of variables, making it memory-intensive to resolve large FTA structures. To overcome this challenge, a possible solution is to use a modularization algorithm that breaks down large FTA structures into smaller ones. By storing only a few FTA modules that are not cut off, this method can efficiently address the issue of high memory consumption [40]. Some studies have explored extensions to FTA, including dynamic FTA, repairable FTA, and extended FTA. Another variant is fuzzy FTA, which utilizes a multi-level state approach by introducing multiple severity levels [41].
Event tree analysis (ETA) is another visual technique to estimate the possible aftereffects of a failure, risk or an initial triggered event. Each branch of the tree consists of a chain of probable consequences from the initiating event to the next events until the outcome [38].
During development of ETA, engineering/expert judiciousness is often used to produce the potential progression of the system responses (scenarios) following an initiating events [42], and each the prompted event is positioned in a route are described as pivotal event [43] as shown in Figure 2.
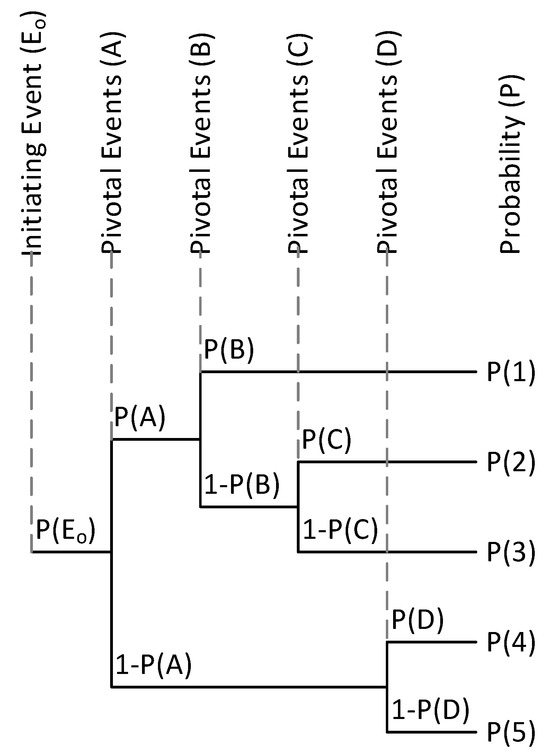
Figure 2.
Event tree analysis (ETA).
Derived from the system structure in Figure 2, the simplified probability expressions are summarized in Table 2, each representing a distinct logical scenario. Each equation represents the probability of a specific state or fault condition occurring within the system, based on combinations of basic component events under the assumption of statistical independence.

Table 2.
Logical decomposition of Event Tree Analysis (ETA) events through Boolean expressions.
Each branch of an event tree results in a specific consequence, which can be analyzed to determine its likelihood of occurring. In safety risk analysis, the events that lead to undesired consequences or failure are considered more significant than scenarios that represent normal system behavior or non-failure scenarios. Various approaches including removal of scenarios [44] are not of concern or use the grouping methods [45].
A bow-tie analysis is another visual technique used for system assessment that combines FTA and ETA methods [46]. It takes into account both the causes and impacts of incident scenarios [47], as illustrated in Figure 3. The figure depicts three main categories of risk: the probability of occurrence, on the left, linked by either an OR or AND relation to cause a risk event; the risk event itself, in the middle, which can result in failure, undesirability, or nonconformance; and the consequences or impacts of the risk event, on the right [48]. Risk mitigations can be classified as either P or D. P represents preventive actions taken before the occurrence of the risk event to prevent or decrease the likelihood of its occurrence, while D represents defensive actions taken after the occurrence of the risk event to protect or minimize the probability of its impact. Since BTA considers both the causes and consequences of a risk, as well as the preventive and protective actions taken, it is considered the most effective visual method for analyzing risks.
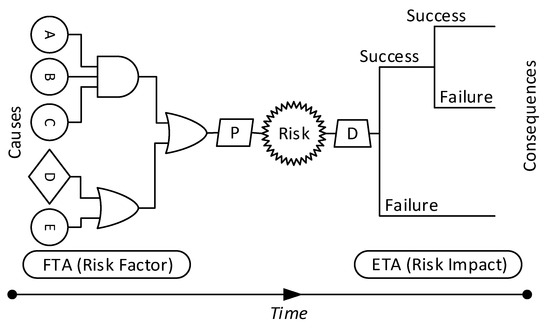
Figure 3.
Bow-tie analysis (BTA).
3.2. Quantitative Methodology
The quantitative methodology using objective and numerical-based calculation. This comprises analytical methods, stochastic methods, Bayes’ theorem, reliability optimization, multi-criteria analysis, and data utilization [30]. The majority of the papers that have been reviewed utilize these quantitative techniques since they are direct applications by using the algorithm.
Analytical methodologies such as limit state function (LSF), first order reliability method (FORM), and second order reliability method (SORM) are commonly used in quantitative methodology to assess reliability. It is essential to solve the algorithm carefully and ensure that its mathematical properties do not interfere with reliability computation [49]. Uncertainty analysis is usually performed using stochastic methods such as Monte Carlo simulation (MCS) and stochastic response surface method (SRSM). Because MCS is time-consuming, SRSM is a better alternative as it significantly reduces the required time compared to MCS [18]. Bayes’ theorem is another quantitative methodology that provides a structured approach to assess the likelihood of new events [49]. Reliability estimation can be updated when new data become available using Bayesian methods.
The reliability-based design optimization (RBDO) methodology, which falls under the category of reliability optimization techniques, is capable of considering the design for a specific risk level and achieving the desired reliability level despite various sources of uncertainty in a quantitative manner [49]. RBDO utilizes probabilistic constraints to establish the correlation between the uncertain variables and design alternatives, resulting in a reliable solution [50]. An alternative technique known as RBRDO can be used to achieve optimal design. This method takes into account the resilience of the objective function and can ensure that the constraints are met within a specific range. In comparison to RBDO, RBRDO aims to reduce the variability in performance, resulting in a narrower distribution of performance by enhancing robustness [51]. Additionally, multi-criteria decision making (MCDM) and multi-attribute decision making (MADM) can be used as part of a multi-criteria analysis approach to evaluate and choose the best result based on different characteristics.
MADM refers to a process of assessing and ranking options based on multiple attributes and criteria, taking into account their quality and significance [52]. This technique involves using data analysis methods such as statistical modeling, databases, and Markov chains, which require data to be gathered and selected appropriately. Typically, the collected data is stored in a database and analyzed using either statistical modeling or Markov chain analysis, with the latter being the most commonly used state-space analysis technique [28] for situations with constant failure and repair rates [29]. Table 3 provides an overview of different risk and reliability methodologies.

Table 3.
Risk and Reliability Methodology.
3.3. Hybrid Qualitative & Quantitative (HQQ) Methodology
The hybrid methodology is a combination of qualitative and quantitative criteria and measurement techniques. It is often an extension of existing methods, incorporating both qualitative and quantitative aspects. This approach can be classified into two categories: table-based and visual analysis methodologies. One example of a table-based hybrid methodology is the failure mode effects and criticality analysis (FMECA), which is an expansion of the failure mode analysis technique to include critical analysis. FMECA includes several additional features that focus on the criticality aspect, such as the occurrence of failure [53]. In comparison to FMEA, FMECA includes extra parameters like the severity of the failure effects, failure mode occurrence, and detectability of the failure cause.
The reliability block diagram (RBD) is an example of visual HQQ method. The RBD provides a visual representation of a system’s elements and how they contribute to the system’s reliability. An RBD is created by establishing paths of successful outcomes between the various blocks that make up the system. This approach breaks down a system into its individual components and illustrates the logical interconnections necessary for the system to function effectively. The RBD methodology employs several basic building blocks, including singleton, series, parallel, K-out-of-N (KooN), and bridge. The underlying assumptions of the RBD methodology are that the system being modeled, as well as each of its components, can only exist in two states—success or failure. The RBD depicts the success state of the modeled system by utilizing success paths, i.e., the connections between the successful outcomes of its components. Additionally, the RBD methodology presumes that the system components are statistically independent [21].
The diagram illustrates the success or failure state of the system based on the working condition of its components. For instance, a basic series alignment requires all elements to be functional for the system to operate, while a basic parallel alignment necessitates at least one functional component for the system to operate. The RBD expands on visual analysis by utilizing algorithms to determine the relationship between each block and others. The RBD uses algebraic rules to describe series and parallel inter-relationships. The RBD is also a hierarchical reliability model that can break larger blocks down into smaller functional blocks [22]. Figure 4a demonstrates a simple serial configuration in which the failure of either component A or B results in system failure. Figure 4b depicts a simple parallel configuration in which the system fails only if both components C and D fail.
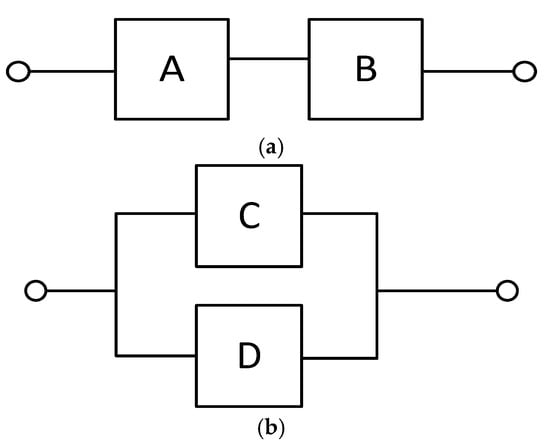
Figure 4.
(a) Simple serial configuration of RBD; (b) Simple parallel configuration of RBD.
The advantages of RBD include its ability to perform sensitivity analysis easily, practicality for large system evaluation, and simplifying the reliability modeling process [54]. On the other hand, the drawbacks include its complexity for more series/parallel blocks and only considering the system state and system fail state [55].
Another expansion of graphical analysis is the Bayesian belief network (BBN). BBN enhance FTA by assigning probabilities to the contributing factors; therefore, BBNs are useful for both risk identification and reliability assessment [30]. Furthermore, the reliability estimation can be updated when new data become available [29].
4. Risk and Reliability Methodology in Photovoltaic (PV) Power Generation
Alternative energy options are increasingly turning towards photovoltaic (PV) power generation. Due to its intermittent nature, reliability assessment is essential [10]. To achieve maximum profitability and optimal generation output, precise risk and reliability assessment are crucial. This motivation has led to discussions on the importance of risk and reliability analysis in the photovoltaic industry. However, while reliability has been a common topic, there have been relatively few discussions on risk analysis.
4.1. Qualitative Methodology in PV Power Generation
As previously discussed, qualitative methods for analyzing the reliability of PV power generation systems include failure mode analysis, hazard analysis, and graphical analysis. For example, FMEA is a systematic approach used in failure mode analysis to understand the causes, effects, and mitigation of rooftop PV system failures, as noted in [56]. Regular maintenance is recommended for the inverter, which is a critical component and generates the highest values of RPN. Graphical analysis methods, such as FTA, ETA, and BTA, can be used to diagnose and predict the weakest link in the PV system, with the inverter being identified as having a significant influence on failure, as mentioned in [57,58]. Safety is a major concern in any system, including PV systems, and the complexity of circuit functions makes them vulnerable to failure. Therefore, it is suggested in [59] that the HAZOP method be used to establish fault characteristics, and that the HAZOP method be combined with FTA for better visualization of risk and reliability.
4.2. Quantitative Methodology in PV Power Generation
Quantitative methodology encompasses a range of analytical techniques including stochastic methods, Bayes’ theorem, reliability optimization, multi-criteria analysis, and data utilization. Types of analytical method within this framework are LSF, SORM, and FORM. Furthermore, the lifetime of photovoltaic modules is evaluated using LSF and simulated stochastic data [60]. Stochastic methods, such as Monte Carlo simulation (MCS), are developed by probability and statistics and involve generating a sampled random number set of grid-connected PV system failure events through computer simulation, as stated in reference [19]. Multi-criteria analysis, such as MADM, is another quantitative methodology that can assist decision-makers in determining the best location for a PV power plant by taking into account important attributes and scenarios [52]
Data utilization methodologies such as the Markov chain are also being used for PV system reliability. According to the Markov chain of stochastic process theory, deterioration in a subject’s performance follows the Markov property. This means that the subject’s future conditions are dependent on their current conditions rather than on their past conditions [61]. Markov chain analysis in forecasting the power generation of the grid-connected photovoltaic system is feasible especially when the statistical sample data is large enough [62]. In the reliability optimization approach such as presented in [63], the sizing process of PV system is dependent on the selection of target-oriented, such as reliability-oriented or cost-oriented design. Given too many variations of variables, the selections of optimum combinations of specific parameters are different from each other. There is also a combination of the quantitative methodology applied in PV system research such as Markov chain Monte Carlo (MCMC). According to [64], MCMC with the acceptance–rejection method is able to successfully synthesize sufficient short-term variations in the generation output weather-dependent PV systems.
4.3. Hybrid Qualitative & Quantitative (HQQ) Methodology in PV Power Generation
The HQQ approach involves utilizing both qualitative and quantitative methods, such as FMECA, RBD, and BBN. For instance, in [23], FMECA was employed to investigate PV modules, revealing a correlation between higher RPN values and the presence of powder on the panel surface. In another study [24], FMECA was combined with fuzzy evaluation of analytic hierarchy process (AHP) to establish a new evaluation index consisting of output power loss (P), fault maintenance costs (W), and fault occurrence (O), resulting in more reliable PV module analysis for maintenance decisions.
RBD was used in to estimate reliability and availability for a large photovoltaic system over a five-year time period [22]. As illustrated in Figure 5, the reliability block diagram (RBD) models for three different photovoltaic (PV) system configurations—string (series), central inverter (parallel), and bridge topology—are derived from the analysis in [25]. The corresponding RBD system reliability values are as follows:
- String (series) configuration, PSIN is 78.8% or 0.788.
- Central inverter (parallel) configuration, PPIN is 87.5% or 0.875.
- Bridge configuration, PBIN is 87.4% or 0.874.
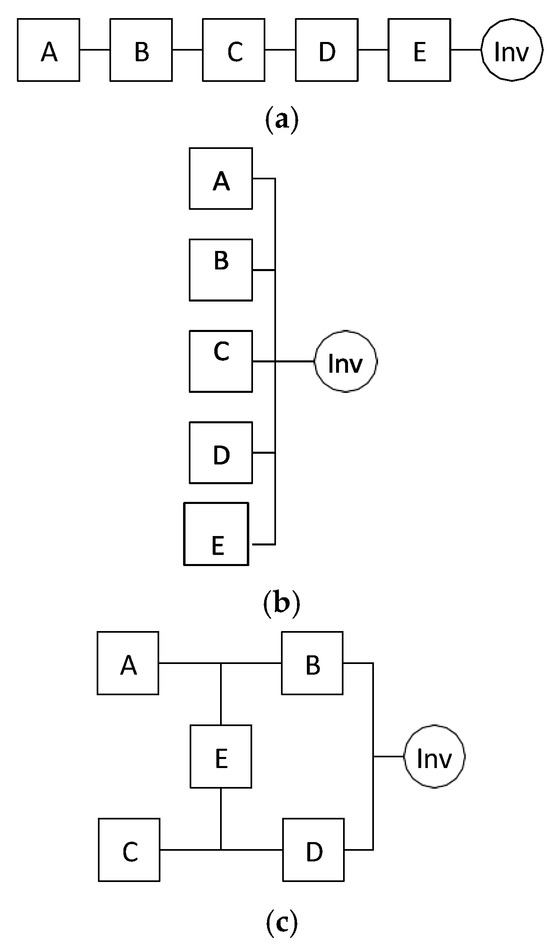
Figure 5.
Reliability block diagram for series parallel and bridge topology. (a) string (series) topology RBD; (b) central inverter (parallel) topology RBD; (c) bridge topology RBD.
The values are taken directly from [25], along with the RBD bridge block equation referenced from [21], both of which offer a comparative reliability assessment of PV inverter topologies using the reliability block diagram (RBD) modeling approach.
The study collected field data, including failure and repair times with their distributions. Additionally, the BBN reliability model was combined with fault tree analysis (FTA) in [20], where FTA was developed first and then translated into BBN to assess the reliability of PV systems. By using this combined HQQ method, the authors claimed that it was possible to conduct reasoning analysis, identify weak points in the system, strengthen its reliability, and improve fault diagnosis and maintenance time.
5. Performance Index Based on Risk and Reliability Methodology in Photovoltaic (PV) Power Generation
The integration of renewable energy sources into the power grid can result in uncertainties due to their intermittent nature. Among these sources, photovoltaic (PV) power generation is the most significant source of uncertainty. Moreover, the output of PV is heavily influenced by various in situ climatological and environmental factors, as noted in [26]. In accordance with [65], light intensity has a significant impact on current parameters but only a minor effect on voltage parameters. Conversely, cell temperature mostly affects voltage parameters and has little effect on current parameters.
There are instances when voltage deviation and reverse power flow occur [66], as well as disturbances originating from the grid network, such as voltage swells and sags. In order to address this issue, ref. [67] proposed a fuzzy logic-based dynamic voltage restorer (DVR) to safeguard critical loads. Meanwhile, ref. [68] utilized incremental conductance (InCond) in conjunction with perturb and observe (P&O), and ref. [69] employed artificial neural network (ANN) to produce better dynamic and steady-state performance, as well as to minimize distortion, compared to existing maximum power point tracking (MPPT) algorithms. ANN is a mathematical model that mimics the structure of the human brain [70]. This results in high power quality, efficiency, and reliability. As per [27], increasing the PV capacity can improve the probability indices and provide large renewable energy resources, not only to meet power demand but also to generate substantial income [71]. The performance of photovoltaic (PV) power generation can be categorized into technical and financial perspectives. Both methods can be applied to the entire generation system or to specific components.
To evaluate the reliability of a system, one can employ various indicators, including mean time between failures (MTBF), mean time to failure (MTTF), and mean time to repair (MTTR). MTBF is a gauge of the reliability of a repairable system, often measured in months or hours [72]. It is equivalent to the inverse of the failure rate (λ) [73].
Mean time to failure (MTTF) is a metric used to determine the average lifetime of a non-repairable component and is usually expressed in hours or months. The decision to classify a component as non-repairable is often based on economic considerations rather than physical impracticality. It is rare for the failure rate (λ) or MTTF to remain constant, as noted by [74].
Figure 6 presents an overview of the key considerations and chronological sequence involved in calculating MTBF (mean time between failures for maintenance). In Equation (3), MTBF is determined by dividing the total duration during which a system operated without any failures by the number of failures that occurred within that same timeframe. The system is initially activated and operates for a certain period before encountering an unexpected failure. Upon detection, repair activities commence, followed by reactivation of the system, subsequent operation, and yet another unforeseen failure. For MTBF calculation purposes, uptime is measured from the beginning of one operational phase to the commencement of the subsequent unplanned downtime. It is important to note that the MTBF calculation specifically excludes repair time, inspections, and planned downtime. The focus remains solely on evaluating the duration of correct system operation under typical conditions.
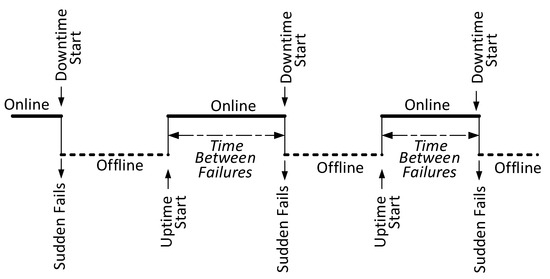
Figure 6.
MTBF timeline.
Figure 7 illustrates an example of the MTTF (mean time to failure) of PV arrays in a typical PV power generation scenario. Among the PV arrays analyzed, PV array A has a lifespan of 20 years; PV arrays B, D, and E have a lifespan of 21 years; and PV array C has a lifespan of 19 years. In total, 100 PV arrays were evaluated. By dividing the cumulative lifespan by the number of arrays (100/5), the calculated MTTF is determined to be 20 h.
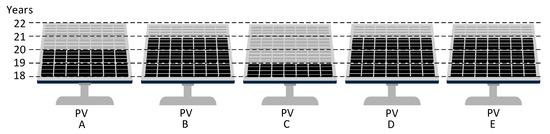
Figure 7.
Photovoltaic (PV) arrays for typical PV power generation.
The rate of expected failures per unit of time, known as failures in time (FIT), is often utilized to indicate the projected number of failures in one billion device hours of operation. This measurement, as per reference [75], can be used to establish the connection between FIT and MTBF, which can be articulated as:
The mean time between maintenance actions (MTBMA) refers to a system reliability parameter that considers the requirement for maintenance personnel. It is calculated by dividing the total number of system life units by the total number of maintenance actions (both preventive and corrective) performed during a specified period.
Mean time between unscheduled removal (MTBUR) is another system reliability parameter that is associated with the need for logistics support. It is determined by dividing the total number of system life units by the total number of unscheduled items that have been removed from the system during a given time frame.
Mean time to repair (MTTR) is a measurement of the repairable system’s serviceability and is usually expressed in minutes or hours. It is generally the time taken from the detection of a problem until the system returns to its normal operating condition [76]. MTTR is also equivalent to the inverse of the repair rate (μ).
Availability is a fraction of time that a system is usable. Steady-state availability (SSA) is equal to MTBF divided by (MTBF+MTTR). It is important to specify whether the availability is inherent, achieved, or operational, as each type of availability considers different factors that contribute to downtime. MTBF, as defined by [55], is the expected time between two failures in a repairable system. MTBF is often used interchangeably with mean time to failure (MTTF), when a failure cannot be repaired [77].
In addition to reliability, other indicators for photovoltaic systems include the system average interruption frequency index (SAIFI) and system average interruption duration index (SAIDI). Enhancing the energy efficiency performance index, such as SAIDI and SAIFI, is a method of increasing reliability [78]. Furthermore, by applying effective early fault detection strategy and reducing the time taken to locate faults can enhance the SAIFI and SAIDI indices [79]. These parameters are evaluated statistically, requiring a significant amount of time to obtain an accurate estimate [80]. As per [67], The system average interruption frequency index (SAIFI) quantifies how often the average customer experiences a sustained interruption. It is calculated as the ratio of the total number of customers interrupted to the total number of customers served. In contrast, the system average interruption duration index (SAIDI) represents the average total duration of interruptions experienced by a customer, computed as the total customer interruption minutes divided by the total number of customers served. The equations for SAIFI and SAIDI are shown in Equations (7) and (8), respectively [66].
The CAIDI (customer average interruption duration index) is a reliability indicator that measures the average time of a disruption. It evaluates the effectiveness of maintenance administrators, operatives, and organizations in responding to emergencies in the electrical power distribution system (PDS) [81]. Simply put, CAIDI is the ratio of the total duration of interruptions (in minutes) to the total number of interruptions, representing the average interruption duration for customers in a year [82]. The equation for CAIDI is as follows:
Other measures of reliability such as index of energy not supplied (ENS), index of average energy not supplied (AENS) [19], average supply availability index (ASAI), ideal supplied energy (ISE), expected supplied energy (ESE), energy availability (Ae), time availability (At), available hours (Tav), down hours (Tdw), derated hours (Tdr) [83], hazard rate (HR), repair rate (RR) [84], loss of load probability (LOLP) [85], and loss of power supply probability (LPSP) [86] are used but not as frequently as SAIDI, SAIFI, and CAIDI [87].
Financial evaluation metrics in the financial category include net present value (NPV), profitability index (PI), benefit-to-cost (B/C) ratio, internal rate of return (IRR), modified internal rate of return (MIRR), simple payback (SP), time-to-net-positive-cash-flow (TNP) payback, annualized monthly bill savings (MBS), levelized cost of energy (LCOE) [88], and levelized avoided cost of electricity (LACE). The initial cost is known as capital expenditure (CAPEX), while the operational and maintenance costs are operational expenditure (OPEX) [89].
The present value (PrV) represents the current value of a future cash flow amount at a particular rate of return. In contrast, the net present value (NPrV) is the current value of the expected returns from an investment, after deducting the costs of acquiring it [90]. When the NPrV of a PrV system reaches zero, it signifies that the expense of generating energy from photovoltaic (PV) is equivalent to the cost or value of energy purchased from the power grid. This milestone is commonly referred to as “grid-parity” [91]. The equation for NPrV is expressed as follows:
Equation (12) incorporates the discount rate, (d) and the variable for years, (t) in each summation. If the NPrV value is zero, it implies that the investment has reached the break-even point for the relevant life cycle period. However, if the NPrV value is greater than zero, it is considered a profitable investment opportunity, and if it is less than zero, it is deemed an unprofitable investment. The levelized cost of energy (LCOE) is a financial metric that determines the minimum possible cost of energy production over the entire lifespan of a power plant. The LCOE indices indicate the financial expenses involved in producing a specific quantity of energy [92]. This LCOE value establishes the lowest price at which electricity could be traded during the plant’s lifetime and is represented as the net present value of the unit cost of electricity. Another term is LACE, the levelized avoided cost of energy [93], which is an amount of revenue for the unit value of energy. The equation for LCOE and LACE, as follows:
For a project to be considered economically viable, the levelized cost of energy (LCOE) must be lower than the levelized avoided cost of energy (LACE). Furthermore, the levelized profit or loss of energy (LPLE), also referred to as the value-to-cost ratio, can be utilized to evaluate the overall profitability of the project over its lifetime. A project is deemed profitable if the LPLE exceeds one. The LPLE is calculated using the following equation:
where LPLE ≥ 1 for profitable plant installation.
The LCOE and LACE represent the discounted cash flow over the project’s lifespan [94]. The LCOE index is frequently employed in industry for reliability evaluation [95]. The conventional method of estimating the LCOE index for photovoltaic plants involves utilizing a percentage of the invested capital (CAPEX). Nevertheless, the LCOE index is heavily influenced by the arrangement of the topology and operational strategy. Dividing the photovoltaic system into multiple locations can maximize power output and financial returns [96].
6. Discussion
This review has evaluated a wide range of methodologies for assessing risk and reliability in photovoltaic (PV) power generation systems. The methods are broadly classified into three categories: qualitative, quantitative, and hybrid qualitative–quantitative (HQQ) approaches, each offering distinct advantages depending on the system complexity, data availability, and application context.
In response to RQ1, this study identified and categorized the principal methodologies for risk and reliability assessment of photovoltaic (PV) power systems into three main groups: qualitative, quantitative, and hybrid qualitative–quantitative (HQQ) approaches. Qualitative methods, such as FMEA, hazard and operability study (HAZOP), and graphical tools including fault tree analysis (FTA) and event tree analysis (ETA), are commonly employed during early-stage system evaluation to identify potential failure points and operational hazards [11,14,38]. These methods are advantageous in contexts with limited data availability, where expert judgment and structured reasoning can provide initial insights.
Quantitative methodologies—including Monte Carlo simulation (MCS), Bayesian inference, and reliability-based design optimization (RBDO)—enable robust probabilistic modeling of system behavior under uncertainty [18,19,51]. These techniques support statistical forecasting and performance optimization by incorporating component failure rates, degradation trends, and environmental variability. While quantitatively rigorous, these methods typically require extensive datasets and computational capacity, which may limit their practical application in early-stage or resource-constrained projects.
Most notably, the review found that hybrid qualitative and quantitative (HQQ) methodologies offer the most effective and adaptable framework for risk and reliability assessment in PV systems. Methods such as failure mode effects and criticality analysis (FMECA), reliability block diagrams (RBD), and Bayesian belief networks (BBN) combine the intuitive and diagnostic advantages of qualitative tools with the analytical precision of quantitative models [20,21,23,24,25]. These integrated approaches enable a more holistic understanding of PV system behavior, allowing simultaneous analysis of component-level failures and system-wide interactions.
Addressing RQ2, the study examined numerous real-world applications of these methodologies in PV system evaluation. For example, FMEA has been implemented in rooftop PV systems to identify high-risk components such as inverters [56]. HAZOP has been used for circuit-level safety assessments, often supplemented with FTA for fault visualization and causal mapping [59]. Quantitative methods like MCS and Markov chain modeling have been applied to simulate failure probabilities and predict long-term energy output under varying operational scenarios [19,61,62]. Hybrid methods have demonstrated practical relevance in diverse settings: FMECA has been applied to model module degradation under environmental stressors [23,24]; RBD has supported comparative analysis of inverter topologies [22,25]; and BBN has enabled dynamic reliability estimation and fault diagnosis in complex PV systems [20].
In response to RQ3, the review identified key performance indicators used to evaluate PV system reliability and economic viability. Technical metrics such as mean time between failures (MTBF), mean time to repair (MTTR), system average interruption frequency index (SAIFI), and system average interruption duration index (SAIDI) are widely adopted to assess system reliability, maintainability, and availability [72,73,74,78,79,80,81,82]. Financial performance is typically evaluated using indicators like net present value (NPV), levelized cost of energy (LCOE), and levelized avoided cost of energy (LACE), which inform investment decisions and long-term project feasibility [88,89,90,91]. When used together, these technical and financial indices support comprehensive risk-informed planning and operational strategies.
Furthermore, the applicability of HQQ methodologies extends beyond component reliability analysis to address emerging systemic challenges in PV deployment, such as grid saturation, energy curtailment, and policy-driven constraints [10,26,27]. These issues demand multi-dimensional assessment frameworks capable of integrating technical, environmental, and regulatory variables—requirements that HQQ methods are uniquely positioned to meet. For instance, FMECA provides prioritization strategies for maintenance, RBD allows for cost-effective modeling of topological variations, and BBN facilitates uncertainty handling and probabilistic reasoning under real-world dynamic conditions.
In summary, while qualitative and quantitative methods each offer important contributions, HQQ methodologies demonstrate the greatest potential for scalable, accurate, and adaptable reliability assessments in PV systems. Their ability to bridge expert-driven insights with empirical modeling makes them particularly well-suited to modern, data-intensive PV infrastructures. As the global deployment of solar energy continues to rise, embracing integrated assessment approaches will be critical for enhancing system resilience, operational efficiency, and long-term sustainability.
7. Conclusions
This paper aimed to systematically review and categorize the prevailing methodologies for risk and reliability assessment in photovoltaic (PV) power generation systems. By conducting structured analysis across qualitative, quantitative, and hybrid paradigms, the study not only achieved its objectives but also contributed a unified framework for evaluating methodological suitability based on system complexity, data availability, and real-world applicability.
Qualitative techniques such as FMEA and HAZOP provide essential early-stage diagnostic tools but are inherently constrained by subjectivity and a lack of quantitative precision. Conversely, quantitative approaches—including Monte Carlo simulation, Bayesian inference, and reliability-based design optimization—deliver statistically rigorous insights but depend heavily on large datasets and computational capabilities. Positioned at the intersection of these two extremes, hybrid qualitative and quantitative (HQQ) methodologies—such as FMECA, reliability block diagrams (RBD), and Bayesian belief networks (BBN)—demonstrate superior capability by merging the strengths of both domains. These methods facilitate comprehensive system modeling that captures both localized failures and broader operational interdependencies.
In addition to methodological classification, the paper underscores the critical role of integrating technical and economic performance indicators—such as the mean time between failures (MTBF), system average interruption frequency index (SAIFI), levelized cost of energy (LCOE), and net present value (NPV)—to support risk-informed, data-driven decision making. The review also draws attention to the emerging need for reliability frameworks that can address macro-level challenges, including energy curtailment, grid saturation, and policy constraints.
Collectively, the findings position HQQ methodologies as the most robust, flexible, and forward-looking tools for comprehensive risk and reliability assessment in PV systems. Their ability to synthesize expert-based reasoning with empirical modeling makes them highly effective in guiding strategic planning, optimizing lifecycle performance, and ensuring long-term resilience of solar energy infrastructure in both developing and established markets. This integrated approach not only advances academic understanding but also provides actionable insights for engineers, system designers, and energy policymakers navigating the future of PV deployment.
Funding
This research received no external funding.
Acknowledgments
The authors gratefully acknowledge the support and assistance of the Renewable Energy Research Laboratory (RENERAL), Universiti Kuala Lumpur (UniKL).
Conflicts of Interest
The authors declare no conflict of interest.
References
- International Energy Agency. World Energy Outlook 2017; International Energy Agency: Paris, France, 2017. [Google Scholar]
- Andersen, O.; Gilpin, G.; Andrae, A.S.G. Cradle-to-Gate Life Cycle Assessment of the Dry Etching Step in the Manufacturing of Photovoltaic Cells. AIMS Energy 2014, 2, 410–423. [Google Scholar] [CrossRef]
- Zhou, P.; Jin, R.Y.; Fan, L.W. Reliability and Economic Evaluation of Power System with Renewables: A Review. Renew. Sustain. Energy Rev. 2016, 58, 537–547. [Google Scholar] [CrossRef]
- Shimura, S.; Herrero, R.; Zuffo, M.K.; Baesso Grimoni, J.A. Production Costs Estimation in Photovoltaic Power Plants Using Reliability. Sol. Energy 2016, 133, 294–304. [Google Scholar] [CrossRef]
- Colli, A. Failure Mode and Effect Analysis for Photovoltaic Systems. Renew. Sustain. Energy Rev. 2015, 50, 804–809. [Google Scholar] [CrossRef]
- Deceglie, M.G.; Silverman, T.J.; Marion, B.; Kurtz, S.R. Real-Time Series Resistance Monitoring in PV Systems Without the Need for I–V Curves. IEEE J. Photovolt. 2015, 5, 1706–1709. [Google Scholar] [CrossRef]
- Birolini, A. Reliability Engineering, 7th ed.; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-642-14951-1. [Google Scholar]
- Alvarez, M.L.; Sarachaga, I.; Burgos, A.; Estévez, E.; Marcos, M. A Methodological Approach to Model-Driven Design and Development of Automation Systems. IEEE Trans. Autom. Sci. Eng. 2018, 15, 67–79. [Google Scholar] [CrossRef]
- MS ISO 9001:2015; Quality Management Systems—Requirements (Second Revision). Malaysian Standard; Department of Standard Malaysia: Sepang, Malaysia, 2015; Volume 43.
- Khan, B.; Alhelou, H.H.; Mebrahtu, F. A Holistic Analysis of Distribution System Reliability Assessment Methods with Conventional and Renewable Energy Sources. AIMS Energy 2019, 7, 413–429. [Google Scholar] [CrossRef]
- Liu, H.; Deng, X.; Jiang, W. Risk Evaluation in Failure Mode and Effects Analysis Using Fuzzy Measure and Fuzzy Integral. Symmetry 2017, 9, 162. [Google Scholar] [CrossRef]
- Carlson, C.S. Effective FMEAs: Achieving Safe, Reliable, and Economical Products and Processes Using Failure Mode and Effects Analysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; ISBN 9781118007433. [Google Scholar]
- Arabian-Hoseynabadi, H.; Oraee, H.; Tavner, P.J. Failure Modes and Effects Analysis (FMEA) for Wind Turbines. Int. J. Electr. Power Energy Syst. 2010, 32, 817–824. [Google Scholar] [CrossRef]
- Marhavilas, P.K.; Filippidis, M.; Koulinas, G.K.; Koulouriotis, D.E. An Expanded HAZOP-Study with Fuzzy-AHP (XPA-HAZOP Technique): Application in a Sour Crude-Oil Processing Plant. Saf. Sci. 2020, 124, 104590. [Google Scholar] [CrossRef]
- Kletz, T.A. Hazop & Hazan: Identifying and Assessing Process Industry Hazards, 4th ed.; Institution of Chemical Engineers: Rugby/Warwickshire, UK, 1999; ISBN 9780852955062. [Google Scholar]
- Reniers, G.L.L.; Dullaert, W.; Ale, B.J.M.; Soudan, K. Developing an External Domino Accident Prevention Framework: Hazwim. J. Loss Prev. Process Ind. 2005, 18, 127–138. [Google Scholar] [CrossRef]
- O Herrera, M.A.d.l.; Luna, A.S.; Augusto da Costa, A.C.; Lemes, E.M.B. Risk Analysis: A Generalized Hazop Methodology State-of-the-Art, Applications, and Perspective in the Process Industry. Vigilância Sanitária em Debate 2018, 6, 106–121. [Google Scholar] [CrossRef]
- Pan, W.; Wang, Z.; Sun, B. Comparison of Stochastic Response Surface Method and Monte Carlo Method for Uncertainty Analysis of Electronics Prognostics. In Proceedings of the 2015 IEEE Conference on Prognostics and Health Management (PHM), Austin, TX, USA, 22–25 June 2015. [Google Scholar] [CrossRef]
- Yang, G.; Li, Y.; Yao, Q.; Yong, R. Study of Reliability of Grid Connected Photovoltaic Power Based on Monte Carlo Method. In Proceedings of the 2011 IEEE Power Engineering and Automation Conference (PEAM), Wuhan, China, 8–9 September 2011; Volume 1, pp. 92–95. [Google Scholar] [CrossRef]
- Xiyun, Y.; Jiawen, C. Application of Bayesian Network to Reliability Assessment of PV Systems. In Proceedings of the International Conference on Renewable Power Generation (RPG 2015), Beijing, China, 17–18 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Carnevali, L.; Ciani, L.; Fantechi, A.; Gori, G.; Papini, M. An Efficient Library for Reliability Block Diagram Evaluation. Appl. Sci. 2021, 11, 4026. [Google Scholar] [CrossRef]
- Collins, E.; Dvorack, M.; Mahn, J.; Mundt, M.; Quintana, M. Reliability and Availability Analysis of a Fielded Photovoltaic System. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Philadelphia, PA, USA, 7–12 June 2009; pp. 002316–002321. [Google Scholar] [CrossRef]
- Catelani, M.; Ciani, L.; Cristaldi, L.; Faifer, M.; Lazzaroni, M.; Rinaldi, P. FMECA Technique on Photovoltaic Module. In Proceedings of the Conference Record—IEEE Instrumentation and Measurement Technology Conference, Hangzhou, China, 10–12 May 2011; pp. 1717–1722. [Google Scholar] [CrossRef]
- Rongbin, Y.; Guixiong, L. Failure Risk Analysis of the Photovoltaic Modules Based on the Improved FMECA Method. In Proceedings of the 2015 Fifth International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC), Qinhuangdao, China, 18–20 September 2015; pp. 1166–1170. [Google Scholar] [CrossRef]
- Abdul Karim, A.Z.; Rahmat, M.K.; Osman, M.S. Innovative Photovoltaics (PV) Bridge Topology Reliability Block Diagram. In Proceedings of the International Conference on Engineering Technology and Technopreneurship (ICE2T), Kuala Lumpur, Malaysia; 2023; pp. 366–372. [Google Scholar] [CrossRef]
- Ramenah, H.; Casin, P.; Ba, M.; Benne, M.; Tanougast, C. Accurate Determination of Parameters Relationship for Photovoltaic Power Output by Augmented Dickey Fuller Test and Engle Granger Method. AIMS Energy 2018, 6, 19–48. [Google Scholar] [CrossRef]
- Song, X.; Zhao, Y.; Zhou, J.; Weng, Z. Reliability Varying Characteristics of PV-ESS-Based Standalone Microgrid. IEEE Access 2019, 7, 120872–120883. [Google Scholar] [CrossRef]
- O’Connor, P.; Kleyner, A. Practical Reliability Engineering, 5th ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; ISBN 9780470979822. [Google Scholar]
- Stapelberg, R.F. Handbook of Reliability, Availability, Maintainability and Safety in Engineering Design; Springer: London, UK, 2009; ISBN 9781848001749. [Google Scholar]
- Leimeister, M.; Kolios, A. A Review of Reliability-Based Methods for Risk Analysis and Their Application in the Offshore Wind Industry. Renew. Sustain. Energy Rev. 2018, 91, 1065–1076. [Google Scholar] [CrossRef]
- Saleem, F.; Nisar, S.; Khan, M.A.; Khan, S.Z.; Sheikh, M.A. Overall Equipment Effectiveness of Tyre Curing Press: A Case Study. J. Qual. Maint. Eng. 2017, 23, 39–56. [Google Scholar] [CrossRef]
- Fabis-Domagala, J.; Domagala, M. A Concept of Risk Prioritization in FMEA of Fluid Power Components. Energies 2022, 15, 6180. [Google Scholar] [CrossRef]
- Yeh, T.M.; Chen, L.Y. Fuzzy-Based Risk Priority Number in FMEA for Semiconductor Wafer Processes. Int. J. Prod. Res. 2014, 52, 539–549. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Liu, N. Risk Evaluation Approaches in Failure Mode and Effects Analysis: A Literature Review. Expert Syst. Appl. 2013, 40, 828–838. [Google Scholar] [CrossRef]
- Kmenta, S.; Ishii, K. Scenario-Based Failure Modes and Effects Analysis Using Expected Cost. J. Mech. Des. Trans. ASME 2004, 126, 1027–1035. [Google Scholar] [CrossRef]
- Saedi, A.M.; Thambirajah, J.J.; Pariatamby, A. A HIRARC Model for Safety and Risk Evaluation at a Hydroelectric Power Generation Plant. Saf. Sci. 2014, 70, 308–315. [Google Scholar] [CrossRef]
- Bambang, S.; Andhika Ayu Valentina, E.; Pringgo Widyo, L. Analysis of Potential Work Accidents Using Hazard Identification, Risk Assessment and Risk Control (HIRARC) Method. In Proceedings of the 2016 2nd International Conference of Industrial, Mechanical, Electrical, Chemical Engineering (ICIMECE), Yogyakarta, Indonesia, 6–7 October 2016; pp. 196–200. [Google Scholar]
- Abad, F.; Naeni, L.M. A Hybrid Framework to Assess the Risk of Change in Construction Projects Using Fuzzy Fault Tree and Fuzzy Event Tree Analysis. Int. J. Constr. Manag. 2020, 22, 2385–2397. [Google Scholar] [CrossRef]
- Ruijters, E.; Stoelinga, M. Fault Tree Analysis: A Survey of the State-of-the-Art in Modeling, Analysis and Tools. Comput. Sci. Rev. 2015, 15, 29–62. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, H.; Guo, B. BDD Algorithms Based on Modularization for Fault Tree Analysis. Prog. Nucl. Energy 2015, 85, 192–199. [Google Scholar] [CrossRef]
- Leung, T.J.; Rife, J. Feature Article: Refining Fault Trees Using Aviation Definitions for Consequence Severity. IEEE Aerosp. Electron. Syst. Mag. 2017, 32, 4–14. [Google Scholar] [CrossRef]
- Zamalieva, D.; Yilmaz, A.; Aldemir, T. A Probabilistic Model for Online Scenario Labeling in Dynamic Event Tree Generation. Reliab. Eng. Syst. Saf. 2013, 120, 18–26. [Google Scholar] [CrossRef]
- Nývlt, O.; Rausand, M. Dependencies in Event Trees Analyzed by Petri Nets. Reliab. Eng. Syst. Saf. 2012, 104, 45–57. [Google Scholar] [CrossRef]
- Mercurio, D.; Podofillini, L.; Zio, E.; Dang, V.N. Identification and Classification of Dynamic Event Tree Scenarios via Possibilistic Clustering: Application to a Steam Generator Tube Rupture Event. Accid. Anal. Prev. 2009, 41, 1180–1191. [Google Scholar] [CrossRef]
- Podofillini, L.; Zio, E.; Mercurio, D.; Dang, V.N. Dynamic Safety Assessment: Scenario Identification via a Possibilistic Clustering Approach. Reliab. Eng. Syst. Saf. 2010, 95, 534–549. [Google Scholar] [CrossRef]
- Wierenga, P.C.; Lie-A-Huen, L.; De Rooij, S.E.; Klazinga, N.S.; Guchelaar, H.J.; Smorenburg, S.M. Application of the Bow-Tie Model in Medication Safety Risk Analysis: Consecutive Experience in Two Hospitals in the Netherlands. Drug Saf. 2009, 32, 663–673. [Google Scholar] [CrossRef]
- Aqlan, F.; Mustafa Ali, E. Integrating Lean Principles and Fuzzy Bow-Tie Analysis for Risk Assessment in Chemical Industry. J. Loss Prev. Process Ind. 2014, 29, 39–48. [Google Scholar] [CrossRef]
- Mettu, S.; Mayorga, R.V.; Peng, W. A FIS Approach to Prioritize Risks in a Chemical Industry. Eng. World 2022, 2, 39–46. [Google Scholar]
- Nikolaidis, E.; Ghiocel, D.M.; Singhal, S. Engineering Design Reliability Handbook; CRC Press: Boca Raton, FL, USA, 2005; ISBN 0849311802. [Google Scholar]
- Huang, Z.L.; Jiang, C.; Li, X.M.; Wei, X.P.; Fang, T.; Han, X. A Single-Loop Approach for Time-Variant Reliability-Based Design Optimization. IEEE Trans. Reliab. 2017, 66, 651–661. [Google Scholar] [CrossRef]
- Park, J.; Yoo, D.; Moon, J.; Yoon, J.; Park, J.; Lee, S.; Lee, D.; Kim, C. Reliability-Based Robust Design Optimization of Lithium-Ion Battery Cells for Maximizing the Energy Density by Increasing Reliability and Robustness. Energies 2021, 14, 6236. [Google Scholar] [CrossRef]
- Haghdadi, N.; Asaei, B. Multi-Attribute Decision Making for New Photovoltaic Power Plant Establishment: Iran Case Study. In Proceedings of the 2012 11th International Conference on Environment and Electrical Engineering, Venice, Italy, 18–25 May 2012; pp. 166–169. [Google Scholar] [CrossRef]
- Odita, T.; Lim, Y.; Chen, G. Application of Model Based Systems Engineering in Aerospace Case Study by Using MADe Software. Hawaii Univ. Int. Conf. 2019, 29, 842. [Google Scholar]
- Shi, X.; Bazzi, A.M. Solar Photovoltaic Power Electronic Systems: Design for Reliability Approach. In Proceedings of the 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Rahmat, M.; Jovanovic, S.; Lo, K.L. Uninterruptible Power Supply (UPS) System Configurations: Reliability Comparison. In Proceedings of the Intelec 2013; 35th International Telecommunications Energy Conference, SMART POWER AND EFFICIENCY, Hamburg, Germany, 13–17 October 2013; pp. 405–410. [Google Scholar]
- Basu, J.B. Failure Modes and Effects Analysis (FMEA) of a Rooftop PV System. Int. J. Sci. Eng. Res. 2015, 3, 51–55. [Google Scholar] [CrossRef]
- Hu, R.; Mi, J.; Hu, T.; Fu, M.; Yang, P. Reliability Research for PV System Using BDD-Based Fault Tree Analysis. In Proceedings of the 2013 International Conference on Quality, Reliability, Risk, Maintenance, and Safety Engineering (QR2MSE), Chengdu, China, 15–18 July 2013; pp. 359–363. [Google Scholar]
- Rahmat, M.K.; Sani, M.N. Fault Tree Analysis in UPS Reliability Estimation. In Proceedings of the 2014 4th International Conference on Engineering Technology and Technopreneuship (ICE2T), Kuala Lumpur, Malaysia, 27–29 August 2014; pp. 240–245. [Google Scholar]
- Wang, Y.; Guo, F.-; Huang, M. Analysis and Countermeasure Study of Photovoltaic System Fault Based on Fault Tree and HAZOP. Appl. Mech. Mater. 2014, 536–537, 1557–1561. [Google Scholar] [CrossRef]
- Laronde, R.; Charki, A.; Bigaud, D. Lifetime Estimation of A Photovoltaic Module Based on Temperetaure Measurement. In Proceedings of the 2nd IMEKO TC 11 International Symposium METROLOGICAL INFRASTRUCTURE, Cavtat, Dubrovnik Riviera, Croatia, 15–17 June 2011; pp. 34–39. [Google Scholar]
- Wei, B.; Guo, C.; Deng, M. An Innovation of the Markov Probability Model for Predicting the Remaining Service Life of Civil Airport Rigid Pavements. Materials 2022, 15, 6082. [Google Scholar] [CrossRef]
- Li, Y.; Niu, J. Forecast of Power Generation for Grid-Connected Photovoltaic System Based on Markov Chain. In Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009; pp. 9–12. [Google Scholar] [CrossRef]
- Ge, H.; Ni, L.; Asgarpoor, S. Reliability-Based Stand-Alone Photovoltaic System Sizing Design-A Case Study. In Proceedings of the 10th International Conference on Probablistic Methods Applied to Power Systems, PMAPS’08, Rincon, PR, USA, 25–29 May 2008; pp. 1–8. [Google Scholar]
- Kim, I. Markov Chain Monte Carlo and Acceptance–Rejection Algorithms for Synthesising Short-Term Variations in the Generation Output of the Photovoltaic System. IET Renew. Power Gener. 2017, 11, 878–888. [Google Scholar] [CrossRef]
- Ramgolam, Y.K.; Bangarigadu, K. Simple and Effective Method for Evaluating Performance of Si Based Photovoltaic Cell Technologies. AIMS Energy 2018, 6, 632–644. [Google Scholar] [CrossRef]
- Shigenobu, R.; Adewuyi, O.B.; Yona, A.; Senjyu, T. Demand Response Strategy Management with Active and Reactive Power Incentive in the Smart Grid: A Two-Level Optimization Approach. AIMS Energy 2017, 5, 482–505. [Google Scholar] [CrossRef]
- Numan, A.H.; Dawood, Z.S.; Hussein, H.A. Theoretical and Experimental Analysis of Photovoltaic Module Characteristics under Different Partial Shading Conditions. Int. J. Power Electron. Drive Syst. 2020, 11, 1508–1518. [Google Scholar] [CrossRef]
- Yasmine, A.; Rafik, B.; Rachid, B.; Adel, M. Grid Connected Photovoltaic System Efficiency and Quality Improvement Using Fuzzy-Incond MPPT. Int. J. Power Electron. Drive Syst. 2020, 11, 1536–1546. [Google Scholar] [CrossRef]
- Attia, H. High Performance PV System Based on Artificial Neural Network MPPT with PI Controller for Direct Current Water Pump Applications. Int. J. Power Electron. Drive Syst. (IJPEDS) 2019, 10, 1329. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, Z.; Liu, D.; Chen, J.; Liu, D.; Hu, X. Degradation Trend Prediction of Hydropower Units Based on a Comprehensive Deterioration Index and LSTM. Energies 2022, 15, 6273. [Google Scholar] [CrossRef]
- Sediqi, M.M.; Howlader, H.O.R.; Ibrahimi, A.M.; Danish, M.S.S.; Sabory, N.R.; Senjyu, T. Development of Renewable Energy Resources in Afghanistan for Economically Optimized Cross-Border Electricity Trading. AIMS Energy 2017, 5, 691–717. [Google Scholar] [CrossRef]
- Gupta, N.; Garg, R.; Kumar, P. Sensitivity and Reliability Models of a PV System Connected to Grid. Renew. Sustain. Energy Rev. 2017, 69, 188–196. [Google Scholar] [CrossRef]
- Boussaid, M.; Belghachi, A.; Agroui, K.; Djarfour, N. Mathematical Models of Photovoltaic Modules Degradation in Desert Environment. AIMS Energy 2019, 7, 127–140. [Google Scholar] [CrossRef]
- Krasich, M. How to Estimate and Use MTTF/MTBF Would the Real MTBF Please Stand Up? In Proceedings of the 2009 Annual Reliability and Maintainability Symposium, Fort Worth, TX, USA, 26–29 January 2009; pp. 353–359. [Google Scholar] [CrossRef]
- Gujarati, A.; Brandenburg, B.B. When Is CAN the Weakest Link? In A Bound on Failures-in-Time in CAN-Based Real-Time Systems. In Proceedings of the 2015 IEEE Real-Time Systems Symposium, San Antonio, TX, USA, 1–4 December 2015; pp. 249–260. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, P.; Goel, L.; Ding, Y. Impacts of Contingency Reserve on Nodal Price and Nodal Reliability Risk in Deregulated Power Systems. IEEE Trans. Power Syst. 2013, 28, 2497–2506. [Google Scholar] [CrossRef]
- Harb, S.; Balog, R.S. Reliability of Candidate Photovoltaic Topologies—A Usage Model Approach. IEEE Trans. Power Electron. 2013, 28, 3019–3027. [Google Scholar] [CrossRef]
- Ramachandradurai, S.; Krishnan, N.; Sharma, G.; Bokoro, P.N. Islanding Detection with Reduced Non-Detection Zones and Restoration by Reconfiguration. Energies 2023, 16, 3035. [Google Scholar] [CrossRef]
- Peter, G.; Stonier, A.A.; Gupta, P.; Gavilanes, D.; Vergara, M.M.; Lung sin, J. Smart Fault Monitoring and Normalizing of a Power Distribution System Using IoT. Energies 2022, 15, 8206. [Google Scholar] [CrossRef]
- Markovskii, P.; Merkushev, A. Investigation into High Voltage Network Reliability Predictive Calculation. In Proceedings of the 2018 19th International Scientific Conference on Electric Power Engineering, EPE 2018–Proceedings, Brno, Czech Republic, 16–18 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Kigsirisin, S.; Pussawiro, S.; Noohawm, O. The Effect of Alternative Power Distribution (Nhánh Tính ENS-PV1). In Proceedings of the 2017 IEEE 30th Canadian Conference on Electrical and Computer Engineering (CCECE), Windsor, ON, Canada, 30 April–3 May 2017; pp. 1–4. [Google Scholar]
- Ayamolowo, O.J.; Mmonyi, C.A.; Adigun, S.O.; Onifade, O.A.; Adeniji, K.A.; Adebanjo, A.S. Reliability Analysis of Power Distribution System: A Case Study of Mofor Injection Substation, Delta State, Nigeria. In Proceedings of the 2019 IEEE AFRICON Conference, Accra, Ghana, 25–27 September 2019. [Google Scholar] [CrossRef]
- Mustafa, A.M.; Omran, W.A.; Hegazy, Y.G.; Member, S. Reliability Assessment of Grid Connected Photovoltaic Generation Systems. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; Volume 5, pp. 1543–1549. [Google Scholar]
- Battistelli, L.; Chiodo, E.; Lauria, D. Bayes Assessment of Photovoltaic Inverter System Reliability and Availability. In Proceedings of the SPEEDAM 2010, Pisa, Italy, 14–16 June 2010; pp. 628–634. [Google Scholar]
- Saengthong, S.; Suttichai, P. A Simple Method in Sizing Related to the Reliability Supply of Small Stand-Alone Photovoltaic Systems. In Proceedings of the Conference Record of the Twenty-Eighth IEEE Photovoltaic Specialists Conference—2000 (Cat. No.00CH37036), Anchorage, AK, USA, 15–22 September 2000; pp. 1630–1633. [Google Scholar]
- Nordin, N.D.; Abdul Rahman, H. A Novel Optimization Method for Designing Stand Alone Photovoltaic System. Renew. Energy 2016, 89, 706–715. [Google Scholar] [CrossRef]
- Aruna, S.B.; Suchitra, D.; Rajarajeswari, R.; Fernandez, S.G. A Comprehensive Review on the Modern Power System Reliability Assessment. Int. J. Renew. Energy Res. 2021, 11, 1735–1747. [Google Scholar] [CrossRef]
- Drury, E.; Denholm, P.; Margolis, R. The Impact of Different Economic Performance Metrics on the Perceived Value of Solar Photovoltaics; Technical Report (NREL/TP-6A20-52197); National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2011; pp. 1–44. [Google Scholar]
- Egli, F.; Steffen, B.; Schmidt, T.S. A Dynamic Analysis of Financing Conditions for Renewable Energy Technologies. Nat. Energy 2018, 3, 1084–1092. [Google Scholar] [CrossRef]
- Dranka, G.G.; Cunha, J.; de Lima, J.D.; Ferreira, P. Economic Evaluation Methodologies for Renewable Energy Projects. AIMS Energy 2020, 8, 339–364. [Google Scholar] [CrossRef]
- Denholm, P.; Drury, E.; Margolis, R. The Solar Deployment System (SolarDS) Model: Documentation and Sample Results; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009; p. 52. [Google Scholar]
- Quijano, A.; Lorenzo, C.; Narvarte, L. Economic Assessment of a PV-HP System for Drying Alfalfa in The North of Spain. Energies 2023, 16, 3347. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration. Levelized Cost and Levelized Avoided Cost of New Generation Resources in the Annual Energy Outlook 2015; U.S. Energy Information Administration: Washington, DC, USA, 2015; pp. 1–5. [Google Scholar]
- Huseyin Murat, C.; Serdar, E. Modified Levelized Cost of Electricity or Energy, MLOCE and Modified Levelized Avoidable Cost of Electricity or Energy, MLACE and Decision Making. Am. J. Mod. Energy 2019, 5, 1. [Google Scholar] [CrossRef]
- Suruhanjaya Tenaga. Guidelines on Large Scale Solar Photovoltaic Plant for Connection to Electricity Networks. Malays. Energy Comm. 2019, 2016, 1–42. [Google Scholar]
- Jo, J.H.; Ilves, K.; Barth, T.; Leszczynski, E. Implementation of a Large-Scale Solar Photovoltaic System at a Higher Education Institution in Illinois, USA. AIMS Energy 2017, 5, 54–62. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).