Abstract
Recent European regulations promote distributed energy resources as alternatives to centralized generation. This study compares utility-scale and distributed photovoltaic (PV) systems coupled with Battery Energy-Storage Systems (BESSs) in the Italian electricity market, analyzing different battery sizes. A multistage stochastic mixed-integer linear programming model, using Monte Carlo PV production scenarios, optimizes day-ahead and intra-day market offers while incorporating PV forecast updates. In real time, battery flexibility reduces imbalances. Here we show that, to ensure dispatchability—defined as keeping annual imbalances below 5% of PV output—a 1 MW PV system requires 220 kWh of storage for utility-scale and 50 kWh for distributed systems, increasing the levelized cost of electricity by +13.1% and +1.94%, respectively. Net present value is negative for BESSs performing imbalance netting only. Therefore, a multiple service strategy, including imbalance netting and energy arbitrage, is introduced. Performing arbitrage while keeping dispatchability reaches an economic optimum with a 1.7 MWh BESS for utility-scale systems and 1.1 MWh BESS for distributed systems. These results show lower PV firming costs than previous studies, and highlight that under a multiple-service strategy, better economic outcomes are obtained with larger storage capacities.
1. Introduction
1.1. Motivation
In recent decades, policymakers have intensified efforts to reduce carbon emissions, leading to significant transformations particularly in the energy-production sector, which accounts for more than three-quarters of total global greenhouse gas emissions [1]. A key outcome of these efforts has been the widespread deployment of Renewable Energy Sources (RESs) worldwide, gradually replacing conventional thermal power plants. This transition has been driven by substantial public and private investments, as well as by international agreements aimed at facilitating the energy transition such as the Paris Agreement [2] and the European Green Deal [3]. Between 2015 and 2024, the effects of these global commitments became evident, as the share of electricity generated from RESs surpassed 30% in 2023, a notable increase from 23% in 2015 [4]. This progress has been primarily driven by the expansion of solar photovoltaic (PV) and wind energy, with PV alone accounting for 11% of total electricity production in Europe in 2024 [5].
This ongoing transition is also driving the decentralization of electricity generation, with increasing numbers of small- and medium-scale production units connected to distribution grids. This trend is particularly pronounced in the European solar power sector, where distributed installations accounted for 58% of new PV capacity added in 2024 [6]. Consequently, decentralized energy systems are gaining prominence in European regulatory frameworks. In Italy, the integration of Distributed Energy Resources (DERs) into electricity markets has been formalized through the Testo Integrato del Dispacciamento Elettrico (TIDE) [7], which establishes market-based mechanisms to compensate DERs similarly to utility-scale generation units. This national framework aligns with broader European legislation, notably Directive 2019/944 [8], which sets out specific guidelines for DERs participation in electricity markets. Central to these regulations is the role of aggregators, who coordinate and manage multiple DERs within Virtual Power Plants (VPPs), enabling their efficient and effective market participation.
However, the increasing penetration of non-programmable renewable resources (NP-RESs) introduces new challenges for grid stability. The inherent uncertainty associated with these energy sources complicates the real-time balance between electricity generation and consumption. Additionally, the low inertia of NP-RESs reduces the system’s ability to counteract frequency fluctuations, thereby impacting overall grid reliability. As a result of the increased demand for real-time balancing energy and of the greater difficulty in finding flexible resources, the costs of ancillary services are expected to increase in future years [9]. These services, purchased by the Transmission System Operator (TSO), are essential for maintaining voltage and frequency stability and preventing grid disturbances or blackouts [10].
One of the most effective solutions to address these challenges is the integration of Battery Energy-Storage Systems (BESSs) with NP-RESs, enhancing system flexibility by decoupling energy generation from consumption throughout the day. BESSs can be installed in two main configurations: front-of-the-meter (FTM) and behind-the-meter (BTM) [11]. FTM batteries, typically large-scale systems connected directly to transmission or distribution networks, contribute to grid stability by enabling energy shifting, supporting peak demand reduction, and facilitating renewable energy integration [12]. These systems also participate in wholesale markets and deliver critical ancillary services such as frequency regulation, voltage control, and black-start capabilities [13]. With advanced inverters, they can enhance system inertia and fault response, helping stabilize increasingly decarbonized power systems [14]. In contrast, BTM batteries are deployed at residential, commercial, or industrial sites and primarily serve end-users [12]. They help optimize self-consumption of on-site renewable generation, reduce electricity bills via peak shaving and time-of-use arbitrage, and ensure supply reliability during outages [15]. Additionally, BTM systems can support local grid operations by providing flexibility services to Distribution System Operators (DSOs), easing network constraints, and deferring infrastructure upgrades [12].
Given the central role that PV systems play in energy transition—both as utility-scale assets and as distributed generation aggregated through VPPs—it becomes increasingly important to assess the economic and operational value of integrating BESSs with PV installations. Such coupling not only has the potential to improve the financial viability of PV projects but also helps reduce output uncertainty and enhance the reliability of the electrical system.
1.2. Literature Review and Research Gaps
Several studies focus on the development of optimization models for the participation of PV systems in electricity markets, aiming to enhance their integration into the power system. Due to the inherent variability of solar irradiance throughout the day, scenario generation to represent possible PV power production profiles is a crucial starting point in many of these works. The scientific literature presents a wide range of methodologies for this purpose, with Monte Carlo methods being among the most commonly employed. Zheng et al. [16] explore various approaches for modelling the power output of PV systems under diverse meteorological conditions, emphasizing that Monte Carlo methods are particularly effective in generating representative probabilistic production scenarios for DERs. To mitigate the computational complexity of handling large scenario sets while preserving key statistical attributes, Shi et al. [17] propose an approach that integrates a reduced Monte Carlo method with k-means clustering. Similarly, Falabretti et al. [18] apply this combined methodology to construct input scenarios for a stochastic mixed-integer linear programming (MILP) model, designed to optimize the bidding strategy of a VPP in both the Day-Ahead Market (DAM) and the real-time market. By explicitly accounting for PV production uncertainty, their study demonstrates significant improvements in profitability while effectively mitigating imbalance costs.
Given the uncertainty in PV power output, other studies apply stochastic or robust optimization models to maximize revenues from PV participation in electricity markets, demonstrating superior performances over traditional deterministic approaches. Stochastic optimization aims to find solutions that perform well on average by incorporating the probability distributions of uncertain parameters. In contrast, robust optimization seeks solutions that remain effective under worst-case scenarios within a defined uncertainty set, without requiring probabilistic information [19]. For instance, Nemati et al. [20] propose a regret-based flexible robust optimization model for a VPP composed of wind, solar PV, and flexible demand, operating in southern Spain. The VPP participates simultaneously in the day-ahead and secondary reserve markets, while accounting for imbalance penalties. Their model allows the operator to control the level of conservatism using a monetary regret limit rather than traditional uncertainty budgets. Results show that the model is economically effective and that it can adapt to different levels of forecast error and market penalties. In contrast Silva et al. [21] develop a multistage stochastic decision-aid algorithm to optimize the bidding strategy of a VPP composed of wind, solar PV, and storage across day-ahead, intra-day, and balancing markets. Unlike previous studies focusing mainly on day-ahead and balancing markets, their approach explicitly includes intra-day market participation to better manage forecast uncertainty. Results show that engaging in all three markets increases VPP profits by 10.1% and reduces imbalances by 63.8%, highlighting the value of coordinated multi-market strategies under uncertainty and the relevance of near-real-time re-scheduling possibility for NP-RESs. Similarly, Visser et al. [22] propose an operational bidding strategy that optimizes the participation of a PV power plant in electricity spot markets, considering day-ahead, intra-day, and imbalance markets. Particularly, they develop a multistage stochastic optimization method using a scenario-generation algorithm. The method is evaluated using both technical and economic metrics, demonstrating a significant improvement over a reference strategy. The study shows that extending market participation to intra-day increases revenues by 22% and reduces imbalance by 50%.
While the optimization of utility-scale PV + BESS systems for participation in electricity markets has been widely studied, the optimization of residential PV + BESS systems also offers significant benefits, particularly in enhancing energy flexibility and improving economic performance [23]. Li [24] develops a genetic algorithm-based method for the optimal sizing of grid-connected PV + BESS systems in residential buildings, incorporating a time-of-use electricity tariff scheme to maximize cost savings. Results show that jointly optimizing PV and battery sizes significantly reduces electricity imports and costs, though optimal system size varies with household consumption profiles and price conditions. Duman et al. [25] propose an optimal PV + BESS sizing model for prosumers equipped with Home Energy Management Systems (HEMS), emphasizing the role of day-ahead load scheduling in increasing self-consumption. The developed MILP model incorporates optimal PV tilt angle selection and load scheduling of various controllable appliances, while accounting for battery degradation and vehicle-to-home functionality. It first minimizes daily electricity costs through demand response and self-consumption, then simulates one year of HEMS operation to evaluate the Net Present Value (NPV) of different PV + BESS configurations. The optimal design is identified as the configuration yielding the highest NPV. Similarly, Zhou et al. [26] explore the allocation of PV and battery capacity in a smart home environment, explicitly considering the impact of electricity pricing mechanisms on system performance and cost-effectiveness. Particularly, the study accounts for various electricity pricing mechanisms—time-of-use (TOU), real-time pricing (RTP), and stepwise power tariffs (SPTs)—as well as PV subsidies and uncertainties in solar generation and seasonal load profiles. A hybrid optimization approach, combining a cataclysmic genetic algorithm with the DICOPT solver in GAMS [27], is employed to identify the optimal configuration. Through six case studies and sensitivity analyses, the results reveal that under SPTs and sufficient subsidies, installing only PV is optimal, whereas under RTP and TOU, both PV and BESSs are necessary to achieve maximum profits. Rezaeimozafar et al. [28] propose a two-stage stochastic optimization framework for operating behind-the-meter PV + BESS systems, aiming to minimize daily grid consumption and battery degradation while accounting for PV output uncertainty. A feed-forward neural network combined with a statistical error analysis technique is used to generate accurate PV power output scenarios, which are then reduced using a backward scenario reduction method to mitigate dimensionality issues in the optimization model. The reduced scenarios are input into the two-stage model to estimate expected electricity costs and degradation. The approach is validated with real-world data from a household in Ireland, demonstrating strong performance under PV variability and results comparable to an ideal forecast scenario.
A key aspect when optimizing commercial PV programs is to assess the economic impact of imbalances. Guo et al. [29] propose an optimal real-time operational framework aimed at minimizing imbalance costs of a VPP. The study highlights that the effectiveness of the adopted strategy depends on the specific imbalance settlement mechanisms in place. Similarly, Marneris et al. [30] investigate the rationale behind strategic bidding and the necessity of accurate forecasting under different imbalance settlement schemes. Their study presents a comprehensive approach to determine the optimal bidding strategy for an RES aggregator operating in the day-ahead and ancillary services markets, where prices are taken as given. To ensure precision in the optimization process, the interactions between the day-ahead market, ancillary services, and real-time balancing mechanisms are explicitly modelled.
Imbalance costs, and price signals coming from different energy markets, should correctly reflect the impact of PV-induced imbalances on the working operations of the power system managed by the TSO. Pierro et al. present a structured analysis addressing the challenges of integrating high shares of PV generation into the Italian power system [31,32,33]. In their earliest work [31], they propose two complementary strategies to mitigate the impacts of rising PV penetration on imbalance volumes: improving PV and net load day-ahead forecasts, and converting conventional PV systems into “flexible PV” plants equipped with remote curtailment capabilities and cost-optimized battery storage. Both strategies are shown to significantly reduce imbalance volumes and costs, with the second capable of eliminating imbalance impacts entirely, all at a cost lower than current imbalance management practices. Building on this foundation, Pierro et al. in [32] outline a broader roadmap to achieve a 100% renewable electricity mix in Italy by transforming intermittent PV production to firm 24/365 power generation. In their most recent contribution [33], the authors focus on the system-wide implementation of flexible PV plants to provide ancillary services through proactive curtailment and battery support. They show that such plants can reduce the national imbalance by 36% compared to 2016 levels with only 6% curtailment of PV production. This can be achieved at or below current dispatching costs. Moreover, a geographically distributed fleet of flexible PV plants ensures optimal regulation performance, with the sizing strategy found to be robust against year-specific variations in load, generation, and market conditions.
Complementing this system-level perspective, Lazard offers a widely referenced benchmark for the cost of transforming PV generation into firm power through battery storage [34]. According to their last report, the Levelized Cost of Electricity (LCOE) for standalone PV in the CAISO market [35] is approximately USD 43/MWh. When battery-based firming is included, this cost rises to USD 141/MWh. The firming cost is defined as the additional expense required to compensate for the non-firm portion of PV output using a firm resource—assumed in this case to be a 4 h lithium-ion battery with a power rating equal to 50% of the installed PV capacity. This definition highlights the context-specific nature of firming and distinguishes it from broader concepts such as dispatchability. Consequently, firming cost estimates must be interpreted with caution, as they depend heavily on local assumptions about resource adequacy, system needs, and market design.
The optimization of bidding strategies for PV plants has been extensively explored in the literature, with various studies addressing participation to different stages of the electricity market. However, very few studies have specifically analyzed the benefits of PV systems participation in IDM focusing on economic profitability and imbalance management. Additionally, while numerous optimization models incorporate the minimization of imbalance quantities and, consequently, imbalance costs, they rarely integrate this aspect with the optimization of BESS sizing. However, these two dimensions are strongly interrelated, as the extent of imbalances is inherently influenced by storage capacity, given that BESSs can mitigate forecasting errors. This comes at the expense of investment and operational costs associated with storage infrastructure which must be carefully evaluated. Moreover, no study has assessed the difference between utility-scale and distributed PV configurations when it comes to market participation and imbalance management, with possible different impacts on the optimal BESS size. The technical and economic performance of distributed PV systems has been widely examined in scientific literature. However, direct comparisons with utility-scale PV power plants, which currently represent the predominant form of PV generation in the power system [36], remain limited.
1.3. Contribution and Novelty
This research investigates the optimal participation of PV + BESS systems within the Italian electricity market. Specifically, it focuses on the optimization of DAM and IDM bidding strategy through a multistage stochastic MILP, followed by a real-time operation phase, in which the flexibility of the battery is leveraged to minimize imbalances. The optimization framework is implemented in Python 3.11, using Pyomo library for mathematical modelling [37] and Gurobi as the solver [38]. To generate PV production scenarios, a Monte Carlo method is applied in combination with k-means clustering.
Two different system configurations are analyzed in this study:
- 1.
- a distributed system of fixed rooftop PV systems located at the Leonardo campus of Politecnico di Milano [39];
- 2.
- a simulated utility-scale plant situated at the same location.
The dataset for estimating daily PV power production profiles is sourced from the EU Photovoltaic Geographical Information System (PVGIS) [40]. To ensure comparability between the distributed and the utility-scale configurations, a fixed installed peak capacity of 1 MW is considered. By clustering 12 groups of days (corresponding to four seasons and three different irradiance conditions per season), the annual performance of the two configurations is assessed. The BESS size varies from 0 to 5 MWh to assess its impact on both system’s economic performance and the resulting imbalance volumes.
This work contributes to the existing literature by providing a comparative analysis of two distinct PV system configurations—utility-scale and distributed—using a consistent methodological framework. While these configurations are not mutually exclusive, the study highlights their respective strengths and limitations in terms of profitability and dispatchability. The analysis evaluates system economic performance in electricity spot markets as a function of BESS capacity, offering insights into optimal BESS sizing and bidding strategies for each configuration. Furthermore, the study explores the trade-off between economic optimization and dispatchability requirements, assessing how an imposed imbalance threshold of 5% influence battery sizing and key economic metrics such as LCOE and NPV. This comprehensive approach provides a deeper understanding of the value of BESS integration in PV systems under varying operational constraints.
Although this study is conducted within the Italian electricity market and focuses on Milan’s PV generation, findings can be easily extended to other regulatory contexts and alternative geographical locations. The remainder of this paper is structured as follows: Section 2 provides an overview of the Italian electricity market, with a particular emphasis on the TIDE regulatory framework. Section 3 details the methodological approach, from scenario generation to the mathematical model used for optimization. Section 4 presents the case study and discusses the results obtained. Finally, Section 5 summarizes the key findings and outlines potential directions for future research.
2. Italian Electricity Market
This research considers the Italian context within the framework of the new TIDE regulatory initiative, ensuring alignment with the evolving European energy landscape. The section begins by outlining the core principles and objectives of TIDE, providing the necessary foundation for understanding its implications on market operations. It then offers an overview of the structure of the Italian electricity spot markets. The Ancillary Services Market (ASM) is excluded from the analysis, as it lies beyond the scope of this study.
2.1. TIDE
TIDE [7], introduced in January 2025, represents a significant step toward aligning the Italian electricity market with the EU regulatory landscape. Developed in compliance with EU Regulation 2017/2195 [41] and other European directives, TIDE establishes new principles and operational frameworks aimed at enhancing competition and liquidity in electricity markets. Particularly, TIDE aims to support the evolving needs of the electricity system as the share of NP-RESs continues to grow. Its primary objective is to implement an economically efficient dispatch model in which all network resources—including consumption units—can, in principle, serve a dual role: their primary function as energy producers or consumers, managed by Balance Responsible Parties (BRPs), and an additional function of providing flexibility services, managed by Balance Service Providers (BSPs). The model promotes competition among all types of resources, centralized or distributed, through organized market platforms that select the most efficient providers of flexibility services. This selection adheres to the principle of technological neutrality, meaning services are procured regardless of the providing technology as long as technical and cost criteria are met.
A key regulatory development introduced by TIDE is the formal recognition of Virtual Aggregated Units (Unità Virtuali Abilitate, UVA) as market participants, enabling aggregated DERs to compete alongside conventional power plants. This allows for greater flexibility in the participation of decentralized assets, ensuring that even small-scale resources can contribute to system balancing and market liquidity.
In summary, TIDE fosters a more inclusive and competitive electricity market by integrating RESs, storage, and distributed systems and simultaneously enhancing system flexibility. This transformation includes a restructuring of market mechanisms, particularly within the spot markets, which are central to this study. The following sections outline the Italian electricity market structure, focusing on DAM, IDM and imbalance settlement within this new regulatory framework.
2.2. Day-Ahead Market and Intra-Day Market
The first phase of the Italian electricity spot market is the DAM, where market participants must submit their energy bids by 12:00 on the previous day (D-1), with market-clearing results published at 12:55 on D-1. Following the DAM, the IDM provides market participants with the opportunity to adjust their commercial positions by submitting additional supply offers or purchase requests. The IDM consists of three scheduled auctions (CRIDA) and a continuous trading session (IDM-XBID) [42].
The three intra-day auction sessions are structured as follows:
- CRIDA1: Opens at 12:55 on D-1 and closes at 15:30 on D-1.
- CRIDA2: Opens at 12:55 on D-1 and closes at 22:00 on D-1.
- CRIDA3: Opens at 12:55 on D-1 and closes at 10:00 on D.
Prior to the introduction of TIDE, the resolution of spot market transactions was one hour, but starting in 2025, this transitioned to a 15 min resolution to with the ASM. Consequently, a market time unit (MTU) of 15 min is adopted in this research.
In terms of spatial granularity, the Italian electricity market is divided into seven market zones: North (NORD), North-Central (CNOR), South-Central (CSUD), South (SUD), Calabria (CALA), Sicily (SICI), and Sardinia (SARD) [43]. This zonal configuration was established by ARERA through Deliberation 103/2019 [44] based on structural congestions identified in the national transmission grid.
In the DAM, operators submit bids that include: the MTU of delivery, the sale or purchase quantities and the respective price. Offers are accepted based on the auction results after the market closes. All supply offers accepted in the DAM are valued at the marginal clearing price of their respective zones. This price is determined for each MTU by the intersection of demand and supply curves and varies across zones when transit limits are saturated. With the introduction of TIDE, all purchasing offers are valued at the PUN Index, calculated by GME ex-post as the average of zonal prices, weighted by purchased quantities in each market zone.
In the CRIDA, demand bids and supply offers are selected based on the same criterion as described for the DAM, employing a system marginal pricing method. In contrast, in the IDM-XBID, bids are matched immediately whenever a sell offer is priced lower than—or equal to—a corresponding buy bid.
This study considers a PV + BESS system that participates in the DAM and adjusts its commercial output in CRIDA2, based on improved PV forecast accuracy between 12:55 (D-1), the gate closure time (GTC) of the DAM, and 22:00 (D-1), the GTC of CRIDA2.
2.3. Imbalance Settlement
The nodal imbalance volume for a single unit is calculated for each Imbalance Settlement Period (ISP)—the time interval over which a BRP imbalance volume is financially settled—as the difference between the actual energy exchanged with the grid and the scheduled energy resulting from market clearing. This deviation, measured in MWh, indicates whether the unit has a positive (overproduction or underconsumption) or negative (underproduction or overconsumption) imbalance. In addition to nodal imbalances, macrozonal imbalances are also considered, which represent the net imbalance volume across all units within the same macrozone, which is defined as the aggregation of one or more pricing area.
Currently, in Italy is employed a static scheme with two macrozones: a north macrozone corresponding to the “NORD” market zone and a south macrozone corresponding to the six remaining market zones. Imbalance volumes are calculated for each 15 min ISP and are economically settled using the Single Pricing methodology. This pricing mechanism, established by ARERA (the Italian Regulatory Authority for Energy, Networks and Environment) through Deliberation 523/2021/R/eel [45], ensures alignment with European regulatory requirements [41]. Under the single pricing mechanism, the imbalance price for each ISP is calculated based on the overall macrozonal imbalance volume. Therefore, a uniform imbalance price is applied to all market participants in a given macrozone, regardless of whether they contribute positively or negatively to the overall imbalance. Particularly, the macrozonal imbalance price is determined as the volume-weighted average price of balancing energy activated by the TSO in response to system needs. Consequently, in a macrozone with positive imbalance, the imbalance price tends to be lower than the DAM price, whereas in a macrozone with negative imbalance, it tends to be higher than the DAM price. This design benefits participants unbalancing in the opposite direction of the macrozone imbalance volume: those who help mitigate it are rewarded with better prices than DAM prices, while those who worsen it face penalties. However, it must be noted that, since the imbalance price depends on real-time system conditions and balancing actions, it is not known during real-time operations [46]. Instead, Terna, the Italian TSO, publishes the official imbalance prices on the day following market execution.
3. Methodology
This section outlines the modeling approach used to simulate the PV + BESS system operations and its interactions with electricity markets. The process begins with the generation of PV production scenarios using a Monte Carlo random sampling method, widely recognized in scientific literature for its flexibility in handling uncertainty and ease of implementation [47]. To manage computational complexity, a scenario reduction technique is also applied, specifically the k-means clustering algorithm. After generating PV scenarios for both DAM and IDM, the next step is to realistically model the knowledge of electricity prices, with particular attention to how imbalance prices are represented at different stages of the optimization. The final step involves the optimization of the PV + BESS system’s market participation through a multistage stochastic MILP. Given the inherent uncertainties in PV generation, the stochastic approach is considered the most suitable solution. The decision to adopt a multistage model is based on the progressive refinement of available information throughout the day, with improved PV production forecasts between DAM and IDM and the resolution of uncertainty during real-time operation.
3.1. PV Scenario Generation
3.1.1. Day-Ahead Market PV Scenarios
Generating PV scenarios is essential to accurately capture the uncertainty associated with solar radiation during the considered day. As previously mentioned, the adopted methodology combines the Monte Carlo method with k-means clustering, following an approach similar to that described in reference [18]. To ensure a robust dataset, the study utilizes three years of historical PV production data with a 15 min resolution.
The first step of the methodology involves classifying days by season. Within each seasonal group, k-means clustering is applied to group days based on solar radiation conditions. This clustering technique partitions a dataset of n observations into k clusters by assigning each observation to the cluster with the nearest mean, which serves as the cluster’s representative. The k-means clustering technique has been selected because it is particularly effective for extracting meaningful patterns from data, enabling the identification of trends in time-series behavior. By grouping similar data points, it reduces computational complexity while preserving the key statistical characteristics of the dataset [48].
To determine the optimal number of clusters for each season, the Elbow Method is applied. This technique, widely used in literature, helps identifying the appropriate number of clusters by analyzing the within-cluster sum of squares (WCSS), which quantifies the total squared distance between each point in a cluster and its centroid. The Elbow Method involves plotting the WCSS on the y-axis against the number of clusters on the x-axis. The “elbow point”—where the decrease in WCSS starts to plateau—indicates the optimal number of clusters.
To maintain consistency and ensure computational efficiency, a common number of clusters is adopted across all four seasons. This choice is justified by the similarity in optimal cluster values obtained for each season and the benefits of uniformity in the subsequent analysis. As a result, the profiles are organized into 4 × N matrices, where 4 represents the seasons and N denotes the number of clusters.
Once the clusters have been identified, the following steps are carried out for each cluster:
- 1.
- Calculation of the average profile of the cluster being analyzed.
- 2.
- Derivation of error profiles as the difference between the various historical profiles and the average profile, with a 15 min resolution.
- 3.
- Application of the Monte Carlo method through a random addition of errors to the average profile. The selected errors must respect the time constraint (an error obtained in a given quarter hour can only be added to the PV production value of the average profile in the same quarter hour) but can belong to different error profiles. The process continues iteratively until the convergence criterion is satisfied.
Scenario generation is terminated when the uncertainty, defined as in Equation (1), reaches a value lower than the imposed threshold:
where i is the number of scenarios generated so far, represents the PV production profile for the k-th scenario, while denotes the average PV production profile over the first i scenarios.
Once the iterations are completed and all scenarios have been generated, a scenario reduction method is applied to limit computational efforts. The optimal number of reduced scenarios is determined using the elbow method, which is reapplied to assess the trade-off between the number of scenarios and the retained variance. After establishing a common number of reduced scenarios for each cluster, the k-means clustering method is employed to group similar scenarios based on daily PV power production. This process results, for each cluster in each season, in a final set of representative scenarios, each assigned a probability, ensuring that the reduced set accurately reflects the statistical properties of the original distribution.
3.1.2. Intra-Day Market Improved PV Scenarios
The main difference between DAM and IDM optimization lies in the improvement in PV forecast accuracy that occurs between the DAM GTC (12:55 on D-1) and the CRIDA2 GTC (22:00 on D-1). However, due to the lack of historical forecast data, this improvement is synthetically simulated. The steps applied, starting from the real profiles, remain the same, except for an additional step introduced between the Monte Carlo method and scenario reduction. Specifically, a subset of the newly generated profiles is selected based on a predefined filtering criterion. The goal is to retain only those scenarios that match more closely the actual PV production for the day being simulated—representative of the specific combination of season and irradiance conditions under analysis—while discarding those that deviate significantly. To achieve this, the normalized Root Mean Square Error (nRMSE) is used as the filtering metric, and an appropriate threshold is chosen to ensure that only the most realistic scenarios are retained. Equation (2) shows the calculation of the nRMSE:
represents the number of time intervals (96 quarter-hour periods), is the power at interval q of the generated scenario, and is the real power production.
This parameter was chosen as it effectively balances differences in both absolute value and shape, making it well-suited for assessing forecast accuracy. Its widespread use in the literature as a standard metric for evaluating forecasting model performance further supports its application in this study. For instance, Ref. [49] applies nRMSE to assess the accuracy of solar radiation forecasts, particularly in comparing different forecasting methodologies, while Ref. [50] analyzes various studies that frequently adopt nRMSE for performance evaluation, highlighting its relevance across different forecasting applications.
3.2. Mathematical Model
Once the scenarios have been generated, they serve as inputs for the mathematical optimization models that simulate the participation of the PV + BESS system in the electricity market. Figure 1 illustrates the sequence of the different optimization phases, along with the respective inputs and outputs. The process begins with the optimization of the DAM commercial program using the generated PV scenarios. This is followed by a refinement step in the IDM, leveraging more accurate PV forecasts. It is important to note that in both stages, the actual imbalance prices are not used. Instead, penalties are applied to both positive and negative imbalances to discourage intentional deviations, reflecting the operator’s uncertainty regarding future imbalance prices. Finally, based on the commercial program defined at IDM closure, the real-time operation of the plant is simulated. The objective in this phase is to minimize imbalances. At this stage, the simulation allows the calculation of daily profits using actual imbalance volumes and prices.
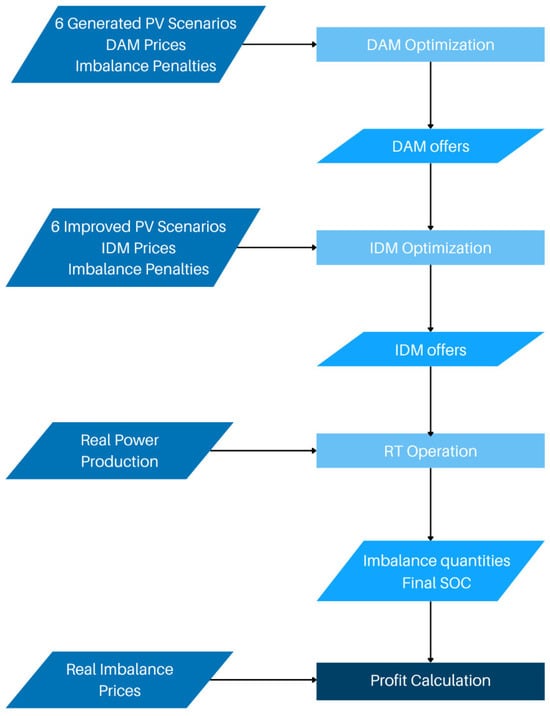
Figure 1.
Optimization sequence.
3.2.1. Day-Ahead Market
The initial PV scenarios, produced using the procedure outlined in Section 3.1.1, along with DAM prices and imbalance penalties, are used as input for the MILP model that optimizes the bidding strategy in the DAM.
Equations (3)–(6) represent the objective function of the first stage of the mathematical model. As shown, the optimal solution corresponds to maximizing the DAM expected profit, while accounting for imbalance costs and battery costs.
The expected profit is calculated as the revenue derived from selling bids submitted in the DAM. Unlike the other two equations, this is not a weighted average across different possible PV production profiles, since the energy offered in the DAM remains the same across all scenarios. In contrast, imbalance quantities and BESS operations vary based on the assumed PV power-production profile. Note that PV scenarios are indexed from 1 to , where indicates the total number of PV scenarios considered in the model. The aim of the optimization is to define a strategy to be submitted to the DAM, representing the best possible compromise for all potential PV daily outcomes before uncertainty is resolved. The term associated with the DAM bid is multiplied by the time interval length (0.25 h) to maintain unit consistency. DAM prices are modeled under a price-taker assumption, given the high market liquidity, and are considered perfectly known in this study. This approach is commonly adopted in the literature for simplifying market modeling and optimizing bidding strategies [51]. Given that the system operates at a 15 min resolution, whereas prices are still at an hourly resolution, a linear interpolation is applied to obtain intermediate values. This choice anticipates the changes expected under TIDE, which will standardize all markets to a single MTU of 15 min.
As described in Section 2.3, Italy follows a single pricing system for imbalance settlement, meaning that imbalance prices depend on the real-time system position for each quarter-hour. However, if perfect foresight were assumed, this pricing mechanism could lead the optimizer to deliberately create imbalances to exploit potential advantages over the DAM price. Since such behavior is unrealistic, given that operators can hardly know imbalance prices in advance, penalties are introduced for both positive and negative imbalances during the DAM and IDM optimization phases. The calculation of the imbalance penalties follows these steps:
- 1.
- Collection of annual DAM prices and imbalance prices.
- 2.
- Calculation of the difference between imbalance prices and DAM prices over each quarter of an hour of the year.
- 3.
- Computation of the annual average imbalance price deviations for each quarter-hour, separately for negative and positive system imbalances.
- 4.
- Finally, each time a day is simulated, imbalance penalties are computed for each quarter-hour by adding the average imbalance price deviations to the actual daily DAM price profile.
Finally, the battery cost is a fictitious compensation term, preventing artificial profits from the energy initially stored in the battery. The calculation assumes that the cost of restoring the initial SOC is based on the DAM annual average price.
To ensure consistency between the physical power flows processed by the PV + BESS system and the commercial dispatch schedule, the following constraint must be imposed:
In Equation (7), the DAM bids remain constant across all scenarios, while the other variables are scenario dependent. To ensure operational coherence, the imbalance power and BESS operation are each modeled using two sets of auxiliary binary variables— and for imbalances, and and for the BESS. The sum of each pair of binary variables is constrained to be less than or equal to one for every timestep q, which prevents simultaneous positive and negative imbalances and avoids charging and discharging the BESS at the same time. It is also important to note that, in this study, the battery is assumed to be charged exclusively by PV generation, with no electricity drawn from the grid.
BESS operations are governed by the following five constraints:
The SOC of the battery can neither exceed nor fall below the threshold in any scenario for any quarter-hour. Excess or insufficient power is converted into positive and negative imbalances, respectively, thereby introducing an economic penalty. Equation (10) defines the SOC update for each quarter-hour based on the BESS-processed power. In particular, the BESS charging and discharging efficiencies are modelled using two-step efficiency curves, following the same methodology outlined in [52], to capture the significant drop in BESS efficiency at low processed power levels. The final two constraints ensure that power flows remain within the maximum allowable limits imposed by the technical specifications of the BESS.
3.2.2. Intra-Day Market
The second stage of the stochastic MILP model consists of solving the IDM. The primary distinction between the two phases is the improvement in PV forecasts. The newly refined forecast scenarios are incorporated as inputs into the model, alongside IDM prices, imbalance penalties, and the bids already submitted in the DAM.
The methodology remains largely unchanged. The objective function follows the same structure of Equation (3), with the only variation concerning the expected profit component, as shown in Equation (13):
In this stage, the additional revenue from IDM transactions is incorporated, complementing the earnings already secured in the DAM. The IDM prices are assumed to be known in advance for the same reasons outlined in the first stage. Given that this study focuses exclusively on participation in the CRIDA2 auction, the corresponding prices are used. To achieve adjustment to the DAM submitted commercial program, IDM bids can take both positive and negative values. A positive IDM bid reflects an additional purchase or an increase in energy injection to compensate for an underestimated DAM position, whereas a negative IDM bid corresponds to a reduction in energy injection or an increase in energy withdrawal, correcting an overestimated DAM position. These adjustments must always remain within the nominal power limits of the system, ensuring feasibility. Additionally, the sum of DAM and IDM bids must never be negative, preserving operational consistency.
Finally, the power balance equation is modified as follows:
3.2.3. Real-Time Operation
The last stage of the mathematical model does not involve an optimization process but rather an operational strategy for real-time management. At this stage, the actual PV power production for each quarter-hour is revealed, fully eliminating uncertainty. Unlike the previous phases, where forecasts and stochastic scenarios influenced decision-making, the real-time strategy relies solely on known values, with no probabilistic components to consider. At each quarter-hour, the model minimizes imbalance quantities as defined in the objective function expressed in Equation (15):
Rather than optimizing for the entire day at once, the model operates sequentially, updating at each time step q. The battery SOC is carried forward from one interval to the next, reflecting a realistic operational framework in which PV production is not known in advance but uncertainty is resolved progressively. To reduce imbalances, the model utilizes the battery’s flexibility. However, due to its physical constraints, long or short imbalances may still occur when the battery reaches either its maximum or minimum SOC.
4. Case Studies and Results
4.1. Analyzed Case Studies
PV production data are sourced from PVGIS [40], a widely used tool that offers significant flexibility in various aspects:
- It allows users to specify the exact geographical location of the PV system; in this study, Piazza Leonardo da Vinci in Milan is selected.
- The time period can vary between 2005 and 2024. In this study, the range 2021–2023 is chosen to ensure a comprehensive representation of production profiles.
- The system type can be customized by selecting fixed panels or tracking systems, allowing further customization of tilt and orientation.
- The installed peak power and system losses can be defined.
The distributed PV power plant analyzed in this study consists of eight fixed rooftop installations located across the Politecnico di Milano Leonardo Campus, with an overall peak power of 1 MW and the characteristics summarized in Table 1. In our azimuth convention, 0° corresponds to south, with positive angles measured westward and negative angles eastward; thus, an azimuth of −180° indicates a north-facing orientation. Please note that the presence of less optimal PV plants not facing south is due to building rooftop architectural constraints.

Table 1.
PV power plants installed at Politecnico di Milano’s Leonardo campus.
The systems employ three main mounting configurations, reflecting the architectural diversity and structural constraints of the selected rooftops. The majority of the systems are rooftop-coplanar, where PV modules are installed flush with the slope and orientation of the existing roof surfaces. Two installations use a ballasted mounting system on flat roofs; in this configuration, modules are secured by weight rather than mechanical anchoring, enabling flexible placement without compromising the roof structure [53]. Finally, one installation is mounted on a barrel-shaped roof, approximated using a simplified model with three tilt sections to represent the curved geometry:
- 50% of the panels positioned at 0° inclination,
- 25% at 15° inclination,
- 25% at −15° inclination (equivalent tilt but opposite azimuth).
Additionally, Figure 2 illustrates the geographical distribution of these rooftop PV systems providing an overview of their spatial layout within the university campus. However, it is important to note that, due to the close proximity of the buildings, PVGIS does not account for localized differences in solar irradiance across the campus. As a result, all rooftop systems are treated as if they are located at the same geographical point, and temporal variations in cloud cover across individual buildings are not captured. Despite this limitation, each system retains its unique tilt and azimuth values, which result in distinct PV production profiles even under the same irradiance conditions. The losses were estimated by observing the actual performance of the systems installed across the university.
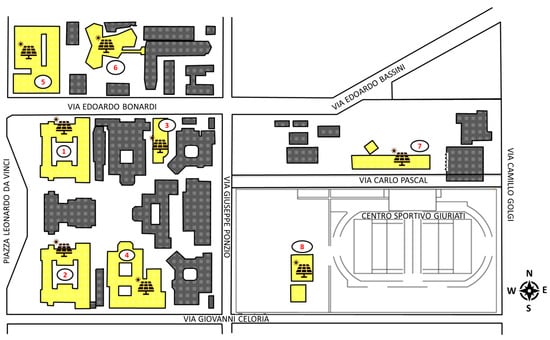
Figure 2.
Map showing the geographical distribution of rooftop PV systems installed at the Politecnico di Milano Leonardo Campus.
Once the system parameters are defined, PVGIS is used to simulate daily PV production profiles for the period 2021–2023. The output from the eight rooftop systems is then aggregated to generate the overall 1 MW production profile representing the distributed PV configuration.
The utility-scale plant considered in this study is a hypothetical ground-mounted system, located at the same geographical site as the rooftop installations and designed with the same peak power of 1 MW to enable a consistent comparison. While the distributed PV systems have varying inclinations and orientations, making the comparison with the utility-scale plant not entirely equivalent, this choice reflects realistic conditions where a VPP includes multiple rooftop systems that cannot all be ideally south-facing. Moreover, this modelling approach allows us to analyze how rooftop geometries affect the overall power-production profile of the VPP, influencing the smoothness of generation compared to the utility-scale system and, consequently, the impact on power-production forecast errors and resulting imbalance volumes.
Moreover, unlike the fixed rooftop systems, this configuration employs a horizontal single-axis tracking system, which allows the PV modules to rotate along a north–south axis. This tracking mechanism follows the sun’s movement from east to west throughout the day, increasing solar exposure and thereby enhancing power production compared to fixed systems [54]. The system is assumed to be installed on flat ground, typical of utility-scale deployments, and system losses are set to 14%, in line with the default value in PVGIS and the assumptions made in ref. [21].
The original PVGIS dataset has an hourly resolution. However, given the 15 min resolution required for following the TIDE regulatory scheme, a linear interpolation method was applied. Although this approach is relatively simple and less precise than more advanced resampling techniques, it is commonly used in the literature [55] and was deemed sufficient here, as increasing time resolution is not the core objective of this study.
As a result, two matrices were constructed, each with dimensions 1095 × 96 (corresponding to three years of daily production profiles, with a 15 min resolution). These matrices represent the complete production datasets for both the rooftop and utility-scale systems.
Once the two matrices have been obtained, they are divided into four seasonal subsets. For each season, the Elbow method is applied to determine the optimal number of clusters for further partitioning the sub-matrices. Figure 3 provides a graphical example of this process for Autumn.
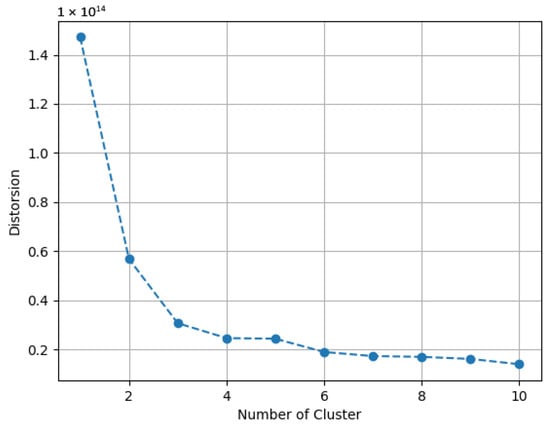
Figure 3.
Determination of the optimal number of clusters for Autumn using the Elbow method.
The analysis identifies three optimal clusters per season, each corresponding to different total radiation levels, influenced by seasonal variations and climatic conditions. Particularly, clusters were defined as Sunny (highest production, clear-sky conditions), Variable (intermediate production, mixed weather), and Cloudy (lowest production, cloudy). This classification led to 4 × 3 = 12 clusters per plant configuration. From each of these 12 clusters, one representative day from 2023 is selected to simulate the market participation of the PV + BESS system. Rather than simulating all days in the year, the analysis is performed only on these 12 representative days, each assumed to typify the operational and production conditions of its corresponding cluster. This methodological choice was driven by both computational and time constraints, allowing for a feasible simulation process while still preserving the seasonal and weather-related variability in solar production. The selected representative days are shown in Table 2.

Table 2.
Selected representative days.
To reconstruct a full-year performance profile from these limited simulations, an occurrence probability is assigned to each cluster based on how frequently it occurs within the three analyzed years. The results obtained from each simulated representative day are then weighted by this probability and scaled to 365 days, effectively allowing the model to approximate annual performance and market participation outcomes from a limited set of representative days. To verify the effectiveness of the method adopted, the Capacity Factor (CF) is calculated as 18.6% for the utility-scale plant and 14.2% for the distributed system, values that are consistent with real-world performance expectations for similar PV installations.
4.2. PV Scenario Generation and Market Data
The first phase of simulating market participation involves generating PV scenarios for DAM using the Monte Carlo method, followed by scenario reduction through k-means clustering, as described in Section 3.1. This process is carried out separately for each selected representative day. It is important to clarify that the scenario-generation method from Section 3.1 is applied using all PV production profiles within the same cluster—meaning all days from the 2021–2023 period that fall under the same category (Sunny, Variable, or Cloudy) and season as the representative day.
To ensure convergence in scenario generation, an uncertainty threshold of 1% is imposed. If this threshold is not reached, the process is automatically terminated after generating 2000 scenarios. These parameters are set to strike a balance between accuracy and computational effort, in line with the values used in similar works [18].
After completing the scenario-generation phase, the number of profiles is reduced using the Elbow method to identify representative cases. Unlike the seasonal clustering, the WCSS curves do not display a clear elbow point, making it challenging to determine the optimal number of scenarios. Nevertheless, six clusters are selected, as this number provides the best trade-off between capturing the key variability in the data and maintaining computational efficiency, with reference to the approach adopted in [18]. As a result, six representative PV production profiles are selected for each of the 12 representative days and for both plant configurations. These profiles represent the forecasted possible PV power-generation scenarios used in the DAM simulation.
To generate the scenarios for the IDM simulation, as detailed in Section 3.1.2, a filtering criterion is introduced. An nRMSE threshold is imposed, varying for each cluster and plant configuration. This differentiation is necessary because a fixed threshold would not be equally effective across all conditions. A threshold that is highly selective for a cloudy day might fail to filter any Monte Carlo-generated scenarios for a sunny day. Conversely, a threshold suitable for a sunny day would eliminate almost all scenarios generated for variable or cloudy clusters. Similarly, the two plant configurations require distinct nRMSE thresholds for the same cluster. To ensure uniformity in the filtering process across all days, the nRMSE threshold is set to retain between 1% and 5% of the generated scenarios. The final step in scenario processing involves further reducing the filtered scenarios using k-means clustering, obtaining six representative scenarios, matching the number used for the DAM, to serve as inputs for the IDM optimization stage.
Figure 4 provides an example of the various processing steps applied to four representative days. The thicker blue line shows the actual PV production on the representative day for the given cluster and is therefore identical for both the DAM and IDM stages. What differs are the six reduced PV scenarios used as inputs for the two stages of the stochastic optimization: the IDM scenarios, produced after the filtering process, are much closer to the actual production profile, while the DAM scenarios show greater deviations since they result from non-filtered Monte Carlo profiles.
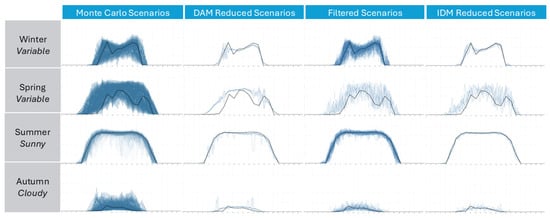
Figure 4.
PV scenario-generation process.
Finally, it is necessary to collect real market price data to provide all the required inputs for the multistage stochastic optimization. The real DAM and IDM prices for the analyzed days were collected from the Italian Energy Market Operator (GME) [56]. The imbalance prices were instead retrieved from Terna’s official database [57].
4.3. Techno-Economic Analysis of PV + BESS Market Participation
The objective of this study is to determine the optimal battery size from both a profitability and a dispatchability perspective. To achieve this, it is crucial to obtain results across a wide range of storage capacities, allowing for a comprehensive evaluation. To avoid excessive computational effort, the Energy-to-Power Ratio (EPR) is fixed at 2. Consequently, storage capacity is varied between 0 and 5 MWh, in steps of 100 kWh. This results in a total of 4 (seasons) × 3 (clusters) × 51 (battery sizes) = 612 market participation simulation, repeated for both plant configurations. At each iteration, the three mathematical models described in Section 3.2 are solved and optimized. The BESS parameters used in the optimization are reported in Table A1 in the Appendix A. Note that, in line with [58], we assume that the modelled lithium-ion BESS operates with a 100% Depth of Discharge (DoD). This assumption reflects our aim to simulate fully unconstrained BESS operation, leaving the optimizer free to exploit the entire available capacity.
The total profit is computed as follows:
where and are the residual imbalances following the system real-time operations.
The total profit is initially calculated for each of the 12 representative days across the different battery sizes. To estimate the annual total profit for each BESS capacity, these daily profits are combined using a weighted average. The weights correspond to the occurrence probabilities of each cluster, which represent how frequently each type of day (Sunny, Variable, or Cloudy) in each season (Winter, Spring, Summer, Autumn) occurs during the 2021–2023 period used to generate the PV scenarios. The occurrence percentages of each cluster, for both the utility-scale plant and the distributed PV system, are presented in Table 3. It is important to note that these percentages differ slightly between the two configurations because the clustering process was performed separately based on their respective PV production profiles. However, since both systems are modeled at the same geographical location, the percentages are quite similar, reflecting consistent radiation level patterns.

Table 3.
Occurrence probabilities of each cluster for both the utility-scale and distributed PV configurations.
In the following sections, we present the results of our analysis assessing the economic impact and improved dispatchability achieved through BESS installation for both configurations. The analysis consists of three steps. First, we determine the minimum BESS size required to reduce annual imbalance volumes—relative to the PV plant’s total production—to below 5%. This threshold is based on [32], which reports that imbalances in Italy accounted for 5.6% of national demand in 2016. To isolate the effect on dispatchability, we run simulations using constant DAM and IDM prices across both stages, so that the optimization focuses solely on minimizing imbalances, excluding any gains from energy arbitrage. This allows us to estimate the net cost of making the PV system dispatchable. In the second step, recognizing that a BESS cannot be financially justified if used solely to reduce imbalances, we assess the system economic performance when the storage is optimally used also for energy arbitrage in DAM and IDM. This allows us to identify the optimal BESS size and associated revenues for both the utility-scale and distributed configurations. Finally, we combine the two perspectives to evaluate the optimal BESS size when a 5% imbalance constraint is enforced. The economic analysis is based on two indicators: the LCOE, which is used to capture the system cost increase due to BESS installation; and the NPV, which estimates the economic returns over the system’s lifetime.
The LCOE is computed as in Equation (21) over a 30-year horizon aligned with the PV plant’s expected lifetime:
In Equation (21) the term represents the PV power production that is sold to the grid during the simulated year, accounting for the BESS round-trip efficiency when the power is not immediately injected but is instead stored and subsequently discharged. PV CAPEX and OPEX are taken from [59]: the Commercial PV category is used for the distributed system (CAPEX = EUR 1300 k/MW, OPEX = EUR 15 k/MW), while the Utility Scale category is used for the utility-scale system with tracking (CAPEX = EUR 950 k/MW, OPEX = EUR 17.5 k/MW). The BESS is assumed to have a 10-year lifetime, requiring two replacements over 30 years and ending without any residual value. BESS CAPEX is modeled as in [52], with an energy-related cost of EUR 250 k/MWh (battery banks) and a power-related cost of EUR 80 k/MW (inverter and grid integration). OPEX is estimated at EUR 5 k/MWh/year. The LCOE denominator includes only the energy exchanged with the grid—i.e., net of BESS round-trip losses in PV + BESS configurations. A discount rate r of 5% is assumed, in line with values adopted in comparable studies [60,61,62].
Based on the same parameters, the NPV can be calculated over a 10-year horizon as follows:
This NPV formulation evaluates whether the BESS investment adds economic value to the system by accounting only for the BESS-related CAPEX and OPEX, as well as the incremental annual revenues generated with the BESS in the simulated year compared to the baseline case without storage. It is assumed that these incremental revenues remain constant and are repeated uniformly over the entire project.
4.3.1. Economic Impact of Dispatchability Constraints
Assuming that only the PV plant participates in the DAM and IDM and using the PV production scenarios described in Section 4.2, the annual imbalance volume for the utility-scale configuration with horizontal single-axis tracking amounts to approximately 11% of total energy production, while for the distributed configuration it is around 8%. As shown in Figure 5, if a BESS is added solely to reduce imbalance volumes below the 5% threshold—acting only in real time to compensate for unavoidable PV forecasting errors—the required storage capacity is 220 kWh for the utility-scale system and 50 kWh for the distributed system. Please note that, for this calculation, the resolution of the BESS sizes analyzed has been refined to 10 kWh increments (from 0 to 300 kWh) to identify more precise capacity values, which would not have been possible with a 100 kWh granularity.
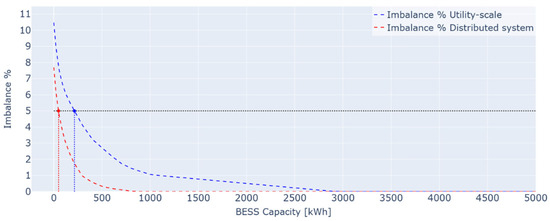
Figure 5.
Normalized imbalance volume as a function of BESS capacity under firming-only strategy.
With a 220 kWh BESS for the utility-scale system and a 50 kWh BESS for the distributed system, the annual imbalance levels are reduced to 4.94% and 4.98%, respectively. Figure 5 also illustrates that, for the distributed system, imbalances could be reduced to negligible levels with a 500 kWh BESS, whereas the utility-scale system would require a 2500 kWh BESS to achieve the same result.
This difference in imbalance volumes is due to the PV scenarios used as input for the DAM and IDM optimization: the PV production profiles are smoother for the distributed system, making it easier to develop a commercial market program that closely matches the range of possible PV production outcomes compared to the utility-scale system. This concept is further discussed in Section 4.3.3.
Figure 6 shows the LCOE for both configurations in the base case (without BESS) and in the firm cases described above. The cost of firming is approximately EUR 6/MWh for the utility-scale system, resulting in a 13.1% increase in LCOE, and around EUR 1.5/MWh for the distributed system, with a 1.94% increase. This means that, to cover their costs over a 30-year lifetime, the firmed PV power plants would require the injected energy to be remunerated at an average electricity price of EUR 52.49/MWh and EUR 77.30/MWh, respectively—levels that would be achievable under current market conditions, considering that the average DAM price for the “NORD” zone in 2023 was EUR 128/MWh.
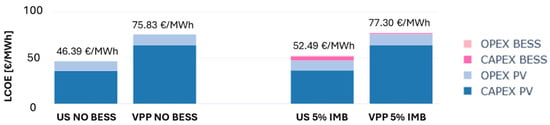
Figure 6.
LCOE increase required to achieve dispatchability without market-based optimization.
However, it is important to highlight that installing such battery sizes solely to minimize imbalances does not generate sufficient revenues to recover the BESS investment costs. Specifically, calculating the NPV using the formulation in Equation (22), under current BESS costs, yields −61 k€ for the utility-scale system and −20 k€ for the distributed one, meaning that installing a BESS under these conditions would result in a significant financial loss compared to simply operating the PV plant alone. This highlights the need to identify additional revenue streams for the BESS, such as using it for energy arbitrage in the DAM and IDM, to make the investment worthwhile.
4.3.2. Unconstrained Optimal BESS Sizing
This section analyzes the optimal operation of the PV + BESS system in electricity markets under varying BESS size and without imposing any constraints on imbalance volumes. Figure 7 presents the annual profit trend and its derivative as battery capacity increases.
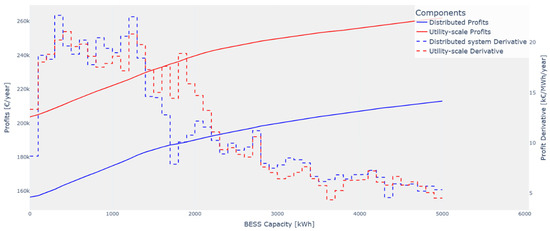
Figure 7.
Annual profit as a function of BESS size under optimal market participation.
As expected, the profit generated by the PV + BESS system increases with battery size. However, the rate of increase is not uniform: for smaller storage capacities, profit grows significantly, whereas for larger capacities, the marginal benefit decreases. This decreasing revenue suggests that increasing BESS capacity beyond a certain threshold no longer provides proportional economic benefits.
To assess the economic feasibility of BESS installation we compute the NPV as in Equation (22). The results indicate that, for any battery size, the NPV remains negative. This suggest that, under 2023 electricity market conditions and assumed battery costs, for a participation limited to DAM and IDM, a battery does not generate sufficient revenue to fully recover its costs. From a strictly economic perspective, the most financially advantageous solution is to operate without a BESS, for both system configurations.
Therefore, we identify the maximum battery bank cost at which at least one PV + BESS configuration remains economically viable, defined as achieving a positive NPV. This threshold is approximately half the current cost, around 125 kEUR/MWh. Figure 8 shows the total 10-year revenue for each battery size after accounting for this reduced BESS cost. The optimal battery sizes that maximize net profit fall within the 1–2 MWh range for both configurations, though differences in profitability within this range are minimal and difficult to distinguish visually. Specifically, the highest net profit is achieved with a 1.4 MWh BESS for the utility-scale system and a 1.3 MWh BESS for the distributed system. For comparison, under current BESS costs, these same configurations would result in NPVs of −239 k€ and −221 k€, respectively.
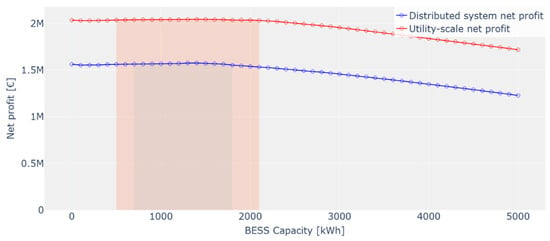
Figure 8.
Overall net profit as a function of BESS capacity considering 125 kEUR/MWh battery bank cost under optimal market participation. The shaded areas indicate the BESS configurations where the PV + BESS system achieves higher economic returns than the PV-only system under the given BESS cost scenario.
The shaded areas in Figure 8 highlight the configurations where the PV + BESS system outperforms the PV-only baseline under the assumed BESS cost scenario. These areas largely overlap, with the utility-scale system exhibiting a slightly broader profitable range. In both cases, installing more than 2 MWh of storage does not yield additional economic benefits because the daily energy available for shifting is limited by the PV system’s 1 MW peak capacity, so adding more storage does not proportionally increase the potential for profitable arbitrage.
4.3.3. Optimal BESS Sizing Under Dispatchability Constraint
This study also aims to investigate how the dispatchability of the system is influenced by increasing battery size under optimal market participation. To achieve this, annual normalized imbalance volumes under optimal market participation are presented for each considered BESS capacity for both the utility-scale plant and the distributed system in Figure 9. As in Figure 5, the graph shows that the utility-scale plant exhibits higher normalized imbalanced volumes than the distributed system for most of the BESS size range.
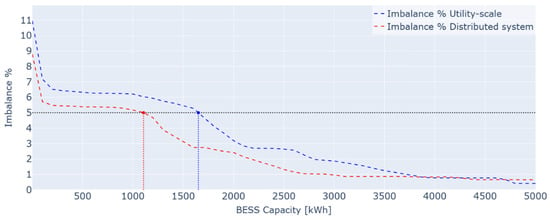
Figure 9.
Normalized imbalance volume as a function of BESS capacity under optimal market participation.
To investigate the reasons behind the imbalance volume differences between the two configurations, we analyze the days with the largest imbalance discrepancies. For this analysis, we select a BESS capacity of 1.4 MWh, identified in the previous section as an optimal size. With this fixed capacity, we collect the seven components of the system’s energy balance at 15 min resolution across 12 representative days: solar production, charging power, discharging power, DAM bids, IDM bids, and both short and long imbalance volumes. Figure 10 and Figure 11 display the corresponding diagrams for the utility-scale and the distributed configurations operating on the representative autumn day with variable conditions.
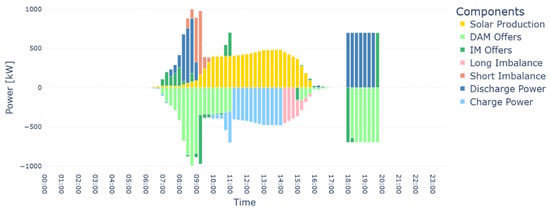
Figure 10.
Energy balance on Autumn Variable Weather Day for a utility-scale system with a 1.4 MWh BESS under optimal market participation.
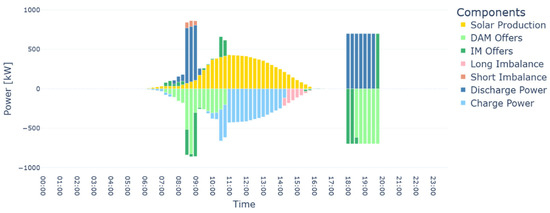
Figure 11.
Energy balance on Autumn Variable Weather Day for a distributed system with a 1.4 MWh BESS under optimal market participation.
It can be seen that the horizontal tracking system of the utility-scale plant produces sharper profiles with two peaks in power production throughout the day. In contrast, the distributed system generally exhibits smoother profiles, with a smaller volume of generated energy. This is further illustrated in Figure 12, which shows the percentage difference in annual PV production between the two systems as function of time. It is clear that the largest production difference occurs at the beginning and end of the day, with the distributed system generating significantly less energy during these periods. This suggests that the utility-scale plant benefits from a longer daily production window, enabling a wider range of production patterns and introducing greater forecast uncertainty. As a result, there is a higher likelihood of committing to a commercial schedule that leads to unavoidable imbalances.
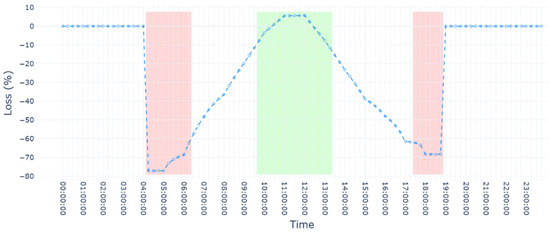
Figure 12.
Average percentage difference in solar power output between the distributed and utility-scale configurations over the year. Red shaded areas indicate time intervals when the utility-scale configuration significantly outperforms the distributed configuration, while the green shaded area highlights periods when the PV power outputs of the two configurations are more comparable.
Referring back at Figure 9, we observe that the minimum BESS sizes required to meet the imposed 5% imbalance threshold, under optimal BESS market participation, are 1.1 MWh for the distributed system and 1.7 MWh for the utility-scale system. This indicates that the dispatchability constraint does not limit the economic optimum for the distributed configuration, as its optimal BESS size (1.3 MWh) exceeds the minimum required (1.1 MWh). In contrast, for the utility-scale system, the optimal size (1.4 MWh) falls below the 1.7 MWh needed for dispatchability, meaning that enforcing this constraint reduces profitability.
As a final step, we aim to determine the cost of making a PV system dispatchable defined as achieving an annual imbalance volume below 5% of total annual production under the condition that the installed BESS must also engage in energy arbitrage to recover its investment costs. Therefore, Figure 13 compares the LCOE of the PV-only system with that of the PV+BESS systems for both the utility-scale and distributed configurations, using the minimum BESS sizes required to keep the relative annual imbalance below the 5% threshold (respectively, 1.7 MWh and 1.1 MWh) and employing current BESS costs.
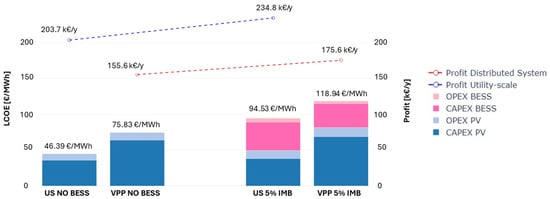
Figure 13.
LCOE increase required to achieve dispatchability with market-based optimization.
It is clear that the LCOE is significantly higher for BESS-integrated solutions in both configurations. For the utility-scale system, the LCOE increases from 46 EUR/MWh to 95 EUR/MWh, while for the distributed system, it rises from 76 EUR/MWh to 119 EUR/MWh. Therefore, if the BESS is also used to maximize system profit through spot market arbitrage, the relative increase in LCOE amounts to 104% for the utility-scale system and 56.9% for the distributed one.
The LCOE increase reflects the cost of firming which the two systems must bear to minimize imbalances at a negligible level when performing energy arbitrage. If the additional profits generated by a larger BESS compensate for this cost increase, the system achieves an optimum in both profitability and dispatchability. For the PV + BESS configurations reported in Figure 13, the NPV under current BESS costs is negative in both cases and much worse than in the pure firming scenario presented in Section 4.3.1: −295 k€ for the utility-scale system compared to −61 k€, and −191 k€ for the distributed system compared to −20 k€. However, assuming reduced BESS costs, as discussed in Section 4.3.2, could make larger BESS capacities more economically viable.
It is also important to note that this analysis considers only revenues from participation in the day-ahead and intra-day markets. Additional revenue streams—such as ancillary services—could further improve the economic performance, particularly if the battery is underutilized in the current configuration. To evaluate this, we compute the battery’s Capacity Factor (CF) as follows:
Here, d represents one of the 12 selected typical days, and represents its corresponding probability of occurrence (see Table 3). A weighted average of the daily contributions is used to determine the total energy exchanged by the battery over an average day. The denominator accounts for the maximum theoretically exchangeable energy in a single day. For battery sizes ensuring imbalance percentages of around 5%, the calculated CF values are 18.6% for the utility-scale plant and 14.2% for the distributed system. These values confirm that the battery is not fully utilized across all operational hours, indicating strong potential for additional service provision.
5. Discussion
This study develops a multistage stochastic optimization framework to assess the participation of a 1 MW PV system coupled with a BESS in the Italian electricity spot markets, accounting for both DAM and IDM operations. Two configurations—utility-scale and distributed—are analyzed to determine the optimal battery size for each.
To explore the technical and economic interplay between storage sizing and system performance, the study investigates the trade-off between dispatchability and profitability. An overview of the economic results in terms of LCOE and NPV for each of the main BESS configurations analyzed in this study is provided in Table A2 in Appendix A.
When considering PV-only systems, the LCOE is calculated at 46.39 EUR/MWh for the utility-scale system and 75.83 EUR/MWh for the distributed one. Introducing a BESS used solely to meet the 5% annual imbalance threshold—without optimizing for market revenues—requires 220 kWh of storage for the utility-scale system and 50 kWh for the distributed system. This increases the LCOE to 52.49 EUR/MWh and 77.30 EUR/MWh, respectively, which remain significantly below the firmed PV LCOE estimated by Lazard in the CAISO context (141 USD/MWh) [34]. For a better comparison, it should be noted that, for the same PV peak power, Lazard’s study assumes a 2 MWh BESS.
However, the firming-only strategy proves economically inefficient with respect to PV stand-alone, as minimizing imbalances alone does not yield sufficient revenue to offset current storage costs, resulting in negative NPVs of −61 k€ and −20 k€, respectively. An alternative approach is to leverage the BESS for energy arbitrage in both DAM and IDM, while also minimizing imbalances in real time. Yet, under current market conditions and battery costs, BESS operation results in negative NPVs across all tested sizes—making PV-only systems the most economically viable option. Nevertheless, future reductions in battery CAPEX, as well as access to additional revenue streams (e.g., frequency regulation services), could significantly improve the financial viability of PV + BESS systems.
To simulate such a future scenario, we assume a 50% reduction in battery bank investment costs—from 250 kEUR/MWh to 125 kEUR/MWh—representing the break-even threshold at which at least one BESS size yields a positive NPV for both configurations. In this scenario, the optimal BESS size (without dispatchability constraints) becomes 1.4 MWh for utility-scale and 1.3 MWh for distributed systems, yielding slightly positive NPVs. For reference, under current BESS costs, the same configurations would result in NPVs of −239 k€ and −221 k€.
Finally, we reintroduce the 5% imbalance constraint while maintaining energy arbitrage strategies. For the utility-scale system, this raises the minimum required BESS size to 1.7 MWh, resulting in a return to negative NPV, even under reduced battery costs. In contrast, the distributed system with a 1.3 MWh BESS remains within the dispatchability threshold, as the minimum required size to meet firm operation is 1.1 MWh. Therefore, no resizing is needed.
Calculating the LCOE under current BESS costs for these minimum dispatchable configurations yields 94.53 EUR/MWh for the utility-scale system with a 1.7 MWh BESS, and 118.94 EUR/MWh for the distributed system with a 1.1 MWh BESS. These higher LCOE values reflect the trade-off between system firmness and storage utilization. Using BESS solely for imbalance minimization would require smaller storage capacities, resulting in lower LCOE but also negative NPVs. Conversely, leveraging the BESS for energy arbitrage—assuming it generates enough revenue to offset its cost—leads to higher LCOE values, but potentially enables positive NPVs.
These findings highlight that distributed systems—due to smoother production profiles—benefit from improved forecast accuracy when using a Monte Carlo scenario-generation approach. This allows them to achieve dispatchability with smaller storage capacities. In contrast, utility-scale systems face more variability and require larger batteries to meet the same dispatchability targets, making investment recovery more difficult.
Several directions for future research emerge from this work, which should be considered alongside its current limitations. First, the study assumes perfect foresight of DAM and IDM prices, an idealization that overlooks real-world price uncertainty; future work could incorporate stochastic or forecast-based price modelling to enhance realism. Second, PV scenario generation could be refined by using historical PV forecasts and actual plant data, allowing for more realistic DAM-IDM transitions and better modeling of forecast uncertainty across time horizons. Third, the imbalance penalties used in the model are artificially defined and could be improved by adopting more realistic market-based or regulatory penalty structures, or by incorporating forecasts of imbalance prices under the single pricing scheme. Additionally, the ancillary services market, especially frequency regulation provision, is not included but would be important to consider for a more complete evaluation of BESS revenue streams. Battery degradation is also omitted in this analysis and should be integrated in future studies to assess long-term performance and cost recovery. Finally, investigating a variable BESS EPR could yield deeper insights into the optimal balance between storage capacity and power availability.
Author Contributions
Conceptualization, A.S., R.P., D.A., G.R., M.D. and F.B.; methodology, A.S., R.P. and F.B.; software, A.S. and R.P.; validation, A.S., R.P., G.R., M.D. and F.B.; formal analysis, A.S. and R.P.; investigation, A.S. and R.P.; resources, A.S., D.A., G.R. and F.B.; data curation, R.P.; writing—original draft preparation, A.S. and R.P.; writing—review and editing, A.S., R.P., D.A., G.R., M.D. and F.B.; visualization, A.S., R.P. and F.B.; supervision, F.B.; project administration, A.S. and F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be made available by authors upon request.
Acknowledgments
During the preparation of this manuscript/study, the authors used ChatGPT-4o mini to improve the English fluency and clarity of the text. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ASM | Ancillary Services Market |
| BESS | Battery Energy-Storage System |
| BTM | Behind-The-Meter |
| CF | Capacity Factor |
| CRIDA | Complementary Regional Intra-Day Auction |
| DAM | Day-Ahead Market |
| DER | Distributed Energy Resource |
| EPR | Energy to Power Ratio |
| EU | European Union |
| FTM | Front-of-The-Meter |
| GTC | Gate Time Closure |
| HEMS | Home Energy Management System |
| IDM | Intra-Day Market |
| ISP | Imbalance Settlement Period |
| LCOE | Levelized Cost Of Electricity |
| MILP | Mixed-Integer Linear Programming |
| MTU | Market Time Unit |
| NP-RESs | Non-Programmable Renewable Energy Sources |
| NPV | Net Present Value |
| nRMSE | normalized Root Mean Square Error |
| PV | Photovoltaic |
| PVGIS | Photovoltaic Geographical Information System |
| RESs | Renewable Energy Sources |
| RTP | Real-Time Pricing |
| SOC | State Of Charge |
| SPT | Stepwise Power Tariff |
| TIDE | Testo Integrato del Dispacciamento Elettrico |
| TOU | Time Of Use |
| TSO | Transmission System Operator |
| VPP | Virtual Power Plant |
| UVA | Unità Virtuale Abilitata |
| WCSS | Within-Cluster Sum of Squares |
| XBID | Cross-Border Intra-Day |
Nomenclature
| Sets | Maximum state of charge (%) | ||
| q | Quarter-hour of the day (from 1 to 96) | Charging efficiency (-) | |
| i | Photovoltaic scenario (from 1 to 6) | Discharging efficiency (-) | |
| Parameters | Battery maximum power (MW) | ||
| DAM price at interval q (EUR/MWh) | PV power at interval q in scenario i (MW) | ||
| IDM price at interval q (EUR/MWh) | Variables | ||
| Negative imbalance penalty at interval q (EUR/MWh) | DAM power offer at interval q (MW) | ||
| Positive imbalance penalty at interval q (EUR/MWh) | IDM power offer at interval q (MW) | ||
| Mean DAM price used as reference (EUR/MWh) | Negative imbalance power at interval q in scenario i (MW) | ||
| Real imbalance price (EUR/MWh) | Positive imbalance power at interval q in scenario i (MW) | ||
| Scenario i probability (%) | Charging power at interval q in scenario i (MW) | ||
| Time interval length (h) | Discharging power at interval q in scenario i (MW) | ||
| Initial state of charge (%) | State of charge at interval q in scenario i (%) | ||
| Battery capacity (MWh) | Binary variables defining if the imbalance is negative or positive (-) | ||
| Minimum state of charge (%) | Binary variables defining if the battery is charging or discharging (-) |
Appendix A

Table A1.
BESS parameters employed in this study.
Table A1.
BESS parameters employed in this study.
| Parameter | Value | Reference |
|---|---|---|
| 55% if BESS power < 15% ; 97.2% otherwise | [52] | |
| 50% if BESS power < 15% ; 86.8% otherwise | [52] | |
| [0, 100, 200, …, 4900, 5000] kWh | [-] | |
| 2 h | [-] | |
| 250 kEUR/MWh | [52] | |
| EUR 80 k/MW | [52] | |
| 100% | [58] | |
| 5 kEUR/MWh/y | [52] | |
| 50% | [-] | |
| 100% | [-] |

Table A2.
Key numerical results for the three scenarios considered in this study.
Table A2.
Key numerical results for the three scenarios considered in this study.
| Utility Scale | Distributed System | ||
|---|---|---|---|
| Firming only | BESS size (kWh) | 220 | 50 |
| LCOE (EUR/MWh) | 52.49 (+13.1% vs. PV-only) | 77.30 (+1.94% vs. PV-only) | |
| NPV (k€) | −61 | −20 | |
| Optimal market participation—no imbalance constraint | BESS size (kWh) | 1400 | 1300 |
| LCOE (EUR/MWh) | 86.60 (+86.7% vs. PV-only) | 125.74 (+65.8% vs. PV-only) | |
| NPV (k€) | −239 | −221 | |
| Optimal market participation + firming | BESS size (kWh) | 1700 | 1100 |
| LCOE (EUR/MWh) | 94.53 (+104% vs. PV-only) | 118.94 (+56.9% vs. PV-only) | |
| NPV (k€) | −295 | −191 | |
(1) LCOE and NPV values are calculated based on current cost estimates for PV and BESS systems. (2) The NPV refers only to the BESS investment, as detailed in Equation (22).
References
- Greenhouse Gas Emissions from Energy Data Explorer—Data Tools—IEA. Available online: https://www.iea.org/data-and-statistics/data-tools/greenhouse-gas-emissions-from-energy-data-explorer (accessed on 8 May 2025).
- The Paris Agreement|UNFCCC. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement (accessed on 8 May 2025).
- The European Green Deal—European Commission. Available online: https://commission.europa.eu/strategy-and-policy/priorities-2019-2024/european-green-deal_en (accessed on 8 May 2025).
- Global Overview—Renewables 2024—Analysis—IEA. Available online: https://www.iea.org/reports/renewables-2024/global-overview (accessed on 8 May 2025).
- Rosslowe, C.; Petrovich, B. European Electricity Review 2025. 2025. Available online: https://ember-energy.org/app/uploads/2025/01/EER_2025_22012025.pdf (accessed on 28 May 2025).
- SolarPower Europe. EU Market Outlook for Solar Power 2024–2028. Available online: https://www.solarpowereurope.org/insights/outlooks/eu-market-outlook-for-solar-power-2024-2028/detail (accessed on 17 March 2025).
- ARERA. TIDE—Testo Integrato del Dispacciamento Elettrico. Available online: https://www.arera.it/area-operatori/produzione-tide (accessed on 8 May 2025).
- European Parliament. Directive—2019/944—EN—EUR-Lex. Available online: https://eur-lex.europa.eu/eli/dir/2019/944/oj/eng (accessed on 8 May 2025).
- ESO. Balancing Costs: Annual Report and Future Projections. Available online: https://www.neso.energy/document/318666/download (accessed on 28 May 2025).
- European Network of Transmission System Operators for Electricity. Balancing Report 2024. 2024. Available online: https://eepublicdownloads.blob.core.windows.net/public-cdn-container/clean-documents/news/2024/240628_ENTSO-E_Balancing_Report_2024.pdf (accessed on 28 May 2025).
- Saldarini, A.; Longo, M.; Brenna, M.; Zaninelli, D. Battery Electric Storage Systems: Advances, Challenges, and Market Trends. Energies 2023, 16, 7566. [Google Scholar] [CrossRef]
- IEA. Batteries and Secure Energy Transitions. Paris. Available online: https://www.iea.org/reports/batteries-and-secure-energy-transitions (accessed on 28 May 2025).
- Hannan, M.A.; Wali, S.; Ker, P.; Rahman, M.A.; Mansor, M.; Ramachandaramurthy, V.; Muttaqi, K.; Mahlia, T.; Dong, Z. Battery energy-storage system: A review of technologies, optimization objectives, constraints, approaches, and outstanding issues. J. Energy Storage 2021, 42, 103023. [Google Scholar] [CrossRef]
- Niu, D.; Fang, J.; Yau, W.; Goetz, S.M. Comprehensive evaluation of energy storage systems for inertia emulation and frequency regulation improvement. Energy Rep. 2023, 9, 2566–2576. [Google Scholar] [CrossRef]
- Rezaeimozafar, M.; Monaghan, R.F.D.; Barrett, E.; Duffy, M. A review of behind-the-meter energy storage systems in smart grids. Renew. Sustain. Energy Rev. 2022, 164, 112573. [Google Scholar] [CrossRef]
- Zheng, K.; Sun, Z.; Song, Y.; Zhang, C.; Zhang, C.; Chang, F.; Yang, D.; Fu, X. Stochastic Scenario Generation Methods for Uncertainty in Wind and Photovoltaic Power Outputs: A Comprehensive Review. Energies 2025, 18, 503. [Google Scholar] [CrossRef]
- Shi, Q.; Li, F.; Kuruganti, T.; Olama, M.M.; Dong, J.; Wang, X.; Winstead, C. Resilience-Oriented DG Siting and Sizing Considering Stochastic Scenario Reduction. IEEE Trans. Power Syst. 2021, 36, 3715–3727. [Google Scholar] [CrossRef]
- Falabretti, D.; Gulotta, F.; Siface, D. Scheduling and operation of RES-based virtual power plants with e-mobility: A novel integrated stochastic model. Int. J. Electr. Power Energy Syst. 2023, 144, 108604. [Google Scholar] [CrossRef]
- Gabrel, V.; Murat, C.; Thiele, A. Recent advances in robust optimization: An overview. Eur. J. Oper. Res. 2014, 235, 471–483. [Google Scholar] [CrossRef]
- Nemati, H.; Sánchez-Martín, P.; Sigrist, L.; Rouco, L.; Ortega, Á. Flexible robust optimization for Renewable-only VPP bidding on electricity markets with economic risk analysis. Int. J. Electr. Power Energy Syst. 2025, 167, 110594. [Google Scholar] [CrossRef]
- Silva, A.R.; Pousinho, H.M.I.; Estanqueiro, A. A multistage stochastic approach for the optimal bidding of variable renewable energy in the day-ahead, intraday and balancing markets. Energy 2022, 258, 124856. [Google Scholar] [CrossRef]
- Visser, L.R.; AlSkaif, T.A.; Khurram, A.; Kleissl, J.; van Sark, W.G.H.J.M. Probabilistic solar power forecasting: An economic and technical evaluation of an optimal market bidding strategy. Appl. Energy 2024, 370, 123573. [Google Scholar] [CrossRef]
- Rancilio, G.; Dimovski, A.; Bovera, F.; Moncecchi, M.; Falabretti, D.; Merlo, M. Service stacking on residential BESS: RES integration by flexibility provision on ancillary services markets. Sustain. Energy Grids Netw. 2023, 35, 101097. [Google Scholar] [CrossRef]
- Li, J. Optimal sizing of grid-connected photovoltaic battery systems for residential houses in Australia. Renew. Energy 2019, 136, 1245–1254. [Google Scholar] [CrossRef]
- Duman, A.C.; Erden, H.S.; Gönül, Ö.; Güler, Ö. Optimal sizing of PV-BESS units for home energy management system-equipped households considering day-ahead load scheduling for demand response and self-consumption. Energy Build. 2022, 267, 112164. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, Y.; Lin, X.; Li, C.; Cai, Z.; Yang, P. Optimal sizing of PV and bess for a smart household considering different price mechanisms. IEEE Access 2018, 6, 41050–41059. [Google Scholar] [CrossRef]
- DICOPT. Available online: https://www.gams.com/latest/docs/S_DICOPT.html (accessed on 24 May 2025).
- Rezaeimozafar, M.; Duffy, M.; Monaghan, R.F.D.; Barrett, E. Residential PV-battery scheduling with stochastic optimization and neural network-driven scenario generation. Energy Rep. 2024, 12, 418–429. [Google Scholar] [CrossRef]
- Guo, Y.; Gong, Y.; Fang, Y.; Khargonekar, P.P. Stochastic minimization of imbalance cost for a virtual power plant in electricity markets. In Proceedings of the 2014 IEEE PES Innovative Smart Grid Technologies Conference, ISGT 2014, Washington, DC, USA, 19–22 February 2014. [Google Scholar] [CrossRef]
- Marneris, I.G.; Ntomaris, A.V.; Biskas, P.N.; Baslis, C.G.; Chatzigiannis, D.I.; Demoulias, C.S.; Oureilidis, K.O.; Bakirtzis, A.G. Optimal Participation of RES Aggregators in Energy and Ancillary Services Markets. IEEE Trans. Ind. Appl. 2023, 59, 232–243. [Google Scholar] [CrossRef]
- Pierro, M.; Perez, R.; Perez, M.; Moser, D.; Cornaro, C. Italian protocol for massive solar integration: Imbalance mitigation strategies. Renew. Energy 2020, 153, 725–739. [Google Scholar] [CrossRef]
- Pierro, M.; Perez, R.; Perez, M.; Prina, M.G.; Moser, D.; Cornaro, C. Italian protocol for massive solar integration: From solar imbalance regulation to firm 24/365 solar generation. Renew. Energy 2021, 169, 425–436. [Google Scholar] [CrossRef]
- Pierro, M.; Perez, R.; Perez, M.; Moser, D.; Cornaro, C. Imbalance mitigation strategy via flexible PV ancillary services: The Italian case study. Renew. Energy 2021, 179, 1694–1705. [Google Scholar] [CrossRef]
- Lazard 2023 Levelized Cost of Energy + Report|Lazard. Available online: https://www.lazard.com/research-insights/2023-levelized-cost-of-energyplus/ (accessed on 9 June 2025).
- CAISO. Home | California ISO. Available online: https://www.caiso.com/ (accessed on 9 June 2025).
- Renewable Energy Progress Tracker—Data Tools—IEA. Available online: https://www.iea.org/data-and-statistics/data-tools/renewable-energy-progress-tracker (accessed on 7 May 2025).
- Pyomo. Available online: https://www.pyomo.org/ (accessed on 24 May 2025).
- Gurobi Optimization. Available online: https://www.gurobi.com/ (accessed on 24 May 2025).
- Politecnico di Milano. PoliGrid—A Smart Grid in Piazza Leonardo. Available online: https://www.polimi.it/en/sustainable-development/environment/energy-and-decarbonisation/energy-committee/translate-to-english-poligrid (accessed on 9 May 2025).
- European Commission. Photovoltaic Geographical Information System (PVGIS). Available online: https://joint-research-centre.ec.europa.eu/photovoltaic-geographical-information-system-pvgis_en (accessed on 9 May 2025).
- Regulation—2017/2195—EN—EUR-Lex. Available online: https://eur-lex.europa.eu/eli/reg/2017/2195/oj/eng (accessed on 9 May 2025).
- GME. Spot Market (MPE). Available online: https://www.mercatoelettrico.org/en-us/Home/Markets/ElectricityMarket/Spot-Market-MPE (accessed on 9 May 2025).
- GME. Vademecum to the Italian Power Exchange. Available online: https://www.mercatoelettrico.org/Portals/0/Documents/en-us/20250101VademecumBorsaElettrica_En.pdf (accessed on 9 May 2025).
- ARERA. Delibera 19 Marzo 2019 103/2019/R/eel. Available online: https://www.arera.it/atti-e-provvedimenti/dettaglio/19/103-19 (accessed on 27 June 2025).
- ARERA. Delibera 23 Novembre 2021 523/2021/R/eel. Available online: https://www.arera.it/atti-e-provvedimenti/dettaglio/21/523-21 (accessed on 9 May 2025).
- Scrocca, A.; Andreotti, D.; Spiller, M.; Rancilio, G.; Bovera, F.; Delfanti, M. Impact of Dynamic Imbalance Pricing on Electricity Market Operators in Italy. In Proceedings of the 2025 21st International Conference on the European Energy Market (EEM), Lisbon, Portugal, 27–29 May 2025; pp. 1–8. [Google Scholar] [CrossRef]
- Abud, T.P.; Augusto, A.A.; Fortes, M.Z.; Maciel, R.S.; Borba, B.S.M.C. State of the Art Monte Carlo Method Applied to Power System Analysis with Distributed Generation. Energies 2023, 16, 394. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Krishnan, N.; Kumar, K.R.; Inda, C.S. How solar radiation forecasting impacts the utilization of solar energy: A critical review. J. Clean. Prod. 2023, 388, 135860. [Google Scholar] [CrossRef]
- Lago, J.; Marcjasz, G.; De Schutter, B.; Weron, R. Forecasting day-ahead electricity prices: A review of state-of-the-art algorithms, best practices and an open-access benchmark. Appl. Energy 2021, 293, 116983. [Google Scholar] [CrossRef]
- Scrocca, A.; Bovera, F.; Rancilio, G.; Delfanti, M.; Zatti, M. Techno-Economic Optimization of Services Stacking for a Battery Participating to Electricity Spot Markets. In Proceedings of the International Conference on the European Energy Market, EEM, Istanbul, Turkiye, 10–12 June 2024. [Google Scholar] [CrossRef]
- Vandewetering, N.; Jamil, U.; Pearce, J.M. Ballast-Supported Foundation Designs for Low-Cost Open-Source Solar Photovoltaic Racking. Designs 2024, 8, 17. [Google Scholar] [CrossRef]
- Barbón, A.; Martínez-Suárez, J.; Bayón, L.; Bayón-Cueli, C. Photovoltaic Power Plants with Horizontal Single-Axis Trackers: Influence of the Movement Limit on Incident Solar Irradiance. Appl. Sci. 2025, 15, 1175. [Google Scholar] [CrossRef]
- Omoyele, O.; Hoffmann, M.; Koivisto, M.; Larrañeta, M.; Weinand, J.M.; Linßen, J.; Stolten, D. Increasing the resolution of solar and wind time series for energy system modeling: A review. Renew. Sustain. Energy Rev. 2024, 189, 113792. [Google Scholar] [CrossRef]
- GME. Esiti Elettricità. Available online: https://gme.mercatoelettrico.org/it-it/Home/Esiti/Elettricita/MGP/Esiti/PUN (accessed on 22 May 2025).
- Terna. SunSet—Area Pubblica. Available online: https://myterna.terna.it/SunSet/Public (accessed on 22 May 2025).
- IRENA. Electricity Storage and Renewables: Costs and Markets to 2030; International Renewable Energy Agency: Masdar City, Abu Dhabi, 2017; 132p, Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2017/Oct/IRENA_Electricity_Storage_Costs_2017.pdf (accessed on 30 June 2025).
- Home|NREL. Available online: https://www.nrel.gov/ (accessed on 22 May 2025).
- Naemi, M.; Davis, D.; Brear, M.J. Optimisation and analysis of battery storage integrated into a wind power plant participating in a wholesale electricity market with energy and ancillary services. J. Clean. Prod. 2022, 373, 133909. [Google Scholar] [CrossRef]
- Mohamed, A.; Rigo-Mariani, R.; Debusschere, V.; Pin, L. Stacked revenues for energy storage participating in energy and reserve markets with an optimal frequency regulation modeling. Appl. Energy 2023, 350, 121721. [Google Scholar] [CrossRef]
- Andreotti, D.; Spiller, M.; Scrocca, A.; Bovera, F.; Rancilio, G. Modeling and Analysis of BESS Operations in Electricity Markets: Prediction and Strategies for Day-Ahead and Continuous Intra-Day Markets. Sustainability 2024, 16, 7940. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).