The Impact of Wind Speed on Electricity Prices in the Polish Day-Ahead Market Since 2016, and Its Applicability to Machine-Learning-Powered Price Prediction
Abstract
1. Introduction
1.1. Literature Review
1.2. Study Contribution
2. Materials and Methods
2.1. Data Acquisition and Preprocessing
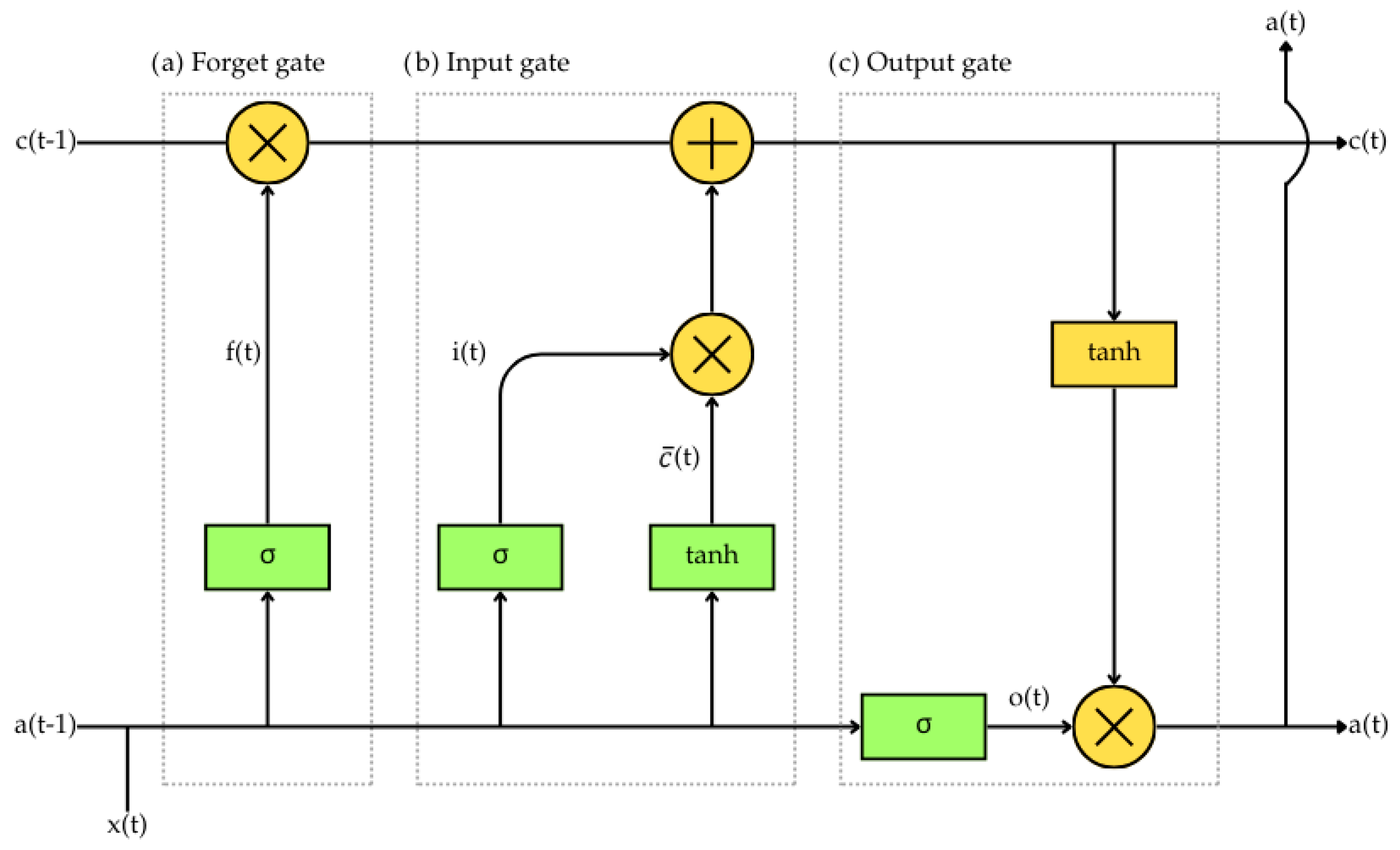
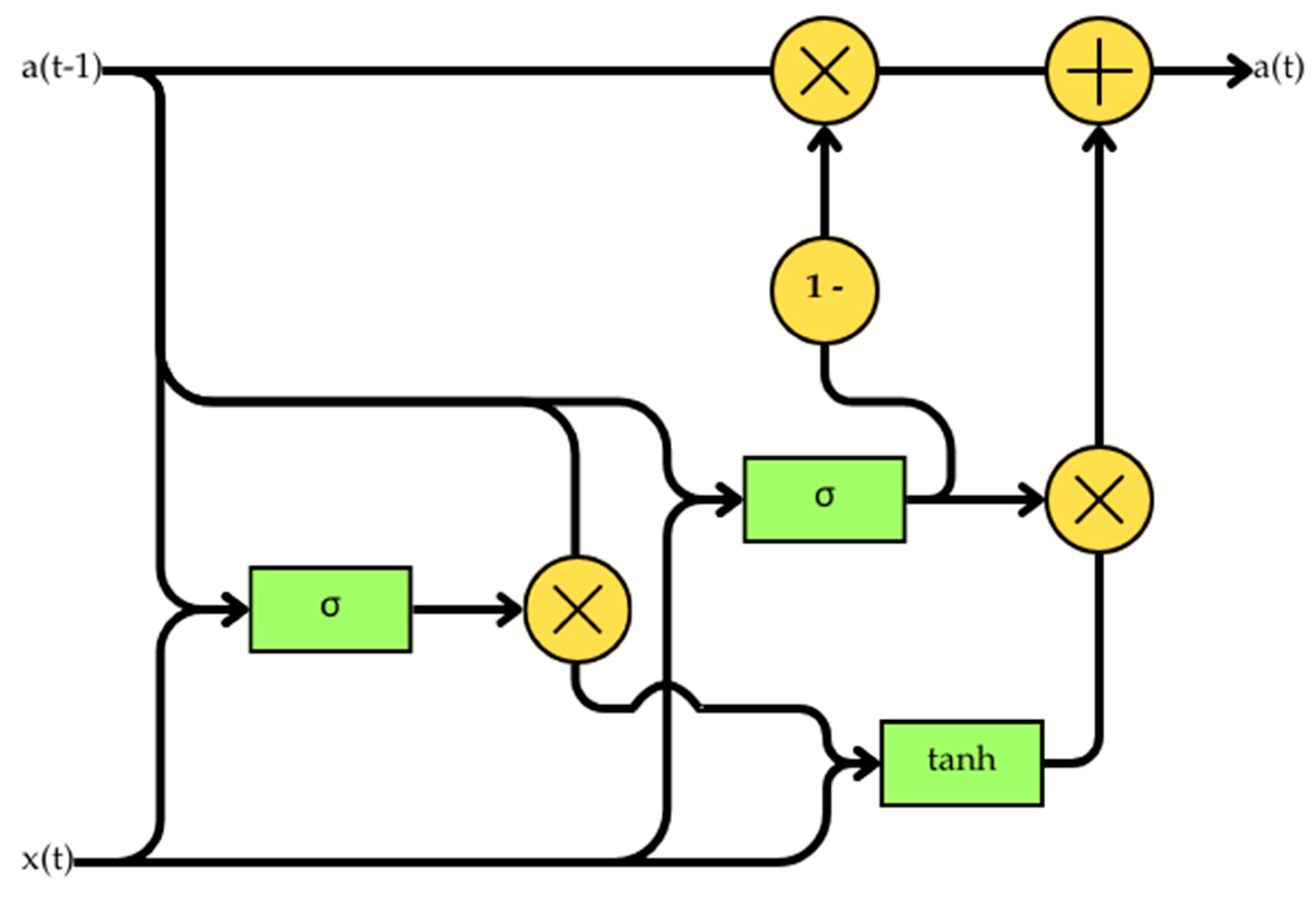
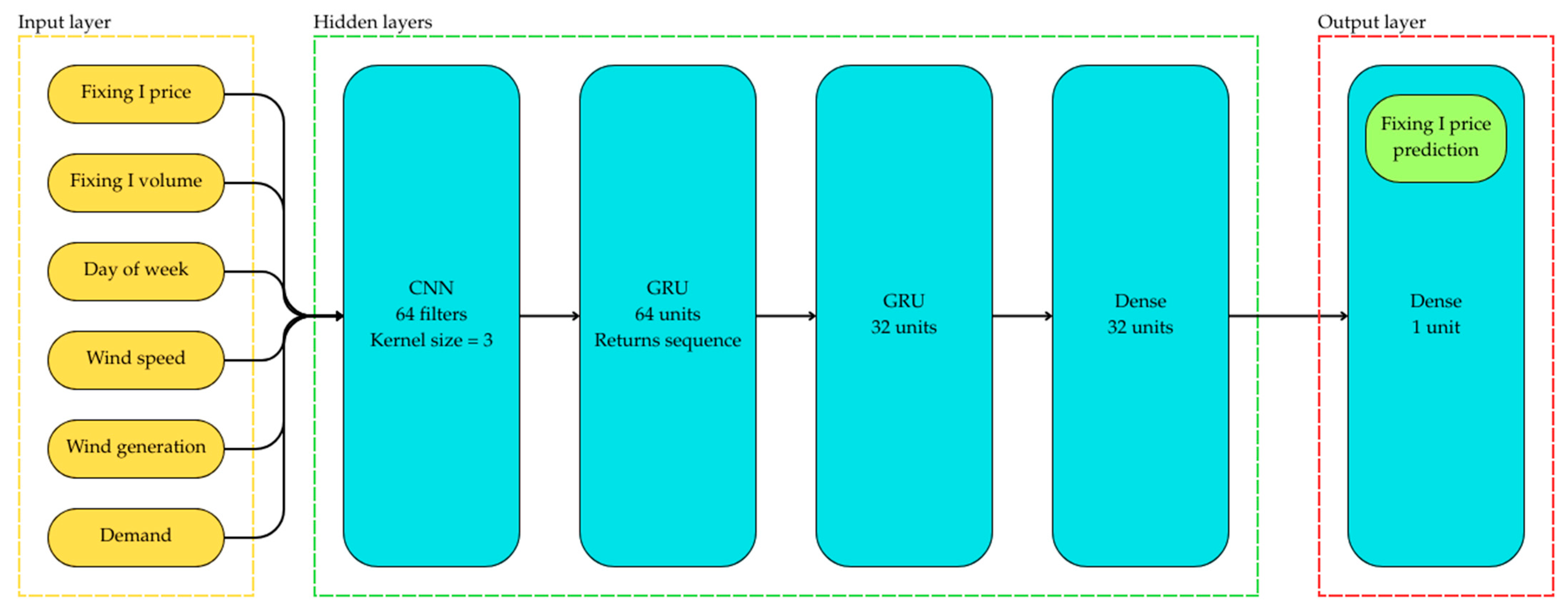
2.2. Machine Learning Models
3. Results and Discussion
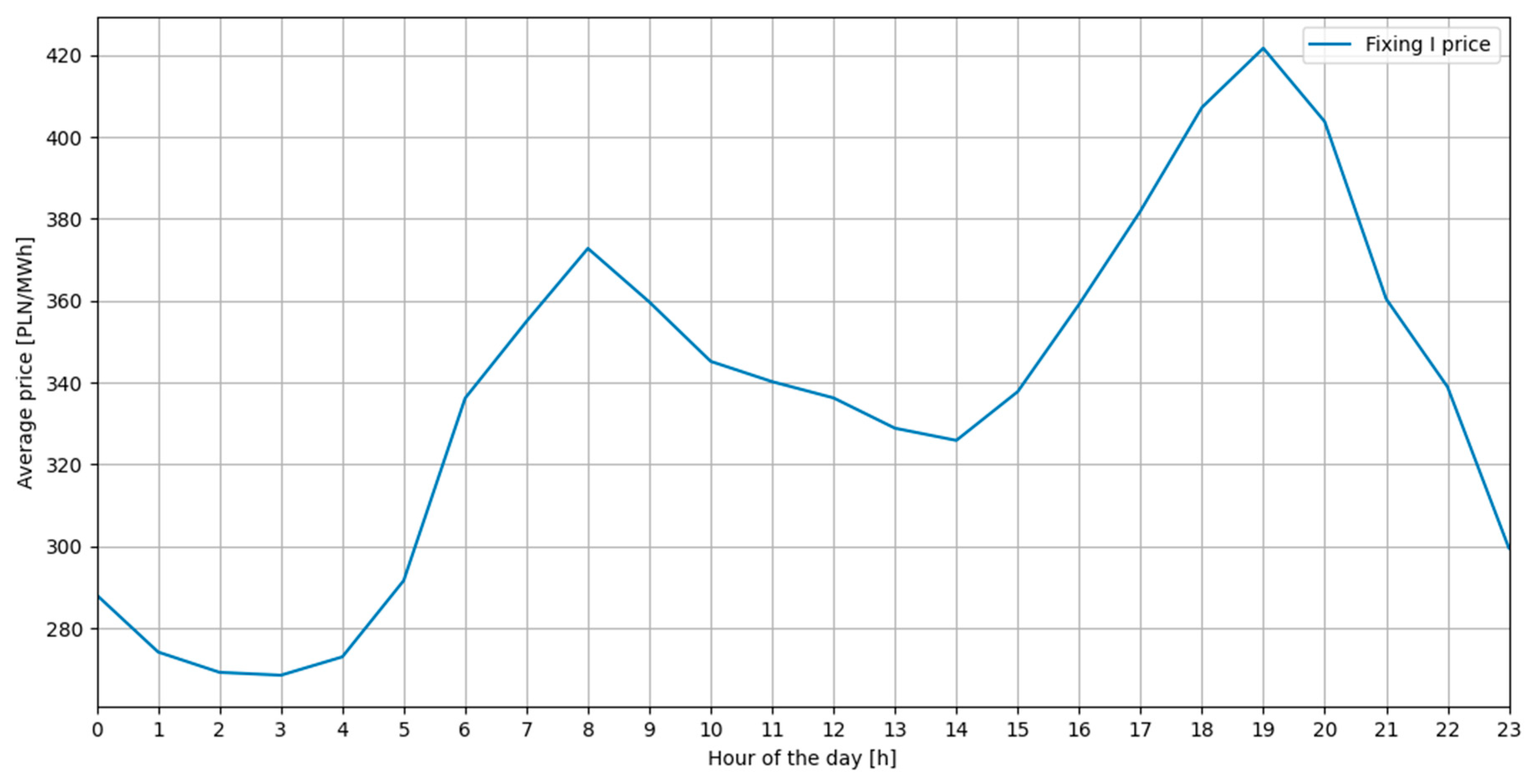
3.1. Price Data Analysis
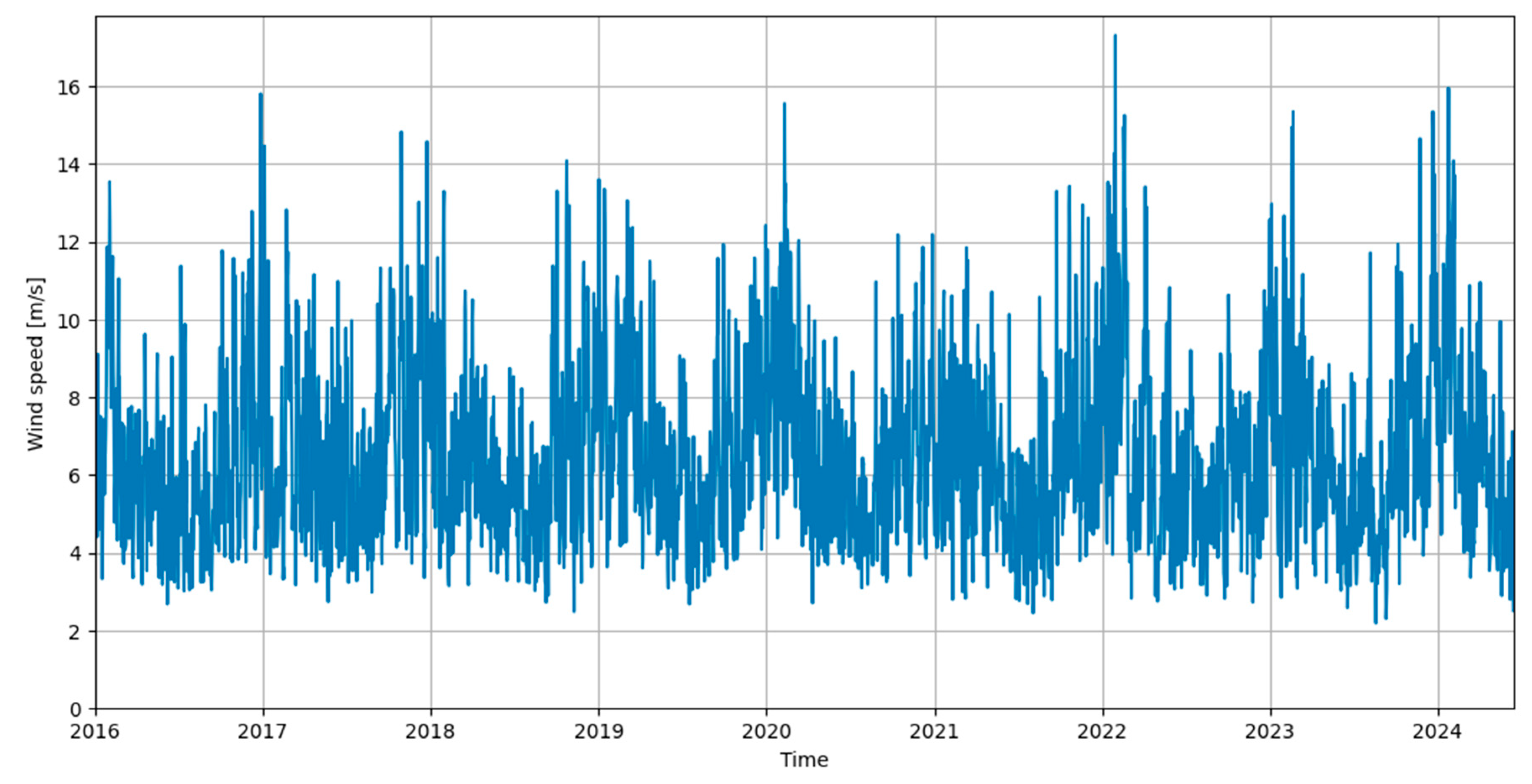
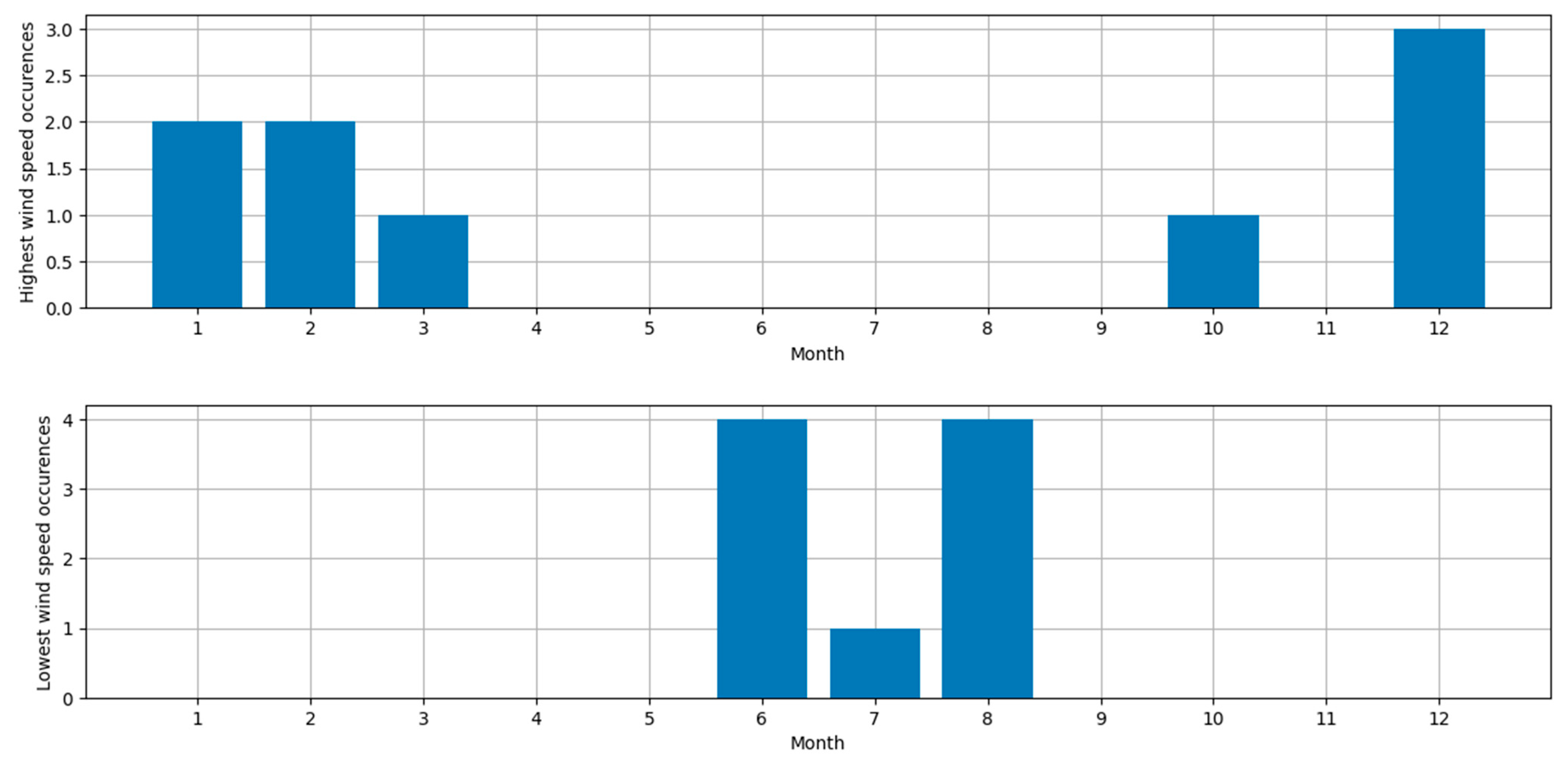
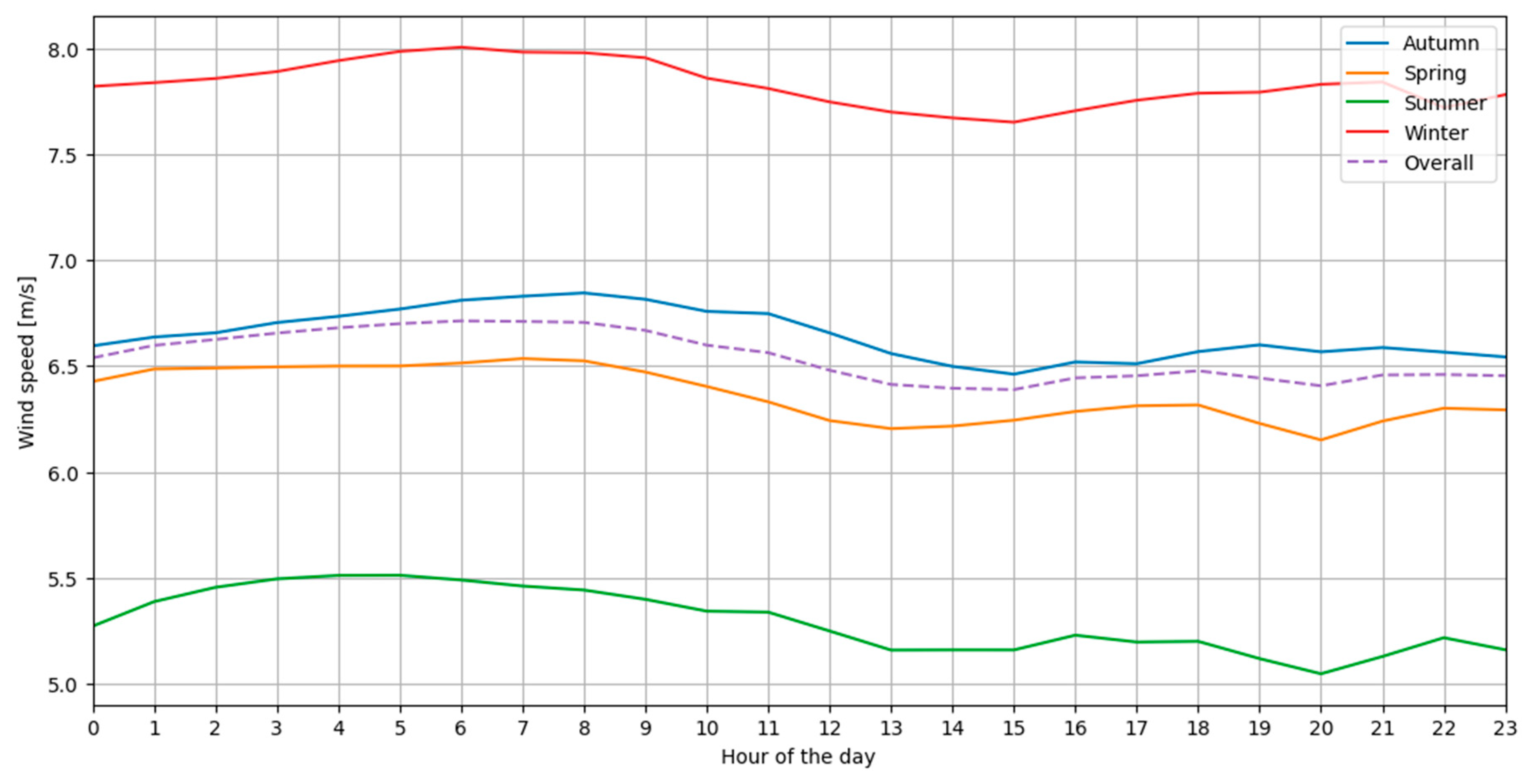
3.2. Wind Speed Data Analysis
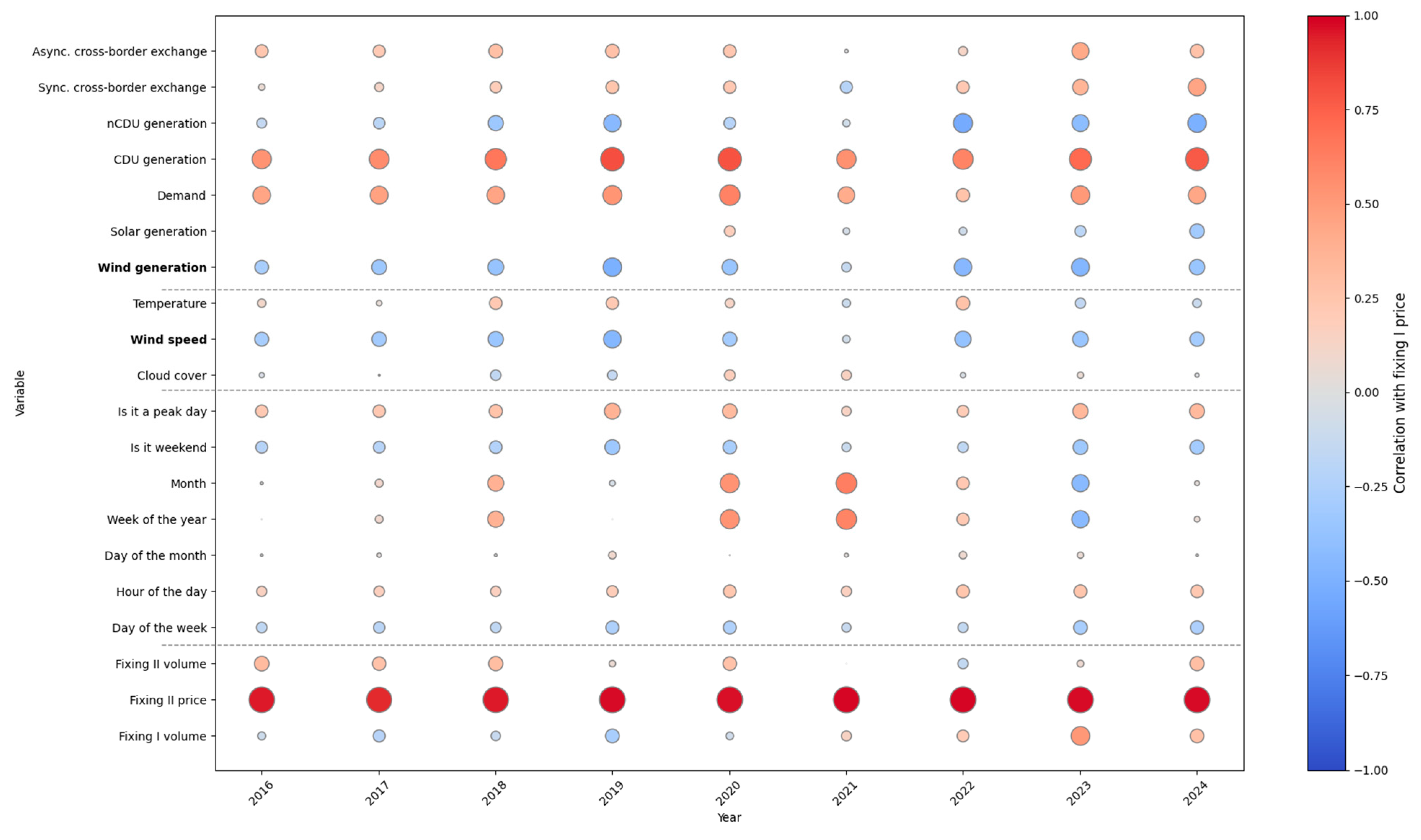
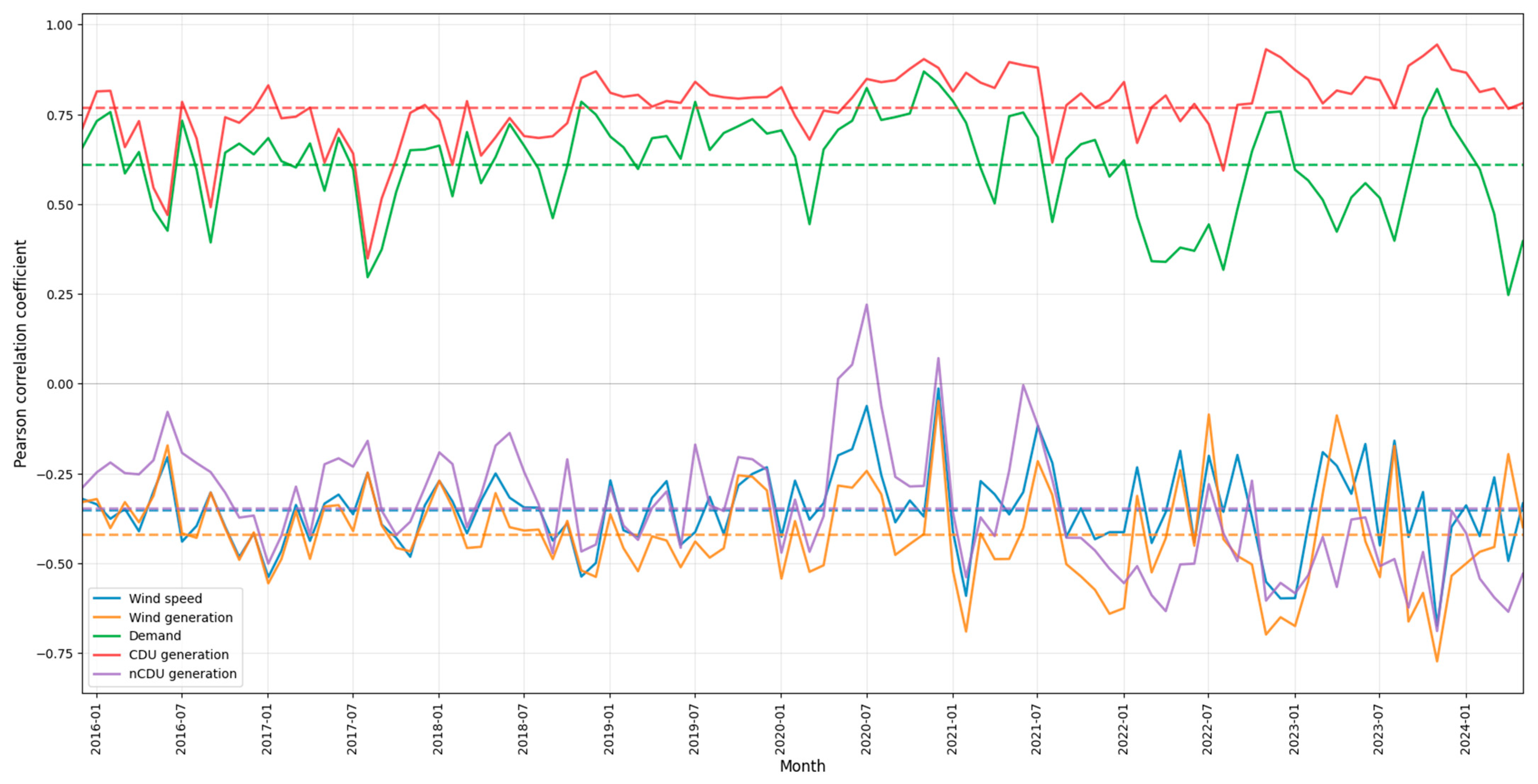
3.3. Statistical Analysis Results
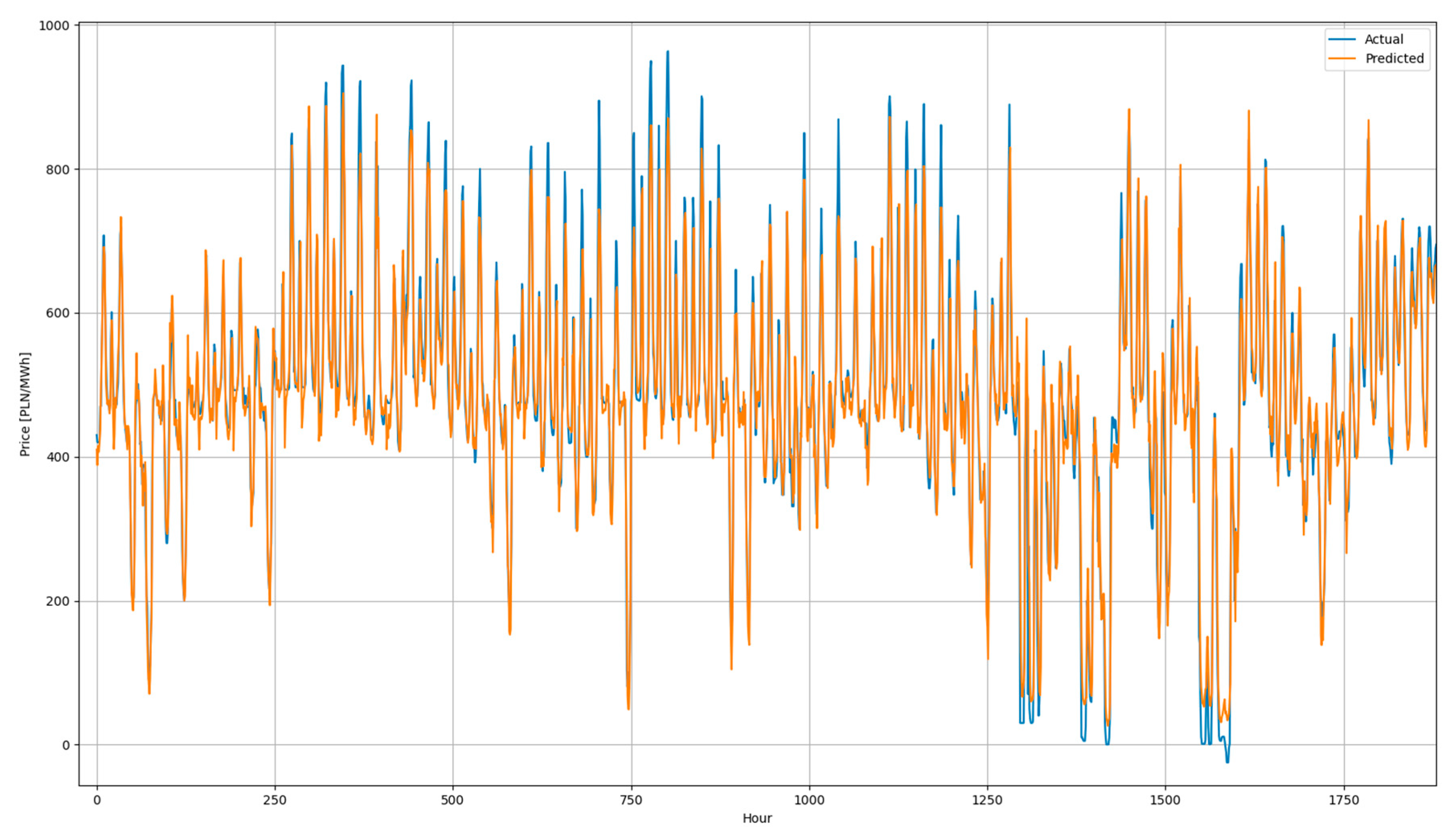
3.4. Prediction Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | Explanations |
| 10H | 10 times the total height of the wind turbine |
| ANN | artificial neural network |
| CDU | centrally dispatched unit |
| CHP | combined heat and power |
| CNN | convolutional neural network |
| csv | comma-separated values |
| EU | European Union |
| EU-27 | European Union of 27 countries |
| FNN | feedforward neural network |
| GLS | generalised least squares |
| grib | grid in binary |
| GRU | gated recurrent unit |
| LSTM | long-short term memory |
| MAE | mean absolute error |
| MSE | mean squared error |
| nCDU | non-centrally dispatched unit |
| NUTS | nomenclature of territorial units for statistics |
| RES | renewable energy sources |
| RNN | recurrent neural network |
| TSO | Transmission System Operator |
| UN | United Nations |
| Symbols | Explanations |
| pointwise addition | |
| pointwise multiplication | |
| α | friction coefficient |
| δ | Huber loss function switching parameter |
| σ | nonlinear activation function (sigmoid) |
| a | single ANN neuron output |
| b | bias |
| c | current ANN neuron state |
| h | height |
| R2 | coefficient of determination |
| tanh | hyperbolic tangent |
| v | wind speed |
| w | ANN layer weight vector |
| x | input |
| y | output |
Appendix A. Statistical Analysis Results for Input Data—Examples
| Variable | ρS | p (ρS) | ρP | p (ρP) | R2 | F-Stat | p (F-Stat) | t-Test β0 | β0 Std. Error | Est. Slope Coef. β | β Std. Error | Omnibus | p (Omnibus) | DW | JB | p (JB) | Condition Number | VIF |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fixing I price | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 4.57 × 1033 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 49,286.07 | 0.00 | 0.05 | 844,942.80 | 0.00 | 691.15 | |
| Fixing I volume | 0.43 | 0.00 | 0.39 | 0.00 | 0.15 | 13,348.42 | 0.00 | 57.75 | 2.58 | 0.11 | 0.00 | 51,005.41 | 0.00 | 0.07 | 1,075,659.57 | 0.00 | 7477.47 | 2.00 |
| Fixing II price | 0.99 | 0.00 | 0.99 | 0.00 | 0.98 | 3,547,233.37 | 0.00 | −0.02 | 0.23 | 1.01 | 0.00 | 39,201.50 | 0.00 | 0.53 | 6,249,838.06 | 0.00 | 689.36 | 2.00 |
| Fixing II volume | 0.16 | 0.00 | 0.05 | 0.00 | 0.00 | 216.42 | 0.00 | 308.33 | 2.15 | 0.03 | 0.00 | 49,276.42 | 0.00 | 0.05 | 827,143.04 | 0.00 | 2108.79 | 1.19 |
| Day of the week | −0.12 | 0.00 | −0.09 | 0.00 | 0.01 | 646.98 | 0.00 | 373.64 | 1.76 | −12.40 | 0.49 | 48,588.08 | 0.00 | 0.05 | 801,105.55 | 0.00 | 6.85 | 2.83 |
| Hour of the day | 0.11 | 0.00 | 0.11 | 0.00 | 0.01 | 854.79 | 0.00 | 289.12 | 1.89 | 4.11 | 0.14 | 47,921.91 | 0.00 | 0.05 | 760,041.72 | 0.00 | 26.14 | 1.72 |
| Day of the month | 0.02 | 0.00 | 0.02 | 0.00 | 0.00 | 45.03 | 0.00 | 324.71 | 2.00 | 0.75 | 0.11 | 48,500.01 | 0.00 | 0.05 | 790,773.86 | 0.00 | 36.86 | 1.10 |
| Week of the year | 0.07 | 0.00 | 0.08 | 0.00 | 0.01 | 532.20 | 0.00 | 297.88 | 1.94 | 1.49 | 0.06 | 48,128.84 | 0.00 | 0.05 | 778,396.53 | 0.00 | 59.35 | 21.80 |
| Month | 0.08 | 0.00 | 0.09 | 0.00 | 0.01 | 595.07 | 0.00 | 292.70 | 2.04 | 6.89 | 0.28 | 48,126.98 | 0.00 | 0.05 | 779,512.89 | 0.00 | 15.34 | 21.43 |
| Year | 0.75 | 0.00 | 0.56 | 0.00 | 0.32 | 34,536.17 | 0.00 | −12,3668.68 | 667.27 | 61.40 | 0.33 | 58,391.44 | 0.00 | 0.07 | 2,052,659.13 | 0.00 | 1,666,030.32 | 2.40 |
| Is it weekend | −0.15 | 0.00 | −0.11 | 0.00 | 0.01 | 837.33 | 0.00 | 354.25 | 1.15 | −62.40 | 2.16 | 48,652.26 | 0.00 | 0.05 | 803,981.14 | 0.00 | 2.44 | 8.18 |
| Is it peak day | 0.16 | 0.00 | 0.12 | 0.00 | 0.01 | 1057.01 | 0.00 | 311.61 | 1.24 | 43.42 | 1.34 | 48,647.01 | 0.00 | 0.05 | 805,297.41 | 0.00 | 2.07 | 8.61 |
| Cloud cover | 0.01 | 0.00 | 0.02 | 0.00 | 0.00 | 21.03 | 0.00 | 322.15 | 3.26 | 2.64 | 0.58 | 48,646.22 | 0.00 | 0.05 | 801,694.46 | 0.00 | 19.45 | 1.35 |
| Wind speed | −0.19 | 0.00 | −0.17 | 0.00 | 0.03 | 2179.17 | 0.00 | 452.82 | 2.67 | −17.79 | 0.38 | 47,892.31 | 0.00 | 0.05 | 769,489.85 | 0.00 | 19.78 | 2.42 |
| Temperature | 0.06 | 0.00 | 0.04 | 0.00 | 0.00 | 141.84 | 0.00 | −82.77 | 35.21 | 1.48 | 0.12 | 48,300.53 | 0.00 | 0.05 | 773,990.08 | 0.00 | 10,188.52 | 5.39 |
| Wind generation | −0.06 | 0.00 | −0.06 | 0.00 | 0.00 | 278.10 | 0.00 | 355.81 | 1.52 | −0.01 | 0.00 | 48,114.13 | 0.00 | 0.05 | 772,899.72 | 0.00 | 3726.30 | 22.26 |
| Solar generation | 0.10 | 0.00 | −0.01 | 0.07 | 0.00 | 3.22 | 0.07 | 485.80 | 1.85 | 0.00 | 0.00 | 19,965.39 | 0.00 | 0.06 | 215,931.74 | 0.00 | 2328.50 | 15.07 |
| Demand | 0.32 | 0.00 | 0.24 | 0.00 | 0.06 | 4683.92 | 0.00 | −54.66 | 5.79 | 0.02 | 0.00 | 48,754.70 | 0.00 | 0.05 | 836,456.60 | 0.00 | 119,131.21 | 201.54 |
| CDU generation | 0.31 | 0.00 | 0.31 | 0.00 | 0.10 | 7955.73 | 0.00 | −7.78 | 3.97 | 0.03 | 0.00 | 45,319.59 | 0.00 | 0.05 | 685,916.43 | 0.00 | 54,040.35 | 209.28 |
| nCDU generation | 0.03 | 0.00 | −0.02 | 0.00 | 0.00 | 36.27 | 0.00 | 353.43 | 2.99 | 0.00 | 0.00 | 48,310.74 | 0.00 | 0.04 | 780,558.39 | 0.00 | 21,223.05 | 157.14 |
| Sync. cross-border exchange | −0.08 | 0.00 | −0.14 | 0.00 | 0.02 | 1554.91 | 0.00 | 333.73 | 0.97 | −0.04 | 0.00 | 48,267.29 | 0.00 | 0.05 | 800,504.24 | 0.00 | 885.53 | 27.55 |
| Async. cross-border exchange | 0.08 | 0.00 | 0.05 | 0.00 | 0.00 | 152.76 | 0.00 | 323.36 | 1.44 | 0.02 | 0.00 | 48,505.60 | 0.00 | 0.05 | 786,934.18 | 0.00 | 1154.56 | 7.66 |
| Season | 0.02 | 0.00 | 0.03 | 0.00 | 0.00 | 55.63 | 0.00 | 326.96 | 1.60 | 6.42 | 0.86 | 48,617.93 | 0.00 | 0.05 | 801,382.42 | 0.00 | 3.66 | 1.72 |
| Variable | ρS | p (ρS) | ρP | p (ρP) | R2 | F-Stat | p (F-Stat) | t-Test β0 | β0 Std. Error | Est. Slope Coef. β | β Std. Error | Omnibus | p (Omnibus) | DW | JB | p (JB) | Condition Number |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fixing I price | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 3.91 × 1032 | 0.00 | 0.00 | 0.00 | 1.00 | 0.00 | 7727.33 | 0.00 | 0.00 | 483,342.70 | 0.00 | 443.72 |
| Fixing I volume | −0.16 | 0.00 | −0.09 | 0.00 | 0.01 | 79.51 | 0.00 | 185.86 | 2.98 | −0.01 | 0.00 | 9763.96 | 0.00 | 0.20 | 1,026,091.70 | 0.00 | 8497.05 |
| Fixing II price | 0.96 | 0.00 | 0.95 | 0.00 | 0.91 | 86781.17 | 0.00 | −2.47 | 0.59 | 1.03 | 0.00 | 5819.44 | 0.00 | 0.76 | 3,599,945.29 | 0.00 | 458.96 |
| Fixing II volume | 0.51 | 0.00 | 0.31 | 0.00 | 0.10 | 962.97 | 0.00 | 123.19 | 1.38 | 0.06 | 0.00 | 10,153.28 | 0.00 | 0.22 | 1,247,658.80 | 0.00 | 1352.76 |
| Day of the week | −0.22 | 0.00 | −0.17 | 0.00 | 0.03 | 253.89 | 0.00 | 177.31 | 1.30 | −5.73 | 0.36 | 9747.71 | 0.00 | 0.20 | 1,059,040.61 | 0.00 | 6.88 |
| Hour of the day | 0.29 | 0.00 | 0.15 | 0.00 | 0.02 | 209.09 | 0.00 | 142.79 | 1.40 | 1.50 | 0.10 | 9881.35 | 0.00 | 0.21 | 1,096,864.57 | 0.00 | 26.14 |
| Day of the month | −0.01 | 0.17 | 0.01 | 0.35 | 0.00 | 0.89 | 0.35 | 158.86 | 1.49 | 0.08 | 0.08 | 9670.02 | 0.00 | 0.19 | 1,001,926.92 | 0.00 | 37.08 |
| Week of the year | 0.00 | 0.84 | 0.00 | 0.99 | 0.00 | 0.00 | 0.99 | 160.10 | 1.48 | 0.00 | 0.05 | 9674.41 | 0.00 | 0.19 | 1,003,423.58 | 0.00 | 62.18 |
| Month | 0.02 | 0.11 | 0.01 | 0.24 | 0.00 | 1.39 | 0.24 | 158.46 | 1.56 | 0.25 | 0.21 | 9672.34 | 0.00 | 0.19 | 1,002,620.88 | 0.00 | 15.98 |
| Is it weekend | −0.29 | 0.00 | −0.21 | 0.00 | 0.04 | 411.79 | 0.00 | 169.25 | 0.84 | −31.94 | 1.57 | 9792.63 | 0.00 | 0.21 | 1,084,337.57 | 0.00 | 2.43 |
| Is it peak day | 0.30 | 0.00 | 0.22 | 0.00 | 0.05 | 462.37 | 0.00 | 148.10 | 0.90 | 20.99 | 0.98 | 9836.19 | 0.00 | 0.21 | 1,109,319.00 | 0.00 | 2.07 |
| Cloud cover | −0.01 | 0.17 | −0.04 | 0.00 | 0.00 | 14.78 | 0.00 | 169.15 | 2.47 | −1.66 | 0.43 | 9651.19 | 0.00 | 0.19 | 991,009.99 | 0.00 | 19.86 |
| Wind speed | −0.34 | 0.00 | −0.29 | 0.00 | 0.08 | 788.11 | 0.00 | 209.41 | 1.89 | −7.91 | 0.28 | 9790.26 | 0.00 | 0.21 | 1,084,228.96 | 0.00 | 18.52 |
| Temperature | 0.07 | 0.00 | 0.11 | 0.00 | 0.01 | 99.45 | 0.00 | −97.24 | 25.81 | 0.91 | 0.09 | 9575.37 | 0.00 | 0.19 | 955,114.49 | 0.00 | 10,079.54 |
| Wind generation | −0.35 | 0.00 | −0.27 | 0.00 | 0.07 | 711.79 | 0.00 | 182.14 | 1.08 | −0.02 | 0.00 | 9834.60 | 0.00 | 0.21 | 1,103,122.05 | 0.00 | 2690.18 |
| Demand | 0.68 | 0.00 | 0.45 | 0.00 | 0.20 | 2249.93 | 0.00 | −27.83 | 4.01 | 0.01 | 0.00 | 10,914.09 | 0.00 | 0.24 | 1,813,384.70 | 0.00 | 117,142.65 |
| CDU generation | 0.76 | 0.00 | 0.54 | 0.00 | 0.29 | 3590.07 | 0.00 | −11.40 | 2.93 | 0.01 | 0.00 | 11,241.77 | 0.00 | 0.27 | 2,150,552.20 | 0.00 | 61,994.77 |
| nCDU generation | −0.10 | 0.00 | −0.15 | 0.00 | 0.02 | 189.79 | 0.00 | 191.64 | 2.40 | −0.01 | 0.00 | 9607.73 | 0.00 | 0.20 | 976,783.51 | 0.00 | 20,481.84 |
| Sync. cross-border exchange | −0.03 | 0.00 | 0.06 | 0.00 | 0.00 | 33.76 | 0.00 | 162.76 | 0.86 | 0.01 | 0.00 | 9611.64 | 0.00 | 0.20 | 979,482.07 | 0.00 | 547.65 |
| Async. cross-border exchange | 0.35 | 0.00 | 0.24 | 0.00 | 0.06 | 533.50 | 0.00 | 144.83 | 0.97 | 0.03 | 0.00 | 9927.12 | 0.00 | 0.21 | 1,116,873.11 | 0.00 | 942.58 |
References
- UNFCCC. Adoption of the Paris Agreement—Paris Agreement; UNFCCC: Bonn, Germany, 2015. [Google Scholar]
- Hardy, J.T. Climate Change: Causes, Effects, and Solutions; Wiley: New York, NY, USA, 2003; p. 247. [Google Scholar]
- Total Net Greenhouse Gas Emission Trends and Projections in Europe|European Environment Agency’s Home Page. Available online: https://www.eea.europa.eu/en/analysis/indicators/total-greenhouse-gas-emission-trends (accessed on 19 March 2025).
- Ember Yearly Electricity Data. Available online: https://ember-energy.org/data/yearly-electricity-data/ (accessed on 19 March 2025).
- Gawlik, L.; Pepłowska, M.; Kowalik, W.; Hubert, W.; Kryzia, D. Energy Transformation of the Silesia Coal Region—Challenges and Coping Strategies. Gospod. Surowcami Miner. Miner. Resour. Manag. 2024, 40, 169–183. [Google Scholar] [CrossRef]
- Directive EU-2023/2413—EN-Renewable Energy Directive—EUR-Lex. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32023L2413&qid=1699364355105 (accessed on 19 March 2025).
- Ministry of Climate and Environment. National Energy and Climate Plan to 2030; Ministry of Climate and Environment: Warsaw, Poland, 2024. [Google Scholar]
- PSESA Reports for 2023. Available online: https://www.pse.pl/dane-systemowe/funkcjonowanie-kse/raporty-roczne-z-funkcjonowania-kse-za-rok/raporty-za-rok-2023#r6_1 (accessed on 19 March 2025).
- Zimny, J.; Laskowski, M. Energetyczna Farma Wiatrowa Barzowice o Mocy 5 MW; Polska Geotermalna Asocjacja: Kraków, Poland, 2007. [Google Scholar]
- EUR-Lex 12003TN02/12/A—P.L. Dziennik Urzędowy L 236. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX:12003TN02/12/A (accessed on 8 July 2025).
- Pieczarko, R.; Sołtysik, M. Analiza Wpływu Generacji Źródeł Wiatrowych Na Poziom Kształtowania Się Cen Energii Elektrycznej Na Rynku SPOT. Prz. Elektrotechniczny 2017, 93, 78–81. [Google Scholar] [CrossRef]
- Polish Energy Regulatory Office. Capacity Installed [MW], as of 2022.12.31; Polish Energy Regulatory Office: Warsaw, Poland, 2023. [Google Scholar]
- Berent-Kowalska, G.; Kacprowska, J.; Gogacz, I.; Jurgaś, A.; Kacperczyk, G. Energia ze Źródeł Odnawialnych w 2011 r.; Central Statistical Office of Poland: Warsaw, Poland, 2012. [Google Scholar]
- Miller, A.; Bućko, P. Analiza Wpływu Generacji Wiatrowej Na Cenę Rozliczeniową Odchylenia Na Rynku Bilansującym w Polsce. Zesz. Nauk. Wydziału Elektrotechniki I Autom. Politech. Gdańskiej 2015, 47, 119–122. [Google Scholar]
- Sejm. Dziennik Ustaw 2—Poz. 724; Sejm: Warsaw, Poland, 2021. [Google Scholar]
- Sliz-Szkliniarz, B.; Eberbach, J.; Hoffmann, B.; Fortin, M. Assessing the Cost of Onshore Wind Development Scenarios: Modelling of Spatial and Temporal Distribution of Wind Power for the Case of Poland. Renew. Sustain. Energy Rev. 2019, 109, 514–531. [Google Scholar] [CrossRef]
- Dziennik Ustaw Poz. 553—Ustawa z Dnia 9 Marca 2023 r. o Zmianie Ustawy o Inwestycjach w Zakresie Elektrowni Wiatrowych Oraz Niektórych Innych Ustaw. Available online: https://orka.sejm.gov.pl/proc9.nsf/ustawy/2938_u.htm (accessed on 19 March 2025).
- Jónsson, T.; Pinson, P.; Nielsen, H.A.; Madsen, H.; Nielsen, T.S. Forecasting Electricity Spot Prices Accounting for Wind Power Predictions. IEEE Trans. Sustain. Energy 2013, 4, 210–218. [Google Scholar] [CrossRef]
- Brancucci Martinez-Anido, C.; Brinkman, G.; Hodge, B.M. The Impact of Wind Power on Electricity Prices. Renew. Energy 2016, 94, 474–487. [Google Scholar] [CrossRef]
- Mulder, M.; Scholtens, B. The Impact of Renewable Energy on Electricity Prices in the Netherlands. Renew. Energy 2013, 57, 94–100. [Google Scholar] [CrossRef]
- Ketterer, J.C. The Impact of Wind Power Generation on the Electricity Price in Germany. Energy Econ. 2014, 44, 270–280. [Google Scholar] [CrossRef]
- Badyda, K.; Dylik, M. Analysis of the Impact of Wind on Electricity Prices Based on Selected European Countries. Energy Procedia 2017, 105, 55–61. [Google Scholar] [CrossRef]
- Igliński, B.; Iglińska, A.; Koziński, G.; Skrzatek, M.; Buczkowski, R. Wind Energy in Poland—History, Current State, Surveys, Renewable Energy Sources Act, SWOT Analysis. Renew. Sustain. Energy Rev. 2016, 64, 19–33. [Google Scholar] [CrossRef]
- Gnatowska, R.; Moryń-Kucharczyk, E. Current Status of Wind Energy Policy in Poland. Renew. Energy 2019, 135, 232–237. [Google Scholar] [CrossRef]
- Brzezińska-Rawa, A.; Goździewicz-Biechońska, J. Recent Developments in the Wind Energy Sector in Poland. Renew. Sustain. Energy Rev. 2014, 38, 79–87. [Google Scholar] [CrossRef]
- Zhong, H.; Member, S.; Tan, Z.; Member, S.; He, Y.; Xie, L.; Kang, C. Implications of COVID-19 for the Electricity Industry: A Comprehensive Review. CSEE J. Power Energy Syst. 2020, 6, 489–495. [Google Scholar] [CrossRef]
- Adolfsen, J.F.; Kuik, F.; Schuler, T.; Lis, E. The Impact of the War in Ukraine on Euro Area Energy Markets; European Central Bank: Frankfurt am Main, Germany, 2022. [Google Scholar]
- Energy Instrat Hourly Electricity Prices (Day Ahead Market). Available online: https://energy.instrat.pl/ceny/energia-rdn-godzinowe/ (accessed on 24 March 2025).
- Olczak, P.; Matuszewska, D.; Kryzia, D. “Mój Prąd” as an Example of the Photovoltaic One off Grant Program in Poland. Polityka Energetyczna 2020, 23, 123–138. [Google Scholar] [CrossRef]
- Benalcazar, P.; Andrade, C.; Guamán, W. Prosumer Policy Options in Developing Countries: A Comparative Analysis of Feed-in Tariffs, Net Metering, and Net Billing for Residential PV-Battery Systems. Polityka Energetyczna Energy Policy J. 2025, 28, 77–98. [Google Scholar] [CrossRef]
- Energy Instrat Installed Capacity of Electricity Sources in Poland. Available online: https://energy.instrat.pl/system-elektroenergetyczny/zainstalowana-moc-are/ (accessed on 24 March 2025).
- IMGW. Index of /Data/Dane_pomiarowo_obserwacyjne/Dane_meteorologiczne/Dobowe. Available online: https://danepubliczne.imgw.pl/data/dane_pomiarowo_obserwacyjne/dane_meteorologiczne/dobowe/ (accessed on 24 March 2025).
- ERA5 Hourly Data on Single Levels from 1940 to Present. Available online: https://cds.climate.copernicus.eu/datasets/reanalysis-era5-single-levels?tab=overview (accessed on 24 March 2025).
- EMHIRES Dataset: Wind and Solar Power Generation. Available online: https://zenodo.org/records/8340501 (accessed on 24 April 2025).
- PSESA TSO Reports/Market Data. Available online: https://raporty.pse.pl/ (accessed on 24 March 2025).
- Shrestha, A.; Mahmood, A. Review of Deep Learning Algorithms and Architectures. IEEE Access 2019, 7, 53040–53065. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation by Simon Haykin. Knowl. Eng. Rev. 1999, 13, 409–412. [Google Scholar]
- Murat, H.S. A Brief Review of Feed-Forward Neural Networks. Commun. Fac. Of. Sci. Univ. Ank. 2006, 50, 11–17. [Google Scholar] [CrossRef]
- Jain, L.C.; Medsker, L.R. Recurrent Neural Networks: Design and Applications; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014. [Google Scholar]
- Wang, X.; Xu, J.; Shi, W.; Liu, J. OGRU: An Optimized Gated Recurrent Unit Neural Network. J. Phys. Conf. Ser. 2019, 1325, 012089. [Google Scholar] [CrossRef]
- Fred Agarap, A.M. A Neural Network Architecture Combining Gated Recurrent Unit (GRU) and Support Vector Machine (SVM) for Intrusion Detection in Network Traffic Data. In Proceedings of the 2018 10th International Conference on Machine Learning and Computing, Macau, China, 26 February 2018; pp. 26–30. [Google Scholar]
- Wu, L.; Kong, C.; Hao, X.; Chen, W. A Short-Term Load Forecasting Method Based on GRU-CNN Hybrid Neural Network Model. Math. Probl. Eng. 2020, 2020, 1428104. [Google Scholar] [CrossRef]
- Uluocak, I.; Bilgili, M. Daily Air Temperature Forecasting Using LSTM-CNN and GRU-CNN Models. Acta Geophys. 2024, 72, 2107–2126. [Google Scholar] [CrossRef]
- Gaur, K.; Kumar, H.; Agarwal, R.P.K.; Baba, K.V.S.; Soonee, S.K. Analysing the Electricity Demand Pattern. In Proceedings of the 2016 National Power Systems Conference, NPSC 2016, Bhubaneswar, India, 19–21 December 2016. [Google Scholar] [CrossRef]
- Bañuelos-Ruedas, F.; Angeles-Camacho, C.; Rios-Marcuello, S. Analysis and Validation of the Methodology Used in the Extrapolation of Wind Speed Data at Different Heights. Renew. Sustain. Energy Rev. 2010, 14, 2383–2391. [Google Scholar] [CrossRef]
- Gelabert, L.; Labandeira, X.; Linares, P. An Ex-Post Analysis of the Effect of Renewables and Cogeneration on Spanish Electricity Prices. Energy Econ. 2011, 33, S59–S65. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Statist. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- StandardScaler—Scikit-Learn 1.6.1 Documentation. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html (accessed on 18 April 2025).
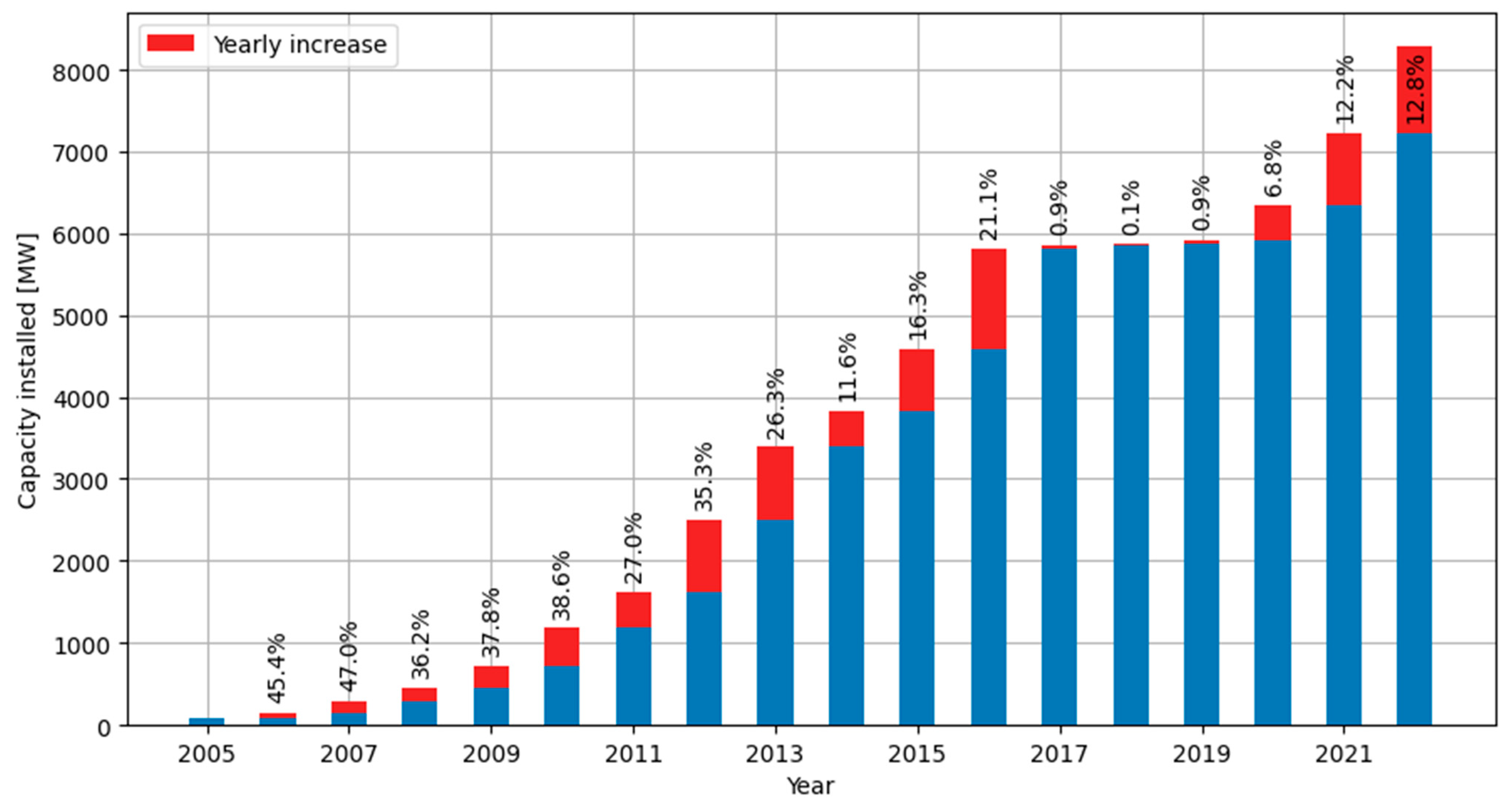
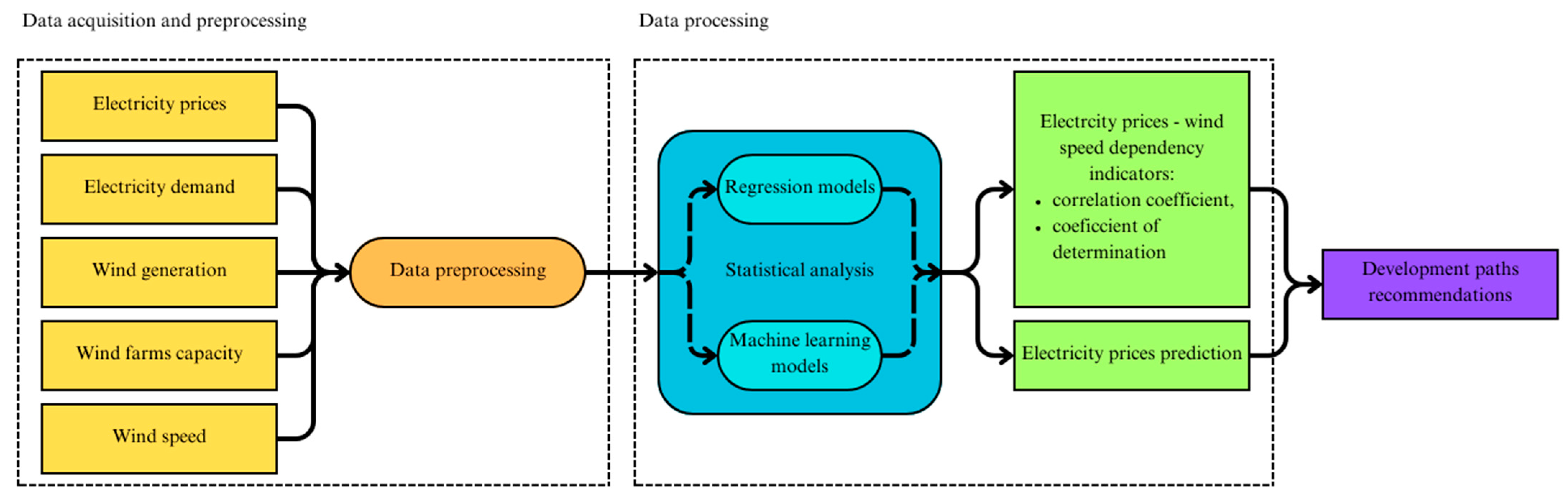
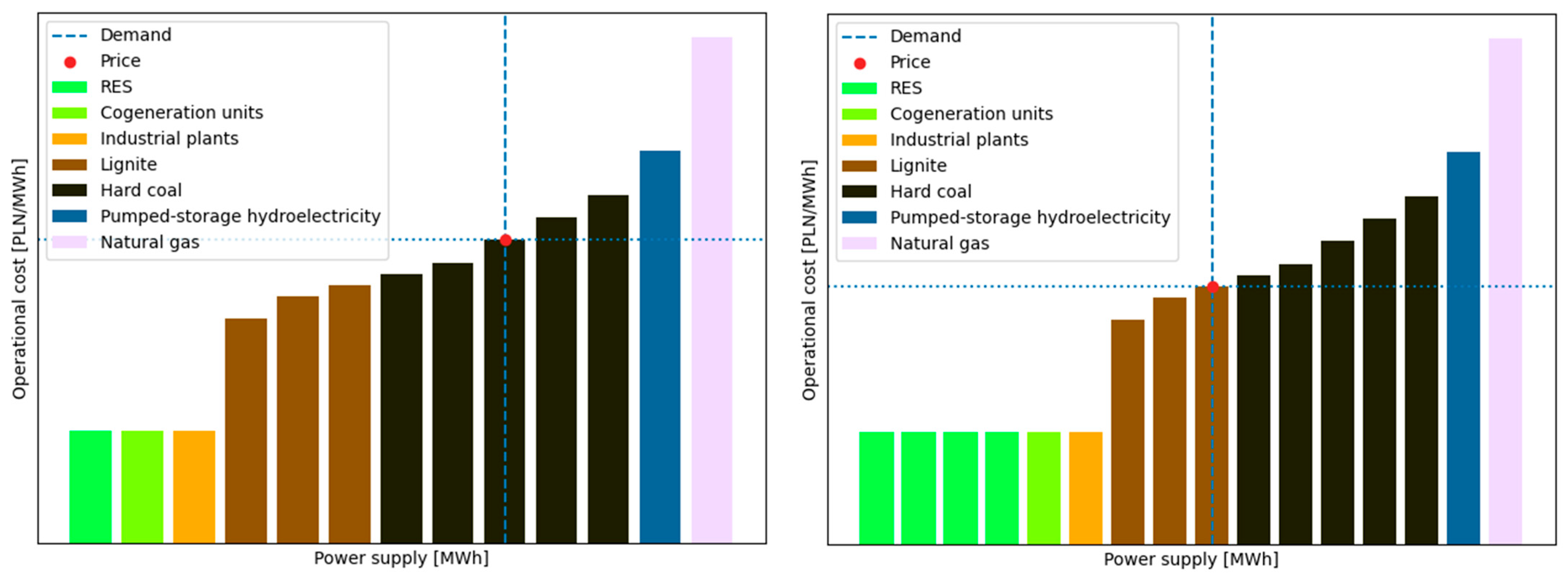
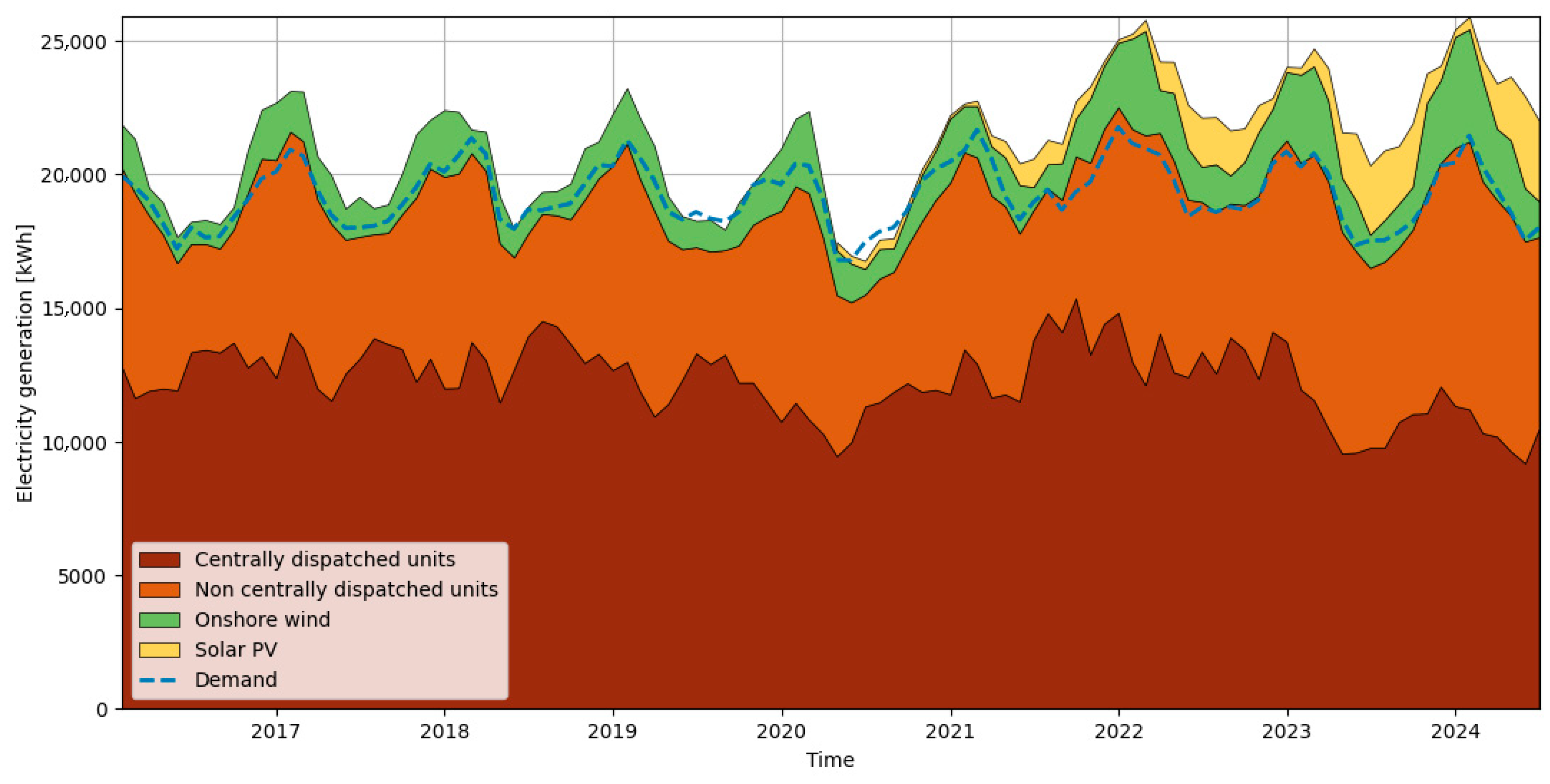
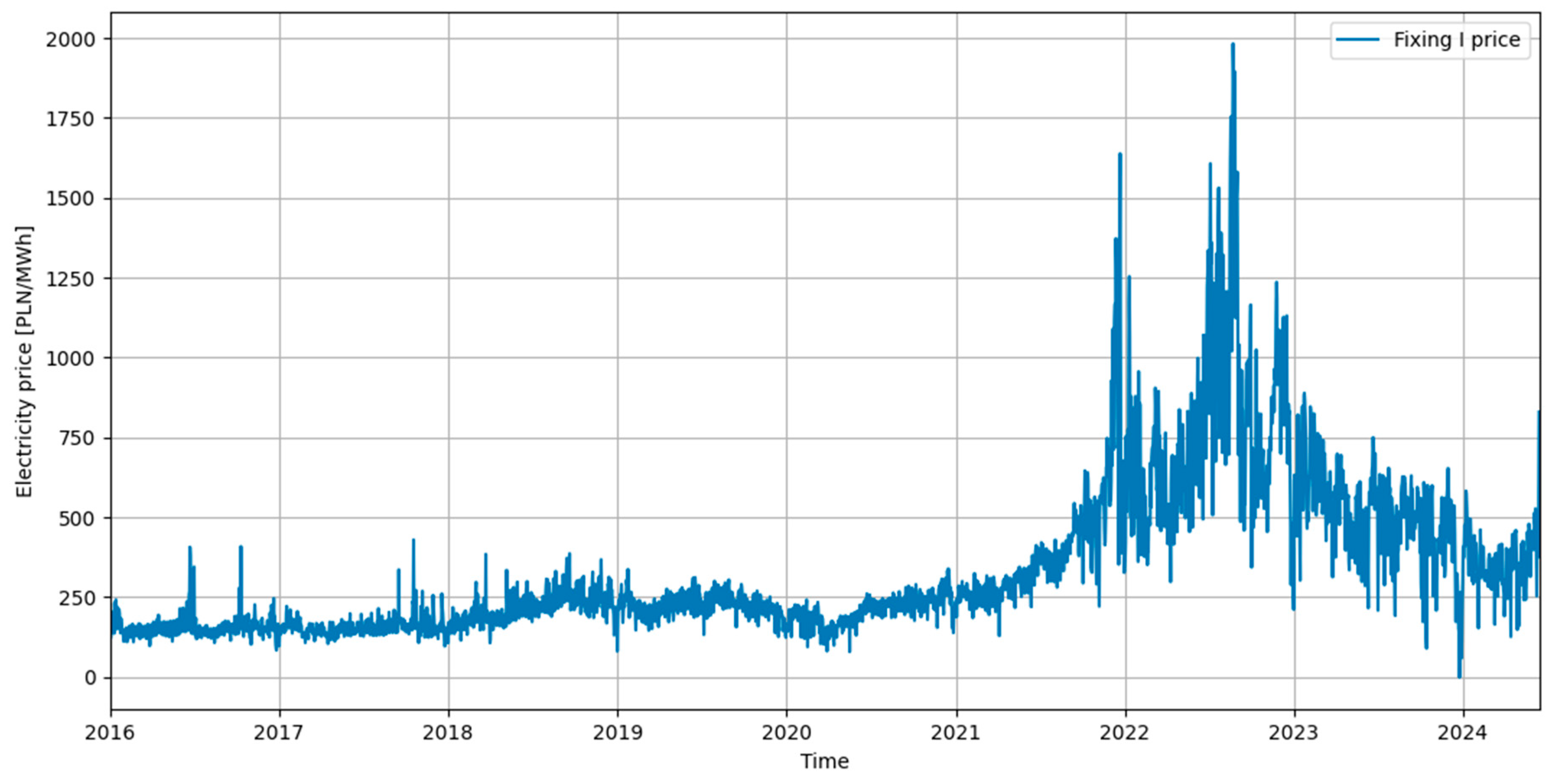
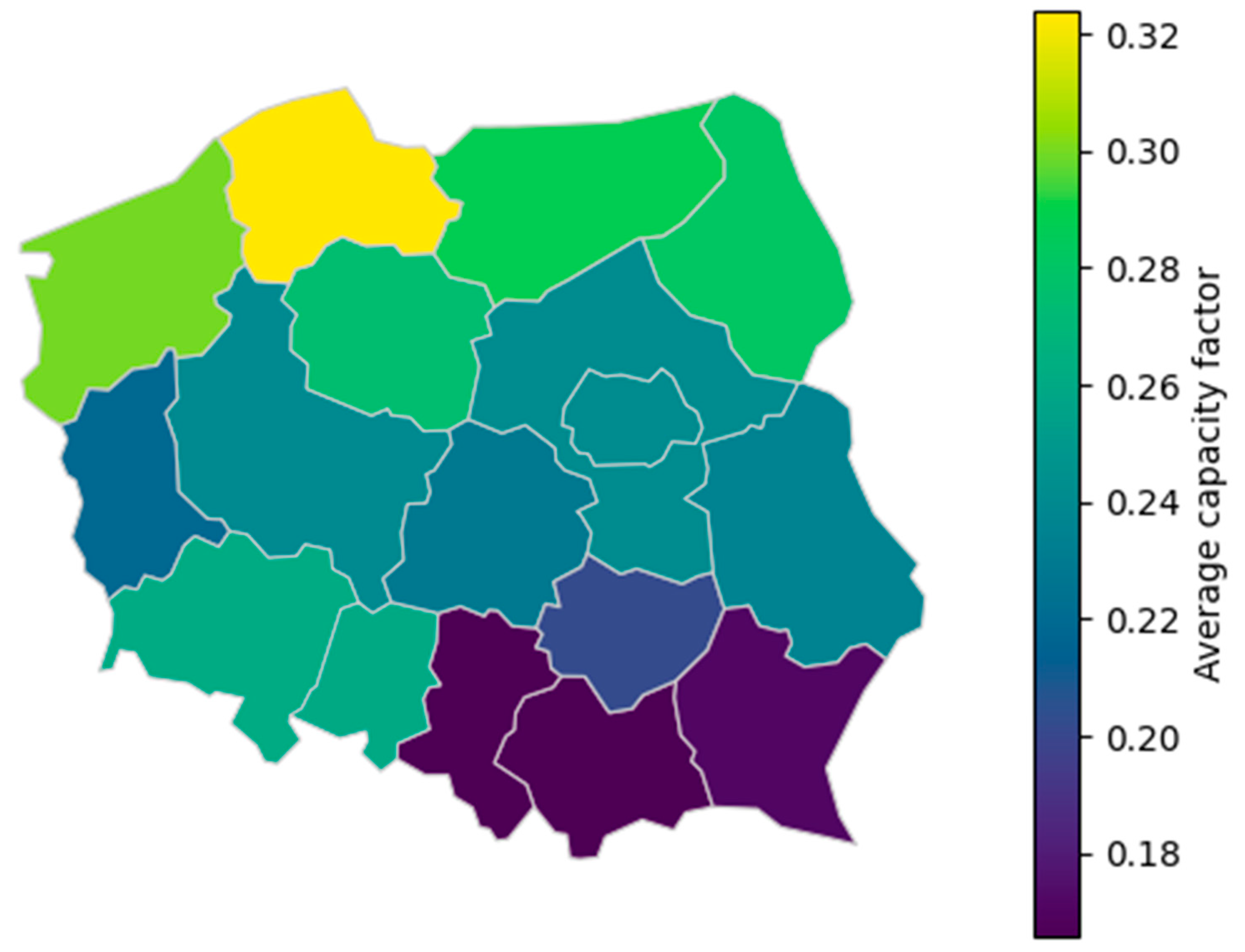
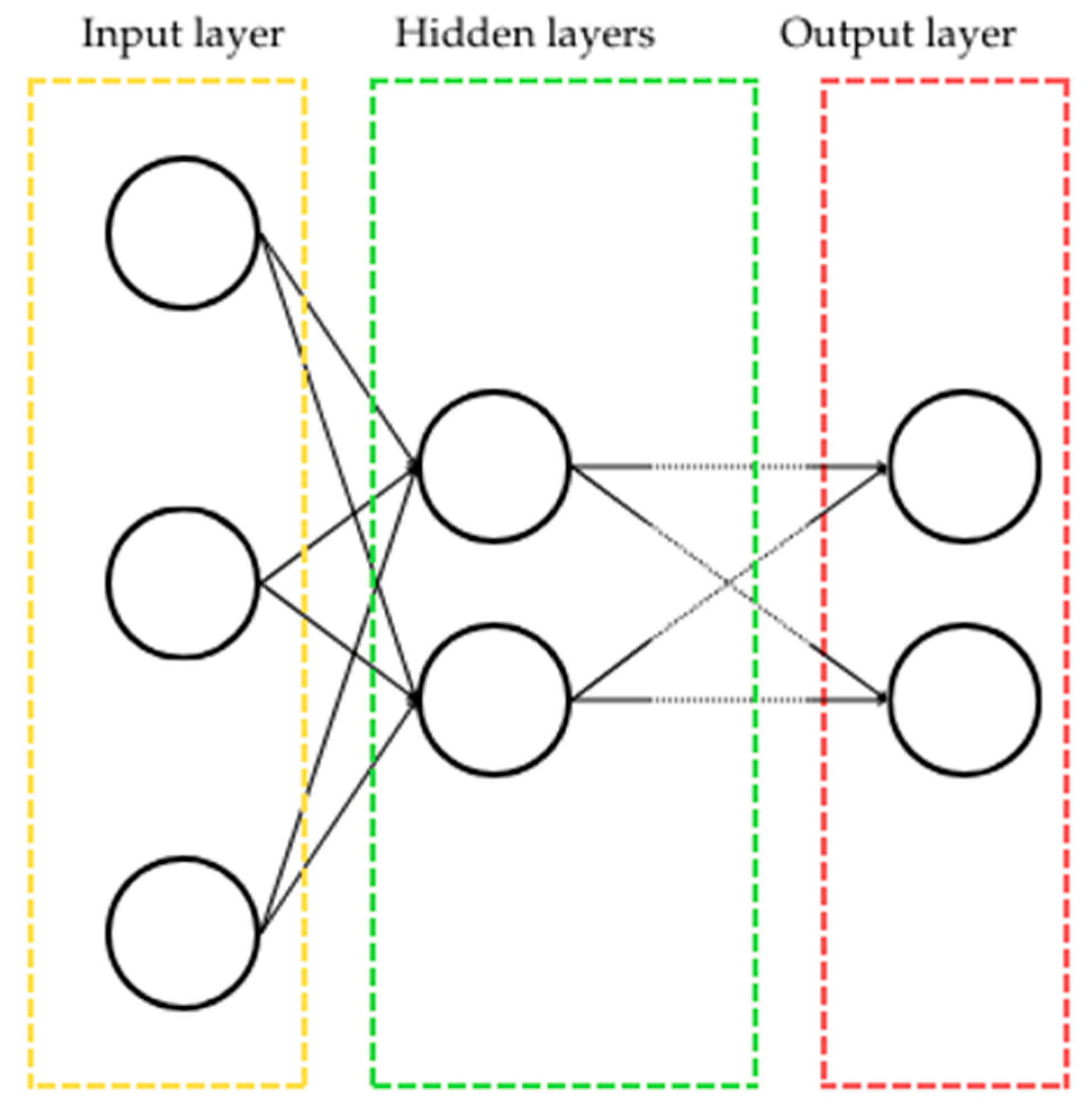
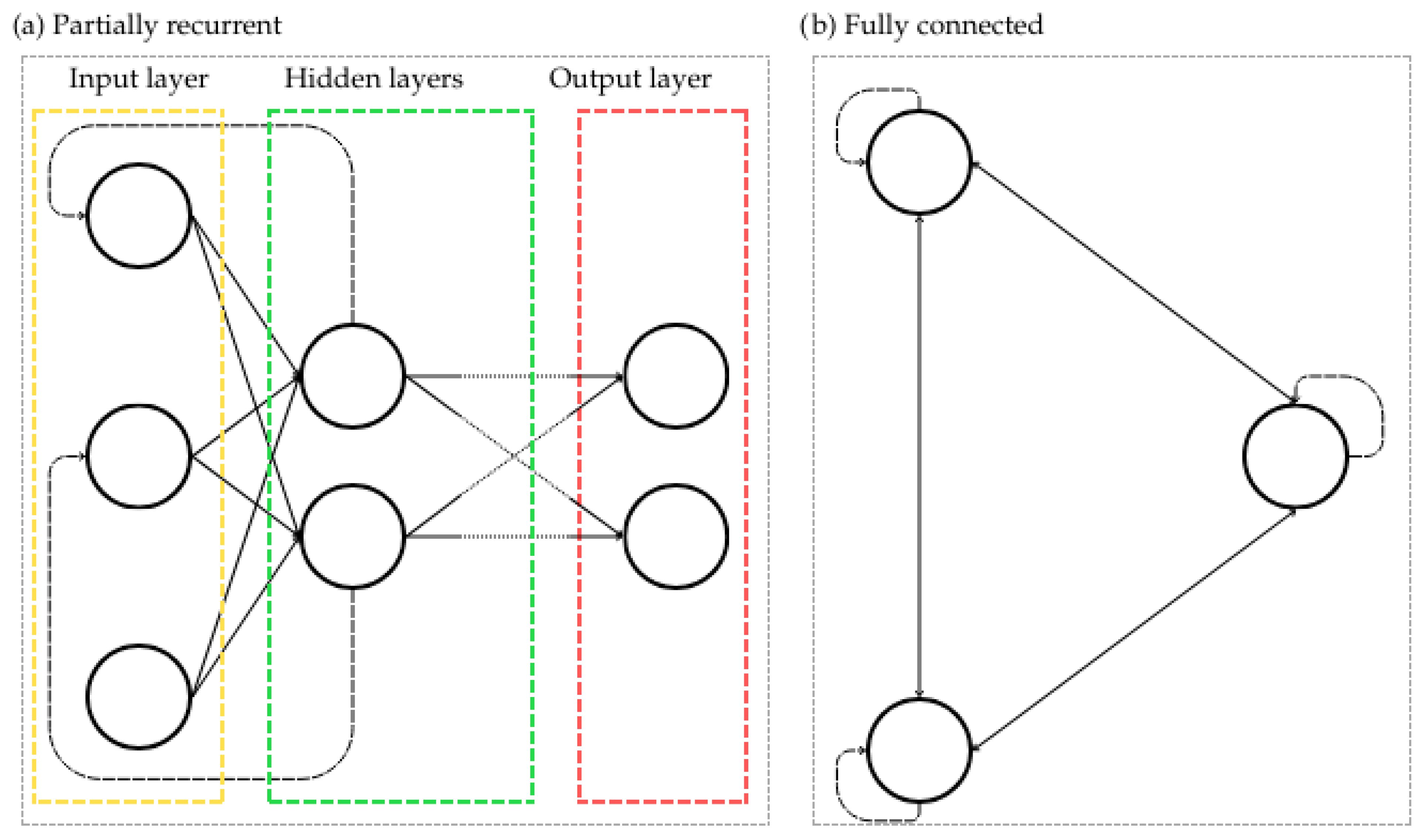
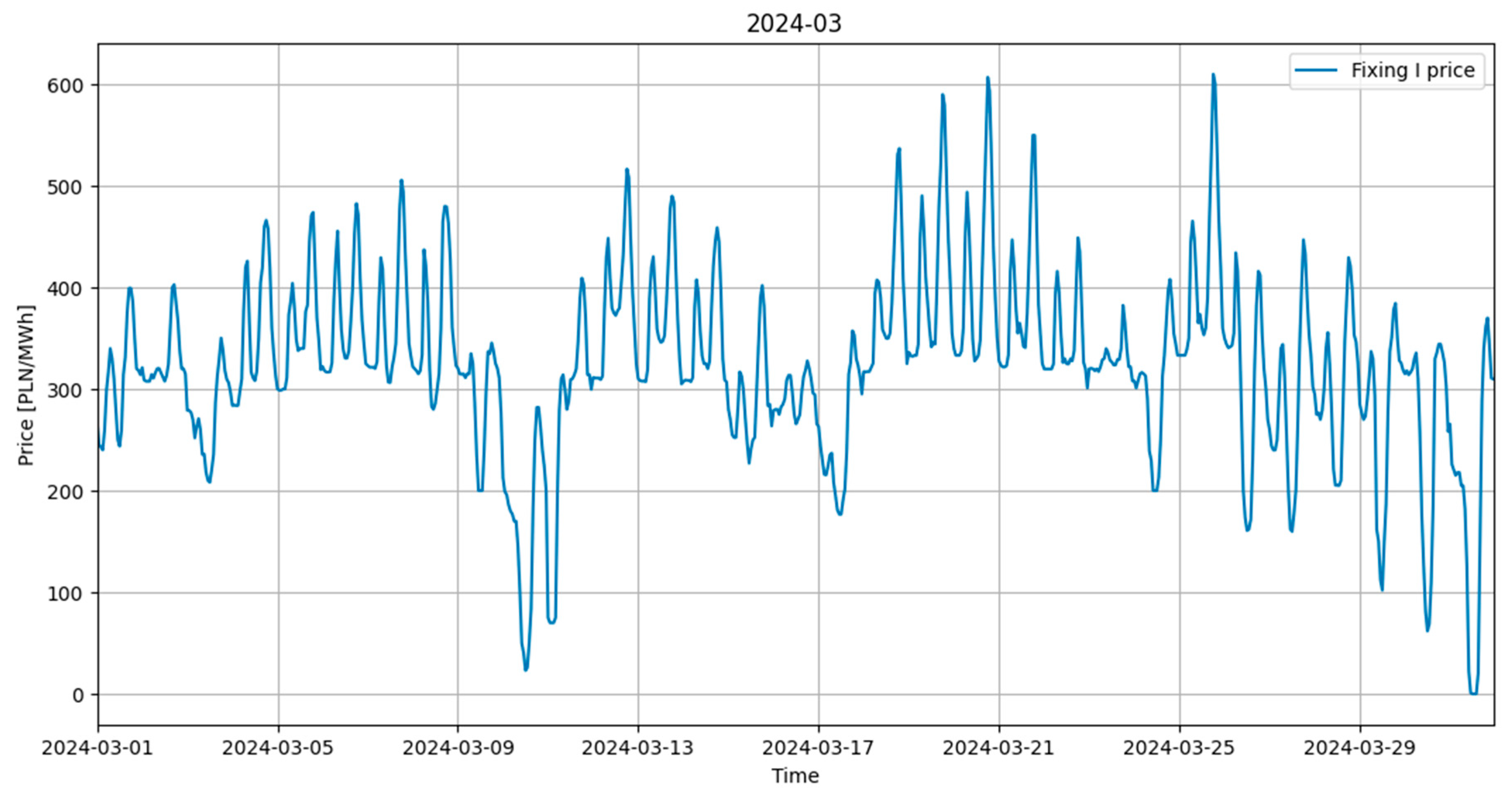
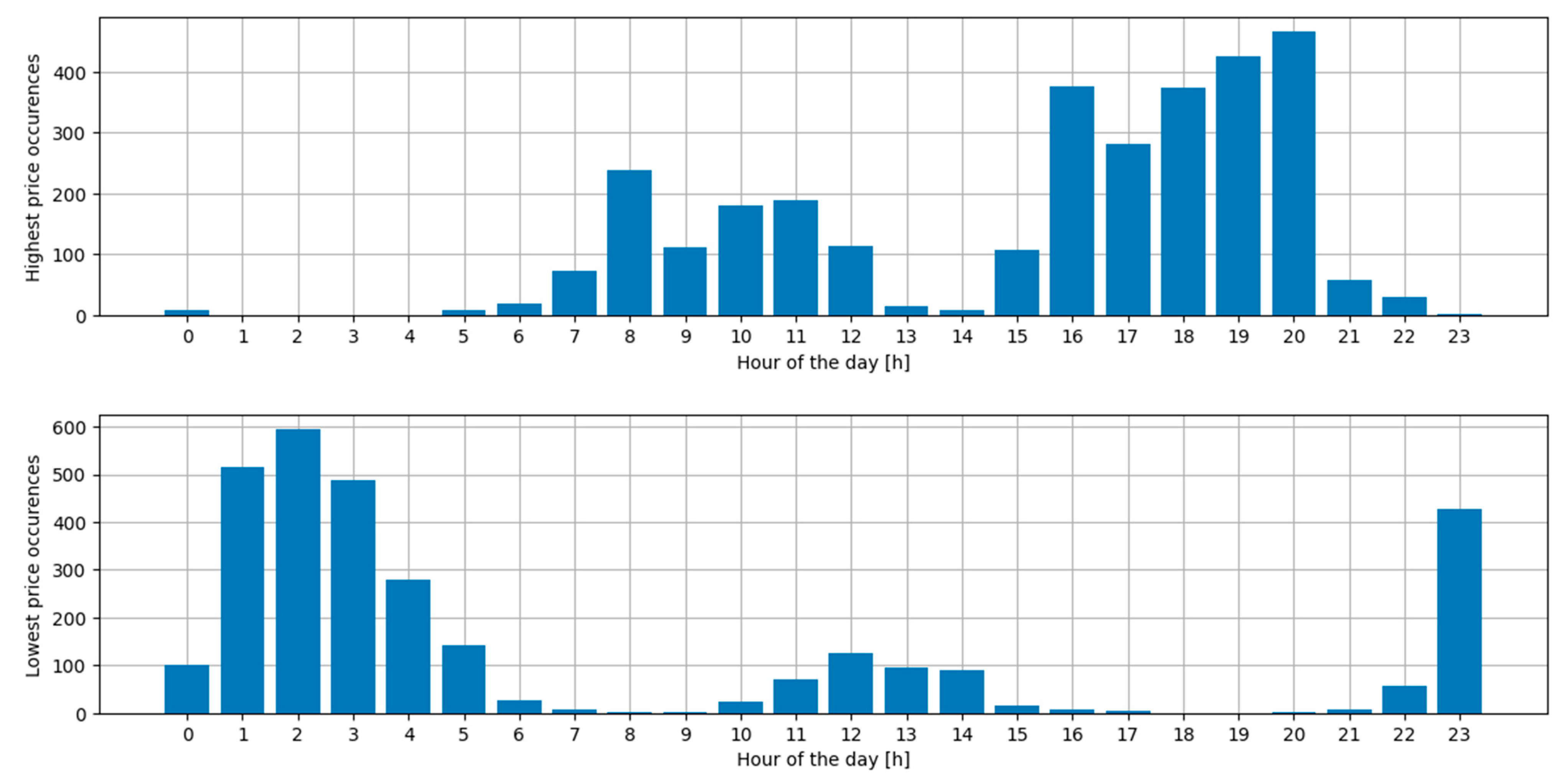
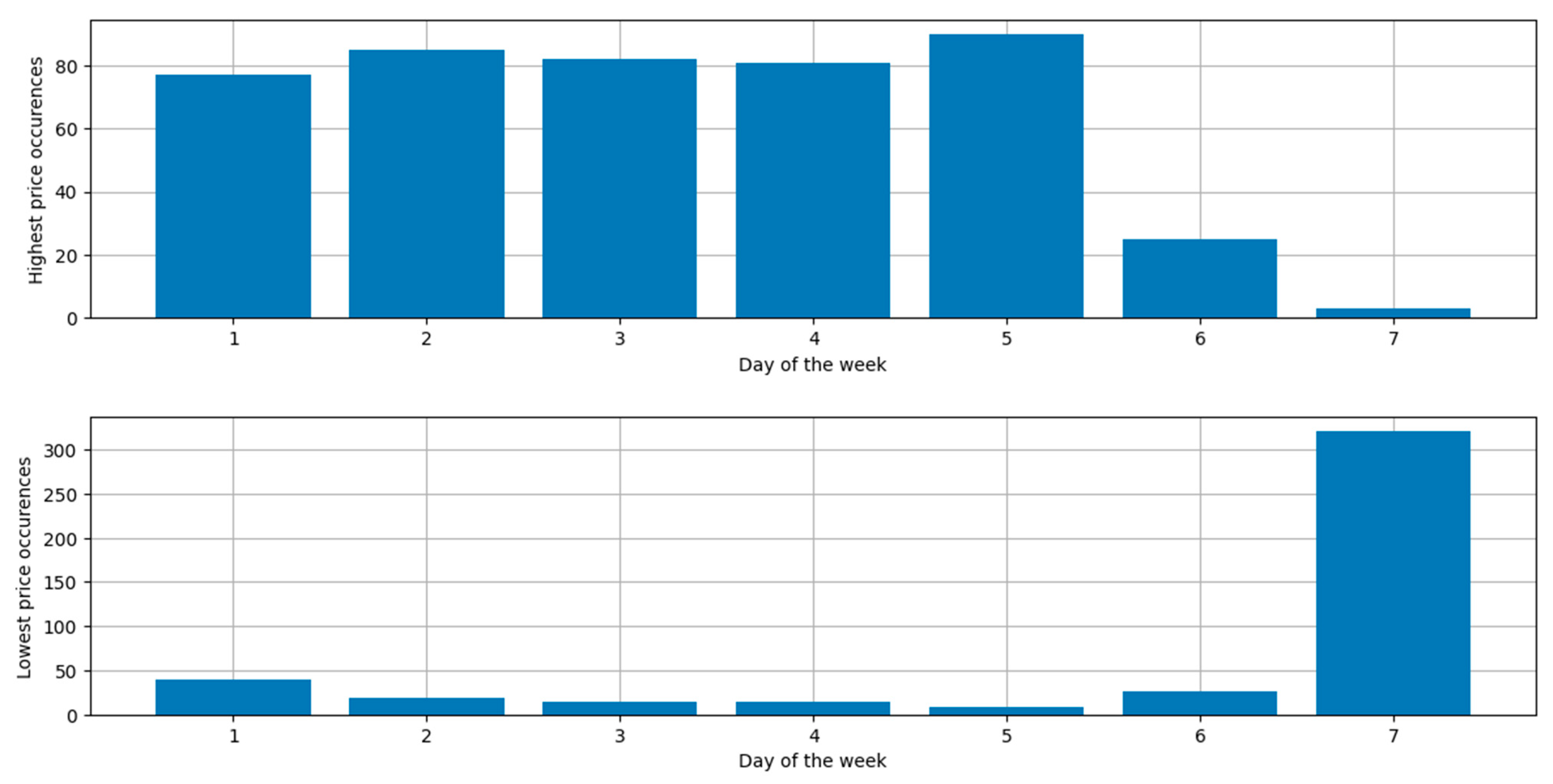
| Day of Week | Average Price [PLN/MWh] |
|---|---|
| Monday | 347.56 |
| Tuesday | 361.53 |
| Wednesday | 361.45 |
| Thursday | 352.58 |
| Friday | 348.13 |
| Saturday | 319.39 |
| Sunday | 264.30 |
| Month | Average Price [PLN/MWh] |
|---|---|
| January | 319.09 |
| February | 295.00 |
| March | 299.93 |
| April | 292.43 |
| May | 303.79 |
| June | 354.04 |
| July | 371.00 |
| August | 402.27 |
| September | 364.10 |
| October | 328.74 |
| November | 354.96 |
| December | 368.99 |
| Month | Average Wind Speed [m/s] | Season | Average Wind Speed [m/s] |
|---|---|---|---|
| December | 7.85 | Winter | 7.83 |
| January | 7.79 | ||
| February | 7.85 | ||
| March | 6.69 | Spring | 6.36 |
| April | 6.51 | ||
| May | 5.90 | ||
| June | 5.29 | Summer | 5.30 |
| July | 5.42 | ||
| August | 5.18 | ||
| September | 5.87 | Autumn | 6.65 |
| October | 7.18 | ||
| November | 6.87 |
| Year | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | 2024 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Correlation coefficient | CDU generation | 0.539 | 0.567 | 0.664 | 0.806 | 0.796 | 0.549 | 0.603 | 0.714 | 0.773 |
| Demand | 0.452 | 0.467 | 0.452 | 0.530 | 0.612 | 0.408 | 0.259 | 0.507 | 0.442 | |
| Wind generation | −0.274 | −0.329 | −0.374 | −0.503 | −0.357 | −0.136 | −0.450 | −0.466 | −0.353 | |
| Wind speed | −0.287 | −0.312 | −0.345 | −0.454 | −0.299 | −0.085 | −0.383 | −0.359 | −0.302 | |
| R2 | CDU generation | 0.290 | 0.321 | 0.441 | 0.649 | 0.633 | 0.301 | 0.363 | 0.509 | 0.597 |
| Demand | 0.204 | 0.218 | 0.205 | 0.281 | 0.374 | 0.166 | 0.067 | 0.257 | 0.195 | |
| Wind generation | 0.075 | 0.108 | 0.139 | 0.253 | 0.127 | 0.018 | 0.202 | 0.217 | 0.124 | |
| Wind speed | 0.082 | 0.097 | 0.119 | 0.206 | 0.089 | 0.007 | 0.146 | 0.128 | 0.091 | |
| Model | Loss Function | Normalisation | MAE 1 h/24 h [PLN/MWh] | Peak Conditions |
|---|---|---|---|---|
| 3 (LSTM (50) + Dropout (0.2)) | MSE | Min–max | 26.85/79.07 | Average |
| 3 (LSTM (50) + Dropout (0.2)) No wind input data | MSE | Min–max | 28.57/85.38 | Average |
| 1 GRU (64) + Dense (32) | MSE | Min–max | 28.06/82.78 | Poor |
| 1 GRU (64) + Dense (32) No wind input data | MSE | Min–max | 27.38/91.03 | Poor |
| CNN (64) + 2 GRU (64, 32) + Dense (32) | MSE | Min–max | 25.79/83.69 | Poor |
| CNN (64) + 2 GRU (64, 32) + Dense (32) No wind data input | MSE | Min–max | 28.22/91.03 | Poor |
| CNN (64) + 2 GRU (64, 32) + Dense (32) | Huber loss fun. | Standard | 24.30/74.15 | Good |
| CNN (64) + 2 GRU (64, 32) + Dense (32) No wind data input | Huber loss fun. | Standard | 24.60/84.87 | Average |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sowiński, R.; Komorowska, A. The Impact of Wind Speed on Electricity Prices in the Polish Day-Ahead Market Since 2016, and Its Applicability to Machine-Learning-Powered Price Prediction. Energies 2025, 18, 3749. https://doi.org/10.3390/en18143749
Sowiński R, Komorowska A. The Impact of Wind Speed on Electricity Prices in the Polish Day-Ahead Market Since 2016, and Its Applicability to Machine-Learning-Powered Price Prediction. Energies. 2025; 18(14):3749. https://doi.org/10.3390/en18143749
Chicago/Turabian StyleSowiński, Rafał, and Aleksandra Komorowska. 2025. "The Impact of Wind Speed on Electricity Prices in the Polish Day-Ahead Market Since 2016, and Its Applicability to Machine-Learning-Powered Price Prediction" Energies 18, no. 14: 3749. https://doi.org/10.3390/en18143749
APA StyleSowiński, R., & Komorowska, A. (2025). The Impact of Wind Speed on Electricity Prices in the Polish Day-Ahead Market Since 2016, and Its Applicability to Machine-Learning-Powered Price Prediction. Energies, 18(14), 3749. https://doi.org/10.3390/en18143749








