Analysis and Design of a Multiple-Driver Power Supply Based on a High-Frequency AC Bus

Abstract

Multi-channel LED drivers are crucial for high-power lighting applications. Maintaining a constant average forward current is essential for stable LED luminous intensity, necessitating drivers capable of consistent current delivery across wide operating ranges. Meanwhile, achieving precise current sharing among channels without incurring high costs and system complexity is a significant challenge. Leveraging the constant-current characteristics of the LCL-T network, this paper presents a multi-channel DC/DC LED driver comprising a full-bridge inverter, a transformer, and a passive resonant rectifier. The driver generates a high-frequency AC bus with series-connected diode rectifiers, a structure that guarantees excellent current sharing among all output channels using only a single control loop. Fully considering the impact of higher harmonics, this paper derives an exact solution for the output current. A step-by-step parameter design methodology ensures soft switching and enhanced switch utilization. Finally, experimental verification was conducted using a prototype with five channels and 200 W, confirming the correctness and accuracy of the theoretical analysis. The experimental results showed that within a wide input voltage range of 380 V to 420 V, the driver was able to provide a stable current of 700 mA to each channel, and the system could achieve a peak efficiency of up to 94.4%.

1. Introduction

With the rapid developments in semiconductor lighting, light-emitting diodes (LEDs) have been extensively applied to lighting equipment and consumer electronic products because of their high luminous efficiency, pollution-free characteristics, and super longevity [1,2]. To achieve sufficient lumens in the aforementioned applications, LEDs are coupled in series and parallel [3]. This configuration yields the requirement of multi-output constant current for LED drivers. It also requires power factor correction (PFC) and electrical isolation to satisfy power quality standards and safety regulations [4,5].

At the present time, approaches for realizing multi-channel constant-current output can be broadly categorized into single-converter and multi-converter schemes [6]. The multi-converter approach, wherein each LED load is driven by a dedicated DC/DC converter, offers flexible control but is often compromised by high system cost, volume, and complexity [7]. Consequently, single-converter multiple-output topologies have been extensively investigated. A key technical challenge for these topologies lies in achieving inherent current balancing among the parallel output branches.

As seen in Figure 1, this two-stage LED driver represents a common option for medium- to high-power applications. PFC converters make up the first stage, and DC/DC converters make up the second stage. Boost, buck, or other converters are often adopted in the first stage to obtain a high power factor and constant output voltage [8,9,10,11]. To address this challenge, this paper focuses on constant-current control multi-output DC/DC LED drivers [12,13] and aims to develop low-cost, high-power density, and high-efficiency solutions [14].

Among existing single-converter multiple-output current-balancing techniques, passive methods, such as those employing resistors or capacitors, feature a simple structure but suffer from poor regulation accuracy and introduce additional power losses [15]. In contrast, active methods, while capable of enhancing accuracy by monitoring and controlling each output channel, necessitate complex control circuitry and a significant increase in component count [16]. In recent years, advanced topologies based on resonant converters, single-inductor multiple-output (SIMO) structures, and electrolytic capacitor-less designs have been successively proposed, effectively enhancing system performance [17,18,19,20]. In particular, schemes that utilize the constant-current characteristics of resonant networks, such as the LCL-T topology, to establish a high-frequency AC bus have demonstrated considerable potential for multi-load applications [21].

Despite some progress in recent years, developing solutions that achieve high-precision current sharing, require minimal components, and feature simple control schemes remains a major challenge. This paper addresses these issues by proposing a novel multi-channel LED driver based on a high-frequency AC bus. The driver employs an innovative series rectifier architecture to achieve inherent current sharing.

A current-sharing scheme of a resonant network is proposed in [21]. Due to the LCL-T constant-current properties, the rectifiers can be designed to function similarly to current sources. In order to provide multiple constant-current outputs, multiple LCL-T rectifiers are coupled to the same high-frequency AC voltage bus. In order to simplify the circuit, increase power density, and reduce costs, more components should be shared among different outputs. The port for the output of the LCL-T passive resonant network can be used to build a high-frequency AC bus in accordance with the circuit duality concept. Each output can also share the passive resonant network apart from the original full-bridge inverter and high-frequency isolation transformer. Thus, as seen in Figure 2, the constant-current multi-output LED driver constructed using a high-frequency AC bus can be built. The focus of this paper is the second-stage DC/DC converter, whose input, U_dc, is provided by a front-end PFC circuit. Figure 2 shows the detailed topology of the proposed DC/DC converter part.

Compared to [21], there are significantly fewer resonant networks, and the circuit structure is significantly simpler. Each string is connected in series before the diode rectifier, so only one output string needs to be sampled and closed-loop controlled. Other output currents can be automatically kept constant since all the strings are driven by the same AC bus. Obviously, high current accuracy can be achieved for multiple LED strings within the change of input and output.

However, for multi-output resonant converters, their stability is of crucial importance. Due to the nonlinear dynamic characteristics of the resonant converter, it is necessary to conduct stability analyses under various working conditions to ensure its stable operation under all conditions. If a linearized system is required, small-signal modeling is indispensable. This method is conducive to the rapid design of an ideal feedback controller [22]. For modern lighting systems, well-designed controllers must achieve high stability, rapid current regulation, provide fast transient response, and—at the same time—prevent current overtones that may damage LED [23]

This paper is organized as follows. Section 2 introduces the proposed DC-fed multi-channel constant-current LED driver. Section 3 elaborates on the parameter design process and provides a comparative stability analysis for the optimization of the PI controller. Section 4 details the implementation of the DC/DC control circuitry and verifies its functionality through experimental results. Finally, Section 5 concludes the paper.

2. The Proposed LED Driver

The topological structure proposed in this paper is an advancement upon and optimization of existing research. The modular topological structure proposed in reference [21] lays the key foundation for this study. This scheme utilizes the constant-current characteristics of the LCL-T network to drive the LED loads in each channel by connecting multiple LCL-T passive resonant rectifier units in parallel to the high-frequency AC voltage bus. This solution provides ideas for further optimization. Specifically, in this solution, each output channel is equipped with a dedicated LCL-T resonator. Therefore, this solution will inevitably increase the total number of components, cost, and physical volume, thereby limiting the power density.

To address the limitations of the aforesaid schemes, this letter presents a topology with a higher degree of integration, the core principle of which is to consolidate multiple resonant units into a centralized resonant network. This architecture utilizes the constant-current characteristics of an LCL-T network to establish a high-frequency AC bus, to which the rectifier bridges of each output channel are connected in series. This series configuration ensures that the output current of each channel is identical, thereby achieving inherent high-precision current balancing. Simultaneously, this approach significantly reduces the component count of passive elements. The final proposed scheme, derived from the analysis of this topology, is depicted in Figure 2.

The DC/AC inverter and the LCL-T passive resonant rectifier are the two components of the proposed DC-provided multi-output constant-current LED driver shown in Figure 2. One LCL-T passive resonant network comes after the DC/AC inverter. After isolation by a transformer, a high-frequency AC bus is formed. Each output string is connected in series with the AC bus through the diode rectifier. Thus, multiple constant-current outputs can be realized with high current accuracy.

Consisting of switches S₁ through S₄, the DC/AC inverter transforms DC electricity into high-frequency AC square voltage. Additionally, Figure 1 shows the output voltage of the first PFC stage, which is the input DC voltage U_dc. An isolation transformer, T, a diode rectifier linked in series with the LED loads, a DC blocking capacitor, C_b, and resonant networks L₁, C₁, and L_a1 make up the LCL-T passive resonant rectifier.

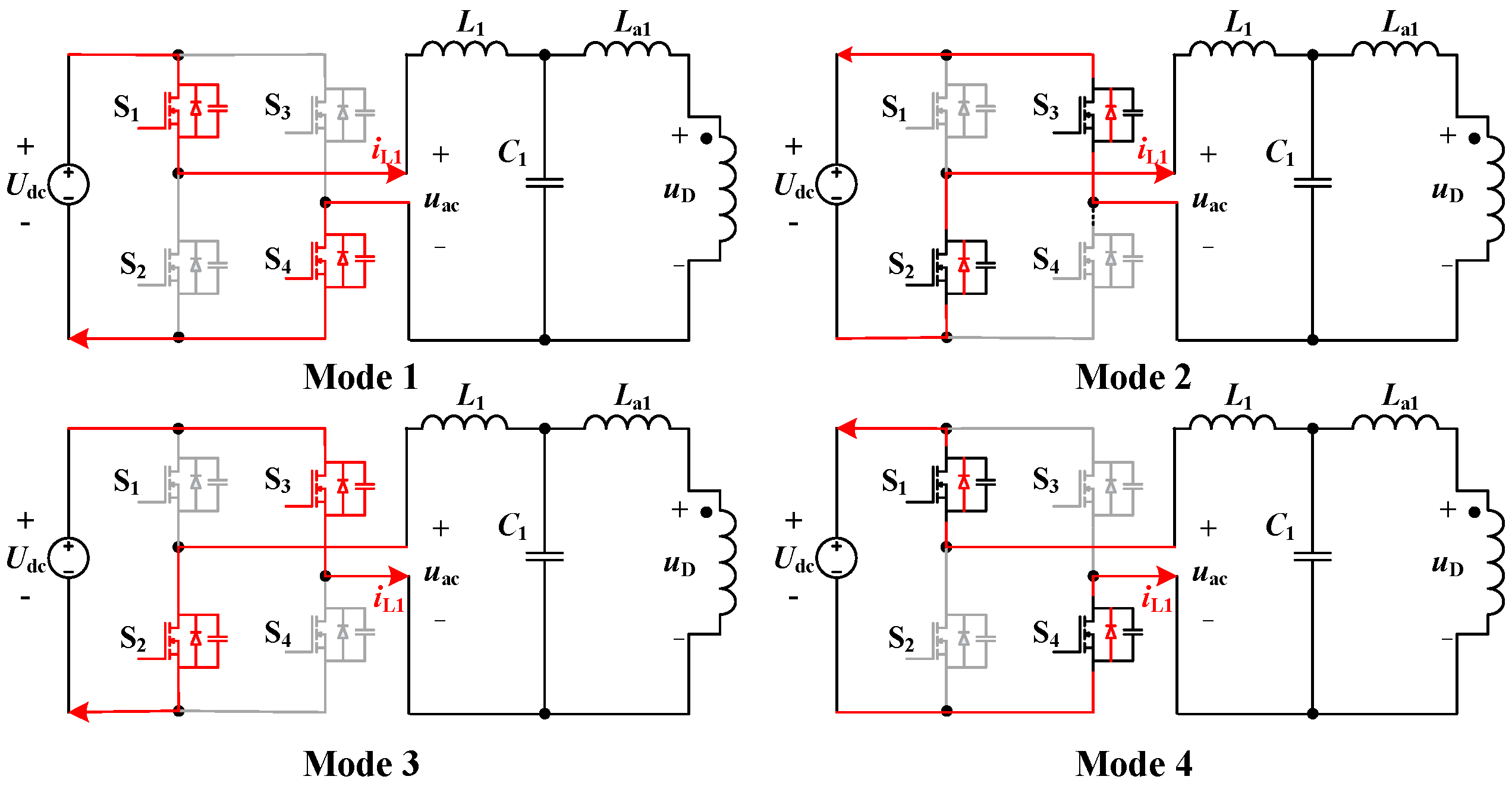
As illustrated in Figure 3, the converter operates in four primary modes within a single switching period, with the current paths highlighted in red and with inactive switching devices marked in gray. By employing phase-shift control, the full-bridge inverter converts the input DC voltage, U_dc, into a high-frequency square-wave voltage, u_ac.

The operational modes are analyzed as follows:

In Mode 1, switches S₁ and S₄ are in the ON state. The DC power source forms a loop through S₁, the LCL-T resonant network, and S₄, transferring energy to the network.

In Mode 2, all the switches are turned OFF. The energy stored in the resonant inductor is released through the freewheeling diodes of S₂ and S₃, allowing the current to continue circulating.

In Mode 3, switches S₂ and S₃ are in the ON state. A reverse DC voltage is now applied to the input of the resonant network, and current flows through S₃, the resonant network, and S₂.

In Mode 4, S₂ and S₃ are turned OFF, and all the switches are once again in the OFF state. The energy in the resonant inductor is released through the freewheeling diodes of S₁ and S₄. This completes one full operational cycle.

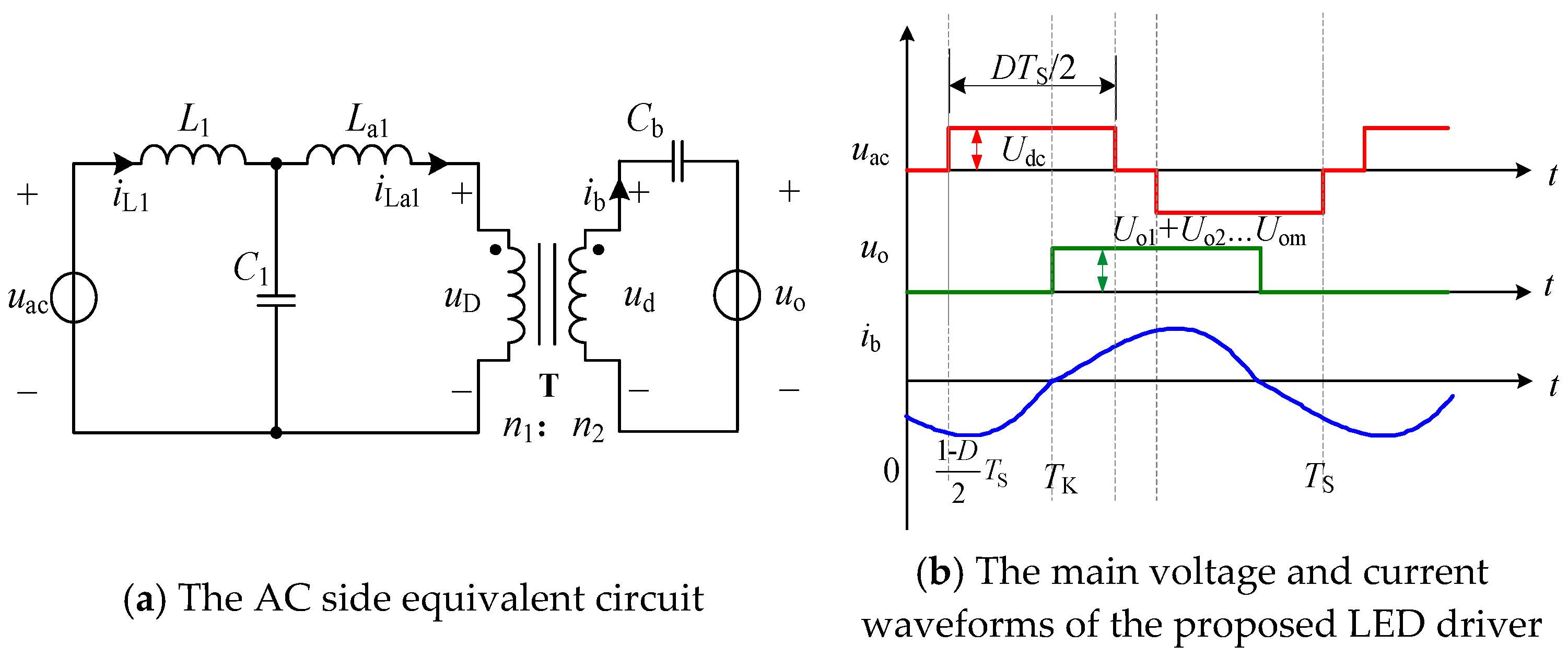
Figure 4a displays the analogous circuit for the AC side. Phase-shifting full-bridge PWM control is applied to switches S₁–S₄. S₁ and S₂, and S₃ and S₄ are turned ON and OFF complementarily, respectively. S₁ and S₃ have the same duty cycle, and their phase difference is 180°. Thus, as seen in Figure 4b, the full-bridge DC/AC inverter’s output voltage is a high-frequency AC square voltage, u_ac. The square voltage, u_o, serves as the diode rectifier’s input voltage. The amplitude of u_o is equal to the sum of the LED load voltages when the current, i_b, is larger than 0. The amplitude of u_o equals 0 when the current, i_b, is smaller than 0.

As described in Figure 4b, the LCL resonant network, u_ac, input voltage can be written as:

$$u_{\mathrm{ac}}=\left\{\begin{array}{l}0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(0<t\le {\displaystyle \frac{1-D}{2}}{T}_{\mathrm{S}}\right)\\ U_{\mathrm{dc}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left({\displaystyle \frac{1-D}{2}}{T}_{\mathrm{S}}<t\le {\displaystyle \frac{T_{\mathrm{S}}}{2}}\right)\\ 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left({\displaystyle \frac{T_{\mathrm{S}}}{2}}<t\le {\displaystyle \frac{2-D}{2}}{T}_{\mathrm{S}}\right)\\ -U_{\mathrm{dc}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left({\displaystyle \frac{2-D}{2}}{T}_{\mathrm{S}}<t\le T_{\mathrm{S}}\right)\end{array}\right.$$

(1)

where D is the switching device’s conduction duty cycle, and T_S is its switching period.

According to the above analysis of the square voltage, u_o, it can be expressed as follows in the first switching cycle.

$$u_{\mathrm{o}}=\left\{\begin{array}{l}0\hspace{1em}\hspace{1em}\left(0<t\le T_{\mathrm{K}}\right)\\ U_{\mathrm{o}}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left(T_{\mathrm{K}}<t\le T_{\mathrm{K}}+{\displaystyle \frac{T_{\mathrm{S}}}{2}}\right)\\ 0\hspace{1em}\left(T_{\mathrm{K}}+{\displaystyle \frac{T_{\mathrm{S}}}{2}}<t\le T_{\mathrm{S}}\right)\end{array}\right.$$

(2)

where U_o = U_o1 + U_o2 +... + U_om, m is the number of output channels, and T_K is the starting delay time of the output voltage, u_o, square wave.

Both u_ac and u_o are AC square voltages, so their Fourier series expansion can be easily obtained as:

$$u_{\mathrm{ac}}={\displaystyle \sum }_{h=1,3,5,7\dots }{U}_{\mathrm{achm}}\sin (h{\mathrm{\omega }}_{\mathrm{S}}t+{\mathrm{\phi }}_{\mathrm{h}})$$

(3)

where

$$\begin{array}{l}{\mathrm{\phi }}_{\mathrm{h}}={\tan }^{-1}{\displaystyle \frac{\sin \left(hD\mathrm{\pi }\right)}{\cos \left(hD\mathrm{\pi }\right)-1}}\\ U_{\mathrm{achm}}=\sqrt{{a_{\mathrm{h}}}^2+{b_{\mathrm{h}}}^2}\\ a_{\mathrm{h}}=\left[\sin \left(D-1\right)h\mathrm{\pi }-\sin \left(Dh\mathrm{\pi }\right)\right]{\displaystyle \frac{U_{\mathrm{dc}}}{h\mathrm{\pi }}}\\ b_{\mathrm{h}}=\left[1-\cos (h\mathrm{\pi })-\cos \left(Dh\mathrm{\pi }\right)+\cos \left(D-1\right)h\mathrm{\pi }\right]{\displaystyle \frac{U_{\mathrm{dc}}}{h\mathrm{\pi }}}\end{array}$$

And the voltage, u_o, can be expressed as

$$u_{\mathrm{o}}={\displaystyle \frac{U_{\mathrm{o}}}{2}}+{\displaystyle \sum }_{h=1,3,5,7\dots }{U}_{\mathrm{ohm}}\sin \left[h{\mathrm{\omega }}_{\mathrm{S}}\left(t-T_{\mathrm{K}}\right)\right]$$

(4)

where

$$U_{\mathrm{ohm}}={\displaystyle \frac{2U_{\mathrm{o}}}{h\mathrm{\pi }}},U_{\mathrm{o}}=U_{\mathrm{o}1}+U_{\mathrm{o}2}+\dots +U_{\mathrm{om}}$$

DC-blocking capacitor C_b filters out the DC component of the high-frequency square voltage, u_o, which is U_o/2. Therefore, the LCL resonant network output voltage, u_D, may be written as

$$u_{\mathrm{D}}={\displaystyle \sum }_{h=1,3,5,7\dots }{U}_{\mathrm{Dhm}}\sin \left[h{\mathrm{\omega }}_{\mathrm{S}}\left(t-T_{\mathrm{K}}\right)\right]$$

(5)

where

$$U_{\mathrm{Dhm}}={\displaystyle \frac{2N{U}_{\mathrm{o}}}{h\mathrm{\pi }}}$$

Additionally, N is the transformer T’s turns ratio, which is equivalent to n₁/n₂.

The output currents of each LED string are identical since they are linked in series via the diode rectifier, which means

$$I_{\mathrm{o}1}=I_{\mathrm{o}2}=\dots =I_{\mathrm{om}}$$

(6)

Figure 2 shows that the precise output current, I_o1-act, is equivalent to half of the average value of the current, i_b, during the positive half-switching phase. So, if the currents i_b or i_La1 can be obtained quantitatively, the exact solution of the output current I_o1-exa can be obtained, which is derived as

$$I_{\mathrm{o}1-\mathrm{exa}}={\displaystyle \frac{1}{2\mathrm{\pi }}}\underset{{\mathrm{\omega }}_{\mathrm{S}}{T}_{\mathrm{K}}}{\overset{{\mathrm{\omega }}_{\mathrm{S}}{T}_{\mathrm{K}}+\mathrm{\pi }}{{\displaystyle \int }}}\left(i_{\mathrm{b}}\right)d{\mathrm{\omega }}_{\mathrm{S}}t={\displaystyle \frac{N}{2\mathrm{\pi }}}\underset{{\mathrm{\omega }}_{\mathrm{S}}{T}_{\mathrm{K}}}{\overset{{\mathrm{\omega }}_{\mathrm{S}}{T}_{\mathrm{K}}+\mathrm{\pi }}{{\displaystyle \int }}}\left(i_{\mathrm{La}1}\right)d{\mathrm{\omega }}_{\mathrm{S}}t$$

(7)

Next, the characteristics of the output current are analyzed considering the fundamental and higher harmonics, respectively.

2.1. Only Considering the Fundamental Harmonic

The ratio of inductors L₁ and L_a1, the resonant angular frequency, ω_o, and its normalized angular frequency, ω_n, are defined as

$${\mathrm{\omega }}_{\mathrm{o}}={\displaystyle \frac{1}{\sqrt{L_1{C}_1}}}, {\mathrm{\omega }}_{\mathrm{n}}={\displaystyle \frac{{\mathrm{\omega }}_{\mathrm{S}}}{{\mathrm{\omega }}_{\mathrm{o}}}}, {\mathrm{\omega }}_{\mathrm{S}}=2\mathrm{\pi }{f}_{\mathrm{S}}, \gamma ={\displaystyle \frac{L_1}{L_{\mathrm{a}1}}}$$

(8)

where f_S is the switching frequency, and ω_S represents its angular frequency.

The LCL-T rectifier functions as an ideal current source if the resonant angular frequency is equivalent to the switching frequency, or ω_n = 1, and only takes into account the fundamental harmonic in voltage u_ac and u_D [21]. Accordingly, as examined in [21], the output current, I_o1, is independent of the output voltage, and it can be expressed as

$$I_{\mathrm{o}1}={\displaystyle \frac{N}{\mathrm{\pi }}}{\displaystyle \frac{U_{\mathrm{ac}1\mathrm{m}}}{{\mathrm{\omega }}_{\mathrm{S}}{L}_1}}$$

(9)

The LCL-T resonant network parameters may be found using Equations (7) and (8). If U_ac1m, N, and I_o1 are known, the inductor, L₁, can be calculated from (8), and the capacitor C₁ can be deduced from (7).

The determination of the inductor, L_a1, is as follows. When γ is equal to 1, the fundamental component of the resonant network input current, i_L1, is in phase with the fundamental component of the voltage, u_ac, as concluded in [21]. The resonant network should be slightly inductive to achieve the zero-voltage switching conditions for switches, so γ needs to be greater than 1. As γ is taken as 2 here, it is also verified that it is a reasonable value in Section 3. Next, L_a1 can be calculated from (8) once L₁ and γ are determined.

2.2. Considering Higher Harmonics

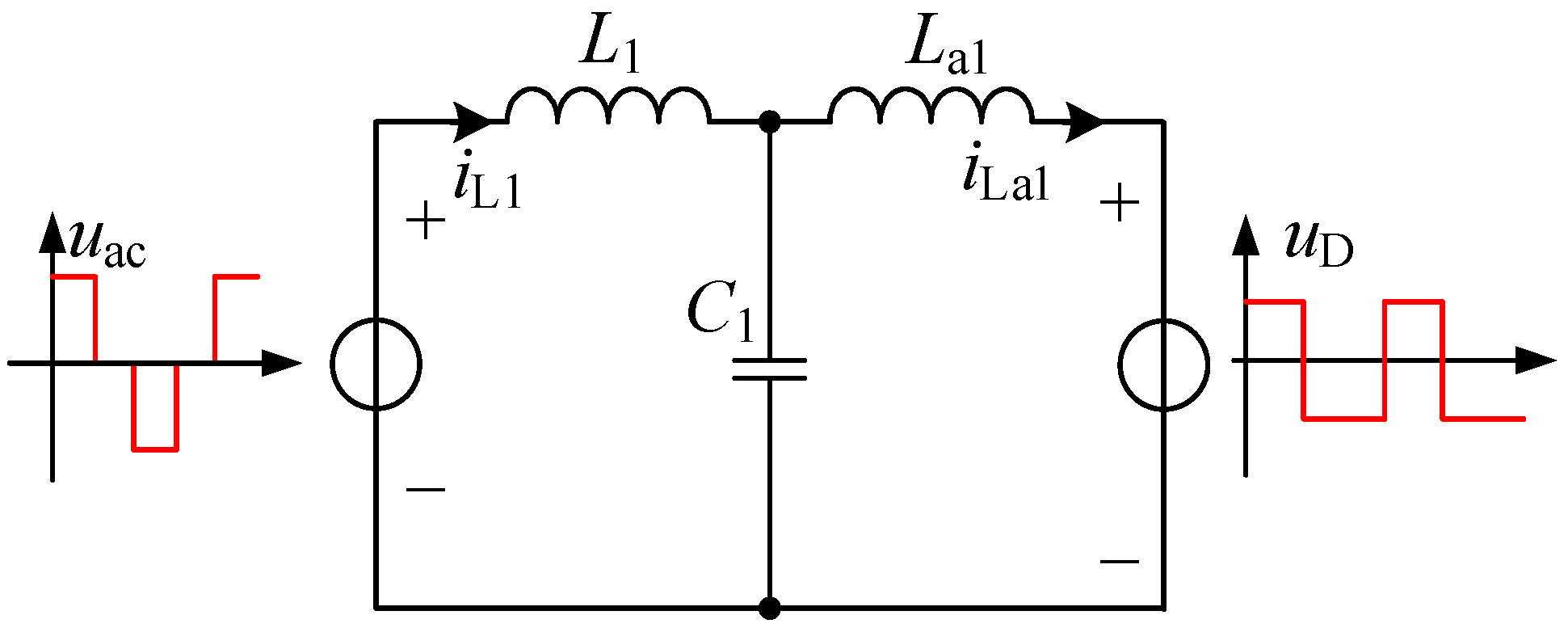
Figure 5 below represents the analogous circuit of the LCL-T resonant network seen in Figure 4a. There are many higher harmonics in the current i_La1 because the voltages, u_ac and u_D, of the LCL-T network correspond to the AC square voltages from (3) and (5), and these include considerably higher harmonics. It is crucial to carefully examine how higher harmonics affect the precision of the output currents, since (7) will have an impact on the accuracy of the precise output current, I_o1-exa.

In Figure 5, i_La1 can be solved when the voltage sources, u_ac and u_D, work separately. Then, the final current, i_La1, can be obtained according to the superposition theorem. The expressions of u_ac and u_D are shown in (3) and (5), and the phase of the AC voltage, u_D, is determined by T_K, which is solved as follows.

The AC voltage, u_D, crosses zero when t = T_K, and the inductor current, i_La1, also crosses zero at this time, that is, i_La1(T_K) = 0. In order to determine the connections between T_K, U_dc, N, and U_o using the frequency domain analysis approach, Equation (10) is obtained from [21]. The output current, I_o1-exa, can thus be precisely solved as (11). Finding the precise current solution and examining the parameters needed to satisfy the output current’s accuracy criteria are the primary uses of Equation (11).

$$-{\displaystyle \sum }_{h=1,3,5,7\dots }^{\infty }{\displaystyle \frac{\gamma U_{\mathrm{achm}}\cos (h{\mathrm{\omega }}_{\mathrm{S}}{T}_{\mathrm{K}}+{\mathrm{\phi }}_{\mathrm{h}})}{h\left[\gamma -\left(h^2-1\right)\right]}}+{\displaystyle \sum }_{h=1,3,5,7\dots }^{\infty }{\displaystyle \frac{\gamma \left(1-h^2\right)U_{\mathrm{Dhm}}}{h\left[\gamma -\left(h^2-1\right)\right]}}=0$$

(10)

After determining U_dc, N, D, and U_o, T_K may be solved using mathematical programs like MATLABR2024a, as stated in [21]. Then, the precise solution of the output current, I_o1-exa, is obtained as follows:

$$\begin{array}{ll}\hfill I_{\mathrm{o}1-\mathrm{exa}}& ={\displaystyle \frac{N}{2\mathrm{\pi }}}\underset{{\mathrm{\omega }}_{\mathrm{S}}{T}_{\mathrm{K}}}{\overset{{\mathrm{\omega }}_{\mathrm{S}}{T}_{\mathrm{K}}+\mathrm{\pi }}{{\displaystyle \int }}}\left(i_{\mathrm{La}1}\right)d{\mathrm{\omega }}_{\mathrm{S}}t\hfill \\ & ={\displaystyle \frac{N}{2\mathrm{\pi }}}\left\{{\displaystyle {\displaystyle \sum }_{h=1,3,5,7\dots }^{\infty }}{\displaystyle \frac{2\gamma U_{\mathrm{achm}}}{h^2\left[\gamma -\left(h^2-1\right)\right]{\mathrm{\omega }}_{\mathrm{S}}{L}_1}}\sin \left(h{\mathrm{\omega }}_{\mathrm{S}}{T}_{\mathrm{K}}+{\mathrm{\phi }}_{\mathrm{h}}\right)\right\}\hfill \end{array}$$

(11)

As indicated by (10) and (11), I_o1-exa is a function of U_dc, U_o, N, D, and L₁. Therefore, the subsequent step is to determine the parameters, N and L₁. The architecture of the LCL-T passive resonant rectifier provides the conditions necessary to achieve zero-voltage switching (ZVS), the realization of which is ensured by the proper selection of the parameter γ.

To validate the preceding theoretical analysis, a corresponding simulation model was constructed. As depicted in Figure 6, the simulation results clearly demonstrate that the input voltage, u_ac, (red trace) is a square wave with an amplitude of ±400 V, while the output voltage, u_D, (blue trace) is also a square wave that lags u_ac. This outcome is in good agreement with the theoretical analysis for the equivalent voltage at the output of the LCL-T resonant network, thus verifying the correctness of the theory presented in this section.

The primary function of the LCL-T resonant network is to perform waveform shaping. Through the analysis and calculation of inductor L₁ and capacitor C₁, its resonant frequency is set to the switching frequency. The network exhibits low impedance to the fundamental component of the square-wave voltage, u_ac, while presenting high impedance to higher-order harmonics. Furthermore, the presence of the inductor, L_a1, effectively attenuates high-order harmonics. The DC-blocking capacitor, C_b, connected in series with the transformer secondary, serves to filter out any DC bias resulting from various factors, thereby ensuring the stable operation of the entire resonant network. In summary, owing to the filtering effect of the LCL-T network and the DC-blocking protection afforded by C_b, the system successfully converts the square-wave voltage into a smooth, high-quality AC.

3. Parameter Design

The stable state model of the whole system, taking into account only the fundamental harmonic, may be obtained using Equations (3) and (9):

$$I_{\mathrm{o}}={\displaystyle \frac{4N{U}_{\mathrm{dc}}}{{\mathrm{\pi }}^2{\mathrm{\omega }}_{\mathrm{S}}{L}_1}}\sin \left(D{\displaystyle \frac{\mathrm{\pi }}{2}}\right)$$

(12)

By linearizing (12) around the steady-state operating point (D, I_o), the influence of a duty cycle perturbation on the output current can be obtained. This is defined as the system’s DC gain, K_dc:

$$K_{\mathrm{dc}}={\displaystyle \frac{\partial I_{\mathrm{o}}}{\partial D}}={\displaystyle \frac{2N{U}_{\mathrm{dc}}}{\mathrm{\pi }{\mathrm{\omega }}_{\mathrm{S}}{L}_1}}\cos \left(D{\displaystyle \frac{\mathrm{\pi }}{2}}\right)$$

(13)

Through the output filtering stage, the system’s low-frequency dynamic properties are established. The output filter for this topology may be roughly represented via the first-order RC low-pass filter, and the transfer function, H(s), is as follows:

$$H(s)={\displaystyle \frac{1}{1+s{R}_{\mathrm{LED}}{C}_{\mathrm{o}}}}$$

(14)

where C_o is the output filter capacitance, and R_LED is the equivalent resistance of the LED load.

By combining the DC gain and low-frequency dynamic characteristics obtained from the above analysis, the small-signal transfer function, G(s), can be obtained as follows:

$$G(s)={\displaystyle \frac{{\widehat{i}}_o(s)}{\widehat{d}(s)}}=K_{\mathrm{dc}}\cdot H(s)={\displaystyle \frac{\frac{2N{U}_{\mathrm{dc}}}{\mathrm{\pi }{\mathrm{\omega }}_{\mathrm{S}}{L}_1}\cos \left(D\frac{\mathrm{\pi }}{2}\right)}{1+s{R}_{\mathrm{LED}}{C}_{\mathrm{o}}}}$$

(15)

Equation (15) was derived using the fundamental harmonic approximation (FHA) method, which represents the open-loop small-signal transfer function of the entire system. This model abstracts the controlled object as a first-order system with variable gain K_dc, primarily used to analyze the low-frequency dynamic characteristics of the system and lay the groundwork for subsequent feedback controllers.

To verify the correctness and accuracy of this theoretical model, a simulation model of the proposed LED driver was constructed in MATLAB/Simulink.

Since the simulation’s circuit parameters act as a direct reference for the practical prototype, they are extremely important. The simulation was configured with a DC input voltage, U_dc, of 400 V and a switching frequency, f_s, of 100 kHz. To reduce the physical volume of the resonant network, the transformer turns ratio, N, was set to 2 after detailed analysis. For a target constant output current, I_o, of 0.7 A, with the normalized angular frequency, ω_n, set to 1 and the inductor ratio, γ, preset to 2, Equations (8) and (9) were used to compute the LCL-T resonance network’s constants. This yielded the following values: L₁ = 364.5 μH, L_a1 = 182.25 μH, and C₁ = 6.96 nF.

To validate the accuracy of the theoretical model, the transfer function, G(s), derived from the theoretical analysis, is compared against Gf(s) obtained from the simulation model. Figure 7 presents a comparison of the theoretical and simulated Bode plots. As illustrated in the figure, the Bode plot derived from the theoretical calculation is in good agreement with the frequency-sweep simulation results, thereby validating the correctness of the established mathematical model in the low-frequency domain.

Following the simulation verification, the subsequent step involves preparing for the experimental implementation. To design a closed-loop controller capable of fast and precise output current regulation, a thorough understanding of the system’s model characteristics is essential. The small-signal function of transfer G(s) from the obligation cycle, d(s), to the output current, i_o(s), demonstrates the traits of a conventional first-order low-pass filter, as per Equation (15):

$$G(s)={\displaystyle \frac{{\widehat{i}}_o(s)}{\widehat{d}(s)}}=K_{\mathrm{dc}}\cdot H(s)={\displaystyle \frac{K_{\mathrm{dc}}}{1+s/{\mathrm{\omega }}_{\mathrm{p}}}}$$

where the pole ω_p = 1/(R_LED · C_o).

By substituting the relevant circuit parameters, it can be calculated that the system pole, f_p, is 19.5 Hz. The system’s dynamic reaction time is quite sluggish because of the pole’s relatively low frequency, which prevents it from meeting the necessary requirements for quick adjustment and quick startup.

Additionally, the duty cycle, D, change affects the DC gain, K_dc. When duty cycle D is zero, the worst-case situation arises, and K_dc achieves its maximum value, represented by K_{dc_max}:

$$K_{\mathrm{dc}\_\max }={\displaystyle \frac{2N{U}_{\mathrm{dc}}}{\mathrm{\pi }{\mathrm{\omega }}_{\mathrm{S}}{L}_1}}$$

Following the above theoretical analysis, the designed PI controller needs to meet four requirements. To enhance the system’s dynamic reaction speed, the bandwidth must first be increased (f_c = 10 kHz). Secondly, it is also necessary to ensure that the system has a sufficient stability margin to resist parameter changes and external disturbances. Thirdly, the compensated system must eliminate the steady-state error, which is the basic requirement for maintaining a constant output current. Fourth, the system also needs to reduce overshoot to protect the LED components and extend their service life.

After analysis, by appropriately adjusting the PI parameters, the proportional–integral controller can meet the above four requirements.

In this section, three distinct PI controller design methods are compared, all based on the worst-case gain scenario. These methods are the zero-pole cancellation method, the phase margin tuning method, and the pole placement method. A comparative analysis of various performance metrics will be conducted to determine the most suitable design approach for the experiment.

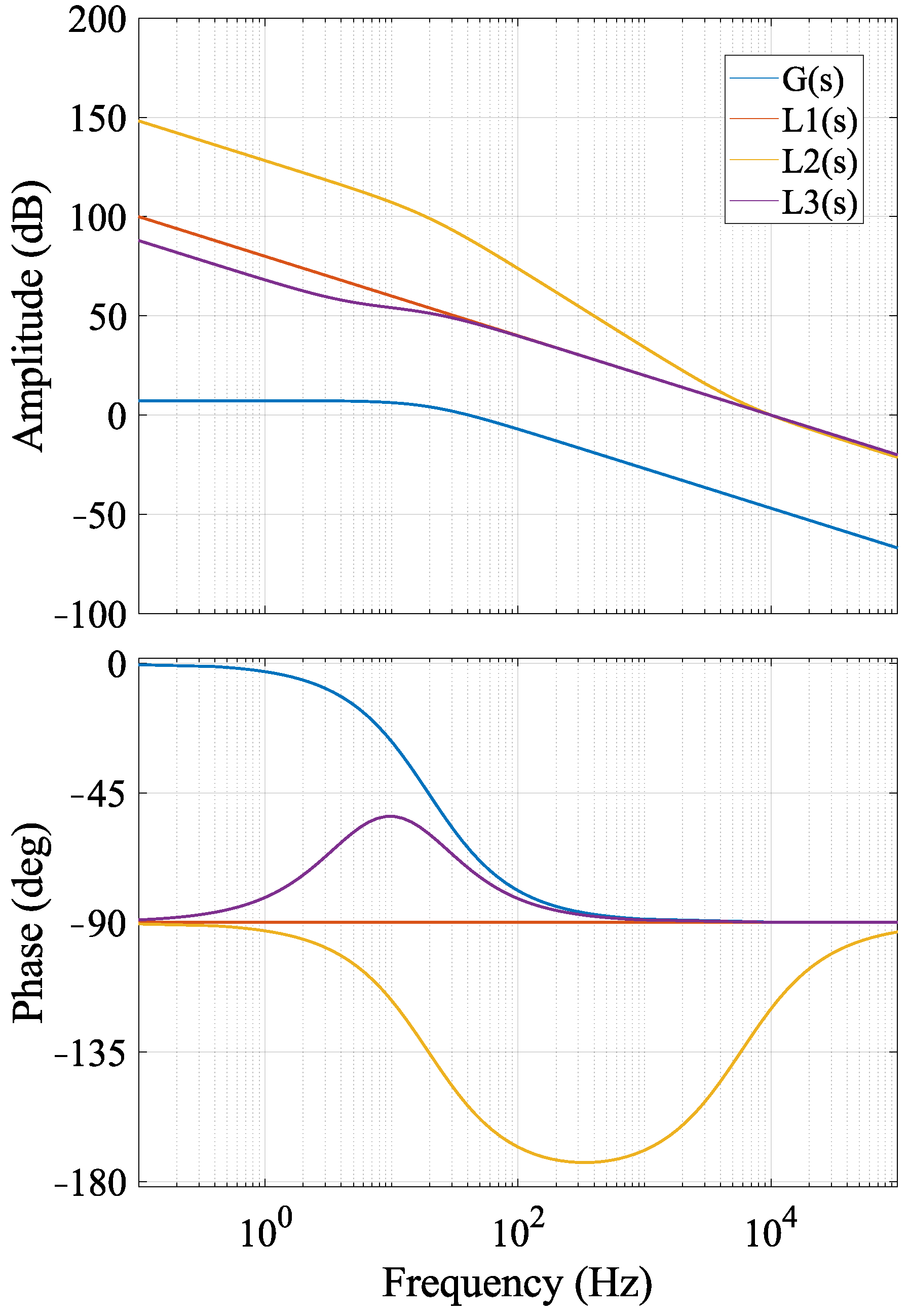
To provide a clear visual comparison, the open-loop transfer functions resulting from each of the three methods are plotted using MATLABR2024a, as shown in Figure 8. In the figure, the uncompensated system is represented by the curve, G(s), while the systems compensated using methods one, two, and three are represented by L₁(s), L₂(s), and L₃(s), respectively. Meanwhile, after calculation, various data of the open-loop curves in the figure are supplemented in

Table 1. Comparative analysis of PI controller design methods.

System	Kp	Ki	fc (kHz)	PM (deg)	Overshoot (%)	Settling Time (μs)
G(s)			0.04	115.6	0.0	9630.6
Method 1	221.4662	27,130.49	10.0	90.0	0.0	62.3
Method 2	191.5795	6,981,061.78	10.0	60.0	24.3	149.8
Method 3	221.4666	6782.64	10.0	90.1	0.0	63.4

for convenient comparison and analysis.

The plant model, based on the system parameters, is:

$$G\left(s\right)=K_{\mathrm{dc}\_\max }/\left(1+s/{\mathrm{\omega }}_{\mathrm{p}}\right)=2.9135/\left(1+s/122.51\right)$$

The resulting open-loop transfer functions corresponding to the curves L₁(s), L₂(s), and L₃(s) are as follows:

For L₁(s): The controller G_c1(s) precisely sets its zero point at the pole of the controlled object, thereby achieving zero-pole cancellation and simplifying the system to a pure integrator form.

$$\begin{array}{l}{L}_1\left(s\right)=G_{\mathrm{c}1}\left(s\right)G\left(s\right)=\left[K_{\mathrm{p}1}\left(s+{\mathrm{\omega }}_{\mathrm{z}1}\right)/s\right]\left[K_{\mathrm{dc}\_\max }/\left(1+s/{\mathrm{\omega }}_{\mathrm{p}}\right)\right]\\ L_1\left(s\right)=\left(K_{\mathrm{p}1}{K}_{\mathrm{dc}\_\max }{\mathrm{\omega }}_{\mathrm{p}}\right)/s\approx 357.0/s\end{array}$$

For L₂(s): By reasonably designing the parameters of controller G_c2(s), the system can achieve the specified phase margin. The complete open-loop transfer function is:

$$\begin{array}{ll}{L}_2\left(s\right)& =G_{\mathrm{c}2}\left(s\right)G\left(s\right)=\left[K_{\mathrm{p}2}\left(s+{\mathrm{\omega }}_{\mathrm{z}2}\right)/s\right]\left[K_{\mathrm{dc}\_\max } \left(1+s/{\mathrm{\omega }}_{\mathrm{p}}\right)\right]\\ L_2(s)& =[(191.58s+6981062)/s][2.9135/(1+s/122.51)]\\ & =(557.9s+20340000)/(0.00816s^2+s)\end{array}$$

For L₃(s): The controller, G_c3(s), uses the pole placement method for its zero location. The complete open-loop transfer function is:

$$\begin{array}{ll}{L}_3\left(s\right)& =G_{\mathrm{c}3}\left(s\right)G\left(s\right)=\left[K_{\mathrm{p}3}\left(s+{\mathrm{\omega }}_{\mathrm{z}3}\right)/s\right]\left[K_{\mathrm{dc}\_\max }/\left(1+s/{\mathrm{\omega }}_{\mathrm{p}}\right)\right]\\ L_3(s)& =[(221.47s+6783)/s][2.9135/(1+s/122.51)]\\ & =(645.2s+19760)/(0.00816s^2+s)\end{array}$$

The transfer functions of L₁(s), L₂(s), and L₃(s) are obtained through the above theoretical calculations. Based on their transfer functions, the corresponding Bode plots can be drawn.

By analyzing the performance metrics of each curve in Table 1 and the frequency response characteristics shown in Figure 8, the zero-pole cancellation method (Method 1) is the most suitable compensation strategy for this application. Its principle lies in aligning the controller’s zero with the main pole of the controlled object, achieving precise cancellation functionally, thereby transforming the open-loop transfer function into an approximate ideal integrator. This method exhibits excellent robustness, characterized by a 90-degree phase margin and zero overshoot characteristics, which protect the LED load from overcurrent hazards. Given the significant advantages of the zero-pole cancellation method, this method is also adopted in the subsequent experimental verification to design the PI controller.

4. Experimental Verification and Analysis

The preceding sections explain the operating principle of the converter, analyze and derive the mathematical model and small-signal model of the system, and design the most suitable PI controller for this paper based on theoretical analysis.

Based on the above system analysis and controller design, this section constructs a complete closed-loop control system, as shown in Figure 9. In order to verify the validity of the aforementioned analysis and parameter design, a five-channel experimental prototype with a rated power of 200 W was constructed, and its detailed specifications are the same as those listed in

Table 2. Experimental parameters of the prototype.

Symbol	Value
Kp	221
Ki	27,130
fS	100 kHz
N	2
m	5
L1	350 μH
La1	175 μH
C1	7 nF
Cb	1 uF
S1–S4	IPP60R099C7
Control board	TMS320F28335

. The corresponding circuit components are also listed in the same table. The control strategy comprises the following: firstly, the current of a single output channel is sampled; secondly, this is compared with a preset reference signal to generate an error signal; thirdly, the error signal is processed by a PI compensator to output a modulating signal; and finally, the modulating signal is compared with a triangular carrier to generate PWM signals to drive the four power switches. The series connection of the output channels via rectifier circuits enables the system to achieve effective closed-loop control of all output currents. As illustrated in Figure 9, the block diagram depicts the closed-loop control system, with its core control unit implemented using a TMS320F28335 digital signal processor. Figure 10 is a photograph of the experimental prototype.

In the control circuitry of the experimental prototype, the isolated gate driver is a critical component. The isolated driver circuit employed in this study is depicted in Figure 11, wherein pwm3 is the PWM input signal. The gate driver IC, IC1 (NSi6602B-DSWR), converts the logic-level pulse (PWM3) from the controller into a high-frequency square-wave drive signal. This conversion is achieved by its internal push–pull output stage, which alternately applies high and low levels across the PWMC and GNDC output terminals, connected respectively to the gate and source of the power MOSFET. The switching frequency of the MOSFET is set to 100 kHz.

4.1. Experimental Waveform Analysis

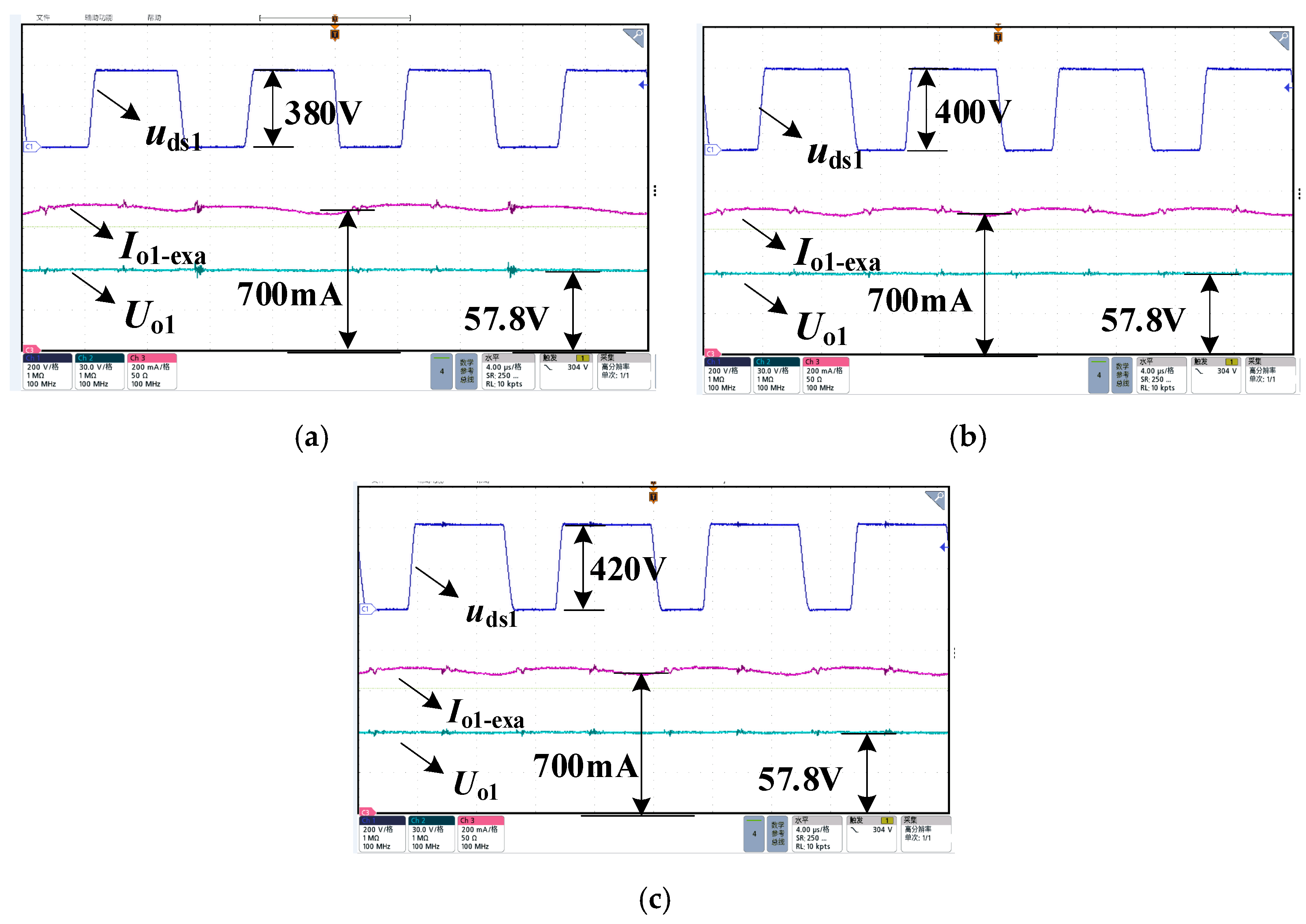
This section presents the performance verification results of the experimental prototype. As shown in Figure 12a–c, the waveform diagrams illustrate the steady-state output waveforms under rated power and different input voltage conditions. The figure shows the experimental waveforms under operating conditions with input voltages, U_dc, of 380 V, 400 V, and 420 V. In each subfigure, the waveforms from top to bottom are the drain–source voltage of switch S₁ (u_ds1), the channel output current (I_o1-exa), and the final output voltage (U_o1). The experimental data indicate that the output current, Io1-exa, remains at a constant level of 700 mA within the input voltage range of 380 V to 420 V. This experimental result validates the effectiveness of the closed-loop control strategy and meets the system design specifications for high-precision output current requirements.

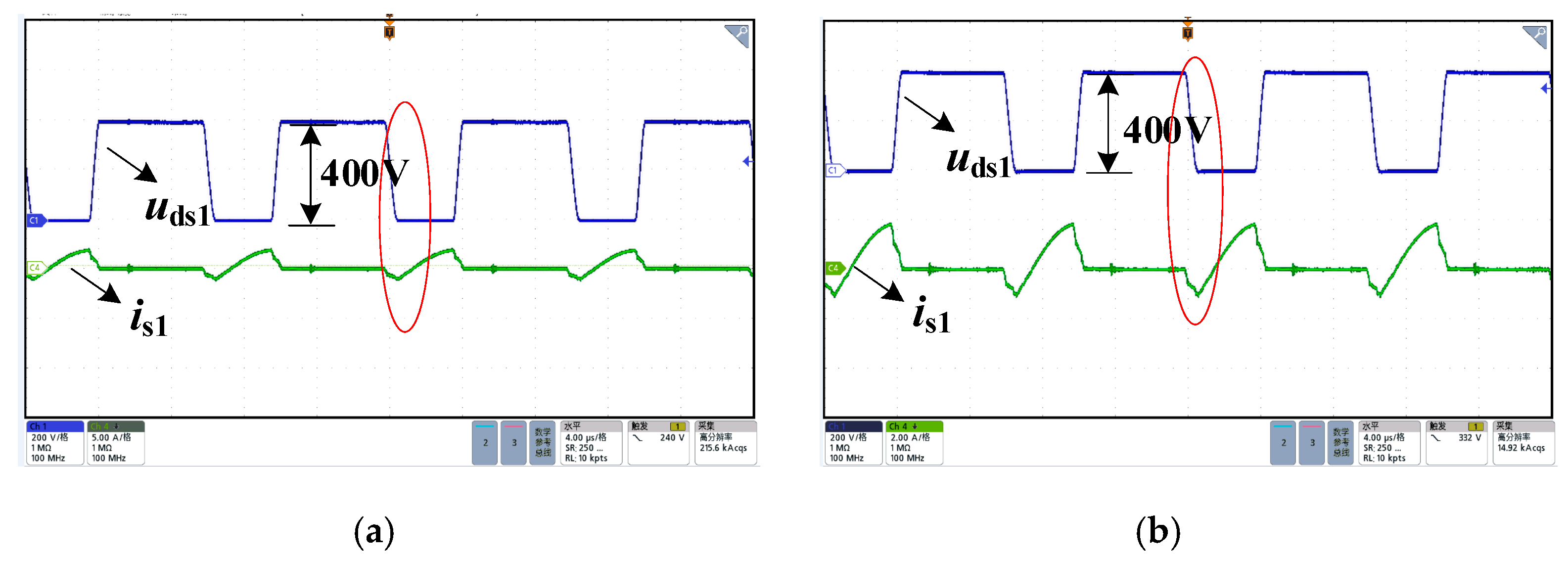
The objective of this study is to verify the zero-voltage switching (ZVS) conditions described in the theoretical analysis of the first part by employing switch transistors S₁ and S₃ as research objects and utilizing experimental characteristic analysis methods. As demonstrated in Figure 13a, under operating conditions of input voltage U_dc = 400 V and output power P = 200 W, the drain–source voltage (u_ds1) and channel current (i_s1) waveforms of switch transistor S₁ were measured. As illustrated in Figure 13b, the measured values correspond to the drain–source voltage (u_ds3) and channel current (i_s3) of switch transistor S₃. The experimental data suggest that the currents, i_s1 and i_s3, are both negative prior to each transistor switching operation. This negative state has been proven to cause the anti-parallel diodes to enter a forced conduction state. This finding confirms that the switching transistors, S₁ and S₃, have successfully achieved zero-voltage switching (ZVS) operation.

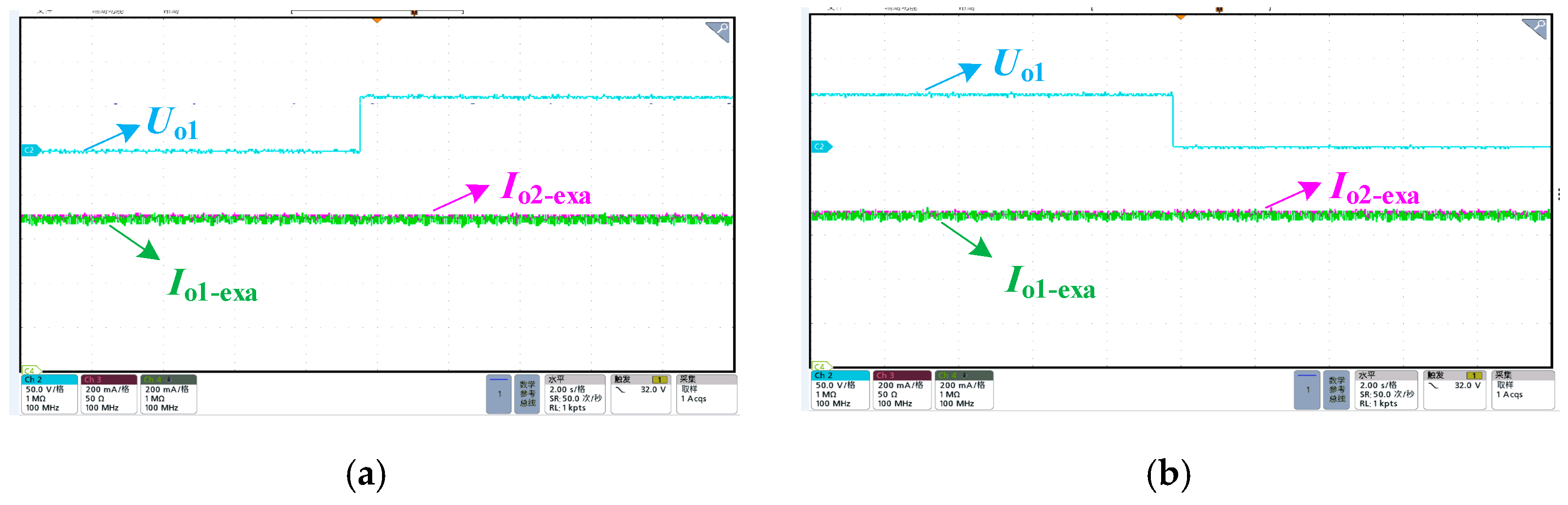
Figure 14 shows transient waveforms when the input voltage, U_dc, changes at rated power 200 W. Figure 15 shows transient waveforms when the output voltage, U_o1, changes. Taking the first and second output channels as an example, the waveforms in Figure 14 are the input voltage, U_dc, and the output currents, I_o1-exa and I_o2-exa. As illustrated in Figure 15, the dynamic waveforms of the output voltage, U_o1, and the output currents, I_o1-exa and I_o2-exa, are also shown. The experiment demonstrates that, in conditions of load disturbance, the output current can rapidly revert to the set value within a brief timeframe. This outcome validates the efficacy of closed-loop control for all output channels and substantiates the accuracy of the output current, which aligns with the design specifications across the entire operational range.

4.2. Loss Analysis and Theoretical Efficiency Estimation

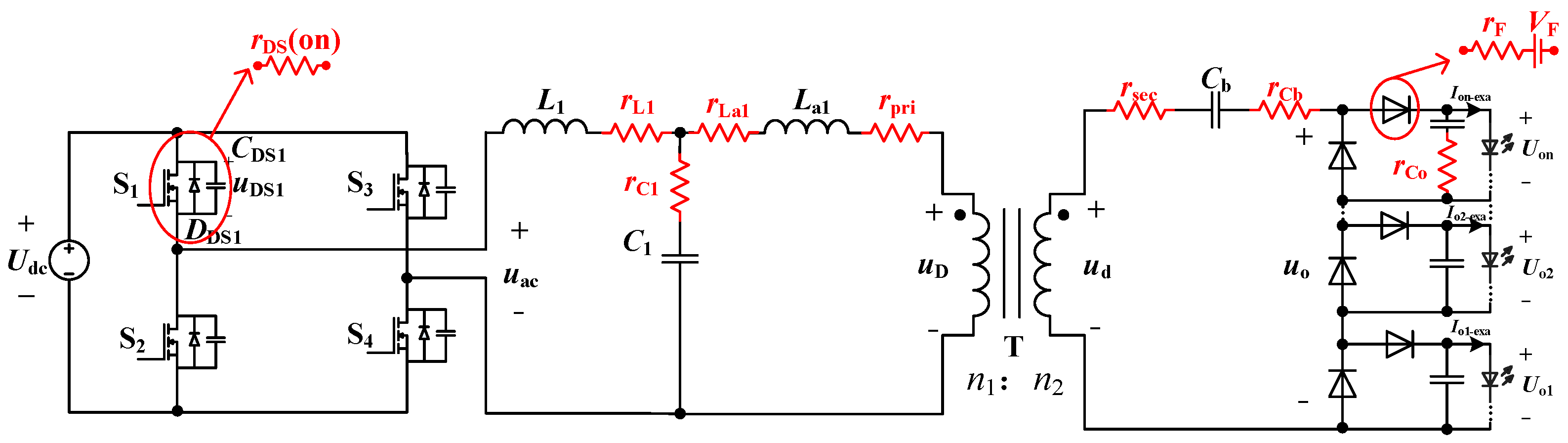
By thoroughly analyzing the wear and tear on each component, we have provided a theoretical basis for proving the high efficiency of the system. Figure 16 illustrates the loss model of the converter, which incorporates the primary parasitic components inherent in the circuit elements. These components include the on-resistance (r_DS(on)) of the MOSFET, the forward voltage drop (V_F) and on-resistance (r_F) of the diode, the parasitic resistance (r_L1 and r_La1) of inductors L₁ and L_a1, the parasitic resistance of capacitors C₁ and C_b (r_C1 and r_Cb), and the primary and secondary winding resistances of the transformer (r_pri and r_sec), which are the fundamental sources of power loss. Based on this model, the power loss calculations for each component are as follows.

The total conduction loss of the four switches can be calculated based on the effective value, I_L1,rms, of the current, i_L1, flowing through the AC side of the inverter:

$$P_{\mathrm{rDS}\_\mathrm{total}}=2\times I_{\mathrm{L}1,\mathrm{rms}}^2\times r_{\mathrm{DS}}(\mathrm{on})$$

(16)

This topology achieves zero-voltage switching (ZVS) through phase shift control, so switching losses can be ignored. Losses mainly originate from the switching process, and the switching loss of a single switch can be expressed as:

$$P_{\mathrm{sw}}=f_{\mathrm{S}}\cdot C_{\mathrm{DS}1}\cdot U_{\mathrm{dc}}^2$$

(17)

where f_S is the switching frequency, and C_DS1 is the output capacitance of the MOSFET.

Therefore, the total MOSFET loss is:

$$P_{\mathrm{Switch}}=P_{\mathrm{rDS}\_\mathrm{total}}+4P_{\mathrm{sw}}$$

(18)

Diode conduction losses are caused by both the forward voltage drop, V_F, and the equivalent dynamic resistance, r_F. The diode loss for a single channel is:

$$P_{{\mathrm{diode},\mathrm{ch}}_{\mathrm{n}}}=V_{\mathrm{F}}{I}_{\mathrm{on}-\mathrm{exa}}+I_{\mathrm{diode},\mathrm{rms}}^2{r}_{\mathrm{F}}$$

(19)

where I_diode,rms is the effective value of the current flowing through a single rectifier diode.

$$P_{\mathrm{Diode}\_\mathrm{total}}={{\displaystyle \sum }}_{n=1}^m{P}_{{\mathrm{diode},\mathrm{ch}}_{\mathrm{n}}}$$

(20)

The loss of inductance is mainly caused by copper loss generated by parasitic resistance, r_L. For inductances L₁ and L_a1 in this circuit, the total loss is:

$$P_{\mathrm{rL}\_\mathrm{total}}=r_{\mathrm{L}1}\cdot I_{\mathrm{L}1,\mathrm{rms}}^2+r_{\mathrm{La}1}\cdot I_{\mathrm{La}1,\mathrm{rms}}^2$$

(21)

where I_L1,rms and I_La1,rms are the effective values of the alternating current flowing through the corresponding inductors.

Capacitor loss is caused by its parasitic resistance, r_C. The total capacitor loss is:

$$P_{\mathrm{RC}\_\mathrm{total}}=r_{\mathrm{C}1}\cdot I_{\mathrm{C}1,\mathrm{rms}}^2+r_{\mathrm{Cb}}\cdot I_{\mathrm{Cb},\mathrm{rms}}^2+{{\displaystyle \sum }}_{n=1}^m(r_{\mathrm{Co}}\cdot I_{\mathrm{Co},\mathrm{n},\mathrm{rms}}^2)$$

(22)

where I_C1,rms, I_Cb,rms, and I_Co,n,rms are the effective values of the alternating current flowing through the corresponding capacitors.

Transformer losses include copper losses and iron losses:

$$P_{\mathrm{T}\_\mathrm{total}}=(r_{\mathrm{pri}}{I}_{\mathrm{pri},\mathrm{rms}}^2+r_{\sec }{I}_{\sec ,\mathrm{rms}}^2)+P_{\mathrm{core},\mathrm{T}}$$

(23)

where I_pri,rms and I_sec,rms are the effective values of the primary and secondary currents, respectively, and P_core,T is the magnetic loss.

Adding up all of the above loss components to obtain the total theoretical loss of the converter results in:

$$P_{\mathrm{loss}}=P_{\mathrm{SW}\_\mathrm{total}}+P_{\mathrm{Diode}\_\mathrm{total}}+P_{\mathrm{L}\_\mathrm{total}}+P_{\mathrm{C}\_\mathrm{total}}+P_{\mathrm{T}\_\mathrm{total}}$$

(24)

To theoretically assess the efficiency of the proposed converter, the theoretical efficiency of the system can be estimated by the following equation:

$${\eta }_{\mathrm{theory}}={\displaystyle \frac{P_{\mathrm{out}}}{P_{\mathrm{in}}}}={\displaystyle \frac{P_{\mathrm{out}}}{P_{\mathrm{out}}+P_{\mathrm{loss}}}}$$

(25)

This section provides a quantitative analysis of the primary power loss sources in the system, based on device datasheets, circuit simulations, and standard engineering estimation methods. Under rated operating conditions, the calculated theoretical total loss is approximately 9.45 W, corresponding to an efficiency of 95.5%. Among these losses, the rectifier diodes account for the largest portion, exceeding 58%, followed by the core loss of the magnetic components (approx. 21%) and the conduction loss of the MOSFETs (approx. 10%).

4.3. Experimental Efficiency Analysis

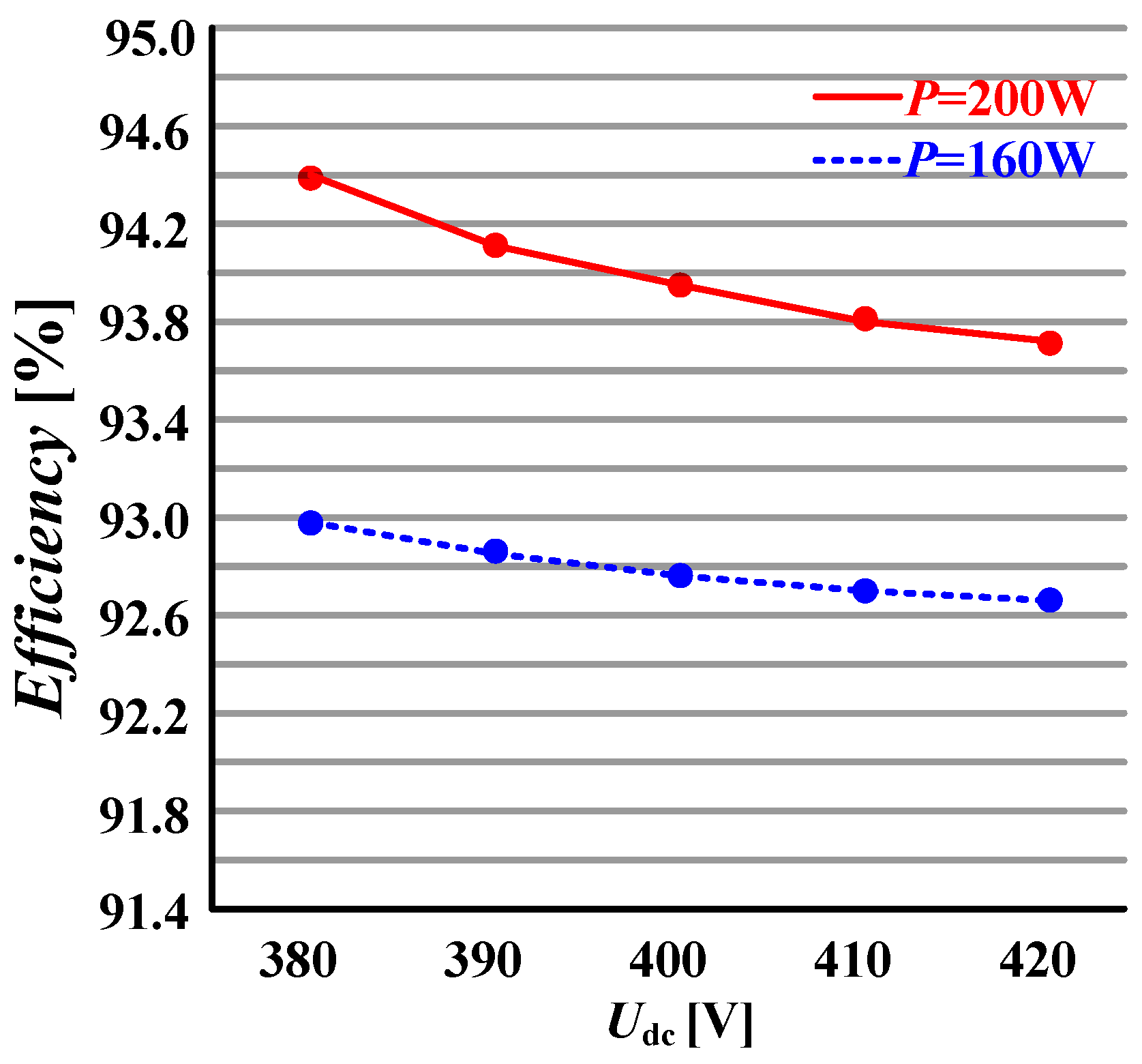
To validate the accuracy of the theoretical analysis, efficiency tests were conducted on the prototype. Figure 17 presents the measured efficiency curves under various input/output conditions. The experimental results indicate that the efficiency of the topology improves significantly as the output load increases, with a measured peak efficiency of 94.4% being achieved under rated operating conditions.

In summary, the experimental tests confirm the precise control capability of the apparatus over the output voltage and current. This measured value is in close agreement with the theoretical peak efficiency of 95.5%, with the minor discrepancy being primarily attributed to unmodeled parasitic parameters and measurement errors. This result further validates the correctness of the design methodology and its practical engineering value.

5. Conclusions

In this paper, the proposed solution is an LED driver with a multi-output configuration that operates on a high-frequency AC bus. Closed-loop regulation of all the series circuits can be achieved by sampling and controlling a single output series circuit. A theoretical analysis of the impact of higher-order harmonics on the constant-current output was conducted, and an exact solution for the output current was derived. After verifying the validity of the topological theory, various PI controller design methods were compared and analyzed, with the zero-pole elimination method ultimately selected. Finally, a five-channel 200 W experimental prototype was constructed, and the effectiveness of the theoretical analysis was validated through test results. The tests demonstrated that all the series circuits meet the high current accuracy requirements.