Abstract
The LLC resonant converter, as an isolated DC-DC conversion topology, has been widely adopted in industrial applications. However, when operating under wide input/output voltage ranges, a broad switching frequency range is required to achieve the desired voltage gain. This wide frequency variation complicates the design of magnetic components, causes loss of soft-switching characteristics, and deteriorates electromagnetic interference (EMI) performance. To address these challenges, this paper presents a detailed analysis of the L-LCLC resonant converter. By controlling the connection/disconnection of additional inductors and capacitors through switching devices, the topology achieves structural reconfiguration to enhance the voltage gain range. Optimal mode transition points are selected to ensure stable operation during mode transitions, thereby reducing design complexity, minimizing transition losses, and suppressing voltage/current stress. The parameter design methodology for the additional reactive components is systematically developed. The converter’s performance is validated with Simulink, and the experimental prototype is established with 100 W. Both simulation and experimental results confirm that the L-LCLC resonant converter achieves a wide voltage gain range within a narrow frequency band while maintaining stable mode transitions.
1. Introduction
The LLC resonant converter has gained widespread adoption as one of the most prevalent isolated DC-DC converter topologies, owing to its high efficiency, high power density, and excellent soft-switching characteristics [,,,]. This topology finds extensive applications in critical domains, including on-board battery chargers (OBCs), server and telecommunication power supplies, industrial automation equipment, medical power supplies, LED lighting drivers, and renewable energy systems [,,]. Figure 1 illustrates the circuit configuration of a conventional full-bridge LLC resonant converter incorporating a full-bridge rectifier stage. In LLC resonant converters, the power transfer mechanism is inherently facilitated through the resonant circuit (comprising inductor Lr and capacitor Cr) and the isolation transformer. As schematically depicted in Figure 1, the application of a square-wave voltage waveform at the VAB node establishes a sinusoidal current profile within the resonant Lr–Cr network. This alternating current is subsequently propagated to the secondary side through magnetic coupling in the transformer, enabling energy delivery to the load [,,]. The voltage regulation mechanism in an LLC resonant converter is realized by modulating the switching frequency of switches Q1–Q4. This modulation dynamically alters the impedance division ratio within the resonant tank, thereby controlling the output voltage []. This operational principle enables precise control of the voltage conversion gain, thereby maintaining a stabilized output voltage Uo under varying load conditions.
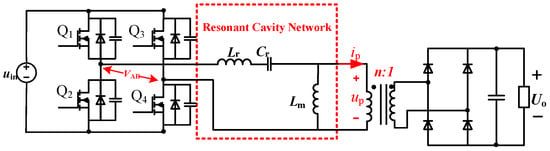
Figure 1.
Full-bridge LLC resonant converter circuit configuration.
Pulse frequency modulation (PFM) is widely used in LLC resonant converters, adjusting the switching frequency to modulate resonant tank impedance []. However, above resonance, PFM-controlled LLC converters exhibit reduced voltage gain sensitivity at higher frequencies, complicating wide voltage-range applications (e.g., on-board chargers and solar systems) [,]. These scenarios require excessively broad frequency ranges to meet strict gain specifications, increasing magnetics complexity, compromising zero-voltage switching, and degrading EMI performance [,,,]. To address these limitations while achieving extended voltage gain within narrow frequency bands, numerous research approaches have been proposed from different technical perspectives.
Based on the modification locations, LLC resonant converters can be categorized into three distinct subcategories: primary-side inverters, resonant tanks, and secondary-side rectifiers. In [], a novel topology was introduced featuring an additional switch integrated into the primary full-bridge inverter, dual independent resonant tanks (Lr/Cr), transformers, and full-wave rectifiers. This configuration enables multi-mode operation through primary switch state regulation, significantly expanding the achievable voltage gain range. However, the incorporation of redundant components, particularly magnetic elements, substantially increases circuit complexity and manufacturing costs while compromising power density. In [,], different basic topologies, such as Buck–Boost and Buck, are cascaded with an LLC resonant converter to achieve extremely high voltage conversion ratios. However, this approach suffers from significant drawbacks, including highly complex system control and potentially slow dynamic response.
A fractional magnetizing inductance with a parallel-connected auxiliary switch was presented in []. By actuating the auxiliary switch, the resonant tank configuration can be dynamically reconfigured to operate in different states. Various secondary-side rectification schemes have been proposed in [,,,,]. Notably, ref. [] replaced the conventional full-wave rectifier with a reconfigurable voltage-doubler rectifier capable of operating in Type-4, Type-5, and Type-6 configurations. Nevertheless, the achievable gain ranges of existing rectification topologies remain constrained, which inevitably expands the required frequency variation range and consequently limits potential application scenarios.
To enable the proposed converter to achieve a wide voltage gain range within a narrow frequency band, this paper introduces a multi-element resonant converter methodology by incorporating one or two additional inductors/capacitors into the conventional LLC resonant tank structure. This approach generates multiple resonant frequencies in the system transfer function, thereby enhancing the gain characteristics. Through comparative analysis of the gain profiles across these derived LLC resonant converter topologies, the configuration with optimal gain performance is selected for detailed investigation. The resonant tank configurations of the proposed LLC-derived topologies are illustrated in Figure 2.
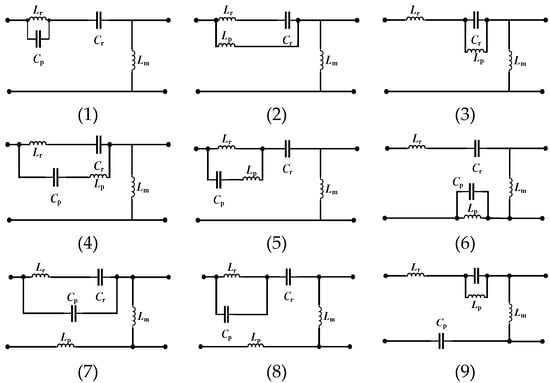
Figure 2.
Resonant tank structure of the derivative resonant converter.
Through systematic modeling and parametric analysis of the voltage gain characteristics for LLC derivative topologies 1 through 9, the gain expression for each topology is established based on the Fundamental Harmonic Approximation (FHA) method. Subsequently, their dynamic voltage gain curves as a function of normalized frequency are plotted using a consistent set of parameters. Building upon this, a comparative analysis is conducted by plotting the gain curves of the derivative topologies alongside those of the conventional LLC resonant converter on the same set of axes. The results are illustrated in Figure 3, where the red curves represent the gain of the derivative topologies and the blue curve corresponds to that of the conventional LLC converter.
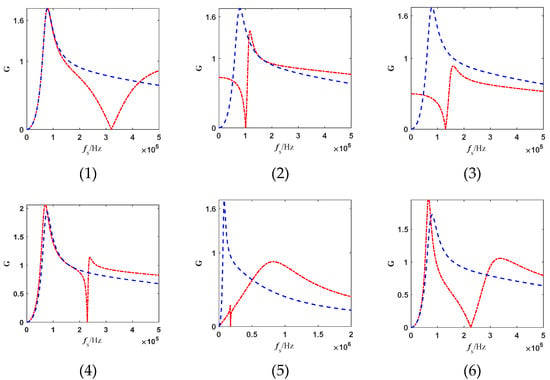
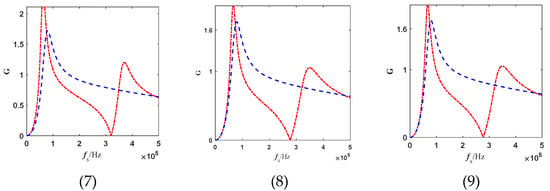
Figure 3.
Voltage gain curves of the derivative resonant converters.
Image analysis reveals that Topology 4 demonstrates significantly superior gain range compared to other configurations. This ultra-steep gain characteristic enables stable high-frequency output under wide input voltage scenarios while allowing substantial voltage regulation through minimal frequency adjustments. Such performance effectively reduces switching device stress, making it particularly suitable for high-dynamic applications. Consequently, Topology 4 is selected as the primary research subject and designated as the L-LCLC resonant converter in this study.
By controlling the connection/disconnection of additional inductors and capacitors through switching devices, the L-LCLC resonant converter achieves structural reconfiguration to enhance the voltage gain range. Compared to the LLC topology, the L-LCLC configuration requires additional reactive components but achieves superior gain characteristics. To optimize overall system efficiency, a hybrid control strategy is implemented: the converter operates in L-LCLC mode when the switching frequency exceeds the resonant frequency, and transitions to LLC mode under sub-resonant conditions. The mode transition occurs precisely at unity voltage gain, where both topologies share identical operating frequencies and gain values. This design methodology effectively minimizes voltage/current stress during mode transitions while maintaining high efficiency across the entire operational range.
The contributions of this study are summarized as follows: (1) This paper presents a detailed analysis of the voltage gain characteristics for the L-LCLC resonant converter, accompanied by a complete derivation of the governing mathematical equations. Furthermore, the soft-switching operational regions of the converter are systematically delineated through a thorough steady-state analysis. Based on these findings, a systematic parameter design methodology is also proposed. (2) A hybrid mode transition strategy is implemented to improve overall system efficiency. The converter seamlessly switches between LLC and L-LCLC modes at the unity gain point, where both topologies share identical operating frequencies and gain characteristics. This design effectively mitigates transient voltage and current surges during mode transitions while maintaining high efficiency across the entire operational range.
The organization of this paper is structured as follows: Section 1 reviews key challenges in LLC resonant converters and explains the motivation for the L-LCLC topology. Section 2 provides a detailed analysis of the L-LCLC converter’s operational principles, covering gain characteristics, soft-switching properties, and hybrid mode transitions. Section 3 proposes a design methodology for critical components, highlighting optimization of the parallel inductor Lp and capacitor Cp. Section 4 validates theoretical analysis via simulations, while Section 5 confirms performance through experimental testing on a 100 W prototype. Section 6 summarizes contributions and practical implications.
2. Principal Analysis of Converter
2.1. The Equivalent Model of the Circuit and the Gain
Figure 4 illustrates the circuit configuration of the L-LCLC resonant converter. Compared to the conventional LLC topology, this configuration incorporates an additional inductor Lp and capacitor Cp within the resonant cavity network.
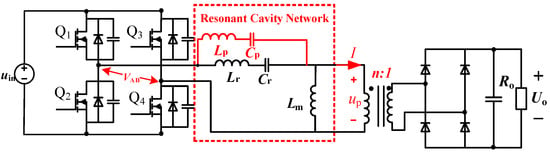
Figure 4.
L-LCLC resonant converter circuit configuration.
The L-LCLC resonant converter is modeled using the fundamental harmonic approximation method. By linearizing the operational characteristics of the high-frequency transformer and composite resonant tank network at the fundamental frequency, an AC equivalent circuit model incorporating core resonant components is established. The simplified equivalent circuit diagram of the L-LCLC resonant converter is illustrated in Figure 5. In Figure 5, Ei represents the input voltage to the resonant tank, while Ip, Ir, and Im are the currents flowing through capacitor Cp, capacitor Cr, and inductor Lm, respectively. Eo denotes the overall output voltage of the resonant converter.
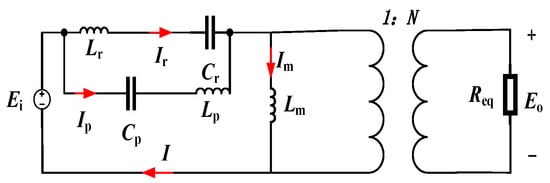
Figure 5.
L-LCLC resonant converter equivalent circuit.
Based on the fundamental harmonic analysis method, the secondary-side equivalent resistance Req of the transformer can be derived as
By formulating the KVL/KCL, the system characteristics can be derived as
By solving the aforementioned system of equations, the following expressions can be derived as
The reciprocal of the L-LCLC resonant converter’s voltage gain in the frequency domain can be formulated as
The L-LCLC resonant converter exhibits three distinct resonant frequencies f1 = 1/2π, f2 = 1/2π, f3 = /2π. The converter’s gain profile is defined by three critical resonant frequencies. At switching frequencies f1 and f2, the converter achieves a unity voltage gain. This occurs because series resonance—between Lr and Cr at f1, and between Lp and Cp at f2—causes the equivalent impedance of the resonant branch to approach zero, allowing the output voltage to approximate the input voltage. When operating at f3, the entire Lr-Cr-Lp-Cp network transitions into parallel resonance, creating an infinite equivalent impedance across the resonant branch. This state effectively blocks energy transfer to the output, and the converter gain is approximately zero.
2.2. Soft-Switching Characteristics Analysis
As derived from Figure 5, the input impedance Zin of the L-LCLC resonant network can be expressed as
The normalized frequencies are defined as fn1, fn2, and fn3, where Rac = Reqn2, fn1 = fs/f1, fn2 = fs/f2, fn3 = fs/f3, and where fs denotes the switching frequency. The structural voltage gain G can be expressed as
where T = /Rac, P1 = (λ1λ3 + λ1λ3)/(λ2 + λ2λ3)fn12 − 1, P2 = 1 − λ1λ3fn12/λ2, P3 = (1 − fn12)/fn1(1 + λ3), λ1 = Lm/Lr, λ2 = Lm/Lp, λ3 = Cp/Cr.
When the input impedance Zin exhibits purely resistive characteristics, the voltage gain becomes inherently resistive and can be derived as
Based on Equations (6) and (7), the inherently resistive voltage gain curves and parametric gain curves for varying T values can be plotted, as illustrated in Figure 6. In the Figure 6, the number 1 represents the blue area, number 2 represents the yellow area, and number 3 represents the pink area.
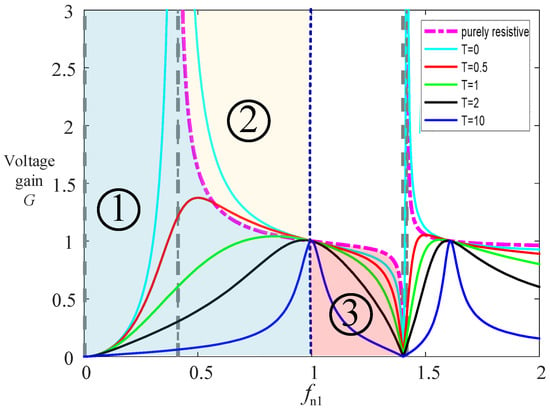
Figure 6.
The voltage gain curve of the L-LCLC resonant converter.
The operational zones of the L-LCLC resonant converter are categorized into three distinct regions, defined by the purely resistive characteristic curve and the boundary line fn1 = 1:
Region 1: Located to the left of both the boundary line fn1 = 1 and the purely resistive characteristic curve, the converter exhibits capacitive behavior and operates in the ZCS mode.
Region 2: Positioned to the left of the boundary line fn1 = 1 and to the right of the purely resistive characteristic curve, the converter exhibits inductive behavior. Here, the voltage gain G > 1, indicating a step-up operation mode, with the system functioning in the ZVS regime.
Region 3: Positioned to the right of the boundary line fn1 = 1 and to the left of the purely resistive characteristic curve, where the voltage gain G < 1 indicates a step-down operation mode, with the system operating in the ZVS regime.
The operational analysis of the L-LCLC resonant converter focuses on switching frequencies below f3, as frequencies exceeding f3 are excluded from practical design considerations. To prioritize ZVS operation, the converter should be designed to operate in Region 3, as established in the preceding analysis.
2.3. Mode Transition Strategy
As illustrated in Figure 7, the voltage gain curves of the two resonant converters reveal distinct operational characteristics. Under the LLC frequency-modulation (FM) mode, the converter operates in a step-up configuration, whereas the L-LCLC structure-variable frequency modulation mode enables step-down operation. Since a mode switch is required, we should select an appropriate switching point.
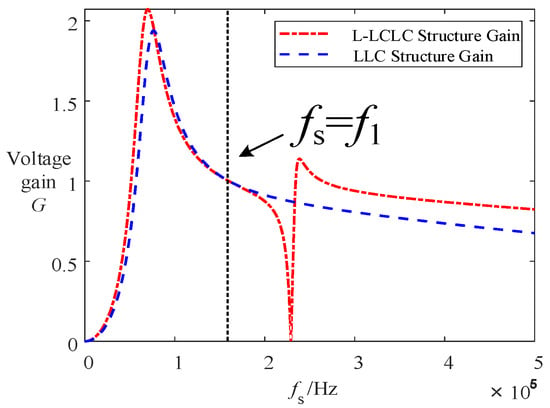
Figure 7.
Composite gain curve graph.
Two conventional methods exist for determining mode transition points. The first is based on equal efficiency between operational modes, requiring loss calculations (conduction/switching) in both modes, but faces computational complexity and numerical instability. The second prioritizes resonant frequency proximity, balancing voltage gain stability and efficiency sensitivity to frequency deviations. In this study, both converter modes operate under frequency modulation control and share a common resonant frequency point. At this specific switching frequency, both modes achieve unity voltage gain with zero frequency deviation, significantly mitigating voltage/current stress during mode transitions. Therefore, this resonant frequency point is selected as the optimal mode transition point.
3. Parameter Design
Extensive research has been conducted by scholars on the circuit parameter design of LLC resonant converters [,,,,]. Building upon these foundations, this paper presents a systematic parameter design methodology for the additional parallel-connected inductor and capacitor introduced in the L-LCLC resonant converter topology.
Based on the hybrid control strategy definition, the LLC FM mode operates under minimum input voltage conditions, achieving the maximum voltage gain Gmax. Conversely, the L-LCLC FM mode functions at maximum input voltage, yielding the minimum voltage gain Gmin. With constant output voltage maintained, the following relationships hold:
As established in the operational characteristics, the LLC frequency modulation mode operates in the step-up region (G > 1), whereas the L-LCLC structure-variable FM mode functions in the step-down region (G < 1). Under these conditions, the voltage gain relationship can be derived as
The peak gain, denoted as Gpeak, is fully utilized by setting Gpeak0 = Gmax. To ensure design robustness, a 20% safety margin is incorporated. The available peak gain Gpeak0 can thus be calculated as
To ensure the converter operates in the LLC FM mode when the switching frequency is below fn1, and achieves steeper voltage gain curves beyond the mode transition point compared to the LLC FM mode, the composite parallel resonant frequency of the Lr-Cr-Lp-Cp network must exceed the series resonant frequency of the Lr-Cr branch. This condition guarantees optimal performance across both operational modes.
To prevent the voltage gain from collapsing to zero, the composite parallel resonant frequency of the Lr-Cr-Lp-Cp network should be designed to exceed the converter’s maximum switching frequency fsmax. This condition ensures operational stability across the entire frequency modulation range while maintaining inherent voltage regulation capability.
The parametric design methodology initiates with selecting an appropriate λ3 value within the typical operational range of 0.1–0.5 for the L-LCLC resonant converter operating in regulated output mode. Based on Equation (6), different λ2 values are sequentially evaluated to satisfy the predefined gain constraints, thereby establishing the feasible λ2 range. Within this range, the optimal λ2 parameter is determined according to specific gain sensitivity requirements. Following λ2 selection, an inverse iterative process is implemented: maintaining the chosen λ2 while re-evaluating λ3 variations under identical gain constraints to determine its optimized range. The final λ2/λ3 parameters are then consolidated through this bidirectional optimization process. Substituting these optimized values into Equations (14) and (15) subsequently yields the concrete specifications for Lₚ and Cₚ components. The systematic parameter selection flowchart is illustrated in Figure 8.
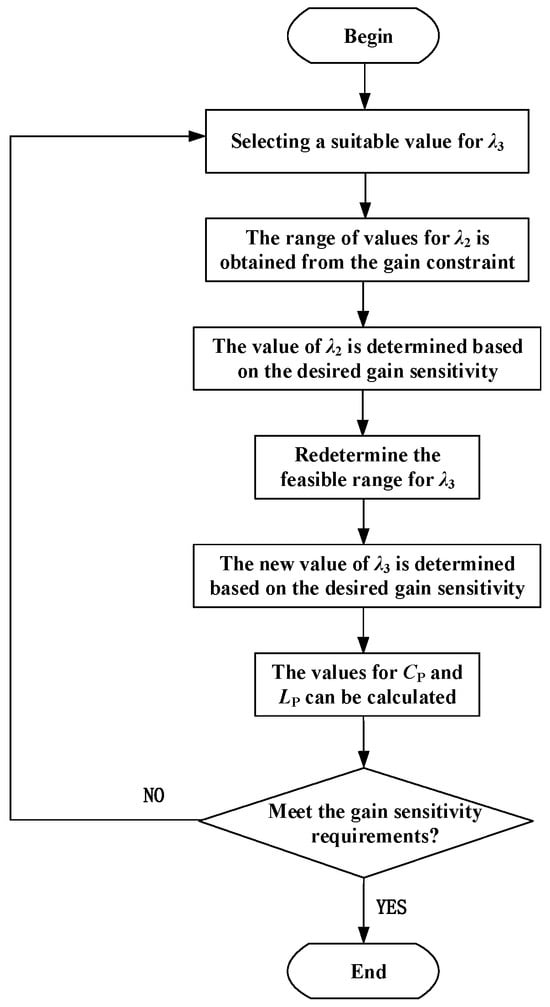
Figure 8.
Parameter design flowchart.
Taking the design process presented in this paper as an example, the design procedure is initiated by setting λ3 = 0.2, followed by evaluating multiple λ2 values to generate the gain profiles illustrated in Figure 9a. The optimal λ2 value of 2.6 is determined based on the specified gain sensitivity requirements. Subsequently, an iterative refinement process adjusts λ3 variations while maintaining the selected λ2, producing the gain characteristics shown in Figure 9b. Through comparative analysis of these gain profiles, λ3 is finalized at 0.25, considering both sensitivity optimization and operational margin. The inductance Lₚ and capacitance Cₚ parameters are then calculated by substituting the optimized λ2/λ3 set into Equations (14) and (15). The final design parameters of the converter, including the optimized Lₚ and Cₚ values, are systematically summarized in Table 1.
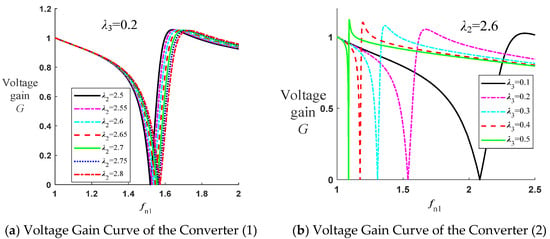
Figure 9.
Voltage gain curves of the L-LCLC resonant converter with parametric variations in λ2 and λ3.

Table 1.
Prototype specifications.
4. Simulation Study
To validate the feasibility of the proposed methodology, a Simulink (MATLAB R2024a version)-based simulation study is first conducted. The simulation was performed using a discrete solver with a sample time of 5 ns. The parasitic capacitance of each primary-side switching device was set to 1.5 nF. The switching frequency is regulated by a Proportional–Integral (PI) controller to maintain a stable output voltage. Furthermore, the engagement of the Lp and Cp branches is dynamically controlled. This is achieved by continuously sampling the input and output voltages to calculate the real-time converter gain. Based on this gain, the branch is disconnected from the circuit when the gain is greater than one and reconnected when the gain is less than one. The key parameters of the converter, including component values and operational specifications, are presented in Table 1.
Figure 10a,b present the simulated waveforms of the capacitor Cr current Icr and output voltage illustrating two operational scenarios: Figure 10a input voltage Uin = 160 ± 20 V with regulated output voltage Uo = 200 V. From top to bottom, the waveforms represent input voltage, output voltage, and capacitor current. As shown in Figure 10b, when Uin decreases from 180 V to 140 V, the output voltage maintains stable regulation around 100 V. Similarly, when Uin increases from 210 V to 250 V, the output voltage remains tightly regulated at 100 V. This demonstrates excellent voltage regulation stability across wide input voltage variations, enabling the converter to adapt to applications requiring different voltage levels.
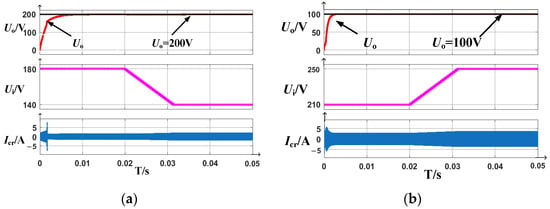
Figure 10.
Simulated waveforms of the capacitor Cr current Icr and output voltage. (a) Dynamic curve graph showing the reduction of input voltage from 180 V to 140 V; (b) Dynamic curve graph showing the increase in input voltage from 210 V to 250 V.
Figure 11a,b present the voltage, current, and power waveforms of primary-side switching devices, along with gate trigger voltage signals, at switching frequencies of 150 kHz and 220 kHz, respectively. As observed in both subfigures, during switch turn-on transitions, no overlap occurs between voltage and current waveforms, resulting in zero turn-on loss. This confirms the successful realization of ZVS, which aligns precisely with theoretical predictions.
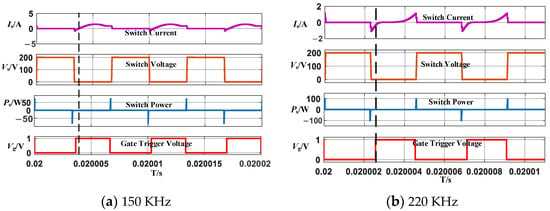
Figure 11.
Simulation curves of soft-switching characteristics for L-LCLC resonant converter.
5. Experimental Result
A 100 W experimental prototype is established to verify parameter design. The specifications of the experimental prototype are consistent with Table 1. Figure 12 shows the photograph of the experimental prototype.

Figure 12.
The prototype of the converter.
Figure 13 presents a comparative analysis of voltage gain characteristics between the LLC and L-LCLC resonant converter modes under a 200 V input voltage. Figure 13a,b illustrate the experimental waveforms of square-wave input voltage VAB and output voltage at a switching frequency of 160 kHz for LLC and L-LCLC modes, respectively. Figure 13c,d display corresponding results at 228 kHz. At 160 kHz, both modes exhibit output voltage fluctuations around 200 V. However, when operating at 228 kHz, the LLC mode produces an output voltage of approximately 130 V, while the L-LCLC mode achieves a significantly lower output voltage of 40 V. This demonstrates the L-LCLC configuration’s ability to extend the voltage gain range by over 300% compared to the conventional LLC topology, validating its superior performance in wide-gain applications.
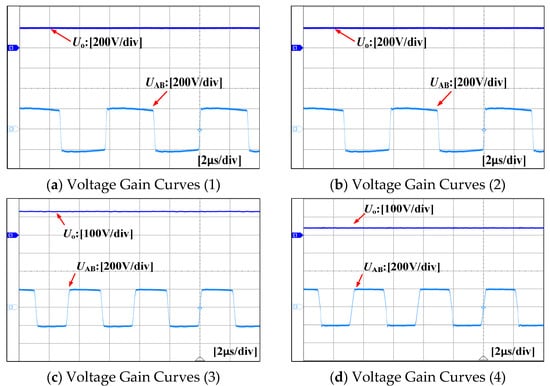
Figure 13.
Comparative voltage gain simulation results of the LLC and L-LCLC resonant converters.
Figure 14a,b illustrate the experimental waveforms of the current I and output voltage under an input voltage of 200 V and switching frequency of 160 kHz, corresponding to output powers of 100 W and 75 W, respectively. From top to bottom, the waveforms represent output voltage, current I, square-wave input voltage VAB, and gate-source voltage of the switches. As shown in the left figure, at full load (100 W), the output voltage remains stably regulated around 200 V. Similarly, the right figure demonstrates that even at reduced load (75 W), the output voltage maintains tight regulation at approximately 200 V. This confirms the converter’s robust voltage regulation capability across varying load conditions, enabling its application in scenarios with diverse power requirements.
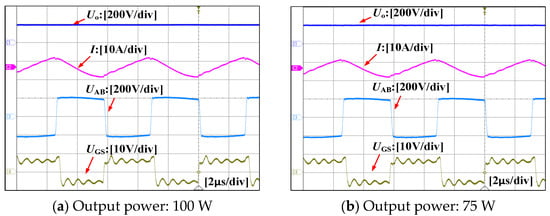
Figure 14.
Experimental Characteristics of L-LCLC Resonant Converter under Load Variations.
As shown in Figure 15, during the transition from LLC to L-LCLC mode, the output voltage remains stably regulated around 200 V, demonstrating excellent transient stability. This confirms the effectiveness of the hybrid control strategy in maintaining output regulation during structural reconfiguration.
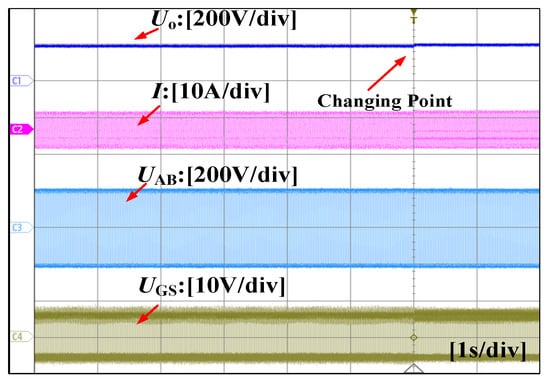
Figure 15.
Transition process from LLC mode to L-LCLC mode.
6. Conclusions
This paper presents a variable-structure LLC resonant converter where an auxiliary switching network enables dynamic configuration transition. By controlling the conduction state of additional switches, the converter operates in LLC FM mode when the voltage gain exceeds unity, and switches to L-LCLC structural-variable FM mode under sub-unity gain conditions. A systematic design methodology for the parallel-connected inductors and capacitors in the L-LCLC configuration is proposed. Simulation and experimental results demonstrate robust output voltage stability at 200 V under input voltage step changes (180 V → 140 V and 210 V → 250 V) and varying load conditions (100 W and 75 W). The L-LCLC topology achieves a wide voltage gain range from 1 to 0.2 within a narrow switching frequency band of 160–228 kHz, compared to the conventional LLC converter’s gain range of 0.65–1 under identical operational conditions. The converter has a wider input-voltage range with a narrow switching frequency range.
Author Contributions
Conceptualization, methodology, data curation, and writing, Q.H., S.T., D.R., C.T. and Q.Z.; analysis, software, and experiments, Q.H., S.T., Z.T. and K.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (52307219) and the Wuhan Science and Technology Bureau Project (2023020201020307).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Gupta, P.P.; Kumar, N.; Nangia, U. Design and Analysis of LLC Resonant Converter and CCCV Topology for Battery Charging. In Proceedings of the 2022 2nd Asian Conference on Innovation in Technology (ASIANCON), Ravet, India, 26–28 August 2022; pp. 1–5. [Google Scholar]
- Wang, Q.; Wang, W.; Shuai, Z.; Peng, Y. Condition Monitoring for Resonant Capacitors in LLC Resonant Converter. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 3545–3550. [Google Scholar]
- Wu, H.; Mu, T.; Gao, X.; Xing, Y. A secondary-side phase-shift controlled LLC resonant converter with reduced conduction loss at normal operation for hold-up time compensation application. IEEE Trans. Power Electron. 2015, 30, 5352–5357. [Google Scholar] [CrossRef]
- Sathya, K.; Guruswamy, K.P. Performance Analysis for LLC Resonant Converter in Electric Vehicle Applications. In Proceedings of the 2023 International Conference on Recent Trends in Electronics and Communication (ICRTEC), Mysore, India, 10–11 February 2023; pp. 1–6. [Google Scholar]
- Nabih, A.; Li, Q. Design of 98.8% Efficient 400-to-48-V LLC Converter with Optimized Matrix Transformer and Matrix Inductor. IEEE Trans. Power Electron. 2023, 38, 7207–7225. [Google Scholar] [CrossRef]
- Zhang, J.; Du, X.; Qian, C.; Du, R.; Hu, X.; Tai, H.-M. Thermal Management of IGBT Module in the Wind Power Converter Based on the ROI. IEEE Trans. Ind. Electron. 2022, 69, 8513–8523. [Google Scholar] [CrossRef]
- He, Y.; Jia, Y.; Gao, L.; Xue, W.; Yang, Y.; Gao, T. A Control Method for Current Sharing in Interleaved LLC Resonant Converter. In Proceedings of the 2024 IEEE 7th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 31 July–2 August 2024; pp. 641–645. [Google Scholar]
- Chen, Z.; Shi, W.; Wang, K. Research on New Wide-input LLC Resonant Converter. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 2145–2149. [Google Scholar]
- Wei, Y.; Luo, Q.; Chen, S.; Sun, P.; Altin, N. Comparison among different analysis methodologies for LLC resonant converter. IET Power Electron. 2019, 12, 2236–2244. [Google Scholar] [CrossRef]
- Vuchev, A.S.; Grigorova, T.G.; Vuchev, S.A. Theoretical Analysis of an LLC Resonant DC-DC Converter at Boost Mode. In Proceedings of the 2023 XXXII International Scientific Conference Electronics (ET), Sozopol, Bulgaria, 13–15 September 2023; pp. 1–4. [Google Scholar]
- Guan, Y.; Li, X.; Wang, W.; Li, B.; Yang, W.; Wang, Y.; Xu, D. A High-Performance 3:1 Conversion Ratio DC–DC Converter: Analysis Method and Modular Adoption. IEEE Trans. Power Electron. 2024, 39, 4412–4425. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Z.; Dou, S. A Novel Resonant DC-DC Converter with Wide Voltage Gain. In Proceedings of the 2023 China Automation Congress (CAC), Chongqing, China, 17–19 November 2023; pp. 1349–1353. [Google Scholar]
- Menke, M.F.; Avila, S.L. Multi-objective Genetic Algorithm Based Optimal Design Methodology for LLC Resonant Converter. In Proceedings of the 2022 14th Seminar on Power Electronics and Control (SEPOC), Santa Maria, Brazil, 12–15 November 2022; pp. 1–6. [Google Scholar]
- Yang, X.; Sha, D. Automatic Current Limit Strategy for LLC DC-DC Converter for Overload Operation. IEEE Trans. Power Electron. 2024, 39, 9917–9928. [Google Scholar] [CrossRef]
- Vuchev, A.; Grigorova, T.; Vuchev, S. Analysis of Continuous Current Mode of an LLC Resonant DC-DC Converter at ZVS. In Proceedings of the 2022 13th National Conference with International Participation (ELECTRONICA), Sofia, Bulgaria, 19–20 May 2022; pp. 1–4. [Google Scholar]
- Zhang, J.; Shen, H.; Sun, H.; Wang, Z. Review on the Thermal Models Applications in the Reliability of Power Semiconductor Device. IET Power Electron. 2025, 18, e70065. [Google Scholar] [CrossRef]
- Zhang, J.; Shen, H.; Du, X.; Chen, R. Condition Monitoring the Inhomogeneous Thermal Fatigue of Multichip IGBT Module Based on the Thermal Attenuation Coefficient. IEEE Trans. Power Electron. 2025, 40, 2114–2125. [Google Scholar] [CrossRef]
- Barbi, I. Analysis of Oscillation Between Transformer Leakage Inductance and Schottky Diode Capacitance in DC–DC Converters. IEEE Trans. Power Electron. 2024, 39, 9127–9131. [Google Scholar] [CrossRef]
- Li, C.; Zhou, M.; Wang, H. An H5-Bridge-Based Asymmetric LLC Resonant Converter with an Ultrawide Output Voltage Range. IEEE Trans. Ind. Electron. 2020, 67, 9503–9514. [Google Scholar] [CrossRef]
- Liu, Q.; Qian, Q.; Ren, B.; Xu, S.; Sun, W.; Yang, L. A Two-Stage Buck–Boost Integrated LLC Converter with Extended ZVS Range and Reduced Conduction Loss for High-Frequency and High-Efficiency Applications. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 727–743. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Zhao, J.; Zhang, P.; Loh, P.C. A Dynamic Control Method for Buck + LLC Cascaded Converter with a Wide Input Voltage Range. IEEE Trans. Power Electron. 2023, 38, 1522–1534. [Google Scholar] [CrossRef]
- Hu, H.; Fang, X.; Chen, F.; Shen, Z.J.; Batarseh, I. A Modified High-Efficiency LLC Converter with Two Transformers for Wide Input-Voltage Range Applications. IEEE Trans. Power Electron. 2013, 28, 1946–1960. [Google Scholar] [CrossRef]
- Wen, H.; Jiao, D.; Lai, J.-S.; Strydom, J.; Lu, B. A MHz LCLCL Resonant Converter Based Single-Stage Soft-Switching Isolated Inverter with Variable Frequency Modulation. IEEE Trans. Power Electron. 2022, 37, 10797–10807. [Google Scholar] [CrossRef]
- Alaql, F.; Alhatlani, A.; Batarseh, I. Multi-Mode Rectifier-Based LLC Resonant Converter for Wide Input Voltage Range Applications. In Proceedings of the 2021 IEEE Applied Power Electronics Conference and Exposition (APEC), Phoenix, AZ, USA, 14–17 June 2021; pp. 349–354. [Google Scholar]
- Shang, M.; Wang, H. A Voltage Quadrupler Rectifier Based Pulsewidth Modulated LLC Converter with Wide Output Range. IEEE Trans. Ind. Appl. 2018, 54, 6159–6168. [Google Scholar] [CrossRef]
- Alaql, F.; Rezaii, R.; Gullu, S.; Elrais, M.T.; Batarseh, I. A Switchable Rectifier-based LLC Resonant Converter for Photovoltaic Applications. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Singapore, 24–27 May 2021; pp. 2093–2098. [Google Scholar]
- Shang, M.; Wang, H.; Cao, Q. Reconfigurable LLC Topology with Squeezed Frequency Span for High-Voltage Bus-Based Photovoltaic Systems. IEEE Trans. Power Electron. 2018, 33, 3688–3692. [Google Scholar] [CrossRef]
- Chen, W.; Xu, M.; Ge, Y.; Guo, Q.; Jiang, T.; Che, X. Parameter Design of High Power LLC Resonant Converter. In Proceedings of the 2022 IEEE 5th International Conference on Electronics Technology (ICET), Chengdu, China, 13–16 May 2022; pp. 421–425. [Google Scholar]
- Yuan, Y.; Xu, L.; Yao, C.; Yuan, J.; Wang, X.; Ruan, X. Simplified Time-Domain Design Methodology for LLC Resonant Converter in EV Charging Station Application. In Proceedings of the 2024 3rd International Conference on Power Systems and Electrical Technology (PSET), Tokyo, Japan, 5–8 August 2024; pp. 332–337. [Google Scholar]
- Hou, Z.; Jiao, D.; Lai, J.-S. An Ultrawide Range Pulse Width Modulated LLC Converter with Voltage Multiplier Rectifiers. IEEE Trans. Power Electron. 2025, 40, 6216–6229. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, C.; Ni, K.; Mi, H.; Yang, J.; Yang, T. A Parameter Design Method for L-LLC Resonant Converter. In Proceedings of the 2023 IEEE 2nd International Power Electronics and Application Symposium (PEAS), Guangzhou, China, 10–13 November 2023; pp. 1205–1210. [Google Scholar]
- Wei, Y.; Pereira, T.; Pan, Y.; Liserre, M.; Blaabjerg, F.; Mantooth, H.A. RMS Current based Automated Optimal Design Tool for LLC Resonant Converters. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022; pp. 2146–2153. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).