Multi-Objective Optimization of Distributed Generation Placement in Electric Bus Transit Systems Integrated with Flash Charging Station Using Enhanced Multi-Objective Grey Wolf Optimization Technique and Consensus-Based Decision Support
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Liturature Review and Research Gaps
1.2.1. DG Optimization in Distribution Networks
1.2.2. Electric Bus Charging Infrastructure Optimization
1.2.3. Grey Wolf Optimizer Applications Optimization
1.2.4. Research Gaps and Motivation
- Limited multi-objective approaches: most DG optimization studies rely on weighted-sum methods, which may not adequately capture trade-offs and require subjective weight selection.
- Static loading assumptions: traditional DG optimization assumes static or simplified loading patterns, failing to account for the dynamic nature of E-bus charging.
- Insufficient decision support: current multi-objective approaches often provide Pareto fronts without adequate guidance for practical solution selection.
- Limited validation: many studies lack comprehensive validation with realistic E-bus operational data and detailed network modeling.
- Methodological Innovation: first application of Euclidean distance-based MOGWO eliminating subjective weight selection while maintaining solution diversity.
- Comprehensive Integration: seamless integration of realistic E-bus operational dynamics with power system optimization, 31-stop routes, flash charging, and multi-bus coordination.
- Advanced Decision Support: five-method consensus approach (TOPSIS, Euclidean distance, weighted sum, compromise programming, hypervolume) for robust solution selection.
- Practical Implementation Focus: automated report generation, multi-stakeholder considerations, and comprehensive implementation guidance, bridging the gap between research and practice.
- Real-world Validation: uses actual E-bus specifications, realistic charging patterns, and comprehensive constraint modeling rather than simplified theoretical scenarios.
1.2.5. Research Objectives
- Develop an enhanced multi-objective grey wolf optimization: create a robust MOGWO variant that eliminates subjective weight selection through Euclidean distance-based fitness evaluation.
- Integrate E-Bus dynamics: incorporate realistic electric bus operational patterns, including route modeling, charging schedules, and dynamic loading scenarios.
- Provide comprehensive decision support: develop multiple compromise solution selection methods to support practical implementation decision.
- Validate performance: demonstrate the effectiveness of the proposed approach through extensive simulation studies and comparative analysis.
- Enable practical implementation: generate actionable insights and recommendations for power system operators and transit agencies.
1.3. Main the Contibutions
- The proposed MOGWO uses Euclidean distance-based fitness to eliminate weight tuning, enhance Pareto diversity, and adapt reference points dynamically. It includes efficient archive management for non-dominated solutions.
- Compromise selection framework is adapted by five methods as TOPSIS, Euclidean distance, equal-weighted Sum, L2-metric, and hypervolume contribution. They are applied to select balanced solutions from the Pareto front.
- Consensus-based decision support: the framework employs a voting mechanism across all five methods to identify consensus solutions, providing.
- Integrated E-bus and DG model with a 31-stop, 62 km route, 600 kW flash charging, and multi-bus coordination with staggered trips and grid interaction.
- Performance evaluation framework Introduces multi-dimensional metrics including hypervolume, diversity, convergence rate, and trade-off analysis, supported by 2D/3D Pareto plots, radar charts.
- Advances multi-objective optimization, sets benchmarks for DG in E-bus systems, and validates nature-inspired methods for smart grid studies.
- Supports utilities in DG planning, transit agencies in flash charging strategies, regulators in performance assessment and advancing sustainable transport.
2. Theory Background
2.1. Power Flow Analysis and Related Modeling of Simulation
2.1.1. Power Flow Equation
2.1.2. Power Balance of the Electrical Power System
2.1.3. E-Bus Flash Charging Modeling
2.1.4. Distributed Generator (DG) Power Injection Model
2.1.5. Voltage Deviation Index (VDI)
2.1.6. Total Real Power Loss ()
2.1.7. Voltage Violations (Vv)
2.2. Energy Management Using Optimization Techniques
2.2.1. Multi-Objective Grey Wolf Optimizer (MOGWO)
2.2.2. Compromised Solution and Normalization
- Objective NormalizationThe difference in the objective function , before applying compromise solution methods, the objective values are normalized. This scales all the objective values into the range [0,1] to ensure comparability across different units.
- Compromise Solution MethodsFrom the generated Pareto optimal set, the need arises to select a single compromise solution that performs well across all objectives. Five advanced methods are employed:
- 1
- Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) that prefers solutions closest to the ideal and farthest from the worst [44,45]. The TOPSIS is consistent with three functions for applications as distance to idea , distance to anti-idea and finding the maximum score of the TOPSIS can expressed in Equations (23)–(25) as follows:
- 2
- Euclidean distance from ideal point use chooses the solution closest to the ideal objective vector and selected by minimum of from each solution and can be expressed as Equation (26) [46].
- 3
- Weighted sum (WS) is adapted by aggregating normalized objectives assuming equal or user-defined priority that can be expressed the WS as Equation (27) [47].
- 4
- Compromise programming (Lp-metric, p = 2) is used by minimizing the L2-norm from the ideal point [48].
- 5
- Hypervolume contribution is used by selecting solutions with the largest added area/volume in objective space [49].
- Consensus-Based Decision SupportThe system assesses all five compromise solution techniques and documents the optimal option determined by each. A consensus-based decision support strategy is used to ascertain the optimal compromise. Within this structure, each method casts a single “vote” for its chosen optimal solution as Equation (30). The option that garners the most votes is chosen by most methods is deemed the ultimate compromise answer as Equation (31). Voting in the context of consensus-based compromise solution selection is based on the solution that each method identifies as its most preferred choice from the set of all non-dominated solutions obtained through multi-objective optimization (Pareto front). This voting-based aggregate guarantees equity and reduces the prejudice inherent in any single approach. The consensus procedure selects the final compromise solution by maximizing the number of votes received, as defined in Equation (32).
3. Methodology of the Multi-Objective Optimization of Distributed Generation Placement in Electric Bus Transit Systems Integrated with Flash Charging Station
3.1. Modified of IEEE 33 Bus and IEEE 69 Bus Testing System
3.2. Definition of Objective Function and Constraints for MOGWO
3.3. Algorithm for Solving the MOGWO for DGs Placement in E-Bus Transit System Integrated with Flash Charging Station
| Algorithm 1: Multi-Objective Grey Wolf Optimizer (MOGWO) for complete pseudocode. | |
| Main Algorithm: Multi-Objective Grey Wolf Optimizer (MOGWO) Input data and network (IEEE 33 bus and IEEE 69 bus) | |
| Begin main algorithm | |
| //Step 1: Initialize MOGWO parameters | |
| CALL Initialize_MOGWO_Parameters () | |
| //Step 2: Initialize wolf population | |
| CALL Initialize_Population () | |
| //Step 3: Main optimization loop | |
| FOR iter = 1 TO max_iter DO | |
| //Step 3.1: Evaluate objectives for all wolves | |
| CALL Evaluate_Objectives () | |
| //Step 3.2: Update reference point for Euclidean distance | |
| CALL Update_Reference_Point () | |
| //Step 3.3: Update alpha, beta, delta wolves | |
| CALL Update_Alpha_Beta_Delta () | |
| //Step 3.4: Update Pareto archive | |
| CALL Update_Pareto_Archive () | |
| //Step 3.5: Record convergence | |
| CALL Record Convergence (iter) | |
| //Step 3.6: Update wolf positions (except last iteration) | |
| If iter < max_iter Then CALL Update_Wolf_Positions(iter) END IF | |
| //Step 3.7: Display progress | |
| PRINT “Iteration”, iter, “: Pareto solutions =”, |pareto_archive | |
| End for | |
| //Step 4: Post-processing and analysis | |
| CALL Generate_Visualizations () | |
| CALL Perform_Compromise_Selection () from Section 2.2.2 | |
| CALL Export_Results () | |
| RETURN pareto_positions, pareto_powers, pareto_reactive_powers, pareto_objectives | |
| End Main Algorithm | |
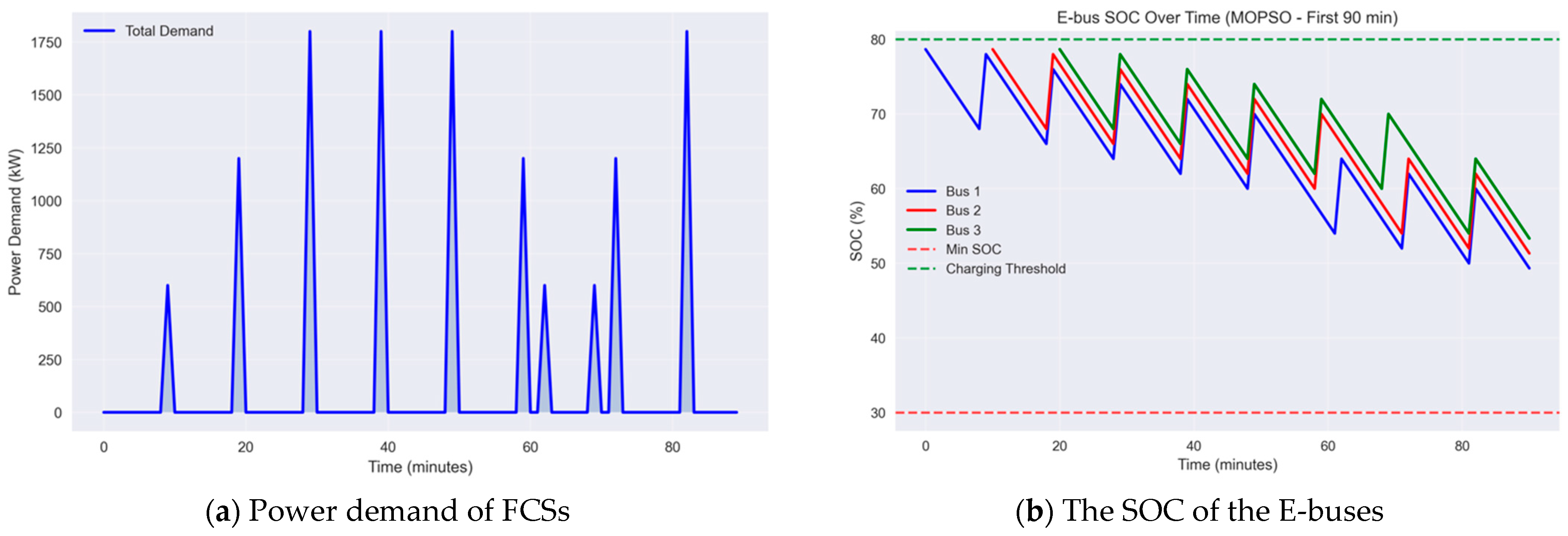
3.4. Scenarios of the MOGWO for Distributed Generation Placement Under Flash Charging of E-Bus
- 2D visualization of simulation results of the objective functions.
- Comparison of the total power loss and voltage violation.
- Comparison of the total voltage deviation and voltage violation.
- Comparison of the quality scores by each method for compromise solution.
- Comparison of the compromise solution votes by each method for consensus-based decision support.
- Comparison of the normalized performance comparison (Radar plot).
- Comparison of the objective function correlation matrix.
- Comparison of all performances and results.
4. Simulation Results
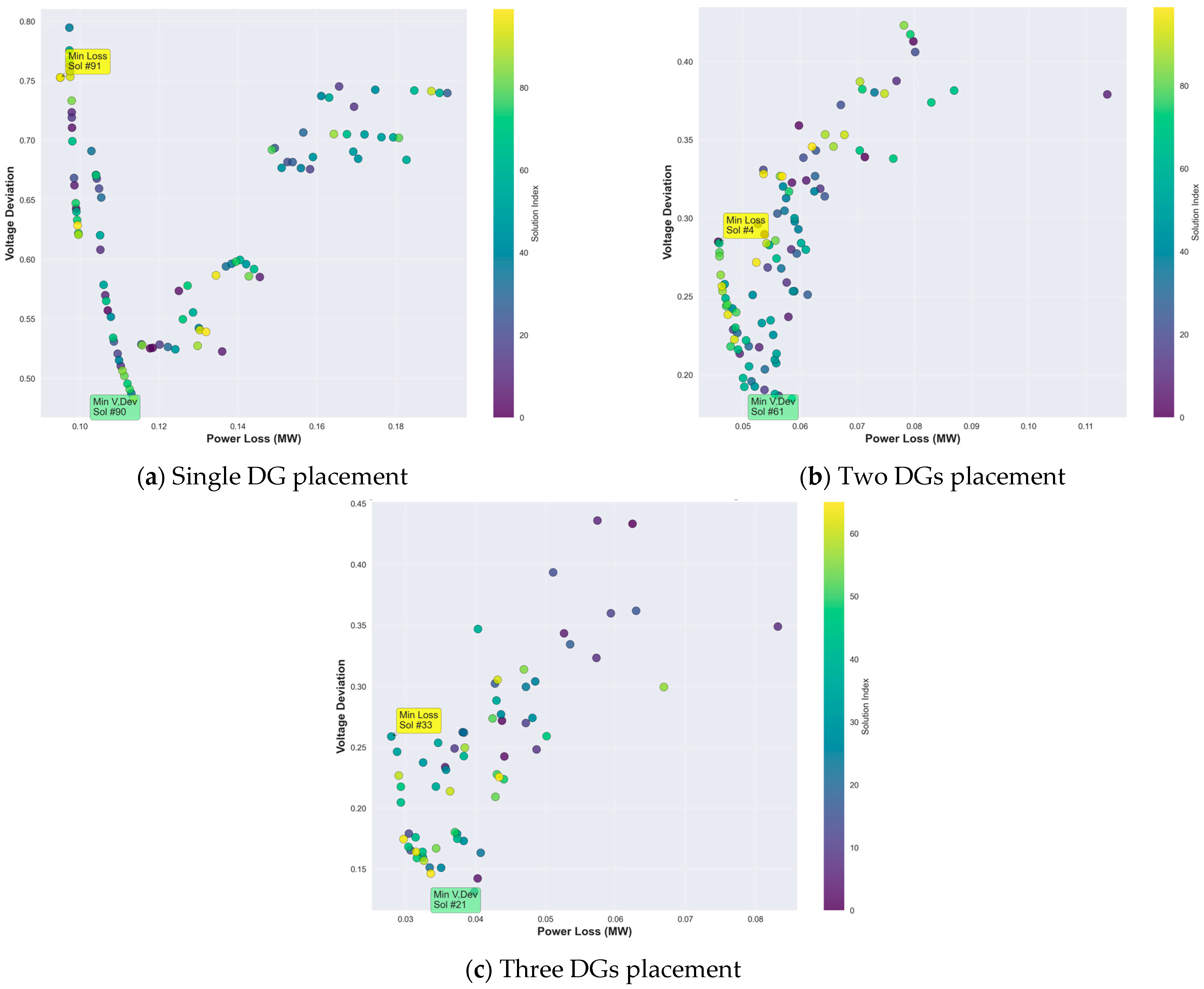
4.1. Comparison of the Simulation Results in 2D Plot
4.1.1. Comparison of the Total Power Loss and Voltage Deviation of the IEEE 33 Bus and IEEE 69 Bus Testing System
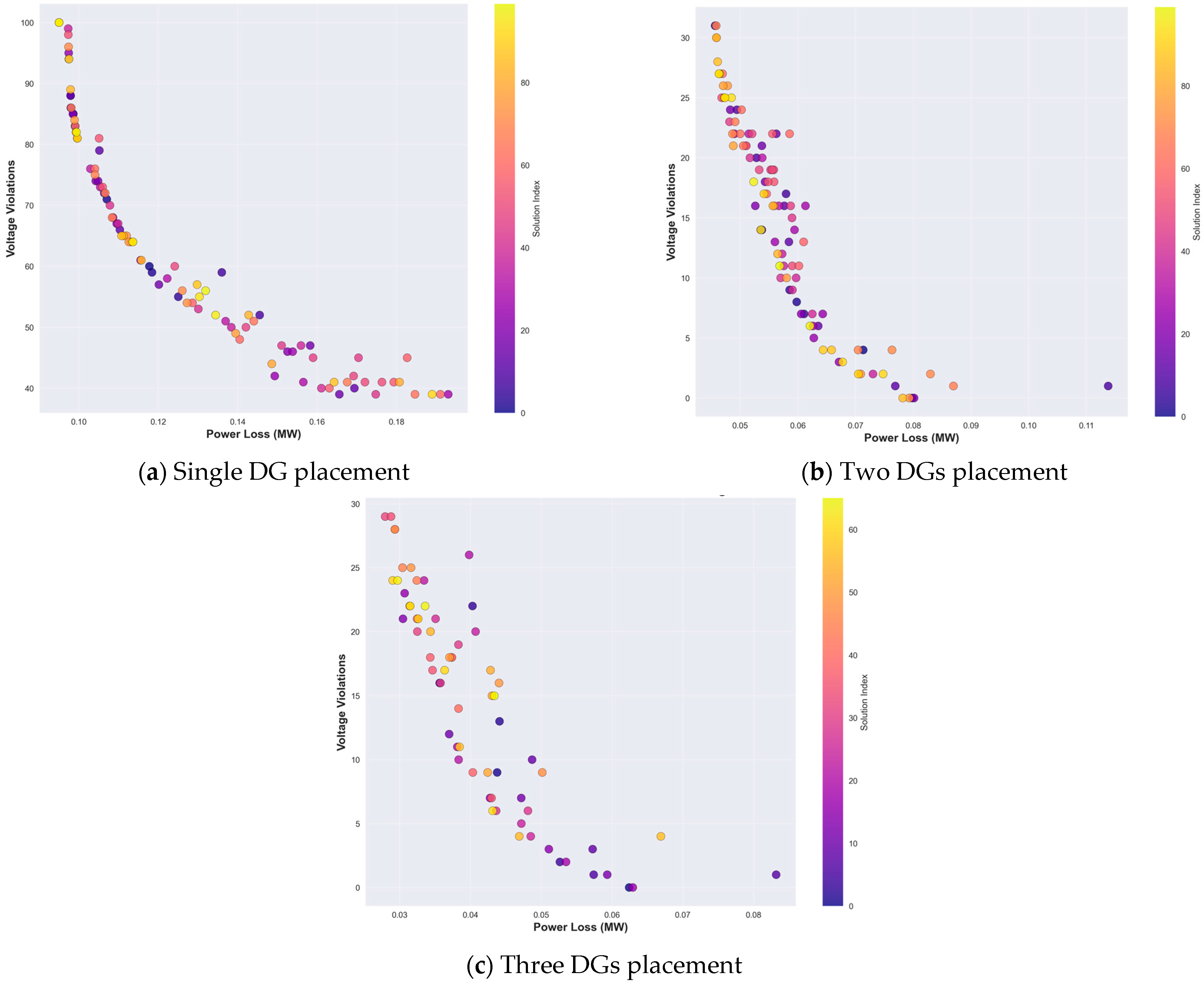
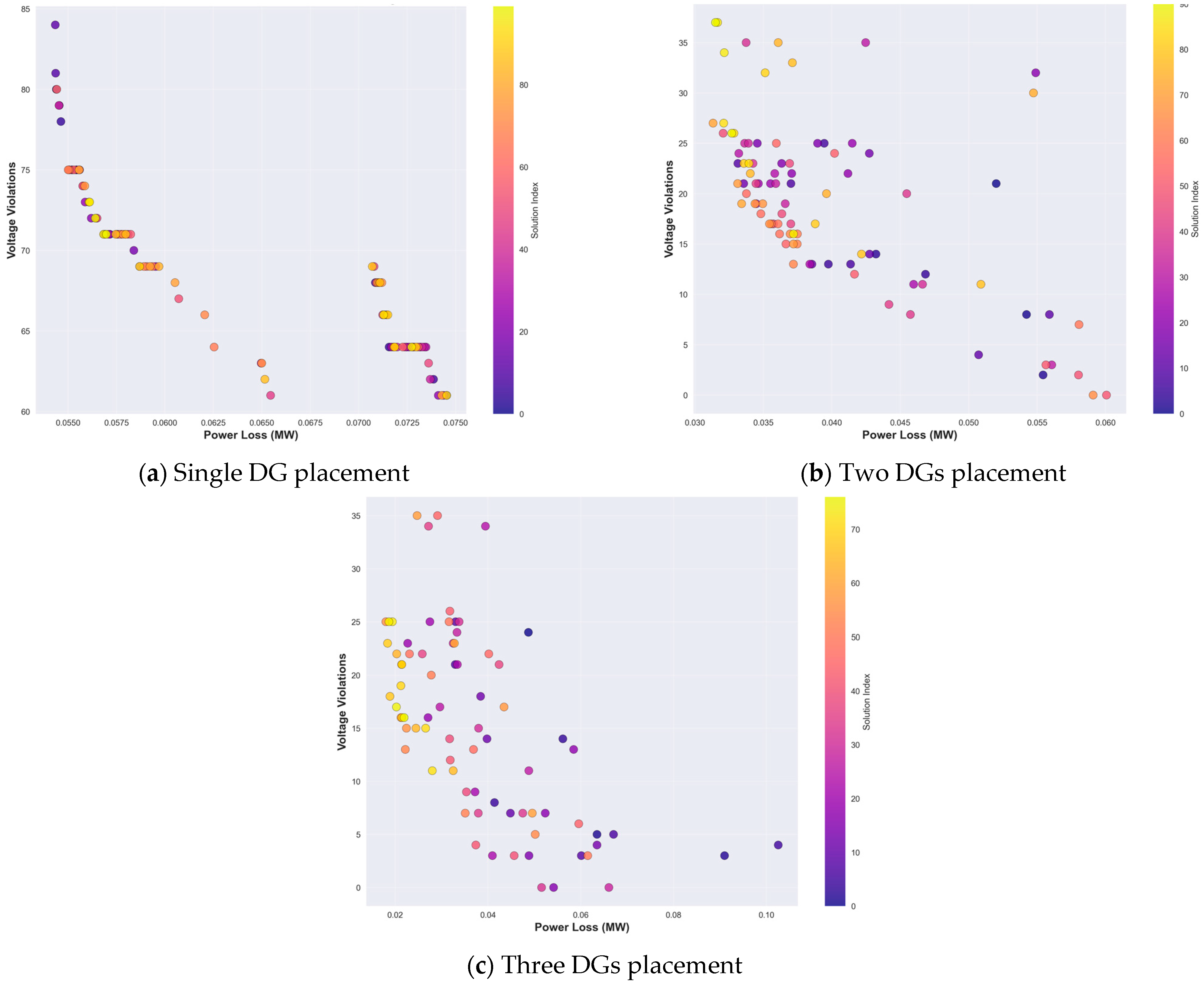
4.1.2. Comparison of the Total Power Loss and Voltage Violation
4.1.3. Comparison of the Total Voltage Deviation and Voltage Violation
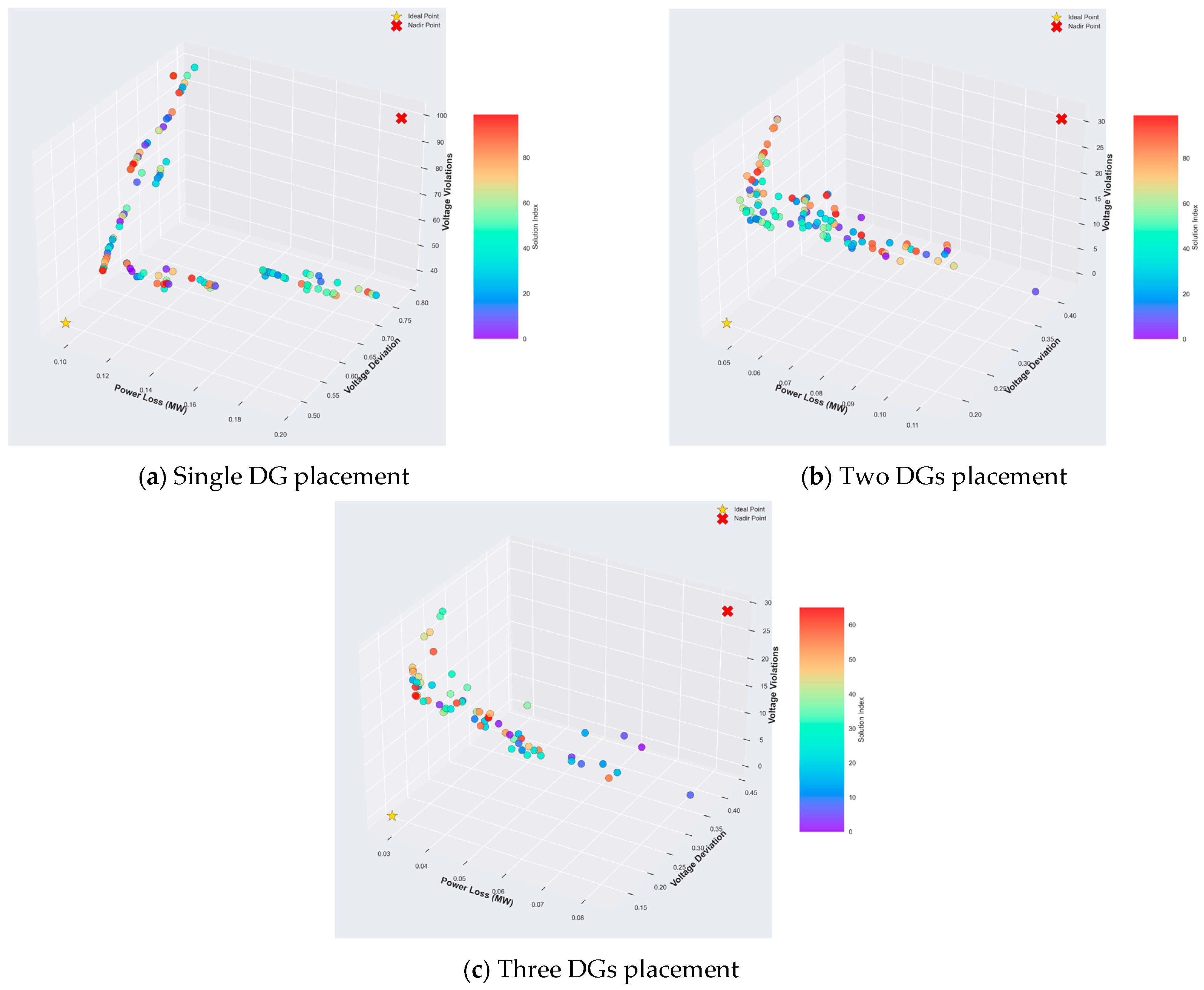
4.2. Comparison of the Simulation Results in 3D Plot
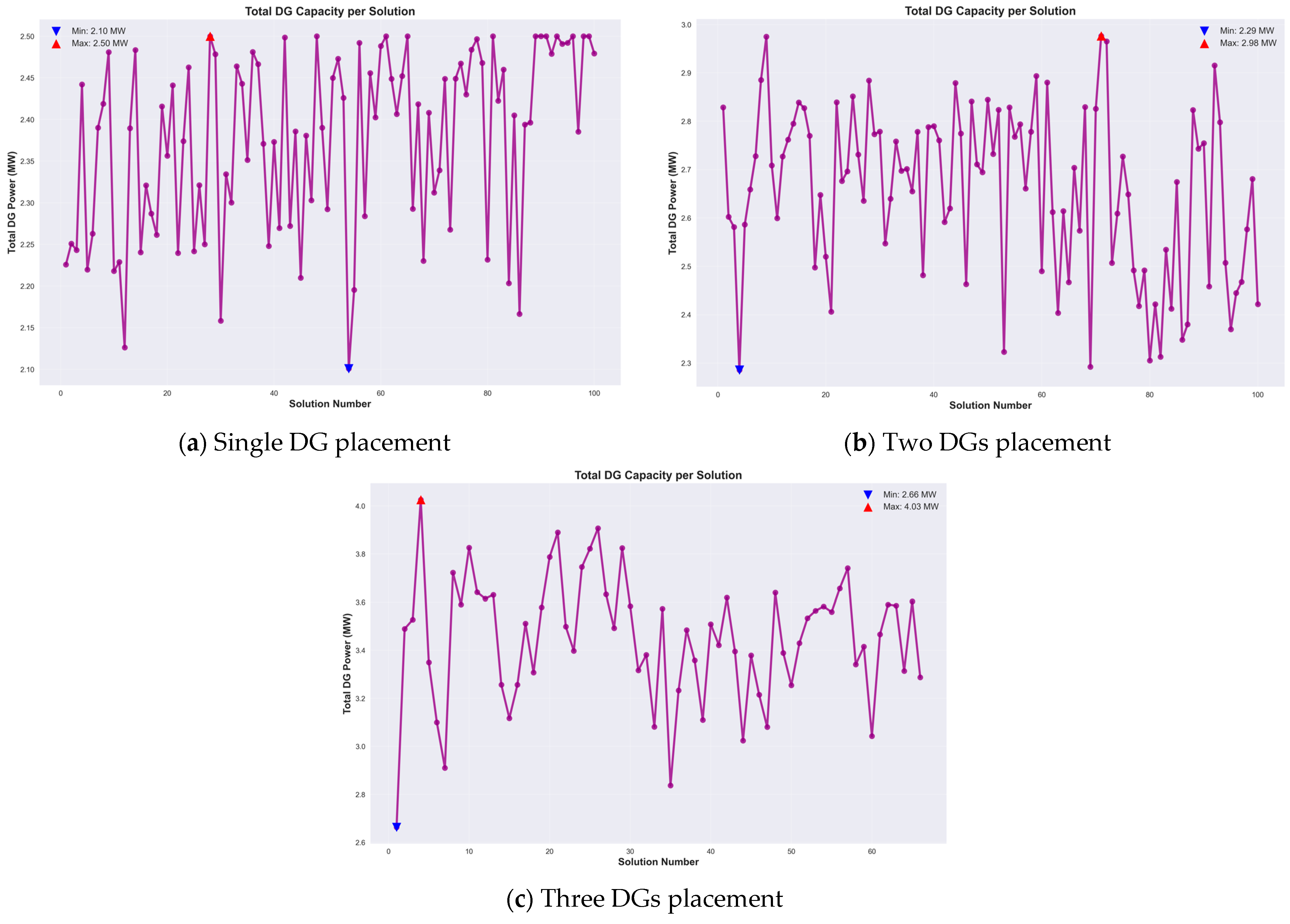
4.3. Comparion the Total DGs Capacity per Solution
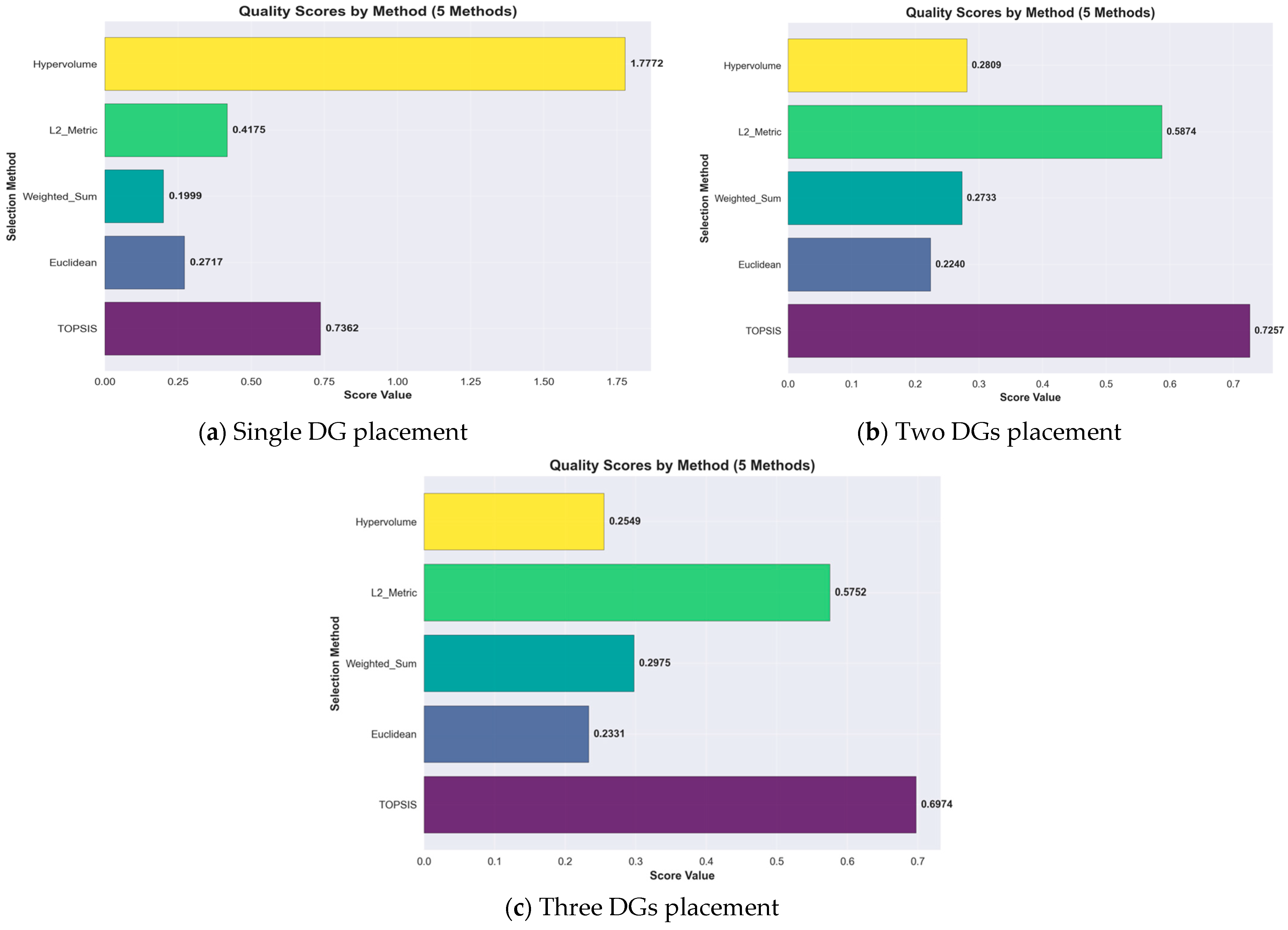
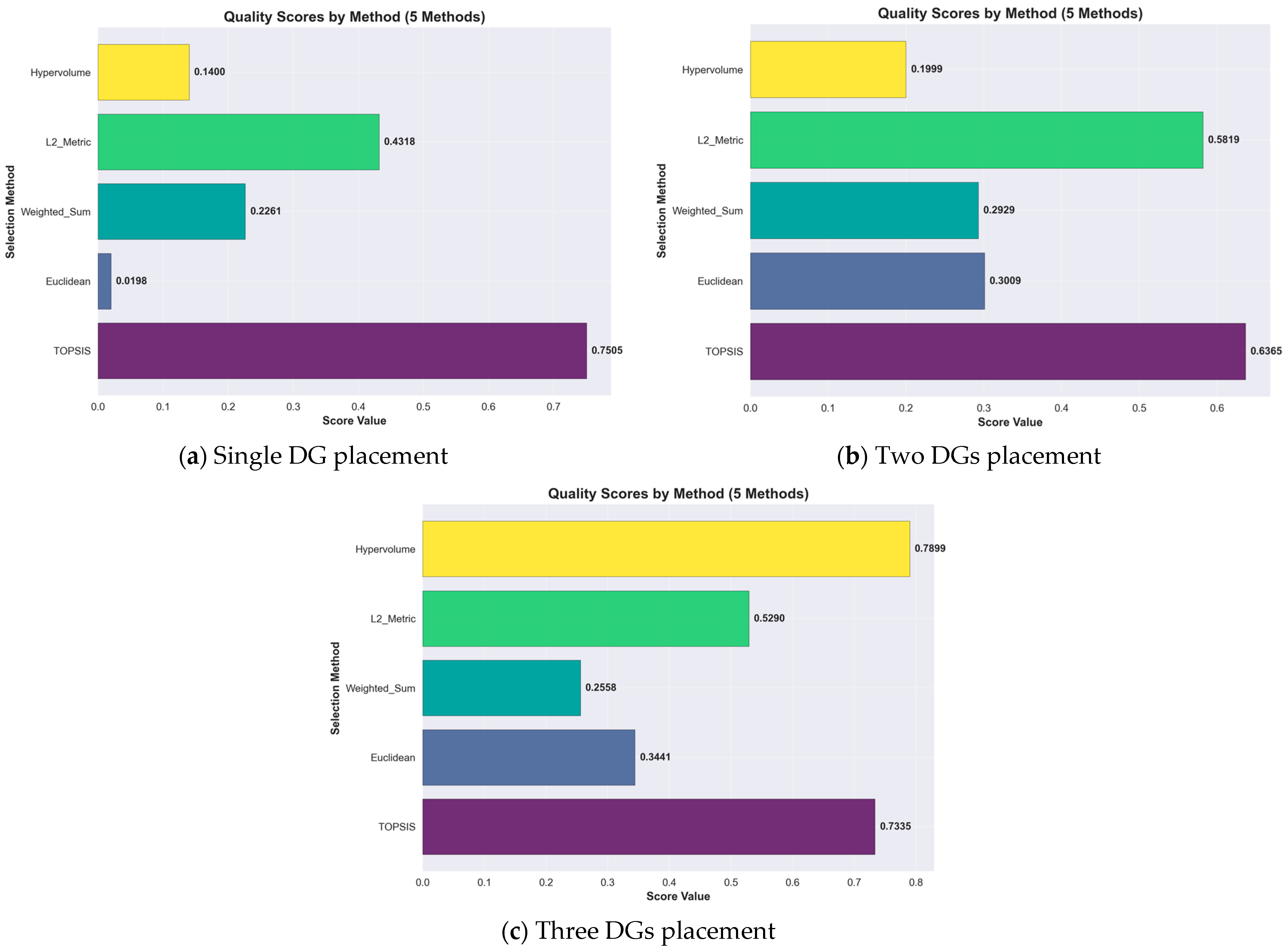
4.4. Comparison of the Quality Scores by Each Method for Compromise Solution
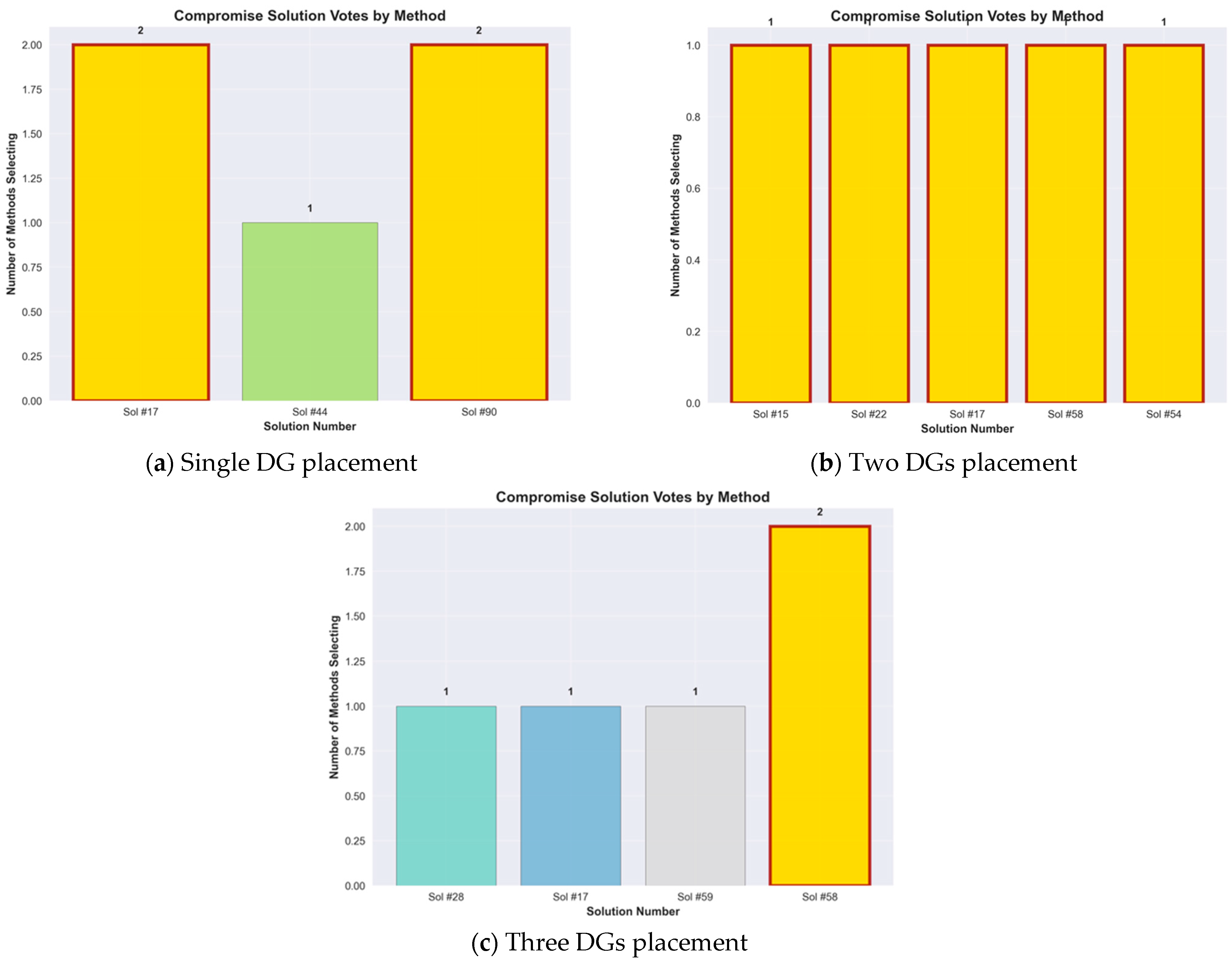
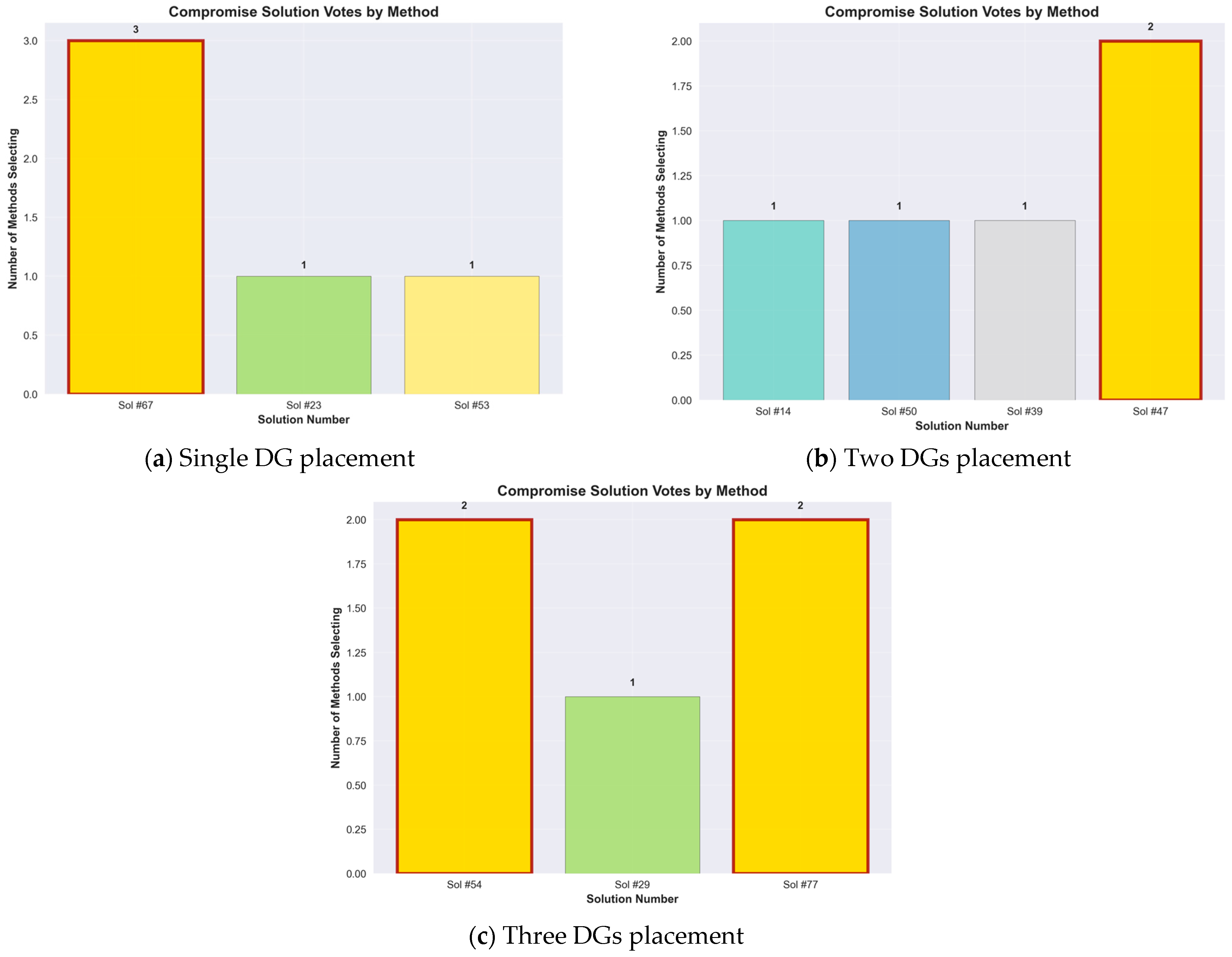
4.5. Comparison of the Compromise Solution Votes by Each Method for Consensus-Based Decision Support
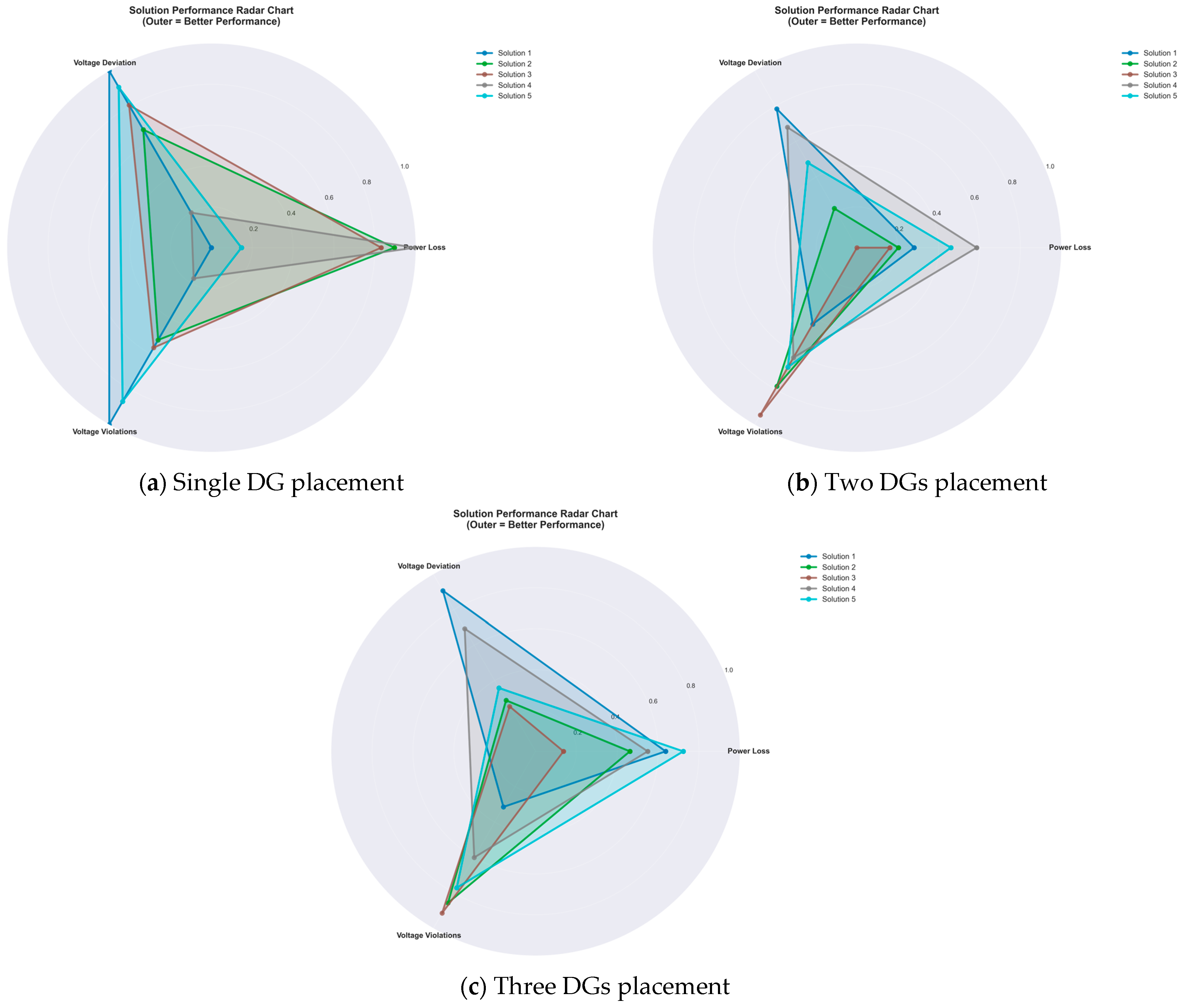
4.6. Comparion the Normalized Performance Comparison (Radar Plot)
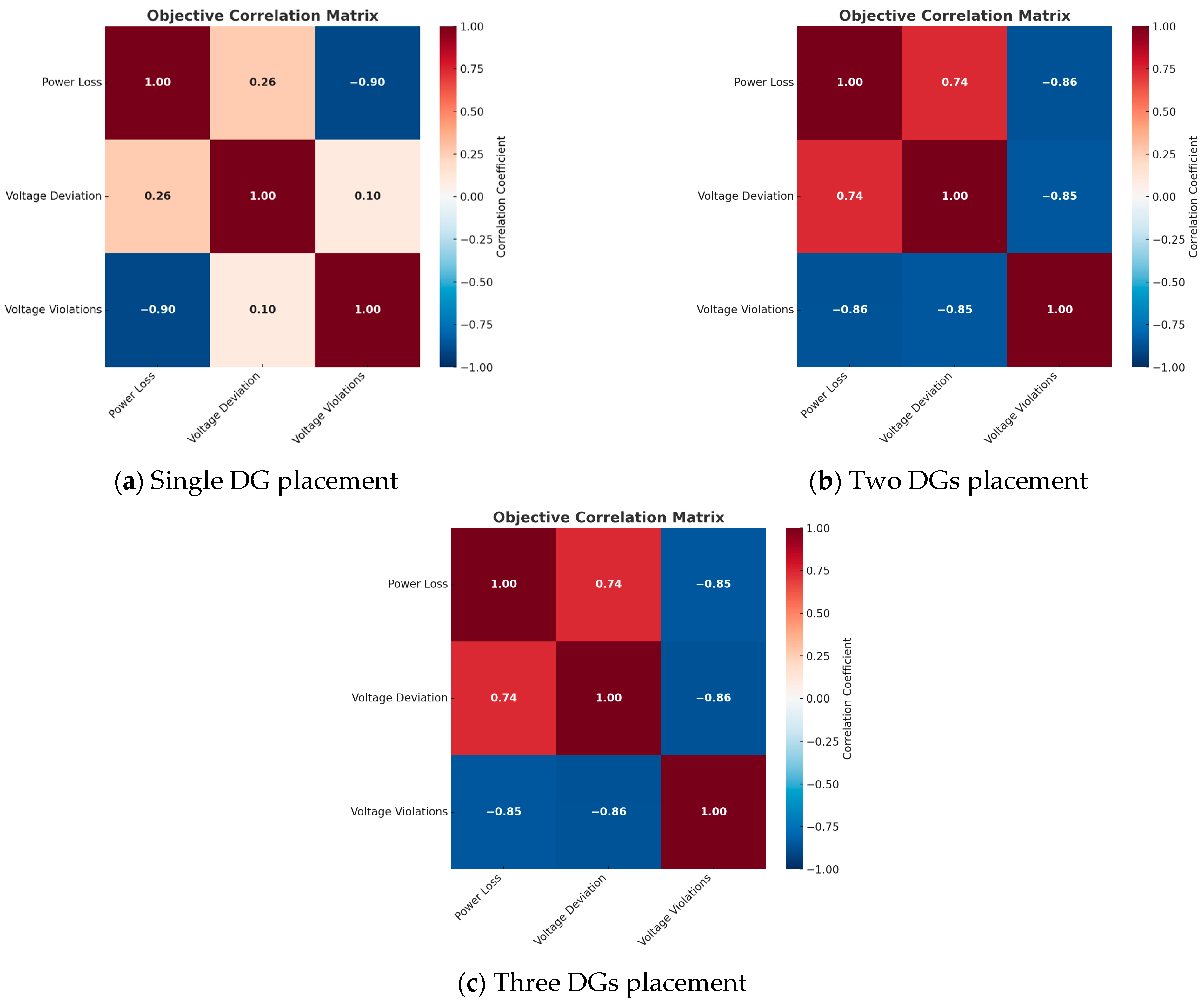
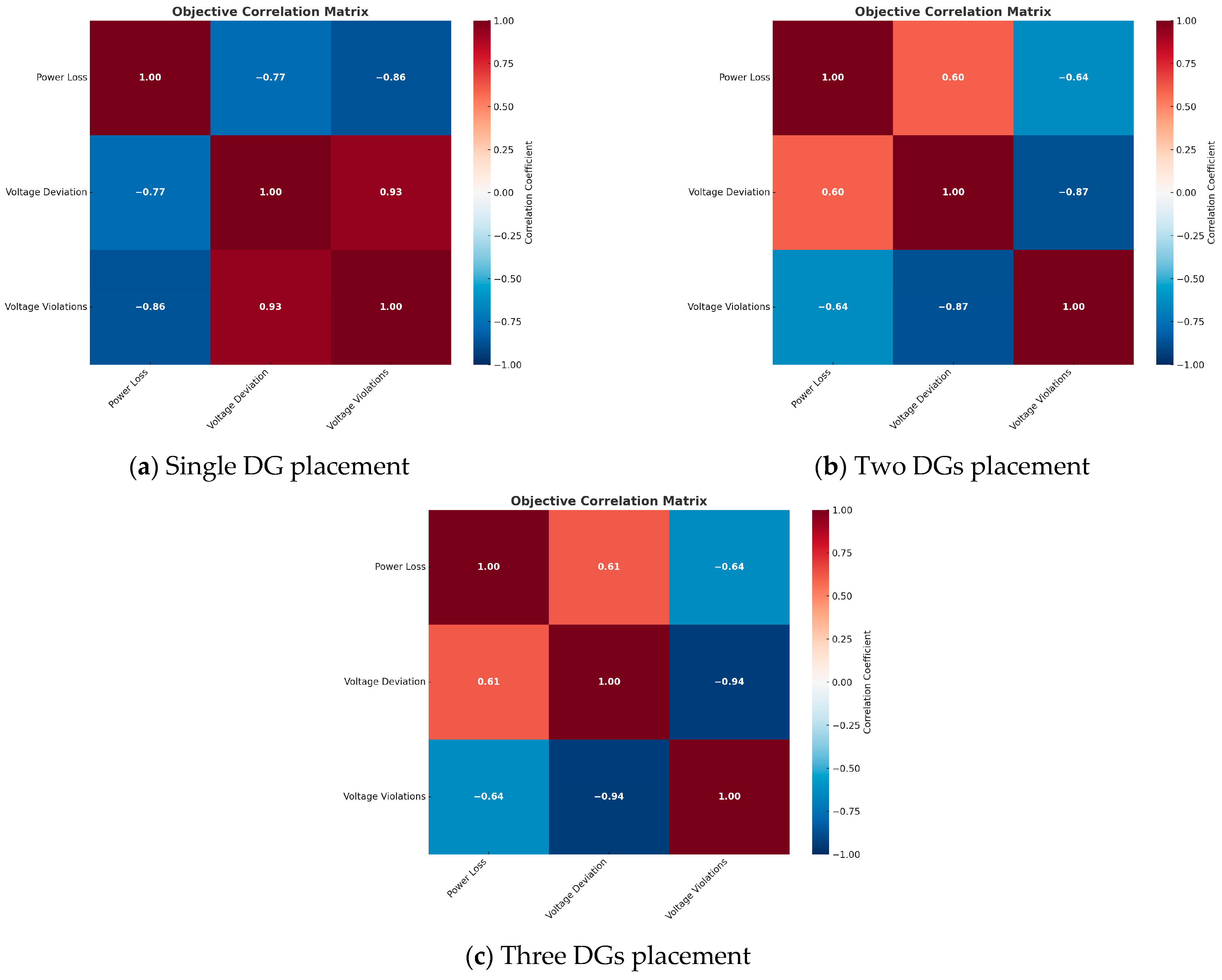
4.7. Comparison of the Objective Function Correlation Matrix
4.8. Comparison of All Performances and Results
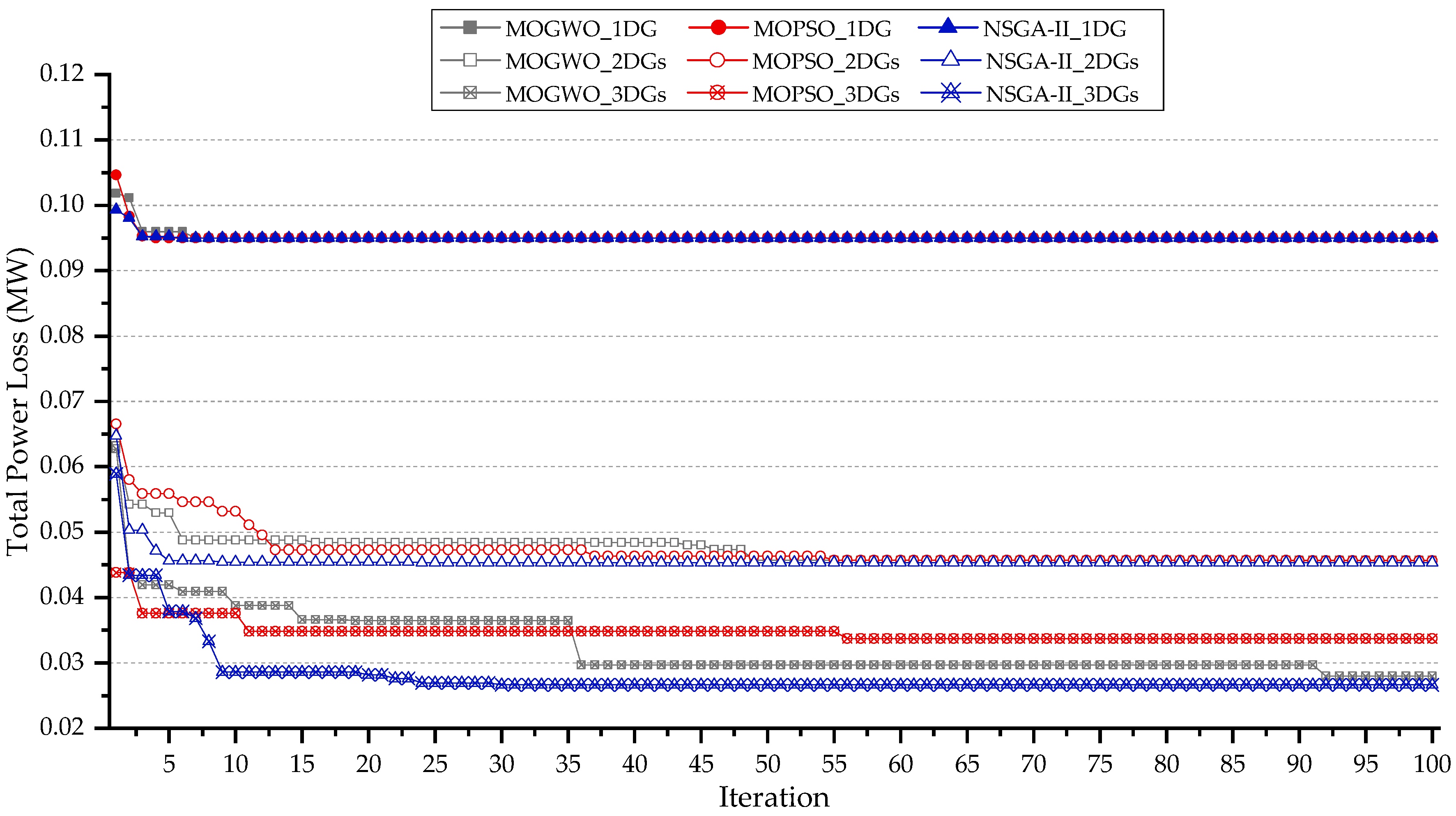
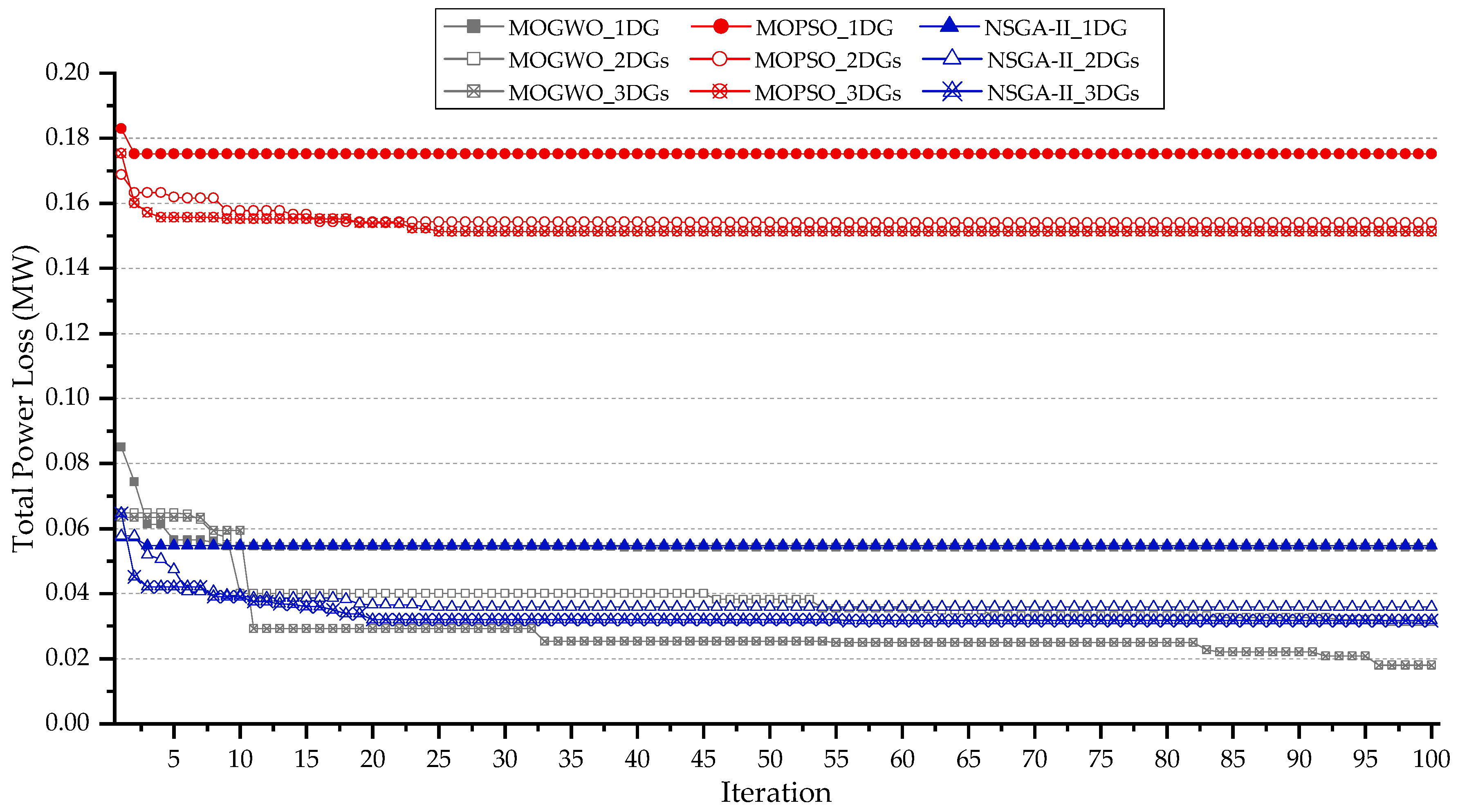
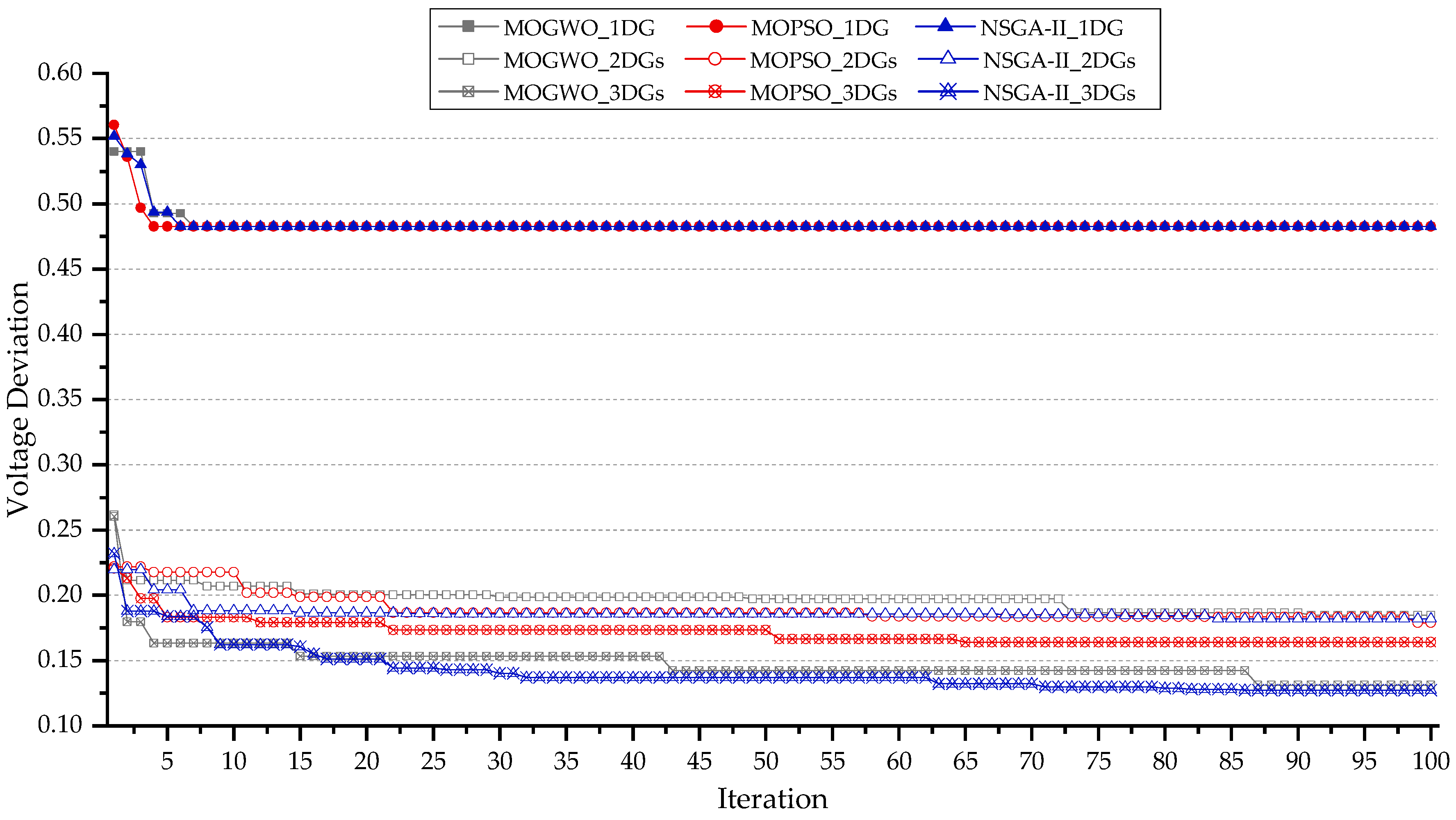
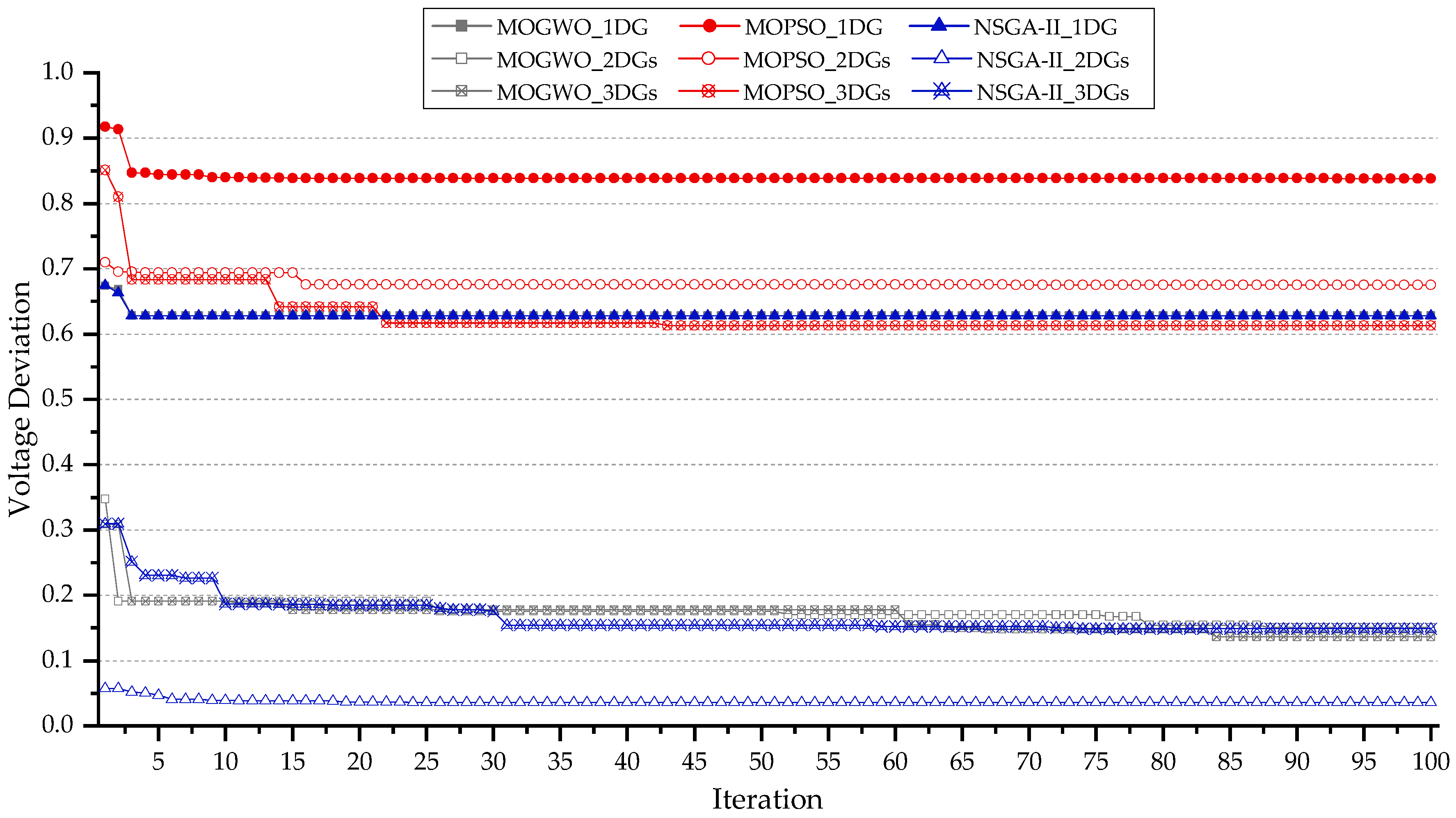
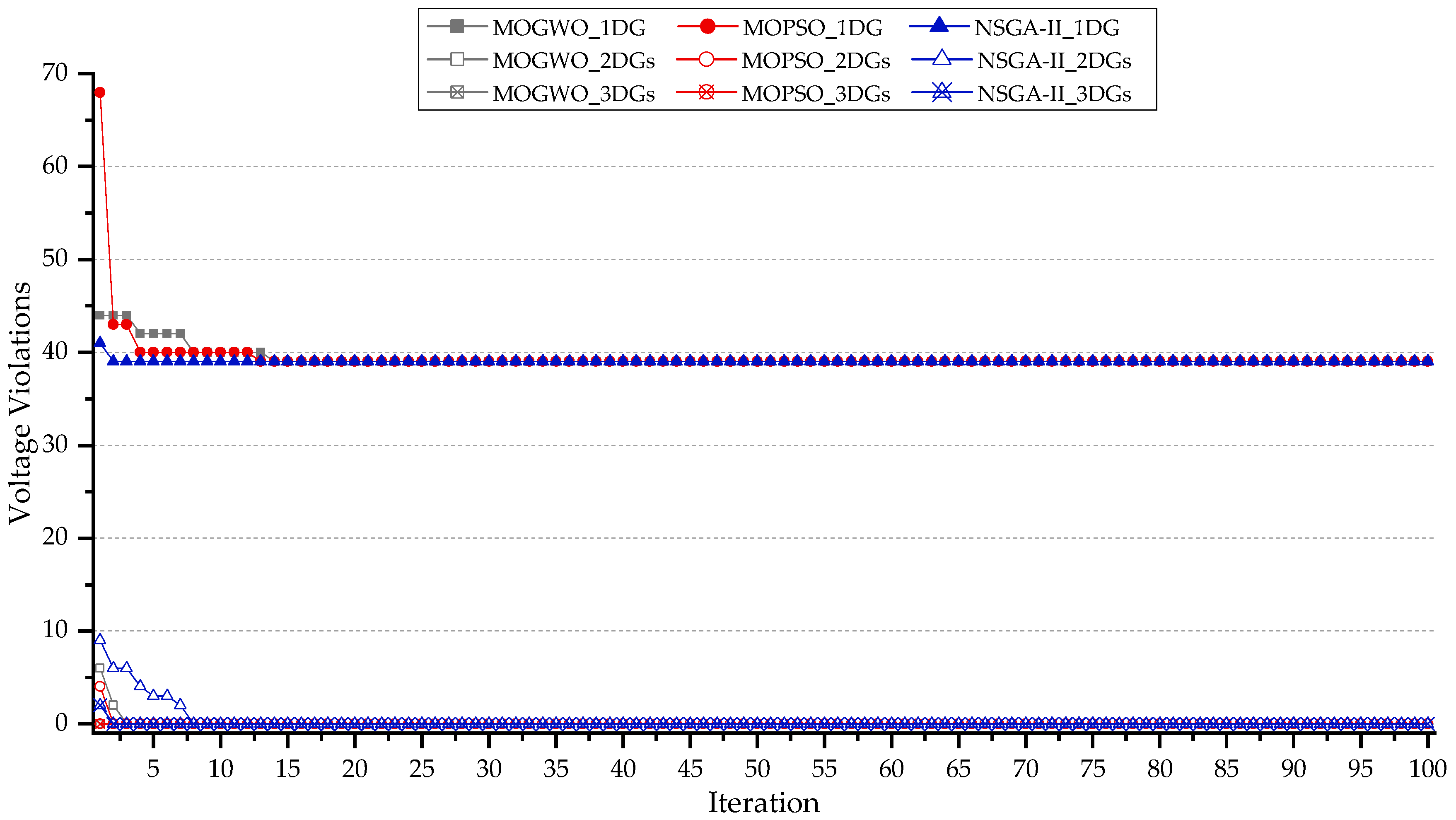
4.9. Performance Comparison of Convergence Behavior and Optimization Results Between MOGWO, MOPSO and NSGA-II
5. Discussion
5.1. Impact of DG Quantity on System Performance
- 0.0950 MW to 0.0279 MW (a 70.6% reduction) in the 33-bus system, and
- 0.0543 MW to 0.0179 MW (a 67.0% reduction) in the 69-bus system.
- 72.8% in the 33-bus system (from 0.4827 to 0.1313), and
- 78.3% in the 69-bus system (from 0.6282 to 0.1362).
5.2. Quality and Selection of Compromise Solutions
5.3. Correlation Evolution Among Objectives
5.4. Optimal DG Sizing and Placement Patterns
5.5. Comparative Algorithm Performance
5.6. Practical Implications and Future Direction
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Total number of buses in the system | |
| Apparent power or complex power injection at bus | |
| Active power or real power | |
| Reactive power or reactive power | |
| From bus and To bus | |
| the voltage magnitudes at bus and . | |
| The phase angle difference between bus i and bus | |
| The conductance between buses and | |
| The susceptance between buses and | |
| The real power from the main generator at bus | |
| The real power from the distributed generator at bus | |
| The real power demand/load at bus | |
| The flash charging power of batteries at bus | |
| The power loss in the transmission lines | |
| The reactive power from the main generator at bus | |
| The reactive power from the distributed generator at bus | |
| The reactive power demand/load at bus | |
| The reactive loss in the transmission lines | |
| Time interval | |
| Total time periods | |
| routed sequence of bus stops | |
| The E-bus stop for services | |
| Distance between consecutive stops | |
| The total route distance | |
| Energy consumption per kilometer | |
| Set of bus locations where flash charging stations are installed | |
| Remaining charging time duration | |
| Current bus stop of E-bus at time | |
| Maximum power rating of the flash charging station | |
| Energy consumed during movement (depends on speed/distance) | |
| Initial energy when the simulation starts | |
| Charging power of the E-bus | |
| Time step (in minutes) | |
| The State of Charge (SOC) of the battery | |
| The set of charging station nodes | |
| The set of buses in the electrical power system | |
| Resistance of line . | |
| The real power flows at line . | |
| The real power flows at line . | |
| Active power of DG power injection model (in MW) | |
| Reactive power of DG power injection model (in MVar) | |
| Comlex power of DG power injection model (in MVA) | |
| a random vector | |
| represents the objective function | |
| The corresponding user-defined weight | |
| Value of the -th objective for the -th solution | |
| The ideal point | |
| The Euclidean distance of a solution to this ideal point | |
| Minimum and maximum of objective | |
| Set of methods | |
| The indicator function | |
| A vote counter for each solution | |
| Solution index selected by method | |
| A reference point beyond the worst values | |
| Select the consensus solution | |
| Bus index where the DG is installed | |
| The vector of decision variables (e.g., DG locations and capacities) | |
| The feasible solution space | |
| The objective functions to be minimized | |
| Represent inequality and equality constraints. | |
| The number of generators |
References
- International Energy Agency. Global EV Outlook 2023: Catching up with Climate Ambitions; International Energy Agency: Paris, France, 2023. [Google Scholar]
- Rogge, M.; Wollny, E.; Sauer, D.U. Fast charging battery buses for the electrification of urban public transport—A feasibility study focusing on charging infrastructure and energy storage requirements. Energies 2015, 8, 4587–4606. [Google Scholar] [CrossRef]
- Kunith, A.; Mendelevitch, R.; Goehlich, D. Electrification of a city bus network—An optimization model for cost-effective placing of charging infrastructure and battery sizing for large-scale fleets. Appl. Energy 2017, 197, 323–331. [Google Scholar]
- Basma, S.; Mansour, S.; Zgheib, D.; Jammal, T.; Bitar, M. Coordination between autonomous electric buses and power distribution networks. In Proceedings of the IEEE Power & Energy Society General Meeting, Portland, OR, USA, 7–9 August 2018; pp. 1–5. [Google Scholar]
- Zhang, R.; Cheng, X.; Yang, L. Flexible charging strategies for electric bus systems considering traffic and grid constraints. IEEE Trans. Transp. Electrific. 2020, 6, 262–276. [Google Scholar]
- Liu, H.; Zhang, Y.; Ge, S.; Gu, C.; Li, F. Day-ahead scheduling for an electric bus system with battery degradation cost consideration. IEEE Trans. Transp. Electrific. 2019, 5, 982–995. [Google Scholar]
- Liu, W.; Liang, S.; Zhang, H.; Liu, X. Distributed charging strategy for electric bus fleet based on dynamic programming. J. Energy Storage 2021, 34, 102112. [Google Scholar]
- Adefarati, T.; Bansal, R.C. Integration of renewable distributed generators into the distribution system: A review. IET Renew. Power Gener. 2016, 10, 873–884. [Google Scholar]
- Ghosh, S.; Ghoshal, S.P.; Ghosh, S. Optimal sizing and placement of distributed generation in a network system. Int. J. Electr. Power Energy Syst. 2010, 32, 849–856. [Google Scholar]
- Moradi, M.H.; Abedini, M. A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R.C. Analytical expressions for DG allocation in primary distribution networks. IEEE Trans. Energy Convers. 2010, 25, 814–820. [Google Scholar]
- Georgilakis, P.S.; Hatziargyriou, N.D. Optimal distributed generation placement in power distribution networks: Models, methods, and future research. IEEE Trans. Power Syst. 2013, 28, 3420–3428. [Google Scholar]
- Das, D. A fuzzy multiobjective approach for network reconfiguration of distribution systems. IEEE Trans. Power Del. 2006, 21, 202–209. [Google Scholar]
- Acharya, N.; Mahat, P.; Mithulananthan, N. An analytical approach for DG allocation in primary distribution network. Int. J. Electr. Power Energy Syst. 2006, 28, 669–678. [Google Scholar]
- Aman, M.M.; Jasmon, G.B.; Bakar, A.H.A.; Mokhlis, H. A new approach for optimum simultaneous multi-DG distributed generation units placement and sizing based on maximization of system loadability using HPSO (hybrid particle swarm optimization) algorithm. Energy 2014, 66, 202–215. [Google Scholar]
- Kaur, S.; Kumbhar, G.; Sharma, J. A MINLP technique for optimal placement of multiple DG units in distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 609–617. [Google Scholar]
- Sedighizadeh, M.; Rezazadeh, A. Using genetic algorithm for distributed generation allocation to reduce losses and improve voltage profile. World Acad. Sci. Eng. Technol. 2008, 37, 251–256. [Google Scholar]
- Tan, W.S.; Hassan, M.Y.; Majid, M.S.; Rahman, H.A. Optimal distributed renewable generation planning: A review of different approaches. Renew. Sustain. Energy Rev. 2013, 18, 626–645. [Google Scholar]
- El-Zonkoly, A.M. Optimal placement of multi-distributed generation units including different load models using particle swarm optimization. Swarm Evol. Comput. 2011, 1, 50–59. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar]
- Viral, R.; Khatod, D.K. Optimal planning of distributed generation systems in distribution system: A review. Renew. Sustain. Energy Rev. 2012, 16, 5146–5165. [Google Scholar]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar]
- AlRashidi, M.R.; El-Hawary, M.E. A survey of particle swarm optimization applications in electric power systems. IEEE Trans. Evol. Comput. 2009, 13, 913–918. [Google Scholar]
- Tran, T.T.; Muttaqi, K.M.; Sutanto, D. Multi-objective optimisation of solar power system integration in distribution networks. IET Gener. Transm. Distrib. 2020, 14, 1–12. [Google Scholar]
- Jian, L.; Xueliang, H.; Jianqiu, Y.; Yongjiang, B.; Ruoli, W. Optimal siting and sizing of electric vehicle charging stations. Int. J. Electr. Power Energy Syst. 2015, 72, 62–70. [Google Scholar]
- Wang, Y.; Chau, K.T.; Chan, C.C.; Li, W. Post-fault operation of redundant flux-switching permanent-magnet motor drive for electric vehicles. IEEE Trans. Magn. 2011, 47, 3051–3054. [Google Scholar]
- Gao, C.; Zhang, L.; Zhou, X.; Chen, Y. Location and capacity optimization of electric vehicle charging stations based on user travel patterns. Energies 2019, 12, 1149. [Google Scholar]
- Yilmaz, M.; Krein, P.T. Review of the impact of vehicle-to-grid technologies on distribution systems and utility interfaces. IEEE Trans. Power Electron. 2013, 28, 5673–5689. [Google Scholar]
- Ahmad, F.; Iqbal, A.; Ashraf, I.; Marzband, M.; Khan, I. Optimal location of electric vehicle charging station and its impact on distribution network: A review. Energy Rep. 2022, 8, 2314–2333. [Google Scholar]
- Li, Z.; Guo, Q.; Sun, H.; Wang, Y.; Xin, S. Emission-concerned wind-EV coordination on the transmission grid side with network constraints: Concept and case study. IEEE Trans. Smart Grid 2013, 4, 1692–1704. [Google Scholar]
- Richardson, P.; Flynn, D.; Keane, A. Local versus centralized charging strategies for electric vehicles in low voltage distribution systems. IEEE Trans. Smart Grid 2012, 3, 1020–1028. [Google Scholar]
- Bi, H.; Gu, Y.; Lu, F.; Mahreen, S. Site Selection of Electric Vehicle Charging Station Expansion Based on GIS-FAHP-MABAC. J. Clean. Prod. 2025, 507, 145557. [Google Scholar]
- Kumar, A.; Bhatti, S.K.; Singh, N.P. A review on electric vehicle technologies. J. Electr. Eng. Technol. 2020, 15, 1497–1531. [Google Scholar]
- ABB Group. ABB’s Flash Charging e-Bus Solution in Geneva. 2020. Available online: https://new.abb.com/news/detail/17282/abb-flash-charging-ebus-solution-reaches-a-new-milestone-of-half-a-million-km. (accessed on 30 May 2025).
- Hitachi Energy. Grid-eMotion® Flash: Fast Charging for e-Mobility. 2022. Available online: https://www.hitachienergy.com/news-and-events/customer-stories/tosa-flash-charging-e-bus-geneva-switzerland (accessed on 30 May 2025).
- ABB Group. Public Transportation Is Electrified. 2020. Available online: https://new.abb.com/news/detail/55599/public-transportation-electrified#:~:text=Revolutionary%20TOSA%20technology&text=They%20are%20charged%20via%20a,charging%20technology%20in%20the%20world (accessed on 30 May 2025).
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar]
- El-Shorbagy, M.A.; El-Refaey, A.A. Hybridization of grasshopper optimization algorithm with genetic algorithm for solving system of non-linear equations. IEEE Access 2020, 8, 220944–220961. [Google Scholar]
- Naderi, E.; Narimani, H.; Fathi, M.; Narimani, M.R. A novel fuzzy adaptive configuration of particle swarm optimization to solve large-scale optimal reactive power dispatch. Appl. Soft Comput. 2017, 60, 441–457. [Google Scholar]
- Faris, H.; Aljarah, I.; Al-Betar, M.A.; Mirjalili, S. Grey wolf optimizer: A review of recent variants and applications. Neural Comput. Appl. 2018, 30, 413–435. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar]
- Qais, M.H.; Hasanien, H.M.; Alghuwainem, S. Enhanced grey wolf optimizer for grid-connected PV system. IEEE Access 2020, 8, 143692–143705. [Google Scholar]
- Chitgreeyan, N.; Marksan, P.; Kongjeen, Y.; Sa-Nga-Ngam, W.; Buayai, K.; Kerdchuen, K.; Marsong, S.; Noppakant, A. An Analysis of the Dg Placement for Primary Radial Distribution System Using Q-Leaning Algorithm. In Proceedings of the 2024 International Conference on Power, Energy and Innovations (ICPEI), Nakhon Ratchasima, Thailand, 16–18 October 2024. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer: Berlin, Germany, 1981. [Google Scholar]
- Sankar, M.M.; Chatterjee, K. A posteriori multiobjective approach for techno-economic allocation of PV and BES units in a distribution system hosting PHEVs. Appl. Energy 2023, 351, 121851. [Google Scholar]
- Opricovic, S.; Tzeng, G.H. The compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar]
- Zeleny, M. Compromise programming. In Multiple Criteria Decision Making; University of South Carolina Press: Columbia, SC, USA, 1973; pp. 262–301. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar]
- Ishibuchi, H.; Pang, L.M.; Shang, K. Solution subset selection for final decision making in evolutionary multi-objective optimization. arXiv 2006, arXiv:2006.08156. [Google Scholar]
- Chitgreeyan, N.; Pilalum, P.; Kongjeen, Y.; Kongnok, R.; Buayai, K.; Kerdchuen, K. Modified MATPOWER for Multi-Period Power Flow Analysis with PV Integration. GMSARN Int. J. 2025, 19, 165–174. [Google Scholar]
- Soliman, I.A.; Tulsky, V.; Abd el-Ghany, H.A.; ElGebaly, A.E. Efficient allocation of capacitors and vehicle-to-grid integration with electric vehicle charging stations in radial distribution networks. Appl. Energy 2025, 377, 124745. [Google Scholar]
- Niu, S.; Yu, H.; Niu, S.; Jian, L. Power loss analysis and thermal assessment on wireless electric vehicle charging technology: The over-temperature risk of ground assembly needs attention. Appl. Energy 2020, 275, 115344. [Google Scholar]
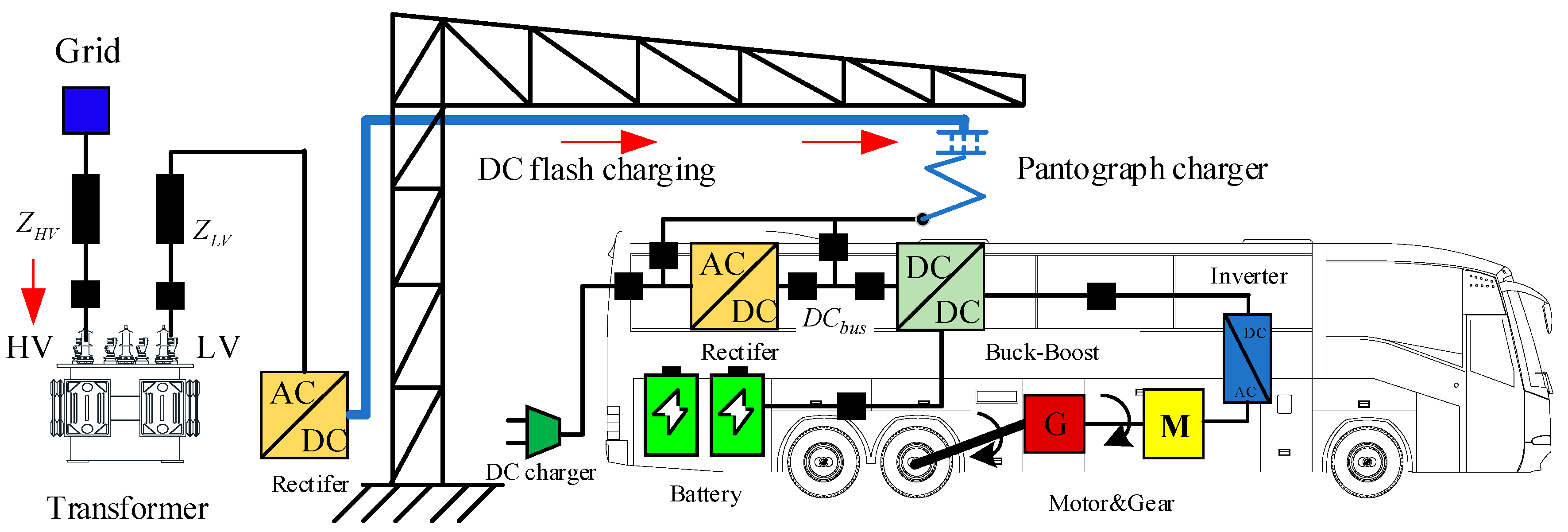









| Charger Type | Power Charger Level (kW) | Charging Time | Application/Use Case | Ref. |
|---|---|---|---|---|
| Depot Charger | 40–150 kW | 4–6 h. | E-bus depot, end-of-line, high-demand E-buses | [33,34] |
| Flash Charger (Pantograph for E-bus) | 600 kW | 20 s–2 min | On-route ultra-fast top-up | [35,36] |
| Fast Charger | 100–600 kW (less common) | 5–10 min (Gas refueling) | Certain bus stop | [33] |
| Criteria | Traditional Single- | Multi-Objective Methods | E-Bus Charging Studies | Recent Integrated Approaches | Proposed MOGWO |
|---|---|---|---|---|---|
| Ref. | [13,14,15,16,17,18,19] | [20,21,22,23,24] | [25,26,27,28,29,30,31] | [32] | |
| Optimization Approach | Single objective | Multiple objectives with | Single objective (charging optimization) | Site selection using spatial MCDA | True multi-objective with Pareto |
| Objective Functions | 1 (Power loss OR | 2–3 (Weighted combination) | 1–2 (Cost/time minimization) | Land use, demand, traffic, grid distance | 3 (Power loss + Voltage deviation + Violations) |
| Weight Selection | Not applicable | Manual/subjective weight assignment | Not applicable | FAHP (fuzzy AHP) weighting | Automatic (Euclidean distance-based) |
| E-Bus Integration | Not considered | Static load assumptions | Detailed charging modeling | Location-based demand assumption | Comprehensive dynamic modeling |
| Charging Dynamics | No charging consideration | No charging patterns | Static charging schedules | Not modeled | Real-time flash charging (600 kW) |
| Route Modeling | Not applicable | Not considered | Simplified routes | Integrated via GIS layers | 31-stop, 62 km realistic route |
| Battery Modeling | Not applicable | Not considered | Basic SOC tracking | Not applicable | Dynamic SOC with constraints |
| Network Constraints | Basic voltage limits | Limited constraint handling | Network treated as passive | Distance to substations only | Comprehensive constraint integration |
| Solution Selection | Single solution | Pareto front provided | Single solution | MABAC method for best site | 5-method consensus selection |
| Decision Support | Minimal | Limited guidance | Problem-specific | Structured MCDA ranking | Comprehensive decision framework |
| Algorithm Type | Not applicable | Manual selection | Not applicable | GIS + FAHP + MABAC | TOPSIS, Euclidean, L2-metric, etc. |
| Optimization Techniques | GA, PSO, ABC | NSGA-II, MOPSO | Heuristic/Mathematical | Multi-Criteria Decision Analysis (MCDA) | Enhanced Grey Wolf Optimizer |
| Convergence | 50–100 | 100–200 | Not applicable | Deterministic MCDA | 100 (Speed up more NSGA-II 31.87%) |
| Scalability | Moderate | Slow (high computational cost) | Fast (simplified problem) | Variable | Fast (50–70 iterations) |
| Validation Scope | IEEE 33/69-bus | IEEE 33/69-bus | Custom networks | National urban planning model (China) | IEEE 33/69-bus with realistic E-bus |
| Real-world Data | Power flow analysis | Multi-objective metrics | Charging performance | GIS, population, traffic data | Comprehensive (Power + E-bus) |
| Time Horizon | Synthetic loads | Theoretical scenarios | Limited real data | Long-term planning | Actual E-bus specifications |
| Fleet Coordination | Static/Peak hour | Static snapshots | Daily scheduling | Not included | 90 min. dynamic simulation |
| Charging Technology | Not applicable | Not considered | Limited coordination | Planning-level assumptions | Multi-bus fleet optimization |
| Performance Metrics | Not applicable | Not considered | Generic charging | GIS scores, distance, land use | Flash charging (1 min. cycles) |
| Visualization | Single metric (loss/voltage) | Multiple but aggregated | Charging-specific metrics | GIS maps + site score layers | Comprehensive multi-dimensional |
| Parameter | Value |
|---|---|
| E-bus system | |
| Battery capacity | 100 kWh |
| Consumption | 2 kWh/km |
| Flash charger | 600 kW (1 min duration) |
| Charger topology | Roof-mounted pantograph charger |
| SOC range | 30–100% |
| Speed | 60 km/h |
| Model type | Discrete-time SOC update based on route and power flow |
| E-bus transits | 3 (E-bus no.1 starts 0 min, E-bus no.2 starts 10 min, E-bus no.2 starts @ 15 min, respectively) |
| Distance per bus stop station | 2 km |
| Flash charging station (Bus no.) | 5, 8, 11, 14, 17, 30, 27, 24, 2 and 20 (10 Station) of IEEE 33 bus |
| 5, 15, 19, 25, 63, 57, 38, 31, 47 and 42 (10 Station) of IEEE 69 bus | |
| Bus stop terminal | S0–S30 (31 Station) |
| Simulation time | 90 min |
| MOGWO | |
| Number of wolves | 100 |
| Max iterations | 100 |
| Possible DG bus No. position [min max] | IEEE 33 bus [2 33] and IEEE69 bus [2 69] |
| Possible DG size [min max] | Active power [0.2 2.5], Reactive power [0.1 0.5] |
| Number of DGs | 1, 2, 3 |
| Criteria | IEEE 33 Bus | IEEE 69 Bus | ||||
|---|---|---|---|---|---|---|
| 1 DG Unit | 2 DG Units | 3 DG Units | 1 DG Unit | 2 DG Units | 3 DG Units | |
| Total DG Capacity (Compromise) (MW) | 2.2869 | 2.7782 | 3.3407 | 2.3317 | 2.7657 | 2.8094 |
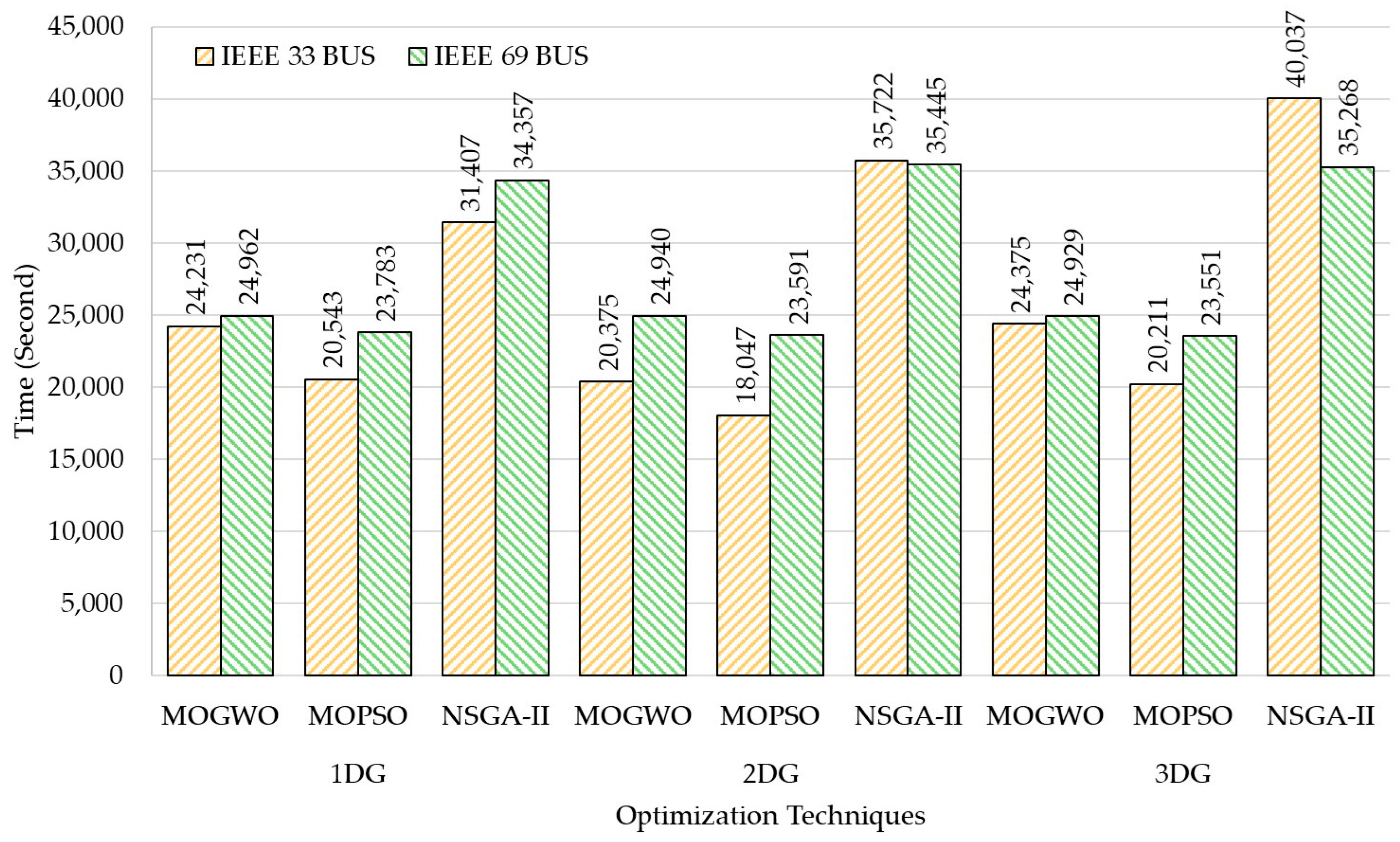
| Optimization Time (s) | 24,231.26 | 24,328.37 | 24,374.62 | 24,961.60 | 24,940.00 | 24,928.99 |
| Pareto Solutions Found | 100 | 100 | 66 | 100 | 91 | 77 |
| Average Inter-Solution Distance | 20.9879 | 10.0189 | 9.8451 | 5.8973 | 9.4496 | 10.2396 |
| Objective | IEEE 33 Bus | IEEE 69 Bus | ||||
|---|---|---|---|---|---|---|
| 1 DG Unit | 2 DG Units | 3 DG Units | 1 DG Unit | 2 DG Units | 3 DG Units | |
| Power Loss (MW) | 0.0950 | 0.0451 | 0.0279 | 0.0543 | 0.0313 | 0.0179 |
| Voltage Deviation | 0.4827 | 0.1847 | 0.1313 | 0.6282 | 0.1509 | 0.1362 |
| Voltage Violations | 39 | 0 | 0 | 61 | 0 | 0 |
| Testing System | No. of DGs Placement | Locations (Bus No.) | Active Powers (MW) | Reactive Powers (MVar) | Total Power Loss (MW) | Voltage Deviation | Violations | Quality Score |
|---|---|---|---|---|---|---|---|---|
| IEEE 33 bus | 1 DG | 9 | 2.2869 | 0.5000 | 0.1202 | 0.5284 | 57 | 0.7055 |
| 2 DG | 14, 28 | 1.1254, 1.6528 | 0.4971, 0.5000 | 0.0602 | 0.2840 | 11 | 0.6300 | |
| 3 DG | 23, 13, 30 | 0.9154, 1.2387, 1.1866 | 0.4774, 0.5000, 0.4817 | 0.0385 | 0.2496 | 11 | 0.06348 | |
| IEEE 69 bus | 1 DG | 60 | 2.3317 | 0.5000 | 0.0607 | 0.6554 | 67 | 0.6984 |
| 2 DG | 21, 60 | 0.6993, 2.0664 | 0.3420, 0.4959 | 0.036351 | 0.241040 | 18 | 0.6322 | |
| 3 DG | 60, 64, 17 | 1.6766, 0.2000, 0.9327 | 0.4537, 0.4460, 0.3892 | 0.0221 | 0.3026 | 13 | 0.6540 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kongjeen, Y.; Pilalum, P.; Deeum, S.; Suthamno, K.; Klayklueng, T.; Marsong, S.; Ratchapan, R.; Buayai, K.; Kerdchuen, K.; Sa-nga-ngam, W.; et al. Multi-Objective Optimization of Distributed Generation Placement in Electric Bus Transit Systems Integrated with Flash Charging Station Using Enhanced Multi-Objective Grey Wolf Optimization Technique and Consensus-Based Decision Support. Energies 2025, 18, 3638. https://doi.org/10.3390/en18143638
Kongjeen Y, Pilalum P, Deeum S, Suthamno K, Klayklueng T, Marsong S, Ratchapan R, Buayai K, Kerdchuen K, Sa-nga-ngam W, et al. Multi-Objective Optimization of Distributed Generation Placement in Electric Bus Transit Systems Integrated with Flash Charging Station Using Enhanced Multi-Objective Grey Wolf Optimization Technique and Consensus-Based Decision Support. Energies. 2025; 18(14):3638. https://doi.org/10.3390/en18143638
Chicago/Turabian StyleKongjeen, Yuttana, Pongsuk Pilalum, Saksit Deeum, Kittiwong Suthamno, Thongchai Klayklueng, Supapradit Marsong, Ritthichai Ratchapan, Krittidet Buayai, Kaan Kerdchuen, Wutthichai Sa-nga-ngam, and et al. 2025. "Multi-Objective Optimization of Distributed Generation Placement in Electric Bus Transit Systems Integrated with Flash Charging Station Using Enhanced Multi-Objective Grey Wolf Optimization Technique and Consensus-Based Decision Support" Energies 18, no. 14: 3638. https://doi.org/10.3390/en18143638
APA StyleKongjeen, Y., Pilalum, P., Deeum, S., Suthamno, K., Klayklueng, T., Marsong, S., Ratchapan, R., Buayai, K., Kerdchuen, K., Sa-nga-ngam, W., & Bhumkittipich, K. (2025). Multi-Objective Optimization of Distributed Generation Placement in Electric Bus Transit Systems Integrated with Flash Charging Station Using Enhanced Multi-Objective Grey Wolf Optimization Technique and Consensus-Based Decision Support. Energies, 18(14), 3638. https://doi.org/10.3390/en18143638












