Abstract
In view of the limitations of traditional offline detection and external excitation online detection of 10 kV cables, this paper proposes a method to evaluate the insulation aging condition of power cables by online measuring of the phase angle of the cable’s ground current, and explores the impact of load fluctuations on cable insulation. By setting the relative permittivity of the cable to characterize the phase variation of the ground current under different aging degrees, and analyzing the phase variation of the cable’s ground current under different load changes at the same aging degree, a load correction-based dynamic dielectric loss evaluation method for cables is proposed. Through the construction of cable simulation models and the processing of field data, the following conclusions have been reached: Under a 1 MW load, the phase angle of the sheath grounding current in the aged phase increases as the dielectric constant of the insulation increases. At the same aging degree, with an increase in load, the phase differences of the aging phase sheath ground current and the steel armor ground current both show a decreasing trend. To eliminate the impact of load, a dynamic dielectric loss load correction method is proposed, and combined with field data analysis, the dynamic dielectric loss of cables under different loads is corrected to a 1 MW load. Specifically: Under 0.3 MW, the correction coefficients k for the sheath and steel armor are 0.609 and 0.778, respectively. Under 3.5 MW, the correction coefficients k for the sheath and steel armor are 1.435 and 1.089, respectively. This study provides a theoretical basis and experimental verification for online cable monitoring methods.
1. Introduction
Due to the rapid development of urbanization, underground cables play an increasingly vital role in urban power supply and are widely used [1]. However, power cables have inherent drawbacks, such as unstable insulation performance during manufacturing, potential insulation damage due to collisions during installation, and long-term exposure to humid underground environments that can lead to water tree aging [2,3], as shown in Figure 1. Statistics show that 32% of urban distribution cables in China have been in operation for over 15 years, and insulation aging accounts for more than 47% of total cable failures. These issues cause insulation degradation, significantly reducing performance and leading to insulation breakdown accidents [4]. It can be seen that the aging of cables has a non-negligible impact on the normal operation of the power grid. Effective fault detection of cables should be carried out as soon as possible to prevent serious losses.

Figure 1.
Insulation damage caused by overheating and moisture.
Extensive research has been conducted on cable insulation aging detection [5,6,7,8]. For example, reference [9] studied water tree and thermal aging in cable insulation, simulating aging experiments on power cable samples and determining aging levels by comparing tanδ-φ curves under different aging conditions. In reference [10], tensile, breakdown strength, infrared spectroscopy, and dielectric spectroscopy tests were performed on XLPE cables, establishing relationships between aging time and parameters such as tensile strength, breakdown strength, hydroxyl index, and dielectric loss factor. Reference [11] proposed an oscillating wave partial discharge detection method for high-voltage XLPE cables using LSTM algorithms, which locates defects by analyzing the time differences between the original and reflected waves. Reference [12] provides a detailed introduction to partial discharge detection methods, including the offline detection of AC test, VLF test, and DAC test, as well as online detection methods such as HFCT, VHF, AE, etc., and introduces their principles and applicability. Although these studies achieved results, most of the offline detection methods are destructive, and have the disadvantages of large test equipment and high operation requirements. Moreover, the online detection methods are affected by serious electromagnetic interference and signal attenuation [13,14,15]. Research on reliable online detection without external excitation remains scarce [16,17,18]. Based on this, this paper aims to propose an online detection method for the variation of the grounding current phase angle of power cables with aging. This method does not require external excitation and compares the phase angle relationships of cable grounding currents under different degrees of simulated aging through simulations and experiments, in order to determine the aging status of the cable.
However, in practical engineering applications, changes in the load side of cable lines can have a certain degree of impact on cable insulation. When the load side equipment runs for a long time, a large amount of heat will be generated and conducted to the cable, causing a sharp increase in cable temperature. High temperature conditions can accelerate the thermal aging process of cable insulation materials, reducing their tensile and bending strength and making them more susceptible to mechanical damage and insulation breakdown [19,20,21]. And when the load size changes, it will directly cause a change in the current size of the cable, thereby causing a change in the phase angle of the cable’s ground current. Therefore, this article establishes aging models for power cables under different loads, analyzes the influence of load on the phase angle of the ground current with aging, and proposes a method for dynamic dielectric loss load correction. By combining field data collection with analysis, the dielectric loss measurements under different load conditions are normalized to a 1 MW reference, thereby mitigating the influence of load variations on detection accuracy. The results can provide a reference for online detection of aging in power cables.
2. Phase Analysis Model for 10 kV Three-Core Pipe-Type Cables
This section builds a 10 kV three-phase cable model based on simulation software, and simulates cable aging by changing the relative dielectric constant of its insulation layer.
2.1. Cable Simulation Model
The 10 kV cable simulation model, shown in Figure 2, consists of a power supply side, input side, and load side. The power supply uses a 110 kV three-phase ideal source, stepped down to a 10 kV equivalent source. The output connects to a 1 MW load to simulate actual usage, while the input side includes current transformers to capture shielding layer and armor grounding currents.
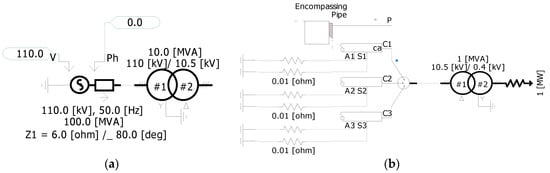
Figure 2.
Simulation model of 10 kV distribution network power cable: (a) power supply side; (b) load side.
2.2. Cable Structure and Aging Simulation
The three-phase cable arrangement and single-cable structure are depicted in Figure 3. A single cable comprises a conductor, inner semiconductor layer, insulation layer, outer semiconductor layer, metal shielding layer, filler layer, inner sheath, armor layer, and outer sheath.
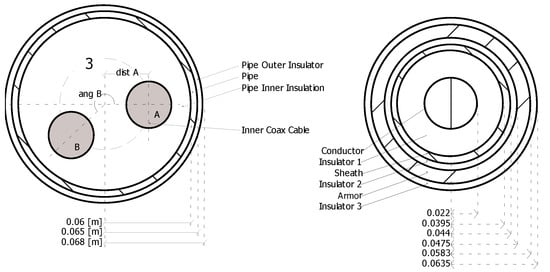
Figure 3.
Structure of 10 kV three-core pipe-type cable.
The simulation focuses on phase angle changes in grounding currents after aging, considering non-uniform single-phase aging. Aging is simulated by adjusting the relative permittivity of the insulation layer: the non-aged phases are set to 2.0, while the aged phase is set to 2.0, 2.4, 2.8, 3.2, and 5.0 to observe phase angle variations in the shielding and armor grounding currents [15].
3. Analysis of Grounding Current Phase Angle Under Cable Aging
In the study of the cable to ground current phase angle, by analyzing the changes in the angle’s amplitude, the aging condition and specific aging phase of cable insulation can be determined. Therefore, in this section, which covers research on the impact of load side on cable insulation, we choose to compare and analyze the changes in the cable to ground current phase angle under single-phase non-uniform aging conditions to verify the sensitivity of the grounding current phase angle to cable insulation aging characteristics and the accuracy of determining the cable insulation’s aging phase.
3.1. Phase Angle Analysis Under 1 MW Load
In simulations using a 1 MW load, the phase angle data for the sheath grounding current of the aged phase (A-phase) is extracted, as shown in Figure 4.
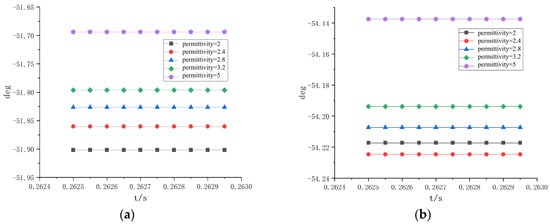
Figure 4.
Grounding current phase angles for aged A-phase: (a) sheath grounding current phase angle; (b) armor grounding current phase angle.
By observing the phase angle changes in the above figure, it can be seen that as the dielectric constant gradually increases from 2 to 5, the phase angle of the aging A-phase sheath to ground current increases from −51.9° to −51.69°, while the phase angle of the steel armor to ground current increases from −54.21° to −54.13°. The amplitude changes of the phase angles of the two currents are 0.21° and 0.09°, respectively, and the phase angle of the sheath current shows a gradually increasing trend. Through comparative analysis, it can be clearly observed that the amplitude change of the phase angle of the sheath to ground current is greater. To further investigate the current phase angle changes of the cable, a phase angle graph of the ground current for phase B of the unaged cable was drawn, as shown in Figure 5.
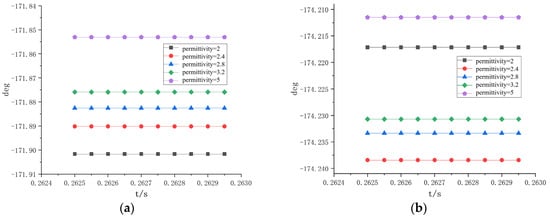
Figure 5.
Grounding current phase angles for non-aged B-phase: (a) sheath grounding current phase angle; (b) armor grounding current phase angle.
From the above figure, it can be seen that as the dielectric constant increases, the phase angle of the unaged B-phase sheath to ground current increases from −171.9° to −171.85°, while the phase angle of the steel armor to ground current increases from −174.217° to −174.211°. The amplitude changes of the current phase angles of the two are 0.05° and 0.006°, respectively. It can be seen that the amplitude changes of the phase angle of the unaged B-phase are relatively small, and the trends of the phase angle changes of the sheath and steel armor currents are inconsistent.
3.2. Phase Angle Analysis Under 2 MW Load
Analogous to the above analysis method, the parameters on the load side are simulated to be 2 MW. By simulating the uneven aging state of the cable, the current phase angle characteristics of cable aging phase A are analyzed, as shown in Figure 6.
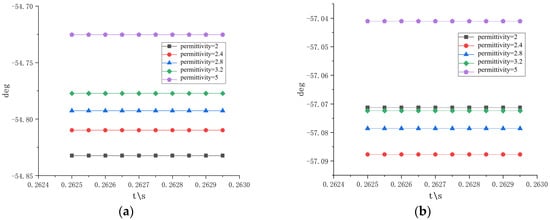
Figure 6.
Grounding current phase angles for aged A-phase: (a) sheath grounding current phase angle; (b) armor grounding current phase angle.
After comparing the above subfigures, it can be seen that as the dielectric constant increases, the phase angle of the cable sheath to ground current increases from −54.83° to −54.72°, while the phase angle of the steel armor to ground current increases from −57.07° to −57.04°. The increases in the phase angle amplitude of the two are 0.11° and 0.03°, respectively. By analyzing the trend of the current phase angle changes in aging phase A, it can be seen that the sheath to ground current phase angle shows a gradually increasing trend, while the changes in the steel armor to ground current phase angle are relatively irregular, and the two trends do not reflect consistency. In order to compare the phase angle variation characteristics of the aged and unaged phases of cables more specifically, a current phase angle variation diagram of the unaged phase B was drawn, as shown in Figure 7.
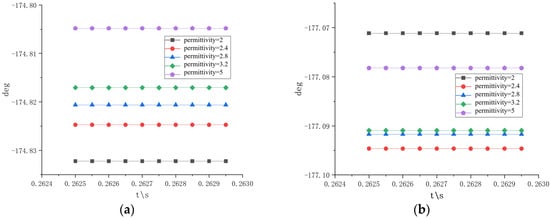
Figure 7.
Grounding current phase angles for aged A-phase: (a) sheath grounding current phase angle; (b) armor grounding current phase angle.
By observing the amplitude changes of the current phase angle during the cable’s B phase, it can be seen that as the dielectric constant increases, the phase angle of the sheath to ground current increases from −174.83° to −174.80°, while the phase angle of the steel armor to ground current decreases from −177.07° to −177.08°. The amplitude changes of the two phase angles are 0.03° and −0.01°, respectively. From the data in the above figure, it can be seen that the phase angle change during the unaged B-phase is relatively small, and there is no correlation between the phase angle change characteristics of the sheath and steel armor currents.
3.3. Phase Angle Analysis Under Different Loads
As can be seen from the previous text, when the cable ages, the phase angle of the grounding current of the cable shows a regular change as the degree of aging increases. Different cable loads can have a certain impact on this pattern, such as changes in the phase angle difference. In order to explore the influence of different loads on the online monitoring of the aging status of the grounding current phase angle of the cable, this section sets four different load side parameters of 0.5 MW, 1 MW, 1.5 MW, and 2 MW for cables under four different working conditions, and compares the phase angle change patterns of the cables under aging compared to normal conditions.
We simulated single-phase aging conditions under four different loads, with a dielectric constant of 2.8 for the aging cable. The phase difference between the grounding currents under normal conditions is shown in Figure 8.
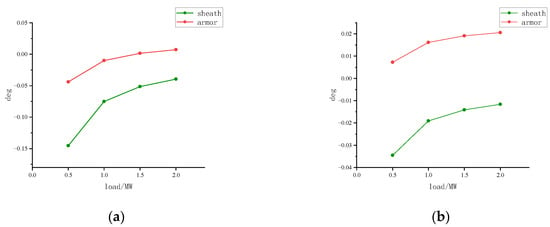
Figure 8.
Grounding current phase differences under different loads: (a) aged phase cable; (b) non-aged phase cable.
As the load increases, the phase difference for the aged phase decreases: the sheath phase difference is reduced from −0.145° to −0.039°, and the armor phase difference decreases from −0.044° to 0.007°. For the non-aged phase, the sheath phase difference decreases from −0.035° to −0.011°, while the armor phase difference increases from 0.007° to 0.02°. The sheath phase difference is most affected by load changes, indicating that load variations can influence the accuracy of online aging detection.
4. Dynamic Dielectric Loss Correction Method Under Different Loads
To mitigate load interference, a dynamic dielectric loss correction method is proposed.
4.1. Dynamic Dielectric Loss Calculation
A vector diagram of three-phase cable currents is shown in Figure 9.
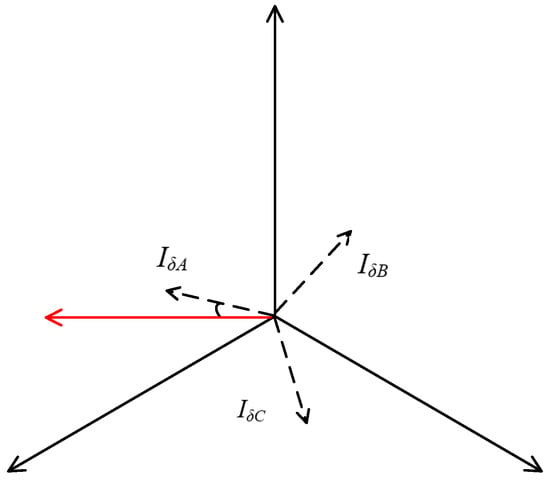
Figure 9.
Cable current phase vector diagram.
Here, IA, IB, and IC are the main currents, while , , and are the grounding currents. The dynamic dielectric loss angle δ is defined as the complement of the angle between the grounding current and the main current:
Under normal cable conditions, distributed capacitance is formed between the conductor of the cable and the insulation and shielding layers. When the insulation is fine, the resistive component of the leakage current is extremely small, while the capacitive component dominates. Therefore, the phase difference between the grounding current and the main current is about 90°. When the cable ages, the insulation resistance decreases, the resistive component of the leakage (grounding) current increases, and the grounding current changes from being mainly capacitive to exhibiting a mixture of resistance and capacitance, resulting in a decrease in the phase difference between the grounding current and the main current, that is, an increase in the dynamic dielectric loss angle and an increase in the dynamic dielectric loss tan. When the cable load increases, the main current increases and the cable heats up, causing changes in insulation resistance and also causing changes in . Therefore, this section studies the method of dynamic dielectric loss discrimination for insulation aging based on load correction, and summarizes its variation pattern through analysis of field data.
4.2. Cable Current Signal Collection and Analysis
The signal of the grounding current of the cable box during the operation of a branch line is collected by using clamp-type transformers and oscilloscopes. A diagram of the current field collection model and a photo of it in the field are shown in Figure 10. The 10 kV branch coaxial cable is transmitted through underground cables, and each phase cable is stripped and led out to the ring-shaped main unit. The model used is ZR-YJV22-8.7/15-3X400. By using current transformers to collect the main current of the cable, the grounding current of the steel cable and the grounding current of the external shield can be used to obtain the current signals.

Figure 10.
Underground cable model and field photo: (a) current collection model; (b) field collection.
The test cable parameters are shown in Table 1. The experiment used three cables with the same operating years under the same branch line. According to the on-site introduction, the F70 cable was used for residential electricity, the F71 cable distributed energy to commercial stores, and the F72 cable was used to supply power to roadside lighting lamps. Due to the on-site time period and relevant personnel, the approximate load situation was understood, and the copper shielding (sheath) grounding current and armor grounding current signals were collected separately.

Table 1.
Test cable parameters.
The phase and dynamic dielectric loss angles of the current signal collected and processed by the oscilloscope are shown in Table 2.

Table 2.
Collected phase and dielectric loss angles.
Based on the above dielectric loss angle calculation method, the dynamic dielectric loss under different loads is normalized and corrected according to a 1 MW load. The correction coefficient k is as follows:
In the formula, represents the dynamic dielectric loss angle under different loads, and represents the dynamic dielectric loss angle under a load of 1 MW. The dynamic dielectric loss and the correction factor are obtained as shown in Table 3.

Table 3.
Dynamic dielectric loss and correction coefficients.
In summary, by correcting the dynamic dielectric loss under different loads, normalized dynamic dielectric loss values can be obtained to evaluate cable aging and eliminate the influence of load on signal acquisition.
5. Conclusions
This paper investigates the phase angle changes of grounding currents in 10 kV three-core cables under aging and varying loads, analyzes the impact of load on aging assessment, and proposes a dynamic dielectric loss correction method. The key conclusions are as follows:
- For single non-uniform aging, the phase of the grounding current of the aging phase sheath shows an increasing trend with increases in the dielectric constant, and the change amplitude is significantly greater than that of the non-aging phase, which can indicate a change in the phase of the aging state.
- Observing the simulation of cable aging under 1 MW and 2 MW loads, the phase angle of the grounding current of the steel cable first decreases and then increases with the deepening of cable aging, and there is no overall regularity. However, the amplitude of the phase angle change of the grounding current during the aging phase of the steel cable is greater than that of the non-aging phase, which can be used to distinguish aged cables.
- When the degree of cable aging is the same, the phase angle changes of the cable grounding current are different under different loads. As the cable load increases, the phase difference of the aging phase grounding current shows a gradually decreasing trend. The phase difference of the sheath grounding current decreases from −0.145° to −0.039°, the phase difference of the armor grounding current decreases from −0.044° to 0.007°, the phase difference of the non-aging phase sheath grounding current decreases from −0.035° to −0.011°, and the phase difference of the armor grounding current increases from 0.007° to 0.02°. Therefore, it can be seen that the load size of the cable will, to some extent, affect the accuracy of online monitoring of cable aging based on the phase difference of the grounding current.
- By defining the dynamic dielectric loss angle , a correction coefficient k based on load normalization is proposed. Experimental data shows that under different loads, the dynamic dielectric loss needs to be normalized to a 1 MW benchmark through the correction coefficient k to eliminate load interference and improve the accuracy of aging assessment under different load conditions.
The phase change of the grounding current can, to some extent, characterize cable aging, of which the phase difference of the sheath current is a key indicator, but it needs to be corrected based on actual load conditions to improve accuracy. This research provides a theoretical basis and experimental verification for online cable detection methods.
Author Contributions
Conceptualization, G.L. and T.Y.; methodology, Y.Z., D.Z., and T.Y.; software, G.L., Y.Z., and P.C.; validation, G.L. and T.Y.; formal analysis, D.Z. and Y.C.; investigation, P.C. and Y.C.; resources, G.L.; data curation, T.Y.; writing—original draft preparation, G.L.; writing—review and editing, Y.Z.; supervision, G.L. and T.Y.; project administration, D.Z.; funding acquisition, D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science Foundation of State Grid Jiangsu Electric Power Company (J2023101).
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Acknowledgments
The authors would like to express their gratitude to Nanjing Institute of Technology for their assistance with this research.
Conflicts of Interest
Authors Gang Liu, Yuanming Zhang, Peigen Cao and Yulan Che were employed by the company State Grid Suqian Power Supply Company. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Li, C.Y.; Tan, X.; Liu, L.G.; Zhang, W.; Yang, Q.M.; Cao, J.Y.; Zhou, E.C.; Li, M.Z.; Song, Z.X. Investigation of Near-Infrared Spectroscopy for Assessing the Macroscopic Mechanical Properties of Cross-Linked Polyethylene During Thermal Aging. Materials 2025, 18, 504. [Google Scholar] [CrossRef] [PubMed]
- Afia, R.S.A.; Mustafa, E.; Tamus, Z.A. Comparison of Mechanical and Low-Frequency Dielectric Properties of Thermally and Thermo-Mechanically Aged Low Voltage CSPE/XLPE Nuclear Power Plant Cables. Electronics 2021, 10, 2728. [Google Scholar] [CrossRef]
- Zhu, X.; Yin, Y.; Wu, J.D.; Wang, X.F. Study on Aging Characteristics of XLPE Cable Insulation Based on Quantum Chemical Calculation. IEEE Trans. Dielectr. Electr. Insul. 2020, 27, 1942–1950. [Google Scholar] [CrossRef]
- Yang, J.; Li, R.Z.; Hu, L.Y.; Wang, W.W. Influence of Thermal Aging on Space Charge Characteristics and Electrical Conduction Behavior of Cross-Linked Polyethylene Cable Insulation. Polymers 2024, 16, 1600. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.F.; Wei, J.H.; Huang, F.B.; Wu, Q.; Tao, X.F.; Wu, K.; Li, Q.; Xue, J.Y. Identification of local thermal aging defects in power cables based on frequency domain reflection coefficient spectroscopy method. J. Phys. Conf. Ser. 2024, 2917, 012007. [Google Scholar] [CrossRef]
- Wang, R.; Pan, R. A Cable Defect Assessment Method Based on a Mixed-Domain Multi-Feature Set of Overall Harmonic Signals. Energies 2025, 18, 83. [Google Scholar] [CrossRef]
- Zhou, K.; Yuan, H.; Li, Y.; Li, M.Z.; Li, Z.R.; Lin, S.Y. Assessing Aging Status and Type of XLPE Cable Insulation With a Graphic Approach Based on PDC Measurement. Ieee Trans. Power Deliv. 2022, 37, 5114–5123. [Google Scholar] [CrossRef]
- Jahromi, A.N.; Pattabi, P.; Densley, J.; Lamarre, L. Medium voltage XLPE cable condition assessment using frequency domain spectroscopy. Ieee Electr. Insul. Mag. 2020, 36, 9–18. [Google Scholar] [CrossRef]
- Kim, C.; Jin, Z.; Huang, X.; Jiang, P.; Ke, Q. Investigation on water treeing behaviors of thermally aged XLPE cable insulation. Polym. Degrad. Stab. 2007, 92, 537–544. [Google Scholar] [CrossRef]
- Ma, F.; Zhang, C. Diagnostic Methods for Insulation Aging of Cross-Linked Polyethylene Cables. Beijing Polytech. Vocat. Coll. 2022, 21, 11–16. [Google Scholar]
- Han, X. Oscillating Wave Partial Discharge Detection Method for High-Voltage Cross-Linked Cable Lines Based on the LSTM Algorithm. Electr. Mach. Control Appl. 2022, 49, 41–46+80. [Google Scholar]
- Suganya, G.; Adolfo, M.; Alfredo, J.A.; Narasimman, P. A review on partial discharge diagnosis in cables: Theory, techniques, and trends. Measurement 2023, 216, 112882. [Google Scholar]
- Fu, H.; Qiu, L.; Ai, Y.H.; Tu, J.; Yan, Y.T. Deep learning-based fault detection and location in underground power cables using resonance frequency analysis. Electr. Eng. 2024, 107, 1–12. [Google Scholar] [CrossRef]
- Nilsson, D.J.; Gubanski, S.M.; Serdyuk, Y.V. Electrical Detection of Degradation in Specimens of HVDC Cable Insulation. Energies 2020, 13, 3963. [Google Scholar] [CrossRef]
- Chen, C.; Cheng, C.H.; Wang, X.; Wu, K. Space Charge Characteristics for XLPE Coaxial Cable Insulation Under Electrothermal Accelerated Aging. IEEE Trans. Dielectr. Electr. Insul. 2022, 29, 727–736. [Google Scholar]
- Wang, Y.; Zhao, A.; Zhang, X.; Shen, Y.; Yang, F.; Deng, J.; Zhang, G. Study of Dielectric Response Characteristics for Thermal Aging of XLPE Cable Insulation. In Proceedings of the International Conference on Condition Monitoring and Diagnosis (CMD), Xian, China, 25–28 September 2016; pp. 602–605. [Google Scholar]
- Chen, H.; Wang, J.J.; Hu, H.J.; Li, X.F.; Huang, Y.Y. Aging Detection of 110 kV XLPE Cable for a CFETR Power Supply System Based on Deep Neural Network. Energies 2022, 15, 3127. [Google Scholar] [CrossRef]
- Wang, X.; Liu, E.H.; Zhang, B. Reflectometry-Based Cable Insulation Aging Diagnosis and Prognosis. IEEE Trans. Ind. Electron. 2022, 69, 4148–4157. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, X.L. Insulation Performance Evaluation of HV AC/DC XLPE Cables by 0.1 Hz Tan δ Test on Circumferentially Peeled Samples. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 3941–3950. [Google Scholar] [CrossRef]
- Rizwan, T.; Ibrahim, A.; Ur, R.A.; Elsayed, T.E.; Muhammad, S.; Ghamry, N.A.; Habib, H. An Optimized Solution for Fault Detection and Location in Underground Cables Based on Traveling Waves. Energies 2022, 15, 6468. [Google Scholar] [CrossRef]
- Sebbane, Y.; Boubakeur, A.; Mekhaledi, A. Influence of Thermal Aging and Water Adsorption on XLPE Cables Insulation Mechanical and Physico-chemical Properties. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 1694–1702. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).