Abstract
The horizontal tube falling film heat exchangers (HTFFHEs), which exhibit remarkable advantages such as high efficiency in heat and mass transfer, low resistance, and a relatively simple structural configuration, have found extensive applications. Complex flow phenomena and the coupled processes of heat and mass transfer take place within it. Given that the heat and mass transfer predominantly occur at the gas-liquid interface, the flow characteristics therein emerge as a significant factor governing the performance of heat and mass transfer. This article elaborates on the progress of experimental and simulation research approaches with respect to flow characteristics. It systematically reviews the influence patterns of various operating parameters, namely parameters of gas, solution and internal medium, as well as structural parameters like tube diameter and tube spacing, on the flow characteristics, such as the flow regime between tubes, liquid film thickness, and wettability. This review serves to furnish theoretical underpinnings for optimizing the heat and mass transfer performance of the horizontal tube falling film heat exchanger. It is further indicated that the multi-dimensional flow characteristics and their quantitative characterizations under the impacts of different airflow features will constitute the focal research directions for horizontal tube falling film heat exchangers in the foreseeable future.
1. Introduction
The horizontal-tube falling film heat exchangers (HTFFHEs) offer several advantages and are widely used in several applications. The advantages include high thermal and mass transfer efficiency, flexible design options, low resistance, simple structure, and a long operational lifespan. Depending on the temperature of the fluid inside the tubes, it can be applied in both absorption and evaporation processes, and is widely used in traditional applications such as refrigeration and air conditioning [1], seawater desalination [2], chemical production [3], and crop drying [4]. In recent years, with the increasing emphasis on achieving carbon peak and carbon neutrality, have gained significant attention in the recovery of waste heat within energy systems [5,6,7] and in energy conservation and emission reduction efforts.
The principles of absorption and evaporation in HTFFHEs are as follows: In the absorption process of HTFFHEs, the solution forms a falling film on the tube outer surface under the influence of gravity, which directly contacts wet air, flue gas, or water vapor. The absorption process is driven by the difference in vapor pressures between the liquid film and the surrounding gas phase, facilitating mass transfer at the gas-liquid interface. Meanwhile, a cooling fluid flows through the inner tube to absorb the heat generated by the absorption process. In contrast, during the evaporation process, a high-temperature fluid flows through the inner tube, while a falling liquid film forms on the outer surface. Heat is transferred from the inner heating fluid to the outer falling film, causing it to evaporate. In both absorption and evaporation, the heat exchanger undergoes a complex coupling of flow dynamics, heat transfer, and mass transfer.
The flow characteristics of HTFFHEs are crucial for the heat and mass transfer efficiency. At low flow rates, “dry spots” may form on the tube surface, leading to incomplete wetting, while at high flow rates, the liquid film becomes thicker, increasing thermal resistance and impeding efficient heat and mass transfer, as illustrated in Figure 1a. As the flow rate increases, the liquid flow transitions through various basic flow patterns, such as droplets, columns, and sheets, between the tubes. Since absorption occurs at the gas-liquid interface, the position and dynamics of this interface vary with different flow regimes, affecting the mass transfer process, as shown in Figure 1b. Additionally, the direction and velocity of the gas flow play significant roles in determining the rates of heat and mass transfer. Notably, when non-absorbed gases are present, an inert gas film may form on the film surface, disrupting the local vapor pressure at the gas-liquid interface and increasing mass transfer resistance, as depicted in Figure 1c. Thus, the interaction between the falling film flow and the heat and mass transfer on the tube outer surface is highly complex. The flow characteristics, in particular, are critical factors influencing the overall performance of HTFFHEs, and this coupling remains a central focus of ongoing research aimed at optimizing heat and mass exchange efficiency.
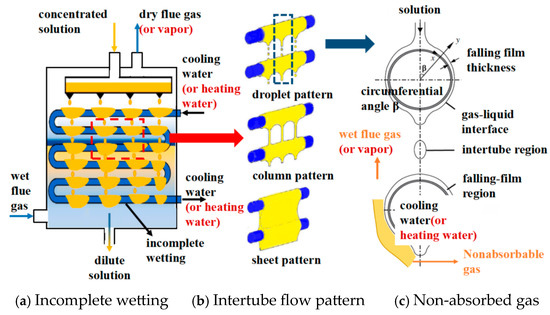
Figure 1.
Local flow characteristics of the falling film on horizontal tubes.
Compared with the review articles on HTFFHE in the past five years [8,9,10,11,12,13], as shown in Table 1, the main difference of this article is that the research fields not only include absorption refrigeration, falling film evaporation, and seawater distillation, but also include chemical production, crop drying, and waste heat recovery; In terms of research objects, a more in-depth analysis of the flow characteristics of falling film evaporation and absorption processes was conducted from the perspective of qualitative and quantitative fitting of relevant equations, and a review of the wetting characteristics of falling films was conducted; In terms of research methods, it covers multiple approaches, including experiments and simulations.

Table 1.
Comparison of the literature review on HTFFHEs in the past five years.
2. Review Methods
The study of falling film flow behavior on the exterior of horizontal tubes primarily focuses on aspects such as inter-tube flow patterns, liquid film thickness, and wettability. These investigations include both experimental approaches and numerical simulations. The articles selected in this review are based on databases such as Web of Science, PubMed, and Google Scholar, covering nearly 15 years of research from 2010 to 2025. The screening criteria include peer-reviewed journal articles.
Regarding liquid film thickness measurement, experimental techniques have evolved significantly over time. Table 2 summarizes the working principles, conditions of applicability, and the advantages and limitations of various measurement methods. In the early stages, direct-contact techniques such as electrical conductivity probes— both insertion-type and embedded-type—were commonly employed to measure liquid film thickness. Hou et al. [14], Tan [15], Zhang et al. [16], and Zhao [17] used insertion-type conductivity probes (illustrated in Figure 2), where the probe is immersed in the liquid film. The resistance between two parallel electrodes correlates to the liquid film thickness, based on the difference in electrical conductivity between the liquid and the surrounding air. While this method is simple and easy to apply, it suffers from relatively low accuracy due to factors such as probe size, fluid temperature, and the disturbance of the liquid film flow. The probe can cause a localized thickening of the film near its surface due to surface tension effects. To minimize such disturbances, Guo et al. [18] introduced an embedded bipolar conductivity probe method, where a cylindrical metal wire (1.5 mm in diameter) is embedded into a falling film tube with an outer diameter of 3.0 mm and an inner diameter of 2.0 mm. This probe consists of an anode and cathode connected to a power supply, as shown in Figure 3. This method improves measurement accuracy compared to the insertion-type probe, but it is more complex to manufacture and has limited applicability. In summary, contact-based electrical conductivity probes are primarily suitable for scenarios involving conductive and relatively thick liquid films.

Table 2.
Liquid film thickness measurement method.
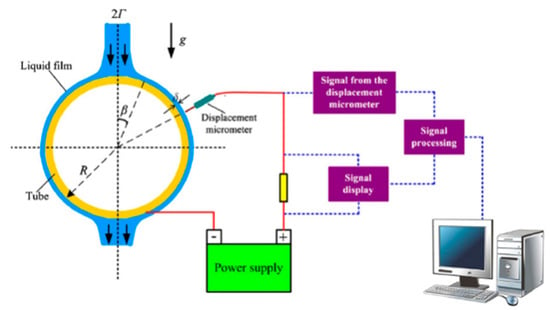
Figure 2.
The principle of the inserted conductivity probe method in Ref. [14] (Hou, 2012).
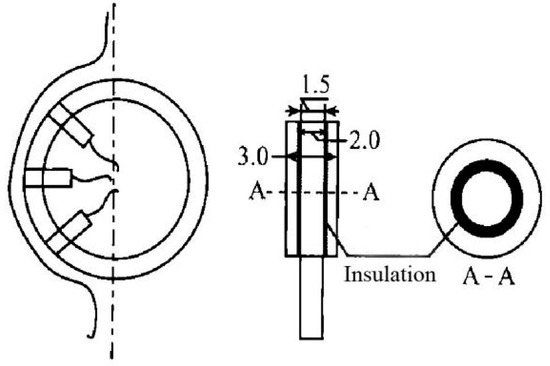
Figure 3.
The principle of the embedded conductivity probe method in Ref. [18] (Guo, 2011).
To avoid disrupting the flow of the liquid film, non-contact methods have been developed. The principal advantage of these techniques is their ability to measure the liquid film thickness distribution and fluctuations without disturbing the flow. Xu et al. [19] and Yu et al. [20] applied capacitive measurement methods to determine liquid film thickness, as shown in Figure 4. In this approach, a metal plate is placed parallel to the tube wall, forming a capacitor, with the capacitance related to the liquid film thickness. This method is non-intrusive and simple in design, but is sensitive to disturbances such as droplet formation and splashing, which can lead to significant errors. With advances in optical technology, non-contact methods such as spectroscopic confocal displacement, fluorescence intensity, and laser-induced fluorescence techniques have been widely utilized. Hazuku et al. [21], Lei et al. [22], Han and Shikazono [23], and Chen et al. [24] employed the spectroscopic confocal displacement method (shown in Figure 5) to measure liquid film thickness. The principle behind this technique is based on lens dispersion and focused imaging. A point light source located above the liquid film emits light that disperses into different wavelengths and focuses at various axial positions along the optical axis. When the monochromatic light at a specific wavelength focuses on the liquid film, it is reflected back and captured by a spectrometer. The position of the spectral peak corresponds to the axial distance of the film, enabling the determination of its thickness.
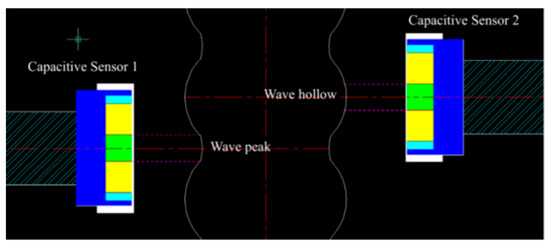
Figure 4.
The principle of the capacitance method in Ref. [20] (Yu, 2017).
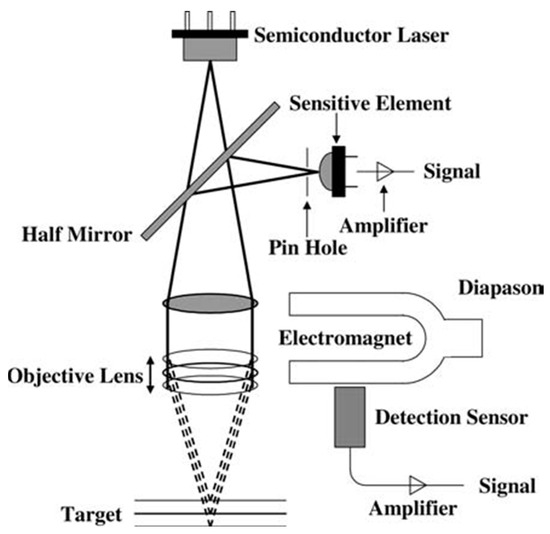
Figure 5.
The principle of the spectral confocal displacement meter method in Ref. [21] (Hazuku, 2004).
This method offers high measurement accuracy, with a laser focus displacement meter achieving a resolution of 0.01 μm, a laser spot diameter of 2 μm, and a response time of 640 μs, with measurement errors confined to less than 1%. However, its measurable thickness (δ) range is limited to 0.05 mm < δ < 0.3 mm. If the thickness is too small, overlapping reflected light peaks prevent accurate calculation, and if the thickness is too large, the lens system cannot resolve the film at higher frequencies. Lei et al. [22] also introduced the fluorescence intensity method (depicted in Figure 6), wherein a fluorescent agent is added to the liquid, and fluorescence is excited using a laser. The liquid film thickness is then inferred from the measured fluorescence intensity, although calibration can be challenging. Gstoehl et al. [25], Chen [26], and Chen et al. [27] combined fluorescence intensity with digital image processing and used laser-induced fluorescence (shown in Figure 7) to measure liquid film thickness. High-definition cameras capture the fluorescence images of the liquid film, which are processed to determine the film thickness. This method is relatively straightforward and effective for thicker films (δ > 0.2 mm), but image processing can introduce significant errors, with relative errors around 5% and absolute errors of approximately 0.0085 mm. Moreover, a substantial number of images must be analyzed to reduce measurement errors. Additionally, experimental studies on inter-tube flow patterns and surface wettability are primarily conducted through visualization techniques [28], combining high-speed cameras and digital image processing to investigate the evolution of flow patterns, as well as the distribution, development, and wetting characteristics of the liquid film.
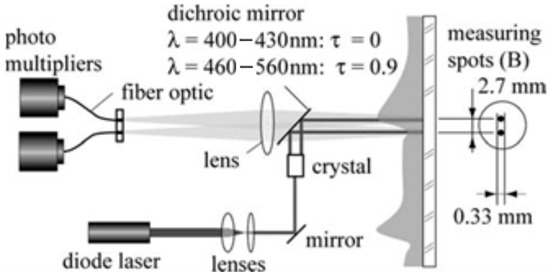
Figure 6.
The principle of the fluorescence intensity method in Ref. [22] (Lei, 2005).
Figure 7.
The principle of laser-induced fluorescence combined with an image processing method in Ref. [27] (Chen, 2015).
Experimental methods can directly characterize real physical processes, verify accurate boundary conditions, and serve as the ultimate validation benchmark for engineering applications. However, they also have disadvantages such as high cost and time investment, limitations in measurement methods and environment. Therefore, they are suitable for studying the characteristics, mechanism verification, and performance testing of flow, heat and mass transfer processes. However, numerical simulations, in comparison to experimental methods, offer advantages such as reduced costs and faster analysis. They also provide an intuitive and efficient means to analyze temperature, velocity, and concentration fields within heat exchangers, enabling predictions of their future trends. These benefits have led to the widespread adoption of numerical simulations to study the local characteristics of falling film flows. Numerical models are based on a set of governing equations for mass, momentum, energy, and component transport. Through specific assumptions, these complex physical problems are transformed into solvable mathematical formulations. In order to simplify the solving process, scholars have made numerous assumptions and approximations, and as computational techniques have advanced, these assumptions have been progressively refined to more accurately reflect real-world phenomena. Models have evolved from two-dimensional models that neglect the axial direction of the tube [29,30,31], to three-dimensional models that account for the actual flow dynamics [32,33,34], from single-tube [35,36,37] to multi-tube models [38,39], and from models that assume a uniform liquid film thickness around the tube [40,41] to those that account for axial and circumferential fluctuations in liquid film thickness [42]. Furthermore, the models have advanced from neglecting the absorption process between tubes [40] to incorporating incomplete wetting effects in falling films [32,43,44], intertube flow patterns [39,44], and gas flow characteristics [45,46]. Both experimental and numerical approaches offer complementary strengths and weaknesses, and as such, research on the performance of falling film heat exchangers often combines both methodologies. In model selection, the VOF (Volume of Fluid) model and Level Set method are widely used to capture the dynamic evolution of gas-liquid interfaces, and combined with wall functions, can accurately simulate the distribution of liquid film thickness. In the simulation of evaporation/condensation phase transition, the Lee model significantly improves prediction accuracy by introducing mass, momentum, and energy transfer through source terms. Research has shown that incorporating latent heat of phase change into the energy equation reduces the prediction error of condensation wall temperature from 15% to within 5% [47]. LES (Large Eddy Simulation) and DNS (Direct Numerical Simulation) methods can analyze the influence of turbulence on liquid film fluctuations, but the computational cost is high. In recent years, the lattice Boltzmann method has shown advantages in microscale multiphase flow simulations, effectively capturing evaporation, condensation, and non-equilibrium phenomena within nanochannels [48].
3. Liquid Film Thickness
Liquid film thickness is a crucial factor influencing heat and mass transfer performance. If the liquid film is too thin, it is prone to rupture, leading to the formation of “dry spots”, which degrade the heat and mass transfer efficiency. Conversely, if the liquid film is too thick, it increases thermal resistance and decreases the mass transfer coefficient. Consequently, researchers worldwide have investigated the distribution and influencing factors of liquid film thickness.
Nusselt [49] was the first to theoretically analyze that both the spray density and the physical properties of the solution jointly determine the distribution of liquid film thickness along the circumference of the outer surface of horizontal tubes, with the minimum film thickness occurring at a circumferential angle of 90°. He proposed an empirical formula, as shown in Equation (1). However, this model neglected the effects of surface tension and inertial forces, leading to significant errors in predicting the liquid film thickness on the lower half of the tube. Later, Gstoehl et al. [25] used laser-induced fluorescence (LIF) to experimentally measure liquid film thickness and demonstrated that the actual minimum liquid film thickness occurs after the 90° circumferential angle.
where δ is the liquid film thickness (m); θ is the circumferential angle of the horizontal tube, as shown in Figure 1 (°).
Since liquid film flow occurs on the outer surface of horizontal falling film tubes, structural parameters such as tube diameter and tube spacing are critical factors affecting the distribution of liquid film thickness. Both Nusselt [49] and Gstoehl et al. [25] only considered fluid properties (e.g., viscosity, flow rate, and density) and inertial forces, ignoring the influence of structural parameters. Hou et al. [14] comprehensively considered the effects of structural dimensions, fluid properties, and inertial forces, experimentally showing that the minimum liquid film thickness occurs at a circumferential angle between 90° and 115°. This refined the liquid film thickness angle range proposed by Gstoehl et al. [25] and compared it with Nusselt’s theoretical results (Figure 8). Hou proposed the theory of asymmetric distribution of liquid film thickness and liquid film velocity and revised the liquid film thickness equation, as shown in Equation (2), which is valid for Ref between 150 and 800.
where C is a constant.
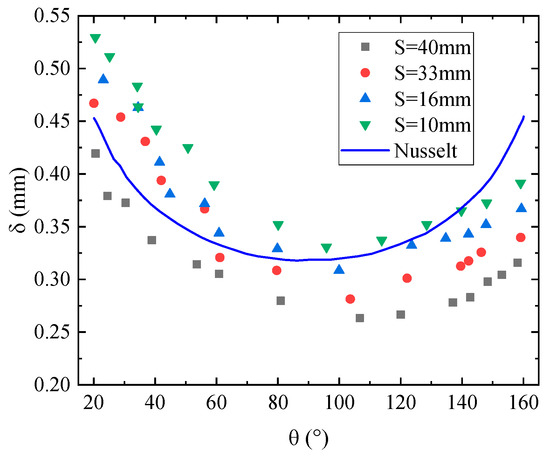
Figure 8.
Variations in film thickness with circumferential angle at different intertube spacings (smooth tube, d = 25.4 mm, Ref = 574) in Ref. [20] (Yu, 2017).
Ji et al. [50] validated the theory of asymmetric distribution of liquid film thickness and velocity through simulations, determining that the minimum liquid film thickness occurs at a circumferential angle of 120°. By utilizing both simulation and experimental data, Ji revised the liquid film thickness equation, as shown in Equation (3), which is valid for Ref between 150 and 260. However, this model did not account for the effects of structural parameters.
Subsequent research by scholars [15,24,27,51] further explored the mechanisms by which tube structural parameters affect the distribution of liquid film thickness. Studies [24,27] show that as the tube spacing increases, the impact of the solution on the lower falling film tube intensifies under gravity, causing the upper half of the liquid film to become significantly thinner. As the circumferential angle increases, the disturbance of the liquid film weakens, and the effect on the lower half of the tube becomes less pronounced. Regarding tube diameter, experimental studies [15,51] indicate that as the diameter increases, the liquid film area expands at a constant spray density, leading to a reduction in liquid film velocity and thickness, which eventually stabilizes. Increasing the spray density amplifies the effect of tube diameter on liquid film thickness. However, Chen [26] conducted experiments and reported that, for a given spray density, the liquid film thickness at the same circumferential angle increases with tube diameter, with the free-flow area of the liquid film increasing, which results in a decrease in velocity and kinetic energy, and consequently, an increase in liquid film thickness.
Chen et al. [52], building on Hou’s work [14], used simulations to suggest that the impact of tube diameter on liquid film thickness is minimal. He derived a corrected correlation for liquid film thickness that accounts for tube spacing, fluid properties, and inertial forces, as shown in Equation (4) (valid for Ref between 600 and 684). This equation does not consider the effect of tube diameter.
where C, n are constants, C = 0.4703, n = −0.2206.
Zhao et al. [53], based on experimental and numerical methods, considered the effects of fluid properties, inertial forces, tube diameter, tube spacing, buoyancy, and gas flow velocity, and established an empirical formula for liquid film thickness across different regions of falling film flow. This formula is given by Equation (5).
where Ar is the dimensionless Archimedes number, representing the ratio of buoyant to inertial forces. Ca, a1, a2, a3, a4, and a5 are constants.
This equation is valid for Ref between 400 and 2485, We between 4.55 × 10−4 and 21.4 × 10−4, Archimedes numbers between 7.17 × 106 and 3.67 × 109, and tube spacing ratios between 0.12 and 2, with the liquid film thickness distribution shown in Figure 9. Killion [54] compared this formula with 261 experimental data points from other researchers and found that the prediction accuracy was 70%.
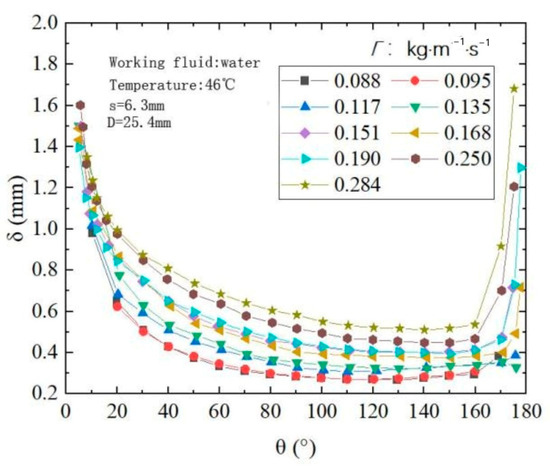
Figure 9.
Variation of the local film thickness with different film flow rate (smooth tube, d = 25.4 mm, s = 6.3 mm) in Ref. [53] (Zhao, 2018).
In recent years, there has been growing attention on the impact of gas flow characteristics (such as direction, velocity, and humidity) on liquid film thickness in horizontal falling film flow. Co-current gas flow significantly increases liquid film velocity and reduces liquid film thickness, shifting the circumferential angle of the thinnest liquid film downward. However, as gas flow velocity increases, the liquid film begins to rupture, leading to the formation of “dry spots”, which deteriorate heat and mass transfer performance [45]. In contrast to co-current flow, counter-current gas flow exerts a lifting effect on the liquid film, decreasing its velocity. As the gas flow velocity increases, the liquid film thickness first increases and then decreases. However, as spray density increases, the gravitational impact on the liquid film becomes stronger, and the influence of gas flow decreases [55,56]. Li [57] conducted three-dimensional simulations and found that as the Weber number of the gas increases, the liquid film thickness decreases, as shown in Figure 10. In falling film absorption processes, an increase in gas humidity results in a higher water recovery rate [32], which lowers the solution concentration, increases temperature, reduces liquid viscosity, and consequently decreases liquid film thickness. Due to the effects of gravity and the curvature of the tube, the liquid film thickness at the bottom of the tube is more significantly influenced by the gas flow than at the top.
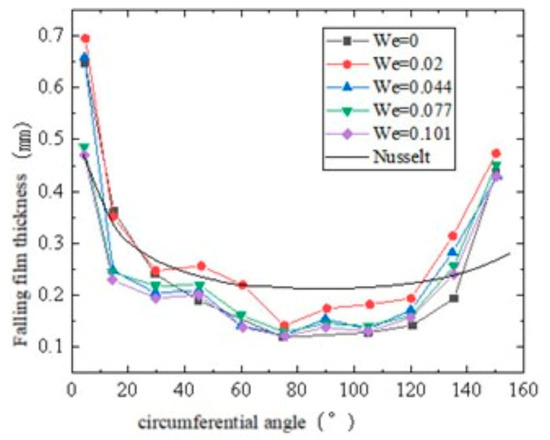
Figure 10.
Variation of the local film thickness with different airflow rates in Ref. [57] (Li, 2013).
Most of the studies mentioned above focus on predicting and characterizing the circumferential distribution of liquid film thickness. In actual flow, however, the liquid film distribution along the axial direction of the tube also exhibits periodic fluctuations, with peaks and valleys whose period length is related to the distance between adjacent liquid droplets or columns in the upper tube. Recent studies have focused on the axial distribution of liquid film thickness. Li [57] used a three-dimensional model to obtain the axial distribution of liquid film thickness for three basic flow patterns. In droplet flow, the upper half of the tube has a more regular liquid film thickness distribution than the lower half; in columnar flow, the upper half exhibits a stable “steady-high-peak-steady” distribution, with the maximum liquid film thickness being twice that of the minimum, and the influence of adjacent liquid columns on the lower half is minimal; in sheet flow, the liquid film thickness at circumferential angles of 45°, 90°, and 135° exhibits a stable wave-peak pattern along the tube axis, with the difference between the maximum and minimum liquid film thickness changing with the circumferential angle. Similarly, Qiu et al. [58] simulated with a three-dimensional model and demonstrated that the liquid film thickness between liquid columns follows a wave-peak distribution, with the maximum liquid film thickness occurring at the center of the columns. Chen et al. [52] also experimentally confirmed that, along the tube axis, as the distance from the center of the liquid column increases, the liquid film thickness increases, reaching a maximum between two adjacent liquid columns, which is shown in Figure 11.
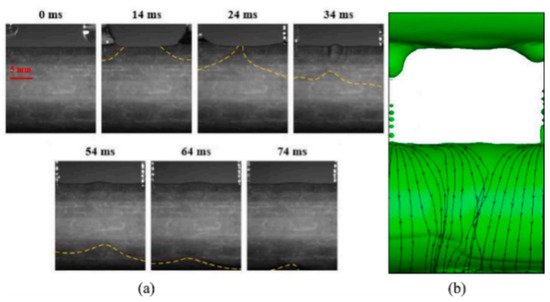
Figure 11.
Axial film thickness distribution under droplet flow pattern Ref = 80 (a) experiment results; (b) simulation results in Ref. [52] (Chen, 2022).
In conclusion, research on the distribution characteristics of liquid film thickness on the outer surface of horizontal falling film tubes has been steadily advancing. The research methods include theoretical analysis, experimental investigation, and numerical simulation. The distribution patterns of liquid film thickness along the tube circumference have been quantitatively characterized using predictive correlations, evolving from models considering only fluid properties and inertial forces to those incorporating a broader range of factors, including tube diameter, tube spacing, buoyancy, and gas flow characteristics. These models have steadily improved in accuracy. Recently, the axial distribution of liquid film thickness has gained attention, but it is still at the qualitative analysis stage. Further research is needed to expand the scope of operational parameters such as fluid types, tube structural parameters, and gas flow characteristics in order to achieve a more comprehensive quantitative characterization.
4. Surface Wettability
The appropriate wettability of the tube surface plays a crucial role in enhancing heat and mass transfer performance. Incomplete wettability on the tube surface can lead to the formation of “dry spots”, reducing the gas-liquid contact area and thus affecting the efficiency of heat and mass transfer. Increasing the solution spray density or flow rate can improve wettability; however, exceeding the optimal values may cause an increase in liquid film thickness, which in turn increases thermal resistance [43]. The key challenge in research lies in enhancing the wettability of the falling film surface while maintaining an appropriate liquid film thickness.
Killion [54] was one of the first to highlight the significant impact of wettability on falling film absorption efficiency. Jeong [42] introduced the concept of the wettability ratio, defined as the ratio of the wetted area of the tube surface to the total surface area, to characterize the wettability. Through two-dimensional simulations of the tube’s circumferential surface, it was shown that the heat and mass transfer coefficients change with the wettability ratio. However, under low flow conditions where droplet flow patterns prevail, the effect of wettability ratio is minimal. Subsequently, Arroiabe et al. [59] developed a three-dimensional model, further validating this conclusion. Castro et al. [60] conducted experimental and simulation studies, demonstrating that the wettability ratio is a key parameter in wettability research and is a function of the contact angle per unit length and the mass flow rate. Ji et al. [50] conducted two-dimensional simulations of the tube’s circumferential surface to evaluate the impact of the static contact angle and spray density on the wettability of hydrophilic tube surfaces (Figure 12) The results showed that the wettability ratio is directly proportional to spray density and inversely proportional to the static contact angle. The liquid film spreading speed increases with an increase in static contact angle, but decreases with an increase in spray density.

Figure 12.
Profiles of LiBr solution over the horizontal tube surface under different ψ (Ref = 42) in Ref. [50] (Ji, 2017).
Most of the above studies were based on two-dimensional simulations or considered only the circumferential distribution of the liquid film, neglecting the axial wettability characteristics of the liquid film. Arroiabe et al. [59], building upon Castro’s work [60], established a three-dimensional transient numerical model to investigate the impact of the contact angle on liquid film wettability under droplet and column flow patterns (Figure 13). The results indicated that for each Reynolds number, there is a corresponding maximum contact angle that ensures complete wetting of the falling film. When the contact angle is smaller than this maximum value, the contact angle has no significant effect on the wettability ratio. However, when the contact angle exceeds this maximum value, the wettability ratio decreases as the contact angle increases. In the application of falling film heat exchangers, if higher wettability and heat transfer characteristics are desired, the surface contact angle cannot be neglected as a key factor.
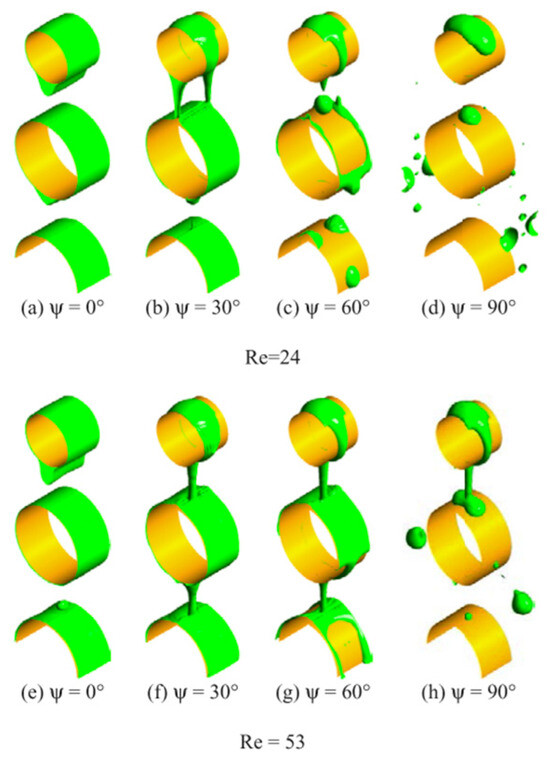
Figure 13.
Film hydrodynamics of the LiBr-H2O solution for different values of ψ in Ref. [59] (Arroiabe, 2018).
Moreover, the material of the falling film tubes, surface treatments, and the presence of additives in the fluid all influence the contact angle and surface tension, which in turn affect the wettability ratio. Martinez-Urrutia et al. [61] compared the wettability of copper, aluminum, and stainless steel through experiments. The results showed that for all materials, both the contact angle and surface tension increase with the concentration of the solution. Compared to copper, aluminum and stainless steel exhibited better wettability characteristics, with a significantly reduced minimum flow rate and liquid film thickness required for complete wetting, resulting in better absorption performance. Lee et al. [62] experimentally studied the influence of micro-porous coatings (Figure 14), demonstrating that pipes with micro-porous coatings required only half the minimum flow rate for complete wetting compared to smooth pipes, with smaller liquid film thickness and higher heat transfer coefficients. Zhang [46] compared the wettability of falling film tubes with two different surfactants and three different surface geometries. The results showed that the wettability area varied with different geometries, with the effectiveness of wettability ranked from high to low as: flower tubes, finned tubes, and smooth tubes. The impact of surfactants on wettability was found to be significantly greater than the effect of surface geometry.

Figure 14.
Comparison of solution wetting and flow modes of (left (a)) plain and (right (b)) porous-layer coated tubes in Ref. [62] (Lee, 2012).
In recent years, micro-/nano-structured surfaces have significantly regulated surface wettability by changing the characteristics of the solid-liquid-gas three-phase contact line, providing a new path for enhancing heat transfer. The superhydrophobic surface reduces the contact area between the liquid film and the wall, promotes rapid droplet rolling, and reduces liquid retention time. The superhydrophilic surface enhances liquid spreading and forms a uniform thin liquid film to reduce thermal resistance. The nanoscale columnar array structure can increase the surface contact angle from 90° to over 160°, achieving self-cleaning and anti-scaling performance [63]. In microchannel heat exchangers, micro-scale groove structures can induce directed flow of liquid film along the channel, reduce local liquid film thickness, and increase heat transfer coefficient by 20–40% [64]. However, the nonlinear relationship between structural scale and wettability still needs to be further studied, such as the possibility of droplet pinning effect caused by excessive density of nanostructures, which may actually inhibit liquid film migration.
Significant progress has been made in optimizing the wetting and heat transfer performance of heat exchangers through surface modification techniques such as grooves, fins, and coatings. The spiral groove tube guides the liquid film to spiral downwards, promoting the thinning and renewal of the liquid film, and increasing the heat transfer coefficient by more than 30% under condensation conditions [65]. Sawtooth-shaped fins increase surface roughness while utilizing the tip effect to accelerate droplet shedding, resulting in a 15–25% increase in heat transfer efficiency compared to straight fins. Biomimetic coating technology simulates the micro-nano composite structure on the surface of lotus leaves or cicada wings to achieve synergistic optimization of superhydrophobicity and anti-icing performance, effectively suppressing frost growth in refrigeration systems. In addition, intelligent responsive coatings (such as temperature/electric field responsive materials) can dynamically adjust surface wettability according to operating conditions, providing innovative solutions for heat exchangers operating under variable loads.
It is important to note that in actual falling film flow conditions, the gas flow rate and direction significantly influence the liquid film thickness and, consequently, the wettability ratio. In recent years, this has attracted increasing attention from researchers. Proper reverse gas flow can improve the liquid film distribution and enhance wettability. However, if the gas flow rate becomes too large, the tube surface may fail to form a steady falling film, leading to the formation of “dry spots” [9]. As shown in Figure 15, the blue regions represent areas where the liquid film thickness decreases under reverse gas flow, making it more prone to dry spot formation. Zhao et al. [9] studied the effect of lateral airflow and found that, in the absence of gas flow, the liquid film along the axis of the falling film tube exhibited a “saddle-shaped” distribution. As the gas flow rate increased, this saddle shape gradually disappeared, and the liquid droplets on the windward side of the tube shifted, worsening the wettability. Ruan et al. [66] showed that when the reverse gas flow rate exceeds 3.5 m/s, the tube surface fails to maintain a steady falling film, resulting in poor wettability. Zhu [67] used high-speed imaging and advanced image processing techniques to investigate the combined effect of operational and structural parameters on wettability, such as solution flow rate, tube array configuration, tube diameter, and inter-tube spacing. Wettability length was introduced to characterize the wettability of the external surface of the tube, defined as the axial spreading length of the liquid film on each tube row. Multi-row wettability of falling films is shown in Figure 16. A predictive correlation between wettability ratio and these parameters was established, as shown in Equation (6), with a prediction error of less than 10%.
where η represents the wettability ratio, which is the ratio of the wetted area to the total surface area of the tube. ε is the tube array coefficient, which varies depending on the number of tube rows.
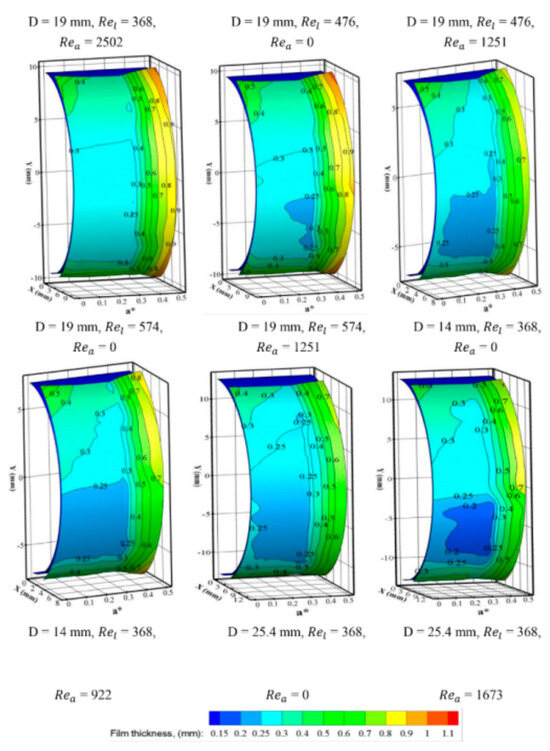
Figure 15.
Contour map of liquid film distribution in Ref. [46] (Zhang, 2022).

Figure 16.
The outer wetted length of the downward film flow in multiple rows of horizontal tubes (Ref = 758) in Ref. [66] (Ruan, 2009).
In conclusion, recent studies on the wettability characteristics of the external surface of falling film heat exchangers have gained significant attention. Research has evolved from two-dimensional studies of smooth tubes to three-dimensional models considering both the circumferential and axial surfaces of the tubes. The research has expanded from studying the material of the falling film tubes, surface treatment processes, and additives, to investigating methods for enhancing the wettability ratio. However, most of the research has been at the qualitative stage, with limited development of quantitative predictive correlations for wettability. Such correlations can be used to predict and assess heat and mass transfer coefficients, providing data support for the design of horizontal falling film heat exchangers. Furthermore, there is limited research on the influence of factors such as fluid properties and gas flow characteristics on wettability. Therefore, a more comprehensive and multi-factorial quantitative approach is needed to characterize the wettability ratio and its relationship with heat and mass transfer processes.
5. Inter-Tube Flow Patterns
Under the influence of factors such as spray density, inter-tube spacing, fluid properties, tube structure, and gas flow disturbances, the liquid film formed between tubes, from the bottom of the upper tube to the top of the lower tube, exhibits different flow patterns. These patterns directly impact the shape and area of the gas-liquid interface, thereby affecting heat and mass transfer performance. As a result, predicting the inter-tube flow pattern and summarizing the transition rules between these patterns are crucial for understanding the thermal and mass transfer characteristics of heat exchangers.
The identification of inter-tube flow patterns has been widely acknowledged among scholars. Mitrovic [68] was among the first to conduct visual experimental studies, demonstrating that with increasing flow rate, the inter-tube flow transitions sequentially through droplet, columnar, and sheet flow patterns. Hu and Jacobi [69] further refined this classification through a series of detailed visual experiments on various fluids, distinguishing flow patterns as droplet, droplet-column, aligned columnar, staggered columnar, column-sheet, and sheet flow. Sun [70] conducted similar flow pattern experiments using water and various concentrations of calcium chloride solution, confirming the same classification, as illustrated in Figure 17.

Figure 17.
Different inter-tube flow patterns in Ref. [70] (Sun, 2013).
The determination of transition points between adjacent flow patterns presents a challenge, as the criteria for evaluation are somewhat subjective and lack universal agreement. As a result, there is no widely accepted formula for flow pattern transitions or a corresponding flow zone map. At present, flow pattern transitions are primarily defined based on the dimensionless liquid film Reynolds number (Ref) at the critical point of pattern change, as expressed in Equation (7):
where Ref is the critical Reynolds number, representing the ratio of inertial force to viscous force; Γ is the spray density (kg/m·s); and μl is the dynamic viscosity of the liquid (Pa·s).
Spray density is a primary factor affecting the critical Reynolds number (Ref) at pattern transitions, though other operational and structural parameters also play significant roles. Armbruster and Mitrovic [71] compared the trends in flow pattern transition for two fluids—water and isopropyl alcohol—using the Galileo number (Ga) to represent the fluid properties. The Galileo number is defined as:
where Ga is the dimensionless Galileo number, representing the ratio of gravitational force to viscous force; ρl is the liquid density (kg/m3); σ is the surface tension (mN/m); and g is the gravitational acceleration (m/s2).
The study [71] indicated that flow pattern transitions depend on both Ref and Ga, and an empirical relationship was established for critical Ref and Ga at flow pattern transitions, as shown in Equation (9) in Table 3.
Later, Hu and Jacobi [69], extending their experiments to include a wider range of fluids such as water, ethylene glycol, hydraulic oil, and their mixtures, determined that the exponent of 1/4 in Equation (9) could not accommodate all fluid types. They revised the formula to a more general form, as Ref = aGab, based on extensive experimental data, which was shown in Equation (10) in Table 3, thus improving the accuracy of predicting critical Ref for various fluids.
Furthermore, research has shown that the transition point for flow patterns differs depending on whether the flow rate is increasing (forward) or decreasing (reverse), a phenomenon known as hysteresis. Sun [70] conducted experiments comparing five different concentrations of CaCl2 solution, demonstrating that under the same flow pattern, the critical Ref for forward flow was greater than that for reverse flow. Additionally, the increase in Ref was more pronounced with higher Ga values. This hysteresis is attributed to the interaction between inertial force, viscous force, and surface tension under different flow patterns.
Earlier studies, however, neglected the impact of tube structural parameters. Roques et al. [72], in an effort to improve prediction accuracy, considered the effects of inter-tube spacing, tube diameter, and fluid type, providing correlation equations that account for and neglect these structural factors. The relationships are expressed as Equations (11) and (12) in Table 3, respectively. Where s is the inter-tube spacing (m), and d is the tube diameter (m).

Table 3.
Equations in the literature.
Table 3.
Equations in the literature.
| Droplet→ Droplet-Column | Droplet-Column→ Column | Column→ Column-Sheet | Column-Sheet→ Sheet | |
|---|---|---|---|---|
| Equation (9) | ||||
| Equation (10) | ||||
| Equation (11) | ||||
| Equation (12) |
Further studies [34,73,74,75] analyzed the impact of structural parameters such as tube diameter and inter-tube spacing on Ref, revealing that Ref increases with tube diameter. However, for relatively small changes in tube diameter (e.g., between 0.019 m and 0.0254 m), the change in Ref was minimal. This is because the area of the liquid film increases with the tube diameter, requiring a higher flow rate to maintain the same inter-tube flow pattern, thus raising Ref. Inter-tube spacing, however, has a greater influence on Ref. With increasing tube spacing, the required flow rate to maintain the corresponding flow pattern also increases, resulting in a higher critical Ref for droplet-to-droplet-column, droplet-column to column, and column to column-sheet flow patterns when the solution flow rate increases [76]. However, reverse flow experiments yielded different results. For instance, Yao et al. [77] found that as inter-tube spacing increases, the critical Ref for sheet-to-sheet-column and column-to-column droplet flow patterns decreased initially before increasing again. This discrepancy arises because inter-tube flow patterns result from the combined effects of inertial force, viscous force, and surface tension, with different dominant factors for each pattern. For low spray densities, such as droplet flow, viscous forces are dominant, while at higher flow rates, inertial forces become more significant.
As horizontal tube falling-film heat exchangers are applied to various fields, such as flue gas heat recovery and seawater desalination, the influence of gas flow characteristics on the inter-tube critical Ref has garnered increasing attention. Gas flow velocities are high in such applications, and flow directions may include reverse, lateral, and other patterns, significantly affecting the inter-tube flow pattern. The Weber number (We) is used to characterize gas flow intensity, as shown in Equation (13):
where We is the Weber number, representing the ratio of gas inertial force to surface tension; ρg is the gas density (kg/m3); vg is the gas velocity (m/s); and σ is the surface tension (mN/m).
Ruan [66] derived a relationship between Ref, Ga, and We for water and ethylene glycol, and proposed an empirical correlation as shown in Equation (14):
where is the critical Reynolds number without the impact of gas flow. m, n, p, and q are constants.
Ruan concluded that, relative to gas flow characteristics, tube diameter has a minor effect on Ref, so this equation neglects the impact of tube diameter but adjusts the constants to account for inter-tube spacing. However, the baseline without gas flow may lead to more complex calculations.
Sun [70] investigated the effects of reverse gas flow, with experimental results showing that as We increases, the critical Ref for droplet-to-droplet-column and droplet-column to column, and column-sheet to sheet patterns increases, while it decreases for column to column-sheet flow. Gas flow influences inter-tube flow patterns differently, and this relationship is not a simple linear one. The gas flow direction affects the droplet displacement or liquid film thickness, influencing the hysteresis phenomenon and ultimately impacting Ref. Zhao [17] highlighted that the lateral gas flow velocity significantly affects inter-tube flow pattern transitions and hysteresis. For sheet flow, the effect of reverse gas flow is more pronounced compared to droplet and column flows. Xie et al. [44] further studied the impact of reverse gas flow in staggered tube bundles, demonstrating that as gas velocity increases from 1.6 m/s to 3.5 m/s, the inter-tube flow pattern gradually shifts from column to droplet-column and droplet flow under the same fluid spray density. They derived a comprehensive empirical correlation considering surface tension, fluid type, and inter-tube spacing for more accurate real-world predictions, as shown in Equation (15).
where a, b, and c are constants, and ξ represents the capillary length, defined as the characteristic length where surface tension and gravity are balanced, as shown in Equation (16):
Zhu [67] extended this research by considering solution properties, gas flow characteristics, tube diameter, and inter-tube spacing, providing an even more accurate predictive correlation as shown in Equation (17), which shows a prediction error of less than 5% compared to experimental values, see Figure 18. This equation is suitable for tube diameters between 16 mm and 25 mm.
where b1, b2, b3, b4, b5, and b6 are constants that vary depending on the transition between different flow patterns, as shown in Table 4.
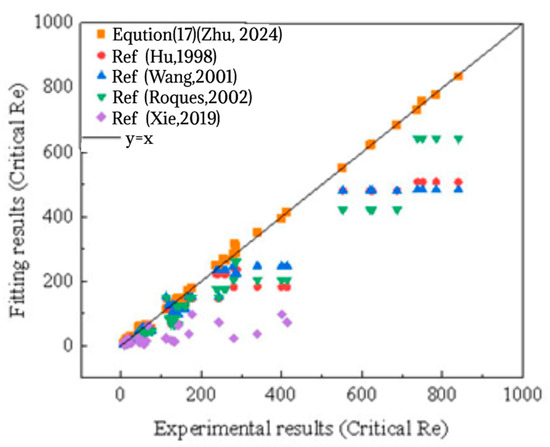
Figure 18.
Comparison between experimental data from the literature and the fitted data from Equation (17) in Refs. [44,67,69,72,73] (Zhu, 2024).

Table 4.
Constants in Equation (17).
Through sensitivity analysis, Zhu et al. [78] determined that the influence factors on critical Ref transition are ranked as follows: solution concentration > inter-tube spacing > reverse gas flow velocity > tube diameter. The prediction accuracy of Equation (17) was validated through comparisons with experimental data from the literature [44,69,72,73], showing relative errors less than 5%. This indicates that Equation (17), which comprehensively considers operational and structural parameters, can accurately predict the critical Ref for various inter-tube flow patterns under different operating conditions.
Under dynamic operating conditions of heat exchangers, fluctuations in fluid flow rate, temperature, pressure, and other parameters have a significant impact on the evolution of gas-liquid two-phase flow patterns, thereby profoundly changing heat transfer efficiency. Droplet flow, column flow, and sheet flow are typical flow patterns in condensation processes, and their transformation mechanisms are comprehensively controlled by fluid properties such as surface tension, viscosity, density, flow velocity, pipeline geometry, and the coupling effect of gravity and shear forces.
From the perspective of the flow pattern transition mechanism, when the gas flow rate is low, the condensate exists in the form of discrete droplets under the action of wall surface tension, forming a droplet flow. After the droplet separates from the wall, a fresh heat transfer surface is exposed, effectively reducing the thermal resistance of the liquid film, resulting in a higher heat transfer coefficient. As the gas flow rate increases, droplets collide and converge with each other, gradually forming a columnar flow. When the flow velocity further increases and the balance between gravity and gas-phase shear force is reached, the condensate eventually spreads on the wall to form a continuous laminar flow. Research has shown that although membrane flow covers a large area, the thermal resistance of the liquid film significantly reduces the heat transfer efficiency; In contrast, droplet flow can increase the heat transfer coefficient by 3–10 times [79].
In actual operation, dynamic changes in working conditions bring many challenges. For example, rapid changes in solution flow rate and pressure during system start-up and shutdown can cause multiple changes in flow patterns in a short period of time, leading to severe oscillations in heat transfer coefficients. Taking a large central air conditioning system as an example, when the load fluctuation range is 30% −100%, the fluctuation amplitude of the heat transfer coefficient can reach 40% during the transition of the flow pattern from droplet to sheet flow. To address this issue, current research focuses on real-time monitoring and intelligent control strategies, such as installing high-speed cameras and pressure sensors to capture flow pattern changes in real time, combining machine learning algorithms to predict flow pattern transition trends, and optimizing heat exchanger operating parameters to improve system stability.
In summary, scholarly understanding of inter-tube flow patterns has deepened progressively. The predictive correlations for critical Ref transitions have evolved from simple considerations of fluid properties to more complex formulations that incorporate fluid properties, tube diameter, inter-tube spacing, and gas flow characteristics. As these predictive formulas become more accurate, their applicability has expanded. However, further research is needed to extend these models to include a wider variety of fluids, structural parameters such as tube diameter and spacing, and additional operational parameters such as liquid flow rates, liquid temperatures, gas flow rates, gas direction and gas humidity content characteristics.
6. Optimization Strategy and Design Suggestions
Based on the analysis above, it is evident that the primary focus of performance optimization and engineering design for HTFFHEs lies in the following aspects:
- (1)
- Collaborative Optimization Design with Multiple Parameters
Accurate matching of spray density and flow rate: Taking into account the requirements of liquid film thickness, inter-tube flow pattern, and wettability, the optimal spray density and flow rate are accurately calculated through experiments or theoretical correlation equations. The curves of liquid film thickness, flow pattern transition, and wettability ratio as a function of spray density and flow rate are plotted to find the parameter combination that maximizes the efficiency of the heat exchanger. And by setting up flow control valves and monitoring devices, the flow rate can be adjusted in real time to enable the system to operate under efficient flow patterns. For instance, in a small experimental setup, the heat and mass transfer coefficients under different parameters are measured through pre experiments to determine the optimal operating conditions; In large-scale industrial applications, by combining on-site debugging and real-time monitoring, the spray density and flow rate can be dynamically adjusted to ensure that the system operates in an efficient range.
Optimize structural parameters: Reasonably design pipe diameter and spacing, considering their combined effects on liquid film thickness and flow pattern between pipes. According to the actual working conditions, if higher heat and mass transfer efficiency is pursued and a certain pressure drop is allowed, the pipe diameter and spacing can be appropriately reduced to promote the rapid flow and renewal of the liquid film; In the pursuit of rapid flow and renewal of liquid film, increasing the diameter and spacing of pipes can reduce the accumulation of liquid film. In the design of pipe length, avoid uneven or unstable thickness of the liquid film at the axial end due to excessively long pipe length. In terms of fluid distribution design, ensure that the liquid is evenly distributed in the axial direction and reduce the fluctuation of liquid film thickness caused by uneven inlet distribution. The axial distribution of the liquid film can be optimized by increasing the accuracy of the distributor and setting up flow guiding structures. At the same time, optimize the layout of tube types and tube arrays, prioritize the use of flower tubes, finned tubes, etc. with good wetting properties, improve the distribution of liquid film between tubes by adopting triangular arrangements, optimize the spacing and arrangement of tubes, and further increase the wetting length and heat transfer area.
Control airflow conditions: Accurately regulate the direction and speed of airflow based on the function and operating conditions of the heat exchanger. For flue gas waste heat recovery devices, the reverse airflow velocity should be controlled below 3.5 m/s to prevent liquid film instability; Reverse airflow, control the speed within a reasonable range (such as below 3.5 m/s) to avoid liquid film instability; For scenes affected by lateral airflow, the contact between airflow and liquid film can be optimized by setting up structures such as wind deflectors and guide vanes, so that the airflow acts evenly on the liquid film and reduces the situation where the local liquid film is too thin or too thick. In addition, in areas where the airflow velocity is high and sensitive to droplet and column flow patterns, it is advisable to increase the tube spacing or adjust the tube diameter appropriately, optimize the gas-liquid contact structure, adopt staggered tube bundle layout, and install distributors at the gas inlet to promote uniform gas-liquid contact and improve heat and mass transfer efficiency.
- (2)
- Optimization of Materials and Surface Treatment
Preferred high wettability materials: When selecting materials, priority should be given to metal materials with good wettability, such as aluminum and stainless steel, or exploring new non-metallic materials such as superhydrophilic polymers. For example, in corrosive environments such as seawater desalination, using stainless steel pipes can not only improve wettability but also ensure corrosion resistance. In the aerospace sector, where stringent requirements are imposed on both weight and performance, attempts are being made to utilize novel polymer materials to enhance wettability and heat transfer efficiency.
Application of surface treatment technology: using micro porous coatings, nano coatings, surfactants and other technologies to improve the surface properties of pipes. Prepare microporous coatings on the surface of pipes through processes such as chemical vapor deposition and spraying, increasing the contact area between the liquid and the surface and reducing the flow rate required for complete wetting; Coating nano coatings on the surface of pipes or adding an appropriate amount of surfactants to fluids can reduce surface tension and improve the spreading ability of liquids. However, attention should be paid to evaluating the impact of surface treatment techniques on fluid properties and system stability, and verifying their actual effectiveness and applicability through experiments.
- (3)
- Strengthen monitoring and intelligent control
Install high-precision sensors to monitor key parameters such as liquid film thickness, flow pattern between pipes, and wettability in real-time. Using high-speed cameras to monitor changes in flow patterns between pipes, measuring liquid film thickness through techniques such as laser-induced fluorescence, and evaluating wettability using image recognition technology. Build an intelligent control system that automatically adjusts operating conditions such as spray density, flow rate, and airflow parameters based on real-time monitoring data and preset optimization objectives. For example, when the liquid film thickness is too thin or “dry spots” are detected, the system automatically increases the spray density; If the flow pattern between the tubes deviates from the efficient range, adjust the flow rate or airflow parameters to achieve dynamic optimization operation of the heat exchanger.
7. Conclusions
This manuscript provides a comprehensive overview of the influence and underlying mechanisms of various operational and structural parameters on the flow performance of horizontal tube falling film heat exchangers. It introduces the experimental methods and numerical simulation techniques commonly employed in current research, and summarizes the research scope and correlation equations related to key parameters such as inter-tube flow pattern transition Reynolds number, liquid film thickness, and wettability ratio. These findings serve as fundamental data for engineering design and applications in traditional fields, while also providing a foundation for the performance optimization of HTFFHEs. Further investigation into scaling laws and criteria is necessary for practical applications. The main conclusions are as follows:
- (1)
- The experimental methods are more intuitive and accurate, evolving from contact-based techniques to non-contact-based ones. The numerical simulations can analyze the internal field distribution and local features, and the accuracy of these models has improved significantly. They have advanced from two-dimensional to three-dimensional models, from single-row to multi-row tube configurations, and from models that neglect inter-tube absorption processes to those that consider more complex factors such as incomplete wetting, inter-tube flow patterns, and gas flow characteristics. Current research typically combines experimental and numerical methods to study flow performance.
- (2)
- The circumferential distribution of liquid film thickness has been quantitatively characterized using predictive correlation equations, which have evolved from considering only fluid properties and inertial forces to incorporating additional factors such as tube diameter, inter-tube spacing, buoyancy, and gas flow characteristics. In contrast, the axial distribution of the liquid film thickness is still largely in the qualitative analysis stage.
- (3)
- Research on the wettability characteristics has evolved from studying the two-dimensional circumferential wettability of smooth tubes to considering the three-dimensional circumferential and axial wettability. Several approaches have been explored to enhance the wettability ratio, including the choice of tube material, surface treatments, and the use of additives.
- (4)
- The predictive correlation equations for the critical Reynolds number of inter-tube flow patterns have become more sophisticated. Initially, these equations considered only fluid properties, but more recently, they have expanded to include factors such as fluid properties, tube diameter, inter-tube spacing, and gas flow characteristics.
Gaps in current research are as follows:
- (1)
- In the axial distribution of the liquid film thickness, further expansion of the research scope to include a broader range of operational factors is needed to achieve a more comprehensive quantitative description.
- (2)
- The studies on the wettability characteristics are primarily in the qualitative analysis phase, with limited development of quantitative correlation equations for wettability. Moreover, in recent years, HTFFHEs have gained attention to utilize deep residual heat from combustion equipment through solution absorption processes; the flue gas composition and flow velocity are critical factors influencing inter-tube flow pattern transitions. Further in-depth studies are needed on the multi-factor quantitative characterization of wettability and the relationship between wettability ratio and heat/mass transfer performance.
- (3)
- While the accuracy of these predictive equations for the critical Reynolds number has improved, their applicability is still limited to a narrower range of fluid types, and the scope of structural and operational parameters needs to be further expanded.
Ideas for future work are as follows:
- (1)
- There is a lack of widely recognized predictive correlations for flow characteristics such as liquid film thickness and wettability, as well as predictive correlations for heat and mass transfer coefficients.
- (2)
- Reinforced tubes have received attention and application, and it is necessary to study and predict the flow pattern transition, liquid film thickness, and wettability of different solutions on reinforced tubes.
- (3)
- The current development of predictive correlation equations for flow characteristics primarily focuses on incorporating more influencing factors. However, the applicability of different correlations remains limited, necessitating the proposal of universal predictive models.
- (4)
- Based on the existing massive data, it is possible to consider using artificial intelligence and other methods to construct a new correlation equation regarding the relationship between flow, heat and mass transfer.
Author Contributions
Conceptualization, M.L.; writing—original draft preparation, Z.W.; writing—review and editing, M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the State Administration for Market Regulation Science and Technology Plan Project (No. 2023MK209) and the Internal Science Foundation of CSEI (No. 202314).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Meijun Li was employed by the company Beijing Tiandi Rongchuang Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wang, W. Research on Enhancing Heat Transfer Performance in Falling-Film Evaporation Outside Horizontal Tubes in Lithium Bromide Absorption Refrigeration System; Chang’an University: Xi’an, China, 2021. [Google Scholar]
- Gong, L.; Shen, S.; Liu, H.; Mu, X.; Chen, X. Three-dimensional heat transfer coefficient distributions in a large horizontal-tube falling film evaporator. Desalination 2014, 357, 104–116. [Google Scholar] [CrossRef]
- Ma, L. Research on the Recovery of Waste Heat from Chlor-Alkali Evaporation Section by Absorption Heat Pump; Dalian University of Technology: Dalian, China, 2004. [Google Scholar]
- Pan, Y.; Ma, S.; Wang, Y. Modeling and performance analysis of vacuum drying system based on open absorption heat pump. Sci. Technol. Eng. 2020, 20, 8568–8572. [Google Scholar]
- Zhang, H. Mechanism and Experiment Study on Water and Heat Recovery Form Low-Temperature Coal-Fired Wet Flue Gas Based on Solution Absorption Method; Shandong University: Jinan, China, 2022. [Google Scholar]
- Cheng, G.; Li, H.; Kang, S.; Zeng, R.; Zhang, G. A study of the CCHP system based on the deep utilization of low temperature flue gas. Sci. Technol. Eng. 2016, 16, 51–57. [Google Scholar]
- Shi, G.; Lin, J.; Tian, Z. Analysis of waste heat recovery from steel plant for heating by reducing return water temperature. Sci. Technol. Eng. 2021, 21, 15035–15042. [Google Scholar]
- Sehgal, S.; Alvarado, J.L.; Hassan, I.G.; Kadam, S.T. A comprehensive review of recent developments in falling-film, spray, bubble and microchannel absorbers for absorption systems. Renew. Sustain. Energy Rev. 2021, 142, 110807. [Google Scholar] [CrossRef]
- Zhao, C.-Y.; Qi, D.; Ji, W.-T.; Jin, P.-H.; Tao, W.-Q. A comprehensive review on computational studies of falling film hydrodynamics and heat transfer on the horizontal tube and tube bundle. Appl. Therm. Eng. 2022, 202, 117869. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, Y.; Wang, S.; Nawaz, K.; Jacobi, A. Falling-film heat exchangers used in desalination systems: A review. Int. J. Heat Mass Transf. 2022, 185, 122407. [Google Scholar] [CrossRef]
- Zhao, C.-Y.; Zheng, C.-M.; Wang, X.-S.; Qi, D.; Jiang, J.-M.; Ji, W.-T.; Jin, P.-H.; Tao, W.-Q. Correlations of falling film hydrodynamics and heat transfer on horizontal tubes: A review. Renew. Sustain. Energy Rev. 2024, 197, 114384. [Google Scholar] [CrossRef]
- Lin, H.-Y.; Muneeshwaran, M.; Yang, C.-M.; Nawaz, K.; Wang, C.-C. On falling film evaporator—A review of mechanisms and critical assessment of correlation on a horizontal tube bundle with updated development. Int. Commun. Heat Mass Transf. 2024, 150, 107165. [Google Scholar] [CrossRef]
- Jia, B.; Yang, L.; Politaeva, N.; Zhou, J.; Sadeghi, K. Review on droplet falling film evaporation in desalination: A focus on heat transfer enhancement of micro-nano structured surfaces. Desalination 2025, 598, 118373. [Google Scholar] [CrossRef]
- Hou, H.; Bi, Q.; Ma, H.; Wu, G. Distribution characteristics of falling film thickness around a horizontal tube. Desalination 2012, 285, 393–398. [Google Scholar] [CrossRef]
- Tan, Q. Study on Film Flow and Enhanced Heat Transfer Characteristics of Horizontal Tube; Southwest University of Science and Technology: Mianyang, China, 2018. [Google Scholar]
- Zhang, Y.; Wang, D.; Liu, Y.; Tang, M.; Zhang, S. Distribution characteristics of falling film thickness around a horizontal corrugated tube. Int. J. Heat Mass Transf. 2020, 154, 119773. [Google Scholar] [CrossRef]
- Zhao, Y. Flow Characteristics of Falling Film on Horizontal Tubes with the Action of Transverse Airflow; Shandong University: Jinan, China, 2021. [Google Scholar]
- Guo, B.; Li, H.; Guo, D. Measurement and analysis of the thickness distributions of falling liquid films around horizontal tubes. J. Eng. Thermophys. 2011, 32, 71–74. [Google Scholar]
- Xu, L.; Wang, S.; Wang, Y.; Ling, Y. Flowing state of liquid films over horizontal tubes and its influences on heat-transfer characteristics. J. Chem. Ind. Eng. 2002, 53, 555–559. [Google Scholar]
- Yu, Y.; Ma, L.; Ye, H.; Zheng, Y.; Ma, Y. Research of non-contact measurement for high viscous fluid falling film thickness on spherical series surface. Measurement 2017, 101, 1–8. [Google Scholar] [CrossRef]
- Hazuku, T.; Fukamachi, N.; Takamasa, T.; Hibiki, T.; Ishii, M. Measurement of liquid film in microchannels using a laser focus displacement meter. Exp. Fluids 2005, 38, 780–788. [Google Scholar] [CrossRef]
- Lel, V.V.; Al-Sibai, F.; Leefken, A.; Renz, U. Local thickness and wave velocity measurement of wavy films with a chromatic confocal imaging method and a fluorescence intensity technique. Exp. Fluids 2005, 39, 856–864. [Google Scholar] [CrossRef]
- Han, Y.; Shikazono, N. Measurement of the liquid film thickness in micro tube slug flow. Int. J. Heat Fluid Flow 2009, 30, 842–853. [Google Scholar] [CrossRef]
- Chen, X. Study on Falling Film Flow and Evaporative Heat Transfer Process of Seawater outside Horizontal Tubes; Dalian University of Technology: Dalian, China, 2015. [Google Scholar]
- Gstoehl, D.; Roques, J.F.; Crisinel, P.; Thome, J.R. Measurement of falling film thickness around a horizontal tube using a laser measurement technique. Heat Transf. Eng. 2004, 25, 28–34. [Google Scholar] [CrossRef]
- Chen, Z. The Thickness Measurement and Heat Transfer Experiment of Falling Film Outside the Horizontal Tube; Huazhong University of Science & Technology: Wuhan, China, 2013. [Google Scholar]
- Chen, X.; Shen, S.; Wang, Y.; Chen, J.; Zhang, J. Measurement on falling film thickness distribution around horizontal tube with laser-induced fluorescence technology. Int. J. Heat Mass Transf. 2015, 89, 707–713. [Google Scholar] [CrossRef]
- Liu, S.; Mu, X.; Shen, S.; Li, C.; Wang, B. Experimental study on the distribution of local heat transfer coefficient of falling film heat transfer outside horizontal tube. Int. J. Heat Mass Transf. 2021, 170, 121031. [Google Scholar] [CrossRef]
- Jiang, C. Analysis of Heat and Mass Transfer of LiBr Solution Falling Film Absorption in Absorber with Horizontal Tube; China University of Petroleum: Qingdao, China, 2007. [Google Scholar]
- Harikrishnan, L.; Tiwari, S.; Maiya, M. Numerical study of heat and mass transfer characteristics on a falling film horizontal tubular absorber for R-134a-DMAC. Int. J. Therm. Sci. 2011, 50, 149–159. [Google Scholar] [CrossRef]
- Rattner, A.S.; Garimella, S. Simple mechanistically consistent formulation for volume-of-fluid based computations of condensing flows. J. Heat Transf. 2014, 136, 071501. [Google Scholar] [CrossRef]
- Li, M.; Lu, Y.; Zhang, S.; Xiao, Y. A numerical study of effects of counter-current gas flow rate on local hydrodynamic characteristics of falling films over horizontal tubes. Desalination 2016, 383, 68–80. [Google Scholar] [CrossRef]
- Qiu, Q.; Zhang, X.; Quan, S.; Zhu, X.; Shen, S. 3D numerical study of the liquid film distribution on the surface of a horizontal-tube falling-film evaporator. Int. J. Heat Mass Transf. 2018, 124, 943–952. [Google Scholar] [CrossRef]
- Liu, S. Inter-Tube Flow Pattern Distribution and Outside-Tube Heat Transfer Coefficient of Horizontal Tube Falling Film; Dalian University of Technology: Dalian, China, 2021. [Google Scholar]
- Sun, F.; Xu, S.; Gao, Y. Numerical simulation of liquid falling film on horizontal circular tubes. Front. Chem. Sci. Eng. 2012, 6, 322–328. [Google Scholar] [CrossRef]
- Subramaniam, V.; Garimella, S. Numerical study of heat and mass transfer in lithium bromide-water falling films and droplets. Int. J. Refrig. 2014, 40, 211–226. [Google Scholar] [CrossRef]
- Zhao, C.-Y.; Ji, W.-T.; He, Y.-L.; Zhong, Y.-J.; Tao, W.-Q. A comprehensive numerical study on the subcooled falling film heat transfer on a horizontal smooth tube. Int. J. Heat Mass Transf. 2018, 119, 259–270. [Google Scholar] [CrossRef]
- Killion, J.D.; Garimella, S. Pendant droplet motion for absorption on horizontal tube banks. Int. J. Heat Mass Transf. 2004, 47, 4403–4414. [Google Scholar] [CrossRef]
- Li, M.; Lu, Y. Numerical and experimental study of local heat mass transfer characteristics of horizontal falling films of CaCl2 solution absorbing vapor from humid air. Int. J. Heat Mass Transf. 2020, 153, 119574. [Google Scholar] [CrossRef]
- Andberg, J.W.; Cliet, G.C. A simplified model for absorption of vapors into liquid films flowing over cooled horizontal tubes. ASHRAE Trans. 1987, 93, 2454–2463. [Google Scholar]
- Choudhury, S.K.; Hisajima, D.; Ohuchi, T.; Sakaguchi, S. Absorption of vapors into liquid films flowing over cooled horizontal tubes. ASHRAE Trans. 1993, 99, 81–89. [Google Scholar]
- Jeong, S.; Garimella, S. Falling-film and droplet mode heat and mass transfer in a horizontal tube LiBr/water absorber. Int. J. Heat Mass Transf. 2002, 45, 1445–1458. [Google Scholar] [CrossRef]
- Zhang, H.; Yin, D.; You, S.; Zheng, W.; Wei, S. Experimental investigation of heat and mass transfer in a LiBr-H2O solution falling film absorber on horizontal tubes: Comprehensive effects of tube types and surfactants. Appl. Therm. Eng. 2018, 146, 203–211. [Google Scholar] [CrossRef]
- Xie, X.; Liu, H.; He, C.; Zhang, B.; Chen, Q.; Pan, M. Deciphering the heat and mass transfer behaviors of staggered tube bundles in a closed wet cooling tower using a 3-D VOF model. Appl. Therm. Eng. 2019, 161, 114202. [Google Scholar] [CrossRef]
- Furqan, T.; Abdelnasser, M.; Muammer, K. Influence of co-current vapor flow on falling film over horizontal tube. Int. J. Therm. Sci. 2021, 159, 106614. [Google Scholar]
- Zhang, H.; Zhou, Y. Effect of wind speed on the spatial distribution of liquid film thickness outside the horizontal falling-film tube. Int. J. Heat Mass Transf. 2022, 187, 122584. [Google Scholar] [CrossRef]
- Wang, X.; Zhan, T.; Dai, S.; Zhang, G.; Wu, J.; Wu, Y. Inundation correlation research on the simulation of two-phase flow and heat transfer in a condenser. J. Phys. Conf. Ser. 2024, 2826, 012026. [Google Scholar] [CrossRef]
- Zeng, L.; Li, Z.; Li, J.; Yan, D.; Huang, F. CFD simulation study of internal mixing and flow of a modified airlift bioreactor. Int. J. Chem. React. Eng. 2024, 22, 571. [Google Scholar]
- Nusselt, W. The surface condensation of water vapor. Mag. Version Ger. 1916, 60, 541–546. [Google Scholar]
- Ji, G.; Wu, J.; Chen, Y.; Ji, G. Asymmetric distribution of falling film solution flowing on hydrophilic horizontal round tube. Int. J. Refrig. 2017, 78, 83–92. [Google Scholar] [CrossRef]
- Zheng, Y. The Flow Characteristics and Heat Transfer Enhancement for Horizontal Tube Falling Film at Low Spray Density on Superhydrophilic Surface; Dalian University of Technology: Dalian, China, 2018. [Google Scholar]
- Chen, X.; Wang, J.; Lu, T.; Sheng, J.; Chen, X. Three-dimensional film thickness distribution of horizontal tube falling film with droplet and sheet flow. Int. J. Multiph. Flow 2022, 148, 103933. [Google Scholar] [CrossRef]
- Zhao, C.-Y.; Ji, W.-T.; Jin, P.-H.; Zhong, Y.-J.; Tao, W.-Q. Hydrodynamic behaviors of the falling film flow on a horizontal tube and construction of new film thickness correlation. Int. J. Heat Mass Transf. 2018, 119, 564–576. [Google Scholar] [CrossRef]
- Killion, J.D.; Garimella, S. A critical review of models of coupled heat and mass transfer in falling-film absorption. Int. J. Refrig. 2001, 24, 755–797. [Google Scholar] [CrossRef]
- Lee, Y.-T.; Hong, S.; Dang, C.; Chien, L.-H.; Yang, A.-S. Effect of counter current airflow on film dispersion and heat transfer of evaporative falling film over a horizontal elliptical tube. Int. J. Heat Mass Transf. 2019, 141, 964–973. [Google Scholar] [CrossRef]
- Xu, X. Research on the Distribution of Liquid Film Thickness and Heat Transfer Characteristics on Horizontal Falling Film of Semi-Elliptical Tube Under Forced Convection; Donghua University: Shanghai, China, 2020. [Google Scholar]
- Li, M. Investigation of the Heat and Mass Transfer of Falling Films over Horizontal Tubes in the Presence of Humid Flue Gas; Institute of Engineering Thermophysics, Chinese Academy of Sciences: Beijing, China, 2013. [Google Scholar]
- Qiu, Q.; Meng, C.; Quan, S.; Jiang, W.; Shen, S. 3D simulation on flow behavior of two adjacent columns outside horizontal tube. J. Eng. Thermophys. 2018, 39, 1044–1048. [Google Scholar]
- de Arroiabe, P.F.; Martinez-Urrutia, A.; Peña, X.; Martinez-Agirre, M.; Bou-Ali, M.M. Influence of the contact angle on the wettability of horizontal-tube falling films in the droplet and jet flow modes. Int. J. Refrig. 2018, 90, 12–21. [Google Scholar] [CrossRef]
- Castro, J.; Oliva, A.; Perez-Segarra, C.D.; Oliet, C. Modelling of the heat exchangers of a small capacity, hot water driven, air-cooled H2O-LiBr absorption cooling machine. Int. J. Refrig. 2008, 31, 75–86. [Google Scholar] [CrossRef]
- Martinez-Urrutia, A.; de Arroiabe, P.F.; Ramirez, M.; Martinez-Agirre, M.; Bou-Ali, M.M. Contact angle measurement for LiBr aqueous solutions on different surface materials used in absorption systems. Int. J. Refrig. 2018, 95, 182–188. [Google Scholar] [CrossRef]
- Lee, S.; Köroğlu, B.; Park, C. Experimental investigation of capillary-assisted solution wetting and heat transfer using a micro-scale, porous-layer coating on horizontal-tube, falling-film heat exchanger. Int. J. Refrig. 2012, 35, 1176–1187. [Google Scholar] [CrossRef]
- Ho, J.Y.; Rabbi, K.F.; Khodakarami, S.; Ma, J.; Boyina, K.S.; Miljkovic, N. Opportunities in nano-engineered surface designs for enhanced condensation heat and mass transfer. J. Heat Transf. 2022, 144, 050801. [Google Scholar] [CrossRef]
- Su, C.; Yang, S.; Ding, C.; Wen, J.; Yang, Z.; Zhang, J.; Xu, L.; Shi, J.; Kuang, C.; Liu, X. Parallel 3D projection lithography of massive tunable nanopillars for functional structures. Optica 2024, 11, 1725–1732. [Google Scholar] [CrossRef]
- Irannezhad, N.; Rossetto, L.; Diani, A. Optimization considerations in the design of shell and tube condensers implementing enhanced tubes: Experimental and theoretical analysis. Appl. Therm. Eng. 2025, 273, 126408. [Google Scholar] [CrossRef]
- Ruan, B.L.; Jacobi, A.M.; Li, L.S. Effects of a counter current gas flow on falling-film mode transitions between horizontal tubes. Exp. Therm. Fluid Sci. 2009, 33, 1216–1225. [Google Scholar] [CrossRef]
- Zhu, C. Experimental Study on the Absorption Performance of Falling Film of Wet Flue Gas Horizontal Tube; China Coal Research Institute: Beijing, China, 2024. [Google Scholar]
- Mitrovic, J. Influence of tube spacing and flow rate on heat transfer from a horizontal tube to a falling liquid film. In Proceedings of Eighth International Heat Transfer Conference; American Press: San Francisco, CA, USA, 1986; pp. 1949–1956. [Google Scholar]
- Hu, X.; Jacobi, A.M. Departure-site spacing for fluid droplets and jets falling between horizontal circular tubes. Exp. Therm. Fluid Sci. 1998, 16, 322–331. [Google Scholar] [CrossRef]
- Sun, W. Experimental Study and Numerical Simulation of Falling Film Flow Outside of Horizontal Tubes; Chinese Academy of Sciences (Institute of Engineering Thermophysics): Beijing, China, 2013. [Google Scholar]
- Armbruster, R.; Mitrovic, J. Patterns of falling film flow over horizontal smooth tubes. In Proceedings of the 10th International Heat Transfer Conference, Brighton, UK, 14–18 August 1994; pp. 275–280. [Google Scholar]
- Roques, J.F.; Dupont, V.; Thome, J.R. Falling film transitions on plain and enhanced tube. J. Heat Transf. 2002, 124, 491–499. [Google Scholar] [CrossRef]
- Wang, L.; You, S.; Wang, S.; Zhang, H. Analysis of LiBr Solution droplet falling film flow between horizontal tubes. J. Tianjin Univ. 2010, 43, 37–42. [Google Scholar]
- Zhang, D. Research on Flow Patterns and Two-Phase Flow Characteristics of Falling Film Evaporation on Horizontal Tubes; Yanshan University: Qinhuangdao, China, 2020. [Google Scholar]
- Zheng, Q. Study on Flow Characteristics and Mechanisms of Horizontal-Tube Falling Film Evaporation; Dalian University of Technology: Dalian, China, 2020. [Google Scholar]
- Zhang, R.; Chen, J.; Niu, R. Experiment study on influential factors of flow pattern among tubes of falling-film-type horizontal-tube. Sci. Technol. Eng. 2016, 16, 43–47. [Google Scholar]
- Yao, N.; Wu, A.; Lin, J. Experimental study on flow pattern conversion between horizontal tubes falling-film evaporator. Refrig. Air-Cond. 2020, 20, 54–58. [Google Scholar]
- Zhu, C.; Li, M.; Duan, L.; Niu, F.; Wang, N. Experimental study on flow characteristics of falling film over horizontal tubes under countercurrent gas flow. Desalination Water Treat. 2024, 318, 100382. [Google Scholar] [CrossRef]
- Yang, J.; Zhong, T.; Yan, X.; Li, H.; He, Z.; Bai, H.; Fang, S. Numerical study of evaporation-condensation heat transfer in finned double pipe heat exchangers. Case Stud. Therm. Eng. 2025, 65, 105667. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).