Abstract
In power grids that integrate renewable energy sources, the virtual synchronous machine (VSM) or synchronverter offers a viable solution to the challenge posed by reduced inertia. This technology employs inverters to transfer power to the electrical network that relies on a control algorithm emulating the dynamic behavior of synchronous machines. Over the past decade, it has been applied in various contexts, leveraging its control structure based on the fundamental equations of synchronous machines. Although several review articles have been published on control strategies for grid-forming inverters, they often lack a specific focus on recent developments related to the synchronverter. Therefore, this paper aims to fill that gap by presenting a detailed review on high-quality research databases to retrieve recent documents published in recent years. These documents were classified according to journals, conferences, and books. A keyword bibliographic analysis was performed to identify the attractive topics related to the synchronverter control strategy. The paper reviews recent improvements in and applications of the synchronverter, identifying emerging trends and new potential use cases to provide a workflow guide for readers and researchers, as the documents are presented in comprehensive tables, streamlining the process of locating specific references. In addition, some advantages and disadvantages of synchronverters are reported.
1. Introduction
1.1. Motivation
Non-conventional renewable energy sources (NCRES) have experienced rapid growth in the past decade [1,2]. Both their initial investment and maintenance costs have decreased significantly since their integration into the electrical grid [3]. As a result, there is an increasing demand for a new generation of inverters that can efficiently manage power exchange between NCRES and the grid. These inverters, known as grid-forming inverters, play a crucial role in this process [4,5,6].
The synchronverter is a type of grid-forming inverter that is specifically designed to mimic the behavior of a synchronous generator (SG) [7]. The synchronverter helps stabilize the grid by replicating the dynamic response of an SG, particularly in systems with a high penetration of renewable energy sources. Over the years, numerous studies have demonstrated its effectiveness in addressing real-world challenges, such as frequency fluctuations in the grid [8] and voltage instability [9], which are common during grid disturbances. As a result, the synchronverter has emerged as a key solution to integrate NCRES in modern power systems.
1.2. Problem Definition
As a recent technology, review papers may be necessary to provide a guide on important topics currently under investigation by other researchers. Several authors have explored the potential of the synchronverter to improve grid resiliency, support power sharing between renewable energy systems, and improve the overall reliability of the electrical grid [10,11].
1.3. Literature Review
The concept of synchronverter has been extensively explored and reviewed in the literature, with numerous studies examining its application and functionality in grid-forming inverters. For example, the review presented in [12] provides a comprehensive analysis of single-phase grid-forming inverters, highlighting the various control structures used to enable synchronization with the power grid. These control strategies are typically categorized into three main approaches: droop control, synchronous machine-based control, and virtual oscillator control, each offering distinct advantages in terms of system stability, scalability, and ease of implementation. The review highlights several commonly used techniques for power estimation, including low-pass filters, hold filters, root-mean-square (RMS) calculation, and second-order generalized integrators (SOGIs). However, the authors did not focus on the three-phase synchronverter.
A comprehensive review of grid-forming inverters was presented in [11], offering an in-depth examination of various control strategies used to enhance the performance and stability of these inverters under different grid conditions. The review covers a wide range of approaches, including droop control, voltage and frequency regulation techniques, model predictive control, and adaptive control. Through a detailed analysis, the authors evaluated the strengths and limitations of each method, considering factors such as system scalability, response time, and robustness to various grid disturbances such as voltage sags, frequency fluctuations, and load variations. Additionally, they assessed the suitability of each control strategy in different operating environments, providing valuable insights into which methods are best suited for specific applications, such as microgrids or large-scale integration of renewable energy. This thorough review not only clarifies the advantages and drawbacks of each control technique but also offers a framework for selecting the most appropriate approach depending on the nature of the grid disturbances encountered and the operational goals of the system. However, this study did not present the synchronverter approach.
Voltage-Source Inverter (VI)-based systems are inverters designed to replicate the behavior of synchronous generators (SGs), typically through three key techniques: (i) virtual synchronous machine (VSM), (ii) virtual synchronous generator (VSG), and (iii) synchronverter. These approaches aim to provide grid-supporting capabilities, such as frequency and voltage regulation, mimicking the dynamic response of traditional synchronous generators. In a detailed study presented in [13], the authors offer an in-depth analysis of the latest advancements, practical applications, and the challenges faced in implementing these technologies. The article serves as a comprehensive overview, addressing not only the theoretical underpinnings of these methods but also real-world considerations. However, while the paper covers a broad spectrum of VI-based inverter technologies, it does not exclusively focus on the synchronverter, providing only a portion of the broader discussion surrounding these techniques.
1.4. Gap, Objective and Novelty
The aforementioned review papers present several classifications concerning control strategies applied to grid-forming inverters and some specific features of the synchronverter. However, no new research documents related to synchronverter applications are reported, which are promising solutions for integrating renewable sources into the power grid.
Therefore, this paper presents a review of recent improvements in and applications of the synchronverter control strategy. The novelty lies in a structured summary that organizes the scientific literature per topic into several classifications. Those classifications can be condensed as mathematical modeling, experimental tests, synchronization, RES, and some other applications related to specific events that may be found in real power grids. The paper also shows the temporal progress in recent years in synchronverter research, as well as its advantages and disadvantages. Finally, some challenges and future prospects are also presented.
1.5. Contributions
- To the best of our knowledge, previous literature reviews have not focused exclusively on the synchronverter. This paper provides a comprehensive review that includes mathematical models, recent improvements, and applications.
- Previous literature dedicated to investigating synchronization techniques and the use of synchronverters. Likewise, this paper also presents the trend in recent years to define interest in the topic and databases that are commonly published documents.
- Previous papers have only been dedicated to reviewing only a few functions of the synchronverter. This detailed review presents applications focused on defining challenges and future prospects.
- Although document [13] shows a table summarizing some merits and demerits of the synchronverter, this review extends the advantages and disadvantages of the synchronverter considering the applications reported through this document.
1.6. Organization
The rest of the paper has been organized into six more sections. Section 2 explains the methodology followed by the authors in this review. Section 3 presents the mathematical model of the synchronverter, representing the original model of the device without the need of an extra synchronization unit, the modes of operation, and the advantages and disadvantages of this device. Next, Section 4 shows improvements in and applications of the synchronverter classified by topics such as renewable energy and storage, stability analysis, and others. In addition, references associated with each subject are presented. Section 5 shows some challenges and future prospects. Finally, Section 6 presents the conclusions.
2. Methodology
This document was prepared following a detailed methodology as presented in Figure 1 and explained in the following section.
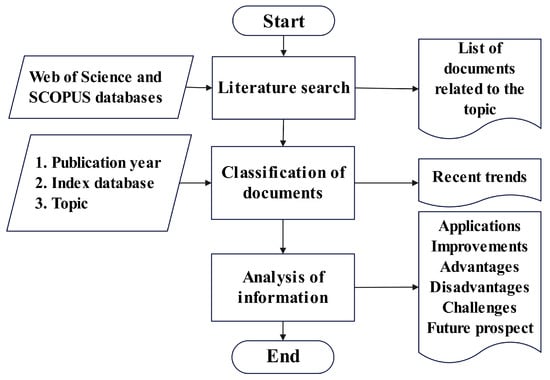
Figure 1.
Review flowchart.
From the results, a detailed classification was realized. Three main classifications were defined: (i) the publication year was useful to create Table 1 and Figure 2 and to observe the publications preferences of the authors; (ii) the index database to display the specific indexing databases where the journals are listed and create Table 1 and Figure 2 and Figure 3. This item may be helpful to new interested researchers in finding journals not only to read but also to publish their findings; and (iii) topics where the synchronverter has been used, such as new improvements to the algorithm or direct applications to several disturbances presented in real power grids.

Table 1.
Number of documents by type, database, and publication year.
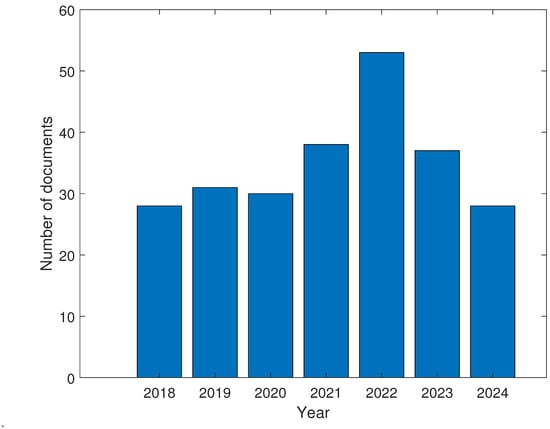
Figure 2.
Number of documents per year.
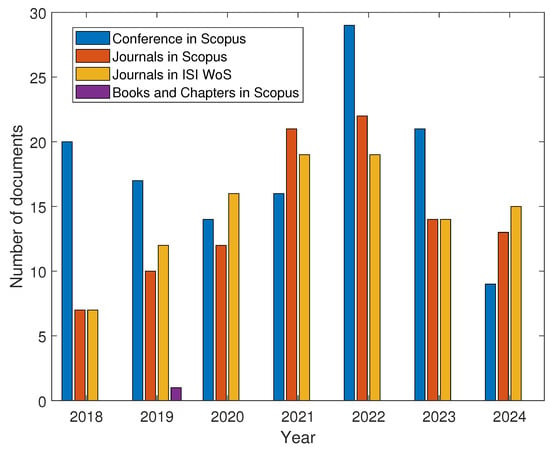
Figure 3.
Number of documents per year according to database and type.
From this point on, the documents that outline the improvements and those that highlight applications in the synchronverter are detailed in Section 4 to highlight the usability of the synchronverter. Recent trends in the use of the synchronverter are also highlighted.
After classifying the documents, an information analysis was performed. The results of the analysis allow for the obtaining of the advantages and disadvantages of using the synchronverter. In addition, challenges and future prospects are obtained and presented in the final section of this paper.
The query to obtain the documents was made in the Scopus and ISI Web of Science databases using the keyword “synchronverter” to visualize the evolution over time of the investigations based on the synchronverter or the virtual synchronous machine. Temporal delimitation was established between 2018 and 2025 to cover the last years, and only documents written in English were selected. It is important to note that the documents consulted in the year 2025 are limited to the date when they are indexed in the databases mentioned above. More documents are expected to be found during 2025, when those papers get indexed. Moreover, there are not enough documents published in 2025, so they are not included in this review.
2.1. Evolution of Synchronverter over Time
Table 1 shows the total number of documents per year classified by Conference—Scopus; Journal—Scopus; Journal—ISI Web of Science (WoS); and Book Chapter—Scopus. It does not have exclusive results from each of the databases. Therefore, for each of these columns, it was considered that the article must be indexed in Scopus or ISI Web of Science. From Table 1, it is observed that the interest in the synchronverter is constant. In addition, the results show a slight increase and are expected to continue to grow in the upcoming years.
The synchronverter has undergone various modifications and new applications that allow us to solve common disturbances in the power system and microgrids with NCRES operating in island mode. Other advances are expected, as most of the documents consulted provided information on future work that is promising for the integration of RES. Figure 2 shows the total number of documents per year in all databases, which were 240 documents in the time frame, limited by the time frame (2018–2024), and the language (English). The year 2022 had a notable increase, but the rest of years have an average of 34 articles per year.
The data presented in Table 1 is illustrated in Figure 3. Although there is no clear upward trend in the number of investigations per year, there is still interest in the time and quality of research aimed at addressing the challenges involved in connecting inverter-based technologies to the interconnected power grid.
Scopus has a higher number of documents, but that is basically because Scopus classifies a larger number of journals compared to ISI Web of Science. In addition, Scopus includes academic conferences that ISI Web of Science does not.
2.2. Bibliographic Analysis
A bibliographic search was conducted in the Scopus and Web of Science databases using the keyword “synchronverter”. The temporal filter covered the period from 2017 to 2024, allowing for the observation of emerging trends in this technology. The search yielded a total of 240 documents, which were processed in RStudio version 4.3.2, using the bibliometrix and biblioshiny packages, to create thematic visualizations and structural metrics.
The analysis was performed using the Walktrap algorithm, which identifies communities within the graph through random walks. This method allows keywords to be grouped into two clusters that reflect significant co-occurrence patterns, facilitating the interpretation of the main trends and thematic relationships in the dataset. This analysis is shown in Figure 4.
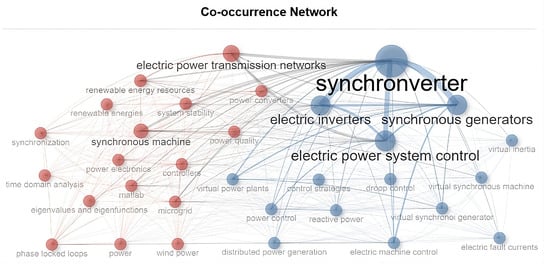
Figure 4.
Keywords Co-occurrence.
The network analysis reveals two distinct clusters. Cluster 1, shown in red, encompasses traditional electrical system concepts such as synchronous machines, electrical power transmission networks, and controllers. In contrast, Cluster 2, in blue, highlights emerging technologies, including terms such as synchronverter, virtual inertia, and electric power system control.
The size of the nodes in the network correlates with PageRank value, indicating a term’s overall relevance. Notably, “synchronverter” stands out as the most prominent node, boasting the highest PageRank (0.101) and betweenness centrality (26.612). This allocates the synchronverter as a crucial thematic bridge connecting both clusters. Other highly influential terms are “electric power system control” (betweenness: 9.443; PageRank: 0.066) and “synchronous generators” (betweenness: 6.379; PageRank: 0.062).
The findings demonstrate how synchronverter research aligns with both established and innovative domains, illustrating a clear transition from traditional synchronous machine-based approaches to advanced control architectures utilizing power converters and virtual systems.
The thematic map shown in Figure 5 illustrates the structural role of each thematic cluster through the analysis of co-occurrence keywords. The centrality (horizontal axis) indicates a topic’s relevance within the field, while the density (vertical axis) reflects its degree of internal development.
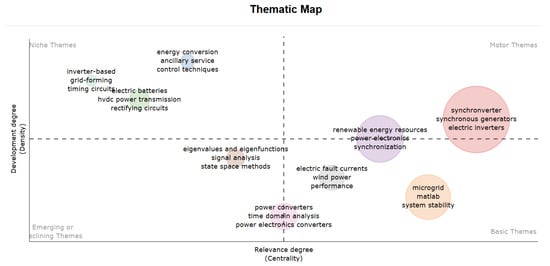
Figure 5.
Keywords of thematic map.
In the upper left quadrant are the Niche Themes, characterized by high internal development but low centrality. These are well-developed topics with weak connections to the core research field. This cluster includes concepts such as inverter-based systems, power electronics, grid-forming, timing circuits, electric batteries, rectifying circuits, design, energy conversion, ancillary services, and control techniques. These themes are often associated with specific applications or technologies and may represent mature research areas with potential for broader integration if their conceptual links are strengthened.
The upper right quadrant features the Motor Themes, which combine high density and high centrality. These are well-developed and essential topics for the structure of knowledge related to energy management and conversion in electrical power grids. Key areas in this group include power control, virtual power plants, and reactive power, crucial for modern distributed generation and advanced electric grid regulation.
The lower right quadrant includes the Basic Themes, exhibiting high centrality but low density. These concepts are fundamental to the overall structure of the field, but require further specialization and thematic development. This group includes terms such as synchronverter, electric inverters, electric fault currents, wind power, voltage control, power converters, time domain analysis, and power. The inclusion of synchronverter in this category confirms its central structural role in the recent literature, highlighting its significance in the technological transition from conventional systems to modern architectures.
Finally, the lower left quadrant contains the Emerging or Declining Themes, showing both low density and low centrality. This suggests they are either losing relevance or are still in early stages of development. This category includes concepts such as energy resources, distributed energy resources, system stability, eigenvalues and eigen functions, and damping. Although these topics currently have less structural weight, they could gain significance if addressed in new research lines, particularly in contexts where system stability and the integration of distributed energy sources are critical.
The thematic map provides an integrated view of the conceptual structure of the field, effectively identifying both well-established areas and those with high development potential. This analytical tool is invaluable for guiding future research, focusing efforts on strategic topics, and recognizing emerging opportunities that can significantly strengthen energy management and control in advanced microgrids.
3. Mathematical Model of Synchronverter
Grid-forming inverters are classified into three main groups: (i) Traditional Control Methods; (ii) Advanced Control Methods; (iii) Other Control Methods. Inside the first group, there are three main types of grid-forming inverters: (a) Droop Control; (b) Voltage-Source Inverter Control; (c) Virtual Synchronous Generator Control (VSG). The synchronverter is part of the second type (VSG) [11].
Zhong and Weiss proposed the mathematical model of the synchronverter [7]. This device is an inverter capable of mimicking an SG. It may mimic a generator where non-conventional renewable energy sources (NCRESs) can participate in both voltage and frequency regulation. A synchronverter comprises two parts: power and control. Figure 6 presents the power part as a three-phase power circuit that contains a three-phase full-bridge inverter connected to a local load as a star-connected impedance , and an LCL filter to smooth the voltage delivered to the grid. This figure shows the equivalent power grid represented by three independent voltage sources: , , and . The DC bus may be fed by photovoltaic arrays, wind turbines, and storage devices; however, it is important that the DC voltage level is controlled.
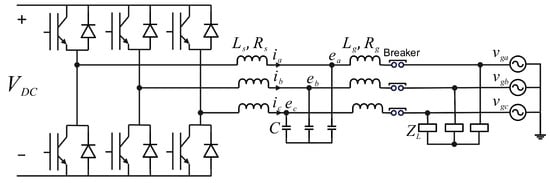
Figure 6.
Synchronverter connected to a local load and the power grid—power part.
Phase voltages (, , and ) and phase currents (, , and ) are measured in the LCL filter. These values are used to calculate the active and reactive power of the inverter ( and ). The induced voltage calculated in the control part triggers the bridge gates.
The original synchronverter was not able to self-synchronize with the power grid without the aid of an independent synchronization unit such as a Phase-Locked-Loop (PLL). The self-synchronization was added by the same authors in [14]. Figure 7 shows the block diagram of the control part used to obtain the magnitude of the induced voltage and its phase angle . This process is accomplished through three loops: the frequency control loop, the voltage control loop, and the synchronization loop.
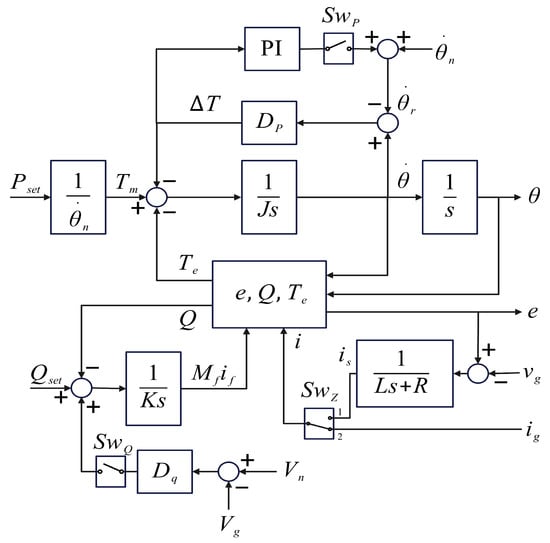
Figure 7.
Control part of the synchronverter with the self-synchronized loop [14].
The loop at the top of Figure 7 represents the frequency regulation control algorithm used in SG. Equation (1) presents the swing equation of an SG. The term is the derivative of the frequency of the grid and J is the moment of inertia. The term is the mechanical torque, and is the electromagnetic torque. In addition, is the damping factor of the machine, and is the frequency of the grid.
The PI controller keeps the difference between the nominal and actual frequencies at zero. Initially, the frequency control loop avoids sharing power between the inverter and the grid and is activated to perform synchronization with the switch . Once the synchronverter is synchronized, this switch must be opened.
The term represents the mutual inductance between the stator and the rotor coil. The term is the field current and i is the three-phase current in the stator. In addition, the term is the active power delivered to the system, is the nominal angular frequency of the grid, and the operators and are given in Equations (4) and (5).
The moment of inertia, together with an integrator , produces the system frequency, which is implemented to obtain the angular velocity . An additional integrator is used to acquire the phase angle , which corresponds to one of the outputs of the control part.
The left-bottom side of Figure 7 is the control loop concerning the excitation of the synchronous machine. The reference value of the reactive power is established as a constant (), and the shared reactive power Q is calculated and fed back into the loop. The voltage magnitude is estimated using Equation (6) and filtered to avoid second-order harmonic ripples [7].
where is the voltage magnitude; , , and are the phase voltages measured in the power grid. The measured voltage is subtracted from the nominal voltage. It is amplified by the voltage droop coefficient , which represents the relationship between the change required in reactive power and the change in voltage . This is activated with the switch to work in mode 1, which uses the reference value of the reactive power, or in mode 2, which is the control of the reactive power droop.
When is open, the amplitude of the excitation voltage is obtained from the tracking error between and Q, and the integrator with gain , where K is the counterpart of J, as observed in Equation (7). When is closed, the error between the grid voltage and the nominal voltage is considered; it activates the reactive power droop control as expressed in Equation (8). The voltage deviation can be observed in Equation (9).
where Q is the reactive power calculated using Equation (10).
The lower right loop in Figure 7 corresponds to the virtual current loop [14]. The virtual current is calculated using the difference between the measured grid voltage and the induced voltage e calculated from the synchronverter. This current is multiplied by the transfer function of the filter inductor impedance . This current is used in Equations (2), (10) and (11) for the synchronization stage. Once the synchronverter is synchronized, the virtual current is no longer used; instead, the measured output current i from the synchronverter replaces it. The switch leads the process. When is in position 1, the virtual current is considered. However, when it is in position 2, the actual current i is used. The second output of the control part is the magnitude of the induced voltage, which is calculated using Equation (11).
The operation modes of the self-synchronized synchronverter are presented in Table 2, based on [14].

Table 2.
Operation modes of the self-synchronized synchronverter.
The switch allows for the transition among the use of virtual or actual current in the synchronverter calculations. The virtual current is used when is in position 1, while the actual measured current is used when is in position 2. From Table 2, it is evident that when is in position 1, the only feasible combination is when is ON and is OFF. As a result, the active power loop ensures that the steady-state error remains at zero between the nominal frequency and the synchronverter frequency, while the reactive control loop tracks the point. This process guarantees the self-synchronization of the synchronverter.
When is in position 2, there are four possible operation modes:
- P-mode and -mode: this mode keeps the steady-state error at zero between the grid and synchronverter frequencies. The reactive control loop is in the droop control mode, which considers changes in Q to adjust the terminal voltage.
- P-mode and Q-mode: there are no changes in the active control loop. The reactive control loop only follows the point .
- -mode and -mode: both power loops are in the droop control mode. The shared powers change to adjust the frequency and the terminal voltage.
- -mode, Q-mode: only the active power droop control is activated, while the reactive control loop follows the point .
The synchronverter is a good choice for emulating synchronous generators that usually work with droop control strategies. The emulation of synchronous machine inertia may help the grid operators to maintain the stability of the system with the aid of the self-synchronization process and the other four operation modes described above. It is important to note that the synchronverter response is faster than conventional synchronous machines, and its primary frequency response and voltage regulation are limited to the source capacity. These are the main reasons why several researchers have focused on new developments to make the synchronverter an even better option for the challenges of the future power grid, which will have many NCRES based in inverters.
After presenting the mathematical model of the synchronverter, Table 3 highlights the most important merits and drawbacks that the synchronverter may have.

Table 3.
Advantages and disadvantages of the synchronverter.
In general, the synchronverter is used as a voltage-controlled source, which is very similar to the feature of the synchronous machine. In addition, advanced control strategies can be integrated to increase the inverter response during events or to protect the physical device against fault currents. In contrast, computation times may be high due to additional settings that might be added to make the synchronverter a more secure control strategy.
Researchers can use the information presented in Table 3 to analyze whether the synchronverter is a solution to the problem they are facing.
4. Recent Improvements and Applications Using the Synchronverter Control Strategy
This section examines some improvements and applications where the synchronverter has been applied. The original synchronverter model works appropriately as long as it is used to connect an inverter to a robust and balanced electrical network. However, the current cases differ from the optimal scenario. Therefore, some improvements have been required in the mathematical model to address the common problems that a real electrical network or a microgrid may have.
4.1. Modifications of the Original Synchronverter and Experimental Tests
Moulichon et al. [15] proposed an observer-based current controller for a virtual synchronous generator (VSG) in the presence of unpredictable and unmeasured loads. It comprises a linear quadratic regulator that incorporates an integrator and a state observer. The intention was to supply some loads that were not known in advance and unpredictable, represented as nonlinear and unbalanced loads. According to the results, this control strategy is necessary to handle common load perturbations in the industry and incorporate a non-simplified synchronous machine model, as VSG may behave similarly to diesel generators. The authors pointed out that some parameters of the VSG must be changed to avoid deterioration of the inverter during harsh events such as faults.
The authors in [16] mentioned that the model predictive control (MPC) is a good tool in real applications. They modeled a photovoltaic power plant together with a synchronverter and demonstrated that MPC may be tied to a synchronverter, improving its response and capabilities, especially because it is possible to state a specific control aim. A drawback of this model may arise when the optimizer finds a solution generated by inaccurate initial conditions due to the switching transistors. The authors stated that more sophisticated filters or state estimation must be designed or used to solve the above issue.
The control of voltage and reactive power can be performed with synchronverters, as exposed in [17]. Ramirez et al. performed hardware-in-the-loop experiments using Matlab/Simulink®. They evaluated the performance of the synchronverter under different operating conditions and became quite relevant when a reactive power control loop is activated.
The IEEE 39-bus test system was used to compare different VSG control strategies [18]. The authors evaluated the following. ISE-Lab, synchronverter, Kawasaki Heavy Industries Model, and power synchronization control. The comparison was based on different network conditions such as ratios, network faults, and load types. The authors implemented the case study in the OPAL-RT real-time simulator. The synchronverter performed better than the other VSG control techniques in each scenario and was more suitable for its integration into distribution power networks because it considered dynamic loads.
Synchronization is commonly preferred before coupling the inverter and the power grid. In [17], the authors proposed a different way to synchronize the synchronverter with the power grid. First, the inverter voltage amplitude is compared with the grid voltage amplitude. To do this, an estimated voltage is obtained using the angle, the mutual inductance of the virtual field, and the field current as follows: . The error of the estimated and the grid voltage passes through a constant called to obtain the necessary reactive power to lead that error to zero. Once the inverter is connected to the grid, becomes zero. The angle is established with the aim of a reset process based on synchronization and connected step. The proposed method was able to share the reactive power satisfactorily using a hardware experimental setup.
Some PLL-less self-synchronization approaches have problems such as the lack of uninterrupted power supply capability during the synchronization process, or delays and uncertainties depending upon grid conditions. In [19], a Fourier analysis-based synchronizer was proposed for the synchronverter. The authors used the uninterrupted power supply capability as a fast solution to synchronize the synchronverter without obtaining the difference between the inverter voltage and the grid voltage. This proposal was compared with the differential root mean square voltage (DRMSV)-based approach, improving the speed and the certainty under perturbed grid conditions.
4.2. Renewable Energy and Storage
Inverters are not only applied to NCRES, as they are useful to compensate the electrical power network, such as static synchronous compensators (STATCOM), dynamic voltage restorers (DVRs), and others. However, based on interest in DG and global warming, investors are playing an important role in integrating NCRES. They are required not only to inject power but also to take an active part in auxiliary services for frequency and voltage regulation.
In [15], a synchronizer based on a fuzzy logic controller is proposed for a grid-connected solar energy system with an adaptive damping factor. A conventional PI control-based synchronverter is not equipped with an adaptive damping factor () or a digitized intelligent controller to manage fast response solar input. The authors proposed a new fuzzy logic controller framework to operate the synchronverter in a grid-connected solar power system. The damping factor is controlled in real time to achieve a balance between speed and stability for frequency error correction based on the frequency difference. The results indicate that the frequency deviation is reduced to at least 0.2 Hz. The authors proposed undergoing works to take advantage of the synchronverter virtual part to increase its performance during harsh events. While a fuzzy logic controller for synchronverters may be helpful in reducing frequency deviations in stability issues, a reduction of only 0.2 Hz may not be enough for grid scenarios where a great amount of NCRES power is injected.
Adaptive virtual inertia is a way to modify the response of a synchronverter. In [20], this concept is employed to control a wind turbine connected to the electrical network through a back-to-back converter. A linear dynamic system for the proposed adaptive virtual inertia was developed, which uses the frequency deviation and the rotor angle deviation of the synchronverter model as state variables and the virtual inertia together with the frequency drop gain as control variables. Additionally, a linear quadratic regulator (LQR) was used to ensure the optimal balance between the fast frequency response and the voltage of the wind turbine during disturbances that may exist on the grid. The frequency deviations were satisfactorily minimized, as shown in the simulations in comparison with the original synchronverter model. Adaptive inertia may not always yield optimal results, as real-world disturbances can be unpredictable and multifaceted.
Wind turbines generally have variable speeds and generate energy regardless of intermittent resources. However, they require a back-to-back device that converts the generated AC into DC and returns it to be converted to a constant-frequency-controlled alternating current. To achieve this, variability in the virtual inertia of the inverter is required. Therefore, in [16], a synchronverter was used with the ability to modify virtual inertia and virtual damping to minimize mechanical loads and achieve a useful life of longer, sufficient to ensure the economical operation of the turbine. The authors proposed a PID control for shaft torque as an additional controller of a variable-speed wind turbine connected to a virtual synchronous machine on the grid side. The results obtained with the simulation indicate that the method is effective when the fastest reach of the steady-state values is optimized individually. However, the objective function could include other goals such as minimize the overshoot, etc.
It is a common practice to install a battery energy storage system (BESS) together with a wind farm to improve virtual damping or simply have energy storage in case it is needed when the natural wind resource is not able. The authors in [21] presented a microgrid model with two main energy sources comprising diesel generators, double-fed induction generator-based wind turbines (DFIG) and a BESS. A complete linearized model considered the resources mentioned above to derive a transfer function between the BESS damper signal and the DFIG torque. A bandpass filter was designed to shift the torsional mode eigenvalues to improve the damping ratio on a complex plane. The dynamic response of the system was tested by means of changes in the load using MATLAB/SIMULINK with very good results. However, the initial costs and ongoing maintenance of battery systems can be prohibitive and their performance can degrade over time, leading to reduced effectiveness in energy storage and management.
The IEEE 14-bus test system was modified to match the parameters of a real hydroelectric power plant in [22]. The authors used this information to emulate the power generated by a DFGI-based wind turbine connected to the system. They developed a comprehensive state-space model to represent both the mechanical and electrical variables of the wind turbine. The synchronverter was selected to operate on the grid-side converter and provide frequency support from the wind turbine by a virtual resistor. The results were obtained from the PSCAD/EMTDC software, demonstrating that the system meets the requirements of the power grid and provides frequency support. The authors pointed out that an optimal tuning method for the parameters of the synchronverter could improve its behavior.
The synchronverter is a suitable choice for integrating NCRES with the power grid, but there are some important concerns to consider. Although advances in inverter technology and control strategies for renewable energy systems show promise, they also present a range of challenges that must be carefully considered. The complexity, costs, and potential reliability issues associated with these systems can outweigh the benefits, making it essential to evaluate alternative approaches to grid management and the integration of renewable energy. Innovative solutions, such as energy storage systems that use advanced battery technologies or hybrid models combining various renewable sources, may offer more sustainable and efficient alternatives to traditional microgrid setups.
4.3. Stability Analysis
Power systems based on synchronous machines are robust due to the rolling inertia reserve in the network. Modern power systems are migrating toward the implementation of power electronics, such as NCRES, energy storage systems, and active grid compensation. They require power conversion from DC to AC or vice versa. They are classified as solid-state devices, so they do not have an inertia reserve. Therefore, VSMs are suitable options to keep the power grid within a stable range.
The transition between grid-connected and island modes of a synchronverter must be smooth to provide reliable use. The concept of distributed energy resources interconnected through inverters is studied in [23]. A new virtual flux link and virtual torque-based synchronization technique are integrated into the synchronverter controller to provide plug-and-play capability of voltage-controlled inverters and their smooth transition between the two operating modes. Comprehensive mathematical modeling, design, and analysis are provided and real-time simulations are used to validate the effectiveness of the proposed technique.
Another important factor for massive integration of NCRES lies in the interoperability of two or more synchronverters. When two synchronverters operate in parallel, they can be synchronized without major problems [24]. The stability robustness of the synchronverters is evaluated with the analysis, resulting in a reduction when they work together. A way to overcome this limitation is to implement virtual variable impedances in the control algorithm. A precise state-space model of the system under study is developed by adopting the component connection method, and robust stability analysis is validated against simulations in the time domain. Experimental results are carried out on a power test bench using hardware-in-the-loop technology.
The probabilistic evaluation of the transient stability of a 13-node IEEE test system with four synchronous virtual machines is presented in [25]. The model used is the limited-frequency synchronverter with an integral voltage controller. Many existing potential failures in a power system with parallel computing of Graphics Processing Units (GPUs) were simulated to ensure convergence of the probabilistic approach. The results quantified the transient stability of the synchronverter system in terms of different locations, penetration levels, and parameter selections with the aim of a Neural Network Predictive Control approach.
In [26], the inertial response is decoupled from the primary frequency response. The authors proposed a condition that allows the inverter to have a critically damped inertial response. They achieved this by improving the damping of the machine and decoupling the active and reactive power control loops. Real-time simulations were performed to evaluate their proposal against the original synchronverter model. These simulations improved stability by enhancing damping, decoupling the power loop, and achieving a better primary frequency response. The model must be evaluated from the point of view of the power system.
Zhong et al. [27] improved the original model to maintain the frequency and voltage of the synchronverter within the specified ranges while maintaining the original functionality. Analytical methods are used to find the stability region given by the system parameter. This lets the proposed method work continuously in the stable region and reach a single equilibrium if the power delivered is within the region. The tests were carried out through real-time simulation with the OPAL-RT hardware for connection to a strong network and a weak network, and the results were satisfactory.
In [28], the authors compared three of the most used grid-forming converters, namely the VSM, the synchronverter, and the grid-forming droop control. They compared their response to that of an SG. Evaluations are conducted to validate that grid-forming converters are much faster than the SG in a system frequency event. The conclusion is that inverters may play an important role in both frequency and voltage control.
The synchronverter is not the only control approach to connect NCRES to the network. There are other techniques such as the virtual synchronous generator [29], droop control [30], and virtual oscillator control [31]. Although these techniques use the swing equation of synchronous machines, the synchronverter explicitly models a physical machine, and both mechanical and electrical characteristics of a synchronous generator. This fact allows grid operators to treat the NCRES as a conventional rotating machine from the perspective of the system.
4.4. Virtual Impedance
Synchronverters can be synchronized with the power grid without requiring a phase-locked loop (PLL). In addition, a virtual impedance can be integrated into the control algorithm to improve the dynamics and current limitation capabilities of the power system. Research has shown that the use of virtual impedance methods combined with inertia control can assist in improving the stability of the power system.
In [32], a variable virtual impedance method is used to guarantee the correct operation of AC microgrids that operate connected to the network or in the island mode. The method proposed by the authors is mathematically modeled and simulated in Matlab®, demonstrating that it is capable of adapting to variations in load and generation.
The original model of synchronverters is based on proportional and integral control. However, in [33], an observer-based current controller is proposed for a VSG to improve its operating performance. This model integrates a PI controller with a state observer. In addition, this model is compared to a traditional PI and a PI with a virtual impedance for the filtering stage. The comparison demonstrates that the proposed method can supply power to unknown and unpredictable loads with the help of the state observer.
In [34], a theoretical comparison of different VSGs implemented in inverters is carried out. The VSG is proposed as a method to add virtual inertia to the grid, emulating the rotating mass of an SG in the control algorithm of an inverter. Virtual impedance is added to the converter output to improve voltage stability issues. In addition, a theoretical comparison is made between different VSG topologies, including the VSM method and the synchronverter.
In [35], the effect of output resistance on the oscillation frequency in a parallel virtual synchronization system is analyzed. It also proposes a method to suppress the active power oscillation by compensating voltage in the transient state. It is concluded that the output power of the VSM is largely determined by its position in the network and that active power oscillation can be suppressed and system stability improved by the proposed method. Voltage changes at the terminals affect the output power of VSMs in a complex network. During the transient state, the voltage output of VSMs is forced to change because of the lack of phase-angle adaptation. The proposed method effectively suppresses the active power oscillation and stabilizes the output voltage.
In [36], a PQ decoupling technique based on a virtual power circle is used for a VSG connected to a weak grid. The proposed technique uses a virtual impedance to independently control the active power (P) and the reactive power (Q). The effectiveness of the proposed scheme is validated using the synchronverter connected to a weak grid in a MATLAB/SIMULINK environment. The addition of a negative virtual impedance may result in a high current when faults occur. The authors mentioned that they will work on a solution in future work.
Virtual impedance, while intended to improve voltage stability, can introduce additional complications and may not be universally effective across different grid conditions, such as (i) nonlinear loads; (ii) mismatched line impedances, which can cause issues with power sharing and voltage compensation, and using a high value of virtual impedance can cause a large voltage drop at the PCC; and (iii) increasing virtual reactance, which can increase the oscillation in the system.
However, adaptive-tuning controls such as robust control theory, Lyapunov stability theory, impedance-based stability analysis, Model Reference Adaptive Control, and others may be implemented.
4.5. Active Compensation
Inverter-based power plants may add active compensation to the power network. This ability can be achieved because the parameters can be changed at any time based on to the circumstances or events that take place on the network. A synchronverter is able to modify some parameters against a fault and then change them again to face a frequency deviation.
In reference [37], the authors proposed a synchronverter to maintain the voltage profile in the PCC and the load of a network with several microgrids that have diesel, solar, and wind generators. Interconnected microgrids are used to overcome the intermittent nature of distributed generation sources. Synchronverters can synchronize distributed energy systems and can improve the stability and performance of microgrids. The frequency and voltage control in synchronverters can keep the voltage profile and other parameters within the appropriate limits.
In [38], a new control method called positive–negative sequence synchronverter applied to unbalanced alternating current networks is proposed. The synchronverter is able to limit the output currents during unbalanced voltage drops and when the network is unbalanced. Additionally, this method helps reduce power oscillations in synchronverters connected to the network when faced with network disturbances. It can be considered as an effective solution to implement in grid converters that emulate synchronous machines in distributed generation applications. The experimental study validated the proposed method through experimental results.
In summary, synchronverters can act as an active filter at the same time they deliver power to the grid. These advances solidify synchronverters as a promising solution for synchronous machine-emulated grid converters, fostering the seamless integration of renewable energy sources and strengthening the resilience of modern power networks.
4.6. Harmonic Reduction
Synchronverters have been investigated for their potential in mitigating harmonics through various control strategies. Through advances in control strategies and system design, synchronverters can effectively minimize harmonic distortions, ensuring the delivery of high-quality power to the grid. For instance, enhancing current loop response times can effectively reduce harmonic distortions.
In [39], the authors applied a low-pass filter to the current feeding loop to enhance the stability of the synchronverter and eliminate power ripples. They used a small signal model of the conventional synchronverter and studied the effectiveness of power ripple elimination. They also analyzed the impact of an unbalanced grid voltage on the conventional synchronverter and proposed a resonance-based strategy to control current harmonics and power ripples in an unbalanced power grid. Comparative experimental studies were conducted to confirm the effectiveness of the proposed strategy in both auto-synchronization and power control modes by reducing the Total Harmonic Distortion (THD) index.
Harmonics at the output of the synchronverter may be decreased by a proper filter design. In [40], the authors designed three filter topologies to reduce both the voltage and current harmonics at the PCC. They used three configurations, such as L-, LC-, and LCL-filter. Finally, they selected the LCL-filter design and validated by means of simulation in MATLAB/SIMULINK that the THD was reduced.
In [41], a fast current controller was proposed and added to the VSM algorithm to provide compensation for delays related to the computation process. It also eliminated both the DC components of the grid-side currents and the zero sequence of the output currents, which helps in the case of unbalanced voltages. A virtual capacitor was also added to diminish the THD at the PCC. This new controller was compared with other current control algorithms, obtaining better results through simulations.
Although the synchronverter can eliminate harmonics delivered to the power grid by selecting the appropriate virtual filters, it may slow the response to transient events. Furthermore, there is a lack of real implementation papers dealing with the reduction in harmonics.
In contrast, dedicated Active Power Filters (APFs) eliminate and adapt to harmonic distortions produced by non-linear loads. However, enhanced synchronverters can both reduce harmonic distortion and manage bidirectional power flow. In addition, APFs require dedicated filters while synchronverters may use the same hardware for voltage support, frequency support, and filtering harmonics.
4.7. Unbalanced Voltage and Asymmetric Faults
Unbalanced voltage conditions can lead to negative components in grid voltage, incorrect operation of different loads, and low performance of voltage source inverters. Synchronverters can contribute significantly to the reliable and efficient operation of power systems.
Some authors have focused on the problem of connecting the synchronverter to unbalanced and unsymmetrical networks. The authors of [42,43] studied the fluctuation of the power and harmonic components of the current in the presence of the negative voltage component in the PCC that only appears when there is a voltage imbalance. In the works mentioned, two similar proposals are presented, where it is required to apply the concept of decomposition of symmetrical components to obtain positive and negative components of both the voltage and the current. Counting on the sequence variables, they proposed adding control loops for voltage and current to calculate a reference current that allows removing power fluctuations, unbalanced current delivered to the network, and balancing voltage profiles in island mode. The most significant difference between the two proposals lies in the reference frame of the coordinates used to perform the control: and , respectively. The authors of these papers used a PLL to synchronize the synchronverter and decompose symmetrical components, taking as a reference the voltage and the phase angle delivered by the PLL. In both cases, a drawback is observed, either the double frequency oscillation of the delivered power or the additional load for the microprocessors responsible for the synchronization of the inverter.
In [44], the operation of a STATCOM based on a synchronverter with voltage unbalance compensation functionality, called S-STATCOM, is presented. This document provides details of the operating modes of the S-STATCOM and its capability to share reactive power. It also mentions the system start and synchronization process and the compensation of voltage imbalances. The proposed device utilizes tilt control to linearly share reactive power and regulate the bus voltage to achieve the desired distribution. S-STATCOM has several operating modes, including the start mode and six power operating modes. The compensation of voltage imbalances is tested using an added inductive impedance in the power circuit of S-STATCOM. The stability of this proposal must be evaluated during frequency disturbances.
In [45], the operation of synchronizing an inverter connected to the power grid is presented using a VSG controller. Different methods for limiting the fault current and maintaining frequency stability are also discussed. Synchronized operation of an inverter connected to the electrical grid using a VSG controller does not change the original operation mode of the electrical grid. The fault current can result in an unbalanced three-phase current or overcurrent and causes frequency fluctuations in the output power. Various control strategies are proposed to limit the current of the fault, such as low voltage ride-through techniques and differential current control. This method has some limitations such as the non-stationarity of current prediction was not considered, and the time control was not studied comprehensively.
In [46], three fault ride-through strategies are proposed for synchronverter-interfaced energy resources to address power oscillations and excessive current generation during unbalanced faults. The first fault ride-through strategy uses an instantaneous active and reactive control to mitigate power oscillations. The second fault ride-through strategy utilizes average active and reactive control to maintain average power delivery and sinusoidal phase currents. The last strategy employs comprehensive instantaneous active and reactive control to eliminate power oscillations and maintain sinusoidal currents. Activation of the PMC controller reduces power generation and limits current generation during voltage drops. The proposed strategies enable the reduction in power oscillations, control the generated peak current, manage the power factor, and regulate the production of active and reactive power according to the conditions of the grid. However, this work shows that although good results are obtained with the proposed strategies, more work must be done regarding the accuracy of the power tracking capability.
Auto-synchronization is complex when the synchronverter is connected to a weak unbalanced power grid. In [47], the authors performed synchronization using the positive sequence of a decomposition into symmetric components. The output variables of the synchronverter can be obtained using the positive sequence. This was possible because the positive sequence contains three balanced signals, as required by the synchronverter control algorithm. But when the voltage imbalance is as high as in faults, it was not possible to follow the voltage magnitude of the grid adequately.
After revising several documents related to the compensation of voltage imbalances due to load unbalance or faults and using a synchronverter model, it can present stability problems, such as frequency disturbances. Additionally, undesired results may arise because it is complicated to predict the non-stationary current, or the adequate activation time of control actions. Finally, it is not possible to completely eliminate active and reactive power oscillations while delivering balanced currents at the same time.
4.8. Parameterization and Design
The synchronverter can also be used to identify the parameters that improve the response of the system. They have been used for the design of electrical systems in conjunction with the synchronverter to obtain better responses to different events.
In [48], the authors present a design of a synchronverter, which functions as a simulated SG and allows renewable energy sources and distributed generation systems to contribute to the control of the frequency and voltage of the grid. They used advanced computer simulations to design and test the synchronverter. The power component converts direct current to alternating current, while the control component manages switching and timing. The synchronverter is evaluated under various operating circumstances using simulation software. This solution maintains consistent voltage and frequency and enhances overall system stability. The solution can integrate multiple inverters into the grid to improve power stability, efficiency, and quality.
In [49], the authors discussed the equivalence of the tuning of microgrid controllers, regardless of the control architecture and the tuning parameters used. It is highlighted how they can be reduced to similar dynamics and how they can be fitted equivalent to the known Droop coefficients. The results show that the resulting dynamic equations and the fitting method guarantee an equivalent parallel active and reactive power distribution, controlling the rate of change in the deduced frequency and voltage signals and their steady-state values. Furthermore, the method is intuitive and easy to implement and represents the physical meaning of each adjustable value of the different controllers.
In [50], a small signal analysis of the improved droop controller in VSG is performed to recommend a practical and tunable maximum power harnessing mode. The simulation is performed in Simulink, and the impact of adjusting the virtual inertia and the time constant of the low-pass filter on the dynamic response of the controller is analyzed. The results show that adjusting the virtual inertia and time constant of the low-pass filter has an effect on the dynamic response of the controller. This research found that adjusting the virtual inertia in the active power loop of the improved droop controller does not affect the response speed of the droop characteristic effectively. An increase in the time constant of the low-pass filter will postpone the maximum power recovery time over a large interval, providing the controller with considerable flexibility in determining the time for post-disturbance maximum power harnessing.
The synchronverter, as most of control algorithms may be adjusted to the circumstances. To do so, it is necessary to select the control parameters in accordance with the purpose to be tackled. This feature allows any distributed generation unit to connect to the power grid, satisfying the network requirements.
4.9. Short-Circuit Analysis and Protection Against Faults
Reliability and security in a power system require a detailed short circuit analysis and the implementation of an optimal protection scheme. Hence, the synchronverter is useful in providing virtual inertia to enhance dynamic stability in power systems. In addition, synchronverters can help system protection schemes minimize the operating time of relays. Furthermore, synchronverters with fault ride-through capabilities enhance microgrid protection during balanced and unbalanced faults.
In [51], optimal control and protection in microgrids are discussed. They employed synchronverters and the theory of modified instantaneous power. It also addresses challenges of power quality and protection faced by microgrids, especially due to the presence of distributed generators interfaced with inverters. In addition, grid codes and the current regulation for distributed generators via the inverter interface are discussed. Synchronverters with the proposed fault ride-through strategies can seamlessly adapt to microgrid operation modes and switch between normal and fault conditions without switching actions. Optimal protection control (OPC) is achieved using the average power control (APC) scheme and the enhanced power control (EPC) scheme in synchronverters. The modified instantaneous power theory is used to obtain the optimal settings of time-inverse overcurrent relays (TIV-OCR) considering the network operation modes, the balanced and unbalanced faults.
In [52], a method is proposed to improve the inertial response in distribution networks with high penetration of renewable energy based on inverters. A protection scheme for the operation of recloser-fuse devices and an algorithm to improve this protection are proposed. The main objective is to prevent the failure of the recloser due to the resistance to the fault in the recloser-fuse protection scheme. Synchronverter-based CESS is used in distribution networks with multiple MG and high penetration of renewable energy to improve the inertial response. The effect of CESS on the protection of the recloser-fuse in distribution networks with multiple MGs is explored. An algorithm is proposed to improve the protection of the recloser fuse and prevent its failure due to fault resistance.
In [53], a single-phase synchronous inverter controller with overcurrent protection is proposed. It uses an active power output calculation method to synchronize with the grid and prevent the oscillation of active power output. The controller also includes a reactive power controller to adjust the reactive power output and contribute to voltage control in the distribution system. Additionally, the controller incorporates a current controller with a latched limit strategy to achieve fault ride-through during instantaneous voltage sag. The proposed controller operates as a GFM inverter without a minor loop during normal operation and avoids controller instability. It also prevents overcurrent overshoot in the event of a grid fault. The effectiveness of the controller was verified through numerical simulations and demonstration experiments.
Despite the fact that the synchronverter may achieve a good control for ride-through scenarios, it may generate unlimited currents during faults if it is not properly adjusted. On the other hand, if the synchronverter is focused on coping with overcurrent problems, it is possible to drag instability issues.
4.10. Microgrids
The synchronverter has also gained significant attention in the use of microgrids. This device can be used when the microgrid is connected to the network or is operating in island mode.
In [54], the synchronverter is used to control the stability of the microgrid with renewable energy sources. It is discussed how renewable energy sources can affect the stability of the power grid and how the synchronverter can solve this problem. The importance of adjusting the values of the synchronverter parameters according to the needs of the network is highlighted. The synchronverter can automatically inject active and reactive power according to the load requirements. However, the importance of conducting more research to evaluate the performance of the synchronverter in microgrids with various renewable energy sources is highlighted.
In [55], a synchronverter is proposed to integrate alternative energy generation systems into the grid and improve the distribution of energy flows. The synchronverter can operate connected to the main grid or isolated under autonomous conditions. The aim is to introduce energy generated by renewable sources into the microgrid.
In [56], the synchronverter is used in a microgrid to control the inverter and regulate the voltage and frequency. In addition, it helps maintain network stability and meets network requirements. The utility of the synchronverter is to efficiently control inverters in microgrids and distributed generation applications. This control system also provides virtual inertia, which helps maintain grid stability during variations in renewable energy generation and changes in load.
Hybrid microgrids combine networks with alternating current (AC) and direct current (DC). A study presented a 3D droop control linked to a VSG, achieving a more resilient system in the event of faults on the utility side [57]. Such a combination improved the stability issues regarding the quasi-static active and reactive power oscillations.
An adaptive virtual inertia was used to improve the dynamic frequency regulation of a microgrid [58]. The adaptive inertia was capable of slowing the dynamic process and improving the frequency nadir when it is outside the normalized value. It was also observed that when the frequency is restored to an acceptable value, the virtual inertia is decreased to accelerate the system dynamics and consolidate a quick transient process. Such results were acquired through an experimental hardware-in-the-loop approach.
An important scenario must be evaluated in future work, as there is a lack of research on the integration of more than three sources. Most of the papers evaluated have two renewable energy sources and a storage system, such as a battery array.
4.11. Other Applications
Several works have been done on more practical and direct approaches, such as electric vehicles [59], single-phase designs to connect solar panels located on the roofs of homes [60], transmission and connection in HVDC [61], among others.
4.12. Summary
Table 4 shows a list of references that improved the original synchronverter model to address the real problems presented in electrical networks, and the applications of the synchronverter in recent years, based on the scientific literature. This table may be used for both junior and senior researchers who are working on grid-forming inverter control strategies. This table contains papers in which the authors developed experimental tests using hardware-in-the-loop approaches or even with real elements. In addition, this table includes works where the researchers used case studies proposed by the IEEE. Furthermore, the table contemplates works in which the authors improved the synchronization process of the VSM.

Table 4.
Recent applications of the synchronverter.
In summary, the synchronverter is a feasible solution to face the challenges of integrating the virtual machine into a power grid with a large number of synchronous machines. The section reviewed improvements to the original mathematical formulation of the synchronverter, addressing limitations of the original model. Some papers show that some experiments and case studies have been conducted using the synchronverter for electrical networks and microgrids. Increasing publications highlight the interest in synchronverters. Some of the applications include power decoupling, primary frequency responses, and damping improvement. Techniques such as virtual impedance and adaptive inertia help manage unpredictable loads and ensure stability, outperforming traditional methods in maintaining system frequency and voltage. Advanced control strategies, such as model predictive control and synchronization improvements, enhance the response of the synchronverter. Diverse approaches, using PLL for synchronization and Fourier analysis, validate effectiveness, aiming to integrate more resilient and adaptive synchronverters into modern electrical grids.
From the consulted documents, there are also some cautions concerning the synchronverter. (i) Some models were evaluated in simulations but might need an assessment from a power system perspective. (ii) Some parameters of the VSG must be changed to avoid deterioration of the inverter during harsh events, such as faults. (iii) When the MPC is integrated with synchronverter, the optimizer may find a solution generated by inaccurate initial conditions due to the switching transistors. (iv) If synchronization is performed only by positive sequences, it may be difficult to properly follow the magnitude of the grid voltage. (v) If an additional unit is required for synchronization purposes, an additional load is added to the microprocessors responsible for synchronization. Therefore, more studies are required to evaluate real scenarios in real power grids and to develop solutions to the drawbacks mentioned here.
In addition, the synchronverter has been modified to fit the practical scenarios required by a real power system. The literature showed some relevant applications of the synchronverter for NCRES, electric vehicles, distribution networks, and transmission networks. The role of grid-forming inverters, such as synchronverters, in maintaining frequency and voltage stability was highlighted. Applications of VSM were reviewed for addressing stability issues, with techniques such as virtual impedance and adaptive controllers. Mathematical modeling and simulation play a crucial role in improving microgrid dynamics and transient stability.
Several challenges such as harmonic distortion were identified, and proposed solutions included enhanced inverter control methods and PQ decoupling. Synchronverters play an essential role in emulating the behavior of traditional synchronous generators, thus aiding in voltage and frequency stability in microgrids, with applications in both grid-connected and islanded systems. Despite progress, further research is required to optimize performance in various renewable energy scenarios.
Finally, the most important gaps found in the literature span theoretical control, practical implementation, and system-level interactions. The following is a list of key gaps for synchronverters is presented below.
- Robustness and stability under diverse and extreme grid conditions.
- –
- Weak grids and low short-circuit ratio (SCR): Synchronverters are often challenging to stabilize in very weak grids, where the coupling between active and reactive power is strong. The development of robust control strategies and parameter tuning methods that guarantee stability across a wide range of SCR values is critical.
- –
- Asymmetrical faults and unbalanced conditions: While some progress has been made, ensuring stable operation and proper fault current contribution during unbalanced faults (e.g., single-phase faults) without excessive current or power oscillations remains a significant challenge. Fault ride-through (FRT) strategies need further refinement for unbalanced conditions.
- –
- Grid resonances and harmonics: Although synchronverters can contribute to harmonic mitigation, their inherent interaction with grid impedance can also lead to or exacerbate harmonic resonances. Robust methods are needed to identify, damp and actively compensate for resonances in various grid grid configurations.
- Adaptive and autonomous parameter tuning.
- –
- Online adaptive control: As grids become more dynamic and uncertain, fixed synchronverter parameters may not be optimal. Developing online, self-tuning, and adaptive control algorithms that ensure stability while optimizing performance (e.g., using AI/optimization-based methods like Reinforcement Learning) is a major gap. The trade-off between adaptation speed and stability guarantees is a key research area.
- –
- Model-Free control: Reducing reliance on precise grid models for tuning, especially in rapidly changing scenarios, is desirable. Exploring more data-driven or model-free adaptive control techniques is an important direction.
- Coordination and interaction in multi-synchronverter systems.
- –
- Scalability and decentralized control: Synchronverters, potentially from different vendors and with varying characteristics, must interact when operating in parallel in a large grid or microgrid. Developing robust decentralized or distributed control strategies that ensure stable power sharing, frequency/voltage regulation, and oscillation damping without extensive communication is crucial.
- –
- Interaction with traditional generators: Managing the transition and dynamic interactions between a diminishing fleet of synchronous generators and an increasing number of synchronverters, especially during disturbances, requires more detailed study and coordination strategies.
- –
- Interoperability: Establishing common standards and protocols for synchronverter communication and control to ensure seamless interoperability between devices from different manufacturers.
- Optimal placement, sizing, and economic viability.
- –
- Grid planning and integration: Developing comprehensive methodologies for optimal placement and sizing of synchronverters in future grids to maximize their benefits (e.g., inertia support, fault current contribution, black start capability) while considering economic factors and grid constraints.
- –
- Cost–benefit analysis: A detailed techno-economic assessment comparing the overall system benefits of synchronverters against their increased complexity and cost compared to traditional grid-following inverters.
- Practical implementation challenges.
- –
- DC-Link dynamics and energy storage integration: The DC-link capacitor plays a crucial role in synchronverter stability and transient response, especially during faults. Optimizing its sizing and integrating energy storage systems (BESS) for enhanced ride-through capability and damping, particularly in dynamic scenarios like variable renewable generation, is an ongoing challenge.
- –
- Mechanical stress in coupled systems (e.g., wind turbines): For direct integration with wind turbines, the emulation of synchronous machine dynamics can sometimes induce mechanical stress on the turbine components (e.g., torsional vibrations). Research is needed to mitigate this without compromising the grid support functions of the synchronverter.
- –
- Hardware-in-the-loop (HIL) and real-time testing: Moving beyond pure simulation, more extensive and standardized HIL and real-time testing frameworks are needed to validate synchronverter performance and stability under realistic and extreme grid conditions before widespread field deployment.
- Advanced ancillary services and grid codes.
- –
- Beyond basic emulation: While synchronverters mimic basic SG functions, exploring how they can provide more advanced ancillary services, such as power oscillation damping (POD), synthetic inertia for specific frequency bands, or enhanced voltage support tailored to specific grid code requirements is an area for further development.
- –
- Harmonic filtering integration: Although mentioned previously, fully integrating robust and comprehensive active filtering capabilities without compromising primary grid-forming functions remains a research gap.
Addressing these gaps will pave the way for synchronverters to become truly foundational elements of future highly inverter-dominated power systems, ensuring stability, reliability, and efficient integration of renewable energy sources.
5. Challenges and Future Prospects
Future research in synchronverters could focus on improving its effectiveness and integration with power systems and microgrids. Here are some potential avenues for investigation.
- When a synchronverter is working in grid mode and suddenly transfers to the standalone- or isolated-mode, the frequency deviation must be immediately controlled. When it operates as a single machine, it can work properly. But when there are more than one grid-following or grid-forming inverters, the response must be joint. It is imperative to explore more parallel control strategies to avoid frequency deviations.
- When the power grid requires more power, the synchronverter must be able to deliver it. The problem arises on the source side, since photovoltaic and wind farms typically work at their maximum capacity to take advantage of the available intermittent power. If the synchronverter does not deliver the of the power, the efficiency is reduced. From the utility company perspective, the maximum cost efficiency is required. Therefore, more studies are indispensable to enhance techniques and topologies to optimize synchronverter capability.
- There is a great need to integrate the synchronverter with the vehicle-to-grid condition. Electric vehicle (EV) sales have increased in the last decade and are expected to continue to increase. EV batteries are crucial for future network planning, because batteries can be charged from the grid at a valley hour and deliver power to the grid at a peak hour. It is important to investigate the support that EV may offer to synchronverters. New control strategies can be developed.
- Synchronverters are cataloged as grid-forming inverters. In the increasing use of microgrids, there are always grid-forming and grid-following inverters. An appropriate ratio between grid-forming vs. grid-following inverters installed in a microgrid must be found to guarantee an operation within the limits permitted by the network codes.
- When there is a voltage imbalance in the PCC, the synchronverter can operate but only under a small imbalance. If the percentage of imbalance is larger, the synchronization becomes an issue, since the auto-synchronization process does not perform well. New algorithms must be developed to allow for phase-independent synchronization.
- The dynamic and uncertain behavior of the loads must be properly modeled to evaluate what the synchronverter is capable of.
- Synchronverters may change their virtual impedances to face different disturbances on the grid. A proper study to evaluate the stability response when those parameters are changed in real time is mandatory.
- Future research on synchronverters should prioritize enhancing their robustness and stability, ensuring reliable performance even under extremely weak or highly unbalanced grid conditions, which are increasingly prevalent in renewable-heavy systems.
- Developing adaptive and autonomous tuning methods is paramount, moving beyond fixed-gain controls towards intelligent, self-optimizing strategies, potentially leveraging advanced AI, to enable seamless operation in dynamic grid environments.
- Addressing the challenges of multi-synchronverter coordination is vital, focusing on decentralized control schemes that ensure stable power sharing and oscillation damping as numerous synchronverters operate in parallel.
- Research is needed to determine their optimal deployment and economic viability across large-scale grids, providing robust methodologies for placement, sizing, and a clear cost–benefit analysis.
- Continuous effort is required in practical implementation refinements, particularly in optimizing DC-link dynamics for improved fault ride-through, mitigating mechanical stresses in directly coupled systems, and expanding comprehensive real-time testing frameworks.
- Future research and development must focus on how synchronverters can robustly contribute to grid-scale frequency and voltage stability in low-inertia environments, optimize fault current contribution and protection coordination for an inverter-dominated grid, mitigate harmonic resonances across vast electrical networks, ensure small-signal and transient stability in increasingly complex power systems, and enhance cybersecurity of critical grid services. Successfully navigating these challenges will solidify the role of the synchronverter as a cornerstone technology to enable the reliable and resilient operation of future power grids.
6. Conclusions
This paper reviewed the current status and recent applications of synchronverter technology, systematically examining publications from the last seven years retrieved from comprehensive online research databases. The documents collected were meticulously categorized by publication type, encompassing journals, conference proceedings, and books, to provide a structured overview of the field’s progression.
The review highlights that significant improvements and specialized applications of the synchronverter have been proposed to address various challenges within electrical networks, both in simulation and in hardware implementations. In particular, the synchronverter emerges as a crucial solution to complex power grid issues, such as seamless integration of renewable energies and the enhancement of the dynamic response of inverter-based systems. Furthermore, its capability for parallel operation in microgrids supports the development of robust energy communities. The reviewed literature also detailed the parameterization methods essential for stability analysis, demonstrating how the synchronverter improves network conditions. Recent contributions have introduced novel solutions for critical grid problems, including synchronization without Phase-Locked Loops (PLLs), effective harmonic reduction, enhanced fault-ride-through capability, stable operation under voltage unbalances, and improved voltage and frequency regulation.
The analysis of the past seven years clearly indicates an emerging and accelerating trend in synchronverter research, evidenced by a consistent increase in the average number of publications. This upward trajectory suggests a highly favorable perspective for continued progress in this domain, with a growing volume of contributions to the subject in the foreseeable future. This review aims to encourage academics to further explore inverter-based solutions incorporating the synchronverter, thereby advancing efforts to reduce the reliance on fossil fuels and improve grid resilience. Specific avenues for future work include mitigating voltage imbalance at the Point of Common Coupling (PCC), validating synchronverter efficacy in various unbalanced distribution networks, integrating its use within economic dispatch optimization, and incorporating advanced digital harmonic filters directly into its current control loops.
Finally, this paper detailed the inherent advantages and existing disadvantages of the synchronverter, along with a comprehensive exposition of critical research gaps. These identified challenges offer precise directions for future research, directly contributing to the advancement and practical implementation of this promising technology.
Author Contributions
Conceptualization, Methodology, Writing, Original Draft and Supervision M.J.Q.-D. and J.E.C.-B.; review and editing M.E.G.-N., S.A.H.-M. and R.F.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Michell J. Quintero-Durán was supported by the Universidad Pedagógica y Tecnológica de Colombia. John E. Candelo-Becerra was supported by the Universidad Nacional de Colombia, Sede Medellín. Mario Eduardo Gonzalez-Niño and Saúl Andrés Hernández-Moreno were supported by the Universidad Pedagógica y Tecnológica de Colombia. Rodolpho Fernando Váz was supported by the Stony Brook University.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Delimpaltadakis, G.; Cortés, J.; Heemels, W.P.M.H. Continuous Approximations of Projected Dynamical Systems via Control Barrier Functions. IEEE Trans. Autom. Control 2025, 70, 681–688. [Google Scholar] [CrossRef]
- Akbari, E.; Zare Ghaleh Seyyedi, A. Multi-functional voltage and current based enhancement of power quality in grid-connected microgrids considering harmonics. Heliyon 2024, 10, e26008. [Google Scholar] [CrossRef]
- Pandey, A.S.; Kallamadi, M.; Shah, K. Cascaded AC–DC Voltage Control to Provide Reactive Power Support for the PV-Driven Grid-Tied Synchronverter. Int. J. Circuit Theory Appl. 2024, 53, 3778–3786. [Google Scholar] [CrossRef]
- Kisinga, D.A.; Makolo, P.; Trodden, P. A modified synchronverter for a weak grid with virtual power circles-based PQ decoupling scheme. IET Renew. Power Gener. 2024, 18, 2723–2736. [Google Scholar] [CrossRef]
- Mahmoudi Rashid, S.; Akbari, E.; Khalafian, F.; Hossein Atazadegan, M.; Shahmoradi, S.; Zare Ghaleh Seyyedi, A. Robust Allocation of FACTS Devices in Coordinated Transmission and Generation Expansion Planning considering Renewable Resources and Demand Response Programs. Int. Trans. Electr. Energy Syst. 2022, 2022, 4331293. [Google Scholar] [CrossRef]
- Akbari, E.; Zare Ghaleh Seyyedi, A. Power quality enhancement of distribution grid using a photovoltaic based hybrid active power filter with three level converter. Energy Rep. 2023, 9, 5432–5448. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Yin, H.; Kustanovich, Z.; Lin, J.; Weiss, G. Synchronverters with Damper Windings to Attenuate Power Oscillations in Grids. IEEE J. Emerg. Sel. Top. Ind. Electron. 2024, 5, 1376–1387. [Google Scholar] [CrossRef]
- Lorenzetti, P.; Reissner, F.; Weiss, G. A Synchronverter-Based Magnitude Phase-Locked Loop. IEEE Trans. Control Syst. Technol. 2025, 33, 32–47. [Google Scholar] [CrossRef]
- Albornoz, M.; Rohten, J.; Espinoza, J.; Varela, J.; Sbarbaro, D.; Gallego, Y. Photovoltaic Power Injection Control Based on a Virtual Synchronous Machine Strategy. Sensors 2024, 24, 4039. [Google Scholar] [CrossRef]
- Rahman, K.; Hashimoto, J.; Orihara, D.; Ustun, T.S.; Otani, K.; Kikusato, H.; Kodama, Y. Reviewing Control Paradigms and Emerging Trends of Grid-Forming Inverters—A Comparative Study. Energies 2024, 17, 2400. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Monfared, M.; Fazeli, M.; Golestan, S. Single-phase Grid-forming Inverters: A Review. In Proceedings of the 2023 International Conference on Computing, Electronics & Communications Engineering (iCCECE), Swansea, UK, 14–16 August 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 7–10. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.Y. Virtual Inertia-Based Inverters for Mitigating Frequency Instability in Grid-Connected Renewable Energy System: A Review. Appl. Sci. 2019, 9, 5300. [Google Scholar] [CrossRef]
- Zhong, Q.-C.; Nguyen, P.L.; Ma, Z.; Sheng, W. Self-Synchronized Synchronverters: Inverters Without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 2014, 29, 617–630. [Google Scholar] [CrossRef]
- Moulichon, A.; Alamir, M.; Debusschere, V.; Garbuio, L.; Rahmani, M.A.; Wang, M.X.; Hadjsaid, N. Observer-Based Current Controller for Virtual Synchronous Generator in Presence of Unknown and Unpredictable Loads. IEEE Trans. Power Electron. 2021, 36, 1708–1716. [Google Scholar] [CrossRef]
- Vetoshkin, L.; Muller, Z. A supervisory MPC for synchronverter. In Proceedings of the 2020 21st International Scientific Conference on Electric Power Engineering (EPE), Prague, Czech Republic, 19–21 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ramirez, J.M.; Montalvo, E.T.; Nuño, C.I. Modelling, synchronisation, and implementation of the virtual synchronous generator: A study of its reactive power handling. Electr. Eng. 2020, 102, 1605–1619. [Google Scholar] [CrossRef]
- Liyanage, C.; Nutkani, I.; Meegahapola, L. A Comparative Analysis of Prominent Virtual Synchronous Generator Strategies Under Different Network Conditions. IEEE Open Access J. Power Energy 2024, 11, 178–195. [Google Scholar] [CrossRef]
- Naeem, M.; Khan, U.A. A PLL-Less Fourier Analysis Based Self-Synchronizer for Synchronverter having Uninterrupted Power Supply Capability. E-Prime Adv. Electr. Eng. Electron. Energy 2023, 5, 100257. [Google Scholar] [CrossRef]
- Phattanakorn, M.; Kumsuwan, Y. Multi-Function Algorithm of Virtual Synchronous Generator. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Republic of Korea, 31 October–3 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 824–829. [Google Scholar] [CrossRef]
- Chiu, B.K.; Lee, K.Y.; Hsu, Y.Y. Battery Energy Storage System Damper Design for a Microgrid with Wind Generators Participating in Frequency Regulation. Energies 2023, 16, 7439. [Google Scholar] [CrossRef]
- Araújo-de Oliveira, J.D.; de Araújo-Lima, F.K.; Nogueira, F.G.; Tofoli, F.L.; Branco, C.G.C. Stability analysis and application of a synchronverter-based control approach to DFIG-based wind energy conversion systems. Electr. Power Syst. Res. 2024, 232, 110403. [Google Scholar] [CrossRef]
- He, L.; Shuai, Z.; Zhang, X.; Liu, X.; Li, Z.; Shen, Z.J. Transient Characteristics of Synchronverters Subjected to Asymmetric Faults. IEEE Trans. Power Deliv. 2019, 34, 1171–1183. [Google Scholar] [CrossRef]
- Li, Y.; Qi, R.; Wang, S. New Control Schemes of Output Power Decoupling Based on Synchronverter. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Republic of Korea, 7–10 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1980–1985. [Google Scholar] [CrossRef]
- Saadatmand, S.; Shamsi, P.; Ferdowsi, M. Power and Frequency Regulation of Synchronverters Using a Model Free Neural Network-Based Predictive Controller. IEEE Trans. Ind. Electron. 2021, 68, 3662–3671. [Google Scholar] [CrossRef]
- Kryonidis, G.C.; Malamaki, K.N.D.; Mauricio, J.M.; Demoulias, C.S. A new perspective on the synchronverter model. Int. J. Electr. Power Energy Syst. 2022, 140, 108072. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Konstantopoulos, G.C.; Ren, B.; Krstic, M. Improved Synchronverters with Bounded Frequency and Voltage for Smart Grid Integration. IEEE Trans. Smart Grid 2018, 9, 786–796. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.; Rueda, J.L.; Palensky, P.; Chamorro, H.R.; Sood, V. Frequency Support provided by Inverted Based-Generation using Grid-Forming Controllers: A Comparison during Islanded Operation. In Proceedings of the 2021 IEEE Electrical Power and Energy Conference (EPEC), Toronto, ON, Canada, 22–31 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 113–118. [Google Scholar] [CrossRef]
- Klink, J.; Helm, S.; Yang, W.; Deblon, F.; Benger, R.; Hauer, I.; Lindemann, A. Instantaneous reserve by battery energy storage systems—A holistic system model to analyze the dynamic power system interactions. Energy Rep. 2025, 13, 3096–3111. [Google Scholar] [CrossRef]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient Stability of Voltage-Source Converters with Grid-Forming Control: A Design-Oriented Study. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1019–1033. [Google Scholar] [CrossRef]
- Luo, S.; Wu, W.; Koutroulis, E.; Chung, H.S.H.; Blaabjerg, F. A New Virtual Oscillator Control Without Third-Harmonics Injection For DC/AC Inverter. IEEE Trans. Power Electron. 2021, 36, 10879–10888. [Google Scholar] [CrossRef]
- Raja Shekhar, K.; Chaudhari, M.A. Operation and control of Synchronverter technique in grid connected and intentional islanding modes for AC micro grids. In Proceedings of the 2020 First International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 3–5 January 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 426–431. [Google Scholar] [CrossRef]
- Moulichon, A.; Alamir, M.; Garbuio, L.; Debusschere, V.; Rahmani, M.A.; Boudinet, C.; Noris, W.; Hadjsaid, N. State observer to improve the VSG control stability. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1698–1703. [Google Scholar] [CrossRef]
- Körner, P.; Reindl, A.; Meier, H.; Niemetz, M. A Theoretical Comparison of Different Virtual Synchronous Generator Implementations on Inverters. In Proceedings of the 24th European Conference on Power Electronics and Applications, EPE 2022 ECCE Europe, Hanover, Germany, 5–9 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 01–09. [Google Scholar]
- Ding, L.; Zhang, Y.; Zhang, F.; Kong, Y. Stability Analysis and Transient Feedback Compensation with Virtual Impedance-Based Method for Parallel-Connected Synchronverters. In Proceedings of the 2022 IEEE 31st International Symposium on Industrial Electronics (ISIE), Anchorage, AK, USA, 1–3 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 380–387. [Google Scholar] [CrossRef]
- Kisinga, D.A.; Trodden, P. Virtual power circle based PQ decoupling technique for a virtual synchronous generator connected to a weak grid. In Proceedings of the 2023 IEEE Belgrade PowerTech, Belgrade, Serbia, 25–29 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Rajan, C.S.; Ebenezer, M. Voltage Profile Improvement of a Multi Microgrid Interconnection Scheme using Synchronverters. In Proceedings of the 2022 IEEE International Conference on Signal Processing, Informatics, Communication and Energy Systems (SPICES), Thiruvananthapuram, India, 10–12 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 217–222. [Google Scholar] [CrossRef]
- Ferreira, R.V.; Silva, S.M.; Brandao, D.I. Positive–Negative Sequence Synchronverter for Unbalanced Voltage in AC Grids. J. Control. Autom. Electr. Syst. 2021, 32, 711–720. [Google Scholar] [CrossRef]
- Wang, X.; Chen, L.; Sun, D.; Zhang, L.; Nian, H. A Modified Self-Synchronized Synchronverter in Unbalanced Power Grids with Balanced Currents and Restrained Power Ripples. Energies 2019, 12, 923. [Google Scholar] [CrossRef]
- Pore, S.; Jadhav, P.R. Filters for Grid Connected Self-Synchronized Synchronverter. In Proceedings of the 2019 4th International Conference on Recent Trends on Electronics, Information, Communication & Technology (RTEICT), Bangalore, India, 17–18 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 551–555. [Google Scholar] [CrossRef]
- Kustanovich, Z.; Yin, H.; Weiss, G. Improvements to the VSM current controller for better grid performance. In Proceedings of the 2022 IEEE 20th International Power Electronics and Motion Control Conference (PEMC), Brasov, Romania, 25–28 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 621–626. [Google Scholar] [CrossRef]
- Zheng, T.; Chen, L.; Guo, Y.; Mei, S. Comprehensive control strategy of virtual synchronous generator under unbalanced voltage conditions. IET Gener. Transm. Distrib. 2018, 12, 1621–1630. [Google Scholar] [CrossRef]
- Li, F.; Liu, G.; Zhu, K.; Wang, W. An Improved Control Strategy of Virtual Synchronous Generator under Unbalanced Conditions. In Proceedings of the 2018 IEEE 4th Southern Power Electronics Conference (SPEC), Singapore, 10–13 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Gomes, L.D.N.; Abrantes-Ferreira, A.J.G.; Dias, R.F.D.S.; Rolim, L.G.B. Synchronverter-Based STATCOM with Voltage Imbalance Compensation Functionality. IEEE Trans. Ind. Electron. 2022, 69, 4836–4844. [Google Scholar] [CrossRef]
- Wang, M.; Li, H.; Li, L. Fault Through Technique of Synchronverter Based on Voltage Feedforward Compensation. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–8 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2056–2061. [Google Scholar] [CrossRef]
- Pola, S.; Azzouz, M.; Awad, A.S.A.; Sindi, H. Fault Ride-Through Strategies for Synchronverter-Interfaced Energy Resources Under Asymmetrical Grid Faults. IEEE Trans. Sustain. Energy 2023, 14, 2391–2405. [Google Scholar] [CrossRef]
- Quintero-Duran, M.J.; Candelo-Becerra, J.E.; Posada, J. Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition. Nonlinear Eng. 2022, 11, 395–410. [Google Scholar] [CrossRef]
- Wijekoon, W.; Pabasara, W.; L, P.; Ranaweera, K.; Welmilla, D. Revolutionizing Renewable Energy Integration with Synchronverters: A Game-Changer for Modern Power Grids. In Proceedings of the 2023 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 9–11 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 491–496. [Google Scholar] [CrossRef]
- Kelada, F.; Buire, J.; HadjSaid, N. Comparative Study of Decentralized Grid-forming Converter Controls For Inverter-based Microgrids. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, M.; Mostajeran, E.; Jatskevich, J. Tuning the Maximum Power Extraction Loop in the Improved Droop Controller of Virtual Synchronous Generators. In Proceedings of the 2023 22nd International Symposium INFOTEH-JAHORINA (INFOTEH), East Sarajevo, Bosnia and Herzegovina, 15–17 March 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Pola, S.; Azzouz, M.; Mirhassani, M. Synchronverters with Fault Ride-Through Capabilities for Reliable Microgrid Protection during Balanced and Unbalanced Faults. IEEE Trans. Sustain. Energy 2024, 15, 1663–1676. [Google Scholar] [CrossRef]
- Yazdaninejadi, A.; Ebrahimi, H. A new protection algorithm for tackling the impact of fault-resistance and cloud energy storage on coordination of recloser-fuse protection. IET Gener. Transm. Distrib. 2023, 17, 1827–1835. [Google Scholar] [CrossRef]
- Sekizaki, S.; Yorino, N.; Sasaki, Y.; Zoka, Y.; Shimizu, T.; Nishizaki, I. Single-phase Synchronous Inverter with Overcurrent Protection using Current Controller with Latched Limit Strategy. IEEJ Trans. Electr. Electron. Eng. 2023, 18, 1001–1014. [Google Scholar] [CrossRef]
- Frasetyo, M.B.; WIjaya, F.D.; Ali, H.R. Hybrid PV-WT Microgrid Stability Control Using Synchronverter Algorithm. In Proceedings of the 2023 15th International Conference on Information Technology and Electrical Engineering (ICITEE), Chiang Mai, Thailand, 26–27 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 365–369. [Google Scholar] [CrossRef]
- Ala, G.; Campagna, N.; Caruso, M.; Castiglia, V.; Di Tommaso, A.O.; Miceli, R.; Nevoloso, C.; Schettino, G.; Viola, F.; Nguyen, M. Stability of Microgrids: An Application of Virtual Synchronous Generator. In Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2023; Volume 602 LNNS, pp. 873–880. [Google Scholar] [CrossRef]
- Kumar, R.; Chaudhari, M.A.; Chaturvedi, P. Analysis of Synchronverter and PLL-Less Control for Three-Phase VSI in AC Microgrids. In Proceedings of the 2024 Third International Conference on Power, Control and Computing Technologies (ICPC2T), Raipur, India, 18–20 January 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 810–816. [Google Scholar] [CrossRef]
- Eisapour-Moarref, A.; Kalantar, M.; Esmaili, M. Control strategy resilient to unbalanced faults for interlinking converters in hybrid microgrids. Int. J. Electr. Power Energy Syst. 2020, 119, 105927. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Zhang, X.; Lu, J.; Wang, P.; Guerrero, J.M. Improvement of Frequency Regulation in VSG-Based AC Microgrid Via Adaptive Virtual Inertia. IEEE Trans. Power Electron. 2020, 35, 1589–1602. [Google Scholar] [CrossRef]
- Jayachandran, M.; Reddy, C.R.; Padmanaban, S.; Milyani, A.H. Operational planning steps in smart electric power delivery system. Sci. Rep. 2021, 11, 17250. [Google Scholar] [CrossRef]
- Sarojini, R.K.; Palanisamy, K.; Sanjeevikumar, P.; Nielsen, J.B. Inertia emulation control technique based frequency control of grid-connected single-phase rooftop photovoltaic system with battery and supercapacitor. IET Renew. Power Gener. 2020, 14, 1156–1163. [Google Scholar] [CrossRef]
- Kanakkayil, M.A.; Kiranmai, K.P.; Shareef, H. Synchronous Machine Emulation of VSC for Interconnection of Renewable Energy Sources through HVDC Transmission. In Proceedings of the 2021 6th International Conference on Renewable Energy: Generation and Applications (ICREGA), Al Ain, United Arab Emirates, 2–4 February 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 131–136. [Google Scholar] [CrossRef]
- Gadgune, S.; Joshi, P.M. Performance Improvement of 3 Phase Inverter Operated as Virtual Synchronous Generator with Closed Loop Active Power Control. In Proceedings of the 2021 International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 19–20 February 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Panda, R.K.; Mohapatra, A.; Srivastava, S.C. Enhancing inertia of solar photovoltaic-based microgrid through notch filter-based PLL in SRF control. IET Gener. Transm. Distrib. 2020, 14, 379–388. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Babu, T.S.; Pouryekta, A. Synchronverter: A Comprehensive Review of Modifications, Stability Assessment, Applications and Future Perspectives. IEEE Access 2020, 8, 131565–131589. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.Y. Grid Integration of Solar Photovoltaic System Using Machine Learning-Based Virtual Inertia Synthetization in Synchronverter. IEEE Access 2020, 8, 49961–49976. [Google Scholar] [CrossRef]
- Ramezani, M.; Li, S.; Musavi, F.; Golestan, S. Seamless Transition of Synchronous Inverters Using Synchronizing Virtual Torque and Flux Linkage. IEEE Trans. Ind. Electron. 2020, 67, 319–328. [Google Scholar] [CrossRef]
- Shivratri, S.; Kustanovich, Z.; Weiss, G.; Shani, B. Virtual synchronous machines with fast current loop. IFAC-PapersOnLine 2020, 53, 12422–12428. [Google Scholar] [CrossRef]
- Palacios, J.; Posada, J. Voltage Converters in Parallel Working as Virtual Synchronous Generators. In Proceedings of the 2019 FISE-IEEE/CIGRE Conference—Living the energy Transition (FISE/CIGRE), Medellin, Colombia, 4–6 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Rosso, R.; Engelken, S.; Liserre, M. Robust Stability Analysis of Synchronverters Operating in Parallel. IEEE Trans. Power Electron. 2019, 34, 11309–11319. [Google Scholar] [CrossRef]
- Roldan-Perez, J.; Rodriguez-Cabero, A.; Prodanovic, M. Design and Analysis of Virtual Synchronous Machines in Inductive and Resistive Weak Grids. IEEE Trans. Energy Convers. 2019, 34, 1818–1828. [Google Scholar] [CrossRef]
- Moulichon, A.; Garbuio, L.; Debusschere, V.; Rahmani, M.A.; Hadj-Said, N. A Simplified Synchronous Machine Model for Virtual Synchronous Generator Implementation. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z. Probabilistic-Based Transient Stability Assessment of Power Systems with Virtual Synchronous Machines. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2117–2122. [Google Scholar] [CrossRef]
- Wang, S.; Qi, R.; Li, Y. Fuzzy Control Scheme of Virtual Inertia for Synchronverter in Micro-Grid. In Proceedings of the 2018 21st International Conference on Electrical Machines and Systems (ICEMS), Jeju, Republic of Korea, 7–10 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2028–2032. [Google Scholar] [CrossRef]
- Yap, K.Y.; Beh, C.M.; Sarimuthu, C.R. Fuzzy logic controller-based synchronverter in grid-connected solar power system with adaptive damping factor. Chin. J. Electr. Eng. 2021, 7, 37–49. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Escobar-Mejía, A.; Hernández, J.C. LQR-Based Adaptive Virtual Inertia for Grid Integration of Wind Energy Conversion System Based on Synchronverter Model. Electronics 2021, 10, 1022. [Google Scholar] [CrossRef]
- Saadatmand, S.; Shamsi, P.; Ferdowsi, M. Adaptive critic design-based reinforcement learning approach in controlling virtual inertia-based grid-connected inverters. Int. J. Electr. Power Energy Syst. 2021, 127, 106657. [Google Scholar] [CrossRef]
- Gunther, K.; Sourkounis, C. Active Damping Control for Variable-Speed Wind Turbines with VSM as Grid-Side Control. In Proceedings of the 2021 22nd IEEE International Conference on Industrial Technology (ICIT), Valencia, Spain, 10–12 March 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 304–309. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.Y. An Adaptive Synchronverter for Ensuring Fault Ride Through Capability of Grid-Connected Solar Power System. J. Phys. Conf. Ser. 2021, 1828, 012054. [Google Scholar] [CrossRef]
- da Silva Santos, M.; Sales Barros, L.; Bezerra Costa, F.; Mara Vital Barros, C.; Penha Silva Junior, G.; Strunz, K. Frequency Droop-Based Synchronverter Without Battery for Primary Support of Microgrids. J. Control. Autom. Electr. Syst. 2023, 34, 40–49. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Venugopal, G.; Guerrero, J.M.; David Agundis Tinajero, G. Synergizing pico hydel and battery energy storage with adaptive synchronverter control for frequency regulation of autonomous microgrids. Appl. Energy 2022, 325, 119827. [Google Scholar] [CrossRef]
- Zhang, Y.; Mou, J.; Zhang, F.; Huang, N. Modeling and Stability Analysis Based on Internal Voltage Dynamics in Synchronverter. Electronics 2023, 12, 700. [Google Scholar] [CrossRef]
- Kustanovich, Z.; Shivratri, S.; Yin, H.; Reissner, F.; Weiss, G. Synchronverters with Fast Current Loops. IEEE Trans. Ind. Electron. 2023, 70, 11357–11367. [Google Scholar] [CrossRef]
- Busada, C.; Jorge, S.G.; Solsona, J.A. Current-Controlled Synchronverter: A Grid Fault Tolerant Grid Forming Inverter. IEEE Trans. Ind. Electron. 2024, 71, 3233–3241. [Google Scholar] [CrossRef]
- Schulze, W.; Weber, P.; Suriyah, M.; Leibfried, T. Grid-forming synchronverter-based control method with current limiting method for grid-side converters of converter-based generation plants. In Proceedings of the 21st Wind & Solar Integration Workshop (WIW 2022), The Hague, The Netherlands, 12–14 October 2022; Institution of Engineering and Technology: London, UK, 2022; pp. 394–401. [Google Scholar] [CrossRef]
- Manjunath, K.; Pandya, V. Single-loop control of grid-tied synchronverter for the desired power injection. In Proceedings of the 2022 IEEE International Power and Renewable Energy Conference (IPRECON), Kollam, India, 16–18 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Lorenzetti, P.; Reissner, F.; Weiss, G. An internal model for tracking a sinusoidal reference with unknown frequency and uncertain plant. In Proceedings of the 2022 IEEE 61st Conference on Decision and Control (CDC), Cancun, Mexico, 6–9 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 2525–2531. [Google Scholar] [CrossRef]
- Wang, M.; Mostajeran, E.; Ebrahimi, S.; Jatskevich, J. An Improved Droop Controller for Virtual Synchronous Generators. In Proceedings of the 2022 IEEE Electrical Power and Energy Conference (EPEC), Victoria, BC, Canada, 5–7 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 273–277. [Google Scholar] [CrossRef]
- Lorenzetti, P.; Weiss, G. A variable frequency internal model controller inspired by synchronverter theory. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 715–720. [Google Scholar] [CrossRef]
- Yin, H.; Kustanovich, Z.; Weiss, G. Attenuation of power system oscillations by using virtual damper windings. In Proceedings of the 2022 IEEE 23rd Workshop on Control and Modeling for Power Electronics (COMPEL), Tel Aviv, Israel, 20–23 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Utkarsha, P.; Swami Naidu, N.K.; Sivaprasad, B.; Yalla, N. Synchronverter based Multifunctional UPQC for Distributed Generation Applications. In Proceedings of the 2023 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 17–20 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Mercado–Uribe, A.; Mendoza-Ávila, J.; Efimov, D.; Schiffer, J. A Control Leonov Function Guaranteeing Global ISS of Two Coupled Synchronverters. In Proceedings of the 2023 62nd IEEE Conference on Decision and Control (CDC), Singapore, 13–15 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 4580–4585. [Google Scholar] [CrossRef]
- Chen, S.; Xia, X.; Jiang, L.; Zhang, Y. Power Oscillation Suppression Method for Multi-Parallel Synchronverters. In Proceedings of the 2023 8th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, 22–25 September 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 468–473. [Google Scholar] [CrossRef]
- Gluščević, J.; Janda, Ž.; Dragosavac, J.; Ristić, L. Enhancing Stability of Grid-Following Inverter for Renewables. In Proceedings of the 2023 22nd International Symposium on Power Electronics (Ee), Novi Sad, Serbia, 25–28 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Yin, H.; Wang, S.; Zhou, Z. Synchronverters with a Virtual Oscillator to Attenuate Power Oscillations. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 1303–1310. [Google Scholar] [CrossRef]
- Sonawane, A.; Umarikar, A. Small-Signal Stability Analysis of PV-Based Synchronverter Including PV Operating Modes and DC-Link Voltage Controller. IEEE Trans. Ind. Electron. 2022, 69, 8028–8039. [Google Scholar] [CrossRef]
- Sonawane, A.J.; Umarikar, A.C. Three-Phase Single-Stage Photovoltaic System with Synchronverter Control: Power System Simulation Studies. IEEE Access 2022, 10, 23408–23424. [Google Scholar] [CrossRef]
- Yap, K.Y.; Lim, J.M.Y.; Sarimuthu, C.R. A novel adaptive virtual inertia control strategy under varying irradiance and temperature in grid-connected solar power system. Int. J. Electr. Power Energy Syst. 2021, 132, 107180. [Google Scholar] [CrossRef]
- Montalvo, E.T.; Sanchez, V.M.; Ramirez, J.M. Synchronverter assessment for the frequency regulation of control areas encompassing Renewable Distributed Generation. Int. J. Hydrogen Energy 2021, 46, 26138–26151. [Google Scholar] [CrossRef]
- Schulze, W.; Zajadatz, M.; Suriyah, M.; Leibfried, T. Emulation of grid-forming inverters using real-time PC and 4-quadrant voltage amplifier. Forsch. Im Ingenieurwesen 2021, 85, 425–430. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, Q.; Zhou, J.; Li, L.; Wang, P.; Guerrero, J.M. Coordinated Control of Networked AC/DC Microgrids with Adaptive Virtual Inertia and Governor-Gain for Stability Enhancement. IEEE Trans. Energy Convers. 2021, 36, 95–110. [Google Scholar] [CrossRef]
- Hariharan, R.; Mishra, M.K. Analysis and design of gradient descent based pre-synchronization control for synchronverter. IET Renew. Power Gener. 2021, 15, 297–312. [Google Scholar] [CrossRef]
- Marthi, P.R.V.; Debnath, S.; Crow, M.L. Synchronverter-based Control of Multi-Port Autonomous Reconfigurable Solar Plants (MARS). In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 5019–5026. [Google Scholar] [CrossRef]
- Dokus, M.; Mertens, A. Sequence Impedance Characteristics of Grid-Feeding Converters. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1216–1223. [Google Scholar] [CrossRef]
- Li, S.; Wu, S.; Xiang, S.; Zhang, Y.; Guerrero, J.M.; Vasquez, J.C. Research on Synchronverter-Based Regenerative Braking Energy Feedback System of Urban Rail Transit. Energies 2020, 13, 4418. [Google Scholar] [CrossRef]
- Rosso, R.; Engelken, S.; Liserre, M. Robust Stability Investigation of the Interactions Among Grid-Forming and Grid-Following Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 991–1003. [Google Scholar] [CrossRef]
- Shuai, Z.; Huang, W.; Shen, Z.J.; Luo, A.; Tian, Z. Active Power Oscillation and Suppression Techniques Between Two Parallel Synchronverters During Load Fluctuations. IEEE Trans. Power Electron. 2020, 35, 4127–4142. [Google Scholar] [CrossRef]
- Liaw, M.J.Y.; Sarimuthu, C.R. Development of a synchronverter for a grid connected photovoltaic system. IOP Conf. Ser. Mater. Sci. Eng. 2020, 767, 012046. [Google Scholar] [CrossRef]
- Dong, S.; Jiang, J.; Chen, Y.C. Analysis of Synchronverter Self-Synchronization Dynamics to Facilitate Parameter Tuning. IEEE Trans. Energy Convers. 2020, 35, 11–23. [Google Scholar] [CrossRef]
- Rodriguez-Cabero, A.; Roldan-Perez, J.; Prodanovic, M. Virtual Impedance Design Considerations for Virtual Synchronous Machines in Weak Grids. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1477–1489. [Google Scholar] [CrossRef]
- Ghosh, R.; Tummuru, N.R.; Rajpurohit, B.S.; Monti, A. Virtual Inertia from Renewable Energy Sources: Mathematical Representation and Control Strategy. In Proceedings of the 2020 IEEE International Conference on Power Electronics, Smart Grid and Renewable Energy (PESGRE2020), Cochin, India, 2–4 January 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Ferreira, R.V.; Silva, S.M.; Antunes, H.M.A.; Venkataramanan, G. Dynamic Analysis of Grid-Connected Droop-Controlled Converters and Synchronverters. J. Control. Autom. Electr. Syst. 2019, 30, 741–753. [Google Scholar] [CrossRef]
- Rosso, R.; Engelken, S.; Liserre, M. Analysis of the Parallel Operation Between Synchronverters and PLL-Based Converters. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2583–2590. [Google Scholar] [CrossRef]
- Li, H.; Zhang, X.; Shao, T.; Zheng, T.Q. Flexible Inertia Optimization for Single-Phase Voltage Source Inverter Based on Hold Filter. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1300–1310. [Google Scholar] [CrossRef]
- Roldan-Perez, J.; Rodriguez-Cabero, A.; Prodanovic, M. Harmonic Virtual Impedance Design for Parallel-Connected Grid-Tied Synchronverters. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 493–503. [Google Scholar] [CrossRef]
- Younis, T.; Ismeil, M.; Hussain, E.K.; Orabi, M. Improved single-phase self-synchronised synchronverter with enhanced dynamics and current limitation capability. IET Power Electron. 2019, 12, 337–344. [Google Scholar] [CrossRef]
- Shao, T.; Zheng, T.Q.; Li, H.; Zhang, X. Parameter design and hot seamless transfer of single-phase synchronverter. Electr. Power Syst. Res. 2018, 160, 63–70. [Google Scholar] [CrossRef]
- Natarajan, V.; Weiss, G. Almost global asymptotic stability of a grid-connected synchronous generator. Math. Control. Signals Syst. 2018, 30, 10. [Google Scholar] [CrossRef]
- Brahma, A.R.; Kumaravel, S.; Thomas, V.; Ashok, S. Impact of System Parameters on the Performance of Synchronverter. In Proceedings of the 2019 IEEE Region 10 Symposium (TENSYMP), Kolkata, India, 7–9 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 120–125. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, S.; Yang, P.; Xiang, S.; Li, S.; He, S. Research on Parallel Operation of Virtual Synchronous Generators in Microgrid. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1659–1664. [Google Scholar] [CrossRef]
- He, L.; Huang, W.; Shuai, Z.; Shen, Z.J. An asymmetrical fault current calculation method of synchronverter. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1805–1809. [Google Scholar] [CrossRef]
- Trujillo, M.D.; Mendez, S.; Ramos, G.; Camarillo-Penaranda, J.; Jurado, E. Real-time Simulation of Synchronverter Connected to the Main Grid. In Proceedings of the 2019 IEEE Workshop on Power Electronics and Power Quality Applications (PEPQA), Manizales, Colombia, 30–31 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–7. [Google Scholar] [CrossRef]
- Kustanovich, Z.; Weiss, G. Synchronverter based photovoltaic inverter. In Proceedings of the 2018 IEEE International Conference on the Science of Electrical Engineering in Israel (ICSEE), Eilat, Israel, 12–14 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Kumaravel, S.; Thomas, V.; Vijay Kumar, T.; Ashok, S. Development of the synchronverter for green energy integration. In Distributed Energy Resources in Microgrids; Elsevier: Amsterdam, The Netherlands, 2019; pp. 343–356. [Google Scholar] [CrossRef]
- Chowdhury, A.; Alam, M.S.; Dey, S.; Ayman, A. Design of a Compact 600VA Sinusoidal Inverter with Battery Storage System. In Proceedings of the 2018 International Conference on Innovations in Science, Engineering and Technology (ICISET), Chittagong, Bangladesh, 27–28 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 13–18. [Google Scholar] [CrossRef]
- Barbosa, D.; Ramos, J.; Rodrigues, J.; Lopes, A.; Esteves Araujo, R. A Practical Comparison of Two Algorithms for Inverter Control with Virtual Inertia Emulation. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), Dublin, Ireland, 11–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Roldan-Perez, J.; Prodanovic, M.; Rodriguez-Cabero, A.; Guerrero, J.; Garcia-Cerrada, A. Finite-gain-current repetitive controller for synchronverters with harmonic-sharing capabilities. In Proceedings of the 2018 18th International Conference on Harmonics and Quality of Power (ICHQP), Ljubljana, Slovenia, 13–16 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Younis, T.; Ismeil, M.; Orabi, M.; Hussain, E.K. A single-phase self-synchronized synchronverter with bounded droop characteristics. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1624–1629. [Google Scholar] [CrossRef]
- Kumar, T.V.; Thomas, V.; Kumaravel, S.; Ashok, S. Performance of virtual synchronous machine in autonomous mode of operation. In Proceedings of the 2018 5th International Conference on Renewable Energy: Generation and Applications (ICREGA), Al Ain, United Arab Emirates, 25–28 February 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 310–314. [Google Scholar] [CrossRef]
- Busada, C.A.; Jorge, S.G.; Solsona, J.A. Shaping the Transient Behavior of Synchronverters. IEEE Trans. Energy Convers. 2023, 38, 735–738. [Google Scholar] [CrossRef]
- Li, G.; Ma, F.; Wu, C.; Li, M.; Guerrero, J.M.; Wong, M.C. A Generalized Harmonic Compensation Control Strategy for Mitigating Subsynchronous Oscillation in Synchronverter Based Wind Farm Connected to Series Compensated Transmission Line. IEEE Trans. Power Syst. 2023, 38, 2610–2620. [Google Scholar] [CrossRef]
- Gawande, S.P.; Meshram, P.M.; Chaturvedi, P.; Daigavane, M.B. An Investigations on Design Dynamics of Synchronverter for P, Q and Frequency Control. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Pawar, R.R.; Jain, T. Controller Hardware-In-Loop Validation of Synchronverter in Islanded Microgrid. In Proceedings of the 2022 22nd National Power Systems Conference (NPSC), New Delhi, India, 17–19 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 260–265. [Google Scholar] [CrossRef]
- Azuara-Grande, L.S.; Gonzalez-Longatt, F.; Tricarico, G.; Wagle, R.; Arnaltes, S.; Granizo, R. Real-Time Implementation of Two Grid-Forming Power Converter Controls to Emulate Synchronous Generators. In Proceedings of the 2022 IEEE Biennial Congress of Argentina (ARGENCON), San Juan, Argentina, 7–9 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Sütő, B.; Divényi, D.; Raisz, D. Comparison and specification-based tuning of two grid-forming inverter controllers providing inertia. In Proceedings of the 2022 IEEE 13th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Kiel, Germany, 26–29 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Farkas, C.; Divenyi, D.; Arnold, A.; Suto, B.; Raisz, D. Extended synchronverter model for PHIL simulation in grid-connected and islanded operation. In Proceedings of the 2022 IEEE 13th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Kiel, Germany, 26–29 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Medina, G.N.I.; Bandeira, C.M.; Azevedo, G.M.S.; Limongi, L.R.; Bradaschia, F.; Barbosa, E.J. Comparative Study of Microgrid Power-Sharing Techniques Based on Synchronous Machine Emulation Carried Out in Real-Time Simulation. In Proceedings of the 2023 IEEE 8th Southern Power Electronics Conference and 17th Brazilian Power Electronics Conference (SPEC/COBEP), Florianopolis, Brazil, 26–29 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Weber, P.; Schulze, W.; Pawlowski, P.; Suriyah, M.; Leibfried, T. Grid-forming synchronverter-based control method with current limiting method for grid-side converters of type 4 wind power plants. In Proceedings of the 22nd Wind and Solar Integration Workshop (WIW 2023), Copenhagen, Denmark, 26–28 September 2023; Institution of Engineering and Technology: London, UK, 2023; pp. 422–429. [Google Scholar] [CrossRef]
- Maurya, S.S.; Jain, T.; Umarikar, A.C. Small-Signal Stability Analysis of Synchronverter-Based AC Microgrid in Islanded Mode. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2024; Volume 1099, pp. 315–334. [Google Scholar] [CrossRef]
- Zare Ghaleh Seyyedi, A.; Mahmoudi Rashid, S.; Akbari, E.; Nejati, S.A.; Khalafian, F.; Siano, P. Co-planning of generation and transmission expansion planning for network resiliency improvement against extreme weather conditions and uncertainty of resiliency sources. IET Gener. Transm. Distrib. 2022, 16, 4830–4845. [Google Scholar] [CrossRef]
- Yari, S.; Khatibi, M. Damping Improvement of Inter-Area Oscillations Using Large-Scale Wind Farms. In Proceedings of the 7th Iran Wind Energy Conference (IWEC2021), Shahrood, Iran, 17–18 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Yan, W.; Cheng, L.; Yan, S.; Gao, W.; Gao, D.W. Enabling and Evaluation of Inertial Control for PMSG-WTG Using Synchronverter with Multiple Virtual Rotating Masses in Microgrid. IEEE Trans. Sustain. Energy 2020, 11, 1078–1088. [Google Scholar] [CrossRef]
- Karray, I.; Kilani, K.B.; Elleuch, M. Advanced Controls for Wind Power Plant Ancillary Services. In Lecture Notes in Electrical Engineering; Springer International Publishing: Berlin, Germany, 2019; Volume 522, pp. 277–292. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Yazdaninejadi, A.; Golshannavaz, S. Transient stability enhancement in multiple-microgrid networks by cloud energy storage system alongside considering protection system limitations. IET Gener. Transm. Distrib. 2022, 17, 1816–1826. [Google Scholar] [CrossRef]
- Hansen, J.B.B.; Osterfelt, S.T.; Randewijk, P.J. The Use of Synchronverters for Fast Frequency Response and Automatic Voltage Regulation in Low Inertia Islanded Power Networks. In Proceedings of the 2021 56th International Universities Power Engineering Conference (UPEC), Middlesbrough, UK, 31 August–3 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Vetoshkin, L.; Müller, Z. A comparative analysis of a power system stability with virtual inertia. Energies 2021, 14, 3277. [Google Scholar] [CrossRef]
- Vetoshkin, L.; Muller, Z. Dynamic Stability Improvement of Power System by Means of STATCOM with Virtual Inertia. IEEE Access 2021, 9, 116105–116114. [Google Scholar] [CrossRef]
- Elshenawy, M.A.; Abdelkader, S.M.; Amin, A.A.; Farghal, S.A. Improved plug–play SV with virtual inertia for enhancing the stability of high RES-penetrated grids. IET Smart Grid 2019, 2, 571–580. [Google Scholar] [CrossRef]
- Blau, M.; Weiss, G. Synchronverters used for damping inter-area oscillations in two-area power systems. Renew. Energy Power Qual. J. 2018, 1, 45–50. [Google Scholar] [CrossRef]
- Dong, S.; Chen, C. Analysis of Feasible Synchronverter Pole-Placement Region to Facilitate Parameter Tuning. IEEE Trans. Energy Convers. 2021, 36, 2782–2793. [Google Scholar] [CrossRef]
- Chowdhury, V.R.; Divan, D. Lyapunov energy function based direct power control of synchronverters under unbalanced grid voltage conditions. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 992–999. [Google Scholar] [CrossRef]
- Moulichon, A.; Debusschere, V.; Garbuio, L.; Rahmani, M.A.; Alamir, M.; Hadjsaid, N. Standardization tests for the industrialization of grid-friendly Virtual Synchronous Generators. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 679–688. [Google Scholar] [CrossRef]
- Karray, I.; Aouini, R.; Ben Kilani, K.; Elleuch, M.; Tran Quoc, T. Advanced Controls of HVDC Interconnection for Ancillary Services Support. In Proceedings of the 2020 17th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 20–23 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 59–64. [Google Scholar] [CrossRef]
- Pola, S.; Azzouz, M.A. Optimal Protection Coordination of Active Distribution Networks with Synchronverters. IEEE Access 2022, 10, 75105–75116. [Google Scholar] [CrossRef]
- de Oliveira, J.D.A.; Lima, F.K.d.A.; Tofoli, F.L.; Branco, C.G.C. Synchronverter-based frequency control technique applied in wind energy conversion systems based on the doubly-fed induction generator. Electr. Power Syst. Res. 2023, 214, 108820. [Google Scholar] [CrossRef]
- Chowdhury, V.R.; An, Z.; Kandula, R.P.; Divan, D.M. Operation and control of Soft Switching Solid State Transformer as a Virtual Synchronous Machine for Photovoltaic application. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.M.; Rueda, J.L.; Palensky, P.; Chamorro, H. Investigations of the Virtual Impedance Control Mode of Synchronverter in the Power Swing. In Proceedings of the 2022 International Conference on Smart Energy Systems and Technologies (SEST), Eindhoven, The Netherlands, 5–7 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Abid, M.S.; Ahshan, R.; Al Abri, R.; Al-Badi, A.; Albadi, M. Photovoltaic unit allocation in synchronverter-integrated microgrids. In Proceedings of the 2023 6th International Conference on Electrical Information and Communication Technology (EICT), Khulna, Bangladesh, 7–9 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Araújo de Oliveira, J.D.; Lima, F.K.d.A.; Castelo Branco, C.G. Synchronverter with Virtual Resistor-Based Frequency Control Technique Applied in Doubly-Fed Induction Generator. In Proceedings of the 2023 IEEE 8th Southern Power Electronics Conference and 17th Brazilian Power Electronics Conference (SPEC/COBEP), Florianopolis, Brazil, 26–29 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Alkhamis, B.T.; Al-Odienat, A. The Application of Synchronverter for the Enhancement of Power System Stability. In Proceedings of the 2023 IEEE Jordan International Joint Conference on Electrical Engineering and Information Technology (JEEIT), Amman, Jordan, 22–24 May 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 44–49. [Google Scholar] [CrossRef]
- Akbari, E.; Zare Ghaleh Seyyedi, A. Improving Power Quality of a Hybrid Grid-Connected Photovoltaic–Wind Microgrid Using Shunt Active Power Filter and Distribution Static Synchronous Compensator. Int. Trans. Electr. Energy Syst. 2024, 2024. [Google Scholar] [CrossRef]
- Kim, K.R.; Lee, S.; Lee, J.P.; Kang, J. An Enhanced Control Strategy for Mitigation of State-Transition Oscillation Phenomena in Grid-Forming Self-Synchronized Converter System with Islanded Power System. Energies 2021, 14, 8453. [Google Scholar] [CrossRef]
- Dong, S.; Chen, Y.C. A Fast Self-synchronizing Synchronverter Design with Easily Tuneable Parameters. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- R, H.; Mishra, M. An Integrated Control of Enhanced-PLL and Synchronverter for Unbalanced Grid. IEEE Trans. Ind. Appl. 2022, 58, 2206–2216. [Google Scholar] [CrossRef]
- Naeem, M.; Ashraf, M.; Khan, U.A. A robust auto-synchronizer for synchronverter. Comput. Electr. Eng. 2022, 98, 107661. [Google Scholar] [CrossRef]
- Tan, Y.; Shen, X.; Xu, M. Pre-Synchronization Control Strategy for Grid Connection of Synchronverter Cluster. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Chandrakar, P.; Saha, S.; Das, P.; Singh, A.; Debbarma, S. Grid Integration of PV System Using Synchronverter. In Proceedings of the 2018 Internat2018 International Conference on Computation of Power, Energy, Information and Communication (ICCPEIC)ional conference on computation of power, energy, Information and Communication (ICCPEIC), Chennai, India, 28–29 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 237–242. [Google Scholar] [CrossRef]
- Hariharan, R.; Mishra, M.K. An Inbuilt Synchronization Controller for Three-Phase Synchronverters. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Manoj, S.; Pradeep Kumar, S.; Ashok Babu, N. Automatic Synchronverter: Inverter Lacking a Devoted Synchronization Unit. Int. J. Eng. Technol. 2018, 7, 20. [Google Scholar] [CrossRef]
- Rashid, U.; Muzzammel, R. Operational Analysis of a Power Electronic Converter as a Virtual Synchronous Machine. In Proceedings of the 2023 2nd International Conference on Emerging Trends in Electrical, Control, and Telecommunication Engineering (ETECTE), Lahore, Pakistan, 27–29 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Venugopal, G.; Guerrero, J.M.; Ekanayake, J.B.; Tiong, S.K. Variable-Speed PICO Hydel Energy Storage with Synchronverter Control to Emulate Virtual Inertia in Autonomous Microgrids. IEEE Syst. J. 2022, 16, 452–463. [Google Scholar] [CrossRef]
- Vasudevan, K.R.; Ramachandaramurthy, V.K.; Venugopal, G.; Guerrero, J.M. Hybridization of battery with pico hydel for frequency regulation of microgrids using synchronverter control. IET Renew. Power Gener. 2022, 16, 274–286. [Google Scholar] [CrossRef]
- Silva Junior, G.P.d.; Barros, L.S.; Barros, C.M.V. Synchronverter coupled to a lithium-ion bank for grid frequency and voltage supports and controlled charge-discharge. Electr. Power Syst. Res. 2021, 197, 107352. [Google Scholar] [CrossRef]
- Chen, J.; Liu, M.; Guo, R.; Zhao, N.; Milano, F.; O’Donnell, T. Co-ordinated grid forming control of AC-side-connected energy storage systems for converter-interfaced generation. Int. J. Electr. Power Energy Syst. 2021, 133, 107201. [Google Scholar] [CrossRef]
- Høstmark, H.; Amin, M. Small-signal modeling and tuning of Synchronverter-based wind energy conversion systems. Int. Trans. Electr. Energy Syst. 2021, 31, 1–21. [Google Scholar] [CrossRef]
- V Marthi, P.R.; Debnath, S.; Xia, Q.; Crow, M.L. Model Based Predictive Control for Frequency Support in Multi-port Autonomous Reconfigurable Solar Plants. In Proceedings of the 2021 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–18 February 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Sharma, N.; Buwa, O.N.; Thakre, M.P. Dynamic Phasor Modeling of Single Phase Roof Top PV with Synchronverter Control. In Proceedings of the 2020 Third International Conference on Advances in Electronics, Computers and Communications (ICAECC), Bengaluru, India, 11–12 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Sharma, N.; Buwa, O.N.; Thakre, M.P. Transient Response Analysis of a Single Phase Roof Top PV with Synchronverter Control. In Proceedings of the 2020 International Conference on Power, Energy, Control and Transmission Systems (ICPECTS), Chennai, India, 10–11 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Perveen, R.; Hassan, A.; Awais, M. A synchronverter-based static synchronous compensator approach to compensate nonlinear loads in wind integrated power system. Int. Trans. Electr. Energy Syst. 2020, 30, 1–15. [Google Scholar] [CrossRef]
- Gunther, K.; Sourkounis, C. Investigation of Virtual Synchronous Machine Control for the Grid-Side Converter of Wind Turbines with Permanently Excited Synchronous Generator. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 2395–2401. [Google Scholar] [CrossRef]
- Nair, N.R.; Kanakasabapathy, D.P. A Three Phase Grid Connected SPV System using Synchronverter. In Proceedings of the 2018 8th IEEE India International Conference on Power Electronics (IICPE), Jaipur, India, 13–15 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, W.; Liu, B.; Nazir, M.S.; Abdalla, A.N.; Mohamed, M.A.; Ding, Z.; Bhutta, M.S.; Gul, M. An Energy Storage Assessment: Using Frequency Modulation Approach to Capture Optimal Coordination. Sustainability 2022, 14, 8510. [Google Scholar] [CrossRef]
- Neupane, D.; Gurung, S.; Neupane, S.; Bhattarai, N. Power Sharing in Solar PV: Microhydro Hybrid System Using Power Angle Control Strategy. J. Control. Autom. Electr. Syst. 2023, 34, 166–176. [Google Scholar] [CrossRef]
- Frasetyo, M.B.; Wijaya, F.D.; Ali, H.R. Islanded Wind Farm Microgrid Stability Control using Synchronverter Algorithm. IEEJ J. Ind. Appl. 2023, 12, 22007270. [Google Scholar] [CrossRef]
- Vilmann, B.; Randewijk, P.J.; Jóhannsson, H.; Hjerrild, J.; Khalil, A. Frequency and Voltage Compliance Capabilities of Grid-Forming Wind Turbines in Offshore Wind Farms in Weak AC Grids. Electronics 2023, 12, 1114. [Google Scholar] [CrossRef]
- Mohamed, M.; Dubuisson, F.; Beram, B.S.; Rezkallah, M.; Hamadi, A.; Chandra, A. Combination of the Synchronverter with Droop Control for Hybrid OFF-grid System. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Vilmann, B.; Hjerrild, J.; Randewijk, P.J.; Khalil, A. Frequency and Voltage Compliance Capability of Grid-Forming Wind Turbines in Offshore Wind Farms in Weak Grids with a Power Imbalance. In Proceedings of the 2022 57th International Universities Power Engineering Conference (UPEC), Istanbul, Turkey, 30 August–2 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–8. [Google Scholar] [CrossRef]
- Frasetyo, M.B.; Danang Wijaya, F.; Firmansyah, E. Islanded Wind Farm Microgrid Stability Control Using Synchronverter Algorithm. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022- ECCE Asia), Himeji, Japan, 15–19 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1567–1572. [Google Scholar] [CrossRef]
- Yap, K.Y.; Hon, H.Y.; Sarimuthu, C.R. Grid Integration of Solar Power System Using Synchronverter-Based Energy Storage System. Appl. Sol. Energy 2022, 58, 444–457. [Google Scholar] [CrossRef]
- Marthi, P.R.V.; Debnath, S.; Xia, Q. Fidelity Analysis of Complex Large-Scale Simulation Models of PEs (MARS) in Future Power Grids. In Proceedings of the 2023 IEEE 24th Workshop on Control and Modeling for Power Electronics (COMPEL), Ann Arbor, MI, USA, 25–28 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Lorenzetti, P.; Kustanovich, Z.; Shivratri, S.; Weiss, G. The Equilibrium Points and Stability of Grid-Connected Synchronverters. IEEE Trans. Power Syst. 2022, 37, 1184–1197. [Google Scholar] [CrossRef]
- Franca, B.W.; Aredes, M.; Silva, L.F.d.; Gontijo, G.F.; Tricarico, T.C.; Posada, J. An Enhanced Shunt Active Filter Based on Synchronverter Concept. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 494–505. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.; Rueda, J.L.; Palensky, P.; Chamorro, H.R.; Abdellah, K. Comparative Performance of Inverted-Based Generation using Synchonverter during Transient Stability Conditions. In Proceedings of the 2022 5th International Conference on Power Electronics and their Applications (ICPEA), Hail, Saudi Arabia, 29–31 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Xu, R.; Wu, S.; Xiang, S.; Zhou, Y.; Xiang, B.; Huang, K. An Optimization Method of Virtual Synchronous Generators Parameter Design Based on Power Equivalent Model. In Proceedings of the 2022 5th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 22–24 April 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 663–669. [Google Scholar] [CrossRef]
- Busada, C.A.; Gomez Jorge, S.; Solsona, J.A. Feedback Linearization of a grid-tied Synchronverter. IEEE Trans. Ind. Electron. 2022, 70, 147–154. [Google Scholar] [CrossRef]
- Lorenzetti, P.; Weiss, G. Saturating PI control of stable nonlinear systems using singular perturbations. IEEE Trans. Autom. Control 2022, 68, 867–882. [Google Scholar] [CrossRef]
- Skinder, K.S.; Kerdphol, T.; Mitani, Y.; Turschner, D. Frequency Stability Assessment of Multiple Virtual Synchronous Generators for Interconnected Power System. IEEE Trans. Ind. Appl. 2022, 58, 91–101. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Bevrani, H.; Ise, T. A Unified Modeling Method of Virtual Synchronous Generator for Multi-Operation-Mode Analyses. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2394–2409. [Google Scholar] [CrossRef]
- Hariharan, R.; Mishra, M.K. Analysis of Synchronverter Control with Virtual Impedance During Grid Voltage Variations. In Proceedings of the 2021 IEEE 2nd International Conference on Smart Technologies for Power, Energy and Control (STPEC), Bilaspur, India, 19–22 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Zheng, Q.; Gao, F. An Enhanced Control Strategy of Bidirectional Interlinking Converters in a Hybrid AC/DC Microgrid. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1087–1094. [Google Scholar] [CrossRef]
- Kustanovich, Z.; Reissner, F.; Shivratri, S.; Weiss, G. The Sensitivity of Grid-Connected Synchronverters with Respect to Measurement Errors. IEEE Access 2021, 9, 118985–118995. [Google Scholar] [CrossRef]
- Vetoshkin, L.; Muller, Z. A comparative study of synchronverter stability. In Proceedings of the 2020 21st International Scientific Conference on Electric Power Engineering (EPE), Prague, Czech Republic, 19–21 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Unamuno, E.; Suul, J.A.; Molinas, M.; Barrena, J.A. Comparative Eigenvalue Analysis of Synchronous Machine Emulations and Synchronous Machines. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3863–3870. [Google Scholar] [CrossRef]
- Rosso, R.; Cassoli, J.; Buticchi, G.; Engelken, S.; Liserre, M. Robust Stability Analysis of LCL Filter Based Synchronverter Under Different Grid Conditions. IEEE Trans. Power Electron. 2019, 34, 5842–5853. [Google Scholar] [CrossRef]
- Dong, S.; Chen, Y.C. A Method to Directly Compute Synchronverter Parameters for Desired Dynamic Response. IEEE Trans. Energy Convers. 2018, 33, 814–825. [Google Scholar] [CrossRef]
- Deepak, D.; Raisz, D.; Musa, A.; Ponci, F.; Monti, A. Inertial Control Applied to Synchronverters to Achieve Linear Swing Dynamics. In Proceedings of the 2019 Electric Power Quality and Supply Reliability Conference (PQ) & 2019 Symposium on Electrical Engineering and Mechatronics (SEEM), Kärdla, Estonia, 12–15 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Rosso, R.; Engelken, S.; Liserre, M. Analysis of the Behavior of Synchronverters Operating in Parallel by Means of Component Connection Method (CCM). In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2228–2235. [Google Scholar] [CrossRef]
- Lewis, P.T.; Grainger, B.M. Electro-Thermal Transient Performance Assessment of SiC Based Distributed Generation Inverters when Governed by Virtual Synchronous Machine Control or Conventional dq Control. In Proceedings of the 2018 9th IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Charlotte, NC, USA, 25–28 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Lorenzetti, P.; Weiss, G. PI control of stable nonlinear plants using projected dynamical systems. Automatica 2022, 146, 110606. [Google Scholar] [CrossRef]
- Segundo Ramírez, J.; Hernández Ramírez, J.; Visairo Cruz, N.; Peña Gallardo, R. Bifurcation Stability Analysis of the Synchronverter in a Microgrid. Energies 2022, 15, 7992. [Google Scholar] [CrossRef]
- Kumar, R.; Chaudhari, M.A.; Chaturvedi, P.; Sekhar, K.S.R. Comparative Analysis of Direct Quadrature (DQ) and Synchonverter Techniques for the Control of 3 − ϕ VSI in AC Micro-Grid. In Proceedings of the 2022 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Jaipur, India, 14–17 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Yin, H.; Lin, J. Phillips-Heffron model and damping torque analysis of synchronverter. In Proceedings of the 2022 IEEE 20th International Power Electronics and Motion Control Conference (PEMC), Brasov, Romania, 25–28 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 137–142. [Google Scholar] [CrossRef]
- Mahafzah, K.A.; Rabab’ah, H.A.; Al-Odienat, A.; Al-Momani, M.; Al-Maitah, K.; Al-Mbaideen, A. The Dynamic Response of SPWM vs. SVPWM Synchronverter. Wseas Trans. Power Syst. 2022, 17, 93–102. [Google Scholar] [CrossRef]
- Maurya, S.S.; Jain, T.; Umarikar, A.C. Small Signal Modelling of Compensator based Virtual Synchronous Generator in Islanded AC Microgrid. In Proceedings of the 2023 International Conference on Circuit Power and Computing Technologies (ICCPCT), Kollam, India, 28–31 October 2018; IEEE: Piscataway, NJ, USA, 2023; pp. 1609–1616. [Google Scholar] [CrossRef]
- Tebib, A.; Boudour, M. Optimal Design of Synchronverter Virtual Capacitor to Achieve Capacitive Output Impedance. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Busada, C.A.; Jorge, S.G.; Solsona, J.A. Output Admittance Synthesizer for Synchronverters. IEEE Trans. Ind. Electron. 2022, 69, 4320–4328. [Google Scholar] [CrossRef]
- Hariharan, R.; Mishra, M.K. An Improved Synchronverter Control for DERs Under Grid Voltage Variations. In Proceedings of the 2021 IEEE 2nd International Conference on Smart Technologies for Power, Energy and Control (STPEC), Bilaspur, India, 19–22 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- da Silva Junior, G.P.; Barros, L.S. Using Synchronverter in Distributed Generation for Frequency and Voltage Grid Support. In Proceedings of the 2019 IEEE 15th Brazilian Power Electronics Conference and 5th IEEE Southern Power Electronics Conference (COBEP/SPEC), Santos, Brazil, 1–4 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- da Silva Junior, G.P.; Barros, L.S. Synchronverter Operation in Active and Reactive Support Mode. In Proceedings of the 2019 Workshop on Communication Networks and Power Systems (WCNPS), Brasilia, Brasil, 3–4 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Sharmini, K.S. A Simplified Pulse Generation Control Algorithm Based upon the Concept of Synchronverter. In Advances in Intelligent Systems and Computing; Springer: Singapore, 2019; Volume 846, pp. 261–269. [Google Scholar] [CrossRef]
- Furqan, S.M.; Nasir, A.; Ashraf, A.; Shami, T.A.; Khalid, N. Design And Implementation of Virtual Synchronous Machine. In Proceedings of the 2018 International Conference on Computing, Electronic and Electrical Engineering (ICE Cube), Quetta, Pakistan, 12–13 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Pandya, V.; Manjunath, K. A Preliminary Study for Realizing Frequency Control Loop of Grid-tied Synchronverter. In Proceedings of the 2022 International Conference on Breakthrough in Heuristics And Reciprocation of Advanced Technologies (BHARAT), Visakhapatnam, India, 7–8 April 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 107–110. [Google Scholar] [CrossRef]
- Kumar, R.; Chaudhari, M.A.; Chaturvedi, P. A Three-Phase Nine-Level MLI for Grid-Tied AC Microgrid with Synchronverter Control. In Proceedings of the 2023 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 17–20 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Chen, J.; Deng, C.; Lin, W.; Qi, Q.; Liu, S.; Sun, X. Calculation of Three-phase Fault Current in Synchronverters Considering Fault ride-through Strategies. In Proceedings of the 2022 5th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 22–24 April 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 442–446. [Google Scholar] [CrossRef]
- Azzouz, M.A.; Zeineldin, H.H.; El-Saadany, E.F. Selective Phase Tripping for Microgrids Powered by Synchronverter-Interfaced Renewable Energy Sources. IEEE Trans. Power Deliv. 2021, 36, 3506–3518. [Google Scholar] [CrossRef]
- Habibullah, M.; Gonzalez-Longatt, F.; Acosta Montalvo, M.N.; Chamorro, H.R.; Rueda, J.L.; Palensky, P. On Short Circuit of Grid-Forming Converters Controllers: A glance of the Dynamic Behaviour. In Proceedings of the 2021 IEEE PES Innovative Smart Grid Technologies Conference—Latin America (ISGT Latin America), Lima, Peru, 15–17 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Zakis, J.; Makovenko, E.; Zeng, H.; Husev, O.; Kutt, L. qZS Inverter as Synchronverter in Small-Scale Micro-Grid. Elektron. Elektrotech. 2018, 24, 58–62. [Google Scholar] [CrossRef]
- Gutierrez, M.; Zuniga, P.; Uribe, F.; Barocio, E.; Puerto-Flores, D.D. Analysis of Synchronverters and Droop Control Scheme During Microgrid Operation: A Performance Comparison Approach. In Proceedings of the 2018 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 14–16 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Ala, G.; Di Tommaso, A.; Miceli, R.; Nevoloso, C.; Scaglione, G.; Schettino, G.; Viola, F. Virtual Synchronous Generator: An application to Microgrid Stability. In Proceedings of the 2022 11th International Conference on Renewable Energy Research and Application (ICRERA), Istanbul, Turkey, 18–21 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 151–157. [Google Scholar] [CrossRef]
- Chida, A.B.; Boukettaya, G.; Cherni, R. Synchronverter as Control Strategy of Grid-Forming Inverter. In Proceedings of the 2023 20th International Multi-Conference on Systems, Signals and Devices, SSD 2023, Mahdia, India, 28–30 May 2021; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023; pp. 61–66. [Google Scholar] [CrossRef]
- Yang, T.; Hu, W. Research on Variable Inertia Control Strategy of Electric Vehicle Based on Synchronverter. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, D.; Zeng, X.; Liu, G. Control method for EV charging and discharging in V2G/V2H scenario based on the synchronvter technology and H ∞ repetitive control. J. Eng. 2019, 2019, 1350–1355. [Google Scholar] [CrossRef]
- Liu, D.; Zhong, Q.; Wang, Y.; Liu, G. Modeling and control of a V2G charging station based on synchronverter technology. CSEE J. Power Energy Syst. 2018, 4, 326–338. [Google Scholar] [CrossRef]
- Yin, H. Gasoline-electric hybrid propulsion system with synchronverter. In Proceedings of the 2022 25th International Conference on Mechatronics Technology (ICMT), Kaohsiung, Taiwan, 18–21 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Zhang, J.F.; Yang, Z.; Liu, B.; Yin, X.; Zhang, Y.X. Design of Ship-applied Grid-Connected Synchronverter. In Proceedings of the 2022 7th International Conference on Power and Renewable Energy (ICPRE), Shangai, China, 23–26 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 635–638. [Google Scholar] [CrossRef]
- Yin, H. Single-phase VSM based on dq coordinate. In Proceedings of the 2022 25th International Conference on Mechatronics Technology (ICMT), Kaohsiung, Taiwan, 18–21 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Wei, J.; Wu, S.; Zhou, Y.; Yang, P.; Kong, Q. Research on Power Electronic Transformers Based on Virtual Synchronous Machine Control. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 669–674. [Google Scholar] [CrossRef]
- Wu, R.; Ran, L.; Weiss, G.; Yu, J. Control of a synchronverter-based soft open point in a distribution network. J. Eng. 2019, 2019, 720–727. [Google Scholar] [CrossRef]
- Oñate, M.; Posada, J.; López, J.; Quintero, J.; Aredes, M. Control of a back-to-back converter as a power transfer system using synchronverter approach. IET Gener. Transm. Distrib. 2018, 12, 1998–2005. [Google Scholar] [CrossRef]
- Arun, P.B.; Bose, K.C. Synchronverter Based HVDC Transmission For Stability Improvement. In Proceedings of the 2019 International Conference on Intelligent Computing and Control Systems (ICCS), Madurai, India, 15–17 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1312–1316. [Google Scholar] [CrossRef]
- Tebib, A.; Boudour, M. An Improved Synchronverter based HVDC System Considering Damper Windings Effect. In Proceedings of the 2018 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Algiers, Algeria, 28–31 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Cunha, A.C.; Souza, M.J.; Alves, F.; Bernhardt, B.; Aredes, M.; Nunes, S.; Leal, G. Connection of Deep Water Oil Extraction Platforms to the Onshore Power Electric System by a VSC-HVDC System Based on Synchronverter Control. In Proceedings of the 2023 IEEE 8th Southern Power Electronics Conference and 17th Brazilian Power Electronics Conference (SPEC/COBEP), Florianopolis, SC, Brazil, 26–28 November 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Sonawane, A.J.; Umarikar, A.C. Voltage and Reactive Power Regulation with Synchronverter-Based Control of PV-STATCOM. IEEE Access 2023, 11, 52129–52140. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).