Thermal Impacts of Air Cavities Associated with Insulated Panels Deployed for Exterior Building Envelope Assemblies
Abstract
1. Introduction
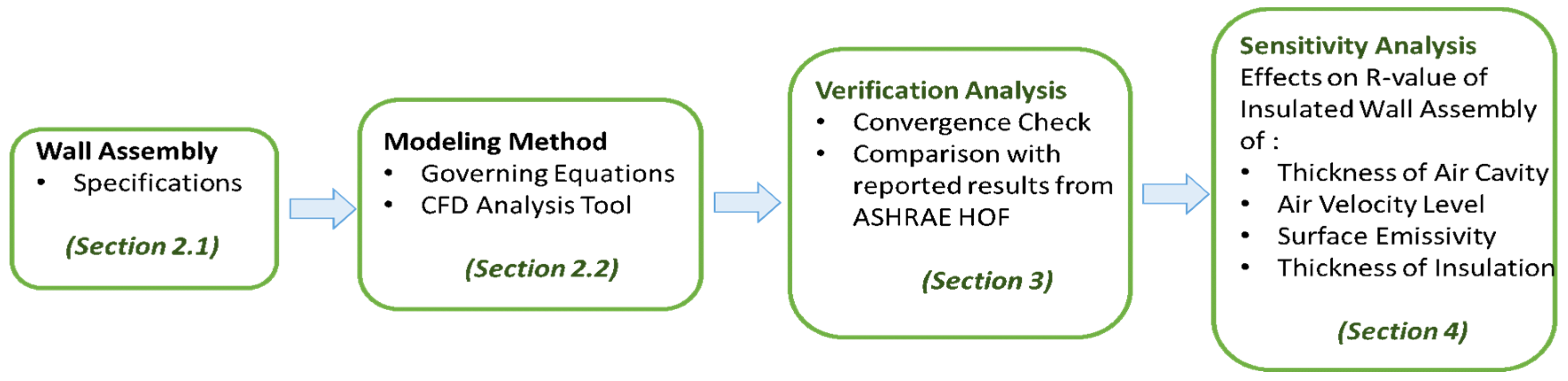
2. Materials and Methods
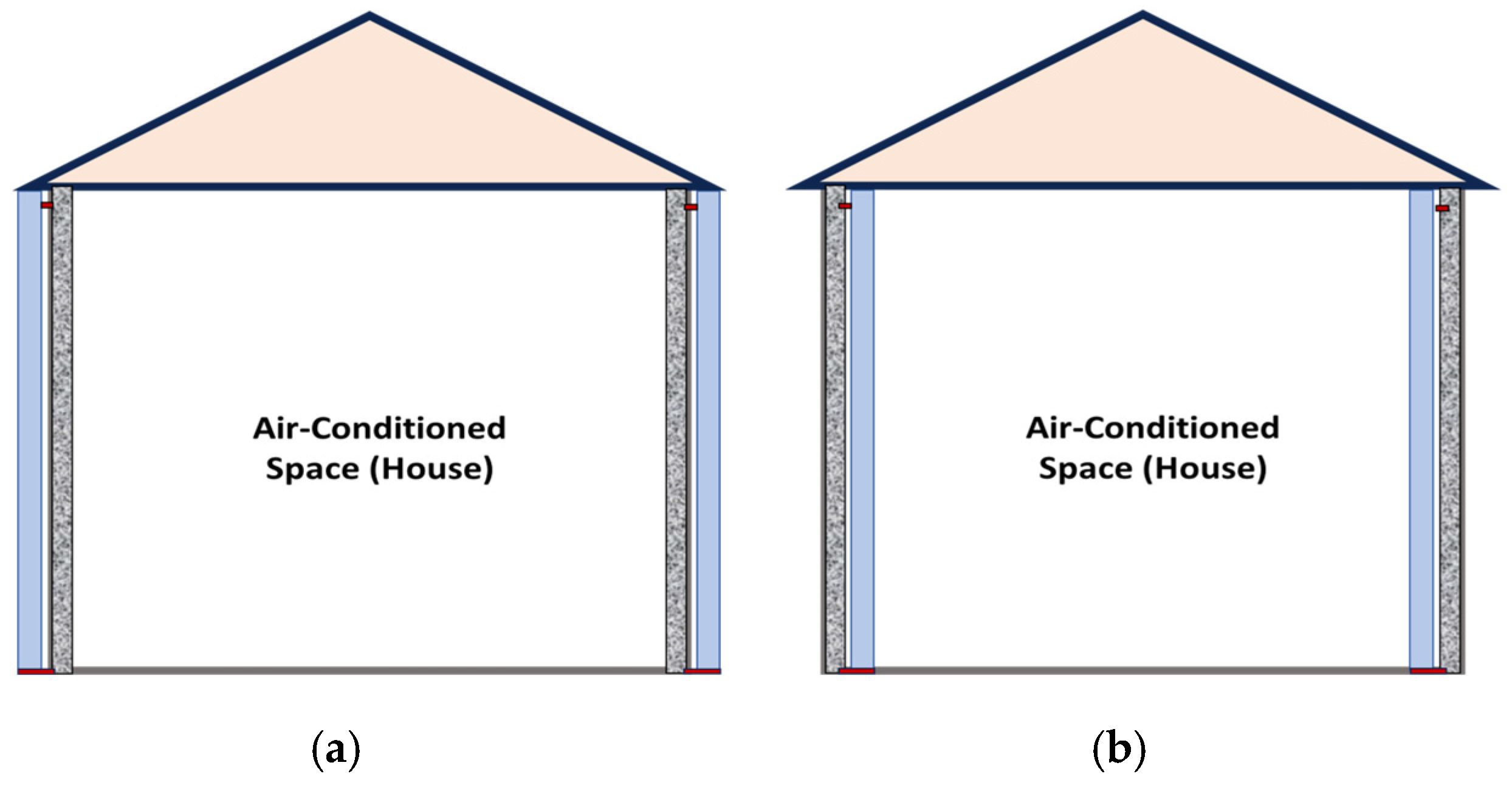
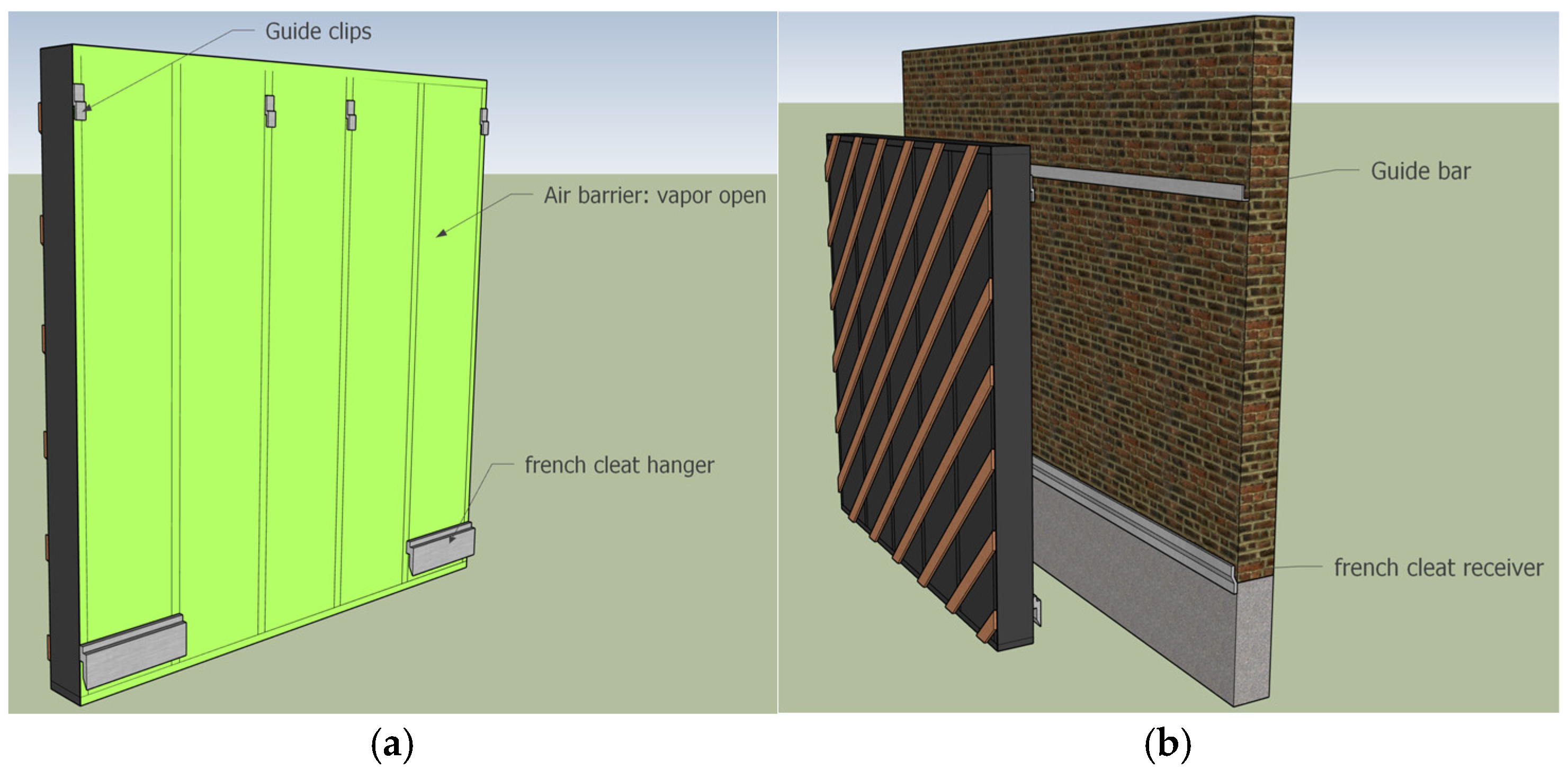
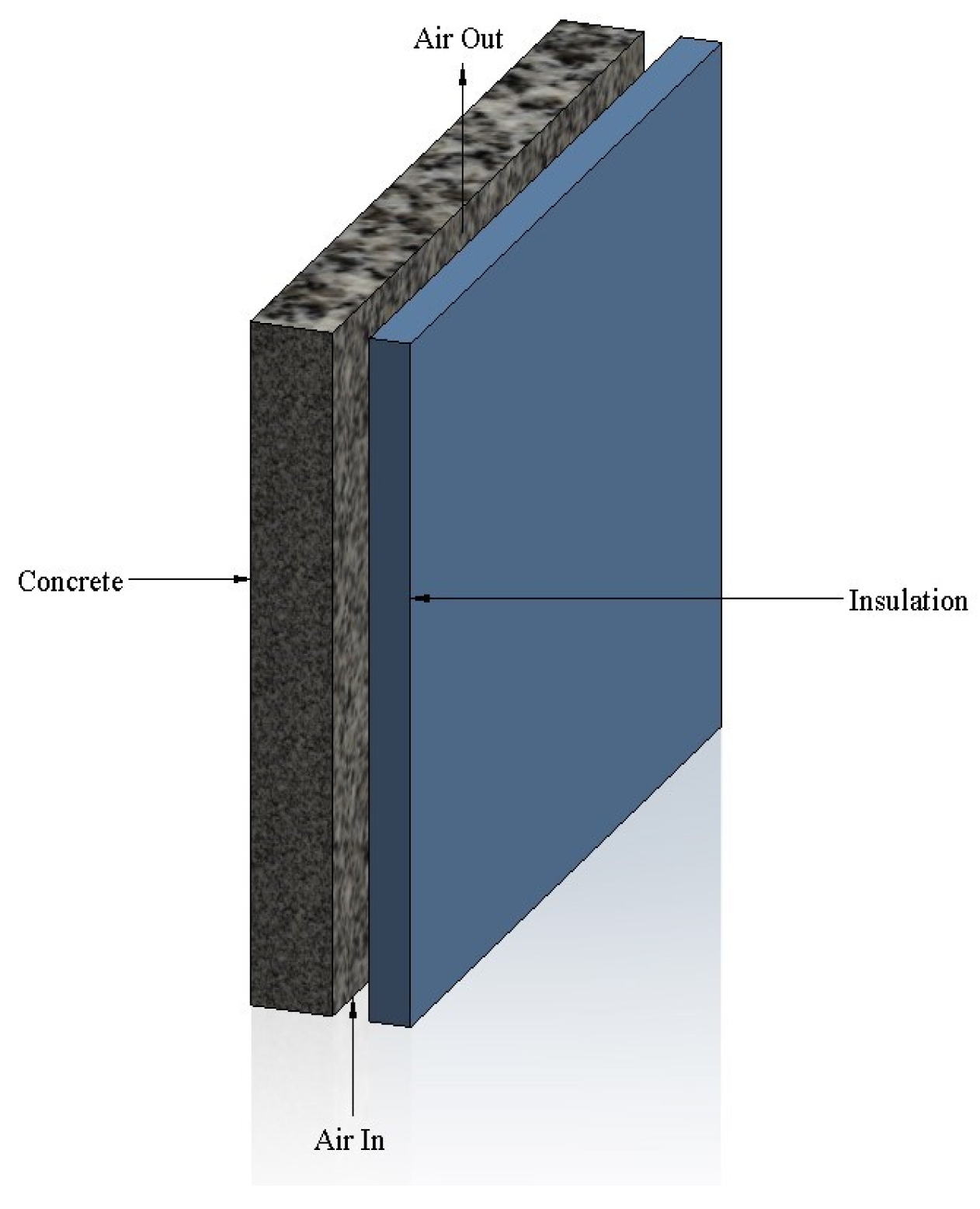
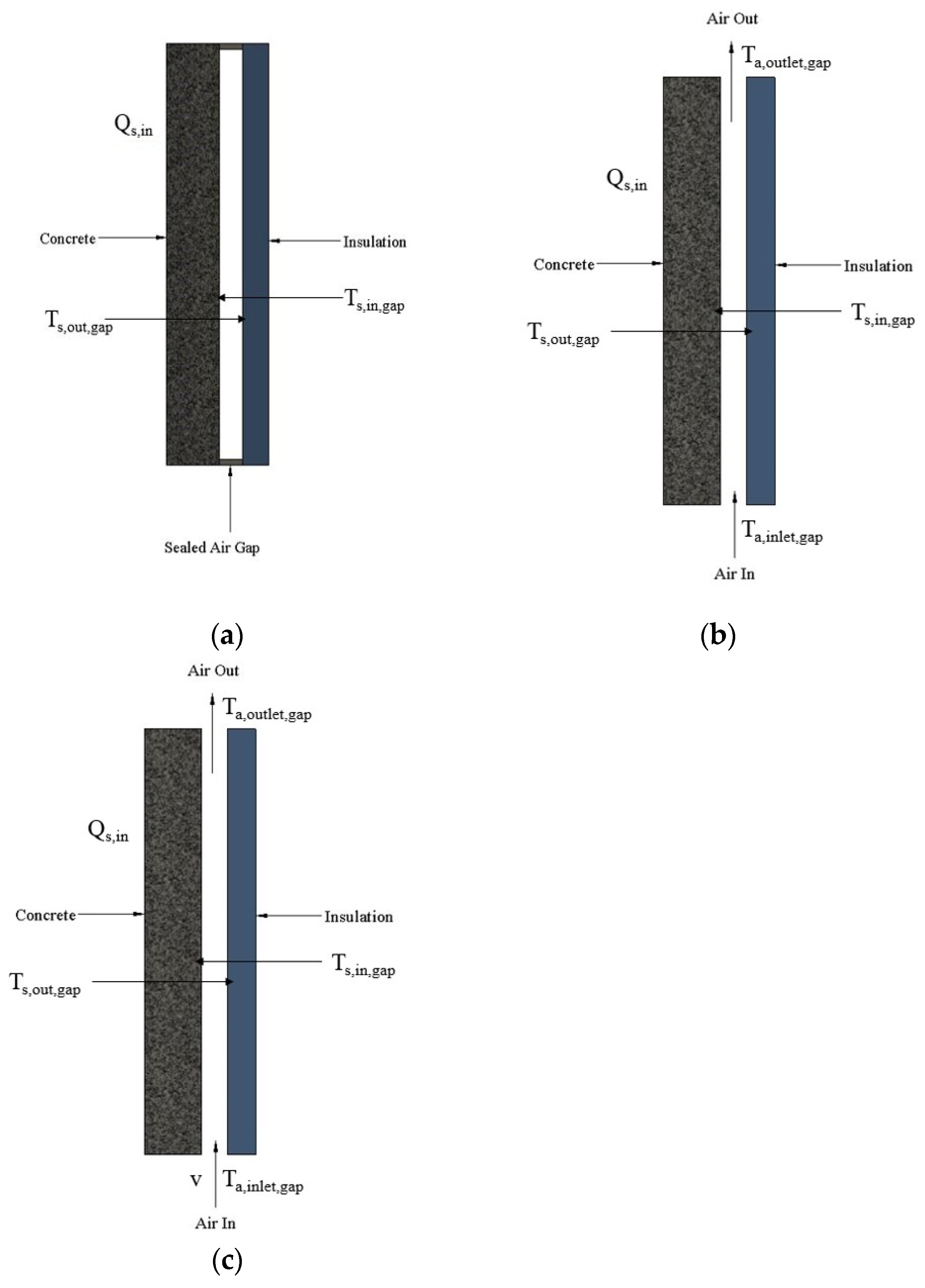
2.1. Wall Assembly Description
2.2. Overview of Modeling Analysis
2.3. Thermal Properties of Wall Assembly
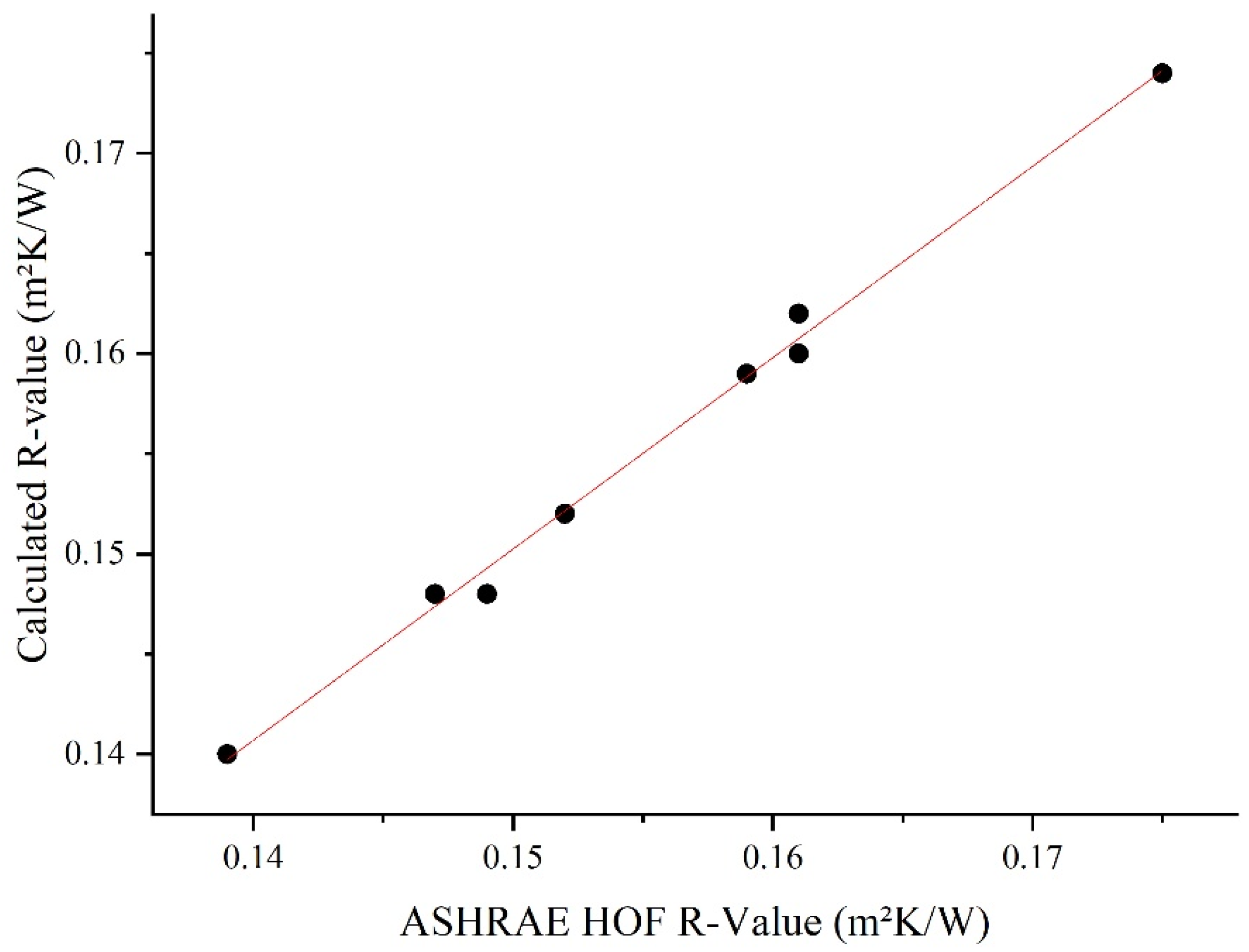
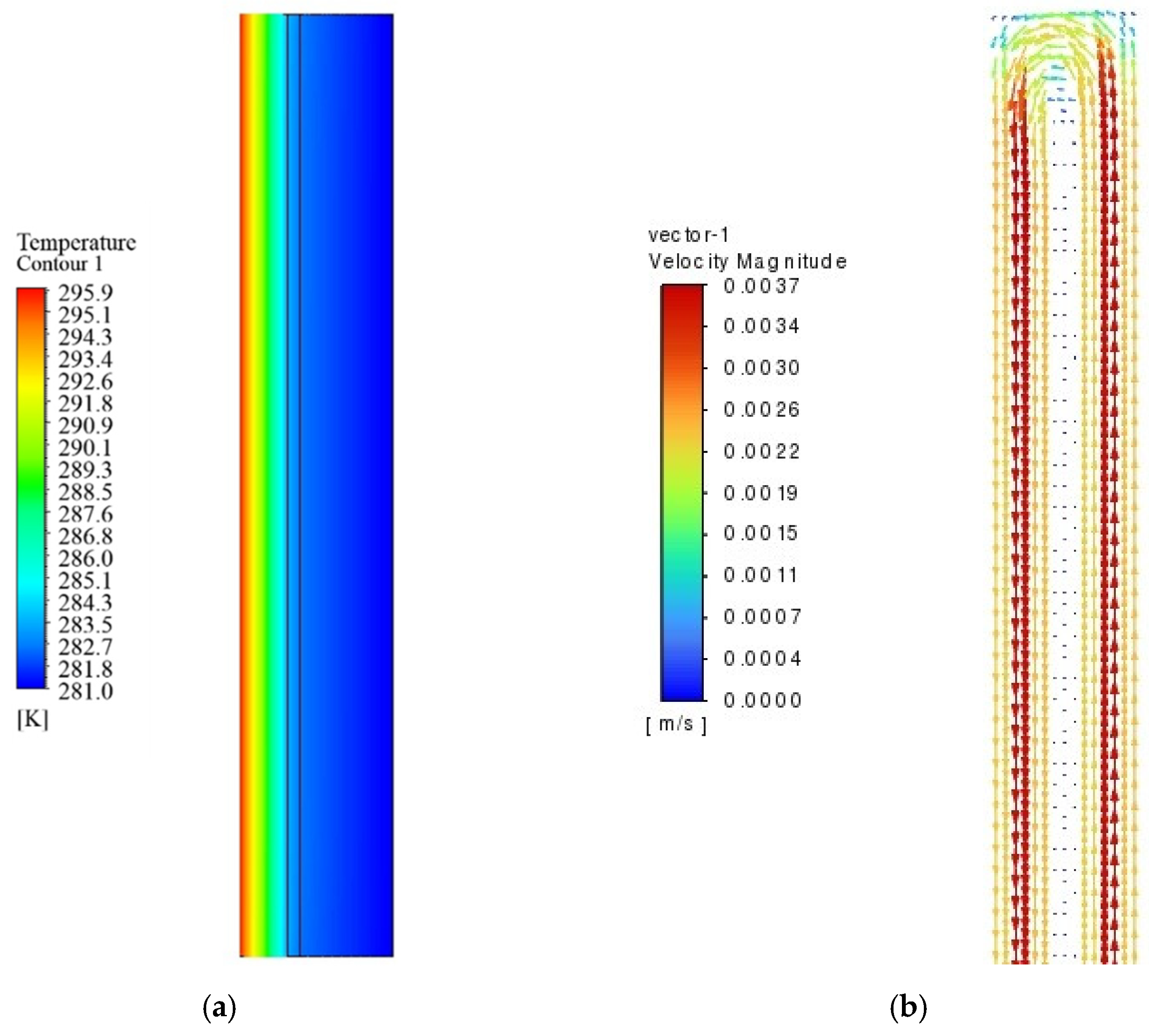
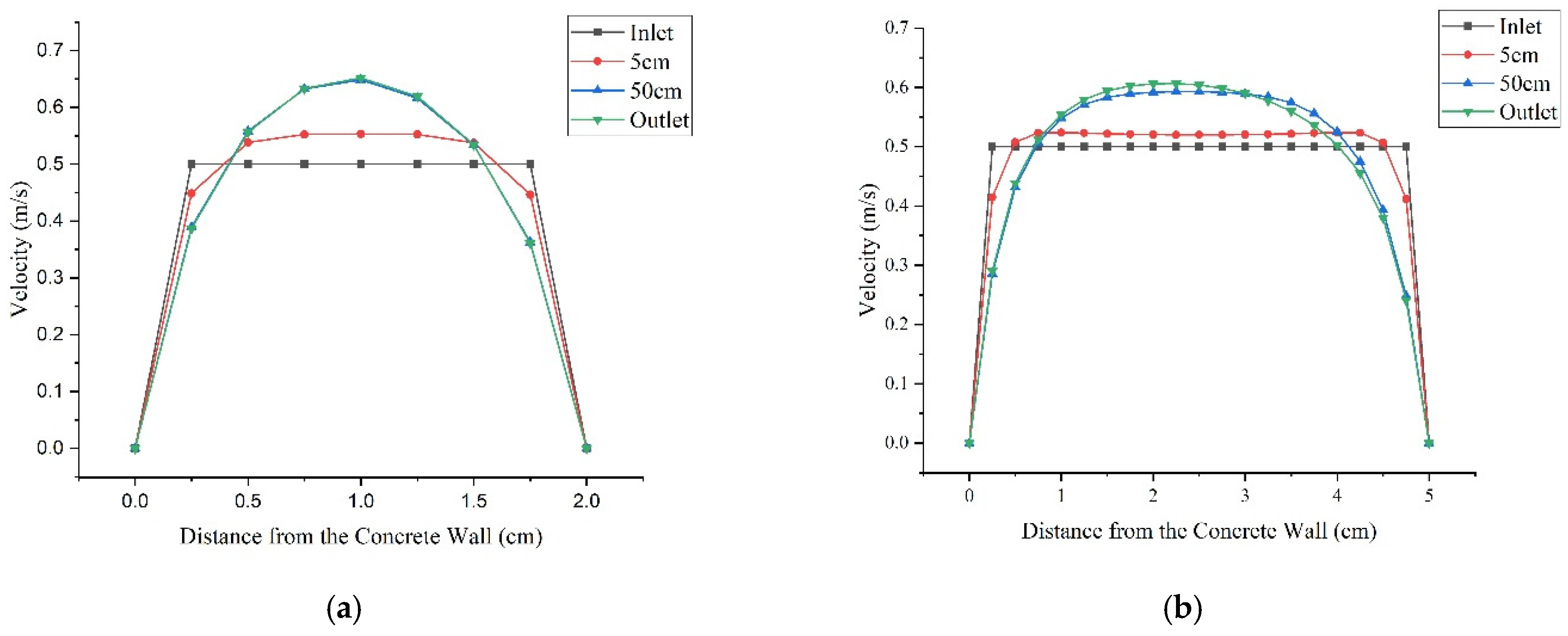
3. Verification Analysis
| Number of Nodes | Number of Elements | Air Gap Temp (K) | Heat Flux (W/m2) | Rwall (m2K/W) | Rairgap (m2K/W) | Computation Time (s) | Error % |
|---|---|---|---|---|---|---|---|
| 238 | 198 | 283.06 | 6.217 | 2.413 | 0.163 | 11.590 | 0.865 |
| 1717 | 1600 | 283.06 | 6.217 | 2.413 | 0.163 | 15.652 | 0.859 |
| 6834 | 6600 | 283.06 | 6.218 | 2.412 | 0.162 | 21.799 | 0.658 |
| 13,556 | 13,247 | 283.06 | 6.218 | 2.412 | 0.162 | 22.598 | 0.562 |
| 17,989 | 17,633 | 283.06 | 6.2185 | 2.412 | 0.162 | 31.615 | 0.535 |
| 25,675 | 25,268 | 283.06 | 6.2186 | 2.412 | 0.162 | 33.579 | 0.503 |
4. Sensitivity Analysis
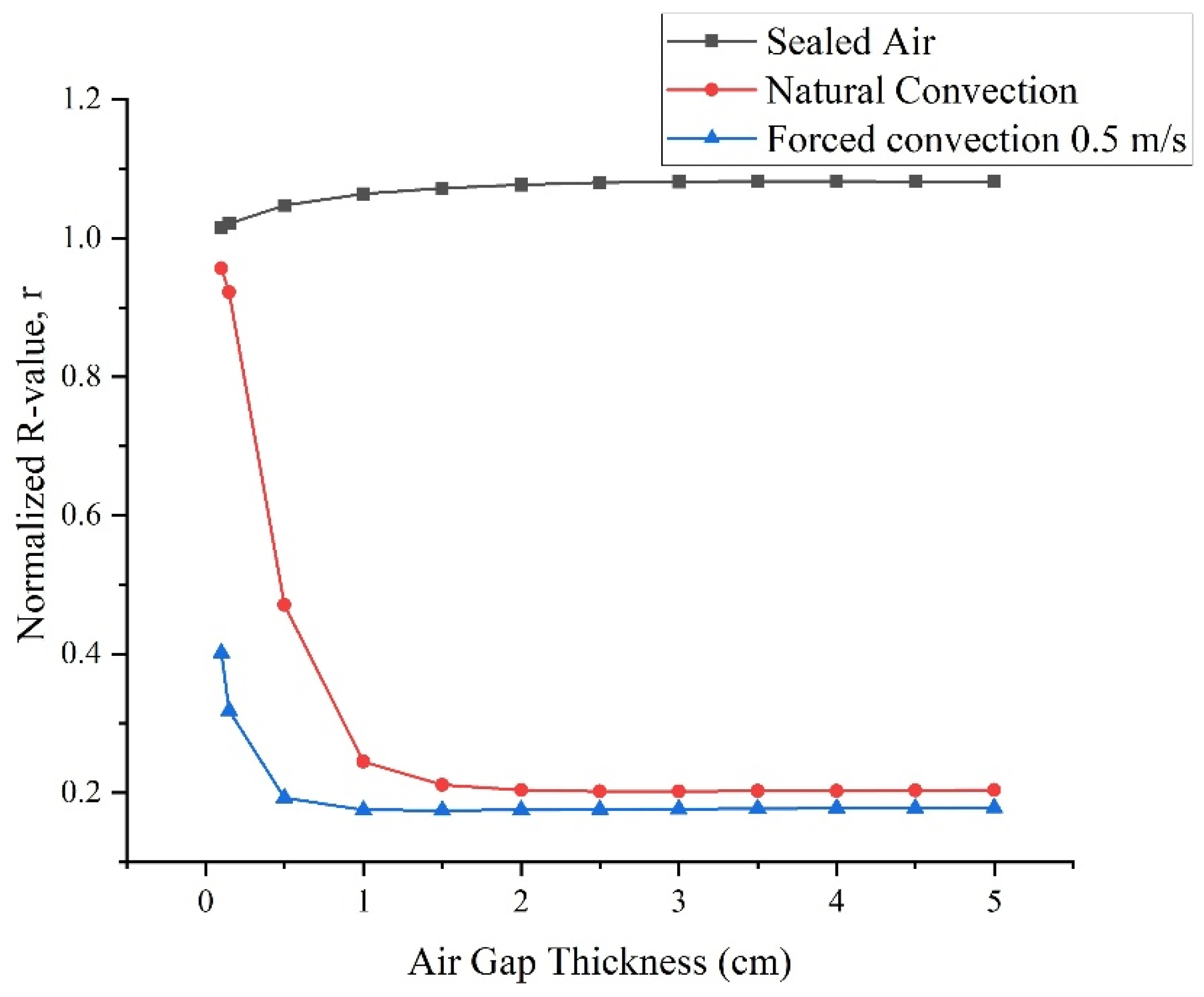
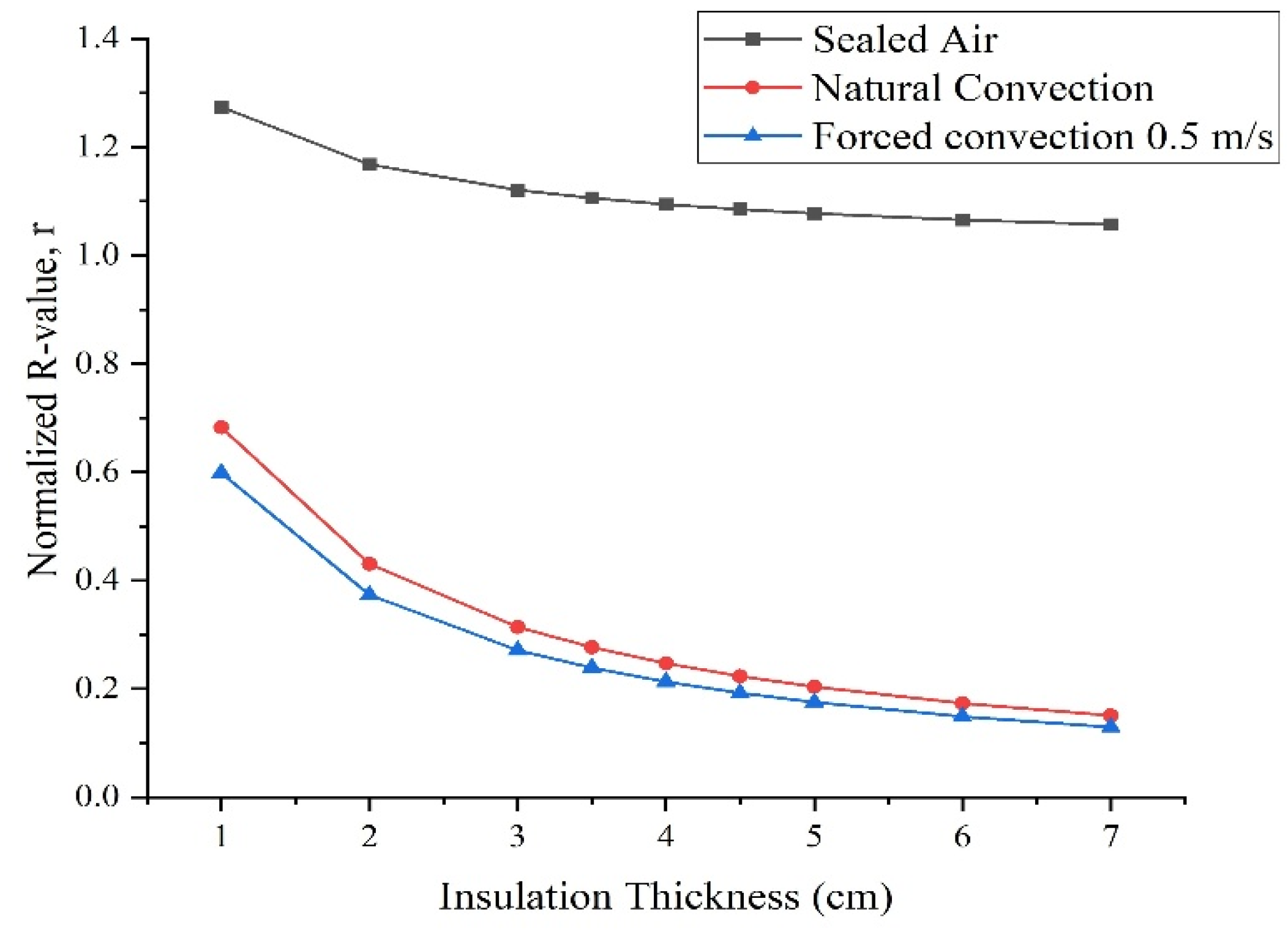
4.1. Impact of Air Cavity Thickness
Heat Transfer Analysis
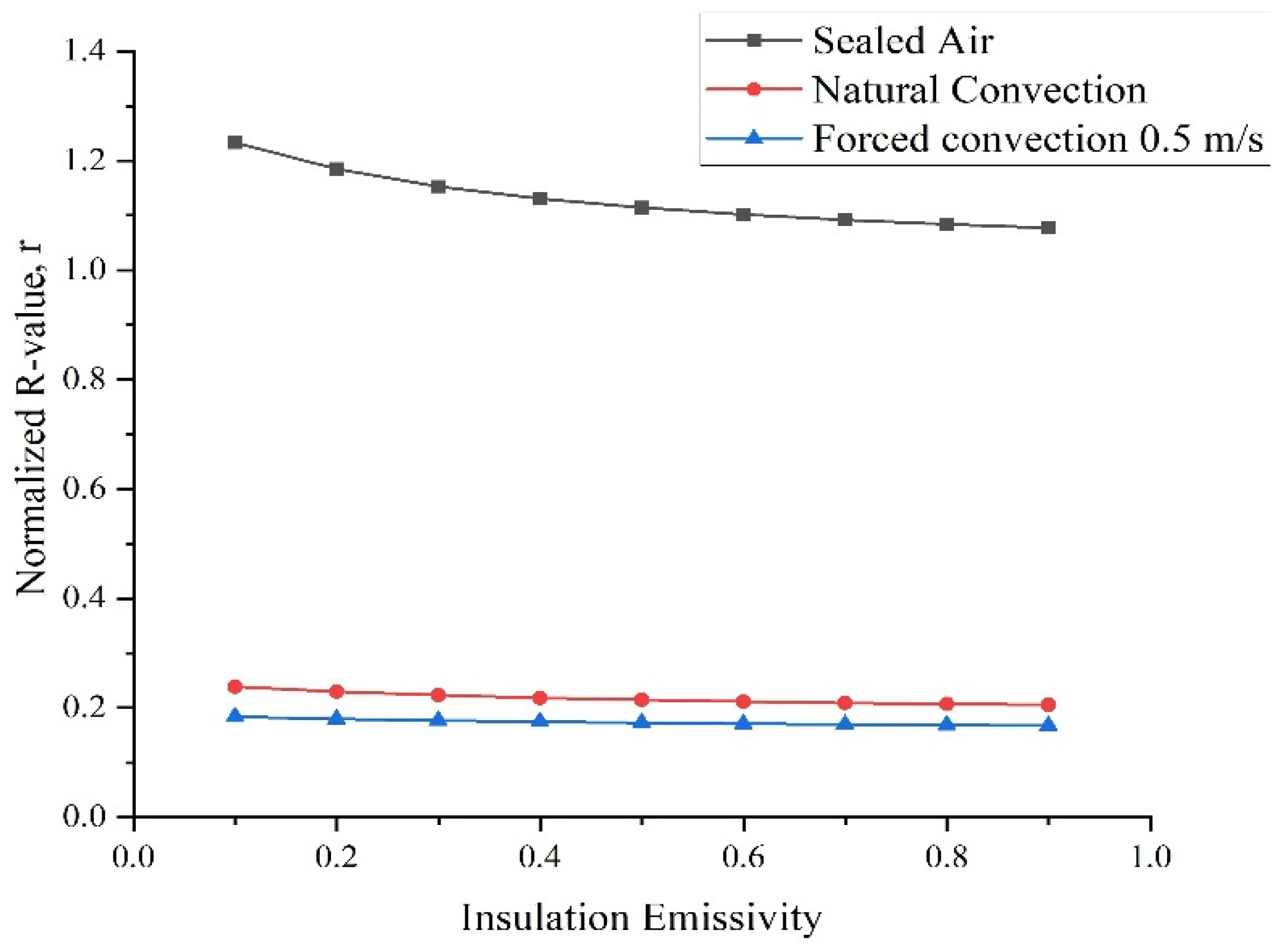
4.2. Impact of Cavity Surface Emissivity
4.3. Impact of Insulated Panel Thickness
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| DO | Discrete Ordinates, a model for radiation in CFD analysis |
| HOF | Handbook of Fundamentals |
| SIMPLE | Semi-Implicit Method for Pressure-Linked Equations |
References
- IEA. World Energy Outlook 2024; International Energy Agency: Paris, France, 2024; Available online: https://www.iea.org/reports/world-energy-outlook-2024 (accessed on 20 June 2025).
- U.S. Energy Information Administration—EIA—Independent Statistics and Analysis. Available online: https://www.eia.gov/pressroom/releases/press542.php (accessed on 29 June 2025).
- Fan, Y.; Fang, C. GHG Emissions and Energy Consumption of Residential Buildings—A Systematic Review and Meta-Analysis. Environ. Monit. Assess. 2023, 195, 885. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Song, J.; Shi, D.; Reyna, J.L.; Horsey, H.; Feron, S.; Zhou, Y.; Ouyang, Z.; Li, Y.; Jackson, R.B. Impacts of Climate Change, Population Growth, and Power Sector Decarbonization on Urban Building Energy Use. Nat. Commun. 2023, 14, 6434. [Google Scholar] [CrossRef]
- Hafez, F.S.; Sa’di, B.; Safa-Gamal, M.; Taufiq-Yap, Y.H.; Alrifaey, M.; Seyedmahmoudian, M.; Stojcevski, A.; Horan, B.; Mekhilef, S. Energy Efficiency in Sustainable Buildings: A Systematic Review with Taxonomy, Challenges, Motivations, Methodological Aspects, Recommendations, and Pathways for Future Research. Energy Strategy Rev. 2023, 45, 101013. [Google Scholar] [CrossRef]
- Liu, Z.-A.; Li, Y.; Hou, J.; Tian, L.; Wang, S.; Hu, W.; Zhang, L. Impact of Exterior Envelope Thermal Performance on Energy Demand and Optimization Strategies for University Teaching-Office Buildings. Sci. Rep. 2025, 15, 15171. [Google Scholar] [CrossRef]
- Shehadi, M. Energy Consumption Optimization Measures for Buildings in the Midwest Regions of USA. Buildings 2018, 8, 170. [Google Scholar] [CrossRef]
- Amani, N. Energy Efficiency of Residential Buildings Using Thermal Insulation of External Walls and Roof Based on Simulation Analysis. Energy Storage Sav. 2025, 4, 48–55. [Google Scholar] [CrossRef]
- Kalhor, K.; Emaminejad, N. Qualitative and Quantitative Optimization of Thermal Insulation Materials: Insights from the Market and Energy Codes. J. Build. Eng. 2020, 30, 101275. [Google Scholar] [CrossRef]
- Fawaier, M.; Bokor, B. Dynamic Insulation Systems of Building Envelopes: A Review. Energy Build. 2022, 270, 112268. [Google Scholar] [CrossRef]
- Song, A.; Kim, Y.; Hwang, S.; Shin, M.; Lee, S. A Comprehensive Review of Thermal Transmittance Assessments of Building Envelopes. Buildings 2024, 14, 3304. [Google Scholar] [CrossRef]
- Bond, D.E.M.; Clark, W.W.; Kimber, M. Configuring Wall Layers for Improved Insulation Performance. Appl. Energy 2013, 112, 235–245. [Google Scholar] [CrossRef]
- Ali, A.; Issa, A.; Elshaer, A. A Comprehensive Review and Recent Trends in Thermal Insulation Materials for Energy Conservation in Buildings. Sustainability 2024, 16, 8782. [Google Scholar] [CrossRef]
- Bhamare, D.K.; Rathod, M.K.; Banerjee, J.; Arıcı, M. Investigation of the Effect of Air Layer Thickness on the Thermal Performance of the PCM Integrated Roof. Buildings 2023, 13, 488. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, H. Heat Transfer Pattern Judgment and Thermal Performance Enhancement of Insulation Air Layers in Building Envelopes. Appl. Energy 2019, 250, 834–845. [Google Scholar] [CrossRef]
- Zhang, T.; Tan, Y.; Yang, H.; Zhang, X. The Application of Air Layers in Building Envelopes: A Review. Appl. Energy 2016, 165, 707–734. [Google Scholar] [CrossRef]
- Liu, Y.-L.; Yang, D.-G.; Wang, D.-H.; Liu, X. Research on Thermal and Heat Insulation Properties of Aerogel Heat-Insulating Reflective Coatings. Appl. Sci. 2023, 13, 9700. [Google Scholar] [CrossRef]
- Peng, Y.; Lai, J.-C.; Xiao, X.; Jin, W.; Zhou, J.; Yang, Y.; Gao, X.; Tang, J.; Fan, L.; Fan, S.; et al. Colorful Low-Emissivity Paints for Space Heating and Cooling Energy Savings. Proc. Natl. Acad. Sci. USA 2023, 120, e2300856120. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Handbook—Fundamentals, SI ed.; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2021. [Google Scholar]
- Roig, O.; Summa, S.; Pardal, C.; Isalgue, A.; Di Perna, C.; Stazi, F. Opaque Ventilated Façades: Energy Performance for Different Main Walls and Claddings. Energy Build. 2024, 314, 114280. [Google Scholar] [CrossRef]
- Ingebretsen, S.B.; Andenæs, E.; Gullbrekken, L.; Kvande, T. Microclimate and Mould Growth Potential of Air Cavities in Ventilated Wooden Façade and Roof Systems—Case Studies from Norway. Buildings 2022, 12, 1739. [Google Scholar] [CrossRef]
- Rahiminejad, M.; Khovalyg, D. Thermal Resistance of Ventilated Air-Spaces behind External Claddings; Definitions and Challenges (ASHRAE 1759-RP). Sci. Technol. Built Environ. 2021, 27, 788–805. [Google Scholar] [CrossRef]
- Rahiminejad, M.; Khovalyg, D. Measuring the Effective Thermal Resistance of Ventilated Air-Spaces behind Common Wall Assemblies: Theoretical Uncertainty Analysis and Recommendations for the Hot Box Method Modifications (ASHRAE 1759-RP). Sci. Technol. Built Environ. 2022, 28, 320–337. [Google Scholar] [CrossRef]
- Amani-Beni, M.; Tabatabaei Malazi, M.; Sahin, B.; Dalkılıç, A.S. Effects of Facades Positioned at Different Angles on Building Thermal Performance and Flow Behaviors. Front. Archit. Res. 2025, 14, 267–281. [Google Scholar] [CrossRef]
- Domínguez-Torres, C.-A.; Suárez, R.; León-Rodríguez, A.L.; Domínguez-Delgado, A. Parametric Energy Optimization of a Ventilated Facade with Windows in Mediterranean Climates. Renew. Energy 2024, 227, 120398. [Google Scholar] [CrossRef]
- Sobieraj, J.; Metelski, D.; Rosłon, J. Thermal Performance Analysis and Design Evolution of Ventilated Stone Facades: A Case Study of the Praski Student House (Akademik Praski) in Warsaw. Buildings 2024, 14, 3558. [Google Scholar] [CrossRef]
- Zhangabay, N.; Oner, A.; Rakhimov, M.; Tursunkululy, T.; Abdikerova, U. Thermal Performance Evaluation of a Retrofitted Building with Adaptive Composite Energy-Saving Facade Systems. Energies 2025, 18, 1402. [Google Scholar] [CrossRef]
- Energiesprong Energiesprong. Available online: https://energiesprong.org/about (accessed on 1 June 2025).
- Biega, K.; Krarti, M. Evaluation of Exterior Insulated Panels for Residential Deep Energy Retrofits. Energies 2024, 17, 3988. [Google Scholar] [CrossRef]
- ANSYS. ANSYS FLUENT, A Fluid Simulation Software, ANSYS Inc 2024, Canonsburg, PA. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 1 June 2025).
- ANSYS. ANSYS FLUENT User’s Guide. ANSYS Inc. 2025. Canonsburg, PA. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 5 June 2025).
- Qin, J.; Pan, H.; Zhu, Z.; Tian, X.; Rahman, M.M. Assessments of SIMPLE and ASIMPLE Algorithms Based on Buoyancy-Driven Cavity Flows. Int. J. Innov. Sci. Res. Technol. 2020, 5, 700–714. [Google Scholar]

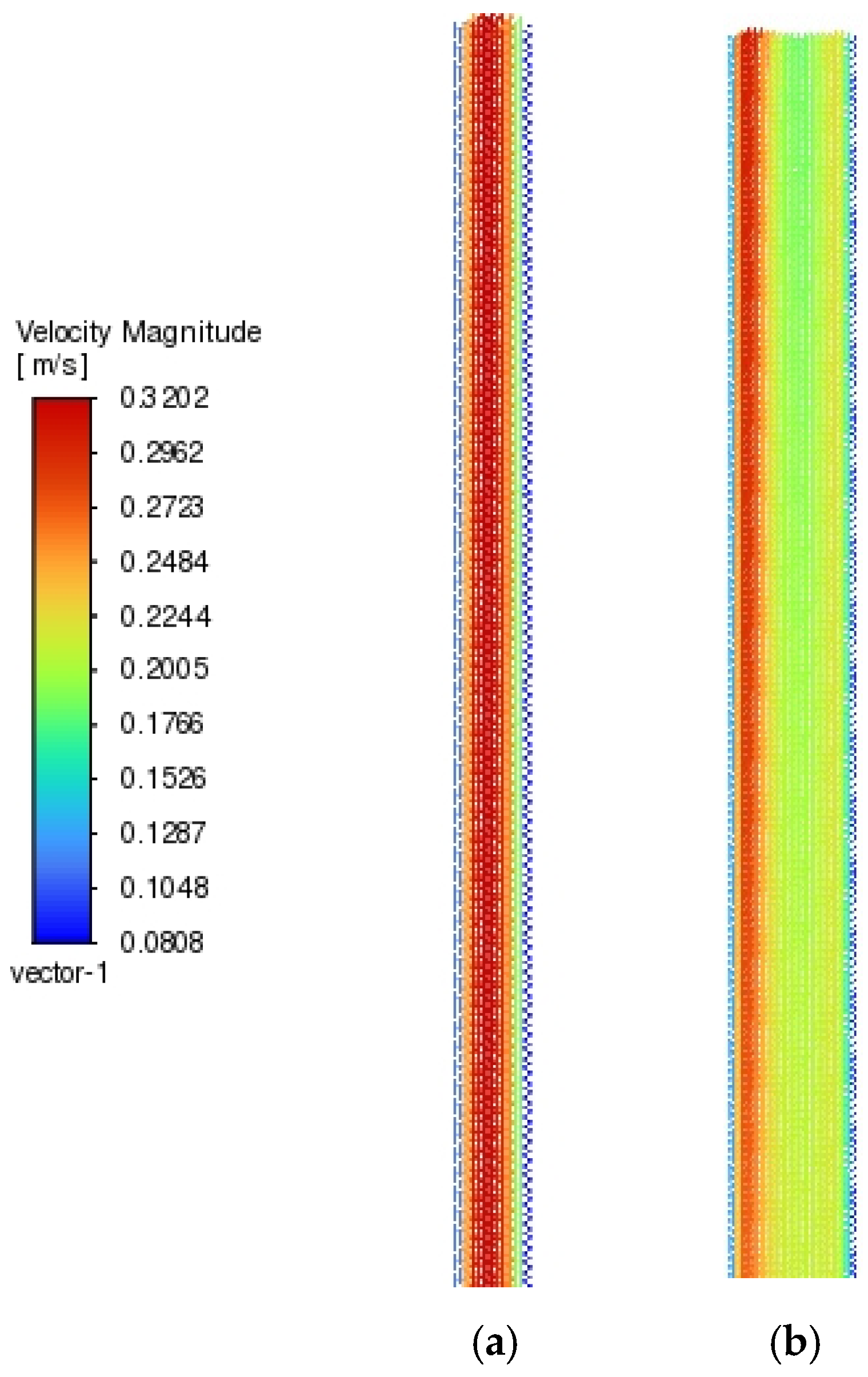

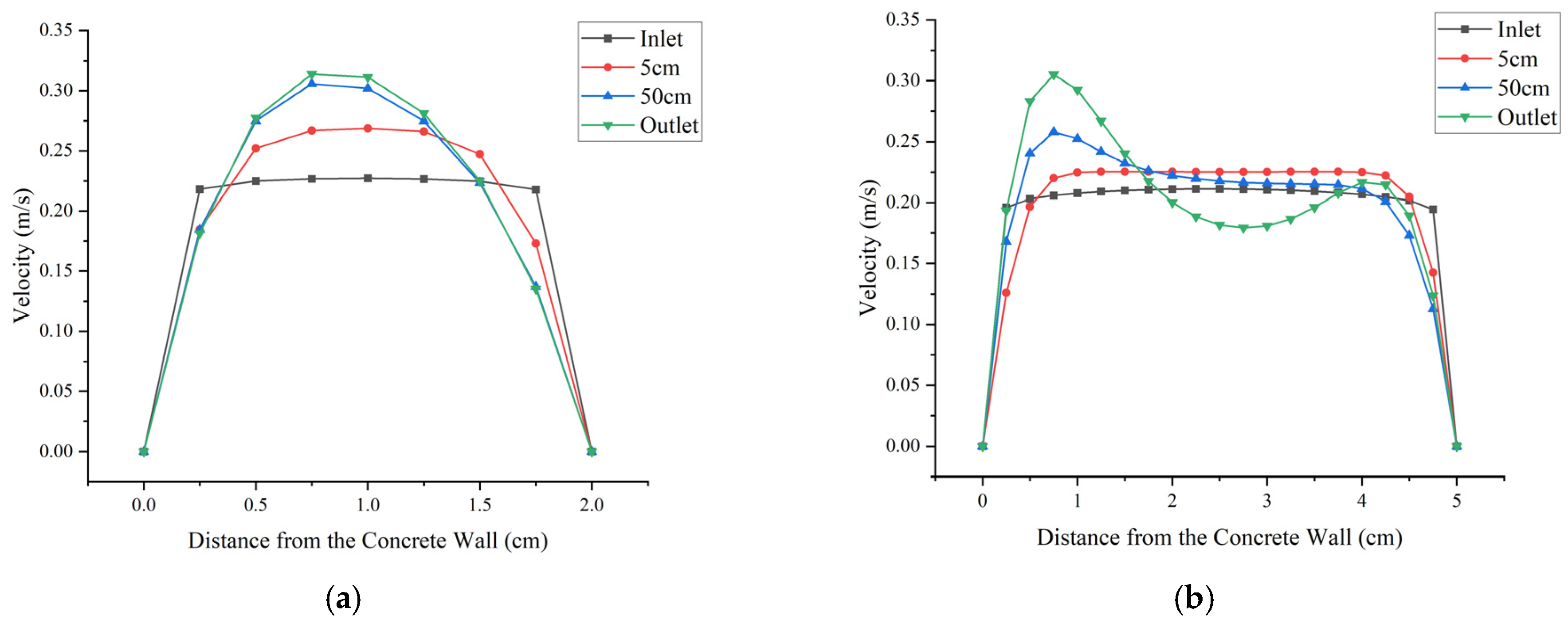

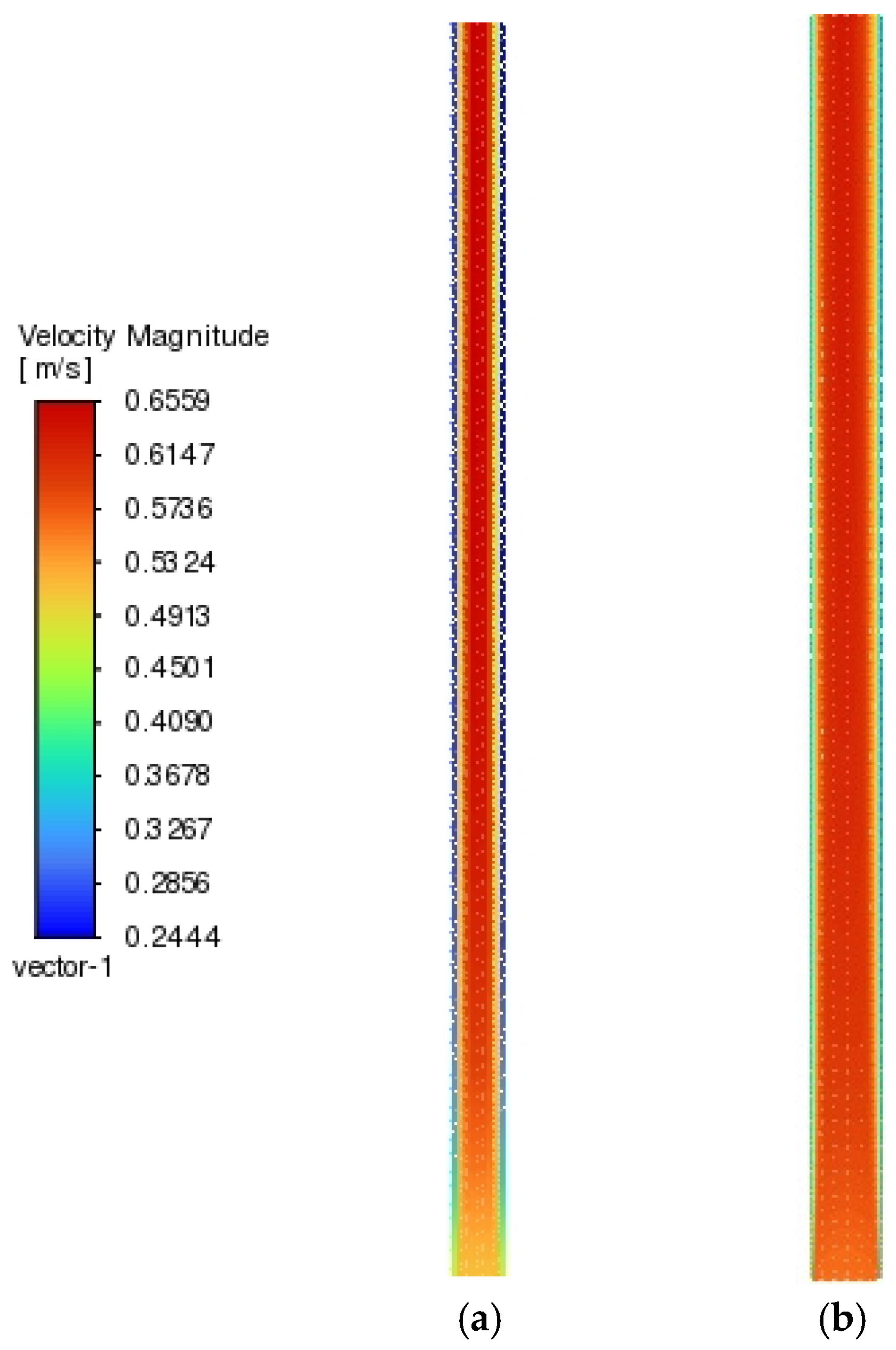
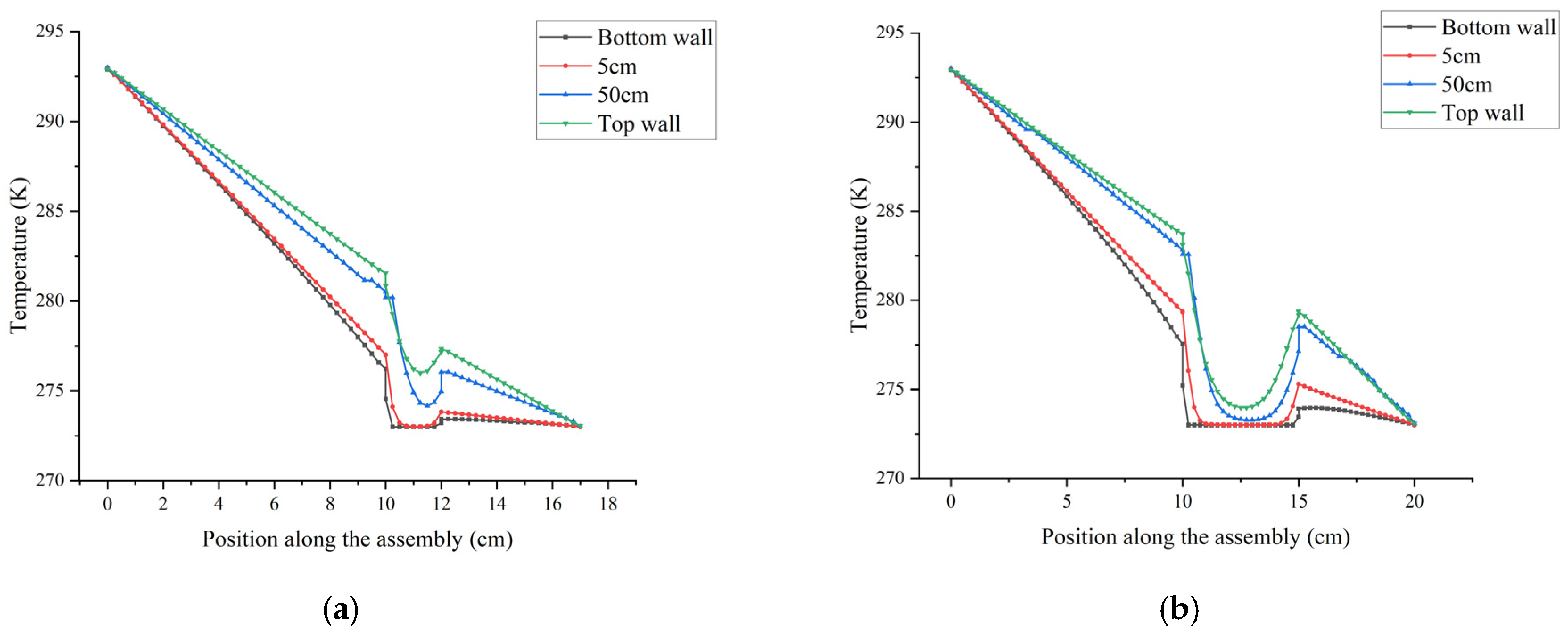
| Material | Density (kg/m3) | Specific Heat Capacity (J/kg K) | Thermal Conductivity (W/m K) |
|---|---|---|---|
| Insulation | 45 | 1500 | 0.025 |
| Concrete | 2400 | 880 | 0.4 |
| Air Space Thickness (cm) | Air Space Temp (°C) | Air Temp Difference (°C) | Effective Emissivity | HOF Rairgap Value (m2K/W) | Estimated Rairgap Value (m2K/W) | Error % |
|---|---|---|---|---|---|---|
| 1.3 | 10 | 15 | 0.82 | 0.161 | 0.162 | 0.701 |
| 1.3 | 10 | 15 | 0.72 | 0.175 | 0.174 | 0.621 |
| 1.3 | 30 | 5 | 0.82 | 0.139 | 0.140 | 0.511 |
| 1.3 | 30 | 15 | 0.72 | 0.152 | 0.152 | 0.416 |
| 1 | 10 | 5 | 0.82 | 0.149 | 0.148 | 0.750 |
| 1 | 10 | 5 | 0.72 | 0.161 | 0.160 | 0.743 |
| 1 | 10 | 30 | 0.82 | 0.147 | 0.148 | 0.680 |
| 1 | 10 | 30 | 0.72 | 0.159 | 0.159 | 0.359 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahal, U.; Krarti, M. Thermal Impacts of Air Cavities Associated with Insulated Panels Deployed for Exterior Building Envelope Assemblies. Energies 2025, 18, 3573. https://doi.org/10.3390/en18133573
Dahal U, Krarti M. Thermal Impacts of Air Cavities Associated with Insulated Panels Deployed for Exterior Building Envelope Assemblies. Energies. 2025; 18(13):3573. https://doi.org/10.3390/en18133573
Chicago/Turabian StyleDahal, Utsav, and Moncef Krarti. 2025. "Thermal Impacts of Air Cavities Associated with Insulated Panels Deployed for Exterior Building Envelope Assemblies" Energies 18, no. 13: 3573. https://doi.org/10.3390/en18133573
APA StyleDahal, U., & Krarti, M. (2025). Thermal Impacts of Air Cavities Associated with Insulated Panels Deployed for Exterior Building Envelope Assemblies. Energies, 18(13), 3573. https://doi.org/10.3390/en18133573






