A Spatio-Temporal Microsimulation Framework for Charging Impact Analysis of Electric Vehicles in Residential Areas: Sensitivity Analysis and Benefits of Model Complexity
Abstract
1. Introduction
- First, neither study evaluates the impact of modeling a synthetic population with mobility patterns explicitly tied to sociodemographic attributes. Instead, mobility profiles are assigned independently of these factors, relying solely on stochastic sampling and random allocation. This risks overlooking systematic behavioral differences between user groups that could significantly affect results. Although the importance of sociodemographic profiling in mobility modeling is increasingly recognized, its specific impact on distribution grid assessments remains insufficiently explored.
- Second, both studies focus only on transformer peak loads and line loadings, although busbar voltage violations often occur earlier and pose a great risk to system stability [11,12]. Busbar voltage violations occur when local voltages at distribution grid busbars fall below thresholds defined by standards such as EN 50160 [13]. Due to the spatial variability and strong dependence on local grid topology, busbar voltages are likely far more sensitive to localized changes introduced by detailed modeling than aggregated transformer loads or line loadings. Therefore, capturing sensitivities in busbar voltages requires a more detailed, spatially resolved modeling approach.
- Third, both studies apply sensitivity analyses to only a single distribution grid, making it difficult to assess variability across different real-world distribution grids. This study addresses this limitation by analyzing three real-world municipalities, allowing for an assessment of the consistency of observed trends across different grid topologies.
- The introduction of the modular simulation framework with a bottom-up modeling approach.
- The modeling of three communities in the suburbs of Stuttgart using real distribution grid data.
- The creation of a synthetic, representative population based on census and microcensus data with a spatial resolution of 100 m × 100 m.
- The modeling of the synthetic population’s mobility behavior using MOP data.
- The modeling of household baseload and a representative, diversified vehicle fleet of BEVs.
- A sensitivity analysis of seven EV charging scenarios, focusing on the impact of model complexity on transformer peak load and busbar voltage for each of the three communities.
- The identification of key impact parameters that most significantly affect transformer peak load and busbar voltage.
- A stochastic load flow simulation considering the identified key impact parameters under varying EV penetration rates for each of the three communities.
2. Materials and Methods
- Population Synthesis Module: Creates a virtual population that closely resembles the actual population. The synthesized population is assigned to buildings, which are connected to the distribution grid.
- Grid Module: Provides distribution grid data from three real-world distribution grids in the suburbs of Stuttgart.
- Mobility Pattern Module: Models the weekly mobility behavior of household residents using MOP data. Since electric vehicle charging does not always occur daily, analyzing continuous weekly mobility patterns provides valuable insights [14].
- Vehicle Fleet Module: Assigns representative vehicles to households. The vehicle parameters depend on real-world data from an electric vehicle database [15].
- Charging Price Module: Provides EEX day-ahead AC charging prices for cost optimized charging strategies.
- Household Loadprofile Module: Assigns annual household baseload profiles with a 15 min resolution. The annual consumption is scaled based on household size.
- Charging Strategy Module: Enables the modeling of different charging strategies.
- Power Flow Computation Module: Performs power flow calculations using Pandapower [19].
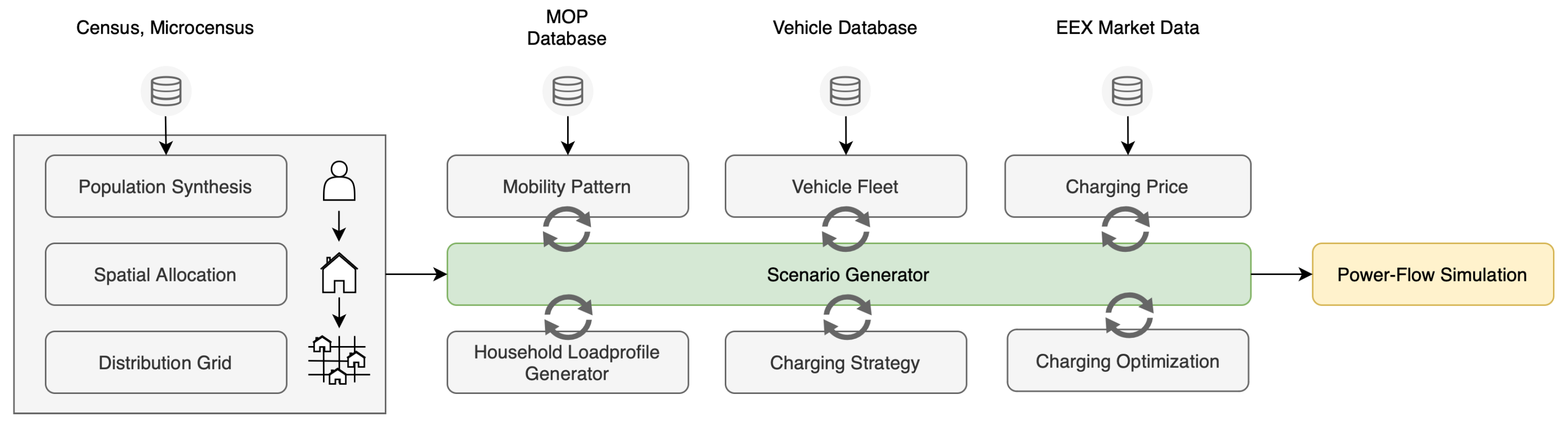
2.1. Population Synthesis Module
- The harmonization of household and population attributes across both geographic levels. Due to privacy restrictions, some household and population attributes in sparsely populated 100 m × 100 m grid cells are slightly modified by the data-providing government agency. To correct these modifications and ensure that the sum across all grid cells matches the municipality-level marginals, a manual harmonization approach is applied. Feasible replacement cells are constructed with minimal adjustments to the attributes, and a simulated annealing algorithm is used to assign these replacements while minimizing both the number of altered cells and the extent of modification.
- An iterative proportional updating (IPU) of household and population attributes.
- The spatial allocation of households to building units connected to the distribution grid.
2.1.1. Household and Population Attribute Harmonization
| Type | Attribute | Characteristic | Geo-Resolution |
|---|---|---|---|
| Household | Total Number | Sum | Municipality, Grid |
| Size | 1, 2, 3, 4, 5, 6+ | Municipality, Grid | |
| Net Income | 5 Groups | Municipality | |
| Person | Total Number | Sum | Municipality, Grid |
| Gender | [m, f] | Municipality, Grid | |
| Age | 9 Groups | Municipality, Grid | |
| Gender × Age | [m, f] × [9 Groups] | Municipality | |
| Employed | yes, no | Municipality |
2.1.2. Iterative Proportional Updating (IPU)

2.1.3. Spatial Household Allocation

2.2. Mobility Module

| Household Type | Vehicle Average Travel Distance [km] | ||
|---|---|---|---|
| Workday | Saturday | Sunday | |
| 1 | 35.0 | 28.6 | 25.6 |
| 2 | 17.8 | 19.0 | 18.3 |
| 3 | 25.7 | 18.6 | 17.3 |
| 4 | 28.5 | 23.8 | 22.7 |
| Household Type | Characteristics | Relative Share [%] |
|---|---|---|
| 1 | 1–2 employed persons. | 43.1 |
| 2 | 1–2 non-employed (retired) persons. | 37.3 |
| 3 | Household with children below 18 years. | 15.3 |
| 4 | Household w/o children. 3+ persons. | 4.3 |

2.3. Household Loadprofile Module

2.4. Vehicle Module
| Vehicle Segment | Relative Share [%] |
|---|---|
| Mini | 7.2 |
| Small | 18.5 |
| Compact | 24.2 |
| Middle | 12.2 |
| Upper Middle | 3.8 |
| Upper + Sport | 2.6 |
| SUV | 19.4 |
| VAN + Utilities | 12.1 |
| Segment | Usable Battery Capacity [kWh] | Mild Weather Consumption [kWh/100 km] | Cold Weather Consumption [kWh/100 km] | Maximum AC Charging Power [kW] |
|---|---|---|---|---|
| Mini | 32.3 | 15.8 | 18.5 | 7.4 |
| Small | 46.3 | 13.6 | 18.9 | 7.4 |
| Compact | 46.3 | 13.8 | 19.3 | 11 |
| Middle | 54 | 15.9 | 21.6 | 11 |
| Upper Middle | 95 | 17.6 | 23.5 | 11 |
| Upper + Sport | 108.4 | 17.5 | 23.7 | 22 |
| SUV | 95 | 17.4 | 23.4 | 11 |
| VAN + Utilities | 90 | 26.1 | 33.3 | 11 |
| Average | 64.4 | 16.6 | 22.2 | 10.4 |
2.5. Charging Strategy
- Reference Strategy: The vehicle is connected to the wallbox after the last trip of each day and remains available for charging until the next trip. The vehicle is charged as quickly as possible without considering any pricing mechanism.
- Min SOC, Weekend Charging: The vehicle is primarily connected to the wallbox after the last trip from Friday to Sunday. The only exception occurs if the SoC falls below the minimum threshold before Friday. In this case, the EV is connected to the wallbox immediately after the last trip of this day. The vehicle is charged as quickly as possible without considering any pricing mechanism.
- Cost-Based: The vehicle is connected to the wallbox after the last trip of each day and charged cost-optimally based on day-ahead EEX electricity prices from 2021. Energy prices are adjusted for taxes and additional fees to ensure realistic end-user costs, averaging approximately 0.32 Euro/kWh in 2021 [32]. Data from 2021 is used, as geopolitical crises have distorted electricity prices in subsequent years.
2.6. Charging Price Module

2.7. Optimization Module
2.8. Power Flow Simulation Module
3. Results
- Municipality Overview:This section provides an overview of the three municipalities and their associated distribution grids. It highlights the key characteristics of the synthetically generated population to illustrate the differences between the municipalities and to establish a contextual foundation for the subsequent sensitivity and load flow analyses.
- Sensitivity Analysis: This section identifies the key modeling parameters that significantly impact transformer load and busbar voltage through a sensitivity analysis of various scenarios.
- Load Flow Analysis: For each municipality, a load flow calculation is performed using the key modeling parameters identified in the sensitivity analysis. Different EV penetration rates are explored to assess their impact on transformer load and busbar voltage.
3.1. Municipality Overview
- Key Findings:
- Synthetic populations were successfully created for all three municipalities.
- The assignment of mobility profiles based on sociodemographic household attributes aims to identify relevant differences in the simulation results. In two of the three municipalities, the household type distribution deviates by more than 10% from the MOP dataset. Consequently, if these differences have a significant impact, they should be reflected in the simulation results.
- The distribution grids are quite diverse and show varying degrees of meshing. These structural differences are expected to result in observable variations in the minimum busbar voltages.
3.1.1. Municipality 1


| Attribute | 1st Quartile (Q1) | Median (Q2) | 3rd Quartile (Q3) |
|---|---|---|---|
| Households | 466 | 469 | 472 |
| Persons | 1036 | 1043 | 1051 |
| Vehicles | 512 | 553 | 605 |
| Attribute | Community Share [%] | MOP Share [%] | Relative Difference [%] |
|---|---|---|---|
| Household Type 1 | 45.7 | 43.1 | +2.6 |
| Household Type 2 | 22.1 | 37.3 | −15.2 |
| Household Type 3 | 19.1 | 15.3 | +3.8 |
| Household Type 4 | 13.1 | 4.3 | +8.8 |
3.1.2. Municipality 2

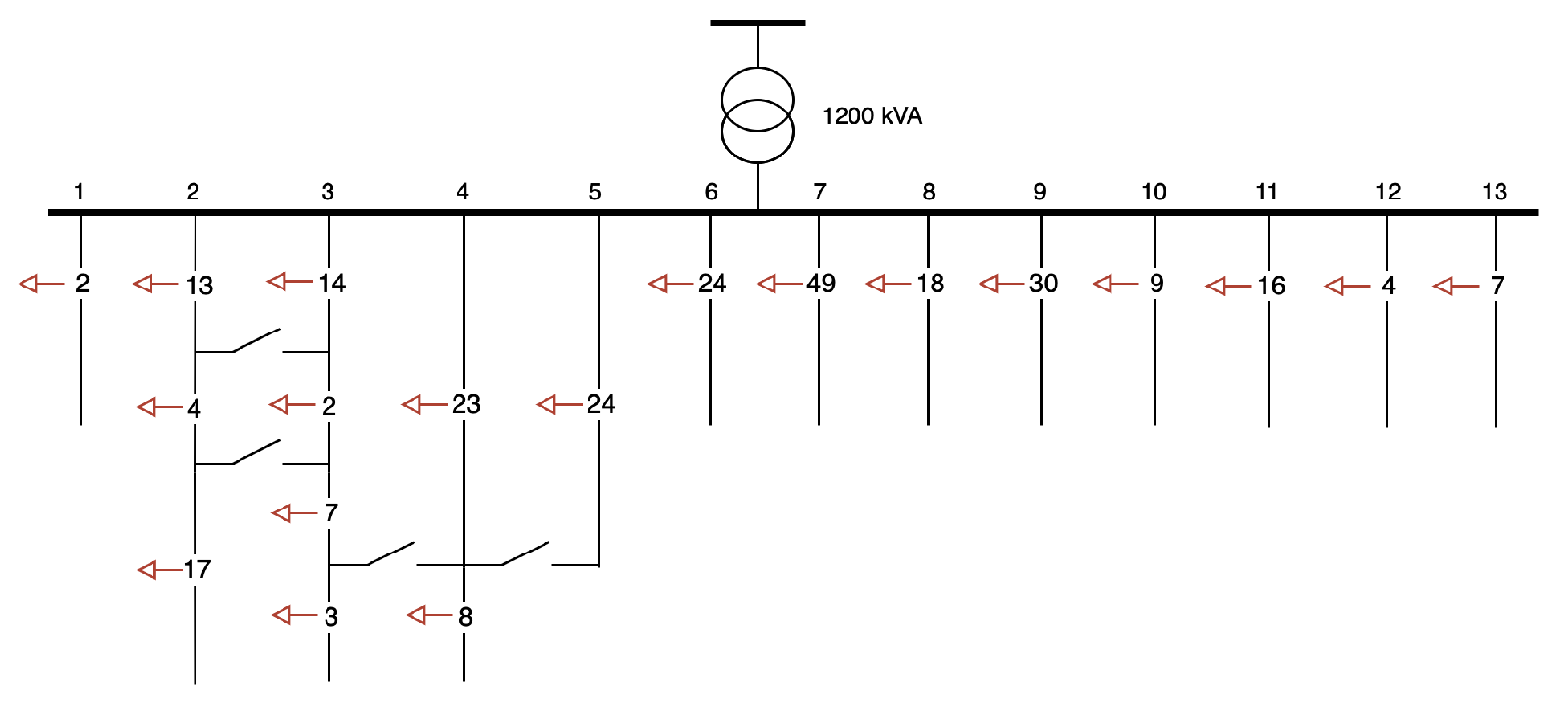
| Attribute | 1st Quartile (Q1) | Median (Q2) | 3rd Quartile (Q3) |
|---|---|---|---|
| Households | 362 | 364 | 366 |
| Persons | 816 | 823 | 830 |
| Vehicles | 387 | 419 | 468 |
| Attribute | Community Share [%] | MOP Share [%] | Relative Difference [%] |
|---|---|---|---|
| Household Type 1 | 28.8 | 43.1 | −14.3 |
| Household Type 2 | 38.3 | 37.3 | +1.0 |
| Household Type 3 | 21.4 | 15.3 | +6.1 |
| Household Type 4 | 11.5 | 4.3 | +7.2 |
3.1.3. Municipality 3
| Attribute | 1st Quartile (Q1) | Median (Q2) | 3rd Quartile (Q3) |
|---|---|---|---|
| Households | 379 | 382 | 385 |
| Persons | 807 | 816 | 825 |
| Vehicles | 401 | 439 | 470 |
| Attribute | Community Share [%] | MOP Share [%] | Relative Difference [%] |
|---|---|---|---|
| Household Type 1 | 37.2 | 43.1 | −5.9 |
| Household Type 2 | 33.6 | 37.3 | −3.7 |
| Household Type 3 | 19.7 | 15.3 | +4.4 |
| Household Type 4 | 9.5 | 4.3 | +5.2 |
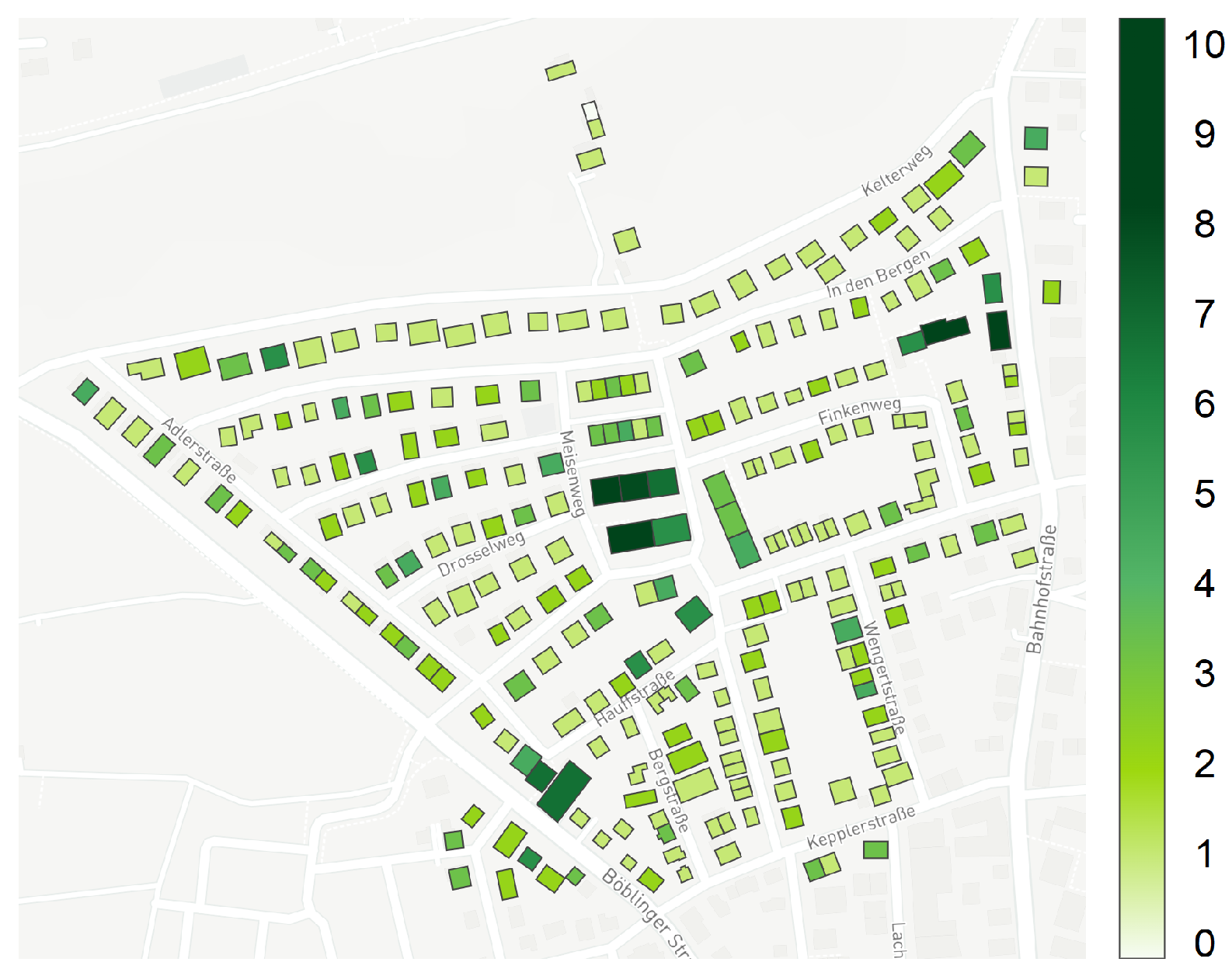
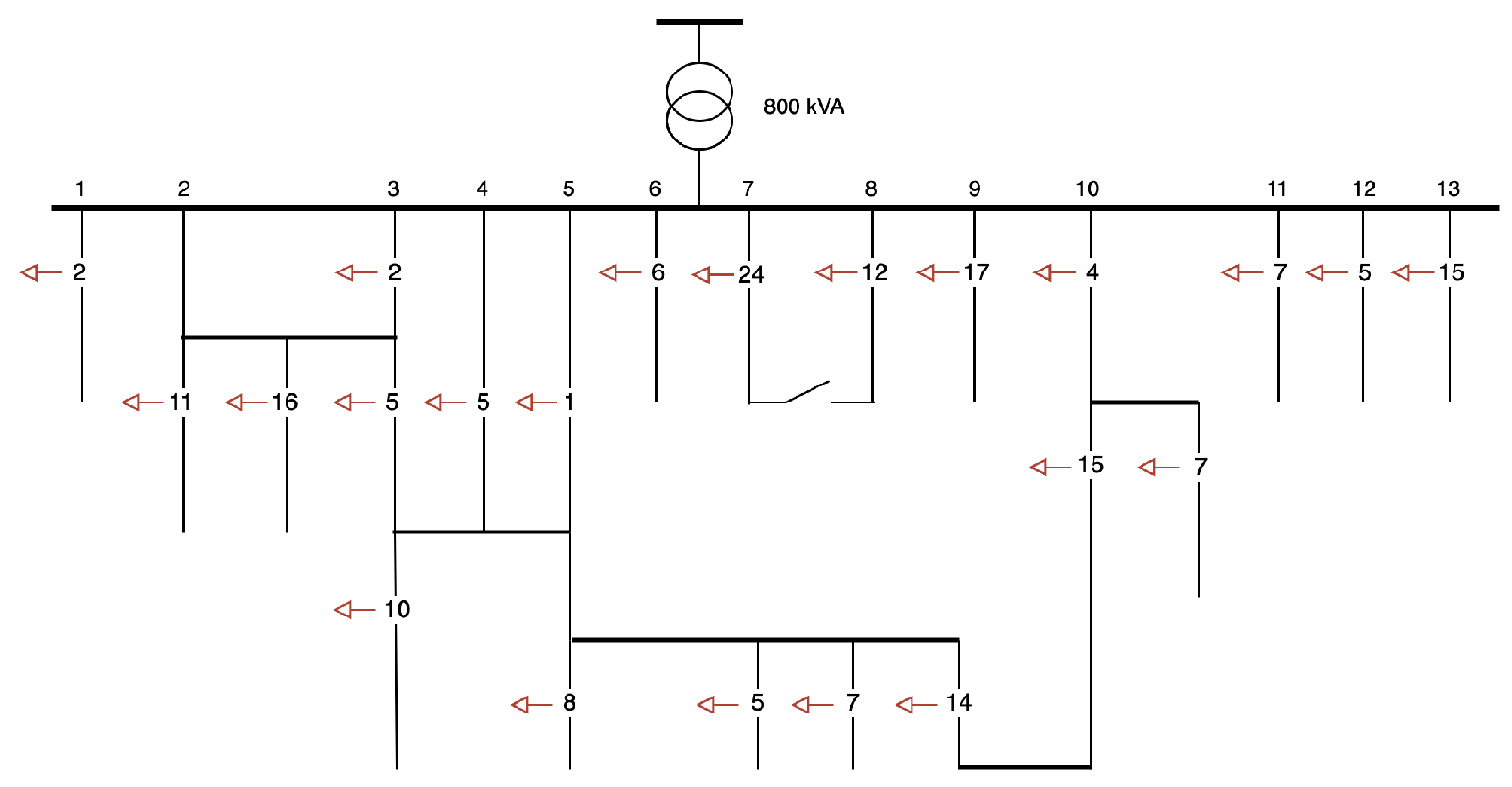
3.2. Sensitivity Analysis
- Charging strategy: Whether EVs are charged daily or exclusively on weekends.
- Seasonal effects: Primarily winter, with increased baseload and elevated EV demand.
- AC charging power: Maximum AC charging power of the vehicle’s AC onboard charger (e.g., 11 kW vs. 22 kW).
- Mobility profile modeling: Assignment based on household size and type, incorporating sociodemographic attributes.
- Biased EV assignment. Higher EV adoption likelihood for single-family and multi-vehicle households.
- Vehicle model: Detailed vehicle class modeling with a diversified and representative vehicle fleet.
| Parameter | Default | Variation |
|---|---|---|
| Model Complexity | Mobility profile assignment based on household size and household type. Unbiased EV assignment |
|
| Charging Strategy | EV charging only at home after the last trip of each day |
|
| Vehicle Model | Diverse and representative vehicle fleet |
|
| Ambient Conditions | Mild Weather CW 34 2021 |
|


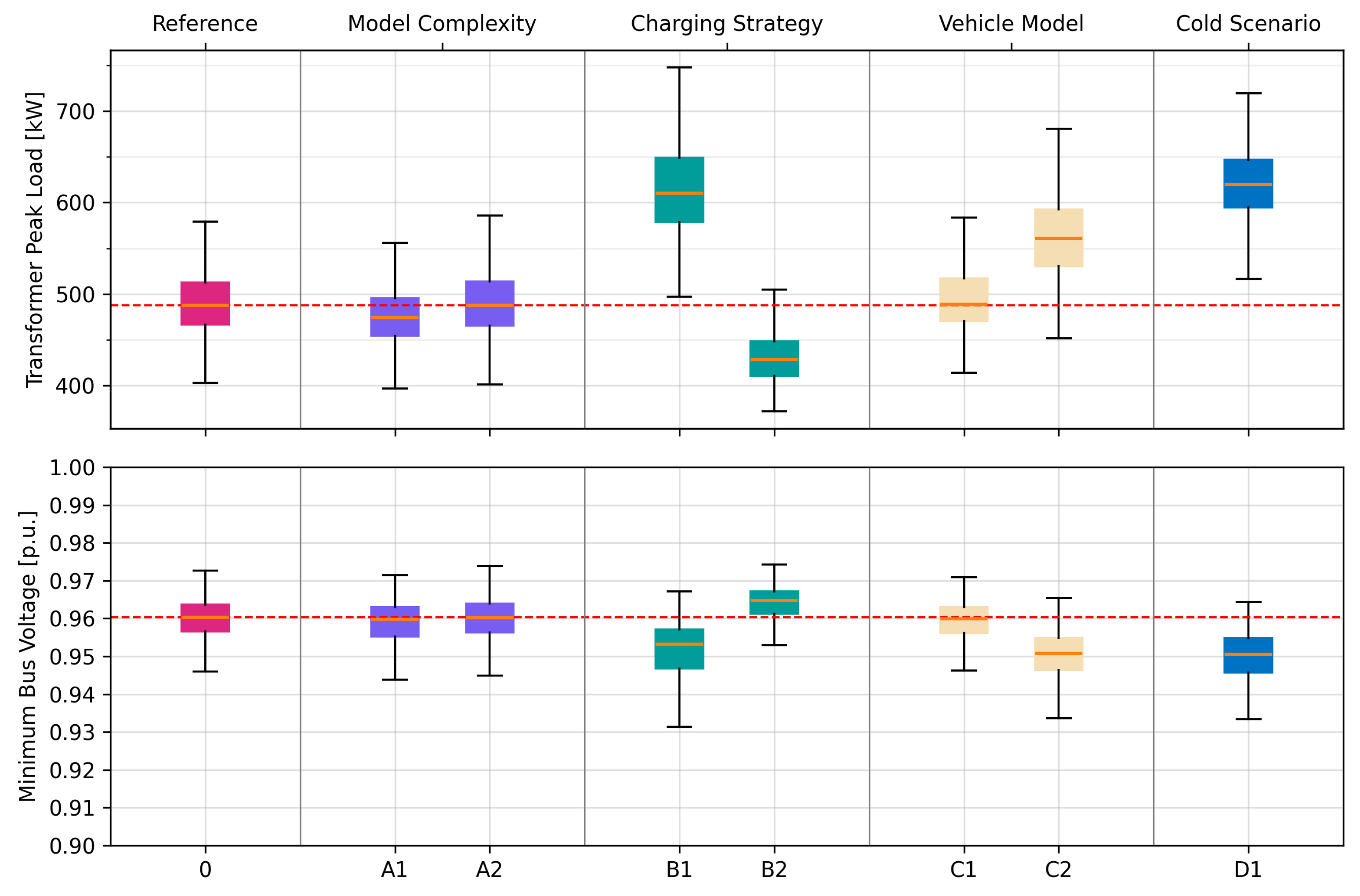
3.2.1. Scenario Variation: Model Complexity
- Scenario A1: Mobility profiles are assigned based solely on household size, without considering household type. All other model assumptions remain consistent with the reference scenario. Table 13 presents the median deviation of scenario A1 from the reference scenario for the three municipalities. The comparison shows that Municipality 1 exhibits the largest deviation in transformer peak load, with a 5.5% reduction compared to the reference scenario. In contrast, the deviations in Municipalities 2 and 3 remain below 3%. The pronounced deviation in Municipality 1 is primarily attributed to a significantly lower proportion of household type 2 (retired households), which is 15% lower than the average in the MOP dataset (see Table 7). However, despite this substantial deviation in population characteristics, the overall simulation results remain largely unaffected. Similarly, busbar voltage deviations are minimal and closely align with those of the reference scenario.
- Scenario A2: Mobility profiles are assigned based on household size and type, but EV ownership is biased toward single-family homes with multiple vehicles, which have a higher likelihood of receiving an EV compared to multi-family homes with only one vehicle per household. All other model assumptions remain consistent with the reference scenario. Table 14 presents the median deviation of scenario A2 from the reference scenario for the three municipalities. An analysis shows that biased EV assignment only impacts the median busbar voltage of Municipality 1. For all other municipalities, there is no measurable effect on transformer peak load or minimum busbar voltage.
| Median Deviation to Reference Scenario | Municipality 1 | Municipality 2 | Municipality 3 |
|---|---|---|---|
| Transformer Peak Load | −5.5% | −1.9% | −2.7% |
| Minimum Bus Voltage | +0.004 p.u. | +0.002 p.u. | +0.001 p.u. |
| Median Deviation to Reference Scenario | Municipality 1 | Municipality 2 | Municipality 3 |
|---|---|---|---|
| Transformer Peak Load | +0.0% | +0.0% | +0.0% |
| Minimum Bus Voltage | −0.004 p.u. | −0.000 p.u. | −0.000 p.u. |
3.2.2. Scenario Variation: Charging Strategy
- Scenario B1: EV charging only at home after the last trip from Friday to Sunday. All other model assumptions remain consistent with the reference scenario. Table 15 presents the median deviation of scenario B1 from the reference scenario across the three municipalities. For all three municipalities, a notable increase in transformer peak load of up to 25% is observed. Additionally, minimum busbar voltages decrease noticeably, and the variance increases. The delayed charging until Friday results in higher energy demand, which not only extends charging times but also increases the likelihood of simultaneous EV charging.
- Scenario B2: EV charging at work and at home after each day’s last trip. Unlike the previous scenarios, the vehicle is now also charged at the workplace. All other model assumptions remain consistent with the reference scenario. Table 16 presents the median deviation of scenario B2 from the reference scenario across the three municipalities. For all three municipalities, a notable decrease in the transformer peak load of more than 12% is observed. Charging at the workplace reduces the amount of charging at home, which mitigates the occurrence of simultaneous charging events. This is reflected in a lower transformer peak load, as well as a more relaxed minimum busbar voltage with reduced variance.
| Median Deviation to Reference Scenario | Municipality 1 | Municipality 2 | Municipality 3 |
|---|---|---|---|
| Transformer Peak Load | +21.2% | +16.7% | +25.1% |
| Minimum Bus Voltage | −0.008 p.u. | −0.003 p.u. | −0.007 p.u. |
| Median Deviation to Reference Scenario | Municipality 1 | Municipality 2 | Municipality 3 |
|---|---|---|---|
| Transformer Peak Load | −12.7% | −9.3% | −12.2% |
| Minimum Bus Voltage | +0.008 p.u. | +0.002 p.u. | +0.004 p.u. |
3.2.3. Scenario Variation: Vehicle Model
- Scenario C1: Average vehicle with maximum AC charging power of 11 kW. In this scenario, the statistical vehicle type modeling is replaced by the average vehicle parameters from Table 5. The average AC charging power of 10.4 kW is replaced with 11 kW, which is the next feasible value for standard onboard chargers available in EVs. All other model assumptions remain consistent with the reference scenario.A comparison of the median deviations in Table 17 reveals that the relative deviation in transformer peak load remains below 4%, while the deviation in minimum busbar voltage is nearly negligible. These results suggest that replacing a detailed vehicle type model with a simplified average vehicle model is a valid approach, as other modeling factors effectively outweigh potential inaccuracies introduced by using an average vehicle model.
- Scenario C2: Average vehicle with maximum AC charging power of 22 kW.In this scenario, the statistical vehicle type modeling is replaced with the average vehicle parameters from Table 5, assuming an AC charging power of 22 kW for every EV. All other model assumptions remain consistent with the reference scenario.As expected, the increase in charging power leads to a significant rise in median transformer peak loads, ranging from 15% to 18%, as shown in Table 18. This also has a considerable impact on the minimum busbar voltages in the distribution grid. Although the charging power is twice as high as in the base scenario, the peak loads for EVs are not doubled. This can be explained by the fact that faster charging reduces the overall charging duration, thereby decreasing the number of simultaneous charging events. A large-scale shift from 11 kW to 22 kW charging power in future EVs would certainly have considerable impacts. However, most current EVs are equipped with 11 kW onboard chargers, and a widespread shift to 22 kW chargers is not yet foreseeable.
| Median Deviation to Reference Scenario | Municipality 1 | Municipality 2 | Municipality 3 |
|---|---|---|---|
| Transformer Peak Load | +3.4% | +3.7% | +0.2% |
| Minimum Bus Voltage | −0.003 p.u. | −0.002 p.u. | −0.000 p.u. |
| Median Deviation to Reference Scenario | Municipality 1 | Municipality 2 | Municipality 3 |
|---|---|---|---|
| Transformer Peak Load | +16.9% | +18.6% | +15.0% |
| Minimum Bus Voltage | −0.024 p.u. | −0.013 p.u. | −0.009 p.u. |
3.2.4. Scenario Variation: Ambient Conditions
- Scenario D1: Scenario D1 models cold weather conditions. Two key factors distinguish this scenario from all others. First, the vehicle consumption is higher, following the values in Table 5. Second, the household load is elevated, due to the winter period. All other model assumptions remain consistent with the reference scenario.Table 19 illustrates that the transformer peak load is approximately 27% higher than in the reference scenario. This effect is also reflected in a more pronounced minimum busbar voltage. These results highlight the critical impact of EV charging during winter periods. In conclusion, cold weather conditions have a huge impact on the power flow simulation results across all three municipalities, far outweighing other modeling factors, such as biased EV assignment or mobility modeling based on sociodemographic attributes.
| Median Deviation to Reference Scenario | Municipality 1 | Municipality 2 | Municipality 3 |
|---|---|---|---|
| Transformer Peak Load | +27.9% | +27.0% | +27.0% |
| Minimum Bus Voltage | −0.015 p.u. | −0.007 p.u. | −0.010 p.u. |
3.3. Power Flow Simulation Results
- Key Findings:
- Cost-optimized charging has the greatest impact on the distribution grids. In two of the three municipalities, transformer overloads occur even at relatively moderate local EV penetration rates of 20 to 25%.
- In all other scenarios, no transformer overloads are expected up to relatively high penetration rates of 75%.
- Minimum busbar voltage violations consistently occur earlier than transformer overloads.
- The degree of meshing in the distribution grids plays a significant role. A clear trend is observed across Municipalities 1 to 3, with increasing meshing corresponding to a decreasing proportion of feeders affected by voltage violations. This underlines the critical importance of detailed distribution grid modeling for accurate impact assessment.
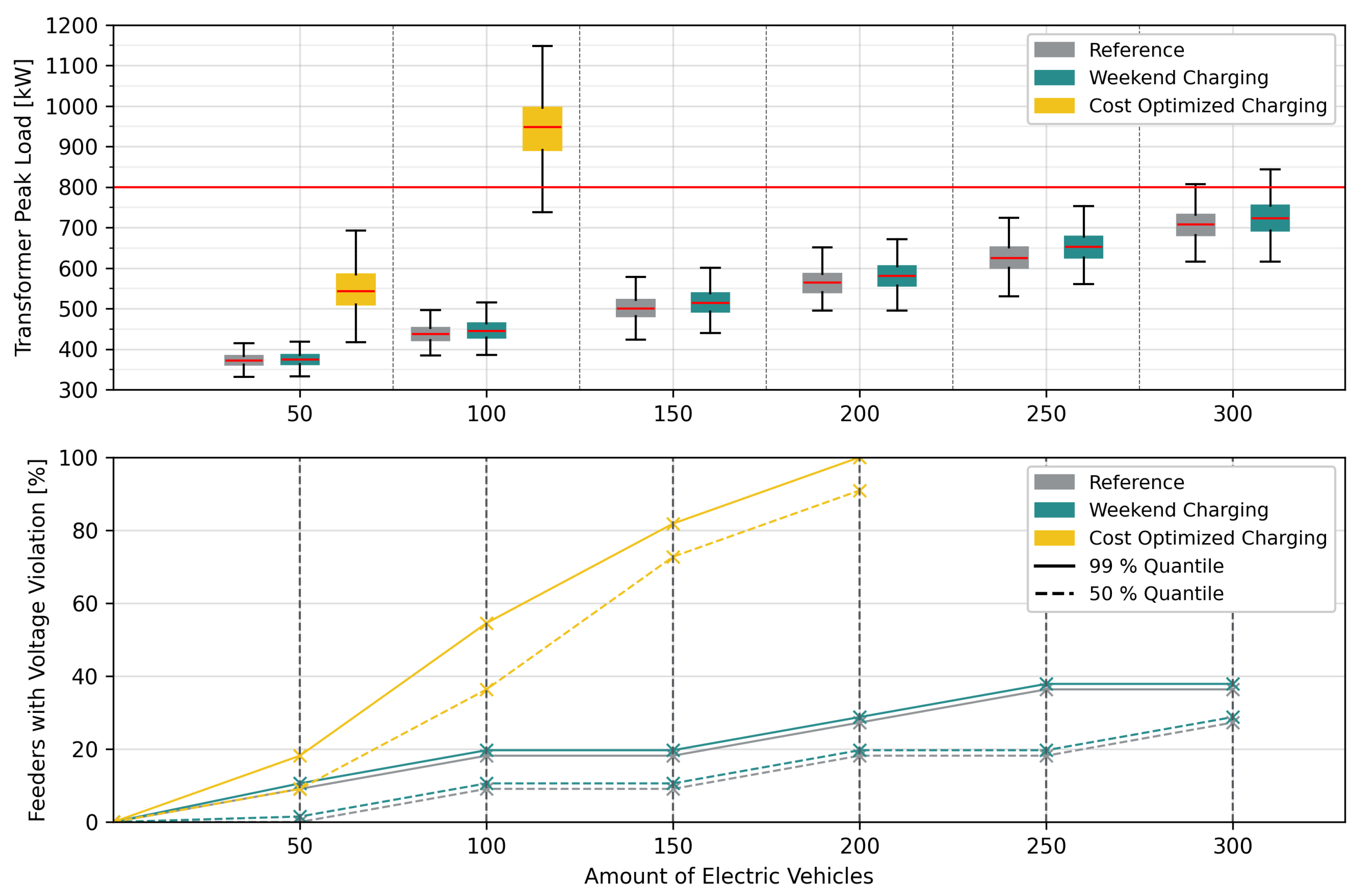
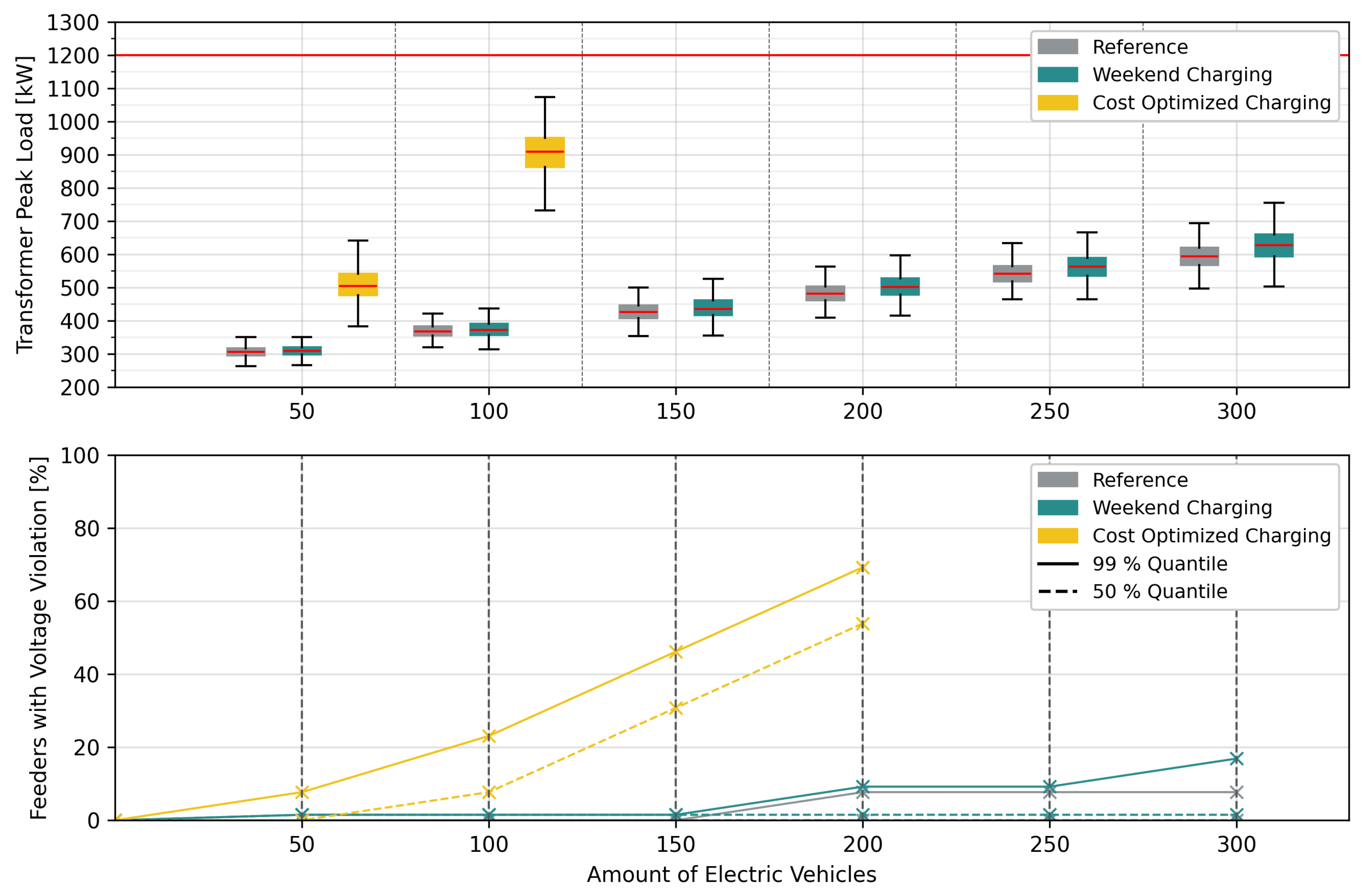

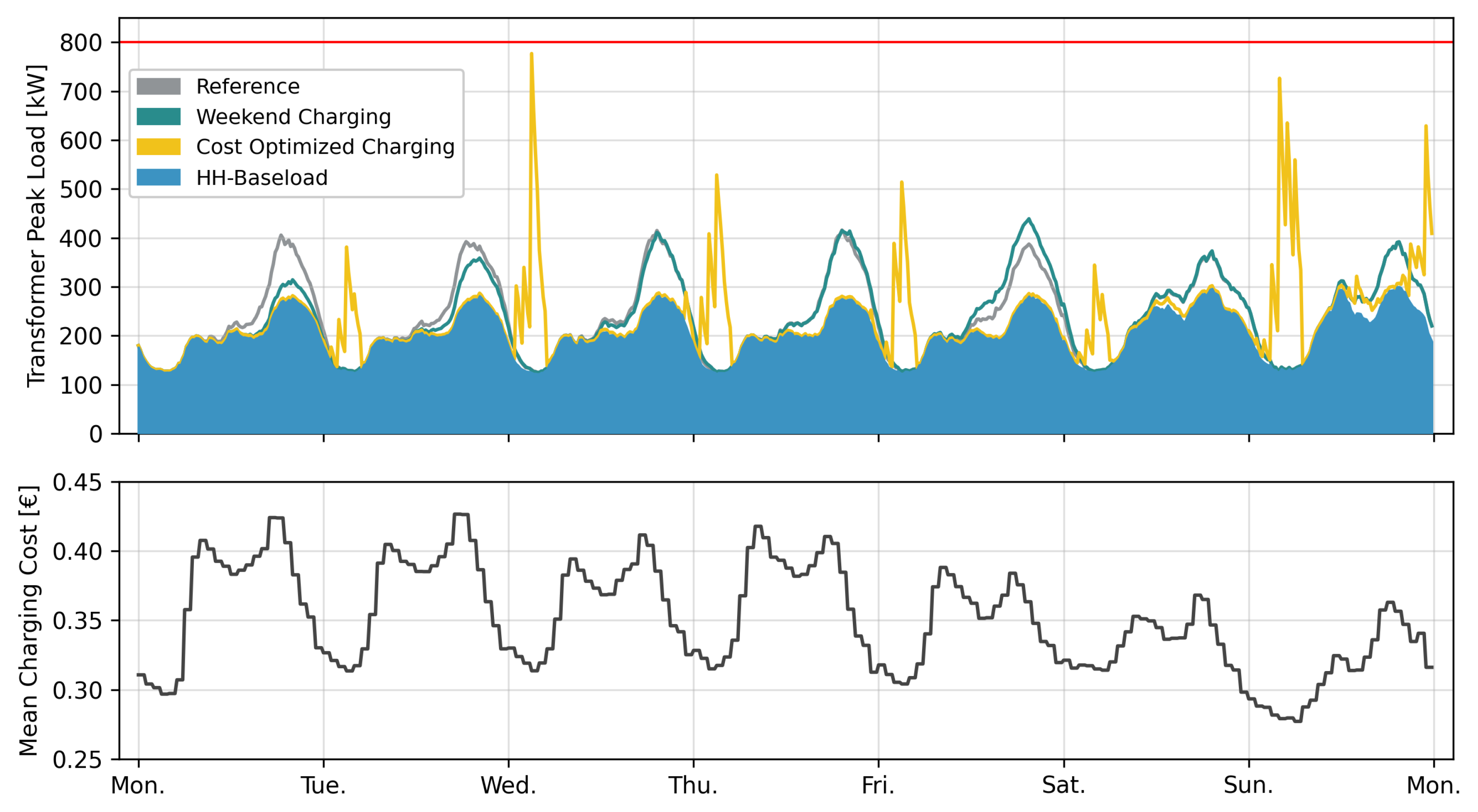
4. Discussion
4.1. Sensitivity Analysis
- Charging Strategy: The choice between charging vehicles at home daily or only on weekends has a comparably strong impact. This observation aligns with findings from Fischer et al. [8] and Stiasny et al. [9], although these studies did not provide detailed sociodemographic modeling or analyze effects on busbar voltage. The results of this study indicate that charging EVs solely on weekends can cause a significant clustering of charging events, leading to an increase in the transformer peak load of up to 25%. Extending the analysis to minimum busbar voltage, we find a relatively small median reduction of approximately 0.01 p.u. However, the variance in voltage deviations increases substantially, with individual events deviating by as much as 0.05 p.u. from the reference scenario. This is a crucial finding, as even rare and unlikely events have the potential to compromise distribution grid stability.Conversely, charging electric vehicles on a daily basis, both at home and at workplaces, can reduce the transformer peak load by up to 13%. The positive impact on minimum busbar voltage is minimal, with changes below 0.01 p.u. and no noticeable increase in voltage variance compared to the reference scenario. Overall, these findings warrant serious consideration, as charging EVs primarily on weekends is both practically relevant and likely, since daily charging often reduces user convenience.
- Seasonal Effects: An increased baseload and higher EV demand during winter led to a relative transformer peak load increase of up to 28%, along with a median reduction of up to 0.015 p.u. in minimum busbar voltage. The high relevance of seasonal effects is increasingly recognized in the literature, as the growing adoption of EVs is expected to coincide with the widespread deployment of heat pumps, further increasing stress on the distribution grid during winter season [34].
- Maximum AC Charging Power: Consistent with the findings of [9], the maximum AC charging power of EVs was found to be a significant factor for transformer peak load. This study builds on their results by also quantifying the impact on minimum busbar voltage, revealing both a notable decrease in the median voltage and a substantial increase in variance. Across the three municipalities studied, equipping all future vehicles with 22 kW AC onboard chargers could lead to up to a 19% increase in transformer peak load and a reduction in minimum busbar voltage by 0.024 p.u. However, from a practical perspective, a widespread shift from 11 kW to 22 kW AC onboard-chargers in future EVs is unlikely. Consequently, compared to the other two findings, this scenario appears primarily theoretical.
- Mobility patterns from the MOP dataset were assigned based on sociodemographic attributes such as household size and household type, indirectly reflecting occupation-related factors known to influence mobility behavior [8]. Previous studies have shown that sampling from different mobility datasets can affect simulation outcomes, although the impact is generally smaller than that of other factors, such as charging behavior, local electric vehicle adoption, and the type of charging infrastructure [9]. The present study confirms this observation. Even when applying detailed modeling based on a synthetic population calibrated for the analyzed municipalities, the influence remains smaller than that of other scenario parameters. Variations in median transformer peak load remained below 6 percent, and changes in busbar voltage stayed within 0.01 per unit across all three municipalities. While it is well established that sociodemographic and socioeconomic characteristics influence individual charging behavior, and that differences between user groups can be observed [8], this study explored how such effects aggregate within real municipal populations, which typically consist of a heterogeneous mix of user profiles rather than uniform groups. The results also align with the findings of [35], who reported impacts of up to 8% on median transformer peak load and less than 1% on busbar voltage deviation when mobility patterns were modeled based on sociodemographic characteristics. However, they also noted that the impact becomes more pronounced when mobility modeling is combined with the allocation of charging points according to sociodemographic attributes. Overall, this study extends previous work by demonstrating that, even with detailed synthetic population modeling and mobility pattern assignment based on sociodemographic data, the effects on transformer peak loads and minimum busbar voltages remain relatively minor compared to other sources of uncertainty. This is a reassuring result, as such modeling requires highly detailed and spatially disaggregated input data, which is rarely available.
- Biased EV Assignment: The preferential assignment of electric vehicles to households with a higher likelihood of adoption, such as those living in single-family homes or owning multiple vehicles, has a limited impact. Similar conclusions were drawn by Stiasny et al. [9], who found that even, mildly clustered, and heavily clustered distributions yielded comparable results. The findings presented here build on this, showing that the conclusion remains valid when more detailed modeling of population and sociodemographic mobility is applied, and when the analysis is extended to include effects on busbar voltage. A potential exception may be individual streets or neighborhoods with an unusually high share of electric vehicles. However, such cases should be manageable for distribution grid operators, as charging points are typically registered. Designing distribution networks universally to account for these rare cases would be excessive and unnecessary.
- Detailed Vehicle Class Modeling: Differentiating between specific vehicle classes results in less than a 3% impact on transformer load and has a negligible effect on busbar voltages. Consequently, modeling vehicles using an average consumption profile, as shown in Table 5, is sufficient for distribution grid analysis. While Fischer et al. [8] observed variations when analyzing small, mid-sized, and large vehicles next to each other, real-world vehicle fleets consist of a mix of vehicle types, leading to an averaging effect. This effect, previously demonstrated by Stiasny et al. [9] for transformer peak loads, is now also confirmed for busbar voltage behavior.
4.2. Power Flow Simulation
4.3. Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EV | Electric Vehicle |
| BEV | Battery Electric Vehicle |
| SoC | State of Charge |
| AC | Alternating Current |
| DC | Direct Current |
| TOU | Time-of-Use |
| SUF | Scientific-Use-File |
| SLP | Standard Load Profile |
| IPF | Iterative Proportional Filtering |
| IPU | Iterative Proportional Updating |
| SAFE | ‘Sichere Anonymisierung für Einzeldaten’: Secure anonymization of individual data |
| GIS | Geoinformation System |
| MiD | Mobility in Germany Dataset |
| MOP | German Mobility Panel Dataset |
| EEX | European Energy Exchange |
| IQR | Interquartile Range |
References
- Umweltbundesamt. Analyse der Umweltbilanz von Kraftfahrzeugen mit Alternativen Antrieben oder Kraftstoffen auf dem Weg zu Einem Treibhausgasneutralen Verkehr; Umweltbundesamt: Dessau-Roßlau, Germany, 2024. [Google Scholar] [CrossRef]
- Hardman, S.; Jenn, A.; Tal, G.; Axsen, J.; Beard, G.; Daina, N.; Figenbaum, E.; Jakobsson, N.; Jochem, P.; Kinnear, N.; et al. A review of consumer preferences of and interactions with electric vehicle charging infrastructure. Transp.Res. Part D Transp. Environ. 2018, 62, 508–523. [Google Scholar] [CrossRef]
- Dubey, A.; Santoso, S. Electric Vehicle Charging on Residential Distribution Systems: Impacts and Mitigations. IEEE Access 2015, 3, 1871–1893. [Google Scholar] [CrossRef]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The Impact of Charging Plug-In Hybrid Electric Vehicles on a Residential Distribution Grid. IEEE Trans. Power Syst. 2010, 25, 371–380. [Google Scholar] [CrossRef]
- Galus, M.D.; Waraich, R.A.; Balmer, M.; Andersson, G.; Axhausen, K.W. A Framework for Investigating the Impact of PHEVS; ETH Library: Zurich, Switzerland, 2009. [Google Scholar] [CrossRef]
- Waraich, R.A.; Galus, M.D.; Dobler, C.; Balmer, M.; Andersson, G.; Axhausen, K.W. Plug-in hybrid electric vehicles and smart grids: Investigations based on a microsimulation. Transp. Res. Part C Emerg. Technol. 2013, 28, 74–86. [Google Scholar] [CrossRef]
- Gschwendtner, C.; Knoeri, C.; Stephan, A. The impact of plug-in behavior on the spatial–temporal flexibility of electric vehicle charging load. Sustain. Cities Soc. 2023, 88, 104263. [Google Scholar] [CrossRef]
- Fischer, D.; Harbrecht, A.; Surmann, A.; McKenna, R. Electric vehicles’ impacts on residential electric local profiles—A stochastic modelling approach considering socio-economic, behavioural and spatial factors. Appl. Energy 2019, 233–234, 644–658. [Google Scholar] [CrossRef]
- Stiasny, J.; Zufferey, T.; Pareschi, G.; Toffanin, D.; Hug, G.; Boulouchos, K. Sensitivity analysis of electric vehicle impact on low-voltage distribution grids. Electr. Power Syst. Res. 2021, 191, 106696. [Google Scholar] [CrossRef]
- Karmaker, A.K.; Behrens, S.; Pota, H. Sensitivity Analysis for Electric Vehicle Hosting Capacity in Distribution Networks. In Proceedings of the 2023 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Chiang Mai, Thailand, 28 November–1 December 2023; pp. 1–7. [Google Scholar] [CrossRef]
- Fani, H.; Hashmi, M.U.; Deconinck, G. Impact of electric vehicle charging simultaneity factor on the hosting capacity of LV feeder. Sustain. Energy Grids Netw. 2024, 40, 101581. [Google Scholar] [CrossRef]
- Held, L.; Märtz, A.; Krohn, D.; Wirth, J.; Zimmerlin, M.; Suriyah, M.R.; Leibfried, T.; Jochem, P.; Fichtner, W. The Influence of Electric Vehicle Charging on Low Voltage Grids with Characteristics Typical for Germany. World Electr. Veh. J. 2019, 10, 88. [Google Scholar] [CrossRef]
- DIN EN 50160:2020-11; Voltage Characteristics of Electricity Supplied by Public Electricity Networks. DIN Deutsches Institut für Normung e.V., Beuth Verlag: Berlin, Germany, 2010.
- BMVI. German Mobility Panel (MOP): Longitudinal Study on the Travel Behavior of the Population; Federal Ministry of Transport and Digital Infrastructure (BMVI): Berlin, Germany. Available online: https://mobilitaetspanel.ifv.kit.edu/english/index.php (accessed on 18 July 2024).
- Electric Vehicle Database. Current and Upcoming Electric Vehicles. Available online: https://ev-database.org/ (accessed on 25 July 2024).
- Bynum, M.L.; Hackebeil, G.A.; Hart, W.E.; Laird, C.D.; Nicholson, B.L.; Siirola, J.D.; Watson, J.P.; Woodruff, D.L. Pyomo–Optimization Modeling in Python, 3rd ed.; Springer Science & Business Media: Cham, Switzerland, 2021; Volume 67. [Google Scholar]
- Hart, W.E.; Watson, J.P.; Woodruff, D.L. Pyomo: Modeling and solving mathematical programs in Python. Math. Program. Comput. 2011, 3, 219–260. [Google Scholar] [CrossRef]
- Bolusani, S.; Besançon, M.; Bestuzheva, K.; Chmiela, A.; Dionísio, J.; Donkiewicz, T.; van Doornmalen, J.; Eifler, L.; Ghannam, M.; Gleixner, A.; et al. The SCIP Optimization Suite 9.0; Technical Report; Optimization Online: Berlin, Germany, 2024. [Google Scholar]
- Thurner, L.; Scheidler, A.; Schafer, F.; Menke, J.H.; Dollichon, J.; Meier, F.; Meinecke, S.; Braun, M. Pandapower—An Open-Source Python Tool for Convenient Modeling, Analysis, and Optimization of Electric Power Systems. IEEE Trans. Power Syst. 2018, 33, 6510–6521. [Google Scholar] [CrossRef]
- Statistisches Bundesamt. Zensus 2011: Ergebnisse des Zensus. Available online: https://www.zensus2011.de/DE/Home/Aktuelles/DemografischeGrunddaten.html?nn=559100 (accessed on 15 June 2024).
- Forschungsdatenzentren der Statistischen Ämter des Bundes und der Länder. Mikrozensus 2011, SUF, Version 0; Forschungsdatenzentren Der Statistischen Ämter des Bundes und der Länder: Wiesbaden, Germany, 2011. [Google Scholar] [CrossRef]
- Statistisches Bundesamt. Nutzer-Kurzinformation zu SAFE. Available online: https://www.zensus2011.de/SharedDocs/Downloads/DE/Merkmale/Nutzerhinweise_safe.pdf?__blob=publicationFile&v=2 (accessed on 15 July 2024).
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Deming, W.E.; Stephan, F.F. On a Least Squares Adjustment of a Sampled Frequency Table When the Expected Marginal Totals are Known. Ann. Math. Stat. 1940, 11, 427–444. [Google Scholar] [CrossRef]
- Konduri, K.C.; You, D.; Garikapati, V.M.; Pendyala, R.M. Enhanced Synthetic Population Generator That Accommodates Control Variables at Multiple Geographic Resolutions. Transp. Res. Rec. 2016, 2563, 40–50. [Google Scholar] [CrossRef]
- Ye, X.; Konduri, K.; Pendyala, R.; Sana, B.; Waddell, P. A Methodology to Match Distributions of Both Household and Person Attributes in the Generation of Synthetic Populations. In Proceedings of the 88th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 11–15 January 2009. [Google Scholar]
- BMVI. Mobilität in Deutschland (MiD). Federal Ministry of Transport and Digital Infrastructure (BMVI). Available online: http://www.mobilitaet-in-deutschland.de/ (accessed on 18 July 2024).
- Uhrig, M. Lastprofilgenerator zur Modellierung von Wirkleistungsprofilen Privater Haushalte. Available online: https://zenodo.org/records/803261 (accessed on 16 July 2024).
- Statistisches Bundesamt. Electricity Consumption of Households by Household Size. Available online: https://www.destatis.de/EN/Themes/Society-Environment/Environment/Environmental-Economic-Accounting/private-households/Tables/electricity-consumption-private-households.html (accessed on 16 July 2024).
- BDEW Bundesverband der Energie- und Wasserwirtschaft e.V. Standardlastprofile Strom. Available online: https://www.bdew.de/energie/standardlastprofile-strom/ (accessed on 16 July 2024).
- Kraftfahrzeugbundesamt. Bestand an Personenkraftwagen nach Segmenten und Modellreihen am 1. Januar 2024 gegenüber 1. Januar 2023. Available online: https://www.kba.de/DE/Statistik/Fahrzeuge/Bestand/Segmente/segmente_node.html;jsessionid=B38FCA08D78A8FA7A5989255DB9FFBEE.live11311 (accessed on 15 July 2024).
- Bundesnetzagentur. SMARD: Marktdaten. Available online: https://www.smard.de/home/downloadcenter/download-marktdaten/ (accessed on 25 July 2024).
- von Bonin, M.; Dörre, E.; Al-Khzouz, H.; Braun, M.; Zhou, X. Impact of Dynamic Electricity Tariff and Home PV System Incentives on Electric Vehicle Charging Behavior: Study on Potential Grid Implications and Economic Effects for Households. Energies 2022, 15, 1079. [Google Scholar] [CrossRef]
- Damianakis, N.; Mouli, G.R.C.; Bauer, P.; Yu, Y. Assessing the grid impact of Electric Vehicles, Heat Pumps & PV generation in Dutch LV distribution grids. Appl. Energy 2023, 352, 121878. [Google Scholar] [CrossRef]
- Gauglitz, P.; Ulffers, J.; Thomsen, G.; Frischmuth, F.; Geiger, D.; Scheidler, A. Modeling Spatial Charging Demands Related to Electric Vehicles for Power Grid Planning Applications. ISPRS Int. J. Geo-Inf. 2020, 9, 699. [Google Scholar] [CrossRef]
- Unterluggauer, T.; Hipolito, F.; Rich, J.; Marinelli, M.; Andersen, P.B. Impact of cost-based smart electric vehicle charging on urban low voltage power distribution networks. Sustain. Energy Grids Netw. 2023, 35, 101085. [Google Scholar] [CrossRef]
- Schachler, B.; Heider, A.; Röpke, T.; Reinke, F.; Bakker, C. Assessing the impacts of market-oriented electric vehicle charging on german distribution grids. IET Conf. Proc. 2021, 2021, 128–136. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmalzl, S.; Frey, M.; Gauterin, F. A Spatio-Temporal Microsimulation Framework for Charging Impact Analysis of Electric Vehicles in Residential Areas: Sensitivity Analysis and Benefits of Model Complexity. Energies 2025, 18, 3530. https://doi.org/10.3390/en18133530
Schmalzl S, Frey M, Gauterin F. A Spatio-Temporal Microsimulation Framework for Charging Impact Analysis of Electric Vehicles in Residential Areas: Sensitivity Analysis and Benefits of Model Complexity. Energies. 2025; 18(13):3530. https://doi.org/10.3390/en18133530
Chicago/Turabian StyleSchmalzl, Stefan, Michael Frey, and Frank Gauterin. 2025. "A Spatio-Temporal Microsimulation Framework for Charging Impact Analysis of Electric Vehicles in Residential Areas: Sensitivity Analysis and Benefits of Model Complexity" Energies 18, no. 13: 3530. https://doi.org/10.3390/en18133530
APA StyleSchmalzl, S., Frey, M., & Gauterin, F. (2025). A Spatio-Temporal Microsimulation Framework for Charging Impact Analysis of Electric Vehicles in Residential Areas: Sensitivity Analysis and Benefits of Model Complexity. Energies, 18(13), 3530. https://doi.org/10.3390/en18133530






