Abstract
A thorough understanding of fuel behaviour is essential for designing and operating thermochemical systems. Thermogravimetric analysis (TGA) is among the most widely used fuel characterization methods, offering parameters like reactivity and ignition temperature, and enabling comprehensive fuel behaviour assessment through combined indices. This study critically examines the applicability of TGA-based indices for predicting coal performance in industrial processes such as gasification and combustion, where devolatilization, ignition, and burnout stages are key. TGA-derived data are compared with results from established methods, including drop tube furnace (DTF), pulse ignition (PI), and entrained flow reactor (EFR) tests. Findings indicate that the Volatile Matter Release Index (D2) effectively predicts DTF behaviour (R2 = 0.938, max residuals: 4.1 pp), proving useful for fast devolatilization analysis. The Flammability Index (C1) and Ignition Index (C3) correlate well with PI results (R2 = 0.927 and 0.931, max residuals: 53.3a °C), making them reliable ignition indicators. While TGA tools showed limited accuracy in burnout prediction, the proposed Modified Burnout Characteristic Index (B1′) achieved reasonable performance (R2 = 0.734, max residuals: 0.062%∙°C−1). Overall, selected TGA-based indices offer strong predictive potential for key thermochemical conversion stages.
1. Introduction
Thermogravimetric analysis (TGA) is a widely used tool for characterizing and evaluating the behaviour of solid fuels under high-temperature conditions. This is due to several factors, including its ability to produce repeatable results across different laboratories (by maintaining a consistent testing procedure), its user-friendly operation that requires minimal expertise, its capability to analyse fuels of diverse origins without equipment modifications, and the small sample weight required for testing.
TGA primarily enables the determination of fuel mass loss as a function of temperature and time. Consequently, its results are often used as an alternative to other methods of proximate analysis [1,2]. Additionally, tracking the dynamics of sample mass changes during the process allows for the determination of further fuel characteristics, such as reactivity, ignition temperature, and burnout time. This approach is increasingly considered a viable alternative to standard methods [3,4], particularly in measuring the minimum ignition temperature of dust clouds [5] and dust layers [6], as well as spontaneous ignition temperature [7].
Beyond analysing individual fuel characteristics, parameters are increasingly combined into indices that comprehensively describe fuel behaviour during different gasification or combustion phases, such as devolatilization, ignition, and burnout. These TGA-based indices are widely used in scientific research, and the following chapter presents a brief mini-review of them. Despite their widespread application, TGA-based indices remain a subject of debate. Concerns have been raised regarding their questionable physical basis [8], as well as their reliability in predicting fuel behaviour under industrial conditions, due to differences in system design, operating principles, and the conditions under which the process is conducted [9,10].
The design of a TGA allows for the analysis of samples ranging from a few milligrams to several grams, typically placed in a crucible as a thin bed layer. Moreover, to minimize the impact of temperature gradients on the process under investigation, it is widely recommended that the thinnest possible fuel layer be formed in the crucible [11,12]. Industrial pulverized coal-fired boilers (PC) and circulating fluidized bed boilers (CFB), however, operate under notably different conditions, being supplied with tens of tons of coal per hour [13], where the fuel takes the form of a dust cloud within the combustion chamber.
TGA analysers are electrically heated, with heating elements transferring heat to the gases inside the reactor and to the top layer of fuel in the crucible through radiation and convection. The remaining layers of fuel are heated primarily by thermal conduction—from the crucible walls and from the already heated, hotter layers of the sample. As a result, heat transfer within the TGA reactor is relatively slow, and the maximum heating rates, depending on other factors, including the properties of the fuel being analysed, typically do not exceed one and a half degrees per second. In contrast, heat transfer in industrial boilers is dominated by thermal radiation from the flame to the fuel particles, resulting in heating rates reaching up to ten thousand degrees per second [10].
TGA experiments last from several to several dozen minutes, during which the fuel remains in continuous contact with high temperatures and the gases filling the analyser chamber. In contrast, in industrial boilers, a fuel particle stays in the high-temperature zone for only a few seconds (PC) up to several tens of seconds (CFB) [14,15].
Depending on their design, TGA analysers allow experiments at maximum temperatures of around 1500 °C, although experiments are most commonly conducted at temperatures up to 1000 °C [16]. In industrial boilers, gas temperatures typically range from 1200 to 1500 °C, while in localized areas known as hot spots, they may reach up to 1800 °C [17,18].
During TGA tests, the reactor chamber is continuously flushed with a carrier gas; therefore, when air is used during fuel combustion experiments, a significant excess of oxidizer relative to the fuel is present. In contrast, in industrial boilers, the oxidizer excess is strictly controlled and, depending on the boiler type, does not exceed values approximately from 1.3 (PC) to 1.5 (CFB) [13].
The composition of gases surrounding the fuel differs markedly. In TGA, this composition depends on the operator and typically includes nitrogen, oxygen, and/or carbon dioxide, according to the experimental setup. Moreover, fuel particles in the lower layers have limited access to the flowing gas, which is especially important during experiments involving an oxidizer. In industrial boilers, however, the atmosphere surrounding fuel particles is determined by both the boiler design and the properties of the fuel being burned, making it significantly more complex. In addition to nitrogen, carbon dioxide, and oxygen, it may also contain, among others, soot, volatile organic compounds, carbon monoxide, sulphur and nitrogen compounds, mercury, and water vapor—some of which may exist in highly reactive free radical forms [19].
As highlighted above, the conditions within a TGA differ significantly from those in industrial boilers. Therefore, the application of TGA results—including TGA-based indices—to extrapolate data to larger-scale systems remains uncertain and should be approached with caution. Nevertheless, the potential to predict the behaviour of industrial boilers based on laboratory-scale studies is appealing, as even limited-accuracy forecasts of fuel behaviour can lead to significant cost savings.
In light of the above, the objective of this study is to evaluate the suitability of commonly used TGA-based indices reported in the literature. To this end, 14 different samples, including lignite, hard coal, and anthracite, were selected and characterized through physicochemical analysis. They were also subjected to thermogravimetric analysis (TGA), drop tube furnace (DTF) tests, pulse ignition (PI) tests, and entrained flow reactor (EFR) tests. Where possible, data from literature sources were also incorporated. Finally, the TGA-based indices were compared with physicochemical data and results from well-established laboratory methods to assess their universality and potential as predictors of fuel behaviour on an industrial scale.
2. Mini-Review of TG-Based Indices
Table 1 presents the most commonly reported TGA-based indices found in the literature. The names of these indices differ from those in the source papers due to inconsistencies in naming conventions. Therefore, for this study, indices describing fuel behaviour during devolatilization are designated with the letter “D”, those related to ignition with the letter “C”, and those related to burnout with the letter “B”.
The susceptibility of fuel to volatile matter release is described using three different indices, D1–D3. The D1 index, referred to in Ref. [20] as the Comprehensive Devolatilization Index, is defined as
The individual parameters comprising the index are determined based on TGA data obtained during fuel heating in an inert atmosphere, with the result expressed in %2∙°C−5.
The D2 index, referred to in Refs. [21,22] as the Volatile Matter Release Index, is defined like D1, except that it does not include the average reactivity during devolatilization:
Similar to the D1 index, it is determined for experiments conducted in inert atmospheres. The resulting value is expressed in %∙°C−4.
The D3 index, also referred to as the Volatile Matter Release Index [23], has an even simpler definition. However, unlike D1 and D2, it is determined based on thermograms obtained under oxidizing conditions, rather than inert ones. The resulting value is expressed in %∙°C−3.
In Ref. [24], this index was used to indicate the fuel’s susceptibility to volatile release during gasification. However, unlike the results presented in Ref. [23], the experiments in Ref. [24] were conducted in a gasifying atmosphere containing both oxygen and water vapor.
Fuel flammability and combustion stability are described by six different indices, C1–C6. The C1 index, referred to in Refs. [25,26] as the Flammability Index, is expressed in %∙°C−3 and defined as
The parameter Rmax.oxd is determined under oxidizing conditions, while the Tign parameter can be determined either from measurements conducted under oxidizing conditions or by comparing thermograms obtained under both oxidizing and inert atmospheres.
The second index, C2, is referred to as the Comprehensive Combustion Index [22,27] or the Combustion Characteristics Index [26,28,29] and is commonly denoted by the symbol S:
The parameters related to reactivity and burnout temperature are determined under oxidizing conditions, while the ignition temperature, as with the other indices, can be determined in various ways, which will be discussed later in this work. The resulting value is expressed in %2∙°C−5.
The next index, C3, is referred to as the Ignition Index [21,22,30], and the resulting value is expressed in %∙°C−1∙s−2.
Notably, two parameters are used that correspond to the time associated with characteristic stages of the process, rather than temperatures, as in the previous indices. When the index was intended for combustion processes, the parameters were determined under oxidizing conditions (e.g., [21,22]), whereas for gasification, they were determined in the presence of gasifying agents [24].
An index very similar to C3 is C4, known as the Combustion Stability Index [25]. Compared to C3, the only difference is that instead of times describing characteristic points, temperatures are used:
The resulting value is expressed in %∙°C−3.
Another index similar to the previous ones is C5, also known as the Ignition Index [31], like C3:
In contrast to C4, it refers to the temperature corresponding to fuel burnout, rather than the temperature at which combustion occurs at the maximum rate.
The last of the analysed indices is the Combustion Stability Index [31], expressed as
Among the four indices used to describe a fuel’s tendency to burnout, two are quite commonly used, namely B1 and B2. The B1 index, known as the Burnout Characteristic Index [28], is described by the following equation and is expressed in s−1:
The B2 index, known as the Burnout Index [21,22], is expressed in %∙°C−1∙s−3 and is defined as follows:
The B3 index, known as the Comprehensive Burnout Judging Index [25], is expressed as
The resulting value is expressed in %∙°C−3.
The last of the used indices, the Burnout Index [32] B4, is dimensionless and is defined as
All the indices used to describe the fuel’s tendency to burnout utilize parameters determined under oxidizing conditions.

Table 1.
Thermogravimetry-based indices published in scientific paper.
Table 1.
Thermogravimetry-based indices published in scientific paper.
| Stage of Combustion | Index | Source |
|---|---|---|
| Devolatilization | D1 | [20,33,34] |
| D2 | [21,22,33,35,36] | |
| D3 | [23,24] | |
| Ignition | C1 | [25,26,31,37,38,39,40,41] |
| C2 | [21,22,26,27,28,29,31,35,37,39,40,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61] | |
| C3 | [21,22,24,30,40,47,53,59,60,62,63,64] | |
| C4 | [25,32,40,60] | |
| C5 | [31,36] | |
| C6 | [31,40,59,60] | |
| Burnout | B1 | [28,29,31,38,46] |
| B2 | [21,22,24,40,53,59,60,63,64] | |
| B3 | [25] | |
| B4 | [32] |
A critical analysis of the definitions of the indices presented above indicates that only C2 has a straightforward physical explanation, derived from the definition of the combustion rate as shown in Ref. [26]. The other parameters were postulated in the form presented above by their authors, and it is difficult to assign a physical interpretation to them.
Among the analysed indices, three—C3, B1, and B2—take into account the duration of specific process stages, such as ignition (tign) or burnout (tb.oxd). These times result not only from the physicochemical properties of the analysed fuels but also from the heating procedure applied to the fuels in the thermogravimetric reactor. Therefore, indices C3, B1, and B2 should only be compared for fuels subjected to the same heating history. Furthermore, it should be noted that depending on the heating rate, the combustion mechanism of the fuel may change. Consequently, the extrapolation of these indices to processes under markedly different conditions may be limited.
The remaining ten indices refer to parameters that are theoretically independent of the heating program, such as fuel reactivity (expressed as %∙°C−1) or temperatures at characteristic stages of the process, making them more universal. Since thermogravimetric techniques allow for processes with maximum heating rates of about 1–1.5 °C∙s−1, these indices are fully justified for predicting fuel behaviour during coke production [65], carbon adsorbent/catalyst production [66,67] or catalyst coking [68,69]. In processes where fuel heating occurs at significantly higher rates, although theoretically possible, the use of TGA-based indices requires careful consideration and in-depth analysis.
The vast majority of indices dedicated to the ignition stage refer in their definition to parameters measured at specific stages of the process, such as the ignition temperature. This approach seems justified for homogeneous fuels, for which these temperatures can be clearly identified. However, in the case of fuels with complex structures or fuel mixtures, individual constituents may undergo reactions independently, making it unreasonable to define a single temperature to describe a given phenomenon. Analysing the definition of the C5 index, it becomes apparent that while two fuels may ignite and burnout at the same temperature and have similar maximum reactivity values, the index will be identical for both, even though their gasification/combustion profiles may differ significantly. In the case of indices D1, D2, D3, C6, B2, B3, and B4, they appear to consider the mass change profile over a broader range by using parameters such as ΔT1/2.dev or ΔT1/3.oxd, making them better suited for describing fuels with complex structures.
Some of the parameters used for TGA-based indices are clearly defined, and the method of their determination is similar across most studies. These include, for example, parameters describing maximum reactivity during devolatilization or combustion, as well as the temperatures associated with these reactivities. However, some parameters are determined differently by various authors, and in many studies, there is a lack of a clear definition of the criteria used. The most glaring example of such a parameter is the ignition temperature, which, depending on the study, is determined based on entirely different criteria.
The method presented, among others, in Ref. [56], is based on TGA and dTG combustion profiles. The ignition temperature is determined by drawing a tangent to the TGA curve at the dTG peak. Its intersection with the baseline from the onset of weight loss marks Tign1, whose temperature is defined as the ignition point. The second method, introduced in Ref. [70], suggests taking the ignition temperature (Tign2) as the temperature at which the TG curves from combustion (oxidative atmosphere) and pyrolysis (inert atmosphere) experiments diverge. According to the third method [23], the ignition temperature is considered the point where the mass loss in an oxidative atmosphere reaches a rate of 1% per minute.
As demonstrated above, some of the TGA-based indices appear to be more universal and suitable for application beyond the areas in which they were originally defined. Additionally, considering their widespread use in scientific literature, it is assumed that further analyses will focus on examining the correlations between D2, C1, C2, C3, B1, and B2 and the physicochemical properties of the fuels, as well as the results of selected laboratory experiments. Furthermore, the analyses will focus on coal-based fuels, as their origin results in more homogeneous gasification/combustion profiles compared to biomass or alternative fuels. This approach will help avoid ambiguities in determining TGA-based indices that rely on parameters such as the onset temperature of devolatilization and the ignition temperature.
3. Experimental Section
3.1. Methods
3.1.1. General Outline of the Adopted Methodology
The scope of the conducted experiments included determining the basic physicochemical parameters of the tested fuel samples using proximate analysis, ultimate analysis, and a bomb calorimeter. Subsequently, the samples were subjected to TGA tests, and the obtained results were used to calculate TGA-based indices.
To verify the applicability of TGA-based indices for describing the devolatilization step in predicting fast devolatilization processes occurring in large-scale units, an attempt was made to correlate these indices with data obtained from a DTF. Although the DTF method is not covered by any standard, it has been widely used for years for the investigation of fast devolatilization [4], and its results are commonly applied for predicting operational parameters of industrial-scale burners [71].
To verify the applicability of TGA-based indices describing ignition as a tool for assessing the minimum autoignition temperature of dust clouds, the obtained results were compared with those determined using a Godbert–Greenwald furnace (the so-called Pulse Ignition Test). The method employing the Godbert–Greenwald Furnace complies with the ISO standard [72] and is widely used.
To verify the applicability of TGA-based indices describing burnout for predicting the fuel conversion rate under utility reactor or boiler conditions, the results were compared with the reactivity of chars produced under near-industrial conditions. For this purpose, chars were first produced using an EFR, which ensured a heating rate of approximately 105 °C∙s−1. The reactivity of the obtained chars was then determined. According to fundamental research in combustion science, char reactivity is a reliable indicator for predicting coal combustion efficiency in utility boilers [73].
3.1.2. Assessment Method of TGA-Based Indices
According to the approach proposed above, the TGA-based indices are categorized into those describing the stages of devolatilization, ignition, and burnout, and assessed separately. For each of these stages, the analysis focused on answering the following questions: (1) Do the basic physicochemical parameters determined through standard analyses—i.e., proximate and ultimate analysis—allow for an effective prediction of fuel behaviour under industrial conditions? (2) Do the basic parameters using TGA—i.e., maximum reactivity during devolatilization/oxidation, the initial temperature of devolatilization, ignition/burnout temperature—allow for an effective prediction of fuel behaviour under industrial conditions? (3) Are the analysed TGA-based indices interrelated? (4) Are the analysed TGA-based indices correlated with basic physicochemical parameters? (5) How do TGA-based indices correlate with results obtained using standardized/well-established methods?
The first two questions aim to determine to what extent the development of TGA-based indices is justified—specifically, whether fuel behaviour at a given combustion stage can be assessed solely based on its basic physicochemical properties or basic TGA parameters. The third question examines whether different indices, describing the same combustion stage, similarly rank the analysed fuels or whether the data obtained through these indices contradict each other. The fourth question evaluates the necessity of determining TGA-based indices by assessing whether similar information can be derived from basic physicochemical parameters obtained through standard analyses. Finally, the fifth question investigates whether TGA-based indices correlate with results from standardized and/or well-established methods and whether they can serve as viable alternatives to these methods.
3.1.3. Statistical Approach
To evaluate the quality of the data correlation, a statistical method was employed. There is no universally accepted method for assessing the goodness of fit, and various approaches can be found in the literature [74,75,76]. For the purposes of this study, the relationships between different parameters were analysed, and an attempt was made to describe these relationships using a regression curve. Subsequently, the fit between the regression curve and the available data was assessed by calculating and analysing the coefficient of determination (R2), the standard error of the regression (SER), and residual of the standard error of the regression.
The R-squared coefficient of determination illustrates the goodness of fit and was calculated using the standard equation:
The R2 coefficient is dimensionless, and when it reaches “1”, it signifies a perfect goodness of fit. The acceptable threshold values for R2 may vary depending on the study’s focus. In this research, the guidelines from Refs. [74,77] were followed, assuming that R2 > 0.91 indicates a very good correlation, 0.71–0.90 represents a good correlation, 0.51–0.70 signifies a moderate correlation, and R2 < 0.5 corresponds to a weak correlation.
SER was used to assess the precision of the model’s predictions and was calculated as follows:
The SER coefficient can take any value and shares the same unit as the y variable. Unlike R2, there is no fixed threshold to determine what SER values indicate a good correlation. However, based on generally accepted principles [78], a correlation was considered valid if 95% of the data points fell within a range of ±1.96∙SER. Since each analysis was performed on a set of 14 fuel samples, all examined materials had to fall within this specified range.
The residuals analysis was conducted to assess whether the discrepancies between the measured and regression-predicted values were random or exhibited a trend. From the perspective of correlation quality, residuals randomly scattered around zero were desirable, as they indicated an unbiased correlation.
The correlation was considered valid if the regression curve showed at least a good fit to the actual data (R2 > 0.71), all samples fell within the defined SER range, and the residuals were randomly distributed around zero.
3.2. Materials and Equipment
3.2.1. Samples
For this study, 14 coals of diverse origins were selected, all of which are used in actual combined heat and power plants as well as conventional power plants. The selection included anthracite (denoted as AA), eleven hard coals (denoted as HA–HK), and two lignite coals (denoted as LA and LB), including eight fuels originating from the Northern Hemisphere and six from the Southern Hemisphere.
3.2.2. Proximate/Ultimate Analysis and Heating Value Determination
Proximate/Ultimate Analysis and Heating Value Determination. The samples were air-dried, ground to a particle size below 75 μm, and thoroughly homogenized. Proximate analysis was performed using laboratory chamber furnaces, following ISO-standardized methods for moisture [79], volatile matter [80], and ash content [81]. Ultimate analysis was conducted using a Perkin Elmer CHNS 2400 analyser (Perkin Elmer, Rodgau, Germany), as described in Ref. [82]. The higher heating value (HHV) was measured with an Ika Werke C2000 calorimeter (IKA Werke, Staufen im Breisgau, Germany) following [83], while the lower heating value (LHV) was calculated using the following formula:
3.2.3. TGA
Tests were conducted using a Linseis STA PT 1600 analyser (Linseis, Selb, Germany). Samples of approximately 10 mg were heated with a flow of 0.833 mL∙s−1 of carrier gas. To investigate the behaviour of the fuels, the samples were placed in an open crucible, heated to 900 °C at a rate of 0.167 °C∙s−1, and held at this temperature for 30 min. To determine the TGA-based indices, two measurements were taken for each fuel under inert conditions and two under oxidizing conditions. The discrepancies between the curves recorded under the same conditions for the same fuel did not exceed 1.5%. Therefore, the results were assumed to be repeatable, and the data from both measurement sessions were averaged. A schematic diagram of the described experimental setups is shown in Figure 1.
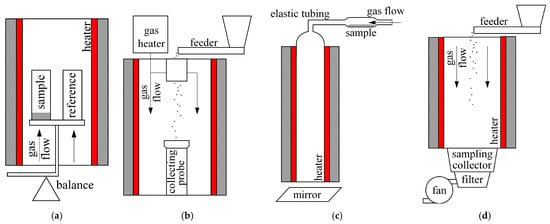
Figure 1.
Schematics of the experimental setups used: (a) TGA, (b) DTF, (c) PI, (d) EFR.
3.2.4. DTF
The experimental setup consisted of a system for preparing the reactor’s gas atmosphere, a probe for introducing the dust, a probe for collecting solid products, a gas heater, a pneumatic powder feeder, electric heating systems for the reaction chamber, and a water-cooling system for the probes. The experiment was based on the continuous flow of fuel particles through a vertical reactor heated by electric heaters. The furnace wall temperature was maintained at a sufficiently high level to ensure exhaust gas temperatures of approximately 1000–1200 °C. The dust particles, mixed with the carrier gas, were fed from the feeder through a water-cooled probe into the reactor, where they were rapidly heated. The tests were conducted for different residence times of the fuel particles in the furnace (up to 50 μs), depending on the varying flow rates of fuel and nitrogen. The particles flowed through the reactor under isothermal conditions and were then drawn from the bottom of the reactor through the water-cooled probe. In the probe, the solid and gaseous reaction products were rapidly cooled in a short time. The solid products were retained in a bag filter. As a result of the measurements, mass loss curves of the fuel were obtained for a given temperature as a function of the particle residence time in the furnace.
3.2.5. PI
The experiments were carried out using a Godbert–Greenwald furnace, which features a 0.27 L test chamber shaped as a vertical ceramic tube, 3.9 cm in diameter and 23 cm high. This chamber was linked to a dust dispersion chamber via elastic tubing. To maintain stable conditions, the test chamber was insulated and equipped with an electric heater regulated by a thermostat. A thermocouple was utilized to monitor and measure the chamber’s preset temperature. Ignition was identified by observing a flame emerging from the furnace’s bottom. A dust sample, with an approximate concentration of 500 g∙m−3, was placed in the dispenser and initially tested at 50 °C. If no ignition took place, the temperature was increased to 100 °C, and the test was repeated under identical conditions. Once ignition was detected, the test temperature was gradually reduced in 25 °C increments to determine both the lowest temperature at which ignition occurs and the highest temperature at which it does not for the given dust concentration. At the highest non-ignition temperature, the dust concentration was adjusted within the range of 300 to 1000 g∙m−3. If ignition was triggered at any concentration at this temperature, the test temperature was further decreased, and testing proceeded accordingly. A minimum of five tests were conducted across various concentrations at the highest temperature where ignition was not observed. At the temperature where ignition did occur, the dust concentration was adjusted to establish the range within which ignition takes place. To ensure data reliability, at least three ignitions at varying concentrations were required at the lowest temperature at which ignition was confirmed.
3.2.6. EFR
The experiments were carried out using a 3-m-long bespoke entrained flow reactor with a diameter of approximately 80 mm. The chars were collected at the bottom of the reactor, while the gases were removed using an exhaust fan. The fuel sample was fed continuously at a rate of ca. 7 g∙min−1 through a feeder located at the top of the furnace. The test was performed at 1000 °C in an air atmosphere. The heating rate of the particles was assumed to be approximately 105 °C∙s−1. The chars obtained from the EFR were then characterized in terms of reactivity through TGA tests conducted in an oxidizing atmosphere.
4. Results and Discussion
4.1. Physicochemical Properties of Fuels
In the following chapter, the results of fuel property determinations are presented along with a brief commentary. Table 2 compiles the results of proximate and ultimate analysis, as well as the LHV value determined based on measurements using a bomb calorimeter.

Table 2.
Proximate and ultimate analysis of investigated fuels (on an analytical basis).
The analysed fuels had a relatively low moisture content, averaging approximately 3.4% in the analytical state, with a maximum of 7.6% observed in sample HB. Other properties varied significantly. For instance, the volatile matter content ranged from 4.8% (AA) to 44.4–46.7% (LA and LB), while the fixed carbon content ranged from 30.7% (HI) to 90.9% (AA). The fuel ratio, defined as the ratio of fixed carbon to volatile matter, ranged from 0.7 to 0.8 for the least carbonized lignite samples (LA and LB), around 1.6–2.2 for hard coals (HA–HK), and up to 18.9 for anthracite (AA). A noteworthy observation is the highly diverse ash content in the hard coal samples, ranging from 7.7% (HG) to 45.7% (HI), depending on the sample. Ultimate analysis showed a fairly strong linear correlation between the fixed carbon content and elemental carbon share. The measured hydrogen content ranged from 2.4% (HI) to 4.9% (HK), nitrogen from 0.5% (LB) to 1.4% (HK), and sulphur from 0.4% (AA) to 1.8% (LA). The heating value ranged from 14.8 MJ∙kg−1 (in the case of the high-ash hard coal HI) to 33.2 MJ∙kg−1 (in the case of anthracite AA).
The TGA-based indices calculated for the analysed samples are summarized in Table 3.

Table 3.
TGA-based indices calculated for analysed samples.
The diverse origins and properties of the analysed samples were reflected in the wide variation in the TGA-based indices. The largest discrepancies among the calculated results were observed for the D2 index, where the highest value exceeded the lowest by more than a factor of 13 (HK: 39.57%∙°C−4∙109 vs. AA: 2.95%∙°C−4∙109). For the C1–C3 indices, the difference between the minimum and maximum values ranged from 2.5 to 3.7 times, while for B1–B2, the differences ranged from 1.4 to 3.2 times.
As presented in the previous chapter, there are several methods for determining the ignition temperature using TGA. Table 4 summarizes the results obtained using the three most common approaches: Tign1 according to Ref. [56], Tign2 according to Ref. [70], and Tign3 according to Ref. [23].

Table 4.
Compilation of ignition temperatures for the samples obtained using TGA.
As noted, all three methods indicate a similar gradation of fuels in terms of their ignition susceptibility, i.e., lignite has the lowest ignition temperatures, followed by hard coal, and finally anthracite. However, depending on the method used, the absolute values of the ignition temperatures differ. Comparing Tign1 and Tign2, it can be observed that Tign1 values are always higher than Tign2, with differences ranging from 31.0 °C (LA) to 74.4 °C (HB). The average discrepancy was approximately 49.4 °C. A similar trend was observed when comparing Tign1 and Tign3, with Tign1 being on average 61.3 °C higher than Tign3, with discrepancies ranging from 37.1 °C (LA) to 82.5 °C (HH). The Tign2 and Tign3 methods generally provided very similar values, with the average difference being 12.9 °C. As demonstrated later in the paper, Tign1 ensured values closest to the minimum autoignition temperature of dust clouds determined by the standard PI method. Therefore, only Tign1 was analysed in the further sections of this work.
The results of the experiments carried out at the DTF, PI, and EFR test stands are presented in Table 5.

Table 5.
Experimental data obtained using DTF, PI, and EFR.
Experiments conducted on the DTF setup indicated that the fuel mass loss under inert conditions ranged from 32.6% for the HJ sample to 62.0% for the LA sample. The minimum autoignition temperature of dust clouds, determined using the standard PI method, ranged from 435 °C for HD to 740 °C for LB, with some results taken from the literature. In the case of the ERF experiments, the reactivity of the char ranged from 0.262 %∙°C−1 for HI to 0.470%∙°C−1 for LB.
4.2. TGA-Based Indices for Devolatilization
Figure 2 and Figure 3 present a comparison of the relationship between the mass of the fuel evolved during the DTF experiments (Δm1000°C(DTF)) and the basic physicochemical parameters characterizing the properties of the analysed fuels.
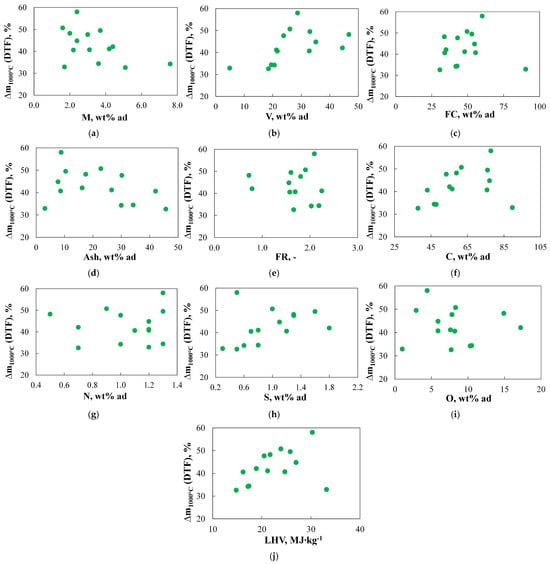
Figure 2.
(a–j) The relationship between the mass of the fuel evolved during the DTF experiments (Δm1000°C(DTF)) and the basic physicochemical parameters.
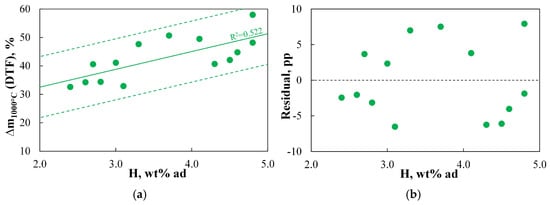
Figure 3.
The relationship between the mass of the fuel devolatilized during the DTF experiments ((a): Δm1000°C(DTF), (b): Residual) and the basic physicochemical parameters (H, wt% ad).
Figure 2 presents examples of results that do not indicate a correlation between the analysed parameters. The lack of correlation demonstrates that it was not possible to determine a regression curve that accurately represents the observed relationships. Consequently, predicting the behaviour of fuel under DTF conditions based on the analysed physicochemical parameters is unjustified. In the following sections of this work, to maintain clarity and conciseness, not all results indicating a lack of correlation between the analysed parameters will be presented in graphs but will instead be discussed. Interestingly, the lack of direct correlation between the volatile matter content in the fuel and the amount of fuel evolved during the DTF experiments, as shown in the analysis, confirms that the volatile matter content is not a particular property of the fuel but depends, among other factors, on the process conditions [87].
A separate figure presents the relationship between the mass of fuel devolatilized under inert conditions, as determined using the DTF, and the hydrogen content in the fuel.
Figure 3a demonstrates that there is a certain relationship between the hydrogen content and the amount of volatile matter devolatilized in the DTF setup, with the regression curve that best represents this relationship described by a linear function. All measurement points lie within the specified SER range, assessing the acceptable precision of the model’s predictions. The calculated residuals indicated an unbiased correlation, although discrepancies between the predicted and actual values are approximately 8.0 pp (Figure 3b). The R2 value of 0.522 indicates that the variation in Δm1000°C(DTF) is only moderately explained by hydrogen content in the regression model. Therefore, it is concluded that predicting DTF mass loss based solely on hydrogen content in the fuel is acceptable only for fuels with similar origin and properties to the analysed materials, and attempts to apply the regression curve outside the indicated range would be unjustified.
The correlation between hydrogen content and DTF results was also discussed in Ref. [88]. Data obtained for 13 analysed coals suggest a potential relationship between the DTF results and a parameter involving hydrogen content (i.e., (H2O)/(C∙S)); however, that study did not confirm this dependency. The existence of a relationship between the aliphatic hydrogen concentration and the mass of fuel devolatilized under DTF conditions is indicated in the article [89]. However, it should be noted that this parameter was determined using FTIR analysis and is not equivalent to the total hydrogen concentration typically measured in the basic ultimate analysis. Considering that both cited works were published over 40 years ago and that no studies currently known to the author indicate the widespread use of predicting devolatilized fuel mass under rapid heating conditions based solely on ultimate analysis, the universality of this approach appears questionable and requires further clarification.
The analysis of the relationship between the mass of fuel devolatilized during DTF experiments and the basic parameters obtained using TGA indicates a linear correlation only between Δm1000°C(DTF) and the maximum reactivity of coal measured under inert conditions. This correlation is presented in Figure 4.
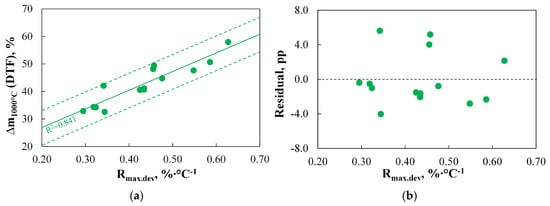
Figure 4.
The relationship between the mass of the fuel devolatilized during the DTF experiments ((a): Δm1000°C(DTF), (b): Residual) and the basic physicochemical parameters (Rmax.dev′ %∙°C−1).
Analysing the results presented in Figure 4a, it can be concluded that the proposed linear regression curve adequately represents the variation in Δm1000°C(DTF), as the R2 value falls within the range of 0.71–0.90. Moreover, the precision of the model’s predictions is acceptable, as all results lie within the specified SER range, and according to Figure 4b, the correlation appears to be unbiased. Based on this, the authors consider the use of the Rmax.dev parameter for predicting the mass of fuel devolatilized during DTF experiments needs to be justified. The use of more complex TGA-based indices for the devolatilization step will only be desirable if the results obtained with these indices allow for even greater accuracy in representing the results obtained using DTF than Rmax.dev.
The key role of Rmax.dev in predicting the effects of the devolatilization process seems to support the assumptions made by the authors of the D1–D2 indices, as both of these indices are, by definition, proportional to this parameter. It is also worth mentioning the validity of replacing the Rmax.dev with the Rmax.oxd parameter, as performed by the authors of the D3 index. The work [90] indicated the lack of a clear relationship between fuel reactivity during combustion under TGA conditions and its tendency to devolatilize under DTF conditions. This study also confirms this lack of correlation, as shown in Figure 5.
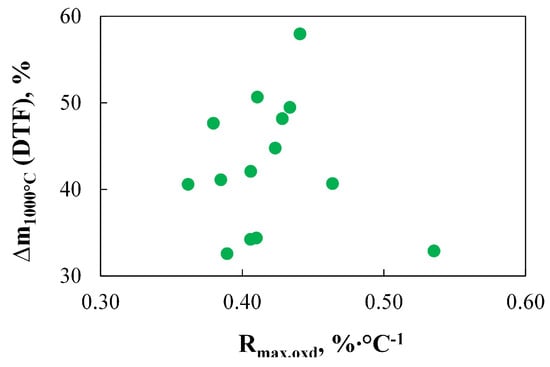
Figure 5.
The relationship between the mass of fuel devolatilized during DTF experiments (Δm1000°C(DTF)) and the maximum reactivity of coal measured under oxidizing conditions using TGA (Rmax.oxd′ %∙°C−1).
Interestingly, the obtained results did not indicate any correlation between Δm1000°C(DTF) and the onset temperature of devolatilization. As indicated in Ref. [91], the onset of devolatilization is expected to be roughly related to coal reactivity, so it could be assumed that fuels characterized by lower Ti.dev parameters would also exhibit higher mass losses under pyrolysis conditions conducted using DTF. This line of reasoning is supported by data presented in Ref. [92]. However, the observed lack of correlation confirms the conclusions from studies [93,94] and suggests that the higher the mass loss, it does not always correspond to a higher volatile matter content.
Since only one TGA-based index, namely D2, was subjected to detailed analysis to predict the stage of devolatilization, no correlation analysis was performed with other TGA-based indices. Figure 6 shows the relationship between the D2 values obtained for different coals and basic physicochemical parameters.
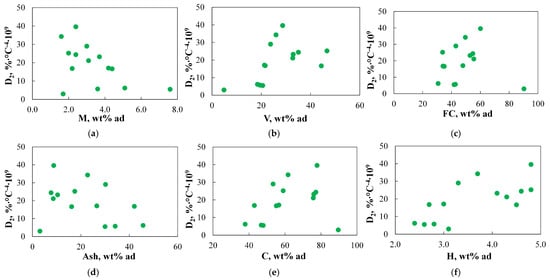
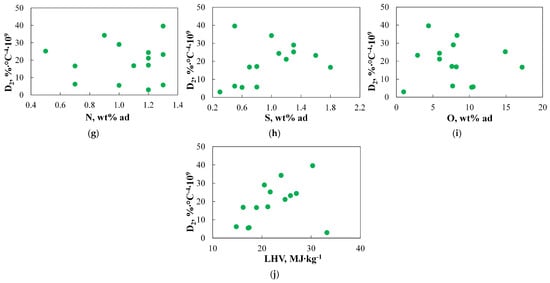
Figure 6.
(a–j) The relationship between the D2 index and basic physicochemical parameters.
As can be observed, the D2 index is not even moderately correlated with the basic physicochemical properties, and therefore, these properties cannot be used to determine it.
To assess the extent to which a TGA-based index can serve as an alternative to the results obtained using DTF, Figure 7 presents the results obtained with both methods.
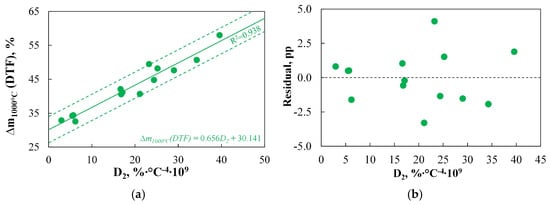
Figure 7.
(a,b) The relationship between the D2 index and the DTF results measured at 1000 °C.
Figure 7 indicates that for the 14 analysed fuels, the D2 index is very well correlated with the results obtained using DTF (at 1000 °C), and the obtained R2 value is 0.938, which is significantly higher than the value obtained when comparing DTF results with Rmax.dev (R2 equals 0.841). Moreover, the correlation is unbiased, and the precision of the model’s predictions is acceptable according to the SER criterion, with discrepancies between the results obtained by both methods reaching a maximum of approximately 4.1 pp.
Typically, when determining DTF results, experiments are conducted at several temperatures. Therefore, Figure 8 presents the mass loss results at 1000 °C, 1200 °C, and 1400 °C for three selected fuels, namely HA, HB, and HC.
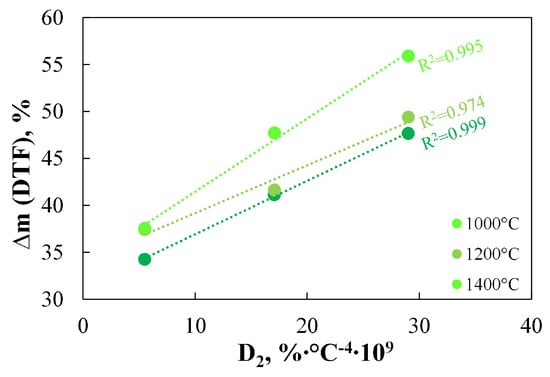
Figure 8.
The relationship between the D2 index and the DTF results measured at temperatures from 1000 °C to 1400 °C.
As can be observed, regardless of the temperature at which the process is conducted, the obtained DTF results show a linear correlation with the D2 index. These observations confirm the validity of using the D2 index in place of Rmax.dev and suggest that the D2 index can be used to predict the behaviour of coals under rapid heating in an inert atmosphere, thus providing a real alternative to the well-established DTF method.
4.3. TGA-Based Indices for Ignition
Figure 9 and Figure 10 present a comparison of the relationship between the minimum autoignition temperature of dust clouds determined using the PI method (MAIT(PI)) and the basic physicochemical parameters characterizing the properties of the analysed fuels.
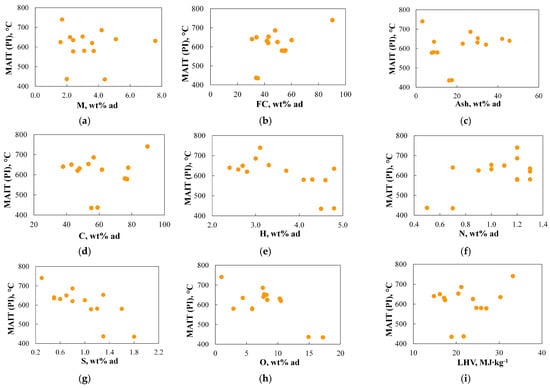
Figure 9.
(a–i) The relationship between the minimum autoignition temperature of dust clouds determined using the PI method (MAIT(PI)) and the basic physicochemical parameters.
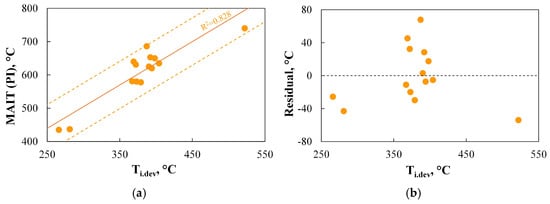
Figure 10.
(a,b) The relationship between the minimum autoignition temperature of dust clouds determined using PI (MAIT(PI)) and the volatile matter content.
Figure 9 shows examples of the lack of correlation between the physicochemical parameters of coal and the autoignition temperature of dust clouds (MAIT(PI)). Interestingly, no clear influence of ash and moisture content on the ignition temperature was found. In general, the presence of ash and moisture negatively impacts energy output by lowering the flame temperature and reducing combustion density; thus, they may reduce the ability of ignition and flame stability [92]. Direct correlations between ash and moisture content and ignition are reported in Refs. [95,96]. However, the observed ambiguous effect of ash and moisture on fuel combustion in this study is not isolated in the literature and has also been observed in Refs. [97,98]. The explanation for this lack of correlation requires further work and analysis.
Moreover, this study did not find a correlation between LHV and ignition temperature. This supports the finding in Ref. [99] that while the heating value may provide insight into flame stability, it alone is not a reliable metric for assessing ignitability and flame behaviour. However, based on the obtained data, it was not possible to verify the information presented in Refs. [100,101,102], which argues that the ignitability of coal can be determined based on the heating value of volatile matter. It should be noted that in this study, the standard heating value was determined for the raw fuel without distinguishing between the heating value of char and volatiles.
Figure 10 shows the only correlation that could be observed between the autoignition temperature of dust clouds (MAIT(PI)) and the analysed physicochemical parameter, i.e., volatile matter content.
As should be emphasized, the R2 coefficient of 0.872 indicates that the proposed linear regression curve effectively represents the variation in MAIT(PI), the precision of the model’s predictions is good (ca. 46.5 °C), and the correlation is unbiased. A similar correlation was found in works [103,104], while [92] even stated that volatile matter content may be used for predicting the ignitability of coal. However, there are also studies in the literature indicating deviations from the linear nature of this relationship for fuels with volatile matter content above 20% [105], or even no correlation at all [106]. The observations presented above require further studies to explain the discrepancies between the results, but they indicate the potential for predicting MAIT(PI) based on basic physicochemical parameters of fuel.
The comparison of results obtained using PI with parameters determined based on TGA signals revealed several interesting correlations, as shown in Figure 11.
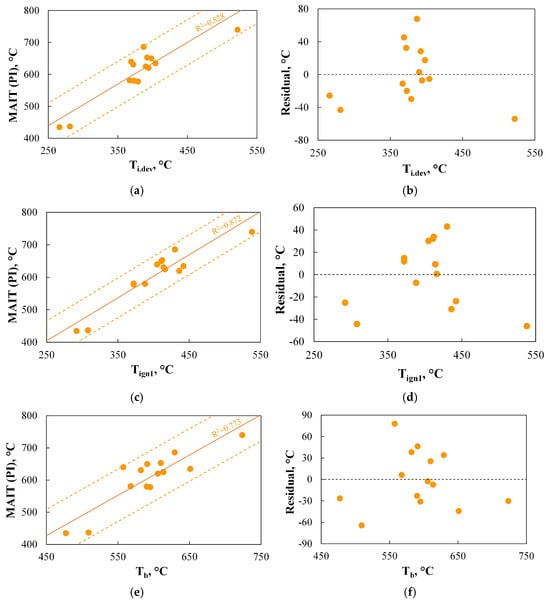
Figure 11.
(a–f) The relationship between the minimum autoignition temperature of dust clouds determined using PI (MAIT(PI)) and the basic parameters determined using TGA.
Figure 11a,b indicate that there is a linear correlation between the minimum autoignition temperature of dust clouds and Ti.dev, which accurately (R2 = 0.828) represents the variation in MAIT(PI). The accuracy of the predicted values is acceptable and amounts to approximately 70 °C. The dependence of the ignition temperature on the onset temperature of devolatilization is also pointed out by other authors, such as Ref. [107], where it is stated that this parameter has the greatest influence on spontaneous ignition. Interestingly, despite the existence of this dependence, none of the six analysed TGA-based indices (C1–C6) include the Ti.dev parameter in their definition.
As shown in the analysis of Figure 11c,d, there is a relationship between the minimum autoignition temperature of dust clouds and the ignition temperature measured using TGA, which can be represented by a linear regression curve. This relationship accurately represents the changes in MAIT(PI) (R2 = 0.872) and allows for results with an accuracy of approximately 45 °C. The results indicate that the TGA method could be a good alternative to the standard PI measurement. Similar conclusions are drawn in the study by Ref. [5], where the authors achieved an accuracy of approximately 66 °C, or Ref. [6], where the accuracy was found to be approximately 6 °C.
The results presented in Figure 11e,f also show a relationship between the minimum autoignition temperature of dust clouds and the burnout temperature. On the one hand, this relationship can partly be explained by the fact that fuels of similar origin and properties, subjected to combustion under similar conditions, will have a similar reaction profile. Therefore, if the fuel ignites at lower temperatures, it should burn more quickly, which, in non-isothermal TGA measurements, will manifest as lower burnout temperatures. The reasoning outlined above seems to align with the definitions of TGA-based indices C2 and C5, which are inherently related to Tb.oxd. Similarly, there are indices responsible for burnout, such as B3, which in their definition refers to the ignition temperature. On the other hand, for example, in the study by Ref. [108], no relationship was found between the ignition temperature and Tb.oxd.
The observations presented above suggest the possibility of predicting MAIT(PI) based on basic parameters obtained via TGA, such as Ti.dev, Tign1, or Tb.oxd. Therefore, the use of more complex TGA-based indices for the ignition step will only be justified if the results obtained using these indices allow for even greater accuracy in representing the data obtained from the PI setup.
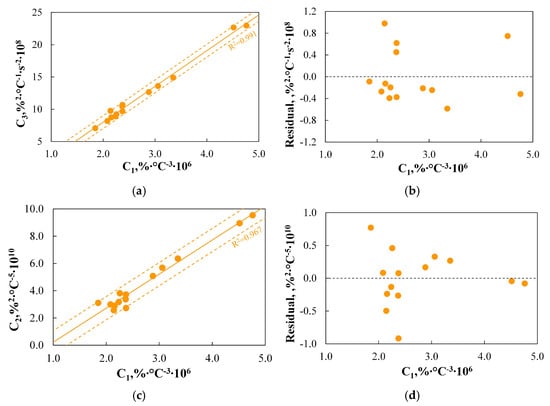
Figure 12.
(a–d) The dependence between TGA-based indices for ignition step.
As shown in Figure 12a,b, the C1 and C3 indices are very well correlated, and by using the determined regression curve, they can be effectively converted. Comparing the definitions of both indices, it should be noted that the C3 index, unlike C1, is based on time parameters, i.e., the time which corresponds to the maximum combustion rate and the ignition time. In the case of the analysed data series, this does not constitute a source of inconvenience, as all measurements were conducted using the same TGA heating program. However, when comparing results obtained from different analysers and using different heating programs, it should be noted that the time-related parameter may introduce discrepancies that are not attributable to the properties of the analysed fuel.
Analysis of Figure 12c,d leads to an interesting observation, indicating that although the R2 value is close to one (0.967) and shows a very good correlation between C2 and C1, one of the analysed fuels is outside the specified SER range. Therefore, it must be concluded that the proposed regression curve is not sufficiently sensitive to changes in C2, and the observed correlation is not valid. Analysis of the source of discrepancy leads to the conclusion that it is caused by the Tb.oxd parameter, whose influence on the ignition step, as previously indicated, is not fully explained.
Figure 13 presents the relationships between the physicochemical properties of the fuel and the C1 index.
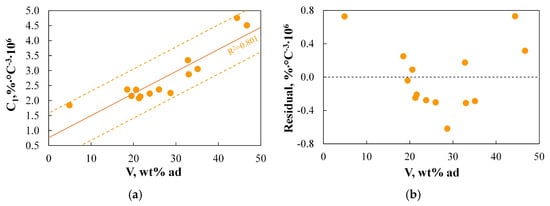
Figure 13.
(a,b) The relationship between the C1 index and basic physicochemical parameters.
Similarly to MAIT(PI), the C1 index is also correlated with only one physicochemical parameter, namely the volatile matter content. The R2 coefficient is 0.801, compared to 0.872 for MAIT(PI). All results fall within the SER range, and the correlation appears to be unbiased. A similar correlation was observed for the C2 and C3 indices, with R2 values of 0.777 and 0.781, respectively. These results indicate that the C1–C3 parameters can be reliably predicted based on basic physicochemical analysis.
Finally, to assess whether the C1–C3 indices could serve as an alternative to the standard method of determining the minimum autoignition temperature of dust clouds, Figure 14 presents a comparison between MAIT(PI) and C1–C3.
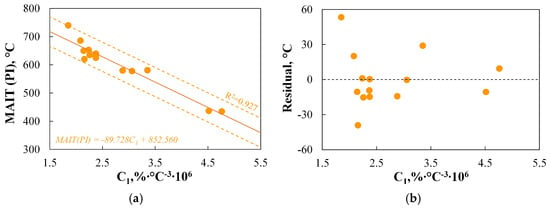
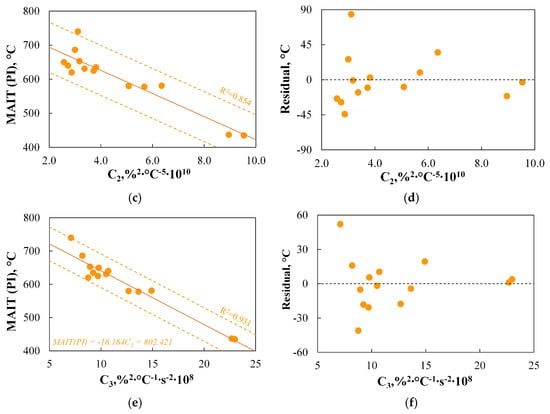
Figure 14.
(a–f) The relationship between the C1–C3 indices and the PI results.
For both the C1 and C3 indices, three conditions were met, allowing the correlation to be considered valid. In both cases, the R2 coefficient exceeded 0.91, indicating a very strong ability of the regression curves to reflect the variability of MAIT(PI). All data points were within the SER range, and the residuals—representing the differences between predicted and actual MAIT(PI) values—did not exceed 53.3 °C. In the case of the C2 index, despite achieving a relatively high R2 value of 0.854, the SER criterion was not met, and, therefore, the correlation was deemed invalid.
Furthermore, when comparing the ability to predict ignition temperature using basic TGA-derived parameters such as Tign1, it should be noted that the TGA-based C1 and C3 indices provide an even more reliable reflection of MAIT(PI) variation, with comparable prediction accuracy of approximately 50 °C.
4.4. TGA-Based Indices for Burnout
Figure 15 illustrates the relationship between the reactivity of chars produced using EFR (Rmax.oxd(EFR)), which serves as an indicator of burnout level under industrial conditions, and selected physicochemical parameters.
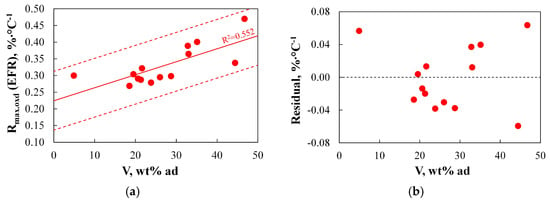
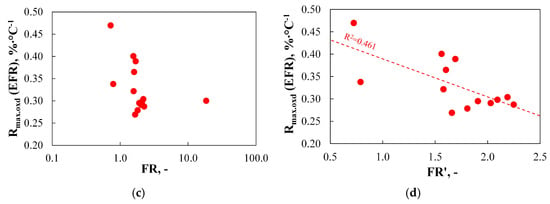
Figure 15.
(a–d) The relationship between the reactivity of chars produced using EFR and basic physicochemical parameters.
Among all the physicochemical parameters analysed for the studied fuels, the only parameter that showed at least a moderate correlation with Rmax.oxd(EFR) was the volatile matter content. The relationships shown in Figure 15a,b demonstrate that the obtained R2 coefficient was relatively low at 0.552, and the discrepancies between predicted and measured results reached approximately 0.057–0.064%·°C−1 in 3 out of 14 cases, corresponding to nearly 20% of the measured values.
The ambiguous influence of volatile matter on coal burnout has also been frequently reported in the literature. In a study by Ref. [109], it was indicated that burnout generally decreased with increasing volatile content in the fuel, and the relationship appeared to be linear. However, for fuels with a low volatile content (around 10%), an unexpectedly high degree of burnout was observed. In Ref. [110], it was shown that adding high-volatile coal to the fuel mixture generally improved burnout, although it did not always have the desired effect. In Ref. [111], test results showed that the volatile content in coal—except for one sample—improved combustion reactivity, and consequently, burnout. The reason behind the occasionally abnormal impact of volatiles on burnout remains unresolved.
In addition to volatile matter, literature also commonly points to a correlation between the fuel ratio (FR) and burnout. As shown in Figure 15c, the data collected in this study do not indicate a straightforward correlation. However, excluding anthracite from the analysis reveals a tendency suggesting that increasing FR leads to lower reactivity, and thus a lower degree of burnout. As illustrated in Figure 15b, this correlation is nevertheless weak. A similar observation was made in the study by Ref. [112], where it was demonstrated that while the fuel ratio is generally considered a good index for assessing carbon burnout, it cannot be universally applied to all types of coal. Slightly fewer objections to the use of fuel ratio were raised in studies [92,95,100,104,113], which provided clear evidence of a correlation between FR and burnout. Conversely, a study by Ref. [99] concluded that a higher fuel ratio does not necessarily indicate a lower burnout level.
The results obtained in this work suggest that physicochemical parameters such as volatile matter content can serve as indicative factors for estimating burnout levels. However, their correlation with Rmax.oxd(EFR) is not strong enough to be considered a reliable predictor of burnout under industrial conditions.
To explore the potential for predicting Rmax.oxd(EFR) based on basic parameters derived from thermograms, Figure 16 presents the most relevant relationships between this index and selected TGA-based parameters.
Figure 16.
(a–c) The relationship between the reactivity of chars produced using EFR and basic parameters determined using TGA.
As can be observed, none of the basic TGA-derived parameters allows for effective prediction of Rmax.oxd(EFR) values. The calculated R2 coefficients for the correlations between Rmax.oxd(EFR) and Ti.dev, Tign1, and Tb.oxd were only in the range of 0.222–0.389.
These findings do not confirm the claims presented in a study by Ref. [83], which suggested that there is a good relationship between the initial temperature from the burning profiles and the carbon burnout determined in the utility boiler. Furthermore, the results only partially support the conclusions from a study by Ref. [91], where the authors stated that the initial temperatures of devolatilization, determined from TGA, relate much better to the carbon burnout of coal on an industrial scale than the burnout temperature and the volatile matter content. The data presented in this work show that volatile matter content is better correlated with burnout (R2 = 0.552) than either the initial devolatilization temperature (R2 = 0.245) or the burnout temperature (R2 = 0.222).
The influence of burnout temperature on the level of burnout also remains a subject for further research. In this study, the correlation between these two parameters was found to be very weak (R2 = 0.222), which is consistent with the findings in a study by Ref. [94]. In contrast, a study by Ref. [114] suggested that coals with lower burnout temperatures have superior burnout levels.
To further analyse the interrelationships between TGA-based indices for the burnout step, Figure 17 was created.
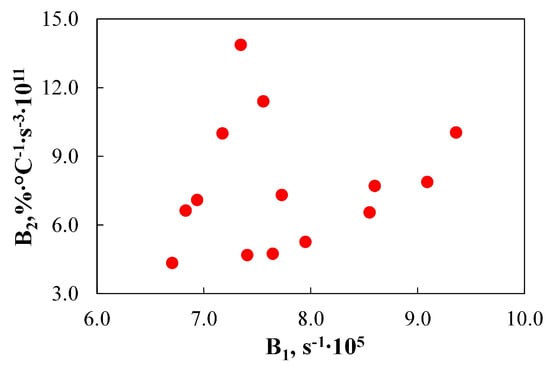
Figure 17.
The relationship between TGA-based indices for the burnout step.
The obtained data indicate that the analysed indices predict fuel burnout susceptibility in different ways. For instance, fuel HA, which has the highest B2 index (13.9 × 1011 %·°C−1·s−3), suggesting it should burn rapidly and therefore achieve a high burnout level, exhibits only an average B1 index (7.3 × 105 s−1). Conversely, the opposite trend was observed for fuel HE, which, despite having nearly the highest B1 index (9.1 × 105 s−1), is characterized by moderate B2 index values (7.9 × 1011%·°C−1·s−3).
Figure 18 presents the extent to which TGA-based indices are correlated with the basic physicochemical parameters of the fuel.
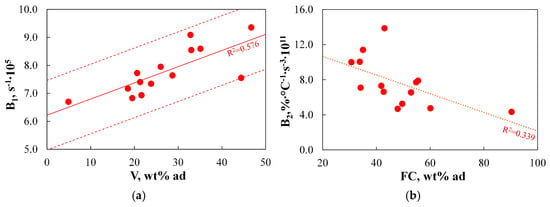
Figure 18.
(a,b) The relationship between TGA-based indices for the burnout step and basic physicochemical parameters.
None of the analysed indices were correlated with any physicochemical parameter to at least a good degree. For the B1 index, a moderate correlation (R2 = 0.576) with the volatile matter content was observed, while for the B2 index, only a weak correlation (R2 = 0.339) with the fuel ratio was found. The correlation of burnout indices with volatile matter content and the FR is supported by the literature (as indicated in the analysis of Figure 15). However, due to significant discrepancies between measured and predicted values, using these physicochemical parameters to determine the B1 and B2 indices would result in considerable inaccuracies and is not recommended.
Finally, to evaluate whether the use of TGA-based indices for predicting reactivity and consequently the degree of burnout in industrial conditions is justified, Figure 19 compares the B1 and B2 indices with Rmax.oxd(EFR).
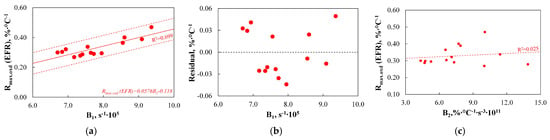
Figure 19.
(a–c) The relationship between the B1–B2 indices and the results obtained on the EFR setup.
As the results show, the B1 index reflects the variability of the Rmax.oxd(EFR) parameter almost good (R2 = 0.699). All analysed coal samples fall within the SER range, and the maximum discrepancies between the measured and predicted values are ±0.50%·°C−1, which corresponds to a maximum difference of 15% compared to the Rmax.oxd(EFR) value obtained using the EFR setup. These data indicate that the B1 index provides a nearly good prediction of the Rmax.oxd(EFR) parameter, which justifies its practical application. However, when comparing the prediction accuracy of the B1 index with that of the D2, C1, and C3 indices, it is evident that predicting the degree of burnout using TGA-based indices is less accurate than predictions related to devolatilization or ignition/combustion steps.
Considering the previously established correlation between Rmax.oxd(EFR) and the volatile matter content in the fuel, a modification of the B1 index definition is proposed below, incorporating a component that accounts for the volatile matter content in the fuel:
The results obtained for the B1′ index are presented in Figure 20.
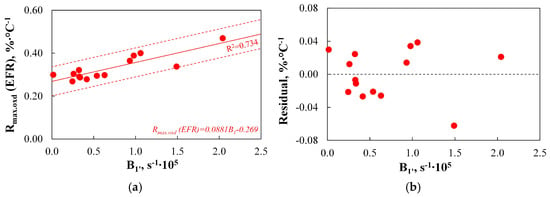
Figure 20.
(a,b) The relationship between the B1′ index and the results obtained on the EFR setup.
The modified B1′ index better reflects the variability of Rmax.oxd(EFR) than the B1 index, as evidenced by the increase in the R2 coefficient from 0.699 to 0.734. Additionally, as with the B1 index, the SER range criterion was met, and a comparison of the residual value plots shows that the average discrepancy between the actual and predicted Rmax.oxd(EFR) values decreased from 0.77% to 0.67%. Nevertheless, it is worth noting that while the maximum discrepancy between the actual and predicted values for the B1 and Rmax.oxd(EFR) correlation was 15%, for the B1′ and Rmax.oxd(EFR) correlation, one of the measurements showed a discrepancy as high as 18%. In summary, the modified B1′ index provides a good representation of Rmax.oxd(EFR) values and can be used to predict fuel reactivity and burnout levels in industrial conditions.
5. Conclusions
As part of this study, the behaviour of 14 coals was analysed across the stages of devolatilization, ignition, and burnout. Experiments conducted using TGA, DTF, PI, and EFR research setups were aimed at assessing the universality of TGA-based indices and evaluating their applicability in predicting fuel behaviour under utility reactor/boiler conditions. The obtained results are summarized in Table 6.

Table 6.
Correlation of results obtained from well-established/standardized methods (DTF, PI, EFR) with basic physicochemical parameters, basic TGA parameters, and TGA-based indices.
In the case of devolatilization, it was confirmed that the tendency of fuels to undergo this process more rapidly could be predicted to a moderate degree based solely on the hydrogen content determined through basic elemental analysis. The coefficient of determination (R2), indicating the strength of the correlation between hydrogen content and the amount of devolatilized fuel as measured using the well-established DTF method, was 0.522. This tendency was captured with significantly greater accuracy by one of the fundamental parameters typically obtained from TGA analysis, i.e., Rmax.dev (R2 = 0.841). However, applying the D2 index led to a further improvement in predictive accuracy, achieving an R2 of 0.938. Taking into account the fulfilment of other statistical criteria, it was concluded that the D2 index provides a very good prediction of DTF results and constitutes a reliable tool for evaluating the behaviour of coal-based fuels.
In the case of ignition, it was confirmed that the tendency of fuels to undergo this process more rapidly could be predicted to a good degree based solely on the volatile matter content determined through basic proximate analysis. The coefficient of determination (R2), reflecting the correlation between volatile content and the minimum autoignition temperature of dust clouds determined using the PI method, was 0.872. Interestingly, the assessment of ignition propensity based on basic TGA-derived parameters such as Ti.dev, Tign1, or Tb.oxd did not lead to improved prediction accuracy (R2 = 0.773 − 0.872). The application of TGA-based indices, specifically C1 and C3, resulted in the highest prediction accuracy, fulfilling all relevant statistical criteria, including achieving R2 values of 0.927–0.931. Notably, the commonly used C2 index, also known as the Comprehensive Combustion Index, which uniquely has a straightforward physical interpretation, did yield a good level of agreement with PI results (R2 = 0.854). However, it failed to provide sufficient predictive accuracy across all analysed fuels, as it did not meet the SER criterion. Therefore, it was concluded that among the indices analysed, C1 and C3 offer a very good predictive capability for PI results and serve as reliable tools for evaluating the ignition behaviour of coal fuels.
In the case of burnout, it was confirmed that the tendency of fuels to undergo this process more rapidly could be predicted to a moderate extent based on the volatile matter content determined through basic proximate analysis (R2 = 0.576). Interestingly, neither the basic parameters obtained from the TGA analysis nor the TGA-based B2 index showed a significant correlation with the reactivity of chars produced under EFR conditions. However, the study confirmed that the B1 index reflected the variability of the EFR results to a nearly good degree (R2 = 0.699) and that a proposed modification to its definition resulted in improved prediction accuracy (R2 = 0.734). Therefore, it was concluded that the B1′ index (a modified version of B1) enables a good-level prediction of EFR outcomes and can be considered a reasonably reliable tool for evaluating the burnout behaviour of coal fuels. Nevertheless, it should be noted that among the three stages analysed, the application of TGA-based tools for assessing burnout is the least accurate.
The observation that TGA-based indices provide reliable predictions of fuel behaviour during the devolatilization and ignition stages, but are less accurate during the burnout stage, aligns well with the classical ‘three-zone’ combustion model introduced in Ref. [115].
Data obtained using TGA and DTF indicate that devolatilization commenced at low temperatures, with its maximum rate achieved before the fuel particles reached 900–1000 °C. Consequently, for both experimental setups, it can be concluded that the overall process rate was limited solely by devolatilization kinetics (i.e., a kinetically controlled regime), making fuel particle temperature the key parameter influencing the devolatilization rate [116]. Hence, ensuring similar fuel particle temperatures allows for comparable results, regardless of differences in device design or operation.
Ignition temperatures recorded in the pulse ignition (PI) setup were below 900 °C, indicating that the ignition of each of the analysed fuels was of a heterogeneous nature [117]. Comparable results were obtained using the TGA setup. The analysis of the devolatilization and combustion curves—conducted in accordance with the methodology described in Ref. [118]—confirms that ignition occurred on the surface of coal particles, where a direct reaction between the solid fuel and oxygen took place. The heterogeneous ignition observed in both setups suggests that the process was limited by film diffusion, with the overall reaction rate controlled by particle–gas interactions. Despite the use of different apparatuses, comparable interphase transport conditions were maintained in both systems; that is, each reactor supplied a substantial excess of oxidizer relative to the fuel, and similar particle temperatures were ensured. This likely accounts for the consistency of the results. Interestingly, in the case of biomass—fuels with a significantly higher volatile content than coal—there is a tendency toward homogeneous ignition, which may not necessarily be observable in either the PI or TGA setups. In such cases, particle size becomes a key factor influencing ignition behaviour, as indicated by Ref. [119], and the C1 and C3 indices may prove less accurate.
In the case of burnout, the active sites responsible for the total conversion rate of char are located inside the pores, on the internal surfaces. Therefore, since pore diffusion effects are slower than reaction kinetics, they become the limiting factor in the overall reaction rate (i.e., the pore-diffusion-controlled regime). Consequently, to ensure comparable oxidation behaviour in both the TGA and EFR setups, it is not sufficient to maintain similar fuel particle temperatures; intra-particle phenomena—including pore diffusion and the evolution of pore structure—must also be considered. As stated in the introduction, during oxidation experiments in the TGA setup, the reactor is continuously purged with oxidizing gas, ensuring a significant excess of oxidizer relative to the fuel. In contrast, the EFR experiments are designed to mimic conditions present in industrial boilers, where the oxidizer-to-fuel ratio is typically maintained at around 1.3–1.5. As a result, due to differing pore diffusion rates, the concentration of oxidizer within the pores varies between the TGA and EFR conditions. This effect is further amplified by the different heating rates applied in each setup, which directly influence the evolution of pore structure [9], and consequently, the efficiency of oxygen diffusion within the pores. Therefore, the accuracy of indices describing the burnout phase is reduced. To improve their reliability, it would be necessary, for example, to limit the amount of oxidizer introduced into the TGA chamber and to analyse the TGA chars previously generated under rapid heating conditions.
In addition to analysing the applicability of TGA-based indices for predicting coal behaviour in utility boilers, this study also evaluates which TGA method for determining ignition temperature yields values most comparable to those obtained using the standard PI method. The results showed that all three investigated methods exhibited a good correlation with the PI data and ranked the analysed fuels in a similar way. However, the method that provided ignition temperatures closest to the MEIT(PI) was the first method (Tign1), which is based on TGA and dTG combustion profiles.
This study did not confirm several dependencies reported in the literature, such as the correlations between DTF results and (H2O)/(C∙S), Rmax.oxd, Ti.dev, or the correlations between PI results and Ash content, M content, or LHV, or between EFR results and FR or Ti.dev. The explanation for this lack of correlation requires further work and analysis.
As demonstrated by the analyses presented above, TGA-based indices offer a valuable tool for assessing the behaviour of coals, which are homogeneous fuels characterized by a reaction profile with a distinct main peak. However, the reliability of results obtained for fuels with complex compositions—such as biomass, waste, and fuel blends—remains an issue that requires further clarification. For such complex fuels, several parameters—such as Rmax.dev, Rmax.oxd, Ti.dev and Tign—raise the question of whether they should be determined separately for each constituent, or whether a single global value should be reported. The approach of determining these parameters for individual components has been applied, for example, to biomass [16]; however, studies that relate such results to data from industrial-scale systems are still lacking. In cases where a single global value is used, the question arises as to which method of calculation provides the most accurate representation of fuel behaviour under industrial conditions.
Moreover, as previously mentioned, the differing properties of certain fuels—such as biomass—can affect ignition and burnout mechanisms, potentially causing significant discrepancies in the results obtained using TGA, PI, or EFR methods. Another source of uncertainty is the potentially substantial influence of moisture on the processes under analysis. For the purposes of this study, all coals were prepared on an analytical basis and did not contain significant moisture. However, for fuels with high inherent moisture content—such as sewage sludge—complete drying is energy-intensive and economically unjustified. As such, these fuels should be analysed in their as-received state, retaining their natural moisture levels. Studies addressing this issue suggest that the impact of moisture is not straightforward, and depending on the type of fuel, there may exist an optimal moisture content for achieving a favorable combustion temperature profile [120,121]. Therefore, while the application of TGA-based indices to fuel groups other than coal is not excluded, it requires thorough investigation. Future studies should also focus on evaluating the applicability of TGA-based indices in predicting results obtained with other well-established techniques, such as layer ignition temperature (LIT) or the crossing-point temperature (CPT).
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| B1 | Burnout Characteristic Index, s−1 |
| B1′ | Modified Burnout Characteristic Index, s−1 |
| B2 | Burnout Index, %∙°C−1∙s−3 |
| B3 | Comprehensive Burnout Judging Index, %∙°C−3. |
| B4 | Burnout Index, - |
| C | Elemental carbon content |
| C1 | Flammability Index, %∙°C−3 |
| C2 | Comprehensive Combustion Index, %2∙°C−5. |
| C3 | Ignition Index, %∙°C−1∙s−2 |
| C4 | Combustion Stability Index, %∙°C−3 |
| C5 | Ignition Index, %∙°C−3 |
| C6 | Combustion Stability Index, %−1∙°C3 |
| CFB | Circulating Fluidized Bed Boilers |
| D1 | Comprehensive Devolatilization Index, %2∙°C−5 |
| D2 | Volatile Matter Release Index, %∙°C−4 |
| D3 | Volatile Matter Release Index, %∙°C−3 |
| DTF | Drop Tube Furnace |
| EFR | Entrained Flow Reactor |
| f1 | Ratio of the particle mass loss to the combustible material at the ignition point, - |
| f2 | Share equal to “1- f1”, - |
| FC | Fixed carbon content |
| FR | Fuel ratio (=FC/V) |
| H | Elemental hydrogen content |
| HHV | Higher Heating Value |
| k | Number of coefficients estimated by the regression (equal to 2) |
| LHV | Lower Heating Value |
| M | Moisture content |
| MAIT(PI) | Experimental data obtained using PI |
| n | Total sample size |
| N | Elemental nitrogen content |
| O | Elemental oxygen content |
| PC | Pulverized Coal-fired Boilers |
| PI | Pulse Ignition |
| R-squared coefficient of determination | |
| Ra.dev | Average reactivity during devolatilization, %∙°C−1 |
| Ra.oxd | Average reactivity, %∙°C−1 |
| Rmax.dev | Maximum reactivity during devolatilization, %∙°C−1 |
| Rmax.oxd | Maximum reactivity during oxidation, %∙°C−1 |
| Rmax.oxd (EFR) | Experimental data obtained using EFR |
| S | Elemental sulphur content |
| SER | Precision of the model’s predictions |
| tb.oxd | Burnout time, s |
| Tb.oxd | Burnout temperature, °C |
| TGA | Thermogravimetric Analysis |
| Ti.dev | Initial temperature of devolatilization, °C |
| tign | Ignition time at ignition temperature, s |
| Tign | Ignition temperature, °C |
| Tmax.dev | Temperature of maximum devolatilization rate, °C |
| tmax.oxd | Time which corresponds to the maximum combustion rate, s |
| Tmax.oxd | Temperature of maximum oxidation rate, °C |
| V | Volatiles content |
| Mean of the actual x values | |
| xᵢ | Actual x value |
| Mean of the observed values | |
| yi | Observed values |
| Predicted values from the regression model | |
| ∆T1/2.dev | Temperature range at a half value of Rmax.dev, °C |
| ∆t1/2.oxd | Time range at a half value of Rmax.oxd, s |
| ∆T1/3.oxd | Temperature range at a one-third value of Rmax.dev, °C |
| ∆Texo | Width of the exothermic peak, - |
| ∆m1000°C (DTF) | Experimental data obtained using DTF |
References
- Czajka, K.M. Proximate analysis of coal by micro-TG method. J. Anal. Appl. Pyrolysis 2018, 133, 82–90. [Google Scholar] [CrossRef]
- ASTM E1131-20; Standard Test Method for Compositional Analysis by Thermogravimetry. ASTM International: West Conshohocken, PA, USA, 2020. Available online: https://store.astm.org/e1131-20.html (accessed on 8 June 2025).
- ASTM E2021-15; Standard Test Method for Hot-Surface Ignition Temperature of Dust Layers. ASTM International: West Conshohocken, PA, USA, 2023. Available online: https://store.astm.org/e2021-15r23.html (accessed on 8 June 2025).
- Annamalai, K.; Ryan, W.; Dhanapalan, S. Interactive processes in gasification and combustion—Part III: Coal/char particle arrays, streams and clouds. Prog. Energy Combust. Sci. 1994, 20, 487–618. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Pochtar, A.S.; Vinogradov, S.V.; Burdukov, A.P. Determination of the ignition temperature of mechanically activated carbon of various degrees of metamorphism and type of grinding. J. Phys. Conf. Ser. 2022, 2233, 012018. [Google Scholar] [CrossRef]
- Paredes, R.; Amez, I.; Leon, D.; Castells, B. Biomass minimum ignition temperature prediction through differential study of thermogravimetric analysis. J. Loss Prev. Process. Ind. 2024, 92, 105486. [Google Scholar] [CrossRef]
- Jankovic, B.; Manic, N.; Stojiljkovic, D.; Jovanovic, V. The assessment of spontaneous ignition potential of coals using TGA–DTG technique. Combust. Flame 2020, 211, 32–43. [Google Scholar] [CrossRef]
- Motiei, P.; Pecchi, M.; Adair, J.L.; Goldfarb, J.L.; O’Connor, J. Pairing combustion experiments and thermogravimetric analysis to uncover timescales controlling cellulose ignition and burnout in a Hencken burner. Combust. Flame 2023, 258, 113092. [Google Scholar] [CrossRef]
- Le Manquais, K.; Snape, C.; McRobbie, I.; Barker, J.; Pellegrini, V. Comparison of the Combustion Reactivity of TGA and Drop Tube Furnace Chars from a Bituminous Coal. Energy Fuels 2009, 23, 4269–4277. [Google Scholar] [CrossRef]
- Czajka, K.M.; Modlinski, N.; Kisiela-Czajka, A.M.; Naidoo, R.; Peta, S.; Nyangwa, B. Volatile matter release from coal at different heating rates –experimental study and kinetic modelling. J. Anal. Appl. Pyrolysis 2019, 139, 282–290. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Koga, N.; Moukhina, E.; Perez-Maqueda, L.A.; Sbirrazzouli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetic. Thermochim. Acta 2020, 698, 178597. [Google Scholar] [CrossRef]
- De Lannoye, K.; Trettin, C.; Belt, A.; Reinecke, E.A.; Goertz, R.; Arnold, L. The influence of experimental conditions on the mass loss for TGA in fire safety science. Fire Saf. J. 2024, 144, 104079. [Google Scholar] [CrossRef]
- Pronobis, M.; Mroczek, K.; Tymoszuk, M.; Ciukaj, S.; Wejkowski, R.; Janda, T.; Jagodzińska, K. Optimisation of coal fineness in pulverised-fuel boilers. Energy 2017, 139, 655–666. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, J.; Liang, H.; Li, Q.; Hu, P.; Wang, D. Modelling on rapid prediction and cause diagnosis of boiler combustion efficiency. Energy 2024, 302, 131848. [Google Scholar] [CrossRef]
- Li, K.; Cheng, L.; Zhao, X.; Wang, B.; Zhang, Q.; Zhu, L.; Kang, Q.; Ma, Z. Experimental study of NH3 and coal Co-firing in a CFB and its nitrogen conversion. Energy 2024, 304, 132156. [Google Scholar] [CrossRef]
- Felix, C.B.; Chen, W.H.; Ubando, A.T.; Park, Y.K.; Lin, K.Y.A.; Pugazhendhi, A.; Nguyen, T.B.; Dong, C.D. A comprehensive review of thermogravimetric analysis in lignocellulosic and algal biomass gasification. J. Chem. Eng. 2022, 445, 136730. [Google Scholar] [CrossRef]
- Khaldi, N.; Chouari, Y.; Mhiri, H.; Bornout, P. CFD investigation on the flow and combustion in a 300 MWe tangentially fired pulverized-coal furnace. Heat Mass Transf. 2016, 52, 1881–1890. [Google Scholar] [CrossRef]
- Glushkov, D.; Paushkina, K.; Vershinina, K.; Vysokomornaya, O. Slagging characteristics of a steam boiler furnace with flare combustion of solid fuel when switching to composite slurry fuel. Appl. Sci. 2023, 13, 434. [Google Scholar] [CrossRef]
- Zhou, B.; Yang, S.; Wang, C.; Hu, X.; Song, W.; Cai, J.; Xu, Q.; Sang, N. The characterization of free radical reaction in coal low-temperature oxidation with different oxygen concentration. Fuel 2020, 262, 116524. [Google Scholar] [CrossRef]
- Ma, J.; Luo, H.; Liu, Z.; Li, D.; Gai, C.; Jiao, W. Pyrolysis kinetics and thermodynamic parameters of the hydrochars derived from co-hydrothermal carbonization of sawdust and sewage sludge using thermogravimetric analysis. Bioresour. Technol. 2019, 282, 133–141. [Google Scholar] [CrossRef]
- Chen, J.; Mu, L.; Cai, J.; Yao, P.; Song, X.; Yin, H.; Li, A. Pyrolysis and oxy-fuel combustion characteristics and kinetics of petrochemical wastewater sludge using thermogravimetric analysis. Bioresour. Technol. 2015, 198, 115–123. [Google Scholar] [CrossRef]
- Chen, J.; Wang, Y.; Lang, X.; Ren, X.; Fan, S. Comparative evaluation of thermal oxidative decomposition for oil-plant residues via thermogravimetric analysis: Thermal conversion characteristics, kinetics, and thermodynamics. Bioresour. Technol. 2017, 243, 37–46. [Google Scholar] [CrossRef]
- Fan, Y.; Zhou, Z.; Cao, Z.; Jiang, X.; Xu, Y. The Influence of High Oxygen Concentration on Ignition Characteristics of Pulverized Bituminous Coal. In Proceedings of the International Conference on Power Engineering-2007, Hangzhou, China, 23–27 October 2007. [Google Scholar]
- Paniagua, S.; Prado-Guerra, A.; Garcia, A.I.; Calvo, L.F. Bioenergy derived from an organically fertilized poplar plot: Overall TGA and index estimation study for combustion, gasification, and pyrolysis processes. Biomass Convers. Biorefin. 2019, 9, 749–760. [Google Scholar] [CrossRef]
- Yan, X.; Wang, X.; Chen, D.; Liu, L. Experimental Investigation for effects of Pulverized-coal Fineness on Combustion Characteristics. In Proceedings of the International Conference on Power Engineering-2007, Hangzhou, China, 23–27 October 2007. [Google Scholar]
- Chen, G.-B.; Li, J.-W.; Lin, H.-T.; Wu, F.-H.; Chao, Y.-C. A Study of the Production and Combustion Characteristics of Pyrolytic Oil from Sewage Sludge Using the Taguchi Method. Energies 2018, 11, 2260. [Google Scholar] [CrossRef]
- Chen, J.; Liu, J.; He, Y.; Huang, L.; Sun, S.; Sun, J.; Chang, K.; Kuo, J.; Huang, S.; Ning, X. Investigation of co-combustion characteristics of sewage sludge and coffee grounds mixtures using thermogravimetric analysis coupled to artificial neural networks modelling. Bioresour. Technol. 2017, 225, 234–245. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z.; Liu, S.; Li, R.-N.; Li, M.-D. Experimental Study on the Oxidation Reaction Parameters of Different Carbon Structure Particles. Environ. Prog. Sustain. Energy 2015, 34, 1063–1071. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Wang, Y.; Mu, M.; Li, X.; Kou, G. Pyrolysis Characteristic Analysis of Particulate Matter from Diesel Engine Run on Diesel/Polyoxymethylene Dimethyl Ethers Blends Based on Nanostructure and Thermogravimetry. Aerosol Air Qual. Res. 2016, 16, 2560–2569. [Google Scholar] [CrossRef]
- Li, X.-g.; Ma, B.-g.; Xu, L.; Hu, Z.-w.; Wang, X.-g. Thermogravimetric analysis of the co-combustion of the blends with high ash coal and waste tyres. Thermochim. Acta 2006, 441, 79–83. [Google Scholar] [CrossRef]
- Song, C.-Z.; Wen, J.-H.; Li, Y.-Y.; Dan, H.; Shi, X.-Y.; Xin, S. Thermogravimetric Assessment of Combustion Characteristics of Blends of Lignite Coals with Coal Gangue. In Advances in Engineering Research (AER), Proceedings of the 3rd Annual International Conference on Mechanics and Mechanical Engineering (MME 2016), Chengdu, China, 16–18 December 2016; Atlantis Press: Paris, France, 2016; Volume 105, pp. 490–495. [Google Scholar]
- Zhang, K.; Zhang, K.; Cao, Y.; Pan, W.-p. Co-combustion characteristics and blending optimization of tobacco stem and high-sulphur bituminous coal based on thermogravimetric and mass spectrometry analyses. Bioresour. Technol. 2013, 131, 325–332. [Google Scholar] [CrossRef]
- Bongomin, O.; Nzila, C.; Mwasiagi, J.I.; Maube, O. Comprehensive thermal properties, kinetic, and thermodynamic analyses of biomass wastes pyrolysis via TGA and Coats-Redfern methodologies. Energy Convers. Manag. X 2024, 24, 100723. [Google Scholar] [CrossRef]
- Nawaz, A.; Kumar, P. Impact of temperature severity on hydrothermal carbonization: Fuel properties, kinetic and thermodynamic parameters. Fuel 2023, 336, 127166. [Google Scholar] [CrossRef]
- Liu, X.; Chen, M.; Yu, D. Oxygen enriched co-combustion characteristics of herbaceous biomass and bituminous coal. Thermochim. Acta 2013, 569, 17–24. [Google Scholar] [CrossRef]
- Shu, Y.; Zhang, J.; Li, W.; Zhao, P.; Zhang, Q.; Zhou, M. Thermogravimetric analysis of the pyrolysis and combustion kinetics of surface dead combustibles in the Daxing’an Mountains. PLoS ONE 2021, 16, e0260790. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.F.; Zhang, Z.E.; Zhang, L.; Zhang, L. Influence of coal properties on the co-combustion characteristics of lowgrade coal and city mud. Glob. NEST J. 2014, 16, 330–339. [Google Scholar]
- Li, Q.; Zhao, C.; Chen, X.; Wu, W.; Li, Y. Comparison of pulverized coal combustion in air and in O2/CO2 mixtures by thermo-gravimetric analysis. J. Anal. Appl. Pyrolysis 2009, 85, 521–528. [Google Scholar] [CrossRef]
- Jin, Y.; Li, Y.; Liu, F. Combustion effects and emission characteristics of SO2, CO, NOx and heavy metals during co-combustion of coal and dewatered sludge. Front. Environ. Sci. Eng. 2016, 10, 201–210. [Google Scholar] [CrossRef]
- Paredes, R.; Castells, B.; Tascon, A. Thermogravimetric Assessment of Biomass: Unravelling Kinetic, Chemical Composition and Combustion Profiles. Fire 2024, 7, 396. [Google Scholar] [CrossRef]
- Qin, Z.; Lei, M.; Zhang, L. Thermogravimetric analysis of the co-combustion of bituminous coal, rice straw and sewage sludge. IOP Conf. Ser. Earth Environ. Sci. 2022, 1011, 012028. [Google Scholar] [CrossRef]
- Luo, S.Y.; Xiao, B.; Hu, Z.Q.; Liu, S.M.; Guan, Y.W. Experimental study on oxygen-enriched combustion of biomass micro fuel. Energy 2009, 34, 1880–1884. [Google Scholar] [CrossRef]
- Lopez-Gonzalez, D.; Fernandez-Lopez, M.; Valverde, J.L.; Sanchez-Silva, L. Kinetic analysis and thermal characterization of the microalgae combustion process by thermal analysis coupled to mass spectrometry. Appl. Energy 2014, 114, 227–237. [Google Scholar] [CrossRef]
- Qing, W.; Yang, X.; Hongpeng, L.; Xiyan, L.; Mingshu, C. Gaseous emission and thermal analysis during co-combustion of oil shale semicoke and sawdust using tg-ftir. Oil Shale 2015, 32, 356–372. [Google Scholar] [CrossRef]
- Qing, W.; Hao, X.; Hongpeng, L.; Chunxia, J.; Jingru, B. Thermogravimetric analysis of the combustion characteristics of oil shale semi-coke/biomass blends. Oil Shale 2011, 28, 284–295. [Google Scholar] [CrossRef]
- Zhang, N.; Ning, X.A.; Zhou, J.; Wei, P.; Luo, J. Investigation on the co-combustion characteristics of pulverized coal and paper mill sludge. Appl. Mech. Mater. 2011, 55–57, 1132–1137. [Google Scholar] [CrossRef]
- Vamvuka, D.; Sfakiotakis, S. Combustion behaviour of biomass fuels and their blends with lignite. Thermochim. Acta 2011, 526, 192–199. [Google Scholar] [CrossRef]
- Mundike, J.; Collard, F.-X.; Gorgens, J.F. Co-combustion characteristics of coal with invasive alien plant chars prepared by torrefaction or slow pyrolysis. Fuel 2018, 225, 62–70. [Google Scholar] [CrossRef]
- Du, Y.; Yu, D.; Wu, J.; Zeng, X.; Xu, M. Co-combustion characteristics of rice husk and different coal. Therm. Eng. 2016, 45, 6–13. [Google Scholar]
- Wang, C.; Wang, F.; Yang, Q.; Liang, R. Thermogravimetric studies of the behaviour of wheat straw with added coal during combustion. Biomass Bioenergy 2009, 33, 50–56. [Google Scholar] [CrossRef]
- Xiu, S.; Rojanala, H.K.; Shahbazi, A.; Fini, E.H.; Wang, L. Pyrolysis and combustion characteristics of Bio-oil from swine manure. J. Therm. Anal. Calorim. 2012, 107, 823–829. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, X.M.; Han, X.X.; Liu, J.G. Combustion characteristics of seaweed biomass. 1. Combustion characteristics of Enteromorpha clathrata and Sargassum natans. Energy Fuels 2009, 23, 5173–5178. [Google Scholar] [CrossRef]
- Wei, Q.; Qiang, X.; Yuyi, H.; Jiatao, D.; Kaidi, S.; Qian, Y.; Jincao, W. Combustion characteristics of semicokes derived from pyrolysis of low rank bituminous coal. Int. J. Min. Sci. Technol. 2012, 22, 645–650. [Google Scholar] [CrossRef]
- Xiong, S.; Zhang, S.; Wu, Q.; Guo, X.; Dong, A.; Chen, C. Investigation on cotton stalk and bamboo sawdust carbonization for barbecue charcoal preparation. Bioresour. Technol. 2014, 152, 86–92. [Google Scholar] [CrossRef]
- Miao, Z.-Y.; Wu, G.-G.; Zhao, N.; Wang, P.-C.; Meng, X.-L. Combustion characteristics of Daqing oil shale and oil shale semi-cokes. Min. Sci. Technol. 2009, 19, 380–384. [Google Scholar] [CrossRef]
- Huang, X.; Jiang, X.; Han, X.; Wang, H. Combustion Characteristics of Fine- and Micro-pulverized Coal in the Mixture of O2/CO2. Energy Fuels 2008, 22, 3756–3762. [Google Scholar] [CrossRef]
- Jiang, X.; Zheng, C.; Qiu, J.; Li, J.; Liu, D. Combustion Characteristics of Super Fine Pulverized Coal Particles. Energy Fuels 2001, 15, 1100–1102. [Google Scholar] [CrossRef]
- Moon, C.; Sung, Y.; Ahn, S.; Kim, T.; Choi, G.; Kim, D. Effect of blending ratio on combustion performance in blends of biomass and coals of different ranks. Exp. Therm. Fluid Sci. 2013, 47, 232–240. [Google Scholar] [CrossRef]
- Wnorowska, J.; Ciukaj, S.; Kalisz, S. Thermogravimetric Analysis of Solid Biofuels with Additive under Air Atmosphere. Energies 2021, 14, 2557. [Google Scholar] [CrossRef]
- Bilkic, B.; Haykiri-Acma, H.; Yaman, S. Combustion reactivity estimation parameters of biomass compared with lignite based on thermogravimetric analysis. Energy Source Part A 2023, 45, 370–383. [Google Scholar] [CrossRef]
- Plis, A.; Lasek, J.A.; Zuwala, J.; Yu, C.C.; Iluk, A. Combustion performance evaluation of Posidonia oceanica using TGA and bubbling fluidized-bed combustor (batch reactor). J. Sustain. Min. 2016, 15, 181–190. [Google Scholar] [CrossRef]
- Sahu, S.G.; Sarkar, P.; Chakraborty, N.; Adak, A.K. Thermogravimetric assessment of combustion characteristics of blends of a coal with different biomass chars. Fuel Process. Technol. 2010, 91, 369–378. [Google Scholar] [CrossRef]
- Li, X.G.; Lv, Y.; Ma, B.G.; Jian, S.W.; Tan, H.B. Thermogravimetric investigation on co-combustion characteristics of tobacco residue and high-ash anthracite coal. Bioresour. Technol. 2011, 102, 9783–9787. [Google Scholar] [CrossRef]
- Ma, B.-G.; Li, X.-G.; Xu, L.; Wang, K.; Wang, X.-G. Investigation on catalyzed combustion of high ash coal by thermogravimetric analysis. Thermochim. Acta 2006, 445, 19–22. [Google Scholar] [CrossRef]
- Diaz-Faes, E.; Barriocanal, C.; Diez, M.A.; Alvarez, R. Applying TGA parameters in coke quality prediction models. J. Anal. Appl. Pyrolysis 2007, 79, 154–160. [Google Scholar] [CrossRef]
- Kisiela-Czajka, A.M. Adsorption behaviour of SO2 molecules on unburned carbon from lignite fly ash in the context of developing commercially applicable environmental carbon adsorbent. Energy 2022, 250, 123741. [Google Scholar] [CrossRef]
- Dasari, H.P.; Patil, S.S.; Kamath, R.S.; Kisiela-Czajka, A.M. Ceria-based electrospun nanofibers and their widespread applications: A review. J. Environ. Manag. 2025, 377, 124656. [Google Scholar] [CrossRef] [PubMed]
- Cherbanski, R.; Kotkowski, T.; Molga, E. Thermogravimetric analysis of coking during dry reforming of methane. Int. J. Hydrogen Energy 2023, 48, 7346–7360. [Google Scholar] [CrossRef]
- Kisiela-Czajka, A.M.; Hull, S.; Albiniak, A. Investigation of the activity of unburned carbon as a catalyst in the decomposition of NO and NH3. Fuel 2022, 309, 122170. [Google Scholar] [CrossRef]
- Tognotti, L.; Malotti, A.; Petarca, L.; Zanelli, S. Measurement of Ignition Temperature of Coal Particles Using a Thermogravimetric Technique. Combust. Sci. Technol. 1985, 44, 5–18. [Google Scholar] [CrossRef]
- Saponaro, A.; Senneca, O.; Cerciello, F.; Brand, D.J.; Torresi, M.; Cesareo, F.; Valenzano, M.; Siena, S.; Rago, G.; Rossiello, G.; et al. CFD modelling: A powerful tool for high efficiency burner design. In Proceedings of the 12th European Conference on Industrial Furnaces and Boilers (INFUB-12), Porto, Portugal, 14–17 April 2020. [Google Scholar]
- ASTM E1491-06; Standard Test Method for Minimum Autoignition Temperature of Dust Clouds. ASTM International: West Conshohocken, PA, USA, 2019. Available online: https://store.astm.org/e1491-06r19.html (accessed on 8 June 2025).
- Roberts, P.T.; Morley, C. Practical Use of Coal Combustion Research. In Fundamentals of the Physical-Chemistry of Pulverized Coal Combustion; Lahaye, J., Prado, G., Eds.; NATO Science Series E; Springer: Berlin/Heidelberg, Germany, 1987; pp. 452–465. Available online: https://link.springer.com/chapter/10.1007/978-94-009-3661-4_20 (accessed on 8 June 2025).
- Singh, R.; Jamwal, N.; Kumar, M.; Luyt, A.S.; Sharma, P.K.; Kumar, R. Theoretical assessment of mechanical behaviour of LDPE/Cu composites using nonlinear polynomial regression analysis. Adv. Mech. Eng. 2025, 17, 16878132251323156. [Google Scholar] [CrossRef]
- Pilatov, A.; Czajka, K.M.; Petraconi Filho, G.; Medeiros, H.S.; Kisiela, A.M. Evaluation criteria for assessment of additives (AlCl3 and ZnCl2) influence on pyrolysis of sunflower oil cake. Waste Biomass Valorization 2017, 8, 2595–2607. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, Z. The general goodness-of-fit tests for correlated data. Comput. Stat. Data Anal. 2022, 167, 107379. [Google Scholar] [CrossRef]
- Moore, D.S.; Notz, W.I.; Flinger, M.A. The Basic Practice of Statistics, 6th ed.; W. H. Freeman and Company: New York, NY, USA, 2013. [Google Scholar]
- McHugh, M.L. Standard error: Meaning and interpretation. Biochem. Med. 2008, 18, 7–13. Available online: https://www.biochemia-medica.com/assets/images/upload/xml_tif/McHugh_ML_-_Standard_error.pdf (accessed on 8 June 2025). [CrossRef]
- ISO 11722:2013; Solid Mineral Fuels—Hard Coal—Determination of Moisture in the General Analysis Test Sample by Drying in Nitrogen. International Organisation for Standardisation: Geneva, Switzerland, 2013. Available online: https://www.iso.org/standard/62610.html (accessed on 8 June 2025).
- ISO 562:2024; Hard Coal and Coke—Determination of Volatile Matter. International Organisation for Standardisation: Geneva, Switzerland, 2024. Available online: https://www.iso.org/standard/86976.html (accessed on 8 June 2025).
- ISO 1171:2024; Coal and Coke—Determination of Ash. International Organisation for Standardisation: Geneva, Switzerland, 2024. Available online: https://www.iso.org/obp/ui/#iso:std:iso:1171:ed-5:v1:en (accessed on 8 June 2025).
- ISO 21663:2020; Solid Recovered Fuels—Methods for the Determination of Carbon (C), Hydrogen (H), Nitrogen (N) and Sulphur (S) by the Instrumental Method. International Organisation for Standardisation: Geneva, Switzerland, 2020. Available online: https://www.iso.org/standard/71332.html (accessed on 8 June 2025).
- ISO 1928:2020; Coal and Coke—Determination of Gross Calorific Value. International Organisation for Standardisation: Geneva, Switzerland, 2020. Available online: https://www.iso.org/standard/75883.html (accessed on 8 June 2025).
- Peta, S. Ignition Characteristics of Low Volatile Quality High Ash Coal. Master’s Thesis, University of Witwatersrand, Johannesburg, SA, USA, 2014. [Google Scholar]
- Rybak, W.; Moron, W.; Czajka, K.M. Report: Selection of Coals and Conducting Proximate, Ultimate, and Petrographic Analyses of Selected Fuels; PWr: Wroclaw, Poland, 2016. (In Polish) [Google Scholar]
- Czakiert, T.; Nowak, W.; Rybak, W. Oxy-Fuel Combustion for Pulverized and Fluidized Bed Boilers Integrated with CO2 Capture: Kinetics and Mechanism of Oxy-Fuel Combustion and CO2 Capture; Wydawnictwo Politechniki Częstochowskiej: Czestochowa, Poland, 2013. (In Polish) [Google Scholar]
- Speight, J.G. The Chemistry and Technology of Coal, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Neoh, K.G.; Gannon, R.E. Coal volatile yield and element partition in rapid pyrolysis. Fuel 1984, 63, 1347–1352. [Google Scholar] [CrossRef]
- Solomon, P.R.; Hobbs, R.H.; Hamblen, D.G.; Chen, W.-Y.; La Cara, A.; Graff, R.S. Correlation of coal volatile yield with oxygen and aliphatic hydrogen. Fuel 1981, 60, 342–346. [Google Scholar] [CrossRef]
- Kim, J.K.; Lee, H.D.; Kim, H.S.; Park, H.Y.; Kim, S.C. Combustion possibility of low rank Russian peat as a blended fuel of pulverized coal fired power plant. J. Ind. Eng. Chem. 2014, 20, 1752–1760. [Google Scholar] [CrossRef]
- Su, S.; Pohl, J.H.; Holcombe, D.; Hart, J.A. Techniques to determine ignition, flame stability and burnout of blended coals in p.f. power station boilers. Prog. Energy Combust. Sci. 2001, 27, 75–98. [Google Scholar] [CrossRef]
- Pisupati, S.V.; Scaroni, A.W. Prediction of combustion behaviour of coal blends in industrial scale boilers from laboratory scale data. In Proceedings of the ICCS’97, DGMK Tagungsberichte 9703, Seattle, WA, USA, 3–8 August 1997. [Google Scholar]
- Pohl, J.H. Fuel Evaluation Report: Obed Mountain Coal; Energy and Environmental Research Corporation: Irvine, CA, USA, 1985. [Google Scholar]
- Pohl, J.H. Fuels Evaluation Report: Gloucester Coals; Energy and Environmental Research Corporation: Irvine, CA, USA, 1984. [Google Scholar]
- Holcombe, D. Interim Test Results for the CRC for Black Coal Utilization; ACIRL Limited: Ipswich, UK, 1998. [Google Scholar]
- Li, L.; Bai, X.; Qu, C.; Zhou, K.; Sun, Y. Effects of Moisture on the Ignition and Combustion Characteristics of Lignite Particles: Modelling and Experimental Study. ACS Omega 2022, 7, 34912–34920. [Google Scholar] [CrossRef]
- Pinchuk, V.A.; Sharabura, T.A.; Kuzmin, A.V.; Pinchuk, S.A. The peculiar influence of the mineral impurities content in coal-water fuel on the regularities of fuel drop ignition and combustion. J. Energy Inst. 2020, 93, 911–921. [Google Scholar] [CrossRef]
- Zheng, W.; Gan, S.; Jia, X.; Liu, X. Effect of Moisture Content on Spontaneous Combustion Characteristics of Bituminous Coal in Wuda Coal Field. In Solid Fuel Chemistry; Dzhemilev, U.M., Ed.; Springer Nature: Berlin/Heidelberg, Germany, 2025; Available online: https://link.springer.com/journal/11985 (accessed on 8 June 2025).
- Skorupska, N.M. Coal Specifications—Impact on Power Station Performance, IEACR/52; IEA Coal Research: London, UK, 1993; Available online: https://www.sustainable-carbon.org/report/coal-specifications-impact-on-power-station-performance-ieacr-52/ (accessed on 8 June 2025).
- Pohl, J.H. Fuels Evaluation Report: SRP Coals; Energy and Environmental Research Corporation: Irvine, CA, USA, 1985. [Google Scholar]
- Breen, B.P.; Dusatko, G.C.; Mann, A.N. Low sulphur cleaned coal as a compliance strategy for existing utility boilers. In Proceedings of the Second International Conference on Effects of Coal Quality on Power Plants, St Louis, MO, USA, 19–21 September 1990. [Google Scholar]
- Su, S.; Pohl, J.H.; Holcombe, D.; Hart, J.A. A proposed maceral index to predict combustion behavior of coal. Fuel 2001, 80, 699–706. [Google Scholar] [CrossRef]
- Hertzberg, M. Autoignition temperatures for coal particles dispersed in air. Fuel 1991, 70, 1115–1123. [Google Scholar] [CrossRef]
- Zeng, H.C.; Yao, B.; Qiu, J.R. Studies of combustion and slagging characteristics of anthracite blends with bituminous coal. Ranshao Kexue Yu Jishu 1996, 2, 181–189. (In Chinese) [Google Scholar]
- Sha, D.; Li, Y.; Zhou, X.; Zhang, J.; Zhang, H.; Yu, J. Influence of Volatile Content on the Explosion Characteristics of Coal Dust. ACS Omega 2021, 6, 27150–27157. [Google Scholar] [CrossRef]
- Ajrash, M.J.; Zanganeh, J.; Moghtaderi, B. Experimental investigation of the minimum auto-ignition temperature (MAIT) of the coal dust layer in a hot and humid environment. Fire Saf. J. 2016, 82, 12–22. [Google Scholar] [CrossRef]
- Wu, K.; Qi, Y.; Chen, Y.; Zhao, P.; Xi, C.; Zhao, Y.; Wang, Q. Dependence evaluation of factors influencing coal spontaneous ignition. Energy Sci. Eng. 2023, 11, 3307–3960. [Google Scholar] [CrossRef]
- Aich, S.; Behera, D.; Nandi, B.K.; Bhattacharya, S. Relationship between proximate analysis parameters and combustion behaviour of high ash Indian coal. Int. J. Coal Sci. Technol. 2020, 7, 766–777. [Google Scholar] [CrossRef]
- Li, H.; Elliott, L.; Rogers, H.; Wall, T. Comparative Study on the Combustion Performance of Coals on a Pilot-Scale Test Rig Simulating Blast Furnace Pulverized Coal Injection and a Lab-Scale Drop-Tube Furnace. Energy Fuels 2014, 28, 363–368. [Google Scholar] [CrossRef]
- Smart, J.P.; Nakamura, T. NOx emissions and burnout from a swirl-stabilized burner firing pulverized coal: The effects of firing coal blends. J. Energy Inst. 1993, 66, 99–105. Available online: https://scispace.com/papers/nox-emissions-anf-burnout-from-a-swirl-stabilised-burner-1paywnfad4 (accessed on 8 June 2025).
- Kim, J.K.; Lee, H.D. Combustion Possibility of Indonesia KBB Coal with High Moisture as a Pulverized Fuel of Thermal Power Plant. J. Chem. Eng. Jpn. 2010, 43, 704–712. [Google Scholar] [CrossRef]
- Oka, N.; Murayama, T.; Matsuoka, H.; Yamada, S.; Yamada, T.; Shinozaki, S.; Shibaoka, M.; Thomas, C.G. The influence of rank and maceral composition on ignition and char burnout of pulverized coal. Fuel Process. Technol. 1987, 15, 213–224. [Google Scholar] [CrossRef]
- Douglas, R.E.; Mai, M.C.; Stoessner, R.D. Effects of increasing coal hardness and volatility on pilot-scale pulverization and combustion performance. In Proceedings of the 7th Annual International Pittsburgh Coal Conference, Pittsburgh, PA, USA, 10–14 September 1990; pp. 837–851. [Google Scholar]
- Carpenter, A.M. Coal Blending for Power Stations; IEA/81; IEA Coal Research: London, UK, 1995. [Google Scholar]
- Walker, P.L.; Rusinko, F.; Austin, L.G.; Eley, D.D.; Selwood, P.W.; Weisz, P.B. Gas reactions of carbon. Adv. Catal. 1959, 11, 133–221. [Google Scholar] [CrossRef]
- Hasse, C.; Debiagi, P.; Wen, X.; Hildebrandt, K.; Vascellari, M.; Faravelli, T. Advanced modelling approaches for CFD simulations of coal combustion and gasification. Prog. Energy Combust. 2021, 86, 100938. [Google Scholar] [CrossRef]
- Yuan, Y.; Li, S.; Li, G.; Wu, N.; Yao, Q. The transition of heterogeneous–homogeneous ignitions of dispersed coal particle streams. Combust. Flame 2014, 161, 2458–2468. [Google Scholar] [CrossRef]
- Chen, Y.; Mori, S.; Pan, W.P. Studying the mechanisms of ignition of coal particles by TG-DTA. Thermochim. Acta 1996, 275, 149–158. [Google Scholar] [CrossRef]
- Li, J.; Paul, M.C.; Czajka, K.M. Studies of ignition behaviour of biomass particles in a down-fire reactor for improving co-firing performance. Energy Fuels 2016, 30, 5870–5877. [Google Scholar] [CrossRef]
- Sitka, A.; Szulc, P.; Smykowski, D.; Anwajler, B.; Tietze, T.; Jodkowski, W. Conversion of post-refining waste mong to gaseous fuel in a rotary gasifier. Sustainability 2024, 16, 4251. [Google Scholar] [CrossRef]
- Huang, Q.; Yu, B.; Qiu, K.; Zhou, G.; Wang, S.; Chi, Y.; Yan, J. Effect of moisture on sewage sludge combustion temperature profile and heavy metal leaching. Dry. Technol. 2016, 34, 1810–1819. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).