Application of Repetitive Control to Grid-Forming Converters in Centralized AC Microgrids †
Abstract
1. Introduction
- Model Predictive Control (MPC) applied to GFCs, which guarantees optimal reference tracking while respecting the converter’s current and voltage constraints [12];
- Distributed coordination schemes that eliminate the need for a central communication infrastructure, ensuring resilient voltage restoration and load sharing [13];
- Machine-learning-based adaptive control techniques, capable of dynamically adjusting virtual inertia and droop parameters in response to varying grid conditions [14];
- Dynamic virtual-impedance loops, which enhance stability margins in low-inertia scenarios and suppress high-frequency disturbances [15].
- Natural reference frame (abc);
- Synchronous reference frame (dq0);
- Stationary reference frame (0).
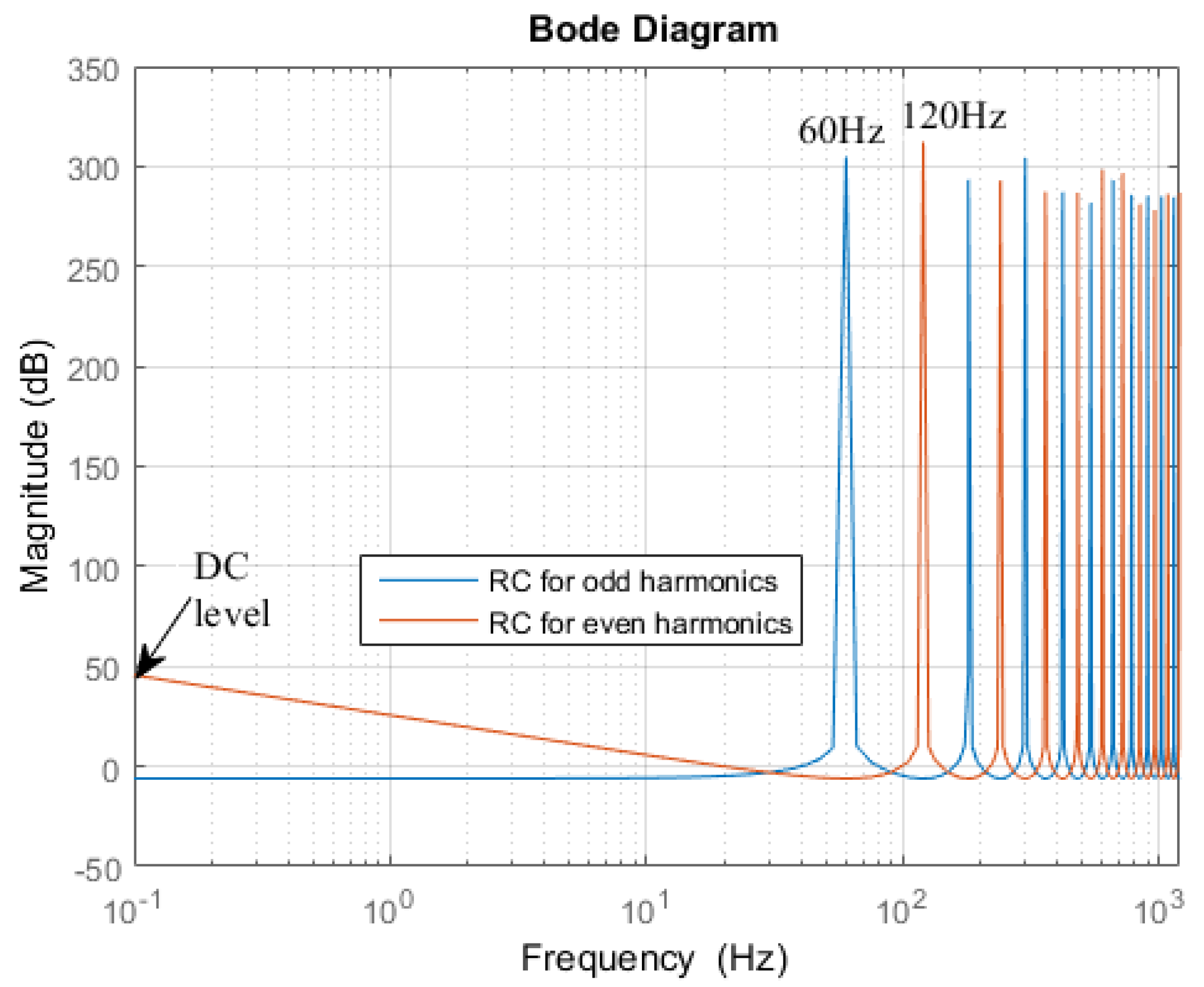
2. Repetitive Controller
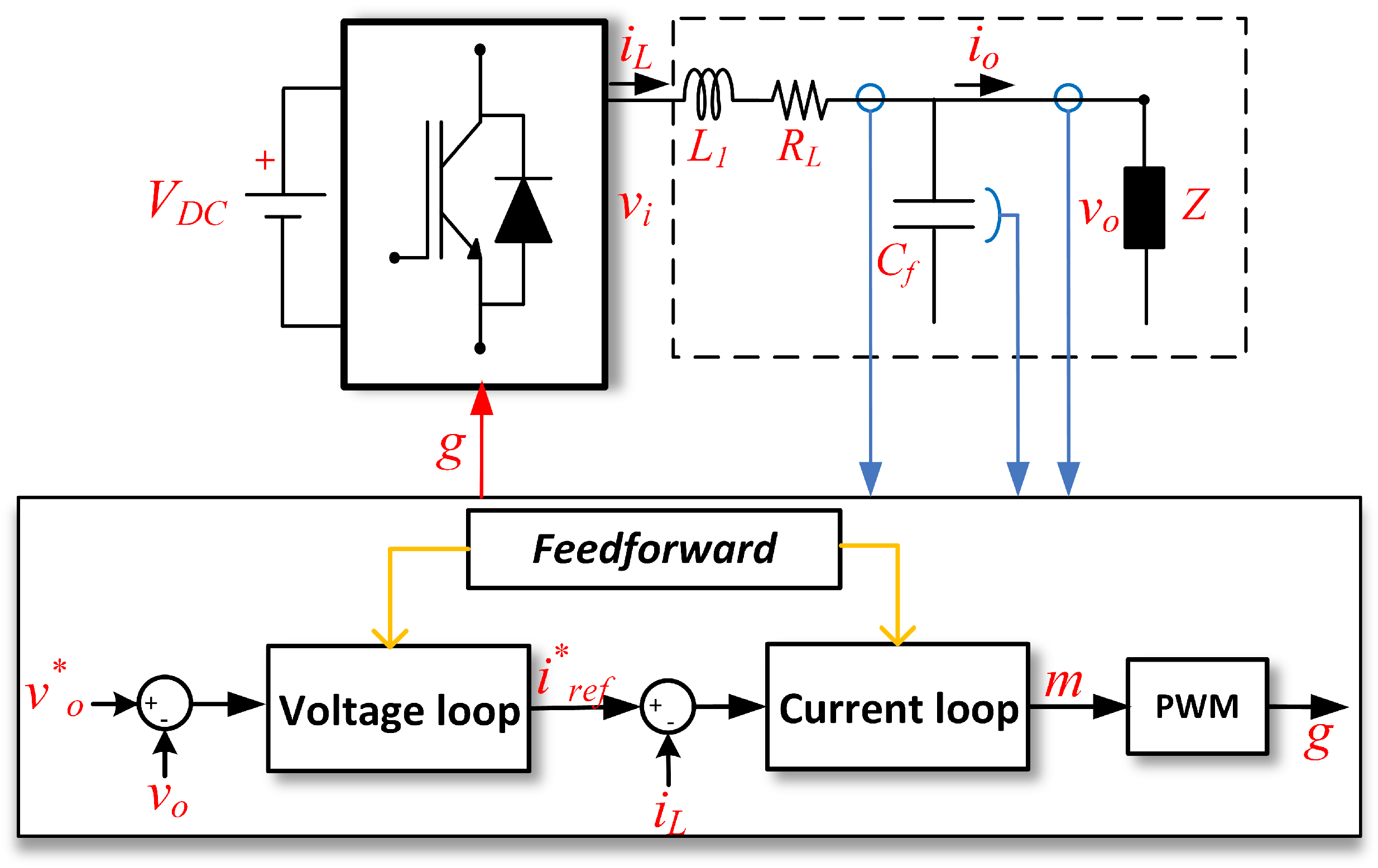
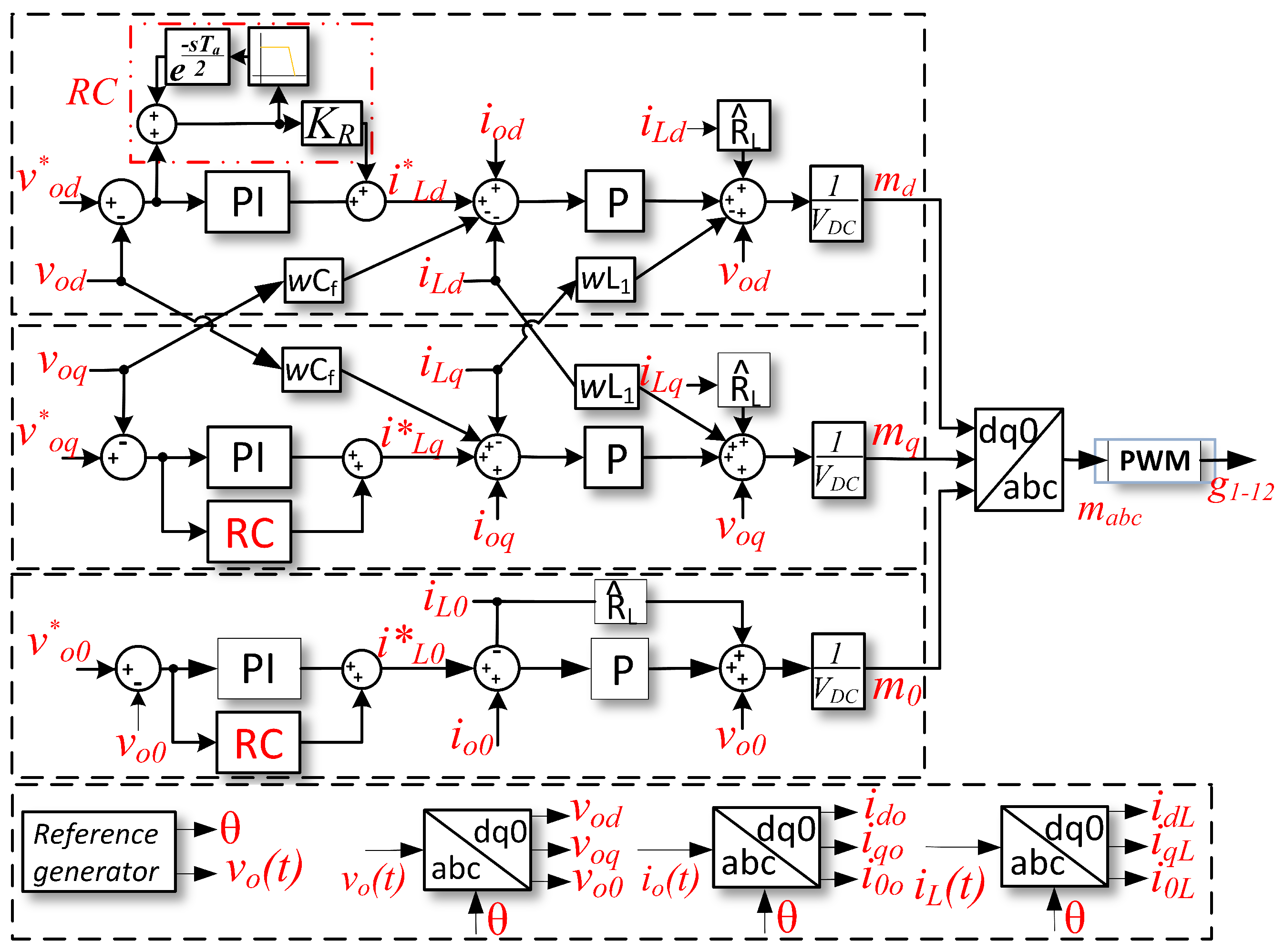
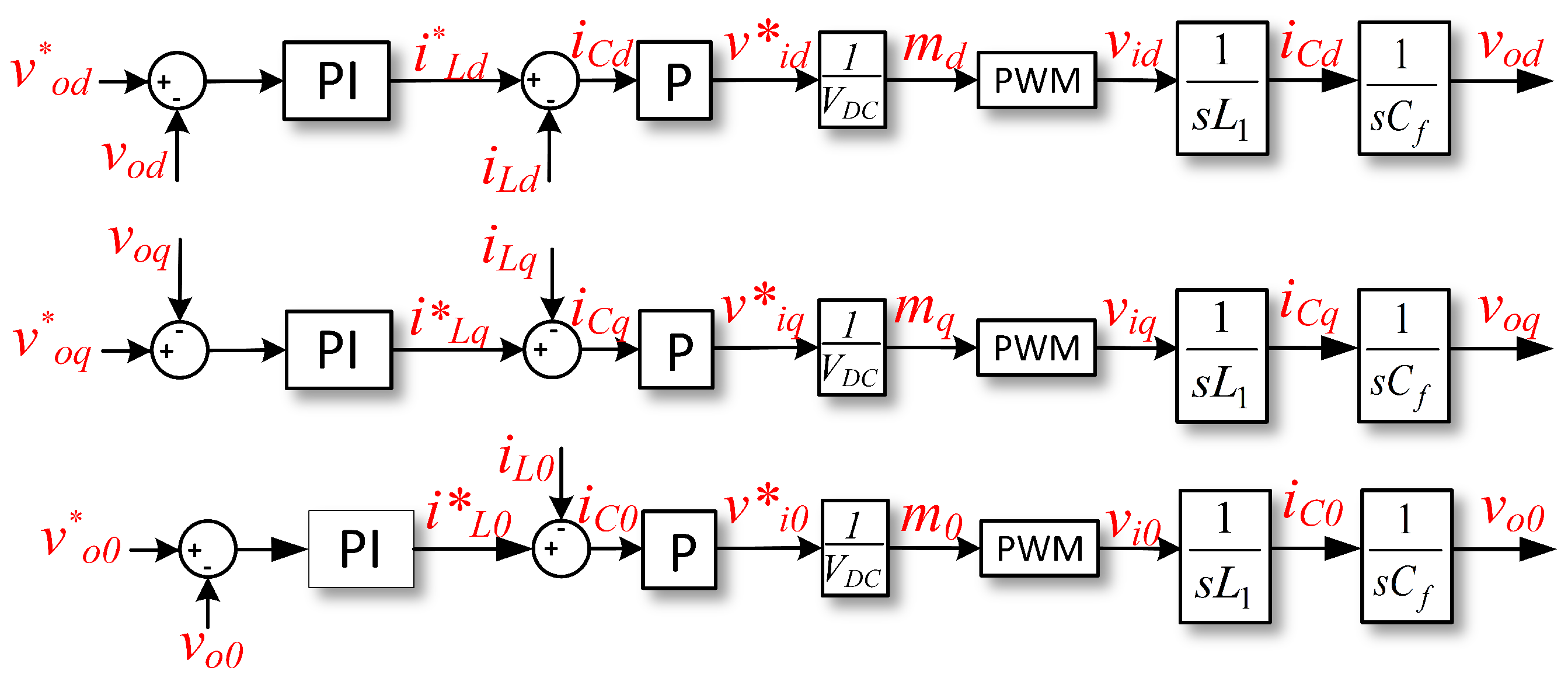
3. Proposed Control for Grid-Forming Converter
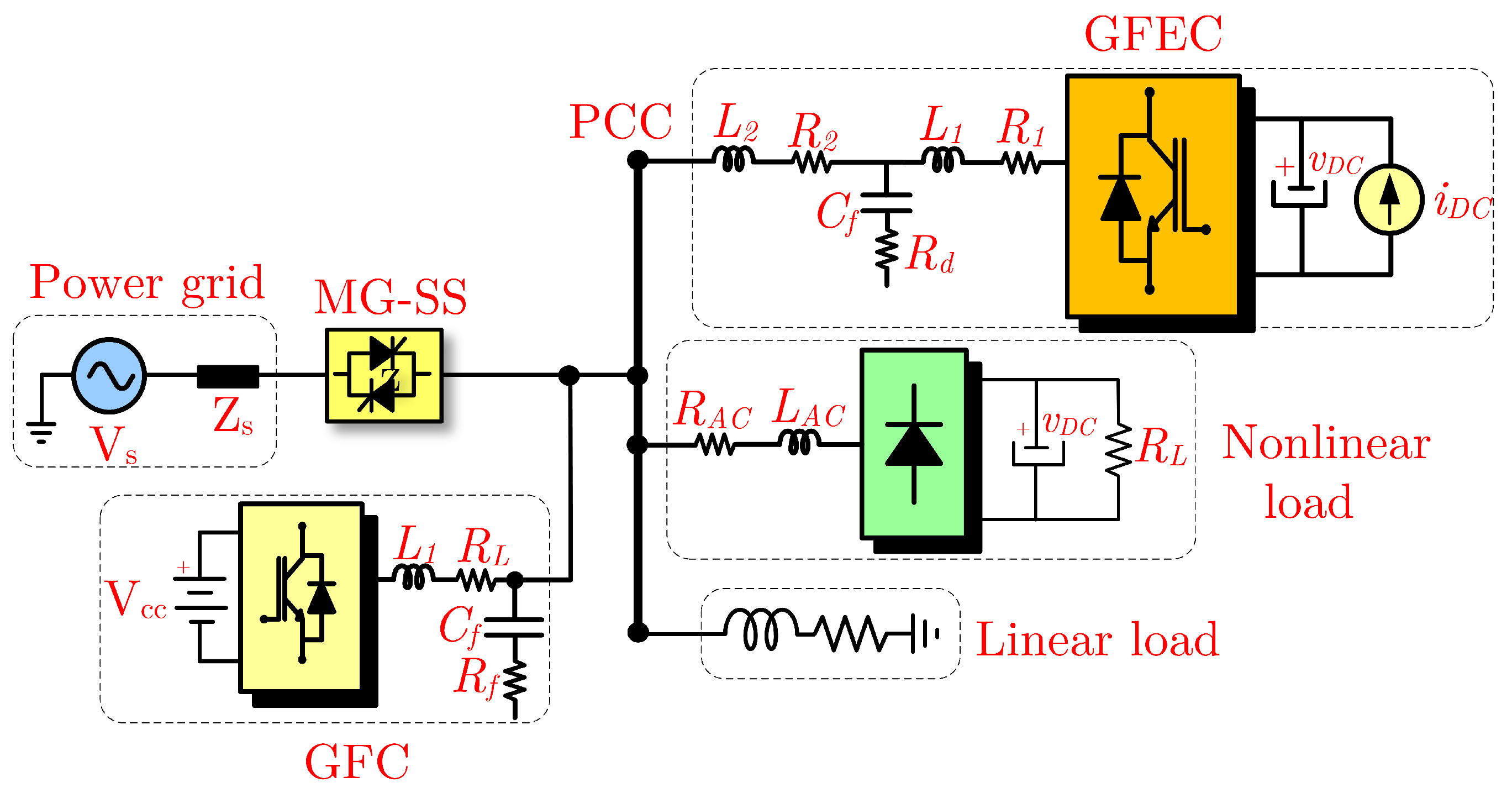
4. Microgrid Architecture Under Analysis
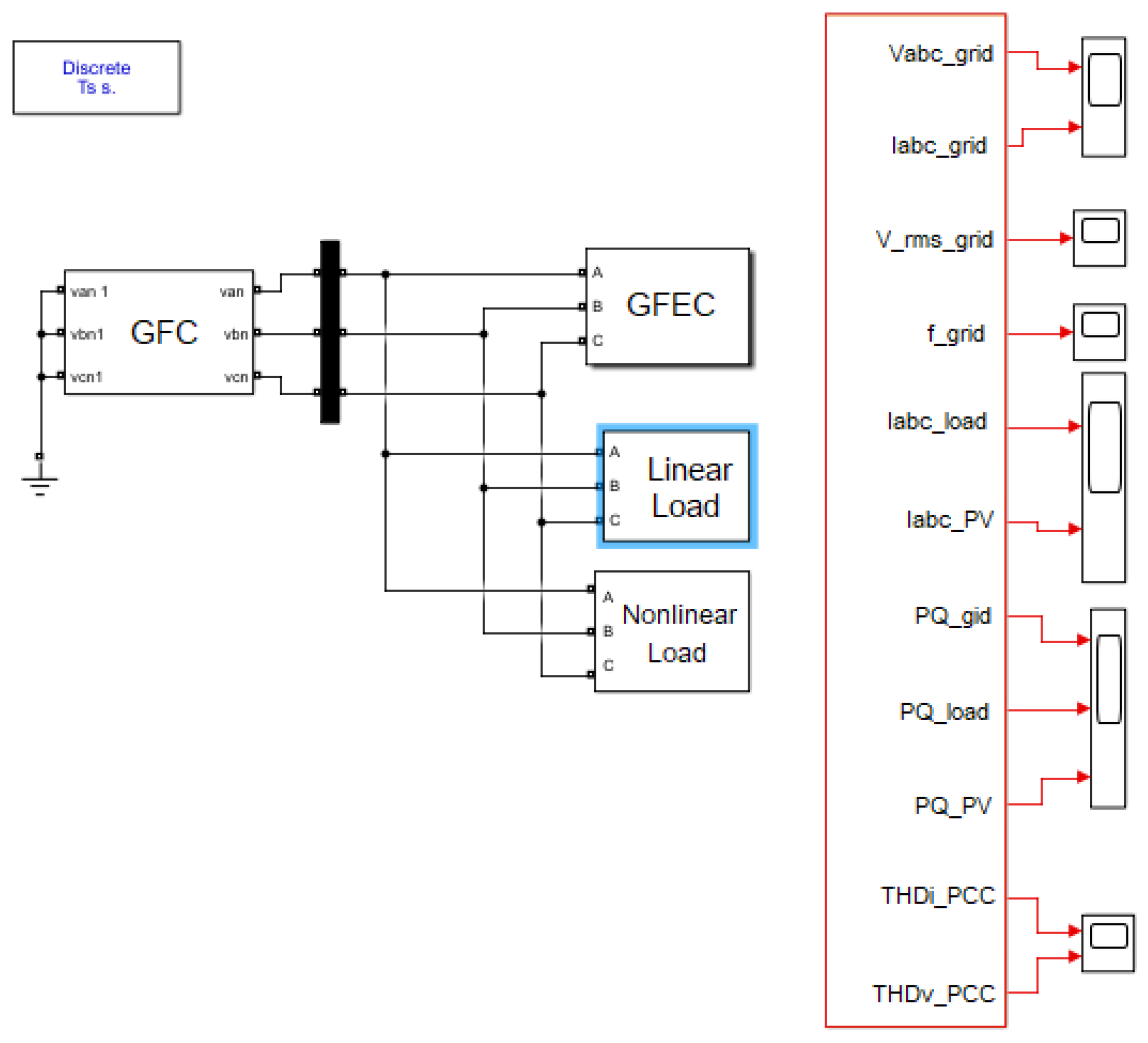
5. Simulation Results of the Microgrid
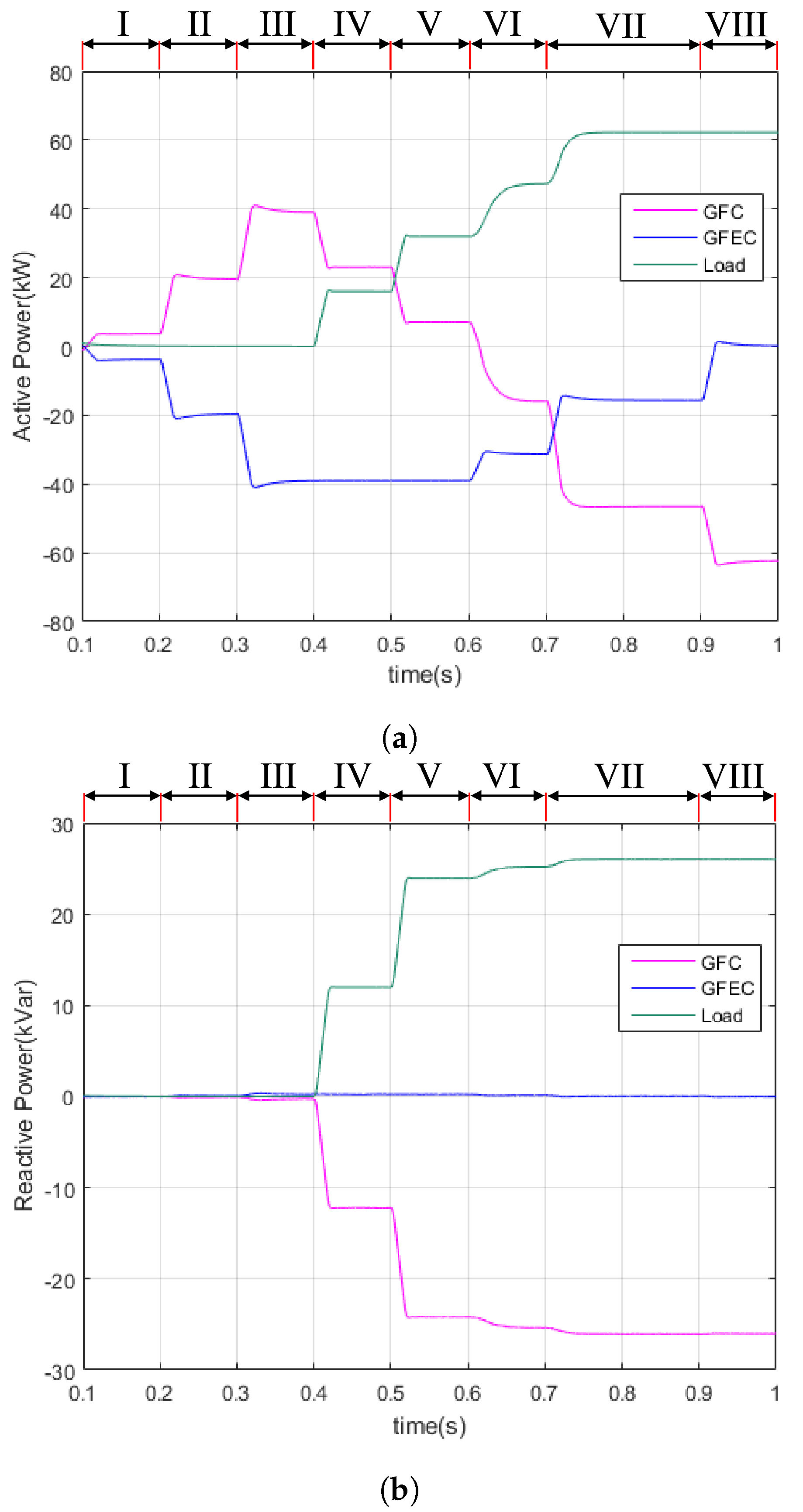
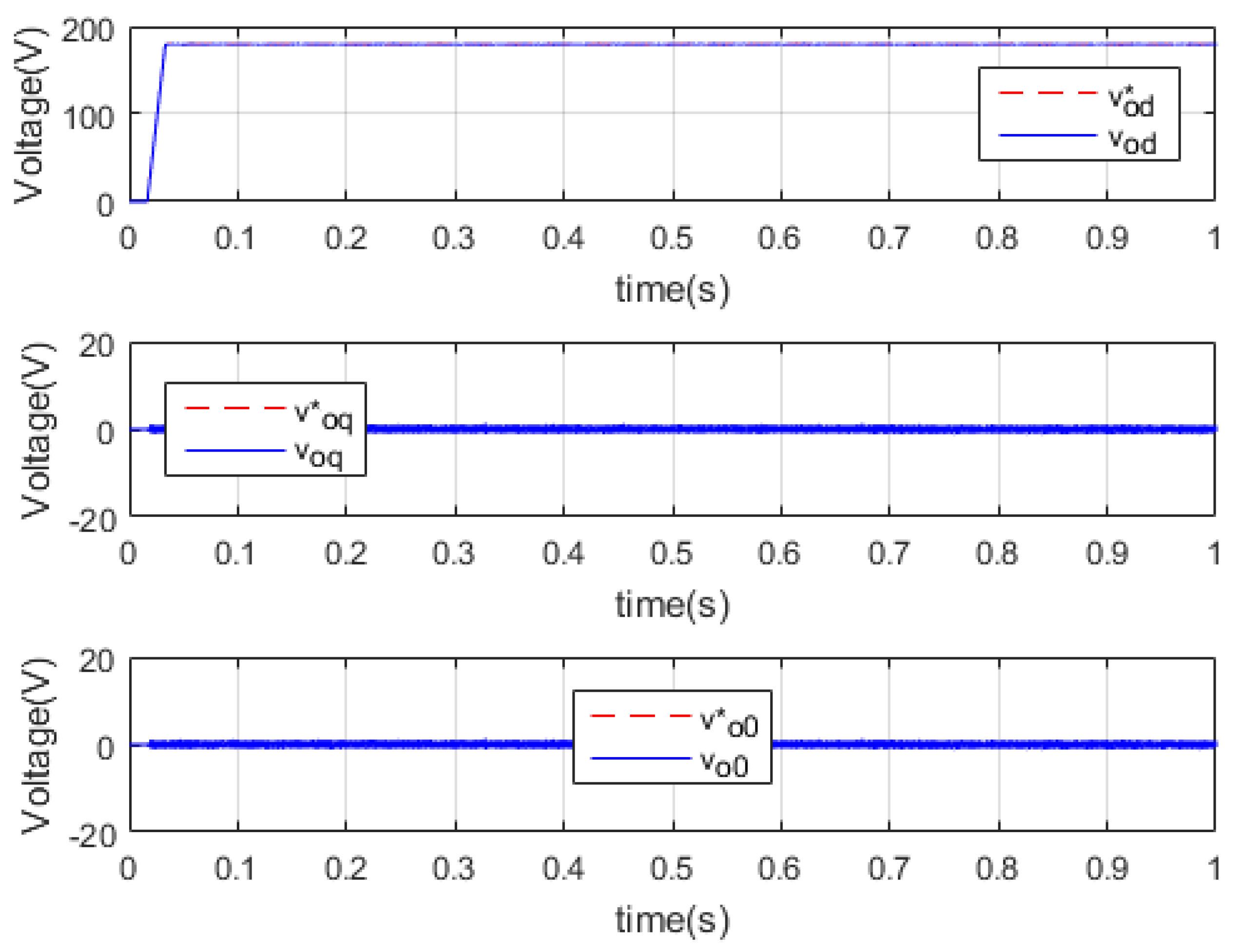
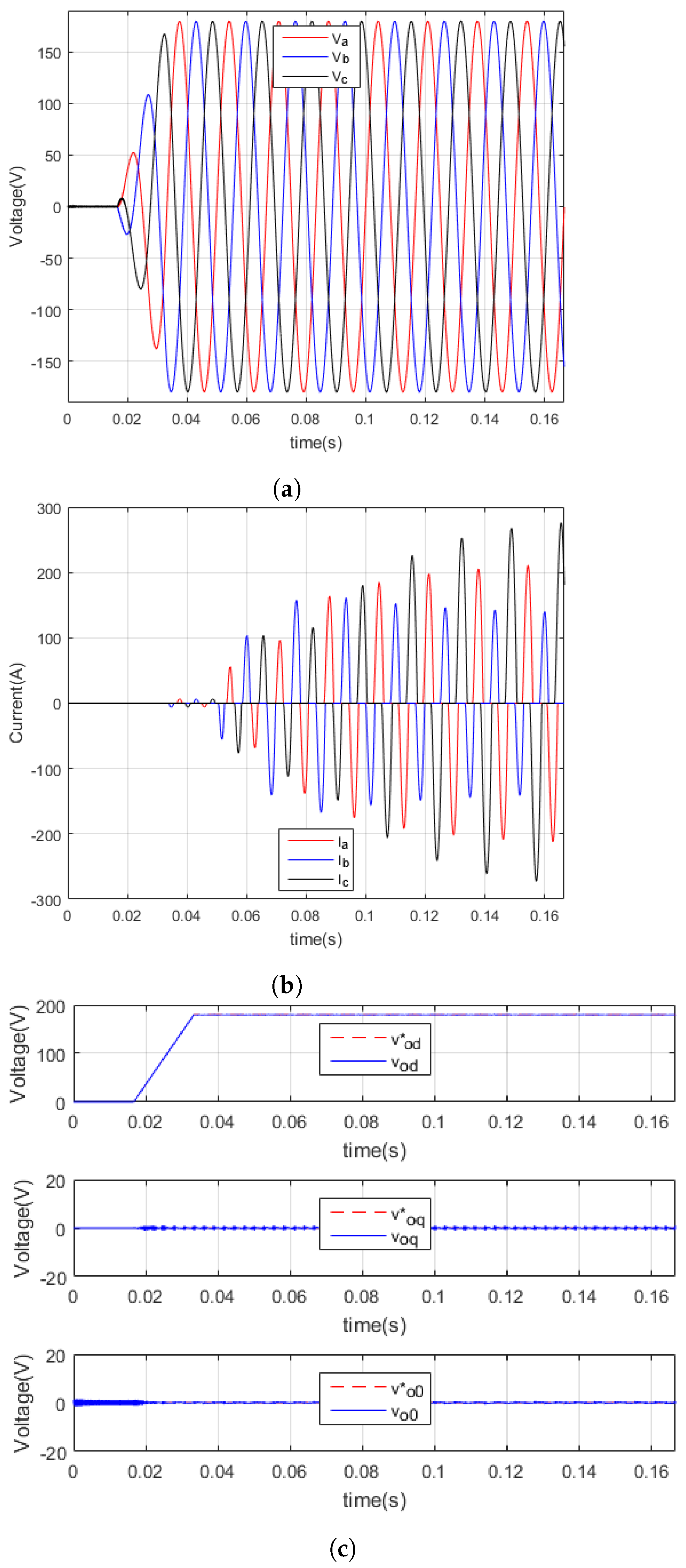
5.1. Scenario I
- t = 0 s—PCC is energized by the GFC;
- t = 0.1 s (I)—DC current in GFEC is adjusted to 8 A;
- t = 0.2 s (II)—DC current in GFEC is adjusted to 40 A;
- t = 0.3 s (III)—DC current in GFEC is adjusted to 80 A;
- t = 0.4 s (IV)—RL load is connected with (16 + j12) kVA;
- t = 0.5 s (V)—RL load is connected with (32 + j24) kVA;
- t = 0.6 s (VI)—DC current in GFEC is adjusted to 64 A and R = 5.6 Ω is connected in DC side of nonlinear load;
- t = 0.7 s (VII)—DC current in GFEC is adjusted to 32 A and R = 2.8 Ω is connected in DC side of nonlinear load;
- t = 0.9 s (VIII)—GFEC is turned off;
- t = 1 s—end of simulation.
5.2. Scenario II
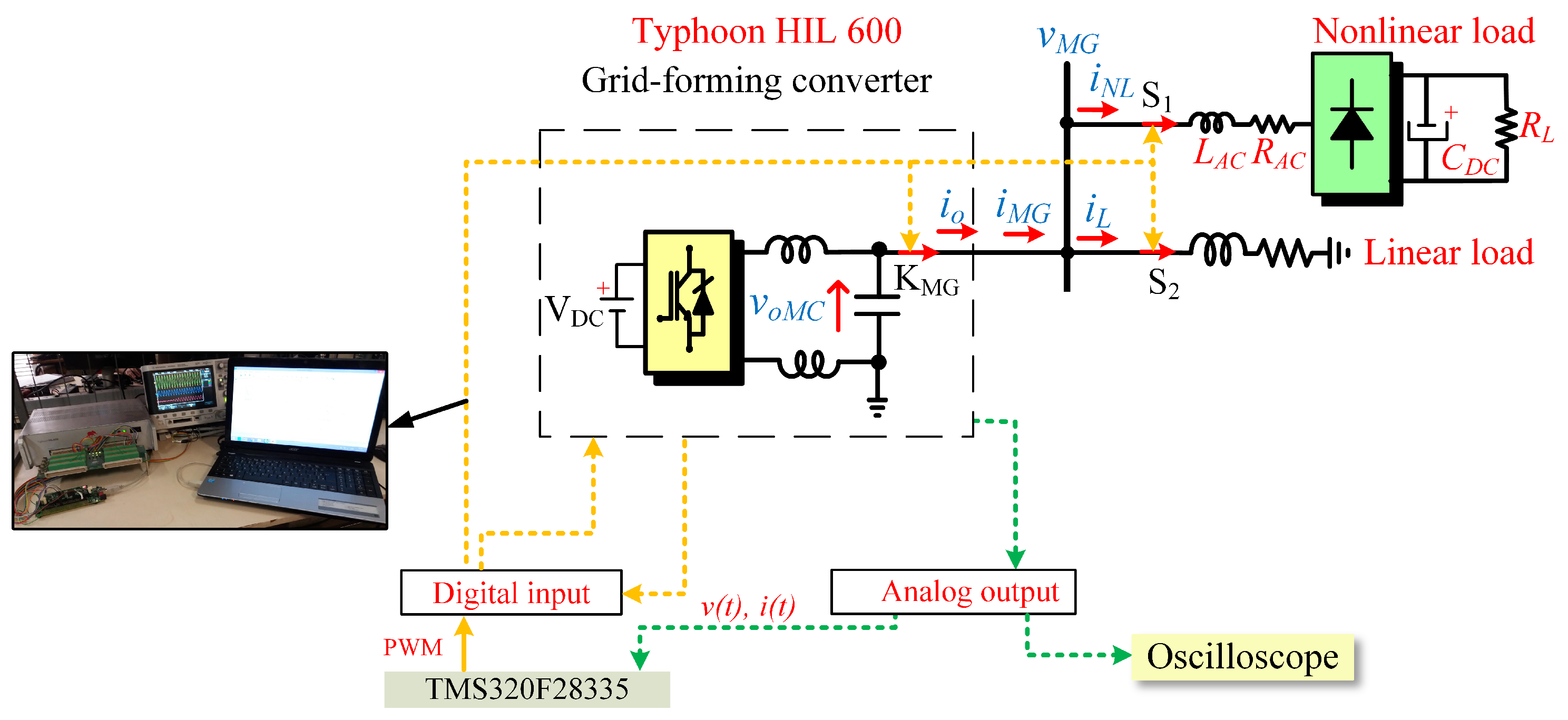
6. Hardware-in-the-Loop Results
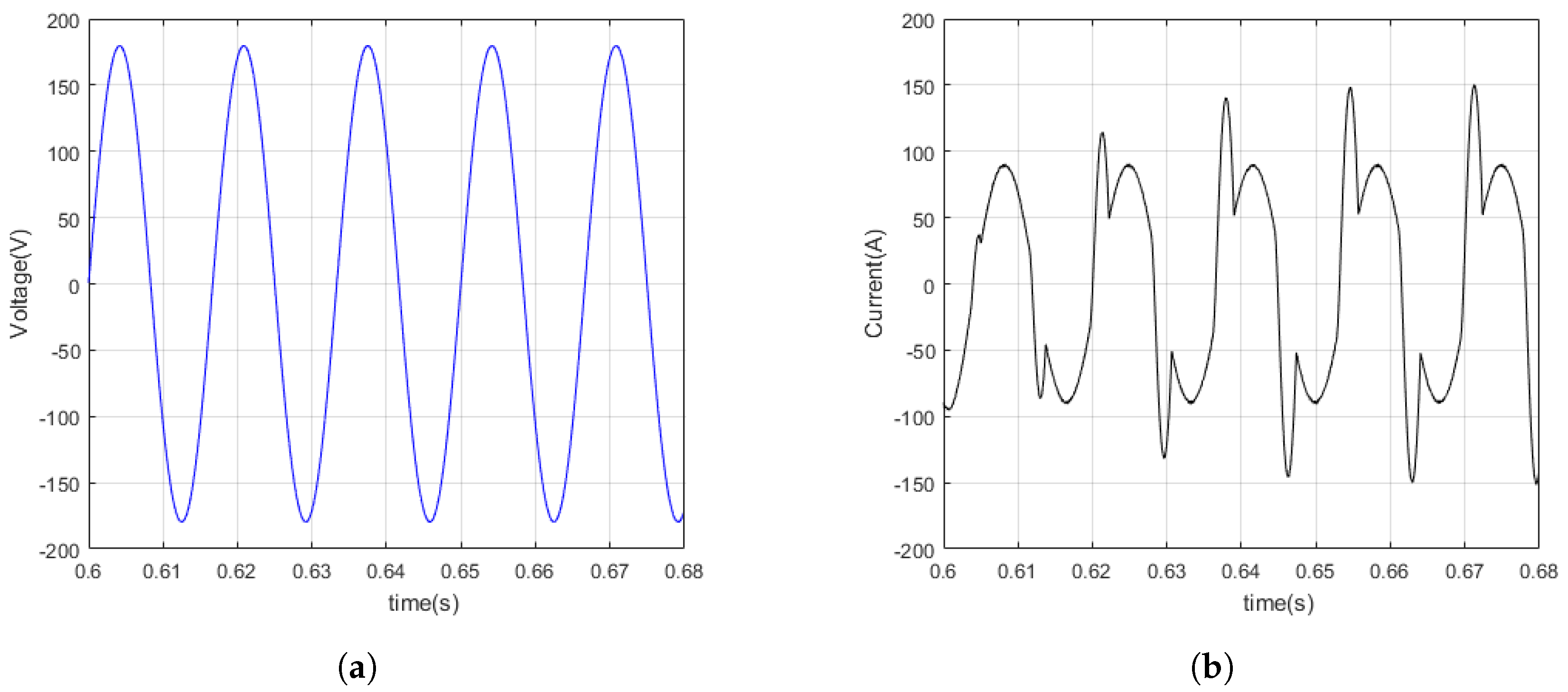
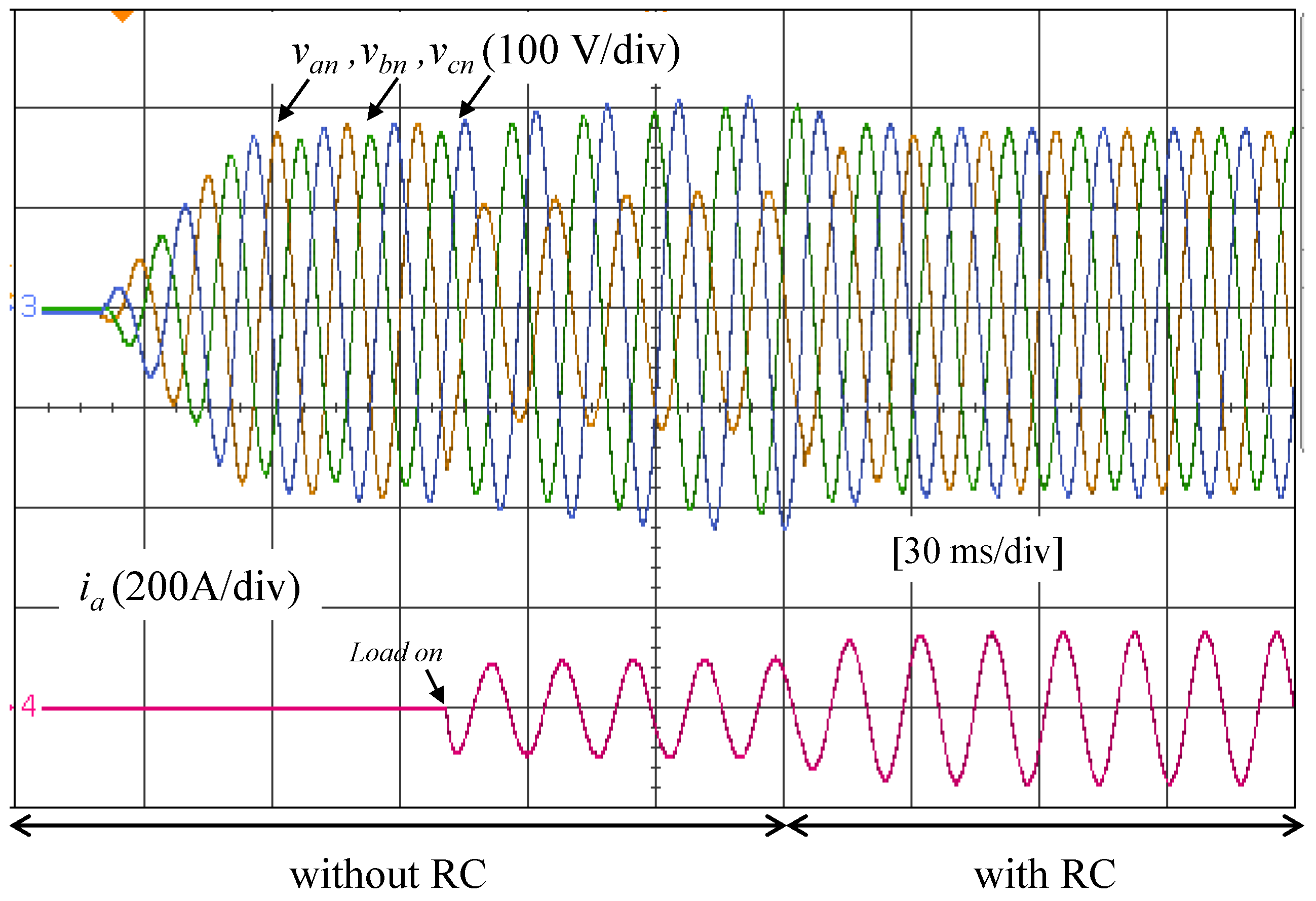
6.1. Scenario III—Single-Phase Linear Load
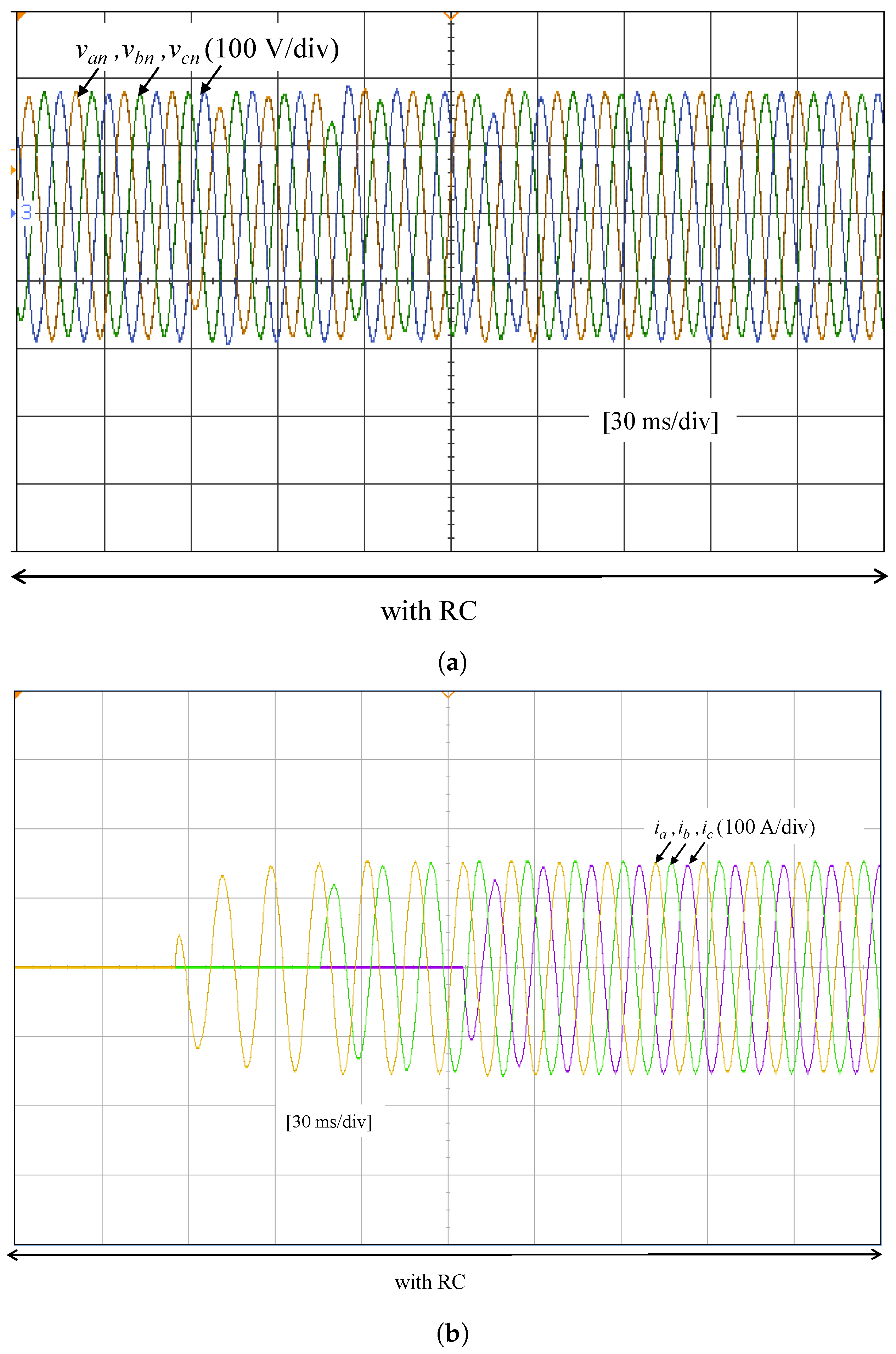
6.2. Scenario IV—Transition Between the Connection of Unbalanced to Balanced Linear Load
- 0–50 ms: Both cases show balanced RMS voltages close to nominal values. However, voltage THD is slightly lower with RC: 0.69% in (with RC) versus 2.44% (without RC).
- 50–100 ms: This period exhibits major differences. Without RC, there is a strong voltage imbalance with V and V, while with RC, voltages remain balanced around 127 V. Voltage THD is significantly reduced from 2.11% to 0.76% in , and current increases from 67.17 A to 106.1 A, reflecting improved power delivery.
- 100–150 ms: Without RC, there is severe imbalance and overvoltage in V, with dropping to 94.77 V. With RC, voltages are nearly nominal and balanced. The THD in improves from 1.99% to 0.68%, and increases from 77.46 A to 107 A, confirming better system behavior with RC.
- 150–300 ms: This steady-state period also benefits from RC. Voltage THD is reduced from 1.31% to 0.50% in , and all three-phase currents show a slight increase: from 103.2 A to 106.4 A, from 101 A to 107.4 A, and from 103.1 A to 106.4 A, indicating enhanced load supply capability.
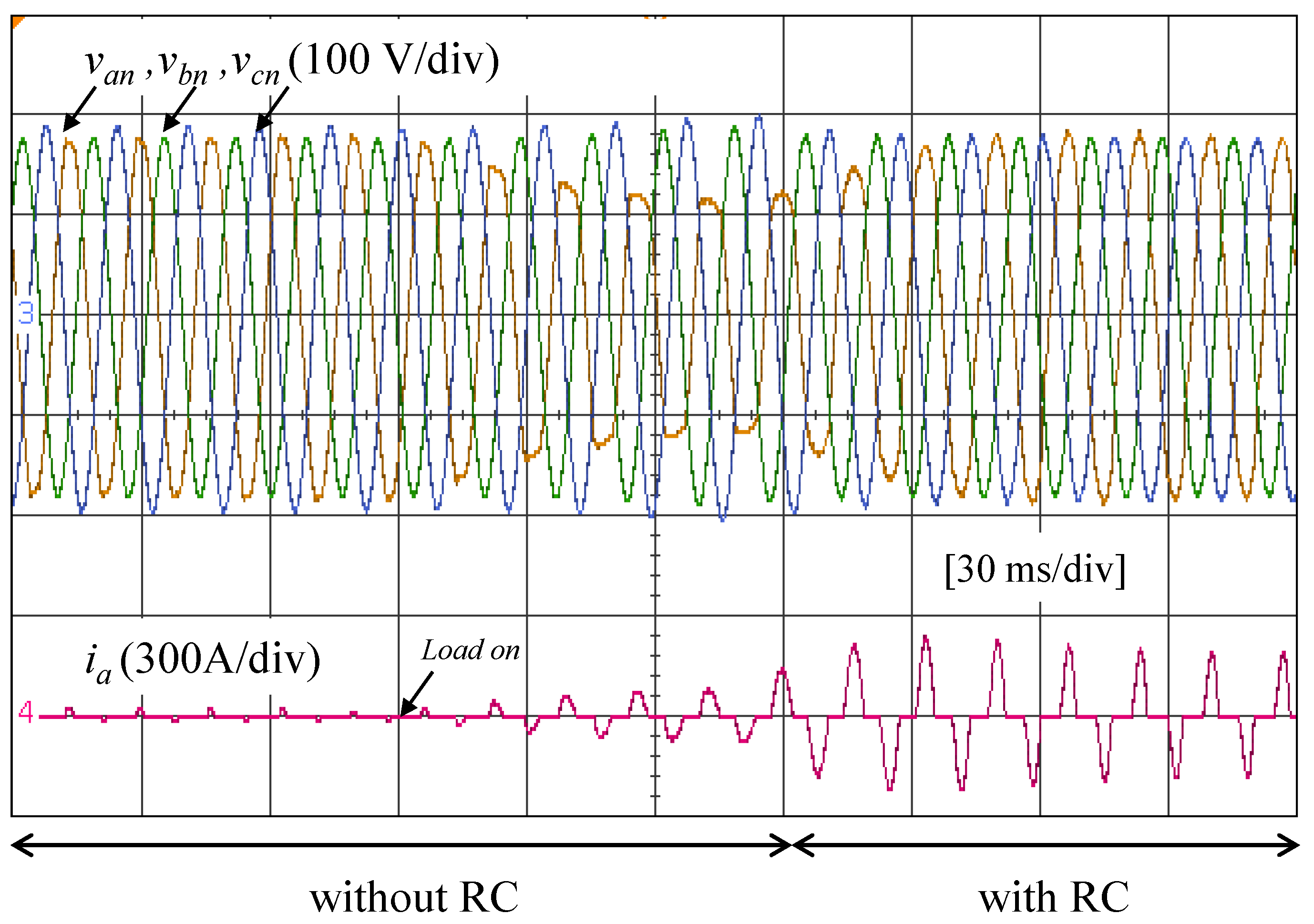
6.3. Scenario V—Single-Phase Nonlinear Load
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hatziargyriou, N.; Asano, H.; Iravani, R.; Marnay, C. Microgrids. IEEE Power Energy Mag. 2007, 5, 78–94. [Google Scholar] [CrossRef]
- Medina, P.; Bizuayehu, A.W.; Catalão, J.P.; Rodrigues, E.M.; Contreras, J. Electrical energy storage systems: Technologies’ state-of-the-art, techno-economic benefits and applications analysis. In Proceedings of the 2014 47th Hawaii International Conference on System Sciences, Waikoloa, HI, USA, 6–9 January 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2295–2304. [Google Scholar]
- Cheng, Q.; Zhang, Z.; Wang, Y.; Zhang, L. A Review of Distributed Energy Systems: Technologies, Classification, and Applications. Sustainability 2025, 17, 1346. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Ansari, S.; Chandel, A.; Tariq, M. A Comprehensive Review on Power Converters Control and Control Strategies of AC/DC Microgrid. IEEE Access 2021, 9, 17998–18015. [Google Scholar] [CrossRef]
- Xu, L.; Miao, Z.; Fan, L. Coordinated control of a solar and battery system in a microgrid. In Proceedings of the PES T&D 2012, Orlando, FL, USA, 7–10 May 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–7. [Google Scholar]
- Lopes, J.P.; Moreira, C.L.; Madureira, A. Defining control strategies for microgrids islanded operation. IEEE Trans. Power Syst. 2006, 21, 916–924. [Google Scholar] [CrossRef]
- Azevedo, G.M.; Cavalcanti, M.C.; Neves, F.A.; Limongi, L.R.; Bradaschia, F. A control of microgrid power converter with smooth transient response during the change of connection mode. In Proceedings of the 2013 Brazilian Power Electronics Conference, Gramado, Brazil, 27–31 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1008–1015. [Google Scholar]
- Salem, Q.; Aljarrah, R.; Karimi, M.; Al-Quraan, A. Grid-Forming Inverter Control for Power Sharing in Microgrids Based on P/f and Q/V Droop Characteristics. Sustainability 2023, 15, 11712. [Google Scholar] [CrossRef]
- Arghir, C.; Jouini, T.; Dörfler, F. Grid-forming control for power converters based on matching of synchronous machines. Automatica 2018, 95, 273–282. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, Y.; Chen, S.; Lan, T. A Fast Repetitive Control Strategy for a Power Conversion System. Electronics 2024, 13, 1186. [Google Scholar] [CrossRef]
- Arjomandi-Nezhad, A.; Guo, Y.; Pal, B.C.; Varagnolo, D. A Model Predictive Approach for Enhancing Transient Stability of Grid-Forming Converters. arXiv 2023, arXiv:2308.01020. [Google Scholar] [CrossRef]
- Häberle, V.; He, X.; Huang, L.; Dörfler, F.; Low, S. Quantitative Decentralized Stability Certificates for Grid-Forming Converter Control. arXiv 2025, arXiv:2503.05403. [Google Scholar] [CrossRef]
- Ngamroo, I.; Surinkaew, T.; Mitani, Y. Intelligence-Driven Grid-Forming Converter Control for Islanding Microgrids. J. Mod. Power Syst. Clean Energy 2025. [Google Scholar] [CrossRef]
- Ribeiro, R.L.d.A.; Oshnoei, A.; Anvari-Moghaddam, A.; Blaabjerg, F. Adaptive Grid Impedance Shaping Approach Applied for Grid-Forming Power Converters. IEEE Access 2022, 10, 83096–83110. [Google Scholar] [CrossRef]
- Wang, C.; Li, X.; Guo, L.; Li, Y. A seamless operation mode transition control strategy for a microgrid based on master-slave control. Sci. China Technol. Sci. 2012, 55, 1644–1654. [Google Scholar] [CrossRef]
- de Araújo, L.S.; Narvaez, D.I.; Villalva, M.G.; de Siqueira, T. Controle Droop para Conversor de Suporte Conectado a Bateria em Microrrede Monofásica de Baixa Tensão. In Proceedings of the VI Simpósio Brasileiro de Sistemas Elétricos, Natal, RN, Brazil, 22–25 May 2016. [Google Scholar]
- Oliveira, A.F.B.O.; Silva, S.M.; Santos, C.H.; Cardoso Filho, B.d.J. Aplicação do controle repetitivo a inversor PWM monofásico com filtro LC de saída utilizado em fonte programável CA. Eletrônica Potência 2013, 18, 1161–1169. [Google Scholar] [CrossRef]
- Michels, L.; Gründling, H.A. Procedimentos de Projeto de Controladores Repetitivos para o Estágio de Saída de Fontes Ininterruptas de Energia. Eletrônica Potência 2005, 10, 39–50. [Google Scholar] [CrossRef]
- Wang, J.; Chang, N.C.P.; Feng, X.; Monti, A. Design of a generalized control algorithm for parallel inverters for smooth microgrid transition operation. IEEE Trans. Ind. Electron. 2015, 62, 4900–4914. [Google Scholar] [CrossRef]
- Kim, T.; Barry, N.G.; Kim, W.; Santoso, S.; Wang, W.; Dugan, R.C.; Ramasubramanian, D. Voltage Balancing Capability of Grid-Forming Inverters. IEEE Open Access J. Power Energy 2022, 9, 479–488. [Google Scholar] [CrossRef]
- de Matos, J.G.; de Souza Ribeiro, L.A.; de Carvalho Gomes, E. Power control in isolated Microgrids with renewable distributed energy sources and battey banks. In Proceedings of the 2013 International Conference on Renewable Energy Research and Applications (ICRERA), Madrid, Spain, 20–23 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 258–263. [Google Scholar]
- Ravanji, M.H.; Rathnayake, D.B.; Mansour, M.Z.; Bahrani, B. Impact of Voltage-Loop Feedforward Terms on the Stability of Grid-Forming Inverters and Remedial Actions. IEEE Trans. Energy Convers. 2023, 38, 1554–1565. [Google Scholar] [CrossRef]
- Cho, Y.; Byen, B.J.; Lee, H.S.; Cho, K.Y. A Single-Loop Repetitive Voltage Controller with an Active Damping Control Technique. Energies 2017, 10, 673. [Google Scholar] [CrossRef]
- Du, Y.; Wang, X.; Zhang, H.; Wen, J. Challenges and potential solutions of grid-forming converters in renewable energy dominated power systems. Front. Energy Res. 2020, 8, 1040781. [Google Scholar] [CrossRef]
- Miveh, M.R.; Rahmat, M.F.; Ghadimi, A.A.; Mustafa, M.W. Power quality improvement in autonomous microgrids using multi-functional voltage source inverters: A comprehensive review. J. Power Electron. 2015, 15, 1054–1065. [Google Scholar] [CrossRef]
- e Silva, F.S.; Ribeiro, L.A.d.S.; de Matos, J.G. Bidirectional DC-AC converter for isolated microgrids with voltage unbalance reduction capabilities. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 4985–4991. [Google Scholar]
- Gkountaras, A.; Dieckerhoff, S.; Sezi, T. Evaluation of current limiting methods for grid forming inverters in medium voltage microgrids. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1223–1230. [Google Scholar]
- Li, X.; Chen, Z.; Kumar, A. Adaptive Grid-Forming Control for Microgrids Under Uncertain Conditions. IEEE Access 2023, 11, 12345–12356. [Google Scholar]
- Liu, Q.; Tao, Y.; Liu, X.; Deng, Y.; He, X. Voltage unbalance and harmonics compensation for islanded microgrid inverters. IET Power Electron. 2014, 7, 1055–1063. [Google Scholar] [CrossRef]
- Ryan, M.J.; Lorenz, R.D. A high performance sine wave inverter controller with capacitor current feedback and “back-emf” decoupling. In Proceedings of the PESC’95-Power Electronics Specialist Conference, Atlanta, GA, USA, 18–22 June 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 1, pp. 507–513. [Google Scholar]
- Natesan, C.; Ajithan, S.K.; Palani, P.; Kandhasamy, P. Survey on microgrid: Power quality improvement techniques. Int. Sch. Res. Not. 2014, 2014, 342019. [Google Scholar] [CrossRef]
- Tang, M.; Caspar, M.; Sonn, G. Application of New Structure Frequency Adaptive Selective Harmonics Repetition Control for Grid-Connected Converter. Energy Convers. Manag. 2021, 251, 114996. [Google Scholar]
- Ufnalski, B.; Straś, A.; Grzesiak, L. High Quality Repetitive Control System for a Grid-Tied Converter under Distorted Grid Voltage Conditions—Design and Implementation. Bull. Pol. Acad. Sci. Tech. Sci. 2021, 69, e136739. [Google Scholar] [CrossRef]
- Straś, A.; Ufnalski, B.; Kaszewski, A. Design of a Repetitive Control for a Three-Phase Grid-Tied Converter under Distorted Grid Voltage Conditions. Energies 2023, 16, 754. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, D. Digital repetitive learning controller for three-phase CVCF PWM inverter. IEEE Trans. Ind. Electron. 2001, 48, 820–830. [Google Scholar] [CrossRef]
- Antunes, H.M.; Silva, S.M.; Brandao, D.I.; Ferreira, R.V.; Braz de Jesus Filho, C. Analysis of a grid-forming converter based on repetitive control in centralized AC microgrid. In Proceedings of the 2017 IEEE 8th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Florianopolis, Brazil, 17–20 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar]
- Francis, B.A.; Wonham, W.M. The internal model principle for linear multivariable regulators. Appl. Math. Optim. 1975, 2, 170–194. [Google Scholar] [CrossRef]
- Cuiyan, L.; Dongchun, Z.; Xianyi, Z. Theory and applications of the repetitive control. In Proceedings of the SICE 2004 Annual Conference, Sapporo, Japan, 4–6 August 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 1, pp. 27–34. [Google Scholar]
- Liang, F.; Lee, H.J.; Zhao, Q. A Novel Fractional Delay Proportional–Integral Multi-Resonant-Type Repetitive Control Based on a Farrow-Structure Filter for Grid-Tied Inverters. Electronics 2023, 12, 4010. [Google Scholar] [CrossRef]
- Shahgholian, G.; Moradian, M.; Fathollahi, A. Droop control strategy in inverter-based microgrids: A brief review on analysis and application in islanded mode of operation. IET Renew. Power Gener. 2025, 19, e13186. [Google Scholar] [CrossRef]
- Zou, Z.; Zhou, K.; Wang, Z.; Cheng, M. Fractional-order repetitive control of programmable AC power sources. IET Power Electron. 2014, 7, 431–438. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, J.; Qian, Z. An improved repetitive control scheme for grid-connected inverter with frequency-adaptive capability. IEEE Trans. Ind. Electron. 2012, 60, 814–823. [Google Scholar] [CrossRef]
- Lu, W.; Zhou, X.; Hu, L.; Fang, W. Generic selective harmonic repetitive control strategy for grid-connected converters. Energy Rep. 2025, 13, 5064–5076. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Silva, S.; Filho, B. Component-minimized voltage sag compensators. In Proceedings of the Conference Record of the 2002 IEEE Industry Applications Conference. 37th IAS Annual Meeting (Cat. No.02CH37344), Pittsburgh, PA, USA, 13–18 October 2002; Volume 2, pp. 883–889. [Google Scholar] [CrossRef]
- Ryan, M.J.; Brumsickle, W.E.; Lorenz, R.D. Control topology options for single-phase UPS inverters. IEEE Trans. Ind. Appl. 1997, 33, 493–501. [Google Scholar] [CrossRef]
- Buso, S.; Mattavelli, P. Digital Control in Power Electronics; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Rahman, S.A.; Varma, R.K. PSCAD/EMTDC model of a 3-phase grid connected photovoltaic solar system. In Proceedings of the 2011 North American Power Symposium, Boston, MA, USA, 4–6 August 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–7. [Google Scholar]
- Reznik, A.; Simões, M.G.; Al-Durra, A.; Muyeen, S. LCL filter design and performance analysis for small wind turbine systems. In Proceedings of the 2012 IEEE Power Electronics and Machines in Wind Applications, Denver, CO, USA, 16–18 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–7. [Google Scholar]
- Vechiu, I.; Curea, O.; Llaria, A.; Camblong, H. Control of power converters for microgrids. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2011, 30, 300–309. [Google Scholar] [CrossRef]
- Cupertino, A.; De Resende, J.; Pereira, H.; Júnior, S.S. A grid-connected photovoltaic system with a maximum power point tracker using passivity-based control applied in a boost converter. In Proceedings of the 2012 10th IEEE/IAS International Conference on Industry Applications, Fortaleza, Brazil, 5–7 November 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–8. [Google Scholar]
- de Matos, J.G.; de Souza Ribeiro, L.A.; Freitas, F.S. Controle da potência gerada em microrredes autônomas e isoladas com fontes de energia renováveis e sistema de armazenamento com bancos de baterias. Eletrônica de Potência 2014, 19, 152–162. [Google Scholar] [CrossRef]
- Trintis, I.; Munk-Nielsen, S.; Teodorescu, R. Single stage grid converters for battery energy storage. In Proceedings of the 5th IET International Conference on Power Electronics, Machines and Drives (PEMD 2010), Brighton, UK, 19–21 April 2010; IET: Stevenage, UK, 2010; p. MO234. [Google Scholar]
- Kelm, P.; Wasiak, I.; Mieński, R.; Wędzik, A.; Szypowski, M.; Pawełek, R.; Szaniawski, K. Hardware-in-the-loop validation of an energy management system for LV distribution networks with renewable energy sources. Energies 2022, 15, 2561. [Google Scholar] [CrossRef]
- Araujo, L.S.; Brandao, D.I. Self-adaptive control for grid-forming converter with smooth transition between microgrid operating modes. Int. J. Electr. Power Energy Syst. 2022, 135, 107479. [Google Scholar] [CrossRef]
- Wang, J.; Pratt, A.; Prabakar, K.; Miller, B.; Symko-Davies, M. Development of an integrated platform for hardware-in-the-loop evaluation of microgrids prior to site commissioning. Appl. Energy 2021, 290, 116755. [Google Scholar] [CrossRef]
- Elrajoubi, A.; Ang, S.S.; Abushaiba, A. TMS320F28335 DSP programming using MATLAB Simulink embedded coder: Techniques and advancements. In Proceedings of the 2017 IEEE 18th Workshop on Control and Modeling for Power Electronics (COMPEL), Stanford, CA, USA, 9–12 July 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Jiang, J.; Li, Y.; Yang, K.; Wang, S.; Wang, S. Stochastic Planning for Resilient Infrastructure of Distribution System Under Extreme Weather Events. IEEE Trans. Ind. Appl. 2024, 60, 2191–2200. [Google Scholar] [CrossRef]
- Xiao, D.; Chen, H. Stochastic Up to Congestion Bidding Strategy in the Nodal Electricity Markets Considering Risk Management. IEEE Access 2020, 8, 202428–202438. [Google Scholar] [CrossRef]

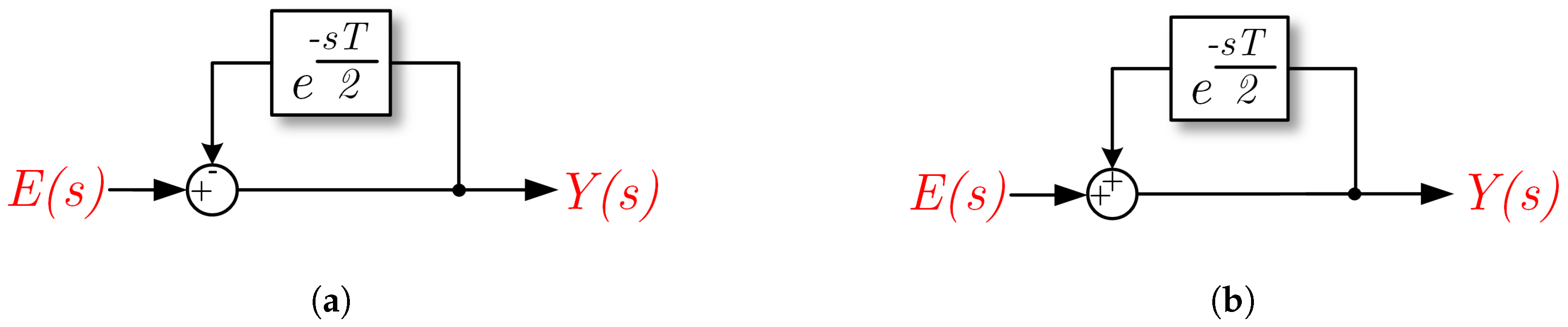







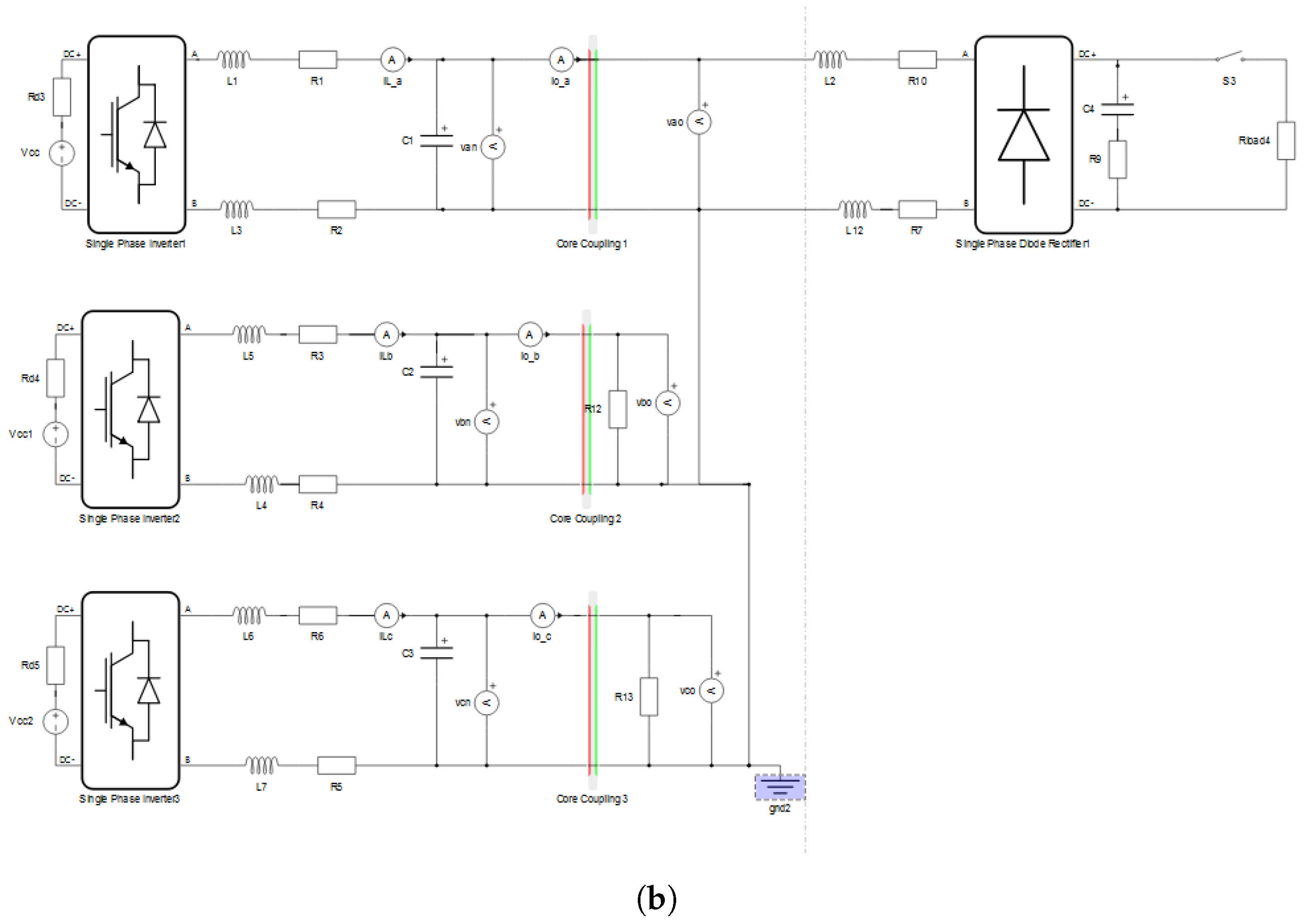

| System | Characteristics |
|---|---|
| GFC | 220 V, 60 Hz, 75 kVA, LC filter: , , , , kHz, |
| GFEC | 40 kVA, 220 V, kHz, LCL filter: , , , , , , , , |
| Linear load | 220 V, 40 kVA, (lagged) |
| Nonlinear load | 220 V, 30 kW, , , , |
| Loop | Gains |
|---|---|
| DC voltage | |
| Current |
| Loop | Gains |
|---|---|
| Voltage | , , |
| Current |
| Interval | RMS (V) | THD (%) | RMS (A) | ||||
|---|---|---|---|---|---|---|---|
| 0–60 ms | 129.0 | 121.9 | 130.3 | 2.53 | 1.76 | 1.88 | – |
| 60–180 ms | 82.33 | 138.4 | 147.7 | 2.15 | 1.09 | 0.80 | 67.9 |
| 180–300 ms | 128.3 | 126.8 | 130.2 | 0.59 | 0.67 | 0.69 | 106.3 |
| Interval | RMS (V) | THDv (%) | RMS (A) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0–50 ms | 129.2 | 122.1 | 130.9 | 2.44 | 1.69 | 1.57 | - | - | - |
| 50–100 ms | 82.44 | 138.5 | 148 | 2.11 | 0.94 | 0.79 | 67.17 | - | - |
| 100–150 ms | 94.77 | 90.68 | 167.5 | 1.99 | 1.73 | 1.86 | 77.46 | 76.3 | - |
| 150–300 ms | 124.7 | 118.1 | 125 | 1.31 | 1.23 | 1.27 | 103.2 | 101 | 103.1 |
| Interval | RMS (V) | THDv (%) | RMS (A) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0–50 ms | 129.4 | 126.7 | 129.2 | 0.69 | 0.77 | 0.79 | - | - | - |
| 50–100 ms | 127.1 | 127.1 | 130.1 | 0.76 | 0.70 | 0.77 | 106.1 | - | - |
| 100–150 ms | 129.3 | 124.7 | 130.5 | 0.68 | 1.53 | 0.70 | 107 | 105.3 | - |
| 150–300 ms | 129.1 | 126.4 | 129 | 0.50 | 0.54 | 0.57 | 106.4 | 107.4 | 106.4 |
| Interval | RMS (V) | THDv (%) | RMS (A) | THDi (%) | ||||
|---|---|---|---|---|---|---|---|---|
| 0–90 ms | 129.8 | 127 | 136 | 3.21 | 0.83 | 1.17 | 6.28 | 126.18 |
| 90–180 ms | 96.06 | 132.6 | 141.8 | 16.39 | 0.96 | 0.76 | 53.18 | 49.97 |
| 180–300 ms | 128.09 | 126.5 | 129.7 | 4.71 | 1.86 | 1.34 | 98.39 | 76.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Antunes, H.M.A.; Piero, R.R.D.; Silva, S.M. Application of Repetitive Control to Grid-Forming Converters in Centralized AC Microgrids. Energies 2025, 18, 3427. https://doi.org/10.3390/en18133427
Antunes HMA, Piero RRD, Silva SM. Application of Repetitive Control to Grid-Forming Converters in Centralized AC Microgrids. Energies. 2025; 18(13):3427. https://doi.org/10.3390/en18133427
Chicago/Turabian StyleAntunes, Hélio Marcos André, Ramon Ravani Del Piero, and Sidelmo Magalhães Silva. 2025. "Application of Repetitive Control to Grid-Forming Converters in Centralized AC Microgrids" Energies 18, no. 13: 3427. https://doi.org/10.3390/en18133427
APA StyleAntunes, H. M. A., Piero, R. R. D., & Silva, S. M. (2025). Application of Repetitive Control to Grid-Forming Converters in Centralized AC Microgrids. Energies, 18(13), 3427. https://doi.org/10.3390/en18133427







