Discrete-Time Impedance Model-Based Dynamic Analysis and Parameter Design for VSG-Controlled Grid-Forming DG System
Abstract
1. Introduction
- Based on a discrete-time power flow model, discrete-time active and reactive power controllers are designed to achieve the desired dynamic response in both the reactive power support and voltage support operating modes of the VSG strategy. The proposed design method can be used as a useful design guideline for the implementation of the VSG scheme in a digital environment.
- The behavior of the closed-loop poles and their sensitivity to VSG control gains are discussed, considering the effect of the system’s equivalent impedance variations and variations in the sampling time.
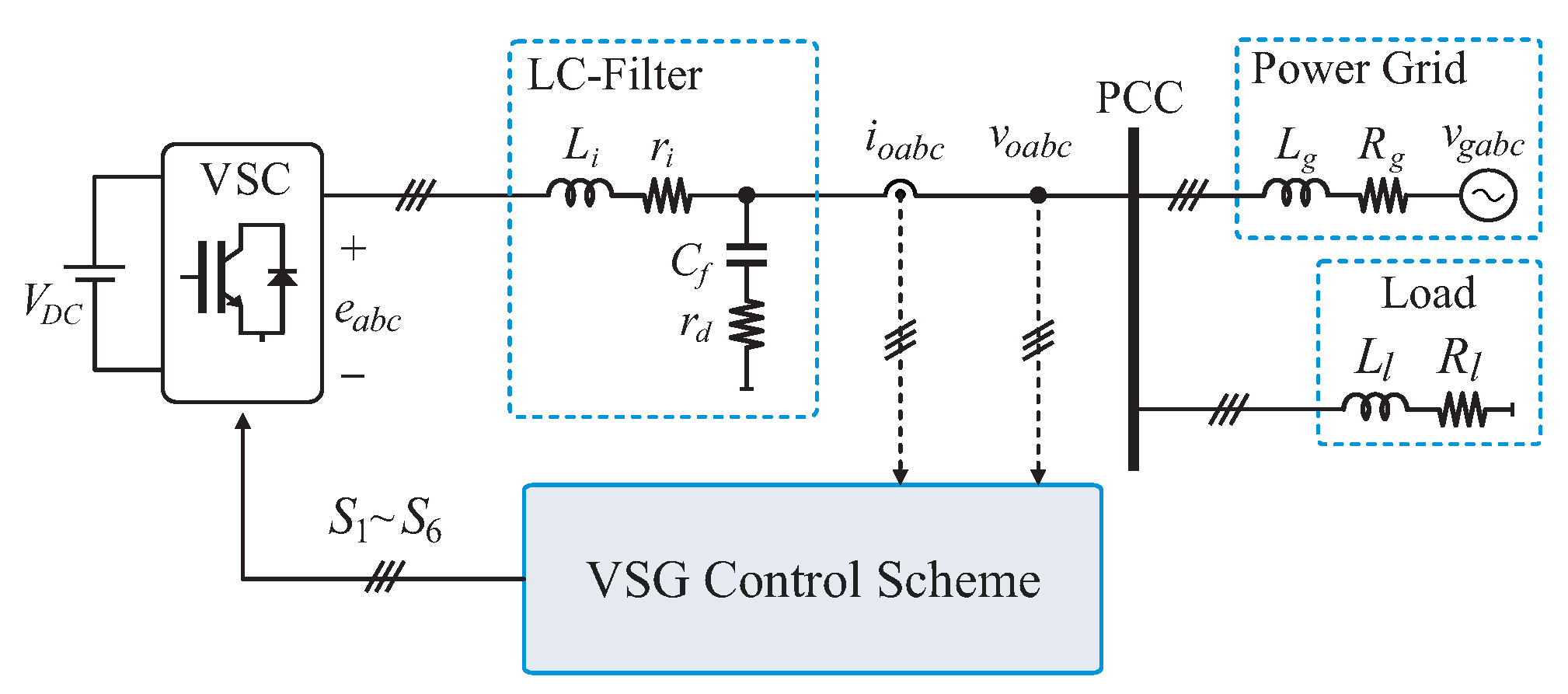
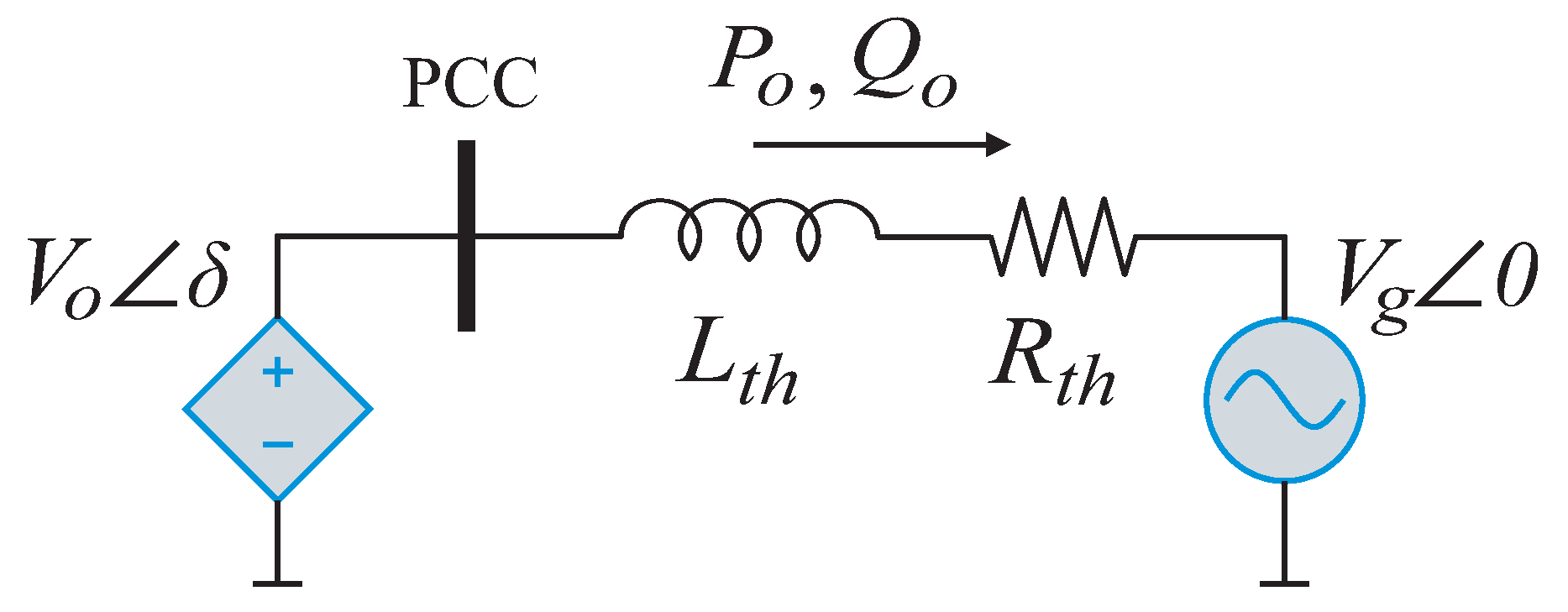
2. System’s Description and Modeling
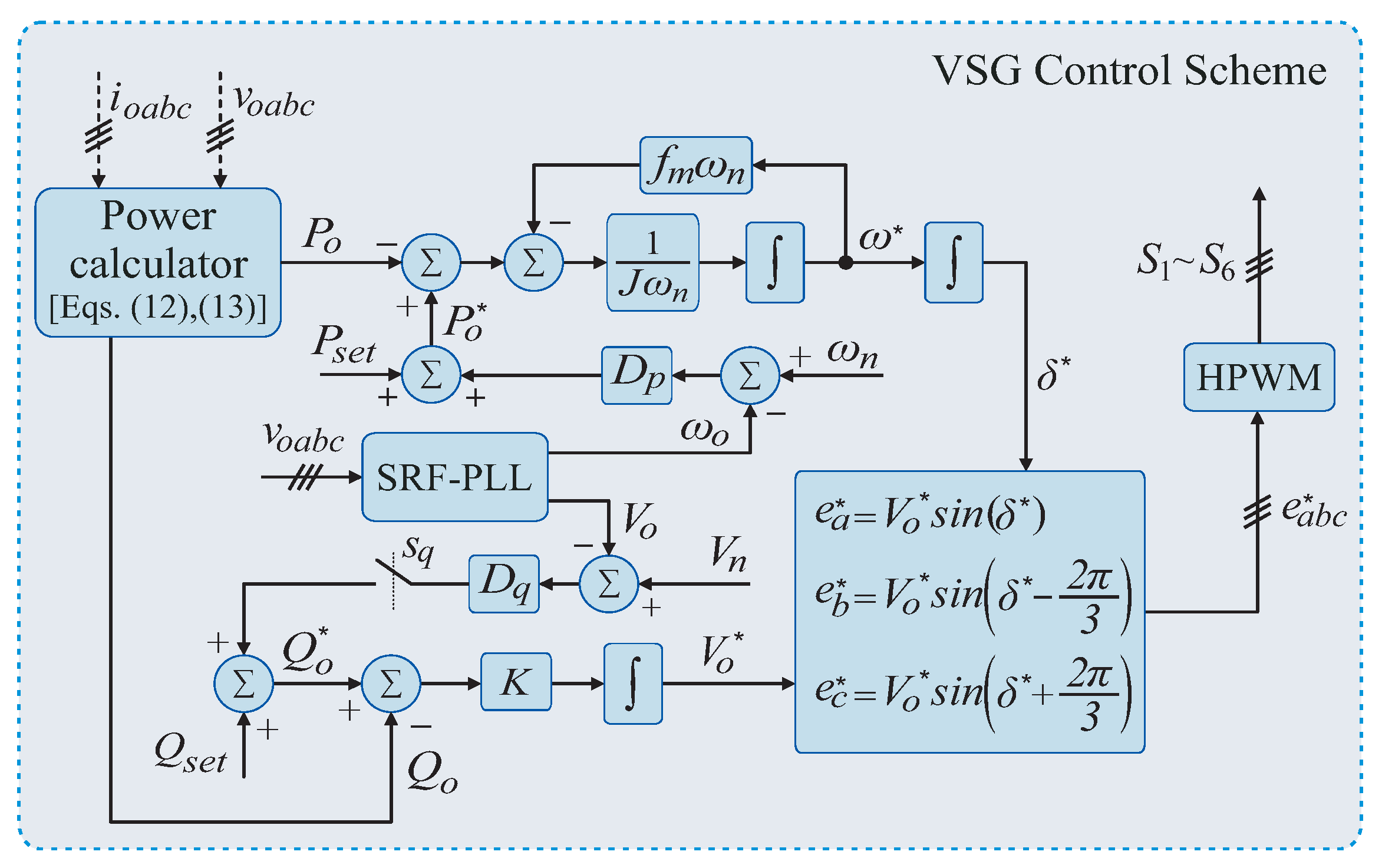
3. Discrete-Time VSG Control Scheme
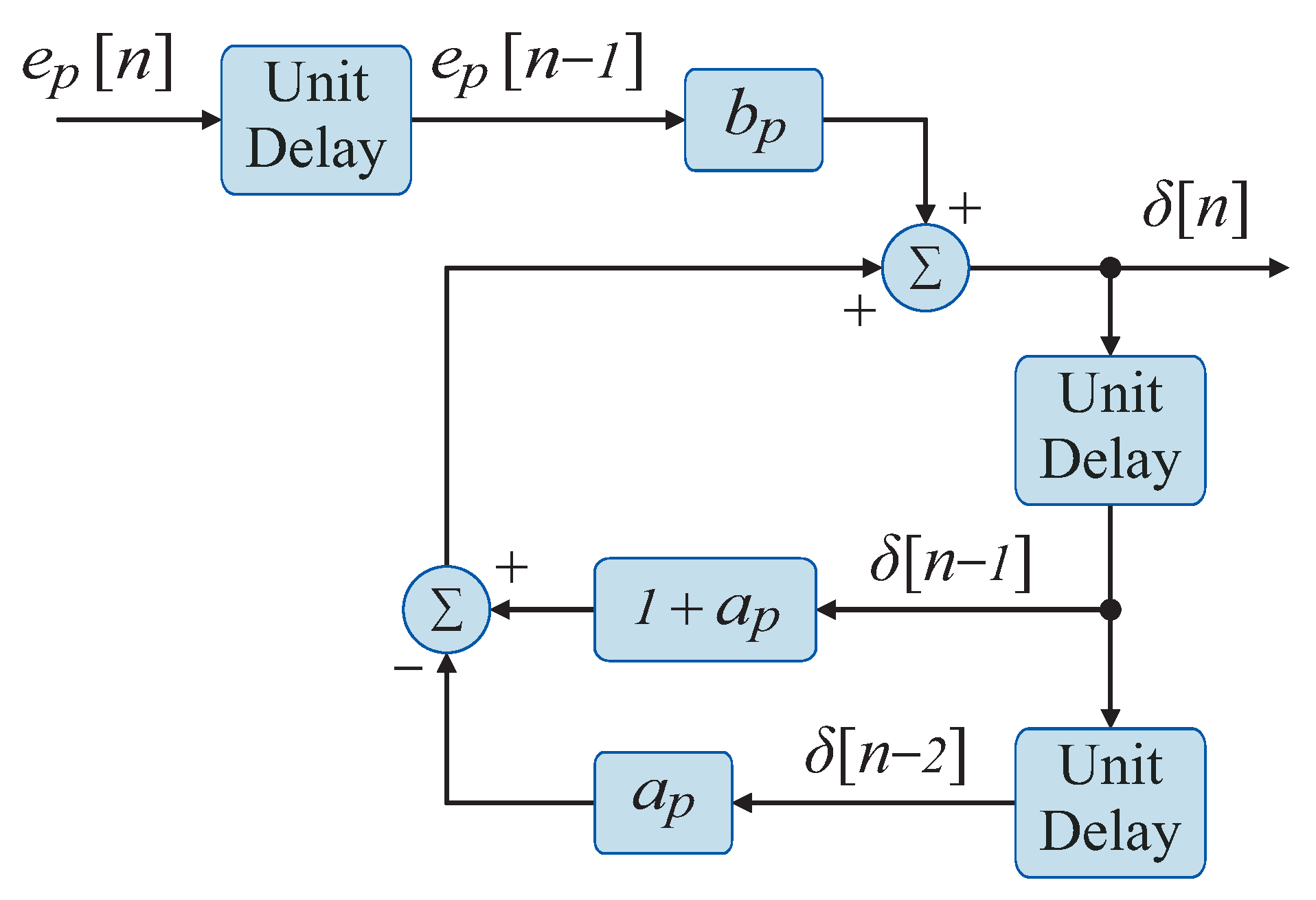
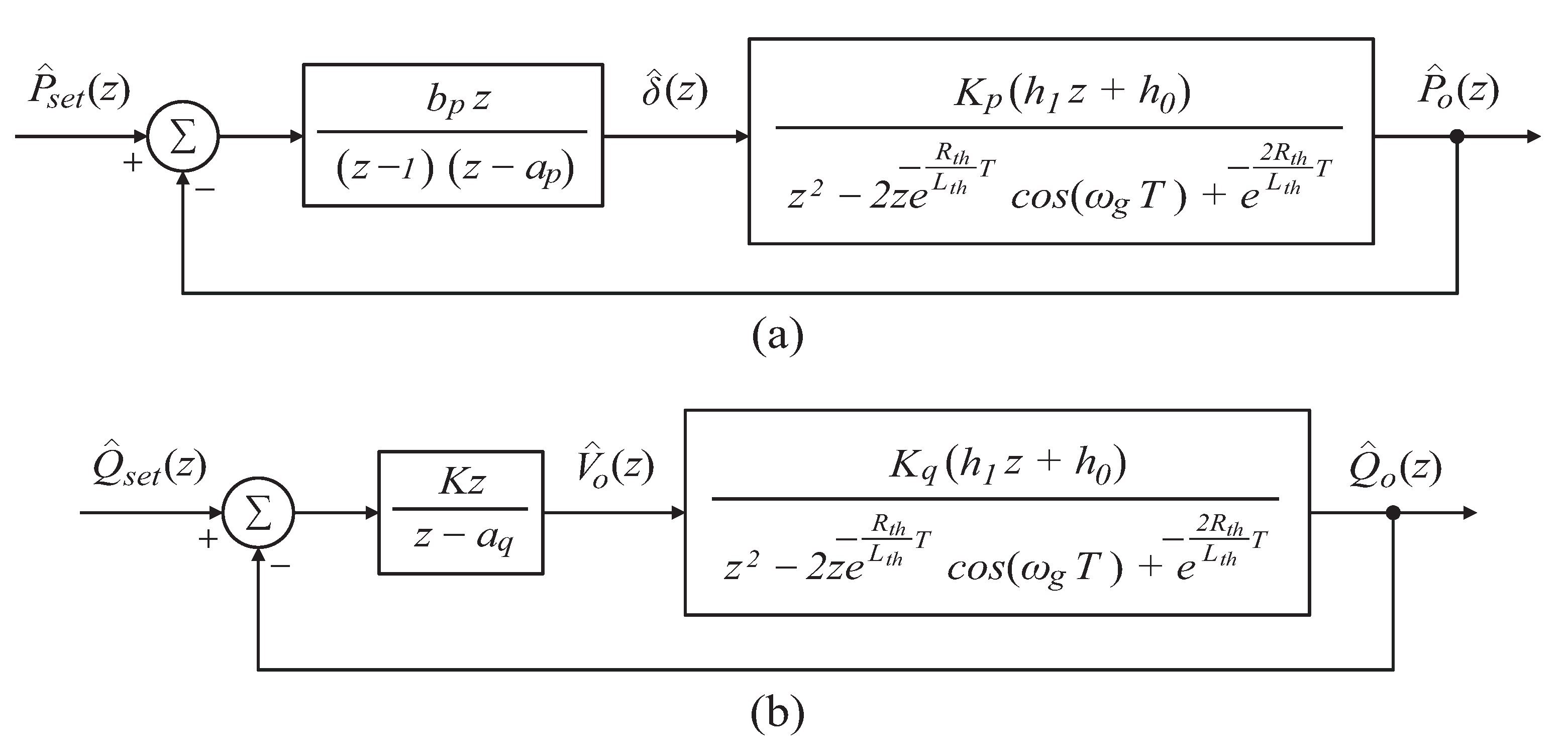
3.1. Discrete-Time Active Power Controller
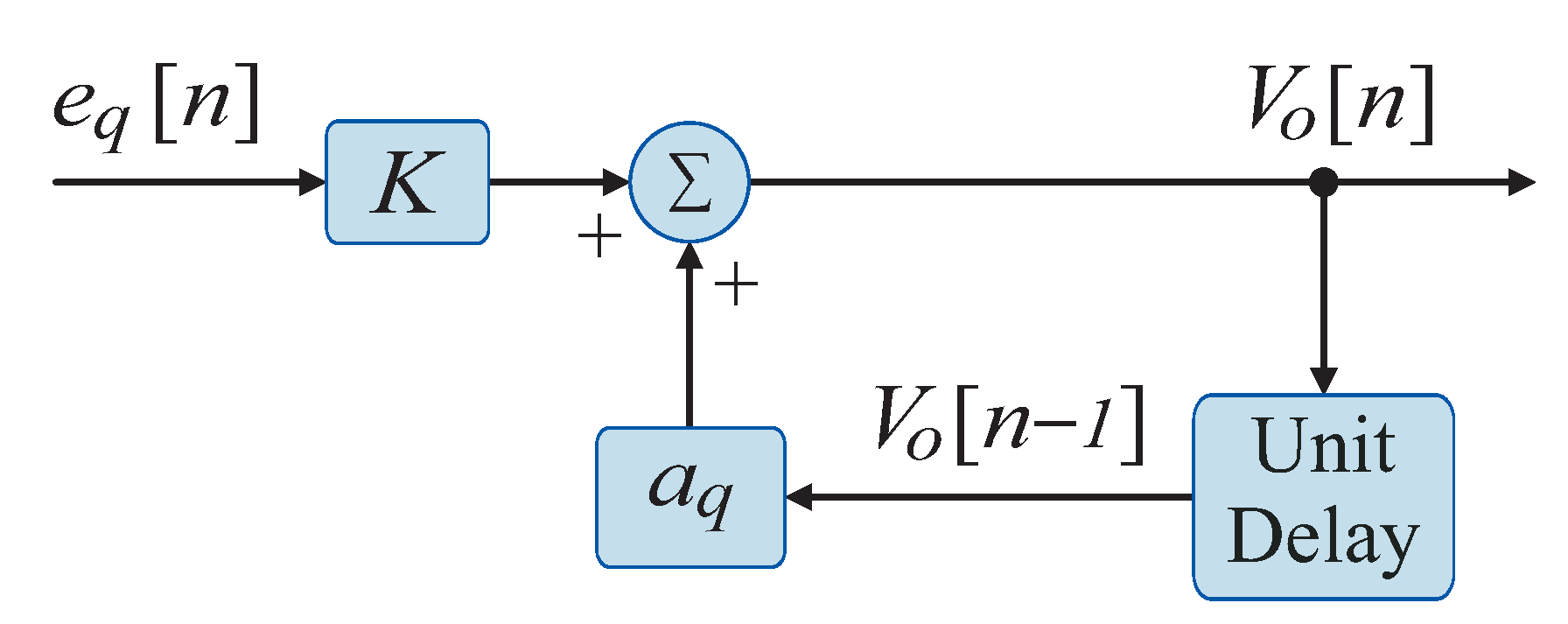
3.2. Discrete-Time Reactive Power Controller
4. VSG Controller Parameter Design
4.1. Active Power Controller Design
4.2. Reactive Power Controller Design
5. VSG-DG Power Control Dynamic Analysis
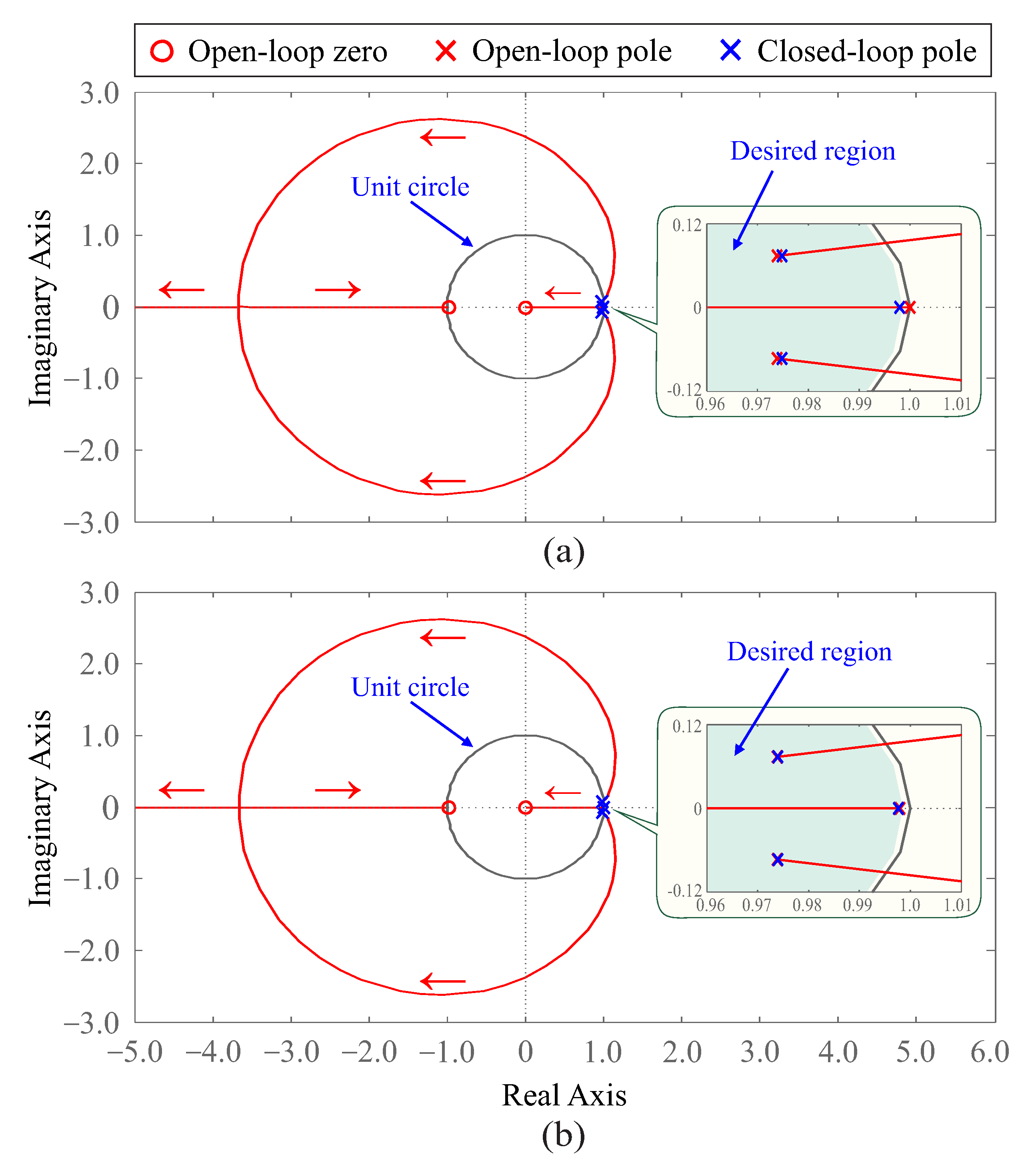
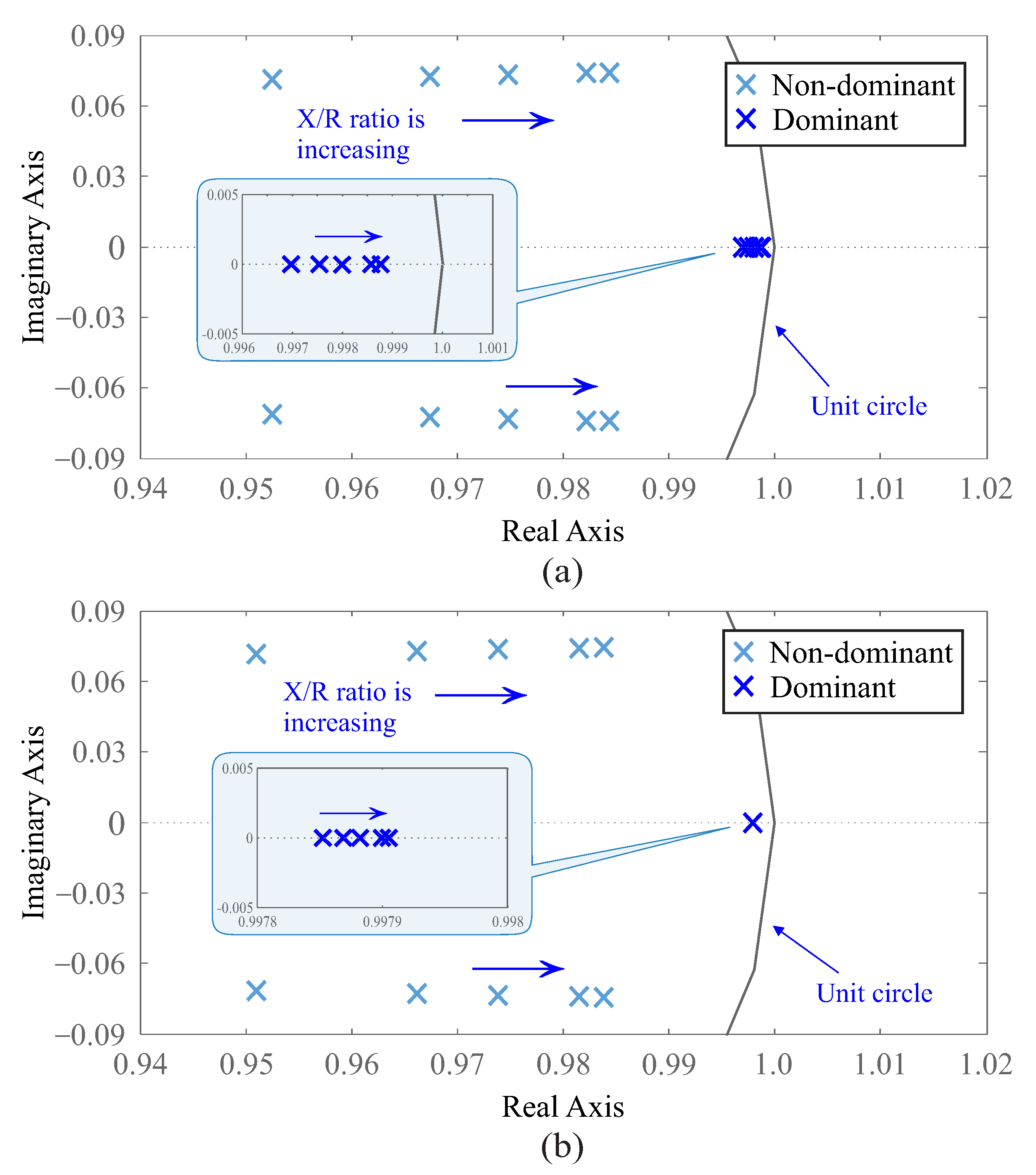
5.1. Closed-Loop Poles Behavior
5.1.1. Active Power Loop
5.1.2. Reactive Power Loop
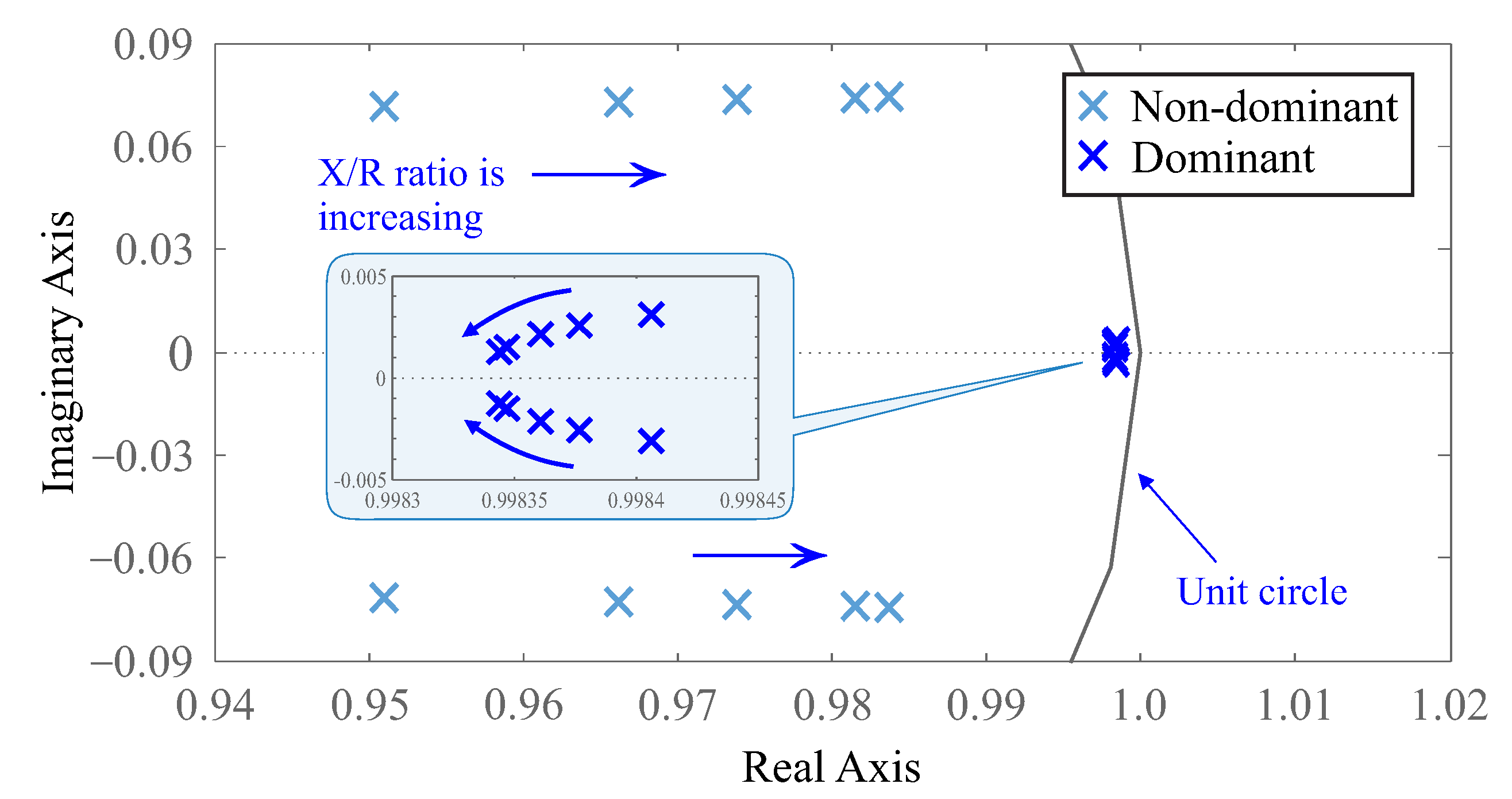
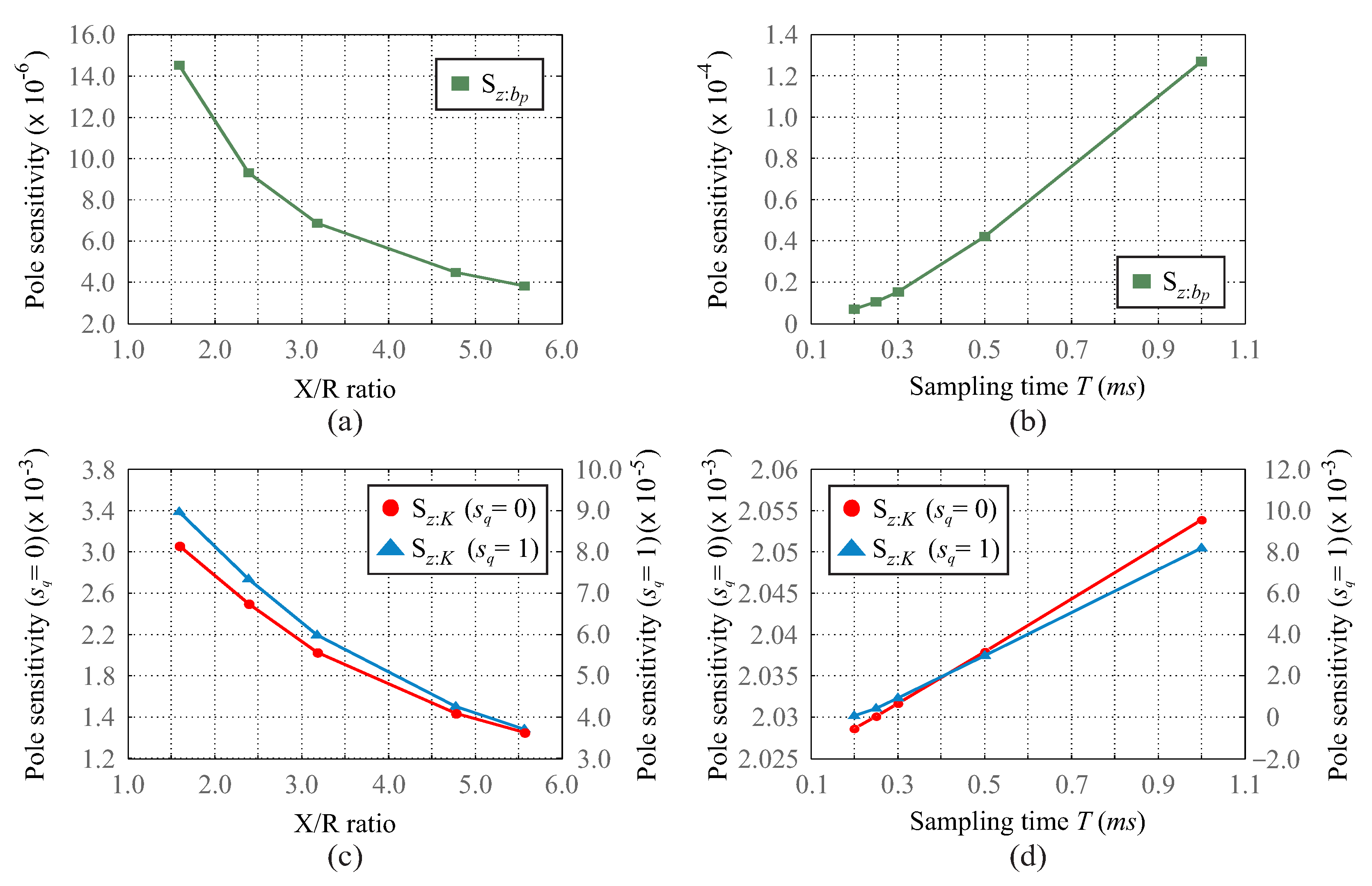
5.2. Sensitivity Analysis
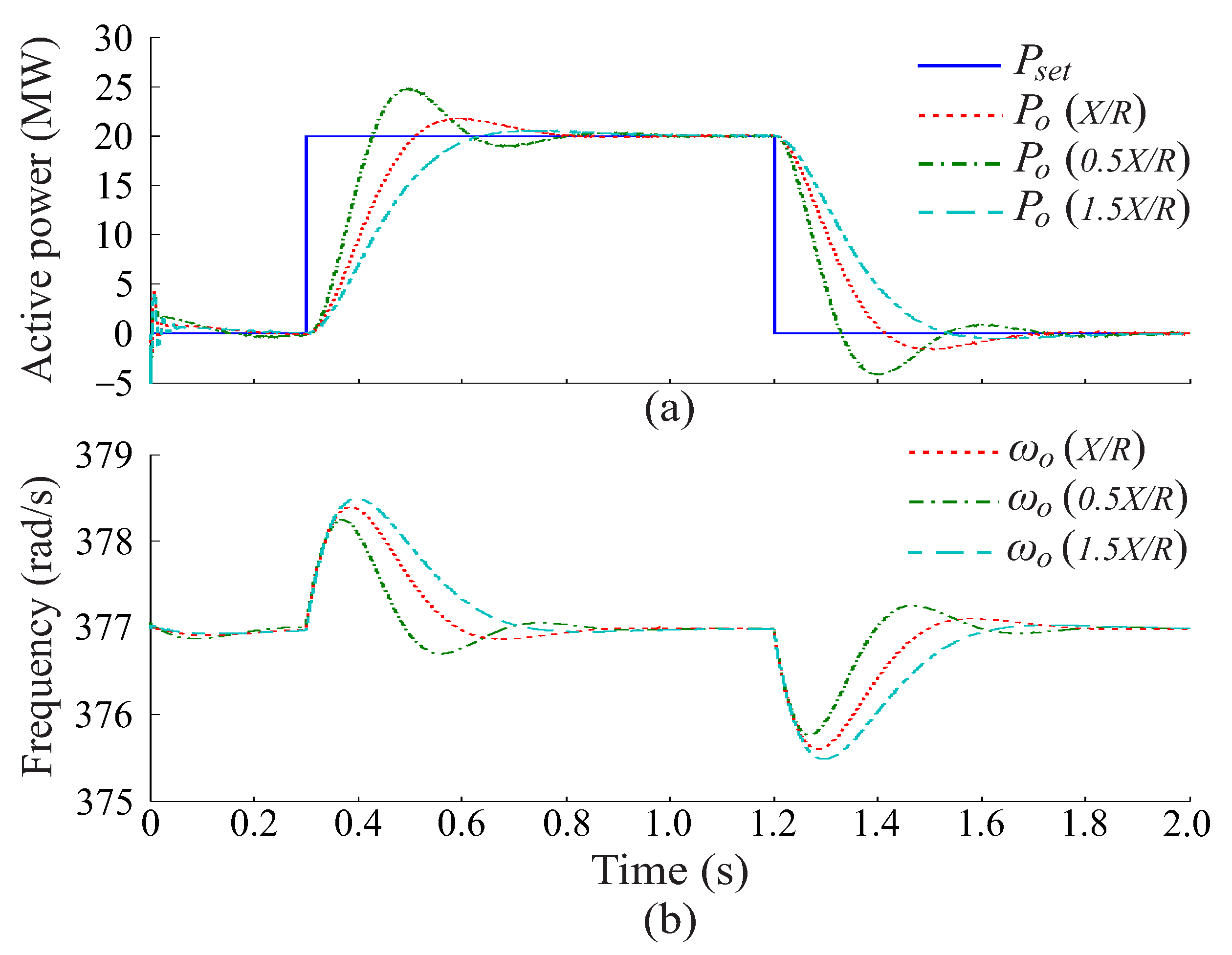
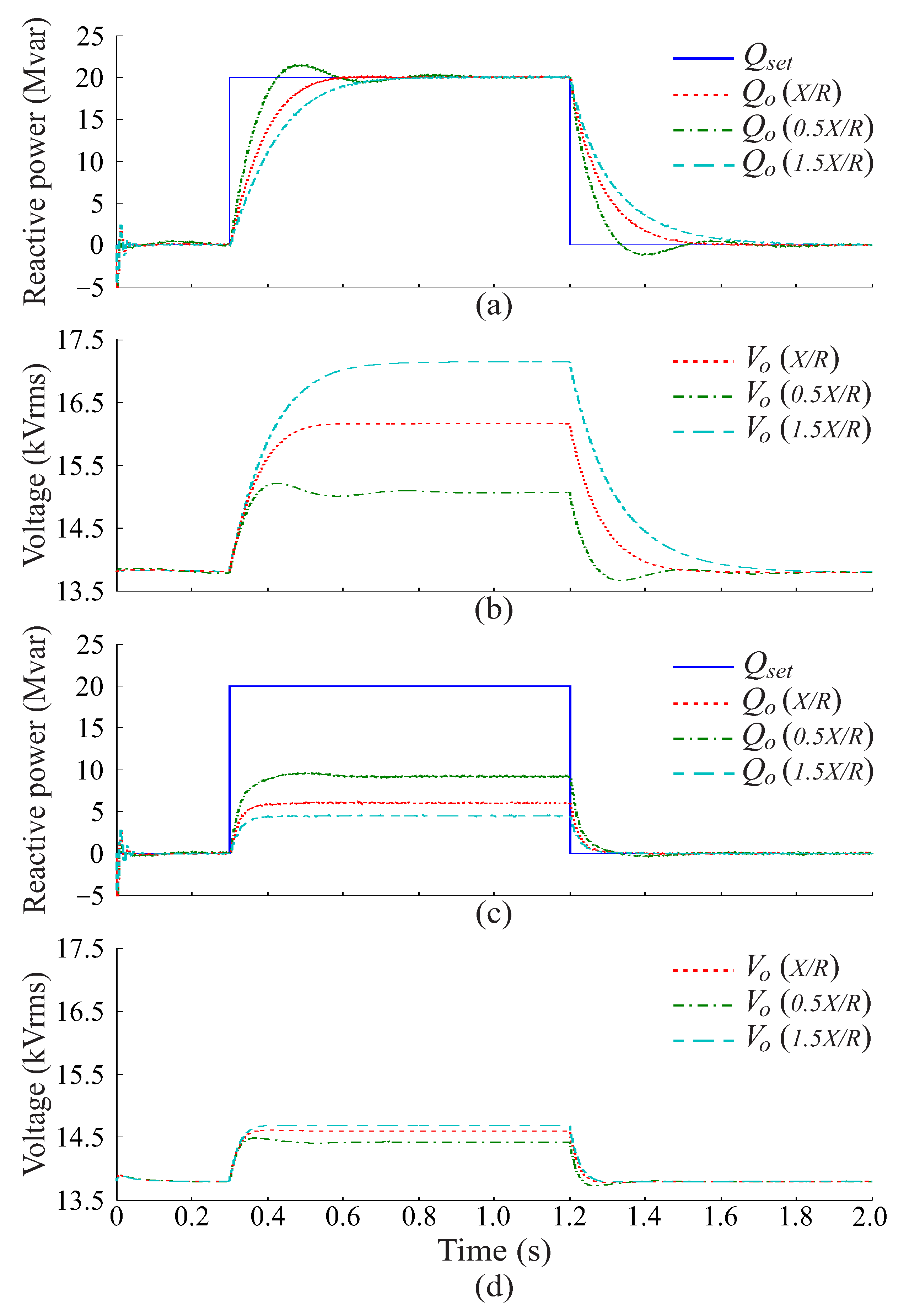
6. Performance Assessment
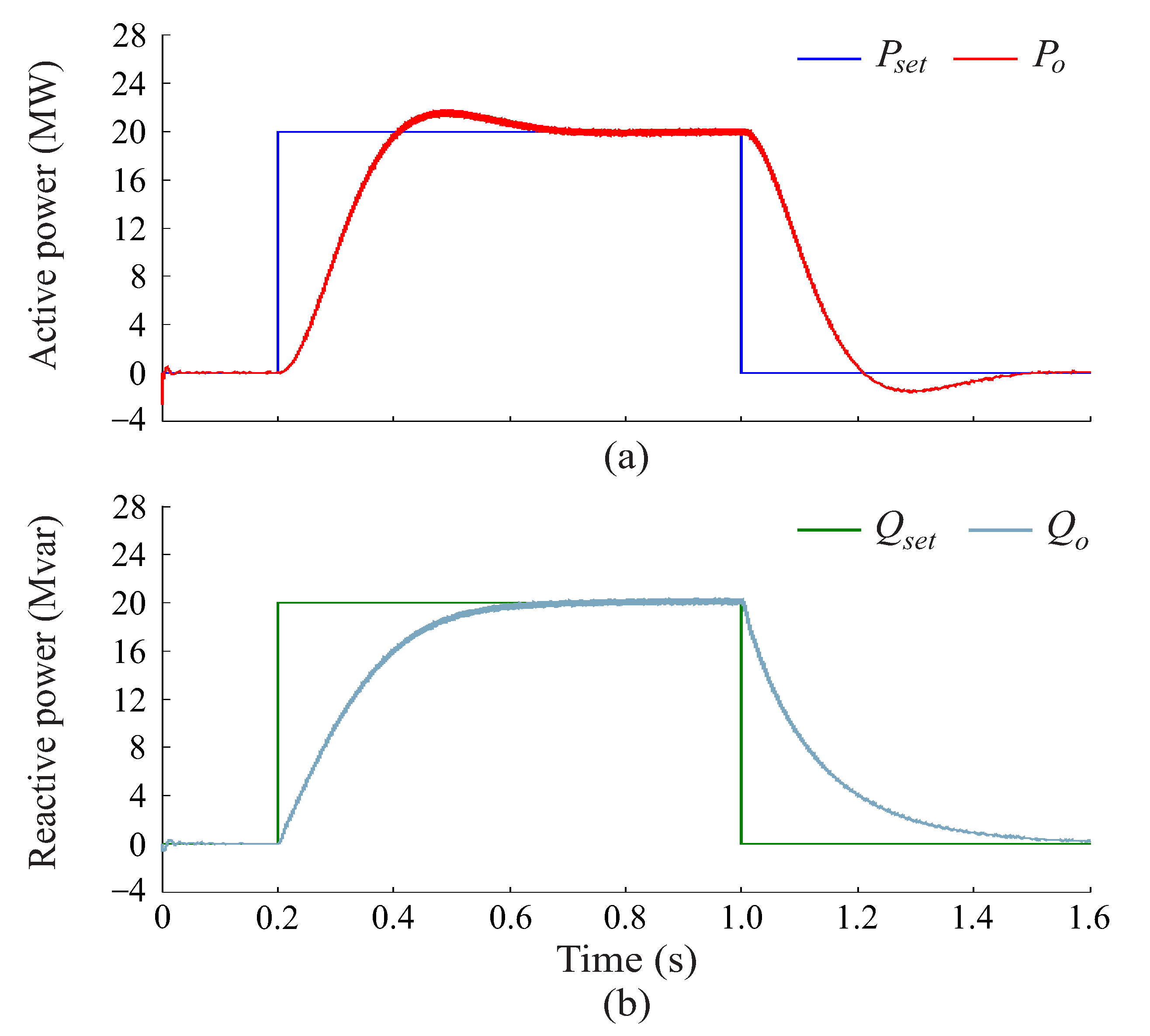
6.1. VSG Controller Performance Analysis
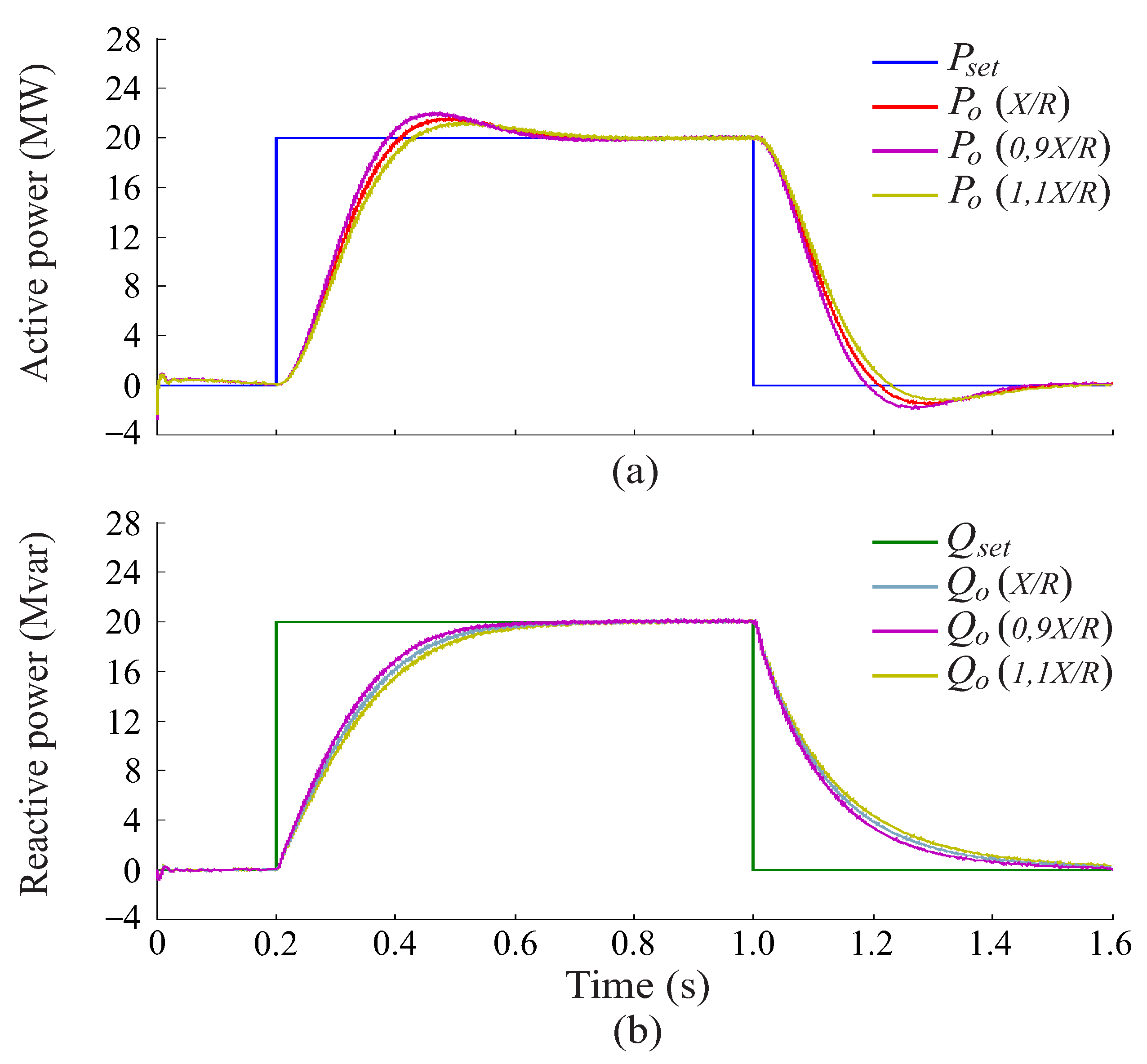
6.2. Performance Analysis for Grid Impedance Variation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DG | distributed generation |
| DC | direct current |
| HPWM | hybrid pulse width modulation |
| PCC | point of common coupling |
| RLM | root-locus method |
| RES | renewable energy sources |
| SG | synchronous generator |
| SRF-PLL | synchronous reference frame phase-locked loop |
| VSG | virtual synchronous generator |
| VSC | voltage source converter |
References
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Shuai, Z.; Sun, Y.; Shen, Z.J.; Tian, W.; Tu, C.; Li, Y.; Yin, X. Microgrid stability: Classification and a review. Renew. Sustain. Energy Rev. 2016, 58, 167–179. [Google Scholar] [CrossRef]
- Azmy, A.M.; Erlich, I. Impact of distributed generation on the stability of electrical power system. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 16 June 2005; Volume 2, pp. 1056–1063. [Google Scholar]
- van Wesenbeeck, M.P.N.; de Haan, S.W.H.; Varela, P.; Visscher, K. Grid tied converter with virtual kinetic storage. In Proceedings of the 2009 IEEE Bucharest PowerTech, Bucharest, Romania, 28 June–2 July 2009; pp. 1–7. [Google Scholar]
- Zhu, J.; Booth, C.D.; Adam, G.P.; Roscoe, A.J.; Bright, C.G. Inertia Emulation Control Strategy for VSC-HVDC Transmission Systems. IEEE Trans. Power Syst. 2012, 28, 1277–1287. [Google Scholar] [CrossRef]
- Torres, M.A.; Lopes, L.A.C.; Morán, L.A.; Espinoza, J.R. Self-Tuning Virtual Synchronous Machine: A Control Strategy for Energy Storage Systems to Support Dynamic Frequency Control. IEEE Trans. Energy Convers. 2014, 29, 833–840. [Google Scholar] [CrossRef]
- Zhong, Q.; Nguyen, P.; Ma, Z.; Sheng, W. Self-Synchronized Synchronverters: Inverters Without a Dedicated Synchronization Unit. IEEE Trans. Power Electron. 2014, 29, 617–630. [Google Scholar] [CrossRef]
- Guan, M.; Pan, W.; Zhang, J.; Hao, Q.; Cheng, J.; Zheng, X. Synchronous Generator Emulation Control Strategy for Voltage Source Converter (VSC) Stations. IEEE Trans. Power Syst. 2015, 30, 3093–3101. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A.; Fosso, O.B. A Virtual Synchronous Machine implementation for distributed control of power converters in SmartGrids. Electr. Power Syst. Res. 2015, 122, 180–197. [Google Scholar] [CrossRef]
- Rodríguez, P.; Citro, C.; Candela, J.I.; Rocabert, J.; Luna, A. Flexible Grid Connection and Islanding of SPC-Based PV Power Converters. IEEE Trans. Ind. Appl. 2018, 54, 2690–2702. [Google Scholar] [CrossRef]
- do Nascimento, T.F.; Salazar, A.O. Improving Transient Response of a Synchronous Generator Emulation Technique Applied to Grid-tied Converters. In Proceedings of the 2021 Brazilian Power Electronics Conference (COBEP), Joao Pessoa, Brazil, 7–10 November 2021; pp. 1–7. [Google Scholar]
- Wang, X.; Li, Y.W.; Blaabjerg, F.; Loh, P.C. Virtual-Impedance-Based Control for Voltage-Source and Current-Source Converters. IEEE Trans. Power Electron. 2015, 30, 7019–7037. [Google Scholar] [CrossRef]
- Du, Y.; Guerrero, J.M.; Chang, L.; Su, J.; Mao, M. Modeling, analysis, and design of a frequency-droop-based virtual synchronous generator for microgrid applications. In Proceedings of the 2013 IEEE ECCE Asia Downunder, Melbourne, VIC, Australia, 3–6 June 2013; pp. 643–649. [Google Scholar]
- Shintai, T.; Miura, Y.; Ise, T. Oscillation Damping of a Distributed Generator Using a Virtual Synchronous Generator. IEEE Trans. Power Deliv. 2014, 29, 668–676. [Google Scholar] [CrossRef]
- Wu, H.; Ruan, X.; Yang, D.; Chen, X.; Zhao, W.; Lv, Z.; Zhong, Q.C. Small-Signal modeling and parameters design for virtual synchronous generators. IEEE Trans. Ind. Electron. 2016, 63, 4292–4303. [Google Scholar] [CrossRef]
- Roldán-Pérez, J.; Rodríguez-Cabero, A.; Prodanovic, M. Design and Analysis of Virtual Synchronous Machines in Inductive and Resistive Weak Grids. IEEE Trans. Energy Convers. 2019, 34, 1818–1828. [Google Scholar] [CrossRef]
- Li, G.; Ma, F.; Wang, Y.; Weng, M.; Chen, Z.; Li, X. Design and Operation Analysis of Virtual Synchronous Compensator. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3835–3845. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Wu, C.; Blaabjerg, F. Characteristics of Parallel Inverters Applying Virtual Synchronous Generator Control. IEEE Trans. Smart Grid 2021, 12, 4690–4701. [Google Scholar] [CrossRef]
- Guo, J.; Chen, Y.; Wang, L.; Wu, W.; Wang, X.; Shuai, Z.; Guerrero, J.M. Impedance Analysis and Stabilization of Virtual Synchronous Generators With Different DC-Link Voltage Controllers Under Weak Grid. IEEE Trans. Power Electron. 2021, 36, 11397–11408. [Google Scholar] [CrossRef]
- Nascimento, T.F.d.; Salazar, A.O. Impedance Model Based Dynamic Analysis Applied to VSG-Controlled Converters in AC Microgrids. IEEE Trans. Ind. Appl. 2023, 59, 2720–2730. [Google Scholar] [CrossRef]
- Nise, N.S. Control Systems Engineering, 6th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Nascimento, T.F.D.; Salazar, A.O. Parameters Design of a Digital VSG Control Strategy for Grid-Forming DG Systems Applications. In Proceedings of the 2023 15th IEEE International Conference on Industry Applications (INDUSCON), São Bernardo do Campo, Brazil, 22–24 November 2023; pp. 1588–1593. [Google Scholar]
- Leon, A.E.; Mauricio, J.M. Control strategy to improve damping and transient response of VSG-based renewable power plants. Electr. Power Syst. Res. 2025, 247, 111802. [Google Scholar] [CrossRef]
- Shaikh, M.S.; Raj, S.; Ikram, M.; Khan, W. Parameters estimation of AC transmission line by an improved moth flame optimization method. Electr. Syst. Inf. Technol. 2022, 9, 25. [Google Scholar] [CrossRef]
- Shaikh, M.S.; Raj, S.; Ikram, M.; Latif, S.A.; Mbasso, W.F.; Kamel, S. Optimizing transmission line parameter estimation with hybrid evolutionary techniques. IET Gener. Transm. Distrib. 2024, 18, 1795–1814. [Google Scholar] [CrossRef]
- ANSI C84.1-2020; Electrical Power Systems and Equipment—Voltage Ratings (60 Hz). American National Standards Institute (ANSI): Washington, DC, USA, 2020.
- Akagi, H.; Watanabe, E.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; IEEE Press: Piscataway, NJ, USA, 2007. [Google Scholar]
- Blasko, V. Analysis of a hybrid PWM based on modified space-vector and triangle-comparison methods. IEEE Trans. Ind. Appl. 1997, 33, 756–764. [Google Scholar] [CrossRef]
- Peña-Alzola, R.; Liserre, M.; Blaabjerg, F.; Ordonez, M.; Yang, Y. LCL-Filter Design for Robust Active Damping in Grid-Connected Converters. IEEE Trans. Ind. Inform. 2014, 10, 2192–2203. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Grid voltage | 13.8 kV rms |
| PCC voltage | 14.3 kV rms |
| Grid frequency | rad/s |
| Thevenin impedance | mH, |
| Rated power | 20 MVA |
| Rated load angle | 0.2 rad |
| Sampling time T | 0.0002 s |
| Switching frequency | 5 kHz |
| Filter inductor | mH, |
| Filter capacitor | 10 F |
| Damping resistance | 2.5 |
| T = 0.0002 s | ||
|---|---|---|
| Controller | Parameter | Value |
| Active power | ||
| Reactive power | ||
| K | ||
| K |
| Controller | Design Criteria |
Values Obtained |
Values Obtained |
Values Obtained |
|---|---|---|---|---|
| Active power | Settling time s | s | s | s |
| Percent overshoot % | ||||
| Reactive power | Settling time s | s | s | s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
do Nascimento, T.F.; Oliveira, J.B.; Villarreal, E.R.L.; Salazar, A.O. Discrete-Time Impedance Model-Based Dynamic Analysis and Parameter Design for VSG-Controlled Grid-Forming DG System. Energies 2025, 18, 3400. https://doi.org/10.3390/en18133400
do Nascimento TF, Oliveira JB, Villarreal ERL, Salazar AO. Discrete-Time Impedance Model-Based Dynamic Analysis and Parameter Design for VSG-Controlled Grid-Forming DG System. Energies. 2025; 18(13):3400. https://doi.org/10.3390/en18133400
Chicago/Turabian Styledo Nascimento, Thiago F., Josenalde B. Oliveira, Elmer R. L. Villarreal, and Andrés O. Salazar. 2025. "Discrete-Time Impedance Model-Based Dynamic Analysis and Parameter Design for VSG-Controlled Grid-Forming DG System" Energies 18, no. 13: 3400. https://doi.org/10.3390/en18133400
APA Styledo Nascimento, T. F., Oliveira, J. B., Villarreal, E. R. L., & Salazar, A. O. (2025). Discrete-Time Impedance Model-Based Dynamic Analysis and Parameter Design for VSG-Controlled Grid-Forming DG System. Energies, 18(13), 3400. https://doi.org/10.3390/en18133400











