Stochastic Demand-Side Management for Residential Off-Grid PV Systems Considering Battery, Fuel Cell, and PEM Electrolyzer Degradation
Abstract
1. Introduction
- This study proposes an innovative SDSM strategy for off-grid PV systems with hybrid Li-ion battery–hydrogen storage that significantly minimizes the degradation of principal components and reduces the levelized cost of energy (LCOE).
- The uncertainty of load predictions is incorporated into the optimization problem using scenario-based generation to enhance the accuracy and robustness of the proposed approach.
- Simulation results validate the economic and operational benefits of the proposed SDSM method, achieving up to a 22.5% reduction in LCOE, zero load shedding, and minimal energy dumping compared to random operation scenarios.
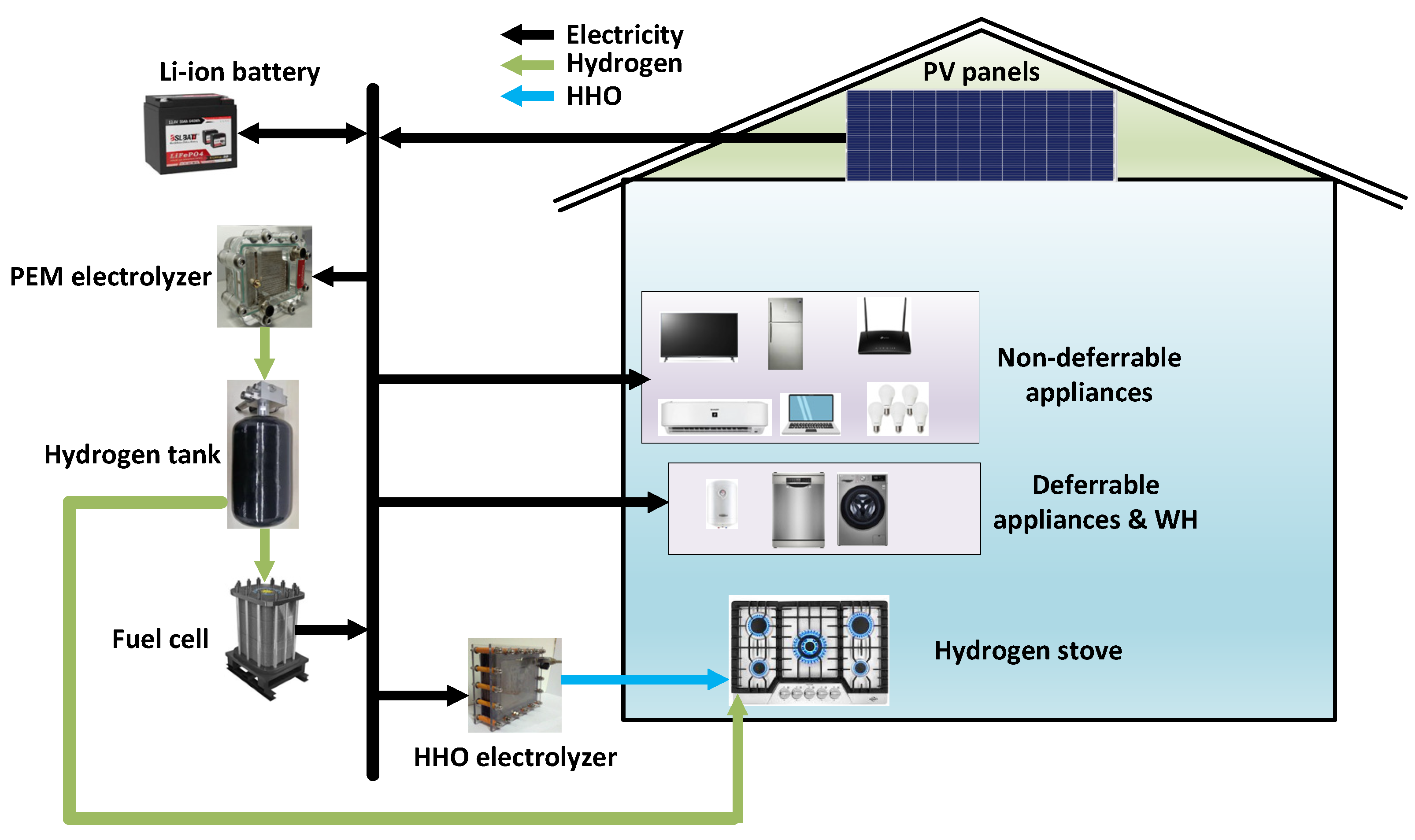
2. Methodology
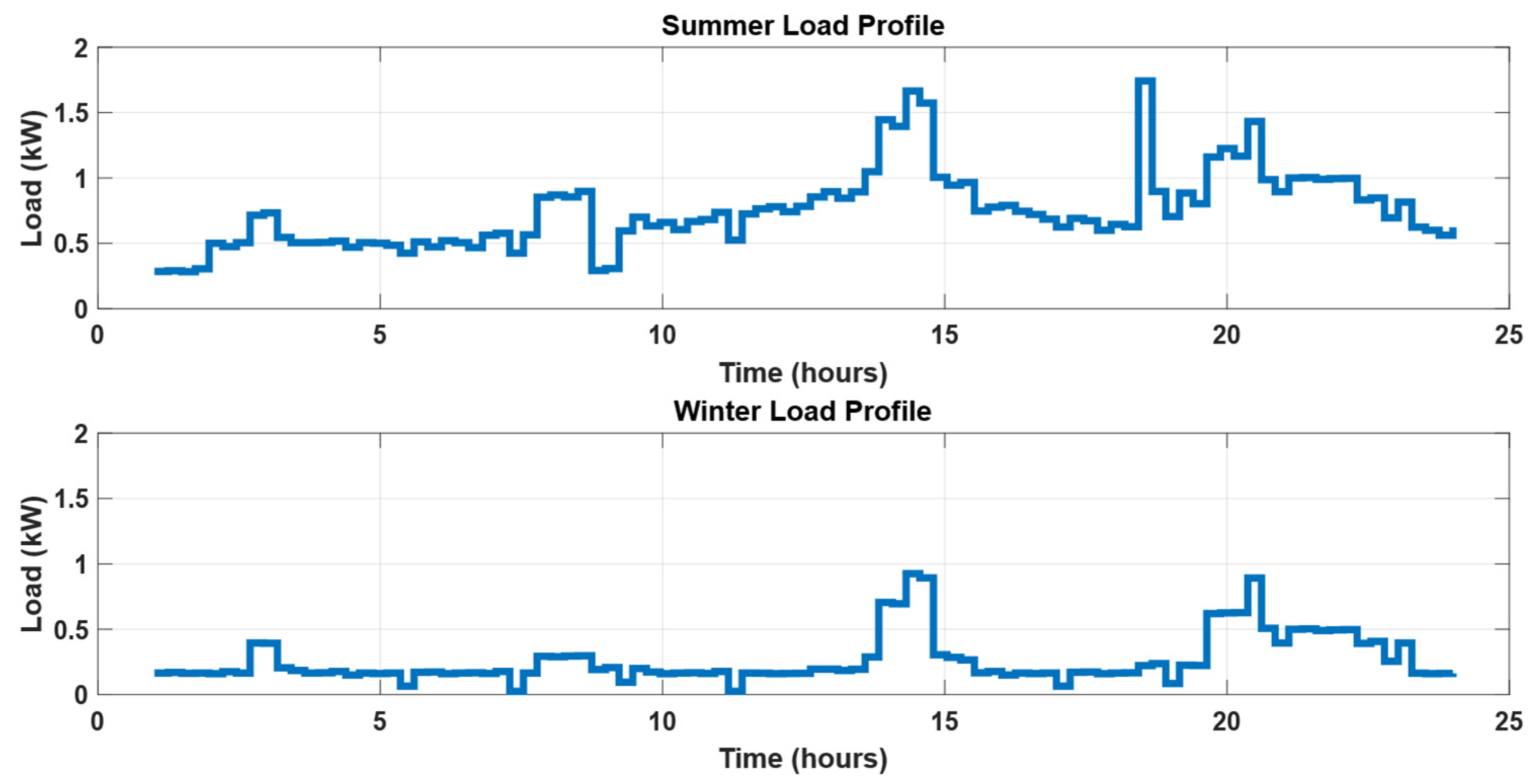
2.1. Typical Electrical Load Profile and Appliance Classification
- Non-deferable loads: These loads cannot participate in SDSM programs due to their non-deferable nature. Examples of loads in this category are lights, fans, personal laptops, televisions, refrigerators, and routers.
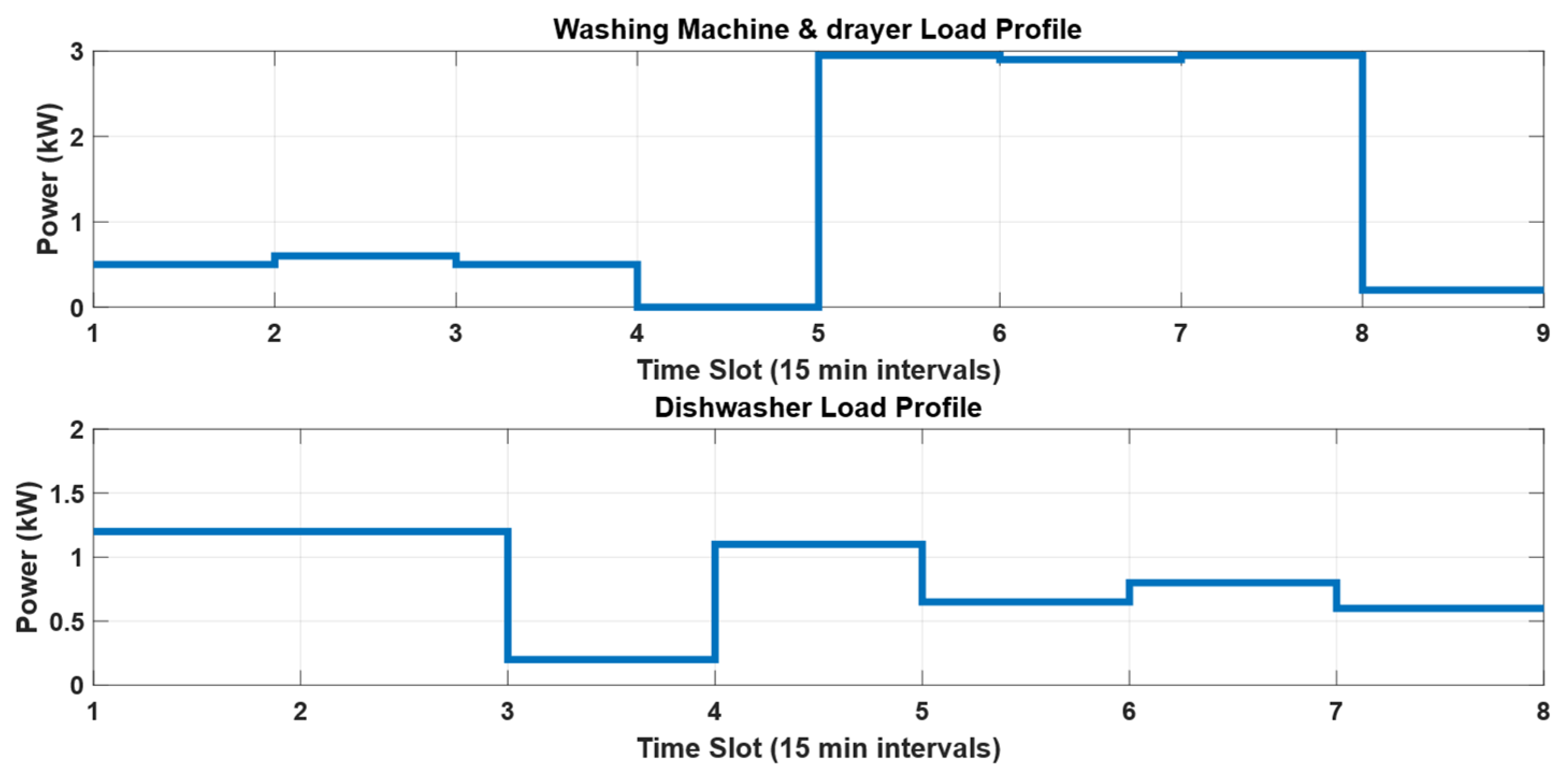
- Deferable loads: The operation of these loads can be scheduled within a predefined time window set by the customer. Once initiated, these loads cannot be interrupted, and they must complete their full operating cycle. Examples of loads in this category include appliances such as washing machine and dryer (WM) and dishwasher (DW).
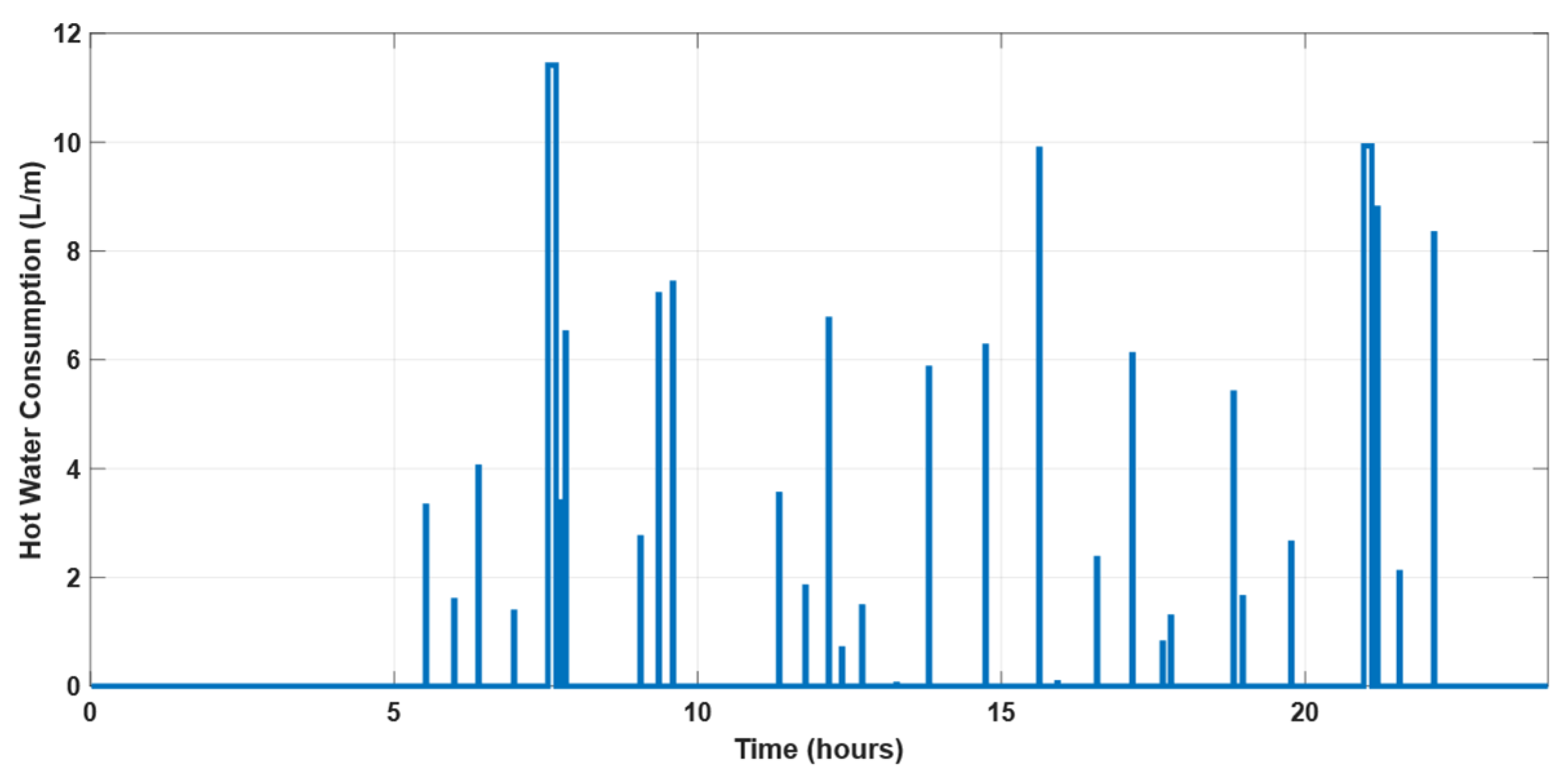
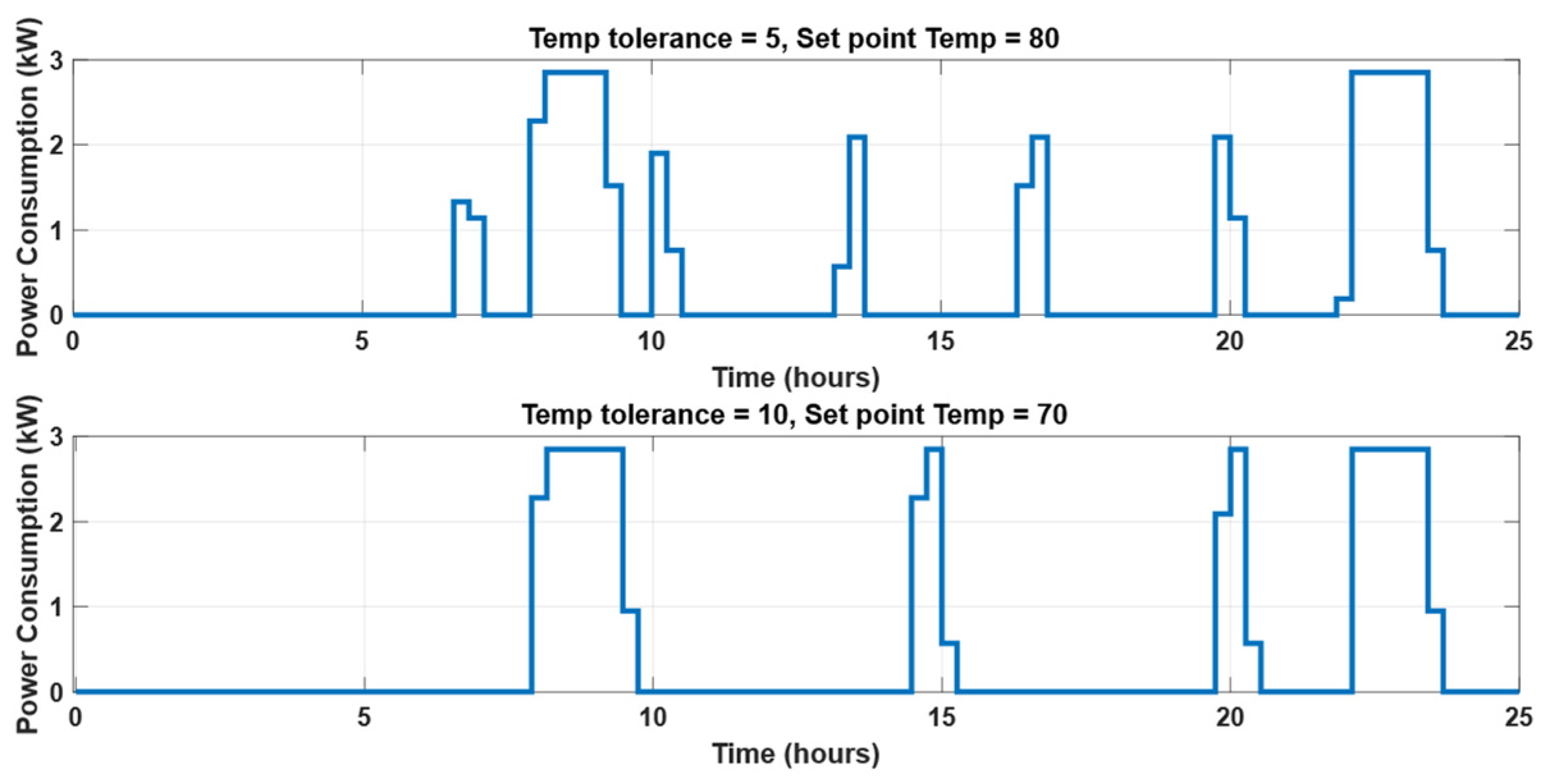
- Thermostatically controlled: These loads can contribute to SDSM due to their thermal capacity and inertia, so their power consumption profile can be controlled without affecting user comfort level. WH is an example of this load category.
- Load profile of non-deferable loads
- 2.
- Load profile of deferable loads
- 3.
- Load profile of water heater
2.2. Energy Consumption Profiling for Cooking Using an HHO Stove
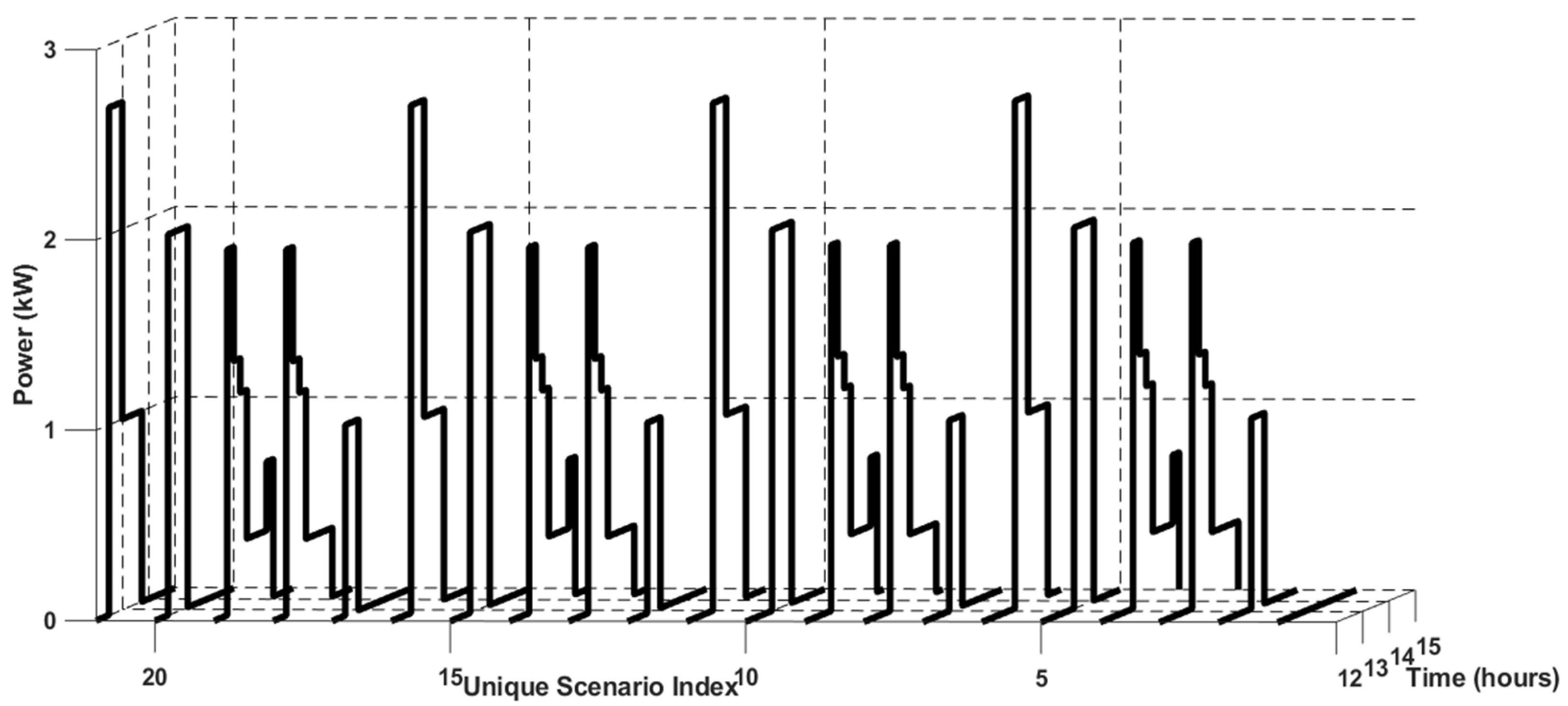
2.3. Stochastic Model Description
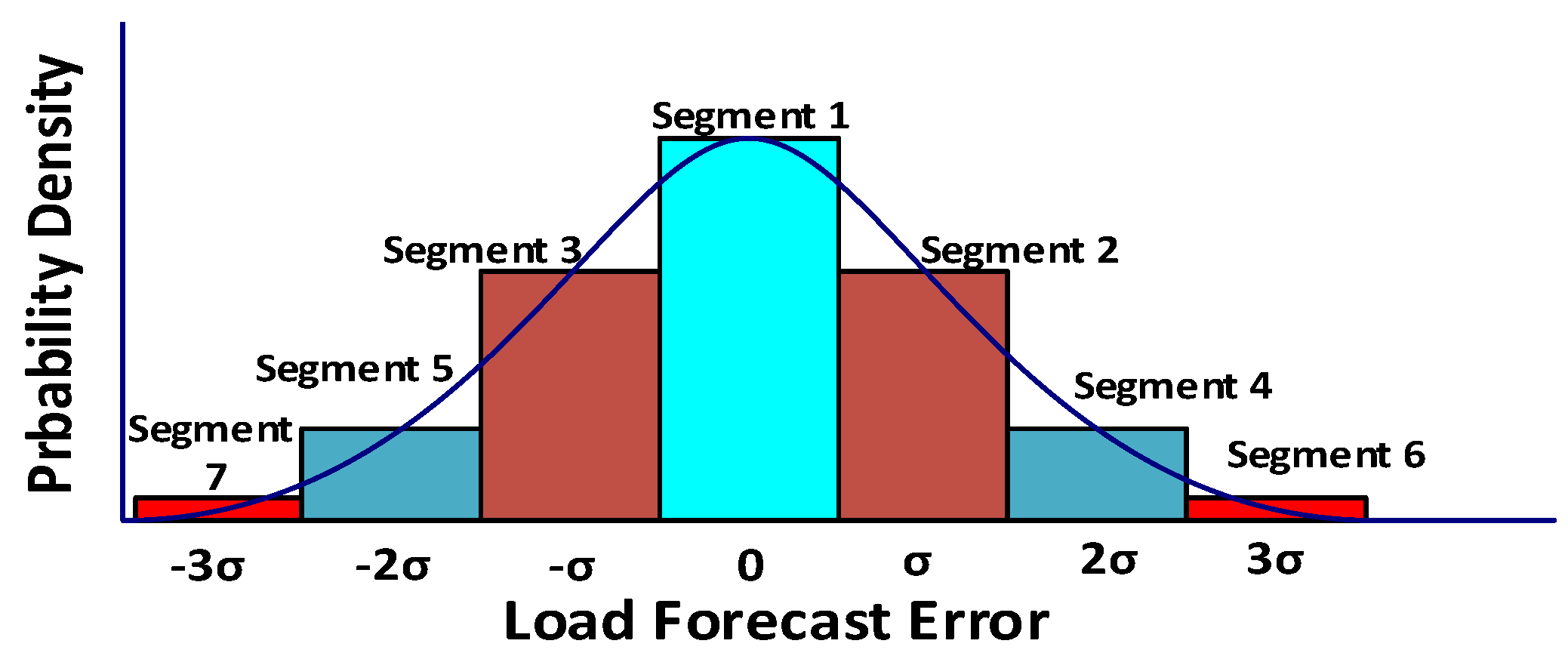
- Scenario generation
- 2.
- Scenario reduction and stooping rule
- 3.
- Combination of cooking and electrical load scenarios
2.4. Sizing of the Proposed System
2.5. The Degradation Model of Different Components
- Li-ion battery degradation model
- 2.
- Fuel cell degradation model
- 3.
- PEM electrolyzer degradation model
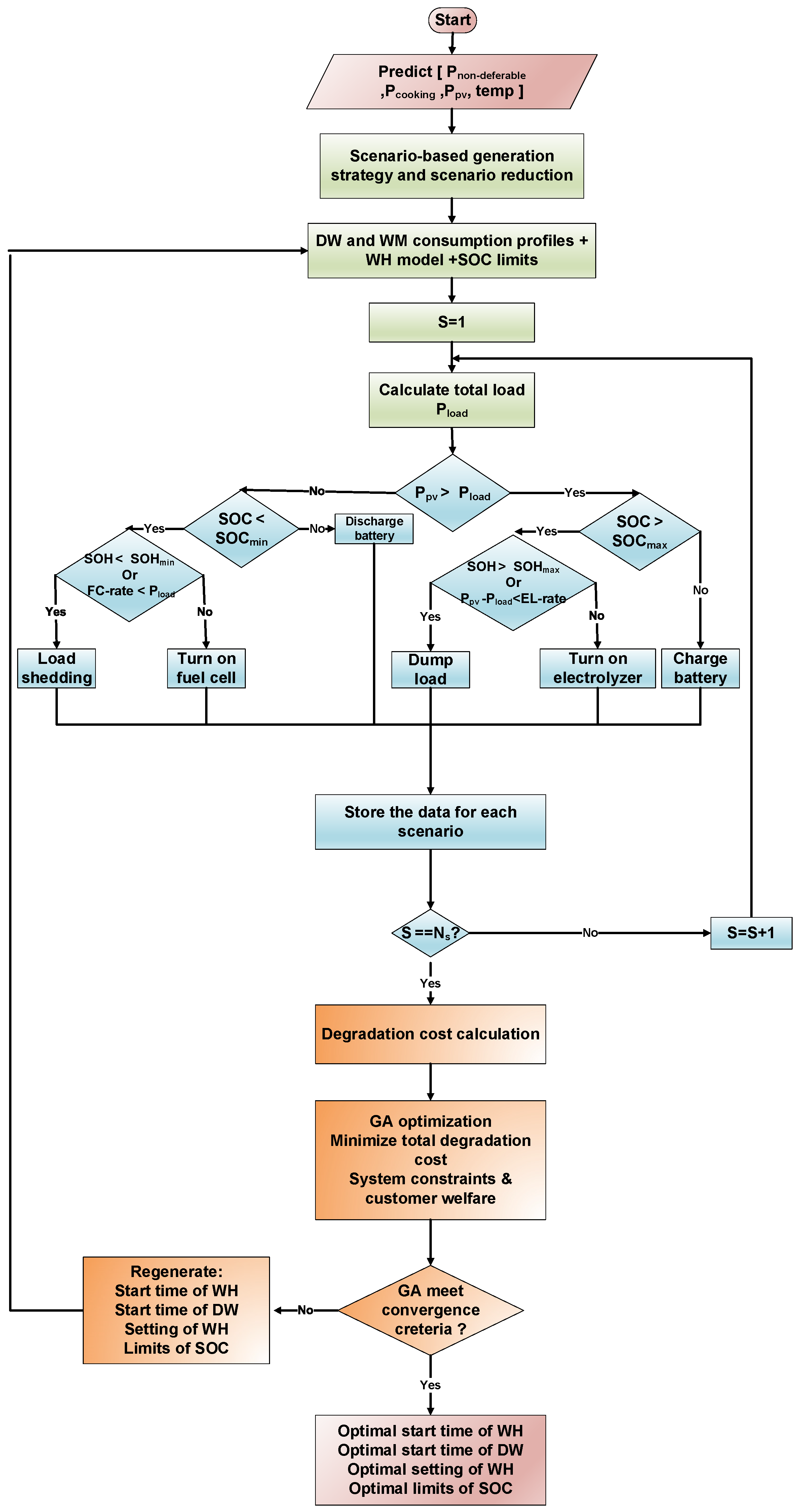
2.6. Integrated Stochastic Optimization Model and Energy Management Architecture
2.7. Economic Indicator: Levelized Cost of Energy
3. Results
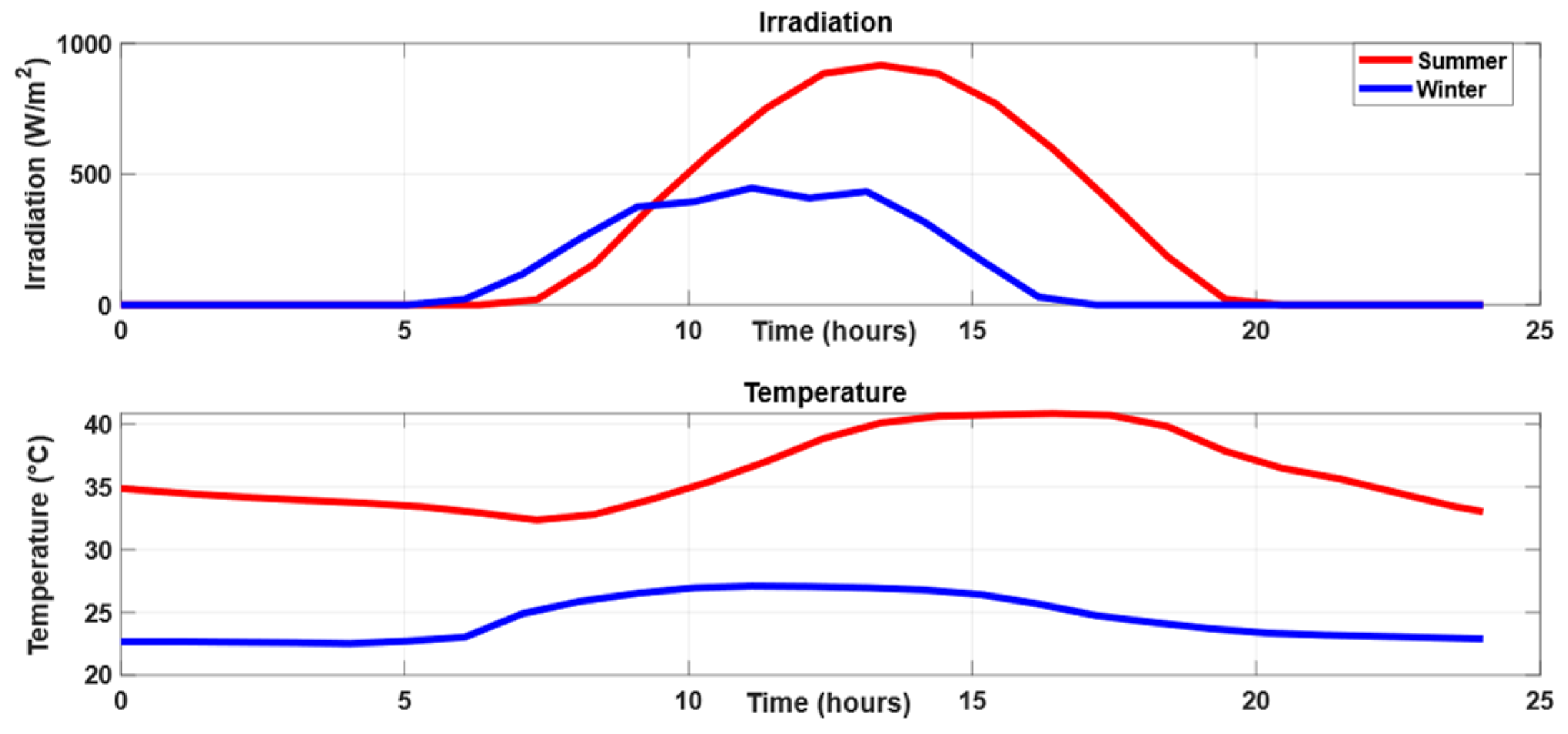
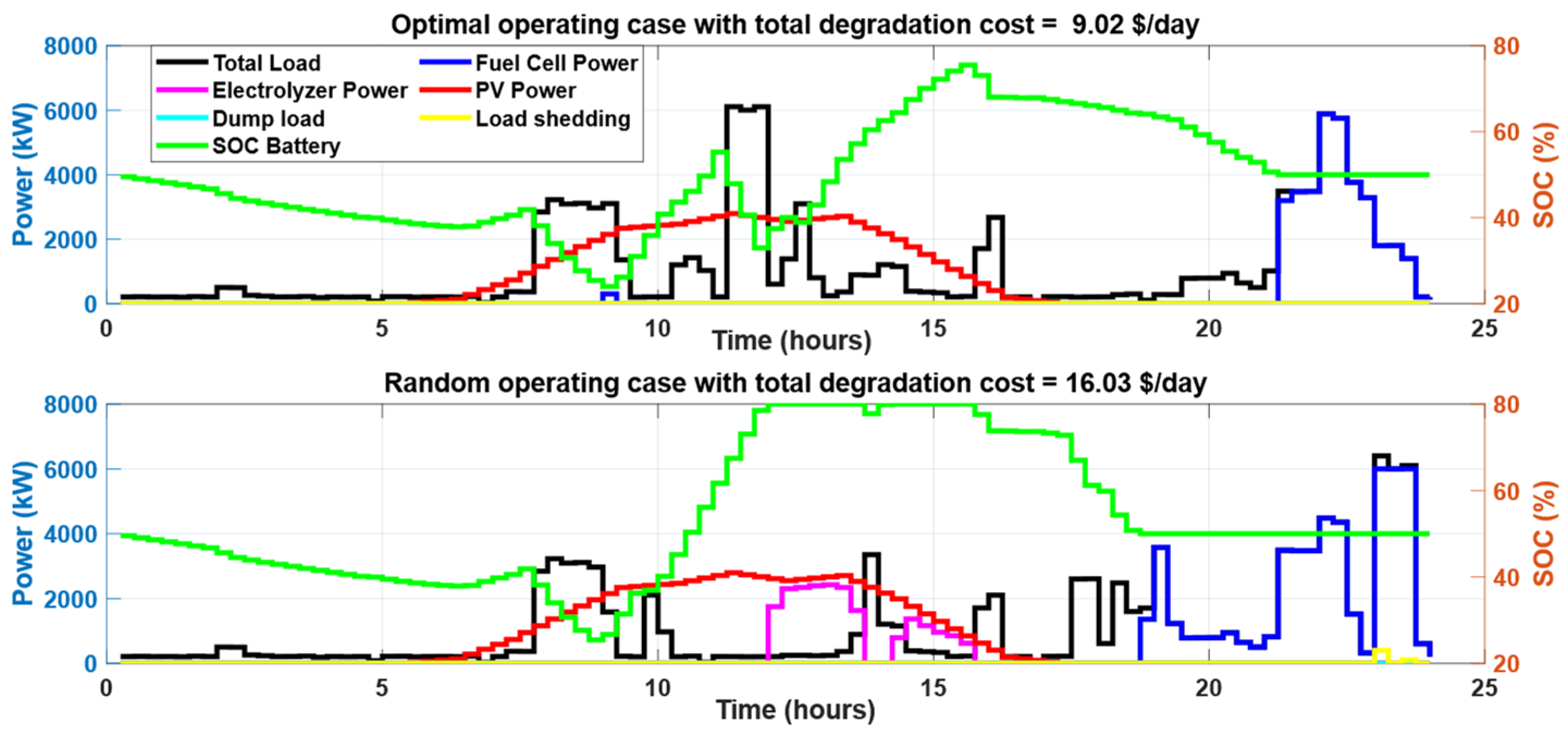
3.1. Optimal Results on Winter Day
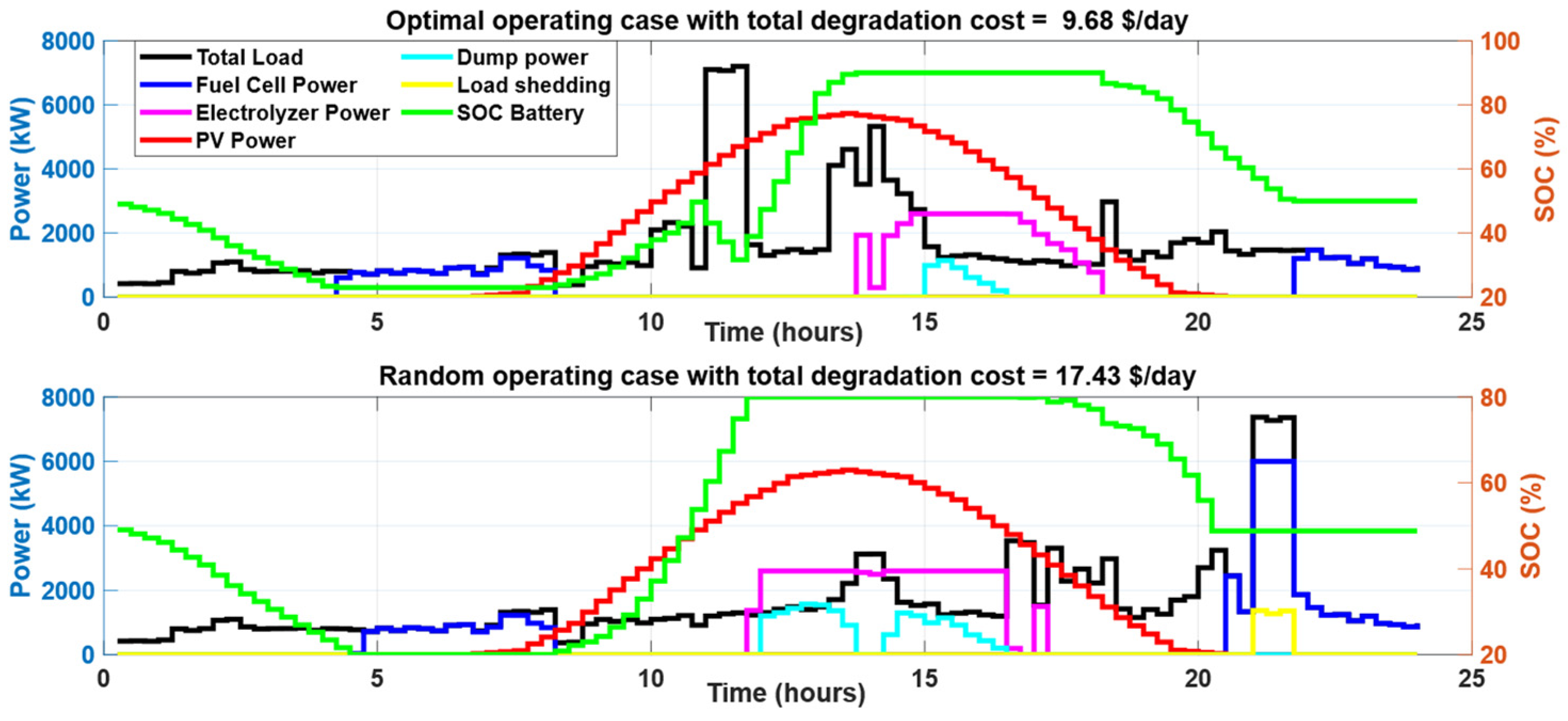
3.2. Optimal Results on a Summer Day
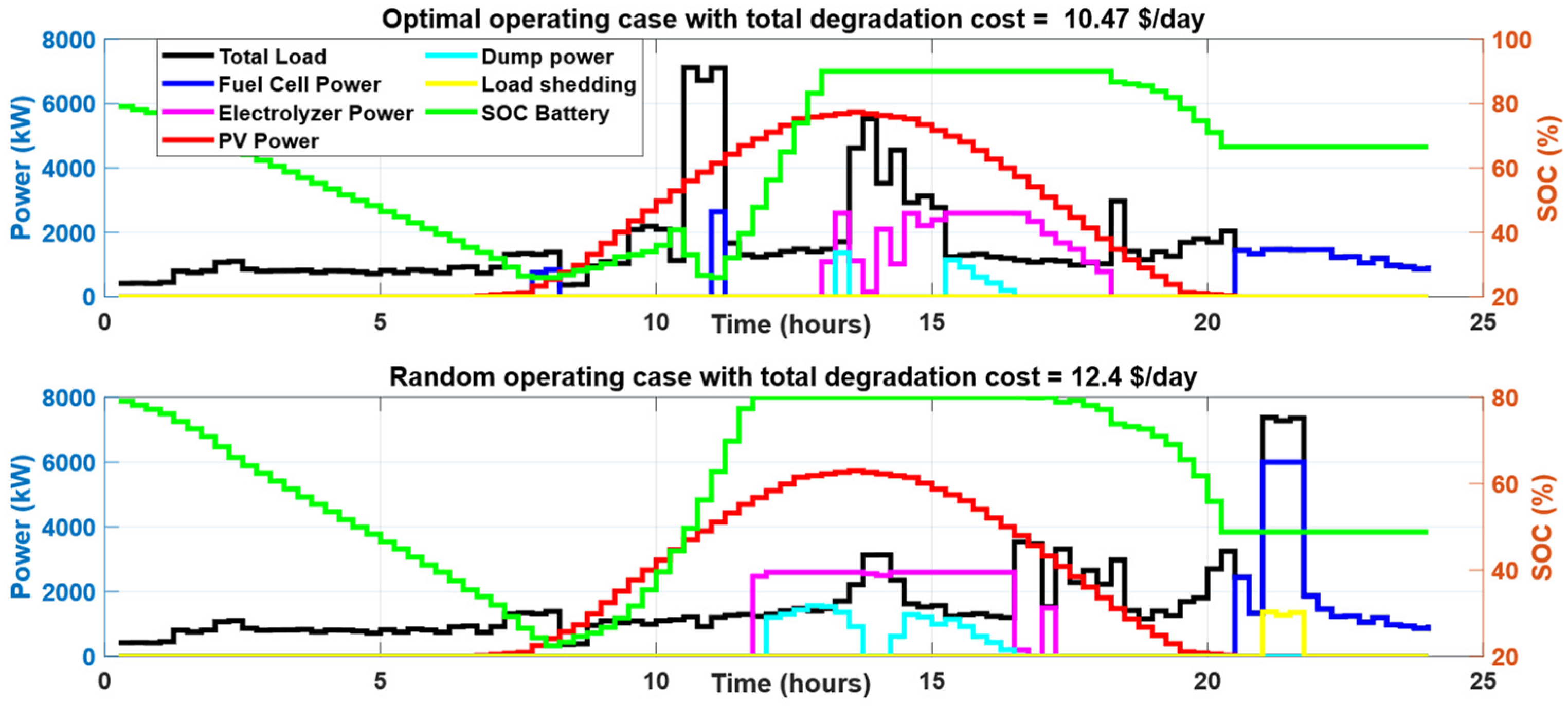
3.3. Effect of the Proposed Technique on Component Lifetime and Cost of Electricity
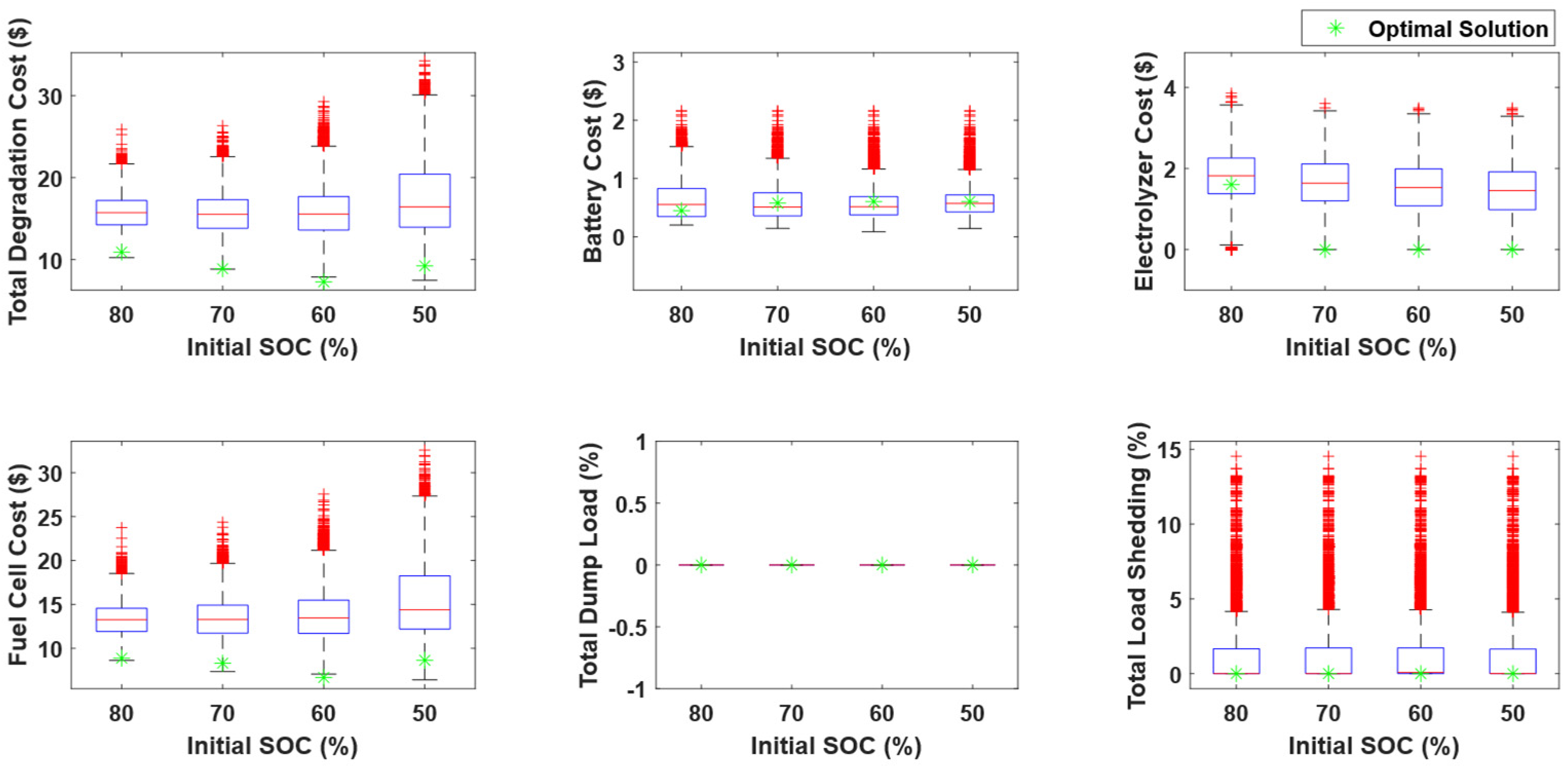
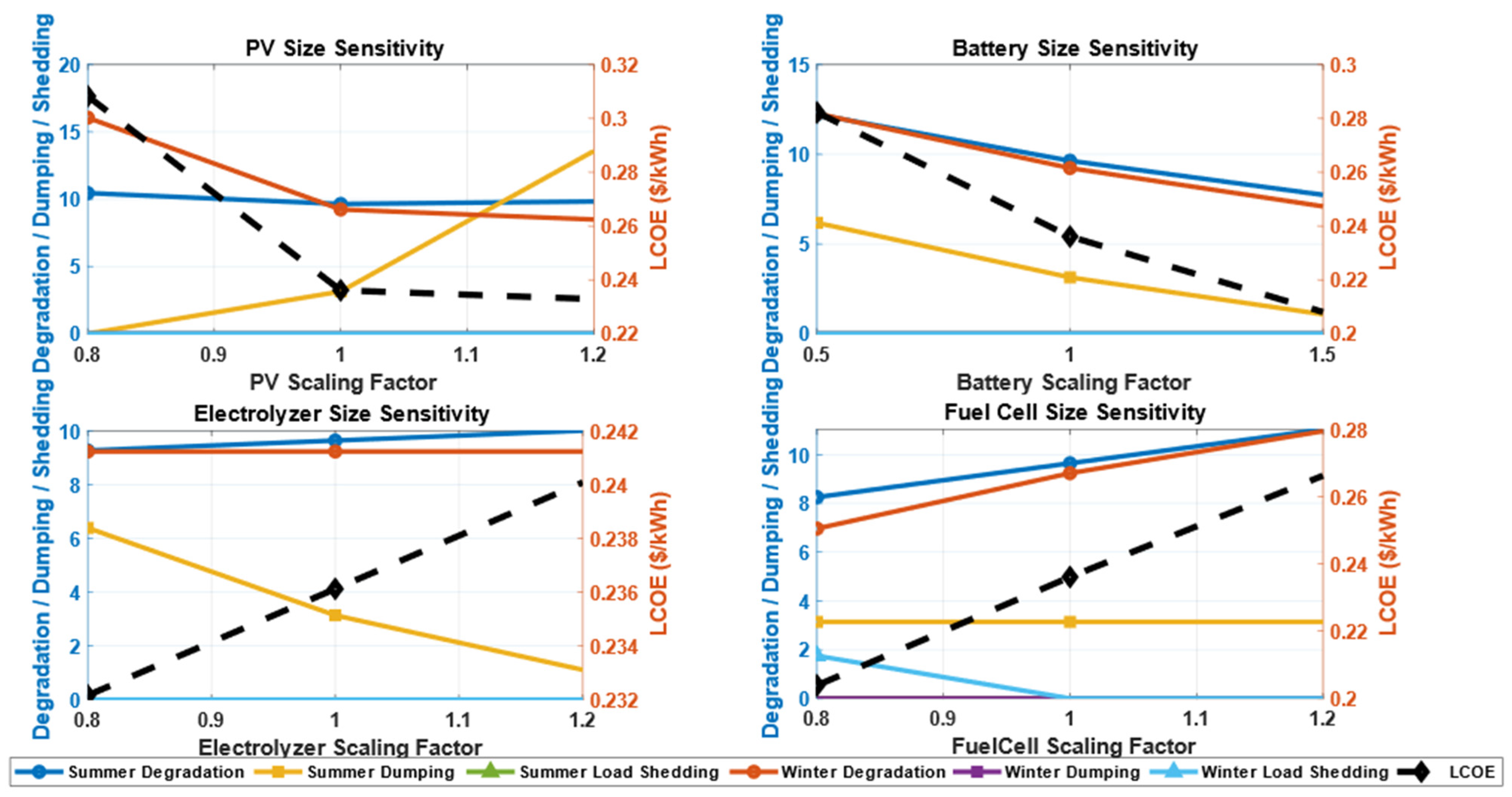
3.4. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Choudhury, S.; Parida, A.; Pant, R.M.; Chatterjee, S. GIS augmented computational intelligence technique for rural cluster electrification through prioritized site selection of micro-hydro power generation system. Renew. Energy 2019, 142, 487–496. [Google Scholar] [CrossRef]
- Grosspietsch, D.; Saenger, M.; Girod, B. Matching decentralized energy production and local consumption: A review of renewable energy systems with conversion and storage technologies. Wiley Interdiscip. Rev. Energy Environ. 2019, 8, e336. [Google Scholar] [CrossRef]
- Li, N.; Lukszo, Z.; Schmitz, J. An approach for sizing a PV–battery–electrolyzer–fuel cell energy system: A case study at a field lab. Renew. Sustain. Energy Rev. 2023, 181, 113308. [Google Scholar] [CrossRef]
- Balat, M. Potential importance of hydrogen as a future solution to environmental and transportation problems. Int. J. Hydrogen Energy 2008, 33, 4013–4029. [Google Scholar] [CrossRef]
- Kovač, A.; Paranos, M.; Marciuš, D. Hydrogen in energy transition: A review. Int. J. Hydrogen Energy 2021, 46, 10016–10035. [Google Scholar] [CrossRef]
- Dodds, P.E.; Staffell, I.; Hawkes, A.D.; Li, F.; Grünewald, P.; McDowall, W.; Ekins, P. Hydrogen and fuel cell technologies for heating: A review. Int. J. Hydrogen Energy 2015, 40, 2065–2083. [Google Scholar] [CrossRef]
- Moreno-Soriano, R.; Soriano-Moranchel, F.; Flores-Herrera, L.A.; Sandoval-Pineda, J.M.; De Guadalupe González-Huerta, R. Thermal efficiency of oxyhydrogen gas burner. Energies 2020, 13, 5526. [Google Scholar] [CrossRef]
- Bielmann, M.; Vogt, U.F.; Zimmermann, M.; Züttel, A. Seasonal energy storage system based on hydrogen for self sufficient living. J. Power Sources 2011, 196, 4054–4060. [Google Scholar] [CrossRef]
- Fumey, B.; Stoller, S.; Fricker, R.; Weber, R.; Dorer, V.; Vogt, U.F. Development of a novel cooking stove based on catalytic hydrogen combustion. Int. J. Hydrogen Energy 2016, 41, 7494–7499. [Google Scholar] [CrossRef]
- Topriska, E.; Kolokotroni, M.; Dehouche, Z.; Wilson, E. Solar hydrogen system for cooking applications: Experimental andnumerical study. Renew. Energy 2015, 83, 717–728. [Google Scholar] [CrossRef]
- Scott, M.; Powells, G. Sensing hydrogen transitions in homes through social practices: Cooking, heating, and the decomposition of demand. Int. J. Hydrogen Energy 2020, 45, 3870–3882. [Google Scholar] [CrossRef]
- Schmidt, O.; Gambhir, A.; Staffell, I.; Hawkes, A.; Nelson, J.; Few, S. Future cost and performance of water electrolysis: An expert elicitation study. Int. J. Hydrogen Energy 2017, 42, 30470–30492. [Google Scholar] [CrossRef]
- Krishnan, S.; Koning, V.; de Groot, M.T.; de Groot, A.; Mendoza, P.G.; Junginger, M.; Kramer, G.J. Present and future cost of alkaline and PEM electrolyser stacks. Int. J. Hydrogen Energy 2023, 48, 32313–32330. [Google Scholar] [CrossRef]
- Maharjan, S.; Zhang, Y.; Gjessing, S.; Tsang, D.H.K. User-centric demand response management in the smart grid with multiple providers. IEEE Trans. Emerg. Top. Comput. 2017, 5, 494–505. [Google Scholar] [CrossRef]
- Al Essa, M.J.M. Home energy management of thermostatically controlled loads and photovoltaic-battery systems. Energy 2019, 176, 742–752. [Google Scholar] [CrossRef]
- Lokeshgupta, B.; Sivasubramani, S. Multi-objective home energy management with battery energy storage systems. Sustain. Cities Soc. 2019, 47, 101458. [Google Scholar] [CrossRef]
- Panda, S.; Mohanty, S.; Rout, P.K.; Sahu, B.K.; Bajaj, M.; Zawbaa, H.M.; Kamel, S. Residential Demand Side Management model, optimization and future perspective: A review. Energy Rep. 2022, 8, 3727–3766. [Google Scholar] [CrossRef]
- Aljohani, T.M. Multilayer Iterative Stochastic Dynamic Programming for Optimal Energy Management of Residential Loads with Electric Vehicles. Int. J. Energy Res. 2024, 2024, 6842580. [Google Scholar] [CrossRef]
- Sridhar, A.; Honkapuro, S.; Ruiz, F.; Mohammadi-Ivatloo, B.; Annala, S.; Wolff, A. Aggregator decision analysis in residential demand response under uncertain consumer behavior. J. Clean. Prod. 2025, 495, 144997. [Google Scholar] [CrossRef]
- Aatabe, M.; El Abbadi, R.; Vargas, A.N.; Bouzid, A.E.M.; Bawayan, H.; Mosaad, M.I. Stochastic Energy Management Strategy for Autonomous PV-Microgrid Under Unpredictable Load Consumption. IEEE Access 2024, 12, 84401–84419. [Google Scholar] [CrossRef]
- Yi, T.; Li, Q.; Zhu, Y.; Shan, Z.; Ye, H.; Xu, C.; Dong, H. A hierarchical co-optimal planning framework for microgrid considering hydrogen energy storage and demand-side flexibilities. J. Energy Storage 2024, 84, 110940. [Google Scholar] [CrossRef]
- Karimi, H. A tri-objectives scheduling model for renewable-hydrogen-based microgrid system considering hydrogen storage system and demand-side management. Int. J. Hydrogen Energy 2024, 68, 1412–1422. [Google Scholar] [CrossRef]
- Youssef, A.R.; Abdelkareem, R.; Mousa, H.H.H.; Ismeil, M.A. Economic and Technical Evaluation of Hydrogen Storage in Hybrid Renewable Systems with Demand-Side Management: Upper Egypt Case Study. IEEE Access 2024, 12, 120250–120272. [Google Scholar] [CrossRef]
- Javid, S.S.M.; Derakhshan, G.; Hakimi, S.M. Energy scheduling in a smart energy hub system with hydrogen storage systems and electrical demand management. J. Build. Eng. 2023, 80, 108129. [Google Scholar] [CrossRef]
- Yousri, D.; Farag, H.E.Z.; Zeineldin, H.; El-Saadany, E.F. Integrated model for optimal energy management and demand response of microgrids considering hybrid hydrogen-battery storage systems. Energy Convers. Manag. 2023, 280, 116809. [Google Scholar] [CrossRef]
- Zakeri, B.; Syri, S. Electrical energy storage systems: A comparative life cycle cost analysis. Energy Rev. 2015, 42, 569–596. [Google Scholar] [CrossRef]
- Mohsenian-Rad, H. Optimal bidding, scheduling, and deployment of battery systems in California day-ahead energy market. IEEE Trans. Power Syst. 2016, 31, 442–453. [Google Scholar] [CrossRef]
- Xu, B.; Zhao, J.; Zheng, T.; Litvinov, E.; Kirschen, D.S. Factoring the Cycle Aging Cost of Batteries Participating in Electricity Markets. IEEE Trans. Power Syst. 2018, 33, 2248–2259. [Google Scholar] [CrossRef]
- Hu, X.; Zou, C.; Tang, X.; Liu, T.; Hu, L. Cost-optimal energy management of hybrid electric vehicles using fuel cell/battery health-aware predictive control. IEEE Trans. Power Electron. 2020, 35, 382–392. [Google Scholar] [CrossRef]
- Pu, Y.; Li, Q.; Zou, X.; Li, R.; Li, L.; Chen, W.; Liu, H. Optimal sizing for an integrated energy system considering degradation and seasonal hydrogen storage. Appl. Energy 2021, 302, 117542. [Google Scholar] [CrossRef]
- Qayyum, F.A.; Naeem, M.; Khwaja, A.S.; Anpalagan, A.; Guan, L.; Venkatesh, B. Appliance Scheduling Optimization in Smart Home Networks. IEEE Access 2015, 3, 2176–2190. [Google Scholar] [CrossRef]
- Nezhad, A.E.; Rahimnejad, A.; Gadsden, S.A. Home energy management system for smart buildings with inverter-based air conditioning system. Int. J. Electr. Power Energy Syst. 2021, 133, 107230. [Google Scholar] [CrossRef]
- Shao, S.; Pipattanasomporn, M.; Rahman, S. Development of physical-based demand response-enabled residential load models. IEEE Trans. Power Syst. 2013, 28, 607–614. [Google Scholar] [CrossRef]
- Pardiñas, Á.; Gómez, P.D.; Camarero, F.E.; Ortega, P.C. Demand–Response Control of Electric Storage Water Heaters Based on Dynamic Electricity Pricing and Comfort Optimization. Energies 2023, 16, 4104. [Google Scholar] [CrossRef]
- Lombardi, F.S.; Riva, F.; Sacchi, M.; Colombo, E. Enabling combined access to electricity and clean cooking with PV-microgrids: New evidences from a high-resolution model of cooking loads. Energy Sustain. Dev. 2019, 49, 78–88. [Google Scholar] [CrossRef]
- Najafi, M.H.; Jenson, D.; Lilja, D.J.; Riedel, M.D. Performing Stochastic Computation Deterministically. In IEEE Transactions on Very Large Scale Integration (VLSI) Systems; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 2925–2938. [Google Scholar] [CrossRef]
- Niknam, T.; Azizipanah-Abarghooee, R.; Narimani, M.R. An efficient scenario-based stochastic programming framework for multi-objective optimal micro-grid operation. Appl. Energy 2012, 99, 455–470. [Google Scholar] [CrossRef]
- Wu, L.; Shahidehpour, M.; Li, T. Stochastic security-constrained unit commitment. IEEE Trans. Power Syst. 2007, 22, 800–811. [Google Scholar] [CrossRef]
- Hendy, M.A.; Nayel, M.A. Sizing and Control of Isolated PV System for Self Sufficient House. In Proceedings of the IEEE Conference on Power Electronics and Renewable Energy, CPERE, Luxor, Egypt, 15–17 February 2023; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Kassem, M.; Bernard, J.; Revel, R.; Pélissier, S.; Duclaud, F.; Delacourt, C. Calendar aging of a graphite/LiFePO4 cell. J. Power Sources 2012, 208, 296–305. [Google Scholar] [CrossRef]
- Purewal, J.; Wang, J.; Graetz, J.; Soukiazian, S.; Tataria, H.; Verbrugge, M.W. Degradation of lithium ion batteries employing graphite negatives and nickel-cobalt-manganese oxide + spinel manganese oxide positives: Part 2, chemical-mechanical degradation model. J. Power Sources 2014, 272, 1154–1161. [Google Scholar] [CrossRef]
- Ecker, M.; Nieto, N.; Käbitz, S.; Schmalstieg, J.; Blanke, H.; Warnecke, A.; Sauer, D.U. Calendar and cycle life study of Li(NiMnCo)O2-based 18650 lithium-ion batteries. J. Power Sources 2014, 248, 839–851. [Google Scholar] [CrossRef]
- Papakonstantinou, G.; Algara-Siller, G.; Teschner, D.; Vidaković-Koch, T.; Schlögl, R.; Sundmacher, K. Degradation study of a proton exchange membrane water electrolyzer under dynamic operation conditions. Appl. Energy 2020, 280, 115911. [Google Scholar] [CrossRef]
- Torkan, R.; Ilinca, A.; Ghorbanzadeh, M. A genetic algorithm optimization approach for smart energy management of microgrid. Renew. Energy 2022, 197, 852–863. [Google Scholar] [CrossRef]
- Bhandari, R. Standalone electricity supply system with solar hydrogen and fuel cell: Possible to get rid of storage batteries? Int. J. Hydrogen Energy 2024, 104, 599–610. [Google Scholar] [CrossRef]
- Available online: https://power.larc.nasa.gov/data-access-viewer (accessed on 15 January 2024).
- Sheikholeslami, R.; Razavi, S. Progressive Latin Hypercube Sampling: An efficient approach for robust sampling-based analysis of environmental models. Environ. Model. Softw. 2017, 93, 109–126. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, Y.; Zhang, W.; Li, Y.; Su, X. Short-term interval prediction strategy of photovoltaic power based on meteorological reconstruction with spatiotemporal correlation and multi-factor interval constraints. Renew. Energy 2024, 237, 121834. [Google Scholar] [CrossRef]
- Zhang, M.; Cai, S.; Xie, Y.; Zhou, B.; Zheng, W.; Wu, Q.; Wen, J. Supply Resilience Constrained Scheduling of MEGs for Distribution System Restoration: A Stochastic Model and FW-PH Algorithm. IEEE Trans. Smart Grid 2025, 16, 194–208. [Google Scholar] [CrossRef]
- Zhang, T.; Zhao, W.; He, Q.; Xu, J. Optimization of Microgrid Dispatching by Integrating Photovoltaic Power Generation Forecast. Sustainability 2025, 17, 648. [Google Scholar] [CrossRef]
- Ma, K.; Yang, J.; Liu, P. Relaying-Assisted Communications for Demand Response in Smart Grid: Cost Modeling, Game Strategies, and Algorithms. IEEE J. Sel. Areas Commun. 2020, 38, 48–60. [Google Scholar] [CrossRef]
- Zhang, H.; Yue, D.; Dou, C.; Hancke, G.P. PBI Based Multi-Objective Optimization via Deep Reinforcement Elite Learning Strategy for Micro-Grid Dispatch with Frequency Dynamics. IEEE Trans. Power Syst. 2023, 38, 488–498. [Google Scholar] [CrossRef]







| Appliance Name | Rating (W) | Quantity | Operating Time (h) |
|---|---|---|---|
| Refrigerator | 140 | 1 | 00:00 to 23:59 |
| Router | 10 | 1 | 00:00 to 23:59 |
| Lights (LED) | 15 | 1 | 00:00 to 23:59 |
| 12 | 2 | 07:00 to 09:00 | |
| 12:00 to 14:00 | |||
| 18:00 to 20:00 | |||
| 15 | 2 | 18:00 to 23:00 | |
| TV | 100 | 1 | 07:00 to 08:00 |
| 13:00 to 15:00 | |||
| 20:00 to 22:00 | |||
| Personal computer | 200 | 1 | 20:00 to 23:00 |
| Fans (summer only) | 100 | 2 | 00:00 to 09:00 |
| 12:00 to 23:59 | |||
| Inverter air conditioner (summer only) | 1500 | 2 | Table 2 |
| Others | 400 | 1 | 2 h ~ Uniform [07:00 to 23:59] |
| (kW) | (°C/kW) | Temperature Set Point | ||
|---|---|---|---|---|
| 1.5 | 0.99 | 0.01 | 0.29 | 24 °C for t ϵ {[0:00–8:00] U [18:00–0:00]} |
| 26 °C for t ϵ {[8:00–18:00]} |
(kW) | (%) | (°C) | (gallon) | ||
|---|---|---|---|---|---|
| 3 | 95 | 14 | 22.29 | 26.45 | 15 |
| Categories | Cat A | Cat B | Cat C [Shower] |
|---|---|---|---|
| Flow rate (L/m) | 1 | 6 | 8 |
| Duration (m) | 1 | 1 | 5 |
| Inc/day | 28 | 12 | 2 |
| σ | 2 | 2 | 2 |
| Dish | Power Range | Average Time Range (Minute) | Average Starting Time Range | |
|---|---|---|---|---|
| 1 | Rice | Boil: HP | 15 | 01:00 PM to 02:00 PM |
| Simmer: LP | 20 | |||
| Steam: very low power | 10 | |||
| Meat | Boil: HP | 40 | ||
| Simmer: LP | 65 | |||
| 2 | Rice | Boil: HP | 15 | |
| Simmer: LP | 20 | |||
| Steam: very low power | 10 | |||
| Chicken | Boil: HP | 40 | ||
| Simmer: LP | 50 | |||
| Frying: MP | 20 | |||
| 3 | Molokhia | MP | 35 | |
| 4 | Chicken pane | MP | 40 | |
| 5 | Vegetables | Boil: HP | 25 | |
| Simmer: LP | 40 | |||
| 6 | Remaining food or fast food | MP | 40 | |
| 7 | Delivery or non-cook food | No power | - |
| Parameters | Value | Component | Size |
|---|---|---|---|
| (kWh) | 5293 | PV (kW) | 6.25 |
| (kWh) | 6205 | Li-io battery (kWh) | 45 |
| (kg/kWh) | 0.0212 | PEM electrolyzer (kW) | 2.6 |
| (kWh/kg) | 23.1 | Fuel cell (kW) | 6 |
| (%) | 80 | Hydrogen tank (kg) | 45 |
| (%) | 75 | ||
| (kW) | 8 | ||
| 182 | |||
| SF (%) | 20 |
| Parameter | Value | Reference | Parameter | Value | Reference |
|---|---|---|---|---|---|
| 90% | 13.79 × 10−6 V | [30] | |||
| 10 kW | 0.07 V | [30] | |||
| J | 20 | 1400 USD/kW | [30] | ||
| 96 | Δ | 32 × 10−6 V/h | [30] | ||
| 0.25 h | 30 × 10−6 V | [30] | |||
| 140 USD/kWh | [30] | 0.2 V | [30] | ||
| 8.662 × 10−6 V/h | [30] | 1260 USD/kW | [30] | ||
| 10 × 10−6 V/h | [30] | 240 USD/kW | [3] | ||
| 40 cells | 200 USD/kg | [3] |
| Initial SOC of Li-Ion Battery (%) | 80 | 70 | 60 | 50 |
|---|---|---|---|---|
| Starting time of WM | 10:15 AM | 10:00 AM | 10:00 AM | 10:00 AM |
| Starting time of DW | 07:45 PM | 10:00 PM | 10:00 PM | 10:00 PM |
| SOC minimum (%) | 22 | 20 | 24 | 24 |
| SOC maximum (%) | 90 | 90 | 90 | 90 |
| Set point of WH | 80 | 75 | 76 | 76 |
| Temp. tolerance of WH | 11 | 2 | 8 | 8 |
| Dump load (%) | 0 | 0 | 0 | 0 |
| Load shedding (%) | 0 | 0 | 0 | 0 |
| Battery degradation cost (USD/day) | 0.447 | 0.578 | 0.604 | 0.604 |
| Electrolyzer degradation cost (USD/day) | 1.6 | 0 | 0 | 0 |
| Fuel cell degradation cost (USD/day) | 8.86 | 8.30 | 6.67 | 8.63 |
| Total degradation cost (USD/day) | 10.91 | 8.81 | 7.28 | 9.23 |
| Initial SOC of Li-Ion Battery (%) | 80 | 70 | 60 | 50 |
|---|---|---|---|---|
| Starting time of WM | 09:30 AM | 09:45 AM | 10:45 AM | 10:00 AM |
| Starting time of DW | 01:30 PM | 01:30 PM | 01:15 PM | 01:15 PM |
| SOC minimum (%) | 26 | 26 | 21 | 23 |
| SOC maximum (%) | 90 | 90 | 88 | 90 |
| Dump load (%) | 3.03 | 2.44 | 3.14 | 3.14 |
| Load shedding (%) | 0 | 0 | 0 | 0 |
| Battery degradation cost (USD/day) | 1.187 | 0.912 | 0.797 | 0.850 |
| Electrolyzer degradation cost (USD/day) | 2.363 | 2.162 | 1.847 | 1.847 |
| Fuel cell degradation cost (USD/day) | 7.222 | 8.537 | 7.751 | 6.943 |
| Total degradation cost (USD/day) | 10.773 | 11.612 | 10.396 | 9.641 |
| Operation Case | Using the Proposed SDSM | Average of 10,000 Random Operation Cases |
|---|---|---|
| Expected battery lifetime (years) | 6.980 | 7.070 |
| Expected fuel cell lifetime (years) | 2.920 | 2.0 |
| Expected electrolyzer lifetime (years) | 7.314 | 4.653 |
| LCOE (USD/kWh) | 0.2694 | 0.3483 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hendy, M.A.; Nayel, M.A.; Abdelrahem, M. Stochastic Demand-Side Management for Residential Off-Grid PV Systems Considering Battery, Fuel Cell, and PEM Electrolyzer Degradation. Energies 2025, 18, 3395. https://doi.org/10.3390/en18133395
Hendy MA, Nayel MA, Abdelrahem M. Stochastic Demand-Side Management for Residential Off-Grid PV Systems Considering Battery, Fuel Cell, and PEM Electrolyzer Degradation. Energies. 2025; 18(13):3395. https://doi.org/10.3390/en18133395
Chicago/Turabian StyleHendy, Mohamed A., Mohamed A. Nayel, and Mohamed Abdelrahem. 2025. "Stochastic Demand-Side Management for Residential Off-Grid PV Systems Considering Battery, Fuel Cell, and PEM Electrolyzer Degradation" Energies 18, no. 13: 3395. https://doi.org/10.3390/en18133395
APA StyleHendy, M. A., Nayel, M. A., & Abdelrahem, M. (2025). Stochastic Demand-Side Management for Residential Off-Grid PV Systems Considering Battery, Fuel Cell, and PEM Electrolyzer Degradation. Energies, 18(13), 3395. https://doi.org/10.3390/en18133395







