Thermo-Hydrodynamic Features of Grooved Heat Sink with Droplet-Shaped Fins Based on Taguchi Optimization and Field Synergy Analysis
Abstract
1. Introduction
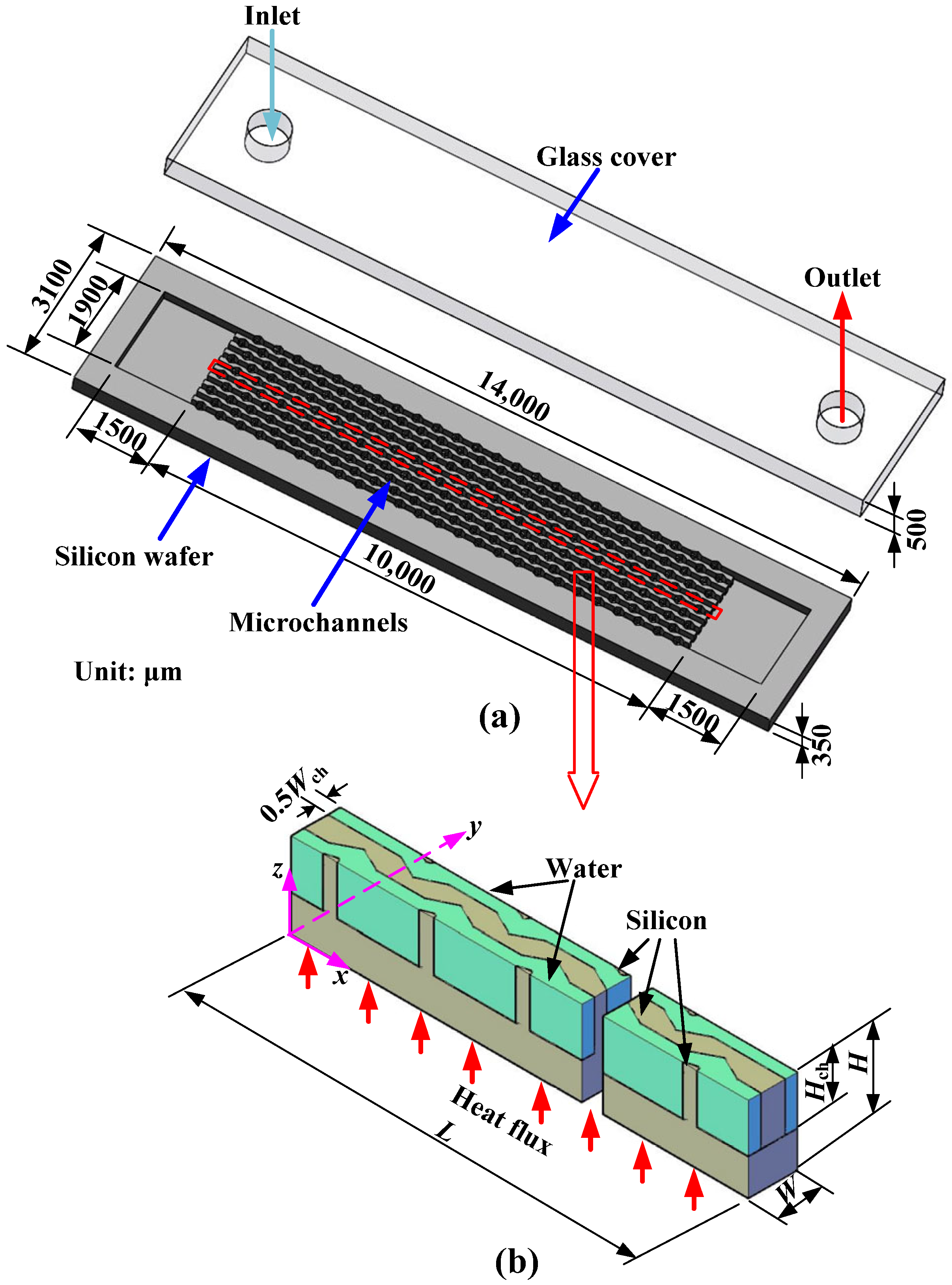
2. Model and Numerical Solution
2.1. Configurations and Orthogonal Experiment
2.2. Governing Equation and Methodology
3. Evaluation Index and Model Verification
3.1. Evaluation Index
3.2. Model Validation
4. Results and Discussion
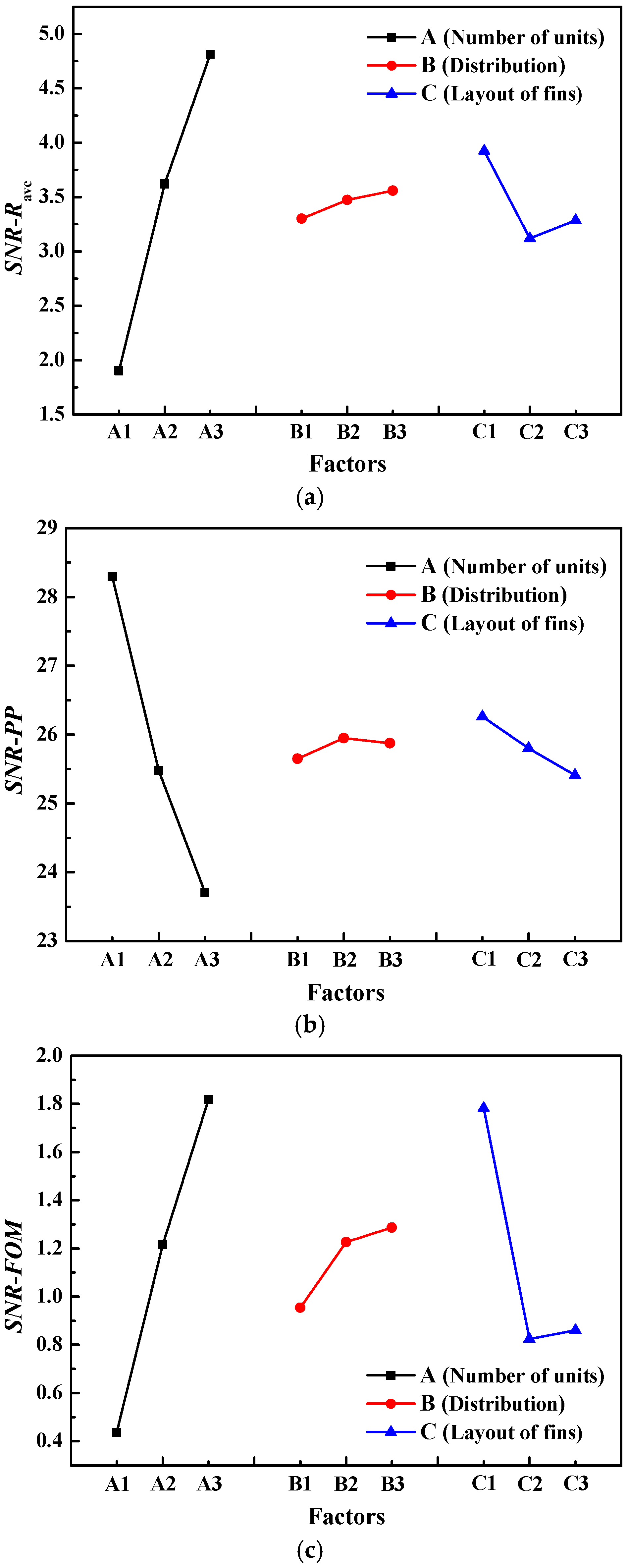
4.1. Taguchi Optimization
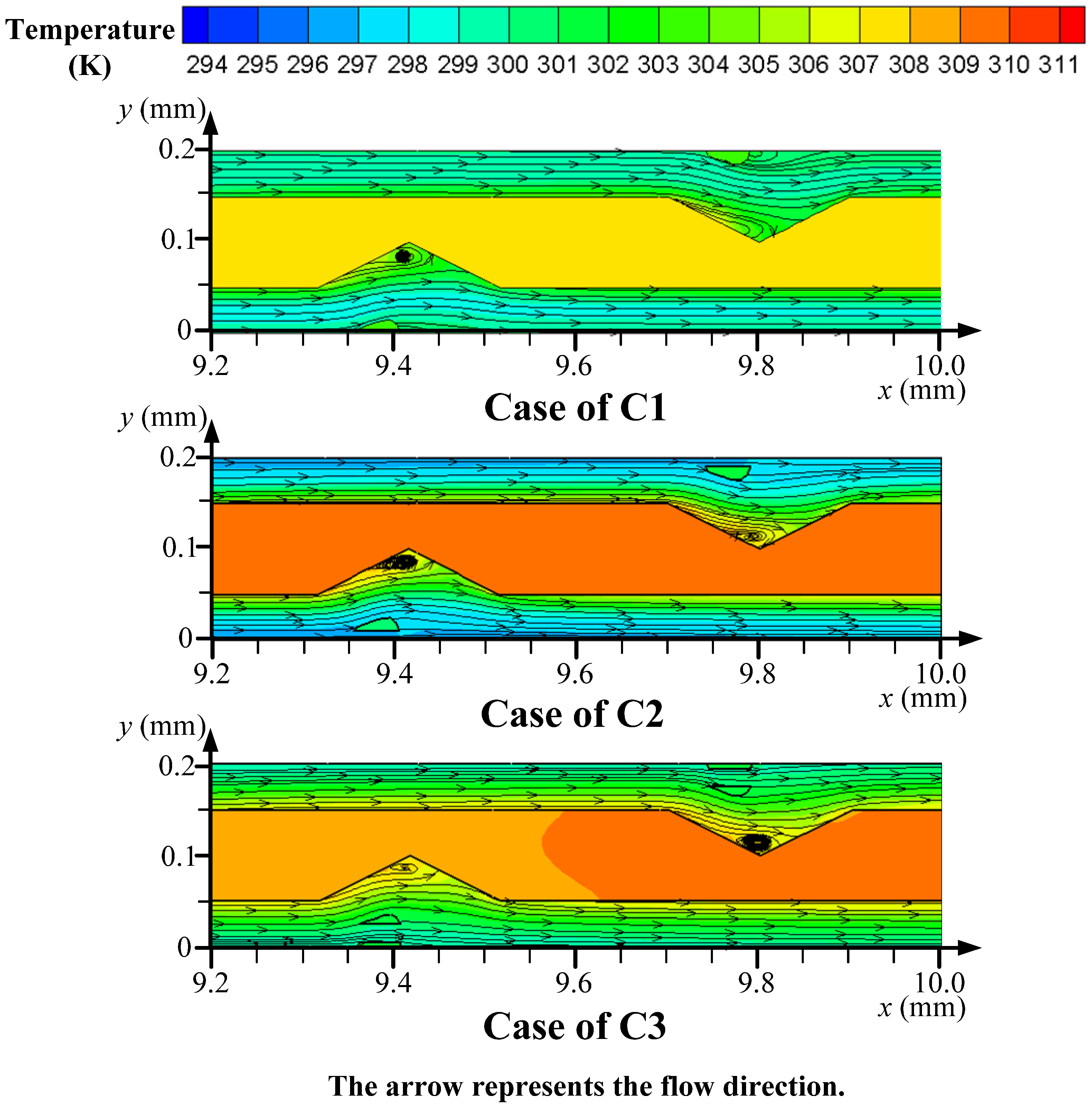
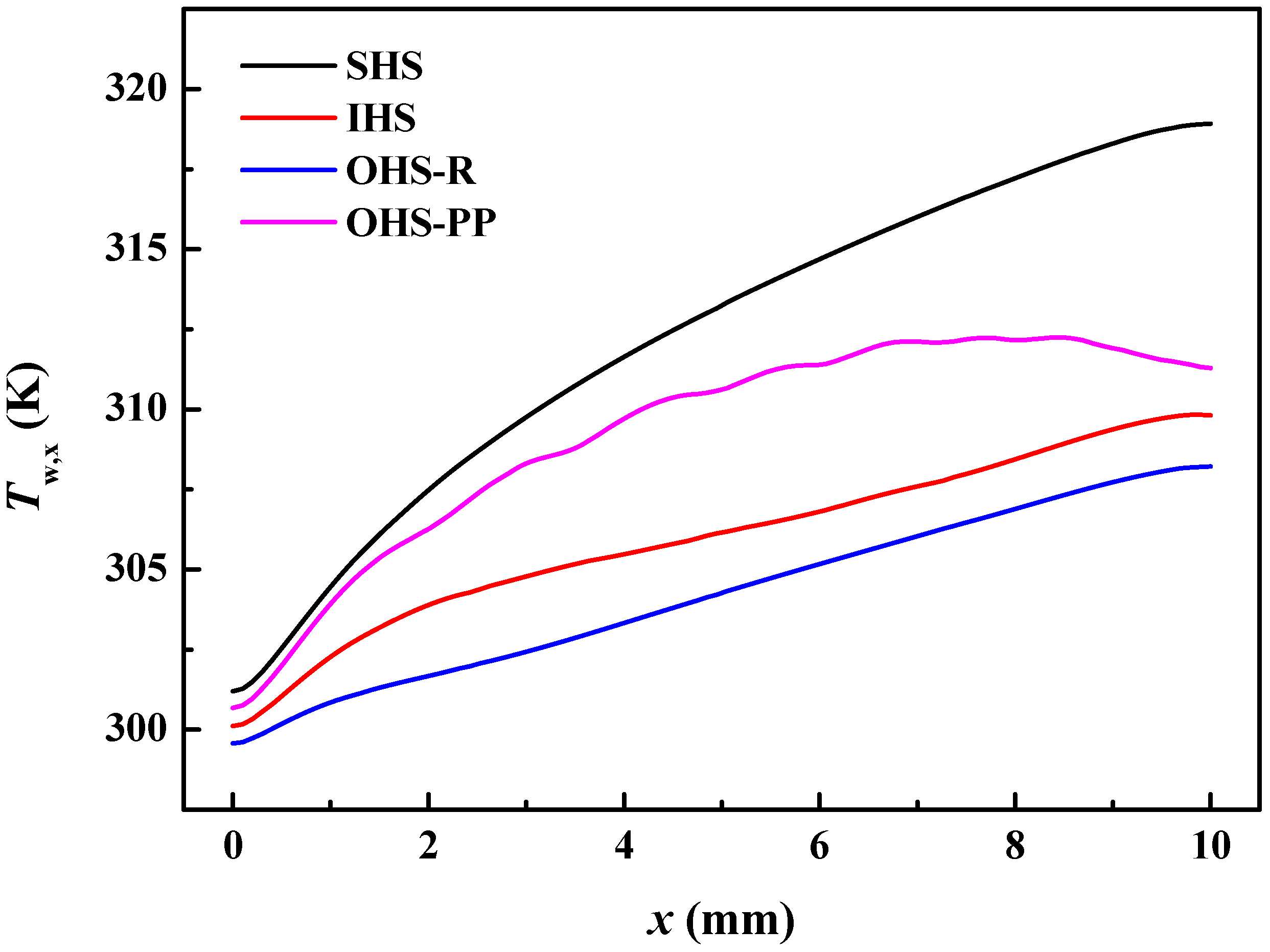
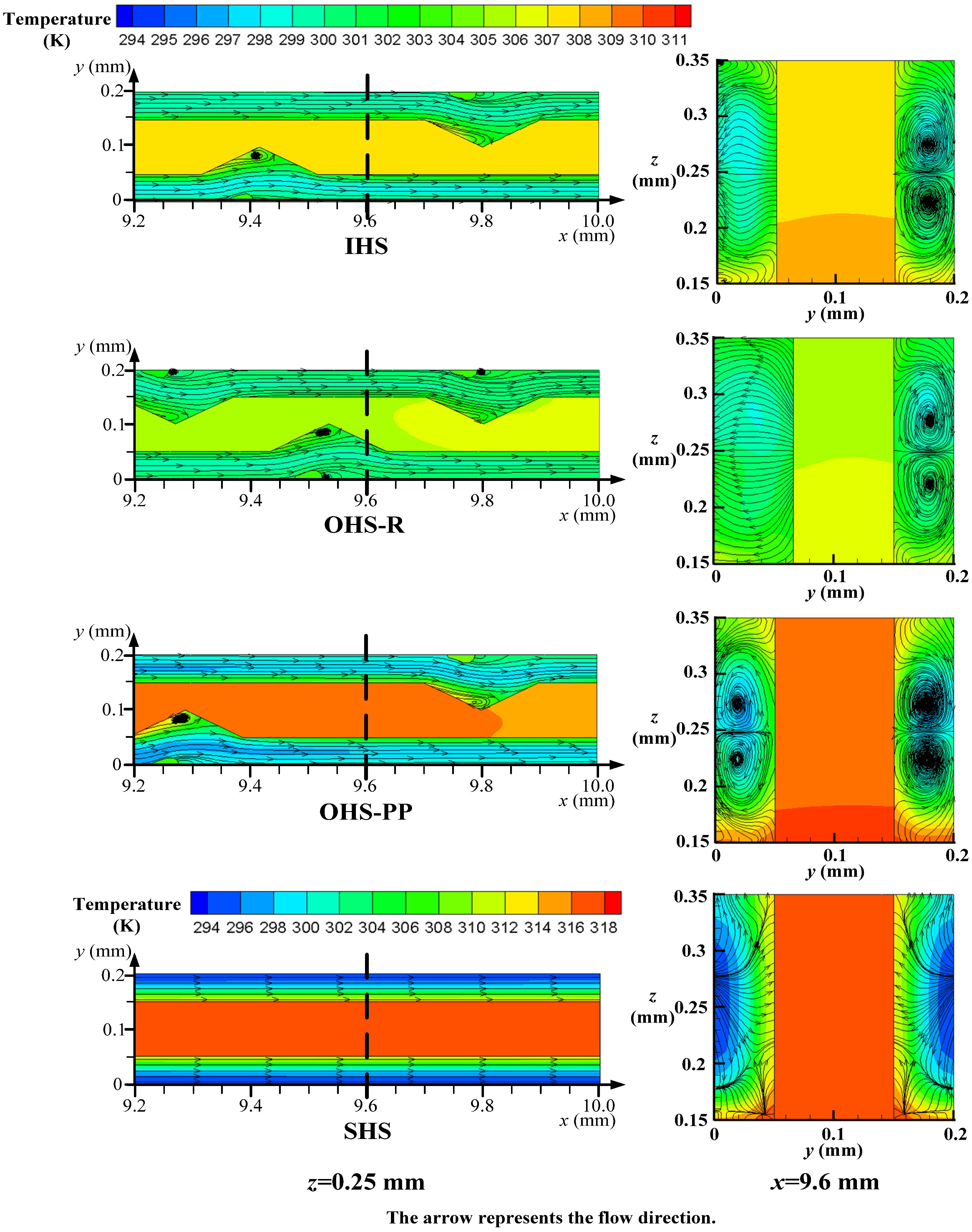
4.2. Thermo-Hydrodynamic Features
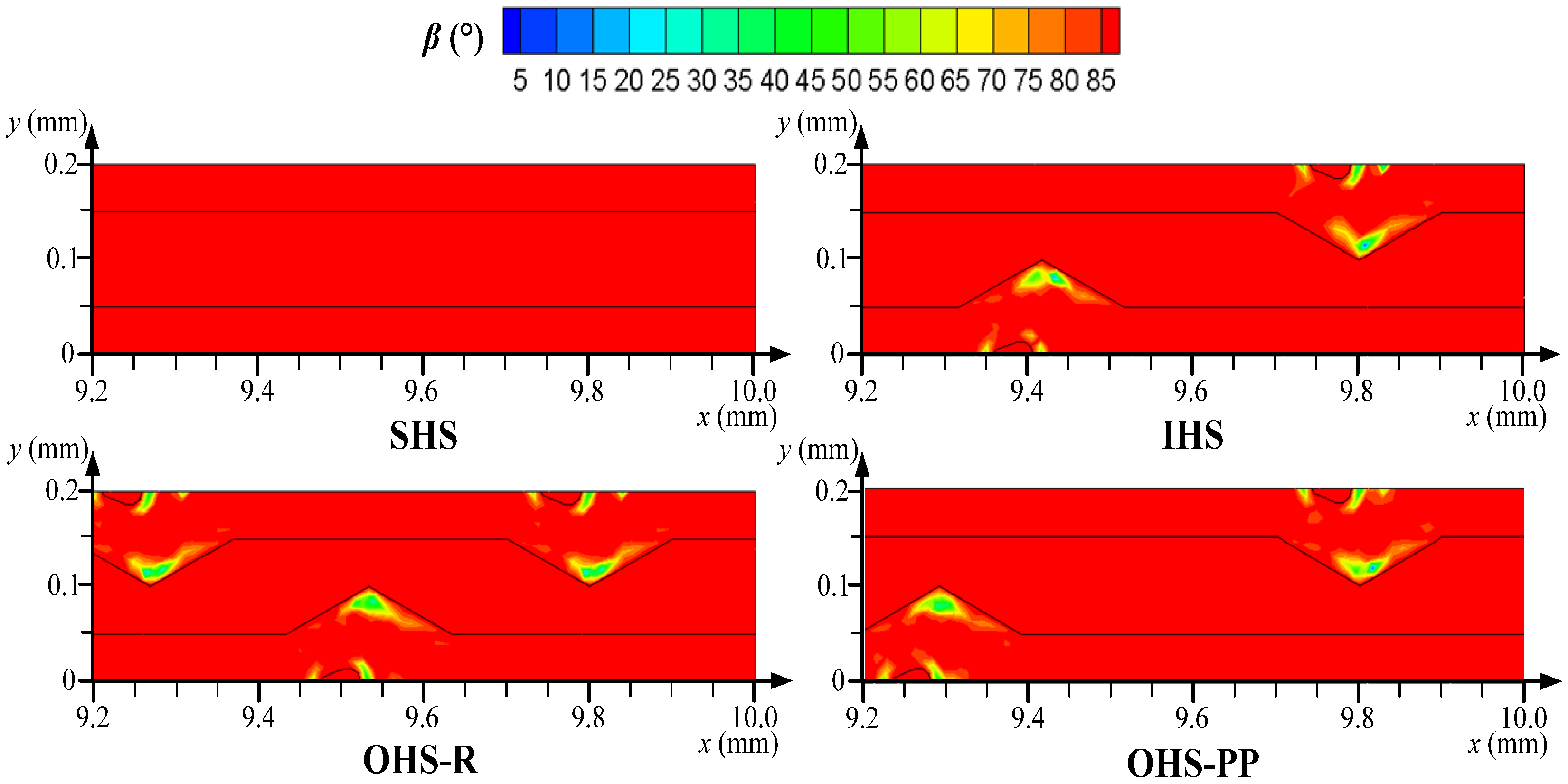
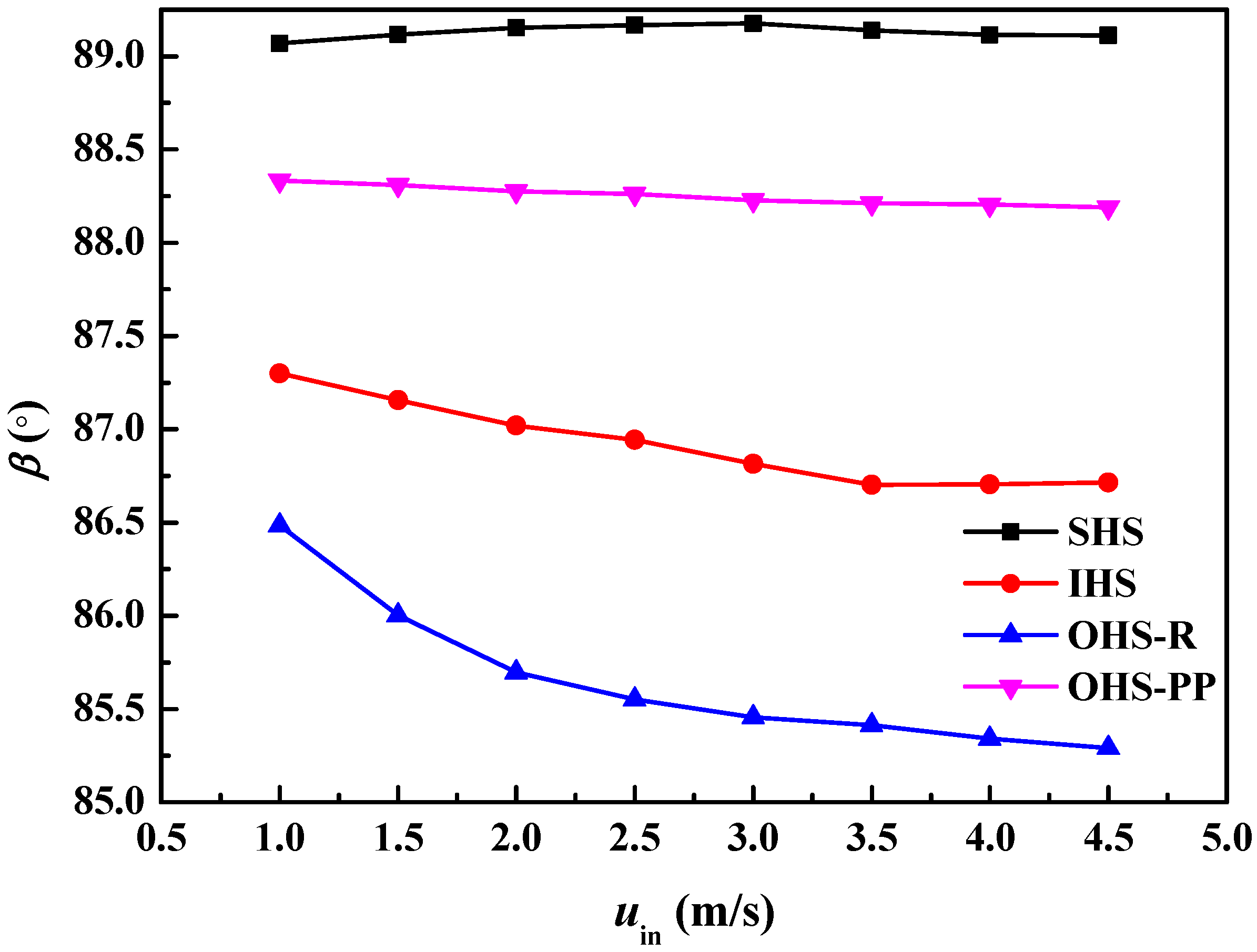
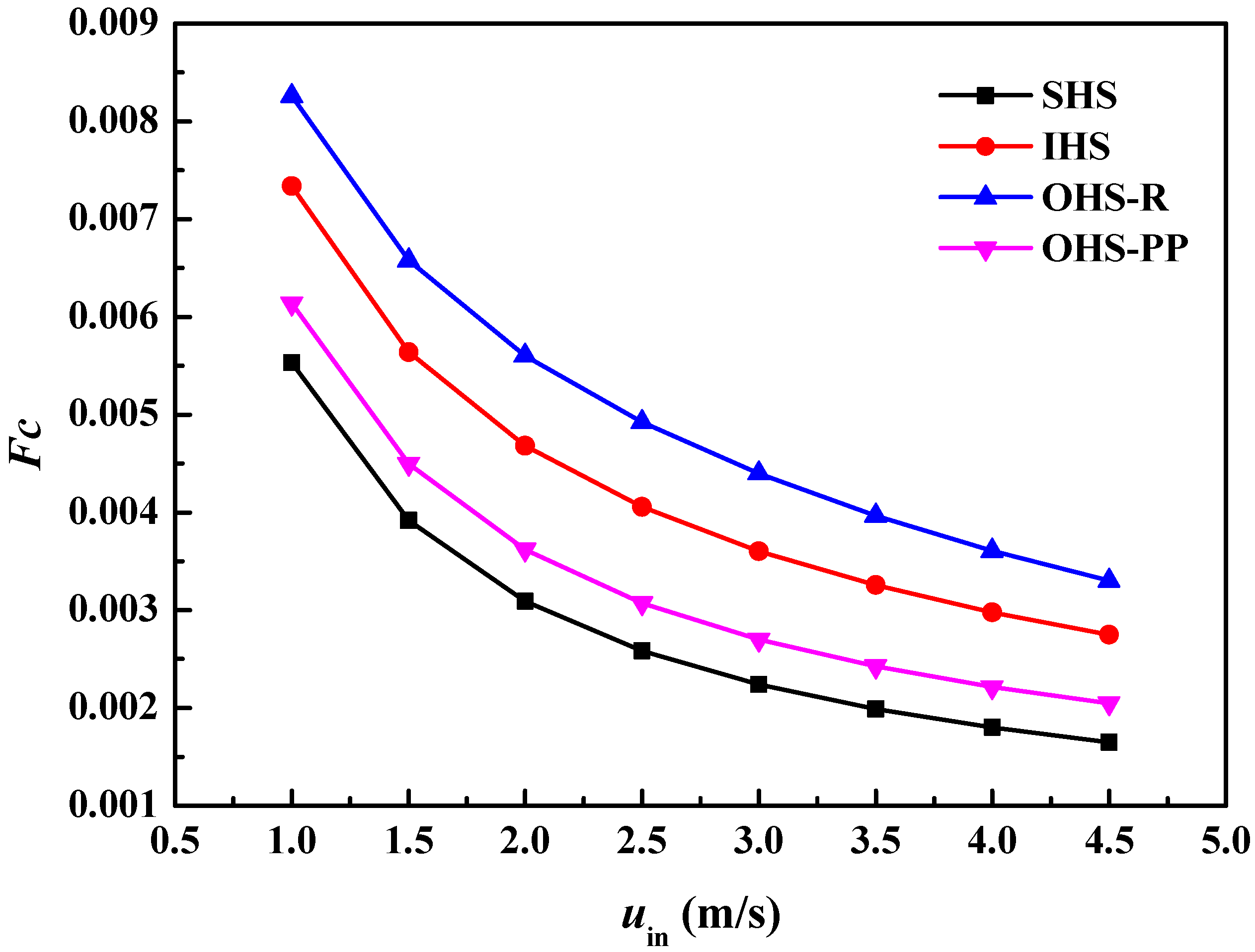
4.3. Field Synergy Analysis
5. Conclusions
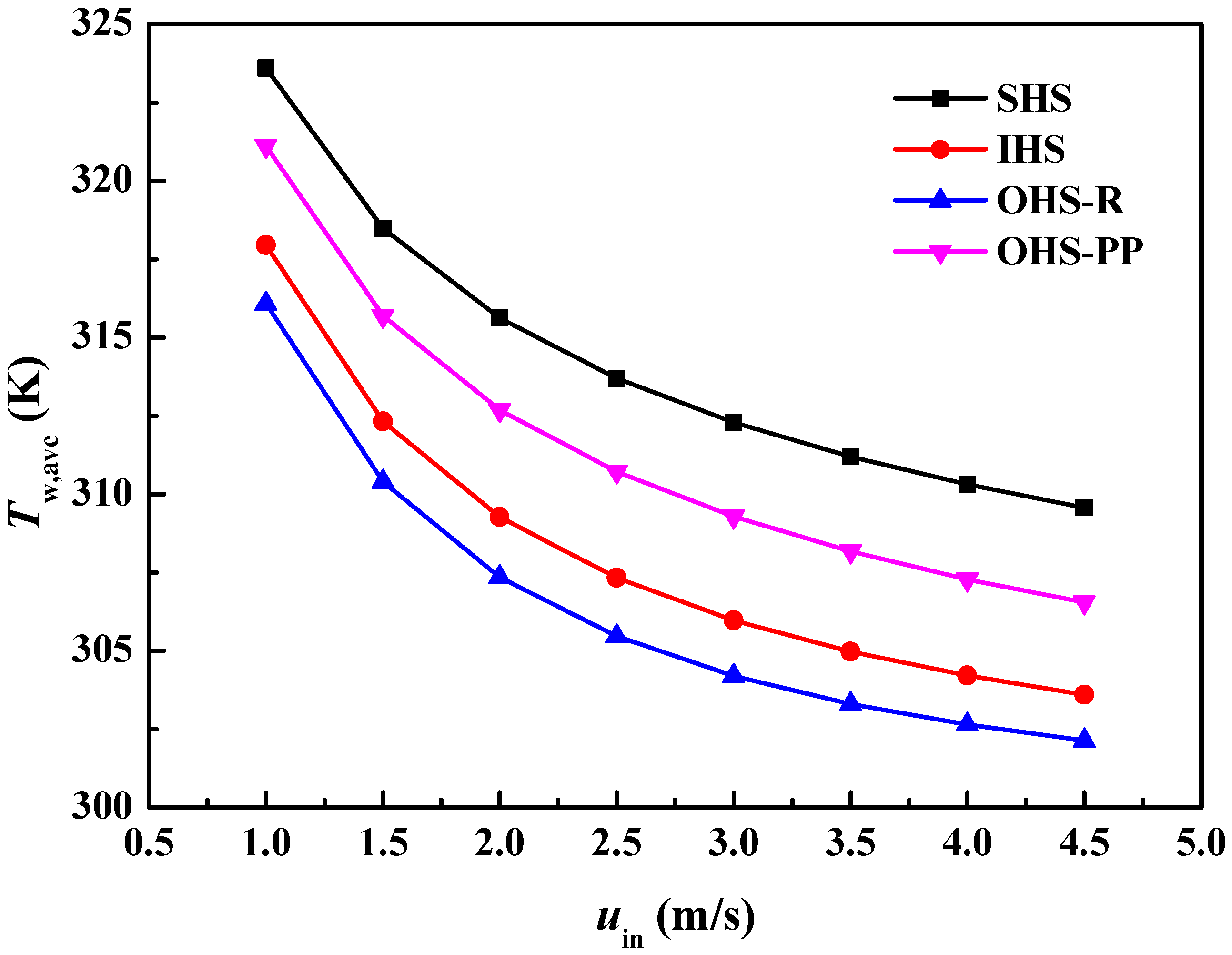
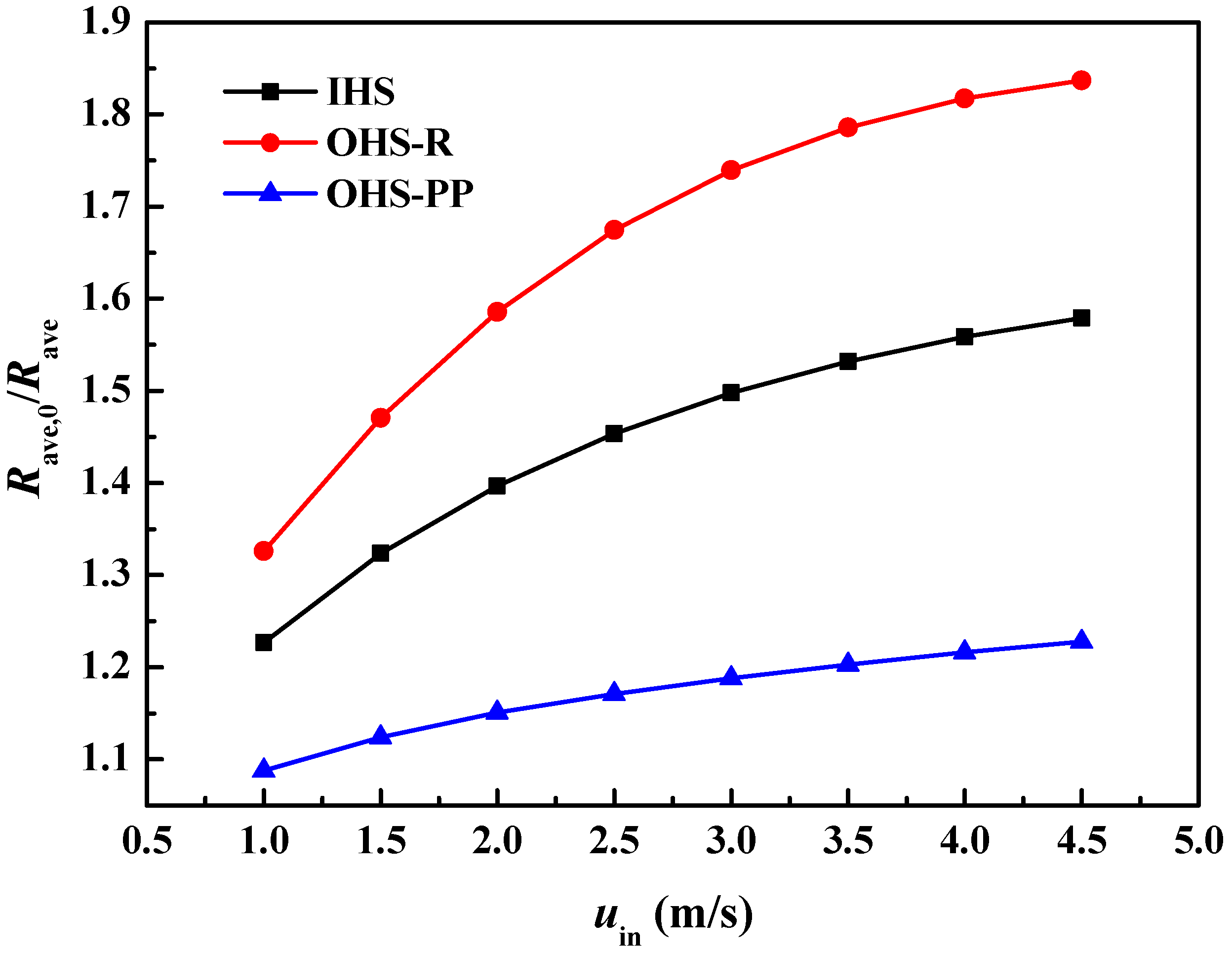
- The number of combined units presents the greatest influence on thermal resistance, pump power, and overall efficiency, followed by the number of fins in each unit. For both thermal resistance and overall efficiency, the optimal configuration is the heat sink with 21 combined units, arranged from dense to sparse, with one fin in each unit (A3B3C1), which shows a 14.05% reduction in thermal resistance and a 8.5% increment in overall efficiency. For pump power, the optimal combination is the heat sink with five combined units, arranged from sparse to dense, with one fin in each unit (A1B2C1), which presents a 27.61% decrease in pump power.
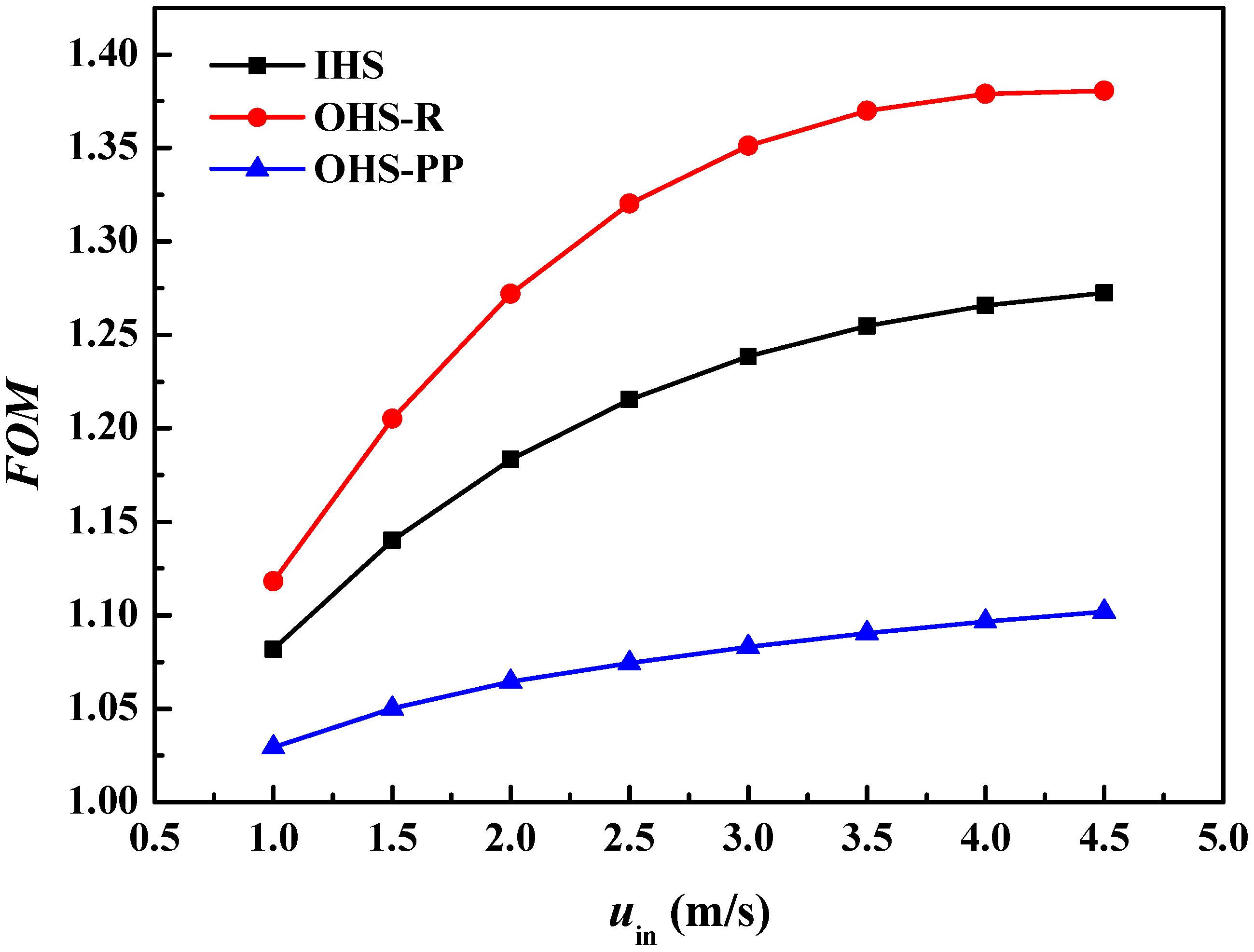
- Compared to the cases with two or three fins in each unit, the single droplet-shaped fin presents superior thermal and hydrodynamic performances because of the enhanced impingement effect and reduced flow friction. The heat removal efficiency of the configuration A3B3C1 is improved because of the better coupling effect of flow and temperature fields with a 4.29% smaller synergy angle β compared to the smooth heat sink. Improving the coupling between the flow and temperature fields is beneficial for enhancing the cooling capability.
- The optimized heat sinks can better balance heat dissipation and energy consumption, which can be applied to heat dissipation of high-power equipment in high-tech fields, e.g., DCs, power batteries, and energy conversion systems, to improve the cost-effectiveness of liquid cooling systems. In addition, the thermophysical properties of the coolant have a direct impact on the overall capability of the cooling systems. Further numerical and experimental studies will be conducted to explore the thermo-hydrodynamic features of novel coolants, e.g., nanofluids, CO2, phase change microcapsule suspension, etc. The cooling efficiency of this kind of heat sink under unsteady heat flux conditions and the intelligent regulation of cooling systems will be analyzed in detail to provide a theoretical basis for advanced thermal management.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | thermal diffusion coefficient [m2/s] |
| A | area [m2] |
| cp | specific heat capacity [J/(kg·K)] |
| CR | contribution ratio [-] |
| Dh | hydrodynamic diameter [m] |
| f | friction coefficient [-] |
| Fc | field synergy number [-] |
| FOM | figure of merit [-] |
| h | heat transfer coefficient [W/(m2·K)] |
| Hch | height of microchannel [m] |
| k | ratio of channel width to height [-] |
| K | Hagenbach’s factor [-] |
| L | length [m] |
| S | space between two grooves [m] |
| m | number of parallel channel [-] |
| N | number of combined units [-] |
| Nu | Nusselt number [-] |
| Δp | pressure drop [Pa] |
| Po | Poiseuille number [-] |
| PP | pump power [W] |
| Pr | Prandtl number [-] |
| qb | heat flux per area [W/m2] |
| Qv | flow rate [m3/s] |
| R | thermal resistance [K/W] |
| Re | Reynolds number [-] |
| SNR | signal-to-noise ratio [-] |
| T | temperature [K] |
| u | velocity in x direction [m/s] |
| V | velocity vector [m/s] |
| Wch | width of microchannel [m] |
| Greek symbols | |
| β | synergy angle [°] |
| λ | thermal conductivity [W/(m·K)] |
| μ | dynamic viscosity [Pa·s] |
| ρ | density [kg/m3] |
| ν | momentum diffusion coefficient [m2/s] |
| Subscript | |
| ave | average |
| b | bottom |
| con | convection |
| f | fluid |
| in | inlet |
| out | outlet |
| s | solid |
| w | wall |
| 0 | smooth heat sink |
References
- Isazadeh, A.; Ziviani, D.; Claridge, D. Thermal management in legacy air-cooled data centers: An overview and perspectives. Renew. Sustain. Energy Rev. 2023, 187, 113707. [Google Scholar] [CrossRef]
- He, Z.Q.; Yan, Y.F.; Zhang, Z.E. Thermal management and temperature uniformity enhancement of electronic devices by micro heat sinks: A review. Energy 2021, 216, 119223. [Google Scholar] [CrossRef]
- Li, Z.Y.; Luo, H.L.; Jiang, Y.G.; Liu, H.; Xu, L.; Cao, K.; Wu, H.; Gao, P.; Liu, H. Comprehensive review and future prospects on chip-scale thermal management: Core of data center’s thermal management. Appl. Therm. Eng. 2024, 251, 123612. [Google Scholar] [CrossRef]
- Pan, M.Q.; Wang, H.Q.; Zhong, Y.J.; Hu, M.; Zhou, X.; Dong, G.; Huang, P. Experimental investigation of the heat transfer performance of microchannel heat exchangers with fan-shaped cavities. Int. J. Heat Mass Transf. 2019, 134, 1199–1208. [Google Scholar] [CrossRef]
- Alfellag, M.A.; Ahmed, H.E.; Fadhil, O.T.; Kherbeet, A.S. Optimal hydrothermal design of microchannel heat sink using trapezoidal cavities and solid/slotted oval pins. Appl. Therm. Eng. 2019, 158, 113765. [Google Scholar] [CrossRef]
- Sun, L.; Li, J.; Hu, H.; Ma, J.; Peng, H. Numerical study on heat transfer and flow characteristics of novel microchannel heat sinks. Int. J. Therm. Sci. 2022, 176, 107535. [Google Scholar] [CrossRef]
- Fathi, M.; Heyhat, M.M.; Targhi, M.Z.; Emadi, A. Semi-porous-fin microchannel heat sinks for enhanced micro-electronics cooling. Int. Commun. Heat Mass Transf. 2024, 157, 107814. [Google Scholar] [CrossRef]
- Cui, H.C.; Fan, W.H.; Wang, J.; Yu, M.J.; Zhang, Z.K.; Liu, Z.C.; Liu, W. Characteristics analysis and structure optimization of a hybrid micro-jet impingement/micro-channel heat sink. Appl. Therm. Eng. 2024, 245, 122769. [Google Scholar] [CrossRef]
- Chen, S.J.; Li, S.W.; Hu, Z.Z. Fluid flow and heat transfer characteristics of manifold microchannel heat sinks with ribs of different shapes. Int. J. Heat Mass Transf. 2025, 251, 127300. [Google Scholar] [CrossRef]
- Bhandari, P. Numerical investigations on the effect of multi-dimensional stepness in open micro pin fin heat sink using single phase liquid fluid flow. Int. Commun. Heat Mass Transf. 2022, 138, 106392. [Google Scholar] [CrossRef]
- Wang, S.S.; Xia, G.D.; Ma, D.D. Thermal-hydraulic performance in novel microchannels with asymmetric cavities and coaxially variable-size water droplet ribs. Int. Commun. Heat Mass Transf. 2024, 159, 108032. [Google Scholar] [CrossRef]
- Liu, L.Y.; Liu, H.T.; Luo, J.; Tang, J. Thermal-hydraulic performance of an imperfectly bonded ultrathin manifold micro pin-fin channel heat sink. Int. Commun. Heat Mass Transf. 2024, 156, 107684. [Google Scholar] [CrossRef]
- Sahel, D.; Boudaoud, W.; Bouabidi, A.; Alem, K. Impact of splitter inserts combined with perforation technique and transversal fins on the performance of micro pin heat sinks. Int. Commun. Heat Mass Transf. 2024, 159, 108094. [Google Scholar] [CrossRef]
- Xue, Z.G.; Yan, Y.F.; Shen, K.M.; You, J.; Zhang, C.; He, Z. Investigation on thermal-hydraulic performance for local hotspot via variable density design of a micro-jet heat sink. Int. Commun. Heat Mass Transf. 2024, 156, 107668. [Google Scholar] [CrossRef]
- Zhou, J.H.; Lu, M.X.; Han, L.; Zhao, Q.; Li, Q.; Chen, X. Topological manifold microchannel cooling for thermal management of divertor in fusion reactor. Energy 2025, 315, 134145. [Google Scholar] [CrossRef]
- Liu, Z.X.; Han, Q.; Han, J.W.; Zhang, Y.; Chen, X.; Li, W. Flow boiling in a relatively large copper heat sink comprised of Tesla microchannels. Int. J. Heat Mass Transf. 2025, 236, 126366. [Google Scholar] [CrossRef]
- Ma, D.D.; Liu, Y.S.; Zhang, X.M.; Xia, G. Experimental and numerical investigation of the thermohydraulic performance of a variable-period sinusoidal microchannel heat sink. Appl. Therm. Eng. 2025, 262, 125234. [Google Scholar] [CrossRef]
- Wang, Z.X.; Tao, W.Q. Heat transfer and pressure drop characteristics of microchannel cold plate in commercial CPU-package cooling system. Int. J. Heat Mass Transf. 2025, 246, 127060. [Google Scholar] [CrossRef]
- Song, H.L.; Han, B.; Wang, Y.; Zhang, Q. Enhanced heat transfer of alveolar biomimetic interlaced hollow lattice metastructures. Energy 2025, 326, 136272. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Li, D.Y.; Wang, B.X. A novel concept for convective heat transfer enhancement. Int. J. Heat Mass Transf. 1998, 41, 2221–2225. [Google Scholar] [CrossRef]
- Yao, P.T.; Zhai, Y.L.; Li, Z.H.; Shen, X.; Wang, H. Thermal performance analysis of multi-objective optimized microchannels with triangular cavity and rib based on field synergy principle. Case Stud. Therm. Eng. 2021, 25, 100963. [Google Scholar]
- Mukherjee, A.; Senapati, J.R.; Barik, A.K. Field synergy and thermodynamic evaluation of a mini-duct with several protrusions utilizing the cross-flow method: A numerical exercise. Int. Commun. Heat Mass Transf. 2023, 145, 106817. [Google Scholar] [CrossRef]
- Bazkhane, S.; Zahmatkesh, I. Taguchi–based sensitivity analysis of hydrodynamics and heat transfer of nanofluids in a microchannel heat sink (MCHS) having porous substrates. Int. Commun. Heat Mass Transf. 2020, 118, 104885. [Google Scholar] [CrossRef]
- Huang, S.; Li, J.Q.; Zhu, K.; Dong, J.; Jiang, Y. Multifactor optimization of medium and deep U-type borehole heat exchanger design using Taguchi method. Geothermics 2023, 109, 102644. [Google Scholar] [CrossRef]
- Shi, Z.R.; Lan, X.; Cao, J.; Zhao, N.; Cheng, Y. Numerical study of variable density and height flow guided pin fin in an open microchannel heat sink. Int. J. Heat Mass Transf. 2024, 225, 125405. [Google Scholar] [CrossRef]
- Tang, Z.G.; Yin, C.; Xiang, Y.; Yu, P.; Cheng, J. Multi-objective optimization of a hybrid nanofluid jet impinging on a microchannel heat sink with semi-airfoil ribs based on field synergy principle. Int. J. Heat Mass Transf. 2024, 225, 125431. [Google Scholar] [CrossRef]
- He, W.; Wang, Z.X.; Li, J.Q.; Li, Q. Investigation of heat transfer performance for through-silicon via embedded in micro pin fins in 3D integrated chips. Int. J. Heat Mass Transf. 2023, 214, 124442. [Google Scholar] [CrossRef]
- Jia, Y.T.; Xia, G.D.; Li, Y.F.; Ma, D.; Cai, B. Heat transfer and fluid flow characteristics of combined microchannel with cone-shaped micro pin fins. Int. Commun. Heat Mass Transf. 2018, 92, 78–89. [Google Scholar] [CrossRef]
- Li, Y.F.; Wang, Z.P.; Yang, J.L.; Liu, H. Thermal and hydraulic characteristics of microchannel heat sinks with cavities and fins based on field synergy and thermodynamic analysis. Appl. Therm. Eng. 2020, 175, 115348. [Google Scholar] [CrossRef]
- Li, Y.F.; Wang, T.Y.; Wang, Z.P.; Yang, J.; Cao, W.; Ma, X. Thermohydraulic performance analysis and parameters optimization of the combined heat sinks with microchannels and micro pin-fins. Appl. Therm. Eng. 2024, 241, 122443. [Google Scholar] [CrossRef]
- Li, Y.F.; Yang, B.; Wang, Z.P.; Guo, Q. Investigation on the thermal and hydraulic characteristics of the micro heat sinks with grooves and pin fins by Taguchi-based sensitivity analysis. Appl. Therm. Eng. 2024, 249, 123454. [Google Scholar] [CrossRef]
- Al-Rashed, A.; Shahsavar, A.; Rasooli, O.; Moghimi, M.A.; Karimipour, A.; Tran, M.D. Numerical assessment into the hydrothermal and entropy generation characteristics of biological water–silver nano–fluid in a wavy walled microchannel heat sink. Int. Commun. Heat Mass Transf. 2019, 104, 118–126. [Google Scholar] [CrossRef]
- Ho, C.J.; Peng, J.K.; Yang, T.F.; Rashidi, S.; Yan, W.-M. Comparison of cooling performance of nanofluid flows in mini/micro-channel stacked double-layer heat sink and single-layer micro-channel heat sink. Int. J. Therm. Sci. 2023, 191, 108375. [Google Scholar] [CrossRef]
- Bi, C.; Tang, G.H.; Tao, W.Q. Heat transfer enhancement in mini-channel heat sinks with dimples and cylindrical grooves. Appl. Therm. Eng. 2013, 55, 121–132. [Google Scholar] [CrossRef]
- Zhai, Y.L.; Xia, G.D.; Liu, X.F.; Li, Y.F. Heat transfer in the microchannels with fan-shaped reentrant cavities and different ribs based on field synergy principle and entropy generation analysis. Int. J. Heat Mass Transf. 2014, 68, 224–233. [Google Scholar] [CrossRef]
- Guo, J.F.; Xu, M.T.; Cheng, L. Second law analysis of curved rectangular channel. Int. J. Therm. Sci. 2011, 50, 760–768. [Google Scholar] [CrossRef]
- Steinke, M.E.; Kandlikar, S.G. Single-phase liquid friction factors in microchannels. Int. J. Therm. Sci. 2006, 45, 1073–1083. [Google Scholar] [CrossRef]
- Chai, L.; Xia, G.D.; Wang, L.; Zhou, M.; Cui, Z. Heat transfer enhancement in microchannel heat sinks with periodic expansion-constriction cross-sections. Int. J. Heat Mass Transf. 2013, 62, 741–751. [Google Scholar] [CrossRef]
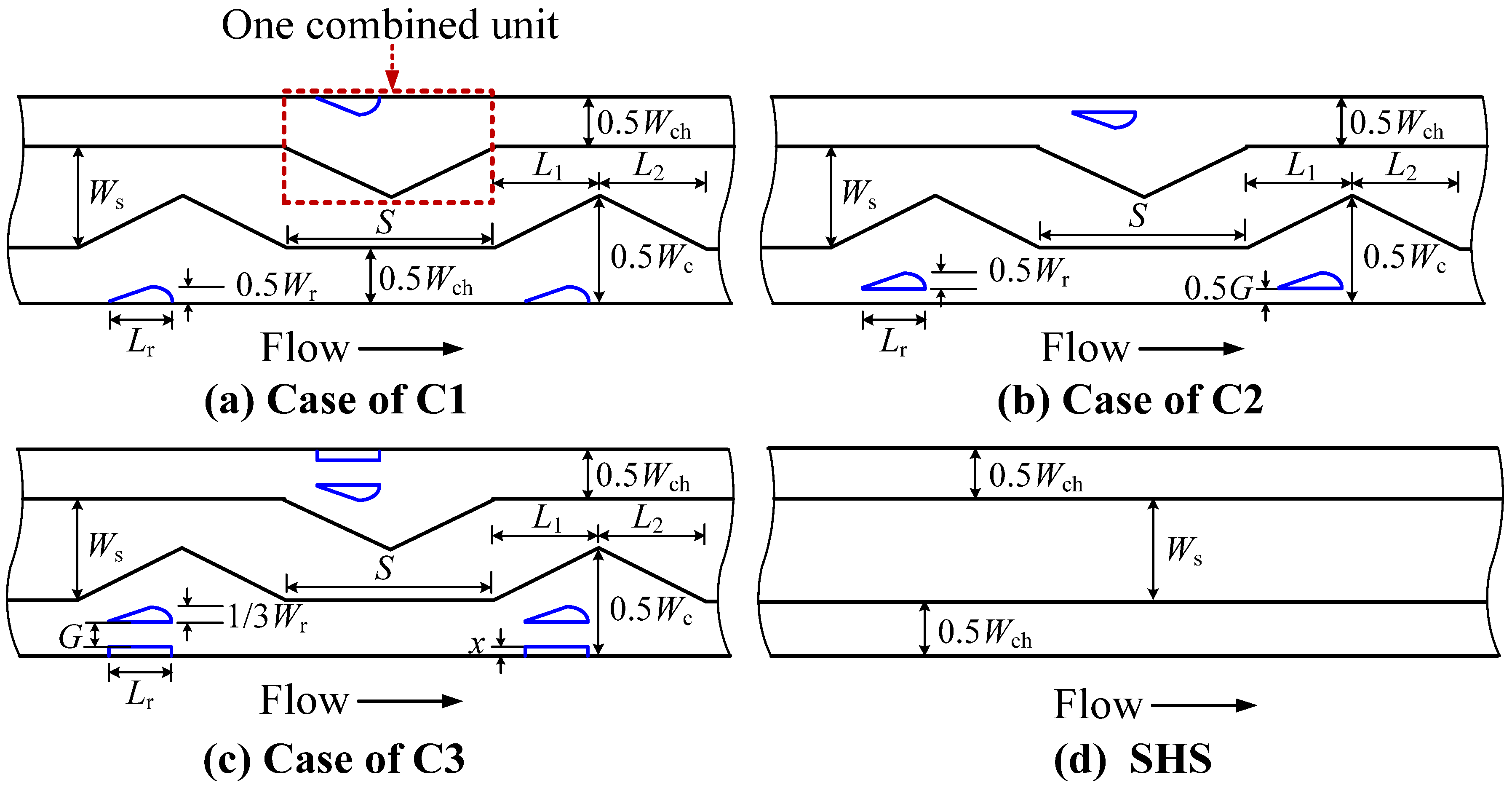




| Case | Design Factors | ||
|---|---|---|---|
| A (Number of Combined Units, N) | B (Distribution of Combined Units) | C (Number of Fins in Each Unit) | |
| 1 | 1 (N = 5) | 1 (uniform distribution) | 1 (one fin) |
| 2 | 1 (N = 5) | 2 (from sparse to dense) | 2 (two fins) |
| 3 | 1 (N = 5) | 3 (from dense to sparse) | 3 (three fins) |
| 4 | 2 (N = 13) | 1 (uniform distribution) | 2 (two fins) |
| 5 | 2 (N = 13) | 2 (from sparse to dense) | 3 (three fins) |
| 6 | 2 (N = 13) | 3 (from dense to sparse) | 1 (one fin) |
| 7 | 3 (N = 21) | 1 (uniform distribution) | 3 (three fins) |
| 8 | 3 (N = 21) | 2 (from sparse to dense) | 1 (one fin) |
| 9 | 3 (N = 21) | 3 (from dense to sparse) | 2 (two fins) |
| Symbol | Size (μm) | Symbol | Size (μm) | Symbol | Size (μm) |
|---|---|---|---|---|---|
| G | 20 | L2 | 100 | Wr | 30 |
| H | 350 | Lr | 60 | Ws | 100 |
| Hch | 200 | W | 200 | x | 5 |
| L | 10,000 | Wc | 200 | ||
| L1 | 100 | Wch | 100 |
| T (K) | μf × 106 (Pa·s) |
|---|---|
| 293 | 1004.0 |
| 303 | 801.5 |
| 313 | 653.3 |
| 323 | 549.4 |
| 333 | 469.9 |
| 343 | 406.1 |
| 353 | 355.1 |
| 363 | 314.9 |
| Parameters | Silicon | Water |
|---|---|---|
| cp (J/(kg·K)) | 712 | 4183 |
| ρ (kg/m3) | 2329 | 998.2 |
| λ (W/(m·K)) | 148 | 0.6002 |
| Location | Value |
|---|---|
| Velocity inlet (uin, Tin) | 1~4.5 m/s, 293 K |
| Pressure outlet (pout) | Pout = 0 Pa (relative pressure) |
| Heat flux at the heating film (qb) | 106 W/m2 |
| Two sides of the computational model | Symmetry |
| Water–silicon interface | Coupled without slip |
| Other surfaces | Adiabatic |
| Mesh | Tw,ave (K) | ΔP (Pa) |
|---|---|---|
| 0.44 million | 0.133% | 4.98% |
| 0.75 million | 0.13% | 1.73% |
| Case | Rave (K/W) | SNR-Rave | PP (W) | SNR-PP | FOM | SNR-FOM |
|---|---|---|---|---|---|---|
| 1 | 0.78 | 2.20 | 0.04 | 28.46 | 1.10 | 0.79 |
| 2 | 0.83 | 1.62 | 0.04 | 28.36 | 1.02 | 0.18 |
| 3 | 0.81 | 1.88 | 0.04 | 28.06 | 1.04 | 0.34 |
| 4 | 0.69 | 3.18 | 0.05 | 25.40 | 1.09 | 0.75 |
| 5 | 0.67 | 3.45 | 0.06 | 25.09 | 1.11 | 0.92 |
| 6 | 0.61 | 4.23 | 0.05 | 25.93 | 1.26 | 1.98 |
| 7 | 0.59 | 4.53 | 0.07 | 23.08 | 1.16 | 1.33 |
| 8 | 0.54 | 5.35 | 0.06 | 24.39 | 1.35 | 2.58 |
| 9 | 0.59 | 4.56 | 0.07 | 23.64 | 1.19 | 1.55 |
| Level | A (Number of Combined Units, N) | B (Distribution of Combined Units) | C (Number of Fins in Each Unit) |
|---|---|---|---|
| 1 | 1.90 | 3.30 | 3.93 |
| 2 | 3.62 | 3.47 | 3.12 |
| 3 | 4.812 | 3.56 | 3.29 |
| Contribution ratio | 73.27 | 6.47 | 20.25 |
| Rank | 1 | 3 | 2 |
| Level | A (Number of Combined Units, N) | B (Distribution of Combined Units) | C (Number of Fins in Each Unit) |
|---|---|---|---|
| 1 | 28.29 | 25.65 | 26.26 |
| 2 | 25.48 | 25.95 | 25.80 |
| 3 | 23.71 | 25.88 | 25.41 |
| Contribution ratio | 79.97 | 5.19 | 14.84 |
| Rank | 1 | 3 | 2 |
| Level | A (Number of Combined Units, N) | B (Distribution of Combined Units) | C (Number of Fins in Each Unit) |
|---|---|---|---|
| 1 | 0.44 | 0.95 | 1.78 |
| 2 | 1.21 | 1.23 | 0.82 |
| 3 | 1.82 | 1.29 | 0.86 |
| Contribution ratio | 51.71 | 12.44 | 35.85 |
| Rank | 1 | 3 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, L.; Shi, J.; Li, Y.; Wang, Z. Thermo-Hydrodynamic Features of Grooved Heat Sink with Droplet-Shaped Fins Based on Taguchi Optimization and Field Synergy Analysis. Energies 2025, 18, 3396. https://doi.org/10.3390/en18133396
Zhong L, Shi J, Li Y, Wang Z. Thermo-Hydrodynamic Features of Grooved Heat Sink with Droplet-Shaped Fins Based on Taguchi Optimization and Field Synergy Analysis. Energies. 2025; 18(13):3396. https://doi.org/10.3390/en18133396
Chicago/Turabian StyleZhong, Lin, Jingli Shi, Yifan Li, and Zhipeng Wang. 2025. "Thermo-Hydrodynamic Features of Grooved Heat Sink with Droplet-Shaped Fins Based on Taguchi Optimization and Field Synergy Analysis" Energies 18, no. 13: 3396. https://doi.org/10.3390/en18133396
APA StyleZhong, L., Shi, J., Li, Y., & Wang, Z. (2025). Thermo-Hydrodynamic Features of Grooved Heat Sink with Droplet-Shaped Fins Based on Taguchi Optimization and Field Synergy Analysis. Energies, 18(13), 3396. https://doi.org/10.3390/en18133396





