Advanced Numerical Validation of Integrated Electrochemical-Thermal Models for PCM-Based Li-Ion Battery Thermal Management System
Abstract
1. Introduction
2. Modeling Process and Methodology
2.1. NTGK Battery Cell Model and Integrated Heat Transfer Modeling
2.1.1. Governing Equations for Potential and Current Distribution
2.1.2. Temperature Dependence of Parameters
2.1.3. Thermal Model of the Battery
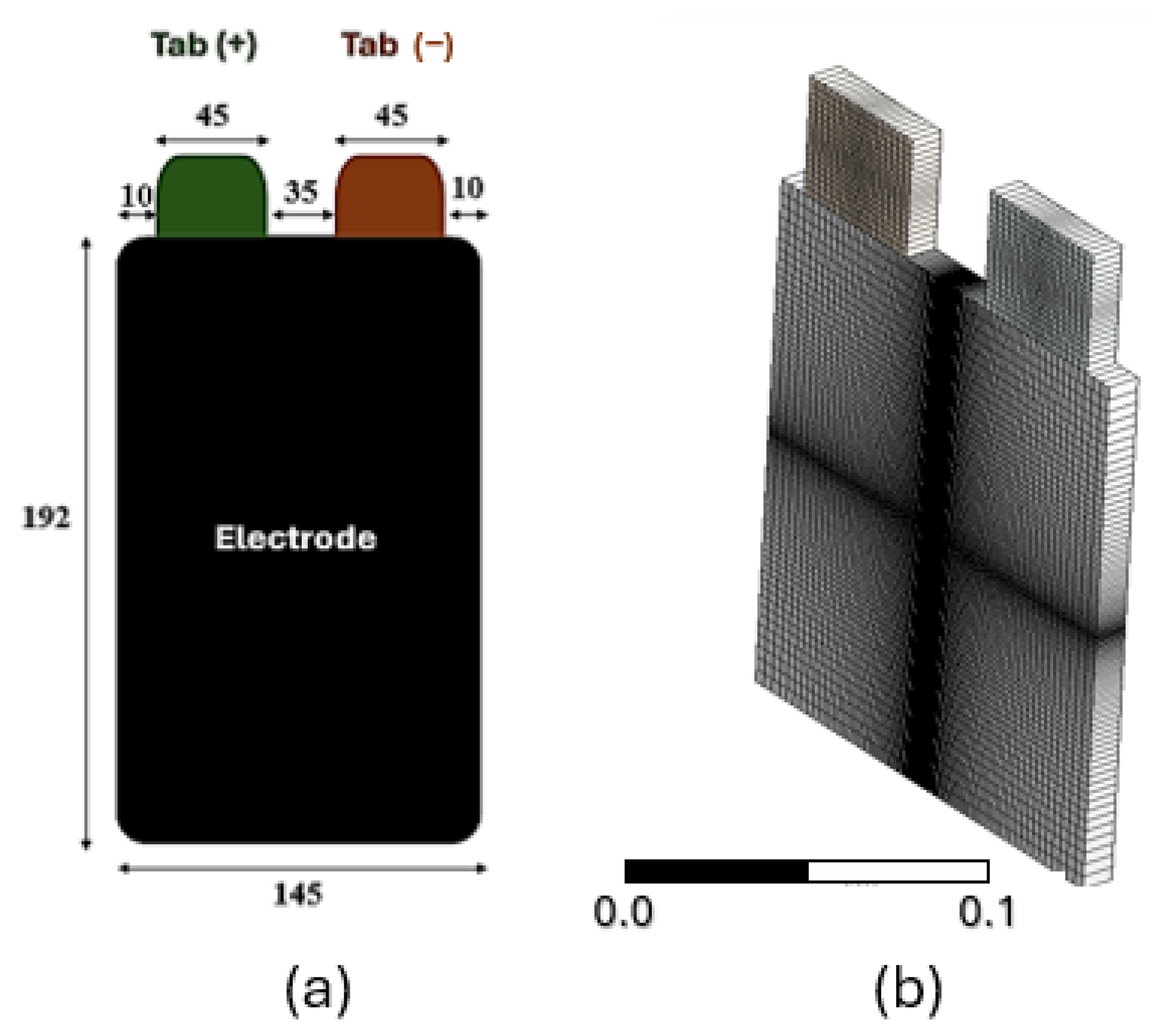
2.1.4. Battery Material Properties and Boundary Conditions
2.2. Phase Change Material Modeling
2.2.1. Governing Equations for PCM
2.2.2. PCM Properties and Implementation
2.2.3. Coupled Thermal Model and Boundary Conditions
3. Results and Discussion
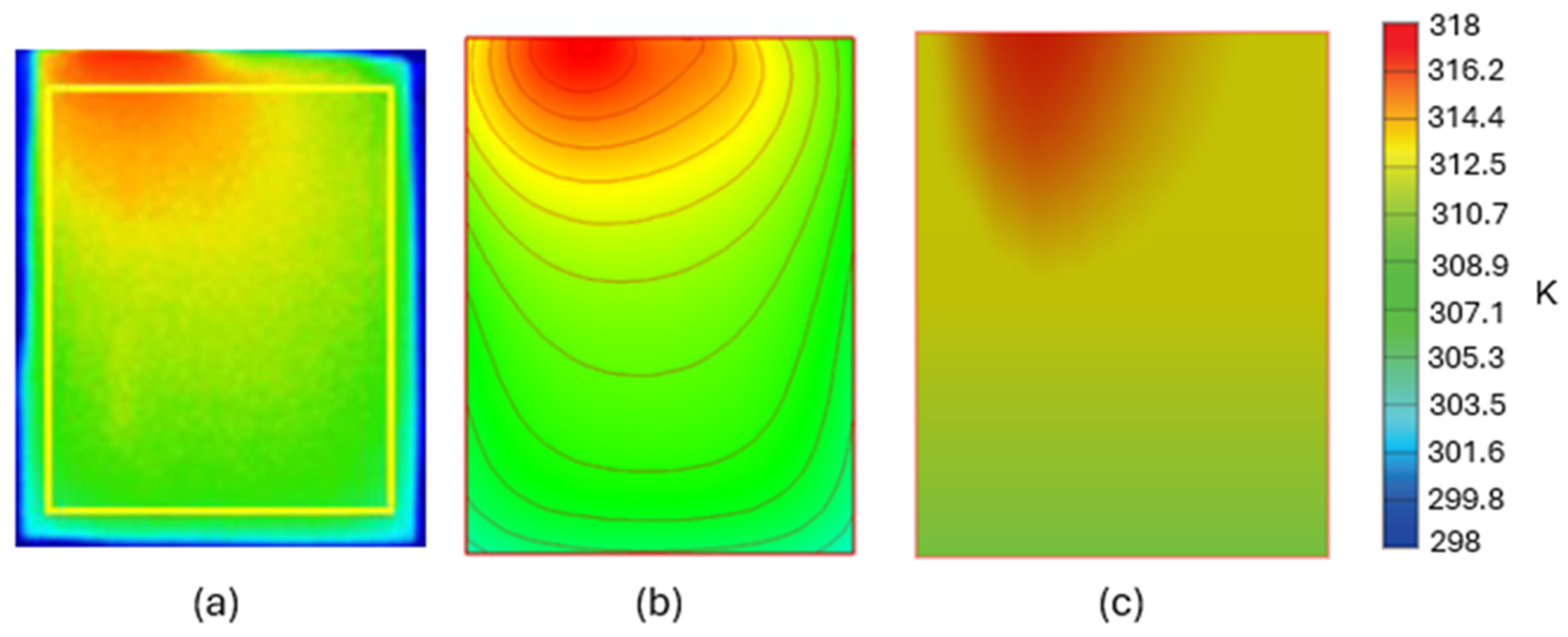
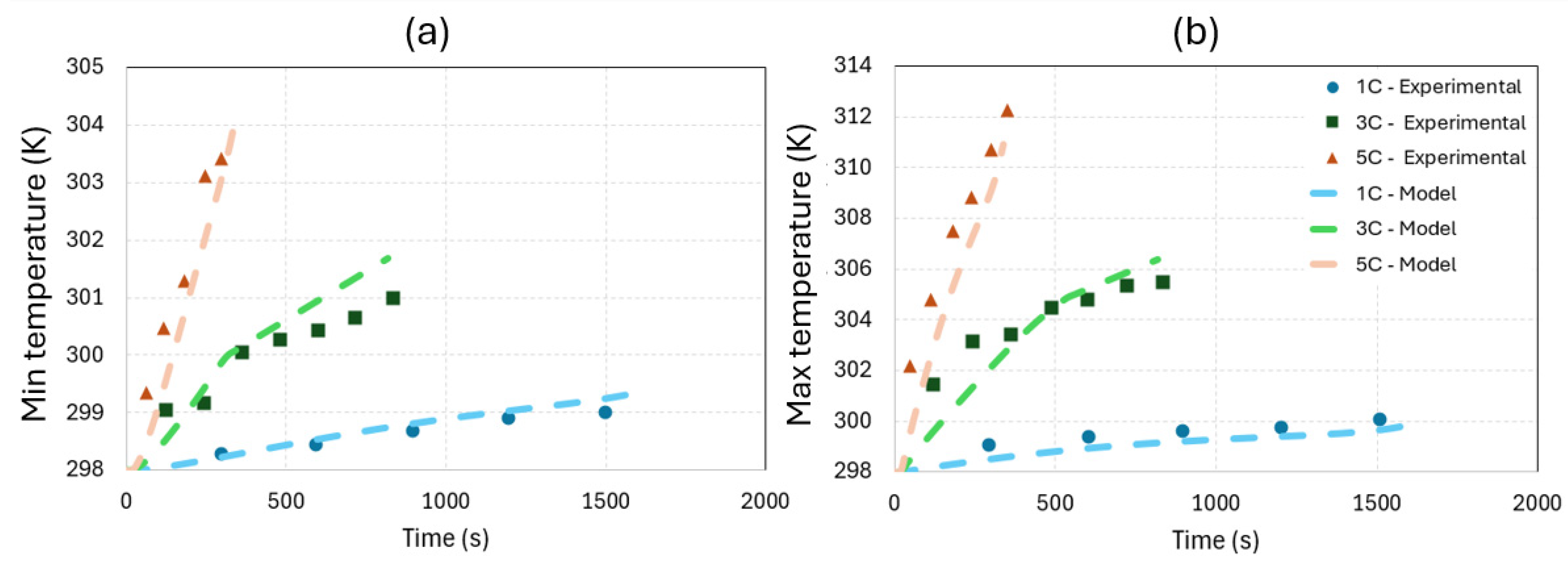
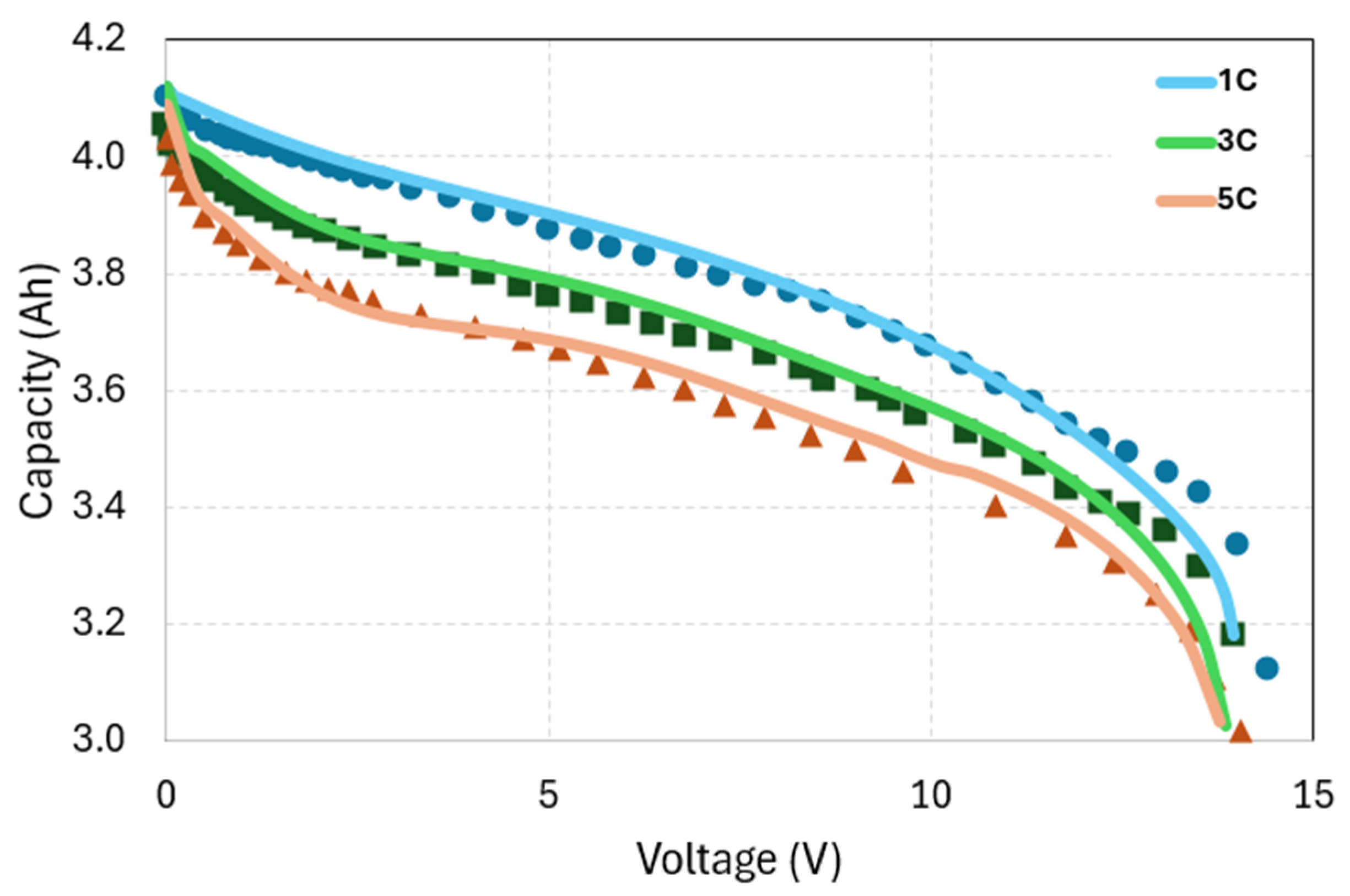
3.1. Battery Model Validation
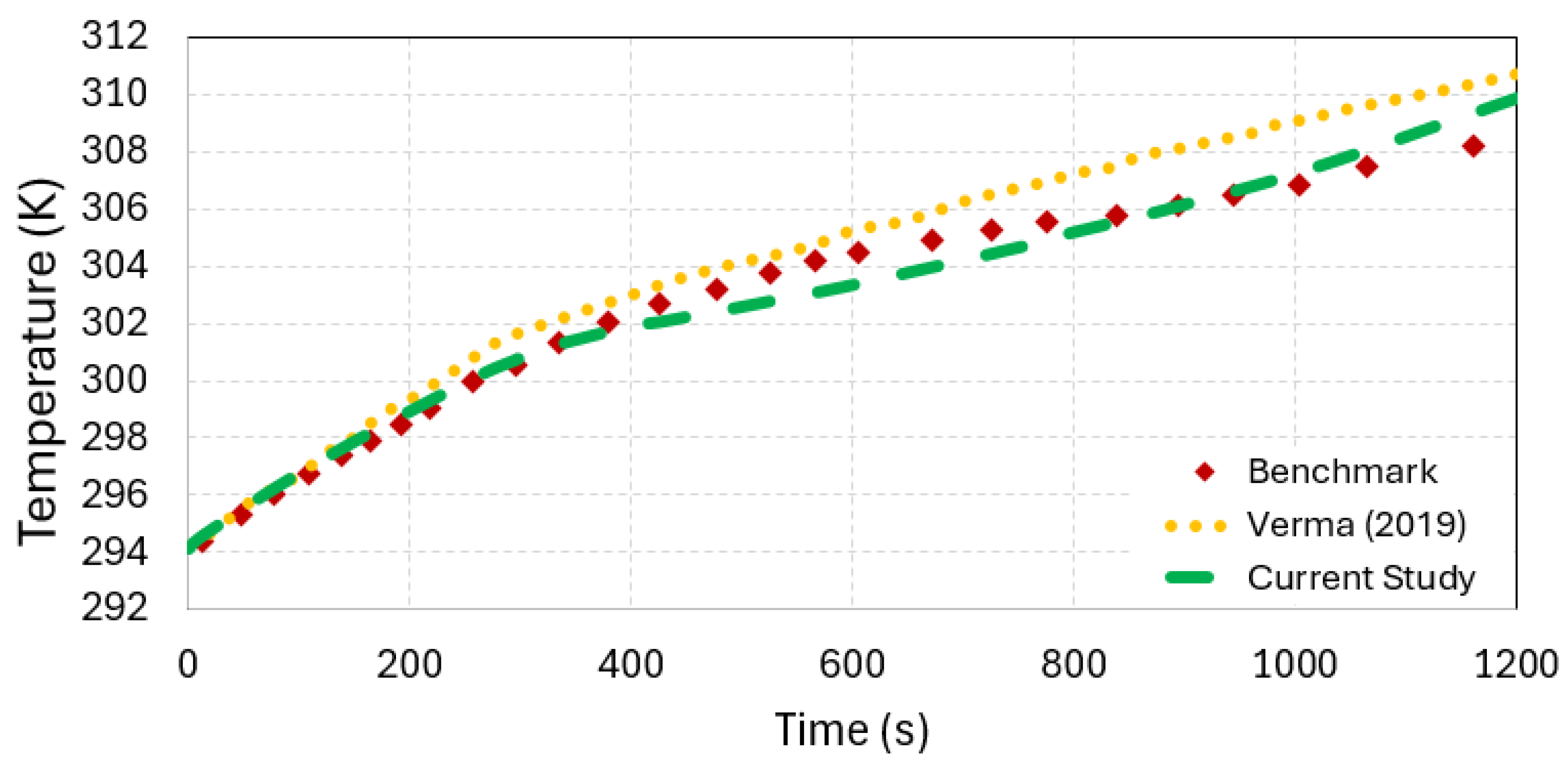
3.2. PCM Thermal Management Model Validation
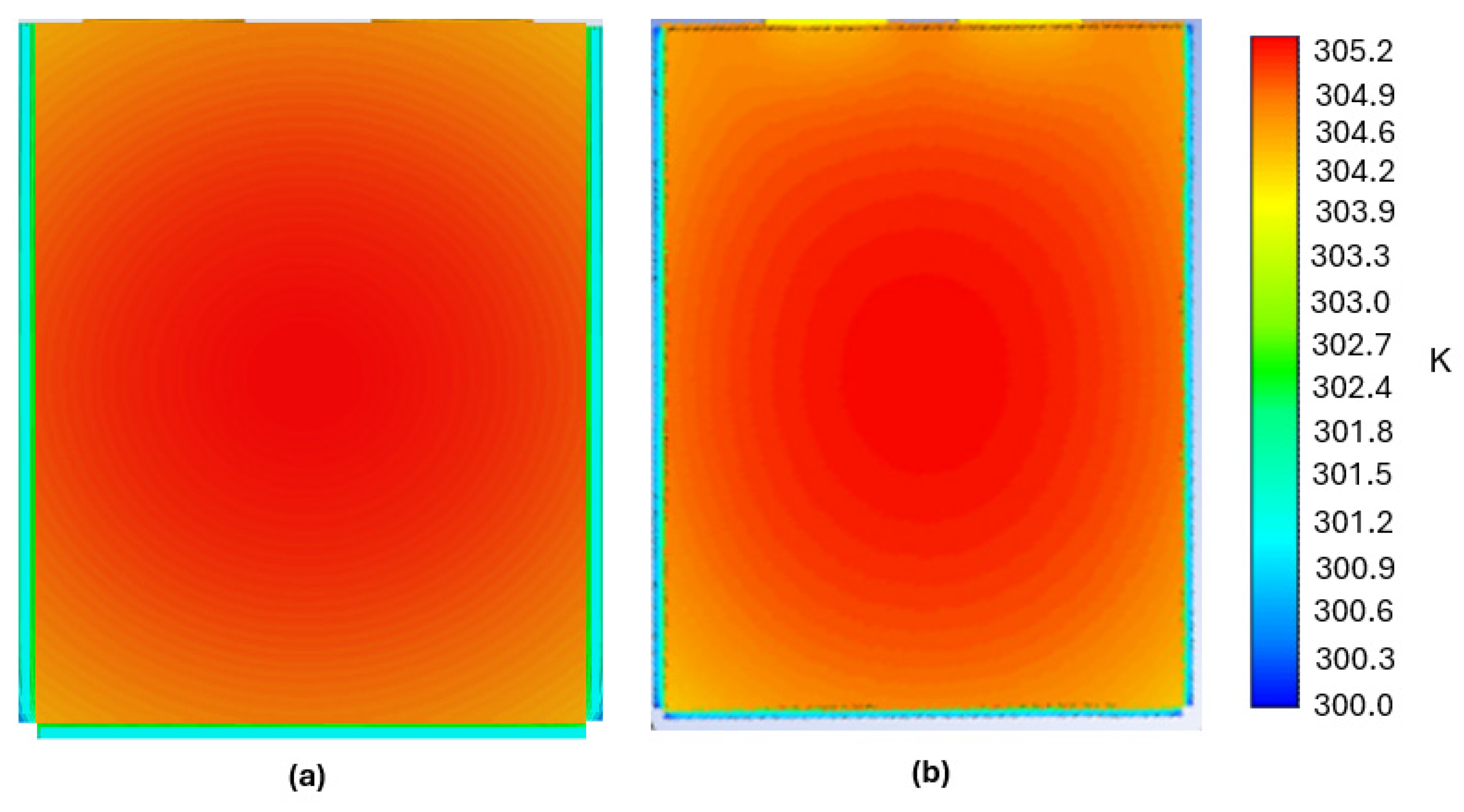
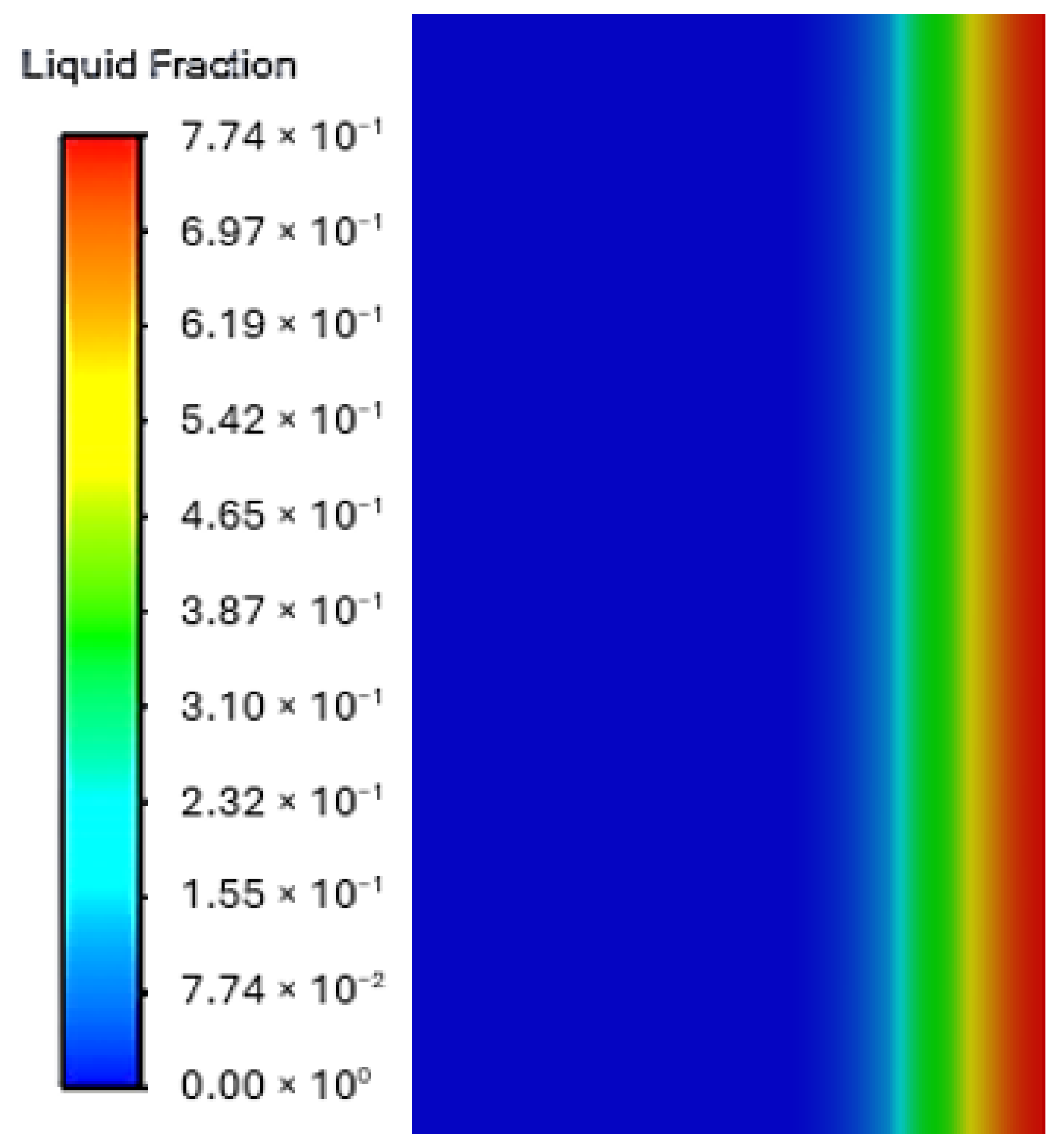
3.3. Phase Change Dynamics and Thermal Performance
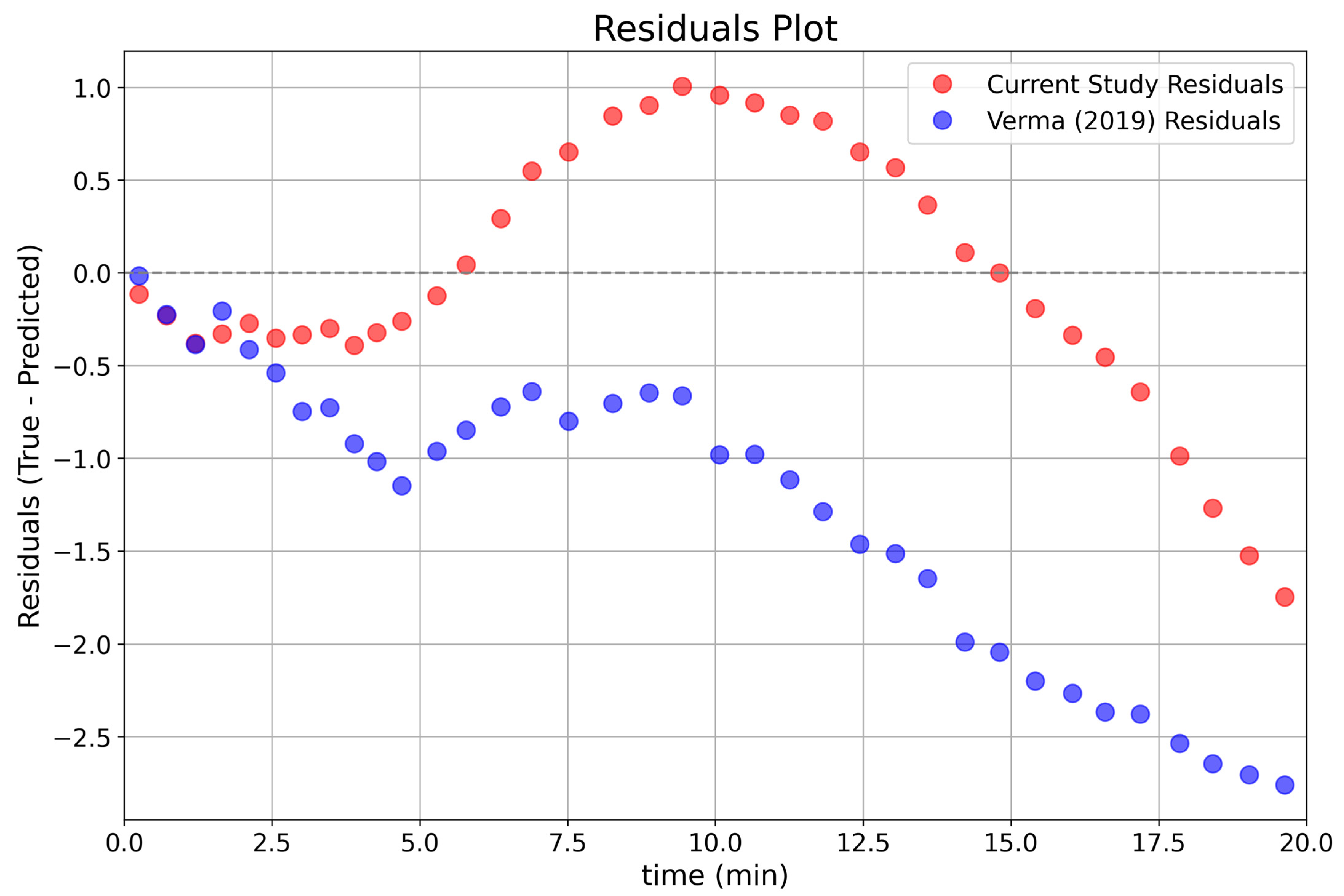
3.4. Comparative Analysis with Previous Studies
3.5. Data Preparation and Interpolation
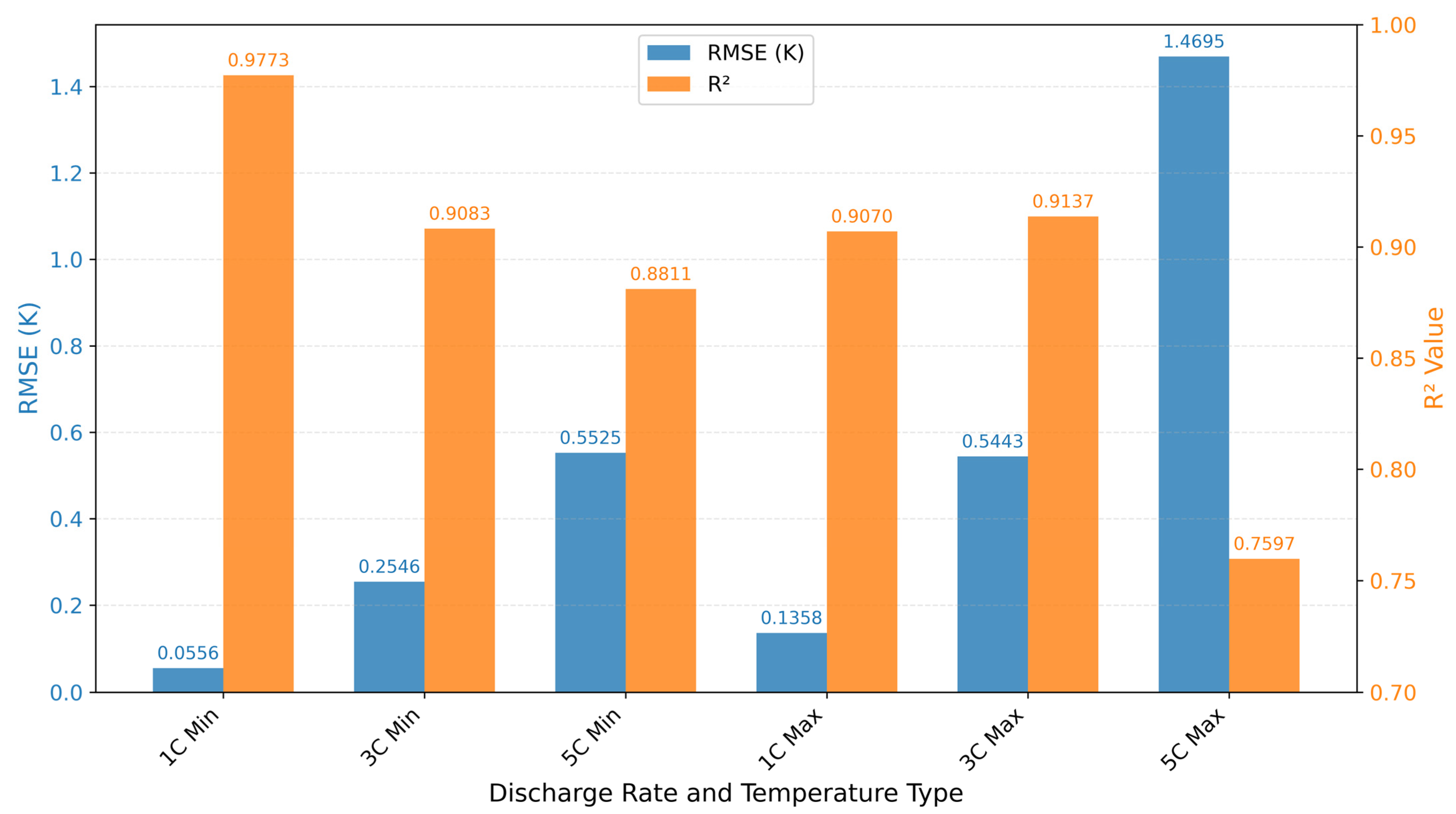
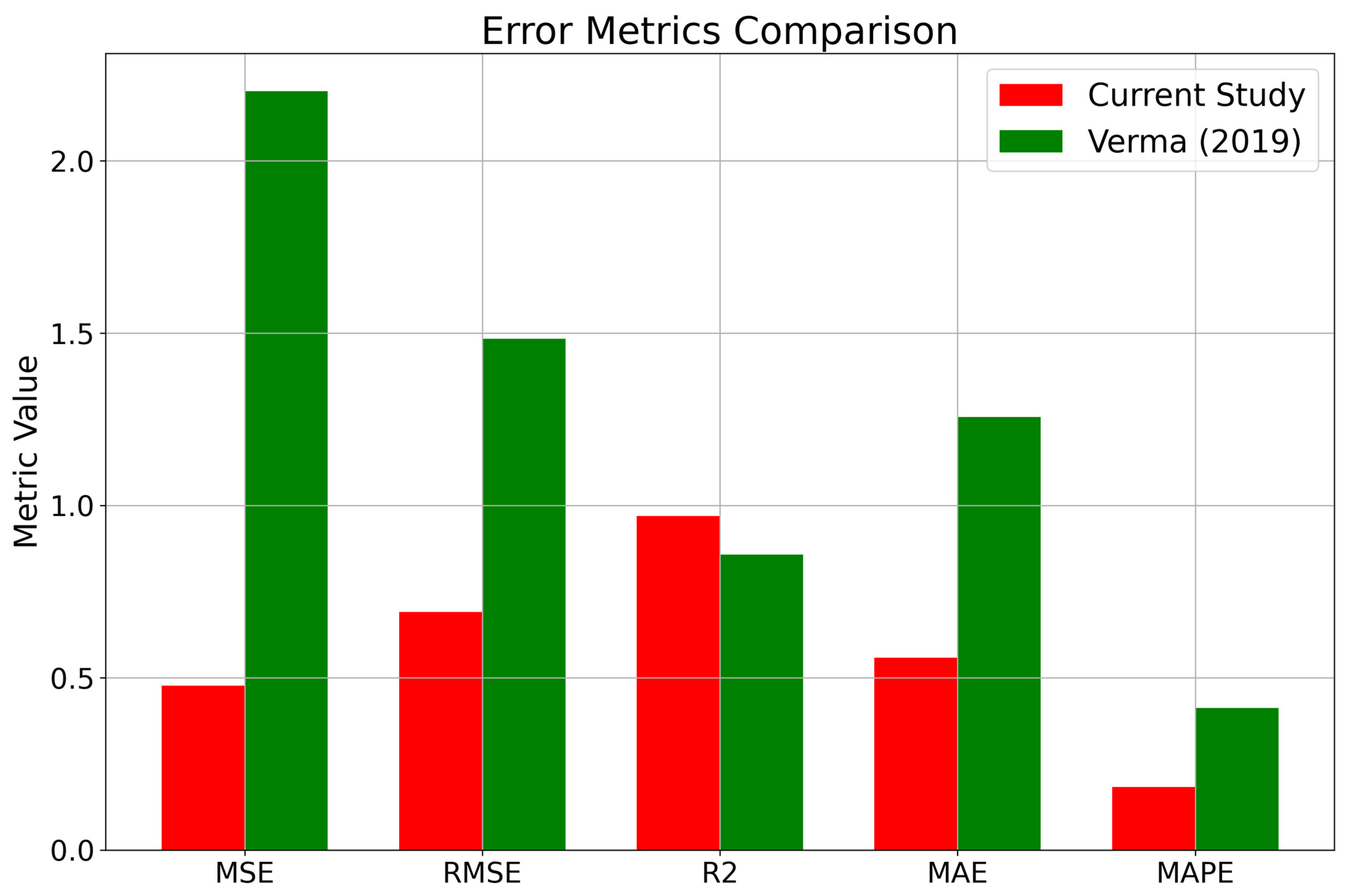
3.6. Error Metrics Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BTMS | Battery thermal management system |
| DOD | Depth of discharge |
| LIB | Lithium-ion battery |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MSE | Mean Squared Error |
| NTGK | Newman–Tiedemann–Gu–Kim |
| PCM | Phase change material |
| RMSE | Root Mean Squared Error |
| TMS | Thermal management system |
| EV | Electric vehicle |
| TR | Thermal runaway |
| Nomenclature | |
| ρ | Density (kg/m3) |
| Cp | Specific heat capacity (J/kg·K) |
| k | Thermal conductivity (W/m·K) |
| σ | Electrical conductivity (S/m) |
| H | Total enthalpy (J) |
| L | Latent heat of fusion (kJ/kg) |
| f | Liquid fraction |
| T | Temperature (K) |
| t | Time (s) |
| q | Volumetric heat generation rate (W/m3) |
| J | Current density (A/m2) |
| δ | Thickness (μm) |
| E | Cell voltage (V) |
| U | Open-circuit potential (V) |
| Y, U | Polarization parameters |
| h | Convective heat transfer coefficient (W/m2·K) |
| DOD | Depth of discharge (dimensionless) |
| a | Specific area of battery (m2) |
| ip, in | Magnitude of current density vectors (A/m2) |
Appendix A. Statistical Error Analysis for Model Evaluation
References
- Khan, F.N.U.; Rasul, M.G.; Sayem, A.S.M.; Mandal, N.K. Design and optimization of lithium-ion battery as an efficient energy storage device for electric vehicles: A comprehensive review. J. Energy Storage 2023, 71, 108033. [Google Scholar] [CrossRef]
- Nasiri, M.; Hadim, H. Battery Thermal Management Systems: Analyzing Today’s Landscape and Tomorrow’s Technology. In Proceedings of the 9th Thermal and Fluids Engineering Conference (TFEC), Corvallis, OR, USA, 21–24 April 2024; ASTFE Digital Library, Begell House Inc.: Danbury, CT, USA, 2024. Available online: https://dl.astfe.org/conferences/tfec2024,2d6c7309626b1193,111d34ff7129638b.html (accessed on 16 September 2024).
- Xu, J.; Cai, X.; Cai, S.; Shao, Y.; Hu, C.; Lu, S.; Ding, S. High-Energy Lithium-Ion Batteries: Recent Progress and a Promising Future in Applications. Energy Environ. Mater. 2023, 6, e12450. [Google Scholar] [CrossRef]
- Sahoo, S.; Timmann, P. Energy storage technologies for modern power systems: A detailed analysis of functionalities, potentials, and impacts. IEEE Access 2023, 11, 49689–49729. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Y.; Zhang, S.; Tang, B. Phase change materials for lithium-ion battery thermal management systems: A review. J. Energy Storage 2024, 80, 110259. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Z.; Luo, L.; Fan, Y.; Du, Z. A review on thermal management of lithium-ion batteries for electric vehicles. Energy 2022, 238, 121652. [Google Scholar] [CrossRef]
- Nasiri, M.; Hadim, H. Advances in battery thermal management: Current landscape and future directions. Renew. Sustain. Energy Rev. 2024, 200, 114611. [Google Scholar] [CrossRef]
- Chen, Y.; Kang, Y.; Zhao, Y.; Wang, L.; Liu, J.; Li, Y.; Liang, Z.; He, X.; Li, X.; Tavajohi, N.; et al. A review of lithium-ion battery safety concerns: The issues, strategies, and testing standards. J. Energy Chem. 2021, 59, 83–99. [Google Scholar] [CrossRef]
- Patel, J.R.; Rathod, M.K. Recent developments in the passive and hybrid thermal management techniques of lithium-ion batteries. J. Power Sources 2020, 480, 228820. [Google Scholar] [CrossRef]
- Ahmadian-Elmi, M.; Zhao, P. Review of thermal management strategies for cylindrical lithium-ion battery packs. Batteries 2024, 10, 50. [Google Scholar] [CrossRef]
- Lamrani, B.; Johannes, K.; Kuznik, F. Phase change materials integrated into building walls: An updated review. Renew. Sustain. Energy Rev. 2021, 140, 110751. [Google Scholar] [CrossRef]
- Jilte, R.; Afzal, A.; Panchal, S. A novel battery thermal management system using nano-enhanced phase change materials. Energy 2021, 219, 119564. [Google Scholar] [CrossRef]
- El Idi, M.M.; Karkri, M.; Tankari, M.A. A passive thermal management system of Li-ion batteries using PCM composites: Experimental and numerical investigations. Int. J. Heat Mass Transf. 2021, 169, 120894. [Google Scholar] [CrossRef]
- Srivastava, G.; Nandan, R.; Das, M.K. Thermal runaway management of Li ion battery using PCM: A parametric study. Energy Convers. Manag. X 2022, 16, 100306. [Google Scholar] [CrossRef]
- Sarmadian, A.; Widanage, W.D.; Shollock, B.; Restuccia, F. Experimentally-verified thermal-electrochemical simulations of a cylindrical battery using physics-based, simplified and generalized lumped models. J. Energy Storage 2023, 70, 107910. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, M.; Dan, D.; Dong, J.; Wright, E. Enhancing battery electrochemical-thermal model accuracy through a hybrid parameter estimation framework. Energy Storage Mater. 2024, 72, 103720. [Google Scholar] [CrossRef]
- Wang, Q.-K.; Shen, J.-N.; Ma, Z.-F.; He, Y.-J. Decoupling parameter estimation strategy based electrochemical-thermal coupled modeling method for large format lithium-ion batteries with internal temperature experimental validation. Chem. Eng. J. 2021, 424, 130308. [Google Scholar] [CrossRef]
- Zhu, X.; Xie, Y.; Chen, H.; Luan, W. Numerical analysis of the cyclic mechanical damage of Li-ion battery electrode and experimental validation. Int. J. Fatigue 2021, 142, 105915. [Google Scholar] [CrossRef]
- Kim, U.S.; Yi, J.; Shin, C.B.; Han, T.; Park, S. Modeling the dependence of the discharge behavior of a lithium-ion battery on the environmental temperature. J. Electrochem. Soc. 2011, 158, A611. [Google Scholar]
- Javani, N.; Dincer, I.; Naterer, G.F.; Yilbas, B.S. Heat transfer and thermal management with PCMs in a Li-ion battery cell for electric vehicles. Int. J. Heat Mass Transf. 2014, 72, 690–703. [Google Scholar] [CrossRef]
- Verma, A.; Shashidhara, S.; Rakshit, D. A comparative study on battery thermal management using phase change material (PCM). Therm. Sci. Eng. Prog. 2019, 11, 74–83. [Google Scholar] [CrossRef]
- Kwon, K.H.; Shin, C.B.; Kang, T.H.; Kim, C.-S. A two-dimensional modeling of a lithium-polymer battery. J. Power Sources 2006, 163, 151–157. [Google Scholar] [CrossRef]
- Bergveld, H.J.; Kruijt, W.S.; Notten, P.H.L. Battery Management Systems. In Battery Management Systems; Springer: Dordrecht, The Netherlands, 2002; pp. 9–30. [Google Scholar] [CrossRef]
- Pals, C.R.; Newman, J. Thermal modeling of the lithium/polymer battery: I. Discharge behavior of a single cell. J. Electrochem. Soc. 1995, 142, 3274. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R.; White, H.S. Electrochemical Methods: Fundamentals and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2022; Available online: https://books.google.com/books?hl=en&lr=&id=4ShuEAAAQBAJ&oi=fnd&pg=PR21&dq=A.+J.+Bard+and+L.+R.+Falkner,+Electrochemical+Methods:+Fundamentals+and+Applications,+2nd+ed.,+John+Wiley+and+Sons,+Inc.,+New+York+(2001).&ots=SJErFYRwsI&sig=S6nTJA9aahmn2H0n2CaOLa5pWmU (accessed on 21 March 2025).
- Song, L.; Evans, J.W. Electrochemical-thermal model of lithium polymer batteries. J. Electrochem. Soc. 2000, 147, 2086. [Google Scholar] [CrossRef]
- Gu, W.B.; Wang, C.Y. Thermal-electrochemical modeling of battery systems. J. Electrochem. Soc. 2000, 147, 2910. [Google Scholar] [CrossRef]
- Srinivasan, V.; Wang, C.Y. Analysis of electrochemical and thermal behavior of Li-ion cells. J. Electrochem. Soc. 2002, 150, A98. [Google Scholar] [CrossRef]
- Kim, U.S.; Shin, C.B.; Kim, C.-S. Effect of electrode configuration on the thermal behavior of a lithium-polymer battery. J. Power Sources 2008, 180, 909–916. [Google Scholar] [CrossRef]
- ANSYS Drive Canonsburg. ANSYS Fluent Advanced Add-On Modules; ANSYS: Canonsburg, PA, USA, 2015; Volume 15317, pp. 724–746. [Google Scholar]
- Benhorma, A.; Bensenouci, A.; Teggar, M.; Ismail, K.A.; Arıcı, M.; Mezaache, E.; Laouer, A.; Lino, F.A. Prospects and challenges of bio-based phase change materials: An up to date review. J. Energy Storage 2024, 90, 111713. [Google Scholar] [CrossRef]
- Wu, W.Y.; Yeap, I.S.; Wang, S.; Tomczak, N.; Lin, M.; Kai, D.; Ye, E.; Thitsartarn, W.; Tan, J.B.; Yin, X.; et al. Advancements in sustainable phase change materials: Valorizing waste for eco-friendly applications. Mater. Today Chem. 2024, 39, 102163. [Google Scholar] [CrossRef]
- Guo, M.; Fei, H.; Li, Y.; He, Q.; Du, W.; Zhou, J. Thermal Performances and Stability of Capric Acid–Stearic Acid–Paraffin Wax Adsorbed into Expanded Graphite in Vacuum Conditions. J. Phys. Chem. C 2024, 128, 6222–6232. [Google Scholar] [CrossRef]
- Kim, U.S.; Yi, J.; Shin, C.B.; Han, T.; Park, S. Modelling the thermal behavior of a lithium-ion battery during charge. J. Power Sources 2011, 196, 5115–5121. [Google Scholar] [CrossRef]
- Jiang, L.; Zhao, L.; Zhang, R.; Zhang, W.; Ma, X.; Niu, Z.; Chen, G.; Li, M. Research of the thermal storage properties of thermally conductive carbon fiber-reinforced paraffin/olefin block copolymer composite phase change materials with thermotropic flexibility. J. Energy Storage 2024, 76, 109761. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasiri, M.; Hadim, H. Advanced Numerical Validation of Integrated Electrochemical-Thermal Models for PCM-Based Li-Ion Battery Thermal Management System. Energies 2025, 18, 3386. https://doi.org/10.3390/en18133386
Nasiri M, Hadim H. Advanced Numerical Validation of Integrated Electrochemical-Thermal Models for PCM-Based Li-Ion Battery Thermal Management System. Energies. 2025; 18(13):3386. https://doi.org/10.3390/en18133386
Chicago/Turabian StyleNasiri, Mahdieh, and Hamid Hadim. 2025. "Advanced Numerical Validation of Integrated Electrochemical-Thermal Models for PCM-Based Li-Ion Battery Thermal Management System" Energies 18, no. 13: 3386. https://doi.org/10.3390/en18133386
APA StyleNasiri, M., & Hadim, H. (2025). Advanced Numerical Validation of Integrated Electrochemical-Thermal Models for PCM-Based Li-Ion Battery Thermal Management System. Energies, 18(13), 3386. https://doi.org/10.3390/en18133386







