Impact Mechanism Analysis of DFIG with Inertia Control on the Ultra-Low Frequency Oscillation of the Power System
Abstract
1. Introduction
2. System Description and Modeling
2.1. System Description
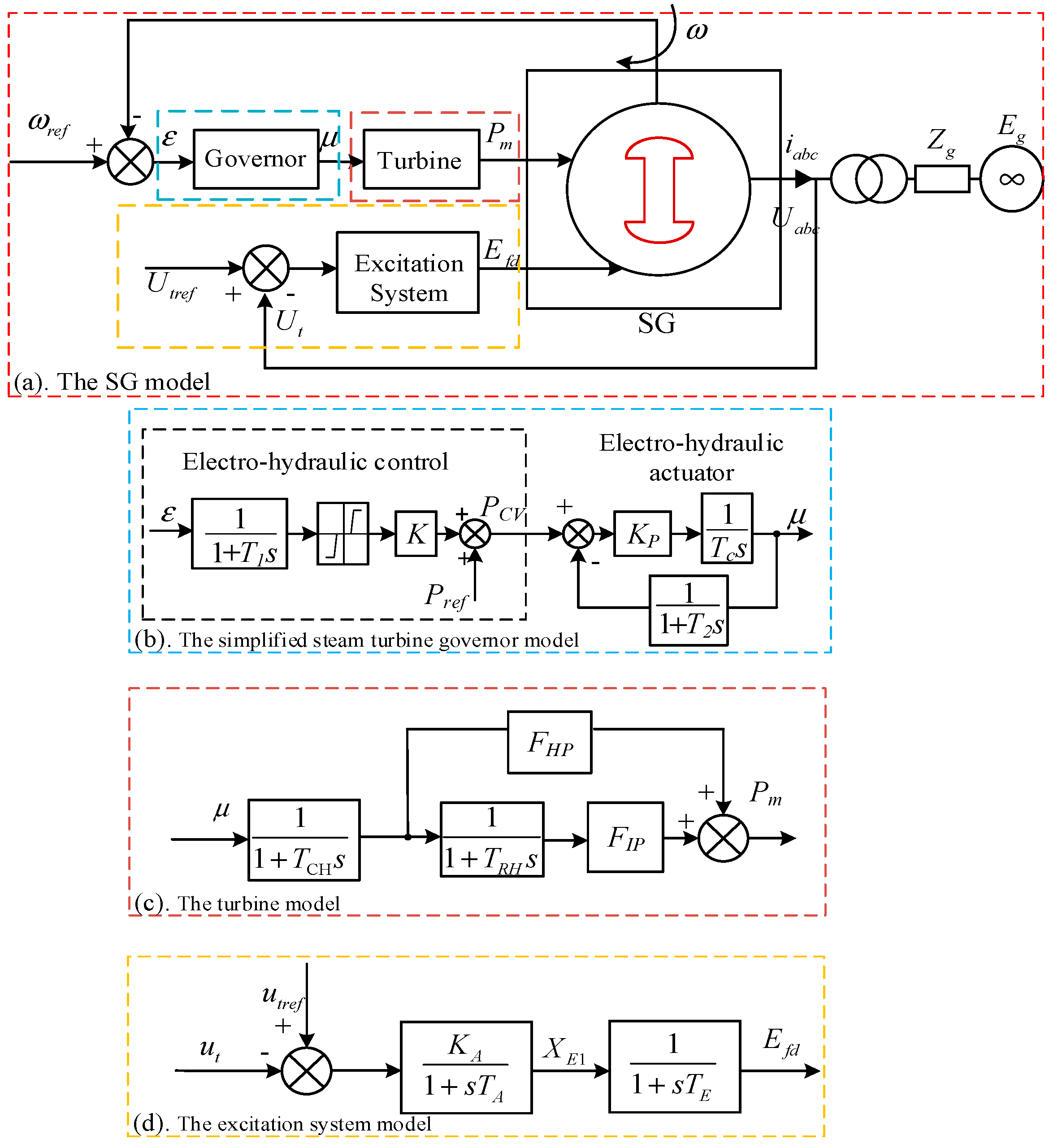
2.2. Modeling of Steam Turbine SG
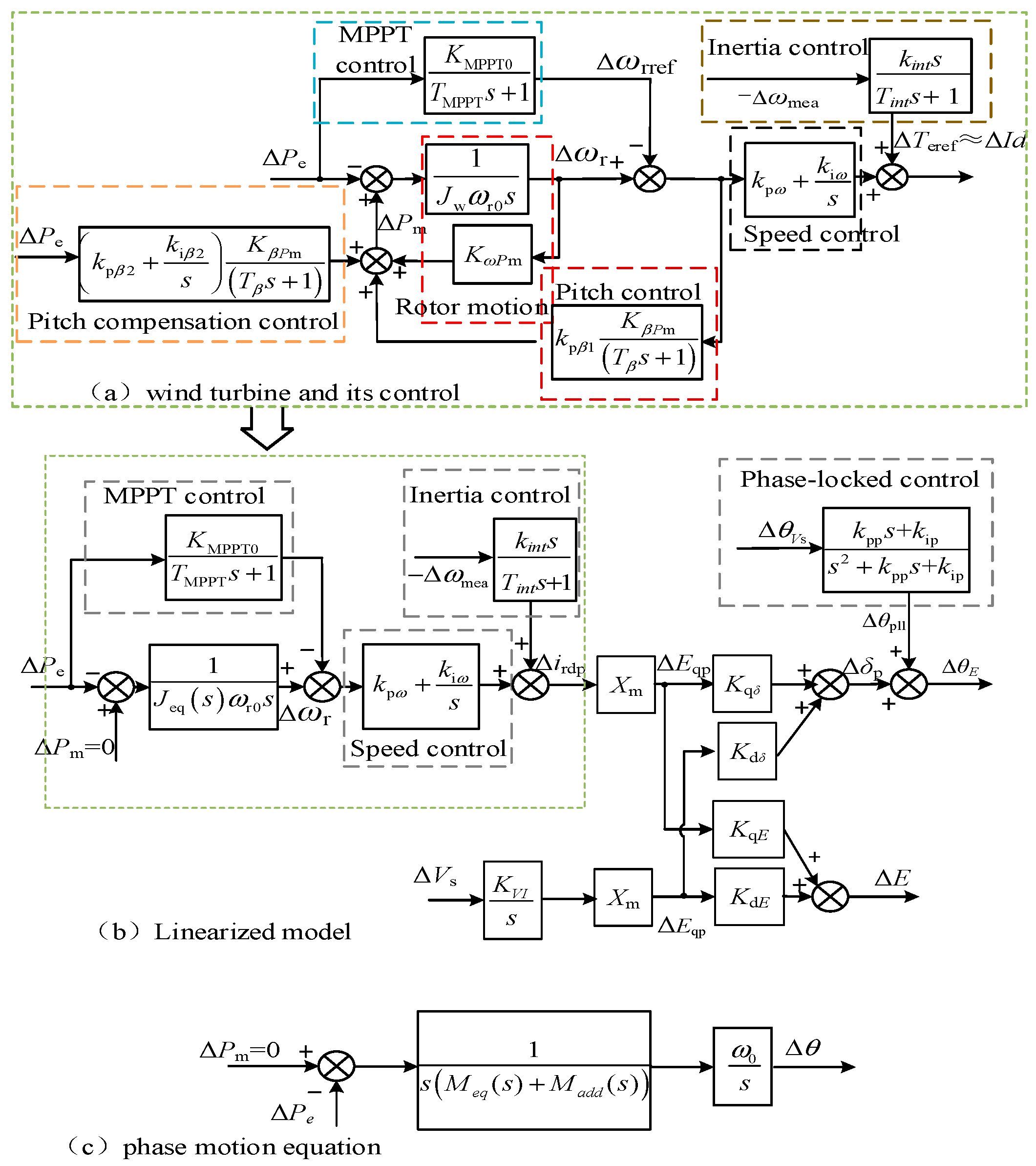
2.3. Modeling of DFIG in the Electromechanical Time Scale
2.3.1. The Internal Voltage of the DFIG
2.3.2. Linearization of DFIG Model
2.4. Phase Motion Equation
3. Analysis Method of the ULFO Caused by Inertia Control of DFIG
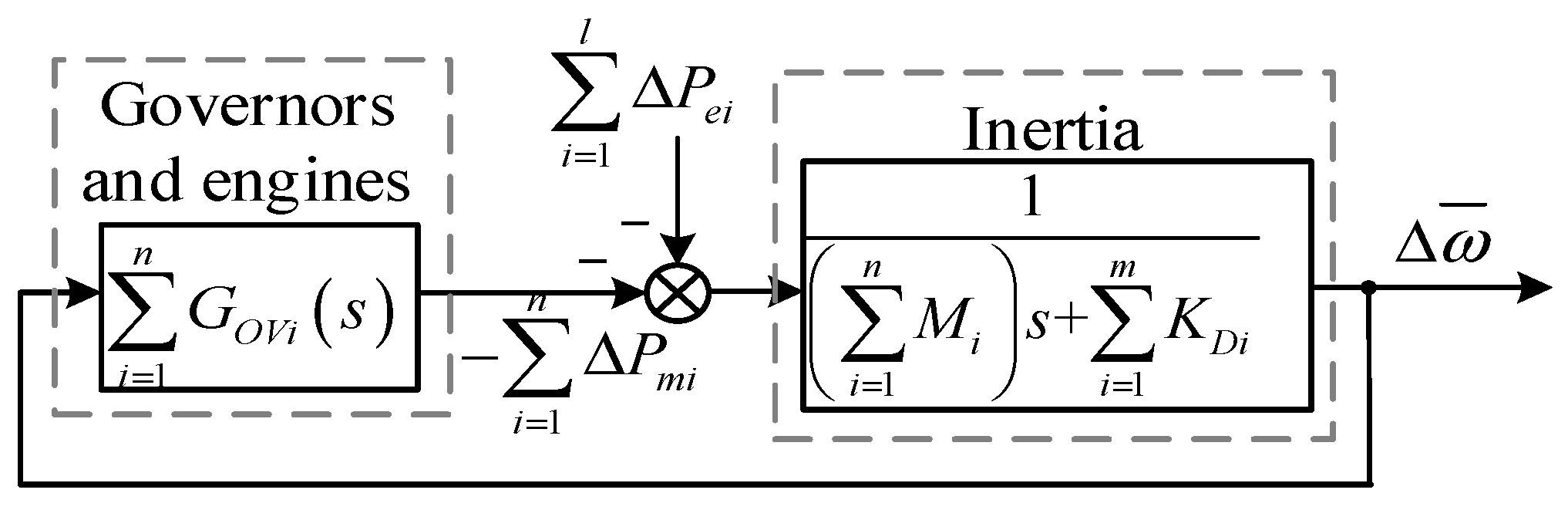
3.1. The Simplified ESFR for the Analysis of the System with DFIG
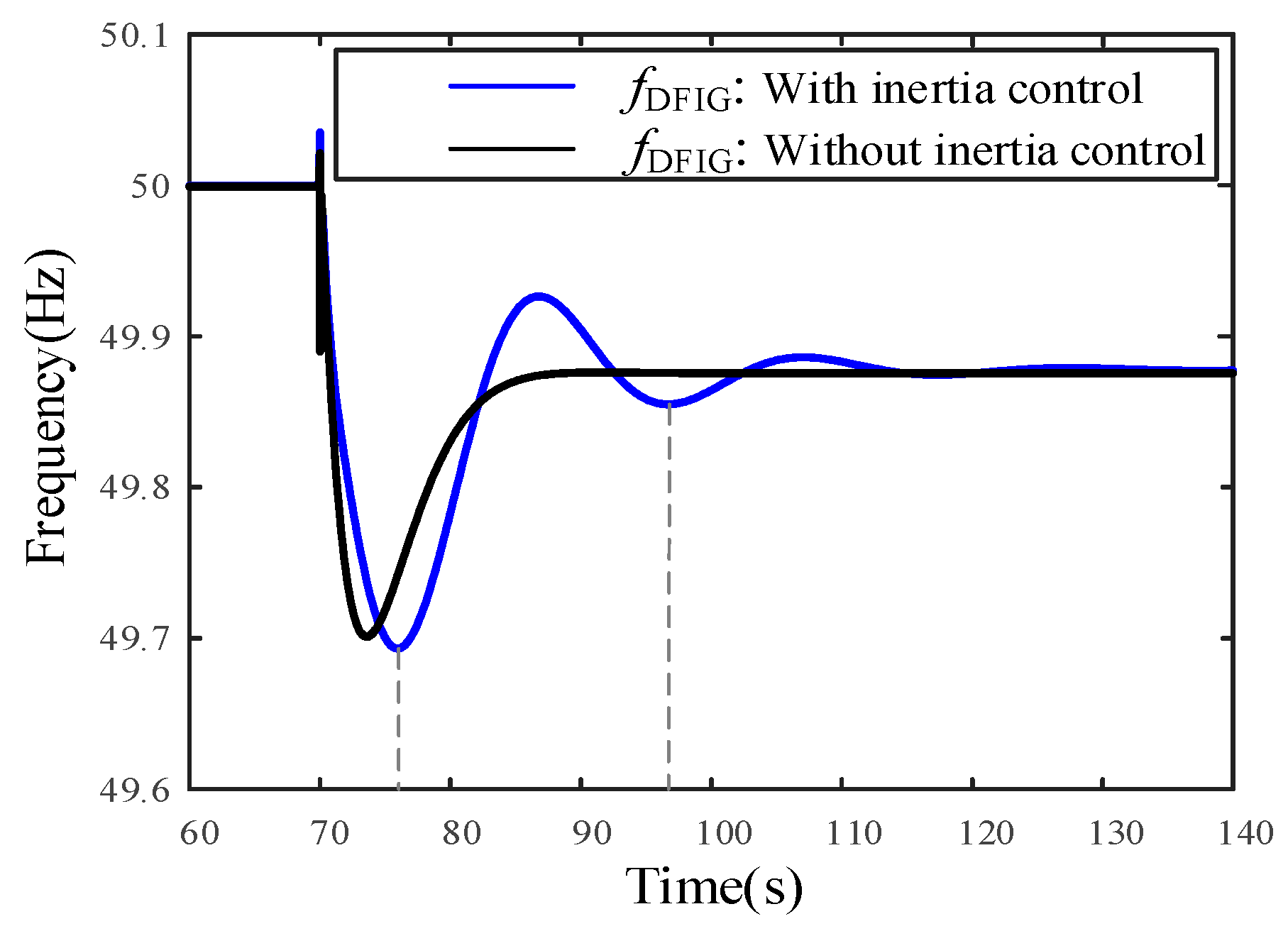
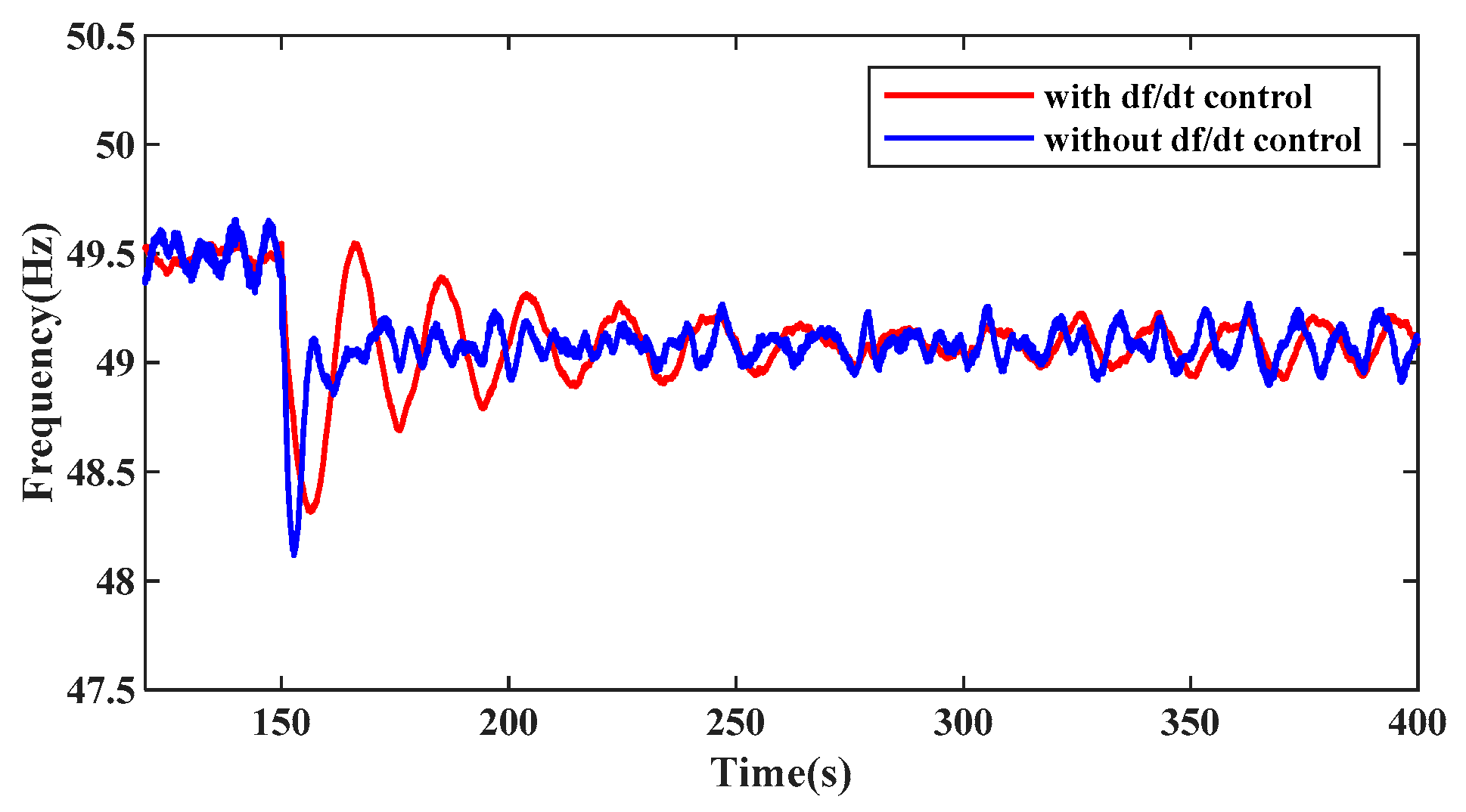
3.2. The ULFO Caused by DFIG with Inertia Control
4. Mechanism Analysis of the ULFO Caused by Inertia Control of the DFIG
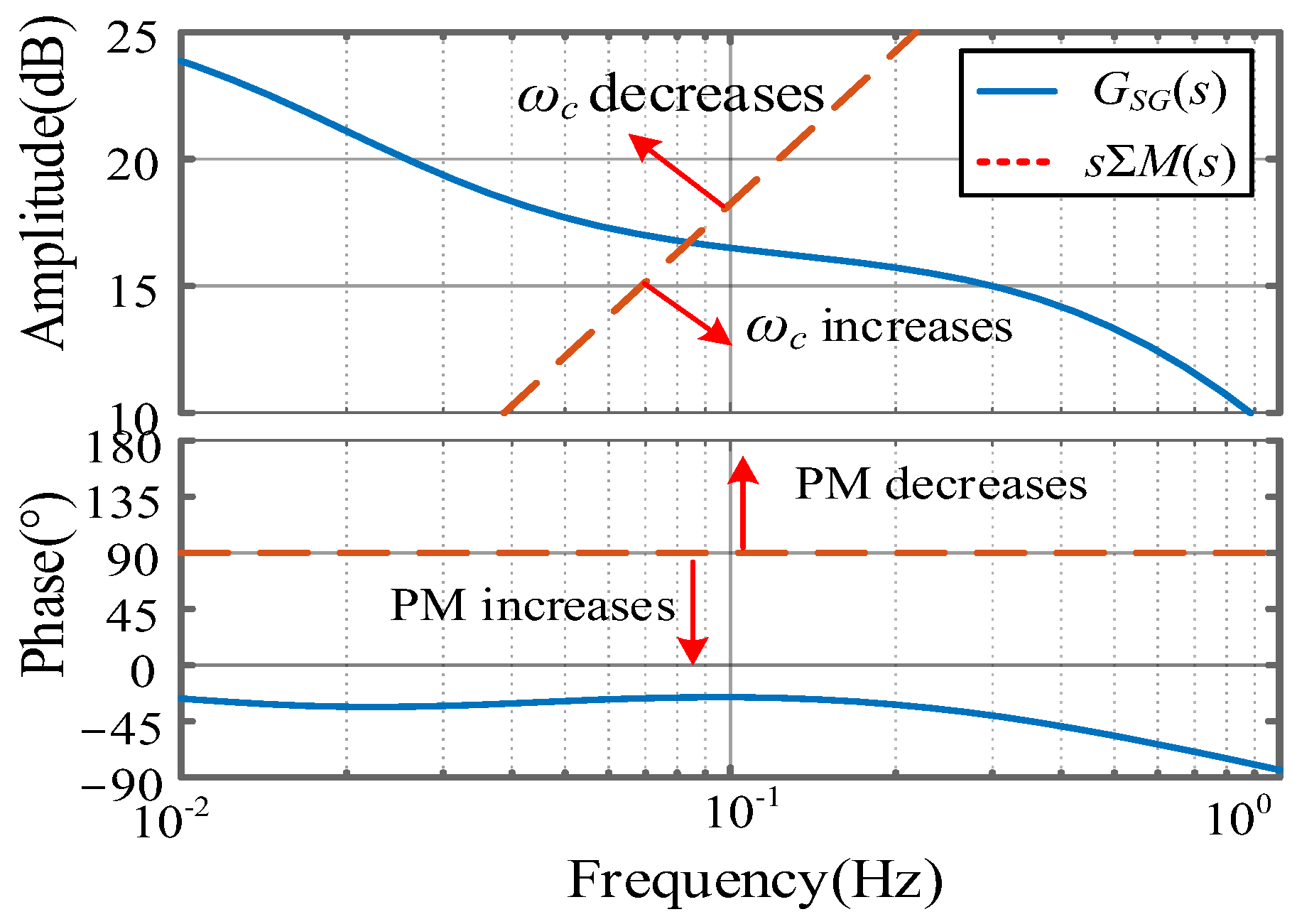
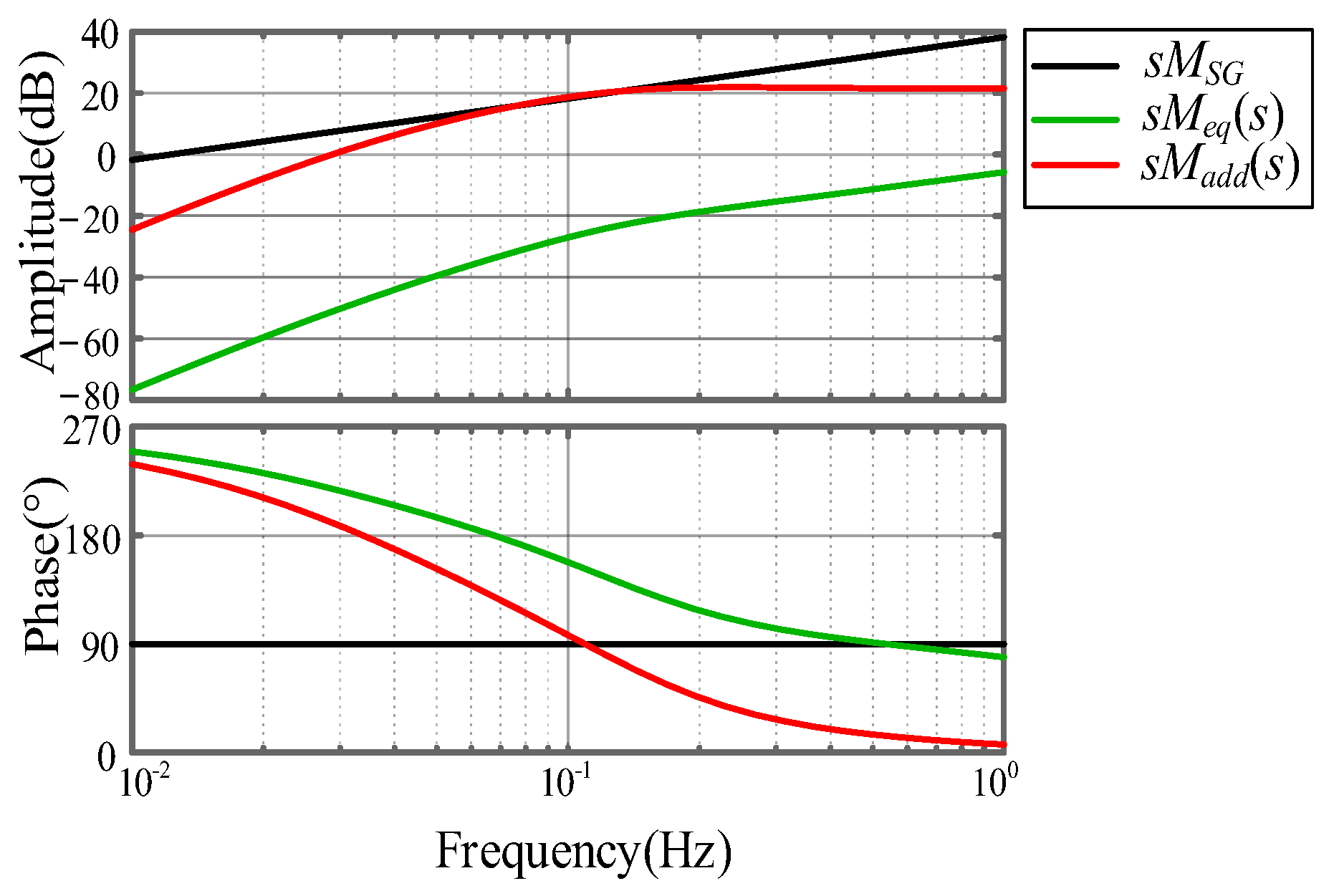
4.1. Relation Between the Additional Inertia and the Stability of the System
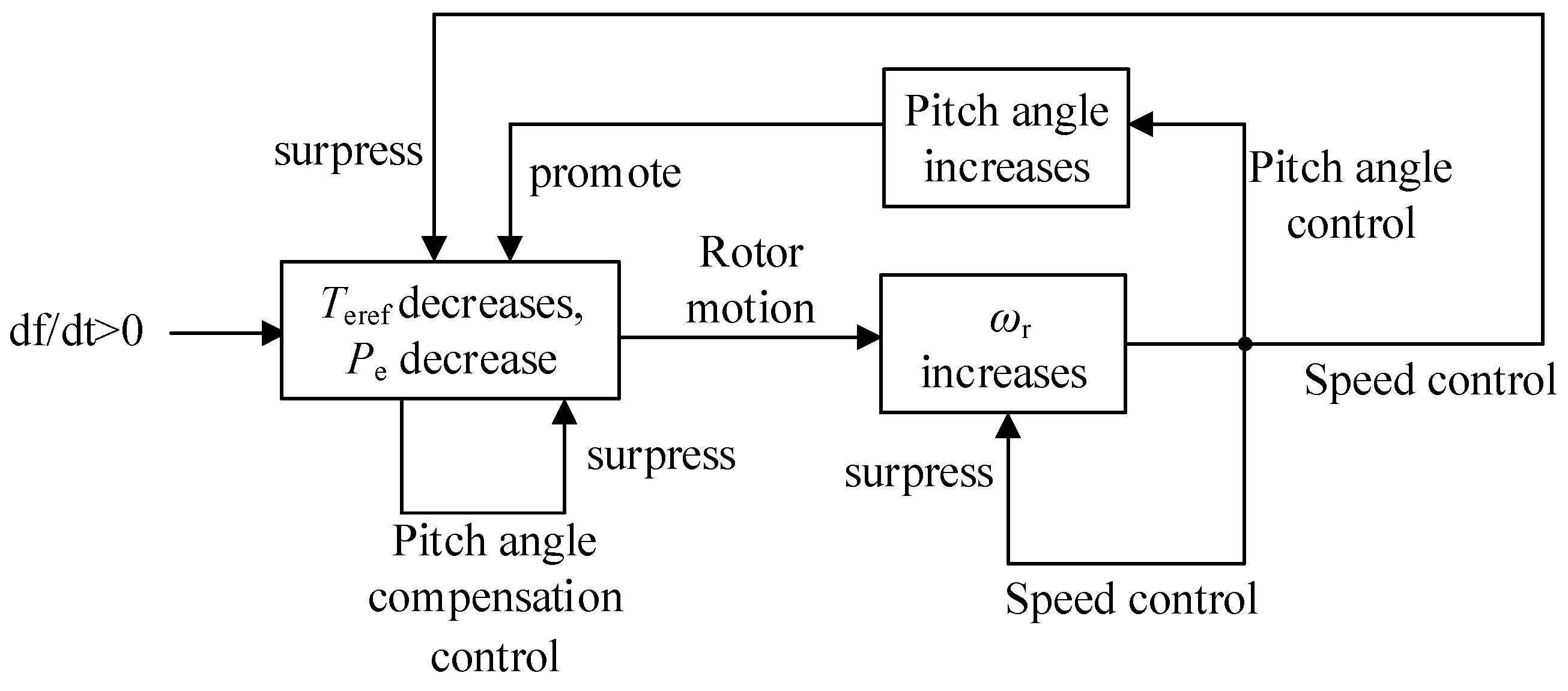
4.2. Mechanism of ULFO Caused by Inertia Control
5. Factors Influencing the ULFO
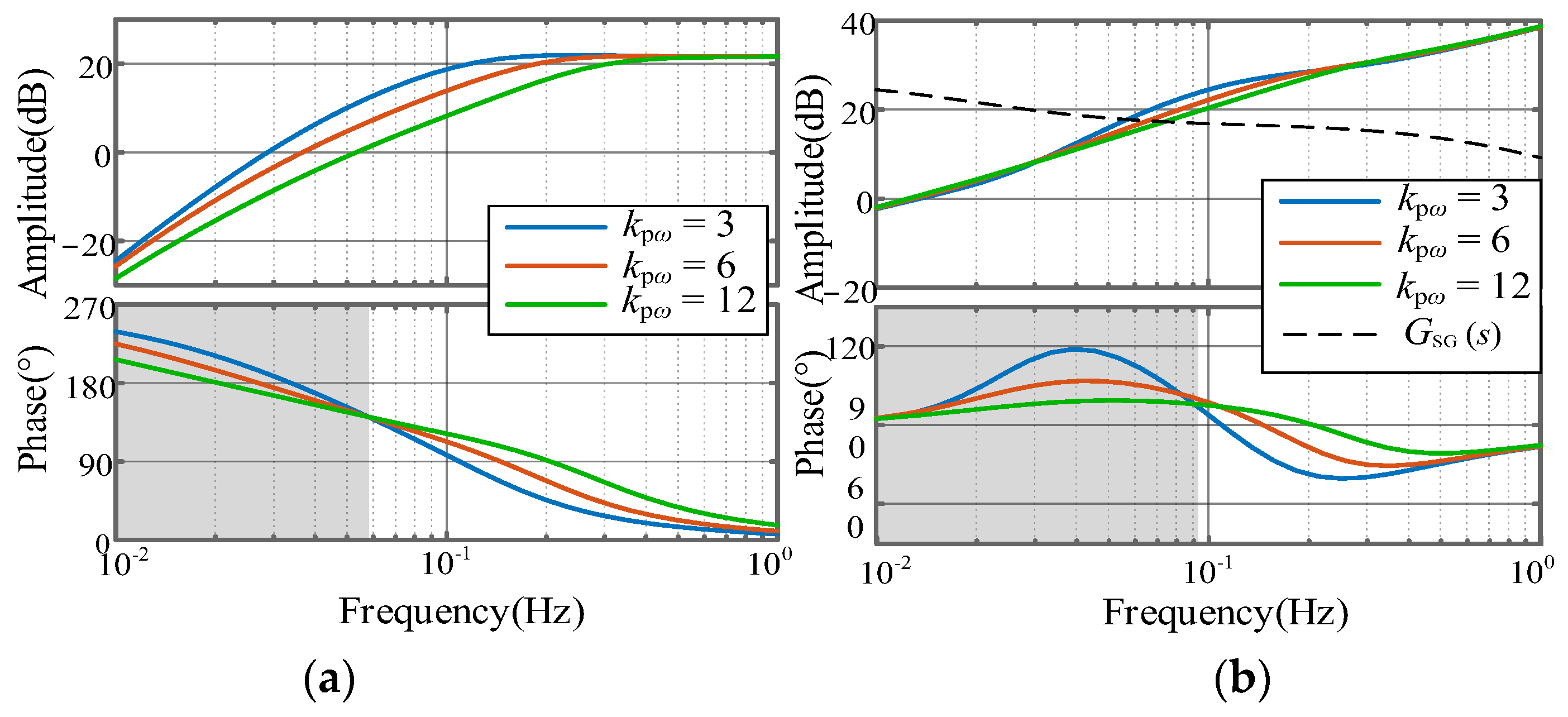
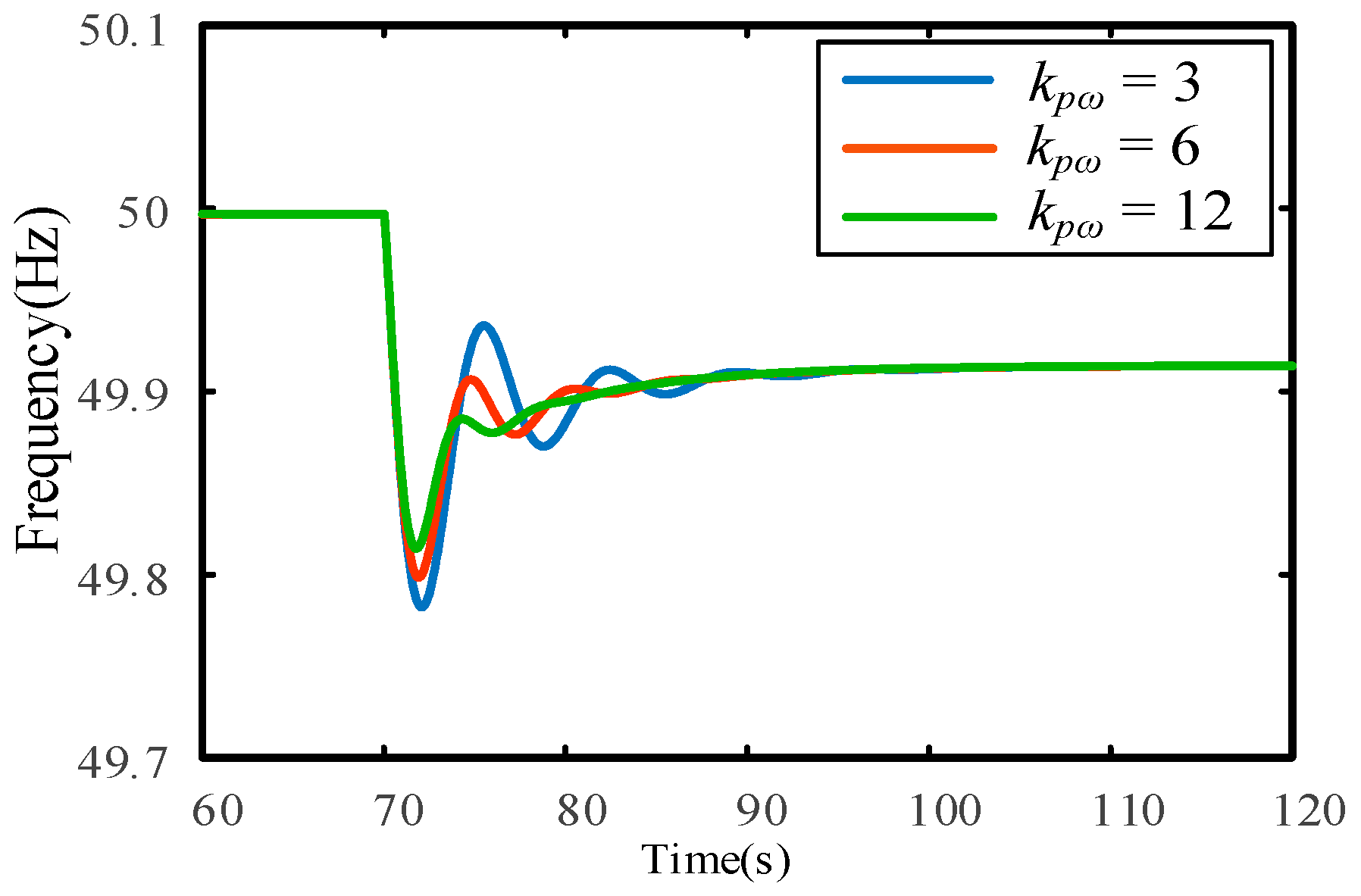
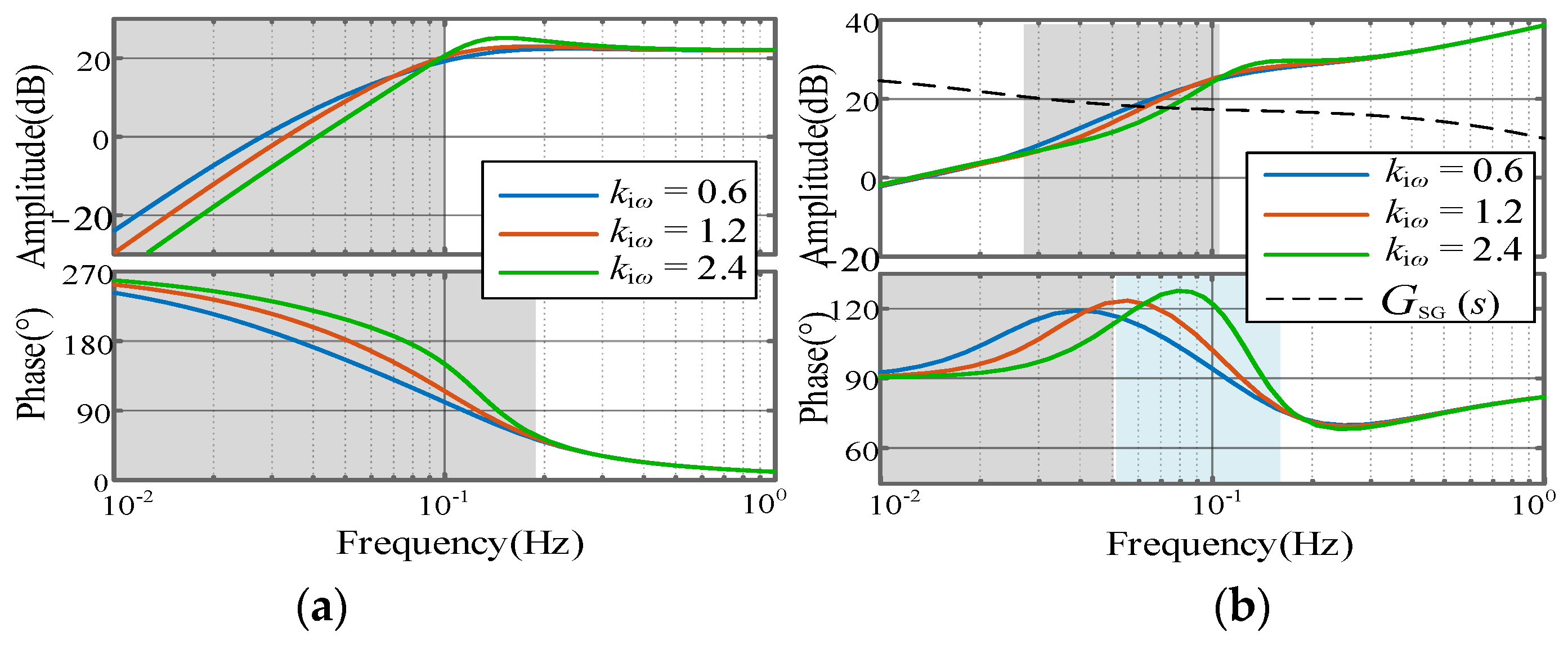
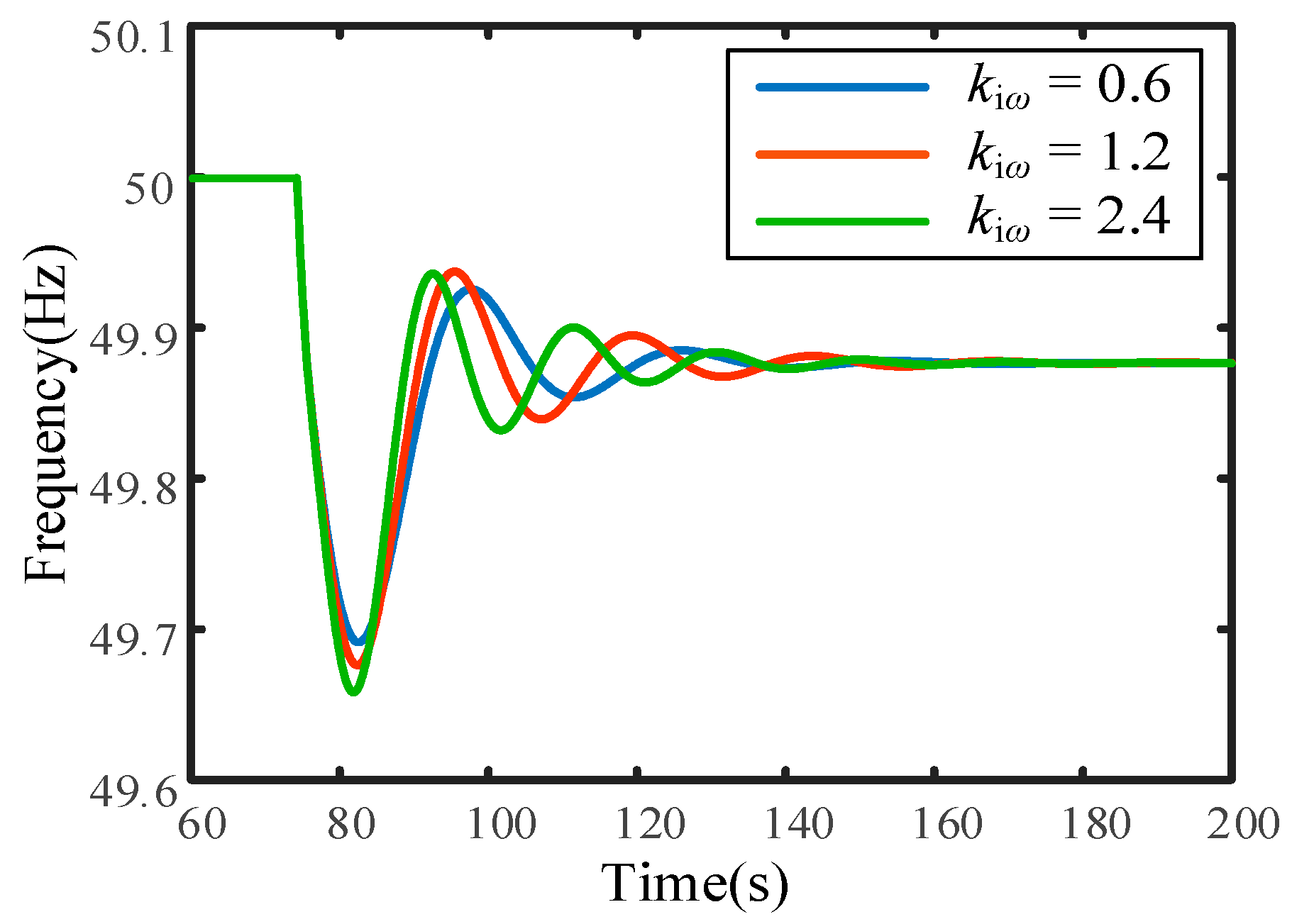
5.1. Impact of Speed Control
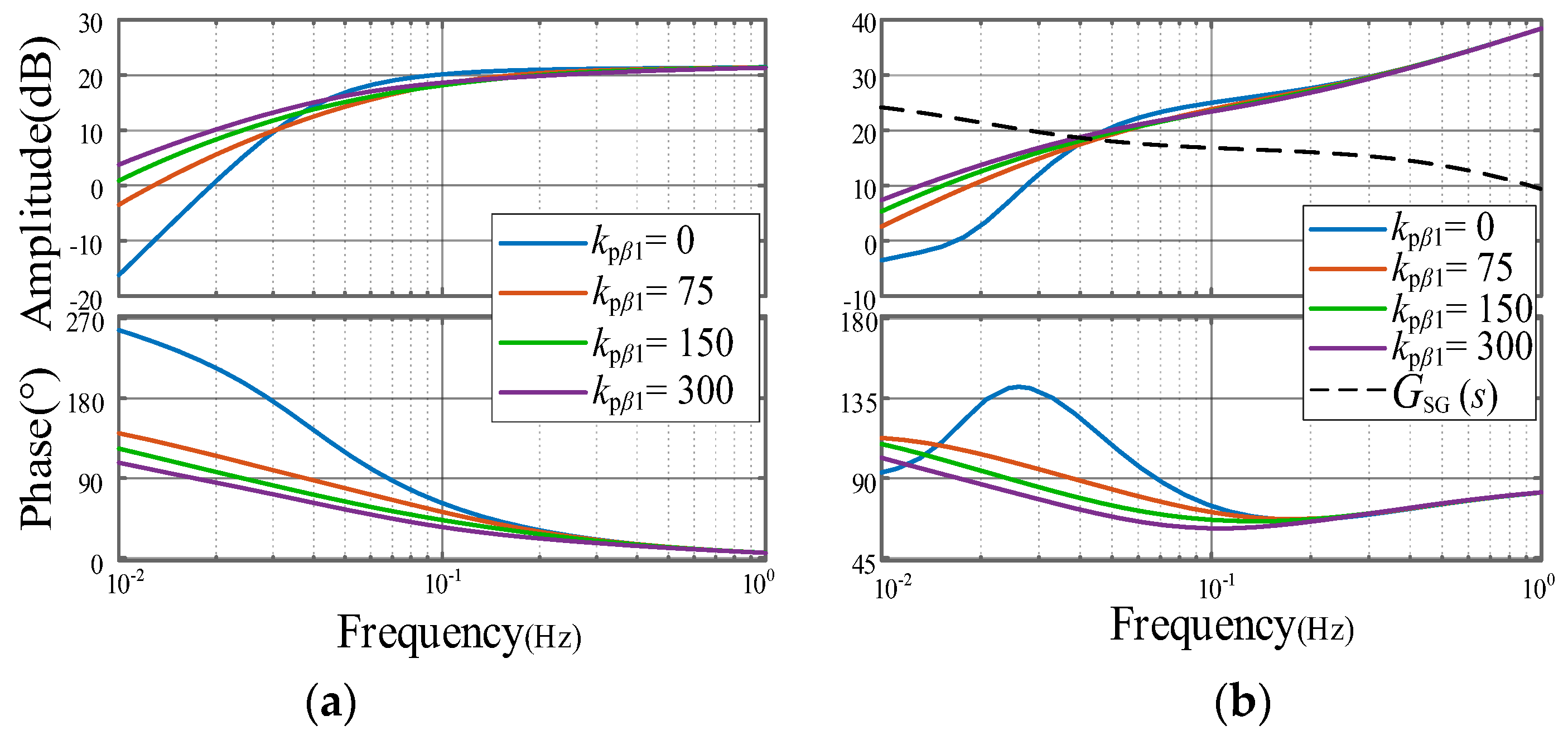
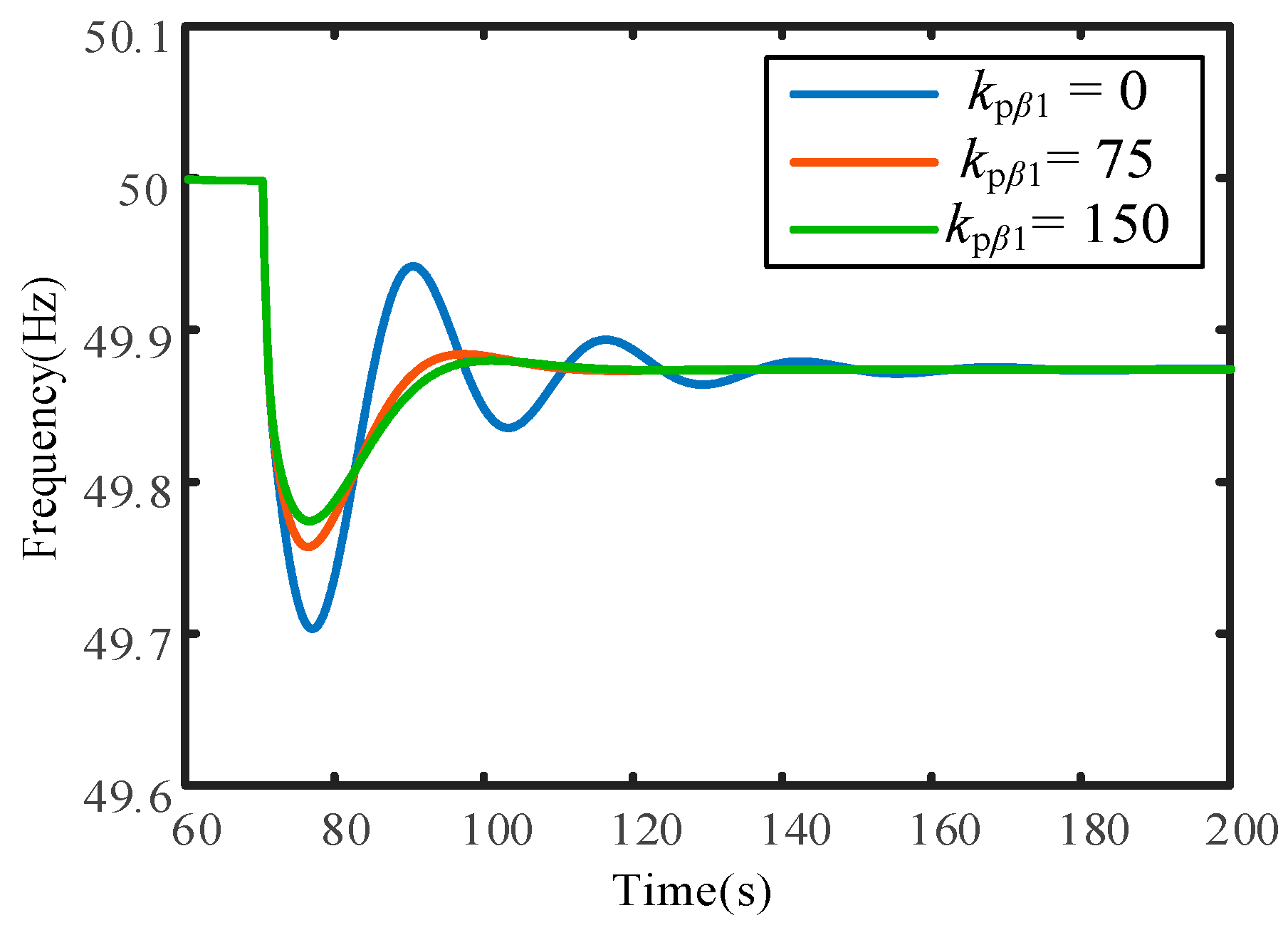
5.2. Impact of Pitch Angle Control
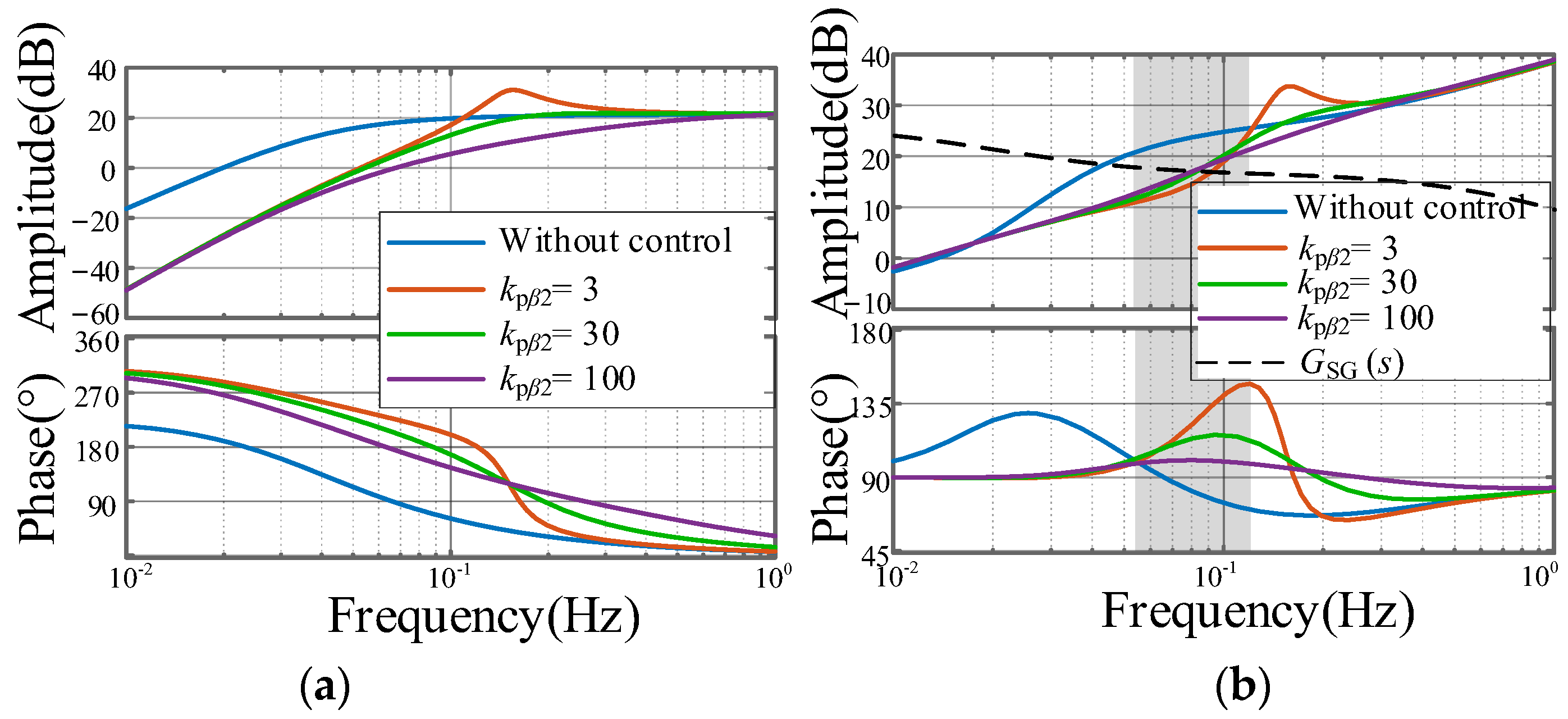
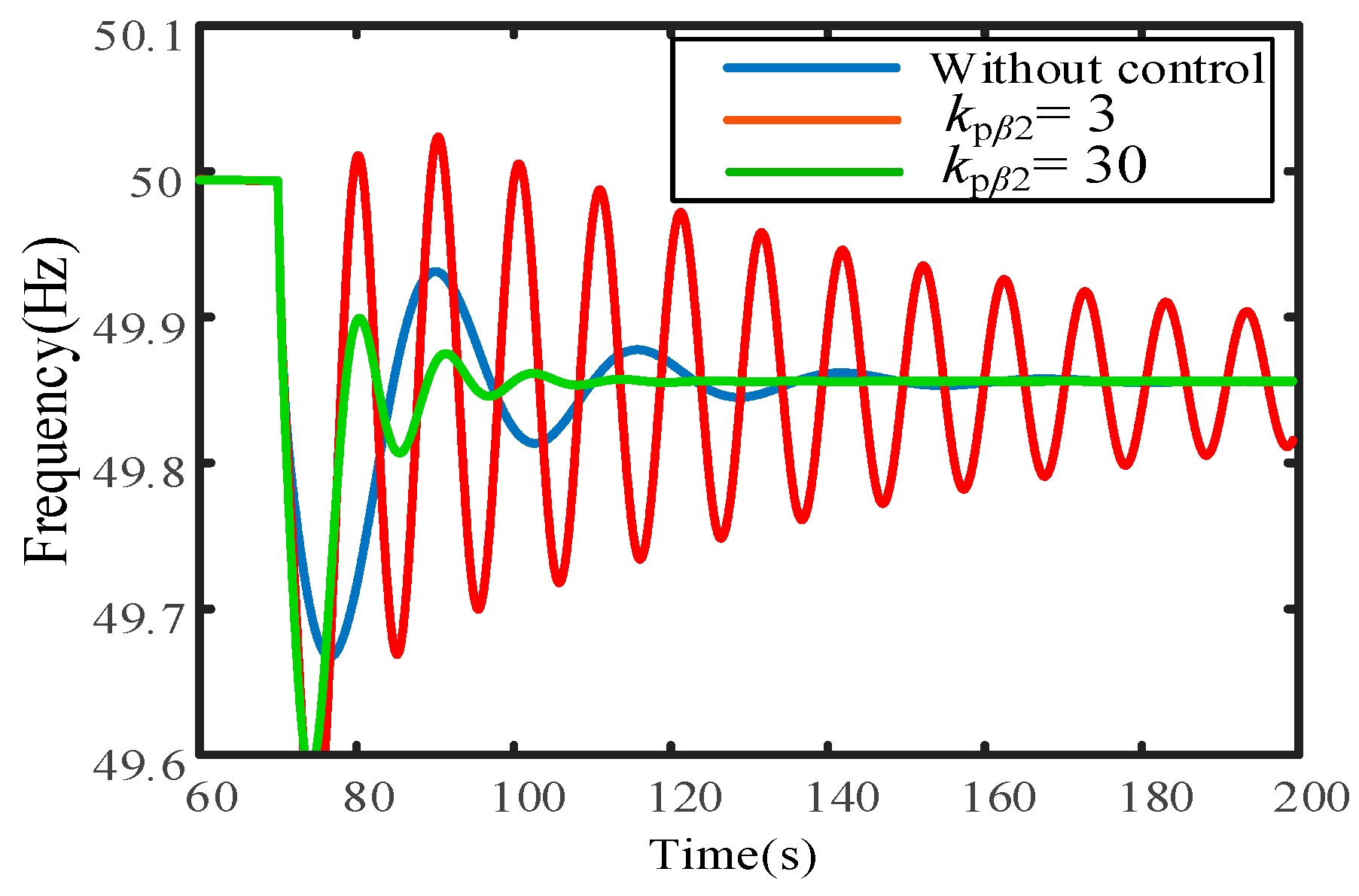
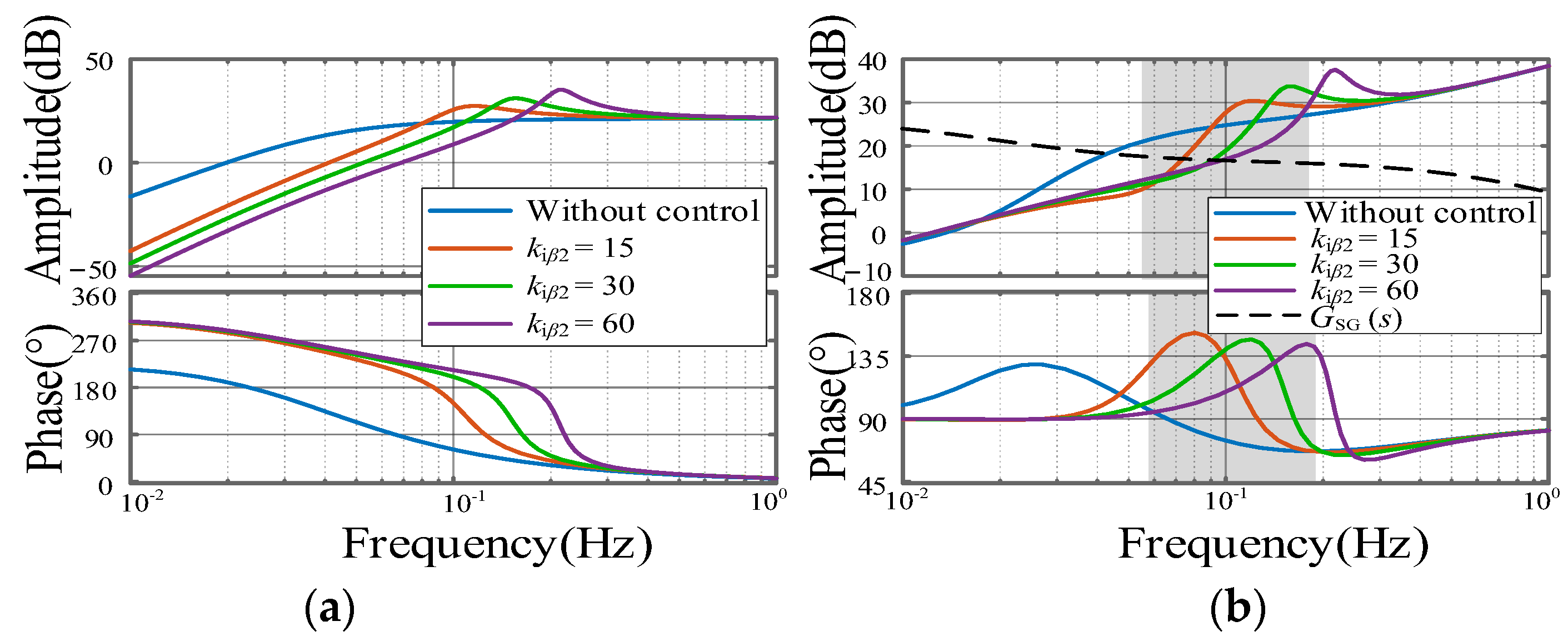
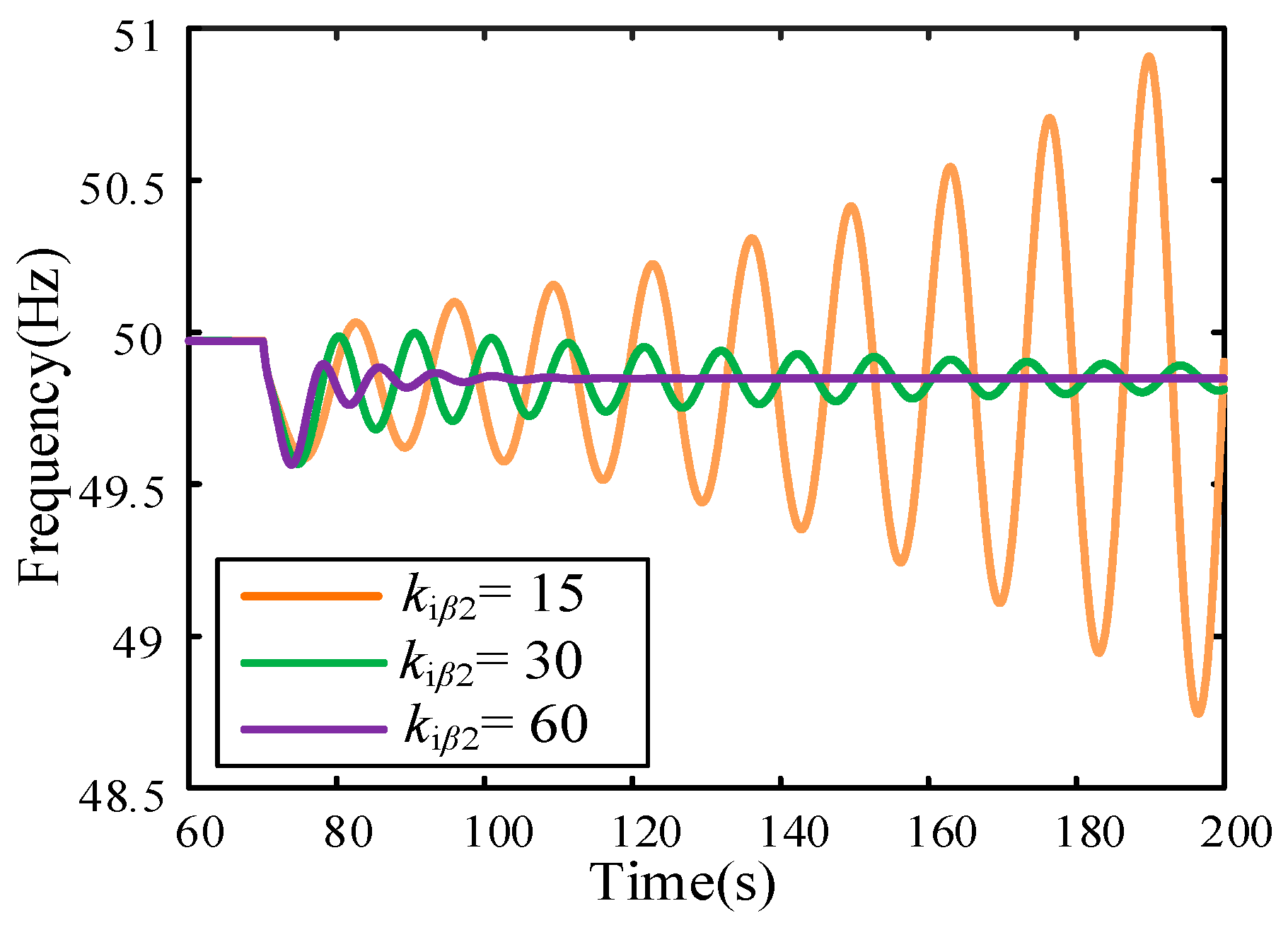
5.3. Impact of Pitch Angle Compensation
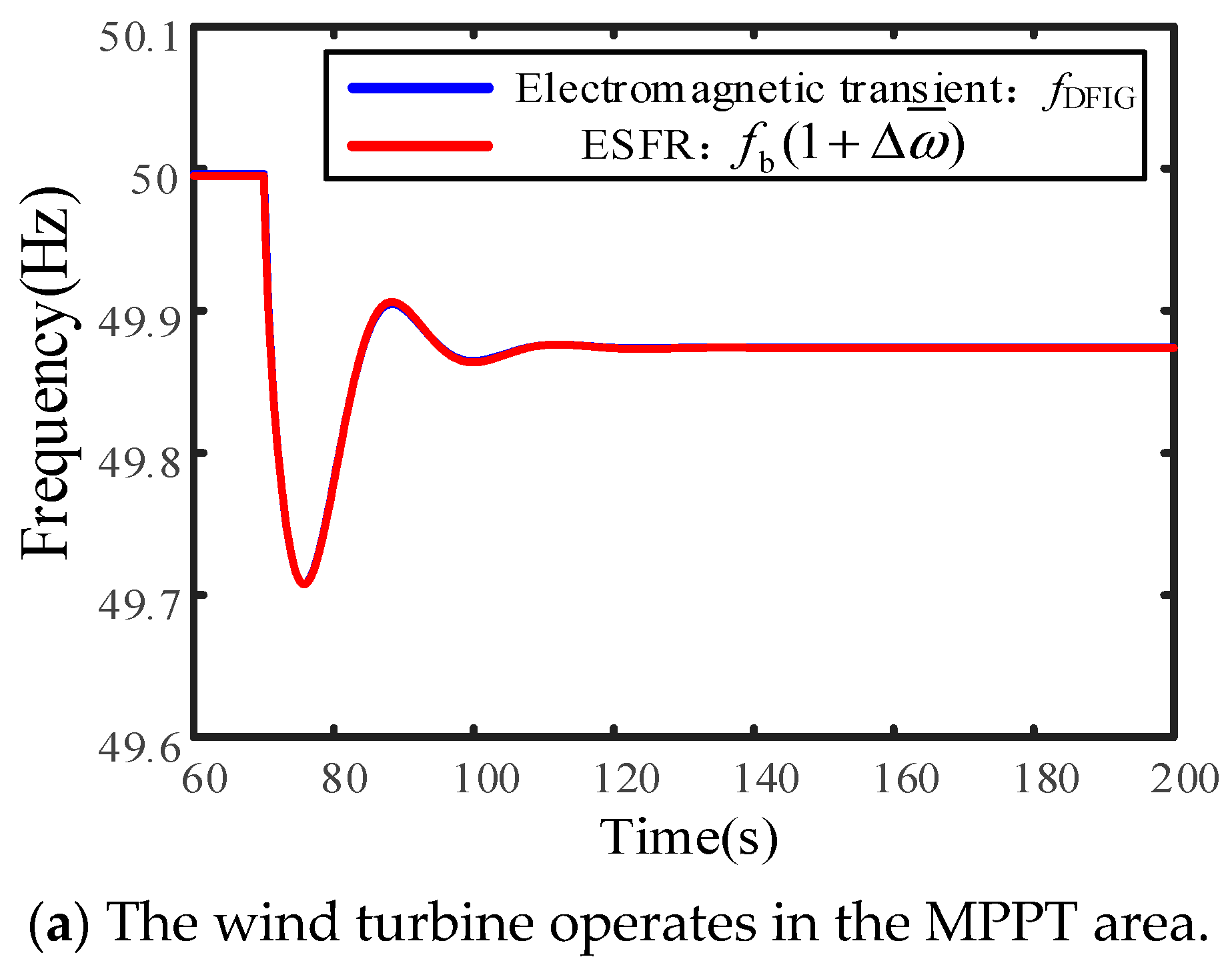
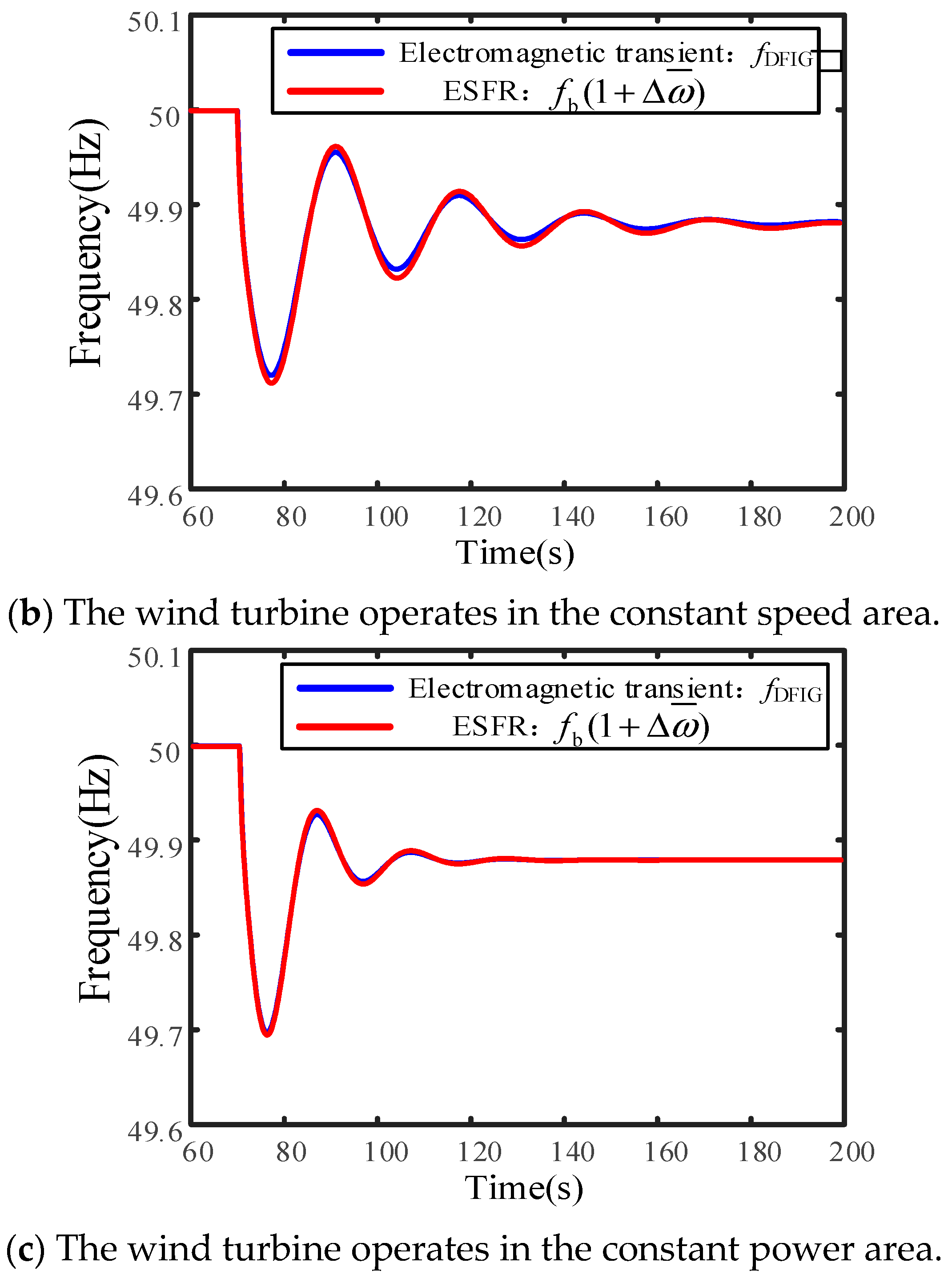
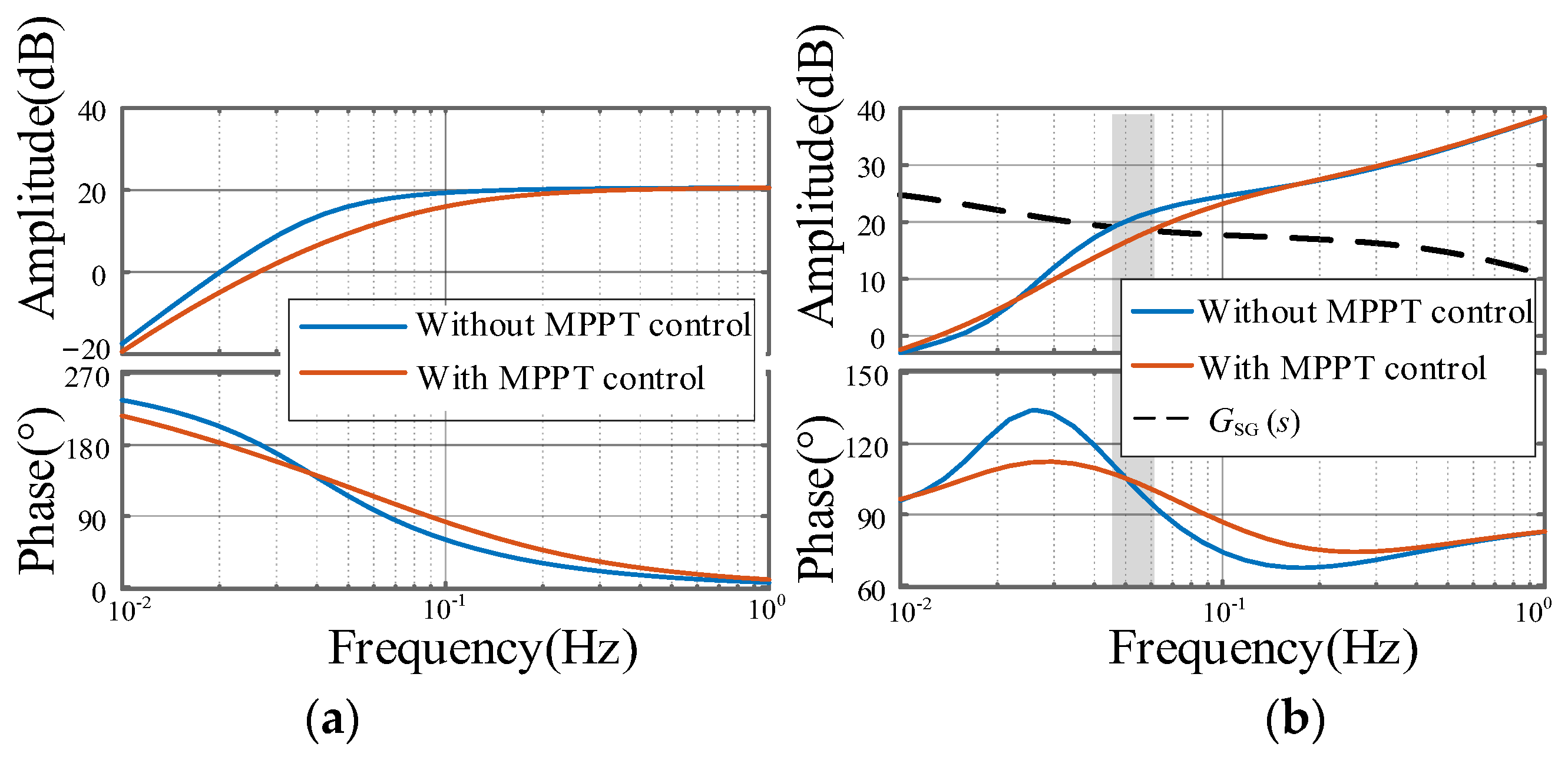
5.4. Impact of the MPPT Control
5.5. Key Influencing Parameters Validation
6. Conclusions
- ULFOs induced by inertia control of DFIG are confirmed using eigenvalue analysis. The result indicates that inertia control in DFIGs is a contributing factor to the emergence of ULFOs.
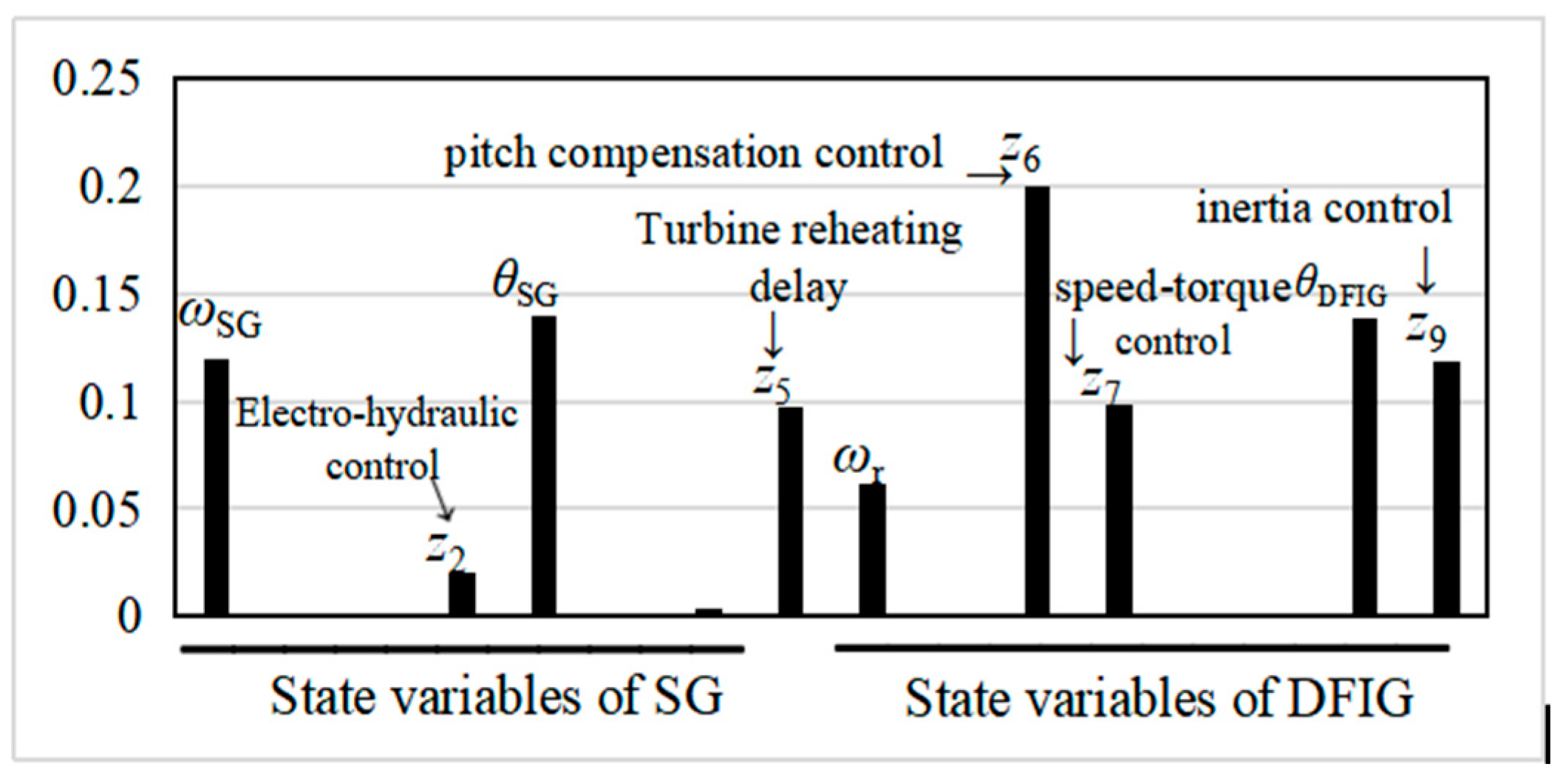
- An ESFR model is proposed and validated to further investigate the mechanism of ULFOs. To evaluate which control has a greater influence on the ULFO modes, the participation factor analysis is conducted.
- Based on this, the factors influencing the ULFO are analyzed. It is found that pitch angle compensation control exerts the predominant impact on such oscillations. With the increase of the parameters kpβ2 and kiβ2, the ULFO can be effectively mitigated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Parameters of the Studied System
| Symbol | Meaning |
|---|---|
| KPTm | The partial derivative of Tm with respect to β |
| KωTm | The partial derivative of Tm with respect to ωr |
| GωP1(s) | Transfer function of pitch angle control 1 |
| GωP2(s) | Transfer function of pitch angle control 2 |
| GωTe(s) | Transfer function of speed control |
| KωPm | The partial derivative of Pm with respect to ωr |
| KβPm | The partial derivative of Pm with respect to β |
| KMPPT0 | The partial derivative of ωrefMPPT with respect to Pe |
| G1(s) | Transfer function between Δωr and ΔPe 1 |
| G2(s) | Transfer function between Δωr and ΔPe 2 |
| G3(s) | Transfer function of Meq(s) |
| G4(s) | Transfer function of Madd(s) |
Appendix A.2. Coefficients and Transfer Functions in the Linearized Model
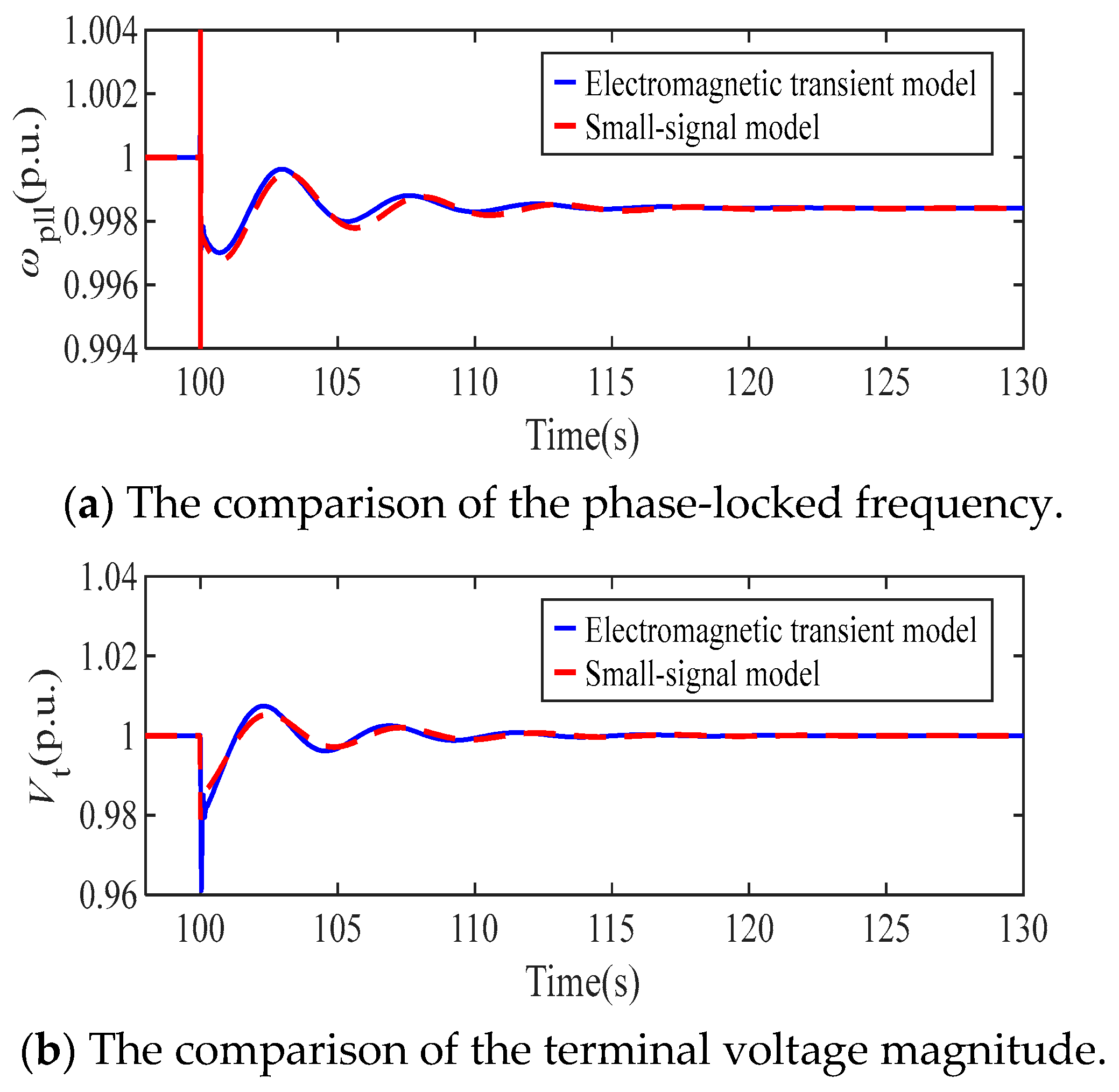
Appendix A.3. The Validation of the Small-Signal Model
References
- Mo, W.; Chen, Y.; Chen, H.; Liu, Y.; Zhang, Y.; Hou, J.; Gao, Q.; Li, C.; Zhao, R. Analysis and Measures of Ultralow-Frequency Oscillations in a Large-Scale Hydropower Transmission System. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1077–1085. [Google Scholar]
- Cebeci, M. The effects of Hydro Power Plant’s Governor Settings on the Turkish Power System Frequency. Master’s Thesis, Department of Electrical & Electronics Engineering, Middle East Technical University, Ankara, Turkey, 2008. [Google Scholar]
- Chen, G.; Liu, C.; Fan, C.; Han, X.; Shi, H.; Wang, G.; Ai, D. Research on Damping Control Index of Ultra-Low Frequency Oscillation in Hydro-Dominant Power Systems. Sustainability 2020, 12, 7316. [Google Scholar] [CrossRef]
- Pico, H.V.; McCalley, J.D.; Angel, A.; Leon, R.; Castrillon, N.J. Analysis of very low frequency oscillations in hydro-dominant power systems using multi-unit modeling. IEEE Trans. Power Syst. 2012, 27, 1906–1915. [Google Scholar] [CrossRef]
- Shen, J.Y.; Gong, K.Q.; Zhou, B. Ultralow Frequency Oscillation Induced by Primary Frequency Modulation of Hydropower and Parameter Optimization. J. Electr. Power 2018, 33, 392–398. [Google Scholar]
- Lu, X.M.; Chen, L.; Chen, Y.P.; Min, Y.; Hou, J.; Liu, Y.S. Ultra-low-frequency Oscillation of Power System Primary Frequency Regulation. Autom. Electr. Power Syst. 2017, 41, 67–70. [Google Scholar]
- Liu, C.X.; Zhang, J.F.; Chen, Y.P.; Zhang, J.X.; Xu, M.; Wang, G.H. Mechanism Analysis and Simulation on Ultra-ow Frequency Oscillation of Yunnan Power Grid in Asynchronous Interconnection Mode. South. Power Syst. Technol. 2016, 10, 29–34. [Google Scholar]
- Wang, P.; Li, B.; Zhao, J.; Liu, T.; Jiang, Q.; Chen, G. The Mechanism of Ultra-Low Frequency Oscillations with the Same Mode Shapes. IEEE Access 2020, 8, 198047–198057. [Google Scholar] [CrossRef]
- Shi, P. Wind Power Integrated Power System Small Signal Stability Analysis Based on Frequency Response Method; Zhejiang University: Zhejiang, China, 2019. [Google Scholar]
- Zhang, G.Z. Research on Low Frequency and Ultra-Low Frequency Stability Analysis and Control Strategy for Power Systems with High Renewable Energy Penetration; University of Electronic Science and Technology of China: Chengdu, China, 2022. [Google Scholar]
- Niasse, M.; Zheng, Q.; Xin, A.; Quan, F.A.F.; Simiyu, P. Mitigating Ultra-Low-Frequency Oscillations in Wind-Penetrated Hydro-dominant Power Grid through Virtual Inertia Emulation Strategy. In Proceedings of the 2020 4th International Conference on Power and Energy Engineering (ICPEE), Xiamen, China, 19–21 November 2020; pp. 130–137. [Google Scholar]
- Sun, L.; Zhao, X. Modelling and Analysis of Frequency-Responsive Wind Turbine Involved in Power System Ultra-Low Frequency Oscillation. IEEE Trans. Sustain. Energy 2021, 13, 844–855. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, T.; Bu, J.; Chen, L.; Xu, Z. Influence Mechanism Analysis of Wind Power Integration on Ultra-low Frequency Oscillation Based on Comprehensive Inertial Control. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; 383–389. [Google Scholar]
- Zhou, Y.; Zhu, D.; Hu, J.; Zou, X.; Kang, Y. Collaborative design of multiloop controllers for DFIG-based wind turbines to optimize inertia characteristics. IEEE Trans. Power Electron. 2025, 40, 6177–6191. [Google Scholar] [CrossRef]
- Liu, L.; Luo, X.; Xiong, L.; Guo, J.; Liu, X.; Liu, Y.; Zhang, H. Preset Power Based Droop Control for Improving Primary Frequency Regulation of Inverters Under Large Disturbances. IEEE Trans. Power Electron. 2025, 40, 9153–9166. [Google Scholar] [CrossRef]
- Li, Z.L. Research and Analysis on Parameter Identification and Power System Stability of Steam Turbine Governing System; North China Electric Power University: Beijing, China, 2020. [Google Scholar]
- Du, Y.W.; Wang, Q.; Jiang, C.M.; Li, Z.H.; Luo, Y.Z. Comparison of Typical Speed Governor Model with Power System Primary Frequency Characteristics. Water Resour. Power 2017, 35, 163–167. [Google Scholar]
- Deng, L.; Gui, S.; Wang, Z.F.; Gao, T. Physics Resolution for Mathematics Model of Synchronous Generator. Northeast. Electr. Power Technol. 2012, 33, 5–7. [Google Scholar]
- Tang, W.; Hu, J.; Chang, Y.; Liu, F. Modeling of DFIG-Based Wind Turbine for Power System Transient Response Analysis in Rotor Speed Control Timescale. IEEE Trans. Power Syst. 2018, 33, 6795–6805. [Google Scholar] [CrossRef]
- Wei, H. Study of Electromechanical-Time Scale Characteristics of Doubly Fed Induction Generator Type Wind Turbine and its Impact on Power System Electromechanical Dynamics; Huazhong University of Science and Technology: Wuhan, China, 2018. [Google Scholar]
- Rimorov, D.; Kamwa, I.; Joós, G. Quasi-Steady-State Approach for Analysis of Frequency Oscillations and Damping Controller Design. IEEE Trans. Power Syst. 2016, 31, 3212–3220. [Google Scholar] [CrossRef]
- Vournas, C.D.; Mantzaris, J.C. Application of QSS Modeling to Stabilizer Design for Interarea Oscillations. IEEE Trans. Power Syst. 2010, 25, 1910–1917. [Google Scholar] [CrossRef]
- Chen, L.; Lu, X.M.; Chen, Y.P.; Min, Y.; Zhang, Y.; Tang, Z.Y. Analysis of Ultra-low-frequency Oscillations in Multi-machine System and Equivalent Method. Autom. Electr. Power Syst. 2017, 41, 10–15. [Google Scholar]
- Li, G.Q.; Liu, X.Z.; Xin, Y.C.; Jiang, T.; Yan, K.F.; Wang, T. Research on Frequency Stability of Power System with High Penetration Renewable Energy: A Review. High Volt. Eng. 2024, 50, 1165–1181. [Google Scholar]


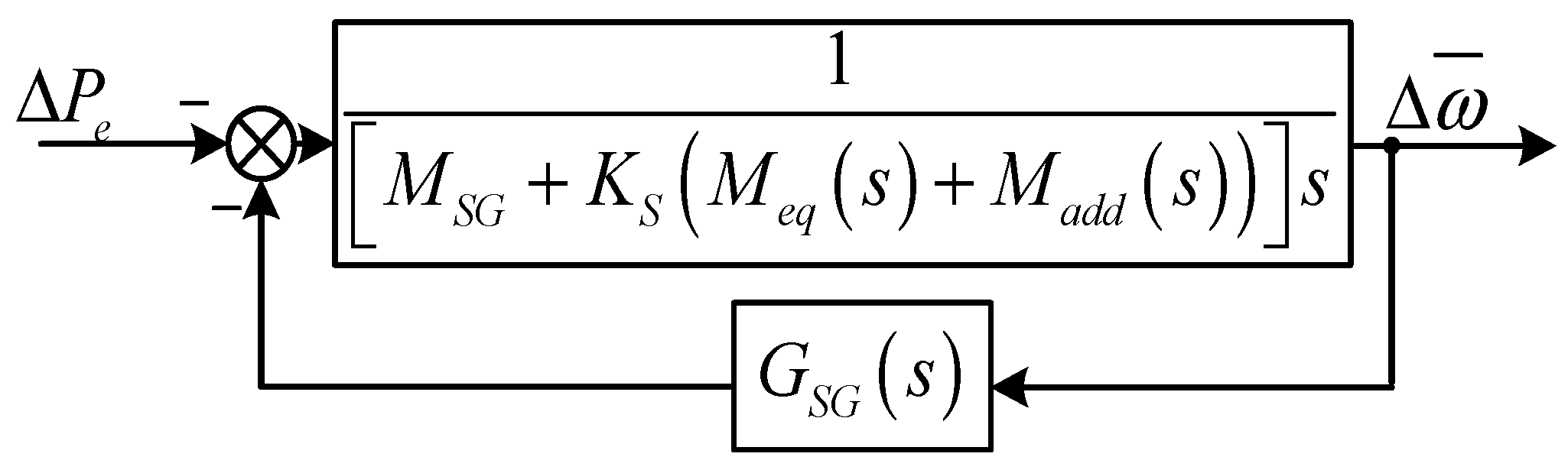
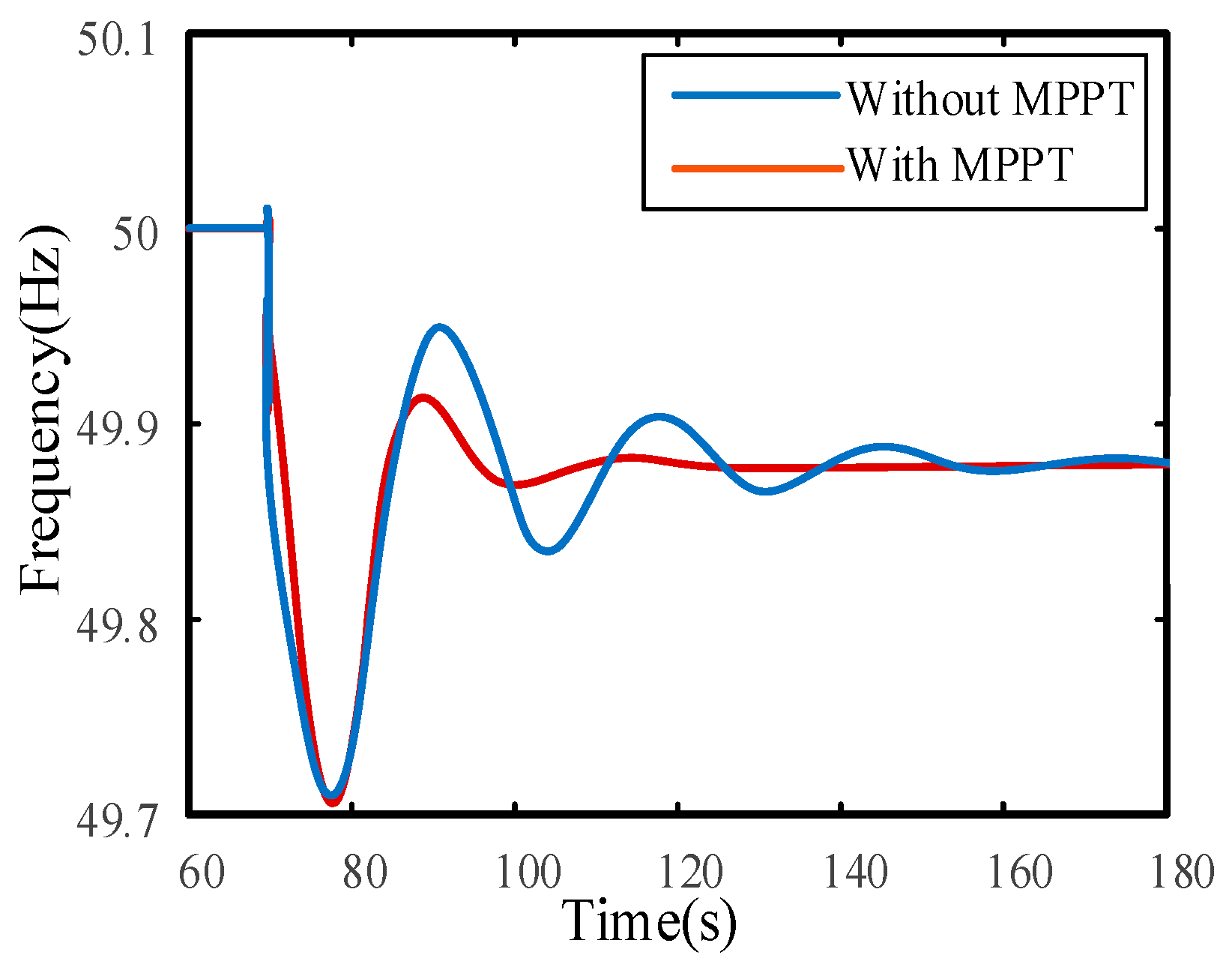
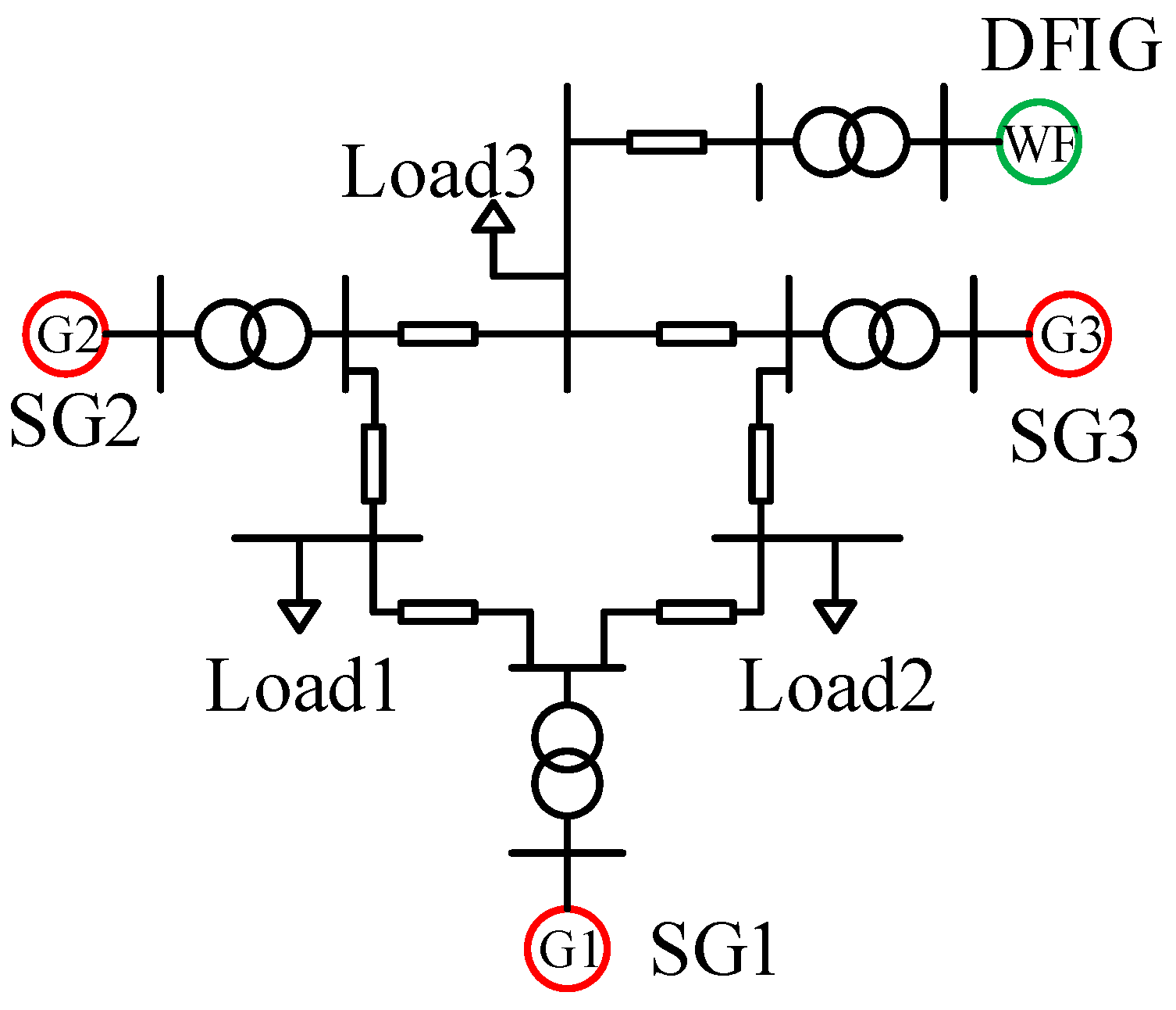
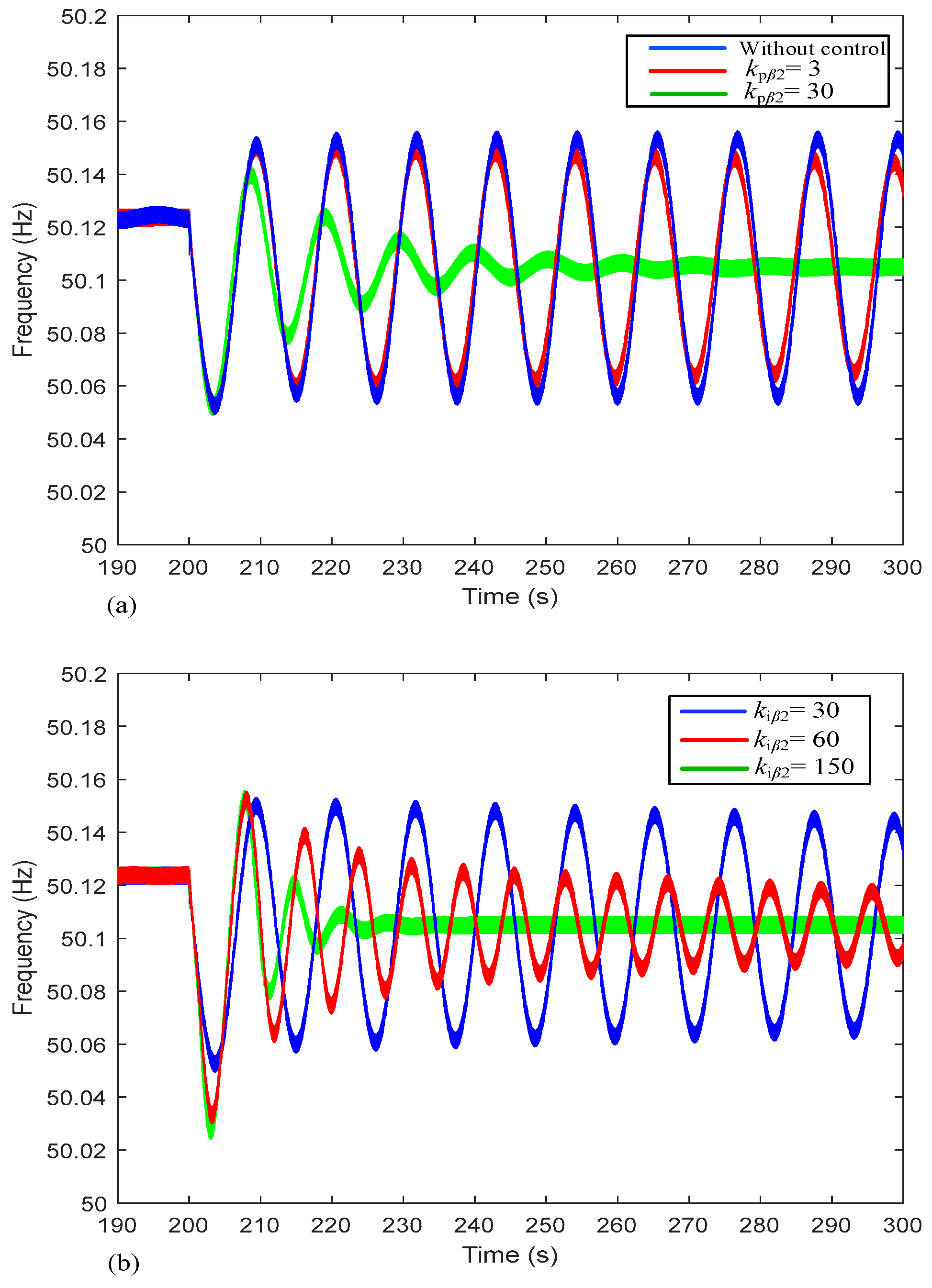
| Modal | Eigenvalue | Oscillation Frequency | Damping Ratio |
|---|---|---|---|
| λ1,2 | −0.336 ± j 0.177 | 0.028 Hz | 0.884 |
| λ3,4 | −0.635 ± j 0.508 | 0.081 Hz | 0.781 |
| λ5,6 | −3.163 ± j 20.43 | 3.252 Hz | 0.153 |
| Modal | Eigenvalue | Oscillation Frequency | Damping Ratio |
|---|---|---|---|
| λ1,2 | −0.092 ± j 0.307 | 0.049 Hz | 0.287 |
| λ3,4 | −0.155 ± j 0.056 | 0.009 Hz | 0.941 |
| λ5,6 | −2.154 ± j 0.868 | 0.138 Hz | 0.928 |
| λ7,8 | −15.09 ± j 15.38 | 2.448 Hz | 0.700 |
| Parameter | kpω | kiω | kpβ1 | kpβ2 | kiβ2 | Introducing MPPT |
|---|---|---|---|---|---|---|
| Oscillation Frequency | ↑ | ↑ | — | ↓ | ↑ | ↑ |
| Oscillation Damping Ratio | ↑ | ↓ | ↑ | ↑ | — | ↑ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, W.; Yi, Y.; Zhu, D.; Zhang, B.; Bao, B.; Zhang, Y. Impact Mechanism Analysis of DFIG with Inertia Control on the Ultra-Low Frequency Oscillation of the Power System. Energies 2025, 18, 3365. https://doi.org/10.3390/en18133365
Fan W, Yi Y, Zhu D, Zhang B, Bao B, Zhang Y. Impact Mechanism Analysis of DFIG with Inertia Control on the Ultra-Low Frequency Oscillation of the Power System. Energies. 2025; 18(13):3365. https://doi.org/10.3390/en18133365
Chicago/Turabian StyleFan, Wei, Yang Yi, Donghai Zhu, Bilin Zhang, Bo Bao, and Yibo Zhang. 2025. "Impact Mechanism Analysis of DFIG with Inertia Control on the Ultra-Low Frequency Oscillation of the Power System" Energies 18, no. 13: 3365. https://doi.org/10.3390/en18133365
APA StyleFan, W., Yi, Y., Zhu, D., Zhang, B., Bao, B., & Zhang, Y. (2025). Impact Mechanism Analysis of DFIG with Inertia Control on the Ultra-Low Frequency Oscillation of the Power System. Energies, 18(13), 3365. https://doi.org/10.3390/en18133365