Smart Grid Self-Healing Enhancement E-SOP-Based Recovery Strategy for Flexible Interconnected Distribution Networks

Abstract

With the development of modern power systems, AC distribution networks face increasing demands for supply flexibility and reliability. Energy storage-based soft open points (E-SOPs), which integrate energy storage systems into the DC side of traditional SOP connecting AC distribution networks, not only maintain power flow control capabilities but also enhance system supply performance, providing a novel approach to AC distribution network fault recovery. To fully leverage the advantages of E-SOPs in handling faults in flexible interconnected AC distribution networks (FIDNs), this paper proposes an E-SOP-based FIDN islanding recovery method. First, the basic structure and control modes of SOPs for AC distribution networks are elaborated, and the E-SOP-based AC distribution network structure is analyzed. Second, with maximizing total load recovery as the objective function, the constraints of E-SOPs are comprehensively considered, and recovery priorities are established based on load importance classification. Then, a multi-dimensional improvement of the dung beetle optimizer (DBO) algorithm is implemented through Logistic chaotic mapping, adaptive parameter adjustment, elite learning mechanisms, and local search strategies, resulting in an efficient solution for AC distribution network power supply restoration. Finally, the proposed FIDN islanding partitioning and fault recovery methods are validated on a double-ended AC distribution network structure. Simulation results demonstrate that the improved DBO (IDBO) algorithm exhibits a superior optimization performance and the proposed method effectively enhances the load recovery capability of AC distribution networks, significantly improving the self-healing ability and operational reliability of AC distribution systems.

1. Introduction

With the rapid development of modern power systems, new energy sources, represented by photovoltaic and wind power, are being extensively integrated into the grid. These new energy sources exhibit significant intermittency and uncertainty, which can lead to power supply interruptions and limited regulation capabilities when relying solely on sectionalizing switches and tie switches in traditional power systems [1,2]. Unlike the traditional distribution network operation mode of “closed-loop design, open-loop operation,” flexible interconnected distribution networks (FIDNs) offer numerous advantages, including closed-loop power supply and controllable power flow. These characteristics enable FIDNs to effectively achieve flexible power exchange, thereby facilitating rapid power supply restoration under fault conditions [3,4,5].

With the rapid development of flexible interconnection devices (FIDs), they have gradually replaced traditional switching devices in distribution networks, making interconnection methods more flexible. Among these, soft open points (SOPs) are the most typical flexible devices. During sudden grid faults, SOPs can respond rapidly and precisely to adjust power distribution across feeders, thereby promoting the integration of new energy sources and enhancing the fault recovery capability of distribution networks [6,7,8].

Self-healing capability is one of the essential characteristics of flexible interconnected distribution networks, particularly when the penetration rate of distributed generators (DGs) increases, necessitating higher requirements for the self-healing capability of distribution networks. When faults occur in distribution networks, islanding phenomena can easily emerge. Consequently, researchers have conducted extensive studies on distribution network island recovery. Zhou et al. [9] introduced network reconfiguration into island partitioning and constructed a model based on binary particle swarm optimization and differential evolution hybrid algorithms to enhance the self-healing capability of distribution networks. Zhan et al. [10] investigated dynamic island partitioning in distribution networks with high proportions of DG integration, comprehensively considering island backup requirements to improve supply reliability.

However, the aforementioned studies did not consider the use of SOPs and still exhibit certain limitations. The authors of [11] proposed an SOP island partitioning method based on node importance ranking, which improved DG utilization and enhanced power system stability. Nevertheless, SOPs have high costs, and distribution network structures are complex, so coordinating SOPs with traditional equipment should be considered. Energy storage-based soft open points (E-SOPs) are an improved version of SOPs, which place energy storage systems (ESSs) on the DC side of SOPs. E-SOPs feature smaller volumes and lower costs while providing better regulation capabilities, warranting further research [12].

Ruonan et al. [13] coordinated on-load tap changers (OLTCs), capacitor banks (CBs), static var compensators, and E-SOPs for optimization, effectively maintaining node voltages within required ranges. Chu et al. [14] established a multi-time scale voltage optimization model for OLTCs, CBs, and E-SOPs, achieving superior voltage control effects. Evidently, E-SOPs demonstrate excellent voltage support capabilities. However, as DG penetration in power grids increases, their randomness directly affects distribution network load supply and island partitioning [15]. Currently, research on FIDN island recovery is limited. Studying FIDN island recovery can improve grid emergency response capabilities and distribution system flexibility, which is significant for the safe and stable operation of power grids.

In summary, this paper proposes an E-SOP-based flexible interconnected distribution network island recovery method. The main contributions of this paper are as follows:

(1)

An E-SOP-based FIDN island recovery method is proposed, which fully considers the power constraints and voltage support capabilities of E-SOPs, effectively enhancing power supply flexibility and the reliability of distribution networks under fault conditions.

(2)

Based on node importance classification, a differentiated recovery strategy is designed, prioritizing the recovery of primary loads to ensure the continuous operation of critical power facilities.

(3)

An improved dung beetle optimizer algorithm (IDBO) is introduced to solve the power supply restoration problem. Through adaptive parameter adjustment, elite learning strategies, local search mechanisms, and chaotic mapping, the optimization effect of distribution network recovery schemes is significantly improved.

The remainder of this paper is organized as follows: Section 2 introduces the mathematical models related to E-SOPs, Section 3 establishes the flexible distribution network power supply restoration model, Section 4 proposes the E-SOP-based power supply restoration method and improves the DBO algorithm, Section 5 verifies the effectiveness of the proposed method through case analysis, and Section 6 summarizes the work of the entire paper.

2. E-SOP Mathematical Model

To analyze the role of E-SOPs in flexible interconnected distribution networks, this section first introduces the basic structure and control methods of SOPs, then elaborates on the mathematical model of E-SOPs.

2.1. SOPs

As a highly modularized integrated power electronic device [16,17,18], SOPs are primarily implemented in three ways—back-to-back voltage source converters (B2B VSCs), static synchronous series compensators (SSSCs), and unified power flow controllers (UPFCs) [19]. This paper mainly focuses on B2B VSCs for research. B2B VSCs primarily consist of two VSCs connected through a DC capacitor, with the specific structure shown in Figure 1. The control methods of B2B VSCs are listed in Table 1.

Figure 1. Diagram of a flexible interconnected system with an SOP.

Table 1. Control Strategies for SOPs.

Mode	VSC1	VSC2	Operating State
1	PQ control	VdcQ control	Normal
2	VdcQ control	PQ control	Normal
3	Vf control	VdcQ control	VSC1 side fault
4	VdcQ control	Vf control	VSC2 side fault

From Figure 1 and Table 1, it can be observed that under normal operating conditions, the SOP consistently maintains the PQ-V_dcQ control mode. When a fault occurs in one of the AC distribution networks (such as a transformer failure or line fault), the affected network loses its main power supply and becomes de-energized. In this scenario, the VSC connected to the faulted distribution network side switches to V_f control mode to provide voltage and frequency support to the de-energized area, while the VSC on the healthy network side maintains V_dcQ control to regulate the DC link voltage and reactive power.

2.2. E-SOPs

The internal structure of an E-SOP primarily consists of converters and an ESS. The specific structure of an E-SOP in a double-ended distribution network is shown in Figure 2.

Figure 2. Structural configuration of an E-SOP in a double-ended distribution network.

E-SOPs placed in distribution networks can effectively replace traditional tie switches. Unlike traditional SOPs, the integration of ESSs enables energy storage functionality during power transmission, thereby enhancing the power flow control capability of traditional SOPs [20]. Additionally, when a transformer in the line fails, the E-SOP can serve as a backup power source to continue providing electricity, ensuring the normal operation of the distribution network.

3. Flexible Distribution Network Power Supply Restoration Modeling

3.1. Objective Function

Distribution network power supply restoration is a typical multi-objective optimization problem. In practical applications, the primary objective of power restoration is to recover as much de-energized load as possible, especially critical loads, to reduce economic losses and operational impacts.

Traditional power supply restoration models typically only consider maximizing the total restored load. However, in a flexible interconnected distribution network containing E-SOPs, it is necessary to simultaneously consider equipment utilization efficiency and system operational safety and stability. Therefore, when establishing the objective function in this paper, we not only focus on the total amount of load restoration but also consider the power margin of the ESS in the E-SOP to ensure the system has a sufficient regulation capability to respond to load fluctuations. Consequently, this paper adopts the maximization of the total restored load as the objective function, which can be represented as follows:

$$\max f_1=S_{\max }^{\mathrm{ESS}}-S_c^{\mathrm{ESS}}$$

(1)

where $S_{\max }^{\mathrm{ESS}}$ is the maximum discharge power of the ESS; $S_c^{\mathrm{ESS}}$ is the power margin of the ESS.

3.2. Constraint Conditions

In practical distribution networks, switchable nodes are typically those equipped with sectionalizing switches, load switches, or other controllable switching devices. The restoration strategy focuses on these controllable nodes, which can be isolated or reconnected based on system requirements and operational constraints. The mathematical formulation presented in this section applies specifically to these switchable nodes, while non-switchable nodes are considered as part of the network topology constraints.

Within the E-SOP device, there exists a certain power constraint between the SOP and ESS. During normal operation, the two converters will operate using different control methods. When both transformers at both ends fail, the converters will switch to Vf mode to provide voltage support for the distribution network. At this time, the ESS functions as a power source for the converters, forming a power constraint between the SOP and ESS during this process, as shown in the following equation:

$$P_{\mathrm{ESS}}+P_{\mathrm{VSC}1}+P_{\mathrm{VSC}2}=0$$

(2)

where P_ESS is the active power output by the ESS device, P_VSC1 is the active power output by VSC1, and P_VSC2 is the active power output by VSC2. This constraint ensures a matching relationship between ESS output power and the power consumption of the two VSCs, which is the fundamental condition for the normal operation of E-SOPs.

In a double-ended distribution network structure, when both transformers fail, although the E-SOP can restore power supply to the fault nodes, considering that both SOP and ESS devices have power limitations, appropriate measures need to be formulated to ensure that the E-SOP will not be damaged due to excessive power. This paper has formulated the following load shedding strategy [21], with specific steps as follows:

(1)

Load power statistical constraint: First, the power of loads to be restored in distribution network 1 and distribution network 2 is set. The purpose of this step is to clarify the total load demand that needs to be restored after the fault, providing a basis for subsequent power allocation, which can be represented using the following equation:

$$\left\{\begin{array}{l}{S}_1^{\mathrm{res}}={\displaystyle \sum _{n\in {\Omega }_1}{S}_i^{\mathrm{load}}}\\ S_2^{\mathrm{res}}={\displaystyle \sum _{n\in {\Omega }_2}{S}_i^{\mathrm{load}}}\end{array}\right.$$

(3)

where $S_1^{\mathrm{res}}$ and $S_2^{\mathrm{res}}$ are the powers of loads to be restored in the two distribution networks; $S_i^{\mathrm{load}}$ is the power of node I; ${\Omega }_1$ is the set of nodes to be restored in distribution network 1; and ${\Omega }_2$ is the set of nodes to be restored in distribution network 2.

(2)

VSC power margin constraint: A power margin refers to the difference between actual output power and maximum power. A larger power margin indicates a greater safety and stability. When the power margin is less than 0, load shedding operations need to be considered. Analyzing the nodes in distribution network 1 and considering the power limitation of VSC1, when supplying power to nodes in distribution network 1, the power margin of VSC1 $S_{\mathrm{vsc}1}^m$ can be represented as follows:

$$S_{\mathrm{vsc}1}^m=S_{\max }^{\mathrm{vsc}1}-S_1^{\mathrm{res}}$$

(4)

where $S_{\max }^{\mathrm{vsc}1}$ is the maximum power that VSC1 can transmit. When the value of $S_{\mathrm{vsc}1}^m$ is greater than 0, it indicates that the power provided by VSC1 can restore the node to its original state, and power supply can continue to the next fault node. When the value of $S_{\mathrm{vsc}1}^m$ is less than 0, it indicates that VSC1 has exceeded its transmission power constraint, and corresponding load shedding operations are required. Similarly, the power limitation of VSC2 needs to be considered. The power margin of VSC2 $S_{\mathrm{vsc}2}^m$ can be represented as follows:

$$S_{\mathrm{vsc}2}^m=S_{\max }^{\mathrm{vsc}2}-S_2^{\mathrm{res}}$$

(5)

where $S_{\max }^{\mathrm{vsc}2}$ is the maximum power that VSC2 can transmit. The calculation logic of the VSC2 power margin is the same as that of VSC1, and the magnitude of the power margin needs to be considered to perform corresponding operations, ensuring that both converters operate within safe operating ranges.

(3)

ESS power margin constraint: Considering the power margin of the ESS in the E-SOP, the ESS is responsible for providing power to VSC1 and VSC2, so the power margin of the ESS $S_c^{\mathrm{ESS}}$ can be represented as follows:

$$S_c^{\mathrm{ESS}}=S_{\max }^{\mathrm{ESS}}-S_1^{\mathrm{res}}-S_2^{\mathrm{res}}$$

(6)

where $S_c^{\mathrm{ESS}}$ is greater than 0, indicating that the ESS can supply power to fault nodes in VSC1 and VSC2, supporting the restoration of more loads. When $S_c^{\mathrm{ESS}}$ is less than 0, it indicates that the ESS can no longer provide further power supply, and load shedding processing is required.

(4)

Node voltage constraint: The node voltage constraints of E-SOPs are considered to ensure that the voltage at each node remains within the allowable range after power supply restoration, as shown in the following equation:

$$U_i^{\min }\le U_i\le U_i^{\max }$$

(7)

where U_i is the voltage at node i, $U_i^{\max }$ is the maximum voltage at node i, and $U_i^{\min }$ is the minimum voltage at node i.

(5)

DG power constraint: Finally, the power constraints of the connected DG need to be considered to avoid equipment damage caused by overload operation, which can be represented as follows:

$${\left(P_i^{\mathrm{DG}}\right)}^2+{\left(Q_i^{\mathrm{DG}}\right)}^2\le {\left(S_i^{\mathrm{DG}}\right)}^2$$

(8)

$$0\le P_i^{\mathrm{DG}}\le P_{i,\max }^{\mathrm{DG}}$$

(9)

where $P_i^{\mathrm{DG}}$ is the active power output of the DG at node i, $Q_i^{\mathrm{DG}}$ is the reactive power output of the DG at node i, $S_i^{\mathrm{DG}}$ is the capacity of the DG at node i, and $P_{i,\max }^{\mathrm{DG}}$ is the maximum active power output of the DG at node i.

Through the establishment of the above constraints, the safe operation of each device during the E-SOP-based distribution network islanding recovery process is ensured, providing complete constraint boundaries for the optimization algorithm and guaranteeing the feasibility and safety of the recovery scheme.

4. E-SOP-Based Power Supply Restoration Method

4.1. Node Recovery Sequence

This research is based on a double-ended distribution network structure. According to the importance of node recovery, the primary loads and secondary loads are defined. When the distribution network experiences a fault, the search begins from the VSC side, prioritizing power supply to primary loads. After all primary loads are fully restored, the search for secondary loads begins, followed by their restoration. This process can be represented as follows:

$$\left\{\begin{array}{l}0\le {\omega }_1\le 1\\ 0\le {\omega }_2\le 1\\ {\omega }_1+{\omega }_2\le 1\end{array}\right.$$

(10)

$$\left\{\begin{array}{l}rec({\omega }_1),if\left(S_{\text{E-sop}}^{\mathrm{load}}\le {\displaystyle \sum _{n\in {\omega }_1}{S}_i^{\mathrm{load}}}\right)\\ rec({\omega }_2),\mathrm{else}\end{array}\right.$$

(11)

where ω₁ represents primary loads; ω₂ represents secondary loads. When ω₁ = 1, the node is identified as a primary load node; when ω₂ = 1, the node is identified as a secondary load node. $S_{\text{E-sop}}^{\mathrm{load}}$ is the power provided by the E-SOP to the fault nodes, ${\displaystyle \sum _{n\in {\omega }_1}{S}_i^{\mathrm{load}}}$ is the sum of power required for restoring primary load fault nodes, and rec(-) is the type of load to be restored. When the power provided by the E-SOP is less than the total power required for restoring primary load nodes, only primary load nodes are restored; when the power provided by the E-SOP is greater than the total power required for restoring primary load nodes, the restoration of secondary load nodes can begin.

4.2. Improved Dung Beetle Optimizer Algorithm

Current research on flexible interconnected distribution network power supply restoration is mostly based on heuristic algorithms. The dung beetle optimizer (DBO) algorithm is a novel biologically inspired algorithm that simulates the behavior of dung beetles finding, making, and rolling dung balls. This algorithm demonstrates good performance in terms of convergence speed and optimization capability [22]. The distribution network power supply restoration problem has the characteristics of strong constraints, multiple variables, and nonlinearity. The standard DBO algorithm has the following deficiencies when solving such problems: (1) the randomness of population initialization leads to the uneven distribution of search starting points, affecting global search performance; (2) fixed parameter settings are difficult to adapt to the needs of different search stages; and (3) the lack of effective local fine search mechanisms. To better solve the power supply restoration scheme of flexible interconnected distribution networks containing E-SOPs, an improved dung beetle optimizer (IDBO) algorithm is proposed, incorporating multiple improvement strategies to enhance the algorithm’s search capability and prevent solution overshot through inherent stability mechanisms. The proposed improvements not only enhance optimization performance but also ensure convergence stability by incorporating controlled search mechanisms that prevent dramatic solution changes and maintain feasibility throughout the optimization process.

(1)

Logistic Chaotic Mapping

Logistic chaotic mapping is a typical one-dimensional chaotic mapping that mainly acts on the algorithm initialization stage, which can avoid the excessive concentration of the initial population in certain areas. For multi-peak optimization problems like distribution network restoration, uniformly distributed initial populations can better cover the solution space, thereby finding the global optimal solution. The mathematical expression of logistic chaotic mapping can be represented by the following equation:

$$\left\{\begin{array}{l}{a}_{n+1}=a_n\theta (1-a_n)\\ \theta \in [0,4]\\ a_n\in (0,1)\end{array}\right.$$

(12)

where a_n is the initial chaotic value, a_n+1 is the updated chaotic value, and θ is the bifurcation parameter. The bifurcation diagram of logistic chaotic mapping is shown in Figure 3.

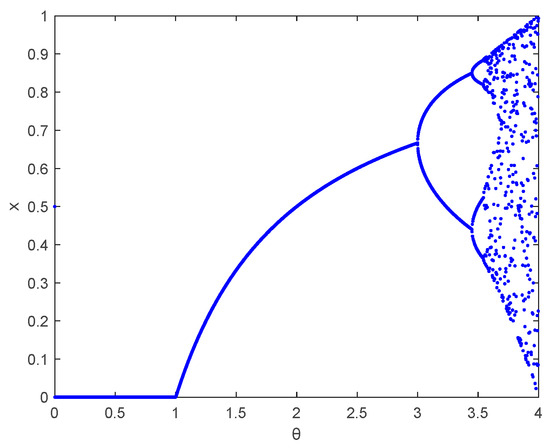
Figure 3. Bifurcation diagram of the logistic chaotic map.

From Figure 3, it can be observed that when θ is between 3.5 and 4, its chaotic characteristics are more pronounced. Therefore, this paper sets θ = 4.

(2)

Adaptive Parameter Strategy

In the DBO algorithm, the dung beetle rolling behavior is controlled by fixed parameters, which limits the algorithm’s search capability. Therefore, an adaptive parameter strategy is introduced for improvement, making the rolling radius dynamically adjust with iteration numbers. This enables the algorithm to conduct large-scale exploration to discover potential areas in the early stage and perform fine searches in the later stage. This strategy is suitable for the characteristics of distribution network solution space with multiple constraints and multiple local optima, which can be represented as follows:

$$r(t)=r_{\max }-(r_{\max }-r_{\min })\times {\displaystyle \frac{t}{T_{\max }}}$$

(13)

where r(t) is the rolling radius of the current iteration, r_max and r_min are the extreme values of the rolling radius, t is the current iteration number, and T_max is the maximum number of iterations.

(3)

Elite Learning Strategy

To accelerate the algorithm’s convergence speed, an elite learning strategy is introduced. The elite learning strategy represents superior load restoration schemes, and by learning the characteristics of these schemes, it can guide other individuals to evolve in better directions, which can be represented as follows:

$$X_{new}^e=\lambda \times X_b+(1-\lambda )\times X_e$$

(14)

where X_e is the position of the elite individual, X_b is the global optimal position, and λ is the learning rate.

(4)

Local Search Strategy

To enhance the IDBO algorithm’s ability to escape local optima, a small-scale local search is performed on some individuals in the population by exchanging the positions of a small number of elements in the solution vector for fine-tuning. This fine-tuning enables load restoration schemes to often achieve better restoration effects while satisfying constraint conditions, which can be represented as follows:

$$X_{new}^l=LocalSearch(X,N_s)$$

(15)

where $X_{new}^l$ is the new position after the local search, X is the current position of the dung beetle, and N_s is the number of exchanged elements.

To verify the effectiveness of the improved algorithm, three test functions are used for testing experiments, labeled as F1, F2, and F3, respectively. The expressions of the test functions are as follows:

$$F_1={\displaystyle \sum _{i=1}^n{([x_i+0.5])}^2}$$

(16)

$$F_2={\displaystyle \sum _{i=1}^{n}i{x}_i^4+random[0,1)}$$

(17)

$$F_3=-20\exp \left(-0.2\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{x}_i^2}}-\exp \left({\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\cos (2\pi x_i)}\right)\right)+20+e$$

(18)

where n is the dimension. Here, the test dimension for all test functions is set to 30, and the number of iterations is set to 500. The optimization results of the IDBO algorithm and the standard DBO algorithm on the test functions are shown in Figure 4, Figure 5 and Figure 6, respectively.

Figure 4. Test results of the F₁ function.

Figure 5. Test results of the F₂ function.

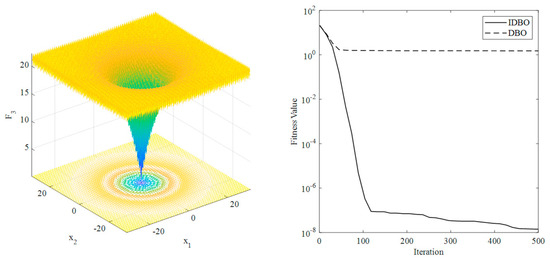
Figure 6. Test results of the F₃ function.

From Figure 4, Figure 5 and Figure 6, it can be observed that the IDBO algorithm can approach the optimal solution more quickly and exhibits a better convergence performance during the optimization process. This indicates that the improvement strategies proposed in this paper effectively enhance the algorithm’s search capability, making it more suitable for solving complex combinatorial optimization problems such as flexible interconnected distribution network power supply restoration.

4.3. Power Supply Restoration Process of Distribution Networks Containing E-SOPs

This paper studies the island recovery of flexible interconnected distribution networks containing E-SOPs, comprehensively considering E-SOP power constraints, voltage constraints, and DG capacity constraints. The specific restoration flow chart is shown in Figure 7.

Figure 7. Flow chart of distribution network island recovery based on E-SOPs.

(1)

Input the basic network parameters after the transformer faults in the double-ended distribution network and initialize the relevant parameters of the DBO algorithm, setting the population size to 30 and the maximum number of iterations to 100.

(2)

Improve the DBO algorithm through logistic chaotic mapping, adaptive parameter adjustment, elite learning strategy, and local search mechanisms, as well as initiating the search for distribution network nodes.

(3)

Determine whether the searched node is a primary load node or a secondary load node. If it is a primary load node, consider node restoration operation; if it is a secondary load node, search again.

(4)

Determine whether the power provided by the E-SOP is greater than the power required by the set of primary load nodes. If less, directly output the restored node set and calculate the restored load size; if greater, proceed with the restoration of secondary load nodes and continue to determine whether the power provided by the E-SOP is greater than the power required by the set of primary and secondary load nodes. If less, directly output the restored node set and calculate the restored load size; if greater, continue searching for secondary load nodes until all fault nodes are restored.

(5)

Determine whether the model satisfies the cycle ending condition. If satisfied, output the optimal solution; if not, re-iterate.

5. Case Analysis

Research and analysis are conducted on the node network shown in Figure 8, where nodes 3, 5, 15, and 18 are assumed to be primary load nodes, and the remaining nodes are all secondary load nodes. Additionally, both transformers in this double-ended distribution network have failed, causing all nodes to lose power.

Figure 8. Flexible interconnected distribution system based on an E-SOP.

The transmission capacities of VSC1 and VSC2 are set to 1300 kW and 1600 kW, respectively, and the transmission capacity of the energy storage device is set to 2500 kW. The voltage fluctuation interval is set to [0.95, 1.05]. To analyze the impact of DG integration on flexible interconnected distribution network island recovery, experiments are conducted with and without DG integration.

5.1. Case Analysis (I)

When both transformers in the double-ended distribution network structure fail, islands will form in the distribution network. Three schemes are set up for load restoration solution.

Case 1: A traversal method based on accurate power flow calculation considering load importance.

Case 2: Standard DBO algorithm for load restoration scheme solution.

Case 3: IDBO algorithm for load restoration scheme solution.

The power supply restoration process of Case 1 is shown in Table 2.

Table 2. Power supply recovery process of an E-SOP.

Distribution Network 1 Restored Nodes	Distribution Network 2 Restored Nodes	VSC1 Power Margin/kW	VSC2 Power Margin/kW	ESS Power Margin/kW
/	/	1300	1600	2500
3	15	1012.4	1279.82	1892.22
3, 5	15, 18	708.41	948.5	1256.91
3, 5, 7	15, 18, 14	526.42	732.5	858.92
3, 5, 7, 6	15, 18, 14, 16	329.73	548.05	477.78
3, 5, 7, 6, 4	15, 18, 14, 16, 17	140.13	336.84	76.97
3, 5, 7, 6, 4, 2	15, 18, 14, 16, 17, 19	−44.8	141.25	−303.55
3, 5, 7, 6, 4	15, 18, 14, 16, 17, 19	140.13	141.25	−118.62

From the results in Table 2, it can be determined that when using E-SOPs for power supply restoration, the set of restored nodes for distribution network 1 is {3, 5, 7, 6, 4}, while the set of restored nodes for distribution network 2 is {15, 18, 14, 16, 17}. The restoration process follows the principle of prioritizing primary nodes before restoring secondary nodes.

However, the direction of node restoration starts from the VSC side and searches from the VSC side towards the remote end, which results in a suboptimal total restored load. Therefore, it is necessary to introduce intelligent optimization algorithms to obtain solutions. In the absence of DG integration, the utilization rate bar chart of flexible interconnection equipment for each scheme is shown in Figure 9, and the solution results using different methods are shown in Table 3.

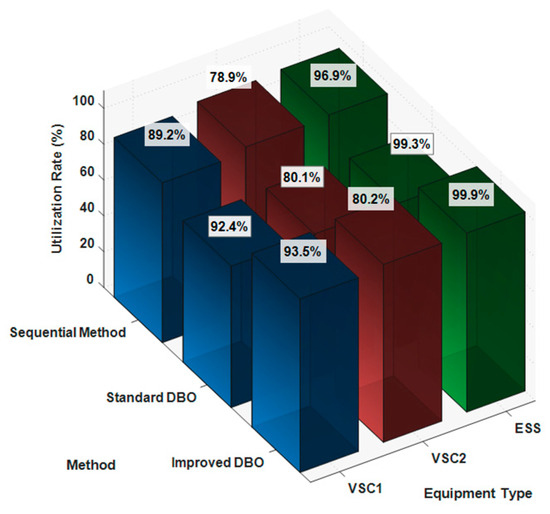
Figure 9. Utilization rate of equipment.

Table 3. Power supply recovery results without DG integration.

Method	Case 1	Case 2	Case 3
Distribution Network 1 Restored Nodes	7, 6, 5, 4, 3	3, 5, 6, 9, 13	3, 4, 5, 8, 9
VSC1 Utilization Power/kW	1159.87	1200.84	1215.09
VSC1 Utilization Efficiency/%	89.2	92.4	93.5
Distribution Network 2 Restored Nodes	14, 15, 16, 17, 18	14, 15, 18, 21, 24	15, 18, 21, 24, 25
VSC2 Utilization Power/kW	1263.17	1281.35	1283.59
VSC2 Utilization Efficiency/%	78.9	80.1	80.2
ESS Utilization Power/kW	2423.04	2482.19	2498.68
ESS Utilization Efficiency/%	96.9	99.3	99.9
Total Restored Load/kW	2423.04	2482.19	2498.68

From the results in Figure 9 and Table 3, it can be seen that the restored load using only E-SOPs for power supply restoration is 2423.04 kW. Using the Case 2 scheme, the restored load is 2482.19 kW, representing a 2.38% increase in restoration. Using the Case 3 scheme, the restored load is 2498.68 kW, representing a 3.03% increase in restoration. This indicates that Case 1 adopts a fixed strategy of searching from the VSC side to the remote end. Although it can guarantee the feasibility of solutions, it is often limited to local optimal solutions. Case 2, while possessing certain global search capabilities, lacks targeted optimization mechanisms when dealing with complex constraints such as E-SOP power constraints and voltage constraints. Case 3, through the introduction of logistic chaotic mapping, adaptive parameter adjustment, elite learning mechanisms, and local search strategies for improvement, not only avoids the path dependency problem of traditional methods but also enables a global search in a larger solution space.

5.2. Case Analysis (II)

To investigate the impact of DG integration on distribution network island recovery, a 300 kW photovoltaic system is connected at node 6 in distribution network 1, and a 400 kW wind turbine is connected at node 19 in distribution network 2. The same two methods are used for analysis. The solution results using different methods with DG integration are shown in Table 4, and the impact of DG integration on power supply restoration is shown in Figure 10.

Table 4. Power supply recovery results with DG integration.

Method	Case 1	Case 2	Case 3
Distribution Network 1 Restored Nodes	7, 6, 5, 4, 3, 2, 1	1, 3, 5, 6, 9, 10, 13	2, 3, 5, 6, 7, 10, 13
VSC1 Utilization Power/kW	1229.73	1285.41	1249.60
VSC1 Utilization Efficiency/%	94.6	98.9	96.1
Distribution Network 2 Restored Nodes	14, 15, 16, 17, 18, 19, 20	15, 18, 19, 21, 23, 26, 27	15, 16, 17, 18, 19, 20, 24
VSC2 Utilization Power/kW	1248.42	1213.93	1250.10
VSC2 Utilization Efficiency/%	78.0	75.9	78.1
ESS Utilization Power/kW	2478.15	2499.34	2499.71
ESS Utilization Efficiency/%	99.1	99.9	99.9
Total Restored Load/kW	3093.59	3114.78	3115.15

Figure 10. Impact of DG integration on power supply recovery.

From the results in Table 4 and Figure 10, it can be determined that without DG integration, the number of restored nodes is only 10, whereas with DG integration, the number of load restoration nodes reaches 14 and the total restored load is significantly increased. This indicates that the integration of DG provides additional power sources for the system, effectively alleviating the power supply pressure on E-SOPs. Meanwhile, using the IDBO algorithm for solving can further improve the load recovery capacity of the distribution network. This demonstrates that the multiple improvement strategies of the IDBO algorithm enable it to automatically adapt to changes in problem structure. When DG integration changes system conditions, chaotic mapping ensures new search starting points, adaptive parameter strategies adjust search behavior, and elite learning strategies quickly adapt to new optimal solution patterns, indicating that the proposed method has a certain feasibility.

6. Conclusions

This paper conducts analyses based on a double-ended distribution network and proposes an E-SOP-based flexible interconnected distribution network island recovery method. First, the mathematical model of E-SOPs is analyzed in detail, and an optimization model with maximizing total restored load as the objective is constructed. Second, logistic chaotic mapping is used to enhance the diversity of the dung beetle population, adaptive parameter strategies are employed to balance the global search and local exploitation capabilities of the DBO algorithm, elite learning strategies are combined to accelerate the convergence process, and local search mechanisms are used to improve the performance of the DBO algorithm. Finally, a differentiated recovery strategy is established based on node importance, clearly defining the recovery sequence of primary and secondary loads. The experimental results show that the proposed method fully considers the operational characteristics of E-SOPs and ensures the feasibility of E-SOP-based flexible interconnected distribution network islanding operation. Compared with traditional methods, it improves load recovery by 3.03%, while enhancing the utilization rate of flexible interconnection equipment. The integration of DG can effectively improve the power supply recovery capability of E-SOPs, and the IDBO algorithm is used to solve the load recovery model. However, this study has not yet considered the impact of wind and solar uncertainty on power supply recovery. Future work will further explore power supply recovery strategies for flexible interconnected distribution networks under uncertainty conditions based on this foundation.